Biomimetic microchannels of planar reactors for optimized photocatalytic efficiency of water purification

Abstract

This paper reports a biomimetic design of microchannels in the planar reactors with the aim to optimize the photocatalytic efficiency of water purification. Inspired from biology, a bifurcated microchannel has been designed based on the Murray's law to connect to the reaction chamber for photocatalytic reaction. The microchannels are designed to have a constant depth of 50 μm but variable aspect ratios ranging from 0.015 to 0.125. To prove its effectiveness for photocatalytic water purification, the biomimetic planar reactors have been tested and compared with the non-biomimetic ones, showing an improvement of the degradation efficiency by 68%. By employing the finite element method, the flow process of the designed microchannel reactors has been simulated and analyzed. It is found that the biomimetic design owns a larger flow velocity fluctuation than that of the non-biomimetic one, which in turn results in a faster photocatalytic reaction speed. Such a biomimetic design paves the way for the design of more efficient planar reactors and may also find applications in other microfluidic systems that involve the use of microchannels.

I. INTRODUCTION

Modern society is experiencing a rapidly increasing demand of pure water supply for both industrial production and household uses. Lots of efforts have been devoted to the technological development of water purification during the past decades. In the process of water purification, reactor plays an important role. In order to improve the reacting efficiency, various microfluidic reactors have been developed in recent years, which can be broadly categorized into four designs: micro-capillary reactors,¹ single-microchannel reactors,² multi-microchannel reactors,^3–5 and planar reactors.^6–8 We refer the readers to a recent review article for more details.⁹ Among them, the planar reactor was demonstrated to have a higher reacting efficiency than the other forms of reactors. The merits of the planar reactor lie in its large contacting surface area, uniform reacting velocity, and simple fabrication process. In the planar reactors, bifurcated microchannels are imperative to lead the flow into and to collect it from the planar reaction chamber so that the flow moves through the reaction surface uniformly. However, the bifurcated microchannels were not well optimized in the previous studies,^6–8 and thus the efficiency of the water treatment is not in their best performance.

In nature, many structures in biological systems perform better than artificial ones. A good example is the tree-branch structure. It obeys the rule of the minimum energy loss in order to absorb more nutrition for photosynthesis, which has been widely applied in many areas including micro-electronics, space flight, and medicine and so on in last century.^10–17 For the microfluidic planar reactors, the minimum energy loss is also important. This is to minimize the effective power that is used to pump the fluids through the reactors. More importantly, the minimum energy loss corresponds to the lowest pressure drop from the inlet to the outlet of the reactor. This is because the power loss is equal to the multiplications of the pressure drop, the cross-sectional area of the inlet, and the flow velocity at the inlet. For practical uses, low pressure is always preferred. This is because the layers of the planar reactor are often joined by bonding; higher pressure tends to cause detachment of the layers and thus leakage of fluids. In addition, the pressure in the reaction chamber would cause the thin top layer to bump up, which is problematic when the reactor is scaled up for large flow flux.

In order to further improve the efficiency, planar reactors whose microchannels followed the biomimetic principle were designed, fabricated, and tested in this work. To compare with the experimental results, rigorous numerical simulation based on the finite element method was also employed to simulate the steady state of the flow process. The flow velocity and the pressure characteristics were carefully and systematically analyzed. It is found that the experimental results agree well with those of theoretical ones. As a conclusion, the biomimetic microchannels can increase the reaction efficiency effectively.

II. THEORY AND EXPERIMENT

A. Biomimetic design of microchannels

In 1926, based on the Darwin's evolution, Murray proposed an equation of principle of minimum work. This equation took the bifurcated system of blood vessel as an example. It is expressed as¹⁰

$$d_0^3=d_1^3+d_2^3,$$ (1)

where d₀ represents the diameter of mother branch and d₁ and d₂ represent the diameters of the daughter generations. Such a relationship was named as the Murray's law. It indicates that when the sum of the cubes of the diameters of the daughter channels is equal to the cubes of the diameter of the mother channel, this system has the minimum energy loss. At the same time, its shear stress is constant.¹⁰ For symmetric systems, the Murray's law can be simplified as

$${d_0}^3=2{d_1}^3.$$ (2)

For multi-generations symmetric system, the Murray's law can be described as

$${d_0}^3=2^n{d_n}^3,$$ (3)

where d_n is the diameter of the nth generation of the channel.

The Murray's law has been used for the analysis of blood vessel, tracheas, trees, and the design of circuit and fluid systems.^12–14 However, the formulae above have some limitations. It works only for circular tubes. In practical applications, non-circular channel models are often employed by researchers. In 1978, Shah and London derived the relations for the rectangular channels with a constant depth¹⁵

$$P_O({\alpha }_n^{*})=24[1–a_1{\alpha }_n^{*}+a_2{\left({\alpha }_n^{*}\right)}^2–a_3{\left({\alpha }_n^{*}\right)}^3+a_4{\left({\alpha }_n^{*}\right)}^4–a_5{\left({\alpha }_n^{*}\right)}^5],$$ (4)

where P_o denotes the Poiseuille number and α_n* is the aspect ratio (α_n) or the reciprocal of the aspect ratio of the n_th generation, respectively. When α_n ≤ 1, it takes the form α_n*= α_n. When α_n > 1, α_n*= 1/α_n. The constant coefficients are a₁ = 1.3553, a₂ = 1.9467, a₃ = 1.7012, a₄ = 0.9564, a₅ = 0.2537.

For laminar flows, the Reynolds number (Re) is less than 2320. In this case, the Murray's law for the rectangular cross-section can be simplified as

$${\alpha }_n(1+{\alpha }_n)P_O\left({\alpha }_n^{*}\right)=2^n{\alpha }_0(1+{\alpha }_0)P_O\left({\alpha }_0^{*}\right).$$ (5)

The length of each generation is often proportional to its diameter (width) or hydraulic diameter. For the rectangular and square channels, the hydraulic diameter is defined as D_h, which can be expressed as¹⁶

$$D_h=4\times area/perimeter.$$ (6)

In this paper, a microfluidic reactor with four generations of symmetric tree-branch microchannel was designed. The whole reactor has a constant depth (d = 50 μm). Each microchannel has a rectangular cross-section. By solving Equations (4) and (5), one can easily get α_n (n = 1, 2, 3, 4) according to the setting width and depth of the 0th generation. Then the width of each branch generation can be obtained from α_n and the constant d. The length of each generation microchannel is proportional to its hydraulic diameter. Table I shows the design parameters of the microchannel reactor with a biomimetic design.

TABLE I.

Parameters of the biomimetic planar reactor.

Generation	0	1	2	3	4
W (μm)	3333	1656	821	404	200
L (μm)	5000	2484	1232	606	300

To prove the advantage of the biomimetic design, a planar reactor whose microchannels do not follow the biomimetic principle was designed as well. The parameters are listed in Table II. In this design, the width of the microchannel is halved from one generation to the next generation. As a result, the total cross-sectional area of every generation is maintained the same. This is a simple rule for designing the tree-branch microchannels and has been widely used in previous studies to give very good photocatalytic performance.^6–9 For fair comparison, the cross-sectional areas of the reaction chambers of both the biomimetic and non-biomimetic reactors are designed the same, i.e., 1 cm². In addition, the heights of all the microchannels and the reaction chambers are set to be identical at 50 μm.

TABLE II.

Parameters of the non-biomimetic planar reactor.

Generation	0	1	2	3	4
W (μm)	950	950	950	650	400
L (μm)	3200	1800	1850	1500	1000

B. Device fabrication and photocatalytic experiment

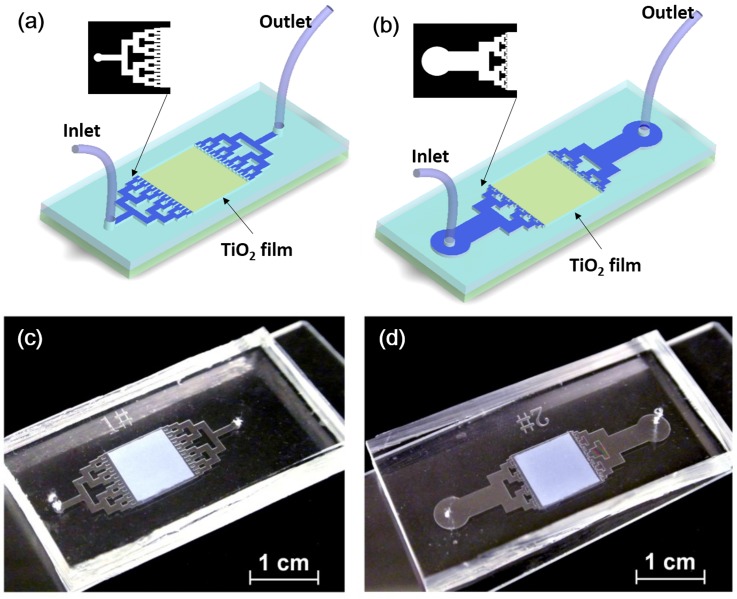
Figure 1 shows the diagrams and photos of the biomimetic reactor and the non-biomimetic reactor. Basically, each reactor consists of three layers, i.e., a top glass slide as the cover, a bottom glass slide as the substrate, and a microstructured layer sandwiched in between the two glass slides to form the microchannels and the reaction chamber. The microchannels were fabricated using the UV cured adhesive (NOA 81, Norland), which is used as spacer and sealant at the same time. The photocatalyst used for the photocatalytic reaction was a layer of highly porous TiO₂ film, which was deposited onto the bottom surface of the reaction chamber by the manual painting method.⁶ The photocatalytic reaction was implemented by employing a solar simulator equipped with an AM 1.5 G filter (Newport 91160, 150w) and the solar irradiation power density is 100 mW/cm². Methylene blue (MB) (Sigma-Aldrich) solution was used as the targeted reactant and was pumped into the reactor by a syringe pump (TS2-60, Longer) with a constant flow flux. It should be noted here that different fluxes can be obtained by changing the applying pressure of the pump, and hence different reaction times can be achieved by varying the input flow flux. After the photocatalytic reaction, the absorption spectra of the degraded MB solutions were analyzed by using a UV-visible spectrophotometer (UV-2550, Shimadzu). The degradation efficiency of the photocatalytic reaction here is defined as how much percent of MB is degraded every second, and hence the unit is %/s. The details of the fabrication and operation can be found elsewhere.⁶

FIG. 1.

Schematic diagrams and photos of the biomimetic and non-biomimetic reactors. (a) and (c) Non-biomimetic reactor (sample #1); (b) and (d) biomimetic reactor (sample #2). Each reactor consists of three layers, a glass top, a microstructured layer, and a glass substrate. At the bottom of the reaction chamber is a TiO₂ film (1 cm × 1 cm × 50 μm). Bifurcate tree-branch microchannels are used to connect the inlet and the outlet to the reaction chamber.

III. RESULTS AND DISCUSSION

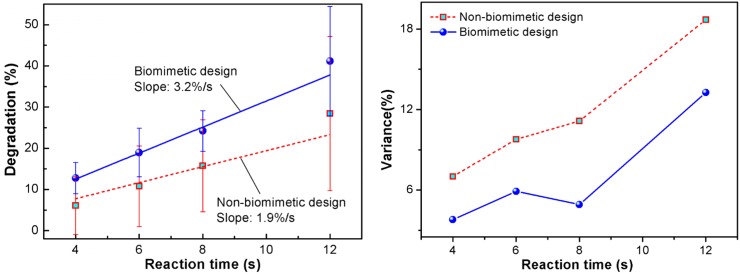
Figure 2 shows the measured degradation efficiency (left) and the variance (right) as a function of the reaction time for both the biomimetic and non-biomimetic reactors. The error bar in the left figure of Fig. 2 is a result of four measurements. Different measurements were conducted under different flow flux conditions and hence different reaction times. In general, the degradation efficiency for the biomimetic design is always higher. After a linear fitting, the biomimetic reactor gives a slope of 3.2%/s, whereas the non-biomimetic reactor is only 1.9%/s. It is seen that the biomimetic reactor is 68% faster than the non-biomimetic reactor. This well proves the effectiveness of the biomimetic design on the enhancement of photocatalytic efficiency. As shown in the right figure of Fig. 2, the variances for both designs increase with the reaction time, and the non-biomimetic design is more severe than the biomimetic design. The large variance may be due to the difficulty and uncertainty in controlling the test conditions. In experiments, the repeated tests were conducted using the same reactor sample. After each test, the reactor was flushed using deionized water to remove the residual MB that may be adsorbed in the NOA sidewalls of microchannels and the TiO₂ film of reaction chamber. However, such cleaning was not always thorough. Therefore, the residual MB severely affects the data and thus causes a large variance of the test data during the repeated tests.

FIG. 2.

Comparison of the measured photodegradation efficiencies (left) and the variances (right) of the biomimetic reactor and the non-biomimetic reactor. The biomimetic design shows significantly lower variances than the non-biomimetic design, indicating its better stability and controllability.

To prove the systematic difference of degradation efficiency between the two designs, we conducted one-way analysis of variance (ANOVA) of the data. The results are listed in Table III. It is seen that the F number is larger than 1 for the reaction times of 4, 6, and 8 s, and becomes a bit smaller than 1 for 12 s. Generally, the F number gets smaller when the reaction time goes longer. Such trend may be still attributed to the MB residue adsorbed on the microchannel sidewalls and the TiO₂ film. A longer reaction time leads to more adsorption and thus a higher fluctuation of the residual MB after flushing. As a result, the variance of degradation efficiency is larger. To suppress the variance, we will adopt a much extended flushing time, more measurements, or a strong oxidant for full removal of the MB residuals.

TABLE III.

The F number of measured degradation efficiency of each reaction time of the biomimetic and non-biomimetic designs.

Reaction time (s)	4	6	8	12
F number	2.11	1.53	1.44	0.92

To further understand why the biomimetic design results in a higher degradation efficiency. The fluidic properties of both designs were simulated by employing finite element method by using the COMSOL Multiphysics software. The whole process is divided into two parts, i.e., the initial state and the steady state. The former is a time-dependent two-phase flow process, i.e., the fluid gradually fills the reaction chamber from the inlet microchannels; the latter represents a one-phase flow process, i.e., the fluid has already filled the entire microchannel reactor. In the modeling, X-axis represents the flow direction and the origin is set at the start position of the reaction chamber. Y-axis is perpendicular to X-axis. Z-axis represents the depth of the microchannels. Two-phase flow (level set) was set in the microfluidic process. Fluid 1 is set as air and fluid 2 as water. In the simulation, the flux at the inlet microchannel was set as the same for both reactors, i.e., 25 μl/min.

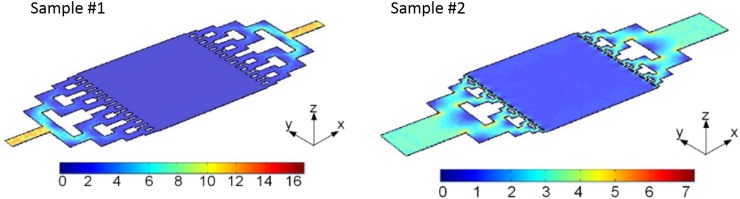
Figure 3 shows the flow velocity distributions in the steady state for both reactors. In comparison, there are two apparent features. One is that the flow velocity at the inlet of the non-biomimetic reactor is much larger than that of the biomimetic ones. This is because the width of the microchannel at the inlet of non-biomimetic reactor is much narrower than that of the biomimetic ones. The other is that the abrupt drop of the flow velocity inside the non-biomimetic reactor. However, the flow velocity inside the reaction chamber is quite uniform for both reactors. Fig. 4 shows the pressure distribution for both reactors. The pressure drop through the whole non-biomimetic reactor (1200 Pa) is much higher than that of the biomimetic reactor (700 Pa). Therefore, the biomimetic design is suitable for practical uses due to its relatively low pressure.

FIG. 3.

Flow velocity distributions for the non-biomimetic reactor (left) and the biomimetic reactor (right). The unit for the flow velocity is mm/s.

FIG. 4.

Pressure distributions for both the non-biomimetic reactor (left) and the biomimetic reactor (right). The unit for the pressure is Pa.

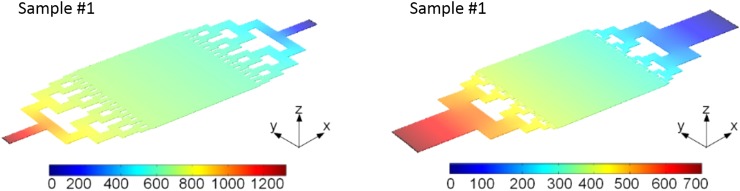
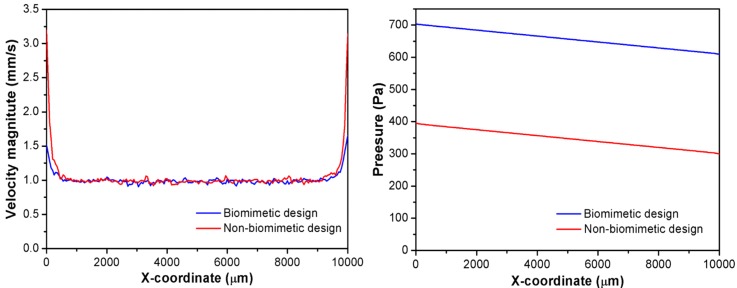
To further study the details, the flow velocity and pressure distribution along the central line of the reaction chamber are extracted and plotted in Fig. 5 for both reactors. From the left figure of Fig. 5, the mean flow velocity of the biomimetic design is calculated to be 1.05 mm/s, which is a little bit higher than that of the non-biomimetic one (1.01 mm/s). However, the standard deviation of the flow velocity is significant different, which are 0.26 mm/s and 0.09 mm/s for the biomimetic and the non-biomimetic design, respectively. The larger standard deviation of the flow velocity infers a larger fluctuation of the flow rate, which in turn results in a stronger oscillating or stirring effect on the fluid and hence enables a more intimate contact of photocatalysts with the reactants. As a result, the photocatalytic reaction process is significantly speeded up. The reason of the large fluctuation of the flow velocity of the biomimetic design may be attributed to the width and positioning of the 4th-generation microchannels, as can be read from the blue curve in the left part of Fig. 5.

FIG. 5.

Comparisons of the flow velocity (left) and the pressure distribution (right) along the X-axis inside the reaction chambers of both reactors.

While for the pressure distribution as shown in the right figure of Fig. 5, the pressure of the biomimetic design falls in the range of 300–400 Pa, while that of the non-biomimetic design is in the range of 600–700 Pa, which is almost twice that of the biomimetic design. However, the pressure drop of the biomimetic design is only a little bit lower (about 20 Pa) than that of the non-biomimetic design. The higher pressure means more energy needs to be consumed from the input side. This indicates that the biomimetic design can achieve a higher photocatalytic efficiency but with a much lower energy consumption. Again, this matches well the design target of biomimetic reactor to achieve the minimum energy loss. Moreover, the output flux for the biomimetic design is about 24.1 μl/min, which is about 0.8 μl/min higher than that of the non-biomimetic one. This means that the biomimetic design has a higher yield while it still can maintain a higher photocatalytic efficiency.

In summary, our biomimetic design achieves the constant shear stress with the minimum energy loss, i.e., the pressure of the whole system is lower than that of the non-biomimetic design. As a result, the velocity drop at the entrance of the reactors for both designs are quite different, they are about 0.45 mm/s and 1.99 mm/s for the biomimetic design and the non-biomimetic design, respectively. Considering the average velocity inside the reactor at the stable state of the biomimetic design is a bit larger than that of the non-biomimetic design, the larger fluctuation of the velocity of the biomimetic design might due to this lower velocity drop at the entrance of the reaction chamber but with a relatively larger average velocity at the stable state. In a word, the constant share stress guarantees a uniform flow velocity but the minimum energy loss enables a relatively larger average velocity with larger fluctuations, which in turn results in a larger reaction efficiency.

IV. CONCLUSIONS

A biomimetic microchannel reactor was designed based on the Murray's law. Experiments and analyses showed that the biomimetic design of the reactor holds several advantages over the non-biomimetic ones, including enhanced photocatalytic efficiency, low power consumption, and high yield. The rigorous simulation by employing the finite element method reveals that the much larger flow velocity fluctuation of the biomimetic microchannel reactor makes the photocatalytic reaction faster. In summary, both theoretical and experimental results show that the biomimetic microchannel reactor has a better performance on photocatalytic reaction, which opens up a new way to improve the microfluidic systems that involve the microchannels.