Particle migration and sorting in microbubble streaming flows

Abstract

Ultrasonic driving of semicylindrical microbubbles generates strong streaming flows that are robust over a wide range of driving frequencies. We show that in microchannels, these streaming flow patterns can be combined with Poiseuille flows to achieve two distinctive, highly tunable methods for size-sensitive sorting and trapping of particles much smaller than the bubble itself. This method allows higher throughput than typical passive sorting techniques, since it does not require the inclusion of device features on the order of the particle size. We propose a simple mechanism, based on channel and flow geometry, which reliably describes and predicts the sorting behavior observed in experiment. It is also shown that an asymptotic theory that incorporates the device geometry and superimposed channel flow accurately models key flow features such as peak speeds and particle trajectories, provided it is appropriately modified to account for 3D effects caused by the axial confinement of the bubble.

I. INTRODUCTION

A wide variety of microfluidics applications require the manipulation of micro-scale objects such as cells and particles. Typically, this manipulation involves control of the position and/or concentration of the objects. The literature contains a large number of methods, both active and passive, to achieve this control. Active methods generally rely on the application of an external force to the microparticle—a non-exhaustive list of examples includes dielectrophoresis,^1,2 optical tweezers,^3,4 and magnetic forces.^5,6 Passive methods, on the other hand, rely exclusively on hydrodynamic forces and typically make use of geometric features such as orifices and barriers within the microfluidic devices in order to alter particle paths.^7–9 All of these techniques force particles to behave differently based on one or more of their properties. In the case of the passive methods, this property is usually the size, with size-dependent sorting and trapping of particles as the main goal. However, this generally relies on the integration of small device features on the order of the particle size and typically requires the particles to pass in close proximity to those features^10,11—this has the significant drawback of limiting the flow rate and throughput through such devices.

In this work, we describe a controllable size-sorter that makes use of hydrodynamic forces in the streaming flow generated by an ultrasonically oscillating microbubble. Such microbubbles have been used in a number of microfluidics applications including transport and trapping,^12,13 micro-mixing,^14,15 and cell deformation and lysis.¹⁶ While the bubbles are actively driven to oscillation, the particles in the bubble streaming flows experience size-dependent effects due to flow forces only, allowing us to trap and sort them passively, without the use of any external forces or small-scale geometric features. In fact, the strength of the bubble streaming flow itself shapes the local flow geometry. The advantages of this approach include high throughput, interactive control, and ease of manufacturing.

Previous work has provided a detailed theoretical description of the bubble streaming flows,^15–17 as well as an overview of their applications towards trapping and focusing particles.^18,19 Here, we combine our theoretical knowledge of streaming with experimental observations and results to elucidate a simple mechanism by which particles of just a few micrometers diameter can be predictably sorted and/or trapped. We also use experimental results to help validate the asymptotic theory used to describe the streaming flow. We make use of recent findings on the three-dimensional geometry of streaming flows^20,21 to show that such 3D effects are necessary for a quantitative explanation of the sorting and that their proper understanding facilitates the development of better sorting devices.

II. EXPERIMENTAL SETUP

The microfluidic devices were manufactured from polydimethylsiloxane (PDMS) using techniques similar to those previously described.^15,18,19 Standard photolithography procedures were used to create 100 μm tall SU-8 molds on silicon wafers. PDMS mixture (90% w/w resin, 10% w/w hardener) is poured onto the SU-8 molds and is allowed to harden for 24 h. These device layers are then peeled from the molds and bonded to a flat PDMS layer using an oxygen plasma treatment. The inlets and outlets are connected using 1/32 in. ID tubing.

A schematic of a typical device design is shown in Fig. 1. Two inlet channels lead into a main channel, which then bifurcates into two outlet channels. Two main channel widths of H = 180 μm and H = 250 μm in the image plane are used. The channel depth D = 100 μm is dictated by the height of the SU-8 layer. A blind side channel of width w = 80 μm is manufactured perpendicular to the main channel. This blind side channel is placed a distance of 150 μm from the main channel bifurcation. When an aqueous solution enters the main channel, the PDMS's hydrophobicity ensures that air is trapped in the side channel, forming an approximately semicylindrical bubble. The bubbles are generally not seen to form anywhere else in the device. The device is bonded to a glass slide to which a piezoelectric transducer (Physik Instrumente, Germany) is then attached. A function generator (model 7075, Hioki) and an amplifier (model 7500, Krohn-Hite, set to 100× amplification) provide sinusoidal signals in order to ultrasonically excite the piezotransducer and thus the bubble. The bubble size can vary due to temperature changes and consequent diffusive transport of gas, but is maintained by modulating the external temperature through evaporative cooling or environmental heating. Growth and shrinkage of the bubble typically occur on diffusive time scales of several minutes,²² allowing temperature modulation and correction to be performed manually by the operator. As a result, the shape of the bubble interface is kept approximately semicylindrical. While the theory described below assumes an exactly semicylindrical shape, the agreement with experiment remains good even if the shape deviates noticeably from this ideal.

FIG. 1.

(a) Illustration of typical device design indicating the inlets, the position of the bubble, and the piezoelectric transducer. The microfluidic channels are accessed through four inlet/outlet ports. (b) Schematic of device inlets and outlets. Particle solution is infused through I₁, while glycerol-water solution without particles enters through I₂. The outlets O₁ and O₂ are connected to the open atmosphere. The dashed blue line represents the stagnation streamline dividing the upper and lower halves of the flow, a straight line in the absence of applied driving. (c) Alternative designs with additional inlets and outlets.

Particle solutions consist of 5 μm and 10 μm diameter polystyrene microparticles (Magsphere) suspended in a density-matched glycerol-water solution (23% glycerol w/w)—we will refer to the size of particles below in terms of their radius a_p. 1% w/w Tween 20 surfactant is added in order to prevent particle agglomeration. The solution has a specific gravity of 1.05 and a dynamic viscosity of 0.00198 Pa s. We use a syringe pump (PHD Ultra, Harvard Apparatus) to infuse equal constant fluid flow rates through each inlet channel. Particle solutions are infused into the bottom inlet in Fig. 1(b) (I₁), while pure glycerol-water solution enters the upper inlet (I₂). A high-speed camera (Phantom v310, Vision Research) is used to capture videos through an inverted microscope (IX71, Olympus). We use Mtrack2 (http://valelab.ucsf.edu/~nstuurman/ijplugins/MTrack2.html), a plugin for the image processing program ImageJ, to record particle trajectories and to count the number of particles reaching each outlet channel.

III. RESULTS AND DISCUSSION

A. Streaming flow

The signal supplied to the piezoelectric transducer drives a periodic pressure variation in the fluid at the driving frequency of f ≈ 20 kHz. As the bubble is compressible, this pressure variation causes the bubble surface to oscillate at the driving frequency f and with amplitude ϵa, where a is the radius of the semicylindrical bubble (a ≈ w/2 = 40 μm). Note that the dimensionless amplitude ϵ is proportional to the driving voltage at the piezo.¹⁵ The oscillatory motion of the bubble interface produces a streaming flow to second order in ϵ. Averaging this over the oscillatory time scales (i.e., by sampling at rates slower than f) produces an observable steady flow. This steady streaming flow consists of two symmetric closed-loop vortices, as shown in Figs. 2(a) and 2(b). Of particular importance is the maximum steady streaming velocity u_max, which is attained at the surface of the bubble. Previous work has shown¹⁷ that this maximum velocity can be expressed as u_max = βu_s, with the streaming speed scale u_s = 2πϵ²af and an O(1) constant β. The streaming flow speed therefore increases quadratically with driving voltage V. It has also been shown¹⁷ that the prefactor β of u_max is well predicted by an asymptotic theory that is briefly described below in Section III D. The dimensionless maximum speed β depends (weakly) on the driving frequency; for the experiments conducted in the present work, the appropriate value is β ≈ 1.6.

FIG. 2.

(a) and (b) Steady streaming flow field generated by bubble oscillations: (a) Experimental streak image generated using tracer particles, and (b) streamlines produced by asymptotic theory, with coordinates indicated. (c) and (d) Flow field produced by combining Poiseuille flow (from left to right) with streaming flow: (c) Experimental streak image, with the separatrix (solid line) shown in red; (d) schematic indicating the stagnation streamline (dashed blue line), which cannot be directly determined in experiment, and the definitions of ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$ and ${\overline{d}}_1$.

In an experiment, u_max is determined by measuring the speeds of particles very close to the bubble (at distances about 2–10 μm from the bubble surface) and extrapolating back to the mean position of the bubble surface. The streaming speed decay with radial distance R is linear to good approximation close to the bubble, so that u_str(R) ≈ u_max(1 − κ(R − a)/a), with κ = O(1), for (R − a) ≪ a.

As previously described, our experimental setup combines the steady streaming flow with an imposed Poiseuille flow. In the two-inlet/two-outlet design described above in Fig. 1, when the piezotransducer is turned off, a stagnation streamline evenly divides the bottom and top halves of the flow, as shown in Fig. 1(b). The fluids entering inlets I₁ and I₂ exit through the outlets O₁ and O₂, respectively. While this remains the case when the streaming flow is turned on, the shapes of the streamlines are greatly altered in the section of the channel surrounding the bubble. Fig. 2(c) shows a representative resultant flow field (Poiseuille flow from left to right). Note that there are now both open streamlines and closed loops in the vicinity of the bubble, and that a large portion of the flow is being focused into a narrow bundle of streamlines near the bubble surface. It should be emphasized that we use “streamline” as a short-hand here for a Lagrangian pathline of a liquid particle (as would be observed in an experiment as a passive-tracer trajectory), averaged over the short (oscillatory) time scale. This Lagrangian flow field therefore contains the proper Stokes drift terms^23–25 that distinguish it from the time-averaged Eulerian field.

While we are limiting our analysis to the two inlet/two outlet design here, it is quite feasible to incorporate additional inlets and outlets, as illustrated in Fig. 1(c). This further divides the flow into a larger number of distinct regions through the introduction of additional stagnation streamlines, and the following analysis can be straightforwardly extended to such cases.

We can expect the overall shape of the flow field to be dictated by the relative strengths of the Poiseuille and streaming flows, as captured by the following parameter:

$$s\equiv \frac{{\overline{u}}_p}{u_{\mathit{m}\mathit{a}\mathit{x}}}\propto \frac{Q}{V^2},$$ (1)

where ${\overline{u}}_p\equiv Q/HD$ is the mean Poiseuille velocity, and Q is the total flow rate imposed by the syringe pump.

As shown in Figs. 2(c) and 2(d), combining streaming and Poiseuille flows divides the flow field into certain distinct regions. There are closed streamline loops upstream and downstream of the bubble. The uppermost point of the upstream vortex marks a hyperbolic point with an associated critical streamline (separatrix). The flow above this separatrix (representing a fraction of flow rate ΔQ) does not pass near the bubble, while all streamlines below it are focused into a narrow bundle between the bubble surface and the upstream loop. The bypass flow ΔQ reduces as s is lowered.

Since we are considering only the time-averaged steady flow, we can define a closest distance ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$ between the bubble surface and the separatrix. By continuity, all fluid below the separatrix must traverse the gap; employing the linear approximation for u_str throughout the gap, we obtain

$$u_{\mathit{m}\mathit{a}\mathit{x}}{\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}\left(1-\frac{\kappa }{2a}{\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}\right)={\overline{u}}_{p}H\frac{Q-\Delta Q}{Q}\hspace{0.17em}.$$ (2)

For the experiments discussed in the present work, we find that ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}/a$ is always very small, so that the left-hand side of the equation is well approximated by $u_{\mathit{m}\mathit{a}\mathit{x}}{\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$, which yields

$${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}=sH\left(1-\frac{\Delta Q}{Q}\right)\hspace{0.17em}.$$ (3)

We also define a second distance ${\overline{d}}_1$ as the closest distance between the bubble surface and the stagnation streamline at its closest approach (refer to the dashed blue streamline in Fig. 2(d))

$${\overline{d}}_1=\frac{\mathit{s}\mathit{H}}{2}\hspace{0.17em}.$$ (4)

Note that if ΔQ = 0, ${\overline{d}}_1={\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}/2$. Note also that the above definition of ${\overline{d}}_1$ requires ΔQ/Q < 1/2.

B. Size sorting of particles

Since particle solution is infused through inlet I₁ only, all particles remain in the lower half of the flow and exit through O₁ in the absence of a driving voltage. If all particles behaved purely as passive tracers, we would expect this to remain the case when the streaming flow is turned on.

In reality, however, size-sensitive sorting and trapping of particles is observed in the presence of a streaming flow. Under appropriate conditions, the particles are faithfully and continuously deflected from the lower half of the flow into the upper half (exit at outlet O₂). We call this type of sorting continuous mode or mode 1 sorting. Under different conditions, a second type of sorting is observed, where particles are intermediately trapped within the upstream vortex before later being released into the upper half of the flow (trapping mode or mode 2 sorting). The latter was reported in Refs. ¹⁸ and ¹⁹, while the former is novel and provides additional insight for a quantitative description of the phenomenon, as explained in Sections III C–III E. In addition, mode 1 is a more versatile and powerful tool in sorting applications, as it allows for (i) continuous sorting without intermittent release of particles after vortex trapping, (ii) is unaffected by much larger particle concentrations than can be used for mode 2, as particles do not accumulate and interfere with each other, (iii) can be used for the separation of particles whose radii are closer than a factor of two (a limitation of mode 2), and (iv) can be used to separate multiple species of particles through the use of multiple outlets such as those depicted in Fig. 1(c). These advantages will be further highlighted below. Continuous deflection of the particles was used in Ref. 19 to focus a stream of (uniform size) particles in a microchannel, but we use it here for the first time for systematic particle sorting. Experimental images of the two sorting modes are given in Figs. 3(a) and 3(b) (Multimedia view). The dynamics of both processes can be observed in the video footage.

FIG. 3.

(a) and (b) Streak images showing particle sorting: (a) Continuous sorting (mode 1)—the particles are continuously deflected into the upper half of the flow. (b) Trapping (mode 2)—the particles are trapped in the upstream vortex and eventually expelled into the upper half of the flow. When the streaming flow is weak or absent, all particles remain in the lower half. (c)–(e) Illustration of geometric sorting mechanism for a given parameter s, i.e., given ${\overline{d}}_1$ and ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$: As particle radius a_p increases, the particles experience (c) no sorting, (d) continuous sorting, and (e) trapping. The shaded regions represent exclusion volumes around the bubble; since particles cannot penetrate the bubble surface, their centers of mass cannot enter this exclusion volume. Videos of both sorting and trapping are available. (Multimedia view) [URL: http://dx.doi.org/10.1063/1.4942458.1] Download video file ^{(5.5MB, avi)} DOI: 10.1063/1.4942458.1 [URL: http://dx.doi.org/10.1063/1.4942458.2] Download video file ^{(4.1MB, avi)} DOI: 10.1063/1.4942458.2

It is apparent that upon passing near the bubble the particles are deflected such that they migrate across streamlines. The precise nature of the hydrodynamic forces acting on the particles is potentially very complex: in the past 50+ years, since the pioneering work of Segré and Silberberg,^26–28 descriptions of forces on particles in many types of flows have been developed, from simple shear flows²⁹ to more general background flows,³⁰ sometimes explicitly taking into account the presence of a nearby wall,^31,32 or the explicit time dependence of the flow.^33,34 Even the behavior of common microparticles in the transport flow through ordinary, ubiquitous microfluidic channels still reveals novel insights today.^35,36 Because the bubbles are driven acoustically in our experiments, one may suspect acoustic radiation forces at work; however, using our typical parameters to evaluate these forces³⁷ and translating them to particle displacements during passage near the bubble, we find that even our largest (a_p = 5 μm) particles would not be displaced perpendicular to streamlines by more than ∼100 nm if the particle and fluid densities were not matched, and far less under the density-matched conditions of our experiment.

The present bubble streaming problem potentially contains all of the complications discussed in the literature on hydrodynamic forces: close proximity of the particles to both no-slip and no-stress walls, the latter (the bubble interface) moving and deforming on fast time scales, and establishing both oscillatory and steady flow components with non-trivial geometry and strong gradients on the scale of the bubble size. We do not attempt here to develop a model that accounts for all these effects, but focus on the fact that the force on the particles must, at least, be able to avoid the interpenetration of the particles and the bubble. Experimentally, the particles are never seen to attach or adsorb to the bubble surface, although they approach very closely (up to about 1 μm, or a fraction of typical particle sizes). Therefore, no matter what the exact force law is, it must exert a strong short-range repulsion, which leads us to propose a geometric mechanism for the observed size sorting: Since particles cannot penetrate the bubble surface, there is an exclusion volume around the bubble that the particles’ center of mass cannot enter (cf. Figs. 3(c)–3(e)). A particle that closely approaches the bubble must therefore cross streamlines and enter the region of the flow outside the exclusion volume, effectively obeying a hard-core repulsion. We can thus use simple geometric principles to formulate sorting criteria based on the particle size.

For continuous sorting to take place, the particle radius must be large enough for its center of mass to be pushed beyond the stagnation streamline. This happens when the following condition is met:

$$a_p>{\overline{d}}_1={\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}\frac{1}{2(1-\Delta Q/Q)}\hspace{0.17em},$$ (5)

where the latter equality follows from (3) and (4). For trapping, the particle center of mass must be deflected beyond the separatrix, leading to the following simple criterion:

$$a_p>{\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}\hspace{0.17em}.$$ (6)

At face value, it might appear that such a sorting mechanism does not in fact solve the problems of low throughput/flow rate suffered by passive sorters with small device features, since the transport flow here is funneled into a narrow bundle of streamlines in close proximity to a boundary. The key difference, however, is that the bubble surface is not a no-slip boundary—as a result, the flow speeds achieved near it are the highest in the entire channel (reaching up to 100 times the average transport flow speed), thus allowing large transport flow rates; if the bubble surface sustained stress, e.g., from surfactant contamination, we would observe very different velocity profiles. Moreover, the stress-free bubble surface precludes the large shear gradients present near a no-slip boundary at a constriction—the particles passing through the gap in our setup do not experience strong shear and are not observed to rotate significantly. Therefore, we do not consider lift forces due to particle rotation, which may be prominent in devices with no-slip constrictions.³⁸ Section III C presents experimental results for the throughput and sorting efficiencies achievable in our devices.

The above criteria for particle sorting transitions were tested by observing the trajectories of particles in experiment. Note that it is very difficult to accurately measure ${\overline{d}}_1$ in experiment, as this would require high-resolution simultaneous observation of the particle behavior close to the bubble and the stagnation points at the walls of the device. Therefore, (5) was rewritten in terms of the directly measurable ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$ and ΔQ—these can be measured by identifying the separatrix from figures such as Fig. 2(c), generated by taking streak images of small tracer particles.

In the experiments, a particle suspension was allowed to flow through a single device at several different flow rates; for each flow rate, the driving voltage supplied to the piezo transducer was varied until the voltages required to transition to mode 1 and mode 2 sorting were identified. To this end, the trajectories of ∼50 particles were followed for each combination of flow rate and driving voltage. The process was repeated using two particle sizes (a_p = 5 μm and 2.5 μm) in two devices with main channel widths of H = 180 μm and H = 250 μm. Note that to avoid confusion, separate experiments were carried out for each of the two particle sizes. By also measuring particle speeds as they approached the bubble, we could identify the critical s values at which the sorting transitions occur; we will call these values s₁ and s₂, respectively.

The results for the four test cases are presented in Fig. 4: The symbols indicate the s values for which approximately 50% of particles were deflected to O₂ (for s₁) or trapped in the vortex (for s₂); the error bars represent the range of s values over which each sorting transition took place: from the largest value for which ∼25% deflection or trapping occurred to the smallest value where sorting or trapping of ∼75% of particles is observed.

FIG. 4.

Values of s at sorting transitions in channels of two different widths H: (a) a_p = 2.5 μm particles and (b) a_p = 5 μm particles. Ratio of s values between mode 1 and mode 2 transitions (s₁/s₂) for (c) a_p = 2.5 μm particles and (d) a_p = 5 μm particles.

The results show good agreement with the sorting mechanism proposed above. We see that despite changing the total flow rate (and thus the mean Poiseuille velocity ${\overline{u}}_p$) fivefold, the sorting transitions take place at close to constant s, as predicted by (3)–(6). Note also that mode 2 transitions consistently take place over a smaller range of s values than mode 1.

Also of interest is the ratio of s values between mode 1 and mode 2 transitions (s₁/s₂); using the aforementioned equations, we predict that (s₁/s₂) = 2(1 − ΔQ/Q). Based on the measured values of ΔQ, we compare these predicted values with experiment in Figs. 4(c) and 4(d) and find them to be in close agreement. In the narrower 180 μm channel, the ratios are essentially indistinguishable from two, since ΔQ is small. For the wider 250 μm channel, this ratio becomes smaller as ΔQ increases, particularly for a_p = 5 μm particles, for which sorting occurs at relatively large s values. The theory captures this trend well and shows its applicability for both the case of appreciable ΔQ and the particularly desirable case of ΔQ → 0, where the entire channel flow participates in the sorting. Note, however, that the accurate prediction of this ratio s₁/s₂ does not necessarily imply accurate modeling of the physical gap width. In Section III E, we will show that a more sophisticated treatment of the flow field allows for the prediction of this width.

We have thus shown that $s={\overline{u}}_p/u_{\mathit{m}\mathit{a}\mathit{x}}$ is a valuable predictor of the sorting, which is under direct experimental control and can be changed both by varying the transport flow rate Q and the piezoelectric driving voltage V. To make more quantitative progress, we outline the implications of an asymptotic theory of steady streaming flow in Section III D.

C. Sorting performance

An extensive investigation into the sorting efficiency and resolution of our devices is outside the scope of this paper, which focuses on understanding the mechanism of particle deflection and sorting. We will, however, briefly present results regarding the separation of a_p = 5 μm and a_p = 2.5 μm particles. Fig. 5 demonstrates that these two particle species can be reliably separated both using mode 1 (Fig. 5(a)) and mode 2 sorting (Fig. 5(b)).

FIG. 5.

Separation of a_p = 2.5 μm particles and a_p = 5 μm particles using (a) mode 1 sorting and (b) mode 2 trapping. Every particle belonging to the larger species in the streak images has been colored red in post-processing. The flow control parameters are s = 0.018 (a) and s = 0.007 (b), respectively, consistent with the thresholds reported in Fig. 4.

In order to quantify sorting performance, a variety of measures are helpful: Aside from the total throughput (particles/time) through the device, the sorting efficiency (percentage of desired particles collected after sorting relative to their concentration in the initial mixture) is an important quantity, as is the enrichment ratio (the factor by which the ratio of concentrations of desired to undesired particles is increased by the sorting process). Our experiments, as detailed above, are designed to deflect the larger species of particle from the mixture, so that the large particles are the “desired” species in the above-mentioned sense (although analogous quantities can of course be defined describing the purification of the small species).

Our sorting experiments were conducted in channels of width H = 250 μm, and the s values were chosen such that mode 1 sorting was selected for each experiment. We used particle solutions of two different concentrations: The first solution contained 1800 a_p = 2.5 μm particles/μl and 900 a_p = 5 μm particles/μl (total volume fraction = 6 × 10⁻⁴). For this solution, the large-particle enrichment ratios of ∼11.5 were obtained for throughputs as high as 360 particles/s. The second solution contained 9000 a_p = 2.5 μm particles/μl and 4500 a_p = 5 μm particles/μl (total volume fraction = 3 × 10⁻³). Here, enrichment ratios of ∼8 were obtained for throughputs above 1400 particles/s. These throughput rates are considerably in excess of what could be demonstrated previously through mode-2 sorting,^18,19 where higher particle concentrations lead to strong particle-particle interactions within the trapping vortex and subsequent expulsion from the vortex that is not fully controllable. In fact, even when the release from the vortex is reproducible, mode-2 trapping leads to potentially deleterious intermittent bunching of the desired particles at the outlet; owing to the continuous nature of mode-1 sorting, the output stream of desired particles is uniform here.

Note that the above enrichment ratios were achieved while maintaining sorting efficiencies above 80%. As with other sorting devices, the enrichment ratios can be greatly increased by compromising on sorting efficiency. For instance, at a sorting efficiency of 52%, we were able to attain an enrichment ratio of 28. Even larger enrichment ratios could be achieved by using multiple bubbles in series within a single device.

Comparing with other passive sorting devices described in the literature,^11,39 we find that these experiments demonstrate competitive enrichment ratios and sorting efficiencies, while offering greater throughput than many approaches discussed previously.^10,40–42

D. Modeling of trajectories using asymptotic theory

In previous publications, we have developed a description of the steady component of streaming flow from a bubble positioned as in this experiment.^15,17,20 In order to accurately model the flow due to the combination of streaming and Poiseuille flows, it is useful to define two kinds of Reynolds numbers (i) Re_s ≡ u_sa/ν, corresponding to the fast streaming flow near the bubble, and (ii) $R{e}_p\equiv {\overline{u}}_{p}H/\nu$, corresponding to the flow gradients over the channel width. It has been shown^43,44 that the streaming flow due to an oscillating cylinder for Re_s ≲ O(100) differs only slightly from the leading order theory (Re_s → 0). In our range of driving parameters, we find 0.3 ≲ Re_s ≲ 7, and 0.05 ≲ Re_p ≲ 0.3. Due to the insensitivity of the streaming to Re_s, and since Re_p is always smaller than unity, we model the net flow, to leading order in Reynolds number, as a linear superposition of streaming and Poiseuille flow fields. However, it is necessary to carefully consider the geometry of the channel and the bubble protruding into it, as the details of the sorting transitions turn out to show some dependence on such considerations.

For a theoretical description of the flow, it is convenient to non-dimensionalize lengths by a, so that the dimensionless channel width and depth are given, respectively, by h ≡ H/a and d ≡ D/a, and radial distances become r = R/a. We additionally non-dimensionalize speeds by the streaming speed scale u_s and use a right-handed coordinate system (x, y, z) centered at the mid-point of the bubble axis, so that y spans the width of the channel, and z is directed along the axis of the bubble.

The unidirectional pressure-driven transport flow through a channel of rectangular cross section in the absence of a bubble is given by Ref. 45. A velocity profile u_x(y, z) of unit mean speed may be written as

$$u_x(y,z)={\left\{\sum _{n=1,3,\dots }^{\infty }\frac{2}{n^4\pi }\left(1-\frac{2h}{n\pi d}\tanh \frac{n\pi d}{2h}\right)\right\}}^{-1}\sum _{n=1,3,\dots }^{\infty }\frac{1}{n^3}\left(1-\frac{\cosh (n\pi z/h)}{\cosh (n\pi d/(2h\left)\right)}\right)\text{sin}(n\pi y/h)\hspace{0.17em}.$$ (7)

We will first consider the combined streaming and transport flow as approximately two-dimensional, as all experimental data are taken with the microscope focused on the channel mid-plane z = 0, with a depth of field of ≈10 μm width about z = 0. This allows us to define an effective stream function governing the Poiseuille flow in the mid-plane, given by

$${\psi }_p^{(0)}(x,y)={\int }_0^{y}u(y\prime ,0)\hspace{0.17em}\mathrm{d}y\prime .$$ (8)

This solution must, however, be modified to also satisfy the bubble boundary conditions (no-penetration and no-stress at the bubble interface). In the following, we develop an iterative procedure to accomplish this task. If we assume that any modification of the flow resulting from the introduction of the bubble at r = 1 is approximately 2D (small axial gradients), the flow in the midplane is given, in the limit of small Re_s, by the linear modification

$${\psi }_p^{(j-1)}\mapsto {\chi }_p^{(j)}={\psi }_p^{(j-1)}+{\xi }_b^{(j)}.$$ (9)

The modification ${\xi }_b^{(j)}$ must satisfy the Stokes equations (${\nabla }^4{\xi }_b^{(j)}=0$), and also no-slip boundary conditions at the wall where the bubble is positioned (y = 0). Thus, ${\xi }_b^{(j)}$ may be expressed as an expansion into no-slip Stokes solutions of the form

$${\xi }_b^{\left(j\right)}(x,y)=\sum _{n=0}^{\infty }\frac{a_n}{r^n}\left(\text{cos}\hspace{0.17em}\left\{n\left(\theta -\frac{\pi }{2}\right)\right\}+{\sigma }_n\hspace{0.17em}\text{cos}\hspace{0.17em}\left\{(n+2)\left(\theta -\frac{\pi }{2}\right)\right\}\right),$$ (10)

where $x=r\hspace{0.17em}\text{cos}\hspace{0.17em}\theta ,\hspace{0.17em}y=r\hspace{0.17em}\text{sin}\hspace{0.17em}\theta$, and

$${\sigma }_n=\{\begin{array}{cc}1,\hfill & n\hspace{0.17em}\hspace{0.17em}\text{even},\\ \frac{n}{n+2},& n\hspace{0.17em}\hspace{0.17em}\text{odd}.\hfill \end{array}$$ (11)

The coefficients a_n are chosen such that both no penetration and no-stress conditions are satisfied at the bubble surface, i.e.,

$$\frac{1}{r}\frac{\partial {\chi }_p^{\left(j\right)}}{\partial \theta }=\left(\frac{{\partial }^2}{\partial r^2}-\frac{1}{r}\frac{\partial }{\partial r}-\frac{1}{r^2}\frac{{\partial }^2}{\partial {\theta }^2}\right){\chi }_p^{\left(j\right)}=0,\hspace{1em}\text{on}\hspace{0.17em}r=1.$$ (12)

In general, the a_n may be obtained analytically for arbitrary n using a Fourier transform in θ of the undisturbed solution at r = 1 (see Ref. 20); here, we determine them numerically by evaluating the boundary conditions on a finite number of points on r = 1 (collocation).

The stream function obtained by this procedure satisfies the bubble boundary conditions and those at the lower wall y = 0, but now introduces velocity components of O(h⁻¹) at the opposite wall y = h. This can be accommodated using a second correction

$${\chi }_p^{(j)}\mapsto {\psi }_p^{(j)}={\chi }_p^{(j)}+{\xi }_w^{(j)}\hspace{0.17em},$$ (13)

where ${\xi }_w^{(j)}(x,y)$ is again a solution of the Stokes equations. If we define the Fourier transform of f(x) by

$$\widehat{f}(k)={\int }_{-\infty }^{\infty }f(x){\mathrm{e}}^{-\mathrm{i}kx}\mathrm{d}x,$$ (14)

the Fourier transform of ${\xi }_w^{(j)}$ is given by

$${\widehat{\xi }}_w^{(j)}(k,y)=\widehat{b}(\sinh ky-ky\cosh ky)+\widehat{c}\hspace{0.17em}y\sinh ky,$$ (15)

where

$$\widehat{b}=\frac{2\mathrm{i}}{k}\frac{\widehat{v}\hspace{0.17em}kh\cosh kh+(\mathrm{i}\widehat{u}\hspace{0.17em}kh+\widehat{v})\sinh kh}{1+2k^2{h}^2-\cosh 2kh},$$ (16)

$$\widehat{c}=-2\frac{\widehat{u}\hspace{0.17em}kh\cosh kh-(\widehat{u}+\mathrm{i}\widehat{v}\hspace{0.17em}kh)\sinh kh}{1+2k^2{h}^2-\cosh 2kh},$$ (17)

and $\widehat{u}$ and $\widehat{v}$ are Fourier transforms, respectively, of $u={\partial }_y{\psi }_p^{(j)}$ and $v=-{\partial }_y{\psi }_p^{(j)}$ evaluated at y = h.²⁰ The function ${\xi }_w^{(j)}(x,y)$ is recovered by an inverse transform of (15). This lets the superposition ${\chi }_p^{(j)}+{\xi }_w^{(j)}$ satisfy wall boundary conditions exactly but violates the boundary conditions at r = 1. The combined application of (9) and (13) completes one iteration ${\psi }_p^{(j-1)}\mapsto {\psi }_p^{(j)}$ and results in a transport flow description that satisfies all boundary conditions to successively greater accuracy, with excellent convergence obtained typically within two iterations for the h considered here.

The time averaged fluid velocity due to the streaming is two-dimensional to first approximation and is confined to planes perpendicular to the bubble axis. The stream function ${\psi }_s^{2d}$ describing the steady streaming flow is given analytically in a half-space (h → ∞) at any driving frequency by a singularity expansion. The details are found in Refs. ¹⁵ and ¹⁷; briefly, for a given bubble size and frequency directly from experiment, we have obtained analytical expressions for all expansion terms describing the stream function governing the bubble streaming flow field. Using a procedure similar to that used for the transport flow (but with opposite spatial symmetry), this solution is also modified for arbitrary channel width h (cf. Appendix A of Rallabandi et al.²⁰).

The net two-dimensional flow satisfying both bubble and wall boundary conditions is given by the superposition

$$\psi ={\psi }_s^{2d}+s\beta {\psi }_p,$$ (18)

where β represents the dimensionless maximum speed (u_max expressed in units of u_s), whose value is one of the results of the modeling of ${\psi }_s^{2d}$. The value of s therefore sets the relative strength between the streaming and transport flows and is consistent with its definition in (1). It is the only control parameter that determines the streamline portrait of the flow field and can be changed in experiment by either changing driving voltage or Poiseuille flow rate.

The motion of finite-sized microparticles is modeled by a passive advection due to the flow (constant value of ψ) in regions where the separation between the particle center and the bubble is greater than the particle radius, i.e., r > 1 + a_p. If the passive advection of the particle results in a violation of this condition, the particle is displaced radially outward at constant θ to a radial coordinate r = 1 + a_p, and the passive advection is continued. This ensures that the particle and bubble surfaces never penetrate each other and are consistent with the proposed geometric size-sorting mechanism depicted in Figs. 3(c)–3(e). The particle advection under a given flow field and initial conditions are computed numerically using a fourth order Runge–Kutta scheme.

A comparison of theoretical predictions for particle transport with a set of experimental conditions (frequency, voltage, and flow rate) requires both a determination of the theoretical flow field (equivalently a value of theoretical s), as well as of the initial particle positions resulting in the experimentally measured trajectories. For a fixed s, one may compute a set of (theoretical) stream function values corresponding to experimentally measured particle positions (x_i, y_i), given by ${\psi }_i^{\mathit{e}\mathit{x}\mathit{p}\mathit{t}}\equiv \psi (x_i,y_i)$. For the same s and some initial conditions, the theoretical particle trajectories assume a set of ψ values as they pass through the experimentally measured x_i, denoted by ${\psi }_i^{\mathit{t}\mathit{h}\mathit{e}\mathit{o}\mathit{r}\mathit{y}}$. The error between the experimental and theoretical trajectories is quantified by the deviation between the two sets of stream function values over all data points i and all particle trajectories. The theoretical value of s (flow field) and initial conditions that provide the best fit between the theory and the experiment is obtained by the global minimum over s and initial conditions of the error functional

$$\mathcal{E}(s,IC)=\sum _i{\left(\frac{1}{{\rho }_i}\frac{{\psi }_i^{\mathit{t}\mathit{h}\mathit{e}\mathit{o}\mathit{r}\mathit{y}}-{\psi }_i^{\mathit{e}\mathit{x}\mathit{p}\mathit{t}}}{{\psi }_i^{\mathit{t}\mathit{h}\mathit{e}\mathit{o}\mathit{r}\mathit{y}}}\right)}^2,$$ (19)

where ${\rho }_i=\left|\right|{\mathit{x}}_{i+1}-\mathit{x}|{|}^{-1}$ is the spatial density of experimental data points. The factor 1/ρ_i permits a comparison between the theory and the experiment at a uniform spatial weighting of the experimental data. Otherwise, as the experimental data are collected at a fixed frame rate, a disproportionately large number of data points would be collected far away from the bubble (slow fluid speed) and very few near the bubble (where the flow is fastest). A high-speed camera was used to capture detailed trajectory data for particles approaching the bubble, including their positions and velocities. These could then be compared with theoretical predictions. The global minimum of $\mathcal{E}$ over s and initial particle positions corresponds to a best-fit between the experiment and the theory, resulting in a theoretically predicted s value, denoted by s_theory.

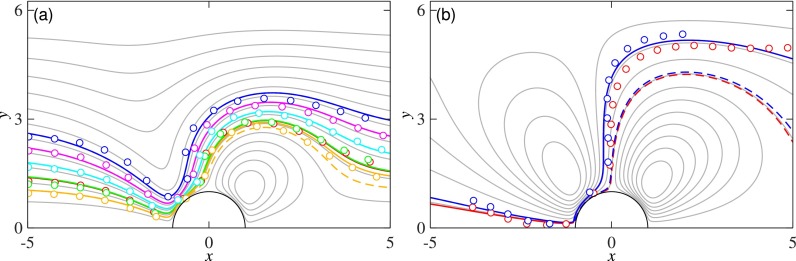
The results of this optimization are presented in Fig. 6 for a driving frequency of 20 kHz and a mean Poiseuille speed ${\overline{u}}_p\approx 1.3\hspace{0.17em}\text{mm}/\mathrm{s}$. We see that the trajectories computed by the asymptotic theory fit the experimental trajectories very well, for the entire range of experimental outcomes from small to large particle deflections. As an additional consistency check, we find that the optimized s_theory values are in close agreement with the experimental s_expt, which were found by directly measuring maximum particle speeds near the bubble. This indicates that the theory is able to predict not only trajectory shapes but also peak flow speeds.

FIG. 6.

Comparison of theoretical trajectories with experimentally measured trajectories of a_p = 2.5 μm particles at f = 20 kHz. The experimental parameters are (a) $\overline{u_p}=1333\hspace{0.17em}\mu \mathrm{m}/\mathrm{s}$, at a voltage of 0.6 V; (b) $\overline{u_p}=1000\hspace{0.17em}\mu \mathrm{m}/\mathrm{s}$ and 0.7 V. The smaller voltage results in a relatively large s > s₁ with small particle deflections (a), the larger voltage represents a value s < s₁ (b), with very strong deflections and sorting of the particles into the upper half of the channel. Distances x and y are normalized by bubble radius. The open circles are experimental data, while the solid lines represent theoretical trajectories. The dashed lines correspond to the streamlines particles would follow if they were not deflected. (a) s_theory = 0.038, s_expt = 0.037; and (b) s_theory = 0.008, s_expt = 0.009. From (4) and ${\overline{d}}_1=a_p$, we estimate s₁ ≈ 0.02, consistent with the characterization of (a) as a non-sorting situation and (b) as sorting.

We can thus conclude that the asymptotic theory is successfully modeling particle motion in the combined bubble streaming and transport flow. Of particular importance is the fact that trajectories are well-modeled close to the bubble—this is the region of most interest for sorting.

E. 3D flow effects on gap size

In Section III B, we computed and compared s values for mode 1 and mode 2 sorting of a_p = 2.5 μm and a_p = 5 μm particles. However, we did not explicitly compute the gap size ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$. This can be done fairly easily using Equation (3).

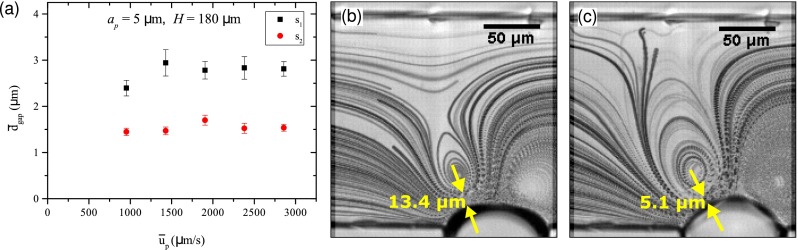
Fig. 7(a) converts the measured s values from Fig. 4(b) into the values of ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$, through (3). The discrepancy between expected and computed gap sizes is striking. Since the particles in question have radius a_p = 5 μm, we would expect the mode 1 and mode 2 sorting transitions to occur at gap sizes of roughly 10 μm and 5 μm, respectively (assuming zero ΔQ). Instead, the average computed d_gap turn out to be 2.75 μm and 1.54 μm.

FIG. 7.

(a) Computed ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$ at sorting mode transitions for a_p = 5 μm particles in 180 μm channel. (b) Measured gap width at the channel center d_gap(z = 0) at mode 1 transition −13.4 μm. (c) Measured d_gap(z = 0) at mode 2 transition −5.1 μm.

To verify these results, the gap widths were measured experimentally using high-speed videography. Stroboscopic videos (frame rate equal to bubble oscillation frequency) were taken through a high-magnification lens, with a_p = 0.5 μm particles being used as tracers. The lens focus was adjusted in order to capture the gap size at the center of the channel d_gap(z = 0). Figs. 7(b) and 7(c) show the results for s values at which a_p = 5 μm particles reached mode 1 and mode 2 sorting transitions. Note that these measured gap widths are in fact slightly larger than the expected values of 10 μm and 5 μm for these particle sizes assuming negligible ΔQ (this assumption is valid, since a H = 180 μm channel was used for these measurements). We suspect that the simplistic assumption of geometric volume exclusion is responsible for this discrepancy, as a physical deflection force on the particles would be somewhat longer range than hard-core repulsion.

Similar experimental gap size measurements were made for a wide range of s. Fig. 8(b) compares these measured center gap widths to the corresponding theoretical ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$. We find that while the measured and computed values are proportional, the computed values are much smaller. On average, the ratio of computed to measured values is 0.325.

FIG. 8.

(a) Gap width as a function of z at s = 0.005, normalized by the mean gap width ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$, showing that the 3D streaming theory predicts a wider gap compared to 2D theory and that the maximum gap width occurs at z = 0. (b) Gap widths at the mid-plane (z = 0) plotted against the mean estimated gap width ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$, showing results from experiments, as well as from 2D and 3D theories of the streaming. The dashed line corresponds to the asymptote of the 3D theory for s ≪ 1. The peak axial velocity component in the 3D theory is ≈0.25 times the maximum in-plane velocity u_max (as measured in Ref. 21), showing that even weak axial effects can enhance the central width of the gap compared to its mean value ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$.

This discrepancy might be explained by taking into account the 3D nature of the flow. The use of (3) to calculate gap size implicitly assumes that (i) the streaming speed is planar and uniform across the depth of the channel, and (ii) that the net flow rate through the gap Q − ΔQ is distributed uniformly through the channel depth. The average gap size ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$ computed using (3) may not therefore adequately represent the flow experienced by the microparticles as they flow past the bubble.

We will now relax the 2D assumption (and thus also the stream function representation of the flow) and consider a broader class of flow superpositions between the streaming and Poiseuille flows of the form

$$\mathit{u}={\mathit{u}}_s+s\beta {\mathit{u}}_p,$$ (20)

where we now allow $\mathit{u}$ to contain non-zero axial gradients and velocity components. This allows us to define more generally a z dependent gap size d_gap(z) as the minimum separation, over the azimuth θ, between the upstream vortex and semi-cylindrical bubble interface, as a function of the axial coordinate z.

As a first approximation, we take into account the z variation of the Poiseuille flow, but retain the 2D solution for the streaming. This is a relatively simple modification and produces quasi-2D flows of the type $\mathit{u}=\{u_x(x,y,z),u_y(x,y,z),0\}$. Following passive tracer elements advected in this version of the flow field starting at different initial conditions across the channel and near the bubble, we record which tracers end up caught in the vortex structures, and which tracers follow open streamlines. The latter are deemed to have passed through the gap, and their closest approach distances to the bubble surface result in a z-dependent gap width d_gap(z) shown as “2D Theory” in Fig. 8(a). While such a superposition predicts that $d_{\mathit{g}\mathit{a}\mathit{p}}(z=0)>{\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$, it still underpredicts the direct experimental measurements of the gap width, as shown in Figure 8(b).

We find, however, that even the introduction of weak axial streaming flow components improves the agreement between the theory and experimental measurements. To model these axial flows, we use a flow superposition of the 2D streaming and axial Stokes solutions, which results in a net 3D streaming flow field.^20,21 The modeling of the 3D streaming is described briefly in the Appendix and in greater detail in Ref. 20. While the axial flow strength in the present experiments is unknown, we assume in our model that the maximum axial components of fluid velocity are ≈0.25u_max, consistent with 3D experimental measurements by Ref. 21 in microchannels of the same make and geometry. We evaluate d_gap(z) in the same fashion with passive tracers advected in this 3D flow field. In Fig. 8(a), the pronounced widening of the gap in the channel center and its reduction to zero near the channel walls is clearly visible. Figure 8(b) shows that this introduction of axial flows in the theory improves the agreement with experiment when comparing experimental gap sizes with d_gap(z = 0). The 3D theory is quite accurate for small s values (small gap widths), while discrepancies become larger for larger s. We suspect that the flow field modeling for very strong transport flow (large gap sizes) does not adequately describe the flow, as the gap becomes comparable to the bubble dimensions. Fortunately, the gap sizes relevant for sorting micron-sized particles (or, e.g., biological cells) are at the low end of the range depicted in Fig. 8(b). The asymptotic result of the 3D theory (s → 0, dashed line) accurately describes the observed gap sizes up to much larger s than expected, perhaps fortuitously.

The justification that d_gap(z = 0) is the relevant indicator for sorting stems from two separate sources. First, the Poiseuille flow speed is fastest at z = 0, so that a greater number of particles reach the bubble per unit time near z = 0, compared with the region of the flow near z = ±d/2. Second, the 3D streaming flow consists of axial flow components that drive fluid towards the mid-plane near θ = 0 and θ = π and towards the walls of the channel near θ = π/2 (see Refs. ²¹ and ²⁰). The flow becomes focused toward z = 0 as it passes through the gap, which must therefore be wider than the average gap width ${\overline{d}}_{\mathit{g}\mathit{a}\mathit{p}}$ in order to accommodate this flow rate. The combination of the experimental measurements of gap widths and the theoretical results from the 3D flow model thus suggests that the maximum gap width d_gap(z = 0) replaces the mean gap width in the geometric model of sorting, explaining the experimentally observed sorting transitions. Similarly to d_gap(z), one can define a z-dependent smallest distance d₁(z) (for all θ) to the stagnation stream surface (the 3D generalization of the stagnation stream line). The z-variation of d₁ is very similar to that of d_gap, and the theoretically predicted ratio of the two at z = 0 is d_gap(z = 0)/d₁(z = 0) ≈ 1.91 for negligible ΔQ. Thus, the predictions for s₁/s₂, experimentally confirmed above, remain valid within the 3D formalism and are consistent with it.

It was shown in Ref. 20 that the axial flow components decay exponentially with radial distance from the bubble surface. Therefore, the corrections are very important near the bubble (and thus for reproducing the observed gap width), but do not substantially alter the particle trajectories farther away from the bubble. Thus, the overall shape of the trajectories is well captured by the simpler 2D theory, as evidenced in Fig. 6.

IV. CONCLUSIONS

We have demonstrated here that steady streaming flows driven by acoustically excited microbubbles can be used effectively for the continuous size-sensitive sorting of particles. By superimposing the streaming flow with a pressure-driven Poiseuille flow through the channel carrying microparticles, we were able to design a continuous size-sensitive sorting device whose throughput is limited only by the flow rate of the Poiseuille flow. Compared to previous microbubble sorting techniques using vortex trapping, the continuous sorting presented here allows for uniform sorting rates, greater size sensitivity, and greater rates of throughput over a range of μm particle sizes particularly relevant in biology- or manufacturing-related lab-on-a-chip applications. Separating even slightly enlarged cells from normal-sized specimens should be within the reach of this method, as well as the simultaneous sorting of more than two species.

A simple geometric sorting mechanism that relies on the inability of particles to penetrate the bubble surface predicts that particles must be deflected across streamlines as they pass through a narrow gap near the bubble. It is verified experimentally that the width of this gap relative to particle size determines the sorting properties of the device. We have shown that the size-sensitivity of the device (controlled by the gap width) may be tuned by varying the relative strength of the streaming to the Poiseuille flow, achieved simply by adjusting the driving voltage of the ultrasound without the need to actively manipulate individual particles or modify the device geometry. The 2D projections of experimental particle trajectories were accurately modeled using an asymptotic description of the flow field. A more sophisticated version of the theory quantitatively describes the flow structure near the bubble (including the gap), as well as the experimentally observed sorting, provided that the axial flow components (driven by the axial confinement of the bubble) are properly accounted for.

We have therefore described, in both experiment and theory, a simple mechanism of particle sorting in microfluidic flows. Contrary to other sorting devices,^7,8,46 the sorting occurs over short length (∼10 μm) and time scales (1 ms) where the flow is the fastest. Future work will focus on quantifying and theoretically describing the detailed hydrodynamic forces acting on particles and leading to their migration, advancing the work toward a more general understanding of particle dynamics in microfluidic flows as well as towards the development of improved devices for particle manipulation.

With a view to applications in the biosciences, we have also begun work on microstreaming in a wider variety of contexts. This includes studies on the sorting behavior of cells and bacteria (including red blood cells, archaeal cells, and Escherichia coli) in bubble streaming flows. Aside from aiding our understanding of effects of particle non-sphericity, motility, or deformability, this research offers great promise for applications such as cytometry or the collection of specifically targeted cells for diagnostic purposes.

APPENDIX: THREE-DIMENSIONAL STREAMING FLOW FIELDS

We briefly summarize the construction of the 3D streaming flow field, given in detail by Rallabandi et al.²⁰ This is accomplished by means of a superposition of the 2D streaming flow field ${\mathit{u}}_s^{2d}$ with axial (3d) solutions $\mathit{v}$ of the Stokes equations

$$\mathbf{\nabla }·\mathit{v}=0,\hspace{1em}{\nabla }^2\mathit{v}=\mathbf{\nabla }p,$$ (A1)

where p is the dimensionless pressure. The axial flow $\mathit{v}$ may be written using a Fourier decomposition in θ and z into modes of the form

$$\begin{array}{c}{\mathit{v}}_{\mathit{m}\mathit{n}}^j=\{u_{\mathit{m}\mathit{n}}^j(r)\hspace{0.17em}\text{cos}\hspace{0.17em}2m\theta \hspace{0.17em}\text{cos}\hspace{0.17em}2n\alpha z,v_{\mathit{m}\mathit{n}}^j(r)\hspace{0.17em}\text{sin}\hspace{0.17em}2m\theta \hspace{0.17em}\text{cos}\hspace{0.17em}2n\alpha z,\hspace{0.17em}{w}_{\mathit{m}\mathit{n}}^j(r)\hspace{0.17em}\text{cos}\hspace{0.17em}2m\theta \hspace{0.17em}\text{sin}\hspace{0.17em}2n\alpha z\},\hspace{1em}j\in \{1,2\},\end{array}$$ (A2)

where α = π/d. Here, the terms with j = 1 and j = 2 represent, respectively, the conservative (curl-free) and non-conservative components of the velocity field. The separation of variables admits the following analytical expressions for the radial functions of ${\mathit{v}}_{\mathit{m}\mathit{n}}^j$

$$\begin{array}{c}{u}_{\mathit{m}\mathit{n}}^1\left(r\right)=-\frac{2n\alpha }{2}\left({\mathrm{K}}_{2m+1}(2n\alpha r)+{\mathrm{K}}_{2m-1}(2n\alpha r)\right),\\ v_{\mathit{m}\mathit{n}}^1\left(r\right)=-\frac{2m}{r}{\mathrm{K}}_{2m}(2n\alpha r),\\ w_{\mathit{m}\mathit{n}}^1\left(r\right)=-2n\alpha {\mathrm{K}}_{2m}(2n\alpha r),\end{array}\}$$ (A3)

and

$$\begin{array}{c}{u}_{\mathit{m}\mathit{n}}^2\left(r\right)=-\frac{m}{2n\alpha }{\mathrm{K}}_{2m+1}(2n\alpha r)+\frac{r}{2}{\mathrm{K}}_{2m+2}(2n\alpha r),\\ v_{\mathit{m}\mathit{n}}^2\left(r\right)=\frac{m+1}{2n\alpha }{\mathrm{K}}_{2m+1}(2n\alpha r),\\ w_{\mathit{m}\mathit{n}}^2\left(r\right)=\frac{r}{2}{\mathrm{K}}_{2m+1}(2n\alpha r).\end{array}\}$$ (A4)

The Stokes solution ${\mathit{v}}_{\mathit{m}\mathit{n}}$ that satisfies no penetration conditions both at the axially confining walls (z = ±d/2) and at the mean position of the bubble interface (r = 1), normalized to have unit maximum axial velocity, is given by the following linear superposition of the modes ${\mathit{v}}_{\mathit{m}\mathit{n}}^{\mathit{j}}$

$${\mathit{v}}_{\mathit{m}\mathit{n}}\equiv {\left(\frac{w_{\mathit{m}\mathit{n}}^1\left(1\right)}{u_{\mathit{m}\mathit{n}}^1\left(1\right)}-\frac{w_{\mathit{m}\mathit{n}}^2\left(1\right)}{u_{\mathit{m}\mathit{n}}^2\left(1\right)}\right)}^{-1}\left(\frac{{\mathit{v}}_{\mathit{m}\mathit{n}}^1}{u_{\mathit{m}\mathit{n}}^1\left(1\right)}-\frac{{\mathit{v}}_{\mathit{m}\mathit{n}}^2}{u_{\mathit{m}\mathit{n}}^2\left(1\right)}\right).$$ (A5)

It has been shown that all the salient features of the 3D streaming flow ${\mathit{u}}_s$ are well represented by a superposition of the 2D streaming solution ${\mathit{u}}_s^{2d}$ with the lowest axial Stokes modes

$${\mathit{u}}_s={\mathit{u}}_s^{2d}+c_{01}{\mathit{v}}_{01}+c_{11}{\mathit{v}}_{11},$$ (A6)

where c₀₁ and c₁₁ are coefficients that set the relative strength of the axial velocity to the flow velocity in the xy plane.^20,21 The experiments of Marin et al.²¹ show that the peak axial speed is ≈0.25u_max, setting c₀₀ = −0.085 and c₁₁ = −0.351.