Technical Note: FreeCT_wFBP: A robust, efficient, open-source implementation of weighted filtered backprojection for helical, fan-beam CT

Abstract

Purpose:

With growing interest in quantitative imaging, radiomics, and CAD using CT imaging, the need to explore the impacts of acquisition and reconstruction parameters has grown. This usually requires extensive access to the scanner on which the data were acquired and its workflow is not designed for large-scale reconstruction projects. Therefore, the authors have developed a freely available, open-source software package implementing a common reconstruction method, weighted filtered backprojection (wFBP), for helical fan-beam CT applications.

Methods:

FreeCT_wFBP is a low-dependency, GPU-based reconstruction program utilizing c for the host code and Nvidia CUDA C for GPU code. The software is capable of reconstructing helical scans acquired with arbitrary pitch-values, and sampling techniques such as flying focal spots and a quarter-detector offset. In this work, the software has been described and evaluated for reconstruction speed, image quality, and accuracy. Speed was evaluated based on acquisitions of the ACR CT accreditation phantom under four different flying focal spot configurations. Image quality was assessed using the same phantom by evaluating CT number accuracy, uniformity, and contrast to noise ratio (CNR). Finally, reconstructed mass-attenuation coefficient accuracy was evaluated using a simulated scan of a FORBILD thorax phantom and comparing reconstructed values to the known phantom values.

Results:

The average reconstruction time evaluated under all flying focal spot configurations was found to be 17.4 ± 1.0 s for a 512 row × 512 column × 32 slice volume. Reconstructions of the ACR phantom were found to meet all CT Accreditation Program criteria including CT number, CNR, and uniformity tests. Finally, reconstructed mass-attenuation coefficient values of water within the FORBILD thorax phantom agreed with original phantom values to within 0.0001 mm²/g (0.01%).

Conclusions:

FreeCT_wFBP is a fast, highly configurable reconstruction package for third-generation CT available under the GNU GPL. It shows good performance with both clinical and simulated data.

1. INTRODUCTION

There is substantial interest in advanced uses of CT that involve quantitative imaging, radiomics, and CAD for lung screening and other applications.^1–9 To ensure that these applications are robust, they should be tested across a wide variety of scanner platforms, acquisition conditions, and reconstruction parameters.^10,11 While phantom studies can be repeated using various acquisition and reconstruction settings, this approach is not generally realizable for patient studies due to radiation dose concerns. However, from a given set of raw projection data resulting from a single patient scan, a number of reconstruction conditions can be evaluated including different reconstruction kernels as well as reconstructed slice thickness, spacing, or simulated reduced-dose conditions.^12–15

When needed, additional reconstructions are often performed at the CT scanner (“on-board” reconstructions), but scanner-based reconstruction has substantial limitations when considering large-scale explorations of reconstruction and acquisition parameter space. First, the scanners are typically only available for research activities outside of clinical operation hours, reducing the time available for large-scale reconstruction projects such as Ref. 11 (396 reconstructions utilizing 33 data sets) or Ref. 16 (10 000 reconstructions of simulated noise realizations). Second, scanner work-flows are optimized for clinical work and not the “batch mode,” high-throughput reconstruction typically required in quantitative imaging research, reducing the number of reconstructions that can be accomplished in any allotted time. Third, the clinical setup typically requires manual changes to many parameters prior to each reconstruction, requiring the constant attention of a researcher, and increasing the likelihood of errors. And finally, if a site upgrades a scanner, a researcher may lose the ability to reconstruct “legacy” raw data associated with that scanner model. Therefore, there is a need to develop customizable tools that allow efficient, large-scale reconstruction of diagnostic CT images independent of the acquisition scanner.

While there are many available options for reconstructing cone-beam CT data using third-party open source software libraries [e.g., RTK,¹⁷ CONRAD,¹⁸ and OSCaR (Ref. ¹⁹)], the options for reconstructing helical, diagnostic CT data are substantially more limited. The only alternative to on-board reconstruction of which the authors are aware, is a standalone reconstruction computer from manufacturers, but these have limited availability and are not widely deployed. Furthermore, the work-flow of these “recon boxes” is typically ill-suited to large-scale reconstruction and rarely customizable to a researcher’s needs. Thus, the standalone reconstruction computer does not represent a satisfactory solution to the problems facing researchers hoping to perform large numbers of reconstructions, and no other alternatives are currently available.

In this work, we present a free and open-source implementation of a commonly used reconstruction concept—specifically weighted filtered backprojection (wFBP)—for third-generation, helical, fan-beam CT in an effort to overcome some of the limitations of the currently available tools. The software is highly flexible, with features such as user-configurable scanner geometries, user-modifiable reconstruction kernels, CPU and GPU implementations, and support for data acquired using sampling techniques such as flying focal spots (FFSs) and quarter-detector offsets (QDOs). In Sec. 2, a more complete description of the software details and features is provided, including a discussion of the implemented algorithm, hardware and software requirements, licensing (freely available under the GNU GPL), and some of the issues around acquiring raw diagnostic CT data. In Sec. 3, the research-readiness of the software is evaluated taking into consideration both speed and accuracy, with Sec. 4 containing a discussion of these results. Finally, in Sec. 5, the work is summarized and planned future developments for the software are discussed.

2. SOFTWARE FEATURES

FreeCT_wFBP is a free, command-line program providing flexible and fast reconstruction of helical, diagnostic CT data using a GPU or CPU. It is written in c and utilizes the Nvidia CUDA framework for GPU-specific code. This section provides an overview of what the software does and its features. For a complete description and to obtain the software, please visit the FreeCT_wFBP website at http://cvib.ucla.edu/freect.²⁰

2.A. The algorithm

FreeCT_wFBP is an implementation of wFBP, a widely used approach for helical CT reconstruction that offers a good trade-off between computational effort, accuracy, and flexibility.^21–25 While wFBP is a relatively simple reconstruction approach to implement, there are many possible variations such as where and how to handle slice-thickness settings, weighting function choices, and weighting “tuning” parameters. FreeCT_wFBP is, specifically, an implementation of weighted filtered backprojection as described in Ref. 22. It is suitable for reconstructing any third-generation, helical CT data (without gantry tilt), including clinical or simulated raw projection data from any manufacturer or software tool, so long as the user can extract that raw data into an appropriate format readable by FreeCT_wFBP and the scanner geometry is configured properly.

While wFBP is a well-known reconstruction method, no details of its parallel implementation have been reported in the literature to date. FreeCT_wFBP’s GPU implementation is highly customized for the computational and data transfer demands of reconstruction. Twenty-two kernels were written to handle parallelizable tasks: eighteen for rebinning (primarily to handle the various flying focal spot scenarios), one for filtering, and two for backprojection; gridding schemes for each kernel were chosen to maximize GPU occupancy while also taking into account size of the raw data. Optimization techniques include the use of CUDA streams to interleave data transfers with compute operations, the use of textures for interpolation operations, shared memory usage, and loop unrolling where possible. A full discussion of GPU implementation and optimizations employed by FreeCT_wFBP and other implementation choices (weighting function, slice thickness handling, etc.) have been made available in the software documentation,²⁰ including equations and pseudo-code.

2.B. Geometry

FreeCT_wFBP reconstructs helical data from third-generation multi-detector CT scanners, currently the most widely employed geometry in clinical diagnostic CT. Third-generation CT scanners utilize a detector with circular curvature in the axial (XY) plane, and no curvature in the longitudinal (Z) direction. FreeCT-wFBP does not currently reconstruct axial scans nor does it reconstruct helical scans acquired with gantry tilt.

2.C. Rebinning and flying focal spots

Weighted filtered backprojection, as described in Ref. 22 utilizes a row-wise fan-to-parallel rebinning process prior to filtering and backprojection. While this requires an extra set of interpolations, it has been shown to have negligible effect on image quality²⁶ while at the same time providing several benefits: (1) simplified geometry for backprojection, (2) artifact reduction (mitigation of cone-beam artifacts) during filtering since the data is recast along the spiral tangent,²² and (3) straight-forward accounting for changes in geometry caused by sampling techniques such as flying focal spots.

Flying focal spots are a technique employed by some CT scanners to improve sampling in the axial and/or longitudinal directions by periodically deflecting the electron beam to different locations on the x-ray tube anode between detector readouts; a depiction of this periodic motion can be found in Fig. 1 of Ref. 28 and Figs. 1, 2, and 5 of Ref. 27. Projections acquired at the different focal spot locations can then be interleaved, effectively doubling the detector grid sampling in the direction of the electron beam deflection. This improved sampling allows the system to satisfy the Nyquist criterion resulting in fewer aliasing artifacts and higher spatial resolution in the reconstructed image; see Refs. ²⁷ and ²⁸ for more details. Use of the in-plane flying focal spot (called the “Phi” flying focal spot) improves in-plane spatial resolution in axial images. Use of the longitudinal flying focal spot (called the “Z” flying focal spot) improves spatial resolution in the longitudinal direction and also reduces windmill artifacts observed in the axial plane near the edges of high-contrast objects.^27,28 Depending on scan configuration (namely, rotation time and collimation), a scanner equipped with flying focal spots may use both Z and Phi, Z only, Phi only, or no flying focal spots to acquire data. Incorporation of the flying focal spot rebinning routines allows the software to reconstruct projection data from a much larger subset of scanners than would otherwise be possible.

2.D. Quarter- and eighth-detector offsets

The QDO is a sampling technique utilized in most modern CT scanners wherein the detector center is shifted by a quarter of the detector width relative to “center” (the point at which a ray traced from the focal spot through isocenter would intersect the detector plane). While the quarter detector offset is most beneficial in axial CT scans (doubled in-plane sampling, improved in-plane resolution, and reduction of in-plane aliasing artifacts) its use in helical CT is also very common.^27,29 FreeCT_wFBP is capable of reconstructing with and without the QDO, as well as with an eighth-detector offset which occurs when the QDO is used in conjunction with the in-plane flying focal spot.²⁷

2.E. Parameter files for configuration

Reconstructions with the software are configured using simple, commentable, text-based parameter files, an example of which is shown in listing 1. Reconstruction parameters are configured using a “.prm” file-type in which settings such as collimation, slice thickness, reconstruction range, and reconstruction kernel are configured. Scanner geometry parameters   can  be   selected   from  a   library   of hard-coded

Listing 1.

Sample input parameter file used to configure a reconstruction with FreeCT_wFBP. Comments begin with a “%” and are ignored when parsed. Note the scanner geometry is defined in the separate file “DefinitionAS.scanner.”

% Input PRM file for reconstructing Phi + Z flying focal spot.

% scan acquired on a Definition AS. Units are millimeters unless otherwise

% specified.

RawDataDir:/home/user/Study_Data/WFBP/raw_data/

RawDataFile:a_ffs.IMA

Nrows:64

CollSlicewidth:0.6

Start Pos:895.5% Smallest possible value: 750.0

End Pos:895.4% Largest possible value: 920.2

SliceThickness:0.6

TableFeed:19.2%mm/rotation

AcqFOV:500.0

Recon FOV:220.0

ReconKernel:3

Readings:51 600

Xorigin:0.0

Yorigin:0.0

Zffs:1

Phiffs:1

Scanner:DefinitionAS.scanner

FileType:3

FileSubType:1

RawOffset:522 960% bytes

Nx:512

Ny:512

scanners included in the source code, or from “.scanner” files included with the software or created by the user. Scanner geometry files have very similar structure to the parameter files however contain parameters such as number of detector channels, number of projections per rotation, tube anode angle, and other measurements.

The use of text files for configuration eliminates the need to recompile the software for simple changes, such as scan range or slice thickness, as well as complex changes, such as adding new scanners, or changes in scanner geometry. Sample reconstruction parameter files, as well as details on parameter (“.prm”) file structure and scanner (“.scanner”) file structure are available in Ref. 20.

2.F. Reconstruction kernels

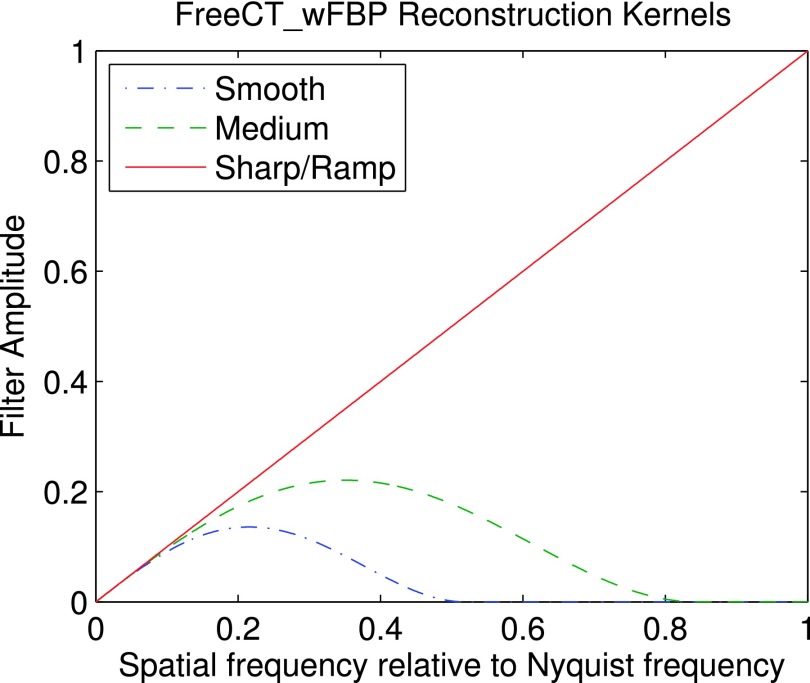
Reconstruction kernels are stored as binary files of single-precision, floating-point data (a vector representing the kernel profile in the spatial domain) and are read in at program runtime making it easy for a user to create and utilize their own filters without needing to recompile source code. Full details on filter creation and installation can be found in the documentation. FreeCT_wFBP comes with three reconstruction kernels and ready for use: smooth, medium, and sharp/ramp. The kernels were developed using the method outlined in Ref. 33 and plots of the kernel profiles in the Fourier domain can be found in Fig. 1. Sample reconstructions using the built-in kernels can be found in Figs. 2–4.

FIG. 1.

Smooth, medium, and sharp/ramp reconstruction kernels provided with the FreeCT_wFBP software package.

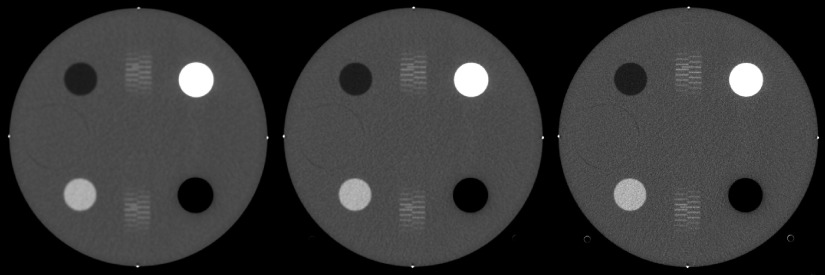
FIG. 2.

CT number module of ACR phantom. Reconstructed with smooth (left), medium (center), and sharp/ramp (right) kernels. Shown with a window/level of 400/0 HU.

FIG. 3.

Uniformity module of ACR phantom. Reconstructed with smooth (left), medium (center), and sharp/ramp (right) kernels. Shown with a window/level of 100/0 HU.

FIG. 4.

Low contrast module of ACR phantom. Reconstructed with smooth (left), medium (center), and sharp/ramp (right) kernels. Shown with a window/level of 100/100 HU.

2.G. GPU/CPU implementation

Due to the computational demands of CT image reconstruction and the need to automate large numbers of reconstructions in an efficient manner, FreeCT_wFBP is first and foremost a GPU-based software package. To extend the functionality and accessibility of the software, a single-threaded CPU implementation has also been created. The GPU implementation is significantly faster and will be most useful for researchers looking to process large numbers of reconstructions; however, the CPU implementation is well suited to running large numbers of reconstructions on distributed clusters that may not have GPUs available. It should be noted that the performance on a single CPU is not expected to be fast enough for large-scale reconstruction projects.

Both GPU and CPU versions are built into one program, and the software is capable of autodetecting the presence or absence of GPU resources and favors GPU computation if available. It can also be set to run on the CPU manually via a simple “--no-gpu” command line option.

2.H. Requirements and dependencies

In this subsection, we provide a brief overview of the resources needed to run FreeCT_wFBP. For a full description of the hardware and software requirements please refer to the documentation.²⁰

2.H.1. Software

FreeCT_wFBP was developed on Linux (Ubuntu 14.04 LTS, Canonical, Ltd, London, UK) and should compile and run on all modern Linux distributions with little to no modification. Only two major external dependencies for building and running the software are required: (1) the Nvidia CUDA toolkit (https://developer.nvidia.com/cuda-toolkit) and (2) the FFTW3 Fourier transform library (http://www.fftw.org/), which are free and compatible with most systems.

2.H.2. Hardware

For both CPU and GPU execution, RAM requirements are minimal: it is recommended to have at least 2 GB of free memory to run FreeCT_wFBP. For GPU execution, a CUDA-capable device and corresponding driver is needed. For clinical raw projection data, a GPU with at least 2 GB of global memory and capable of running 1024 threads per block is recommended. Actual global memory requirements will depend on the size of the data being reconstructed (number of detector rows and channels, and number of projections per rotation) and thus may be more or less than 2 GB in practice. Thread and block dimensions are set to default values optimized for the hardware and data used for the reconstructions in this work; however, gridding is user configurable for the raw data being reconstructed and GPU being utilized. The CPU implementation is single-threaded and thus CPU clock speed and cache size will have the largest impact on reconstruction speed.

2.I. Raw CT projection data

Research in diagnostic CT can be limited by a lack of access to raw projection data. If raw data can be exported from the scanner, it is typically stored in a proprietary format not readily readable by the user without access to proprietary, manufacturer-provided software libraries. Duan and McCollough have recently proposed a vendor neutral raw data format based on the DICOM standard which will ultimately support their efforts to develop a library of freely available diagnostic CT patient and phantom projection datasets.³⁰ The reader library packaged with FreeCT_wFBP is capable of directly reading this open-format DICOM raw data as well as binary files of floating-point data. Furthermore, all of the raw data files and necessary parameter files used in this publication are available for download from the FreeCT_wFBP website.²⁰ Exact specifications for how data are read into the software can be found in the documentation, further providing users the opportunity to supply their own raw data through simulation or other means.

2.J. Licensing

FreeCT_wFBP is freely distributed under GNU GPL v2.0 in an effort to encourage further research and education using diagnostic CT. In short, licensing under the GPL v2.0 means that users are free to copy, distribute and modify the software provided changes are identified and dated in the source code and any modifications are made freely available under the same license. To provide stability for users doing research with the software, FreeCT_wFBP will be maintaining individual, versioned releases through the website and GitHub, which will provide a consistent “history” needed for reproducibility. For those interested in developing or modifying the software, FreeCT_wFBP is an ongoing effort open to feedback, suggestions, and contributions from the larger community.

3. SOFTWARE PERFORMANCE EVALUATION

3.A. Methods

All reconstruction and evaluation were performed on an Alienware Aurora R4 computer with an Intel i7-4960X CPU (3.6 GHz, 15 MB L3 cache), 32 GB of RAM and an Nvidia GeForce GTX 780 GPU with 3 GB of global memory. GPU reconstructions were acquired by running the software with the standard settings (auto-detection and use of GPU resources), and CPU reconstructions were acquired using the “--no-gpu” command line option, forcing all reconstruction to take place on the CPU.

Speed was evaluated using timing benchmarks for each step of the reconstruction process for a given set of reconstruction/acquisition conditions. Reconstruction speed (i.e., computational performance) is dependent on many factors, including but not limited to collimation, flying focal spot configuration, and slice thickness; column 5 of Table I (“Rebinned Projections for 32 Slices”) is included to highlight how collimation and flying focal spot settings, in particular, can have a large impact on parameters the user does not directly control (i.e., number of projections required to fully reconstruct a volume) but do affect reconstruction speed. FreeCT_wFBP reconstruction speed was evaluated by reconstructing 512 × 512 × 32 voxel volumes from scans of the ACR accreditation phantom (Model 464, Gammex, Middleton, WI) performed on a 3rd generation CT scanner (Definition AS 64, Siemens Healthcare, Forchheim, Germany) under all FFS combinations available on that scanner: (a) no FFS, (b) Phi FFS only, (c) Z FFS only, and (d) both Z and Phi FFS as described in Table I. Slices were reconstructed to thicknesses matching detector collimation. Code profiling for both the CPU and GPU implementations was performed using the Nvidia Visual Profiler included with the CUDA toolkit.

TABLE I.

Summary of scan parameters for speed profiling scans. The number of rebinned projections required for each reconstruction are shown and reflect the effects of collimation and flying focal spot settings, which are influenced by the reconstructed voxel size relative to the size of the effective detector thickness (e.g., 16 × 1.2 mm).

FFS	Collimation (mm)	Rotation time (s)	Recon slice thickness (mm)	Rebined projections for 32 slices
No FFS	16 × 1.2	0.5	1.2	3840
Phi-only	16 × 1.2	1	1.2	3712
Z-only	64 × 0.6	0.5	0.6	2624
Phi and Z	64 × 0.6	1	0.6	2528

Image quality and accuracy were evaluated according to the current ACR CT Accreditation Program (CTAP) criteriafor CT number evaluation, CT number uniformity, and contrast-to-noise ratio (CNR) using the methods and formulas described in Ref. 31. The ACR phantom was scanned under the “Phi and Z” conditions described in Table I, using a routine adult abdomen protocol, and the central slice of each module of the ACR phantom was reconstructed (using the GPU) to a thickness of 5 mm using the included smooth, medium, and sharp/ramp kernels from the FreeCT_wFBP package. The reconstructed slices of each module were then evaluated to see if they fell within ACR-acceptable ranges.

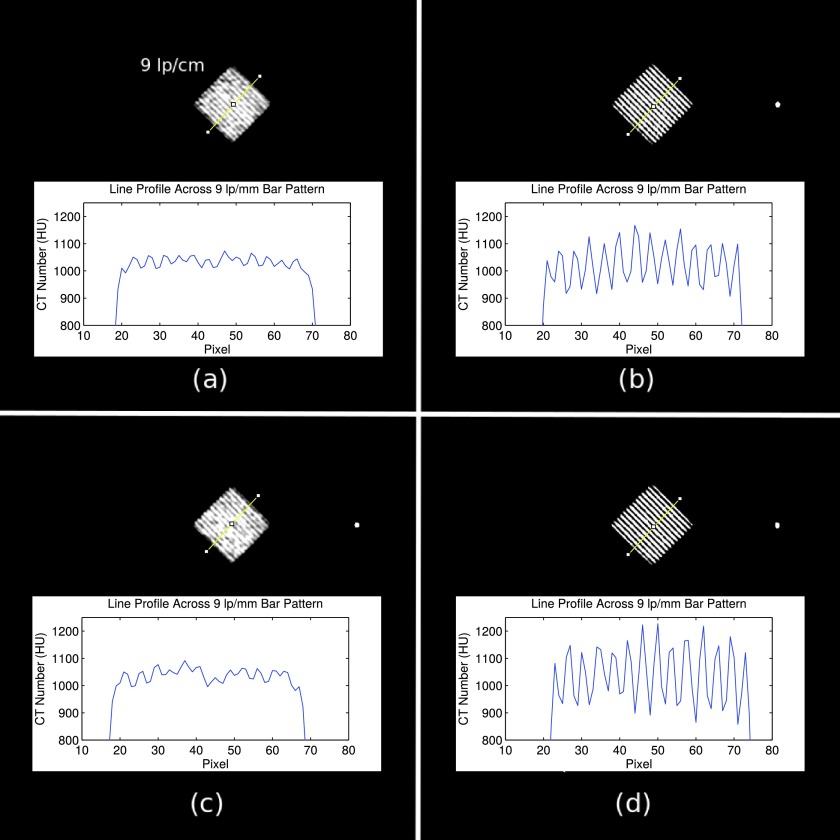
While spatial resolution is no longer evaluated as part of the ACR CTAP, the spatial resolution module of the phantom was used to ensure proper implementation of flying focal spot rebinning. A slice through the middle of the spatial resolution module from each of the scans listed in Table I was reconstructed to a 1.2 mm slice thickness and a 100 mm field of view centered on the 9 lp/cm bar pattern. A sharp/ramp filter was used to maximize spatial resolution. Each reconstructed image was evaluated for changes in in-plane resolution and changes in windmill artifacts. If implemented correctly, an improvement in in-plane resolution with activation of the Phi flying focal spot, and a reduction of windmill artifacts with the activation of the Z flying focal spot, should be observed.

Finally, reconstruction accuracy was evaluated using a reconstruction of a simulated FORBILD thorax phantom³² for which attenuation values were known exactly. The FORBILD thorax phantom data was generated with a simulated, 80 keV, monochromatic beam without flying focal spots, and reconstructed using the included sharp/ramp kernel. The attenuation value of water at 80 keV (mass attenuation coefficient of 0.0183 mm²/g) was used to create the phantom. Without scaling the reconstructed image to Hounsfield units (HUs), a ROI was placed over a region of simulated water and the mean value (mass attenuation coefficient) was compared to the value used in the simulation.

3.B. Results

Tables II and III summarize the GPU and CPU reconstruction times, respectively. Rebinning and filtering are a hybrid process in the FreeCT_wFBP implementation and thus are combined into one step for timing purposes. Note that GPU reconstruction times are in seconds and CPU reconstruction times are in minutes.

TABLE II.

Sample speed results for GPU reconstruction for different flying focal spot (FFS) configurations. Note that times are given in seconds.

	GPU
FFS	Rebin and filter (s)	Backprojection (s)	Total (s)
No FFS	2.7	13.8	16.5
Phi FFS	2.9	13.8	16.7
Z FFS	7.9	9.9	17.8
Phi and Z FFS	8.8	9.9	18.7

TABLE III.

Sample speed results for CPU reconstruction for different flying focal spot (FFS) configurations. Note that times are given in minutes.

	CPU
FFS	Rebin and filter (min)	Backprojection (min)	Total (min)
No FFS	0.5	93.5	94.0
Phi FFS	3.0	93.4	96.4
Z FFS	4.6	64.8	69.4
Phi and Z FFS	8.2	64.9	73.1

Tables IV–VI summarize the imaging performance of the smooth, medium, and sharp reconstruction kernels using the ACR testing protocols. Figures 2–4 show the reconstructed slices that were used for evaluation, all windowed and leveled to the values recommended in the ACR testing protocols.

TABLE IV.

Summary of CT number performance for each reconstruction kernel provided with FreeCT_wFBP. All values are within acceptable ACR ranges. All values are in HU.

	Polyethylene	Bone	Acrylic	Air	Water
Smooth	−88.3	869.3	123.6	−989.1	−0.4
Medium	−88.3	869.0	123.5	−988.7	−0.4
Sharp	−88.1	866.6	123.4	−988.1	−0.3
Acceptable range	−107 to −84	850 to 970	110 to 135	−1005 to −970	−7 to 7

TABLE V.

Summary of uniformity measurements for each reconstruction kernel. All values are in HU and well within the −5 to +5 HU range specified by the ACR.

	Uniformity (maximum difference from center)
Smooth	−0.3
Medium	0.6
Sharp	0.9
Acceptable range	−5 to 5

TABLE VI.

Summary of CNR values for FreeCT_wFBP. The smooth and medium reconstructions are well above the ACR limit of 1.0.

	CNR
Smooth	2.6
Medium	1.3
Sharp	0.4
Acceptable range	>1.0

The effects of flying focal spot usage on reconstruction quality are shown in Figs. 5 and 6. In Fig. 5, an improvement in spatial resolution is observed when the Phi flying focal spot is utilized [Figs. 5(b) and 5(d)], allowing the 9 lp/cm bar pattern to be clearly resolved. When the Phi flying focal spot is not used [Figs. 5(a) and 5(c)], the 9 lp/cm bar pattern can no longer be precisely resolved.

FIG. 5.

Spatial resolution reconstructions using (a) no flying focal spots, (b) Phi flying focal spot, (c) Z flying focal spot, and (d) Z and Phi flying focal spot. In (b) and (d), the Phi flying focal spot is active and spatial resolution is qualitatively improved and line profiles across the bar pattern further indicate the improved ability to distinguish fine detail. All images are of the 9 lp/cm bar pattern of the ACR phantom spatial resolution module. Shown with a window/level of 100/1000 HU.

FIG. 6.

Z flying focal spot comparison using (a) no flying focal spots, (b) Phi flying focal spot, (c) Z flying focal spot, and (d) Z and Phi flying focal spot. Large, red arrows highlight windmill artifacts off of a high contrast centering bead, while smaller black arrows highlight their absence in (c) and (d) when the Z flying focal spot is active. Shown with a window/level of 125/−1000 HU. High frequency artifacts (most pronounced in top right image) are due to the ramp filter reconstruction combined with the high, in-plane resolution offered with the Phi flying focal spot; note their disappearance when the Phi and Z flying focal spots are utilized together.

In Fig. 6, the image is windowed and leveled to highlight the impacts of Z flying focal spot usage. Usage of the Z flying focal spot manifests itself in the axial plane as a reduction of windmill artifacts. In Fig. 6, a high contrast bead produces windmill artifacts when the Z flying focal spot is not utilized (top row, highlighted with the larger red arrow), which then disappear with the activation of the Z flying focal spot (highlighted with the smaller, black arrows). The higher frequency noise in the right column is due to the increased in-plane resolution with the Phi flying focal spot combined with the ramp filter reconstruction.

Finally, Fig. 7 shows the unscaled axial, sagittal, and coronal FreeCT_wFBP reconstructions of the FORBILD thorax phantom for which all attenuation values are known exactly. The ROI’s mean value of 0.0183 mm²/g agrees to within 0.0001 (0.5%) of the value used to simulate the data.

FIG. 7.

Sample axial (left), coronal (top right), and sagittal (bottom right) reconstructions of a simulated FORBILD thorax phantom (monochromatic, 80 keV beam energy) are shown. An elliptical ROI is placed of a region of simulated water showing a reconstructed attenuation value of 0.0183 mm²/g. Shown with a window/level of 0.005/0.0183 mm²/g, which corresponds to a window/level of approximately 272/0 HU. Residual aliasing artifacts caused by high-frequency components in the noise-free data are visible due to the use of a ramp kernel.

4. DISCUSSION

Actual reconstruction times for 512 × 512 × 32 voxel volumes are provided in Tables II and III; however, a user will often wish to reconstruct a larger region of data. Reconstruction times for full volumes will be dependent on many factors; however, approximate times can be determined from the following equation:

$${\displaystyle t_{\text{total}}\approx \left(\frac{\left|Z_{\text{end}}-Z_{\text{start}}\right|}{32\ast S}+1\right)\times t_{32},}$$ (1)

where $\left|Z_{\text{end}}-Z_{\text{start}}\right|$ is the full reconstruction length in mm, S is the collimated slice width in mm, and t₃₂ is the time required to reconstruct a 32 slice volume with slice thicknesses equal to the collimated slice thickness. For example, a 100 mm (z-axis length) reconstruction performed on the GPU from 64 × 0.6 mm projection data would take approximately $\left(100/\left(32\ast 0.6\right)+1\right)\ast 18=112$ s, or roughly 2 min with a minimum available slice thickness of 0.6 mm. The same reconstruction using 16 × 1.2 mm projection data would take approximately $\left(100/\left(32\ast 1.2\right)+1\right)\ast 17=61$ s, or a little over 1 min; however, the minimum available slice thickness will be 1.2 mm. Reconstruction times are largely independent of the final number of reconstructed slices and reconstructed slice thickness. While Eq. (1) is a good starting point for approximate reconstruction times, users should remember that due to the complexity of the GPU hardware (namely, optimized memory access, caching, block and thread dimension optimization, etc., all of which changes for different scanner geometries and acquisition parameters) reconstruction times will vary.

As expected, CPU reconstruction takes a substantially longer time than GPU reconstruction; between approximately 250 and 350 times longer. The rebinning and filtering times in both the CPU and GPU cases reflect the relative complexity of rebinning the different flying focal spot configurations; however, it is also important to note the larger number of rows in the projection data in the cases where the Z flying focal spot is active also increases the rebinning and filtering times. In both the CPU and GPU reconstructions, backprojection times for the cases where collimation is 16 × 1.2 mm (“No FFS” and “Phi FFS”) are approximately 40% longer than the cases where the collimation is 64 × 0.6 mm. This is due to the greater number of projections required to reconstruct the requested volume (see Table I).

The authors would also like to highlight that despite advanced computing hardware being used for development and testing in this work, lower-cost personal computers have been tested and achieved the same reconstruction speeds. Modern GPUs capable of taking full advantage of FreeCT_wFBP’s parallelization can also be added to most desktop computer systems. More information on GPU hardware, GPUs known to work with FreeCT_wFBP, and performance results can be found in Ref. 20.

The effects of Phi and Z flying focal spot usage on spatial resolution and windmill artifacts, respectively, have been demonstrated. Reconstructions utilizing the Phi flying focal spot displayed improved spatial and usage of the Z flying focal spot lead to fewer windmill artifacts around high contrast objects. This qualitatively agrees with the effects of flying focal spot reconstruction observed in Refs. ²⁷ and ²⁸.

To provide an initial verification that the software was yielding acceptable results, reconstructions of the ACR phantom were performed and analyzed. These reconstructions (Figs. 2–4) were performed using the smooth and medium reconstruction kernels and met or exceeded all of the ACR accreditation standards (Tables IV–VI). The CNR of the sharp/ramp kernel did not pass the adult abdomen standard (>1.0); however, ramp kernels are not used clinically due to the fact that they over-enhance high-frequency noise. The sharp/ramp kernel met all other ACR accreditation standards and provided the highest spatial resolution. Using a reconstruction of a simulated scan (80 keV, monochromatic beam) of a FORBILD thorax phantom (Fig. 7), it was shown that the software reconstructs accurate attenuation values. Therefore, while FreeCT_wFBP may not represent the exact reconstruction algorithms employed in clinical scanners, and ACR-acceptable performance, and accurate reconstruction of physical attenuation values in a known phantom indicate its readiness for use in scientific research, such as Ref. 16 where the software was used to perform 10 000 volumetric reconstructions to assess lesion detectability in lung screening scans.

5. CONCLUSIONS

A software package dedicated to reconstructing helical, third-generation CT data using weighted filtered backprojection has been described and tested. Many free and open source CT reconstruction packages exist; however, none exist that are dedicated to reconstructing modern, third generation, helical, diagnostic CT. FreeCT_wFBP not only offers software dedicated diagnostic CT reconstruction but does so in a highly flexible and configurable package capable of handling complex imaging setups including detector offsets, flying focal spots, and multiple scanner geometries. While this package may not represent the exact reconstruction algorithms employed by clinical CT scanners, an initial assessment demonstrated that FreeCT_wFBP can provide acceptable performance on the ACR phantom as well as accurate reconstruction of attenuation values. FreeCT_wFBP’s GPU implementation allows for fast reconstruction of clinical CT data and is well suited to large-scale explorations of reconstruction parameter space. FreeCT_wFBP’s CPU implementation makes the software capable of running on almost any modern computing hardware (albeit at substantially reduced speed) and provides a more intuitive entry point for a user hoping to understand the code. Since both the CPU and GPU versions are command line based and configured through parameter files, FreeCT_wFBP can easily be automated (e.g., via Bash, Python, and matlab) to perform large numbers of reconstructions without the need for user intervention or extensive access to clinical scanners.

At release, FreeCT_wFBP is intended for use on Linux systems. While there are no definitive plans to port the software to Windows or Mac OS at the time of writing, FreeCT_wFBP’s simple, low-dependency design should make porting relatively straightforward. Mac OS’s Unix underpinnings and tools such as MinGW for Windows should provide any POSIX-type dependencies, and CUDA and FFTW are available on all platforms. Potential users are also reminded that Linux distributions are freely available and simple to dual-boot or boot from an external USB or CD drive on which FreeCT_wFPB could be installed. For ease of use with FreeCT_wFBP, the authors recommend the distribution Ubuntu, under which FreeCT_wFBP was developed and an automated install script has been developed; however, other distributions should work as well (e.g., Debian, Fedora, Arch Linux).

More information, including documentation, detailed licensing, and source code, can be found via FreeCT_wFBP’s website.²⁰ The website also hosts contact information for bug reporting, a list of any known bugs, as well as a list of planned updates, and version history. Finally, through the website all of the raw data, parameter files, and scanner files necessary to reproduce the testing done in this publication are available for download.