A PEDIATRIC AIRWAY ATLAS AND ITS APPLICATION IN SUBGLOTTIC STENOSIS

Abstract

Young children with upper airway problems are at risk for hypoxia, respiratory insufficiency and long term morbidity. Computational models and quantitative analysis would reveal airway growth patterns and benefit clinical care. To capture expected growth patterns we propose a method to build a pediatric airway atlas as a function of age. The atlas is based on a simplified airway model in combination with kernel regression. We show experimental results on children with subglottic stenosis to demonstrate that our method is able to track and measure the stenosis in pediatric airways.

1. INTRODUCTION

Abnormalities of the upper airway in infants and children may lead to life threatening respiratory difficulties, poor growth, delay in speech development and long term morbidity. In these airway disorders, therapy is typically directed by the clinician’s experience and preference, rather than based on normalized physiologic or anatomic metrics. Methods of evaluating and determining optimal management for upper airway anomalies would be of tremendous benefit for improved clinical care and outcomes [1].

To track and measure these anomalies, a pediatric airway atlas built from normal subjects is needed as a reference. Such an atlas would generally provide a domain for understanding airway growth patterns; it could also be customized to specific patients to capture airway stenoses. We propose a method to construct a pediatric airway atlas based on normal subjects. This method makes use of a simplified airway model and allows age-adapted atlas computations through kernel regression combined with the computation of weighted percentiles. The result is typically straightforward for physician interpretation.

The first challenge for building a pediatric airway atlas is to find the correspondence among various airways. Our work is based on computed tomography (CT) images of the upper airway. Normal control subjects are scanned for a variety of non-airway related reasons. Therefore the subject positioning is variable and so is the positioning of the airway. This makes airway comparisons between subjects challenging. Furthermore, subjects are of varying ages and therefore at different stages of growth. The second challenge comes from the limited number of datasets while the airway geometry is high dimensional. For such high dimension, low sample size data dimension reduction is necessary to allow classical data analysis. Therefore, we use a simplified airway model to convert a 3D airway geometry into a 1D representative curve, a function of airway cross-sectional area over the length of the airway, similar to the image processing in [2, 3].

Based on a group of extracted curves from normal subjects we apply kernel smoothing [4] to overcome the size limitation of our current dataset and smoothly regress weighted percentiles of airway size as a function of age. They can also be regressed with respect to other variables, such as weight or body mass index. We build a subject-age-specific airway atlas and demonstrate its application to the analysis of patients with subglottic stenosis (SGS), a very specific, commonly encountered and high risk anomaly in pediatric upper airways [1].

2. SIMPLIFIED AIRWAY MODEL

Our simplified airway model includes three components: airway segmentation from a CT image, airway representation with a centerline and cross sections, and feature extractions from the simplified structure for further analysis.

2.1. Airway segmentation

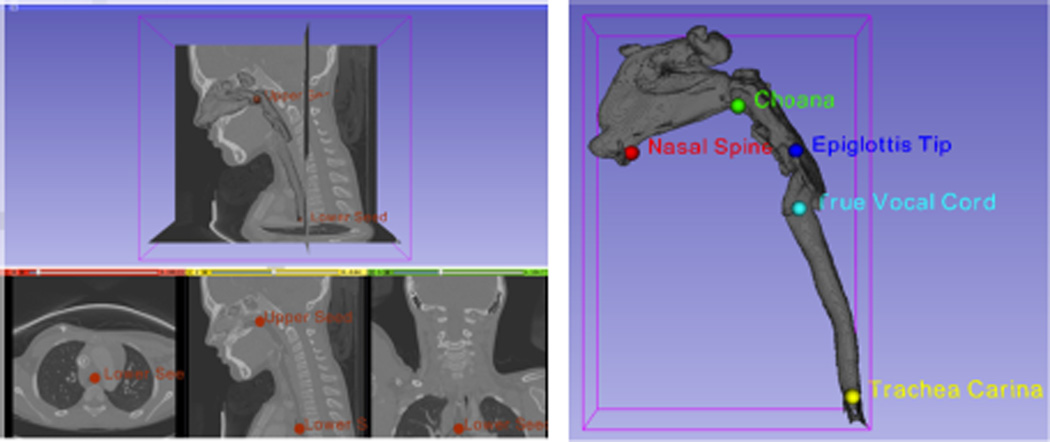
We segment the airway from CT images using Otsu-thresholding and two manually chosen seeds that bracket the upper airway. Fig. 1 illustrates the result of our airway segmentation which is integrated into Slicer 3D.

Fig. 1.

Our automatic airway segmentation (left) and an airway geometry with five landmarks (right).

2.2. Centerline and cross sections

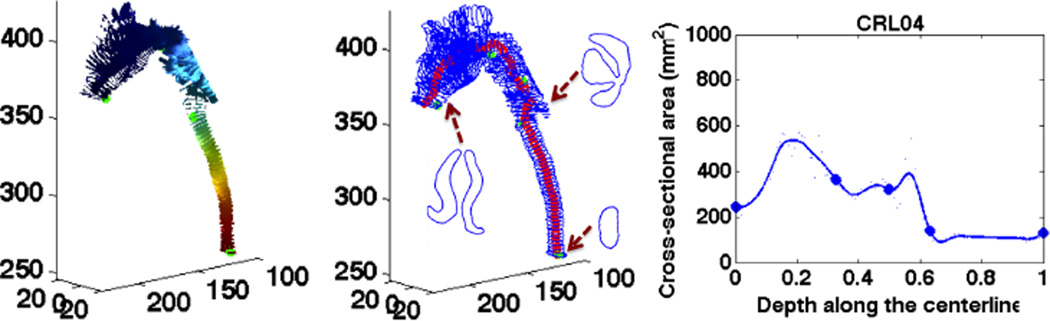
The upper airway, like any tube-like structures, can be approximated by a centerline with cross sections. The centerline is inferred based on the heat distribution along the airway flow that is solved by a Laplace equation. As shown in Fig. 2, we extract iso-surfaces from the Laplace’s solution and make the centerline go through the centers of the iso-surfaces. Cross sections are cut from the airway geometry using planes that are orthogonal to the tangent of the centerline.

Fig. 2.

The iso-surfaces (left), the centerline and cross sections (middle), and the 1D curve (right) for a control subject.

2.3. Feature extraction

In clinical diagnosis, subglottic stenosis is usually graded by measuring the diameter of the lumen [5]. Similarly, we take the cross-sectional area as the airway’s main feature. For each point on the centerline, it has a distance x from the nostrils which is normalized to 1 over the length of the airway, and a cross-sectional area y. Our 1D function for airway geometry is the curve c(x) that smoothly passes through all these points, (x, y), as shown in the right image of Fig. 2.

3. PEDIATRIC AIRWAY ATLAS

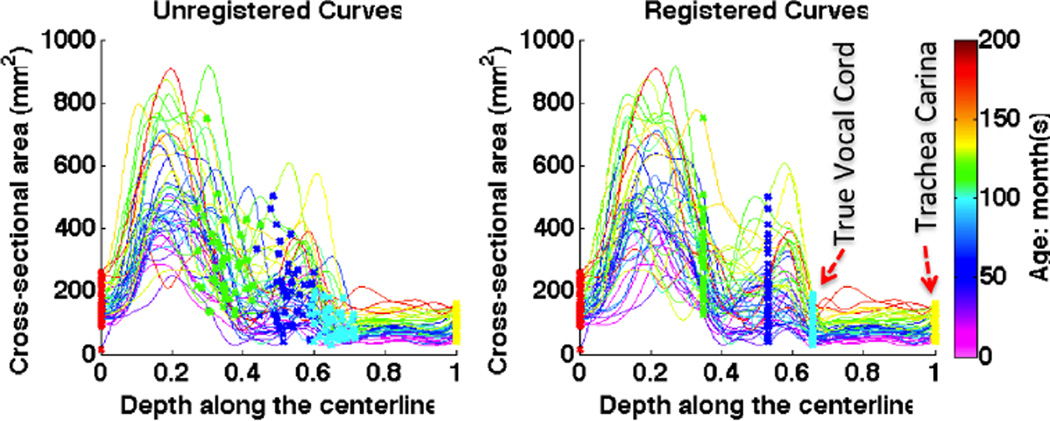
To analyze the airway of a patient with subglottic stenosis, a customized atlas from normal airways is useful for comparison. Fig. 3 shows a population of curves that are extracted from 44 normal subjects using the simplified airway model. To build the pediatric airway atlas based on these curves, the first step is to find the point correspondence for them.

Fig. 3.

The unregistered (left) and registered (right) curves.

3.1. Curve registration

We align curves based on five key anatomic landmarks: nasal spine, choana, epiglottis tip, true vocal cord (TVC) and trachea carina, marked in Fig. 1. For each landmark j, there is a physical position x_j, projected from its 3D coordinate onto the centerline, and a mean position x̄_j of that landmark on all cases. The landmark-based curve registration [6] is to estimate a warping function h_i for each curve c_i, which is strictly monotonic and smoothly passes through these five points (x̄_j, x_j). With the constructed warping functions, curves can be transformed with $c_i^{*}(x)=c_i[h_i(x)]$, shown in Fig. 3.

3.2. Principle component analysis (PCA)

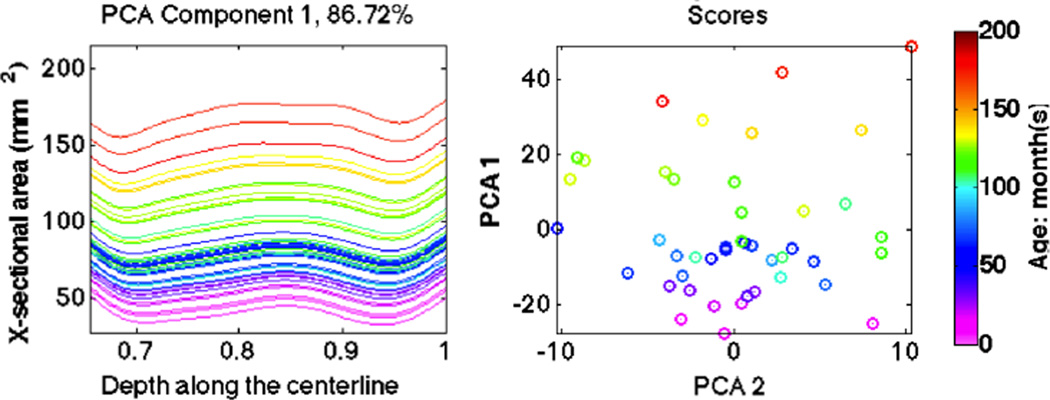
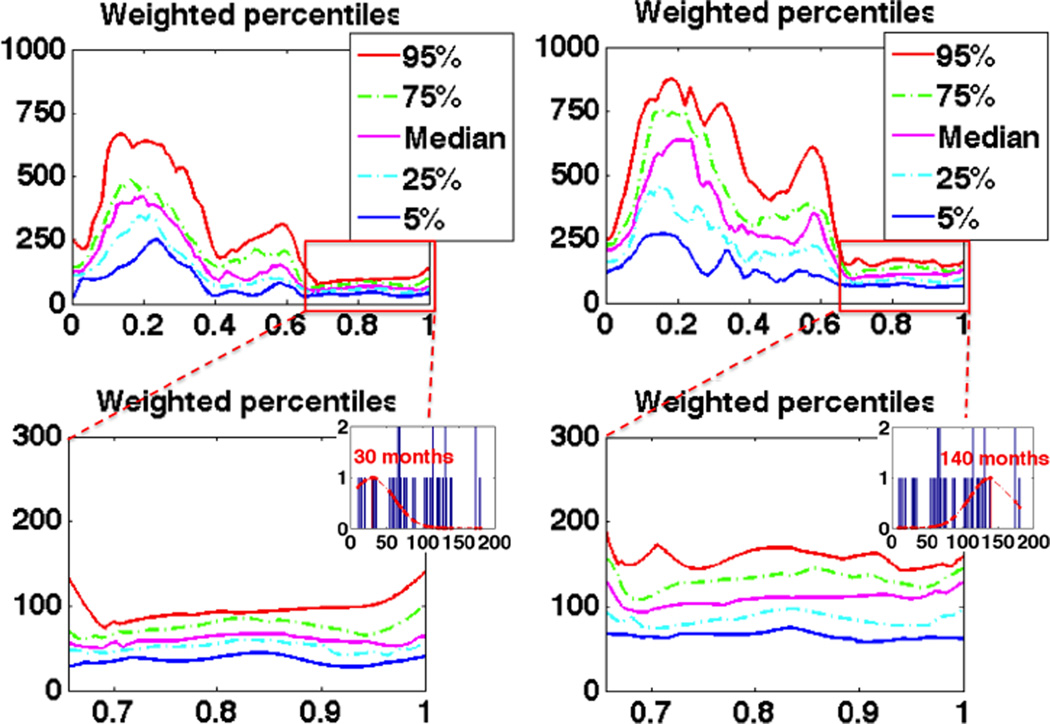
To explore population variations of the registered curves, we apply PCA to display modes of variation that are strongly represented in the data. Since subglottic stenoses occur within the subregion from TVC to trachea carina, we focus our analysis on this part of the curves. The first component of PCA shown in Fig. 4 has 86.72% variance and is dominant compared with the 6.36% variance for the second one. Furthermore, curves move up when children grow up, which means they capture the relation of increasing airway size with age. Therefore, it makes sense to build an airway atlas based on patient age.

Fig. 4.

The first principle component of PCA on curves between TVC and trachea carina. Colors represent age, which is clearly a predictor of airway size.

3.3. Weighted percentiles

Due to the limited number of datasets available to us and our goal of building an atlas over time, we propose the weighted percentile based on kernel regression [4] to generate a continuous and smooth atlas as a function of age, as [7] for images.

For a specified age ā in months, we calculate the weight for each curve c_i based on the Gaussian function:

$$w_i(a_i;\sigma ,\overline{a})=e^{-{((a_i-\overline{a})}^2/2{\sigma }^2}$$ (1)

where a_i is the age in months for curve i, and σ is set to 30 months in all the experiments. The sum of the weights is normalized to 1 by w_i = w_i/ ∑_i w_i.

The median curve is composed by point-wise weighted medians of cross-sectional areas from all curves, that is, the point on the median curve at the depth x_k is defined by

$$c_{i^{*}}(x_k)=\underset{i=1:n}{\text{argmin}}\sum _{j=1:n}{w}_j|c_i(x_k)-c_j(x_k)|$$ (2)

where i, j are the curve indices, n is the number of the curves, and i* is the index for the curve minimizing the weighted median criterion (2).

To calculate the curve at the percentile q, we first sort the cross-sectional areas of all curves at depth x_k in ascending order, resulting in y′_1:n(x_k) and weights w′ in the new order. The percentile q is defined by

$$c^q(x_k)=c_p(x_k),\mathit{\text{ if}}\sum _{s=1:p}{w}_s^{\prime }\le q\&\sum _{s=p+1:n}{w}_s^{\prime }\ge q$$ (3)

Five commonly used percentiles are chosen to build the pediatric airway atlas: 5%, 25%, median, 75% and 95%, and two atlases at 30 months and 140 months respectively are shown in Fig. 5. The change in percentile along the increasing age is consistent with the PCA result and reveals the growth patterns of pediatric airways.

Fig. 5.

Pediatric airway atlas at 30 (left) and 140 (right) months represented by weighted percentiles, for which x-axis is the depth along the centerline and y-axis is the crosssectional area (mm²).

4. EXPERIMENTS

We built the age-based atlas with 44 CT images of normal subjects (27 boys and 17 girls) aging from several months to 15 years old, and tested our method with CT scans from 11 SGS subjects (6 boys and 5 girls) before and/or after surgery.

4.1. Comparison between pre and post surgery

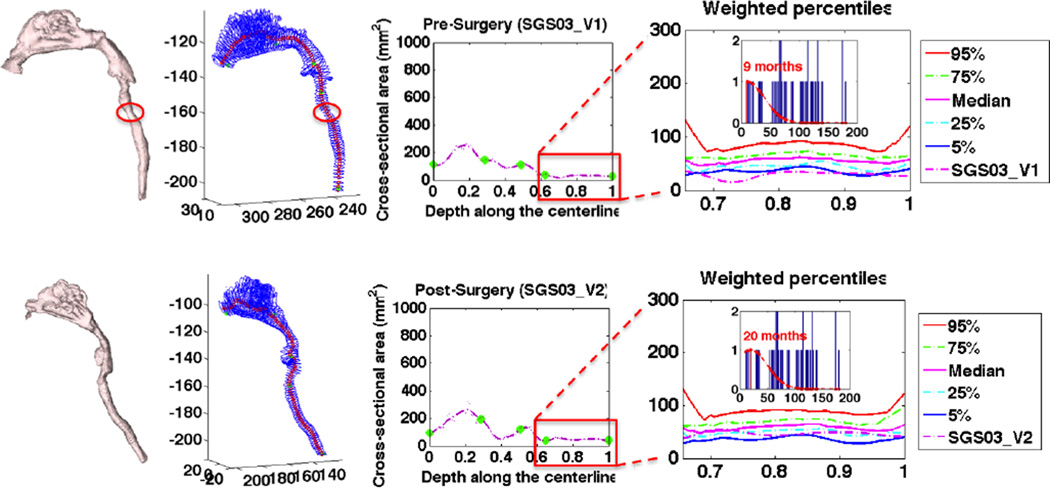
For each SGS case, we first represented it with a curve generated by the simplified airway model, then registered the curve to the population of control curves, and finally built a subject-specific airway atlas at the age of this patient. Fig. 6 shows the simplified model and the airway atlas for SGS03’s pre and post surgery. As we can see, before surgery there is an obvious stenosis in the simplified model and this region is below the 5th percentile. After corrective surgery, the curve moves up with respect to the atlas, correlating with a successful surgery.

Fig. 6.

Comparison of SGS03 between pre and post surgery.

4.2. Quantitative measurements

The Myer-Cotton system [5] is one of the most popular grading systems in clinical diagnosis for subglottic stenosis. It is performed using endotracheal tubes and describes the stenosis based on the percent relative reduction in cross-sectional area of the subglottis. Our measurements were inspired by this grading system. We took the position that had the minimal cross-sectional area between TVC and trachea carina as subglottic stenosis and calculated its percent relative reduction in airway cross-sectional area with respect to the atlas.

In Tab. 1, we measured the minimal cross-sectional area for the stenosis and calculated its percent relative reduction with respect to the mean value of the airway cross-sectional areas from TVC to trachea carina at the 5th percentile, the median, and the 95th percentile respectively. These SGS subjects belong to two groups, pre and post surgery. As we can see from the scores of these measurements, the pre-surgery group had more constricted airways (higher percentage values) in comparison to the post-surgery group. We performed a t-test between the pre and the post surgery measurements and obtained highly statistically significant results (p-value < 1e–3) indicating that our pediatric airway atlas could measure a difference in these two populations with respect to airway cross-sectional areas and that the surgery had on average a beneficial effect.

Table 1.

Measurement results on curves between TVC and Trachea Carina for subglottic stenosis.

Patient Id	Age in months	Gender	Surgery	Minimal area (mm2)	Area reduction (%)* w.r.t.
					5%	median	95%
SGS03_V1	9	M	pre	15.3	56.8	72.1	82.3
SGS07	6	M	pre	19.5	44.8	64.2	77.2
SGS11	10	F	pre	19.8	43.9	63.9	77.1
SGS12	6.5	M	pre	23.2	34.4	57.5	73.0
SGS13	102	M	pre	43.2	25.7	48.1	68.5
SGS03_V2	20	M	post	42.8	0.0	24.8	52.3
SGS05	39	M	post	50.7	0.0	20.3	48.2
SGS06	122	F	post	59.9	3.5	35.7	58.5
SGS08	106	F	post	75.8	0.0	10.5	45.0
SGS09	122	M	post	47.4	23.6	49.1	67.1
SGS10	94	F	post	54.5	4.1	31.7	59.1
SGS14	92	F	post	54.8	0.0	30.8	56.5

Area reduction (%)*: the percent relative reduction in the airway cross-sectional area.

5. CONCLUSIONS AND FUTURE WORK

In this paper, we proposed a simplified airway model and the weighted percentiles of the cross-sectional area to build a pediatric airway atlas as a function of age. Using a customized atlas for SGS patients, the experimental results showed that our method could capture and measure the stenosis in the pediatric airway. Due to the limited size of our current dataset for normal subjects, we chose the point-wise weighted percentiles to generate a smooth airway atlas. In future work, once we have a sufficiently large number of normal control subjects, we may use the curves themselves as data objects to build the atlas. Our atlas-building method is general and can be used to regress with respect to other variables than age. In our future work we will also explore using additional features such as subject weight and airway pressure.