Sub-diffuse optical biomarkers characterize localized microstructure and function of cortex and malignant tumor

Abstract

This study uses a sub-diffusive light transport model to analyze fiber-optic measurements of reflectance spectra to recover endogenous tissue biomarkers and to correct raw fluorescence emissions for distortions from background optical properties. Measurements in tissue-simulating phantoms validated accurate recovery of the reduced scattering coefficient [(0.3–3.4 mm⁻¹), error 10%], blood volume fraction [(1–3 vol%), error 7%], and a dimensionless metric of anisotropic scattering, γ, that is sensitive to submillimeter tissue ultrastructure [(1.29–2.06), error 11%]. In vivo sub-diffusive optical data acquired during clinical neurosurgeries characterize differences in microstructure (γ), perfusion (blood volume), and metabolism (PpIX fluorescence) between normal cortex and malignant tumor.

Fiber-optic probe sampling of reflectance and fluorescence in tissue can be used to characterize microscopic aspects of tissue function and structure. Optical measurements of absorption provide insight into vascular physiology, while measurements of scatter provide insight into the composition and orientation of intracellular ultrastructure and the extracellular matrix. These endogenous tissue parameters may offer contrast between tissue types and could become a tool to diagnostically assess pathologies. Additionally, localized reflectance measurements produce estimates of tissue optical properties that correct measurements of fluorescence emissions for absorption and scattering-induced distortions. An important application for localized optical measurements occurs in neurosurgery, which uses tissue optical biomarkers to guide intracranial tumor resection. Optical measurements obtained clinically have reported contrast based on (1) quantitative assessment of aminolevulinic acid-induced protoporphyrin IX (PpIX) fluorescence, which provides contrast between normal cortex and malignant tumor within the surgical field [1], and (2) tissue parameters that describe differences in vascular physiology between normal cortex and malignant tumor in the brain [2]. The current study uses a sub-diffuse reflectance model of light transport to provide a more accurate and complete description of the microscopic optical properties in tissue and, in turn, a more exact estimation of endogenous biomarkers and exogenously induced fluorescence assessed in the brain.

Optical approaches that use small fiber optics to sample reflectance remission in tissue interrogate a localized volume, which reduces averaging of potentially informative tissue heterogeneities. However, quantitative interpretation of optical properties (i.e., reduced scattering, ${\mu }_s^{\prime }$, and absorption, μ_a, coefficients) from reflectance sampled near the source location is complicated by the collection of weakly scattered photons that make the measured intensity sensitive to the directional probability of scattering events, which are defined by the scattering phase function, P(θ). While analytical modeling of the sub-diffuse (SD) signal requires knowledge of the exact form of P(θ) [3], this information is not known a priori in tissue, and existing approaches use empirically derived models that describe anisotropic behavior of backscattered reflectance near the source with the parameter $\gamma =\frac{1-g_2}{1-g_1}$ [4-8], where g₁ and g₂ are the first and second Legendre moments of P(θ) . Alternatively, Kim et al. [9] analyzed reflectance sampled at multiple distances within 1 mm of the source through a constrained formulation of the diffusion approximation (CDT) to the radiative transport equation, which required that (1) a monotonically increasing relationship exists between reflectance intensity and ${\mu }_s^{\prime }$, and (2) a minimum threshold ${\mu }_s^{\prime }$ is sampled for each source-detector separation to minimize sensitivity to P(θ). While the CDT model has been used extensively in the brain [1,2], the approach cannot resolve tissue microstructure that may be characterized by γ. Moreover, previous studies have shown that incorrect assumptions of anistoropic transport can introduce error into estimates of ${\mu }_s^{\prime }$ and μ_a [8]. In this Letter, we develop an SD model of reflectance that is sampled by a fiber-optic probe at multiple submillimeter source-detector separations, validate the approach using tissue-simulating phantoms in comparison with results from CDT, and apply the approach to a pilot clinical dataset obtained during neurosurgery.

A customized Monte Carlo (MC) model characterized the relationship between reflectance intensity sampled by a fiber-optic probe and optical properties contained within the sampled medium. The MC model applied the modified Henyey–Greenstein formulation of the scattering phase function, which was constructed to sample g₁ = [0.75; 0.85; 0.95] and γ = [1.3–1.9] in steps of 0.1. The scattering coefficient was selected to achieve reduced scattering coefficient values in the range of ${\mu }_s^{\prime }$ = (1 – g₁)μ_s = [0.3, 0.5, 1, 3, 5, 10] mm⁻¹, and absorption was characterized over the range μ_a = [0 – 1] mm⁻¹. The model geometry considered source and detector fiber optics, each with an inner diameter of 200 μm and numerical aperture of 0.22, and source-detector separations of 260 and 520 μm. The resulting data generated a 3D look-up table, and upon input of parameters ${\mu }_s^{\prime }$, γ, and μ_a, the Matlab function interpn returned the corresponding reflectance intensity; this represents a modified extension of the work by Hennessy et al. [10] into the SD transport regime.

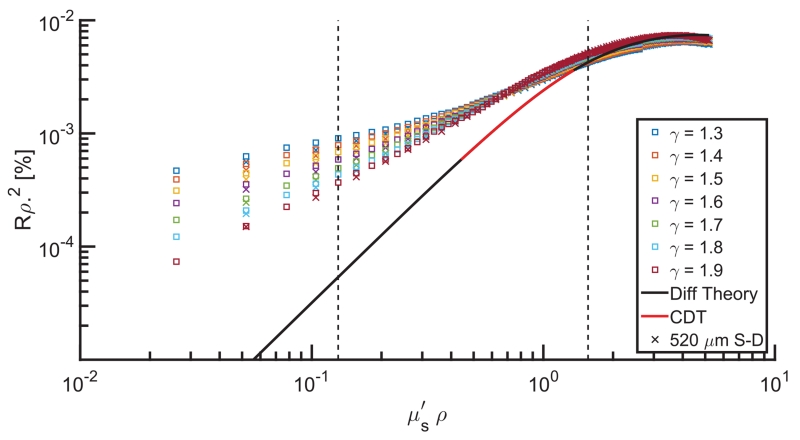
Figure 1 shows dimensionless reflectance, given as the product of reflectance intensity and the square of source-detector distance, ρ, versus dimensionless reduced scattering, given as the product of ${\mu }_s^{\prime }$ and ρ. MC estimates exhibit a γ-specific proportionality between reflectance and scattering, where reflectance is stratified by P(θ) and increases for moderate to low scattering (i.e., ${\mu }_s^{\prime }$ρ < 1) with decreases in γ. Diffusion theory (black line) is uninformed by γ, and estimates show a substantial (and increasing) error associated with decreases in ${\mu }_s^{\prime }$ρ. The CDT model (red line) limits the range of ${\mu }_s^{\prime }$ to a region less sensitive to γ effects but still shows deviation from MC estimates and covers only about half of the biologically relevant ${\mu }_s^{\prime }$ range (dashed lines). These data indicate the profound influence of anisotropic light transport on SD light reflectance—a behavior that cannot be described with a diffusion theory analysis (i.e., CDT).

Fig. 1.

Dimensionless reflectance intensity versus dimensionless reduced scattering as returned by MC estimates of multiple γ values (markers) and as estimated by diffusion theory (black line) and CDT (red line). □ represents data collected 260 μm from the source, and x represents data collected 520 μm from the source. Vertical dashed lines bracket the expected range of ${\mu }_s^{\prime }$ in tissue (0.5–3 mm⁻¹).

Experimental validation was performed using measurements in tissue-simulating optical phantoms. Scattering phantoms were prepared from solutions of polystyrene beads (Bangs Laboratories) with fractal dimensions of D_f = [3.85, 4.35, 4.85] selected to create P(θ) similar to tissue [11] with values of γ(450 nm) = [1.67, 1.51, 1.40] for ${\mu }_s^{\prime }$(450 nm) = [2.74, 3.10, 3.45] mm⁻¹, respectively. Each phantom was diluted with phosphate-buffered saline (PBS) to achieve ratios of [1, 0.75, 0.5, 0.25], resulting in 12 optical phantoms with ${\mu }_s^{\prime }$ = [3.45 – 0.31] mm⁻¹ and γ = [1.67–1.29]. Additionally, a set of nine phantoms were formed using Intralipid as the scattering source, with total lipid volume fraction = [1.25, 1, 0.75]% and whole bovine blood as the background absorber, with blood volume fraction (BVF) = [3, 2, 1]%, yielding ${\mu }_s^{\prime }$ = [2.31 – 0.92] mm⁻¹ and γ = [2.06 – 1.77]. Optical measurements were recorded with a customized hand-held probe [12] having four fiber optics of 200 μm in diameter connected to a spectrophotometer (USB2000+, Ocean Optics), a blue LED (405 nm) source (LedEngin Inc.) with center to center separation of 260 μm and two fibers leading to a white LED light source (LedEngin Inc.) spaced 260 and 520 μm center to center from the detection channel. Reflectance intensity (I), sampled over 450–650 nm, was corrected for dark signal, normalized by integration time, and calibrated by a ratio of the intensity (I_ref) and model estimated reflectance (R_ref) in a phantom with known optical properties, yielding calibrated values in units of (photons/area). The SD model inverted the MC-generated look-up-table values to fit reflectance sampled at both fiber separations at once, returning a coupled estimate of ${\mu }_s^{\prime }$ and γ and an fiber-averaged estimate of μ_a. The CDT model used the analytical expression defined previously [9] to fit reflectance sampled at each fiber separation sequentially and return ${\mu }_s^{\prime }$ and μ_a.

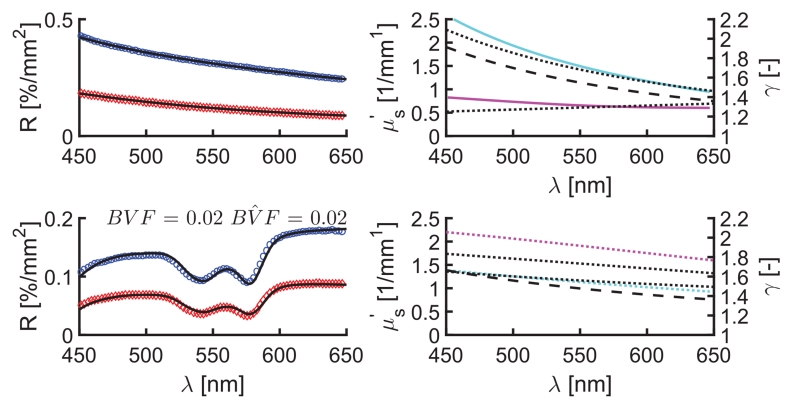
Figure 2 (top) shows representative reflectance spectra, SD model fits, and estimates of ${\mu }_s^{\prime }$ and γ in a polystyrene bead-based phantom. The fitting algorithm estimated ${\mu }_s^{\prime }$(λ) using a power law = a(λ/550)^−b and estimated γ(λ) by assuming a linear function between the wavelength bounds of 450 and 650 nm. To evaluate the sensitivity of reflectance models to changes in P(θ), all phantoms were analyzed using each dilution of the D_f = 4.35 phantom as a calibration. The mean absolute percentage errors in estimated optical parameters across all calibration permutations are listed in Table 1. In aggregate, the polystyrene bead data have increased error in ${\mu }_s^{\prime }$ estimated by CDT (<35%) compared with SD (<10%), with higher errors found in lower scattering phantoms, as expected since measurements made with lower values of ${\mu }_s^{\prime }$ρ exhibit increased sensitivity to the γ spectrum. The CDT model assumes a linear proportionality between R and ${\mu }_s^{\prime }$ that is defined a priori via the calibration; therefore, disparity in the ${\mu }_s^{\prime }$ or γ spectrum between the calibration and the sample introduces error into the CDT estimates. Conversely, the SD model accounts for the specific influence of γ in both calibration and sample, mitigating these distortions. This investigation was extended to phantoms containing background absorption from whole blood, and Fig. 2 (bottom) presents representative fitted reflectance spectra and parameter estimates from an Intralipid-blood phantom. The bottom of Table 1 shows increased accuracy obtained in recovered ${\mu }_s^{\prime }$ and BVF with the SD relative to the CDT model. Furthermore, the SD model also recovers accurate γ, even in the presence of strong background absorption. While SD and CDT estimates of optical parameters showed absolute differences, values were highly correlated with average Pearson product-moment correlation coefficients (r) of 0.89 and 0.92 for ${\mu }_s^{\prime }$ and BVF across all phantoms and calibrations tested, respectively.

Fig. 2.

Representative model fits to sampled reflectance spectra in polystyrene bead (top) and Intralipid (bottom) phantoms. Left panels show reflectance data (circles) and overlapping SD model fits (black lines), and right panels show ${\mu }_s^{\prime }$, and γ spectra. Legend: 260 μm (blue) and 520 μm (red) SD fiber reflectance data, known ${\mu }_s^{\prime }$ (cyan) and γ (magenta), SD (dotted line) and CDT estimates (dashed line).

Table 1. Comparison of SD and CDT Model Estimates of Optical Parameters from Measurements in Polystyrene Bead and Intralipid Optical Phantoms^a.

		Error [%]
Range (450–650 nm)		${\mu }_s^{\prime }$		γ
γ	${\mu }_s^{\prime }$ [mm−1]	CDT	SD
Df = 4.85	3.45–1.24	29 ± 24	7 ± 5	6 ± 3
r = 1.40 – 1.29	2.59–0.93	22 ± 20	7 ± 6	6 ± 2
	1.73–0.62	24 ± 16	5 ± 4	9 ± 6
	0.86–0.31	57 ± 44	10 ± 9	11 ± 6
Df = 4.35	3.10–1.24	26 ± 24	6 ± 7	7 ± 5
γ = 1.51 – 1.42	2.32–0.93	21 ± 20	6 ± 6	4 ± 3
	1.55–0.62	25 ± 18	7 ± 5	5 ± 4
	0.78–0.31	60 ± 47	20 ± 16	8 ± 6
Df = 3.85	2.74–1.24	25 ± 22	5 ± 4	12 ± 7
γ = 1.67 – 1.58	1.37–0.62	27 ± 18	7 ± 5	5 ± 4
	0.69–0.31	60 ± 46	16 ± 14	4 ± 3
Intralipid	2.31–0.92	24 ± 3	9 ± 9	11 ± 3
γ = 2.06 – 1.77	BVF	27 ± 4	7 ± 4

^aError is phantom-specific and averaged across multiple calibrations using the D_f = 4.35 dilution series.

This study also analyzed in vivo data acquired in a clinical trial that is investigating the use of optical biomarkers, including PpIX, to provide surgical guidance during intracranial tumor resection. The Institutional Review Board at Dartmouth–Hitchcock Medical Center approved the protocol, and all patients participated under informed consent. This Letter reports optical data acquired from five patients, each sampled with two measurements on normal cortex and two measurements on tumor as identified by the operating surgeon (DWR). Biopsies of tumor tissue were taken during surgery to confirm tumor type and grade based on the World Health Organization (WHO) grading scale. Of the patients sampled, one had a meningiothelial meningioma WHO grade I, one had a diffuse astrocytoma WHO grade II, one had an oligo-astrocytoma WHO grade II, one had anaplastic astrocytoma WHO grade III, and one had anaplastic oligo-astrocytoma WHO grade III. The pilot set of 20 spectra were analyzed using both SD and CDT models, and estimated parameters were compared between groups of normal cortex and malignant tumor using the Kruskal–Wallis statistical test.

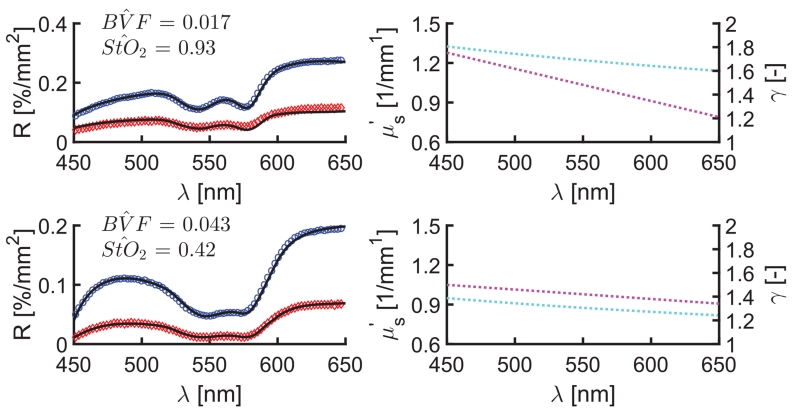
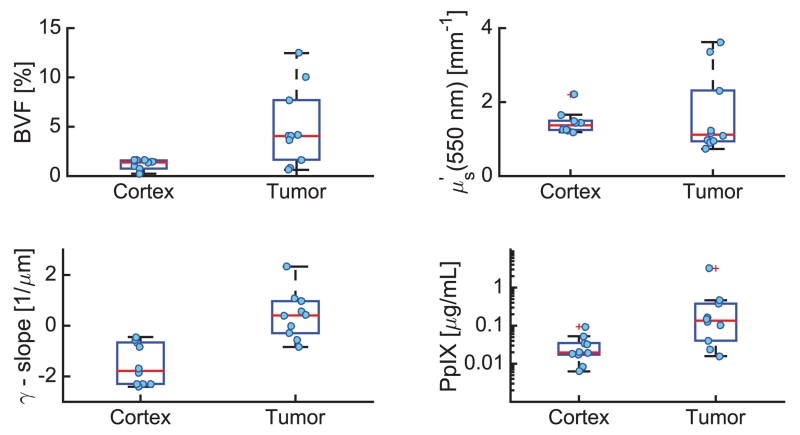
Figure 3 shows representative reflectance spectra and SD model fits, as well as the corresponding optical parameter estimates for normal cortex (Fig. 3, top) and malignant tumor (Fig. 3, bottom), respectively. Figure 4 presents the comparison of tissue optical biomarkers in normal cortex and tumor for all five patients. Differences in vascular physiology are evident in the absorption-based spectral signatures for normal cortex and tumor locations in Fig. 3. Specifically, increased BVF was observed in tumor tissue in all patients (p < 0.01), which is indicative of increased angiogenesis that is classically found in tumor tissue [2]. Inspection of ${\mu }_s^{\prime }$(550 nm) data shows substantial intermeasurement variability in tumor, which is consistent with more heterogeneous tissue composition of dys-regulated tumor tissue. With such biological variability, no significant difference in ${\mu }_s^{\prime }$ (p < 0.17) was found. Interestingly, inspection of γ estimates show a significant decrease in the wavelength-dependent slope of γ in tumor compared with normal tissue (p < 0.001). A decrease in γ is associated with an increased number of small particles that effectively act as Rayleigh scatterers, suggesting that spectroscopic analysis of sub-diffusive scatter may reveal endogenous contrast associated with tissue microstructure. The SD model also yields different tissue biomarkers in vivo compared with CDT, with deviations in BVF of < 29% [range (−119%–40%)] and in ${\mu }_s^{\prime }$ (550 nm) of <15% [range (−28%–43%)].

Fig. 3.

Representative reflectance data (circles), SD model fits (black lines), and estimated ${\mu }_s^{\prime }$ and γ spectra from in vivo cortex (top) and tumor (bottom) measurements. Legend: 260 μm (blue) and 520 μm (red) SD fiber reflectance data, and estimates of ${\mu }_s^{\prime }$ (cyan) and γ (magenta).

Fig. 4.

Comparison of tissue optical biomarkers estimated in normal cortex and malignant tumor, including BVF (top, left), ${\mu }_s^{\prime }$(550 nm) (top, right), γ slope (bottom, left), and PpIX concentration (bottom, right).

In vivo optical measurements also collected PpIX fluorescence emissions, revealing significantly elevated PpIX concentrations in tumor compared with normal tissue (p < 0.0065). While this contrast is representative of metabolic-based selectivity of the exogenously induced endogenous fluorescence marker, inspection of the raw fluorescence shows no difference between normal and tumor tissue (p < 0.94) due to attenuation by background optical properties. Recovery of quantitative fluorescence exploits the coupled interpretation of localized reflectance and fluorescence [12] where ${\mu }_s^{\prime }$ and μ_a are obtained from reflectance analysis to inform a model-based correction which mitigates absorption and scattering based distortions of the raw fluorescence emissions. However, fluorescence is insensitive to anisotropic aspects of scattering [13], and the correction must be informed by optical properties that are not confounded by P(θ) effects. Comparisons of the quantitative fluorescence recovered using optical properties returned by SD and CDT models were highly correlated (r = 0.99), but substantially different in values with a mean absolute difference of <28% [range (−69 to 58)]. Additionally, the majority of the in vivo data were composed of measurements from patients with low-grade tumors, which are known to have little visible fluorescence, further emphasizing the importance of quantitative techniques.

The data presented in this Letter show important advantages to analyzing localized reflectance using an SD model, including improved estimates of BVF, novel insight into scatter-based assessment of tissue microstructure, and a fluorescence correction that is informed by more-accurate optical properties. This study is the first to report SD optical biomarkers sampled in normal cortex and malignant tumor in the brain.