Appearance Normalization of Histology Slides

Abstract

This paper presents a method for automatic color and intensity normalization of digitized histology slides stained with two different agents. In comparison to previous approaches, prior information on the stain vectors is used in the plane estimation process, resulting in improved stability of the estimates. Due to the prevalence of hematoxylin and eosin staining for histology slides, the proposed method has significant practical utility. In particular, it can be used as a first step to standardize appearance across slides and is effective at countering effects due to differing stain amounts and protocols and counteracting slide fading. The approach is validated against non-prior plane-fitting using synthetic experiments and 13 real datasets. Results of application of the method to adjustment of faded slides are given, and the effectiveness of the method in aiding statistical classification is shown.

1. Introduction

Stains are often used to highlight distinct structures in microscopy slides of tissue samples. Frequently two stains, such as eosin and hematoxylin, are applied for purposes such as discriminating cell nuclei and cytoplasm. Standardized staining protocols help to reduce variations in staining results, however, various factors can affect stain color and intensity in practice. For example, stains can fade over time, stain colors may differ slightly, or different imaging equipment may be used.

Standard stains absorb light. The concentrations of the various stains on a sample will determine its appearance when illuminated under a microscope, with higher concentrations appearing darker. The amount of light absorbed by a stain is wavelength dependent, and each stain can be characterized by its absorption coefficients. These coefficients form a vector (the stain vector) of dimension equal to the number of wavelengths in the imaging sensor (three for a standard RGB camera). Given the stain vectors, an image can be decomposed into components of each idividual stain via color deconvolution (Ruifrok and Johnston, 2001). These components can be adjusted and recomposed into an image which appears to have different amounts of each stain than before. This paper proposes a method for automatic stain vector estimation and slide appearance normalization (both color and intensity). This can improve quality both for viewing the slides as well as quantitative analysis of the slides.

Previous approaches to extract stain vectors include manual region of interest definition, methods relying on non-negative matrix factorizations (Rabinovich et al., 2003), and working in the optical density domain, including plane fitting (Macenko et al., 2009) and learning perimage vectors from manually segmented regions Magee et al. (2009).

Stain vector estimation is not the only approach used for normalization of histology slides. Reinhard et al. (2001) transform images into the Lab colorspace and normalize the mean and standard deviation of each channel of an image to a target image. Magee et al. (2009) propose an extension to this method which first segments the pixels into multiple classes based on color and then normalizes each class separately. This method uses a prior obtained by computing the mean of each pixel class over a set of manually segmented images. Another common approach is equalization of color histograms. Kothari et al. (2011) use a modification of this approach which normalizes using rank functions of unique colors rather than all colors present in an image.

Methods which do not use prior information often have trouble dealing with images which do not fit the assumptions made by their models. Histogram-based methods assume that two images are similar in the amount of stain present. Stain vector estimation via plane-fitting becomes unstable in the cases where the number of pixels with each stain are highly unbalanced. The method of Magee et al. (2009) which does include prior information on stain vectors requires per-image manual segmentations of each stain.

This paper addresses these issues by introducing prior information to the plane-fitting algorithm of Macenko et al. (2009). This is an extension of the work by Niethammer et al. (2010) with additional applications and validation. Novel contributions include: (1) a rigorous theory for the color model used, (2) the introduction of prior information for the stain vector taking into account varying amounts of stain (such as that encountered in the case of sparsely distributed nuclei on large amounts of stained background tissue), (3) an alternating optimization method and its connection to a sub-problem from trust region optimization, (4) a novel twist on Otsu thresholding (Otsu, 1975) which also includes prior information, and (5) quantitative validation on synthetic and real datasets.

The rest of this paper is organized as follows: section 2 gives background information on the stain vector model used, section 3 describes the basic plane optimization problem, section 4 adds prior information to this optimization, section 5 describes the prior-based clustering method, section 6 describes the digital restaining procedure, section 7 gives results from a variety of experiments, section 8 describes several applications of this method, and section 9 gives conclusions and discussion.

2. Stain Vector Model

According to the Beer-Lambert law, the transmission of light through a material can be modeled as

$$I=I_0{e}^{-\alpha cx},$$ (1)

where I₀ is the intensity of the incident light, I is the intensity of the light after passing through the medium, α is the absorption coefficient, c the concentration of the absorbing substance, and x the distance traveled through the medium. The optical density (OD) or absorbance is

$$OD=\alpha cx=-\text{log }\left(\frac{I}{I_0}\right).$$ (2)

We assume that α and x are constant for a specimen and a given stain, but that a stain’s concentration c may change both locally and between slides. For a multispectral image, such as an RGB image captured with three wavelengths, equation 1 becomes vector-valued

$$\mathit{I}={\mathit{I}}_{\mathbf{0}}\odot e^{-\mathit{\alpha }cx},$$ (3)

resulting in an OD vector

$$\mathit{O}\mathit{D}=-\text{log}(\mathit{I}\oslash {\mathit{I}}_0)=\mathit{\alpha }cx.$$ (4)

Here, the absorption coefficients α_i are color dependent, and ⊙ and ⊘ represent element-wise vector multiplication and division. Note that dark intensities will correspond to large optical density values and bright image parts where no absorption occured will have small values. Each stain has a characteristic vector α of absorption coefficients. Given a traced distance x the optical density OD is linearly related to the absorption coefficient, with a proportionality constant given by the stain concentration, i.e., OD = αxc. Applying the vector-valued Beer-Lambert law to the case of a two-stain color image, such as one stained by eosin and hematoxylin, yields

$$\mathit{I}={\mathit{I}}_{\mathbf{0}}\odot e^{-({\mathit{\alpha }}_1{c}_1{x}_1+{\mathit{\alpha }}_2{c}_2{x}_2)}$$ (5)

where subscripts denote values for the two distinct stains. The optical density can be computed as

$$-\text{log}(\mathit{I}\oslash {\mathit{I}}_0)={\mathit{\alpha }}_1{c}_1{x}_1+{\mathit{\alpha }}_2{c}_2{x}_2.$$ (6)

This shows that, for a given illumination I₀, the obtainable intensity vectors I lie in the plane spanned by the absorption coefficients, or stain vectors, α_i. Since cⁱ ≥ 0, xⁱ ≥ 0, and the αⁱ are linearly independent, any color which can be represented by the imaging model must lie in the convex cone

$$𝒞=\{\mathit{x}|\mathit{x}=q_1{\alpha }_1+q_2{\alpha }_2,q_1,q_2\ge 0\}$$ (7)

If all possible optical density vectors are normalized, all points must lie inside

$${𝒞}_N=\{\tilde{\mathit{x}}|\tilde{\mathit{x}}=\frac{\mathit{x}}{\Vert \mathit{x}\Vert },\mathit{x}\in \stackrel{\circ }{𝒞}\},$$ (8)

where 𝒞̊ denotes 𝒞 \ 0. Geometrically, 𝒞_N = 𝒮² ∩ 𝒞, the intersection of 𝒞 and the three-dimensional unit sphere, which is the sector of a great circle.

3. Plane Fitting

In the previous section, we described a method for transforming an RGB image into optical density space. As shown in figure 1, when an image stained with two stains is transformed into OD space, the image colors lie in the convex cone defined by the two stain vectors. The following sections develop a method for estimating both this plane and the associated stain vectors.

Figure 1.

Distributions of image colors in RGB space (left) and OD space (right). The colors lie on a curved surface in RGB space yet are planar when transformed into OD space.

By definition, the convex cone spanned by the stain vectors is a subset of a plane ℘ passing through the origin

$$\wp =\{\mathit{x}:{\mathit{n}}^T\mathit{x}=0\},$$ (9)

where n is the plane’s unit normal. The signed distance of any point to the plane can be computed as

$$d(\mathit{x},\wp )={\mathit{n}}^T\mathit{x}.$$

The plane which minimizes the sum of squared distances to all given optical density vectors is given by minimizing

$$E(\mathit{n})=\sum _i{({\mathit{n}}^T{\mathit{x}}_i)}^2={\mathit{n}}^T\left(\sum _i{\mathit{x}}_i{\mathit{x}}_i^T\right)\mathit{n}={\mathit{n}}^{T}S\mathit{n},\mathrm{s}.\mathrm{t}.\Vert \mathit{n}\Vert =1.,$$ (10)

Since S is positive semi-definite, n is the eigenvector of the smallest eigenvalue of S. This unconstrained optimization was proposed in Macenko et al. (2009).

The results of this estimation are only reliable when a sufficient amount of both stains is present in the sample. When this assumption does not hold, additional constraints are needed. Adding prior information helps to ensure the estimator performs well. While introducing prior information gives up the convenience of a closed-form solution, it has clear benefits for increasing the stability of the plane estimation (see section 7). We use an EM-style alternating optimization approach with efficient solutions for both stages.

4. Plane Prior Information

To introduce prior information, we penalize the deviation from a given reference plane $({\mathit{n}}_p^T\mathit{x}=0)$ through a reference normal n_p. The energy to be minimized now becomes

$$E(\mathit{n})=(\frac{1}{2{\sigma }^2}\sum _{i=1}^n{d}^2({\mathit{x}}_i,\wp ))+\frac{1}{2{\sigma }_0^2}{\Vert \mathit{n}-{\mathit{n}}_p\Vert }^2,\mathrm{s}.\mathrm{t}.\Vert \mathit{n}\Vert =1,$$ (11)

where σ is the standard deviation for the measured points (assumed to be independent) and σ₀ is the standard deviation of the prior (assumed to be Gaussian).

Equation 11 shows how, as n → ∞, the effect of the prior shrinks. The distribution of points will only be approximately planar when there are a large number of measurements for both stains. This distribution cannot be guaranteed, especially if working with smaller sub-regions of a stained slide which may contain low amounts of nuclei and high amounts of stained background. In this case, without the stabilizing effect of the prior information, the plane that is fit will be heavily biased towards the cluster with a large number of points and will be a poor fit to the actual stains present. This problem can be overcome by weighting the data points assigned to a stain vector.

Assuming the partitioning of these data points into two clusters (one for each stain) is known, the minimization energy (up to constants) is given by

$$E(\mathit{n})=\sum _{j=1}^2(\sum _{i\in P_j}^{n_j}\frac{d^2({\mathit{x}}_i,\wp )}{2{\sigma }^2}+\frac{\alpha }{2{\sigma }_0^2}{\Vert \mathit{n}-{\mathit{n}}_p\Vert }^2)w_j,$$ (12)

where the w_i are the weights, P_i the partitions, and n_i the number of points in each partition. The partitioning method used is described in section 5.

The weights are chosen based on several conditions. The weights must take into account whether there are a sufficient number of data points in each cluster, and should simplify back to equation 11 if the clusters are of equal size. The following conditions are placed upon the weights for these properties to hold:

$$\alpha w_1+\alpha w_2=1\hspace{1em}(\text{first limit condition}),$$

$$w_1\frac{n}{2}+w_2\frac{n}{2}=n\hspace{1em}(\text{second limit condition}),$$

$$\frac{\gamma }{n_1}=w_1\hspace{1em}(\text{first cluster size condition}),$$

$$\frac{\gamma }{n_2}=w_2\hspace{1em}(\text{second cluster size condition}).$$

The first two conditions ensure that equation 12 simplifies back to equation 11 for equal size clusters, and the second two set the weights inversely proportional to the cluster sizes. These conditions are fulfilled for $\alpha =\frac{1}{2},w_1=\frac{2n_2}{n}$, and $w_2=\frac{2n_1}{n}$. This allows clusters to contribute equally even when the cluster sizes are uneven, while simplifying back to the original equation when they are equal, as desired. Substituting these values into Equation 12, rearranging, and rescaling by 2σ²n/(4cn₁n₂), the energy to be minimized becomes

$$E(\mathit{n})={\mathit{n}}^T(\frac{1}{2n_1}\sum _{i=1}^{n_1}{\mathit{x}}_i{\mathit{x}}_i^T+\frac{1}{2n_2}\sum _{i=1}^{n_2}{\mathit{x}}_i{\mathit{x}}_i^T)\mathit{n}+\frac{n}{4n_1{n}_2}\frac{{\sigma }^2}{{\sigma }_0^2}{\Vert \mathit{n}-{\mathit{n}}_p\Vert }^2$$

which is of the general form

$$E_p(\mathit{n})={\mathit{n}}^{T}S\mathit{n}+\frac{1}{{\sigma }^2}{\Vert \mathit{n}-{\mathit{n}}_p\Vert }^2,\hspace{1em}\mathrm{s}.\mathrm{t}.\hspace{1em}\Vert \mathit{n}\Vert =1,$$

a weighted covariance matrix and cluster-dependent weighting of the prior term, and assumes at least one point per cluster. Additional conditions for the weights could be used to remove this condition if desired. This optimization problem is closely related to finding a minimum over a boundary in trust-region optimization (Nocedal and Wright, 2006) and can be solved as such. The overall solution alternates between solving this optimization problem and reclustering the data points until convergence.

5. Clustering

The plane-fitting algorithm described in section 4 requires a clustering method to partition the set of data points into two classes. K-means(Macqueen, 1967) is one of the most popular clustering methods. Standard kmeans clustering minimizes

$$S={\text{argmin}}_{\{S_k\}}\sum _k\sum _{i\in S_k}{\Vert x_i-{\mu }_i\Vert }^2$$ (13)

over all possible cluster sets S_k. For the case when only two classes are sought, k-means simplifies to

$$E=\sum _{i\in S_1}{\Vert x_i-{\mu }_1\Vert }^2+\sum _{i\in S_2}{\Vert x_i-{\mu }_2\Vert }^2,$$

where ${\mu }_k=\frac{{\sum }_{i\in S_k}{\Vert x_i-{\mu }_k\Vert }^2}{|S_k|}$ are the cluster centers. Prior information can be added to this two-class case to obtain

$$E=\left(\sum _{i\in S_1}{\Vert x_i-{\mu }_1\Vert }^2\right)+\frac{1}{{\sigma }_1^2}{\Vert {\mu }_1-{\overline{\mu }}_1\Vert }^2+\left(\sum _{i\in S_2}{\Vert x_i-{\mu }_2\Vert }^2\right)+\frac{1}{{\sigma }_2^2}{\Vert {\mu }_2-{\overline{\mu }}_2\Vert }^2,$$

where $\sigma =\frac{{\sigma }_k^{\mu }}{{\sigma }_k}$ is a user-defined constant and μ̅₁ and μ̅₂ are priors for the cluster centers.

In the standard k-means algorithm, elements are assigned to a current estimate of the cluster centers. From this new partitioning, new cluster centers are calculated as the means of the current clusters, and this process is iterated until convergence. This optimization is non-convex, and so is not guaranteed to reach a global minimum. When seeking two cluster centers for one-dimensional features, however, k-means simplifies to Otsu thresholding. Otsu thresholding (Otsu, 1975) computes the globally optimal separation between two classes by searching the feature histogram for the threshold which minimizes the intraclass variance.

A one-dimensional feature suitable for clustering the points in the plane-fitting algorithm is angle in the fitting plane with respect to a reference direction; in this case, the midpoint of the projections of the stain vector priors. Prior stain vector information is used to prevent mis-clustering when the number of data points for one stain direction clearly dominates the other. The actual stain vectors are extreme directions specifying the boundaries of the optical density cone. These directions of pure color are not the norm, as most colors are a mixed combination of these two extremes. For this reason, the stain vectors themselves are not chosen as the priors for clustering. Instead, priors are chosen to be slightly inward from the cone boundaries. Given two stain vectors s₁ and s₂, the priors are chosen as the angles with respect to the reference direction of the projections $\prod \{{\mathit{q}}_i\}={\mathit{q}}_i-{\mathit{q}}_i^T\mathit{n}\mathit{n}$ onto the current estimate of the fitting plane, where q₁ = (1 − α)s₁ + αs₂ and q₂ = αs₁ + (1 − α)s₂, α ∈ [0, 0.5) are directions moved slightly inward from the cone boundary. Including this prior information, the minimization problem becomes

$$E(I\le I_{\theta },{\mu }_1,{\mu }_2)=\left(\frac{1}{{\sigma }_1^2}\sum _{i\in j:I_j\le I_{\theta }}{(I_i-{\mu }_1)}^2\right)+\left(\frac{1}{{\sigma }_2^2}\sum _{i\in j:I_j>I_{\theta }}{(I_i-{\mu }_2)}^2\right)+\frac{1}{{({\sigma }_2^{\mu })}^2}{({\mu }_2-{\overline{\mu }}_2)}^2+\frac{1}{{({\sigma }_1^{\mu })}^2}{({\mu }_1-{\overline{\mu }}_1)}^2,$$ (14)

which is computed for all thresholds I_θ. For a given partitioning, the optimal values for μ₁ and μ₂ are

$${\mu }_i=\frac{{\sigma }_i^2}{{\sigma }_i^2+{({\sigma }_i^{\mu })}^2{n}_i}{\overline{\mu }}_i+\frac{{({\sigma }_i^{\mu })}^2{n}_i}{{\sigma }_i^1+{({\sigma }_i^{\mu })}^2{n}_i}{Ī}_i,$$ (15)

where n_i represents the numbers of points in a cluster and Ī_i the mean angles in the cluster. Note that μ₁ and μ₂ are not simply the foreground and background means, but a weighted average of the means and priors. Algorithm 5 gives an overview of the plane fitting algorithm with prior.

Algorithm 1.

Algorithmic description of the optimal plane-fit algorithm.

Data: σ/σ0, s1, s2
Result: Normal vector for plane fit: n
Compute prior normal vector ${\mathit{n}}_p=\frac{{\mathit{s}}_1\times {\mathit{s}}_2}{\Vert {\mathit{s}}_1\times {\mathit{s}}_2\Vert }$;
Initialization n = np ;
repeat
	Project data points onto plane ${\mathit{n}}_p^T\mathit{x}=0$;
	Project priors q1 and q2 onto the plane (computed from s1, s2);
	Express all points (including the priors) in angular coordinates ;
	Perform globally optimal Otsu thresholding with priors in angular domain;
	Compute new scatter matrix (based on clustering) ;
	Compute new data variance (based on clustering) ;
	Compute optimal normal vector n;
until convergence (i.e., cluster assignments no longer change);

6. Restaining

Once an image’s stain vectors have been computed, it can be restained to better match a target image. As stated in section 2, the relationship between an image’s optical density OD, its stain vectors α_i, and the amounts of each stain q_i is given by the equation

$$\mathit{O}\mathit{D}=\mathit{\alpha }q={\mathit{\alpha }}_{\mathbf{1}}{q}_1+{\mathit{\alpha }}_{\mathbf{2}}{q}_2.$$

Once the α_i have been estimated, the concentration of each stain present in each pixel can be solved for. The stain concentrations are given by

$$q_i={\mathit{\alpha }}_{\mathit{i}}^{-1}\mathit{O}\mathit{D}$$ (16)

In order to restain the image to a different color space, these concentrations must be rescaled to match a desired distribution. This is done by adjusting the concentrations so that their median m_q matches a desired median $m_{\hat{q}}:\hat{q}=\left(\frac{m_{\hat{q}}}{m_q}\right)q$. Given these adjusted saturations and a set of desired stain vectors α̂, the restained image is given by

$$Î=e^{-({\hat{\mathit{\alpha }}}_{\mathbf{1}}{\hat{q}}_1+{\hat{\mathit{\alpha }}}_{\mathbf{2}}{\hat{q}}_2)}$$ (17)

In practice, pixels with nearly no stain are thresholded out for stability reasons.

7. Experiments and Results

This section presents results on several different experiments done to validate the effectiveness of the proposed method. Section 7.1 demonstrates how the method performs when estimating the plane normal direction for a synthetic data set. Section 7.2 shows how incorporating prior information improves the consistency of the plane estimation on a real dataset. Section 7.3 shows the effectiveness of the method in restaining slides which have faded over time. Section 7.4 shows how normalization improves the performance of feature extraction and classification.

7.1. Plane Normal Estimation

Figure 2 shows the results of a synthetic experiment to estimate the plane normal. Three methods are compared: (1) estimation without a plane normal prior (corresponding to the method in Macenko et al. (2009)), (2) estimation with a plane normal prior, but without the clustering step, and (3) the full algorithm. Estimation results shown are deviations (in degrees) of the estimated normal vector n̂ with respect to the ground truth normal vector. To assess the influence of varying cluster sizes and normal priors, two stain vectors s₁, s₂ were chosen at a 30 degree angle

$$s_1=\left(\begin{array}{c}\hfill -\text{ sin }\gamma \hfill \\ \hfill \text{cos }\gamma \hfill \\ \hfill 0\hfill \end{array}\right)\hspace{1em}{s}_2=\left(\begin{array}{c}\hfill \text{sin }\gamma \hfill \\ \hfill \text{cos }\gamma \hfill \\ \hfill 0\hfill \end{array}\right)\hspace{1em}\text{with}\hspace{1em}\gamma =\pi \frac{15}{180}.$$ (18)

Priors q₁ and q₂ were then determined by rotating them in the plane by angle Φ, i.e.,

$$q_1=\left(\begin{array}{c}\hfill -\text{sin}(\gamma +\mathrm{\Phi })\hfill \\ \hfill \text{cos}(\gamma +\mathrm{\Phi })\hfill \\ \hfill 0\hfill \end{array}\right)\hspace{1em}{q}_2=\left(\begin{array}{c}\hfill \text{sin}(\gamma -\mathrm{\Phi })\hfill \\ \hfill \text{cos}(\gamma -\mathrm{\Phi })\hfill \\ \hfill 0\hfill \end{array}\right)$$ (19)

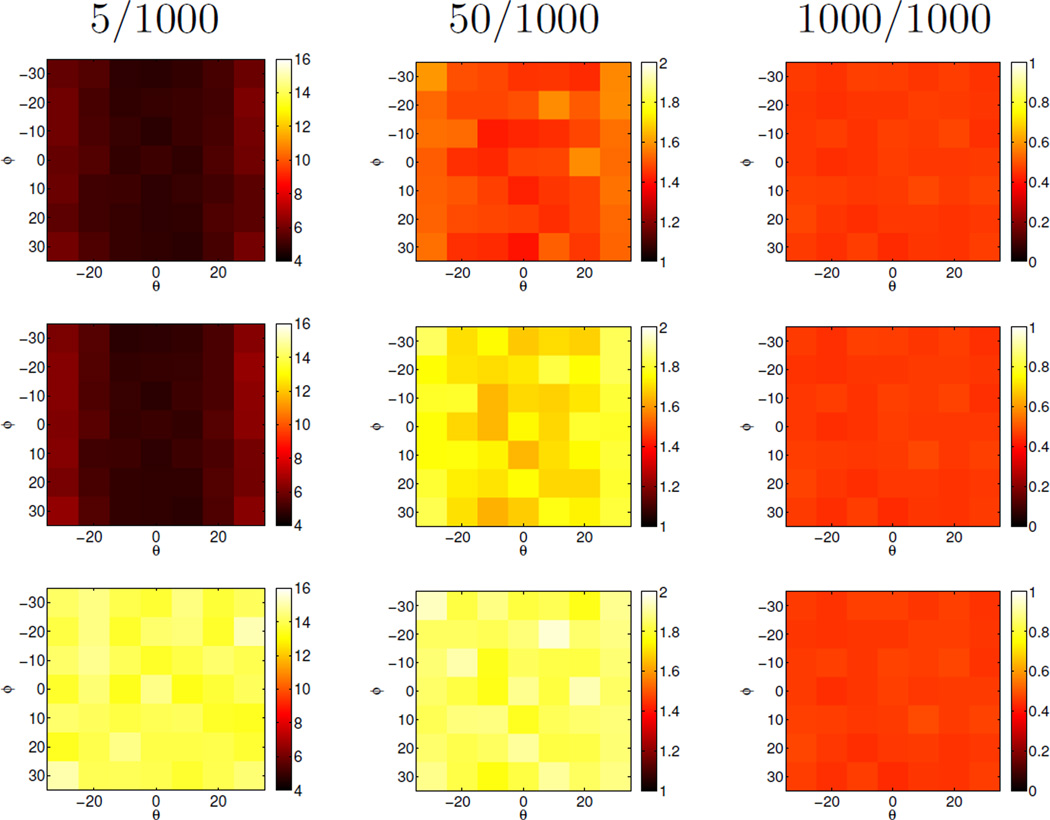
and subsequently tilting them with respect to the plane that they define by an angle θ. For testing purposes the such created priors were used directly, but the stain data was generated by creating samples using an isotropic Gaussian distribution with the respective means of the stain vectors (s₁ and s₂) and standard deviation of 0.1 (which is comparable to what we observe in real datasets). For each combination of (θ, Φ) we created 1000 datasets to evaluate the mean performance of the different estimation methods in recovering the true normal vector of the plane defined by s₁ and s₂, $\mathit{n}=\frac{s_1\times s_2}{\Vert s_1\times s_2\Vert }$. The estimation performance was tested for different distributions of stains. For s₂ 1000 sample points were created while for s₁ the number of sample points was 5, 50, or 1000. The estimation algorithms had no knowledge of this unequal distribution. Only for (θ, Φ) = (0, 0) are the priors correct. Otherwise they indicate various levels of deviation to assess the behavior of the estimators for inaccuracies in the prior. As shown in Figure 2, all three methods to determine the plane normal have similar performance for clusters of equal size (1000/1000) with angular errors of less than one degree. However, prior information improves the results greatly for uneven point distributions. In the most extreme case of a 5/1000 sample point distribution the error of the proposed method is on average about 10 degrees smaller than the error of the method using a plane fit only. Such imbalances are expected to occur for example in regions with sparsely distributed nuclei. In cases where the effect of the prior is most pronounced, the clustering further improves estimation results slightly.

Figure 2.

Synthetic experiments: Angle difference (in degrees) between the estimated normal vector and the ground truth. Top row: proposed method. Middle row: plane fit with prior without clustering. Bottom row: plane fit without prior. Estimates are average results over 1000 random datasets for different priors and varying numbers (5/1000, …) of points in the two stain clusters. The proposed method performs best. For equal stain distributions all three method perform well. The difference is most striking for a highly unbalanced stain distribution (5/1000). Note that the results are fairly insensitive to the prior itself and that the clustering step improves results over the prior slightly.

7.2. Consistency of Estimation

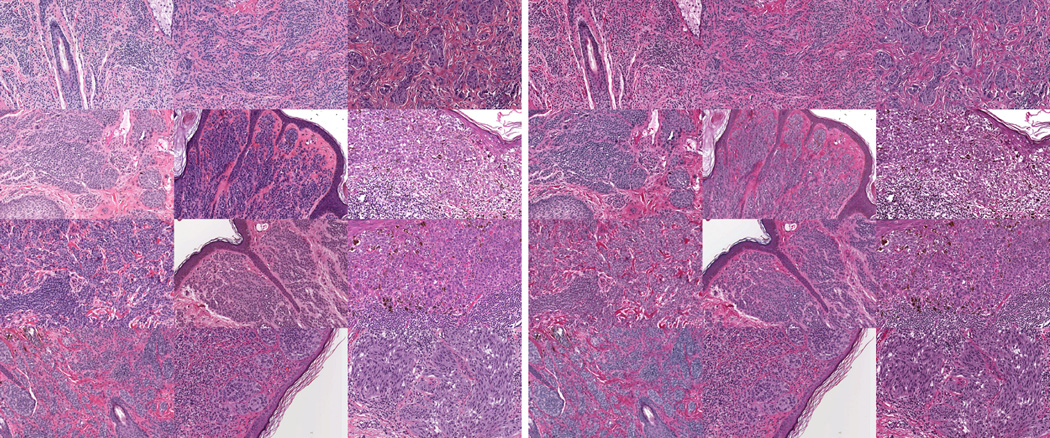
Figure 3 shows the performance of the method on thirteen slides compared to the direct plane fitting without a plane prior as in Macenko et al. (2009). These slides were randomly selected from a study of melanocytic lesions and were scanned digitally using an Aperio ScanScope. The histology images were subdivided into areas of 1000×1000 pixels and were independently adjusted for stain intensity and stain direction using the two methods. Figure 3 shows the estimation consistency for the two methods by comparing the mean deviation from the mean normal vector across a slide (mean with respect to the tiles). Estimation consistency is statistically significantly better for the proposed method (with p < 1e − 4 using a t-test or nonparametric permutation test). The mean deviation from the prior was around 11 degrees for the method using prior information and 20 degrees for the method not using the prior information. The tight distribution for the consistency results for the proposed method demonstrates that the prior was not chosen to dominate the results. Figure 4 shows the results of application of the methods with and without prior information on a slide. Figure 5 shows the results of using the method with prior to normalize the appearance of 12 images.

Figure 3.

Estimation consistency for the proposed method and the method not using prior information (Macenko et al., 2009) comparing the mean deviation from the mean normal vector across a slide (with respect to the tiles) in degrees. Smaller values and a tighter distribution demonstrate the advantage of the proposed method. Results are statistically significantly different.

Figure 4.

Restaining of a real dataset using the proposed method (right) and the method not using prior information (middle).

Figure 5.

A set of 12 slides before (left) and after (right) normalization.

7.3. Faded Slide Normalization

An application of this method is normalizing the color of slides which have faded over time. Figure 6 shows the results of an experiment on 23 pairs of images of cutaneous melanomas taken 2–7 years apart. The second scans show fading of stain intensities compared with their original scans to varying degrees. The two scans were registered to each other using a similarity transform computed from specified landmarks to allow direct comparison of corresponding image regions. The images were then downsampled by a factor of 10 to ease computation, but the method can work on full-size images if desired. This data is available online at http://midas3.kitware.com/midas/folder/11138.

Figure 6.

Results of the 4 different unfading schemes on the groups with low, medium, and high fading. In each graph, the first box is the difference between the original and unadjusted faded image. The next three show difference between the original and adjusted faded images using the local, global, and mixed restaining schemes. The last shows the difference between the original and faded images, both adjusted to a third color space.

Stain vectors and intensities are estimated for the original scan and the faded scan is adjusted to more closely match the original. Effectiveness of this method is measured by computing the distance between a pair of images before and after the faded image is adjusted. Distance is computed by calculating the earth mover’s distance (EMD) between the color histograms of the image. EMD represents the minimum energy needed to turn one histogram into another. A simpler, equivalent computation is taking the distance between the quantile functions of the two histograms (Levina and Bickel, 2001). For this experiment, the images were registered and subdivided into 100 patches (10 × 10 grid). An average EMD is computed on the R, G, and B channels for each patch. These patch-wise distances are then averaged over all patches, giving a total image-to-image distance.

There are several ways to estimate the stain vectors and intensity scalings needed to perform these adjustments. If the images are treated in a purely local manner, the stain vectors and scalings are estimated and applied on a patch-wise basis. This local approach typically yields good improvement in the image distance metric, but the resulting images often show artifacts of this local treatment, especially on images with more severe fading. An alternative approach treats the images from a purely global perspective, estimating a single set of stain vectors and intensity scalings and globally adjusting the faded image to match. This yields smooth restained images, but at the cost of lower quantitative performance. By computing the stain vectors of the original image globally, but performing intensity adjustment locally, a middle ground between the two previous methods offers better performance than the purely global approach while giving smoother images than purely local. It is also possible to restain both the original and faded images to a third, separate color space instead of adjusting one to match the other. The results of this approach using a local restaining scheme are included as well.

Examining the distances between the original and faded images prior to adjustment reveals that the pairs fall into three distinct clusters, representing low, medium, and high levels of fading. Figure 8 shows examples of each of these three classes and the results of the various methods described above on each. The low fading class shows small improvement across all methods, which is expected since there is only small room for improvement. The classes with medium and large fading show much more significant improvements across all methods. In general, the more local methods show the most improvement in distance, while the more global methods produce visually smoother images.

Figure 8.

Examples of restained faded images. From top to bottom: images that show low, medium, and high fading. In each subfigure:a) the unadjusted faded image, b) the original image, c) faded image with global restaining, d) faded image with mixed restaining, e) faded image with local restaining, f) original image restained to new space, and g) faded image restained to new space.

Figure 6 shows the results of these different unfading schemes on a set of 23 pairs of images. The first plot shows results for 11 pairs of images which show low amounts of fading, all of which were scanned approximately 2 years apart. The second plot shows results for the 8 pairs which show moderate amounts of fading, and the third shows the 4 pairs with high amounts of fading. Both the medium and high fading groups were scanned approximately 7 years apart. In each plot, the first box shows the distribution of EMDs between the faded and nonfaded images. The following boxes show EMDs between the nonfaded and adjusted images in the local, mixed, global, and separate color space schemes respectively.

Figure 7 shows the results of evaluating our method against 3 others for the task of restaining faded slides. R is the method of Reinhard et al. (2001), K the method of Kothari et al. (2011), M the method of Macenko et al. (2009), and O is our method. The results are on the set of slides which showed medium fading and all restaining is done globally. Methods R and K show small or no improvement overall. The M method (plane fitting with no prior information) shows good overall improvement in the mean but at the cost of high variation. Our method shows a similar improvement in mean but much lower variation, demonstrating the additional stability provided by the prior.

Figure 7.

Comparison of our method with others on slides with medium fading. Boxes are B (base distance), R (Reinhard et al.), K (Kothari et al.), M (Macenko et al.), and ours.

Figure 8 shows the results of our restaining on typical images from each of the three classes. As can be seen, the global method provides a smoother result, but recovers less information overall than methods which include a local component.

The weight of the prior, here defined as its standard deviation σ₀, is an important parameter in determining the effectiveness of the restaining. The results above were computed by setting σ₀ = 0.5 globally, which is a moderate weight for the prior. The results for the low fading class stay consistent across a wide range of prior values. The medium class is somewhat less robust to change in the prior. A somewhat tighter distribution is obtained for this class near σ₀ = 0.2, but the difference in mean EMD is small (77.4 vs 80.1). For the class with high fading, a marked improvement is seen at much lower standard deviations, such as σ₀ = 0.01. In these cases, the higher prior weight seems to stabilize the estimation of stain direction when there is only a small amount of stain information present. This effect is much more strongly seen in global schemes rather than local. These results suggest that adaptively choosing σ₀ based on the initial difference between the faded and unfaded images in a pair could be desirable.

7.4. Effect on Classification

Another important application of slide appearance normalization is in statistical analysis. Figure 9 shows the effect of color normalization on statistical classification. The goal of this analysis is to classify slides as containing either melanoma or benign nevi. This experiment compares 31 slides containing nevi and 21 containing melanoma. Each image has approximately 10 regions identified by a pathologist. In each of these regions, cell nuclei are segmented and then features are extracted based on these nuclear segmentations using the process described in Miedema et al. (2012). Classification was done using three different processing methods: (1) no appearance normalization, segmentation and feature extraction done on original slides, (2) normalized slides used for segmentation, features extracted from original slides, and (3) normalized slides used for both segmentation and feature extraction.

Figure 9.

Classification accuracy and AUROC for varying levels of normalization. None uses no normalization, partial normalizes for segmentation but not feature extraction, and full normalizes for both.

As figure 9 shows, for distance-weighted discrimination (DWD)(Marron et al., 2007) classification with 10-fold cross-validation, there is clear improvement when normalization is added. In particular, normalization yields improvement in both the segmentation and feature extraction steps.

The significance of the difference in AUROC value between the normalized and unnormalized data is evaluated using a bootstrapping approach. Bootstrapping is done by, for a population of size n, randomly sampling n values from the population with replacement. From this resampled population, a statistic of interest (in our case, AUROC) can be computed. If this process is iterated, a distribution of these values can be created and analyzed.

We perform bootstrapping on both the normalized and unnormalized data to get distributions of AUROC values for both populations. We perform a two-sample t-test in order to assess the significance of the difference between the two populations. For 100 resamplings, we find significant difference between the two populations at the p = 0.01 level.

Projecting the data onto the DWD separating direction and looking at the receiver operating characteristic (ROC) shows similar results. Figure 9 shows the area under the ROC curve (AUROC). While this shows little difference in the segmentation step, it again shows improvement when using the normalized images over the original for feature extraction.

7.5. Variation Between Manufacturers

Computing a plane fit using prior information is desirable due to the variations in stains between batch and manufacturer. If the stain directions were always identical, estimation would be unnecessary as one could simply take the stain directions as fixed.

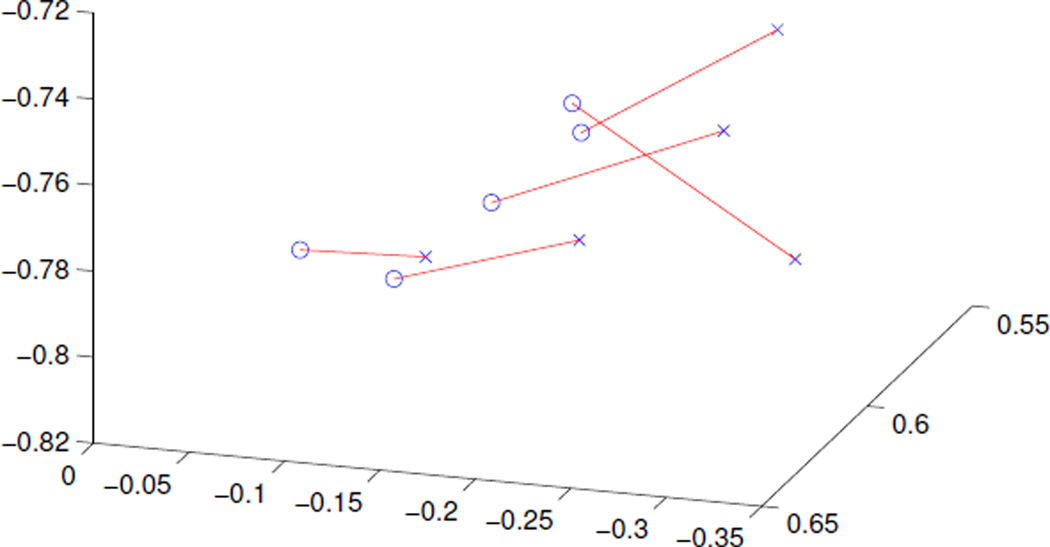
Five slides of normal skin were stained using stains from two different manufacturers. For the first group, the eosin and hematoxylin were from Richard-Allan with other reagents from Fisher. For the second, the stains and other reagents were from Leica. For each pair of images, we convert them to OD space and compute a PCA of the resulting data. In each case, the third principal component explains less than 1% of the variation, indicating that the data is highly planar. We define the plane of the data as the plane spanned by the first two principal components.

The normal to these planes are compared for each pair of images. In each case, the normal varies from 3 to 10 degrees, with an average deviation of 6.5 degrees. While this difference is not large, is it consistent. Figure 10 shows that the normals in each case show a consistent direction of movement, going from the left side of the plot to the right in each case. This demonstrates the need for estimating the stain directions rather than taking them as constant in order to correct for this bias.

Figure 10.

Normal directions for slides stained from two manufacturers: one set in blue, the other in red. The colored lines are drawn between the two normals computed for each slide. Notice there is a consistent left-to-right shift going from blue to red.

8. Applications

The method proposed in this paper has a variety of applications. One such application is the restaining of slides which have faded over time as discussed in the results section. While its application here was in pairs of faded and nonfaded slides, the method could also be used to unfade slides for which there is no nonfaded image available, thus allowing them to be analyzed more easily.

Another application is the restaining of a population of images to a common color space. This adjustment would allow for easier comparison and statistical analysis of a group of images. The extra constraint provided by the prior information would help to stabilize this adjustment for statistical purposes.

Another possible application would be the restaining of an image into a new color space for visualization purposes.

9. Conclusions

This paper presented a method to automatically adjust the appearance of stained histology slides. It described a novel way of adding prior information for the stain vectors and how to deal with unequal stain distribution through a clustering process which is a novel adaptation of Otsu thresholding to include prior information. The underlying optimization problem is related to trust-region optimization, and is therefore well studied and easy to solve. Experiments on real and synthetic data show the superior performance of the method developed compared with methods which use no prior information. Results of applying the method to slides which have faded over time show a potentially powerful application of this method. Normalization of histology slides is shown to improve performance of statistical classification of those slides.

Highlights.

• A method for normalizing the appearance of histology slides is given.

• The method uses prior information to stabilize stain direction estimation.

• The effectiveness of the method over those not using prior information is shown.

• The method is shown to be effective in normalizing the appearance of faded slides.

• Normalization is shown to improve the performance of statistical classification.