Application of multivariate statistical techniques in microbial ecology

Abstract

Recent advances in high-throughput methods of molecular analyses have led to an explosion of studies generating large scale ecological datasets. Especially noticeable effect has been attained in the field of microbial ecology, where new experimental approaches provided in-depth assessments of the composition, functions, and dynamic changes of complex microbial communities. Because even a single high-throughput experiment produces large amounts of data, powerful statistical techniques of multivariate analysis are well suited to analyze and interpret these datasets. Many different multivariate techniques are available, and often it is not clear which method should be applied to a particular dataset. In this review we describe and compare the most widely used multivariate statistical techniques including exploratory, interpretive, and discriminatory procedures. We consider several important limitations and assumptions of these methods, and we present examples of how these approaches have been utilized in recent studies to provide insight into the ecology of the microbial world. Finally, we offer suggestions for the selection of appropriate methods based on the research question and dataset structure.

Introduction

The past decade has seen significant progress in ecological research due in part to the advent and increased utilization of novel high-throughput experimental technologies. With approaches such as high-throughput “next generation” sequencing, oligonucleotide and DNA microarrays, high sensitivity mass spectrometry, and nuclear magnetic resonance analysis, researchers are able to generate massive amounts of molecular data even in a single experiment. These methods have created an especially powerful effect on the field of microbial ecology, where we now can apply DNA, RNA, protein, and metabolite identification and measurement techniques to the whole microbial community without a need to separate or isolate individual community members. These technologies provided foundation to many groundbreaking advances in our understanding of microbial community organization, function, and interactions within a community and with other organisms. Examples include the assessment of marine microbiota response to the Deepwater Horizon oil spill (Mason et al., 2014), functional analysis of microbiomes in different soils (Fierer et al., 2012), identification of enterotypes in the human intestinal microbiota (Arumugam et al., 2011), detection of seasonal fluctuations in oceanic bacterioplankton (Gilbert et al., 2012), and discovery of the loss of gut microbial interactions in human gastrointestinal diseases (Shankar et al., 2013; Shankar et al., 2015).

Because large amount of data is generated even in a single high-throughput experiment, powerful statistical tools are needed to examine and interpret the results. Because many different variables such as species, genes, proteins, or metabolites are measured in each sample or site, the analysis of these datasets is generally performed using multivariate statistics (definitions of most commonly used terms are provided in Box 1). Indeed, many types of standard multivariate statistical analyses have been employed for the assessment of such high-throughput datasets, and novel approaches are also being developed. The multitude of possible statistical choices makes it a daunting task for an investigator not experienced with these tools to pick a good technique to use. In this review, we provide short descriptions of the most frequently used multivariate statistical techniques, we compare different methods, and we present examples of how these approaches have been utilized in recent studies. This text is not meant to serve as an exhaustive overview of existing methods, as the landscape of currently available multivariate analyses is vast and growing. Rather, our goal is to familiarize the reader with the most commonly used approaches and to provide background on the differences among techniques and possible selection choices. While this review will primarily focus on the application of multivariate statistics to microbial ecological research, these techniques can be successfully applied to a wide variety of datasets in other ecological disciplines.

Box 1. Terminology used in multivariate statistical analyses.

• Biplot – a two-dimensional diagram of the ordination analysis output that simultaneously shows variable positioning and object positioning in a reduced dimensionality space.

• Canonical analysis – a general term for statistical technique that aims to find relationship(s) between sets of variables by searching for latent (hidden) gradients that associate these sets of variables.

• Constrained and unconstrained ordination – the constrained multivariate techniques attempt to ‘explain’ the variation in a set of response variables (e.g., species abundance) by the variation in a set of explanatory variables (e.g., environmental parameters) measured in the same set of objects (e.g., samples or sites). The matrix of explanatory variables is said to ‘constrain’ the multivariate analysis of the dataset of response variables, and the output of constrained analysis typically displays only the variation that can be explained by constraining variables. In contrast, the unconstrained multivariate techniques only examine the dataset of response variables, and the output of unconstrained analysis reflects overall variance in the data.

• Gradient analysis – this term describes the study of distribution of variable values in the dataset along gradients. Since the goal of ordination analysis is to order objects along the main gradients of dispersion in the dataset, both of these terms can be used synonymously. Two different types of gradient analysis are usually recognized:

  • Indirect gradient analysis utilizes only one dataset of measured variables. This term is synonymous with ‘unconstrained ordination’.

  • Direct gradient analysis in contrast uses additionally available data to guide (direct) the analysis of the dataset of measured variables. It produces axes that are constrained to be a function of explanatory variables. This term is synonymous with ‘constrained ordination’.

• Data transformation – this term describes the process of applying a mathematical function to the full set of measured values in a systematic way. See Box 2 for a description of common data transformations.

• Distance – it quantifies the dissimilarity between objects in a specific coordinate system. Objects that are similar have small in-between distance; objects that are different have large distance between them. For normalized distances, Distance(X, Y) can be related to Similarity(X,Y) as either D=1-S, D=√(1-S), or D=√(1-S²). Many different mathematical functions can be used to calculate distances among objects or variables (Legendre, Legendre, 2012). The choice of distance measure has a profound effect on the output of multivariate analysis and should be chosen based on the characteristics of the studied ecological dataset.

• Eigenvector and eigenvalue – in ordination methods such as PCA, eigenvectors represent the gradients of dataset dispersion in ordination space and are used as ordination axes, and eigenvalues designate the ‘strength’ of each gradient.

• Explanatory/predictor/independent variable – all these terms describe the type of variables that explain (predict) other variables.

• Ordination – a general term that can be described as ‘arranging objects in order’ (Goodall, 1954). The goal of ordination analysis is to generate a reduced number of new synthetic axes that are used to display the distribution of objects along the main gradients in the dataset.

• Orthogonal – mathematical term that means ‘perpendicular’ or ‘at right angle to’. Due to this feature, the orthogonal variables are linearly independent (Rodgers et al., 1984).

• Randomization tests – a group of related tests of statistical significance that are based on the randomization of measured data values to assess if the value of a calculated metric (such as species diversity) can be obtained by chance.

• Response/dependent variable – both of these terms describe the main measured variables in a study. Many multivariate analyses examine the relationship between these variables and other variables that are said to ‘predict’ or ‘explain’ these measured variables (such as environmental factors). Thus, the measured variables are ‘dependent on’ or ‘responding to’ the values of the explanatory/predictor variable(s).

• Triplot – a two-dimensional diagram of the multivariate analysis output that in addition to response variables and objects shown on biplot also displays explanatory variables.

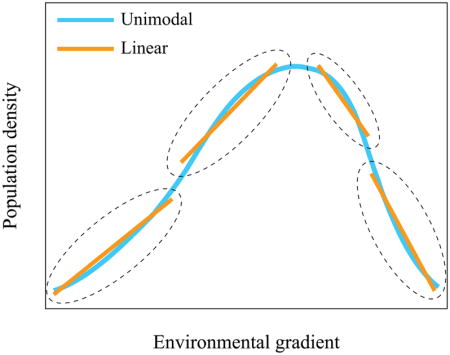
• Unimodal distribution – a distribution with one peak on the variable density plot.

• Variance, variability, and variation – the differences in the use of these three related terms can be described by the following statement: ‘Variance is a statistical measure of data variation and dispersion, which describe the amount of variability in the dataset’.

Types and properties of high-throughput ecological datasets

Although many different experimental tools can be utilized to obtain high-throughput ecological data, the output in most cases is presented as a matrix of positive numbers each representing either a measured value for variable i (e.g., mRNA or protein level, metabolite concentration, or species abundance) in object j (e.g., sample or site), or a ratio of two measured x_i values between two objects. The former dataset structure is common for outputs from high-throughput sequencing, mass spectrometry, NMR-based metabolomics, and single-sample microarrays. The latter is usually obtained from two-color microarrays or high-throughput quantitative PCR. The type and distribution of data should match the assumptions of a particular statistical technique, and in some cases data should be transformed prior to performing further tests and statistical analyses. We describe common statistical assumptions and few of the most widely used data transformation methods in Box 2.

Box 2. Statistical assumptions and common data transformations.

Generally, statistical approaches and tests can be divided into parametric and non-parametric. The parametric methods make an assumption that the data come from a population with a particular underlying probability distribution of the measured variable, and parametric statistics make inferences about the parameters of such distribution. This allows parametric tests to have higher statistical power and to make more accurate estimates. However, the measured variables have to meet the underlying assumptions for parametric methods to be properly applied. The most wide-spread assumptions are:

• The population follows a defined distribution (this is often substituted by the expectation that sampled values follow a defined distribution). In most cases, either linear or unimodal distribution is expected.

• Variables are independent from each other.

• Population variances are equal or at least similar.

• Samples are drawn randomly from the population.

Unfortunately, biological datasets rarely conform to these assumptions. Most datasets are not normally distributed, variables that are displayed on the relative scale are no longer independent from each other, and often variances in different populations are not equal. In such cases, the original dataset values can be transformed so that the scale and the distribution of transformed values conform better to the assumptions of a particular parametric statistic. Most common data transformations include:

• Log transformation x′_i=log_b(x_i+c) – very useful for ratios; log bases 2, e, or 10 are used most often; c is a small number added to deal with x_i=0 cases.

• Root transformation x′_i=(x_i)^1/n – with n ≥ 1, it compresses the spread of values in the right tail of the distribution.

• Power transformation x′_i=(x_i)ⁿ – with n ≥ 1, it has opposite to root transformation effect.

• Arcsin transformation x′_i=arcsin(x_i) – is usually applied to percent and proportion values.

These transformations are very useful for continuous variables, but are less suited for discrete response variables including count data (O’Hara, Kotze, 2010). In addition, if the dataset matrix contains many zero values (e.g., species missing from a particular habitat), many common methods of multivariate analysis such as PCA or RDA are not appropriate as they can create false distributions and outputs. For ecological data with many zeroes, (Legendre, Gallagher, 2001) recommend two special transformations that will allow these ordination techniques to be applied to the dataset:

• Chord transformation: x′_ij= x_ij/√(Σx²_ij).

• Hellinger transformation x′_ij= √(x_ij/Σx_i+); where i − species, j − object, and i+ denotes all i’s.

Alternatively, because non-parametric statistics are not based on parameterized probability distributions (they are “distribution-free”), they can be directly applied to the original dataset, albeit with a loss of statistical power (they are thus less likely to find a statistically significant difference). Examples of non-parametric methods are permutation tests and rank-based statistical analyses.

Another important distinction among different dataset structures is whether data points represent absolute or relative values. The former are usually raw signal values obtained through experimental measurements, while the latter are most frequently derived by scaling individual recorded signals to obtain the same total measured signal across objects. The need for signal transformation into a relative scale is often driven by the limitations of the experimental techniques. For example, multi-step template preparation protocols used in high-throughput sequencing and microarray analyses can introduce an artificial bias into the observed sequence counts (Paliy, Foy, 2011). Thus, we cannot compare raw signal values for the same variable across multiple samples and make comparative conclusions, because the observed higher or lower sequence abundance includes not only true DNA amount in the sample, but is also influenced by confounding variables such as sample DNA quality, amplification biases, variability in sequencing or hybridization efficiency and DNA concentration measurements, etc. The effects of many such confounding factors can be removed if raw signal values for each object are converted into relative values through a simple x′_i = x_i/Σ(x_i) transformation. While this transformation is very useful for simple across-object comparisons, it causes individual variables to lose their independency, which is one of the main assumptions in many statistical tests and analyses (see Box 2). We describe the issues that can arise from the use of such compositional data, and approaches to mitigate these issues in Box 3.

Box 3. Pitfalls of the use of compositional data.

Many types of biological and ecological data are expressed as relative-to-total values, such as relative abundances of different microbial taxa in a soil site, or fraction of particular metabolite in the metabolic profile of a sample. The widespread use of relative values stems from the technical limitations of employed experimental methods, which do not allow direct comparison of the raw measured values of a particular variable (such as gene mRNA level or microbe abundance) between samples. In many cases an assumption is made that the overall measured signal should be the same among different samples, and the levels of variables are expressed as a fraction of the total. Unfortunately, such transformation of raw data into relative form gives rise to the phenomenon of constant-sum constraint, which violates the assumption of variable independence made in many statistical tests. Specifically, because the sum of all values in a sample has to equal a pre-defined value (for example, 1 or 100%), a change of one of the variables in that sample will cause reciprocal changes in the calculated relative values for other variables (Faust et al., 2012). This will produce a negative correlation effect between such variables (see Box Table). If the assumption of the equal overall sum of all measured values among objects is indeed true, such use of compositional data can lead to biologically valid interpretations. However, if ‘equal sum’ assumption can only be technically but not biologically justified, the use of compositional data can produce false discoveries (see Box Table), since the joint probability distribution of compositional variables cannot describe the distribution of the underlying absolute variables (Lovell et al., 2014). Ordination techniques can similarly produce erroneous results because many of these techniques are based on the calculation of the matrix of pair-wise distances or dissimilarities which are often a function of correlation (Lovell et al., 2014). Rank-based non-parametric statistical measures can diminish the effects of outliers, random noise, and deviations from expected probability distribution on the correlation estimates (Shevlyakov, Smirnov, 2011). They, however, still suffer from the possible lack of congruency between absolute and relative data distributions as shown by (Lovell et al., 2014).

Several approaches are available to mitigate the described issues in compositional data analysis.

Absolute values
	V1raw	T2raw	T3raw	T4raw	T5raw	T6raw	average Rp V-vs-T
S1	10	10	11	10	9	10	−0.07
S2	30	11	10	11	9	9	average Rs V-vs-T
S3	50	10	9	9	10	10	−0.16
S4	70	9	9	9	9	9
S5	110	11	11	9	11	9
Relative values
	V1comp	T2comp	T3comp	T4comp	T5comp	T6comp	average Rp V-vs-T
S1	0.17	0.17	0.18	0.17	0.15	0.17	−0.99
S2	0.38	0.14	0.13	0.14	0.11	0.11	average Rs V-vs-T
S3	0.51	0.10	0.09	0.09	0.10	0.10	−1.00
S4	0.61	0.08	0.08	0.08	0.08	0.08
S5	0.68	0.07	0.07	0.06	0.07	0.06

S1…S5 – individual samples; V – variable with varied abundance; T- stable variable (10±1); R_p - Pearson correlation coefficient, R_s - Spearman correlation coefficient

1. A centered log-ratio transformation can be applied to the compositional dataset as x′_i=log(x_i/(∏x_i)^1/n), where (∏x_i)^1/n is the geometric mean of all variables x_i (i=1…n) in an object (Aitchison, 1986; Lovell et al., 2014). This transformation removes effect of constant-sum constraint on the covariance and correlation matrices; such log-ratio transformed dataset can be subjected to multivariate analyses such as PCA (Kucera, Malmgren, 1998). The use of this transformation is however challenging for datasets with many zeroes (Friedman, Alm, 2012), and a zero-replacement procedure has been proposed (Aitchison, 1986).

2. The variance of log-ratio transformed data was used as a basis for the SparCC (Sparse Correlations for Compositional data) approach of correlation network inference (Friedman, Alm, 2012). SparCC was shown to be very accurate on simulated data and was applied to high-throughput sequencing datasets from Human Microbiome Project to reveal robust taxon-taxon interaction networks.

3. A specific method to allow construction of correlation networks for ecological compositional data, called CCREPE (Compositionality Corrected by REnormalization and PErmutation), has also been recently developed (Gevers et al., 2014). Taking into account the constant-sum constraint, CCREPE adjusts p-values assigned to similarity measures (such as correlation coefficient) through a Z-test comparison of the observed similarity distribution with the null distribution generated through permutation and renormalization of the data. This approach reduces the number of spurious correlations and false discoveries.

Different types of multivariate approaches

Different available methods of large scale dataset analyses can be organized into groups based on various criteria such as technique goal (e.g., explore variance, interpret relationships, discriminate groups, test statistical significance), type of mathematical problem (regression, (partial) ordination, calibration, classification), or variable response model (e.g., linear, unimodal, mixture distribution) (ter Braak, Prentice, 1988). Clear separation of the methods is hard to achieve, because the same technique can be used for several different purposes, methods can utilize different sets of parameters or inter-object distance calculations, and many approaches are mathematically related. In this review, we distribute the described techniques into three categories based on the primary research objective of multivariate analysis.

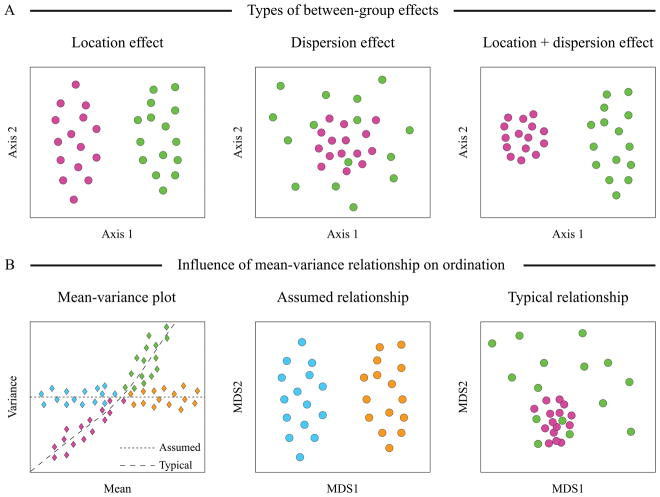
(1) Exploratory methods are used to explore the relationships among objects based on the values of variables measured in those objects. For example, soil samples (objects) collected in different landscapes can be compared based on the abundances of soil microbial species (variables) (Hartmann et al., 2014). These methods provide a useful visualization of object similarities, since similar objects are usually positioned close on the visualization plot, and dissimilar objects are apart from each other. Major gradients of data variation as well as object similarity can be evaluated. This category includes different unconstrained ordination techniques (see Box 4) as well as cluster analyses.

Box 4. Introduction into ordination techniques.

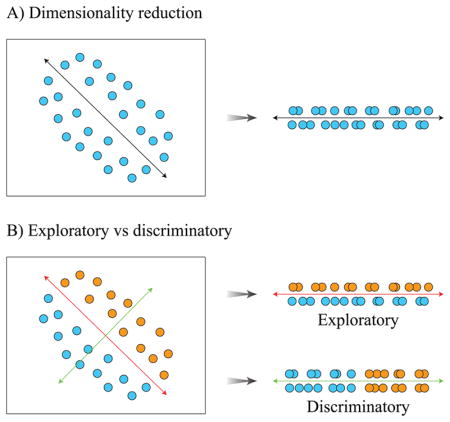
Ordination methods are a group of multivariate statistical approaches that attempt to order objects based on the values of variables measured in these objects (Goodall, 1954). Ordination methods are also often called gradient analyses, because these algorithms look for the main gradients of variation in multidimensional data space, and then arrange the objects in a new system of coordinates with each gradient serving as an axis as shown in Box Figure 1A. Often, the few largest gradients account for the majority of the variance in the data. Thus, a large data matrix can be displayed in just 2 or 3 dimensions with relative positioning of the objects representative of the relationships among the variables measured in these objects. This dimensionality reduction coupled with the straightforward interpretation of visual distribution of objects on an ordination plot (close objects have similar values of variables, distant objects - different) make these ordination techniques a popular choice in ecological studies.

Exploratory ordination methods look for the largest gradients of the scatter in the data, and object distribution in the ordination space represents the largest sources of dispersion (red arrow in Box Figure 1B). Examination of this output can reveal groups of similar objects, and it can show whether the main gradients of variance correspond to the expected sources of data variation. Alternatively, if the potential sources of data variation have been measured, these additional predictor variables can then be used to guide the analyses using one of the ‘constrained’ ordination techniques. In these methods, the goal is to look specifically for gradients in the multidimensional data space that are associated with the observed variation of predictor variables. If the additional variable describes the distribution of objects among different classes, discriminatory ordination analysis will maximize the separation of objects belonging to different classes (green arrow in Box Figure 1B).

Often, there are many different predictor variables that all influence measured response variables. This can make interpretation of ordination results difficult as it is harder to estimate the contribution of each predictor variable to the observed object distribution (see Figure 6A for an example). To more specifically assess the relationship between particular predictor variable(s) and response dataset, partial ordination analysis can be performed (ter Braak, 1988). In this approach, one or few predictor variables are chosen, and the rest are treated as covariates. Contribution of covariates to the variability in response variables is factored out, and ordination is then performed on the residual variability. Partial ordination can reveal how much of the total variation in response variables is attributed specifically to the chosen predictor variable(s), and it can remove the effects of undesired or accidental predictors (Liu, 1997). Partial ordination can be extended further and used as a basis of variation partitioning (Borcard et al., 1992). This approach allows one to partition the total variation in the dataset of response variables into components uniquely as well as jointly described by individual (groups of) predictor variables. The total variation is then displayed as pie chart or Venn diagram, with each section representing the fraction of total variance explained by each (group of) predictor(s). This reveals which predictors have the highest effect on the response variables, and it also shows any joint effects between predictor variables. (Volis et al., 2011) and (Hildebrand et al., 2013) provide examples of variation partitioning analysis.

(2) Interpretive methods are ‘constrained’ techniques, which in addition to the main set of measured variables, also use another set of additional explanatory variables (for example, known environmental gradients among objects) during the analysis. The aim of constrained ordination analyses is to find axes in the multidimensional dataset space that maximize the association between the explanatory variable(s) and the measured variables (called response variables). Thus, the ordination axes are constrained to be functions of the explanatory variables. Coefficients for each explanatory variable used to calculate each ordination axis indicate the contribution of that variable to observed object dispersion along that axis. Constrained ordination techniques can be seen as testing specific hypotheses of how environmental variables determine response variable values. Visualization of constrained ordination analysis allows interpretation of these relationships and reveals object similarity. This group of methods also includes several multivariate statistical tests that are used to assess if the observed data distribution can be expected due to chance.

(3) Discriminatory methods are an extension of the interpretive multivariate techniques and are usually called discriminant analyses (DA). The goal of DA is to define discriminant functions (synthetic variables) or hyperspace planes that will maximize the separation of objects among different classes (see Box 4). For example, in a linear discriminant analysis, the measured variables serve as a set of explanatory variables, and the response variable defines the class of each object. The discriminant function(s) are constrained to be specific combinations of explanatory variables. Variable coefficients (often called weights or loadings) used to calculate each discriminant function indicate the relative contribution of each of the explanatory variables to the observed object separation along each discriminant function. This can provide biological insight into the determinants of the (dis)similarity among object classes. Using the calculated discriminant functions, DA algorithms also generate prediction models that permit predictive classification of new objects into one of the classes based on the values of the measured explanatory variables.

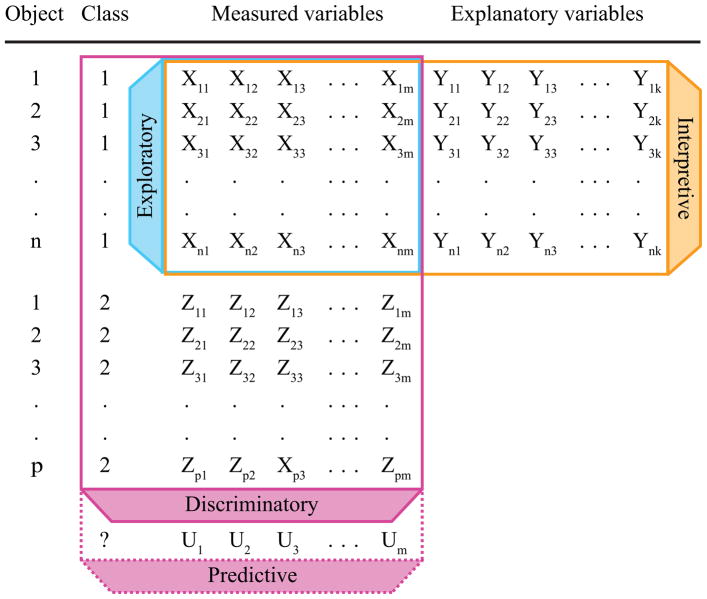
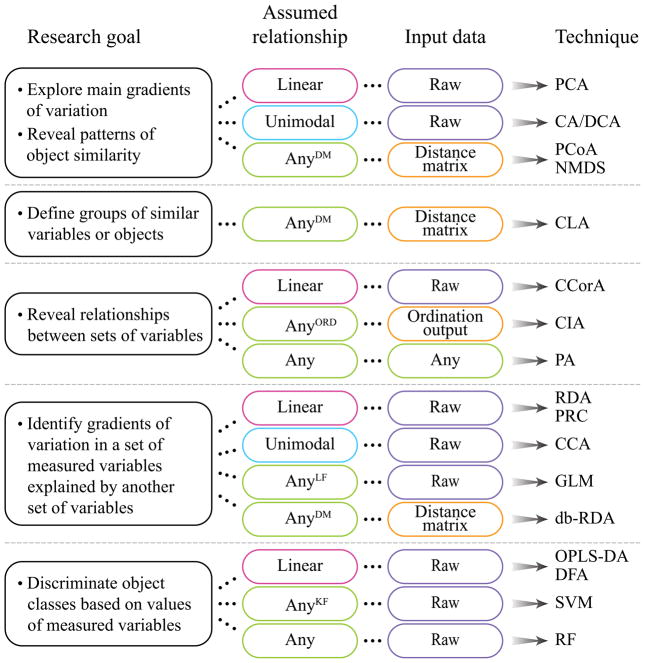
This review aims to provide a short description of the most widely used multivariate statistical approaches in microbial ecology. These methods are listed in Table 1, together with the classification of each method, expected data structure, and availability of Matlab and R scripts to run each algorithm. Figure 1 provides an illustration of the input expectations for each category of multivariate techniques. A more in-depth description of these and other multivariate analyses can be obtained from available literature (Borcard et al., 2011; James et al., 2014; Legendre, Legendre, 2012; Manly, 2004; Šmilauer, Lepš, 2014) and online sources such as GUSTA ME (Buttigieg, Ramette, 2015). Standalone software packages such as CANOCO (Šmilauer, Lepš, 2014), PRIMER v6 (Clarke, Gorley, 2005) and PAST (Hammer et al., 2001) are available as alternatives to Matlab and R scripts.

Table 1.

Common multivariate statistical tools

Technique	Assumed relationship*	Input	R script#	Matlab script#
Exploratory
PCA	Linear	Raw data	prcomp (stats) ca (mva)	princomp (built-in)
CA/DCA	Unimodal	Raw data	decorana (vegan)	CAR†
PCoA	AnyDM	Distance matrix	pcoa (ape)	f_pcoa (Fathom toolbox‡)
NMDS	AnyDM	Distance matrix	metaMDS (vegan)	mdscale (built-in)
Hierarchical clustering	AnyDM	Distance matrix	hclust (stats)	pdist + linkage + cluster (built-in)
K-means clustering	AnyDM	Distance matrix	kmeans (stats)	kmeans (built-in)
Interpretive
CCorA	Linear	Raw data	CCorA (vegan)	f_CCorA (Fathom toolbox‡)
CIA	AnyORD	Ordination output	coinertia (ade4)	coinertia.m€
PA	Any	Any	procrustes (vegan)	f_procrustes (Fathom toolbox‡)
RDA	Linear	Raw data	rda (vegan)	f_rda (Fathom toolbox‡)
db-RDA	AnyDM	Distance matrix	capscale (vegan)	f_rdaDB (Fathom toolbox‡)
CCA	Unimodal	Raw data	cca (vegan)	CAR†
PRC	Linear	Raw data	prc (vegan)	-
GLM	AnyLF	Raw data	glm (stats)	glmfit (built-in)
Mantel test	Any	Distance matrix	mantel (vegan)	f_mantel (Fathom toolbox ‡)
ANOSIM	Any	Distance matrix	anosim (vegan)	f_anosim (Fathom toolbox‡)
PERMANOVA	Any	Distance matrix	adonis (vegan)	f_npManova (Fathom toolbox‡)
Discriminatory
DFA	Linear	Raw data	candisc (candisc)	DA (Classification toolbox ¥)
OPLS-DA	Linear	Raw data	oplsda (muma)	osccalc + pls (PLS_toolbox®)
SVM	AnyKF	Raw data	ksvm (kernlab) randomForest	svmtrain (built-in) classRF_train
RF	Any	Raw data	(randomForest)	(RF_MexStandalone±)

^*denotes expected relationship among variables.

^#entries indicate functions for the respective platforms. Names within brackets represent the package that contains the function.

^†described in (Lorenzo-Seva et al., 2009).

^‡described at http://www.marine.usf.edu/user/djones/matlab/matlab.html and available from: http://www.marine.usf.edu/user/djones/.

^€described in (Doledec, Chessel, 1994).

^¥described in (Ballabio, Consonni, 2013).

^±available at https://code.google.com/p/randomforest-matlab/.

^DMassumed relationship depends on the distance metric used.

^ORDassumed relationship depends on the ordination technique used.

^LFassumed relationship depends on the link function used.

^KFmodel can be linear or non-linear if a non-linear kernel function is incorporated.

Figure 1. Expected input data structure for the multivariate ordination techniques.

Exploratory techniques (blue rectangle) are used to discern patterns within a single m x n matrix of measured variables and objects. Interpretive techniques (orange rectangle) are used to explain variation in a set of dependent variables (measured variables) by another set of independent variables (explanatory variables). Discriminatory techniques (pink rectangle) are used to separate objects between different classes based on the values of measured variables. Predictive approaches are an extension of discriminatory techniques that allow classification of a new object based on the generated discrimination model.

Exploratory methods

Principal components analysis (PCA)

Principal components analysis is one of the most widely used and one of the oldest methods of ordination analyses (Pearson, 1901). The general principle of PCA is to calculate new synthetic variables called principal components based on the matrix operations applied to the original dataset of quantitative variables. Each principal component (PC) is a linear combination of original variables calculated so that the first PC represents an axis in the multidimensional data space that would produce the largest dispersion of values along this component (see Box Figure 1A). Other principal components are calculated as orthogonal to the preceding components and similarly are positioned along the largest remaining scatter of the values. Thus, PCA creates a rotation of the original system of coordinates so that the new axes (principal components) are orthogonal to each other and correspond to the directions of largest variance in the dataset.

By definition, the first PC axis of the PCA output represents the largest gradient of variability in the dataset, PC2 axis – the second largest, and so forth, until all dataset variability has been accounted for. Each object can thus be given a new set of coordinates in the principal components space, and the distribution of objects in that space will correspond to the similarity of the variables’ scores in those objects (see Box 4). Displaying objects in only the first two or three PC dimensions is often sufficient to represent much of the variability in the original dataset. In fact, looking at the percent of dataset variance that is ‘explained’ by each principal component can tell us if there are any dominant gradients in the dataset. We can also infer whether few (first few PCs explain almost all variance) or many (variance ‘explained’ by each successive PC is distributed along a shallow curve) effects influenced the observed data distribution.

Because PCA uses Euclidean distance to measure dissimilarity among objects, care should be taken when using PCA on a dataset with many zeroes, as is often the case for data with long gradients. As described in detail by (Legendre, Gallagher, 2001), when run on such datasets, PCA can generate severe artifacts such as horseshoe visualization effect (see (ter Braak, Šmilauer, 2015) and (Legendre, Legendre, 2012) for examples). With this artifact, objects at the edges of the environmental gradient actually appear close to each other in the ordination space (Novembre, Stephens, 2008). While the horseshoe effect can be partially reduced by processing of the original data values through a chord or Hellinger transformation before running PCA (see Box 2 and (Legendre, Gallagher, 2001)), the use of correspondence analysis is usually advocated for such datasets (ter Braak, Šmilauer, 2015).

PCA can be used as a simple visualization tool to summarize dataset variance and show the dominant gradients in low-dimensional space. PCA results are usually displayed as a two- or three-dimensional scatter plot, where each axis corresponds to a chosen principal component, and each object is plotted based on its corresponding PC values. While it is typical to show PC1-vs-PC2 and/or PC2-vs-PC3 scatter plots, any two or three principal components can be chosen for visualization. Examples of PCA use in microbial ecological studies are provided by (Hong et al., 2010), (Ringel-Kulka et al., 2013), and (Shankar et al., 2013).

Correspondence analysis (CA)

Correspondence analysis is an exploratory technique designed to find relationships (correspondence) between rows and columns of a matrix of tabulated data (often called contingency table) and to represent these relationships in an ordination space (Hill, 1973; Hill, 1974). While the goal of CA is similar to that of PCA, important differences exist between these methods:

1. PCA maximizes the amount of explained variance among measured variables, while CA maximizes the correspondence (measure of similarity of frequencies) between rows (represent measured variables) and columns (represent objects) of a table (Yelland, 2010). Thus, transposing the data matrix prior to running CA produces the same result, while this is not true for PCA (Choulakian, 2001). This property leads to CA results ordinarily displayed in a biplot, where both row (variables such as taxa, genes, metabolites, etc) and column (objects such as samples, sites, etc) variables are jointly depicted on the same ordination chart. For each variable, the position of the point on a plot represents its estimated optimum along the gradient.

2. While PCA expects a linear relationship among variables, CA is based on a unimodal model. This is a very important distinction as we describe in detail in Box 5, and the choice between PCA and CA should depend on the type of variables being analyzed, assumed response model, and the lengths of the gradients and variable distributions (Šmilauer, Lepš, 2014).

3. The distances among objects in full CA ordination space are equal to a variant of Euclidean distance, called the weighted Euclidean distance or χ²-distance. The calculation of χ²-distance does not take into account cases where the value of a variable in two different objects is zero. Thus, CA is well suited to the analysis of datasets of species composition and abundance, where sites at both ends of environmental gradient usually lack many common species. Note, however, that as described in detail by ter Braak and Šmilauer (2015), true χ²-distance between objects is only visualized in the full CA ordination space. In two dimensions and with detrending applied, the inter-object distances now represent actual ecological distances (ter Braak, Šmilauer, 2015).

Box 5. Models of variable response to environmental gradients.

The goal of ecological studies is to assess and contrast the relationships between (groups of) biological entities (species, metabolites, proteins, etc) and their environment. To accomplish this, parametric statistical techniques need to make a specific assumption of the type of the relationship, generally called variable response model, in order to define the appropriate mathematical calculations. While linear relationships are the simplest (the relationships are modeled by a straight line), true linear gradients are rare in nature (Whittaker, 1967). Instead, current evidence shows that biological variables tend to display a non-monotonic relationship with the environment and have an optimum and low density areas (Whittaker, 1956; Whittaker, 1967). For example, consistent with the ecological niche model, species distribution along a gradient (spatial, temporal, response to perturbation, etc) usually displays a unimodal shape with higher population density in the middle of the distribution area and fewer members towards the edges of the territory (Austin, 2007; Whittaker et al., 1973). The standard statistical methods that assume linear relationships are thus not appropriate for the analyses of such variables. Instead, Gaussian models, first promoted by (Gauch, Whittaker, 1972), were found to be a good approximation of the distribution of ecological variables. These models are also well suited to deal with compositional data, data with many zeroes, and binary (presence/absence) variables (ter Braak, Verdonschot, 1995). There are, however, two caveats. First, linear-based methods can be used on some non-linear response datasets if the data can first be transformed to linearity (see Box 2). Secondly, note that over a narrow range of environmental gradient, distribution of response variable can approximate linear function, and thus linear methods such as PCA might be appropriate (Box Figure 2). Further discussion of this topic can be found in (Austin, 2007). An excellent guide for the gradient length-based choice between unimodal and linear based ordination approaches can be found in (Šmilauer, Lepš, 2014).

Based on considerations described above, several different types of response models can be chosen. Linear response models are implied in the Euclidean distance based methods such as PCA and RDA. Unimodal responses can be described explicitly with maximum likelihood estimators of Gaussian curves, or heuristically with weighted averaging estimators (ter Braak, Looman, 1986; ter Braak, Prentice, 1988). The ordination methods based on the former approach are available but have generally not been used often due to complexity (Yee, 2004). Weighted averaging estimators are much simpler and were used as a basis for the “reciprocal averaging” method (correspondence analysis) developed by (Hill, 1973) as an approximate solution to Gaussian ordination. Finally, a number of ordination methods such as PCoA, db-RDA, and NMDS are not based on specific underlying model of variable-environment relationship, but instead rely on the user-defined matrix of (dis)similarities among all objects.

While CA does not suffer from the horseshoe effect described above for PCA, unmodified CA ordination output can often produce a noticeable “arch” effect (see (ter Braak, Šmilauer, 2015) for an example). Arch effect is a mathematical artifact where distribution of objects along the first canonical axis is also partially mirrored in the second axis, because CA axes are constrained to be uncorrelated but not necessarily unrelated of each other (Hill, Gauch, 1980). The arch effect can be eliminated by the use of a detrended CA (DCA) technique, which attempts to remove residual axis 1 variance from axis 2 object scores (Hill, Gauch, 1980; Lockyear, 2000; ter Braak, Šmilauer, 2015). Detrending can also correct the shrinking of inter-object distances at the ends of ordination axes and can reduce the influence of uncommon variables (e.g., rare species). Note that while often useful, the detrending procedure does not always lead to an ordination output that better reflects the observed environmental gradients (see (Legendre, Legendre, 2012) for an in-depth discussion).

CA and DCA were shown to approximate well the ecological niche model and the typically expected Gaussian distribution of ecological variables (ter Braak, 1987; ter Braak, Looman, 1986). These techniques have been applied in ecology to analyze species distribution across many sites and samples, and to visualize sample similarity based on the presence and absence of different species (Prideaux et al., 2013). Other examples of CA use can be found in (Jones et al., 2007), (Perez-Cobas et al., 2014), and (Thureborn et al., 2013).

Principal coordinates analysis (PCoA)

Principal coordinates analysis is a conceptual extension of the PCA technique described above. It similarly seeks to order the objects along the axes of principal coordinates while attempting to explain the variance in the original dataset. However, while PCA organizes objects by an eigen analysis of a correlation or covariance matrix, PCoA can be applied to any distance (dissimilarity) matrix (Gower, 1966). PCoA has gained recent popularity in microbial ecology due to its ability to use phylogenetic distance (e.g., UniFrac distance (Lozupone, Knight, 2005)) and community composition (e.g., Bray-Curtis distance (Bray, Curtis, 1957)) measures to calculate (dis)similarity among microbial populations. Another potentially good choice of a distance measure is a recently introduced distance correlation metric dCor, which is able to robustly capture non-linear relationships between variables (Szekely et al., 2007). Because PCoA uses distance matrix as its input, it is not possible to directly relate any of the measured variables to individual principal coordinate axes (Ramette, 2007). An indirect correlation or regression analysis of object PC values vs object scores for a particular variable can instead be used to estimate the contribution of that variable to object dispersion along a particular PC axis (Koenig et al., 2011).

A particularly useful implementation of PCoA analysis for the microbial ecology studies has been developed by Rob Knight group (Lozupone, Knight, 2005). This PCoA uses a measure of phylogenetic community distance, called UniFrac metric, calculated as the fraction of total branch lengths on a community phylogenetic tree that are unique to one microbial population or the other. Thus, if the two populations are identical and the same members are found in both, all the phylogenetic tree branches are shared, and the UniFrac value is 0. If no member is shared by two populations, then all of the branches are unique, thus providing the maximum possible UniFrac distance. The calculated UniFrac distance metric can therefore be used as a measure of the phylogenetic similarity of the community structure between populations. A variant of the algorithm, called weighted UniFrac (Lozupone et al., 2007), was also introduced, which weighs the tree branches according to the abundance of each community member. Examples of PCoA use in ecological research are provided by (Fierer et al., 2012), (Koren et al., 2013), and (Schnorr et al., 2014).

Non-metric multidimensional scaling (NMDS)

Multidimensional scaling (MDS) is a unique ordination technique in that a (small) number of ordination axes are explicitly chosen prior to the analysis and the data are then fitted to those dimensions. Thus, if only 2 or 3 axes are chosen, there will be no non-displayed axes of variation at the end of the analysis. Similar to PCoA, a matrix of object dissimilarities is first calculated using a chosen distance metric. In non-metric MDS, ranks of these distances among all objects are calculated. The algorithm then finds a configuration of objects in the chosen N-dimensional ordination space that best matches differences in ranks (Kruskal, 1964).

Because NMDS is a numerical rather than an analytical technique, it does not produce a unique solution. A ‘stress’ parameter is computed to measure the lack of fit between object distances in the NMDS ordination space and the calculated dissimilarities among objects. The NMDS algorithm then iteratively repositions the objects in the ordination space to minimize the stress function (Dugard et al., 2014). Stress values ≤ 0.15 are considered generally acceptable (Clarke, 1993).

NMDS makes few assumptions about the distribution of data, and is often used for molecular fingerprinting techniques such as denaturing gradient gel electrophoresis (DGGE) and terminal restriction fragment length polymorphism (TRFLP) (Littman et al., 2009). For datasets with many different gradients of variance, NMDS ordination can be superior to that of other ordination techniques (Minchin, 1987). That is because with N_axis=2 all dataset variance is utilized to distribute objects in a two-dimensional NMDS ordination plot, whereas the first two dimensions of the PCA/CA/PCoA ordination only display a part of that variance (Legendre, Legendre, 2012). NMDS, however, does not perform a simultaneous ordination of both variables and objects. Note that NMDS is not an eigenvector based gradient analysis technique but rather is a mapping method. Each of its ordination axes does not correspond to a particular gradient in the original dataset, and its goal is to represent ranks of pair-wise dissimilarities among objects. Examples of how NMDS has been utilized in ecological research can be found in (Mason et al., 2014) and (Ushio et al., 2015).

Cluster analysis (CLA)

The goal of cluster analysis is to separate variables into groups based on the similarity of variables’ scores among objects, so that variables within each group (cluster) are more similar to one another than to variables in other groups (Driver, Kroeber, 1932). The algorithms minimize the within-group distances and maximize between-group distances. The same approach can also be used to distribute objects into groups. After objects/variables are clustered into individual groups, all members of the same group can be considered together. This facilitates the interpretation of high-throughput data. CLA has been particularly popular in the analyses of high-throughput microarray gene expression data, because it is more straightforward to examine just a few different types of gene expression responses after environmental perturbation instead of analyzing each individual gene behavior separately (Withman et al., 2013). Because CLA allows the use of any distance metric that can generate (dis)similarity measures, this approach can be equally well suited to ecological data (Gajer et al., 2012; Shankar et al., 2014). Below we describe the two most common types of CLA.

i) Hierarchical clustering (HCA)

Hierarchical clustering produces a joint tree-like organization of variables, with organization and length of branches indicative of the relative similarity of different variables. HCA is usually accomplished through an agglomerative approach where single variables that are most similar to each other are first successfully joined into common nodes, which are then joined with other nodes and so forth. This process continues iteratively until all variables have been incorporated into nodes that form a single connected structure. The order of how the nodes were formed and joined is displayed through the organization of the nodes into a ‘hierarchy’ tree (called dendrogram). The connectivity and length of tree branches reflect the similarity between variables and nodes. There are several different methods to compute the distances between nodes (e.g., single linkage, complete linkage, and average linkage, the latter is generally used most often), which influences relative node positioning and tree branching (Ferreira, Hitchcock, 2009). HCA provides a simple way to visualize similarities among variables, and the dendrogram structure can be used to make inferences about grouping of variables. A special case of hierarchical clustering is bi-clustering (sometimes called two-way clustering), which produces simultaneous clustering of rows and columns of the data matrix. Bi-clustering can find features (genes, microbial taxa, etc) that correlate only in a subset of objects but not in the rest of the dataset (Shankar et al., 2015; Sridharan et al., 2014).

ii) Disjoint clustering

We use this term to describe a number of related clustering techniques that aim to separate all variables or objects into individual, usually mutually exclusive, and in most cases unconnected clusters. One of the most frequently used disjoint clustering methods, K-means clustering, seeks to partition all variables into pre-defined K number of individual clusters. The initial cluster reference profiles (variable’s value for each object) are either generated randomly, defined by user, or a single random variable is chosen in the beginning to seed each cluster. All variables are then assigned to one of these pre-defined clusters based on the shortest distance of each variable to cluster centroids. Each cluster reference profile is then recalculated based on the mean of the variables in that cluster, and all variables are repartitioned into clusters. This process is repeated until a stable solution is achieved. Because initial cluster reference profiles are often chosen randomly, K-means clustering is considered nondeterministic, so repeats of this procedure on the same dataset can produce somewhat different results. Thus, it is advisable to run K-means algorithm multiple times and then choose the clustering result that achieves the lowest total error sum of squares (sum of squared distances among variables within each cluster; represents how ‘tight’ variables are within each cluster) (Arthur, Vassilvitskii, 2007). The chosen number of K clusters has a large impact on cluster profiles, and there are mathematical approaches to define the optimal number of clusters (Hastie et al., 2001). K-means clustering was used to define groups of genera that are modified by the fecal microbiota transplantation in patients with Clostridium difficile associated disease (Shankar et al., 2014), and to associate glycan degradation patterns with microbial abundances in mammalian gut (Eilam et al., 2014). Other clustering techniques are available such as TWINSPAN (Hill, 1979), self-organizing maps (Kohonen, 1982), and DBSCAN (Ester et al., 1996).

Interpretive methods

Interpretive methods described in this section can be further subdivided into three types. Symmetric approaches compare two datasets and do not distinguish variables between explanatory and response. These include canonical correlation analysis, co-inertia analysis, and procrustes analysis. Asymmetric approaches also use two different sets of variables but designate one set as explanatory (independent) variables and another as response (dependent) variables. Discussed asymmetric techniques are redundancy analysis, canonical correspondence analysis, principal response curves, and generalized linear models. Finally, we also include in this group three techniques that are focused on the statistical significance testing of multivariate datasets.

Canonical correlation analysis (CCorA)

Canonical correlation analysis is a multivariate extension of simple correlation analysis. The goal of this method is to investigate the associative relationship between two sets of variables. If we have two sets of variables, X=(x₁, x₂,…,x_n), and Y=(y₁, y₂,…,y_n), and there are correlations among the variables, then CCorA will aim to find linear combinations of the x’s and the y’s that would provide maximum correlation between X and Y. Since the goal is to find correlations, there is no assumption of which variables are predictive and which are responsive. CCorA output is a set of orthogonal canonical variates with a corresponding set of canonical correlations. The first canonical correlation is between the first canonical variates X_CV1 and Y_CV1 and has the largest value, the second – between the second canonical variates and has the second largest value, and so forth. Once the canonical variates are calculated, we can assess how each original variable contributed towards each canonical variate based on the weight coefficient of that variable. This is usually done for X_CV1 and Y_CV1 variates, since they show the strongest correlation in comparison to other pairs. The level of overall association between two variable sets can be assessed by the fraction of their joint covariance explained by all pairs of canonical variates. Examples of the use of CCorA in microbial ecology can be found in (Guan et al., 2013), (Schwartz et al., 2012), and (Wang et al., 2012b).

Co-inertia analysis (CIA)

The goal of CIA, similarly to CCorA, is to find the strongest associations between two sets of variables. The method was developed by (Doledec, Chessel, 1994) to specifically study species-environment interactions. In contrast to CCorA, the relationships are based on the co-variance rather than on a correlation. In a typical CIA approach, both sets of variables are first subjected to a gradient analysis such as PCA or CA. Using each ordination output, an axis of variance (inertia) is then found in each ordination space so as to achieve the maximum covariance between the projected object values along each axis. Further pairs of axes that maximize the remaining co-variance can be calculated under orthogonality constraints. Co-inertia is thus a measure of the similarity of object distribution in both ordination spaces and is quantitatively defined by an RV coefficient (Dray et al., 2003a; Heo, Gabriel, 1998). CIA allows each variable set to be analyzed by a different ordination algorithm (Dray et al., 2003a). Co-inertia analysis has been used in several recent studies to reveal relationships between human-associated microbiome and metabolome datasets in the gut of the elderly (Claesson et al., 2012), on the intestinal mucosal surface (McHardy et al., 2013), and in obese subjects (Zhang et al., 2015).

Procrustes analysis (PA)

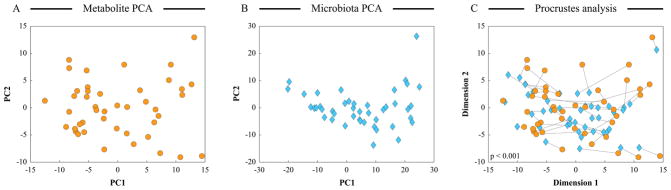
Procrustes analysis is a statistical method of comparing the distributions of multiple sets of corresponding objects (Gower, 1975; Hurley, Cattell, 1962). Because each dataset can be depicted as a cloud of objects in a multidimensional space, this analysis is also referred to as comparison of shapes. The aim of this technique is to superimpose structures, and then move, rotate, and scale them so as to achieve the best match (the smallest difference in shapes). In microbial ecology studies, Procrustes analysis is usually used to compare the distributions of the same set of objects in different ordination spaces. Here, PA minimizes the square root of sum of squared distances (sometimes called Procrustes distance) between the positions of the same object in different ordination outputs. For example, we have carried out microbial and metabolite profiling of the same set of fecal samples obtained from several cohorts of children (Shankar et al., 2013; Shankar et al., 2015). Several different ordination analyses indicated that samples could be separated largely based on their cohort assignment in both microbiota and metabolite datasets. By employing Procrustes analysis of the distributions of samples in PCA plots based on these two datasets, we showed that the separation of samples was congruent between metabolite and microbial datasets. Position of a particular sample in microbiota-based ordination plot was generally close to its placement in the metabolite-based ordination chart (Figure 2). By randomly changing the object IDs in one of the sets, a statistical significance of the observed minimized Procrustes distance was obtained (Shankar et al., 2015). Similar to CIA, PA can be applied to outputs from any ordination method. Thus, it can also be used to assess if multiple ordination techniques applied to the same object-by-variable dataset produce similar results (Bassett et al., 2015). Other examples of PA use are provided in studies by (Claesson et al., 2012), (McHardy et al., 2013), and (Zhang et al., 2015).

Figure 2. Use of procrustes analysis to test for congruency between ordination outputs.

PCA was performed on centered log-ratio transformed compositional metabolite binned data (panel A) and compositional microbiota phylotype data (panel B) for the same set of human fecal samples. Raw metabolite and microbiota datasets were taken from (Shankar et al., 2015). PCA results were provided as input to procrustes analysis to compare object positioning in PCA ordination spaces. Panel C displays the first two dimensions of the PA output. The distance between each sample position on two PCA plots is indicated by connecting line. Shorter lines represent more similar object positioning on both PCA plots. P-value for statistical significance of observed object separation congruency was generated using randomization of object labels.

All three symmetrical techniques described above are closely related. Compared to CCorA, both CIA and PA impose no constraints on the number of variables in the datasets compared to the number of objects, and they have fewer assumptions (Legendre, Legendre, 2012). CIA provides a more readily interpretable quantitative assessment of the strength of the global association (RV coefficient), while PA can be run on a wider range of input tables. Both CIA and PA can be applied to more than 2 datasets simultaneously (Bady et al., 2004; Ten Berge, 1977). An approach merging CIA and PA within the same analysis has been proposed (Dray et al., 2003b).

Redundancy analysis (RDA)

Redundancy analysis is a type of constrained ordination that assesses how much of the variation in one set of variables can be explained by the variation in another set of variables. It is the multivariate extension of simple linear regression that is applied to sets of variables (Rao, 1964; Van den Wollenberg, 1977). RDA is based on similar principles as PCA, and thus assumes linear relationships among variables. RDA is in fact a canonical version of PCA where the principal components are constrained to be linear combinations of the explanatory variables. If the expected relationship between response variables and environmental gradients is unimodal rather than linear (see Box 5), then the canonical correspondence analysis described below is more appropriate.

A combination of two datasets is required to run RDA: the first dataset contains response (dependent) variables (species presence or abundance, metabolite levels, etc) and the other set contains explanatory (predictive) variables (such as environmental variables or experimental treatments measured in the same samples or sites; see Figure 1). “Redundancy” expresses how much of the variance in the set of response variables is explained by the set of explanatory variables. The fraction of the total variance observed in response variables that is explained by all the explanatory variables is a useful indication of how much variance in the species distribution, for example, is due to differences in environmental factors between sites. The output of RDA is an ordination that is usually shown on a two-dimensional ‘triplot’, with constrained RDA dimensions used as axes. Each object is depicted by a point, response variables are represented by arrows originating from the coordinate system origin, and explanatory variables by either arrows (quantitative variables) or points (categorical variables). Because triplots display a lot of data on a single plot, their interpretation is more challenging. On a distance triplot, distances between objects represent the between-object similarity; the angles between arrows of response variables and arrows of explanatory variables represent the found associations between those variables. Finally, the projection of an object onto an arrow approximates the value of the corresponding variable in this object. A detailed description of the interpretation of ordination diagrams can be found in (ter Braak, Verdonschot, 1995) and (Šmilauer, Lepš, 2014). Alternatively, to simplify interpretation, one can carry out partial constrained ordination such as principal response curves analysis described below (see also Box 4).

A special variant of RDA, called distance-based RDA or db-RDA, can be used when the response data are available as dissimilarity matrix, or when the use of Euclidean distance is inappropriate (Anderson, Willis, 2003; Legendre, Anderson, 1999). db-RDA is thus a constrained version of PCoA, and it provides an opportunity to use phylogenetic and ecological distances in constrained ordination analysis (Shakya et al., 2013). Examples of the use of RDA for constrained analysis of ecological datasets are available in the works by (Rajilic-Stojanovic et al., 2010), (Ringel-Kulka et al., 2013), and (Zhang et al., 2012a).

Canonical correspondence analysis (CCA)

The goal of the CCA is similar to that of RDA as it too aims to find the relationship between two sets of variables X and Y. However, whereas RDA assumes a linear relationship among variables, CCA expects a unimodal relationship. Thus, CCA is a canonical form of correspondence analysis of the response variable set that is constrained by the set of explanatory variables (ter Braak, 1986). Note that canonical correlation analysis can also be abbreviated as CCA in the literature. These are, however, two different techniques. The visual output of CCA is a triplot similar to that of RDA, where in addition to objects and variables typically shown on a CA plot, the explanatory variables are also shown as either arrows (quantitative variables) or points (categorical variables). An example of CCA plot interpretation is provided below. Examples of CCA utilization in ecological studies can be found in (Wang et al., 2012a), (Yan et al., 2015), and (Zhang et al., 2013).

Principal response curves (PRC)

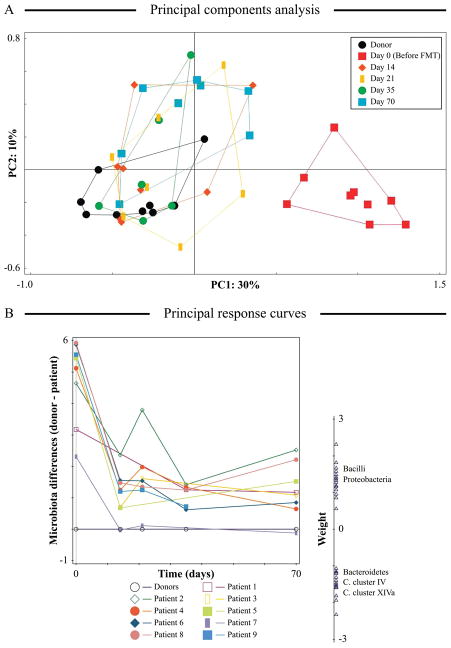
When datasets contain a large number of explanatory and response variables, interpretation of RDA and CCA plots can become quite challenging, especially when there are interaction effects among explanatory variables (ter Braak, Šmilauer, 2015). In such cases, an influence of any individual explanatory variable on the observed distribution of objects is not readily identified. To facilitate visual representation of such complex constrained analyses and to limit interpretation to a single effect (single explanatory variable) and an interaction with a second effect, principle response curves method can be used (not to be confused with a distinct “principal curves” technique proposed by (De’ath, 1999)). PRC was initially developed by (van den Brink, ter Braak, 1999) to visualize and interpret differences between treatment and control communities over time. PRC algorithm carried out a partial RDA ordination (see Box 4) to partition the variance between individual effects and their interaction term. The canonical coefficients obtained in RDA for each sample were then displayed in a line chart (principal curve) with time plotted on the X axis (van den Brink, ter Braak, 1999). PRC is especially useful for the analysis of longitudinal series of measurements, since time-dependent effects can be clearly isolated in PRC from other effects (see Figure 6B). PRC was further extended by (van den Brink et al., 2009) to use a single reference point as control for each series of measurements, allowing longitudinal analysis of individual communities. Multiple sets of objects can be displayed on the same chart as separate response curves, and time can be substituted by other gradient present in the experimental design or the dataset (ter Braak, Šmilauer, 2015; van den Brink et al., 2009). The congruency between each variable response pattern and computed principal response curve is provided by variable weights which are displayed on a separate chart (see Figure 6B; (van den Brink, ter Braak, 1999)). Though PRC is yet to be extensively utilized in microbial ecology research, few examples are provided in the reports by (Zhang et al., 2012b) and (Fuentes et al., 2014).

Figure 6. Application of principal components and principal response curves analyses to visualize changes in microbial compositions over time.

(Panel A) PCA was performed on log-transformed HITChip microarray data to assess microbiota composition similarity between pre- (day 0) and post-FMT (day 14 to day 70) fecal samples from Clostridium difficile infected patients and fecal samples from FMT donors. (Panel B) Principal response curves analysis performed on the same dataset. X axis shows collection time points. Microbial community changes over time are depicted on Y axis as the difference between microbiota composition of a given patient sample and that of the corresponding donor. Variable weights for individual microbial groups are depicted on the weight scale. The figure was adapted with permission from Figure 6 provided in the study by (Fuentes et al., 2014).

Generalized linear modeling (GLM)

Generalized linear modeling is a term that describes a statistical approach to relate response variable(s) to the linear combinations of the explanatory (predictor) variable(s) (Nelder, Wedderburn, 1972). GLM is an extension of the standard linear models such as regression and analysis of variance (ANOVA). The power of GLM lies in its ability to generate not only regression models for continuous response variables, but also models for discrete and categorical response variables (Nelder, Wedderburn, 1972). In GLM, the values of response variable are ‘predicted’ from a linear combination of explanatory variables by connecting them via a so-called link function. Many different link functions can be chosen (examples include log, inverse, power, root, and logit functions), and several different distributions of the response variable may thus be defined (examples include linear, Gaussian, logistic, and beta distributions). This provides GLM with a tremendous flexibility. The output of GLM is i) a set of regression coefficients defining the modeled relationship between explanatory and response variables, and ii) statistical assessment of the fit of the model to the data (Fox, 2008). The generated model can then be evaluated to reveal the strength and statistical significance of the relationship between each predictor variable and the response variable. Multivariate extension of GLM is available (Warton, 2011), an ordination algorithm based on GLM dimensionality reduction has been developed (Yee, 2004), and further extension of GLM, called generalized additive modeling, has been made (Hastie, Tibshirani, 1986). Several recent studies have indicated that for ecological datasets that often contain many zeroes, GLM carried out on the dataset of measured variables performed better than standard parametric analyses conducted on log- or power-transformed values (O’Hara, Kotze, 2010; Warton et al., 2012).

Mantel test, analysis of similarities (ANOSIM), and permutational multivariate analysis of variance (PERMANOVA)

Mantel test, ANOSIM, and PERMANOVA are multivariate statistical tests of significance. Mantel test typically compares two distance matrices that were calculated for the same set of objects but that are based on two independent sets of variables (e.g. a species dissimilarity matrix and site distance matrix) (Mantel, 1967). The test calculates the correlation between values in the corresponding positions of two matrices. Significance of the linear relationship between matrices is assessed through permutation of objects (see Box 6). The goal of Mantel test is similar to that of CCorA, CIA, and PA (Lisboa et al., 2014).

Box 6. Resampling tests of statistical significance.

In many cases, after running a particular multivariate statistical analysis, an investigator desires to obtain some measure of confidence in the observed relationship or object separation. Such measure of confidence is usually acquired through a statistical test for significance. In parametric methods, the output is compared to the probability distribution model that was used as a basis for a particular technique. The probability of observing the obtained output by chance is then represented by a p-value. While this approach works well for methods such as regression and correlation analyses, for many ordination techniques no expected data distribution is defined before running the analyses. Thus, parametric statistical testing cannot be applied to these techniques.

For such cases, one approach to assess statistical confidence of the obtained output is through the use of resampling methods that include bootstrap, jackknife, and permutation tests (Desu, Raghavarao, 2003; Efron, 1979; Tukey, 1958). The principle of these techniques relies on the random resampling of the actual measured data to generate a reference distribution, which the observed distribution is tested against. In bootstrap tests a subset of data is drawn randomly with replacement from a set of data points; in jackknife tests a subset of data points is left out systematically and the analysis output remeasured; in permutation tests object labels are randomly exchanged. The statistical significance (i.e., probability of observing the calculated output by chance) is then computed as the fraction of all simulated outcomes that are at least as extreme as the one originally observed. Because these tests make no assumptions about data distribution, they can be used practically on any dataset irrespective of the assumed relationship among variables.

For example, we have incorporated the permutation analysis of inter-class distance based on the Davies-Bouldin (DB) cluster separation index (Davies, Bouldin, 1979) to assess the statistical significance of the observed object separation between classes in principal components analysis (Shankar et al., 2013; Shankar et al., 2015). Specifically, we calculated the DB distance metric as the ratio of the average inter-class distance among all objects to the average of all intra-class distances. The permutation algorithm then randomly reassigned the object labels, and the DB distance metric was again computed. This process was repeated 10,000 times to produce a reference distribution of DB metric. The significance of object class-based separation observed in PCA ordination was calculated as the fraction of all permuted DB metric values that were equal or higher than the one obtained for the original dataset (Shankar et al., 2013).

For constrained analyses, the significance of the constrained ordination model can be obtained by first calculating the fraction of total variance in the dataset of response variables that is explained by canonical axes, and then comparing this statistic to the distribution of such fractions obtained through a permutation analysis of the dataset (Šmilauer, Lepš, 2014).

ANOSIM tests for significant difference between two or more classes of objects based on any (dis)similarity measure (Clarke, 1993). It compares the ranks of distances between objects of different classes with ranks of object distances within classes. The basis of this approach is similar to the NMDS ordination technique described above. Since ANOSIM is based on ranks, it has fewer assumptions compared to the regression techniques such as multivariate analysis of variance (MANOVA).

PERMANOVA is a non-parametric method to conduct multivariate ANOVA and test for differences between object classes (Anderson, 2001). Any dissimilarity metric can be used, and the test statistic is calculated from the comparison of dissimilarities among inter-class objects to those among intra-class objects. Significance levels (p-values) are obtained through permutation (see Box 6).

Note that most ordination techniques can also assess the statistical significance of observed object distribution via permutation-based analysis (see Box 6).

Discriminatory methods

Discriminant function analysis (DFA)

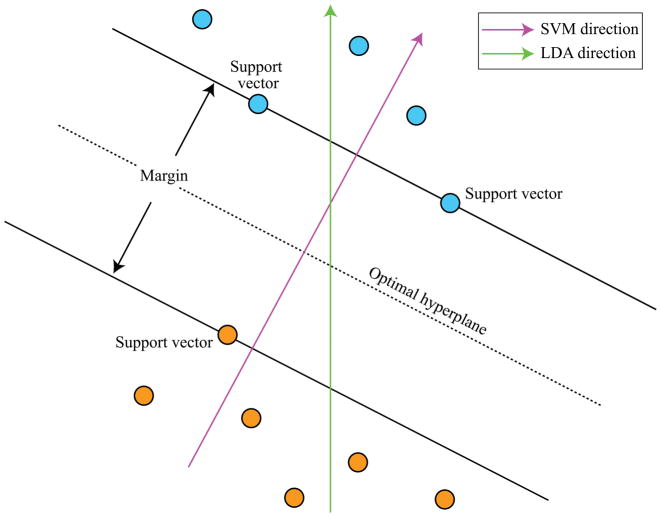
Discriminant function analysis comprises a group of ordination techniques that find linear combinations of observed variables that maximize the grouping of objects into separate classes (Fisher, 1936). Here, the measured variables are the predictor variables, and the variable that defines object classes is treated as the response variable (also called grouping variable). In literature, DFA is also called either linear discriminant analysis (LDA), or canonical discriminant analysis (CDA, also called multiple discriminant analysis; usually implies that more than two classes of objects are available). Algorithmically, DFA methods generate latent variables (called discriminant functions or DFs) that maximize the formation of coherent, well-separated clusters of objects. Multiple discriminant functions can be extracted, each orthogonal to the others, until their number equals the number of predictor variables or the number of object classes minus one, whichever is smaller. An eigenvalue associated with each DF defines the discriminating “power” of that function. DFA techniques are related to PCA; however, unlike PCA which summarizes total variation in the dataset, LDA and CDA derive synthetic variables that specifically maximize the between-class group dispersion. Because each discriminant function is a weighted linear combination of the measured predictor variables, the weights (called discriminant coefficients) can be used to define the contribution (i.e., importance) of each predictor variable to the observed discrimination between classes of objects. Results of the DFA can be visualized through a scatter plot with discriminant functions serving as synthetic axes.

Like PCA, DFA is based on the non-iterative, eigenvector-based solution. As a result, it is more computationally efficient than iterative methods, and is appropriate for extremely large datasets. A model of class prediction can also be generated during discriminant analysis. Such model can be used to provide predictions for new (‘unknown’) object based on the values of measured variables in that object (Putnam et al., 2013). Examples of the use of different DFA variants in ecological studies are available in the reports by (Gilbert et al., 2012) and (Koenig et al., 2011).

Orthogonal projections to latent structures discriminant analysis (OPLS-DA)

OPLS-DA is based on the principle of partial least squares (PLS) regression; PLS itself is an extension of the multiple linear regression model (Wold, 1966). The goal of PLS regression is to predict response variable(s) Y from a (large) set of predictor variables X. PLS regression reduces the set of predictor variables to a smaller set of uncorrelated components and then performs least squares regression on these components. In the process, both variables X and Y are projected to a new space. This process is called projection to latent (hidden) structures (Abdi, Williams, 2010). Compared to multivariate regression, PLS has fewer assumptions (it can use predictor variables that are collinear and not independent) (Tobias, 1995). An additional modification to the PLS regression was developed by Trygg and Wold (Trygg, Wold, 2002), who introduced a way to remove systematic variation from the predictor variable dataset X that is not correlated to the response variable dataset Y, i.e., to remove variation within X that is orthogonal to Y. The advantage of such orthogonal projections to latent structures (OPLS) method is that a single latent variable (designated “T”) is used as a predictor of the Y. All variability in X is separated into predictive (T) and uncorrelated information (T_orthogonal), and the two components can be analyzed separately. In OPLS discriminant analysis, the Y is a binary class-designating variable, and the analysis aims to find the best separation between classes of objects along the T axis, while all variation unrelated to class separation is distributed along the T_orthogonal axes (Westerhuis et al., 2010). Similar to DFA, each variable’s loading indicates its contribution to the OPLS model. The generated model can then be applied to a new object to predict its class given the values of its X variables. The OPLS-DA output provides measures of the model fit (R²), model predictive power (Q²), and model accuracy based on a cross-validation procedure. Examples of OPLS-DA use in multivariate ecological analyses can be found in (Ramadan et al., 2014) and (Shankar et al., 2013).

Support vector machine (SVM)

Support vector machine is a supervised machine learning algorithm that can be used for both classification and regression (Cortes, Vapnik, 1995; Vapnik, 1979). Using a training set of objects separated into classes, the SVM algorithm finds a hyperplane in the data space that produces the largest minimum distance (called margin) between the objects that belong to different classes. The larger the margin, the lower the expected prediction (i.e., misclassification) error. As shown in Figure 3, in comparison to DFA, which uses differences in class means to separate objects (Welling, 2005), SVM only considers the objects on the edges of the margin (these are called support vectors). This increases class separation and reduces expected prediction error. SVM can be used for both linear and non-linear based discriminatory analyses (Gu et al., 2010), and is considered to be a superior DA method for high-dimensionality datasets with small sample size, especially when variable selection and filtering are included in the algorithm (Gokcen, Peng, 2002; Knights et al., 2011). While SVM has yet to be used extensively in microbial ecology, at least one example of its use in microbial ecology is available (Yang et al., 2006).

Figure 3. Directions of class discrimination in linear and support vector machine based discriminant analyses.

Binary classification problem is depicted. Colored circles represent different objects separated into 2 classes. The figure was adapted with permission from Figure 1 provided in the (Gu et al., 2010) study.

Random forest (RF)

Random forest is an ensemble learning approach based on the use of decision (classification) trees. Decision tree learning seeks to construct a statistical model to predict the values of response variable(s) based on the given values of predictor variables. The model is obtained by iteratively partitioning the space of predictor variables and establishing a value of the response variable within each partition (Loh, 2011). The result of such partitioning can be represented as a decision tree containing a set of if-then logical conditions. Random forest ‘grows’ many different decision trees for the same dataset and thus is a type of ensemble classifier. The existing dataset is used to build predictive classification trees and ‘train’ the algorithms. To classify a new object, the input data (values for all predictor variables) are provided to each tree, which then generates an output classification (called a vote). The RF then chooses the classification that garnered the most votes among all the trees in the forest.

Random forest has been shown to achieve very high discriminating power and accuracy of classification (Cutler et al., 2007). This is because RF voting consolidates decisions across thousands of individual trees that together provide very high overall classification accuracy despite potentially low classification accuracy of some individual trees. This technique also does not suffer from high variance or bias that single classification model can have. The accuracy of the constructed model can be calculated by the cross-validation technique (Japkowicz, Shah, 2014), while the similarities among objects can be assessed by computing the average proximity (fraction of trees where objects occupy the same position on a particular tree) for each pair of objects. Variable importance in the classification model can be estimated in RF by permutation tests (see Box 6). Specifically, the values of one of the predictor variables are randomly swapped in the dataset and the number of votes for the correct assignment in all trees is then calculated. The difference in the number of votes between the ‘untouched’ forest and the variable-permuted forest represents the importance score of that variable in the RF model. Results of RF analysis can be visualized as a MDS scatterplot of matrix of proximities among objects. Random forest has been used in several recent studies as described by (Lozupone et al., 2013), (Shankar et al., 2013), and (Yatsunenko et al., 2012).

In a recently published article, Knights and colleagues compared the performance of several different discriminatory and classification techniques (Knights et al., 2011). Data describing the community composition of human-associated microbiota were used as benchmarks, and several different algorithms including SVM and RF were compared. RF achieved the best performance among the compared techniques, followed closely by SVM applied to a filtered set of OTUs (Knights et al., 2011).

Examples of the use of multivariate techniques in microbial ecology research

Study example 1: PCoA

Koren et al. assessed the relative composition of human fecal microbial communities by exploratory ordination (Koren et al., 2013). The authors performed PCoA using Jensen-Shannon divergence metric calculated on high-throughput 16S rRNA gene sequence data obtained from the set of Human Microbiome Project fecal samples. The position of samples in the PCoA ordination space was found to reflect the relative abundances of key members of fecal microbial communities. To illustrate this concept, the authors visualized on a PCoA plot the relative abundances of different genera in each fecal sample according to a color gradient as shown in Figure 4. Three prominent genera of human gut microbiota – Bacteroides, Prevotella, and Clostridium – revealed the most striking abundance gradients. Specifically, distribution of samples across PC1 axis reflected samples’ Bacteroides relative abundances; sample distribution along PC2 axis corresponded to samples’ Prevotella abundances. A similar strong gradient was observed for genus Clostridium, however this effect contributed to the sample dispersion observed along both PC1 and PC2 axes (see Figure 4). Thus, the exploratory PCoA analysis revealed that the abundances of Bacteroides and Prevotella served as the main drivers of variation in the fecal microbiota composition, concordant with their role as keystone genera of gut microbiota enterotypes (Arumugam et al., 2011).

Figure 4. Application of PCoA to arrange fecal human samples based on microbiota structure.

Jensen-Shannon divergence metric was used to calculate distances among all fecal samples obtained in the Human Microbiome Project (Peterson et al., 2009). Associations of sample distribution in PCoA space with relative abundances of genera Bacteroides (panel A), Prevotella (panel B), and Clostridium (panel C) are shown. Each sample point is color-coded based on the abundance of the corresponding genus according to the color gradient as shown in each figure legend. Samples are represented as either circles or triangles to denote microbiota enterotype cluster. The figure was adapted with permission from the Supplementary Figure S13 provided in the (Koren et al., 2013) study.

Study example 2: CCA

The utility of canonical correspondence analysis was demonstrated by ter Braak and Verdonschot, who applied CCA to the macroinvertebrate distribution data from two man-made stream tributaries (ter Braak, Verdonschot, 1995). The goal was to identify major environmental gradients and their effects on the species distribution patterns. The dataset consisted of counts data for species collected from each site as well as measurements of several environmental variables. While this example does not describe a microbial system, it offers an excellent illustration of the interpretation of gradient analysis plots. The following insights can be made from the CCA triplot (Figure 5):

Figure 5. Interpretation of CCA to relate macroinvertebrate species distribution to environmental sites and gradients.

The figure displays a CCA triplot showing the relationships among sites (circles), species (triangles), and environmental variables (arrows and squares). Site labels (U and L) and colors (orange and cyan) represent the stream designations; site number denotes the ranked distance from the stream source. Black arrows denote quantitative environmental variables; black squares represent qualitative environmental variables. Black triangles indicate distribution optimum for each species. Select species are displayed on the plot and are abbreviated as follows: Ct – Ceratopogonidae, Dl – Dendrocoelum lacteum, Et – Erpobdella testacea, Gc – Glossiphonia complanata, Hl – Haliplus lineatocollis, Hd – Helodidae, Ma – Micropsectra atrofasciata, Mf – Micropsectra fusca, Ms – Micropterna sequax, Po – Prodiamesa olivacea, and Ss – Stictochironomus sp. The figure was adapted with permission from Figure 3 provided in (ter Braak, Verdonschot, 1995) study.

1. The distance between site and species position on the triplot is indicative of the abundance of that species at that site: “the inferred abundance of a species is maximal if the site point coincides with the species point and decreases in all directions the farther away the site point is” (ter Braak, Verdonschot, 1995). Thus, we can conclude that species Et is abundant in sites U15 – U19, whereas sites L15–L20 are optimal for Ms, Ss, and Hd species (see Figure 5 legend for species abbreviations).

2. Interpretation of quantitative environmental variables can be summarized as “the arrow points in the direction of maximum change in the value of the associated variable, and the arrow length is proportional to this maximum rate of change” (ter Braak, Verdonschot, 1995). Thus, the “source distance” variable designates the distance of each site from the stream source, and the site ranking is consistent with the direction of the arrow. The difference in species distribution between L and U sites is small near the stream source (low ranks) but increases progressively the farther from the source the sites are (higher site ranks).

3. The relative positioning of environmental variables and species triangles indicates the optimum of species distribution along these environmental gradients. For example, for species Dl and Et, the distribution optimum is located the farthest along the gradient of electric conductivity. A similar interpretation can be extended to the qualitative variables. As stated by the authors, “sites that belong to a particular class” (“shrub” or “no shrub”) “are scattered around the class point, simply because, by definition, each class is at the centroid of the sites that it contains”. By this interpretation, sites L15 – L20 have high shrub coverage.

This example demonstrates how CCA triplots can provide a large number of insights and valuable interpretations, and such methods of direct gradient analyses are well suited to examine the relationships between environmental gradients and response variables (e.g., species).

Study example 3: PRC

Principal response curves analysis was used by Fuentes et. al. to depict the time-dependent changes in distal gut microbiota composition of patients with Clostridium difficile infection (CDI) who have undergone fecal microbiota transplantation (FMT) (Fuentes et al., 2014). The HITChip phylogenetic microarray was used to determine the distal gut microbiota composition from feces collected from CDI patients before (day 0) and after FMT (day 14 to day 70) and from their corresponding donors. Principal components analysis was first performed on the log-transformed microbiota dataset (probe signal intensities) to visualize main gradients of variability (Figure 6A). PC1 clearly separated all patient pre-FMT samples from donor and post-FMT samples. However, the samples of the latter group were all clustered together, which did not allow the assessment of the effect of factors such as time, interpersonal differences, and donor variability on the distribution of samples in PCA space. To assess such possible effects more specifically, PRC analysis was used to isolate the relationships between a single environmental variable (time) and the observed microbiota changes (Figure 6B). Assessment of the PRC chart indicated that gut microbiota changes occurred quickly after FMT procedure and community maintained similarity to that of the donor for at least 70 days, confirming a previously reported observation (Shankar et al., 2014). Additionally, the authors utilized the weights assigned by PRC analysis to different microbial groups to determine the main drivers of the changes in the microbiota profiles between pre- and post-FMT time points. Groups with positive weights such as Bacilli and Proteobacteria were shown to be higher in pre-FMT samples and were depleted as a function of time in the post-FMT samples, while groups with negative weights such as Bacteroidetes and Clostridium clusters IV and XIVa followed the opposite profile.

This study presented an excellent example of the utility of PRC to visualize time-dependent changes in community organization, and showcased how partial ordination analysis can facilitate the interpretation of ordination results of complex datasets.

Study example 4: Random forest

Random forest discriminatory analysis was employed by Lozupone and colleagues to assess the distinctiveness of fecal microbiota between healthy subjects and HIV-infected patients (Lozupone et al., 2013). The authors utilized high-throughput sequencing of 16S rRNA gene to profile fecal microbiota from healthy controls and patients with chronic untreated HIV. The sequencing data were clustered to generate operational taxonomic unit (OTU) tables and subsequently subjected to random forest analysis. RF generated a class prediction model (healthy vs HIV), which was then used to classify unknown samples. Classification of ‘unknown’ samples achieved a 96% accuracy rate. This indicated that HIV-associated fecal microbiota displayed specific differences between healthy and HIV gut. Taking advantage of random forest’s ability to assign an importance score to each OTU variable, the authors identified discriminatory OTUs that marked sample donors as healthy or HIV. OTUs from genus Bacteroides were found to be depleted in HIV patients compared to healthy controls. Conversely, members of Erysipelotrichaceae, Veillonellaceae, and Ruminococcoceae were enriched in HIV patients. In summary, RF analysis generated a model that used fecal microbiota OTU abundances to distinguish between healthy and HIV-infected subjects.

Limitations of multivariate analyses

Despite their undoubted usefulness, multivariate analyses also exhibit some limitations. The outputs of these algorithms are more difficult to interpret compared to those generated by univariate analyses (though it is much less time consuming to interpret single multivariate analysis then hundreds of individual univariate outputs), and the assumptions of a particular method are sometimes not easy to assess or meet. It is also important to remember that revealed associations among variables and patterns of object distribution do not inherently imply causality (unless explanatory variables are experimental treatments), and that synthetic ordination axes or cluster groups might not necessarily match any biological effects or gradients. Finally, many multivariate techniques are very computationally demanding and require significant computing resources when applied to very large datasets.

The majority of multivariate statistical techniques discussed here define similarities and/or distances among objects based on the distribution of variables’ values across these objects. The values of different variables are combined to generate the object distance or dissimilarity matrix. How different variables are combined impacts the output and interpretation of multivariate statistical techniques and can generate artifacts as described in detail by (Warton et al., 2012). The authors point out that in real datasets different variables (taxon abundance, metabolite concentration, etc) usually display unequal mean-variance relationships. This inequality can lead to the ordination displaying dispersion effects (differences among object classes in variables’ variances) instead of the location effects (differences among object classes in variable means), because most distance-based techniques are not able to distinguish between these two effects (see Figure 7). The main limitation is not the ordination technique itself, but the distance metric used, and the authors show that most currently used distance metrics do not account correctly for the mean-variance relationship when combining data across variables. Note that the location-vs-dispersion effects are less prominent in the constrained ordination, because constraints specifically focus on location differences in the dataset (ter Braak, Šmilauer, 2015).

Figure 7. Influence of mean-variance bias on the separation of location and dispersion effects in ordination analyses.

Panels in section A show schematic representation of ordination results of object separation that display location, dispersion, or location and dispersion effects. Panels in section B display a schematic presentation of the effect of different mean-variance relationships on the object distribution in Euclidean distance based MDS ordination. Assumed vs typical mean-variance relationships are shown on the left panel; diamonds represent different variables. Distribution of variables along the ‘mean’ axis represents the described difference (location effect) in the values of variables between classes of objects. Middle panel shows the visualization of ordination results when the equal variance assumption is correct. The right panel shows the ordination results for a more typically observed mean-variance relationship. Colored circles represent different objects separated into 2 classes. The figure is based on Figures 2 and 3a in (Warton et al., 2012).

Well chosen data transformation applied to the data prior to statistical analysis (discussed in Box 2) can lessen the extent of mean-variance bias in multivariate datasets, but it does not remove it completely. Standardization of variable variances prior to multivariate analysis is not very helpful, because it reduces the effect of differences in variable means among classes and thus reduces true biological differences and statistical power of the analysis. Two solutions to the issue of unequal mean-variance distributions were offered by the authors. Standardization of within-class variance for each variable during the analysis solves the mean-variance issue but is very computationally intensive especially for techniques that use permutation to derive statistical significance of class separation (see Box 6). Alternatively, multivariate generalized linear modeling (Warton, 2011) allows the choice of different mean-variance functions and was shown to perform well (O’Hara, Kotze, 2010; Warton et al., 2012). To avoid possible artifacts in the multivariate analysis output, we recommend that the within-class variances for each variable are compared among all object classes, and are adjusted if found to be unequal.

Choice of the multivariate analysis

The multitude of different multivariate analytical techniques that were described above provides many choices for the selection of an algorithm to analyze a particular large scale dataset. In Figure 8 we offer suggestions of some of the appropriate choices based on the research goal, data input structure, and expected relationships among variables. Exploratory methods are in general applied first to extract the main gradients of variation in the data with unconstrained ordination techniques, and to identify groups of similar variables and/or objects with cluster analyses. To relate variability observed in the response variables to the values of additional explanatory variables, constrained gradient analysis should be performed. If the goal is to differentiate among a priori known classes of objects based on variable scores and/or to predict class membership of new/future observations, discriminant analyses and decision trees can be used.

Figure 8. Diagram of potential choices of multivariate techniques based on the research goal, assumed relationship among variables, and input data structure.

DM – assumed relationship depends on the chosen distance metric; ORD – assumed relationship depends on the ordination technique used; LF – assumed relationship depends on the chosen link function; KF – SVM model can be linear or non-linear if a non-linear kernel function is used.

The choice of a particular technique within a category usually depends on the input data structure and the assumed relationship among variables as we describe in Figure 8. While available evidence based on the analysis of simulated datasets with known gradients does not provide a clear consensus on the best approach among linear, unimodal, and distribution-free techniques (Austin, 2013), several suggestions can be made.

In general, to analyze short environmental gradients and continuous variables expressed as absolute values, linear methods such as PCA and RDA are used most often (see Box Figure 2). To model long environmental gradients as well as relative abundances and count data, the application of unimodal ordination techniques such as (D)CA and CCA is usually advised (Austin, 2007; Ramette, 2007). Log-ratio transformation applied to the raw data can address the problem with data compositionality (see Box 3). For datasets not conforming to most common statistical assumptions or distribution models, the use of non-parametric (distribution-free) methods is appropriate. When similarities among objects are desired to be assessed based on one of the ecological distance calculations, the use of PCoA, NMDS, and db-RDA techniques is advocated.

When several different ordination outputs are available for the same set of objects, co-inertia and procrustes analyses can be used to assess the congruency of the results. To determine the fraction of the total variation in measured (response) variables attributed specifically to different environmental gradients, variation partitioning can be carried out (see Box 5).

To find which variables are responsible for the observed differences among classes of objects, discriminatory analyses can be employed. OPLS-DA, SVM, and RF all showed good performance in different comparative studies, with RF currently being favored in microbial community comparisons (Knights et al., 2011). To avoid the problem of model overfitting, model regularization and variable selection and filtering should be applied during discriminatory analyses, especially for datasets with large number of variables (e.g., OTU tables) (Chen et al., 2015).

Closing comments

The development and continuing advances in the high-throughput molecular approaches have led to a dramatic shift in the type and amount of data generated by microbial researchers. It is a less common case now where experimental results can be analyzed manually or with the use of simple parametric statistics and univariate analyses. Instead, the experimental data are often represented by large matrices of data points. This large-scale structure of obtained data limits researcher’s ability to interpret the results without significant reduction in dataset complexity. Multivariate analyses described in this review are well suited for this task, and we provided a general overview of the most frequently used multivariate statistical methods to assist ecologists and other researchers in the choice of appropriate approaches for the analyses of their datasets.

The popularity of multivariate analyses continues to increase as more and more researchers start to take advantage of high-throughput experimental platforms. While the initial high-throughput studies tended to employ simpler exploratory techniques such as PCA and PCoA, there is a recent trend to move to interpretive and discriminatory ordination approaches and to perform more rigorous multivariate hypothesis testing. The use of more recently developed techniques including principal curves and surfaces (De’ath, 1999; Hastie, Stuetzle, 1989), dynamic factor analysis (Zuur et al., 2003), random-effect ordination (Walker, Jackson, 2011), coreferentiality (Fesel, 2012), multidimensional fuzzy set ordination (Roberts, 2009) and fuzzy clustering (Bezdek, 1981), elastic net regression (Zou, Hastie, 2005), and regularized discriminant analyses (Chen et al., 2015; Friedman, 1989; Zhao, Wong, 2014) is expected to further advance these studies and improve the validity and robustness of the outcomes. All these techniques provide exciting opportunities to link ecological and functional measures of microbial communities with environmental gradients, host (patient) information, and time and space variables. Ecological theories can be tested at the whole community level, and microbial community structure and function can now be used to facilitate discrimination between different sites, environments, or between human health and disease (Lozupone et al., 2013; Shankar et al., 2015). All of such studies provide deeper appreciation for the importance of ecological analyses of biological systems, and will reveal further mechanisms of interactions among members of complex communities and between host and microbial partners.