Theoretical estimates of exposure timescales of protein binding sites on DNA regulated by nucleosome kinetics

Abstract

It is being increasingly realized that nucleosome organization on DNA crucially regulates DNA–protein interactions and the resulting gene expression. While the spatial character of the nucleosome positioning on DNA has been experimentally and theoretically studied extensively, the temporal character is poorly understood. Accounting for ATPase activity and DNA-sequence effects on nucleosome kinetics, we develop a theoretical method to estimate the time of continuous exposure of binding sites of non-histone proteins (e.g. transcription factors and TATA binding proteins) along any genome. Applying the method to Saccharomyces cerevisiae, we show that the exposure timescales are determined by cooperative dynamics of multiple nucleosomes, and their behavior is often different from expectations based on static nucleosome occupancy. Examining exposure times in the promoters of GAL1 and PHO5, we show that our theoretical predictions are consistent with known experiments. We apply our method genome-wide and discover huge gene-to-gene variability of mean exposure times of TATA boxes and patches adjacent to TSS (+1 nucleosome region); the resulting timescale distributions have non-exponential tails.

INTRODUCTION

One of the crucial contributor to cellular function and fate is the ‘state’ of its chromatin, which is a dynamic structure formed of DNA and myriads of proteins (1–3). The key constituents of the chromatin are nucleosomes—DNA wrapped around histone octamer (4). It is thought that one major role of nucleosomes is to occlude certain DNA sequences from getting exposed and thereby prevent uncontrolled binding of non-histone proteins at various crucial locations (5). However, during important cellular processes (e.g. transcription, replication and DNA-repair), nucleosome disassembly paves the way for local DNA accessibility (6,7). Once these processes are completed, the DNA typically wraps back and reassembles into nucleosomes (8). This constant wrapping, unwrapping and relocation of nucleosomes are assisted by ATP-dependent chromatin remodelers (e.g. RSC, SWI/SNF, ACF) (9–12). Thus the interplay of nucleosome dynamics and binding of non-histone proteins regulate the ‘state’ of chromatin and its corresponding functionality.

A major focus of many recent experiments has been to understand the nature of positioning of nucleosomes along DNA and the factors that control this positioning. This is achieved by measuring a physical quantity known as nucleosome occupancy (8,13–18). It is the probability of coverage of a base pair (bp) of DNA by a nucleosome, obtained from an ensemble of cells under same conditions, using MNase digestion, chemical cleavage, etc. (13–15,18,19). Such studies over years have shown that the in vivo positioning is influenced by a number of factors such as ATP-dependent molecular machines (11,13), DNA sequence (15,20–22) and ‘barriers’ that create nucleosome free region (NFR) near transcription start site (TSS) (13,23,24). Even though the occupancy gives us an idea about the spatial heterogeneity of occluded regions along DNA, the quantity results from superposition of several frozen snapshots. Hence, it cannot give us information about the temporal variability of the occluded regions and accessibility of DNA, which is crucial for many cellular processes like gene regulation.

It is known that gene regulation, transcription, etc. are kinetically driven processes with many non-histone proteins (transcription factors (TFs), TATA-binding protein (TBP) and RNA polymerase (RNAp) complex) binding on to the DNA competing with the nucleosomes. One crucial factor that controls the binding of these proteins is the availability of continuously exposed (empty, having no proteins bound) patches of DNA. The kinetics of nucleosomes play an important role in regulating this continuous exposure (25–27). For example, disassembly of nucleosomes is known to be important for exposure of TATA sites in promoters (19,28,29), while dynamics of +1 nucleosome is likely to influence the accessibility near TSS (30). Sliding of nucleosomes (31,32) as well as partial unwrapping/wrapping (33) of DNA at nucleosome edges may also contribute toward creating exposed regions along DNA. All such kinetic activities, which are stochastic, can collectively influence transcription levels and noise in gene expression.

In this context, it is important to stress the difference between the study of temporal versus static positioning (occupancy) of nucleosomes. As shown in Figure 1(A and B), nucleosome with two sets of kinetic rates: (i) k₊ = k₋ = 0.1s⁻¹ or (ii) k₊ = k₋ = 0.01s⁻¹, would have the same steady-state occupancy. Yet the kinetic histories of protein competing with nucleosome to bind on a DNA site may be distinct for distinct nucleosomal activities in cases (i) and (ii) (see Supplementary Material section 1 and Supplementary Figure S1 for detailed discussion). Treating nucleosomes as extended objects (not merely point-like (25,26)), and considering the full problem of kinetically competing nucleosomes and non-histone proteins to access a target DNA patch, is a complex mathematical problem. In this paper we address a crucial part of the problem of estimating the exposure time of a target DNA patch influenced solely by the nucleosome kinetics, since such a quantity indicates the ease of accessibility of regulatory proteins to the patch.

Figure 1.

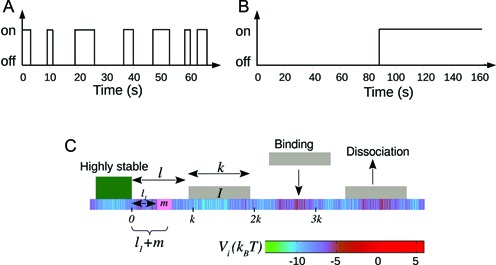
(A and B) Figure comparing two different nucleosome kinetic histories: switching from nucleosome ‘off’ (exposed) to ‘on’ (covered) state happens with a mean time 1/k₊, and ‘on’ to ‘off’ state happens with mean time 1/k₋. The rates are chosen such that (i) k₊ = k₋ = 0.1s⁻¹ and (ii) k₊ = k₋ = 0.01s⁻¹. Due to equality of binding and unbinding rates, both (A and B) lead to average occupancy of 50%. Yet the protein binding kinetic histories may be quite different for (A) as compared to (B)—see section 1 of Supplementary Material for details. (C) A schematic figure of the kinetic model studied in this paper is shown. Effective histone-DNA binding potential V_i (see Equation 1) is represented by color gradient, whose magnitudes (in k_BT) are shown in the horizontal bar. Dark green block depicts a highly stable barrier while light gray blocks represent nucleosomes of size k = 147. The target patch of size m at distance l₁ from the barrier is marked pink on the DNA lattice.

There exists only a limited number of studies that probe the kinetic nature of nucleosomes. FRET experiments have investigated local DNA exposure as a result of single nucleosome dynamics (6,31,32). There are also a few recent experiments investigating nucleosome turnover kinetics (34) and how nucleosomes influence transcription factor binding (35). These studies are still far from understanding how kinetics of multiple nucleosomes influence the DNA exposure and thereby regulate gene expression. While detailed experimentation is absolutely necessary, theories of nucleosome kinetics also need to be developed to address kinetics of DNA exposure. The existing studies which explicitly incorporate kinetics (36–39), mostly focus on understanding nucleosome occupancy.

In this paper we investigate the kinetics of DNA exposure along the genome of Saccharomyces cerevisiae, taking into account the effect of DNA sequence, ATP-dependent nucleosome remodeling and wall-like barriers. Using experimentally known information from chromatin biochemistry and ideas from theory of stochastic processes, we formulate an analytical theory that can predict exposure times of important locations (target patches) along the genome, like TF binding sites or TATA boxes in promoters, or patches near +1 nucleosome close to TSS. Given that our method does not rely on any time-consuming computer simulations, we employ it to predict exposure timescales genome-wide and find huge gene-to-gene variability. Before arriving at such global trends, we do case studies of some specific genes to understand how various factors—initial local organization of nucleosomes, their collective dynamics, the DNA sequence and finally ATPase activity—affect patch exposure times. In particular we find that exposure times do not follow simple expectations of being inverse of local nucleosome occupancies. Nor are they dictated by kinetics of a single nucleosome (a notion prevalent in the literature (40–42)), but rather by the cooperative kinetics of multiple nucleosomes. By studying the exposure times at TATA boxes in GAL1 and PHO5 promoters, we quantitatively compare the promoter activities of the two genes—our results echo findings from earlier experiments.

MATERIALS AND METHODS

Model for nucleosome kinetics

As known from the literature, nucleosomes are highly dynamic units—they stochastically bind, dissociate and slide along the genomic DNA, aided by ATP-dependent remodeling machines, particularly in promoters (9,19,25,26). Since the main aim of the paper is to understand occlusion and exposure of DNA arising out of the dynamics of multiple nucleosomes, we start with the following minimal model (Figure 1C): we consider DNA as a 1-dimensional lattice where each lattice site denotes one base-pair. At any instant, multiple nucleosomes are bound on the DNA, with each one occluding k = 147 bp of space. From a surrounding pool, histone proteins bind on the DNA lattice and form nucleosomes, randomly, at any empty stretch of length ≥147 bp. Each binding process happens with an intrinsic rate k_on = k₀. Since nucleosomes are known to have high affinity toward any natural DNA (43,44) and experiments indicated a single dominant timescale of assembly of nucleosomes (43,45), we assume k_on to be independent of local DNA sequence. However, since nucleosome positioning is known to be DNA sequence and ATPase remodeling activity dependent (13,16), we construct nucleosome removal rates (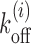) to accommodate these effects (see details below); in this removal process the whole nucleosome is assumed to disassemble from the DNA. Such a model of sterically interacting k −mers has been studied as a Percus fluid for its equilibrium properties (36,39,46–49). Given that this model has been highly successful in reproducing experimentally observed nucleosome occupancy, for a wide range of problems (23,27,36–38,48,50), it would be natural to investigate kinetic quantities based on this model.

Apart from binding and dissociation, other possible kinetic events are sliding and partial unwrapping of nucleosomes (10,33,51–54). Since nucleosome kinetics near TSS (promoters) is dominated by nucleosome removal and re-assembly (9,28,55–57), we mainly focus on these two events in our study. However, we also perform limited simulations to investigate how sliding and partial unwrapping might modify our results (see ‘Discussion and Conclusion’ section and also sections 6 and 10 of Supplementary Material).

Sequence-dependence and local remodeling of nucleosomes

Nucleosome dissociation rate 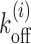discussed above incorporates the effects of DNA sequence and ATP-dependent remodeling such that:

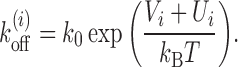(1)

Here V_i is the sequence-dependent effective potential, obtained from the work of Kaplan et al. (15), representing the nucleosome-DNA binding affinity between site i and i + k − 1 in the presence of basal remodeling activity. From (15) one can get the relative affinity, i.e., probability P_i that a nucleosome starts from the i^th bp. By submitting sequence of interest (obtained from NCBI database) to the online server http://genie.weizmann.ac.il/software/nucleo_prediction.html, one may obtain the sequence dependent potential V_i = −k_BTlnP_i experienced by a single nucleosome. Since V_i is the relative affinity, its average value may be fixed from the physical constraint that the gene regions have an observed density of ≈88% in yeast, a steady state value assumed to be achieved within biologically relevant timescales. Assuming the binding rate based on single molecule experiments as discussed above, we consider 〈V_i〉 ≈ −7k_BT which accounts simultaneously for the bare histone–DNA interaction energy and some basal remodeling activity, which is assumed to be a constant (see (27,37) for details). However, depending upon the nucleosome density and remodeling activities in different species, the value of 〈V_i〉 may vary, as considered in the Supplementary Material. Such an approach has been successful in obtaining static occupancy patterns (27,37). In Equation 1, U_i denotes the additional remodeling activity due to locally recruited ATPases (12,58), histone modifications (59,60), histone exchange (e.g. H2A ↔ H2A.Z (61)) or DNA methylation (62,63), which essentially modifies nucleosome stability. Magnitude of U_i being positive (or negative) would result in lesser (or greater) local stability of the nucleosome. Local remodeling, in general, can be time-dependent as this may be activated/deactivated depending on different signals such as TF binding or chemical modification. However, once the switch to active/inactive state happens (e.g. for PHO5 gene, when cells are phosphate-starved or vice versa), one can assume that the remodeling may be captured by a static potential U_i over a time window. Within this time window, one may study various kinetic properties as we do in this work.

Locating the TATA boxes and TSS

The TSS positions for all the genes were obtained from ref. (64). Genes on the ‘Crick’ and ‘Watson’ strands were treated separately, such that the coding part always lies to the right of the TSS, allowing us to study 5160 genes of S. cerevisiae. For the studies involving TATA-containing genes, we referred to (65) to obtain the 8 bp TATA sequence. Since (65) gives TATA positions with respect to ATG sequence, while we needed the positions with respect to TSS, we further locate the desired TATA sequence (using Perl script) specific to every gene. Unambiguous sequence recognition was not possible for all the 1492 TATA containing genes appearing in (65). Moreover we rely for calculations of exposure timescales of TATA on an analytical theory (see below) which assumes their position to be not further than a nucleosome length from a barrier. These restrictions finally limited our genome-wide study of TATA site exposure, to only 356 TATA containing genes.

Modeling ‘barriers’ in gene regions

Throughout this paper, we would be examining the ‘exposure’ of a small patch of DNA in the presence of multiple dynamic nucleosomes near a ‘barrier’. Stable protein-complexes acting as a barrier for nucleosome positioning have been highlighted in many experiments. For example, a stable nucleosome–RSC complex behaves as a barrier in both the repressed and inducing conditions of the gene (40,66). In another study +1 nucleosome is found more stable than other nucleosomes and is called a barrier (67). Similarly ‘locked’ nucleosomes at other locations are also described as barriers (68). A set of non-histone proteins (e.g. remodeling complex, TFs) binding next to TSS at NFR region is commonly referred as a barrier (69,70). In these cases the ‘barrier’ is considered as long-lived and it affects the nucleosome positioning in its vicinity.

Motivated by these examples, we model the barrier as a hard core particle representing a non-histone/histone protein complex that is highly stable and sterically occludes binding of nucleosomes (see Figure 1C). We consider the dissociation rate of the barrier protein to be zero in most of the cases; some simulations are also done for small but finite barrier dissociation rates.

Definition of quantities studied

In this study, we consider a target DNA patch of size m located at a distance l₁ away from the barrier (see Figure 1C). At t = 0, the first nucleosome from the barrier (labeled as nucleosome I in Figure 1C), is located at a distance l ≥ l₁ + m. Starting from this initial condition, we allow all nucleosomes to dissociate and bind according to their respective rates and ask the following question: what is the mean time it takes for the target patch of size m to be covered (either partially or fully) by a nucleosome for the first time? This is the mean first passage time (71) of a nucleosome covering the m-patch, and will be denoted by T_l for a given l. If the length l is not held fixed but drawn from a distribution P_in(l), the mean exposure time T_av of the m-patch would be a weighted average over the mean times T_l:

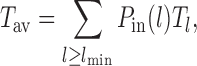(2)

where l_min = l₁ + m. If no experimental bias is introduced, P_in(l) is expected to be the steady state gap distribution P_ss(l − l_min) for the hard k-mers (which is an exponential function, see (46) and Supplementary Material (section 2 and Supplementary Figure S2). We use this form of P_in(l) in our simulations and theory below.

Simulation and analytical methods

Simulation method

We simulated a system of nucleosomes having the kinetic moves described in the section ‘Model for nucleosome kinetics’ above. We start by considering a DNA lattice of 5000 bp assuming a barrier at its edge, and nucleosomes are distributed on the lattice with inter-nucleosome gaps chosen from the steady state distribution P_ss(l − l_min) as discussed in the Supplementary Material section 2. At t = 0, we ensure that the target patch of size m is l₁ bp away from the barrier, not covered by any nucleosome. Starting from such initial conditions, we evolve the system using kinetic Monte-Carlo method, allowing the binding (with rate k_on = 12s⁻¹ (45)) and dissociation events (with respective sequence- and ATP-dependent rates 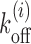, as in Equation 1) of nucleosomes. Then we compute the first passage time—the time up to which the m-patch remains exposed, before getting covered for the first time. Averaging over 2 × 10⁵ independent histories, we compute the mean T_l.

We also did some simulations for three special cases: (i) apart from binding and dissociation, nucleosomes are allowed to slide with rate 0.0017s⁻¹ (38,51), (ii) the barrier is not permanent and can dissociate and bind with rates comparable to nucleosomes, and (iii) smaller sized nucleosomes (k = 120 bp to k = 147 bp) are studied to mimic the partially unwrapped states.

Analytical method

Apart from the simulations, we have also formulated equations to analytically calculate the mean exposure time T_l and compared the results with simulation data. While simulations give accurate estimates of T_l, they involve multiple nucleosome kinetics and using them particularly for ATP and sequence-dependent kinetic events are time-consuming. Therefore, developing an analytical approximation for T_l is of practical importance on two counts: a quick theoretical estimate of T_l makes it easy to evaluate T_av (Equation 2) genome-wide; it also gives us insight into the temporal composition of the mean T_l, event-by-event, helping us understand the collective dynamics of multiple nucleosomes. In the theoretical literature of stochastic processes, a general theory exists for mean first passage times as derived from the backward Master equation formalism (71–73). Although relaxation kinetics in a system of hard k-mers has been studied (46,74–77), a theory for the first passage problem discussed in this paper was not developed for the system earlier. We do so below, and set up linear recursion relations between various T_ls for different l, under certain approximations.

We assume that the location of the m-patch with respect to the barrier is not further than the size k = 147 bp of a nucleosome, i.e. l_min < k. Since the initial barrier-nucleosome separation l has an exponentially decaying distribution P_ss(l − l_min) (see Supplementary Figure S2, large gaps are rare—hence in our analysis, we only retain lengths l ∈ [l_min, 3k). Over this range, we may classify the gap lengths l into four types (see Figure 2A–2D)—each lead to a distinct kinetic history. From the Figure 2A–2C, we see that a dissociation event of the nucleosome I, leads to the initial gap length l being replaced by a new gap length . Similarly, a binding event (light gray blocks with dashed boundary) produces a new gap l′ (Figure 2C–2D), unless of course the m-patch is covered (Figure 2B). Thus we may write recursive equations (Equations 3-6) relating the T_ls, as gap lengths successively change following dissociation and binding of nucleosomes. For all the equations in general, the mean exposure time T_l has two parts—(i) the mean survival time to persist within the initial gap l, added to (ii) the ‘weighted’ mean exposure times (e.g. ) of the new gaps (e.g. 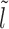). The weighting factors are not easy to obtain exactly and we have used effective approximations for those, as indicated below (for details, see section 3 of Supplementary Material).

Figure 2.

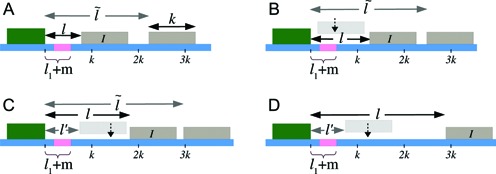
Initial configurations corresponding to Equations 3-6: (A) l ∈ [l_min, k), (B) l ∈ [k, l₁ + m + k), (C) l ∈ [l₁ + m + k, 2k), (D) l ∈ [2k, 3k). The barrier (dark green color) and the right flanking nucleosome (marked as I) have initial separation l. After nucleosome I dissociates, the distance to the next nucleosome from the barrier is 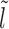, and if l ≥ k, another nucleosome (light gray) may bind in the l-gap either covering the m-patch (B), or missing it and thus creating a gap of length l′ (C and D).

Case 1: Figure 2A, l ∈ [l_min, k)—the mean persistence time of the initial gap state is 1/k_off (needed for the dissociation of nucleosome I), while we approximate the probability weight to make transition to a new gapped (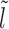) state with new exposure time 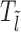, as 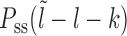. Thus we have for multiple possible :

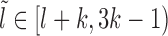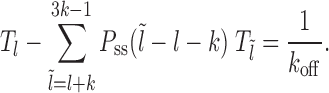(3)

Case 2: Figure 2B, l ∈ [k, l₁ + m + k)—the mean persistence time is 1/λ_l, where λ_l = k_off + k_on(l − k + 1) corresponding to the dissociation event of nucleosome I and (l − k + 1) distinct binding events. The binding events immediately cover the patch, while the dissociation events lead to exposure in new gapped states as in Equation 3. The probability weights of the transitions are :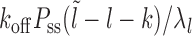

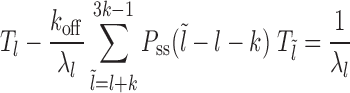(4)

Case 3: Figure 2C, l ∈ [l₁ + m + k, 2k)—apart from same terms as in Equation 4, there is a new (second) term in Equation 5. Binding may lead to a new gap of length l′ ∈ [l₁ + m, l − k] without covering the m-patch, with weight of transition k_on/λ_l. The exposure times in these new gapped states are well approximated by 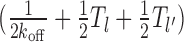(see section 3 of Supplementary Material):

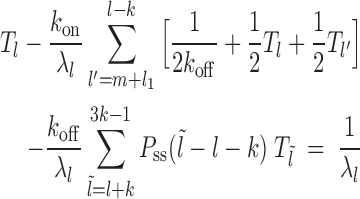(5)

Case 4: Figure 2D, l ∈ [2k, 3k)—dissociation events are ignored all together as they produce gaps of size 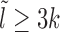(which we do not consider from the start). Binding events happen with weight factor k_on/λ_l. If new gap l′ ≥ k, the exposure time is 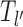and is dominated by subsequent binding events covering the patch. But if l′ < k patch coverage has to rely on further dissociation events and instead of 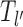we found the following to be a good approximation (see section 3 of Supplementary Material) to the subsequent exposure time—note that if 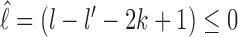, 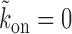in Equation 6 and 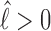, in Equation 6:

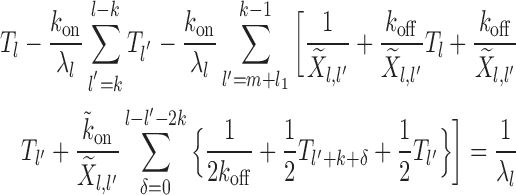(6)

where, 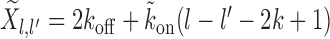. The Equations 3-6 for T_l over the range l ∈ [l_min, 3k) form a system of coupled linear equations which can be easily solved.

The analytical method developed above may be extended to include the effect of DNA sequences and local remodeling, by using the location dependent nucleosome dissociation rate 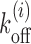(see Equation 1) (15,27,37). Thus we need to replace the uniform k_off in Equations 3-6 with local values of 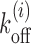—see the explicit forms of the modified equations in section 4 of Supplementary Material. In what follows, we would first study the exposure times of an uniform sequence, and then those of DNA patches on promoters and coding regions of specific genes (using the relevant V_i and U_i). Finally, we would apply our method to a genome-wide study for yeast.

RESULTS

Collective kinetics of nucleosomes determine the exposure times: a study of uniform sequence

We computed the average exposure time T_l using kinetic Monte Carlo simulations, as discussed above, assuming rates mentioned in the caption of Figure 3. In this subsection, the spatial DNA sequence and local remodeling effects are ignored (i.e. V_i = 〈V_i〉 and U_i = 0 for all i)—those would be considered from the next subsection onward.

Figure 3.

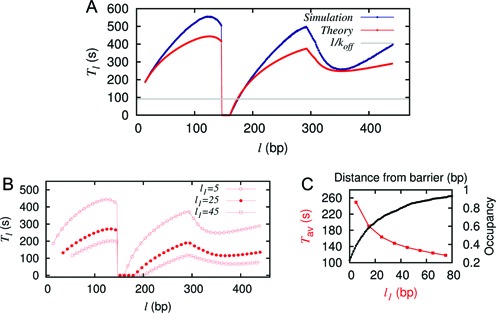
(A) The timescales T_l versus l from simulation (blue) and theory (red). The flat gray line indicates 1/k_off. Here k_off = 12 × e⁻⁷s⁻¹, k_on = 12s⁻¹, k = 147, m = 10, l₁ = 5. (B) T_l versus l for various choices of l₁ with all other parameters same as in (A). (C) Comparison of the variation of T_av (red) and average nucleosome occupancy (black) with distance from the barrier shows an inverse relation.

In Figure 3A, we present the simulation data for T_l (upper curve, blue). We note that it has a characteristic ‘butterfly-like’ (BL) shape with two ‘wings’ (for l < k and l ≥ (k + l₁ + m)) and the values of T_l are typically much higher than 1/k_off (shown by the flat line). However, for k ≤ l < (k + l₁ + m), the timescales are much lower (see Supplementary Figure S3) and are inversely proportional to k_on. Thus the patch exposure timescales T_l vary strongly and non-monotonically with the initial barrier-nucleosome separation l.

From the T_l data, we can compute the l-independent average exposure time, T_av = 259s, using Equation 2. The value of T_av obtained here is completely distinct from other timescales in the problem, namely single kinetic off-timescale (1/k_off = 91.4s) or the on-timescale (1/k_on = 0.083s). The underlying reason is that the exposure time of a DNA patch arises out of successively coupled events in space and time, and the mean value T_av may be viewed as a weighted composite of multiple timescales associated with those events.

We also calculate T_l analytically using Equations 3-6 (see the lower red curve in Figure 3A). Given that some approximations were involved, the match to the simulation is not perfect but close and the overall BL shape is reproduced. Moreover, using the theoretical values of T_ls in Equation 2, we get T_av = 249s, which compares reasonably well to the value of 259s from simulation mentioned above. We have tested this for many different parameters and found that the match between theory and simulation results are very close. Thus from now on, we may rely on the theory to get a reasonably reliable quantitative estimate of T_av, and avoid tedious simulations. A qualitative physical understanding of the BL shape of the T_l versus l curve following the Equations 3-6 is provided in section 3 of Supplementary Material.

Since the distance of the binding site (m-patch) from the barrier may vary from gene to gene, it is important to know what happens to the exposure timescales as a function of the patch location l₁. From theory (and also from simulation whose data is not shown), one can clearly see (Figure 3B) that the T_l versus l curve retains its shape but diminishes in value with increasing l₁. The mean exposure time T_av (calculated using Equation 2) is thus a decreasing function of l₁ (Figure 3C, red curve) for the uniform sequence. Note that nucleosome occupancy goes up with distance from the barrier (Figure 3C, black curve). This fits a simple intuition that enhanced static occupancy should correspond to shorter patch exposure time. Yet what we would see soon, is that such simple intuitive correspondence breaks down for spatially non-uniform dissociation rates—i.e. for real DNA sequence and local remodeling.

Above we have considered the barrier as a highly stable entity that does not dissociate. However, it is interesting to consider the case where the barrier has a finite dissociation rate and ask how this would affect our results. Modifying the model studied above, we introduce kinetics for the barrier too—we allow the barrier along with nucleosomes to do on-off dynamics. This introduces explicit competition between nucleosomes and the barrier. The results are shown in Supplementary section 5 and Supplementary Figure S5. We find that on making the barrier less stable, the exposure times reduce, but nonetheless remain comparable. Moreover, the BL shape of the curve is preserved.

As discussed earlier, thermally driven DNA wrapping/unwrapping at the entry/exit sites of the nucleosomes may result in fluctuating number of DNA bps occupied in one nucleosome. One way to indirectly model this effect is to vary the size of nucleosomes in our theory. As shown in Supplementary Figure S6, for various choices of k from 120—147, there is marginal change in T_av. Thus such wrapping/unwrapping events would not change our exposure time estimates significantly (see section 6 of Supplementary Material for more discussion).

Exposure times for target patches in specific promoters and coding regions

Stability of +1 nucleosome is reflected in exposure times of DNA patches downstream of TSS

Kinetics of +1 nucleosomes are of great interest in chromatin biology (30,78,79) with some of the recent studies exploring the role of +1 nucleosome stability in gene regulation (30) and the influence of +1 nucleosome position in mRNA production (80). To explore the influence of kinetics of +1 nucleosomes, in this section we study the exposure times of DNA patches downstream of TSS.

For a highly expressed gene YIL018W we look at patches downstream of TSS. Please note that the identity of the gene appears in the calculations through the sequence dependent potential V_i (see ‘Materials and Methods’ section). The NFR region upstream of TSS is modeled as an effective barrier (48,81,82) (see Figure 4A, top). In the figure, l is a schematic representation of the gap between NFR and the +1 nucleosome. Since we use an exponential distribution for the gaps (see Supplementary Figure S2), in practice, l is quite small (〈l〉 ≈ 30 bp). Through study of T_l versus l (Figure 4B), we arrive at estimates of average exposure time T_av = 122s (theory, red curve) and 136s (simulation, blue curve), indicating that nucleosomal activity is reasonably fast for this gene (all relevant parameters are specified in the figure caption). Interestingly the curve (T_l versus l) preserves an overall BL shape (similar to Figure 3A-red without sequence), and importantly, the values of T_l are quite different from local off-rates 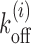(the gray curve, bottom). This shows that, similar to the uniform-sequence case, the exposure times are determined by correlations in kinetics of multiple nucleosomes downstream of TSS. Our calculations indicate the necessity of going beyond this—here we see that cooperative kinetic positioning of the +1 and +2 and other nucleosomes downstream of TSS in successive on-off events escalate the average exposure time of nearby DNA patches. We also present results accounting for the local remodeling of the +1 nucleosomes that reduces its stability (U_i = 1k_BT, for i = l₁ + m to i = l₁ + m + k) (see Figure 4A, bottom); the overall reduction of timescales (Figure 4B, green curve) imply that well exposed DNA patches need a stable +1 nucleosomes in its vicinity.

Figure 4.

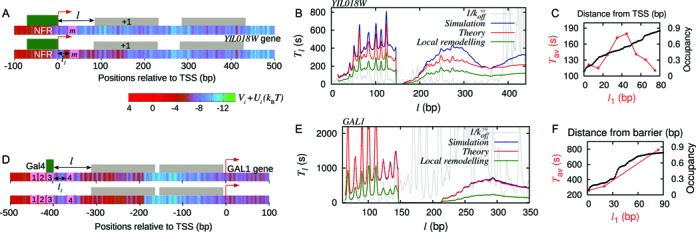
Effect of DNA sequence and local remodeling. (A) Upper panel: schematic figure of gene YIL018W with the m-patch (pink block) downstream of TSS, and a barrier (green block) in the NFR region; here U_i = 0. Lower panel: same gene with local remodeling over a region of 147 bp to the right of the m-patch—note the change in color, more red showing more positive potential (see the color gradient of V_i + U_i). (B) T_l versus l curve for exposure of the m-patch—simulations (blue), theory (red), 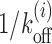(gray), corresponding to upper panel in (A); theory with local remodeling that makes the +1 nucleosome less stable (green), corresponding to lower panel in (A). Parameters are k = 147, l₁ = 5, m = 10, k_on = 12s⁻¹ and U_i = 1k_BT. (C) T_av versus l₁ (red) rises and falls whereas static occupancy increases with distance (black). (D) Schematic figure of GAL1 promoter with four Gal4 (TF) binding sites (pink patches, 1, 2, 3 and 4). One bound TF (green block) at patch 3 is shown. Lower panel shows the local remodeling in the region downstream of site 4. (E) T_l versus l curve for patch 4 in (D) with m = 17 bp and l₁ = 47 bp. Note that the theory (red) and simulation (blue) curves match very well in this case and shows very different behavior from 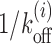(gray). Green curve shows the T_l with local remodeling (U_i = 1k_BT) downstream of 4 with other parameters same as red curve. (F) T_av versus l₁ (red), for Gal4 (barrier) fixed at patch 1 and the m-patch being at locations 2 (l₁ = 2 bp), 3 (l₁ = 20 bp) and 4 (l₁ = 84 bp). The curve shows an unexpected rise with l₁ which is not an inverse behavior of the nucleosome occupancy (black) (see explanation in Supplementary section 9)).

Could we have guessed our results by computing occupancy? We find that although nucleosome occupancy rises monotonically with the distance from the barrier (black curve in Figure 4C), the average coverage times T_av do not fall monotonically with l₁ as in Figure 3C red curve, for the case without sequence. Instead we see a non-monotonic behavior (see red curve in Figure 4C)—a reflection of how sequence effects can influence kinetic quantities very differently.

Similar study for gene YCR012W (see Supplementary Materials, section 7 and Figure S7) gave us very different T_av values for a same sized patch at the same distance l₁ from TSS; we got T_av = 1590s (theory) and 1722s (simulation) indicating that its nucleosomal activity is comparatively slower. This points toward enormous gene-to-gene variability of T_av, as would be discussed later in the paper.

Since 〈V_i〉 and U_i could differ for different species and cell types, we also checked the sensitivity of our results on varying these parameters. In Supplementary Figure S8A and B, we present T_l vs l and T_av for 〈V_i〉 between −5k_BT to −9k_BT for a uniform sequence. We did the same for gene YIL018W and found that T_av varies between 18s to 800s. In our model, varying U_i is same as varying V_i locally. Effects of such local variation would appear in our genome-wide studies below. In principle, similar to TFs (83–87), the nucleosome binding rate k_on may also depend on the local DNA sequence. To test the sensitivity of our results to changes in k_on, we varied the binding rate by a factor of 10, and found that there is no big change in T_l vs l, and T_av remains of the same order (see Supplementary Figure S8C and D).

Study of exposure times in promoter of GAL1 gene

Promoter regions are important for gene regulation, as many proteins have to access their target sites in a cooperative fashion. Some of the targets are TF binding sites. Here we consider a specific example of GAL1 promoter which has four Gal4 (TF) binding sites (88) (see pink patches in Figure 4D, top). Cooperativity in TF binding mediated by nucleosomes has been an interesting topic of study (39,49,89–91). To address the temporal aspects of cooperativity of Gal4 binding, we pose the following question: if one Gal4 is already bound to one of the target sites (say patch 3 in Figure 4D, top), in the presence of nucleosome kinetics, how long will another Gal4 binding site (say patch 4) be exposed? Size of the target is m = 17 bp and distance between patches 3 and 4 is l₁ = 47 bp. For various initial placements of a nucleosome from patch 4 at distance l, calculations of T_l versus l are shown in Figure 4E—theory (red curve) and simulation (blue curve) data has a spectacular match in this case. As in previous cases, the BL shape persists, and the values of T_l arising out of cooperative kinetics are visibly distinct from (gray curve) and remodeling inducing instability (see Figure 4D, bottom) of nucleosomes lower the T_l values (green curve). Using the T_ls, one can obtain T_av which in this case (without local remodeling) is 961s.

Such estimates of T_av can be obtained for other chosen barriers and target patches. In Figure 4F (red curve), the timescales corresponding to targets at patches 2, 3 and 4 with a stable TF (barrier) at 1 are shown—quite contrary to intuition, the timescales rise (instead of falling) with the separation (l₁) of two TF binding sites. Note that occupancy of nucleosome rises as per intuition (black curve in Figure 4F). Thus we see that cooperative kinetics of nucleosomes along with the specific genomic sequence of GAL1 produces a non-intuitive co-operativity (see section 9 of Supplementary and Figure S9 for further explanation) in TF binding kinetics.

Exposure timescales of TATA sequences

In many genes, TATA sequences are one of the important regulatory patches (∼20% of the genes in S. cerevisiae) (65). It has been proposed that for TATA containing genes, binding of TBP at the TATA sequence is followed by recruitment of RNAp and other transcription machineries (92). If the TATA sequence is covered by a nucleosome, it occludes the region for TBP binding and hence hinders the transcription process (93). Thus, it is important to study the exposure timescales of the TATA region in the presence of dynamic nucleosomes.

TATA exposure with barrier at upstream activating sequence (UAS)

Experiments suggest that in GAL1 promoter a nucleosome–RSC complex sits very stably at the UAS and behaves like a barrier (40,66). For this particular situation (see Figure 5) we can find the exposure time of the TATA sequence (pink-patch) treating the protein complex (green-block) at the UAS as the barrier.

Figure 5.

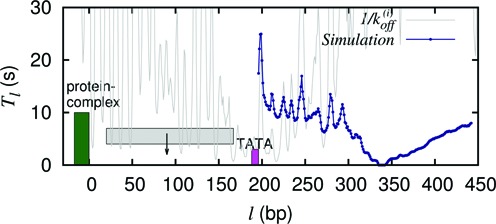
T_l versus l curve for GAL1 promoter where nucleosome–RSC complex (green block) sitting at the UAS acts as a barrier and the m patch is the TATA region (pink-patch). In this situation l₁ = 188 bp and m = 8 bp. Since the l₁ > k, a nucleosome (gray block) can sit in between the barrier and the patch and act as a short lived barrier.

Since the distance from the UAS to the TATA sequence is 188 bp which is greater than the size of a nucleosome, we cannot employ our theory directly to calculate T_l in this problem. Thus, we perform simulations with l₁ = 188 bp and m = 8 bp. The results for T_l are shown in Figure 5 (blue curve), which traces a rough BL shape. The timescales (T_l) are low and T_av = 14.5s. This is mainly because the large l₁ allows the coverage of the patch directly through a nucleosome binding in multiple ways. Nonetheless T_av is much greater than 1/k_on = (1/12)s because occasionally a nucleosome (gray block) may also bind in the gap between the UAS and the TATA sequence and act like another temporary barrier with a finite lifetime.

Comparing TATA box exposure times of PHO5 and GAL1, assuming a stable +1 nucleosome

Doing a comparative study of intrinsic noises in gene expressions in PHO5 and GAL1, Raser et al. (94) proposed a two-state switching model between ‘active’ and ‘inactive’ states of the promoter. They proposed that due to slow chromatin remodeling of positioned nucleosomes near TATA box of PHO5, it has a slow promoter activation or deactivation as opposed to GAL1. Here we do a comparative study of the two genes to quantify this behavior.

In our model, we assume that the switching between active and inactive promoter states is equivalent to the exposed and occluded TATA box. Therefore, the timescale of dissociation of a nucleosome that covers the TATA box is approximately the timescale of switching of the promoter from inactive to active state. The average 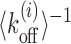for a −1 nucleosome containing the TATA boxes are 97.28s and 11.52s for PHO5 and GAL1, respectively. On the other hand, finding the deactivation timescale to switch from active to inactive state, requires a detailed calculation based on cooperative kinetics of various proteins like TFs, TBPs and nucleosomes. However, assuming that the effects of many of the non-histone proteins are essentially to remodel nucleosome kinetics in a location-dependent manner, we may obtain estimates for deactivation times in terms of the patch exposure under nucleosome kinetics as discussed in the paper. Since +1 nucleosomes for many genes are known to be long-lived (30), we consider +1 nucleosomes (Figure 6A, dark green block) as barriers for these calculations. We calculate exposure times of the TATA boxes (pink-patch) situated upstream of TSS for PHO5 and GAL1 genes (see Supplementary Figure S4 for the method). There is no knowledge of U_i, for these genes, a-priori. However, it is known that in the active versus the repressed states of GAL1 and PHO5 promoters, the nucleosome occupancies around TATA are different (19,40), which is a reflection of local remodeling activity. Comparison of the experimentally known occupancies before and after induction shows similar enhancement (approximately four times) in GAL1 and PHO5 promoter occupancies. This makes us assume same magnitude of remodeling potential |U_i| for both the promoters. Without any local remodeling (U_i = 0) and with nucleosome stabilizing (U_i < 0) or destabilizing (U_i > 0) local remodeling, the timescales for exposure of the TATA boxes are compared for the two genes in Figure 6B. We see consistently in every case PHO5 has larger timescales than GAL1, showing that deactivation rates for PHO5 would be a lot smaller. Thus we provide quantitative support to the picture put forward in (94) about the distinct nature of promoter activities in PHO5 and GAL1.

Figure 6.

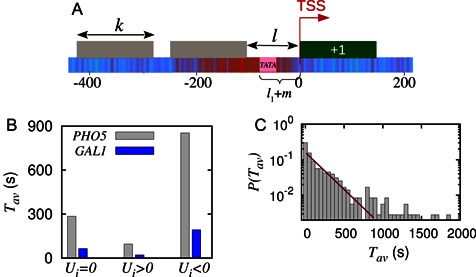
(A) Schematic showing TATA box (pink) as the m-patch situated in a gap of length l and a stable +1 nucleosome as the barrier (dark green block). (B) Comparison of timescales for PHO5 and GAL1 genes without (U_i = 0), and with local remodeling (U_i ≠ 0) done to the left neighborhood of their TATA boxes. Here we consider +1 nucleosome as the barrier and distance of the TATA box from TSS is −58 and −80 bp, for PHO5 and GAL1 respectively, |U_i| = 1k_BT. (C) Probability distribution of average exposure time of the TATA sequence when a barrier is fixed in the coding region starting at TSS. Here, m = 8, l₁ varies with gene to gene depending upon the position of TATA sequence; number of genes = 356.

Genome-wide exposure timescales of TATA boxes

Having studied behavior of specific genes above, we now turn toward study of TATA containing genes, genome-wide. The location of the TATA sequences were obtained from the ref. (65) (see ‘Materials and Methods’ section). In the promoters (upstream TSS) of 356 genes we compute the exposure timescales of TATA boxes assuming +1 nucleosome as the barrier (see schematic Figure 6A). In Figure 6C we plot the distribution of T_av values thus obtained. From the distribution we calculate an average TATA exposure timescale across genes, i.e. genome-averaged 〈T_av〉_genes ≈ 347s. Interestingly, this estimated time forms a close upper bound to the TBP binding timescales known from experiments (52,95)—which is 10–300s (for the TBP concentration range 20–600 nM).

Genome-wide study of exposure timescales downstream of TSS, assuming a barrier at NFR

We continue the genome-wide study to explore how variability in genomic sequence may effect exposure timescales of target patches on DNA. We studied 5160 genes of S. cerevisiae for which the sequence dependent potentials were obtained by using the method discussed in ‘Materials and Methods’ section. For all the genes we used the same initial condition—we assumed a barrier at NFR ending at TSS, a target patch of size m = 10 bp at a fixed distance l₁ = 5 bp downstream of each TSS (see Figure 4A, upper panel). The average exposure timescales T_av of different genes form a distribution shown in Figure 7; the large width of the distribution indicates great diversity of values. Moreover the curve does not have a simple exponential tail (reminiscent of non-exponential relaxations in disordered and glassy physical systems (96,97)), indicating the absence of a typical value of timescale in an ensemble of heterogeneous genomic sequences.

Figure 7.

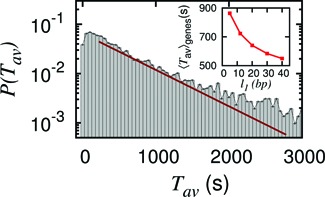
Genome-wide probability distribution of average exposure time, 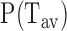, of a patch downstream of the TSS shows huge diversity. Parameters are: m = 10 bp, l₁ = 5 bp, number of genes = 5160. The distribution deviates from simple exponential (red line—showing guide to eye), reflecting the heterogeneity in genomic sequence. Inset: 〈T_av〉_genes versus l₁ showing typical behavior as seen in the case without sequence (Figure 3C red curve).

Are there still some generic trends left in genome-wide behavior, which go beyond the sequence identity of the genes? We saw earlier that for specific genes, the exposure times do not necessarily decay monotonically with the distance l₁ of the patch from the barrier (see Figures 4C and F). In Figure 7 inset, the mean exposure times 〈T_av〉_genes, averaged over 5160 genes, decrease monotonically with increasing distance l₁. Thus the genome averaged generic behavior of 〈T_av〉_genes is distinct from the irregular behavior of T_av seen in specific genes.

Suggestion for experiments to test our predictions

Predictions from our calculations can be tested, in principle, in appropriately designed experiments. Here we provide a few pointers toward some of the potential experiments. Since FRET experiments are one of the standard ways of measuring DNA–protein binding kinetics, a suitable FRET experiment may be designed in the presence of multiple nucleosomes. Another set of experiments may rely on the expected dependence of the probability of TBP binding to the TATA box on the exposure time, T_av, studied in this paper. If the rate of TBP binding can be regulated by, for example, increasing the concentration of the TBPs, we expect that the probability of TBP binding would saturate; this saturation value and the binding rate at the saturating concentration will depend on the T_av we computed. Alternatively, one may experimentally reduce the stability of the nucleosome (using DNA sequence with different affinities or location-specific remodeling) adjacent to the target patch of interest, and thereby bring down the probability of TBP binding for a fixed concentration of TBP (i.e. constant TBP binding rate). This will verify our specific prediction that the T_av will decrease as the adjacent nucleosomes become more unstable.

DISCUSSION AND CONCLUSIONS

Recent experiments show that, in promoters, nucleosome numbers and positions are stochastic. In the induced state as well as the repressed state, the number of nucleosomes vary over a 600 bp region in promoters (19,26,29). Moreover, the turnover studies during a cell cycle show the genome-wide kinetics of nucleosomes (34,98). These facts suggest that a stochastic model with dynamic nucleosomes may be appropriate for gene regions. Most of the existing studies focus on the spatial organization of nucleosomes—e.g. nucleosome positioning/occupancy (8,13–18). However, as we mentioned in the introduction, for processes like transcription factor-binding on to the DNA and gene regulation, what would matter is not just the occupancy but also the kinetics of nucleosomes. To demonstrate this point we performed an explicit calculation for a TF binding to a single site competing with nucleosomes. The accessibility of the TF to the site has a marked variation with variation in nucleosome kinetics (for same nucleosome occupancy)—see Supplementary Material section 1. This provides motivation to go beyond the spatial aspects, and study the more complex problem of temporal organization of multiple, spatially extended, nucleosomes in gene regions.

In this paper, we have investigated how nucleosome dynamics regulates accessibility of certain regions in S. cerevisiae genome by computing exposure times at various crucial locations near the promoters and +1 nucleosome regions. We study the mean time (T_av) of continuous exposure of a DNA patch before coverage by a nucleosome. An analytical method is developed to estimate it using the theory of stochastic processes. Our theory takes into account genomic specificity (DNA sequence effects), remodeling effects of ATPases and the effect of stable barrier-like proteins. Competition between nucleosomes and TFs are not considered explicitly. We expect that higher T_av values would imply higher probability of TFs binding to target patches.

From our analytical theory and computational investigations, we make a set of important conclusions: we show that the initial nucleosome organization (in particular the barrier-nucleosome separation l) plays a crucial role in determining the mean exposure time T_l. Such curves have a generic BL shape. Going beyond the prevalent picture of a well-positioned nucleosome regulating the accessibility of the region it covers, we show that the exposure and accessibility are results of a collective nucleosomal dynamics involving multiple nucleosomes near the region of accessibility. We further show how DNA sequence and local ATPase activity influence the exposure times of specific genes. In particular, depending on sequence, we find that exposure times may even increase with distance (l₁) of the patch from the barrier. For GAL1 promoter, we have studied the influence of a remote stable nucleosome–RSC complex at the UAS on exposure times of its TATA box. Our calculations show that the promoter activity of PHO5 and GAL1 genes are markedly different—effective switch to an inactive promoter via TATA box coverage involves very different timescales. Estimates of TATA box exposure times as a genome-wide average tally well with known timescales of TBP binding. Genome-wide study of exposure times in the +1 nucleosome region reveals a huge gene-to-gene variability.

Our results may be extended in a few possible directions. Given that we have developed an analytical method that can calculate the exposure times very fast (compared to computer simulations), our method may be used (as we demonstrated for S. cerevisiae) to compute accessibility of locations genome-wide, for any organism. The only input needed is the sequence-dependent potential information which is often available in the literature/databases (15,17,18,99). One may also extend this problem to incorporate the binding of TFs and their competition with nucleosomes (70). Moreover, our exposure time calculation is a first step toward understanding the timescale of promoter states switching from active to inactive states (e.g. via TATA box coverage); this may be further developed to gain a better understanding of the dynamics of promoter states and the resulting gene expression.

To examine how sliding, partial wrapping/unwrapping of nucleosomes, as well as the finite lifetime of the barrier affect our results, we performed additional simulations. (i) We found that sliding does not change the overall picture and understanding developed in this paper (see section 10 of Supplementary Material and Figure S10). In many cases where active local remodeling ensures fast disassembly and turnover of histones (like +1 regions and promoters), the rate of sliding is much smaller than the rate of removal; hence the removal timescales dominate and the sliding can often be neglected. (ii) The partial wrapping/unwrapping of nucleosomes happen over timescales of milliseconds and proteins like TBP bind onto the DNA with a timescale of seconds or minutes. Therefore, such fast kinetics may not be relevant directly for binding of proteins like TBP. However, by changing the nucleosome size we have tried to indirectly imitate this phenomenon and found a very marginal change in T_av (see Supplementary Material section 6). (iii) Throughout this study, we have considered barriers as infinitely stable entities, however, all barriers will have a finite lifetime. In Supplementary Material section 5 and Supplementary Figure S5, we show that on making the barrier dissociate with finite rates (slightly lesser than the nucleosome dissociation rate), exposure timescales still remain comparable. The overall BL shape is also retained, indicating that the resulting exposure timescales can still be accounted for in terms of cooperative kinetics of the nucleosomes. Also, non-histone proteins binding at different non-specific locations may affect the nucleosome positioning (70,83)—this interesting open question may be studied in future.

We look forward to wide applicability of the general theoretical method developed in this paper to deal with temporal activity of DNA-nucleosome assembly. In particular it would be a crucial step toward understanding the underlying molecular basis of coarse-grained few-promoter-state switching models.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

CSIR India [03(1326)/14/EMR-II to D.D., 37(1582)/13/EMR-II to R.P.]; UGC India (to J.P.). Indira Foundation toward Faculty Mobility Program of Indian Institute of Technology Bombay (to R.P.). Funding for open access charge: CSIR, India(37(1582)/13/EMR-II for R.P.); Indian Institute of Technology Bombay (IRCC funding for D. D.).

Conflict of interest statement. None declared.