Independent validation test of the vote-counting strategy used to rank biomarkers from published studies

Abstract

Aim

Vote counting is frequently used in meta-analyses to rank biomarker candidates, but to our knowledge, there have been no independent assessments of its validity. Here, we used predictions from a recent meta-analysis to determine how well number of supporting studies, combined sample size and mean fold change performed as vote-counting strategy criteria.

Materials & methods

Fifty miRNAs previously ranked for their ability to distinguish lung cancer tissue from normal were assayed by RT-qPCR using 45 paired tumor-normal samples.

Results

Number of supporting studies predicted biomarker performance (p = 0.0006; r = 0.44), but sample size and fold change did not (p > 0.2).

Conclusion

Despite limitations, counting the number supporting studies appears to be an effective criterion for ranking biomarkers. Predictions based on sample size and fold change provided little added value. External validation studies should be conducted to establish the performance characteristics of strategies used to rank biomarkers.

Background

Most biomarker studies begin by surveying published studies for potential candidates. All too often, however, these studies present a confusing picture of which biomarkers would perform best in an independent validation test. The results are frequently conflicting and difficult to interpret due to differences in patient demographics, biospecimen type, sample processing and storage, assay method, normalization and data analysis method and the criteria used to assign significance [1–4]. The results can also be difficult to have confidence in due to small effect sizes, small numbers of subjects relative to number of markers tested, multiple clinical endpoints and the absence of a test cohort [1–6]. To overcome these difficulties, a number of strategies and procedures have been developed to rank biomarker candidates systematically [7–13]. One of the most common and frequently cited strategies is vote counting [10].

Vote counting is based on the intuitive idea that a biomarker robust enough to show significance across multiple studies deserves higher ranking. Although many studies have likely incorporated this logic in their selection of candidates without referencing the vote-counting strategy per se, studies that do reference it tend to cite Griffith et al. [10]. As proposed by Griffith et al., the vote-counting strategy ranks biomarkers on the basis of one principal and two secondary criteria. The principal criterion is number of supporting studies in which each study showing significant differential expression in the same direction (either up- or downregulated) for a given biomarker counts as a vote in favor of that biomarker being real. The votes are tallied, and the biomarkers are ranked from highest count to lowest. This approach has obvious shortcomings, such as ignoring negative votes and the potential for selection bias arising from the criteria used to choose the studies and the biomarker candidates within those studies. Nevertheless, vote counting is popular because the computation is simple and the data needed are readily accessible, whereas more rigorous methods typically require requests for unpublished data.

Because vote counting frequently leads to ties, Griffith et al. also proposed two secondary criteria. One is total subject sample size summed across all of the supporting studies, the assumption being that studies based on larger sample sizes tend to be more reliable and thus biomarker candidates supported by larger combined sample sizes should be more reliable as well. The other criterion is mean fold change, based on the idea that large differences in biomarker expression are more likely to be confirmed than small differences. How these two criteria should be weighted with respect to each other in the vote-counting strategy is not discussed.

The goal of this study was to determine how well these three criteria predicted biomarker performance in an actual external validation test (i.e., independent of any association with the research group that implemented the strategy). External testing is important to establishing the validity and performance characteristics of the vote-counting strategy because vote counting requires decisions regarding what studies to include and what significance threshold to use, which are subjective choices that can potentially be manipulated consciously or unconsciously to support internal validation.

We conducted our test of the vote-counting strategy by measuring the performance of the miRNAs ranked by Guan et al. [2] for distinguishing lung cancer tissue from normal lung tissue. We chose this study because of our laboratory’s long-standing expertise in lung cancer and ongoing efforts to validate miRNAs as biomarkers for early detection, The literature on miRNAs for this purpose is extensive, consisting of approximately 40 studies (tissue and nontissue) published over a period of about 6 years prior to the Guan et al. analysis. The Guan et al. meta-analysis involved surveying the literature, identifying 14 studies that met their inclusion criteria (e.g., tissue studies only, test cohort used, nonoverlapping datasets) and applying the vote-counting strategy to the 182 biomarkers that showed significant differential expression in at least one study. Their analysis encountered many of the challenges noted above, and their ranking embodies the challenges faced by biomarker researchers in general, making it well suited for testing the vote-counting strategy.

A second meta-analysis of miRNAs for distinguishing lung cancer tissue from normal was conducted independently by Vosa et al. [3] at the same time. This meta-analysis used different criteria than Guan et al. for selecting their studies and focused on applying a robust rank aggregation method to prioritize the biomarkers. It also included a vote count of supporting studies, and 14 of their 15 biomarker candidates were ones that we tested. Therefore, we used their vote-count numbers and the fold-change data from the studies in their analysis to test the reproducibility of our findings.

The overall aim of this study was to conduct an external validation test of the vote-counting strategy. It was not designed to necessarily confirm or disconfirm these miRNAs as biomarkers of lung cancer. It was designed principally to test for a significant correlation between the biomarker rankings predicted by vote counting and the rankings observed in our external test. To our knowledge, this represents the first independent test of the vote-counting strategy or any other strategy for ranking biomarker candidates.

Materials & methods

Tissue preparation

Samples of surgically resected, lung cancer tissue and adjacent lung tissue were collected from 45 patients with non-small cell lung cancer: 23 cases of adenocarcinoma and 22 cases of squamous cell carcinoma. Demographically, the patients were: 51% males, average age 68 years (SD 10 years) and 90% former or current smokers (18–100 pack years). Use of these samples was obtained by written consent for biomarker analysis in accordance with protocols approved by the University of Colorado’s Institutional Review Board for the Anschutz Medical Campus (Pulmonary Nodule Biomarker Trial IRB #09–1106, Lung Cancer Tissue Bank Trial IRB #04–0688). The samples were embedded in Tissue-Tek Optimal Cutting Temperature Compound and immediately transferred to liquid nitrogen for storage. At the time RNA was needed, a cryostat thoroughly cleaned with DisCide disinfectant and precooled to −25°C was used to cut ten sequential 20 μm sections from each tissue block. All ten sections were gathered together using forceps cleaned with DisCide and placed in a precooled, prelabeled, 2-ml cryovial. Seven hundred microliters of Qiazol reagent (Qiagen, MD, USA) was added and vortexed thoroughly until all tissue was visibly dissolved. The mixture was stored on dry ice temporarily and at −80°C for longer term storage.

miRNA extraction

The samples were thawed and any unhomogenized pieces were ground up using a sterile, disposable, plastic pestle (Kimbal Chase, TN, USA). RNA and miRNA were extracted using a miRNeasy Mini Kit (Qiagen, CA, USA) per the manufacturer’s instructions and eluted using 30 μl of RNase-free water. There was no DNase treatment. The nucleic acid concentration was measured using a NanoDrop UV-Vis spectrophotometer (Thermo Fisher Scientific, MA, USA), and the samples were stored at −80°C.

Real time-quantitative PCR (RT-qPCR)

Under standard nuclease-free conditions, 300 ng of nucleic acid from each sample was reverse transcribed into cDNA using a custom primer pool supplied with custom TaqMan miRNA microarray cards for running 48 qPCR assays simultaneously and the TaqMan miRNA Reverse Transcription kit (Applied Biosystems, NY, USA) according to manufacturer’s supplied protocol. Reverse transcription reaction volume was 15 μl. The Taqman primers were designed by the manufacturer for high specificity, which has been independently confirmed by Mestdagh et al. [14]. We tested for artifactual amplification by including no-reverse-transcriptase control reactions. The full 15 μl of cDNA product was combined with Applied Biosystems ‘TaqMan Universal PCR Master Mix No Amp Erase UNG 2X to a final volume of 100 μl for each reaction. The cDNA and Master Mix reaction solution were loaded on the cards and run on an Applied Biosystems 7900HT Fast Real-Time PCR system real-time thermocycler according to the manufacturer’s protocol. The Ct values were extracted using Applied Biosystems’ RQ Manager 1.2.1 software. A threshold value of 0.23 and a baseline of 3 to 15 cycles were used for all miRNAs. Cts > 40 were imputed with a Ct value of 40. We used the expression mean of let-7g and let-7i for normalization to calculate the ΔCt values for each sample based on the recommendation of Normfinder [15], which ranks each normalization factor candidate for use individually or paired on the basis of having a low ‘stability value,’ derived by modeling and combining the expression variation within groups and the expression difference between groups. To check for potential effects of poor RNA extraction efficiency on our ΔCt values, we conducted technical replicates on 16 tumor and normal samples (eight patients) having the lowest RNA concentrations. The replicates gave nearly identical ΔCts with correlation coefficients ranging from 0.93 to 0.99 (mean of 0.97) and a mean difference in ΔCt of only 0.25.

Of the 52 miRNAs ranked by Guan et al., we tested 50 and excluded two due to limited space on our custom RT-qPCR cards. MiR-30a was excluded because it was nearly identical in sequence to miRs 30b, c and d that we tested; all three of these reached statistical significance with similar fold change and p-values (Tables 1 & 2). MiR-92b was excluded because its values in Guan et al. were intermediate for number of supporting studies (3), total sample size (151) and mean fold change (3.71). Consequently, excluding it would be expected to have negligible impact on our correlation tests.

Table 1.

Statistical significance of biomarker candidates ranked by Guan et al. (2012) and supported by three or more studies.

miRNA‡	Guan et al. meta-analysis†		t-test results this study
	Number of supporting studies§	Total sample size (n)	p-values (1-tailed)#	Fold change¶
miR-126 (3p)	10	587	6.0 × 10−10	−3.85
miR-210 (3p)	9	796	7.3 × 10−8	2.76
miR-486–5p††	8	563	1.7 × 10−8	−4.72
miR-21 (5p)	7	448	7.5 × 10−11	2.96
miR-182 (5p)	6	496	2.2 × 10−6	2.68
miR-31 (5p)	6	425	4.5 × 10−4	3.38
miR-451 (451a)	6	265	2.6 × 10−8	−4.30
miR-205 (5p)	5	417	5.8 × 10−5	8.10
miR-139–5p‡‡	5	371	1.9 × 10−10	−4.20
miR-200b (3p)	5	262	0.13	1.20
miR-30d (5p)	5	154	2.6 × 10−4	−1.99
miR-183 (5p)	4	388	1.4 × 10−6	2.89
miR-145 (5p)	4	362	4.7 × 10−10	−3.28
miR-143 (3p)	4	310	2.5 × 10−10	−2.73
miR-203 (203a)	3	347	0.095	1.33
miR-196a (5p)	3	317	4.0 × 10−10	11.2
miR-708 (5p)	3	301	5.2 × 10−8	3.89
miR-126* (126–5p)	3	280	0.0055	−1.82
miR-140–3p	3	179	6.4 × 10−9	−2.08
miR-138 (5p)	3	164	4.8 × 10−5	−2.33
miR-193b (3p)	3	149	2.6 × 10−4	1.89
miR-30b (5p)	3	132	4.4 × 10−4	−1.71
miR-101 (3p)	3	87	0.0026	−1.35

^†Data extracted from Tables 2 and 3 of Guan et al. [2].

^‡The miRNA names are those used by Guan et al. [2]. Updated designations according to miRBase (www.mirbase.org) are shown in parentheses.

^§The number of studies reporting significant differential expression of the miRNA in the same direction (up- or downregulated).

^#p-values < 0.00069 (6.9 × 10⁻⁴) are shown in exponential notation to indicate statistical significance (α < 0.05) in the direction expected after strict Bonferroni correction (0.05/72 miRNAs tested).

^¶Negative fold change values indicate expression levels that were lower in tumor than control.

^††The Guan et al. data for miR-486 and miR-486–5p were combined because they are the same miRNA.

^‡‡The Guan et al. data for miR-139 and miR-139–5p were combined because they are the same miRNA.

Table 2.

Statistical significance of biomarker candidates ranked by Guan et al. (2012) that were supported by two studies.

Guan et al. (2012) meta-analysis†		t-test results this study
miRNA‡	Total sample size	p-value (1-tailed)§	Fold change#
miR-106a (5p)	279	0.034	1.20
miR-125a (5p)	279	0.0058	−1.31
miR-198	273	0.42	−1.07
miR-21* (3p)	271	2.2 × 10−6	2.26
miR-144* (5p)	271	6.2 × 10−8	−4.10
miR-140 (5p)	248	1.5 × 10−7	−1.71
miR-218 (5p)	246	7.5 × 10−9	−2.82
miR-135b (5p)	222	7.0 × 10−6	2.26
miR-32 (5p)	220	(0.054)	(1.24)
miR-96 (5p)	218	5.5 × 10−4	2.19
miR-17-5p	136	0.27	1.05
miR-338 (3p)	133	1.4 × 10−4	−3.06
miR-20b (5p)	117	(0.019)	(−1.54)
miR-18a (5p)	114	0.0039	1.37
miR-200a (3p)	111	0.13	1.22
miR-93 (5p)	111	6.5 × 10−4	1.35
miR-99a (5p)	111	0.15	−1.16
miR-130b (3p)	108	4.6 × 10−10	2.99
miR-200c (3p)	101	0.0091	1.53
miR-195 (5p)	98	1.5 × 10−6	−1.93
miR-497 (5p)	98	5.9 × 10−7	−2.09
miR-30c (5p)	86	1.5 × 10−6	−1.82
miR-375	86	(0.21)	(−1.38)
miR-20a (5p)	83	0.033	1.25
miR-130a (3p)	81	0.0084	−1.39
miR-18b (5p)	80	7.3 × 10−5	1.56
miR-16 (5p)	76	3.4 × 10−6	−1.51

^†Data extracted from Tables 2 and 3 of Guan et al. [2].

^‡The miRNA names are those used by Guan et al. [2]. Updated designations according to MirBase (www.mirbase.org) are shown in parentheses.

^§p-values < 0.00069 (6.9 × 10⁻⁴) are shown in exponential notation to indicate statistical significance (α < 0.05) in the direction expected after strict Bonferroni correction (0.05/72 miRNAs tested). The three p-values in parentheses are 2-tailed and fold change was in the opposite direction from expected.

^#Negative fold change values indicate expression levels that were lower in tumor than control. Values in parentheses indicate changes that were in the opposite direction from expected.

Statistics

The statistical significance of differential expression was assessed using 1-tailed, paired-sample t-tests, which is consistent with the univariate analyses used to define the statistical significance of each biomarker in the supporting studies. To correct for testing 72 biomarker candidates, we used a strict Bonferroni-corrected p-value of 0.00069 (0.05/72) as our threshold for statistical significance. The differential expression also had to be in the direction expected from the supporting studies (hence the 1-tailed tests).

For the purpose of conducting the correlation analyses, we transformed the p-values in Tables 1 & 2 to a negative logarithm scale and used these as an index of biomarker performance, not as p-values. A second transformation was necessary for three of the miRNAs to indicate performance that was opposite from the direction expected and disconfirming rather than confirming. This directional change was indicated by changing the sign of their performance values from positive to negative. All correlation coefficients are Pearson coefficients.

The methods used to identify outliers and recalculate the Guan et al. mean fold-change values are detailed in Supplementary Methods (see online at www.futuremedicine.com).

Results

We conducted RT-qPCR expression assays on 72 mature miRNAs selected from the literature as promising biomarker candidates for distinguishing lung cancer tissue from adjacent, noncancer lung tissue (paired tumor-normal). All miRNAs were tested against the same 45 paired tumor-normal samples (90 samples total). Of the 72 candidates, 50 were selected from the meta-analysis by Guan et al. [2], which ranked 52 candidates supported by two or more studies according to the vote-counting strategy (the two miRNAs not tested are discussed in section ‘Materials & methods’). The 22 other miRNAs tested were ones that we chose on the basis of being promising candidates in the literature that were not ranked by Guan et al. (17 studies total; Supplementary Table 1). We included these miRNAs to compare the performance of unranked candidates to ranked candidates. Performance was assessed by univariate analysis (Student’s t-test) to match how these miRNAs were originally identified as being significant biomarkers that distinguish tumor samples from normal.

Of the 22 unranked candidates, only let-7a, with p = 2.0 × 10⁻⁴ (Supplementary Table 1), exhibited differential expression between tumor and normal tissue that met our criterion for statistical significance after Bonferroni correction (see section ‘Materials & methods’). In sharp contrast, this criterion was met by 33 of the 50 biomarkers ranked by Guan et al. (Tables 1 & 2). This enrichment for significant biomarkers suggested that Guan et al.’s ranking of candidates represented a near-complete list of the top biomarker candidates in the literature. This suggestion was further supported by Vosa et al. [3], which used different study criteria for their meta-analysis resulting in the inclusion of eight additional studies and the exclusion of two. Nevertheless, all 15 miRNAs that Vosa et al. identified as their top biomarker candidates in the literature were also ranked by Guan et al. That nearly all of the top candidates in the literature have been ranked suggests that the candidates we tested are highly suitable for assessing the vote-counting strategy.

Number of supporting studies

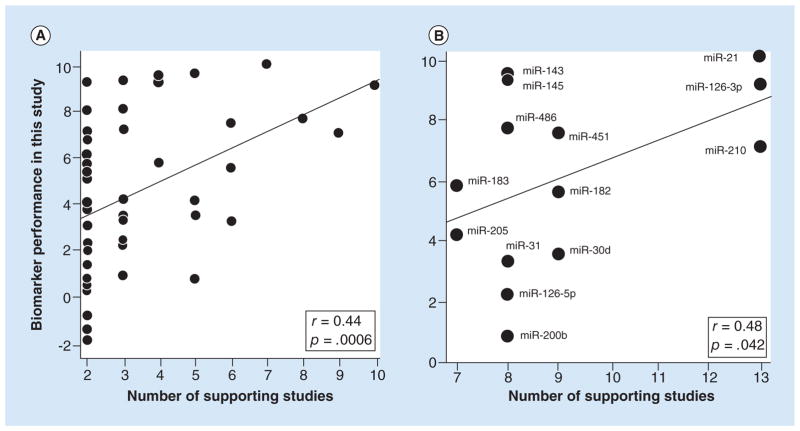
The principal criterion for ranking biomarker candidates according to the vote-counting strategy is number of supporting studies, defined as the number of studies reporting significant differential expression in the same direction (either up or down regulated). We examined this criterion by testing for a significant correlation between number of supporting studies, as counted by Guan et al., and the statistical performance of the biomarker candidates tested against our set of 45 paired tumor-normal samples (Tables 1 & 2). We found that number of supporting studies, ranging from 2 to 10, was indeed a predictor of performance with a highly significant p-value of 0.00061 for the correlation. However, it was only a modest predictor considering that the correlation coefficient (r) was 0.44 (Figure 1), and thus the variance explained (r²) was only 19%.

Figure 1. Scatter plots showing that number of supporting studies predicted the performance of biomarker candidates.

The performance values (y-axis) were derived by rescaling the differential expression p-values in Tables 1 & 2 and using negative values for three of the miRNAs because their expression in tumor versus normal was opposite from the direction expected (see statistics methods). The lines are the best fit lines from the Pearson correlation analysis, the r’s are correlation coefficients and the p’s are the significance values of the correlations (1-tailed). (A) Correlation with the number of supporting studies determined by Guan et al. [2]. n = 50 miRNA biomarkers. (B) Correlation with the number of supporting studies determined by Vosa et al. [3]. n = 14 miRNA biomarkers.

Most of the biomarker candidates (27 of 50) in the above correlation test were supported by two studies, suggesting that the high concentration of these markers could be having a disproportionately large effect on the analysis. Therefore, we asked if a positive correlation was still present when we considered only biomarker candidates supported by three or more studies. It was, with r = 0.36 and p = 0.045 (n = 23).

Independent of Guan et al., Vosa et al. [3] also counted number of supporting studies for 14 of the miRNAs that we tested. Their counts ranged from 7 to 13, whereas the range in Guan et al. for these candidates was 4 to 10. In spite of this difference and the difference in criteria used to select the studies and the analysis being limited to only 14 biomarker candidates, we found that number of supporting studies was still a significant predictor of biomarker performance (Figure 1B) (p = 0.042). The correlation coefficient of 0.48 was also very similar to the correlation of 0.44 noted above. Therefore, number of supporting studies was a significant predictor of biomarker performance for counts determined in two independent studies.

Total number of samples

We then tested whether total sample size (summed across the supporting studies) predicted biomarker performance. However, as evident in Table 1, there was a very high correlation between total sample size and number of supporting studies (r = 0.83, p < 10⁻¹³; see Supplementary Table 2 Correlation Matrix). This correlation arises because total sample size increases proportionally with increases in supporting studies. Therefore, it was not too surprising that total sample size also predicts biomarker performance, and the correlation coefficient of 0.44 and its p-value of 0.00065 were virtually identical to what we observed for number of supporting studies. Therefore, assessing the predictive value of total sample size per se required uncoupling it from number of supporting studies.

To uncouple total sample size, we conducted a correlation analysis using only the biomarker candidates supported by two studies according to Guan et al. (Table 2), corresponding to 27 candidates. Uncoupling by this method is also consistent with total sample size being defined in the vote-counting strategy as a secondary criterion for breaking ties when the number of supporting studies is the same. As shown in Table 2 and Figure 2, the total sample sizes ranged appreciably from 79 to 279 patients, yet total sample size was not a significant predictor of biomarker performance (r = 0.11, p = 0.29). Therefore, contrary to the expectations of the vote-counting strategy, total sample size was not a useful secondary criterion for ranking biomarker candidates.

Figure 2. Scatter plot showing that total sample size in supporting studies did not predict the performance of biomarker candidates.

The performance values (y-axis) were derived by rescaling the differential expression p-values in Table 2 and using negative values for three of the miRNAs because their expression in tumor vs. normal was opposite from the direction expected (see statistics methods). The line is the best fit line from the Pearson correlation analysis, r is the correlation coefficient and p is the significance value of the correlation (1-tailed). Each miRNA biomarker was supported by two studies as determined by Guan et al. [2]. n = 27 miRNA biomarkers (two markers coincide at point 111, 1).

A similar analysis of the biomarker candidates ranked by Vosa et al. could not be performed because not enough candidates had the same number of supporting studies: the largest sample size available (for eight supporting studies) was only six (Figure 1B).

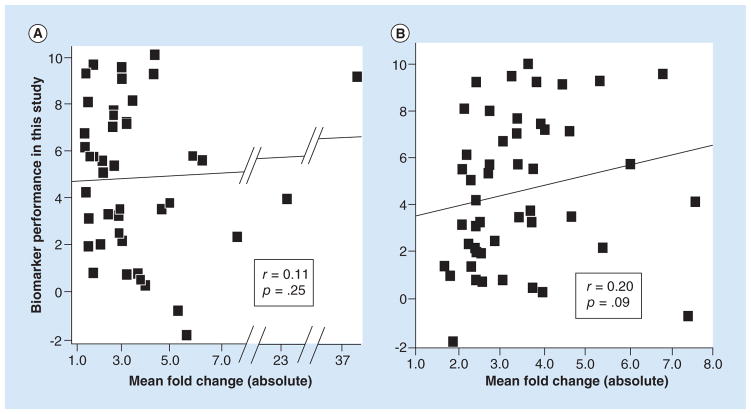
Mean fold change

We then tested whether mean fold change calculated from the supporting studies was a useful criterion for predicting biomarker performance. We first used the fold-change values reported by Guan et al. [2], which they calculated for 44 of their ranked biomarkers. All but three values were distributed across a fivefold range of variation (1.5 to 7.8 absolute scale). As shown in Figure 3A, mean fold change did not correlate with biomarker performance (r = 0.11, p = 0.25). However, as detailed in section ‘Supplementary methods,’ we noticed potential problems with how mean fold change was calculated. Therefore, we also calculated the mean fold-change values ourselves (Supplementary Tables 3 & 4), which resulted in appreciable differences from Guan et al. with an overall correlation of only 0.44 (Supplementary Tables 2, 3 & 4). Nevertheless, the mean fold-change values that we calculated still suggested no correlation with biomarker performance (r = 0.12, p = 0.22, n = 47).

Figure 3. Scatter plots showing that fold change in supporting studies did not predict the performance of biomarker candidates.

The performance values (y-axis) were derived by rescaling the differential expression p-values reported in Tables 1 and 2 and using negative values for two of the miRNAs because their expression in tumor versus normal was opposite from the direction expected (see statistics methods). The line is the best fit line from the Pearson correlation analysis, r’s are the correlation coefficients and the p’s are the significance values of the correlations (1-tailed). (A) Correlation with the biomarker candidates ranked by Guan et al. [2] using the mean fold-change values reported by Guan et al. [2]. n = 43 miRNA biomarker candidates. One biomarker candidate with an expected fold change of 171.6 was excluded as an outlier. If this marker were included, the correlation coefficient would be slightly negative: −0.06 (p = 0.72, two-tailed). (B) Correlation with the biomarker candidates ranked by Guan et al. [2] using the mean fold-change values that we calculated using the supporting studies in Vosa et al. [3]. n = 48 miRNA biomarker candidates.

We also calculated the mean fold-change values using the supporting studies in Vosa et al. As shown in Figure 3B, the correlation with biomarker performance was considerably better (r = 0.20) but still did not reach statistical significance at p < 0.05 (p = 0.09, n = 48).

Discussion & future perspective

To our knowledge this study is the first independent test of a strategy commonly used to rank and select biomarker candidates from published studies for external validation, an extremely difficult hurdle for most biomarkers even after they have been validated internally. The three criteria used in the vote-counting strategy are highly intuitive and many biomarker studies have likely used one or more of these criteria without referencing the vote-counting strategy per se. By independent test, we mean that our laboratory had no involvement in the biomarker rankings or votes counted by Guan et al. or Vosa et al., and our cohort of 45 patients was unrelated to the cohorts used in their analyses. The objectivity of an external test is important because subjective choices must be made in the vote-counting strategy when deciding on the study criteria and what counts as a significant level of differential expression. That the rankings by Guan et al. and Vosa et al. were conducted independent of each other suggests that our test results are not peculiar to the subjective choices made in a single study.

We assessed each criterion in the vote-counting strategy on the basis of how well it predicted biomarker performance defined on the basis of the univariate statistical significance of the differential expression observed using our paired tumor-normal samples. Consistent with expectations, we found that the primary criterion used in the vote-counting strategy, number of supporting studies, is a statistically significant predictor of biomarker performance. That we detected this relationship with a p-value of 0.0006 for a correlation coefficient of only 0.44 demonstrates that our sample size of 90 was more than adequate for testing this relationship and the relationships with total sample size and mean fold change. Although the relationship was highly significant for number of supporting studies, the variance explained was only about 20% (r² = 19% for the 50 candidates ranked by Guan et al. and r² = 23% for the 14 candidates ranked by Vosa et al.), suggesting only modest power to predict rankings.

It is also important to recognize that ranking biomarkers according to the number of supporting studies in the literature has potential for bias if the biomarker candidates tested in later studies are strongly selected for on the basis of success in earlier studies. Such bias could result in top biomarker candidates not receiving multiple votes because they were not tested repeatedly. As done in our study, therefore, it might be prudent when screening candidates to include a sampling of markers that did not achieve two or more votes. It is also worth noting that recently it has been shown that biomarkers can still perform well as part of a multiple-biomarker signature even if they do not perform well individually [22].

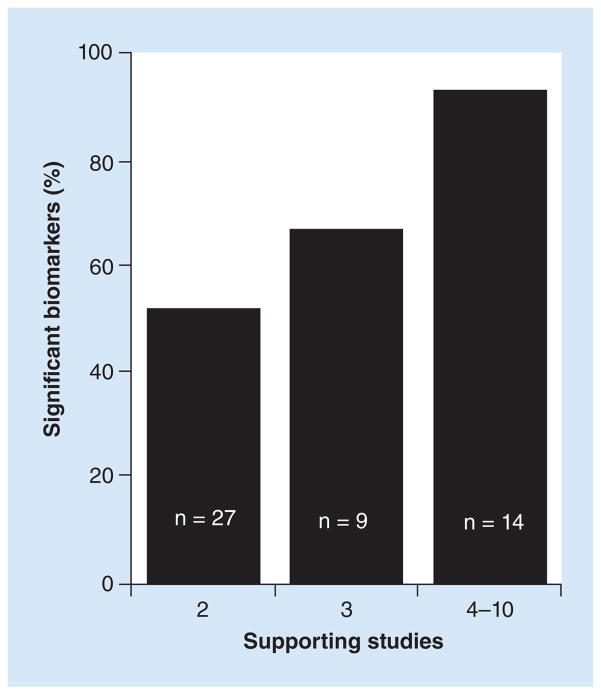
Given these caveats, the relationship between number of supporting studies and biomarker performance can potentially be used to crudely estimate the expected probability of a biomarker candidate reaching statistical significance in an external validation test. For example, we observed that about 90% (13 of 14, Table 1) of the ranked biomarker candidates reached statistical significance if they were supported by four or more studies (the mean and median was six supporting studies, Figure 4). Similarly, the biomarker candidates that reached statistical significance (~95% confidence level) in Vosa et al. according to their robust rank aggregation method (one of the rigorous methods for ranking biomarker candidates that typically requires access to unpublished data) were associated with at least seven supporting studies. For biomarker candidates supported by just two studies, the observed frequency of reaching statistical significance was only 14 of 27 (50%) by our significance criteria (Table 1, Figure 4). With a larger sample size, it’s conceivable that the biomarkers with p’s < 0.05 would also be confirmed, which would increase the confirmation rate to 70% (19/27). This value is in good agreement with the value of 73% estimated by Griffith et al. (2006) in their Monte Carlo simulation. The biomarkers supported by three studies exhibited an intermediate probability of being confirmed: 6 of 9 or 67% (Table 1 & Figure 4) by our significance criteria and potentially 8 of 9 (89%) using p < 0.05, which is also not that different from the value of 99% estimated by the Monte Carlo simulation of Griffith et al. (2006). In contrast, our 22 unranked biomarkers, selected on the basis of at least two promising studies that were not necessarily based on using tissue samples as required by Guan et al., showed only a 5–14% chance of being confirmed by the same criteria. Although these observed frequencies need refinement using data from more studies like ours, they represent a basis for estimating the yield of significant biomarkers expected from vote counting. They also indicate that in spite of its shortcomings and the modest correlation (r = 0.44) between the predicted and observed rankings, vote counting can be remarkably effective at identifying biomarkers likely to reach statistical significance in an external test.

Figure 4. Graphical representation of the observed frequency of statistically significant biomarkers as a function of the number of supporting studies.

The proportion of candidate biomarkers that reached statistical significance according to our study criteria increased from approximately 50% (2 supporting studies) to 90% (4 to 10 supporting studies) as the number of supporting studies increased. The number of supporting studies from four to ten had a mean and median of six studies (Table 1).

In contrast to number of supporting studies, total sample size per se (summed across supporting studies) after controlling for the number of supporting studies was not a predictor of biomarker performance (r = 0.11, p = 0.29). This negative finding could be due to the fact that assessments of statistical significance already take sample size into account. Therefore, sample size is not normally used to predict that one significant result deserves more confidence than another; typically, the p-value is used for this purpose. However, sample size does affect confidence when nonstochastic variation is suspected, which is more likely when there is no test cohort. In this regard, most of the biomarker studies used as the basis for the Guan et al. and Vosa et al. rankings included test cohorts.

We also found that contrary to the vote-counting strategy and intuition, fold change was not a predictor of biomarker performance. This result was particularly surprising because fold change tends to be a strong correlate of statistical significance within studies. Indeed, fold change was a highly significant correlate of biomarker performance in this study: r = 0.65 and p = 2.0 × 10⁻⁷ (1-tailed, n = 50; Supplementary Table 2). Our fold-change values also showed significant correlation with the fold-change values that we calculated from the studies in Guan et al. (r = 0.44, p = 0.002, n = 47) and Vosa et al. (r = 0.44, p = 0.001, n = 48). Therefore, even though the fold-change values from the supporting studies were significant predictors of the fold-change values that we observed, fold change was still not a predictor of biomarker performance. A straightforward interpretation could be that the biomarker candidates associated with larger fold changes also exhibited larger amounts of variability across studies; hence, they are not more likely to reach statistical significance in an external test. Consistent with this interpretation, larger mean fold changes were strongly associated with greater variability across studies (measured as the standard deviation) for the studies in both Vosa et al. (r = 0.89, p = 4 × 10⁻¹⁶, 1-tailed, n = 43) and Guan et al. (r = 0.65, p = 4.8 × 10⁻⁵, 1-tailed, n = 30). Another formal possibility could be that the larger fold-change means were associated with smaller sample sizes (i.e., smaller n’s used to calculate the means), but this was not the case; the correlation between the fold change means and the n’s used to calculate them did not suggest a significant relationship (p’s ≥ 0.2 using either the Guan et al. values or the values that we calculated from the studies in Guan et al. and Vosa et al.).

In conclusion, just as promising biomarkers are typically subjected to external validation, the criteria used to rank biomarkers should be independently tested as well to establish their validity and performance characteristics. In this study we found that counting the number of supporting studies was indeed an effective criterion for ranking and selecting biomarker candidates. At the same time, however, we found that rankings on the basis of total sample size or fold change, which were not even tested by Griffith et al. (2006), appear to have little, if any, value. Although there are possible conditions under which these two criteria could be more informative as alluded to above, there is currently no experimental support for their utility.

Executive summary.

Background

• Different strategies have been used to rank the expected performance of biomarkers on the basis of results aggregated across published studies. To our knowledge, however, none of these strategies has been validated externally.

• Here, we conducted an independent, external test of the vote-counting strategy – a commonly used, simple, highly intuitive approach that ranks expected performance on the basis of the number of supporting studies in the literature, the total sample size represented by those studies and the mean fold change.

Methods & results

• The three ranking criteria were tested using the rankings and data from two published meta-analyses conducted by two separate research groups with whom we have no affiliation.

• We tested the performance of 50 ranked and 22 unranked miRNAs assayed by RT-qPCR for their ability to distinguish lung cancer tissue from normal lung tissue.

• All 72 biomarkers were tested against the same 45 paired tumor-normal samples (90 samples total).

• Number of supporting studies was a significant predictor of biomarker performance (p = 0.0006, r = 0.44).

• Biomarkers supported by two studies showed approximately a 50–70% probability of reaching statistical significance; those supported by three studies showed a 70–90% probability, those supported by four or more studies showed a 90–100% probability. In contrast, our unranked markers showed only a 5–14% probability of being confirmed.

• The other two ranking criteria, total sample size and mean fold change calculated from the supporting studies, were not significant correlates of biomarker performance (p = 0.29, r = 0.11 and p = 0.22, r = 0.12, respectively).

Conclusion

• To our knowledge, this study is the first to show by external validation that counting the number of supporting studies in the literature is an effective strategy for predicting biomarker performance.

• Given certain caveats, it appears that this strategy can markedly enrich for biomarkers likely to be confirmed by independent testing. This knowledge can thus be used to judiciously select biomarkers for clinical validation.

• In contrast, selecting biomarkers on the intuitive basis of a larger total sample size in the supporting literature or a larger mean fold change appears to provide little, if any, added value.