Abstract
Current cochlear implant (CI) strategies carry speech information via the waveform envelope in frequency subbands. CIs require efficient speech processing to maximize information transfer to the brain, especially in background noise, where the speech envelope is not robust to noise interference. In such conditions, the envelope, after decomposition into frequency bands, may be enhanced by sparse transformations, such as nonnegative matrix factorization (NMF). Here, a novel CI processing algorithm is described, which works by applying NMF to the envelope matrix (envelopogram) of 22 frequency channels in order to improve performance in noisy environments. It is evaluated for speech in eight-talker babble noise. The critical sparsity constraint parameter was first tuned using objective measures and then evaluated with subjective speech perception experiments for both normal hearing and CI subjects. Results from vocoder simulations with 10 normal hearing subjects showed that the algorithm significantly enhances speech intelligibility with the selected sparsity constraints. Results from eight CI subjects showed no significant overall improvement compared with the standard advanced combination encoder algorithm, but a trend toward improvement of word identification of about 10 percentage points at +15 dB signal-to-noise ratio (SNR) was observed in the eight CI subjects. Additionally, a considerable reduction of the spread of speech perception performance from 40% to 93% for advanced combination encoder to 80% to 100% for the suggested NMF coding strategy was observed.
Keywords: cochlear implant, nonnegative matrix factorization, speech enhancement, vocoder, speech recognition, babble noise
Introduction
Cochlear implants (CI) are electrical devices that help to restore hearing to the profoundly deaf. The main principle of CIs is to stimulate the auditory nerve via electrodes surgically inserted into the inner ear. With the development of new speech processors and algorithms, CI users benefit more and more from their implants (Wilson & Dorman, 2007; Zeng, 2004), and many of them are even able to communicate via telephone. However, average speech perception performance of CI users is still far below that of normal-hearing (NH) listeners, especially in the presence of background noise. This may occur because there are information transmission bottlenecks (Olshausen & Field, 2004), both in the CI device itself and in the impaired auditory system, which limit acoustic information transmission to auditory neurons (Greenberg, Ainsworth, Popper, & Fay, 2004). Examples of such bottlenecks include the smaller dynamic range of CIs, relative to NH, and the limited number of electrodes.
There are currently two main ways by which speech processing algorithms aim to improve CI performance: one focuses on noise reduction preprocessing by trying to enhance speech and suppress noise (Hendriks & Martin, 2007; Hussain, Chetouani, Squartini, Bastari, & Piazza, 2007; Mauger, Arora, & Dawson, 2012; Mauger, Dawson, & Hersbach, 2012; Roberts, Ephraim, & Lev-Ari, 2006; Wouters & Berghe, 2001); the other focuses on redundancy reduction using different coding strategies (Buchner, Nogueira, Edler, Battmer, & Lenarz, 2008; Buechner et al., 2011; Li, 2008; Li, Lutman, Wang, & Bleeck, 2012; Loizou, Lobo, & Hu, 2005; Nie, Drennan, & Rubinstein, 2009) to make better use of the limited transfer capacity in the CI electrical-auditory system. Speech has a high degree of redundancy (Cooke, 2006; Kasturi, Loizou, Dorman, & Spahr, 2002), and humans can understand speech based on partial information and in difficult environments. This phenomenon has been explored and modeled using, for example, glimpsing (Cooke, 2006) or binary masking (Wang, Kjems, Pedersen, Boldt, & Lunner, 2009). Existing CI strategies, such as continuous interleaved sampling (Wilson et al., 1991), spectral peak (Seligman & McDermott, 1995) and the advanced combination encoder (ACE; Clark, 2003; Patrick, Busby, & Gibson, 2006), already take advantage of the redundancy properties of speech by selecting only few channels or only using envelope information for stimulation. Li and colleagues (Li, 2008; Li et al., 2012) demonstrated that these strategies deliver stimulation in a sparse representation of the speech and they introduced a SPARSE strategy, in which an algorithm based on independent component analysis is applied to the spectral envelope. Their results were promising, showing that the SPARSE strategy improved speech intelligibility for some CI users even with very limited familiarity with the stimulation strategy (Li, 2008; Li et al., 2012). The redundancy properties of speech were further investigated in Hu et al. (2011) by introducing an enhanced SPARSE strategy. Both objective measures and subjective listening tests with vocoder CI simulation in NH showed that the SPARSE strategy is a potential candidate for a future stimulation algorithm (Hu et al., 2011; Li, 2008; Li et al., 2012).
Nonnegative matrix factorization (NMF) (Lee & Seung, 1999, 2000) is an alternative algorithm that produces a sparse representation. It has recently attracted interest across many scientific and engineering disciplines, such as image processing, speech processing, and pattern classification (Cichocki, Zdunek, Phan, & Amari, 2009; Mohammadiha, Gerkmann, & Leijon, 2011; Potluru & Calhoun, 2008; Shashanka, Raj, & Smaragdis, 2008; Smaragdis & Brown, 2003; Spratling, 2006; Wang, Cichocki, & Chambers, 2009). NMF is useful for transforming high-dimensional data sets into a lower dimensional space (Potluru & Calhoun, 2008). Moreover, instead of developing holistic representations, NMF usually conducts parts-based decomposition and reconstruction using nonnegativity constraints (Lee & Seung, 1999). A nonnegative approach is suitable for envelope representations, which cannot be negative.
Motivated by the nonnegativity feature of the signal envelopes in CI channels and the positive firing rate of auditory neurons, a sparse coding strategy based on NMF is proposed in the current study, and we investigate whether it can improve the performance of CI users in noisy environments. Considering the computational complexity of NMF and an envisaged real-time implementation, a basic NMF method with a sparse constraint λ (Hoyer, 2002) is applied. The choice of λ to deal with the trade-off between sparseness and intelligibility, and thus to maximize the performance of the whole algorithm, is a substantial challenge.
The proposed algorithm is evaluated in eight-talker babble noise with both objective measures and experimental listening tests, using specific λ values to assess the effect of λ on the algorithm output. The article is organized as follows: First, the sparse NMF algorithm is presented after a short introduction to NMF. The ACE strategy and how the proposed sparse NMF strategy is embedded are described. Second, the objective evaluation methods and subjective tests for both NH and CI subjects are described. Subsequently, the evaluation results are provided. Finally, a discussion and the conclusions are presented.
Algorithm
NMF is a method to factorize a nonnegative matrix Z into the basis matrix W and component matrix H so that . To perform the factorization, a cost function is usually defined and minimized. There are many possibilities to define the cost function and various procedures for performing the subsequent minimization to derive meaningful factorizations for specific applications (Cichocki, Zdunek, & Amari, 2006; Févotte, Bertin, & Durrieu, 2009; Zdunek & Cichocki, 2008). The general notation of the minimization is:
where and are regularity functions for basis matrix W and component matrix H. The most common regularizations are motivated by the sparseness of the signal (Hoyer, 2004; Rennie, Hershey, & Olsen, 2008; Schmidt, 2008; Virtanen, 2007) and the correlation of the signal over time (Mysore, Smaragdis, & Raj, 2010; Virtanen, 2007). In this article, a squared Euclidean distance is used as the cost function (Cichocki et al., 2006). It is then combined with a L1 regularized least-squares sparseness penalty function through a least absolute shrinkage and selection operator framework; that is, the sparsity is measured by the L1 norm (Hoyer, 2002, 2004).
Principle of Sparse NMF in Envelope Domain
In our application, Z is a matrix consisting of the envelopes of CI channels in multiple frequency bands, referred to as envelopogram. NMF is applied to factorize the envelopogram into two matrices consisting of NMF basis vectors W and the NMF components H representing the activity of each basis vector over time. Although standard NMF usually provides sparseness of its components to a certain degree, an additional sparseness constraint is applied to explicitly control the sparsity of the NMF component matrix H. The L1 norm of H is used as the sparsity measure and the optimization algorithm proposed by Hoyer (2002, 2004) is applied to obtain nonnegative matrices W and H.
Problem formulation
Let Z denote an envelopogram of one analysis block, where N and M indicate the number of channels and the number of frames, respectively. Given the nonnegative envelopogram matrix Z, NMF aims to obtain the basis matrix W and component matrix H such that
| (1) |
is minimized, under the constraints where
zij is the envelope-time bin in the channel of the frame, denotes the column of W, .
The sparseness constraint λ in equation (1) is an important parameter that handles the compromise between the NMF approximation and the sparsity. One goal of the current study is to choose λ to maximize the performance of the algorithm, assessed in objective evaluation and subjective psychophysical experiments in the following sections.
Algorithm description
As proposed by Hoyer (2002, 2004), an iterative algorithm is implemented to minimize the cost function in equation (1), in which the basis matrix W and the component matrix H are updated by gradient descent and multiplicative update rules, respectively. There is no training stage in this study. The whole algorithm can be described as follows:
Initialize basis matrix W and component matrix H with random positive matrices and , and rescale each column of to unit norm.
- Iterate until convergence:
- Rescale each column of W to unit norm, so that
The variable μ is the step size, a small positive constant, which should be set appropriately to achieve reasonable optimization time and good resolution in obtaining the optimal values of W. Here, μ = 1 was chosen.
Sparse NMF Strategy for CIs
The suggested sparse NMF strategy was integrated with a research ACE strategy which served as a comparison framework. It was implemented in the Nucleus MATLAB Toolbox (NMT) v4.20 (Cochlear Technology, 2002; Swanson, 2008). NMT is a set of MATLAB scripts provided by Cochlear Limited and allows researchers to derive or modify speech processing strategies either at the speech processing strategy level or at a lower level to create sequences of electrode stimulation patterns and programmatically stream the patterns directly to Nucleus devices or simulators.
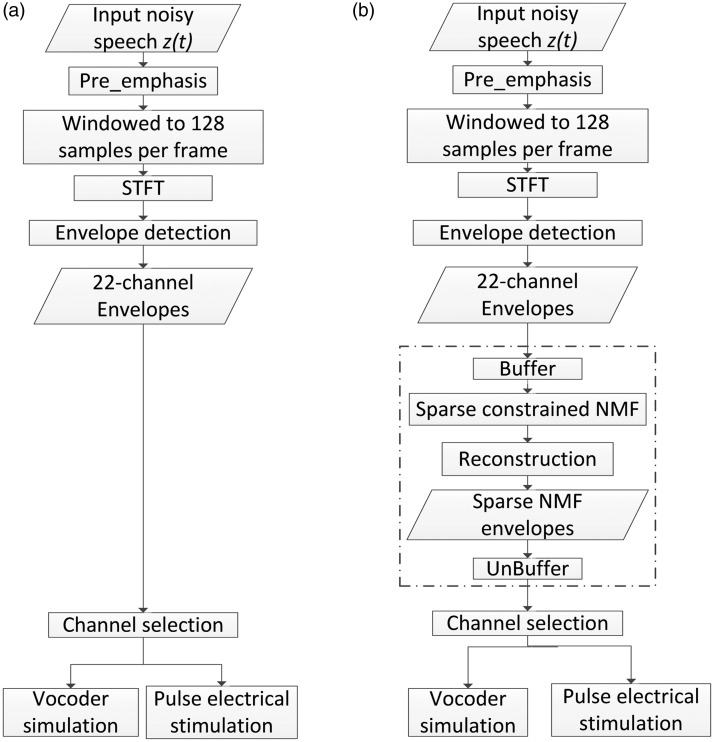
Figure 1a illustrates a basic block diagram of the research ACE strategy. is the measured noisy speech signal sampled at 16 kHz after applying a preemphasis filter. The preemphasis filter attenuates low frequencies and amplifies high frequencies, to compensate for the dB/octave natural slope in the long-term average speech spectrum. Then a filter bank, which is implemented with a short-time Fourier transform, is applied to the previously windowed audio signal; 128-point Hanning windows are used. After transforming the input speech signal into a spectrogram, the 22-channel envelopogram is extracted by summing the weighted short-time Fourier transform bin powers of a certain number of frequency bins within each channel. The envelope of channel i is calculated as:
| (2) |
Where is the fast Fourier transform (FFT) bin power, , . For the first channel, and is used, which means only the third frequency bin is selected and the corresponding weight is 0.98, while the other frequency bins have weightings of . For the channel, the starting nonzero weighting frequency bin is , the number of ascending bins is Li; thus the end frequency bin is ; the corresponding nonzero weights for these selected Li bins FFT powers are listed in Table 1 (Cochlear Technology, 2002; Swanson, 2008).
Figure 1.
Flowcharts of the ACE strategy and the proposed sparse NMF strategy: (a) illustrates the research ACE strategy, (b) shows the flowchart of the proposed sparse NMF algorithm and how it is integrated with the research ACE strategy.
Table 1.
Number of FFT Bins and Weightings .
| Band number | Number of bins L | Gain gz | Band number | Number of bins L | Gain gz |
|---|---|---|---|---|---|
| 1 | 1 | 0.98 | 12 | 2 | 0.68 |
| 2 | 1 | 0.98 | 13 | 2 | 0.68 |
| 3 | 1 | 0.98 | 14 | 3 | 0.65 |
| 4 | 1 | 0.98 | 15 | 3 | 0.65 |
| 5 | 1 | 0.98 | 16 | 4 | 0.65 |
| 6 | 1 | 0.98 | 17 | 4 | 0.65 |
| 7 | 1 | 0.98 | 18 | 5 | 0.65 |
| 8 | 1 | 0.98 | 19 | 5 | 0.65 |
| 9 | 1 | 0.98 | 20 | 6 | 0.65 |
| 10 | 2 | 0.68 | 21 | 7 | 0.65 |
| 11 | 2 | 0.68 | 22 | 8 | 0.65 |
In the channel selection block, a subset of envelopes with the largest amplitudes is selected for stimulation. In the vocoder simulation block, the noise vocoder in the NMT is used for the generation of the vocoded speech. The extracted envelopes from 22 channels after the maxima selection process are used to modulate pink noise signals, which have been band-pass filtered by fourth-order Butterworth filters corresponding to the analysis channels. Finally, all the modulated channels are summed to produce the vocoded stimuli (Dorman, Loizou, Spahr, & Maloff, 2002; Swanson, 2008). Although the simulations cannot model individual CI users’ performance perfectly, it has been shown that these simulations are still useful tools for evaluation new algorithms in their initial stages (Loizou, 2006).
In the CI stimulation block, the electrical stimulation pulses are modulated by the envelopes of the signals in the corresponding frequency bands. In addition, the pulse trains are separated in time and interleaved in order to minimize electrical interaction among the electrodes.
Figure 1b shows the flow chart of the proposed sparse NMF algorithm using a modified ACE strategy framework. The new modules are highlighted by the dashed frame of Figure 1b. The sparse NMF algorithm is applied to the envelopogram on a block-by-block basis by buffering a certain number of continuous frames in each channel. The envelopes are reconstructed from the modified sparse NMF components. The same maxima selection process as used in the research ACE strategy is applied on the reconstructed envelopogram after sparse NMF processing.
Each column of Z consisted of channel envelope bins. Except in the simulation part of Algorithm section (Figures 2–4), the buffer length used in each analysis block was frames, which was the same as used in Hu et al. (2011) and is short enough to allow for a real-time implementation. The resulting throughput delay caused by buffering (considering a frame length of 8 ms and 75% overlap) was around 20 ms. The total delay imposed by the algorithm is equal to the sum of the buffering time and processing time for each block. In the MATLAB implementation, the processing of each block takes roughly 10 ms (with 100 iterations to obtain NMF) using a PC with 3.4 GHz Intel CPU and 16 GB RAM.
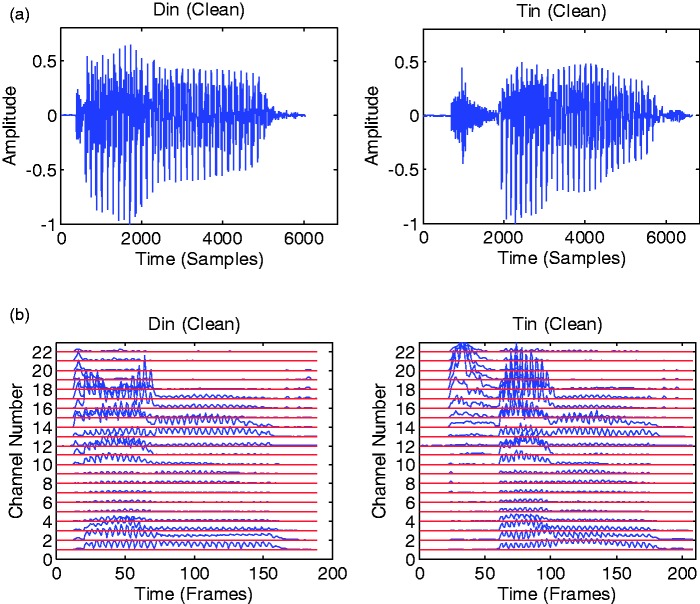
Figure 2.
Example sounds (Din, Tin) in the time and envelope domains: (a) waveforms of the words with x-axis is time in samples with a sample rate of 16 kHz (b) envelopogram of the corresponding words with x-axis and y-axis being time in frames and channel number, respectively.
Figure 3.
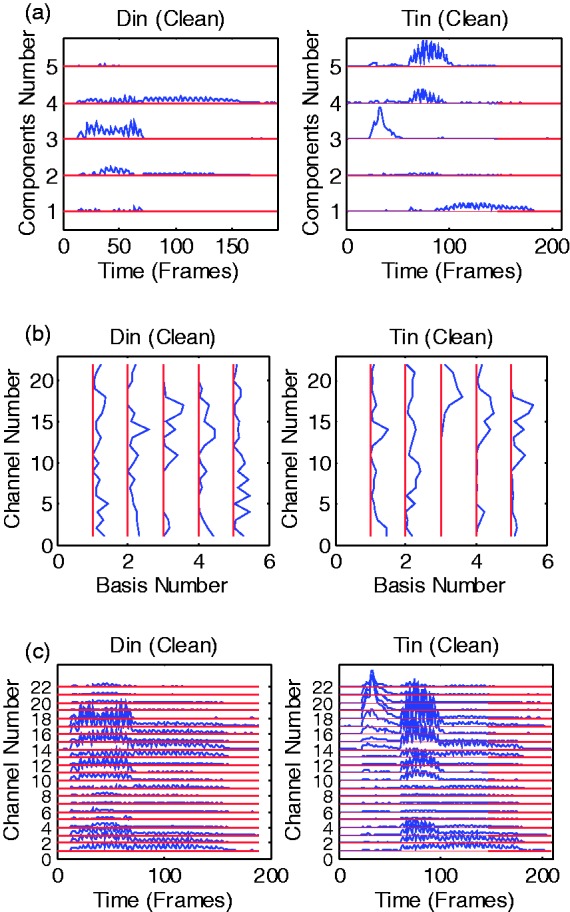
Decomposition and reconstruction by sparse NMF of the envelopogram of the words “Din” and “Tin”: (a) component matrices H with x-axis and y-axis being time in frames and number of components; (b) basis matrices W with x-axis and y-axis being number of basis and channel number; (c) reconstructions with all the components with x-axis and y-axis being time in frames and channel number.
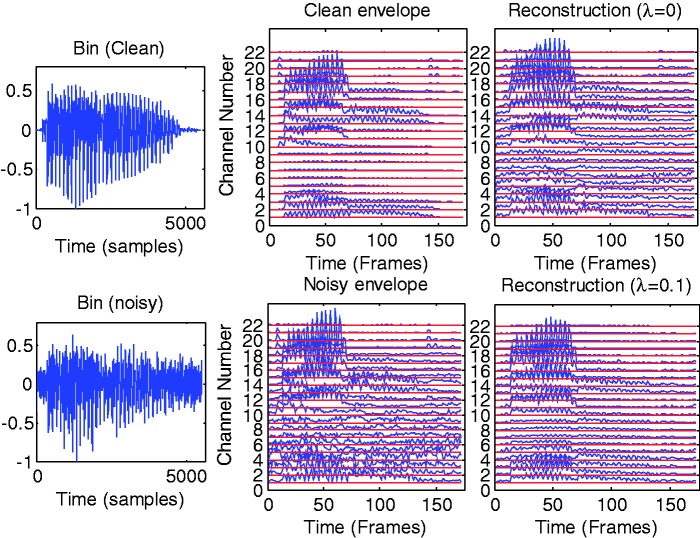
Figure 4.
Reconstruction of sparse NMF envelopograms in babble noise. The bottom left and bottom middle panels are waveform and envelopogram of noisy speech “Bin” (SNR = 5 dB). The top left and top middle panels are the corresponding subplots of the clean speech. The top right and bottom right panels are the reconstructed noisy envelopograms for (top) and (bottom), respectively.
To visualize the NMF decomposition of the envelopogram of both clean and noisy speech signals, monosyllabic words taken from Foster and Haggard (1979) as used in Lutman and Clark (1986) were assessed. The block length was the length (L in samples) of the corresponding word. The total short-time frame number for each individual word is , with 75% overlap. Figure 2a shows the waveforms of two clean words (Din, Tin). The x-axis shows the time in samples at a sample rate of 16 kHz. Figure 2b shows the corresponding envelopograms of 22 channels extracted according to Figure 1a. The x-axis is time in frames, y-axis is channel number. The 22 intra-cochlear electrodes are numbered from 1 to 22 in the basal to apical direction, so that channel 22 is the lowest frequency channel.
Figure 3 shows the decomposition and reconstruction of the envelopogram with (no sparsity constraint). Here, five basis and component vectors are calculated (Hu, Krasoulis, Lutman, & Bleeck, 2013) for each envelopogram. Figure 3a shows the component matrix H, which determines the activity of different basis vectors over time. The x-axis and y-axis show the time in frames and the number of components showing the parts-based decomposition of these monosyllabic words (Lee & Seung, 1999). Each NMF component reflects part of the patterns in the envelopogram along time dimension for both words. Figure 3b shows the basis vectors W for different words. The x-axis and y-axis show the number of basis and the channel numbers. Note that the basis vectors are different for different words, and there are no obvious patterns. Additionally, as illustrated in Figure 3a, the inherent correlation in the speech signal is conserved in the component matrix after applying NMF. The NMF components (the activity of basis vectors) tend to be continuous over time; in other words, if a basis vector is active (meaning that its corresponding coefficient is relatively large in the component matrix) at a specific time-frame, it will often remain active for several time-frames. This illustrates that the representation in the NMF domain is more sparse than in the time domain, indicating that NMF can reconstruct speech with reduced information by choosing only few components (Hu et al., 2013). Moreover, this also reflects the fact that speech has a high degree of redundancy and only few components are necessary to reconstruct an intelligible speech signal, at least in quiet (Cooke, 2006; Kasturi et al., 2002).
For noisy signals, it can be assumed that the factorization of the envelopogram into the basis and component matrices yields some components that mainly correspond to the speech source while others are mainly produced by the noise source. The application of sparse NMF can be interpreted by assuming either that the smaller NMF components correspond to the noise basis vectors, or they do not contribute significantly to the intelligibility of speech. By normalizing each basis vector to unit norm and by applying different sparseness constraint λ to the factorization, the small NMF components will be removed and hence a more sparse signal will be obtained while effectively performing noise reduction and reducing redundancy. The sparseness of the reconstructed signal can be controlled via tuning λ.
Figure 4 shows simulation results of the application of NMF on the envelopogram of the word “Bin” in noisy situations for two sparsity levels () to demonstrate the effect of λ on the sparse NMF reconstruction. The subplots in the bottom left and bottom middle panels are the waveform and the corresponding envelopogram in eight-talker babble noise with . As a comparison, the corresponding subplots of the clean speech are shown in the top left and top middle panels. The subplots in the right panels are the reconstructed noisy speech envelopograms for (top) and (bottom), respectively. As expected, more information is removed using a larger sparsity constraint () than no constraint (). The NMF reconstructed envelopogram appears more similar to the clean envelopogram than the unprocessed noisy one, for both λ values. Thus the processed envelopogram is less noisy.
Methods
Three experiments were designed to evaluate the proposed sparse NMF algorithm with a specific λ and to compare the results with the research ACE strategy. To mimic a more realistic (and more difficult) scenario, eight-talker babble noise instead of Gaussian noise was used in this study. In Experiment I, a wide range of values for λ was selected for objective evaluation in order to narrow down the λ range for the subjective listening tests with NH and CI subjects. In Experiment II, speech reception thresholds (SRT) were assessed (Hu et al., 2012) in NH subjects. Noise vocoder simulated signals produced with the NMT software (shown in Figure 1) were used in Experiments I and II. In Experiment III, CI subjects were recruited to evaluate the proposed algorithm.
Experiments for both NH and CI subjects were performed at the Institute of Sound and Vibration Research, Southampton, and were approved by National Health Service ethics committee (ref 09/H0504/116) and Institute of Sound and Vibration Research Human Experimentation Safety and Ethics Committee (ref 2346).
Experiment I: Objective Measures
Objective measures were applied to assess the effect of λ on the algorithm output as a preselection stage. A wide range of λ values between 0.01 and 0.2, with a step size of 0.01 was used. The objective measures aimed to evaluate the sparsity and to predict speech intelligibility. As applied by Li (2008), kurtosis was used to assess sparsity. Since it is unclear which objective evaluation method better predicts speech perception for vocoded speech, a two-step parameter selection procedure was developed based on Hu et al. (2012), where the results of the objective measures were used to set a smaller range of λ for a further SRT (Plomp & Mimpen, 1979) experiment for NH listeners. Results from Hu et al. (2012) showed that both the normalized covariance metric (NCM) and short-time objective intelligibility (STOI) could predict the performance of intelligibility for noise vocoded speech in some instances. This finding is consistent with Chen and Loizou’s (2011) study, where it was demonstrated that the coherence-based and speech transmission index-based measures are good tools for modeling the intelligibility of vocoded speech. Therefore, kurtosis, NCM, and STOI were all used here to explore the possible effect of λ on the speech perception prior to the subjective listening tests.
Speech material
Bamford-Kowal-Bench (BKB) sentences (Bench, Kowal, & Bamford, 1979) were used. BKB sentence lists are standard British speech materials with 21 lists. Each list contains 50 keywords in 16 sentences. Eight-talker babble noise was added to the speech material at three different long-term SNRs (0, 5, and 10 dB). The noise vocoder as described in Figure 1 was applied to the whole sentence corpus, on their output envelopes either from the ACE strategy (baseline condition) or from the sparse NMF strategy.
Kurtosis
Kurtosis based on equation (2) was used as a measure of sparseness (Li, 2008):
| (2) |
where x is the amplitude, μ is the mean, and σ is the standard deviation of the signal. For a normalized Gaussian (non-sparse) distribution with and , the kurtosis is by definition ; for other signals, the kurtosis may be larger than zero for a super-Gaussian or smaller than 0 for a sub-Gaussian process. If the kurtosis becomes larger, the sparseness of the signal increases.
Normalized Covariance Metric
The NCM measure was used as one of the objective measures for speech intelligibility. NCM is similar to speech transmission index (Steeneken & Houtgast, 1980), which is based on the covariance between the input and output envelope signals. It is expected to correlate highly with the intelligibility of vocoded speech due to similarities in the NCM calculation and CI processing strategies: Both use information extracted from the envelopes in a number of frequency bands while discarding fine-structure information (Chen & Loizou, 2010; Goldsworthy & Greenberg, 2004). For computing the NCM value, the stimulus was first band-pass filtered into bands spanning the signal bandwidth. The envelope of each band was computed using the Hilbert transform, anti-aliased using low-pass filtering and then down-sampled to limit the envelope modulation frequencies.
Short Time Objective Intelligibility
The STOI is based on a correlation coefficient between the temporal envelopes of the clean and the degraded speech in short-time overlapping segments (Taal, Hendriks, Heusdens, & Jensen, 2011). The input of STOI is the clean and the processed signal in the time domain, and the output is a scalar value which has a monotonic relation with the average intelligibility of the processed signal (Taal et al., 2011). In our case, since vocoded speech signals were the test materials for NH subjects, the first input is the vocoded NMF processed signal and the second is the corresponding vocoded ACE clean speech.
Experiment II: SRTs for NH Subjects
In this experiment, NH subjects were recruited to evaluate the sparse NMF strategies in different combinations of SNR and λ values.
Subjects
A total of 10 NH subjects (with NH thresholds between and 15 dB HL, as established by pure tone audiometry between 500 Hz and 8 kHz; 6 males, 4 females; age 18–26 years) were recruited. All participants were native English speakers with no previous experience of BKB sentence lists.
Speech material
The same noise-vocoded BKB sentences and babble noise as in Experiment I were used. Based on the results of Experiment I, three sparsity levels were selected for the listening tests. The parameters of the ACE strategy and three NMF strategies with different sparsity conditions are listed in Table 2. Condition 1 was the ACE strategy that does not use λ. Conditions 2 to 4 are the NMF strategies with three constraints: (NMF008), 0.10 (NMF010), and 0.13 (NMF013) for SNR (from to 10 dB).
Table 2.
The NH Subjective Experiment Conditions.
| Condition | Strategy | λ |
|---|---|---|
| 1 | ACE | – |
| 2 | NMF008 | 0.08 |
| 3 | NMF010 | 0.10 |
| 4 | NMF013 | 0.13 |
Equipment and procedures
All experiments were performed in a sound-isolated room with diotic sounds presented through Sennheiser HDA 200 headphones using a Creek OBH-21SE headphone amplifier. The vocoded BKB sentence lists of a female speaker were used. A two-up one-down adaptive procedure was used to find the SNR required for 70.7% correct recognition in each condition. The speech presentation level was fixed, while the SNR was varied adaptively with a 1-dB step size by changing the noise level (Dahlquist, Lutman, Wood, & Leijon, 2005). The sentence list was randomized for each participant. A sentence was classified to be correctly identified when at least two keywords were correctly repeated. The participants were trained for a few minutes with noise vocoded clean BKB sentences to become familiar with the test procedure.
Experiment III: Word Identification Tests for CI Subjects
In this experiment, CI subjects were recruited to evaluate the sparse NMF strategies in babble noise with different combinations of SNR and λ values.
Subjects
A total of 10 participants were recruited from the University of Southampton Auditory Implant Service database. Two (one male, one female, aged 65 and 55) underwent the pilot experiments for fine-tuning of the experimental setup and parameters, and the other eight (two males, six females, aged between 30 to 87 years) took part in Experiment III formal tests. Only the data from these eight participants are included and analyzed in the results. All of them were native English speakers and unilaterally implanted (four left sided, four right sided) with a Nucleus 24 CI. The hearing threshold levels of their unimplanted ears were at least 90 dB (as established by pure tone audiometry between 500 Hz and 8 kHz). They all had been implanted for more than 1 year (ranged 3–12 years) and had BKB sentence scores in quiet .
Speech material
Considering that the participants might have experienced the BKB sentences previously as a part of their CI assessment and rehabilitation process and to avoid learning effects, an alternative sentence set known as IHR sentence lists (Faulkner, 1998) was used in these experiments. Again, eight-talker babble noise was used as masker. Both the IHR database and BKB database have the same structure and same talker; they contain a similar level of complexity in both vocabulary and syntax. Eighteen sentence lists were used, each containing 15 sentences, with 3 keywords each. One sentence list was used for each condition. The sentence list used in each condition was randomized across participants. BKB sentences were used for practice.
Sparsity parameter λ
Because of large individual differences in speech perception performance in quiet among CI users, the same sparsity level might not be appropriate for different CI users. Thus, three different sparsity levels were generated in the CI experiments. First, the “optimal” λ values were obtained in the same way as in Experiment I (Figure 6). According to the results of Experiment I, the λ values obtained with the NCM and the STOI at 5 dB SNR (Table 4) are similar; they are equally good in predicting the speech recognition performance of the NH participants in Experiment II (Figure 7). Since NCM gives a larger optimal λ at than STOI, it indicates that the algorithm is more sparse or “aggressive” in lower SNR conditions. A previous study (ur Rehman Qazi, van Dijk, Moonen, & Wouters, 2012) showed that CI subjects generally tolerate higher levels of distortion than NH subjects, and therefore, more aggressive noise reduction may be appropriate for CI recipients. To set more varied sparsity levels for CI subjects, NCM was used to initialize the λ values in Experiment III. First, an optimal curve was obtained according to the NCM measure; then a higher and a lower sparsity level were introduced based on curve fitting.
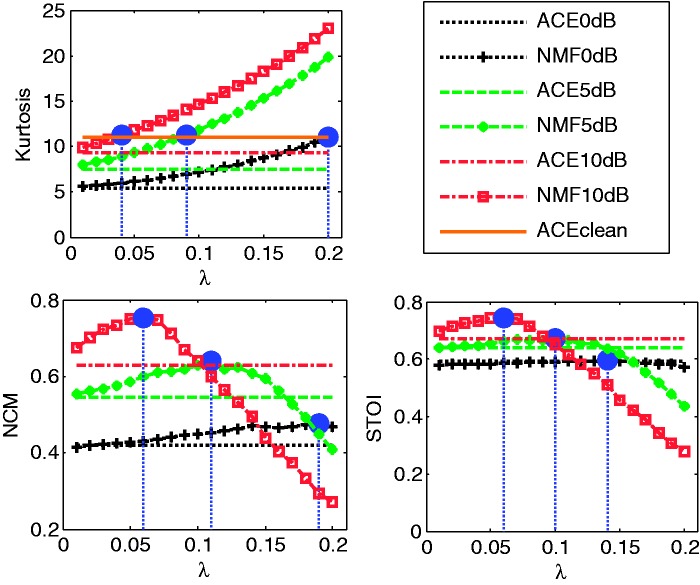
Figure 6.
Kurtosis, NCM, and STOI of vocoded speech reconstructed from different strategies at three SNRs: 0, 5, and 10 dB. Top left panel: Kurtosis. Bottom left panel: NCM. Bottom right panel: STOI. Red dash-dotted line: SNR = 0 dB from ACE. Green dashed line: SNR = 5 dB from ACE. Black dotted line: SNR = 10 dB from ACE. The corresponding marked curves are from sparse NMF (“□,” “o,” “+”). In the top left panel, the brown solid line is the kurtosis of vocoded clean speech using ACE; the values marked with blue dots are those with the same kurtosis as observed for clean vocoded speech of ACE. In the bottom panels, the blue dots indicate the maximum values of each objective measure under different SNR conditions.
Table 4.
The Optimal λ of Different Conditions.
| 0 dB | 5 dB | 10 dB | |
|---|---|---|---|
| Kurtosis | 0.2 | 0.09 | 0.04 |
| NCM | 0.19 | 0.11 | 0.06 |
| STOI | 0.14 | 0.10 | 0.06 |
Note. NCM = normalized covariance metric; STOI = . short-time objective intelligibility.
Figure 7.
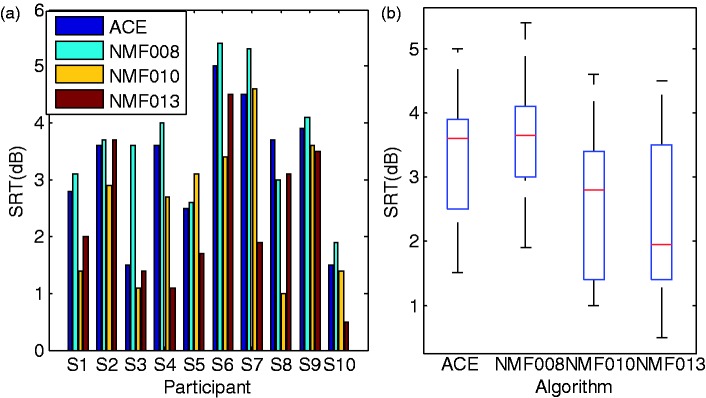
SRTs of the 10 NH participants for ACE and the 3 NMF strategies with different sparsity levels. (a) Individual SRTs of the 10 NH participants (S1–S10). The category is the participant index and the vertical axis shows the SRT in dB. (b) Boxplot of the results (median, inter-quartile ranges, and overall range). Here, the category axis indicates the algorithms (ACE, NMF008, NMF010, and NMF013).
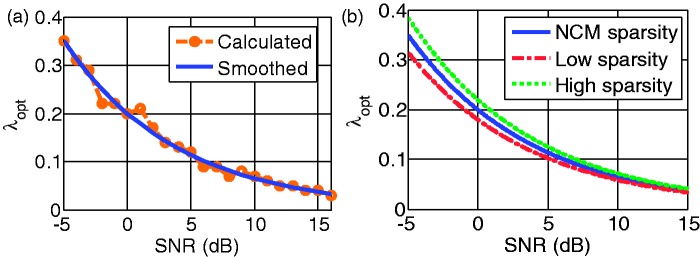
Figure 5a shows λ for different conditions obtained from NCM. The SNR was in the range from to 16 dB in 1-dB steps. Each SNR condition was tested for a range of λ values, for example, for dB, . The brown dotted curve shows the optimum values obtained from NCM. The blue solid curve shows a fitted exponential curve of these optimum λ values as a function of SNR. The approximated least-squares solution is
| (3) |
where ρ represents the SNR in dB, . An increased or a decreased value for G means a higher or lower sparsity level, respectively. In this experiment, G in equation (3) was increased or decreased by 0.02.
Figure 5.
(a) Optimum λ values as a function of the SNR. The brown dotted curve shows the optimum values obtained from NCM of vocoded speech using sparse NMF strategy. The blue curve shows a fitted exponential decay function. (b) Optimum λ values and two alternatives, one for a higher sparseness constraint and one for a lower sparseness constraint.
Table 3 shows the sparsity values λ used in Experiment III for four different SNRs that are derived from the three fitting curves shown in Figure 5b. Three sparse NMF strategies corresponding to these three sparsity levels (named NMFhigh, NMFncm, and NMFlow) under four SNR scenarios (0, 5, 10, 15 dB) were tested, resulting in 16 conditions in the following experiment.
Table 3.
The Sparsity λ Used in the CI Experiments for Each Condition.
| SNR | Low | NCM | High |
|---|---|---|---|
| 0 | 0.108 | 0.2 | 0.22 |
| 5 | 0.102 | 0.114 | 0.126 |
| 10 | 0.059 | 0.065 | 0.071 |
| 15 | 0.033 | 0.037 | 0.041 |
Note. SNR = signal-to-noise ratio; NCM = normalized covariance metric.
Equipment and procedure
The Nucleus Implant Communicator (NIC) software (provided by Cochlear Corporation) was used to communicate with the Nucleus implant and to send stimulus sequences to the implanted electrodes through a research processor (L34) via the standard hardware. The NIC is a set of software modules and libraries associated with NMT, which allows encoding of the envelopogram to stimuli sequences of electrode stimulation and programmatically streaming these sequences to the L34 processor (Swanson, 2008). The L34 processor acts as hardware for communicating between the PC and the Nucleus implant and controlling transmission of radio frequency pulses to the subject’s implant. All stimulus sequence files were generated individually according to existing individual CI map settings and saved for each participant and each condition offline.
All experiments were performed in a sound proof room. During the experiment, participants were asked to repeat whatever they recognized after each presented sentence, and the correctly identified keywords were recorded by the experimenter. A percentage keywords correct rate (KCR) was then calculated and stored at the end of each condition. Participants were offered breaks after each condition or when they experienced any fatigue during the experiment. The duration of the break was determined by the participant. Five BKB practice sentences from each condition at 15 dB SNR were presented before the formal experiments to get used to the new stimulation pattern. This familiarization lasted around a minute, and it thus cannot be assumed that participants were fully acclimatized to the new sounds. The order of presentation of all the 16 conditions was randomized. Total testing time varied between participants between 1 and 2 hours.
Results
Results of Experiment I
Figure 6 shows the kurtosis, NCM, and the STOI outputs of the speech processed by the ACE strategy and the sparse NMF strategies with a range of λ at three SNRs (0, 5, and 10 dB). The x-axis represents λ and the y-axis shows the corresponding objective measure output value. Each value is the average across all BKB sentences. Although ACE is independent of λ, different horizontal lines are plotted in order to compare the results from the ACE processed vocoded speech signals: the red dash-dot line is for SNR = 0 dB, the green dashed line is for SNR = 5 dB, and the black dotted line is for SNR = 10 dB. The corresponding marked curves (“□,” “o,” “+”) are calculated from the sparse NMF processed vocoded speech signals, with corresponding λ showed in the x-axis. The solid blue dots indicate the optimal λ values obtained with different objective measures as criteria at different SNRs.
The top left panel in Figure 6 shows the kurtosis values of clean and noisy conditions at three SNRs, respectively. The average kurtosis values of the vocoded ACE noisy speech signals () are 5.4, 7.5, and 9.3, which correspond to the three horizontal lines. The average kurtosis value of the ACE vocoded clean speech is 11.7 and is shown as a horizontal brown solid line. Overall, the kurtosis value increases with the SNR. The other three curves are the functions, under three SNR conditions of vocoded sparse NMF speech. It is expected that the kurtosis increases for higher λ in each condition given that the signal becomes increasingly sparse. One could assume that speech intelligibility for the processed noisy speech approaches that of the clean speech when the sparseness of the processed noisy speech approaches the sparseness of the clean speech. Therefore, the optimized λ values according to kurtosis are those where the processed noisy speech has the same kurtosis as the corresponding clean speech. The solid blue dots in the top left panel show where the NMF processed vocoded speech and the ACE processed vocoded clean speech have the same kurtosis values. In this case, the optimal λ values are 0.2, 0.09, and 0.04 for corresponding SNRs (), respectively.
The bottom left and right panels in Figure 6 show the NCM and the STOI values of the clean and noisy conditions. The NCM and the STOI values of the ACE processed noisy speech signals () are (0.42, 0.55, 0.63) and (0.60, 0.65, 0.67), which are represented as the three horizontal lines in the corresponding panels. Both the NCM and STOI values increase with the SNR for the ACE processed vocoded speech. For different NMF strategies, the three curves in each panel show that both the NCM and the STOI increase first with λ, then decrease after reaching a peak at a specific λ for each SNR condition. Consequently, the optimized values under the three SNR conditions according to NCM and STOI are obtained by finding the maxima of the three and three curves, indicated by the blue solid dots. The corresponding optimal λ values (x-axis) of these maxima are (0.19, 0.10, 0.06) and (0.14, 0.11, 0.06) for NCM and STOI, respectively. Table 4 lists the optimal λ obtained according to these three measures in three SNR scenarios.
According to Table 4, the λ obtained with the NCM and the STOI at 5 dB SNR are 0.11 and 0.1, respectively. They are very similar to each other and also close to λ (0.09) obtained from kurtosis analysis, where the NMF processed vocoded speech has a similar kurtosis as that of the clean ACE vocoded speech. But for 0 dB SNR, NCM-based optimal λ (0.19) is closer to the kurtosis (0.2). Overall, the optimized λ for according to these three measures is around 0.09 to 0.11.
Results of Experiment II
Figure 7a shows the individual SRT of the 10 NH participants in four conditions (indicated by different colors). The results show large individual performance differences. Figure 7b shows the results as a box plot (median, inter-quartile ranges and overall range). On average, there was a 0.74 dB improvement for NMF010 and a 0.92 dB improvement for NMF013 compared with the ACE strategy. A one-way repeated measures ANOVA shows a significant effect of strategy, . Post hoc tests with Benjamini-Hochberg’s false-discovery rate adjustment (5%) show that the NMF013 strategy outperforms the ACE strategy (p = .023). Moreover, both NMF010 and NMF013 strategies outperform the NMF008 strategy (p = .006 and p = .011, respectively) and there is no significant difference between NMF010 and NMF013.
In summary, the proposed algorithm with individually selected λ can outperform ACE for NH subjects listening to noise-vocoded speech. Objective measures at 5 dB SNR predicted a λ range between 0.08 and 0.13. This is in line with the results from the NH test. According to the NH data, λ can be slightly larger than 0.13, but this needs to be further evaluated in future, for example, by testing . The implication is that larger λ values may be needed for lower SNRs, such as 0 dB. Consequently, although both NCM and STOI can predict speech perception of noisy vocoded speech quite well, in this article, the optimal λ according to NCM is used in the CI experiment to give a larger sparsity constraint λ at SNR = 5 dB in comparison to optimization based on STOI.
Results of Experiment III
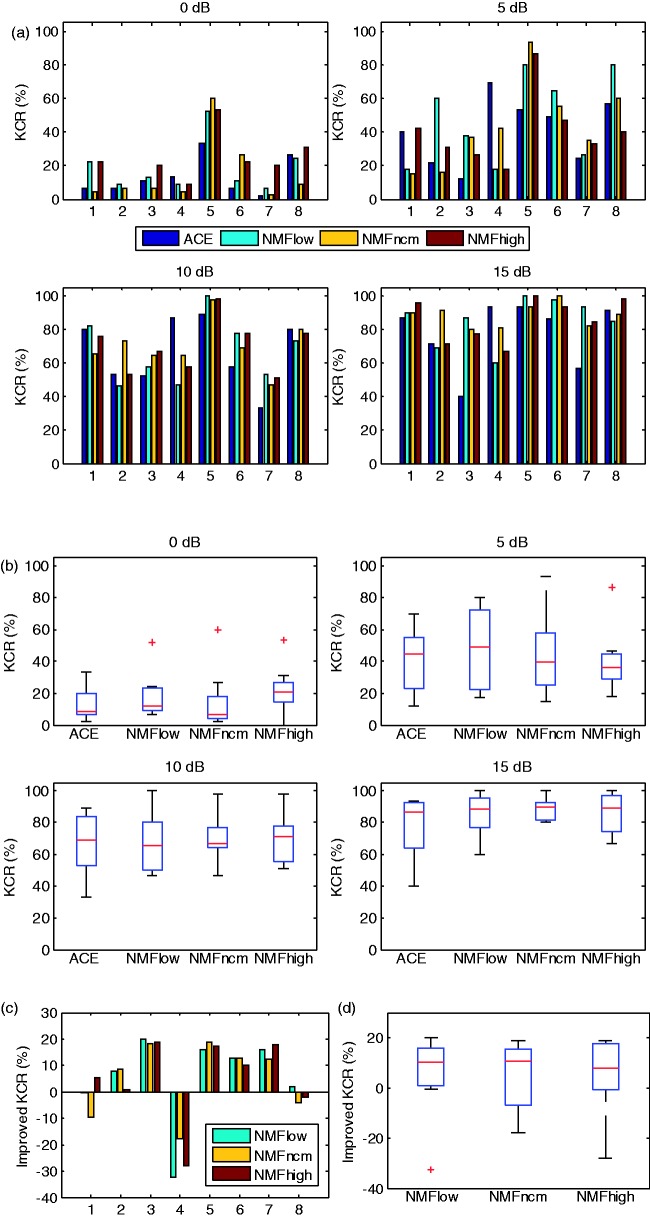
Figure 8a shows the results of the KCR speech of the eight CI participants for ACE, NMFlow, NMFncm, and NMFhigh (indicated by the different colors). The four subpanels in Figure 8a are the results for the four different SNR conditions 0, 5, 10, and 15 dB. The results show large variability between subjects, demonstrating that individual participants do not benefit equally from all NMF conditions; for different SNRs, a different NMF condition might be optimal for each participant. Figure 8b shows the boxplot of the KCR results for the different algorithms. Figure 8c shows the individual KCR improvement for the different algorithms compared with ACE averaged over all SNRs and Figure 8d shows the corresponding boxplot of the KCR improvement for the different algorithms compared with ACE averaged over all SNRs and participants.
Figure 8.
Keyword correct rate (KCR) results for the CI participants: (a) Individual KCR for the eight participants with the different coding strategies (indicated by the colors) at the four SNRs (sub panels); (b) boxplot of KCR for the four coding strategies at the different SNRs in the same style as in (a). (c) KCR improvement for the three NMF coding strategies compared with ACE averaged over all SNRs. (d) boxplot of KCR improvement compared with ACE averaged over all SNRs and participants.
It appears that the CI users who show worst performance with ACE may benefit most. In fact, Participant 4 (who benefits least) is a top performing CI user (using ACE) at SNRs of 5 dB and above, while Participant 3 (who benefits most) has the lowest speech recognition score in 15 dB SNR and was so impressed with the sound quality that he asked if he could have our experimental coding strategy as his standard setting.
However, due to the variability of the individual results and the small number of participants, the overall effect of coding strategy is not statistically significant: a two-way repeated-measures ANOVA showed no significant effect of strategy, , and a highly significant effect of SNR, . There was no significant interaction, . Post hoc pairwise comparisons with Benjamini-Hochberg’s false-discovery rate adjustment (5%) showed that all SNR conditions were significantly different from each other.
Assuming CI users were allowed to choose the optimal coding strategy among the three NMF options and ACE in the fitting practice based on their performance, only Participant 4 would use ACE instead of NMFncm. In total, seven out of eight participants performed better with at least one of the NMF strategies than with the ACE strategy. However, it should be noted that such a result could occur by chance if all algorithms perform similarly, given that there are three NMF alternatives.
Although there is no significant effect of coding strategy, there is still a trend and reduced variability in the data, at least at the highest SNR (15 dB). While for ACE, there is considerable spread in the speech perception performance with a range of 40% to 93% (see Figure 8a), for NMFncm, all subjects perform in the range 80% to 100% with little spread and are on average 11 percentage points better than for ACE. Accordingly, the improvement of NMFncm over ACE may be largest for the participants with lowest ACE performance.
Discussion and Conclusions
A novel CI coding strategy has been proposed in which sparse NMF is applied to the envelopes of CI channels in order to improve the performance of CI users in noisy environments. Babble noise was used in both objective and subjective speech intelligibility assessments. Subjective listening experiments with 10 NH listeners and noise vocoder CI simulation demonstrated that the proposed sparse NMF strategy could significantly outperform the existing ACE strategy when using appropriate sparsity constraints. The objective measures of vocoded speech imply that an SNR-dependent sparsity constraint λ might produce better results.
The proposed sparse NMF algorithm also showed improved speech recognition performance for seven out of eight CI users in babble noise with at least one of the NMF strategies. However, the individual optimum NMF strategy varied strongly across subjects, and there was no significant improvement for any of the three NMF settings over ACE. As a trend, the highest KCR improvement averaged across all eight participants of 11 percentage points was observed for the NCM λ constraint at the highest SNR of 15 dB, with all subjects showing a speech perception performance in the range 80% to 100%. Note that this was the case, although there was minimal familiarization with the stimulus. The improvements are smaller at lower SNR, but we expect that acclimatization may lead to further improvement. This needs to be shown in a future study. It has been shown that listeners need acclimatization periods on the order of days if not weeks to get the full benefit of any new strategy. Our listeners had been listening to ACE for years, but had virtually no exposure to the new stimulation, which also changed every few minutes due to randomization of conditions.
The current trend of improved speech perception in near-quiet (+15 dB SNR) indicates that NMF might be suited to overcome the CI-auditory-nerve bottleneck by selecting crucial speech information. But there are large individual performance variations; possible reasons might be differences in the number of surviving spiral ganglion cells, variable brain plasticity, and ability to adapt to the coding strategy among participants. The smaller improvements in the noisy situations, however, indicate that the power of the proposed NMF strategy as noise reduction might be limited to higher SNRs. Therefore, further improvements might be achieved by combining NMF with noise reduction algorithms like beamforming or by developing more intelligent NMF component selection techniques instead of pure energy-based methods.
The power of the experiment including all participants was low () because of the small effects being measured, the small number of participants and large variability among them. A fully powered experiment () would require around 100 participants under the same circumstances. Note, however, that any algorithm that would help some, but not all, CI users would be helpful, potentially more so if they could fine-tune it to suit their own auditory characteristics and the current listening conditions.
Although there was no statistically significant improvement for any of the NMF conditions over ACE, nevertheless a particular sparseness condition (supported by the trend for improvement with NMFncm in the current data) might be best for each participant. If future results support this trend, for clinical applications, such an optimal coding strategy might have to be selected by comparing speech reception scores in quiet for the different NMF strategies and ACE.
Overall, the study shows that the NMF algorithm may have the potential to confer better real-world speech recognition performance for at least some CI users. It might be preferable to optimize the trade-off between the sparseness and reconstruction for each individual CI user in the future, perhaps under user control. This approach needs to be evaluated with more CI subjects using a real-time sparse coding system (Hu et al., 2013), which would allow individual parameter tuning, daily acoustic scenario training over prolonged periods, and online speech testing for CI subjects in real time.
Acknowledgments
The authors would like to thank Professor Arne Leijon, Nasser Mohammadiha, and Jalil Taghia for their collaboration on part of the work during the first author’s visit in Sound and Image Processing Lab, KTH, Stockholm, Sweden. They would also like to thank Prof Bastiaan Kleijn, Victoria University of Wellington, New Zealand, for the original suggestion to explore using NMF. We further appreciate the valuable comments and suggestions by the anonymous reviewers and by the editor Andrew Oxenham. The authors thank Cochlear Europe for providing the NMT software and NIC streaming application. They are very grateful to Frances Pedley and Falk-Martin Hoffmann for collecting some of the data and to their subjects for participating in these experiments.
Declaration of Conflicting Interests
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding
The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by the European Framework 7 project Digital Signal Processing in Audiology (PITNGA- 2008-214699) and Cochlear Europe. It is currently partly supported by EU FP7 under the Advanced Bilateral Cochlear Implant Technology (ABCIT: grant No. 304912) and DFG SFB TRR 31.
References
- Bench J., Kowal A., Bamford J. (1979) The BKB (Bamford-Kowal-Bench) sentence lists for partially-hearing children. British Journal of Audiology 13(3): 108–112. [DOI] [PubMed] [Google Scholar]
- Buchner A., Nogueira W., Edler B., Battmer R. D., Lenarz T. (2008) Results from a psychoacoustic model-based strategy for the nucleus-24 and freedom cochlear implants. Otology & Neurotology 29(2): 189–192. [DOI] [PubMed] [Google Scholar]
- Buechner A., Beynon A., Szyfter W., Niemczyk K., Hoppe U., Hey M., Smoorenburg G. (2011) Clinical evaluation of cochlear implant sound coding taking into account conjectural masking functions, MP3000. Cochlear Implants International 12(4): 194–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F., Loizou P. C. (2010) Analysis of a simplified normalized covariance measure based on binary weighting functions for predicting the intelligibility of noise-suppressed speech. The Journal of the Acoustical Society of America 128(6): 3715–3723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F., Loizou P. C. (2011) Predicting the intelligibility of vocoded speech. Ear and Hearing 32(3): 331–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cichocki, A., Zdunek, R., & Amari, S. (2006). New algorithms for non-negative matrix factorization in applications to blind source separation. Paper presented at the IEEE International Conference on Acoustics, Speech and Signal Processing, 5.
- Cichocki A., Zdunek R., Phan A. H., Amari S.-i. (2009) Nonnegative matrix and tensor factorizations: Applications to exploratory multi-way data analysis and blind source separation, West Sussex, Engalnd: Wiley. [Google Scholar]
- Clark G. (2003) Cochlear implants: Fundamentals and applications, New York, NY: Springer. [Google Scholar]
- Cochlear Technology (2002) Nucleus MATLAB toolbox 4.2 software user manual (Vol. N95246F), New SouthWales, Australia: Cochlear Limited. [Google Scholar]
- Cooke M. (2006) A glimpsing model of speech perception in noise. The Journal of the Acoustical Society of America 119: 1562–1573. [DOI] [PubMed] [Google Scholar]
- Dahlquist M., Lutman M. E., Wood S., Leijon A. (2005) Methodology for quantifying perceptual effects from noise suppression systems. International Journal of Audiology 44(12): 721–732. [DOI] [PubMed] [Google Scholar]
- Dorman M. F., Loizou P. C., Spahr A. J., Maloff E. (2002) A comparison of the speech understanding provided by acoustic models of fixed-channel and channel-picking signal processors for cochlear implants. Journal of Speech Language and Hearing Research 45(4): 783–788. [DOI] [PubMed] [Google Scholar]
- Faulkner A. (1998) BKB and IHRSL sentence lists and NWAS continuous speech, Nottingham: IHR Products. [Google Scholar]
- Févotte C., Bertin N., Durrieu J. L. (2009) Nonnegative matrix factorization with the Itakura-Saito divergence: With application to music analysis. Neural Computation 21(3): 793–830. [DOI] [PubMed] [Google Scholar]
- Foster, J. R., & Haggard, M. P. (1979). FAAF – An efficient analytical test of speech perception. Paper 1A3 presented at the Proceedings of the Institute of Acoustics, London, 9–12.
- Goldsworthy R. L., Greenberg J. E. (2004) Analysis of speech-based speech transmission index methods with implications for nonlinear operations. The Journal of the Acoustical Society of America 116(6): 3679–3689. [DOI] [PubMed] [Google Scholar]
- Greenberg S., Ainsworth W. A. (2004) Speech processing in the auditory system: An overview. In: Popper A. N., Fay R. R. (eds) Speech processing in the auditory system Vol. 18 New York, NY: Springer, pp. 1–62. [Google Scholar]
- Hendriks R. C., Martin R. (2007) MAP estimators for speech enhancement under normal and Rayleigh inverse Gaussian distributions. IEEE Transactions on Audio, Speech, and Language Processing 15(3): 918–927. [Google Scholar]
- Hoyer, P. O. (2002). Non-negative sparse coding. Paper presented at the Proceedings of the 12th IEEE Workshop on Neural Networks for Signal Processing, 557–565.
- Hoyer P. O. (2004) Non-negative matrix factorization with sparseness constraints. The Journal of Machine Learning Research 5: 1457–1469. [Google Scholar]
- Hu H., Krasoulis A., Lutman M., Bleeck S. (2013) Development of a real time sparse non-negative matrix factorization module for cochlear implants by using xPC Target. Sensors 13(10): 13861–13878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu, H., Li, G., Chen, L., Sang, J., Wang, S., Lutman, M. E., & Bleeck, S. (2011). Enhanced sparse speech processing strategy for cochlear implants. Paper presented at the 19th European Signal Processing Conference (EUSIPCO 2011), 491–495.
- Hu, H., Mohammadiha, N., Taghia, J., Leijon, A., Lutman, M. E., & Shouyan, W. (2012). Sparsity level in a non-negative matrix factorization based speech strategy in cochlear implants. Paper presented at the 20th European Signal Processing Conference (EUSIPCO 2012), 2432–2436.
- Hussain A., Chetouani M., Squartini S., Bastari A., Piazza F. (2007) Nonlinear speech enhancement: An overview. In: Stylianou Y., Faundez-Zanuy M., Esposito A. (eds) Progress in nonlinear speech processing Vol. 4391 Berlin, Heidelberg: Springer, pp. 217–248. [Google Scholar]
- Kasturi K., Loizou P. C., Dorman M., Spahr T. (2002) The intelligibility of speech with “holes” in the spectrum. The Journal of the Acoustical Society of America 112(3): 1102–1111. [DOI] [PubMed] [Google Scholar]
- Lee D. D., Seung H. S. (1999) Learning the parts of objects by non-negative matrix factorization. Nature 401(6755): 788–791. [DOI] [PubMed] [Google Scholar]
- Lee, D. D., & Seung, H. S. (2000). Algorithms for non-negative matrix factorization. Paper presented at the Advances in Neural Information Processing (NIPS 2000), 556–562.
- Li, G. (2008). Speech perception in a sparse domain (PhD dissertation). University of Southampton, Southampton, UK.
- Li G., Lutman M. E., Wang S., Bleeck S. (2012) Relationship between speech recognition in noise and sparseness. International Journal of Audiology 51(2): 75–82. [DOI] [PubMed] [Google Scholar]
- Loizou P. C. (2006) Speech processing in vocoder-centric cochlear implants. In: Møller A. R. (ed.) Cochlear and brainstem implants Vol. 64 New York, NY: Karger, pp. 109–143. [DOI] [PubMed] [Google Scholar]
- Loizou P. C., Lobo A., Hu Y. (2005) Subspace algorithms for noise reduction in cochlear implants. The Journal of the Acoustical Society of America 118(5): 2791–2793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lutman M. E., Clark J. (1986) Speech identification under simulated hearing-aid frequency response characteristics in relation to sensitivity, frequency resolution, and temporal resolution. The Journal of the Acoustical Society of America 80(4): 1030–1040. [DOI] [PubMed] [Google Scholar]
- Mauger S. J., Arora K., Dawson P. W. (2012) Cochlear implant optimized noise reduction. Journal of Neural Engineering 9(6): 065007. [DOI] [PubMed] [Google Scholar]
- Mauger S. J., Dawson P. W., Hersbach A. A. (2012) Perceptually optimized gain function for cochlear implant signal-to-noise ratio based noise reduction. The Journal of the Acoustical Society of America 131(1): 327–336. [DOI] [PubMed] [Google Scholar]
- Mohammadiha, N., Gerkmann, T., & Leijon, A. (2011). A new linear MMSE filter for single channel speech enhancement based on nonnegative Matrix Factorization. Paper presented at the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA 2011), 45–48.
- Mysore G., Smaragdis P., Raj B. (2010) Non-negative hidden markov modeling of audio with application to source separation. In: Vigneron V., Zarzoso V., Moreau E., Gribonval R., Vincent E. (eds) Latent variable analysis and signal separation Vol. 6365 Berlin, Heidelberg: Springer, pp. 140–148. [Google Scholar]
- Nie K., Drennan W., Rubinstein J. (2009) Cochlear implant coding strategies and device programming. In: Snow J. B., Wackym P. A. (eds) Ballenger’s otorhinolaryngology head and neck surgery, Shelton, CT: People’s Medical Publishing House, pp. 389–394. [Google Scholar]
- Olshausen B. A., Field D. J. (2004) Sparse coding of sensory inputs. Current Opinion in Neurobiology 14: 481–487. [DOI] [PubMed] [Google Scholar]
- Patrick J. F., Busby P. A., Gibson P. J. (2006) The development of the nucleus freedom cochlear implant system. Trends in Amplification 10(4): 175–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plomp R., Mimpen A. M. (1979) Improving the reliability of testing the speech reception threshold for sentences. International Journal of Audiology 18(1): 43–52. [DOI] [PubMed] [Google Scholar]
- Potluru, V. K., & Calhoun, V. D. (2008). Group learning using contrast NMF: Application to functional and structural MRI of schizophrenia. Paper presented at the IEEE International Symposium on Circuits and Systems, 2008 (ISCAS 2008).
- Rennie, S. J., Hershey, J. R., & Olsen, P. A. (2008). Efficient model-based speech separation and denoising using non-negative subspace analysis. Paper presented at the IEEE International Conference on Acoustics, Speech and Signal Processing, 2008 (ICASSP 2008).
- Roberts W. J. J., Ephraim Y., Lev-Ari H. (2006) A brief survey of speech enhancement. In: Whitaker J. C. (ed.) Microelectronics, 2nd ed Boca Raton, FL: CRC Press, pp. 1–11. [Google Scholar]
- Schmidt, M. N. (2008). Single-channel source separation using non-negative matrix factorization (PhD dissertation). Technical University of Denmark, Lyngby, Denmark.
- Seligman P. M., McDermott H. J. (1995) Architecture of the spectra 22 speech processor. Annals of Otology, Rhinology and Laryngology 104(suppl. 166): 139–141. [PubMed] [Google Scholar]
- Shashanka M., Raj B., Smaragdis P. (2008) Probabilistic latent variable models as nonnegative factorizations. Computational Intelligence and Neuroscience 2008: 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smaragdis, P., & Brown, J. C. (2003). Non-negative matrix factorization for polyphonic music transcription. Paper presented at the 2003 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, 177–180.
- Spratling M. W. (2006) Learning image components for object recognition. The Journal of Machine Learning Research 7: 793–815. [Google Scholar]
- Steeneken H. J., Houtgast T. (1980) A physical method for measuring speech transmission quality. The Journal of the Acoustical Society of America 67(1): 318–326. [DOI] [PubMed] [Google Scholar]
- Swanson, B. A. (2008). Pitch perception with cochlear implants (PhD dissertation). Faculty of Medicine, The University of Melbourne.
- Taal C. H., Hendriks R. C., Heusdens R., Jensen J. (2011) An algorithm for intelligibility prediction of time frequency weighted noisy speech. IEEE Transactions on Audio, Speech, and Language Processing 19(7): 2125–2136. [Google Scholar]
- ur Rehman Qazi O., van Dijk B., Moonen M., Wouters J. (2012) Speech understanding performance of cochlear implant subjects using time-frequency masking-based noise reduction. IEEE Transactions on Biomedical Engineering 59(5): 1364–1373. [DOI] [PubMed] [Google Scholar]
- Virtanen T. (2007) Monaural sound source separation by nonnegative matrix factorization with temporal continuity and sparseness criteria. IEEE Transactions on Audio, Speech, and Language Processing 15(3): 1066–1074. [Google Scholar]
- Wang W., Cichocki A., Chambers J. A. (2009) A multiplicative algorithm for convolutive non-negative matrix factorization based on squared Euclidean distance. IEEE Transactions on Signal Processing 57(7): 2858–2864. [Google Scholar]
- Wang D., Kjems U., Pedersen M. S., Boldt J. B., Lunner T. (2009) Speech intelligibility in background noise with ideal binary time-frequency masking. The Journal of the Acoustical Society of America 125(4): 2336–2347. [DOI] [PubMed] [Google Scholar]
- Wilson B. S., Dorman M. F. (2007) The surprising performance of present-day cochlear implants. IEEE Transactions on Biomedical Engineering 54(6): 969–972. [DOI] [PubMed] [Google Scholar]
- Wilson B. S., Finley C. C., Lawson D. T., Wolford R. D., Eddington D. K., Rabinowitz W. M. (1991) Better speech recognition with cochlear implants. Nature 352(6332): 236–238. [DOI] [PubMed] [Google Scholar]
- Wouters J., Berghe J. V. (2001) Speech recognition in noise for cochlear implantees with a two-microphone monaural adaptive noise reduction system. Ear and Hearing 22(5): 420–430. [DOI] [PubMed] [Google Scholar]
- Zdunek R., Cichocki A. (2008) Fast nonnegative matrix factorization algorithms using projected gradient approaches for large-scale problems. Computational Intelligence and Neuroscience 2008: 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng F. G. (2004) Trends in cochlear implants. Trends in Amplification 8(1): 1–34. [DOI] [PMC free article] [PubMed] [Google Scholar]