Motion Planning for a Three-Stage Multilumen Transoral Lung Access System

Abstract

Lung cancer is the leading cause of cancer-related death, and early-stage diagnosis is critical to survival. Biopsy is typically required for a definitive diagnosis, but current low-risk clinical options for lung biopsy cannot access all biopsy sites. We introduce a motion planner for a multilumen transoral lung access system, a new system that has the potential to perform safe biopsies anywhere in the lung, which could enable more effective early-stage diagnosis of lung cancer. The system consists of three stages in which a bronchoscope is deployed transorally to the lung, a concentric tube robot pierces through the bronchial tubes into the lung parenchyma, and a steerable needle deploys through a properly oriented concentric tube and steers through the lung parenchyma to the target site while avoiding anatomical obstacles such as significant blood vessels. A sampling-based motion planner computes actions for each stage of the system and considers the coupling of the stages in an efficient manner. We demonstrate the motion planner's fast performance and ability to compute plans with high clearance from obstacles in simulated anatomical scenarios.

I. Introduction

Lung cancer, which kills over 150,000 people each year in the United States alone, is the leading cause of cancer-related death [1]. Early diagnosis is critical to survival. Medical imaging can detect nodules that are potentially cancerous, but biopsy is required for a definitive diagnosis [2]. Unfortunately, currently available biopsy techniques have significant downsides, especially when nodules are detected in the peripheral zone of the lung (i.e., near the ribs). Percutaneous approaches (i.e, needle insertion between the ribs) require puncturing the pulmonary pleura, the membrane surrounding the lung [3], and hence carry a significant risk of pneumothorax (lung collapse), a serious complication [4]. Current transoral approaches (i.e., inserting a bronchoscope through the mouth into the lungs) has a low risk of pneumothorax but cannot reach many sites in the peripheral lung due to the bronchoscope's diameter and the constraint of staying within the bronchial tubes.

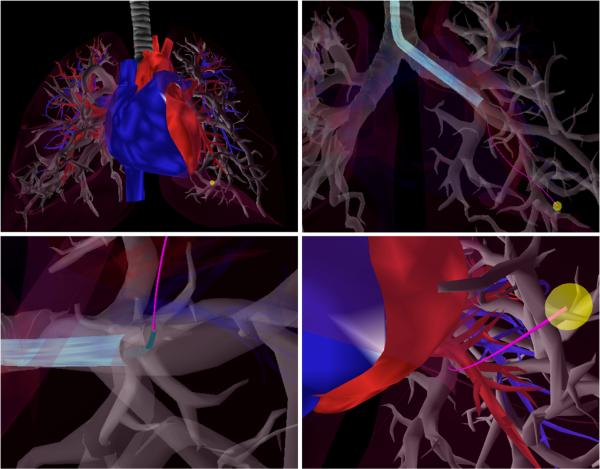
To enable safe and effective lung biopsies for definitive early stage lung cancer diagnosis, a new multilumen transoral lung access system is being developed [5]. This new device provides the benefits of the transoral approach (e.g., low risk of pneuomothorax since the pulmonary pleura is not punctured) while enabling access to peripheral lung nodules. The device uses three stages, as shown in Fig. 1. In the first stage, a bronchoscope is inserted transorally and steered to a bronchial tube near the nodule. In the second stage, a concentric tube robot deploys through the bronchoscope, pierces the bronchial tube, enters the lung parenchyma (i.e., the lung's functional tissue), and is oriented toward the nodule. In the third stage, a bevel-tip steerable needle deploys through the concentric tube robot and steers through the lung parenchyma to the nodule while avoiding significant blood vessels. This system, shown in Fig. 2, has the potential to enable safe access to peripheral lung nodules, but the strong coupling between each stage of the system makes operation of the system difficult for a human operator.

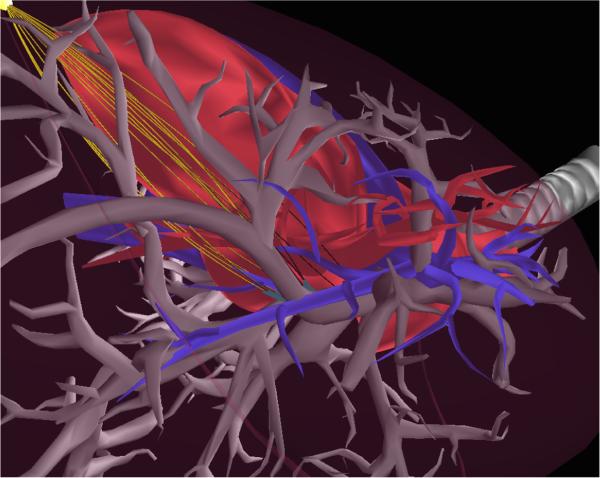
Fig. 1.

Example motion plan for the multilumen transoral lung access system reaching a lung nodule (yellow) while avoiding significant blood vessels (red and blue). Upper Left: Anatomical environment. Upper Right: The first stage of the system, a bronchoscope (light blue), is deployed through a bronchial tube. Lower Left: The second stage of the system, a concentric tube robot (green), is deployed through the bronchoscope and pierces the bronchial tube, entering the lung parenchyma. Lower Right: The third stage of the system, a bevel-tip steerable needle (pink), is deployed from the concentric tube robot and steers through the parenchyma to reach the lung nodule while avoiding anatomical obstacles. Each stage in this coupled system must be considered when computing a safe motion plan.

Fig. 2.

The multilumen transoral lung access system consisting of (A) a bronchoscope, (B) a 2-tube concentric tube robot, and (C) an asymmetric-tip steerable needle.

In this paper, we introduce a motion planner for this new multilumen transoral lung access system. The motion planner computes actions for each of the system's stages to enable the device to safely reach a biopsy target, as shown in Fig. 1. The motion planner explicitly considers the coupling between the stages, e.g., the location of the tip of the bronchoscope and the configuration of the concentric tube robot both greatly affect the reachable workspace of the steerable needle and its ability to safely reach the nodule. The input to the motion planner includes specifications of the structure of the bronchial tubes, the target nodule location, and the anatomical obstacles (e.g., significant arteries and veins in the lung), all of which can be either manually or automatically segmented from medical imaging before a procedure [6]. To decrease the risk of internal bleeding, we prefer motion plans in which the steerable needle in the third stage has greater clearance from the anatomical obstacles as it maneuvers to the target nodule.

The motion planner runs in an anytime manner, computing better and better motion plans as computation time is allowed to rise. We use a sampling-based motion planner that builds a variant of a Rapidly-Exploring Random Tree (RRT) [7] and considers the coupling of the stages in an efficient manner. The plan computed by the motion planner could be used by a physician as a guideline for controlling the device manually or could be used with a feedback controller for automatic execution. We demonstrate the performance of the motion planner in simulation for nodules in the peripheral zone of a lung and show that high quality motion plans can be computed in only a couple of minutes using a standard PC.

II. Related Work

Motion planning for the multilumen transoral lung access system requires modeling and computing plans for each of the stages of the system. We use sampling-based motion planning, an approach that has been very successful for robots with many degrees of freedom for a variety of applications [8].

The first stage of our system is a bronchoscope, an endoscopic device that is typically inserted into a patient's airway via the mouth and can maneuver through large-diameter bronchial tubes. Rosell et al. use haptic feedback and visual navigation for virtual bronchoscopy [9] and demonstrate successful guidance of a bronchoscope toward lesions in the bronchi. We are interested in positioning the bronchoscope to deploy other tools to reach points beyond the bronchi.

The second stage of our system deploys a concentric tube robot via the working channel of the bronchoscope. Concentric tube robots consist of thin, nested, pre-curved nitinol tubes. As the tubes are individually rotated and translated, the entire shape of the robot changes, enabling the robot to curve around anatomy to reach surgical sites unreachable by traditional straight tools. Deploying concentric tube robots through tendon-actuated endoscopic devices has recently been shown to effectively increase surgical dexterity [10], [11]. Controlling the motion of a concentric tube robot is difficult due to the complicated mechanics of the tubes’ interactions. Kinematic modeling of concentric tube robots has rapidly developed to consider bending and torsional interactions among the tubes [12], [13], [14]. Prior work has also achieved position control [14], [13], [15] and obstacle avoidance [16] with these robots. In our work, we use a mechanics-based kinematic model [13] to compute the concentric tube robot's shape during planning.

The third stage of our system deploys an asymmetric-tip steerable needle via the concentric tube robot. Asymmetric-tip steerable needles, such as those with a bevel tip, are flexible and exert an asymmetric force on soft tissue when inserted, causing them to achieve curved paths through the body [17]. The needle can be steered by axially rotating the needle, which changes the direction of the bevel tip. Kinematic models of varying complexity have been proposed for steerable needles [17]. Park et al. proposed a unicycle model on which our work is based [18], and various kinematic models were analyzed and experimentally validated by Webster et al. [19]. We can vary the turning radius during insertion of steerable needles using duty cycling [20].

Both control and motion planning for steerable needles have received a lot of attention [21], [22]. Park et al. developed a path-of-probability algorithm for steerable needle control based on error propagation [23]. Hauser et al. proposed a control method to account for tissue deformation during needle insertion by adapting helical trajectories [24]. Bernardes et al. achieved closed-loop control using feedback from medical imaging for planar needle steering [25]. Closed-loop control of steerable needles has also been achieved without knowledge of needle curvature properties using a sliding mode controller [26]. Seiler et al. accounted for uncertainty during insertion through fast trajectory correction [27]. Variations on the Rapidly-exploring Random Tree (RRT) algorithm have been successfully applied to steerable needles for a variety of applications. Obstacle avoidance in 3D with closed-loop feedback has been achieved through high-frequency replanning [28], [29]. We use the planning approach of Patil et al. [28] to quickly generate many different candidate paths.

The primary concern of this paper is combining the motion planning for each of these three individual stages into a single cohesive algorithm. Computing a motion plan for the entire system can be considered a special case of a hybrid system; Branicky et al. provide a general framework for using RRTs for hybrid system planning [30]. We introduce a specialized approach that explicitly considers the coupling across different stages of the multilumen transoral lung access system.

III. Problem Definition

Our motion planner requires as input a specification of the geometry of the relevant patient anatomy, including the target site and obstacles to avoid. Prior to lung biopsy procedures, physicians typically obtain a volumetric medical image (e.g., a CT scan) from which this data can be obtained via manual or automatic segmentation of the patient anatomy [6]. Specifically, we require (1) the geometry of the bronchial tubes B, (2) the geometry of significant blood vessels V in the lung, including arteries and veins, whose puncture would result in clinically significant internal bleeding, and (3) a point specifying the target site p_goal ∈ ${\mathbb{R}}^3$. In our implementation, we assume B and V are represented using polygonal surface meshes. We define the set of anatomical obstacles O for needle steering in the parenchyma as the union of B and V, since the needle should not pierce a significant blood vessel and should also avoid bronchial tubes that would cause the needle to deflect from its intended path.

The multilumen transoral lung access system consists of three stages, and the configuration of the system encodes the degrees of freedom of each stage. The first stage of the system, the bronchoscope, is deployed via the patient's airway to a specific point p_scope inside the bronchial tubes. The second stage of the system, the concentric tube robot, is deployed through the bronchoscope, exiting at its tip, p_scope. We parameterize the 2-tube concentric tube robot's configuration by the vector m = {β₁, β₂, θ₁, θ₂}^T where β_κ ∈ $\mathbb{R}$ for κ ∈ {1, 2} is the insertional degree of freedom of the κ'th tube and θ_κ ∈ [0, 2π) is the rotational degree of freedom of the κ'th tube. The third stage of the system is a steerable needle deployed through the concentric tubes. We describe the configuration of the steerable needle by the pose of the needle tip, which we represent by the 4 × 4 matrix

$$\mathbf{X}=\left(\begin{array}{cc}\hfill \mathbf{R}\hfill & \hfill \mathbf{p}\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$

where R ∈ $\mathcal{SO}$(3) is the rotation matrix representing the orientation of the needle tip and p ∈ ${\mathbb{R}}^3$ denotes the needle tip's position in the coordinate frame of the medical image. The configuration of the entire system can then be described by the tuple

$$\mathbf{q}=({\mathbf{p}}_{\text{scope}},\mathbf{m},\mathbf{X})$$

where $\mathbf{q}\in \mathcal{Q}={\mathbb{R}}^8\times {\left({\mathbb{S}}^1\right)}^2\times \mathcal{SO}\left(3\right)$.

In the stage bevel-tip steerable needle is controlled by inserting the needle and axially rotating it about its base. Because the needle is flexible and has an asymmetric tip, it curves in the direction of the bevel [18], [19]. We define the control input to the steerable needle as u = {l, ϕ, κ}^T where $l\in \mathbb{R}$ is an insertion distance, ϕ ∈ [0, 2π) is the axial rotation angle of the asymmetric tip (which corresponds to the angle defining the plane of the needle's curvature when inserted), and $\kappa \in {\mathbb{R}}^{+}$ is the curvature achieved using duty cycling [20]. We note κ has an upper bound of κ_max, which is a property of a specific steerable needle in lung tissue.

The system is designed such that the location of the bronchoscope tip p_scope is set first and fixed, then the concentric tube robot configuration m is set and fixed, and finally the steerable needle is controlled such that its tip pose X maneuvers to the target site while avoiding obstacles. We define a motion plan Π as the sequence of configurations of the system {q_o, q₁,...,q_T} and the corresponding control inputs for each stage of the system.

To maximize safety, we prefer motion plans that guide the steerable needle along paths with greater clearance from the anatomical obstacles. We define the cost of a motion plan as

$$c(\Pi )={\int }_{{\mathbf{p}}_0}^{{\mathbf{p}}_T}\frac{1}{\text{clearance}(\mathbf{p},O)}d\mathbf{p}$$ (1)

which is the integration over the curve of the clearance between the tip of the steerable needle and the closest anatomical obstacle over the continuous path of the tip resulting from Π. The objective of our motion planner is to compute a motion plan Π such that the final position p_T of the needle tip at configuration q_T reaches p_goal, the obstacles O are avoided, and cost c(Π) is low.

IV. Method

Our motion planner (Alg. 1) computes motions for each stage of the lung access system, including the bronchoscope, the concentric tube robot, and the steerable needle, to enable access to the physician-specified goal. The motion planner first searches for an optimal placement of the bronchoscope and the concentric tube robot by setting the deployment variables p_scope and m. A desirable (p_scope, m) pair places the steerable needle's start state X_start such that the needle can follow a collision-free path to the goal with large clearance from anatomical obstacles. We evaluate this property of a sampled (p_scope m) pair by using a sampling-based motion planner to find steerable needle controls (u₁, u₂, . . . ) that create a collision-free path to the goal point p_goal. We re-execute the motion planner for the entire system repeatedly for a given amount of time, leveraging randomization to create many different motion plans and then selecting the one with lowest cost (i.e., greater clearance from obstacles).

A. Planning Deployment of the Bronchoscope

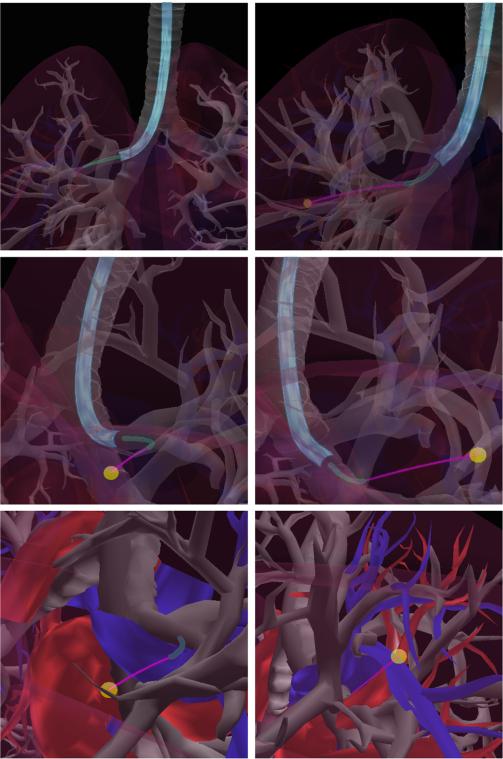
We use a sampling-based approach to create candidate placements of the bronchoscope tip p_scope within the bronchial tree. For efficiency, we leverage the fact that the bronchial tubes form a tree, which is a linear structure, and create a mapping between a parameter $y\in \mathbb{R}$ and the point p_scope in the world coordinate system. We assume that all possible bronchoscope placements must lie on the medial axis of the bronchial tree (which can be constructed automatically [31], although in our results an approximation was constructed manually). In practice, in certain wide-diameter bronchial tubes it may be possible to manipulate the bronchoscope such that its tip is not on the medial access, which will be a topic of future work. We uniformly sample points from the line segments of the medial axis by placing the medial axis's line segments s_i = $({\mathbf{p}}_i,{\mathbf{p}}_i^{\prime })$ in an arbitrarily ordered sequence (s₁, . . . , s_n) and then viewing this sequence of segments as a piecewise linear (and discontinuous) space curve parameterized by arc length $y\in [0,{\sum }_i\Vert {\mathbf{p}}_i-{\mathbf{p}}_i^{\prime }\Vert ]$. We can sample a parameter y from the domain of this space curve to generate a placement for the bronchoscope tip p_scope in the bronchial tree, and can then directly map y to p_scope via the mapping from the medial axis to the world coordinate system. The bronchoscope's ability to move through different branches of the bronchial tree broadens the set of reachable goals in the lung (Fig. 3).

Fig. 3.

Accessing goals in the right lung, the bronchoscope utilizes different branches in the bronchial tree: the upper right branch (left images) for one goal and the lower right branch (right images) for another goal. Top to bottom show the same paths from different angles and with different transparencies for visualization.

B. Planning Deployment of the Concentric Tube Robot

The sampled placement p_scope of the bronchoscope tip describes the start point of deployment of the concentric tube robot. From this point, we wish to sample possible deployments of the concentric tube robot, where deployments are parameterized by the vector m = {β₁, β₂, θ₁, θ₂} to encode each component tube's axial rotation and translation. Due to physical constraints of our system and the desire for follow-the-leader trajectories that do not significantly deform tissues, we disallow relative rotation between the tubes. Hence, we can parameterize deployment with one rotation θ. A deployment m corresponds to sequentially performing the following actions: (1) rotating the tubes to required angle θ, (2) inserting both tubes at the same rate until the outermost tube reaches its stopping point β₂, and then (3) inserting the inner tube past the outer tube until it reaches its stopping point β₁.

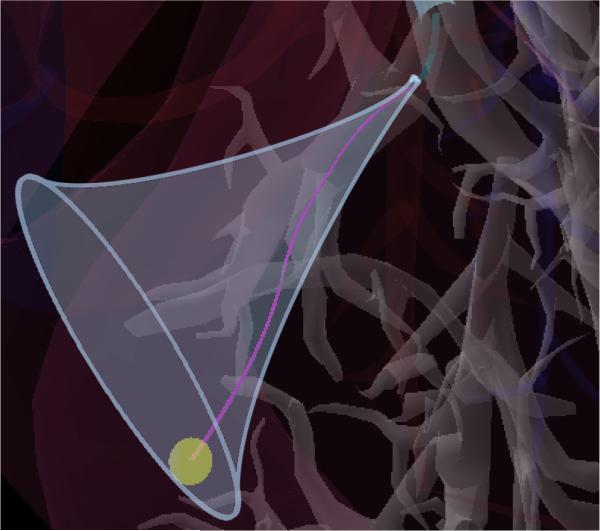
We use a mechanics-based kinematic model [13] to compute the tip frame of the concentric tube robot after deployment. This tip frame marks the initial configuration X_start of steerable needle deployment. If the goal point p_goal lies outside of the reachable workspace of the steerable needle when deployed from X_start (see Fig. 4), we reject this proposed bronchoscope and concentric tube robot deployment.

Fig. 4.

The reachable workspace of the steerable needle is a trumpet shaped volume defined by its start configuration and the maximum curvature κ_max it is capable of achieving in the tissue.

C. Steering the Bevel-tip Needle to the Goal Point

A proposed placement (p_scope, m) of the bronchoscope and concentric tube robot fully specifies the start state X_start of the steerable needle. We evaluate the placement (p_scope, m) by attempting to find a steerable needle trajectory starting at X_start that reaches the goal while avoiding anatomical obstacles. We search for this trajectory using a sampling-based motion planning algorithm for steerable needles developed by Patil et al. [28].

This motion planner is based on a Rapidly-exploring Random Trees (RRT) motion planner [8]. RRT incrementally builds a tree of robot states that are reachable from X_start by collision-free paths. At each iteration, RRT samples a state X_sample in the robot's state space, uses a distance function distance to select the nearest state X_near already in the tree, and uses a function steer to compute a control input u that, when applied to X_near results in a new state X_new nearer to X_sample. If the motion between X_near and X_new is collision-free, X_new is added to the tree. RRT iterates these steps until either (1) the tree connects to the goal, or (2) the algorithm exceeds its time allotment.

To compute the steer function, we compute the unique control u_steer that directly connects the state X_near to the 3D position of X_sample, and then clamp the insertion length of u_steer to a maximum of l_max to generate the resulting control u. To compute the distance function between two states X and X′, we compute the control u_steer that connects X to the 3D position of X′ as above and return the insertion arc length of u_steer. We check whether the motion between two states is collision-free by using the Flexible Collision Library (FCL) [32] for collision detection between the needle and the anatomical obstacles.

In order to more quickly generate motion plans to the goal p_goal, we introduce a strong goal bias; after each iteration of RRT, we perform an additional RRT iteration using p_goal as X_sample in order to bias growth of the tree toward the goal.

Additionally, due to stresses on surrounding tissue, bevel-tip steerable needle insertion is impeded if the orientation of the needle tip is oriented more than 90° from its orientation at X_start. As such, controls that produce such states are discarded as invalid.

We allow the RRT to search for a collision-free path to the goal point for 0.05 seconds. This time limit is based on an intuition that the RRT either finds a path very quickly or not at all in this scenario. If a path is found, we use the path's clearance metric from Eq. 1 to quantify the cost of this particular placement (p_scope, m) of the bronchoscope and concentric tube robot. In practice, we approximate the integral in Eq. 1 by finely discretizing the needle's path and using the trapezoidal rule. We compute the clearance function using FCL [32]. If the RRT fails to find a collision-free path in the allotted time, we discard X_start.

D. Motion Planning for the Entire System

After generating a placement p_scope of the bronchoscope, a deployment m of the concentric tube robot, and appropriate control inputs (u₁, u₂, . . .) for the steerable needle, we concatenate these operations to form a motion plan Π of a collision-free sequence of configurations (q₁, q₂, . . .) and associated control inputs for the entire multilumen lung access system.

The approach above generates a single plan, but we can repeat the process to generate new, different plans due to the randomization in the algorithm. We iteratively create new motion plans Π and evaluate their quality, always saving the best motion plan found so far. We repeat until we exhaust the time allotted for plan computation.

V. Results

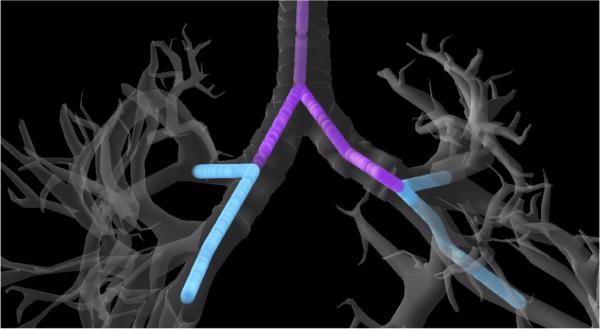
We evaluated our motion planner in a simulated lung biopsy scenario. The scenario consists of a commercially available anatomical model which includes the bronchial tree, both the left and right lungs (evaluated separately), the heart, and large vasculature. We sampled valid bronchoscope access points with the manually approximated medial axis shown in Fig. 5. While the bronchoscope can physically access both the blue and purple segments in the figure, we did not consider the purple segments because exiting the bronchus from points along these segments would require puncturing the pulmonary pleura and increase the risk of pneumothorax. We blocked off deeper parts of the bronchial tree where a bronchoscope's diameter would typically impede further progress due to the narrowing of the bronchial tubes. We used a maximum needle steering curvature κ_max = (0.121m)⁻¹ in accordance with the physical prototype in prior work [33], [5]. We also used concentric tube robot design parameters that matched this prior work.

Fig. 5.

Positions from which the bronchoscope can safely deploy the latter stages of the system without puncturing the pulmonary pleura are shown in cyan. These positions can be reached via the airways shown in purple.

In Fig. 1, we show the output of our motion planner, which computes the bronchoscope tip position, concentric tube robot configuration, and steerable needle control inputs to guide the device to a nodule while avoiding obstacles. Depending on the computation time allowed, our method may generate large numbers of motion plans to a target. In Fig. 6, the method computed 15 feasible motion plans to the target nodule in 5.63 seconds. This set allows our motion planner to select the best plan given the cost function. The motion plans in the set span multiple homotopic classes.

Fig. 6.

The first 15 solutions (in gold) found to a single goal spanning multiple homotopic classes.

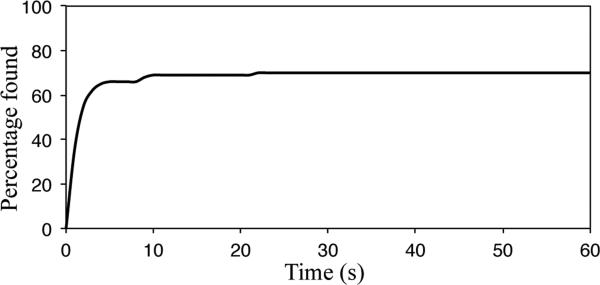
We evaluated the ability of our motion planner to compute plans to reach nodules across the peripheral zone of the lung. We randomly sampled 50 lung nodule locations in the periphery of each lung (100 total nodules) as shown in Fig. 7. For each query nodule, we ran our motion planner for 1 hour. We show the percentage of nodules reached using our motion planner as a function of computation time (first 60 seconds) in Fig. 8. For 36% of the lung nodules, our motion planner computed a valid motion plan to reach them in the first second of planning. By 60 seconds, our motion planner found valid plans reaching 70% of the nodules and by 1 hour valid plans were found to 75% of the nodules. We note that, with a steerable needle of tighter curvature (a subject of future work regarding the mechanical design), the percentage of nodules for which a plan is found would likely increase substantially.

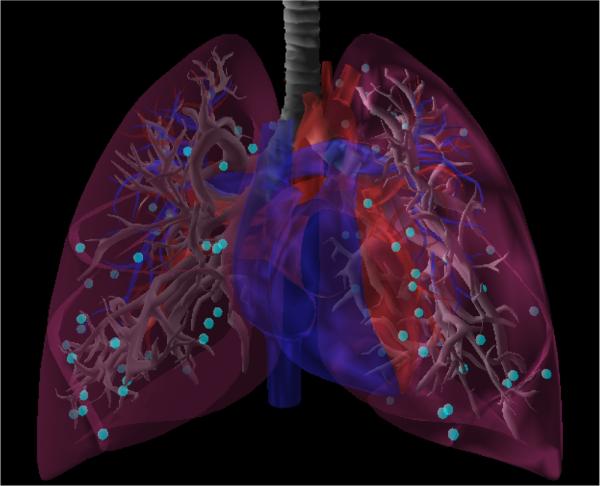
Fig. 7.

Lung nodule query locations (shown in teal) used for the reachability experiment.

Fig. 8.

Percentage of randomly sampled peripheral lung nodules (100 nodules) to which a motion plan has been found as a function of computation time.

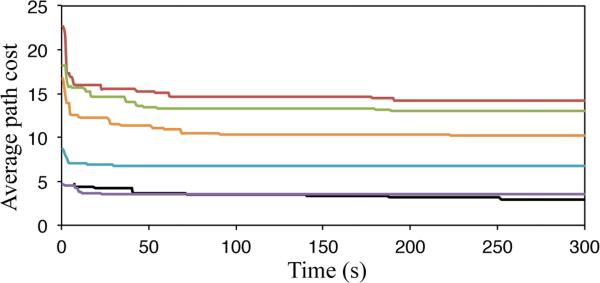
We also investigated how motion plan quality increases as we increase computation time. We selected 6 of the reachable lung nodules found in the experiment above and executed 3 instances of our motion planner on each nodule for 300 seconds per instance. In Fig. 9, we show the best costs found by the motion planner over time for each considered nodule.

Fig. 9.

Over six distinct goals (three from each lung), the cost of the best path found by time averaged over three runs each.

Recall that we only consider placements (p_start, m) of the bronchoscope and concentric tube robot that place p_goal in the workspace of the steerable needle. We demonstrate the computational speedup of this algorithm design choice by leaving it out of our algorithm and comparing the results. With the placement rejection scheme, we found 15 paths to the goal shown in Fig. 6 in 5.63 seconds; without the placement rejection scheme, it took 42.62 seconds to find 15 paths to the goal.

To justify our choice of T_RRT, we ran an additional experiment where we allowed each instance of the RRT 2 seconds to find a solution. We found that a large percentage of valid RRTs were found very quickly, with more than 95% of valid plans being found within the first 0.05 seconds.

VI. Conclusion

We introduced a motion planner for a three-stage multi-lumen transoral lung access system. The planner computes actions for deployment of a bronchoscope into the bronchial tubes, followed by concentric tube robot deployment into the lung parenchyma, and finally deployment of a bevel-tip steerable needle to reach a goal site while avoiding collisions with anatomical obstacles. Our sampling-based motion planner quickly computes plans with high clearance from obstacles in a simulated clinical scenario involving biopsy of lung nodules.

In future work, we will consider additional anatomical obstacles (such as lung fissures) to further decrease risk to the patient. We also plan to quantify the reachable space of the robot in the lung model and to investigate different sampling strategies and motion planning paradigms. We also plan to relax some of our restrictive assumptions on the concentric tube robot and consider approximate follow-the-leader plans that provide added control but are still safe to perform in the lung. Most importantly, we plan to integrate this motion planner with the hardware developed by Swaney et al. [5] and evaluate the efficacy of the algorithm and system using tissue phantoms and porcine lung tissue.

Algorithm 1.

Motion planner for the multilumen lung access system.

	input : T: time to execute outer loop; TRRT: time allotted to an individual RRT; B: surface mesh of bronchial tubes; V: surface mesh of blood vessels; κmax: maximum needle curvature; pgoal: target site position
	output: Π: best motion plan computed by time T
1	Π ← Ø;
2	while elapsed time < T do
3	pscope ← sample_bronchial_medial_axis();
4	θ1 = θ2 ← uniform_random(0, 2π);
5	β1, β2 ← random_tube_translations();
6	m ← {β1, β2, θ1, θ2};
7	Xstart ← CTR_tip_frame(pscope, m);
8	if pgoal is in workspace of needle at Xstart then
9	Πneedle ← RRT(Xstart, TRRT, B, V, κmax, pgoal);
10	if Πneedle ≠ null then
11	Π′ ← (pscope, m, Πneedle);
12	if c(Π′) < c(Π) then
13	Π ← Π′
14	end
15	end
16	end
17	end
18	return Π;