Total retinal blood flow measurement by three beam Doppler optical coherence tomography

Abstract

We present measurements of total retinal blood flow in healthy volunteers using a three beam Doppler optical coherence tomography (D-OCT) technique. This technology has the advantage of a precise determination of the flow vector without the use of any a-priori information on the vessel geometry. Circular D-OCT scans around the optic disc were recorded and venous as well as arterial total blood flow was determined and compared for each subject. The reproducibility of the method was assessed in 6 subjects by repeated measurements. Only small deviations of around 6% between the measurements were found which indicates the high precision of the proposed method.

1. Introduction

Alterations in the retinal blood circulation were recently shown to be connected to the development of several serious eye diseases such as glaucoma, diabetic retinopathy and age related macular degeneration [1–3]. In the case of glaucomatous optic neuropathy (GON), two principal theories have been described [4]. The mechanical theory suggests that increased intraocular pressure (IOP) leads to GON, while the vascular theory suggests that insufficient ocular blood supply causes its development. While some findings indicate that increased IOP is sufficient to diagnose GON, pathologies like normal-tension glaucoma cannot be explained by the mechanical theory alone, but show a decrease in ocular blood flow (OBF), supporting the vascular theory. Furthermore a reduction in OBF can often be measured before the damage to the retina gets irreversible [4].

Therefore information on OBF has its importance not only in the diagnosis and treatment control, but might bring additional insight to the development and pathophysiology of these diseases. Several different techniques have been developed over the last few decades to evaluate OBF in the human eye in vivo [5]. As a non-invasive approach, optical coherence tomography (OCT) allows to evaluate OBF in a quantitative way by using either phase-sensitive or non-phase-sensitive methods.

Non-phase-sensitive methods extract quantitative velocity information by analyzing time varying speckle or intensity fluctuations of backscattered light with autocorrelation techniques [6, 7], but are unable to detect the direction of moving particles. Dynamic light-scattering OCT [8] on the other hand allows the extraction of axial and transverse flow velocities, but requires high computational effort and long measurement times.

As a phase-sensitive approach, Doppler optical coherence tomography (D-OCT) yields both high resolution and superior quantitative velocity information with high sensitivity [9–11]. Intrinsic to the method, D-OCT measures the velocity of moving scatterers parallel to the direction of the incident beam. To reconstruct the actual flow velocity, the Doppler angle (θ) between the beam direction and the flow orientation needs to be known. For retinal imaging the incident beam will be nearly perpendicular to the imaged vessel and the reconstruction of the velocity vector is highly dependent on the accurate measurement of θ. Furthermore D-OCT can only measure velocities within a certain range of Doppler angles. This angular range depends on the minimum and maximum resolvable velocity of the D-OCT system and the absolute velocity of the moving scatterer and is highly non-linear [12]. To address this problem and to retrieve accurate measurements of the velocity vector, both, single and multi-beam (MB-) D-OCT approaches were reported.

Single-beam approaches often measure θ from the 3-D vessel geometry, which can be retrieved by extraction of the vessel gradient between two adjacent cross-sectional scans (B-scan) in the OCT intensity image. The gradient can either be retrieved from circular B-scans with different radii [13, 14] or from volume scans, acquired with high speed OCT systems [15, 16]. Derived from a single beam method, the beam can be divided into path length encoded sections with different Doppler angles, by using thickness-sectored glass plates in the sample arm [17–19]. Transversal D-OCT, on the other hand, employs a four channel quadrant detector [20]. However, as stated in the literature, conventional single-beam approaches extract the vessel geometry from consecutive B-scans and are therefore prone to motion, while the path length encoded methods need to rely on calibration measurements and suffer from significantly reduced depth range for imaging.

Several MB-D-OCT approaches were published to assess the total retinal blood flow in human eyes. Using a second beam with a different angle of incidence eliminates one spatial degree of freedom. If the angle between the plane, spanned by the two beams, and the flow direction is small, the actual blood velocity can be retrieved without direct extraction of the vessel geometry [21, 22]. Blatter et al. [23] used a rotating Dove prism to align the surface normal of the plane parallel to a circular scan pattern around the optic nerve head (ONH). By assuming a radial vessel distribution, spreading from the ONH, total blood flow can be retrieved with a single circular scan. Doblhoff-Dier et al. [24] used a dual beam system with rotatable beams, allowing for vertically and horizontally oriented B-scans around the ONH along with an integrated vessel analyzer to extract the vessel diameter. However, with dual beam methods, the optimal orientation of the plane with respect to the vessel orientation cannot be guaranteed, introducing errors to the flow calculations.

Recently we reported a novel three beam phase sensitive spectral domain D-OCT system [25, 26], capable of measuring the absolute velocity vector and flow in human retinal vasculature. The method illuminates the sample with three independent measurement beams focused in a mutual focus spot. This enables the reconstruction of the velocity vector without any a-priori knowledge on the vessel geometry, through the measurement of three linear independent velocity vector components. Promising results for the measurement of mean absolute flow within retinal vessels were demonstrated in vivo using a circular scan pattern [26]. However the system had several shortcomings preventing measurements of total retinal blood flow. One limitation was the slow A-scan rate of 20 kHz, which prevented velocity measurements in the larger vessels due to phase washout. Another limitation was the restriction to small scanning angles for various reasons: the mechanical specifications of the 2-D MEMS scanning mirror limited the optical scanning angle to 6°. Furthermore the incidence angle on the MEMS mirror caused scanning distortions [27], which needed to be compensated, limiting the maximum scanning angle even further. Finally, a constant beam geometry was assumed which, however, is valid only for small scan angles. All these factors prevented a full circular scan pattern around the ONH, a prerequisite for total flow measurements.

The purpose of this work was to improve the system to overcome these limitations and to enable total retinal blood flow measurements in clinical situations. This is done by increasing the system speed, optimizing the scanning system, and accounting for the variable beam geometry of the three scanning beams by introducing a scan angle dependent beam geometry matrix. We demonstrate the capabilities of the system and evaluate its performance by measuring and imaging 20 eyes of 10 healthy volunteers employing a circular scan pattern around the ONH. The mean total retinal flow was measured for arteries and veins and the in- and outflows were quantitatively compared. Furthermore the reproducibility of the method was evaluated for total retinal blood flow and for flow/velocities within each individual vessel. Finally, we discuss implications on applications in diseases like GON, diabetic retinopathy (DR), branch and central retinal vein occlusion and nonarteric ischemic optic neuropathy (NAION).

2. Methods

The three beam spectral-domain D-OCT system (Fig. 1) consists of three independent Michelson OCT sub-systems. The use of three independent superluminescent diode (SLD) sources (Exalos) in parallel effectively eliminates any cross talk and provides full imaging depth for each channel. The sources are operated at a central wavelength of 840 nm with a bandwidth of 50 nm and coupled into three miniature fiber collimators (Oz Optics Ltd. LPC 05-840-5/125-S-0.5-2.6CL-40-3A-1-1-SP) resting in a specially designed brass mount to generate a specific beam geometry to reconstruct the 3D velocity vector. The beams emitted by the collimators are aligned parallel to each other, with the three beams placed on the corners of an equilateral triangle. Mounting the collimators in a single block mount has the advantage that all optics and mirrors are shared by all three beams. This ensures a high phase stability and equal phase jitter for Doppler analyses in all channels. (The setup is not limited to an equilateral triangle geometry, other triangle geometries might be used as well.)

Fig. 1.

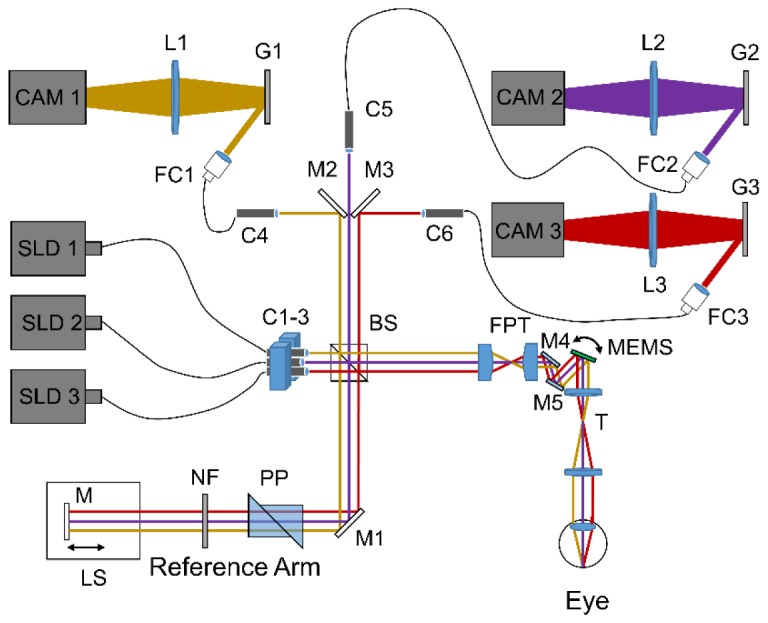
Three beam D-OCT system. C: Miniature Fiber Collimator, FC: Fiber Collimator, L: Lens, G: Grating, BS: Beamsplitter, M: Mirror, PP: Dispersion-compensating Prism Pairs, NF: Neutral Density Filter, FPT: Facet Prism Telescope, T: Telescope, MEMS: two-axis gimbal-less scanning mirror, LS: Linear Stage, SLD: Superluminescent Light Emitting Diode, CAM: Line Scan Camera.

2.1 Interferometer setup

The three beams are split into reference and sample beam via a bulk optics 90:10 (R:T) beam splitter. In the reference arm, hardware dispersion compensation is achieved by insertion of dispersion-compensating prism pairs (N-BK7). Neutral density filters are used to set the light power near the saturation limit of the line scan cameras.

In the sample arm we exchanged the two-axis gimbal-less MEMS mirror (Mirrorcle Technologies, Inc.) for a newer smaller model of the same manufacturer (3 mm diameter), since it allows for larger scanning angles than the previously used mirror. The 2D-MEMS mirror is advantageous compared to a 2-D galvo scanner, because both scanning axes are already in the same imaging plane. Due to the physical separation of 2-D galvo scanners an additional telescope needs to be placed between the scanners to achieve a similar effect. Otherwise the physical separation of the scanners will introduce additional phase shifts that will influence the Doppler evaluation. The MEMS mirror is driven with rather high voltages ranging from 0 to 136 Volts. By applying different voltages to the x- and y- inputs, different scan patterns can be realized (linear, raster, circular and resonant patterns). Maximum optical scan angles of ± 11.5° can be achieved. Since a 2-D scanning mirror introduces scanning distortions (as every scanning mirror), special care needs to be taken with regard to the incident angle of the beams on the mirror [27]. An incident angle of 45°, which is normally used, causes significant distortion for circular scan patterns, resembling an ellipse rather than a circle. Therefore the angle of incidence was changed to 22.5°, which we found to be sufficient to produce a circle without further compensation.

In order to minimize the influence of the introduced phase shifts, as scanning is performed in an off-pivot condition for every beam, it is necessary to reduce the initial beam separation of approximately 4.4 mm, given by the collimator block mount, to around 1.6 mm. This is achieved with a three facet prism telescope (FPT) which allows to control the beam separation on demand, by moving one prism with respect to the other. Contrary to a regular lens based telescope the beam diameter and therefore the lateral resolution of the system is maintained. Further details on the FPT can be found elsewhere [26].

The second 50:80 telescope (lens telescope) sets the final beam separation and diameter of the sample beams. After the telescope, the beam separation was set to 2.55 mm with a beam diameter of 0.8 mm, corresponding to a lateral resolution of ~25 µm for retinal imaging. This configuration was chosen, because it allows the penetration of an undilated pupil, while maintaining a substantially different beam inclination (~3.5° for retinal imaging) when the beams are focused on the sample.

After interference, the three beams are coupled into separate fibers and guided to three independent spectrometer units. Each spectrometer consists of a collimator, a blazed reflective grating (1200 lines/mm), a focusing lens (f = 200 mm) and a line scan camera (Basler spL2048-70km). The camera is operated at 50 kHz during measurements, compared with the old system the A-scan rate is therefore improved by a factor of 2.5. The systems sensitivity is 93.5 dB in each channel measured at 50 kHz and a beam power of 233 µW per channel.

2.2 Beam geometry and scan pattern calibration

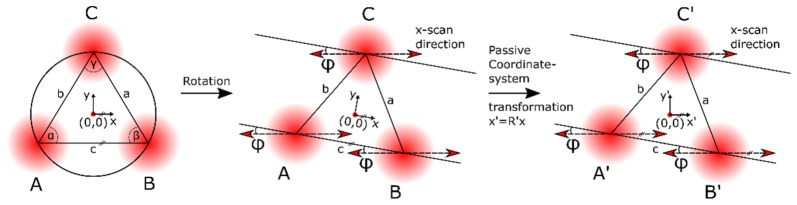
Using the three beam technique the flow vector can be determined in three dimensions. However, the exact geometry of the three beams with respect to the coordinate system of the instrument needs to be known. This geometry may be changed through scanning of the beams over the sample. In the following we describe how this can be measured and be corrected. First it is important that the position of the beams at the pupil plane of the eye are kept constant. This is achieved through the 2D MEMS mirror and the telescope that images the pivot point of the scanner onto the pupil plane of the eye (i.e. the focal plane of the second lens of the lens based telescope). Since a telescope and a 2-D MEMS mirror are used for scanning, the beams show nearly no movement in the focal plane of the second lens of thelens based telescope. At this plane the pupil of the eye is placed for a measurement. In the ideal case the beam geometry resembles an equilateral triangle at the entrance pupil of the eye. In our case the geometry did not resemble a perfect equilateral triangle. However the geometry greatly influences the extracted flow measurements. Therefore it is necessary to measure the exact beam geometry. The beam geometry is defined by the three vectors a, b, c (cf. Fig. 2). Each vector originates at the beam position at the pupil plane (A, B, C in Fig. 2) and meets the other vectors (in the ideal case) at the focal spot on the retina. As mentioned above, an arbitrary base triangle geometry between the beams can be used, as long as the triangle is not degenerated (angles must not be 0 or 180°) and the three vectors are linearly independent. However, maximum angle separation between the triangle points (60°, equilateral triangle) is preferred since more independent information is retrieved for bigger angular separation.

Fig. 2.

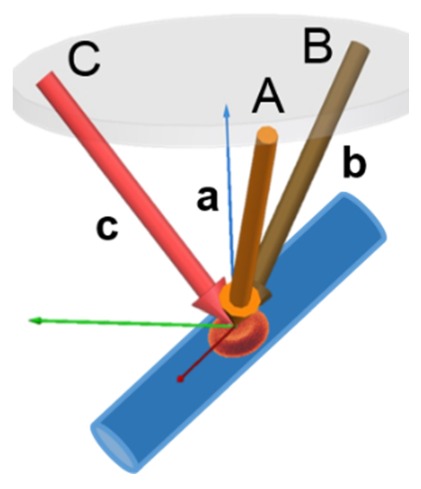
Illustration of the beam geometry of the three beams illuminating the sample. A, B, C entrance location of the beams at the pupil plane of the eye. a, b, c vectors indicating the direction of each beam towards the sample.

To use an arbitrary triangle geometry, the three side lengths of the triangle need to be measured. This can be done using a beam profiler that is placed at the location of the pupil plane of the eye. It must be noted that the geometry of the triangle will be changed through scanning. Therefore for each scanning location the exact geometry needs to be measured as will be described later on. Figure 3 shows an illustration of the corresponding measurement. With the side lengths of the triangle and the law of cosines the three angles of the triangle can then be calculated. After this step, the base triangle is defined (Fig. 3, left). To calculate the corresponding vectors a, b, c (Fig. 2) that span the pyramid and which are necessary to calculate the velocity vector, we introduce a coordinate system. The z-axis of this coordinate system is defined through the position of the common focal spot of the three beams and the center of the circumscribed circle of the base triangle of the pyramid. The positive x-axis is first defined along the horizontal triangle side c in the direction of an x-scan with positive voltage applied to the x-input of the scanning mirror. The positive y-axis is defined perpendicular to the x-axis in the direction of a y-scan when positive voltage is applied.

Fig. 3.

Beam geometry at the plane of a beam profiler. Red gradient dots: Indicate the three sampling beams. A, B, C: the three beams. a, b, c: side lengths of the triangle. α, β, γ: angles of the corresponding vertices. Lines with two arrows: Movement of the beams that is introduced through x-scanning measured with a beam profiler that is axially placed slightly out of position of the pupil plane of the eye. φ: angle between triangle base and x-scan direction. Left: ideal base geometry. x-axis of the coordinate system is aligned parallel to c and the x scanning direction. Center: The x-axis of the coordinate system is not parallel to the x-scanning direction, as observed with the beam profiler. Right: Using a passive coordinate transformation a new coordinate system x', y', z' can be introduced with an x-axis that is parallel to the x-scanning directions. Performing this transformation yields new coordinates A', B', C' for the beam locations at the pupil plane of the eye.

In the ideal case, the x-scan direction would be parallel to the triangle base c (x-axis), but the triangle, as in our case, might be rotated about the z-axis. To account for this rotation the angle (φ in Fig. 3) between c and the x-scan direction needs to be measured. Therefore a beam profiler was placed at a location along the z-axis outside the position of the pupil plane of the eye (at a distance greater than the focal length away from the second lens of the lens based telescope) because no motion of the beams can be detected at the location of the pupil plane of the eye. An x-scan was performed to indicate the x-scan direction on the beam profiler and φ was retrieved (Fig. 3, center). A passive coordinate transformation was then performed to account for the rotation of the triangle (Fig. 3, right). The vectors a, b, c shown in Fig. 2 take the following form in the new coordinate system (Eq. (1)), where α, γ and b are defined as in Fig. 3 (left). f indicates the distance between pupil plane and retina.

$$\mathit{a}\text{'}=\left(\begin{array}{c}-\frac{c}{2}\frac{\sin \left(\gamma +\phi \right)}{\sin \left(\gamma \right)}\\ -\frac{c}{2}\frac{\cos \left(\gamma +\phi \right)}{\sin \left(\gamma \right)}\\ -f\end{array}\right);\mathit{b}\text{'}=\left(\begin{array}{c}\frac{c}{2}\frac{\sin \left(\gamma -\phi \right)}{\sin \left(\gamma \right)}\\ -\frac{c}{2}\frac{\cos \left(\gamma -\phi \right)}{\sin \left(\gamma \right)}\\ -f\end{array}\right);\mathit{c}\text{'}=\left(\begin{array}{c}b\cos \left(\alpha -\phi \right)-\frac{c}{2}\frac{\sin \left(\gamma +\phi \right)}{\sin \left(\gamma \right)}\\ b\sin \left(\alpha -\phi \right)-\frac{c}{2}\frac{\cos \left(\gamma +\phi \right)}{\sin \left(\gamma \right)}\\ -f\end{array}\right)$$ (1)

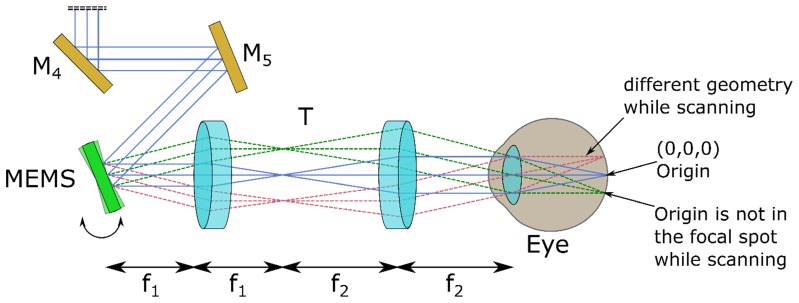
In the case of a circular scan pattern, for example around the ONH, a distortion of the original geometry can be observed for each scan location which needs to be corrected (Fig. 4). Therefore the coordinates of the three vectors (in the coordinate system of the instrument) need to be calculated for every A-scan to resemble the actual beam geometry at every position of the circular B-scan. In order to do so the radius of the circular scan on the retina needs to be known. To calibrate the scanning angle a model eye consisting of a lens and a beam profiler at the location of the retina was used. The beam displacement was then recorded on the beam profiler for several voltage inputs in x and y. With the known focal length of the lens and the measured displacement on the beam profiler, the scanning angle can be calculated. In our case the relationship between voltage and scan angle was found to be linear. For each eye the scanning angle has to be translated into distances on the retina. However, the corresponding distances will depend on the individual eye lengths, more precisely on the distance between the nodal point to the retina. This length was retrieved via biometry (Partial coherence interferometry [28, 29], using a Zeiss IOLMaster), subtracting the anterior chamber depth from the total axial eye length. The radius of the circle on each individual retina was then calculated in a geometric way to allow easy intercomparison. To increase accuracy, various described eye models might be used as well (e.g [30–32]).

Fig. 4.

Simplified illustration of the scanning geometry in the sample arm. M: mirrors. MEMS: 2-D gimbal less scanning mirror. T: telescope. f: focal length. Blue lines: Geometry of the three beams without scanning. Dotted lines: Beam geometry while scanning. The beam geometry is different for every position of the scan.

After the radius of the circle is retrieved we performed an active transformation on the three vectors (a’, b’, c’) for every position within the circular B-scan. First the angular position of every A-scan along the circle needs to be known (Eq. (2)): g = 2π/N_a (Number of A-scans),

$$N_a=\left(\begin{array}{c}0\\ 1\\ .\\ .\\ {\mathrm{N}}_{\mathrm{a}}-1\end{array}\right), g=\mathrm{g}{\mathbf{N}}_{\mathbf{a}}$$ (2)

then the vectors are transformed for every A-scan position (Eq. (3)) using the parametric circle equation

$${\mathit{a}}_{\mathit{i}}\text{'}\text{'}=\left(\begin{array}{l}a{\text{'}}_x+r·\cos \left(g_i\right)\hfill \\ a{\text{'}}_y-r·\sin \left(g_i\right)\hfill \\ -f_{eye}\hfill \end{array}\right);{\mathit{b}}_{\mathit{i}}\text{'}\text{'}=\left(\begin{array}{l}b{\text{'}}_x+r·\cos \left(g_i\right)\hfill \\ b{\text{'}}_y-r·\sin \left(g_i\right)\hfill \\ -f_{eye}\hfill \end{array}\right);{\mathit{c}}_{\mathit{i}}\text{'}\text{'}=\left(\begin{array}{l}c{\text{'}}_x+r·\cos \left(g_i\right)\hfill \\ c{\text{'}}_y-r·\sin \left(g_i\right)\hfill \\ -f_{eye}\hfill \end{array}\right)$$ (3)

with a_i”, b_i”, c_i” building the beam geometry vectors in Fig. 2 for every position of the circular B-scan (i = 0 - 6143, since a B-scan consists of 6144 A-scans) and a’, b’, c’ are the components of the beam coordinates after the passive coordinate system transformation of Eq. (1). After this step the vectors are normalized. Equation (4) shows the final form of the beam geometry matrix. A different beam geometry matrix BGM_i is used for every position i of the circular B-scan. In total there are 6144 different beam geometry matrices. The 3-D velocity vector can then be calculated by solving the linear equation system as described in Trasischker et al. Eq. (3) [25], but with a different BGM for every B-scan position.

$$BG{M}_i=\left(\begin{array}{c}{\frac{{\mathit{a}}_i\text{'}\text{'}}{\Vert {\mathit{a}}_i\text{'}\text{'}\Vert }}^T\\ {\frac{{\mathit{b}}_i\text{'}\text{'}}{\Vert {\mathit{b}}_i\text{'}\text{'}\Vert }}^T\\ {\frac{{\mathit{c}}_i\text{'}\text{'}}{\Vert {\mathit{c}}_i\text{'}\text{'}\Vert }}^T\end{array}\right)=\left(\begin{array}{c}{{\mathit{e}}_{{\mathit{a}}_{\mathit{i}}}}^T\\ {{\mathit{e}}_{{\mathit{b}}_{\mathit{i}}}}^T\\ {{\mathit{e}}_{{\mathit{c}}_{\mathit{i}}}}^T\end{array}\right)=\left(\begin{array}{ccc}{e}_{a_{x_i}}& e_{a_{y_i}}& e_{a_{z_i}}\\ e_{b_{x_i}}& e_{b_{y_i}}& e_{b_{z_i}}\\ e_{c_{x_i}}& e_{c_{y_i}}& e_{c_{z_i}}\end{array}\right)$$ (4)

2.3 In vivo measurements and data evaluation

Twenty healthy eyes of 10 volunteers were measured and evaluated with regard to total arterial and venous blood flow. The measurements taken are part of a study which was approved by the institutional ethics board and is in agreement with the tenets of the Declaration of Helsinki. Informed consent was obtained from all subjects. During in vivo measurements the combined power of the beams illuminating the eye was set to 700 µW to agree with the laser safety standards [33, 34].

The head of the subject was supported by a standard chin/headrest with the possibility to adjust x-, y- and z- positions. For alignment a raster scan pattern was used. The pupil of the eye was placed at one focal distance away from the second telescope lens. This corresponds to the position where the beam movement on the entrance pupil is least, as can be seen in Fig. 4. To find this position a video camera with sensitivity in the near infrared was used. After alignment a fixation target was displayed to the contralateral eye of the volunteer. With the aid of this target and a raster scan, the location of the ONH was centered in the en-face projection of the OCT. When the correct position was found, the scan pattern was switched to a circle with a diameter corresponding to a field of view of 10° revolving around the ONH. Forty circular B-scans were recorded in approximately 4.9 seconds, while ten consecutive scans were used for evaluation.

Standard FD-OCT data processing (re-scaling, zero padding, dispersion compensation, FFT) was performed on the measured spectra and amplitude and phase of each A-scan were extracted. The phase difference between corresponding depth pixels of consecutive A-scans was calculated to form the D-OCT image. Only B-scans within one cardiac cycle were taken. To select these B-scans, the maximum phase difference value of an artery was assumed to occur in the systolic peak. This B-scan and all consecutive B-scans were taken for averaging until the next systolic peak appeared (which was discarded, ~8-10 B-scans for averaging). Averaging was performed in complex space [35]. The B-scans were registered manually, because we found this to be more accurate than the cross correlation algorithm used in Haindl et al. [26].

Since none of the three beams is positioned at the pivot point of the scanning mirror, scanning will introduce an additional phase difference background. This phase difference background depends on the applied scan pattern. The D-OCT image will show a constant offset for a linear and a sinusoidal background for a circular scan pattern, as illustrated on the left side of Fig. 5. Hence it is necessary to subtract this phase background. In order to do so, the inner limiting membrane (ILM) is segmented in the intensity image (Fig. 5, top, green line) and a histogram of the phase difference values of the first 10 pixels from the ILM towards the outer retina is recorded to find the most probable phase difference background value for every A-scan. This A-scan specific background value is then subtracted from the original D-OCT image to get a background free D-OCT image, as can be seen on the right side of Fig. 5. This specific background subtraction not only compensates for the scanning offset, but also for bulk motion. If the vessel is very close to the ILM the phase background subtraction might not work. If this is the case, the phase value of the pixel with the brightest intensity might be chosen as reference [36]. Depending on the eye length the distance between two adjacent A-scans equals approximately 2 µm. This causes an overlap of adjacent sampling points, resulting in each point inside a vessel being sampled ~15 times. The sampling was chosen empirically since it influences the necessary amount of circular B-scans for averaging (8-10 times in one cardiac cycle). Furthermore a higher amount of A-scans slows down the MEMS mirror reducing the phase offset introduced by non-pivotal scanning.

Fig. 5.

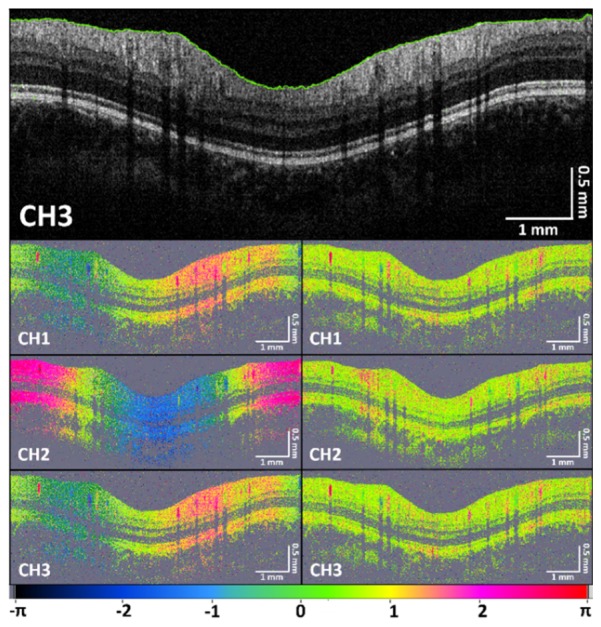
Phase difference background subtraction. Top: circular OCT intensity B-scan of channel 3, consisting of 6144 A-scans. Bottom left: Original phase difference images for all 3 channels. Bottom right: Phase difference images with subtracted phase offset and bulk motion compensation.

The processing and calculation of the mean blood flow, as well as the determination of the 3-D velocity vector were described previously for single vessels using a line scan or in vessel bifurcations using a circular scan pattern [25, 26]. In this work all major vessels emerging from the ONH were evaluated with regard to mean blood velocity, mean blood flow and diameter. A vessel was considered to be major, when it was clearly visible in the OCT intensity image and showed a non-negligible phase-difference value in the D-OCT image (~11 vessels per eye). Furthermore we used a separate BGM for every A-scan (Eq. (4)) to increase the accuracy of the 3-D velocity vector reconstruction. The 3-D velocity vector can still be calculated as described in Eq. (3) in Trasischker et al. [25], but the linear equation system is now solved with a different BGM for every B-scan position.

In order to calculate the mean blood velocity v_mean, the vector norm of the mean x-, y- and z- components of the 3-D velocity vector are used. The vessel’s absolute mean blood flow Q can be calculated as in Eq. (5),

$$Q=\frac{v_{mean}{D}^2\pi }{4}$$ (5)

where D represents the vessel diameter, which was extracted from the D-OCT image (in axial direction). Since the mean flow calculation is highly sensitive to changes in the vessel diameter (quadratic dependence), the diameter was measured five times and averaged values were used. The total retinal blood flow was calculated individually from the sum of the mean venous and also from the mean arterial flows. To evaluate the reproducibility of the technique, 4 independent measurements were carried out in 6 eyes of different subjects. Flow data reproducibility was evaluated for all individual major vessels emerging from the ONH, as well as for the total flow.

3. Results

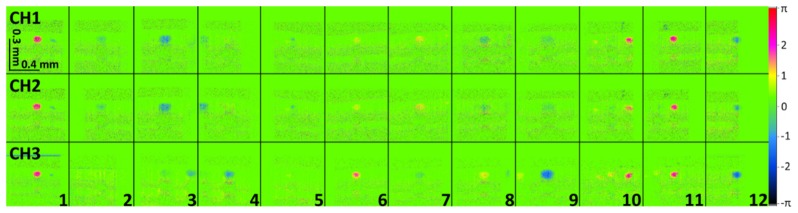
Figure 6 shows phase difference images of all major vessels and all channels of the circular scan around the ONH of a healthy eye (corresponding intensity and phase difference images in Figs. 5 and 7). The D-OCT phase difference images in the regions of interest (ROI’s) around the evaluated vessels were averaged 8-10x in complex space, using manual vessel registration. A ROI consists of ± 250 A-scans with the vessel in its center. The phase difference profiles inside the vessels resemble a parabolic shape for most cases, which is in compliance with Hagen-Poiseuille’s law. Since the beams of all three channels have a different angle of incidence on the blood vessel, the obtained phase difference images will in general look different. This information is used to reconstruct the total velocity vector. Only phase difference values inside the vessels are taken to calculate the velocity vector.

Fig. 6.

D-OCT phase difference images. All major vessels from all three channels in the circular B-scan from Fig. 5 are visualized. Images are averaged 10x in complex space. No unwrapping was applied. Horizontal rows: Vessels from the respective channel numbered from 1 to 12. Black boxes correspond to the size of the ROI.

Fig. 7.

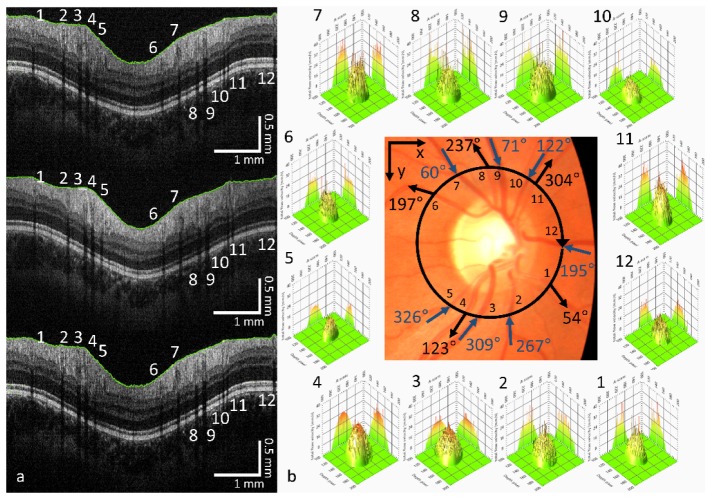
3-D velocity profile evaluation. (a) single circular B-scan for every channel, consisting of 6144 A-scans each. White numbers, vessel numbering. Green lines, segmentation lines for phase offset subtraction. (b, center) Color fundus photo. Black circular arrow indicates the direction and the path of the circular scan. Black inner numbers: Vessel numbering. Arrows with numbers: calculated vessel orientation from the 3 beam D-OCT data. (b, surrounding) Reconstructed velocity profiles for the corresponding vessels around the ONH after phase offset subtraction, phase unwrapping and averaging over 10 B-scans. x-axis: A-scans (200, zoomed view on the vessel location, steps of 40), y-axis: Depth pixel (100, steps of 20), z-axis: Velocity (mm/s, 0 - 40, steps of 8).

Figure 7 shows a compilation of typical OCT intensity images acquired by all channels, a color fundus photo and the velocity profiles for the corresponding vessels. As can be seen in the intensity images on the left side, the line rate of the cameras is fast enough to avoid fringewashout. The black circular arrow in the color fundus photo indicates the approximate scan path. The tail of the circular arrow indicates the start position, while the arrow tip marks the end of the circular scan. All evaluated vessels are numbered on the inside of the circle. The small arrows on the outside of the circle illustrate the calculated vessel orientations, which are in good agreement with the vessel orientations in the fundus photo. Blue labeling indicates a vein, while black labeling indicates an artery. The vessel orientations are readily available after the 3-D velocity vector is calculated. In the surrounding of the fundus photo, the velocity vector profiles inside the labeled vessels are illustrated. Most velocity profiles allow for a parabolic fit (as in this case), but some might resemble a non-parabolic shape. This can be caused by non-optimal registration of the vessels due to motion between B-scans, especially ifthe vessel changes its orientation in the surroundings of the beam path. This will cause a distortion in the averaged phase difference image and therefore in the velocity profiles. Furthermore if a vessel is imaged near to or exactly at a bifurcation, a non-parabolic shape of the velocity profile is expected. This was further explained by Aschinger et al. [37]. In this case the flow might be non-laminar.

The total blood flow was calculated for arteries and veins independently. To do so, the mean velocities inside the vessels were calculated and multiplied with the averaged vessel diameters, retrieved from the D-OCT images. In the case of the eye in Fig. 7 the total venous blood flow was 47.6 µl/min, while the total arterial blood flow was 49.2 µl/min. A comparison between mean venous and arterial total blood flow, averaged over all 20 eyes, can be found in Fig. 8. The mean total venous blood flow was 47.1 ± 2.7 µl/min (mean ± SD) ranging from 42.44 to 51.92 µl/min, while the mean total arterial blood flow was 47.1 ± 2.4 µl/min ranging from 42.42 to 50.17 µl/min. The mean absolute deviation of the venous from the arterial flow was 1.03 ± 0.93 µl/min or 2.2 ± 2% (mean ± SD).

Fig. 8.

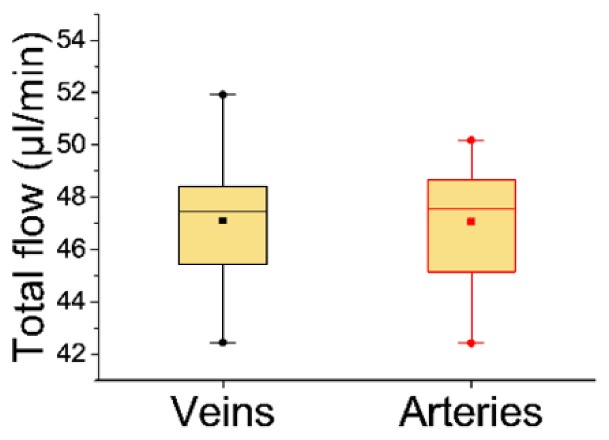
Box-Whiskers plot of the total retinal mean blood flow (20 eyes) in veins and arteries. Filled square: Average. Horizontal line: Median. Filled circles: Maximum and minimum measured flow. Box: 25th and 75th percentile. Whiskers: 1.5 times the interquartile distance – ( + ) the 25th (75th) percentile. If this value is smaller (greater) or equal to the smallest (largest) value in the data set, the whisker is drawn at this position.

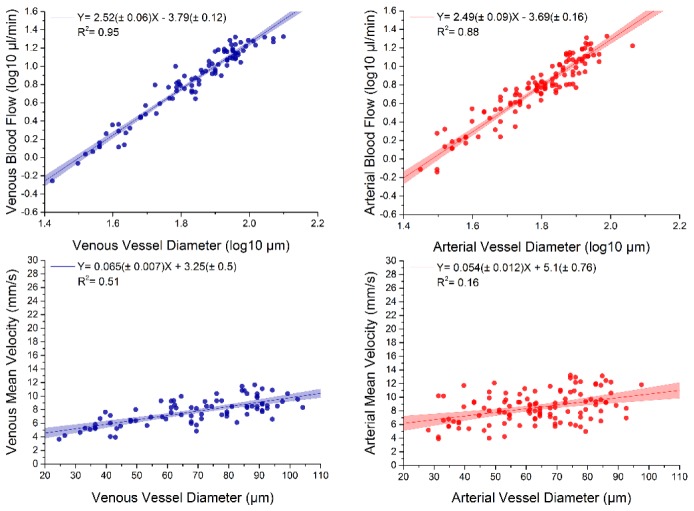
A paired two-sample t-test was performed to evaluate if the retrieved values for the two flows show a significant difference. Since the p-value was found to be high (p > 0.96), the null hypothesis cannot be rejected. This indicates, as expected, that there is no significant difference between venous and arterial blood flow for the measured healthy subjects. Figure 9 shows a linear regression analysis between the logarithmic venous/arterial blood flow and the logarithmic vessel diameter. The regression analysis gave a slope of 2.52 ± 0.06 (R² = 0.95) for veins and 2.49 ± 0.09 (R² = 0.88) for arteries. A moderate linear correlation with a slope of 0.065 ± 0.007 (R² = 0.51) was found between the venous blood velocity and the vessel diameter and a weak linear correlation with a slope of 0.054 ± 0.012 (R² = 0.16) between arterial blood velocity and the vessel diameter.

Fig. 9.

Blood flow rate versus vessel diameter (log-log plot) and mean velocity versus vessel diameter. Upper left: venous blood flow. Upper right: arterial blood flow. Lower left: venous velocity. Lower right: arterial velocity. Filled area: 95% confidence interval of the fit. Vessel diameters are determined from the D-OCT phase difference images.

To evaluate the reproducibility of the method, 4 independent measurements each were evaluated for 6 healthy eyes of different volunteers. For every eye the mean velocities, flows and diameters were calculated for the individual major vessels emerging from the ONH. Then the coefficients of variation were calculated and averaged to quantify reproducibility. Furthermore total venous and arterial flow variations were calculated using mean diameters (5 measurements) for the individual vessels (Table 1).

Table 1. Reproducibility evaluation. Mean coefficients of variation for the mean velocity v, vessel diameter D and mean flow Q retrieved by averaging the coefficients of variation obtained from 4 individual measurements each in every single vessel of 6 different eyes. Total flow variation for veins Q_v and arteries Q_a retrieved by 4 individual total flow measurements.

Eye	v	D	Q	Total Qv	Total Qa
1	0.13	0.08	0.13	0.05	0.06
2	0.09	0.07	0.14	0.08	0.06
3	0.09	0.07	0.12	0.05	0.04
4	0.12	0.05	0.12	0.09	0.06
5	0.11	0.10	0.11	0.08	0.03
6	0.11	0.11	0.12	0.03	0.05
Mean	0.11	0.08	0.12	0.06	0.05

4. Discussion

A critical parameter to accurately measure quantitative blood flow with D-OCT is the vessel diameter, since this parameter enters the flow calculation in a quadratic fashion. The vessel’s diameter might be underestimated if it is measured using the D-OCT phase difference images, due to the phase difference dropping below the noise floor near the vessel borders [24]. Therefore we extracted the vessel diameter from the D-OCT phase difference image near a systolic peak where the phase difference values are high, even at the vessel borders. Furthermore the diameter was measured five times to reduce measurement errors.

The total mean retinal blood flow, 47.1 ± 2.7 µl/min averaged over 20 healthy eyes, reported in this work, lies well within the range of previously published values determined by laser Doppler velocimetry (LDV), where values between 33 µl/min to 64.9 µl/min were measured [38, 39]. Wang et al. were upon the first to measure total retinal blood flow with a double-circle scanning pattern and a single beam using D-OCT. The values obtained with this method were 45.6 ± 3.8 µl/min (n = 10) and 47.6 ± 5.4 µl/min (n = 20) [40, 41]. Sehi et al. reported mean total retinal flow values of 46.5 ± 10.6 µl/min (n = 27) [42]. The values obtained with our three beam method agree well with these findings.

The linear regression analysis (log-log plot) shows a similar slope for veins (2.52 ± 0.06) and arteries (2.49 ± 0.09) and lies within the range of values reported in literature. Wang et al. reported a slope of 1.97 [43], and 2.13 [41], while Grunwald et al. reported a slope of 2.87 [44], similar to the findings of Riva et al., 2.76 ± 0.16 for arteries and 2.84 ± 0.12 for veins [45]. Garcia et al. (3.35 ± 0.23) [46], and Doblhoff-Dier et al. (3.7 for arteries and 2.8 for veins) [24] reported higher values. According to theory [47], the simplest requirement for maximum efficiency in the circulation is that the blood flow scales with the cube of the vessel radius (slope of 3). Most of the reported values indicate that a slope smaller than 3 is likely. Further research is necessary to determine if the deviation is caused by systematic errors in the measurement of blood flow, or if the principle of minimum work is not entirely sufficient to describe retinal circulation. Furthermore theory suggests that the blood velocity should resemble a linear relationship to the vessel’s diameter [47]. Such a relationship was found for veins, while only a weak positive relation was found for arteries. This is possibly caused by differing velocities for arteries within one cardiac cycle and might indicate that more B-scans need to be recorded within one cardiac cycle to minimize velocity variance and to confirm this relationship. Wang et al. did not find a linear relation between blood velocity and diameter, while Doblhoff-Dier et al. reported a linear trend.

In order to apply the three beam method to patients, the accuracy needs to be sufficiently high to detect deviations from the regular blood flow in healthy eyes. Some reports on blood flow alterations due to certain diseases were already described in literature. Sehi et al. reported 34.6 ± 12.2 µl/min (74% of the total retinal flow in comparison to normal eyes measured with this method) in glaucomatous eyes with single-hemifield damage [42]. Wang et al. also reported total retinal blood flow values for pathological eyes, showing decreased blood flow for patients with GON (34.1 ± 4.9 µl/min, 71%), NAION (28.2 ± 8.2 µl/min, 59%) and branch retinal vein occlusion (18.6 µl/min, 39%) and (34.8 µl/min, 73%) [41]. Retinal blood flow for diabetic patients might also be decreased, but were within the variance for the two measured patients. DR in general seems to be closely associated with early retinal vascular dysregulation [3]. Patients with proliferative DR (15.8 ± 10.1 µl/min, 33%) showed severely depressed blood flow [41]. These changes in total retinal blood flow are much higher than the variance in total retinal blood flow measurements of our system (~6%). Therefore it should be possible to evaluate such pathologies in the future with our technology.

Since a strong linear correlation between logarithmic flow and logarithmic diameter was observed, it should be possible to detect deviations from normal flow rates in single vessels. Grunwald et al. reported, that the correlation coefficient for healthy subjects r = 0.96 was significantly higher compared to diabetic patients with background diabetic retinopathy r = 0.83. When the relation between flow and diameter was investigated in each subject separately, the r value was also found to be significantly smaller, r of 0.93 ± 0.06 (range, 0.77-1.00) with greater variance, than in healthy subjects r of 0.98 ± 0.01 (range, 0.97-1.00). As stated above, patients with DR are known to show changes in retinal architecture and/or blood rheology and therefore the normal relationship between flow and diameter might be altered [44]. This relationship might be exploited for DR diagnosis and monitoring with the three beam D-OCT system. Furthermore the correlation should be evaluated for other eye diseases as well, since it might eventually support the vascular theory of GON development.

5. Conclusion

The three beam D-OCT technique allows to directly measure total retinal blood flow and the corresponding three dimensional velocity vector independent from any prior knowledge on the vessel geometry. The line scan rate of the spectrometers is fast enough to avoid fringe washout and to calculate the total mean velocity without parabolic interpolation of the phase pattern. Therefore it is possible to acquire 8 - 10 B-scans within one cardiac cycle and measure the mean blood flow and velocity profiles in all arteries and veins emerging from the ONH.

This work shows that the flows retrieved for arteries and veins show no significant difference for healthy subjects. Furthermore the average total flow variance between measurements is sufficiently low to detect deviations of ~6%. The system should therefore be sensitive enough to detect retinal blood flow alterations in various pathologies like GON, NAION, branch and central retinal vein occlusion and possibly in diabetic patients with background diabetic retinopathy. Three beam D-OCT may aid in the early diagnosis of these pathologies and evaluate the relevance of targeting ocular blood flow in treatment modalities. Furthermore three beam D-OCT might be the proper tool to advance the theory behind GON and resolve the ongoing discussion about mechanical and vascular theories of GON development.