Low-dose, phase-contrast mammography with high signal-to-noise ratio

Abstract

Differential phase-contrast X-ray imaging using a Talbot-Lau interferometer has recently shown promising results for applications in medical imaging. However, reducing the applied radiation dose remains a major challenge. In this study, we consider the realization of a Talbot-Lau interferometer in a high Talbot order to increase the signal-to-noise ratio for low-dose applications. The quantitative performance of π and π/2 systems at high Talbot orders is analyzed through simulations, and the design energy and X-ray spectrum are optimized for mammography. It is found that operation even at very high Talbot orders is feasible and beneficial for image quality. As long as the X-ray spectrum is matched to the visibility spectrum, the SNR continuously increases with the Talbot order for π-systems. We find that the optimal X-ray spectra and design energies are almost independent of the Talbot order and that the overall imaging performance is robust against small variations in these parameters. Discontinuous spectra, such as that from molybdenum, are less robust because the characteristic lines may coincide with minima in the visibility spectra; however, they may offer slightly better performance. We verify this hypothesis by realizing a prototype system with a mean fringe visibility of above 40% at the seventh Talbot order. With this prototype, a proof-of-principle measurement of a freshly dissected breast at reasonable compression to 4 cm is conducted with a mean glandular dose of only 3 mGy but with a high SNR.

1. Introduction

The adoption of grating-based, differential phase-contrast X-ray imaging (gbDPCi) to polychromatic X-ray tubes [1] has recently shown promising results for applications in medical imaging [2–4]. In contrast to conventional, attenuation-based X-ray imaging, gbDPC imaging measures not only the attenuation by a sample, but also the (differential) phase shift of the X-rays as well as the dark-field signal, which is related to small-angle scattering by the sample. The interferometer comprises three binary gratings, as is shown in Fig. 1. One of the gratings is moved in a phase stepping approach [5,6] to simultaneously record the three images.

Fig. 1.

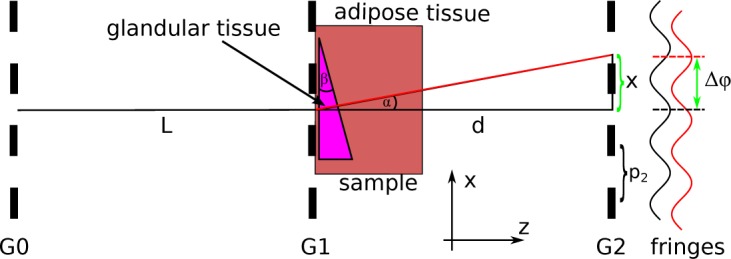
Principle of gbDPCi using a Talbot-Lau interferometer. The X-ray is refracted (from the black to red path) by the sample with height h(x) at a fixed angle α that is translated into a lateral shift x of the interference pattern. The shift x increases with increasing distance d. After the sampling with G₂, this shift is translated into a phase shift of the stepping curve Δφ.

Currently, there is an increasing interest in applying gbDPCi to mammography and several pre-clinical prototypes have been developed recently [2,4,7]. However, most studies conducted so far, have used a radiation dose that exceeds the clinically acceptable limit with approximately 26 and 66mGy in [2] and [4], respectively. As these prototypes were not yet fully optimized, such a high dose was necessary to obtain a sufficiently high signal-to-noise ratio (SNR) in the differential phase-contrast images to be clinically useful. In a recent study [8], related to this work, Scherer et al. reported a major dose reduction by hard- and software improvements specific for their setup. This paper describes a more general approach and outlines a feasible method to decrease the applied radiation dose below the 2.5mGy limit stipulated as per European guidelines [9] while still providing sufficiently high image quality in terms of SNR.

Although the refractive index decrement δ is several orders of magnitude larger than the imaginary part β, which determines the attenuation, current gbDPC systems cannot completely utilize this potential because δ is indirectly measured as a phase shift of the interference pattern introduced by refraction. Therefore the measured differential phase signal is highly dependent on the sensitivity S of the interferometer. In contrast, the attenuation signal is dependent on the X-ray energy and the detector only. The sensitivity is defined by the period p₂ of the analyzer grating (G₂) and the propagation distance d from the beam-splitter-grating (G₁) to G₂ via $S=2\pi \frac{d}{p_2}$ [10, 11]. However, the dependence of the phase signal on the sensitivity is not a limitation but an opportunity, because it offers the possibility of amplifying the measured phase signal and, therefore, the SNR by optimizing the sensitivity of the interferometer. A second crucial parameter is the visibility v of a Talbot-Lau interferometer, which is defined as the ratio of the amplitude of the stepping curve to the mean intensity $v=\frac{I_{max}-I_{min}}{I_{max}-I_{min}}$, with I_min and I_max being the maximum and minimum intensities of the obtained stepping curve. High visibility is crucial for accurate phase signal retrieval even in the case of low photon statistics such as those encountered for low-dose applications such as mammography. To obtain high SNR, both the sensitivity and the visibility have to be simultaneously optimized.

This paper aims to optimize the visibilities of interferometers operated at high fractional Talbot orders [12, 13] because those systems provide increased sensitivities; they are therefore promising candidates for low-dose applications. As discussed recently in [14] and [15], only beam splitter gratings with a π-phase shift as opposed to a π/2-shift are suitable for higher Talbot orders. In addition, we will only consider symmetric systems as they are the most sensitive ones for a fixed grating period of G₂.

We first analyze the influence of the Talbot order on the energy-resolved visibility spectrum for Talbot-Lau-interferometry through a general approach. This analysis is a valuable tool for identifying the quality-limiting factors of a given system. Second, as the imaging performance of the interferometer can be defined by the achievable SNR, this parameter is optimized for a system dedicated to applications in mammography. As a figure of merit, the SNR is optimized through simulations for different design parameters such as grating periods, design energies E_d and X-ray spectra. These steps will be thoroughly discussed in section 3.

As our third step, in section 4, we develop a pre-clinical, high-Talbot-order mammography prototype on the basis of the knowledge obtained through the aforementioned simulations. With this prototype, a gbDPC-mammography of a full human breast specimen with a clinically compatible mean glandular dose of 3mGy is conducted. Finally, in section 5 we discuss the current limitations of our prototype and outline further improvements.

2. Methods & materials

2.1. Simulation tool

The simulations presented in this paper are based on a planar wave optical model of X-rays that are propagated via a Fresnel propagator [16] and interact with the optical elements in the beam path, including the gratings and sample, via their complex transmission function. This function explicitly considers the finite thicknesses of the grating bars. The simulation is performed monochromatically for all X-ray energies of interest. For all energies, a visibility v(E) can be calculated through a virtual phase stepping approach. The energy-resolved visibility v(E), sometimes also referred to as the visibility spectrum, is a valuable tool for analyzing the influence of the applied X-ray spectrum on the resulting performance. The resulting visibility, as it would be recorded by a conventional X-ray detector, is obtained by a weighted average of the visibility spectrum with the X-ray spectrum (energy-integrated visibility). Furthermore the simulation calculates the effective values for the differential phase shift and the attenuation images by taking the full x-ray spectrum into account. Prior to this study, the simulation framework was carefully validated by reproducing the measurements of plastic phantoms of known composition and geometry described in [17].

2.2. Signal-to-noise ratio

Photon noise is considered to be the dominant source of noise and is implemented in the simulation as Poisson noise on the number of applied X-ray photons per energy bin. The resulting photon noise of the simulated effective differential phase shift Δφ_eff for a grating interferometer with a total number of N_total detected photons was found to follow the model introduced in [18]:

$${\sigma }_{\text{photon},\mathrm{\Delta }{\phi }_{eff}}^2\propto \frac{1}{v^2}\cdot \frac{1}{N_{total}}\cdot$$ (1)

The noise scales inversely with the visibility v and the square root of the number of recorded photons N_total, whereas Δφ_eff is proportional to the sensitivity S. The SNR can therefore be defined as

$$\text{SNR}=\frac{\mathrm{\Delta }{\phi }_{eff}}{{\sigma }_{\text{photon},\mathrm{\Delta }{\phi }_{eff}}}\propto S\cdot v\cdot \sqrt{N_{total}}.$$ (2)

As the applied radiation dose D is directly proportional to the number of X-ray photons we can introduce the following relationship to emphasize that the dose D, which is needed to achieve a fixed SNR value, scales in an inversely quadratic manner with both the sensitivity S and the visibility v of the gbDPC system:

$$D\propto \frac{{\text{SNR}}^2}{S^2\cdot v^2},$$ (3)

Therefore, a simultaneous optimization of these two parameters is required to reduce the radiation dose without affecting the image quality in terms of the SNR. This optimization is done by considering the the sensitivity S(m) and the visibility v(m) as functions of the Talbot order m in the following.

In general, the spatial resolution would be an important factor when describing image quality, too. To reduce the complexity, we restrict our optimizations to systems with a fixed length and geometry; and therefore with a fixed spatial resolution. This allows us to use the SNR as a measure of the image quality. Alternations in the grating periods do not affect the spatial resolution of the system as discussed in [1].

2.3. Phantom for SNR analysis

A numerical phantom (shown in Fig. 1) is designed for the analysis of the SNR. The phantom comprises a wedge of glandular tissue embedded in a block of adipose tissue. The material data were taken from [19] and [20], and the tissue composition was taken from [21]. The wedge has an opening angle of β = 45°. The constant slope generates a constant differential phase signal Δφ, which enables the calculation of a mean value for the signal and the standard deviation caused by simulated photon noise that is required to define the SNR.

2.4. Dose calculation

Following suggestions from [22], the mean glandular dose that is applied to the phantom is calculated in a Monte Carlo approach via the GE software CatSim [23]. The calculation considers the inherent filtration of the X-ray spectrum by the gratings and their substrates.

3. Simulation results

3.1. Visibilities of π and π/2 Systems at High Talbot Orders

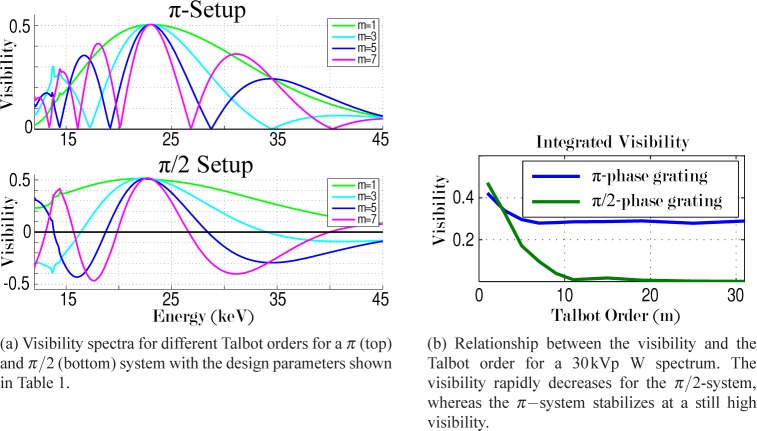
Yashiro et al. [24] suggested decreasing the grating periods (which results in higher Talbot orders for systems with a fixed length) to improve the SNR when working with monochromatic x-rays. In this study we want to optimize the SNR in polychromatic systems with very high Talbot orders. In contrast to the monochromatic case, where the system can always be tuned to have the maximum visibility at the actual x-ray energy, the polychromatic case has to consider and adjust the entire visibility spectrum of the system. Therefore, a detailed study of the visibility spectrum as a function of the Talbot order, m, is performed. As recently shown in [14], there is a major difference between the performance of systems with π and π/2 phase shifts. Therefore, two different systems were simulated with a π and π/2 phase shift, respectively. The attenuation gratings are assumed to be made of 70-µm-high Au bars (see Table 1). As shown in Fig. 2(a), the energy resolved visibility curves are computed for Talbot orders from m = 1 to m = 31. From these curves, the integrated visibilities are calculated for a 30kVp tungsten spectrum considering a 300-µm-thick Gadox screen as a detector as shown in Fig. 2(b).

Table 1.

Simulation parameters for the general comparison of the π and π/2-systems.

Parameter	Phase Shift	Ed	Spectrum	Detector
Value	π (π/2)	23keV	30kVp W	300μm Gadox
Parameter	p1 [μm]	p0/p2 [μm]	Length [m]	Att. gratings
Value	2.4 (1.2)	2.4	1	70µm Au

Fig. 2.

Differences between π and π/2 gratings operated at higher Talbot orders.

Since a π-phase grating does not introduce an alternation [14] in the Talbot carpet, its visibility spectrum does not include “negative” parts such as those observed the lower plot of Fig. 2(a). Nevertheless, the integrated visibility still decreases for higher Talbot orders but is found to stabilize at 60–70% of the value obtained for m = 1 (blue curve in Fig. 2(b)). The decrease can be explained by the increased number of local minima in the visibility spectrum for higher Talbot orders. For m > 7, the visibility becomes saturated as the increased number of minima is balanced by a decrease of their width. This leads to an almost constant filling factor of the area under the curve with respect to the curve for m = 1.

It must be noted, that this result highly depends on the applied X-ray spectrum. If the X-ray spectrum is not matched to the visibility spectrum, also the π−system visibility may be affected at the higher Talbot orders; for example, if a characteristic X-ray line from the tube target coincides with a minimum in the visibility spectrum. Therefore, the influence of the X-ray spectrum on the performance is analyzed as the next step.

3.2. X-ray spectrum and design-energy optimization

As the X-ray spectrum itself has a major influence on the resulting visibility and image quality in terms of the SNR, a study is performed to find the most suitable X-ray spectrum for gbDPCi mammography. For two targets (tungsten and molybdenum), the tube voltage and design energy E_d of the interferometer are varied. The system length is fixed at 66cm, as this is the typical system length of a commercial mammography system. Therefore, according to [10], the grating period decreases with the given equation when increasing the Talbot order:

$$p_2\propto \sqrt{\frac{1}{m}}$$ (4)

The calculation is terminated when the period falls below the limit of 1.8µm. The attenuation gratings are assumed to be made of 50µm high gold bars with duty cycles of 0.5 and 0.66 for G₂ and G₀, respectively. The increased duty cycle of G₀ improves the visibility and, for the same tube power and exposure time, also reduces the dose to the sample. To apply the same effective dose, the tube power and/or exposure time need to be increased accordingly [15]. A fixed dose of 2mGy MGD is applied to the 4-cm-thick phantom for all spectra and the resulting SNR is calculated as a figure of merit. The energy integrating detector is assumed to be 100% efficient for all energies (see Table 2 for a summary of the simulation parameters).

Table 2.

Simulation parameters for the optimization of the X-ray spectrum and design energy specific for gbDPC mammography.

Parameter	Phase Shift	Spectrum	Detector	Dose	Length	Phantom
Value	π	Mo / W	100% efficient	2mGy	0.66m	4cm tissue wedge

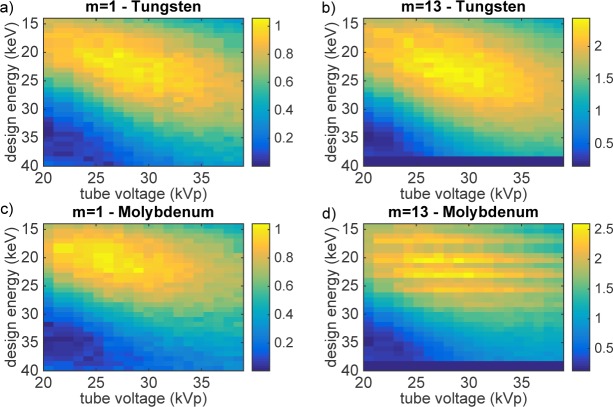
For two example Talbot orders (m = 1 and 13) and two different targets, the resulting SNR is shown in Fig. 3 as a function of design energy and tube voltage. The first important result is that there actually is a maximum in the SNR that is, in addition, very broad even for the higher Talbot orders. This indicates that the system performance remains unaffected by minor variations in either the tube voltage or the design energy. However, the latter conclusion only holds for tungsten. Due to the strong characteristic lines of the molybdenum target around 17keV, such an interferometer is highly sensitive to changes in the design energy as for several design energies, the characteristic lines may coincide with a minimum of the visibility spectrum. This results in the horizontal banding observed in Fig. 3(d). Working with molybdenum targets is therefore more challenging than working with a broad and smooth spectrum such as tungsten. However, molybdenum enables slightly better performance (see Fig. 4) because the visibility can profit from a narrower X-ray spectrum as long as the design energy of the interferometer is appropriately selected.

Fig. 3.

Optimization results for the realistic mammography system. The maximum in the SNR is very broad for both Talbot orders, but contains local minima and maxima (vertical lines) in the case of high Talbot orders with the molybdenum target (d). In b) and d), some values exceed the lower limit of 1.8μm for the grating periods and are therefore skipped in the calculation (dark-blue points at the bottom).

Fig. 4.

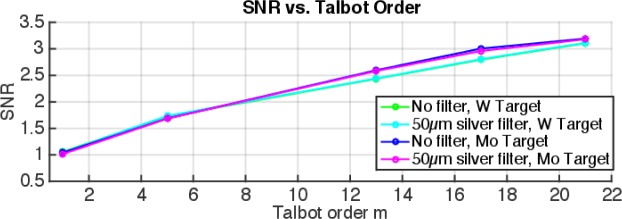
SNR vs. Talbot order for different target and filter combinations. The SNR values are taken from the maximum in each dataset of Fig. 3. The SNR increases with increasing Talbot order. Additional K-edge filtering by 50µm silver does not significantly influence performance. The two tungsten lines are very close together and not distinguishable in the figure.

The second result is that the position of the maximum in the SNR is almost independent of the Talbot order. The highest SNR is always reached for a tube voltage close to 29 kVp and a design energy of approximately 24 keV for tungsten and approximately 26kVp and 22keV for molybdenum. These results are in good agreement with the findings in [25].

When comparing the position of the maximum SNR to the data for the differential phase signal Δφ and the visibility v, the data shows that the maximum is neither at the position of the highest visibility nor at the position of the highest phase signal, which both lie in a region of much smaller kVp. The photon count rate shifts the optimum to higher tube voltages, where the breast becomes more transparent. For the same deposited mean glandular dose in the breast, more photons can reach the detector and therefore reduce the photon noise.

To study the performance of a potential high-Talbot-order mammography system, the maximum SNR value is calculated for each Talbot order. Furthermore, this study is repeated with an additional k-edge filter (50µm silver), as shown in Fig. 4. When choosing the appropriate tube voltage and design energy, it is feasible to continuously increase the SNR with the Talbot order. An additional k-edge filter, as usually applied in conventional mammography, does not significantly affect the performance, but requires an adjustment of tube voltage and design energy. Moreover, the data shows that molybdenum as a target offers slightly higher SNR values., which is due to the narrower X-ray spectrum with lower mean energy.

4. Proof-of-principle experiment: low-dose gbDPCi mammography

As a proof-of-principle, a low-dose imaging system is realized on the basis of the findings mentioned in previous chapters. Due to the limited availability of gratings at the time of the experiment, the highest Talbot order that could be realized was a system in the seventh Talbot order (see Table 3 for all system parameters). The system has a total length of approximately 2m in a symmetric configuration. To enable similar performance at shorter lengths, gratings with a smaller period are necessary. The proof-of-principle images shown in Fig. 5(a) are generated with 11 phase steps and a tube voltage of 30kVp (pre-filtered by 50µm silver) with a conventional rotating molybdenum anode and a photon counting PILATUS 200k detector. In this configuration, a visibility of approximately 40% is achieved. At the time the sample was available for imaging, only a coarse estimate of the optimal tube voltage had been determined, which was thereby used for image acquisition. A later, more detailed analysis, as presented in section 3.2, revealed the actual optimum to be slightly lower.

Table 3.

Configuration for the low-dose gbDPC mammography system as used in the proof-of-principle experiment.

parameter	value	parameter	value	parameter	value
Grating periods	5.4 µm	L	102 cm	Spectrum	30 kVp Mo
Phase shift	π	d	102 cm	Detector	PILATUS 200k
Talbot order	m = 7	visibility	>40%	Filter	50µm Ag

Fig. 5.

New (a) and old (b) gbDPC mammography images of a 4-cm-thick human breast. The darkfield and attenuation images are given as the neg. logarithm of the normalized visibility and intensity respectively. As can be seen from the color-bars, the optimized sensitivity results in much higher values for both the differential phase and darkfield images in the new system. The attenuation image profits mostly from an increased soft tissue contrast due to the reduced energy in the x-ray spectrum (30kVp vs. 40kVp in the old settings).

The study is conducted in accordance with the Declaration of Helsinki and was approved by the local ethics committee (Ethikkommission of the Ludwig-Maximilian-University, Munich). After an adequate explanation of the study protocol, the participant provided written consent prior to participation. Indication for breast surgery followed the recommendation of the interdisciplinary tumor board of the University of Munich breast center.

The sample shown in Fig. 5(a) is a 4-cm-thick female mastectomy breast specimen, imaged with a total mean glandular dose of only 3mGy. As this example is presented only to verify the feasibility of low-dose imaging with high SNR, no further histopathological evaluation of the obtained images is provided herein. Two experienced radiologists rate the images as highly complementary. As depicted in the magnified view, high image acutance is gained in the phase image, while tissue borders are distinctly depicted in the dark-field channel.

4.1. Comparison to old system

To visualize the improvements obtained by the optimization, the same sample was also measured in the old system with the same imaging protocol as presented in [4]. The resulting images are shown in Fig. 5(a) and 5(b) for the new and old system respectively. The images from the old system were conducted with a mean glandular dose of about 60mGy but a recent study [8] showed, that this very high dose was mainly needed to compensate unnecessary detector noise, introduced by hard- and software issues. Therefore the old “high-dose” images still appear more noisy than the new “low-dose” images. As can be seen from the color-bars in Fig. 5(b), the optimized sensitivity results in much higher signals for both the differential phase as well as the darkfield images. The contrast in the attenuation images profits mostly from the reduced energy of the x-ray spectrum, which was 40kVp in the old settings and only 30kVp (plus the silver K-edge filter) in the new approach. As discussed in section 3.2, the effective differential phase shift is larger for low-energy spectra and therefore additionally contributing to higher signals in the images. A direct quantitative comparison between the datasets is not meaningful due to the several shortcomings of the old system. In particular for the phase image it is impossible, due to differential nature of the images, which makes it impossible to define a proper region of interest for a SNR-analysis. Independent of the dose discussion, the experienced radiologists rated the new images as superior in terms of clinical usage.

5. Discussion

In this study, we showed that it is feasible to build a low-dose, differential phase-contrast system at a high Talbot order when choosing a π-phase grating as the beam splitter grating. Due to negative visibility contributions encountered for π/2-phase gratings, the latter systems should only be operated at the first Talbot order wherein they even outperform the π-systems in terms of achievable visibilities, especially when working with wide X-ray spectra. Based on the recent findings in [14], we could show by simulations that the visibility decreases only to 60–70% of the value obtained at the first Talbot order when going to higher Talbot orders for a π-phase grating. As the gain in sensitivity outweighs this loss, a continuous increase of the SNR was observed for higher Talbot orders. Thus, we could realize a preclinical prototype system at the seventh Talbot order with a visibility above 40%.

The exposure time for the proof-of-principle experiment was very long (approximately 3min for every sub-image, from which the full image was generated by stitching). This is a substantial amount of time to deliver a dose of only 3mGy. This is the result of a combination of several shortcomings of our prototype. The X-ray tube output is rather low compared to a state-of-the-art mammography tube and the long system length results in a major loss of photons. A further flux limitation was the additional filtering by the K-edge filter, the grating substrates and the sample holder. For a shorter system with a state-of-the-art X-ray tube, a dedicated mammography detector, and thin grating substrates, the exposure time can be decreased to 4–5 times the conventional exposure time, as this is the amount of radiation that is “sacrificed” in the two attenuation gratings.

The detector used in this experiment was rather sub-optimal. The superior read-out-noise reduction due to the photon counting feature of the Pilatus detector was wasted by the low detection efficiency of the 1-mm-thin silicon sensor. In total, the efficiency was only 56% for the filtered X-ray spectrum. Using a more efficient detector would result in a significant reduction of both the measurement time as well as the applied radiation dose.

The simulation showed that working at high Talbot orders offers the possibility of decreasing the necessary dose, as the SNR increases continuously with the Talbot order for a fixed dose. If a certain SNR is necessary for a specific application (e.g., for clinical images to be of diagnostic value), the applied radiation dose can be reduced below the clinically acceptable limit by increasing the Talbot order. Since a compact setup is desired for most applications, the increase in the Talbot order should be realized by smaller grating periods rather than an increase in the setup length, as realized in the proof-of-principle measurement presented herein. The two limits of this approach are reached when the dose is so low that statistical phase wrapping occurs or when the grating periods become so small that they cannot be fabricated anymore. As the typical signal strength of features in the breast was observed to cover only 5% of the dynamic range of the interferometer, “over-engineering” of the sensitivity and, therefore, phase-wrapping due to too-small grating periods is not considered to be a potential problem.

Another limitation might be the field of view, which becomes very small for cone beam systems and flat gratings with very small periods due to shadowing effects. Working with bended gratings whose performance is not affected by shadowing is therefore strongly recommended.

In contrast to [7] we propose a gbDPCi mammography system in a symmetric configuration, as this is the most sensitive one for a given grating period. To achieve a sensitivity that is similar to the prototype presented herein, but at a length of only 66cm, the gratings should have a period in the order of 2µm. To realize a symmetric configuration, the G₁ grating has to be mounted above the compression plate in the middle of the beam path. This configuration would be similar to the magnification mode of current state-of-the-art mammography systems. Furthermore, a compression of the breast in the direction of G₁, rather than the conventional detector direction would improve the sensitivity by minimizing the distance to the grating.

Due to the nature of the magnification, this approach would be a field-of-interest imaging rather than a full-field imaging approach if the conventional mammography system geometry is preserved. Nevertheless, this would also relax the constraints on the fabrication of larger gratings, although the published technological progress of grating fabrication is developing fast with the first bent and stitched gratings already available. Therefore we believe that the realization of a clinical prototype scanner with the aforementioned parameters should be the next task on bringing differential phase-contrast imaging one step closer to clinical applications.