Fast interferometric second harmonic generation microscopy

Abstract

We report the implementation of fast Interferometric Second Harmonic Generation (I-SHG) microscopy to study the polarity of non-centrosymmetric structures in biological tissues. Using a sample quartz plate, we calibrate the spatially varying phase shift introduced by the laser scanning system. Compensating this phase shift allows us to retrieve the correct phase distribution in periodically poled lithium niobate, used as a model sample. Finally, we used fast interferometric second harmonic generation microscopy to acquire phase images in tendon. Our results show that the method exposed here, using a laser scanning system, allows to recover the polarity of collagen fibrils, similarly to standard I-SHG (using a sample scanning system), but with an imaging time about 40 times shorter.

1. Introduction

In recent years, Second Harmonic Generation (SHG) microscopy has emerged as a powerful technique to probe non-centrosymmetric structures in biological tissues [1–4]. This type of laser scanning microscopy is characterized by an intrinsic sub-micron spatial resolution, due to the confinement of the excitation in the focal volume, robust upon light scattering which provides a high penetration depth within biological tissues [5,6]. SHG is a coherent process that radiates at exactly half the fundamental wavelength and scales quadratically with the number of aligned molecules [7,8]. Importantly, as SHG does not involve population transfer, it considerably reduces phototoxicity and is free from photobleaching [9,10]. Finally, this technique is highly specific for dense non-centrosymmetric media [3,11]. Therefore, SHG microscopy appears to be a very sensitive and specific structural probe, both ex vivo and in vivo, of the macro-molecular architecture of a wide variety of tissues [12–15].

Specifically, SHG microscopy has been used to image connective tissues rich in fibrillar collagen such as tendon [16,17], cornea [18,19], skin [20,21], fascia [22,23], cartilage [24,25]. In addition, SHG signals have been obtained from the myosin band in skeletal muscles [14,26] and from tubulin forming the microtubules in cultures of neurons [27,28] or during cell mitosis [1,29]. The common property of these three proteins (fibrillar collagen, myosin and tubulin) is their non-centrosymmetric structure at the macro-molecular scale. Interestingly, if the polarity of these non-centrosymmetric components are opposite relative to each other, the SHG signal emitted would be π phase shifted [30] due to the opposite sign of the achiral component of their second order non-linear susceptibility tensor χ⁽²⁾. Therefore, measuring the relative phase of the SHG signal carries important structural information about the observed tissues. Unfortunately, this cannot be done in a standard SHG microscope since it only detects the signal intensity and not the phase.

Interferometric Second Harmonic Generation (I-SHG) microscopy overcomes this limitation and probes the relative polarity of harmonophores in tissues. This technique has been originally proposed to characterize non-centrosymmetric materials such as Beta Barium Borate microcrystals [31], organic crystals [32] or periodically poled crystals [33]. Recently, its potential for tissue imaging has been demonstrated. In particular, I-SHG has been used to investigate the bipolarity of myosin filaments in skeletal muscles [26] and the polarity switch in collagen fascicles in tendon [34]. Note that only few other techniques allow to probe the relative polarity in tissues such as holographic SHG [35,36] or interferometric sum-frequency generation (SFG) [37]. However, in its first implementation, I-SHG suffered from two important drawbacks. First, the picosecond pulses excitation [26,34], used to simplify the interferometric part of the setup, decreased drastically the imaging contrast in tissues because of the smaller excitation peak intensity obtained. In practice, while this low contrast was enough to image highly organized structures such as tendon or muscles, it limited the investigation of more complex architectures such as skin or cartilage. Secondly, images were recorded using a translation stage instead of the more classical laser scanning system, based on galvanometric mirrors, because this latter would modify the relative phase to be measured. The use of a sample scanning system decreases imaging speed considerably, which prevents the investigation of dynamical processes. We recently solved the first issue by implementing a new microscope based on a femtosecond excitation and optimizing the temporal overlap between the two beams by compensating the group velocity delay in the microscope [38].

In the present study, we address the second issue by implementing a fast I-SHG imaging setup using the classical laser scanning system to reconstruct images of the sample. We show that, using a model sample, it is possible to calibrate the variable phase shift introduced by the galvanometric mirrors in order to correct the phase image obtained in biological tissues. Finally, we imaged mice tail tendon, a well characterized collagen-rich tissue, and showed that fast I-SHG microscopy recovers the same phase distribution as sample scanning I-SHG, but with an imaging speed approximately 40 times faster. In addition, analyzing the phase distribution as a function of the reference phase step, we optimized the number of images acquired, which allowed us to gain another factor 6 on the imaging time. Altogether, this study validates the use of fast I-SHG in biological tissues and opens avenues for dynamical studies of the relative polarity in a wide range of tissues.

2. Materials and methods

2.1 Experimental setup

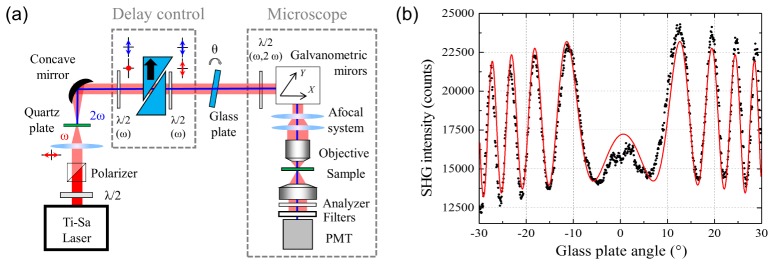
Interferometric SHG imaging was performed using a custom-built laser scanning inverted microscope [Fig. 1(a)], based on a femtosecond Titanium-Sapphire laser (Tsunami, Spectra Physics) delivering 150fs pulses at 80MHz repetition rate. The excitation wavelength was set to 810nm. The average power on the sample was adjusted to 30mW, using a half-wave plate and a polarizer. A 5cm focal lens is used to focus the laser on a 20-µm BBO crystal (θ = 29.2°, Eskma Optics) to generate a reference SHG beam outside the microscope. Moving the crystal closer or further from the focal point allowed to adjust the reference SHG intensity. Both the fundamental and the reference SHG were collimated using a metallic spherical mirror. A half-wave plate at 810nm, full-wave plate at 405nm is then used to rotate the fundamental polarization. Two calcite wedges, with optical axis placed in the reference polarization direction, are used to introduce a negative delay between the fundamental and reference beams. This allows to pre-compensate for the group velocity dispersion introduced by all the following optics, especially the microscope objective. A second half-wave plate at 810nm, full-wave plate at 405nm, was used to set the fundamental and reference beam polarization back together. A 1.5mm thick BK7 glass plate, placed on a rotating mount, was used to control the phase between the reference and fundamental beam. Finally, a half-wave plate (at 810nm and 405nm) is used to rotate the incident polarization on the sample. Two galvanometric mirrors (TillPhotonics GmbH) are used to scan the laser on the sample. A telescope increases the beam size to fill the back aperture of the microscope objective (Olympus UAPO, 40xW3/340, water immersion, NA 1.15) providing a typical lateral and axial resolution of 0.35x1.2 µm² at 810 nm. Mechanical and piezoelectric motors, for coarse and fine adjustments respectively, were used to vertically move the objective, allowing acquisition of z-stacks in the sample. Finally, signals were collected in the forward direction using a condenser (NA 0.55) and detected on a photomultiplier tube (R6357, Hamamatsu Photonics) set at 550V for crystal experiments and at 800V for tissue imaging. The SHG signal was selected using appropriate spectral filters (two FF01-720/SP-25 and a FF01-405/10-25, Semrock). An analyzer was placed before the detector. Images were recorded in the forward direction using 10µs pixel dwell-time and typically 300 nm pixels size.

Fig. 1.

Experimental setup used for fast I-SHG microscopy. a) Experimental setup and b) characterization of the glass plate used to extract the relative phase.

2.2 Phase extraction

I-SHG technique retrieves, pixel by pixel, the relative phase of the SHG signal in the sample by measuring its interference with a reference SHG beam.

The three conditions required to optimize interferences are spatial overlap, temporal overlap, and identical polarization. In this setup, the use of a collinear geometry ensures the spatial overlap of the reference SHG with the sample SHG signal. Also, the two calcite wedges allow to correct for the group velocity dispersion introduced by the microscope and therefore provide the temporal overlap between the fundamental pulses at ω and the reference pulses at 2ω. Finally, the analyzer ensures that only the SHG with a specific polarization is detected on the photomultiplier tube. As a consequence, the modulation between the sample and the reference SHG beams is maximized compared to the background SHG signal, which ensures a high interferometric contrast.

To extract the interferometric term from the raw SHG images acquired with I-SHG setup, we subtract two raw images taken at π shifted reference phases:

$$I\left({\phi }_{ref}\right)-I\left({\phi }_{ref}+\pi \right)=4\sqrt{I_{ref}{I}_{\mathrm{samp}}}\cos \left({\phi }_{\mathrm{samp}}-{\phi }_{ref}\right)$$ (1)

where I_ref and I_samp are the reference and sample SHG intensities respectively and φ_ref and φ_samp their phases. This eliminates the background SHG signals (I_ref + I_samp), independent from the reference phase, and doubles the interferometric contrast. The acquisition of 24 pairs of images, with reference phase varying from 0° to 345° by 15° phase step, allows to interpolate the amplitude and relative phase of the interferometric contrast. For every pixel, we determine the reference phase corresponding to the maximum amplitude, which provides an image of the relative phase in the sample. As a convention, a red (resp. green) color will be assigned to the negative (resp. positive) phase values in all the following images.

The reference phase (φ_ref) is controlled by rotating the BK7 glass window. However, this requires to calibrate the nonlinear relationship between the glass plate angle and the resulting φ_ref values. To that end, we set another y-cut quartz plate in place of the sample in the focus of the objective. As only the relative phase is relevant here, the zero value for the reference phase was assigned to an arbitrary value. Rotating the glass plate allows to retrieve the typical interferometric pattern [Fig. 1(b)] as described by Stolle et al. [39], which provides the relative value of φ_ref for any glass plate angle.

2.3 Sample preparation

Samples were obtained from 8 weeks old male C57/Bl6 mice. The tails were harvested and fixed in 4% PFA for 6 to 8 hours at 4°C. Using a surgical scalpel, samples were cut in few mm pieces and tail tendon compartments were opened and exposed under a Nikon dissection scope with 0.7-83 zoom lens. After harvesting, tail tendons were embedded in OCT-compounds Tissue-Tek (Electron Microscopy Sciences, Hatfield, PA) and 10 µm section was cut using a Leica cryostat CM3000 (Leica Microsystems, Wetzlar, Germany). The sections were transferred onto a 150-µm thick coverslips (VWR International, West Chester, PA; 25_60 mm, No. 1) treated with 3-aminopropyltriethoxysilane or gelatin-chromium potassium sulfate solution (gelatin type A, and chromium potassium sulfate; both Sigma, St. Louis, MO) for optimal tissue adhesion.

3. Results

3.1 Fast I-SHG in periodically poled lithium niobate

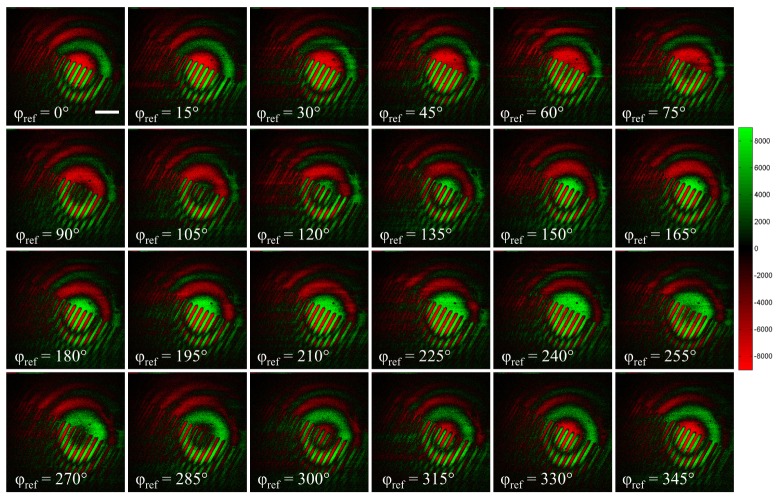
To validate our measurements, we used Periodically-Polled Lithium Niobate (PPLN) crystal as a model sample. Figure 2 shows the 24 subtraction images acquired. As expected, we directly observe different phases (represented in red and green), corresponding to the χ⁽²⁾ domains in PPLN. However, we also observed a circular pattern indicating variations of the relative phase within the field of view.

Fig. 2.

Subtraction stack obtained in PPLN sample. Red and green colors stand respectively for negative and positive values after the subtraction. Therefore, red and green colors reflect the sign of the cosine term in Eq. (1) and denote π phase shifted sample phase. Scale bar: 50µm.

This circular pattern is attributed to the dispersion introduced by the microscope objective. Indeed, using two galvanometric mirrors to acquire the image, we change the incident angle of the excitation beam on the back pupil of the objective. This changes the optical path within the microscope, in particular the objective, which is virtually equivalent to the rotation of the glass plate used to scan the phase. Therefore, when scanning the laser beam in the microscope, the phase shift between the reference and the sample beams varies from one pixel to another. This explain the circular pattern observed in Fig. 2 since a given incident angle corresponds to a constant dispersion. For a fixed φ_ref, the reference and pump beams are gradually phase shifted as we progress further from the center of the interferometric pattern, which eventually leads to destructive interferences appearing as black circles in Fig. 2.

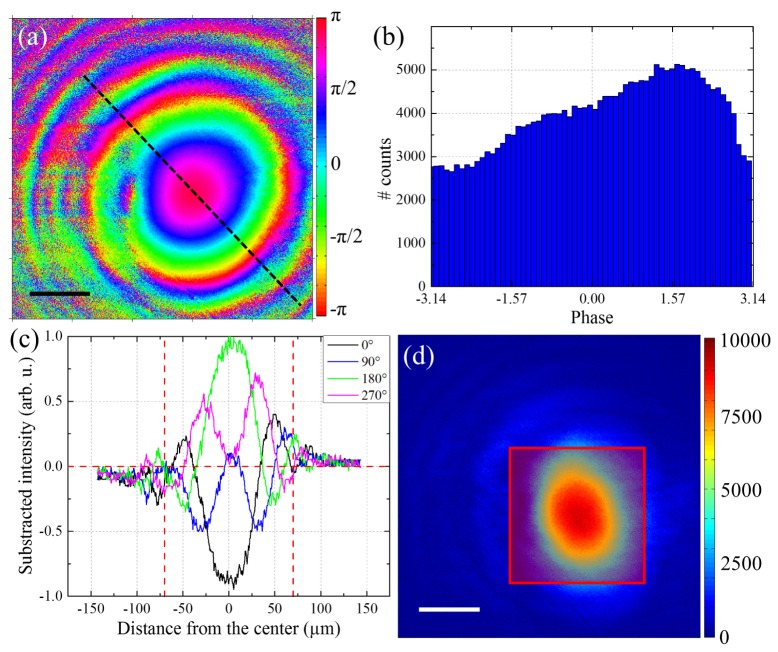
Interestingly, the phase shift introduced by the microscope depends only on the excitation geometry and not on the sample used. Therefore, using a known sample, it is possible to calibrate this effect and correct it in the phase image. This is achieved using another 350 µm y-cut quartz plate as a sample, the same configuration previously used for the calibration of the glass plate. Measuring the interference obtained between the signal generated in the reference and the sample quartz, we directly image the phase shift introduced during the laser scanning. Figures 3(a) and 3(b) show the resulting phase image and the corresponding phase histogram. In particular, Fig. 3(b) shows a very broad phase distribution, while an unbiased phase measurement would have showed a very narrow peak in such a crystalline sample. Figure 3(c) shows the profiles within the subtracted images, along the black dashed line in Fig. 3(a), for different reference phases (i.e. different positions of the glass plate). These profiles are very similar to the one shown in Fig. 1(b), which confirmed that changing the angle of the laser beam on the back pupil of the objective has a similar effect than the rotation of the glass window outside the microscope. All in all, the zero phase value in Fig. 1(b), chosen while calibrating the glass plate angle, can only recover the sample relative phase correctly in the center of the circular fringes in Fig. 3(a).

Fig. 3.

Impact of the sample scanning in phase measurement. a) Phase calibration in a sample quartz plate. b) Histogram of the relative phase measured in the sample quartz plate. c) Profile of the subtracted images, calculated along the black dashed line in (a), as a function of the distance from the center of the circular pattern, for various reference phases. d) Interferometric contrast in the field of view. Scale bars: 50µm.

In addition, Fig. 3(c) shows a decrease of the interferometric contrast as we progress further from the center of the circular pattern. This is due to the delay introduced by the microscope objective between the fundamental beam and the reference SHG. Importantly, the calcite wedges used to pre-compensate for the delay brought by the microscope, which optimizes the temporal overlap between fundamental and reference pulses, introduce the same correction in the whole field of view. This results in a maximum contrast in the center of the circular pattern, where the temporal overlap is optimized, as observable in Fig. 3(c), but a drastically decreased contrast in the border.

Figure 3(d) shows an image of the interferometric contrast (amplitude of the cosine modulation following Eq. (1) obtained in the sample quartz. As the contrast very rapidly decreases in the border of the image, it appears that only a small portion of the field of view can be effectively used to perform I-SHG. The size of the exploitable part of the image depends on the sample imaged. Indeed, in PPLN, the very well organized crystalline domains result in a very high interferometric contrast, which remains sufficient to extract the relative phase in a large field of view (approximately 200x200µm²). On the contrary, in biological tissues, the contrast is usually lower which imposes a sharper limit (typically 100x100µm²). Interestingly, the interferometric contrast obtained in the center of the image is similar to the one reported previously [38] using the sample scanning system. Therefore, this approach will be applicable in disorganized collagen structures such as skin or cartilage, but with a limited field of view. Finally, it is worth noting that the slightly elliptical shape observed in Fig. 3(d) is attributed to the chromatic aberrations introduced by the microscope objective, which results in a small spatial shift between the reference and the fundamental beam. Note that this spatial shift is likely to contribute to the decrease of contrast in the edge of the field of view.

3.2 Phase correction

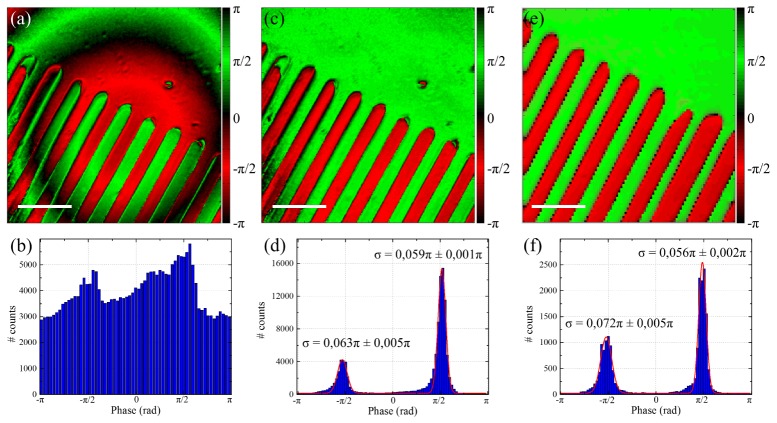
Measuring the phase introduced by the microscope allows to correct the phase images obtained with the laser scanning system. In all the following images, we limit our field of view to 100x100µm², where the interferometric contrast is sufficient to accurately extract the relative sample phase. Figures 4(a) and 4(b) show respectively the phase image and histogram obtained in PPLN. After a subtraction of the phase introduced by the microscope, we obtained the corrected phase image and histogram shown in Figs. 4(c) and 4(d). As the phase extracted is only relative, the actual position of the peaks is not relevant as it depends on the choice of the zero reference phase. However, the peak width is very important as it has been shown to provide information about the polarity of non-centrosymmetric structures in the sample [26,34]. Therefore, in all the following phase distribution, the origin of the phase was chosen to ensure that the two peaks are located at ± π/2. Using a bi-Gaussian fitting of the phase distribution in Fig. 4(d) we found the two peaks width to be σ = 0.063π ± 0.005π and σ = 0.059π ± 0.001π respectively.

Fig. 4.

Phase correction in PPLN. Phase a) image and b) histogram measured in PLLN sample before correction. Phase c) image and d) histogram after correction of the phase shift introduced by the microscope. Phase e) image and f) histogram measured in PPLN sample using the former sample scanning I-SHG setup. The red straight lines in d) and f) are bi-Gaussian fittings of the phase distributions used to retrieve the peaks width σ. Scale bars: 25µm.

To validate our phase correction, we compared our results to the ones obtained previously using the sample scanning I-SHG microscope [34]. Figures 4(e) and 4(f) show the phase image and histogram of the same PPLN sample (but not the exact same ROI) acquired with sample scanning instead of laser scanning. We obtained very similar results, especially for the peaks width σ = 0.072π ± 0.005π and σ = 0.056π ± 0.002π respectively. This demonstrates that the phase correction used with laser scanning allows to recover the exact phase distribution in the sample.

3.4 Fast I-SHG in tendon

To validate our approach in biological tissues, we measured the phase distribution in tendon. Using the sample scanning set-up, I-SHG microscopy has previously shown that in tendon the SHG phase is preserved over long distances in the fibril direction and switches very rapidly in the transverse direction [34]. Figure 5(a) shows the uncorrected phase image, obtained with the laser scanning system, in which the phase shift introduced by the microscope is directly observable. In particular we observe a sharp switch of the phase from –π/2 to π/2 (or vice versa) along the fibrils, which is in contradiction with the previous observation. Again, the region of interest is limited to 100x100µm² to maintain a high interferometric contrast in the whole image. Figure 5(b) shows the phase after correction. It shows that the correction allows to recover the expected behavior in the tendon images and therefore to extract the relative phase information in the whole image. It is worth noting that, since the phase correction to apply is determined in a crystalline sample, the accuracy of the relative phase measurement is not significantly modified compared to the former sample scanning.

Fig. 5.

Fast I-SHG imaging of a mice tail tendon. a) and b) Phase images before and after correction respectively. c) Corrected phase distribution obtained in tendon. Red straight line is the bi-Gaussian fitting used to retrieve the peaks width σ.

Finally, Fig. 5(c) shows the phase distribution in the corrected image. It is worth noting that this distribution is remarkably similar to the one obtained with sample scanning [34]. In particular, the bi-Gaussian fitting of the phase distribution provides the width of the two peaks σ = 0.218π ± 0.003π and σ = 0.247π ± 0.003π, which are in very good agreement with the previously reported values [34].

Importantly, images obtained with the galvanometric mirrors were acquired at 5s/frame, while, for the exact same field of view and pixel size, images were acquired at 195s/frame with the sample scanning system. Since image acquisition is 39 times faster with laser scanning than with sample scanning, the implementation of a laser scanning capable of retrieving an accurate phase in the sample is a significant improvement for I-SHG microscopy. Altogether, since we acquired here 36 images to extract the phase, the phase image in Fig. 4(c) was acquired in 180 seconds whereas the phase image in Fig. 4(e) was acquired in about 2 hours.

3.5 Optimization of the phase step

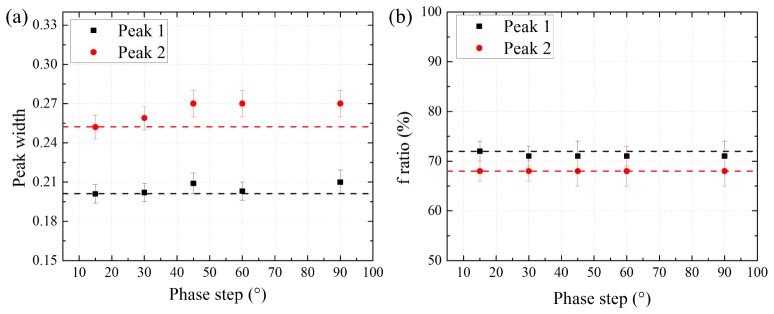
In addition, to reduce even more the imaging time, the number of images acquired can be significantly reduced. Indeed, Fig. 4(c) and e has been acquired using 15° reference phase step, which corresponds to 36 images. Increasing the phase step would reduce the number of images and therefore significantly decrease the imaging time. However, this might result in a decrease of the phase determination accuracy. To evaluate this effect we measured the width of the two peaks of the phase distribution from tendon sample as a function of the phase step. Results are displayed in Fig. 6(a), showing that the peak width does not change significantly, even with a phase step of 90° corresponding to only 6 images acquired.

Fig. 6.

Impact of the reference phase step on the peak width determination. a) Peak width measured in tendon as a function of the reference phase step used for the image acquisition. b) Ratio of fibrils pointing in opposite direction (f ratio) as a function of the reference phase step. Black squares and red circles correspond to the first peak (centered at –π/2) and the second peak (centered at π/2) respectively. Red and black straight lines indicate the more precise value obtained with a 15° reference phase step.

Finally, the peak widths measured in Fig. 6(a) allow to extract the ratio of fibrils pointing in opposite direction [34,38].

$$f=\frac{N\left(+{\chi }^{(2)}\right)}{N\left(+{\chi }^{(2)}\right)+N\left(-{\chi }^{(2)}\right)}$$ (2)

where N( + χ⁽²⁾), resp. N(-χ⁽²⁾), stands for the number of collagen fibrils having a positive, resp. negative, nonlinear susceptibility. Indeed, previous work has demonstrated that the f ratio is directly related with the width of the phase distribution. It is worth noting that the value of the f ratio extracted does not significantly change with the reference phase step, as shown in Fig. 6(b). Therefore, at least in tendon, only 6 images are required to probe efficiently the phase distribution, which, using the laser scanning and the phase correction, limits the imaging time to 30s.

5. Conclusion

We reported here the first implementation of fast I-SHG microscopy using a scanning system based on galvanometric mirrors. To that end, we calibrated the phase shift introduced by the scanning system in the microscope. As a proof of concept, we imaged the phase in periodically poled lithium niobate and showed that the phase correction allows to retrieve the expected phase distribution, in particular the peaks width. Finally, we successfully imaged the phase distribution in mice tail tendons which demonstrates that this set-up allows to probe efficiently the distribution of polarity in tissues with an imaging speed 39 times faster than the sample scanning. This imaging time improvement can be even push further to 234 by reducing the number of images acquired, without significant loss of precision. We anticipate that this improvement will serve as a significant enhancement to current I-SHG microscopy, allowing to image the phase variations in dynamical processes.