Assessing the imaging performance of light sheet microscopies in highly scattering tissues

Abstract

Light sheet microscopy (LSM) has emerged as an optical-imaging method for high spatiotemporal volumetric imaging of relatively transparent samples. While this capability has allowed the technique to be highly impactful in fields such as developmental biology, applications involving highly scattering thick tissues have been largely unexplored. Herein, we employ Monte Carlo simulations to explore the use of LSM for imaging turbid media. In particular, due to its similarity to dual-axis confocal (DAC) microscopy, we compare LSM performance to point-scanned (PS-DAC) and line-scanned (LS-DAC) dual-axis confocal microscopy techniques that have been previously shown to produce high-quality images at round-trip optical lengths of ~9 – 10 and ~3 – 4 respectively. The results of this study indicate that LSM using widefield collection (WF-LSM) provides comparable performance to LS-DAC in thick tissues, due to the fact that they both utilize an illumination beam focused in one dimension (i.e. a line or sheet). On the other hand, LSM using confocal line detection (CL-LSM) is more analogous to PS-DAC microscopy, in which the illumination beam is focused in two dimensions to a point. The imaging depth of LSM is only slightly inferior to DAC (~2 – 3 and ~6 – 7 optical lengths for WF-LSM and CL-LSM respectively) due to the use of a lower numerical aperture (NA) illumination beam for extended imaging along the illumination axis. Therefore, we conclude that the ability to image deeply is dictated most by the confocality of the microscope technique. In addition, we find that imaging resolution is mostly dependent on the collection NA, and is relatively invariant to imaging depth in a homogeneous scattering medium. Our results indicate that superficial imaging of highly scattering tissues using light sheet microscopy is possible.

1. Introduction

Light sheet fluorescence microscopy (LSM) has emerged as an important optical-imaging technique that provides some degree of optical sectioning and rejection of out-of-focus light for relatively transparent specimens, but with the added benefit of improved imaging speeds, reduced photobleaching, and larger fields of view as compared to alternatives such as confocal laser scanning microscopy (CLSM) and two-photon microscopy [1]. To date, LSM has had the most impact in fields such as developmental biology, where studies have focused primarily on the imaging of transparent or optically cleared specimens due to geometric constraints (i.e. only small samples may be mounted in a gel and imaged at the intersection of orthogonally arranged illumination and collection beams), and degradation of image quality due to beam-steering and light scattering [2–7]. Due to these limitations, there has been little investigation into the feasibility of using LSM to image samples that are highly scattering, such as most human tissues. However, the LSM imaging geometry is similar to dual-axis confocal (DAC) microscopy methods (both may be viewed as natural developments of the confocal theta microscope proposed by Stelzer et. al. [8]), which have successfully been utilized for reflectance and fluorescence imaging of thick, highly scattering tissues in a number of ex-vivo and in-vivo studies [9–14]. Furthermore, recent reports have demonstrated LSM in novel “open-top” or “inverted” imaging geometries that are more compatible for the imaging of conventionally mounted specimens of arbitrary size [15–17], as well as the use of confocal line detection for improved contrast in scattering samples [18]. Given these recent developments in LSM, the similarity of LSM to DAC microscopy, and the ability of DAC microscopy to provide high-quality fluorescence images of highly scattering tissues, here we assess the performance of LSM for imaging large and highly scattering in-vivo and ex-vivo tissues using Monte Carlo simulations.

2. DAC and LSM imaging geometries

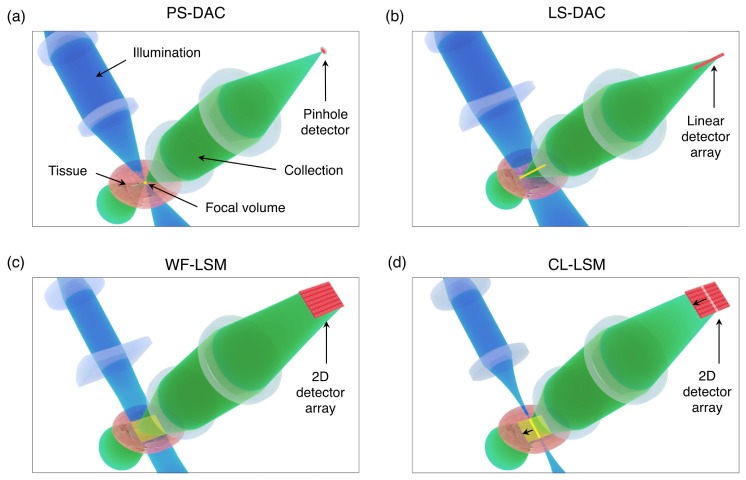
To highlight the similarity between the DAC and LSM techniques, we present representative illustrations of a point-scanned dual-axis confocal microscope (PS-DAC), line-scanned dual-axis confocal microscope (LS-DAC), wide-field detection light-sheet microscope (WF-LSM), and confocal line detection light-sheet microscope (CL-LSM) in Fig. 1.

Fig. 1.

The illumination, collection, focal volume, and detector configurations for the PS-DAC, LS-DAC, WF-LSM, and CL-LSM microscope geometries. In (a), the PS-DAC geometry uses a moderate numerical aperture to illuminate a single point within the tissue, and a similar collection NA to image that point to a pinhole detector. In (b), the LS-DAC geometry uses a moderate illumination NA focused to a line, rather than a point within the tissue volume. This focal line is then imaged onto a linear detector array. In (c), the WF-LSM geometry uses a low illumination NA to provide a sheet of illumination (a low-NA line focus) within the tissue volume, which is imaged with a higher NA onto a two-dimensional (2D) image sensor. In (d), the CL-LSM geometry is shown, in which an illumination sheet identical to that in (c) is created over time by scanning a low-NA point-focused illumination beam, which is synchronized with the rolling shutter (line-by-line acquisition) of a 2D image sensor.

In Fig. 1(a), the geometry for a PS-DAC system is shown. A moderate illumination and collection numerical aperture (NA) ~0.15 – 0.25 are used to illuminate and collect signal from a point within the tissue, and to image that focal point onto a pinhole detector, respectively. This configuration is fully confocal in all three dimensions, but images only a point and requires scanning in two dimensions to build a two-dimensional (2D) image. The LS-DAC geometry is shown in Fig. 1(b). Again a moderate illumination NA ~0.15 – 0.25 (is utilized. However, in this case, a line focus is illuminated within the tissue volume (by using cylindrical focusing optics), which is imaged onto a linear detector array. In this case, the focal line only needs to be scanned in one dimension to build a 2D image, allowing for increased imaging speeds at the cost of a loss in confocality along one dimension. In Figs. 1(c) and 1(d), the WF-LSM and CL-LSM configurations are shown. For both, a low illumination NA < 0.10 is used to provide a sheet of illumination with a long depth of focus within the tissue while a moderate or high NA (greater than the illumination NA) is used for collection. For WF-LSM, the illumination sheet is created directly with cylindrical optics or indirectly by scanning a spherically focused beam [19], and a 2D image is captured of the entire light sheet. The CL-LSM configuration is analogous to WF-LSM using a scanned beam, except in this case the scan is synchronized with the rolling shutter (line-by-line acquisition) of a 2D detector array to indirectly image a sheet within the tissue, where the successive lines of active pixels during the camera readout serve as linear-array detectors. The benefit of this latter configuration, in comparison to WF-LSM, is that confocal detection is achieved along two dimensions (all except the illumination axis) [18].

3. Methods

3.1 A generalized imaging geometry for Monte Carlo simulations

Given the similarities of the DAC and LSM configurations, the generalized imaging geometry shown in Fig. 2 can be used to describe all four techniques for simulation purposes. An illumination beam enters the tissue from the left, exciting fluorescence, which is collected to the right by a collection lens. The NA of the illumination and collection paths are given by NA_i and NA_c respectively, and the half-crossing angle of both beams relative to the normal of the tissue, θ, is 45 degrees, i.e. the illumination and collection are perpendicular to one another, a fundamental property of LSM. This differs slightly from the previously reported DAC methods, in which θ = 30 degrees, but for the purposes of comparison using the generalized imaging geometry, in this study θ = 45 degrees was used for all DAC and LSM simulations [9–14, 20, 21]. Therefore, the only fundamental differences between the four imaging methods lies in the shape of the illumination beam (point focusing for PS-DAC and CL-LSM vs. line focusing for LS-DAC and WF-LSM), the detection scheme (see Fig. 1), and the illumination numerical aperture, NA_i (although NA_c may also vary slightly). For a Gaussian beam, the NA dictates the radius of the beam waist, w_o = λ/πNA, and the Rayleigh range, z_R = w_o²π/λ, which provides a measure of the depth of focus (given by 2z_R) along the illumination axis, z_i. As is well-known for Gaussian beams, there exists a fundamental trade-off between the thickness and depth of focus of the beam, which is plotted in Fig. 3. Note that while there is a dependence of both parameters on the wavelength (λ), a single wavelength of 500 nm was used as a representative wavelength for all cases in this study.

Fig. 2.

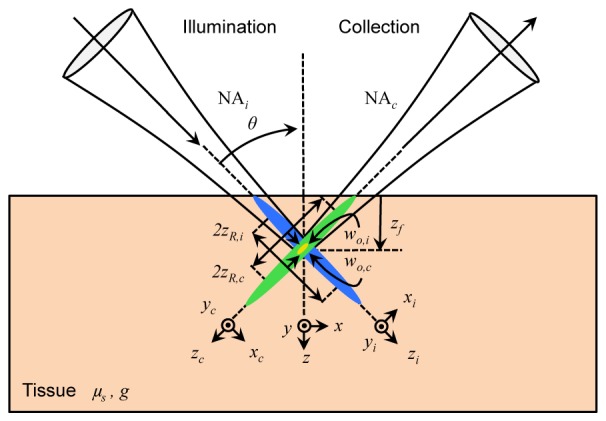
The general microscope geometry for the DAC and LSM methods is shown. The illumination beam (blue) enters the tissue from the left, at an angle θ from the normal, along the illumination coordinate axes denoted by x_i, y_i, and z_i. Similarly, light is collected (green) to the right at an angle θ from the normal, along the collection coordinate axes x_c, y_c, and z_c. The effective focal volume is shown for illustrative purposes (yellow). The numerical aperture of each optical path is given by NA_i and NA_c respectively, which dictates the corresponding beam waists, w_o,i and w_o,c and Rayleigh ranges z_R,i and z_R,c. Both beams are focused at a depth, z_f, into tissue with scattering coefficient μ_s, and scattering anisotropy, g. The coordinate axes of the tissue are given by x, y, and z.

Fig. 3.

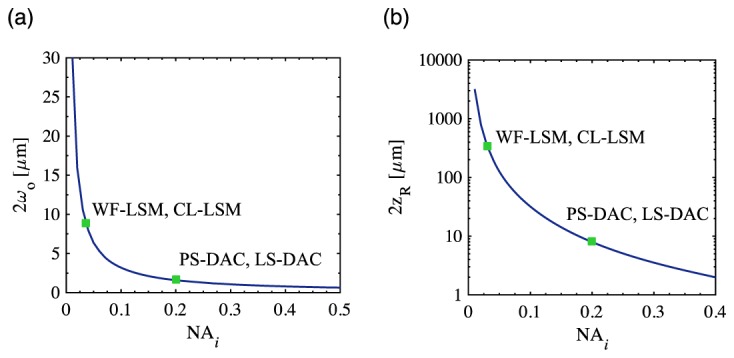
In (a) and (b), the illumination beam thickness, 2w_o and depth of focus, 2z_R are plotted for the PS-DAC, LS-DAC, WF-LSM, and CL-LSM microscope geometries, respectively.

The NAs used for the simulations of each microscope geometry, and the corresponding beam waists and Rayleigh ranges are denoted in Fig. 3 and summarized in Table 1. For the PS-DAC geometry, NA_i and NA_c of 0.20 were used, similar to previous reports [9–13]. The LS-DAC geometry was identical to the PS-DAC geometry, except that in this case (as described previously) a line of illumination was used, i.e. focusing was performed in the x_i dimension only, which allows for direct imaging along the y_i dimension [14, 20, 21]. Similarly, for WF-LSM, a low NA_i of 0.03 (focused only in the x_i dimension), coupled to a higher collection NA_c of 0.30 was used, similar to what has been used previously by other groups [2–4, 16]. This reduction in NA_i results in an extended Rayleigh range (z_R,i) along the z_i axis which allows for the direct imaging of a 2D sheet oriented in the y_i-z_i plane, with a correspondingly larger beam waist (w_o,i). Finally, the CL-LSM geometry is similar to the WF-LSM geometry, except that the illumination beam is now focused along both the x_i and y_i dimensions, and is scanned along the y_i direction in order to create an indirect light sheet over time. For CL-LSM, it is assumed that a rolling shutter is used for line-by-line confocal imaging of a light sheet [18, 22, 23]. Irrespective of the NAs, the geometric focus of the illumination and collection beams are centered at a focal depth, z_f, inside a thick tissue with a scattering coefficient, μ_s, and scattering anisotropy, g. For this study, a range of focal depths were studied to assess imaging performance as a function of depth in tissue (50 – 450 μm in 50 μm increments), the scattering coefficient was assumed to be 10 mm⁻¹, and the scattering anisotropy 0.9, which are representative of a generic human tissue [24]. For generalization to other scattering properties and imaging depths, the focal depth and scattering coefficient can also be incorporated into a dimensionless optical length, defined as L = 2μ_sz_f, which is equal to the total number of mean free paths traversed by ballistic photons on a perpendicular round-trip path from the tissue surface to the focus. The values of z_f and μ_s used in this study correspond to optical lengths of L = 1, 3, 5, 7, and 9. Finally, simulations were also performed in the absence of a tissue sample (no scattering) to assess the ideal performance of each microscope geometry, i.e. L = 0. Note that for simplicity, the refractive index mismatch between the tissue and the surrounding air was not modeled, i.e. only the effects of tissue scattering on ideally focused beams were investigated and aberrations were not considered.

Table 1. Summary of simulation parameters used for each microscope geometry at λ = 500 nm.

Microscope geometry	Refs.	Focusing direction(s)	NAi,	2wo,i [μm]	2zR,i [μm]	NAc	2wo,c [μm]	2zR,c [μm]
PS-DAC	[9–13]	xi and yi	0.20	1.60	7.96	0.20	1.60	7.96
LS-DAC	[14, 20, 21]	xi only	0.20	1.60	7.96	0.20	1.60	7.96
WF-LSM	[2–4, 16]	xi only	0.03	10.62	353.68	0.30	1.06	3.54
CL-LSM	[18, 22, 23]	xi and yi	0.03	10.62	353.68	0.30	1.06	3.54

3.2 Simulation architecture

Previous Monte Carlo characterizations of DAC performance in scattering media have utilized a commercially available optical simulation software (FRED, Photon Engineering, Tucson, AZ) [11, 25, 26]. This approach has the advantage that accurate ray tracing can be performed along an entire optical circuit (from source to detector), modeling aberrations intrinsic to a specific optical system. However, the software cannot model the diffraction effects of a focused Gaussian beam while running in a Monte-Carlo simulation mode (i.e., the rays in a transparent medium will not be distributed within a finite beam waist, but will instead converge to an exact focus, which is not realistic). While the effects of a diffraction-limited spot size in a scattering medium may be negligible in the fully diffuse regime (L >> 10), for the optical lengths investigated in this study (L ≤ 9) the light transport contains a mixture of ballistic and diffuse light, and accurate modeling of the finite Gaussian spot size provides more accurate results. Furthermore, since FRED is not well equipped to model fluorescence in an efficient manner, only reflectance-based imaging was modeled in previous studies. While this previous method was amenable to experimental validation (e.g. with Intralipid and bead phantoms) [27], our current study utilizes an alternative approach to model the performance of a fluorescence-based system.

A number of Monte Carlo codes have been developed for the simulation of light transport in scattering media, (e.g., MCML, MCX, MMC) [28–30]. However, here we employ the GEANT4 architecture for medically oriented simulations (GAMOS) due to its flexibility, ease of use, and recent extension to tissue optics [31, 32]. In particular, we have further extended its functionality to microscopy applications by incorporating a ray-optic model that accurately simulates the propagation of a focused Gaussian beam. The details of the method for modeling a focused beam are provided elsewhere, but in short, an accurate focused Gaussian spot is generated by modeling the positional and directional distribution of the rays at the pupil plane and beam focus [33, 34]. To validate this Gaussian-modeling method, we simulated the 2D irradiance distribution for a focused Gaussian beam in air with NA_x = NA_y = 0.10 at λ = 500 nm, and compared it to the analytical form of the beam intensity predicted by Gaussian beam optics. The results are shown in 4(a). The expected beam waist, w_o = 1.59 μm is in close agreement with the simulated beam waists in the x and y directions, w_o,x = w_o,y = 1.60 μm.

To accurately and efficiently model fluorescence detection, we employed the widely used adjoint method [35–37], in which the illumination and collection beams are both treated as illumination beams, and the product of the simulated illumination beam irradiance profile, S_i, and collection beam profile, S_c, at every image voxel yields the point spread function, S_i,c (PSF) of the microscope in the presence of scattering. For each simulation, we recorded the response functions in a 100 × 100 × 100 μm³ scoring volume, with a voxel size of 0.25 × 0.25 × 0.25 μm³ and 10⁶ total rays. Each S_i or S_c simulation was run on a computer running Linux (single processor - AMD Opteron 4386, 3.1GHz), with a simulation time ranging from 3 – 24 minutes depending on the given focal depth and NA. Finally, we calculated 3D PSFs for each imaging method as a function of the various optical lengths, S_i,c(x,y,z,L). A representative schematic of the adjoint method is shown in Fig. 4(b).

Fig. 4.

In (a), using a ray-optics model that accurately simulates Gaussian beam profiles, the irradiance profile is simulated at the focal plane of a beam with NA_x = NA_y = 0.10 at λ = 500 nm, along with plots of the x and y line profiles through the focus. The measured beam waists, w_o,x = w_o,y = 1.60 μm, are in close agreement to the expected beam waist of 1.59 μm. In (b), the principle of the adjoint method is shown, where the PSF, S_i,c is calculated by multiplying the illumination fluence, S_i, by the reversed collection fluence, S_c.

3.3 PSF analysis

To evaluate the effect of scattering on resolution, line profiles along the x, y, and z axis through the center of various simulated PSFs were plotted. The full-width at half-max (FWHM) width of the PSFs were quantified as a function of optical scattering. It is important to note that while in traditional LSM studies, the response is often analyzed along the x_i,c, y_i,c and z_i,c directions, when imaging in a thick tissue using an “open-top” or “inverted” configuration, the response in the tissue’s x, y, and z coordinates is more appropriate to evaluate. In addition, to evaluate the optical-sectioning performance of each microscopy geometry, the axial response of the system to a planar object was calculated by summing the PSF in the x-y plane, and plotting this sum as a function of axial distance, z, from the focal plane for each optical length, thus yielding S_i,c(z,L) for each microscope geometry. This is analogous to the axial response (reflectance) to a plane mirror, except in this case the axial response to a thin fluorescence sheet is simulated. Finally, the signal-to-background ratio (SBR) was evaluated by taking the ratio of S_i,c at the focus, and at the end of the axial scan where the planar sheet is translated far from the focus (i.e. the ‘signal’ is considered the peak value of the PSF, and the ‘background’ is taken as the value of the PSF at the edge of the axial scan).

3.4 Fluorescent bead phantom

Since the adjoint-method Monte Carlo simulations yield a full 3D PSF, it is possible to calculate the response of the modeled systems to any arbitrary fluorescence source distribution. In particular, it is straightforward to simulate the imaging response to a fluorescent bead phantom, a technique that has been commonly used experimentally in LSM and other methods to evaluate the effects of scattering and other parameters on microscope performance [38–41]. To realize this, we initialized a digital phantom, P(x,y,z), with a scattering coefficient and anisotropy analogous to that of the tissue phantom used to generate the PSFs (μ_s = 10 mm⁻¹, g = 0.9), which is 200 × 200 × 450 μm³ in size, with a voxel size of 0.25 × 0.25 × 0.25 μm³. The values at all voxels were first set to 0 (i.e. no fluorescence), and sub-resolution fluorescent beads were then randomly distributed inside the phantom by setting groups of voxels to 1 at a “concentration” of 1% v/v. With the voxel size in all simulations set to 0.25 μm, this is equivalent to using 250 nm diameter beads, which is below the diffraction limit at the NA_c values used in this study. The simulated imaging performance for each microscopy geometry can then be approximated by convolving the PSF at a given optical length, L_p (or depth, z_p) with the phantom: I(x,y,z) = P(x,y,z_p) ∙ S_i,c(x,y,z,L_p). The contrast as a function of z_p was then evaluated over the entire xy plane as C = (I_max - I_min)/(I_max + I_min) for each microscope geometry.

3.5 Varying illumination and collection numerical aperture

In order to fully explore the parameter space of the generalized imaging geometry, simulations were also executed to calculate the PSF as a function of optical length for a wider array of illumination and collection numerical aperture combinations (NA_i = 0.01, 0.03, 0.05, 0.07, and 0.09 and NA_c = 0.10, 0.20, 0.30, 0.40, and 0.50). The FWHM of the resulting PSFs were calculated to assess the effect of NA_i or NA_c on resolution, and the fluorescent bead phantom procedure described in Sec. 3.4 was used to assess the effect of NA_i or NA_c on the imaging contrast.

4. Results

4.1 Effect of scattering on PSF

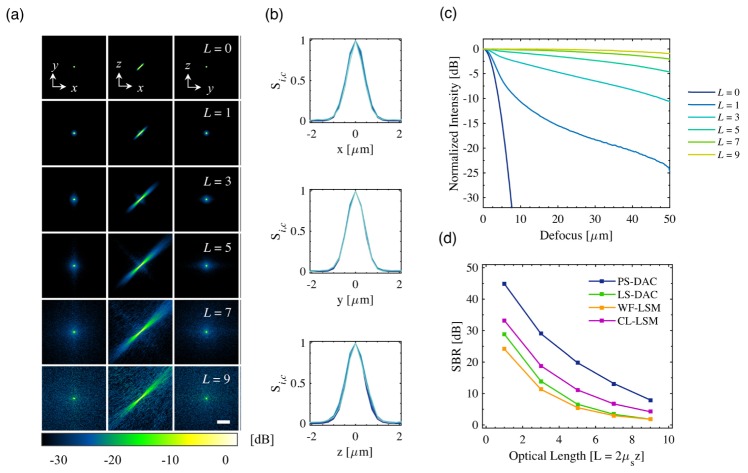
The PSF results for the WF-LSM microscope geometry are shown in Fig. 5. The self-normalized x-y, x-z, and y-z cross-sections of the PSF for all optical lengths are shown in Fig. 5(a) from −30 to 0 dB (10log₁₀) scale). In the x-z plane, the asymmetric PSF is due to the large difference in NA_i and NA_c and corresponding 2w_o,i and 2w_o,c (10.62 and 1.06 μm respectively). As expected, as the optical length is increased, the corresponding background signal around the original PSF grows both in magnitude and extent due to increased optical scattering. However, as has been shown previously using Monte Carlo simulations of DAC microscope geometries, analysis of the PSF along the x, y, and z axes reveals that the full-width at half-maximum (FWHM) in all three directions does not degrade with increasing optical length, FWHM_x = 0.98 ± 0.04 μm, FWHM_y = 0.97 ± 0.07 μm, FWHM_z = 0.98 ± 0.04 μm [25, 26]. The corresponding fluorescence axial scan, S_i,c(z,L), for the WF-LSM geometry is plotted in Fig. 5(c). As can be seen on the dB scale, the background signal outside of the central lobe of the PSF increases as a function of optical length. A corresponding decrease in the SBR is apparent as the optical length is increased. Similar results as those shown in Figs. 5(a)-5(c) were obtained for the other three imaging geometries. This information, for all four microscope geometries, can be summarized by plotting the SBR as a function of optical length, as shown in Fig. 5(d). The highest SBR is achieved by the PS-DAC geometry, followed by the CL-LSM, LS-DAC, and WF-LSM geometries.

Fig. 5.

In (a), the PSFs, S_i,c(x,y,z,L), are shown for the WF-LSM geometry. Each is self-normalized and displayed on a dB scale (10log₁₀) down to −30 dB (10⁻³). In (b), the corresponding x, y, and z line profiles through the focus are plotted for each optical length, L. The corresponding axial scans S_i,c(z,L) are shown in (c). In (d), the contrast (SBR) of the PS-DAC, LS-DAC, WF-LSM, and CL-LSM are plotted as a function of optical length. The scale bar in (a) represents 20 μm.

3.2 Effect of scattering on imaging contrast

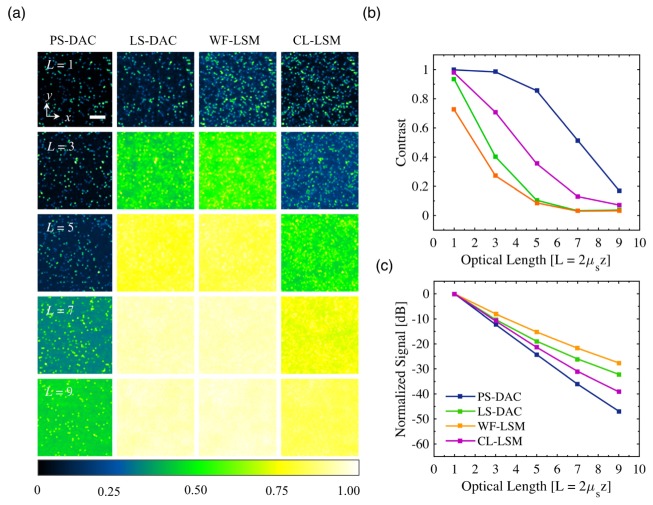
The results of the simulated fluorescent bead phantom images are shown in Fig. 6(a) for the PS-DAC, LS-DAC, WF-LSM, and CL-LSM microscope geometries at optical lengths of L = 1, 3, 5, 7, and 9. Each image is self-normalized such that the maximum pixel value is equal to 1. The images reveal a number of interesting features. As expected from the SBR plot, the PS-DAC geometry is able to maintain the highest contrast even at an optical length of 9. Although the contrast is reduced due to the increasing background, the beads are still visible. This is in comparison to the LS-DAC and WF-LSM geometries, where an image of equivalent contrast is reached at an optical length of just 3. By re-establishing confocality in the y dimension, the CL-LSM microscope geometry is able to obtain better contrast relative to the WF-LSM microscope geometry. An image of comparable contrast to the WF-LSM at an optical length of 3 is obtained by the CL-LSM at an optical length of 5. However, with the exception of the PS-DAC geometry, all other geometries are unable to form a usable image past an optical length of 5. The resulting plot of contrast as a function of optical length, calculated from the planar fluorescent bead images, is shown in Fig. 6(b). Finally, in Fig. 6(c) the un-normalized peak signal of the PSFs of each microscopy geometry is plotted as a function of optical length. For the PS-DAC configuration, the peak signal decays exponentially at a rate of 1/(Lcosθ) corresponding to exponential attenuation (Beer-Lambert law) due to scattering of the ballistic photons. On the other hand, the rate of peak-signal decay is decreased for the CL-LSM, LS-DAC, and WF-LSM systems (deviation from Beer-Lambert law decay) due to increased collection of background photons as the optical length is increased.

Fig. 6.

For each microscopy method, x-y sections of a fluorescent bead phantom, convolved with the appropriate PSF, are shown in (a), self normalized to a maximum value of 1.0. In (b) and (c), the calculated contrast of the images is plotted, as well as the decay in the peak signal of the PSFs as a function of optical length. The scale bar in (a) represents 20 μm.

4.3 Effect of illumination and collection numerical aperture

The FWHM of the PSFs as a function of the array of NA_i and NA_c combinations are shown in Table 2 for the x, y, and z directions respectively. As in the representative case shown in Fig. 5, the FWHM is largely independent of scattering and optical length. The standard deviation in FWHM across all optical lengths for each configuration is denoted in the table. While the results for the resolution as a function of the NAs in Table 2 is for WF-LSM specifically, the results for the CL-LSM configuration are equivalent (except for a slight change in FWHM along the y axis due to the difference between a cylindrically or spherically focused illumination beam). This slight difference has been discussed previously for PS-DAC and LS-DAC microscopes [20]. Table 2 also highlights that for the LSM regime (i.e., NA_i < NA_c) the FWHM is dictated mostly by the higher NA_c.

Table 2. Summary of the FWHM values as a function of NA_i and NA_c for WF-LSM for the x (top), y (middle), and z (bottom) directions.

		NAc
FWHM [μm]		0.10	0.20	0.30	0.40	0.50
NAi	0.01	x: 2.81 ± 0.07 y: 2.82 ± 0.17 z: 2.78 ± 0.07	1.43 ± 0.04 1.36 ± 0.03 1.43 ± 0.06	0.96 ± 0.03 0.97 ± 0.07 1.00 ± 0.05	0.77 ± 0.01 0.75 ± 0.01 0.77 ± 0.06	0.66 ± 0.01 0.65 ± 0.01 0.64 ± 0.06
	0.03	2.74 ± 0.14 2.82 ± 0.17 2.69 ± 0.12	1.37 ± 0.05 1.36 ± 0.03 1.38 ± 0.07	0.98 ± 0.04 0.97 ± 0.07 0.98 ± 0.04	0.76 ± 0.03 0.75 ± 0.01 0.76 ± 0.05	0.65 ± 0.03 0.65 ± 0.01 0.65 ± 0.05
	0.05	2.64 ± 0.19 2.82 ± 0.17 2.59 ± 0.16	1.36 ± 0.04 1.36 ± 0.03 1.36 ± 0.07	0.94 ± 0.04 0.97 ± 0.07 0.97 ± 0.04	0.77 ± 0.02 0.75 ± 0.01 0.81 ± 0.05	0.66 ± 0.02 0.65 ± 0.01 0.72 ± 0.04
	0.07	2.50 ± 0.23 2.82 ± 0.17 2.48 ± 0.21	1.34 ± 0.03 1.36 ± 0.03 1.34 ± 0.05	0.93 ± 0.03 0.97 ± 0.07 0.96 ± 0.03	0.76 ± 0.02 0.75 ± 0.01 0.77 ± 0.05	0.65 ± 0.02 0.65 ± 0.01 0.66 ± 0.04
	0.09	2.32 ± 0.24 2.82 ± 0.17 2.34 ± 0.29	1.32 ± 0.02 1.36 ± 0.03 1.34 ± 0.05	0.93 ± 0.02 0.97 ± 0.07 0.97 ± 0.05	0.76 ± 0.01 0.75 ± 0.01 0.76 ± 0.07	0.65 ± 0.01 0.65 ± 0.01 0.66 ± 0.06

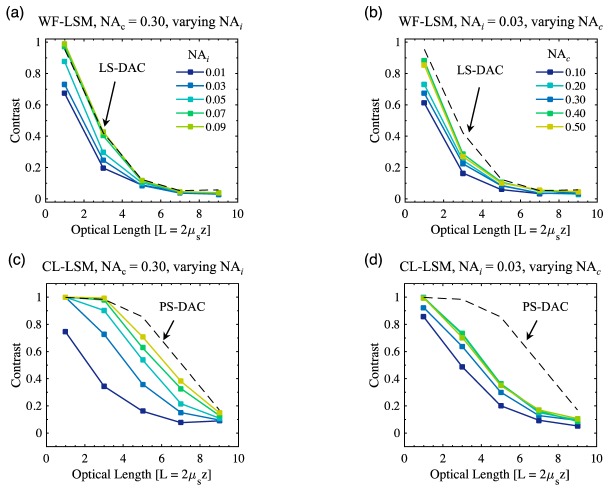
The contrast values as a function of optical length in the fluorescent bead phantom for WF-LSM and CL-LSM are shown in Fig. 7, for various combinations of NA_i and NA_c. For WF-LSM, using a fixed NA_c = 0.30 with an increasing NA_i from 0.01 to 0.09 provides performance that approaches that of the LS-DAC case, in which NA_i = NA_c = 0.20. The corresponding results for a fixed NA_i = 0.03, while varying NA_c from 0.10 to 0.50, are shown in Fig. 7(b). While the performance is increased as a function of increasing NA_c, the improvement is less dramatic than the improvement due to an increase in NA_i.

Fig. 7.

Image contrast values as a function of optical length in the fluorescent bead phantom are plotted for: (a) WF-LSM as a function of NA_i for a fixed NA_c = 0.30, (b) WF-LSM as a function of NA_c for a fixed NA_i = 0.03, (c) CL-LSM as a function of NA_i for a fixed NA_c = 0.30, (b) CL-LSM as a function of NA_c for a fixed NA_i = 0.03. For (a-b), the dashed line represents the performance of LS-DAC where NA_i = NA_c = 0.20, and in (c-d) the dashed line represents the performance of PS-DAC where NA_i = NA_c = 0.20.

Similar results for CL-LSM are shown in Figs. 7(c) and 7(d). For a fixed NA_c = 0.30, increasing NA_i from 0.01 to 0.09 shows performance which approaches that of the PS-DAC case where NA_i = NA_c = 0.20. Again, although the imaging performance is improved by increasing NA_c at a fixed NA_i = 0.03, the improvement is not as significant as increasing NA_i. Therefore, for LSM, contrast is dictated mostly by NA_i, which is typically much lower than NA_c.

4. Discussion and conclusions

We have utilized Monte Carlo simulations to quantitatively assess the performance of LSM in comparison to previous DAC methods for the imaging of highly scattering tissues. By using a customized version of the GAMOS tissue-optics plug-in to GEANT4, the responses of LSM and DAC microscope geometries have been modeled with the ability to account for the finite spot size of a focused Gaussian beam, as well as fluorescence detection (using the adjoint method). In agreement with previous studies, the results of this study show minimal change in the FWHM of the PSFs in the x, y, and z directions as a function of increasing optical length. For a LSM system, the FWHM is instead dictated primarily by NA_c, as is highlighted by the results presented in Table 2. Finally, for all imaging geometries, as would be expected, the contrast (SBR) was found to decrease significantly with increasing optical length, as is shown in Fig. 5(d).

It is often difficult to visualize how optical simulations translate to actual imaging performance. Therefore, due to the fact that the adjoint method used in this study results in a full 3D PSF, the PSFs for each imaging method were convolved with a digital phantom containing sub-resolution fluorescent beads to produce in-silico imaging results. This is similar to the methodology of a recent study by Abdellah et. al. on the development of a computational workflow for in-silico analysis of LSM for brain models [42]. The simulated images of this study were used to generate plots of image contrast (SBR) as a function of optical length, which highlights the achievable imaging depth in tissue for each microscope geometry. For PS-DAC microscopy, the maximum imaging depth was found to be approximately ~9 – 10 round-trip optical lengths, in agreement with previous experimental reports where images were obtained to a depth of ~450 – 500 μm in esophageal tissue (assuming a scattering coefficient of ~10 mm⁻¹) [11]. For LS-DAC microscopy, the ultimate imaging depth was found to be ~3 – 4 optical lengths, also in agreement with a recent experimental study where a LS-DAC system was able to image down to an optical length of ~4 in ex-vivo mouse tissue [20]. While there exists no thorough experimental studies in highly scattering tissues for which the WF-LSM simulations can be compared, the results suggest that imaging performance would be comparable to LS-DAC (in that an ultimate imaging depth of ~2 – 3 optical lengths may be achieved). However, the resolution of a WF-LSM microscope in the z direction would be degraded slightly due to the asymmetric, elongated PSF shown in Fig. 5(a). This is somewhat visible in Fig. 6(a), where the optical sectioning of the WF-LSM system at an optical length of 1 is worse than that of the LS-DAC system (i.e., more out-of-plane beads are visible).

The CL-LSM method exhibits significantly improved imaging performance and rejection of background signal, compared with the LS-DAC and WF-LSM methods, due to additional confocality in the y dimension. This allows for deeper imaging down to optical lengths of ~6 – 7, or an approximate doubling in contrast at any given optical length over WF-LSM. This is in agreement with initial reports comparing CL-LSM to WF-LSM [43]. Therefore, while NA_i has an impact on the image contrast, and NA_c primarily dictates the resolving power of the various microscope geometries, the limiting factor when imaging in thick tissues is the suppression of background signal that can be achieved by introducing confocality along various dimensions. Interestingly, in this study this takes the form of a first tier of imaging performance for PS-DAC and CL-LSM, where there is confocality in the x, y, and z dimensions, and a second tier for LS-DAC and WF-LSM, where there is only confocality in the x and z dimensions (see Fig. 7). However, in the case of WF-LSM and CL-LSM, the illumination NA is reduced, which allows for extended imaging along the z_i axis, at the cost of reduced image contrast compared to the corresponding DAC microscopy methods.

In terms of practical design considerations, it is apparent that there exist inherent tradeoffs between speed, contrast, and imaging depth for a potential DAC or LSM microscope. For example, due to point collection, PS-DAC offers the best contrast, but will have limited imaging speed due to the need to scan in 2D, whereas WF-LSM and CL-LSM offer the worst contrast, but enable fast imaging speeds and the ability to obtain 3D images with only 1D scanning. Therefore, the results in this study suggest that while the ultimate imaging depth may be reduced, volumetric superficial imaging in thick, highly scattering tissues is possible using either the WF-LSM or CL-LSM imaging geometry.

One limitation in the current study is the assumption of a homogenous scattering medium. Although this assumption is commonly made for optical Monte Carlo simulations in both the ballistic and diffuse regime, beam steering due to inhomogeneous scatterers (e.g. organelles, glands, and vascular structures) is a known phenomenon that is difficult to model in a traditional ray-tracing Monte Carlo simulation, but has been investigated using various alternative methods [27, 44–48]. In addition, note that our results assume that the imaging is limited by SBR (contrast) and not limited by SNR (a photon-limited situation). However, in certain cases, especially when imaging weak fluorescent structures, the imaging depth may be limited by insufficient signal (poor SNR), rather than too much background (poor SBR), and the optical throughput of the imaging system should therefore be considered. Finally, alternative illumination schemes other than the Gaussian beams modeled within this study have also been reported in the literature (structured illumination, Bessel and Airy beams, multi-photon, etc.) [49–52], which may be explored using similar methodologies in future studies.