Scanning, non-contact, hybrid broadband diffuse optical spectroscopy and diffuse correlation spectroscopy system

Abstract

A scanning system for small animal imaging using non-contact, hybrid broadband diffuse optical spectroscopy (ncDOS) and diffuse correlation spectroscopy (ncDCS) is presented. The ncDOS uses a two-dimensional spectrophotometer retrieving broadband (610-900 nm) spectral information from up to fifty-seven source-detector distances between 2 and 5 mm. The ncDCS data is simultaneously acquired from four source-detector pairs. The sample is scanned in two dimensions while tracking variations in height. The system has been validated with liquid phantoms, demonstrated in vivo on a human fingertip during an arm cuff occlusion and on a group of mice with xenoimplanted renal cell carcinoma.

1. Introduction

Diffuse optical spectroscopies [1] have demonstrated their feasibility for non-invasively monitoring in vivo tissue hemodynamic changes. Diffuse optical spectroscopy (DOS) provides information about microvascular total haemoglobin concentration, blood oxygen saturation, tissue scattering and other chromophores. Diffuse correlation spectroscopy (DCS) [1, 2] monitors the movement of the moving scattering particles in the tissue, mainly red blood cells, by looking at the speckle fluctuations generated by the interference of coherent light diffused through the tissue. This provides a blood flow index (BFI), which has been shown to be in good agreement with other flowmetry techniques [1, 3]. These techniques have been validated both in human studies [4–9] and pre-clinical research on animal models [10, 11] for assessing deep tissue (>1 cm) hemodynamic changes.

One interesting application of this technology is pre-clinical work on small animals, most often rats and mice where the requirement for non-invasive measurements at penetration depths greater than few millimetres – the traditional limitation of microscopy and mesoscopy – calls for diffuse optics. In these models, the required source-detector separations, which roughly define the depth penetration of the technique, are sub-centimetre and broadband DOS systems have been proven to be feasible and practical [12]. Contact, probe-based broadband DOS, which fits the known absorption spectra (µ_a) and the exponentially decaying scattering (µ_s') to the measured spectra to obtain concentrations of chromophores, systems have been successfully employed in humans e.g. for monitoring haemodynamic and drug concentrations during photodynamic therapy [13] and for characterising colon polyps [14] as well as on small animal models e.g. for monitoring in vivo tissue hemodynamics [15, 16], quantifying therapeutic agents for dosimetry [17–19] and quantifying fluence rate for cytotoxicity evaluation [20]; demonstrating its capacity as a research tool. Our broadband reflectance spectrometer system is based on earlier [21, 22] and recently developed optical instrumentation [23] with the original design principle developed by Wilson et al. [24].

Non-contact broadband DOS systems, which rely on hyperspectral imaging acquisition, where the data is acquired from several wavelengths either along a line in a single frame (pushbroom) or in two-dimensional (2D) images one by one, have also been implemented for retrieving in vivo tissue hemodynamic data on humans, e.g. lip measurements [25], monitoring wound healing [26] and determination of tissue perfusion [27], as well as in animal models, e.g. monitoring laparoscopic surgery [28], identification of residual tumour on surgery [29] and xenograft prostate tumour detection [30].

DCS only systems for small animals have been applied on pre-clinical research, e.g. with a contact probe for monitoring of haemodynamics during brain ischemia and concussion injuries [31, 32], hind limb occlusion and reactive hyperaemia [33] and with non-contact systems for assessment of photodynamic therapy [34, 35], retrieving information about changes in blood flow which exploit the possibility to assess tissue evolving during studies.

First non-contact DCS and frequency domain DOS have been introduced to the field and demonstrated its utility small animals by Refs [36–38]. A tomographic approach was also demonstrated by the same group [38, 39]. Hybrid, contact [40] and non-contact systems [10, 41, 42] that combine broadband DOS and DCS have also been implemented on humans and small animals for providing a more complete set of hemodynamic and metabolic information of a given location with the possibility to monitor over different locations to assess hemodynamic heterogeneities in a single device to improve the sensitivity and specificity of the studies. Combined DOS and DCS have for example been used to study preterm infants [43] and for monitoring of chemotherapy in breast cancer [44]. In our group, a contact broadband DOS-DCS hybrid system with a self-calibrated probe [45] has been validated previously for studies on phantoms and on murine cancer models. The system has provided a rich data set and has been proven to be useful in monitoring anti-angiogenic therapy response.

Apart from pointwise and scanning measurements, DOS and DCS with multiple sources and detectors can be used for diffuse tomographic imaging in the forms of diffuse optical tomography [1, 46, 47] and diffuse correlation tomography [48–50], which, while not as high-resolution as low-scattering tomographic techniques such as X-ray computed tomography, can provide a more accurate quantification of the distribution of hemodynamics with differentiation in depth.

In this work, we present a different approach which overcomes some of the drawbacks inherent in contact systems; (1) variations in probe pressure can introduce an artificial variability in the estimated hemodynamic parameters which pose problems for longitudinal studies, (2) uniform contact of the probe surface with tissue is difficult due to small tissue volumes (e.g. a tumour) of interest and/or curved tissue surface affecting data quality and (3) it is difficult to estimate the heterogeneity of the hemodynamic parameters in a repeatable fashion.

We achieve this by using a non-contact pushbroom, hyperspectral technique for DOS [51–53] (ncDOS) which images the tissue surface directly to the spectrometer surface and acquires spectral and spatial data simultaneously. This allows the use of up to fifty-seven (twelve used for the studies presented herein) source-detector separation pairs for broadband DOS rather than the finite number of fibres used on the probe. We note that most current hyperspectral systems utilise wide field illumination, which primarily probes the very superficial tissue. However, by using a light source focussed to a spot on the measured tissue, our spatially resolved measurements can provide information from deeper tissue. We also incorporate a relatively simple, real-time tissue height map tracking for mapping the measurements positions to the tissue surface accurately and, if needed, to introduce corrections to the physical model [54] used in data analysis. We combine this with non-contact DCS (ncDCS) using the same optical paths. Finally, we have validated the system on tissue simulating phantoms and in-vivo by a dynamic study of a human fingertip during an arm-cuff occlusion test and by scanning a group of mice with implanted tumours.

2. Material and methods

2.1 System description

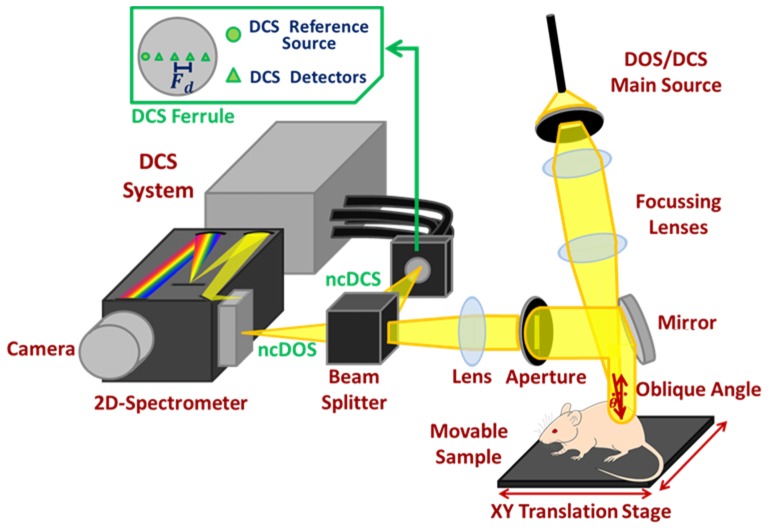
Figure 1 shows the combined system. The broadband ncDOS system uses as a source a 250W broadband incandescent continuous lamp (QTH source model 66499, lamp model 6334NS, Oriel Instruments, Newport Corporation, USA), filtered with an optical long-pass filter (FSQ-OG515, Newport Corporation, USA) in order to avoid second order diffraction from wavelengths shorter than 500 nm. The light is coupled to a multimode 400 µm core fibre and is focused, while avoiding saturation or blooming, to an about 0.5 mm diameter spot on the target via a pair of near infrared achromatic lenses with anti-reflectance coating (AC254-100-B - f = 100.0 mm, Ø1” Achromatic Doublet, Thorlabs GmbH, Germany), incising with an oblique angle. The diffusely reflected light is collected along a line through an aperture and an identical achromatic lens and then split by a beamsplitter (CM1-BP108, Thorlabs GmbH, Germany). The ncDOS light branch is focussed to the entrance slit of a 2D-spectrometer (Acton Insight, 550 to 1050 nm with CCD PIXIS eXcelon 400B, Princeton Instruments, USA) which images a line along the sample. The optical resolution of the ncDOS system, determined from a 60% contrast in a resolution target (R3L3S6P, Thorlabs GmbH, Germany), was 9.6 line pairs/mm (line width: 52 µm). The system provides even intensity on the CCD in the spatial direction when the measured area is evenly illuminated.

Fig. 1.

System overview. Laser and broadband light are alternatingly sent and focussed through a set of achromatic lenses on a spot on the target. The diffusely reflected light is captured along a line from the source spot, split by a beamsplitter and focussed by another achromatic lens to the slit of a spectrometer and an array of DCS detector fibres. Scanning is done by translational movement of the target.

In Fig. 2, we present a set of hyperspectral images taken by our contact (Fig. 2(a)) and non-contact (Fig. 2(b)) setups to illustrate the concept. Figure 2(a) shows data collected from contact measurements were the spatial distribution over the CCD surface is limited by the physical ferrule design, whereas in Fig. 2(b) the CCD surface is used in its entirety since an image of a line along the sample (16 mm length with incoming light incising at 2 mm position) at the whole set of wavelengths (550 to 1050 nm) is mapped onto the sensor surface.

Fig. 2.

Typical hyperspectral data acquired with our systems. Complete usage of the CCD with the non-contact system (b) provides many source-detector separations compared to the contact system (a) with discrete number of detectors placed at a certain source-detector separation.

For all the studies that we present on this work, a wavelength range from 610 to 900 nm and a set of twelve source-detector separations over distances ranging from 2 to 5 mm were employed for ncDOS. The same wavelength range was used for contact DOS measurements with a set of six source-detector pairs over the same range of distances instead. The CCD dark level was measured and subtracted from all DOS spectra.

The ncDCS system uses a 785 nm long coherent length near infrared laser (DL785-120-S, CrystaLaser, USA) as light source. Light is delivered to the target through the same optical setup as the ncDOS system and is collected in the same way. After the abovementioned beamsplitter, the ncDCS path is imaged to a ferrule with one multimode 200 µm reference source fibre for distance calibration and four single mode fibres as detection fibres plugged to a custom-built 4-channel DCS system using avalanche photodetectors (SPCM-AQRH, Excelitas Technologies, USA) and a correlator board (Correlator.com, USA) [1]. The ncDCS measurements were performed by means of a custom designed single source and four detectors ferrule with dynamic source-detector distances (typically ranging from 2 to 7 mm) due to the system’s demagnification factor and object geometry, whereas for the contact DCS measurements, a set of two sources and three detectors for distances ranging from 2 to 5 mm were used. This is further described below.

The sample to be scanned is mounted on a pair of software controlled orthogonal translation stages (MTS50, Thorlabs GmbH, Germany) for two-dimensional scanning with two millimetres step-size, which is variable. System demagnification is set to 0.5 in order to allow the light spot to remain on the CCD while the height of the measured object varies. A detailed description of the systems is shown in Fig. 2 and summarized in Table 1.

Table 1. Summary of the system parameters for DOS-DCS measurements.

Parameter	Contact system	Non-contact system
	Used	Used	Max. or Min. Allowed
DOS systems description
Independent bandwidth (nm)	610 - 900	610 - 900	550 - 1050
Wavelength resolution (nm)	5	5	5
Optical Resolution (OR) (µm)	—	200	74
Source-detector separation (mm)	2 - 5	2 - 5	†
# of source-detector pairs	6	12	57 @ 60% contrast
Dynamic range (dB)	96	96	96
Spot size on the object (mm)	0.2	<1	—
Depth of focus (mm)	—	± 4	± 4
Field of view (mm)	—	≈45x20	‡
Scanning resolution (mm)	—	2	0.2
Integration time per frame (s)	4	2	>0.1
DCS systems descriptions
Source wavelength (nm)	785	785	785
Source-detector separation (mm)	2-5	2-7	†
# of source-detector pairs	6	4	4
Integration time per frame (s)	3	3	>0.1
	DOS + DCS
Total time per frame, still (s)	8	6	1
Total time per frame, moving* (s)	20	8	3

†: Dynamic parameter that depends on the system demagnification and optical path

‡: Dynamic parameter that depends on the sample size

*Probe replacement for contact system and translation for scanner system respectively

2.2 Calibration of source-detector separations and tissue height map tracking

The system’s focal plane or the demagnification factor can be modified according to the region of interest (ROI) by means of changing the optical path; such flexibility turns into a set of potential source-detector separations. The demagnification factor has to be measured for each experiment and is given by an image analysis from printed pattern of dark lines separated by 2 mm placed at the focal plane. This pattern shows up on the CCD as a train of square signals and the number of pixels between the edges of each square signal is proportional to the physical separation between lines. For ncDOS, the source-detector separation distances, ρ (mm), are given by the image analysis of these lines which defines the calibration factor (spatial size per pixel), S_r (mm/pixel), and the pixel position of light peak on the CCD.

The object geometry is recovered from the change, Δx in pixels, of the reemitted light peak tracked on the CCD (Fig. 3) according to Eq. (1)

$$\Delta h=-\frac{\Delta x\times S_{\text{r}}}{\tan \left(\theta \right)}$$ (1)

where Δh is the height difference in millimetres relative to a reference position and θ is the angle of the incoming light relative to the object’s normal. This allows us to determine the height of a diffusely reflecting object within ± 0.5 mm accuracy.

Fig. 3.

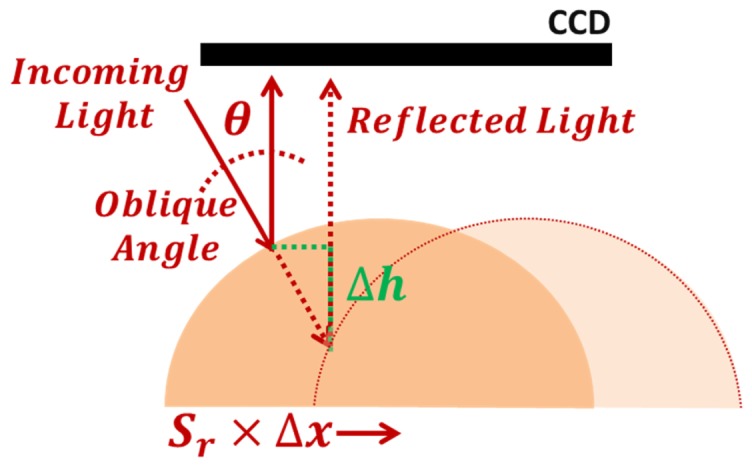
The height change of the object relative to a reference position is a function of the light peak displacement on the CCD and the incoming angle of light.

For estimation of ncDCS source-detector separation distances, the DOS light source is shone in parallel through both the reference source in the ncDCS ferrule and the main DOS/DCS source (Fig. 1) to merge them into a single spot (<1 mm). The source-detector separations ρ_i, where i refers to the number of detector (i = 1,2,…N), will depend on the physical distance between ncDCS detectors (F_d), the system demagnification (0.5), the light peak displacement (Δx) and the calibration factor (S_r) according to Eq. (2)

$${\rho }_i=\frac{i\times F_{\text{d}}}{0.5}-\left(\Delta x\times S_{\text{r}}\right).$$ (2)

2.3 Data analysis

The light intensity at a distance ρ (cm) from the source position was assumed to be proportional to a Green’s function, G, for the diffusion equation in a semi-infinite geometry with a P₃ approximation [55, 56]

$$G=\frac{3{\mu }_s^{\prime }}{4\pi }\left(\frac{\exp \left(-{\nu }^{-}{r}_1\right)}{r_1}-\frac{\exp \left(-{\nu }^{-}{r}_2\right)}{r_2}+\frac{\exp \left(-{\nu }^{-}{r}_3\right)}{r_3}-\frac{\exp \left(-{\nu }^{-}{r}_4\right)}{r_4}\right)$$ (3)

where the attenuation coefficient ${\nu }^{-}={\left[\left({\nu }_{\beta }-{\left\{\left|{{\nu }_{\beta }}^2-{\nu }_{\gamma }\right|\right\}}^{1/2}\right)/18\right]}^{1/2}$ with, neglecting the anisotropy factor of the scattering, ${\nu }_{\beta }=55{\mu }_a\left({\mu }_a+{\mu }_s^{\prime }\right)+35{\left({\mu }_a+{\mu }_s^{\prime }\right)}^2$ and${\nu }_{\gamma }=3780{\mu }_a{\left({\mu }_a+{\mu }_s^{\prime }\right)}^3$. The model uses two source-sink pairs with $r_1={\left[{\rho }^2+{\left(1/{\mu }_s^{\prime }\right)}^2\right]}^{1/2}$ being the distance to a virtual, isotropic point source in the tissue and $r_2={\left[{\rho }^2+{\left(2z_b+1/{\mu }_s^{\prime }\right)}^2\right]}^{1/2}$ the distance to a corresponding mirror point sink above the extrapolated boundary $z_b=\frac{2}{{\mu }_s^{\prime }}\frac{1+R_{eff}}{3\left(1-R_{eff}\right)}$. The effective reflection coefficient is set to R_eff ≈0.47 for the index of refraction mismatch of air over water or tissue. The distance to the real source is r₃ = ρ and the distance to a mirror point sink for the real source is $r_4={\left[{\rho }^2+{\left(2z_b\right)}^2\right]}^{1/2}$. For tissue, the reduced scattering coefficient µ_s' (cm⁻¹) was assumed to adhere to a Mie-like function containing a Rayleigh scattering term, A₂ (cm⁻¹) [57],

$${\mu }_s^{\prime }=A_1{\left(\lambda /{\lambda }_0\right)}^{-b}+A_2{\left(\lambda /{\lambda }_0\right)}^{-4}$$ (4)

while the Rayleigh term was assumed to be negligible for the tissue simulating liquid phantoms.

The absorption coefficient µ_a (cm⁻¹) in tissue was assumed to be the sum of the molar absorption coefficients for oxygenated (HbO₂) and deoxygenated (Hb) haemoglobin (610 – 800 nm: [58], 800 – 900 nm: [59]) and water [60] times their concentrations c_i (haemoglobin: µM, water: %). For the optical phantoms, µ_a was assumed to be the sum of water and ink absorption times their concentrations. Numerical fitting was done for A₁, A₂, b and c_i in the wavelength range 610 – 900 nm for the ratio of the Green’s functions of two distances at a time, G(A_i, b, c_i, ρ)/G(A_i, b, c_i, ρ₀) with ρ₀ going from 2 to 3 mm in steps of 0.2 mm and ρ = ρ₀ + 2 mm for a total of 12 source-detector separations used. To improve signal-to-noise ratio, seven pixels were averaged for each distance, corresponding to band lengths of approximately 0.2 mm. By using the ratio of spectra at two different distances, the spectral shape of the CCD sensitivity and the lamp emission, as well as other systematic effects along the optical path that do not belong to the measured object, is cancelled out. For the contact probe, a further calibration was done by a source fibre at an equal distance to all detector fibres in order to take the differences in light transmission between the fibres and differences in their coupling to the tissue into account. The numerical fitting was done in Matlab (MathWorks, US) using a nonlinear least square method (LSQNONLIN with Levenberg-Marqardt algorithm). Total Haemoglobin Concentration (THC) and Tissue Oxygen Saturation (S_tO2) were retrieved from fitted concentrations, whereas water concentration was fixed at 70% in all fits.

For DCS, the normalized electric field autocorrelation function of the signal was assumed to conform to the expression [1] given below, which is the solution of the correlation diffusion equation for the semi-infinite geometry:

$$g_1=\left(\frac{\exp \left(-K(\tau )r_1\right)}{r_1}-\frac{\exp \left(-K(\tau )r_2\right)}{r_2}\right)/\left(\frac{\exp \left(-K(0)r_1\right)}{r_1}-\frac{\exp \left(-K(0)r_2\right)}{r_2}\right)$$ (5)

$$\text{Where}\hspace{0.17em}K(\tau )={\left[3{\mu }_a{\mu }_s^{\prime }+6\alpha D_b\tau {{\mu }_s^{\prime }}^2{\left(2\pi n/\lambda \right)}^2\right]}^{1/2}$$ (6)

Here, τ (s) is the autocorrelation delay time, α (-) the fraction of moving scatterers, D_b (cm²/s) the Brownian diffusion coefficient for the liquid phantoms, n (-) the index of refraction, which is assumed to be 1.33 for both phantoms and tissue, and λ (cm) the vacuum wavelength of the laser light. For living tissue, the red blood cells responsible for the decorrelation of the function at this time scale are flowing rather than diffusing. Despite this, the term αD_b has been found to be proportional to the actual microvascular blood flow in the tissue and is thus called blood flow index, BFI, for the tissue measurements. The measured DCS signal, g₂, is related to the theoretical g₁ through the Siegert equation

$$g_2=1+\beta {\left|g_1\right|}^2$$ (7)

where β (-) is a system-dependent constant that can be estimated from short delay times in static or low-flow scattering media, i.e. when K(τ) ≈K(0), or from numerical fitting to the measured g₂. The latter was done in this study with the same least square method as for the DOS (Matlab, LSQNONLIN with Levenberg-Marqardt algorithm). The values for µ_a and µ_s' were taken from the corresponding DOS measurements.

2.4 Phantom tests

Tissue-simulating liquid phantoms were made with varying amounts of a scattering emulsion (Lipofundin 20%, B. Braun, Germany) and Brilliant Blue FCF food colouring E133 (Vahiné Azul, Vahiné, France) prediluted to 0.01%. The concentrations of Lipofundin and ink were mixed in three levels, 2.5 – 5 – 7.5% for Lipofundin (i.e. 0.5 – 1.5% lipids) and 5 – 10 – 15% for diluted ink, in a 2x2 design matrix with a middle point at 5% Lipofundin and 10% diluted ink. A region of 1x1 cm² was scanned in a total of thirty-six points. Each measurement took 3 minutes. Since there are no static scatters in the phantoms, α = 1.

2.5 Arterial cuff occlusion test

In order to test the system in vivo, measurements were made on the blood-rich palmar side of the tip of the index finger of an adult volunteer. After two minutes of baseline measurement, the arm was occluded by an inflatable cuff at 180 mmHg for three minutes after which it was released and measurements proceeded for three more minutes. The DOS and DCS measurements were taken quasi-simultaneously, switching between the systems for each time point.

The use of human subjects for testing of the system has been approved by the ethical board of Hospital Clinic i Provincial de Barcelona and the subject gave informed consent before the procedure.

2.6 Mouse scanning

Seven male athymic nude mice (Harlan Laboratories, Spain, weight: 26.7 – 33.5 g) with xenoimplanted clear cell renal cell carcinoma (RCC) tumours were used to compare the contact and non-contact systems. After a small midline incision, small pieces (2 x 2 x 2 mm) of a RCC tumour from a human patient cell line (786O- cells) had been sutured on the left kidney of each mouse under Isoflurane anaesthesia and left to grow to a volume of approximately 1000 mm³ before measurement. Areas of about 20 x 45 mm covering the tumour and the upper parts of the foreleg and hind leg were scanned in steps of 2 mm for each mouse. The measurements were compared to measurements from the same specimen made with a self-calibrating probe [45] using the same spectrometer and DCS system as the scanner. During the measurements the mouse was anesthetized with 2% Isoflurane in 2 L/min oxygen and kept warm by a rectal temperature-controlled heating pad (HBsM, Panlab Harvard Apparatus, Spain). The measurement sessions took approximately 40 minutes each. After the probe measurements, the mice were allowed to rest about three hours before scanner measurements commenced in order to let them recover from the Isoflurane and allow time for rearranging the system.

The animal research had been approved by IDIBELL’s animal research committee and accepted by the local Catalan government (Generalitat de Catalunya, Departament de Medi Ambient i Habitatge, Direcció General del Medi Natural, Protocol number 4899, PI: Oriol Casanovas). The results were compared with a double-sided paired t-test for each of the three regions that were measured.

3. Results

3.1 Data & fit quality

DOS signal-to-noise ratio (SNR) was calculated from the cuff test measurement where the noise was estimated as the standard deviation over time during the baseline period and the signal from the corresponding mean. The results, filtered wavelength-wise with a 10 point Hanning filter, for the longest and shortest source-detector separations are presented in Fig. 4, where examples of spectral fits for the same measurement also are given. The residuals (difference between the measurement and fit) are very flat in the used region with just a small valley around 635 nm possibly corresponding to methaemoglobin which was not accounted for in the fits [58].

Fig. 4.

(a) Signal-to-noise ratio as mean divided by standard deviation over time (2 min) for the longest and shortest source-detector separations used. (b) Spectral fits for two different source-detector combinations. (c) Residuals for the fits. A small peak around 635 nm can be seen, possibly corresponding to methaemoglobin [58].

3.2 Phantom tests

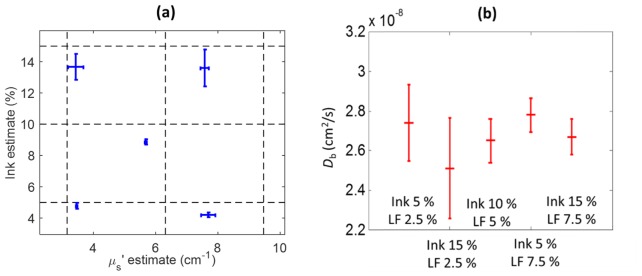
Results from the liquid phantoms are shown in Fig. 5, where estimations for ink concentrations are in acceptable agreement with expectations with an average underestimation of 10% (range: 4 – 16%) of the ink concentrations. On the other hand, the reduced scattering coefficient values are underestimated for larger scatterer concentrations. We note that the latter quantity has not been independently verified on these specific phantoms whereas the ink absorption spectrum was verified with a spectrophotometer. The particle Brownian diffusion coefficient, D_b, is not expected to change between titrations since we have not explicitly induced any changes in temperature, viscosity or scatterer size. Indeed, the diffusion coefficient shows good stability along the scanned surface of each phantom with a mean D_b of 2.7 × 10⁻⁸ cm²/s, standard deviation between the phantoms of 0.10 × 10⁻⁸ cm²/s and an average standard deviation of 0.15 × 10⁻⁸ cm²/s over the phantom surface. The error bars are calculated along different measurement points on each phantom’s surface. Overall, these results are comparable in their relationship to the expected values to those previously reported by the contact approach [45].

Fig. 5.

Results from the five liquid phantoms with varying concentrations of diluted blue ink and Lipofundin (LF). (a) Estimated values of ink concentration and µ_s' at 785 nm. Dashed lines mark expected ink and reduced scattering coefficient values. (b) Estimated D_b values. Error bars are standard-deviation over the scanning positions.

3.3 Arterial cuff test

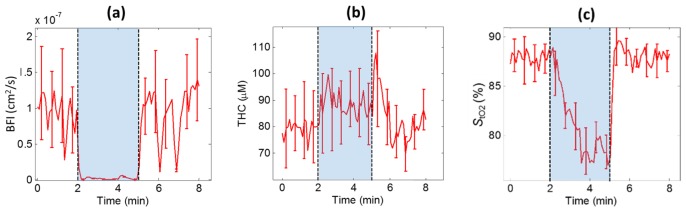
The results from the occlusion test can be seen in Fig. 6. The expected drop in BFI and gradual decay in S_tO2 can readily be seen in the estimates over time whereas THC estimates are relatively unchanged.

Fig. 6.

Results from occlusion test in fingertip. Stasis was induced after 2 minute of baseline measurement and maintained for 3 minutes. (a) BFI drops to almost 0 during the occlusion while (b) THC stays relatively unchanged and (c) S_tO2 gradually decays over time as expected. (Error bars are s.d. over source-detector separations, displayed for every fifth time point.)

3.4 Mouse scanning

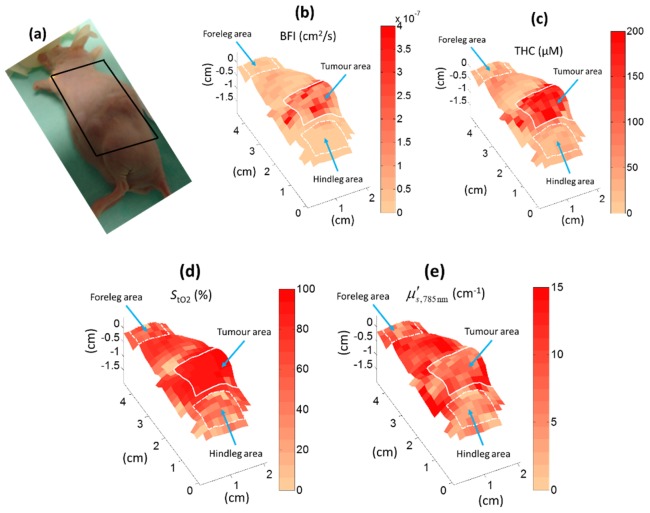
An example mouse scan is shown in Fig. 7. The location of the tumour can be seen by the elevated area where the tumour pushes the skin up though it also extends deeper in the tissue. We have found this particular type of tumour to have very high microvascular blood oxygen saturation, possibly due to arterio-venous shunts and altered metabolism. THC and BFI are also higher in the tumour area than in the surrounding tissue.

Fig. 7.

Scanning of renal cell carcinoma tumour. Regions of interest for comparison with probe measurements are marked with white outlines. Each pixel corresponds to the approximate middle of the line between the light source and the detector points for each measurement.

The tumour, the hind leg and the foreleg areas (about 0.5 – 1.5 cm², illustrated in Fig. 7) were chosen as regions-of-interest for comparison between the scanning and the contact probe in all seven mice. The results are illustrated in Fig. 8 and Table 2 for all seven mice. The estimates are similar, albeit often statistically significantly different, for the probe and the scanning system though the THC and BFI estimates tend to be somewhat lower for the scanning measurements.

Fig. 8.

Comparison of median values for (a) blood flow index (BFI), (b) total haemoglobin concentration (THC), (c) tissue oxygen saturation (S_tO2) and (d) the reduced scattering coefficient at 785 nm obtained from the scanning system (S) and a self-calibrating optical probe (P) in seven mice. The boxplots represent the variability over the mice, visualized by median (central line), quartiles, i.e. the 25 and 75-percentiles (box edges), data range within one time of the interquartile range from the quartiles (whiskers) and all data points (crosses and stars).

Table 2. Tabulation of results from non-contact and contact measurements are shown for the seven mice. BFI, THC, S_tO2 and µ_s' are reported for the tumour, hind leg and foreleg areas. Differences (Diff: probe – scanner results) are reported together with corresponding statistics for paired t-tests. s.d. denotes standard deviation over the named quantity.

n = 7		Non-contact scanner			Contact probe
Tumour	Mean	± s.d. within animal	± s.d. between animals		Mean	± s.d. within animal	± s.d. between animals		Diff	p (paired t-test)
BFI (10−7cm2/s)	0.93	1.64	0.43		1.24	1.66	0.10		0.31	(0.1)
THC (µM)	125	52	34		176	57	65		51	(0.054)
StO2 (%)	89	11	4		87	7	4		−2	(0.08)
µs',785 nm (cm−1)	6.91	4.61	1.22		4.35	1.59	1.21		−2.56	0.004
Hind leg
BFI (10−7 cm2/s)	0.17	0.12	0.06		0.26	0.17	0.07		0.09	0.048
THC (µM)	33	13	17		56	17	7		23	0.01
StO2 (%)	63	13	15		62	12	16		−1	(0.81)
µs',785 nm (cm−1)	5.88	3.55	1.64		5.46	2.46	1.94		−0.42	(0.61)
Foreleg
BFI (10−7 cm2/s)	0.23	0.14	0.09		0.42	0.42	0.13		0.19	0.033
THC (µM)	37	11	14		49	8	9		12	(0.12)
StO2 (%)	61	12	13		59	10	9		−2	(0.71)
µs',785 nm (cm−1)	7.33	3.32	2.89		6.52	5.11	0.84		−0.81	(0.52)

4. Discussion

In this paper, we have presented a hybrid non-contact scanner system with diffuse correlation spectroscopy and pushbroom, broadband diffuse optical spectroscopy for small animal imaging. We have described the set-up in details and demonstrated its functioning on tissue simulating liquid phantoms, in vivo on human fingertip as well as on a group of mice with implanted tumours. Overall, the results show that the system is capable of retrieving the tissue optical properties and hemodynamics across the scanned tissue and the results are comparable, albeit with a statistically significant difference, to those of a contact probe within physiological and experimental variability. We note that, as mentioned above, there are three hours between measurements and the scanner results represent the second time the mouse was anesthetized in one day which could lead to a stressed animal and unstable hemodynamics, also, the pressure applied by the probe alters the local hemodynamics. The different variability between two methods for different measurement sites and variables can also be due to similar factors.

A benefit of the pushbroom approach is that the light intensity for a large number of wavelengths can be obtained at once along a line of detector positions for each source spot. This provides us with a rich data set that improves the quantitative results and also paves the way for future applications where three dimensional diffuse optical tomography algorithms can be used. Alternatively, liquid crystal tuneable filters or a monochromator can be used instead of a spectrometer grating [61, 62]. This allows the collection of a 2D image of the light intensity around each source spot but at a limited number of wavelengths and with the different wavelengths measured at slightly different times as they have to be measured sequentially. An advanced hybrid approach that also can be used is to use patterned light sources to obtain spatially resolved data over a 2D region by use of spatial frequency encoding alongside the wavelength information [63].

In this set-up, we have opted to use translation stages to move the measured object rather than more traditional scanning by moving the optical elements, for instance, using galvanometer-style rotating motors [64, 65]. This approach could be implemented in our system as well but it adds extra complexity since optics for a broadband light source, a coherent laser as well as a CCD-based spectrophotometer and an array of single-mode would be shared and scanned. With translation stages, it is straightforward to let both laser and broadband light illuminate the sample through an oblique angle and thus avoid specular reflections in the lenses to degrade the measurements. Such reflections would be required to be filtered out with crossed polarizers, a method utilized in other non-contact systems [17], complicating the design and reducing light intensity. The samples we study, i.e. rodents, are anesthetized, are relatively small and, therefore, two dimensional mechanical scanning of the sample is a reasonable compromise.

The source-detector distances used are selected to match our previously built contact probe and provide a relatively limited measurement depth as the largest separation is 5 mm. However, the scanner system can in principle be adjusted to arbitrary source-detector separations by adjusting the optics, thus providing a deeper measurement. To maintain a sufficient signal-to-noise ratio and stay within the dynamic range of the system, at larger distances, it is however likely that the source spot must be kept out of the field of view, adding requirements to keep track of its position. As mentioned earlier, one of the motivations of a scanning system is to have topographic mapping which allows us to work with smaller tumours that mimic human tumours more closely – in relative size to the mice.

The non-contact system poses its own challenges but also provides us with significant advantages. A contact probe provides better light-coupling to/from the tissue, does not suffer from stray light effects and is easy to implement [45, 66]. On the other hand, it is difficult and time consuming to systematically scan large fields-of-view, suffers from variations in the applied probe pressure which changes the tissue hemodynamics and is harder to ensure repeatability for longitudinal studies over long periods of time. The non-contact system suffers from the above-mentioned limitations but does not alter the tissue hemodynamics, it is straightforward to scan large tissue volumes and longitudinal studies can be readily tackled even while the tumour size changes. Furthermore, the animals can be manipulated while measurements are being carried on, treatments such as photo-dynamic or photo-thermal therapy can be applied or other non-contact measurements can be taken without obscuring the field of view like a contact probe would.

We have used wavelengths up to 900 nm and refrained from fitting for water as our system was not optimized for wavelengths above 900 nm leading to a severe underestimation of water when using the scanner system. This problem was more severe in the non-contact system, possibly due to stray light affecting this spectral region of relatively low signal-to-noise ratio. A possible strategy for improving the signal-to-noise ratio at especially longer wavelengths is to move the light spot off the CCD axis [67] as higher light intensities can be used without saturating the CCD. However, this approach makes it more difficult to keep track of the source-detector separations in the geometry. It is more desirable to employ stray light corrections [62, 68] and/or a better optimized spectrophotometer which are now available on the market. These approaches could readily be implemented in future versions of the system.

We note that the analysis in this paper is done assuming semi-infinite geometries with a P₃ approximation for DOS which we primarily have found to improve scattering estimates for short source-detector separations. On the other hand, a straightforward photon diffusion model (P₁) for DCS in the semi-infinite geometry was used. We did not implement a P₃ model for DCS which would have, presumably, provided a better model for short source-detector separations and higher absorption since due to the nature of DCS physics we are able to focus on higher scattering events by looking at early delay times [69]. This could be included and tested in the future. In the future, we can also utilize more advanced models that uses photon transport models or Monte Carlo simulations to improve the results in these short source-detector separations. Furthermore, since the tissue outline is measured in real-time by our system and it could also be used to generate heterogeneous, arbitrary geometry models using either fine-elements or Monte Carlo [1, 70].

As shown in Fig. 4, the fits for the spectra are very good with just a small valley at 635 nm. This probably corresponds to methaemoglobin [58] which is oxidized haemoglobin usually present in small amounts in the blood and continuously converted back to functional haemoglobin. We have found this component to be small when included and it was thus omitted from the analysis here. Other chromophores we have tested are lipids [71] and collagen [72] which are important components in fatty tissues likes breast and bone tissues. Their impact on the spectral fitting in this range on these tissues was negligible, probably due to their relatively low absorption. In future, if needed, they could be included in this type of analysis with a broadband system designed particularly for their spectral signatures.

The ink concentrations in the phantoms are underestimated by about 10% (Fig. 5), which is a similar magnitude of error as in other DOS systems [13, 56]. There are some systematic differences in the estimates of the parameters between probe and scanner measurements (Table 2) that we would like to reduce but these differences are within the intra- and inter-mice variability. We suspect that much of the variability is due to the time difference between two measurements and the instability of the mice as about three hours have passed between the probe and the scanning measurements.

It can be noted that both the muscle tissue of the limbs and the renal cell carcinoma tumours are relatively low-scattering tissue. Baran et al. [73] has reported a µ_s' of approximately 8 cm⁻¹ at 785 nm for human renal cell carcinoma and muscle tissue is generally reported to have around 5 cm⁻¹ at 785 nm [74, 75].

The tumours scanned in this paper were very blood-rich (Fig. 7). Furthermore, clear cell renal cell carcinoma is a tumour type with reduced mitochondrial activity [76]. In other words, they rely on glycolysis for their metabolism and do not extract much oxygen from the blood. These two factors probably explain the high blood oxygenation in the tumour which is in agreement with our results from a different study with the contact-probe [45]. As another example, Hull et al. measured mammary adenocarcinoma in rats with contact DOS and found S_tO2 values about 75% [15]. Other types of tumours may show less contrast to the surrounding tissue or have other characteristics as some tumours have higher THC and/or S_tO2 and others lower compared to benign tissue as shown in an extensive review by Bydlon et al. [77]. For example, Yu et al. measured murine fibrosarcoma with contact probe DOS and found S_tO2 values about 36% in the tumours [17]. Breast cancer tumours have enhanced mitochondrial activity [78] and could thus be expected to show lower oxygen saturation, which has been found in some studies [79, 80] though in others did not found a contrast between the oxygenation breast tumours and surrounding healthy breast tissue [81, 82].

Very high S_tO2 values can also be noted in the palmar side of the fingertips. This is likely due to the rich presence of arterio-venous anastomoses [83] which help cooling the body by shunting superficial blood directly from the arteries to the veins and thus bypasses the oxygen-extracting capillary network. The oxygen saturation of venous blood in the fingertip has been estimated to be approximately 86% [84], which is similar to the values obtained in this study.

The varying height of the mouse means that not all of it will be in the focal plane. We have found our estimates to be relatively unchanged when changing the height of a phantom or tissue within 1 cm of the focal plane. Therefore, we do not believe this has affected the scanning results. We are testing auto-focusing methods which cost more time but are feasible since our height-tracking method provides data in real-time which would eliminate this issue.

In this paper, we present two-dimensional scans of tissue but the system could also be used for three-dimensional diffuse optical tomography. This could be verified and developed using heterogeneous phantoms with inclusions of differing static and dynamic properties, of different sizes and contrasts which is beyond the scope of the current paper. In fact, in collaboration with others, we have recently presented a similar system as this for diffuse correlation tomography in mice [85]. Finally, the system could also be adapted to fluorescence spectroscopy [86] by adding a suitable excitation laser or other monochromatic light source [87].