Tissue thickness calculation in ocular optical coherence tomography

Abstract

Thickness measurements derived from optical coherence tomography (OCT) images of the eye are a fundamental clinical and research metric, since they provide valuable information regarding the eye’s anatomical and physiological characteristics, and can assist in the diagnosis and monitoring of numerous ocular conditions. Despite the importance of these measurements, limited attention has been given to the methods used to estimate thickness in OCT images of the eye. Most current studies employing OCT use an axial thickness metric, but there is evidence that axial thickness measures may be biased by tilt and curvature of the image. In this paper, standard axial thickness calculations are compared with a variety of alternative metrics for estimating tissue thickness. These methods were tested on a data set of wide-field chorio-retinal OCT scans (field of view (FOV) 60° x 25°) to examine their performance across a wide region of interest and to demonstrate the potential effect of curvature of the posterior segment of the eye on the thickness estimates. Similarly, the effect of image tilt was systematically examined with the same range of proposed metrics. The results demonstrate that image tilt and curvature of the posterior segment can affect axial tissue thickness calculations, while alternative metrics, which are not biased by these effects, should be considered. This study demonstrates the need to consider alternative methods to calculate tissue thickness in order to avoid measurement error due to image tilt and curvature.

1. Introduction

Developments in ocular imaging technologies, particularly optical coherence tomography (OCT) [1], mean that the tissue layers of the eye’s anterior and posterior segment can be visualized reliably with high resolution cross-sectional (or volumetric) images [2]. Analysis of OCT images provides qualitative and/or quantitative assessment of the morphology and physiology of the eye in vivo in a non-invasive manner. In addition to the fundamental visualization of tissue morphology/structure with OCT instruments, the information obtained from OCT can also be used for different applications, including functional imaging of the retina [3], visualization and estimation of blood flow of the retina [4, 5] and choroid [6, 7] as well as the extraction of the optical properties of the ocular tissue [8]. Despite these developments, OCT thickness values remain one of the most widely used quantitative clinical and research metrics derived from ocular OCT images.

Analysis of thickness data from OCT imaging has expanded our knowledge of the eye’s normal anatomical characteristics, including developmental [9, 10] and age-related [11, 12] changes that occur in ocular tissues throughout life. OCT derived thickness metrics have also contributed towards our understanding of the ocular changes associated with the development and progression of refractive error [13, 14] and a variety of ocular diseases [15, 16]. From a clinical perspective, OCT thickness metrics are commonly used in the diagnosis and monitoring of ocular diseases [17, 18], and to evaluate treatment efficacy [19]. Clinical diagnostic methods typically involve the comparison between global or local layer thickness in a diseased eye, with that of a normative database (or with a previous baseline measurement of the same eye when monitoring disease treatment and/or progression), which underscores the importance of reliable methods for the calculation of tissue thickness.

The rapid development of image processing techniques to segment layer boundaries [20], has resulted in growing interest in thickness mapping of ocular tissue, since there are now a wide variety of methods available to rapidly and automatically segment OCT data, particularly posterior segment images, which include the retinal layers [21, 22] and choroidal tissue [23, 24]. These image segmentation algorithms are also available in current commercial instruments [25] and facilitate the application of 3-D volumetric scanning protocols and rapid quantification of OCT images, making tissue layer 3-D thickness mapping of the eye a common clinical procedure.

Despite the importance of thickness measures derived from ocular OCT images and the number of sophisticated methods available for layer segmentation, no studies have directly compared different approaches for calculating tissue thickness from OCT images. Most current methods utilize an axial based thickness calculation (i.e. thickness along the A-scan) to quantify tissue thickness. Although the axial calculation is intuitive, and requires minimal computational power, these thickness values can be biased by the shape of the measured tissue or the tilt of the image [26–28]. Hence, axial thickness metrics may not always be the most appropriate method to estimate the ocular tissue thickness and alternative metrics should be considered. This is of particular significance given recent developments in retinal OCT imaging which allow wide-field imaging of ocular tissue, using optical methods [29], sophisticated emitting lasers [30–34] or image processing techniques to montage the data from different regions of the eye [35–37]. Taking into account that the posterior segment of the eye is curved, image curvature and tilt increases as a wider region is imaged, presenting a particular challenge for thickness calculations. In this paper, five different metrics to calculate tissue thickness from OCT images are proposed and compared with the standard axial thickness method used in commercial OCT instruments. Some of these metrics have been proposed in clinical OCT studies [38–41], while others have been adapted from other imaging modalities such as MRI [42, 43]. To date, a systematic evaluation of these different metrics for calculating tissue thickness has not been published.

The organization of the paper is as follows; Section 2 presents the data set (and the montaging method to produce wide-field data) as well as the different metrics used to calculate the thickness. Section 3 compares the performance of the proposed set of metrics for calculating tissue thickness from the wide-field retinal and choroidal data, while concluding remarks are given in Section 4.

2. Materials and methods

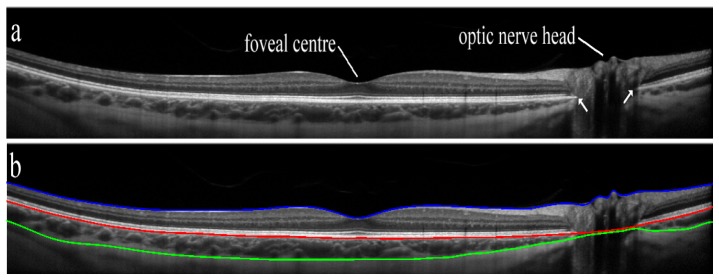
Figure 1 shows an example wide-field OCT B-scan of the human retina. The data was captured using the optical method proposed in [29], which uses a high powered condensing lens in front of the objective lens of a commercial OCT to obtain a wide-field image of the posterior eye, providing a magnification of about 1.5-fold, resulting in a 45° OCT image. The image is shown in a 1:1 ratio to illustrate the curvature of the posterior segment of the eye that is observed as more peripheral regions beyond the central portion of the posterior segment are imaged. The three layers of interest used to determine choroidal and retinal thickness in the current study (inner limiting membrane-ILM, retinal pigment epithelium-RPE and chorio-scleral interface-CSI) are also marked in the figure (Fig. 1(b)). We define the choroidal thickness as the separation between the RPE and the CSI, whereas the retinal thickness is the separation between the ILM and the RPE. An overview of the actual thickness calculations is presented below (section 2.3).

Fig. 1.

Example of a 45° wide-field single B-scan captured with the spectral domain OCT using the instrument’s high resolution scanning protocol (a) with the segmented (b) B-scan with the three boundaries of interest (inner limiting membrane (ILM) [blue line], retinal pigment epithelium (RPE) [red line] and chorio-scleral interface (CSI) [green line]). The image was segmented using graph-search algorithms [10, 21, 23]. White arrows in (a) mark the opening of Bruch's membrane.

It is important to highlight that OCT images are affected by a number of artefacts, such as refraction, the scanning procedure and the curvature of the intermediate tissue layers up to the depth of interest [44, 45]. Thus, the image provided by OCT instruments does not represent the true shape of the tissue. Using optical models of the true OCT scan paths (i.e. modelling the imaged eye), Kuo and colleagues [46] developed sophisticated methods to correct the measured ocular shape in posterior segment OCT images. Their algorithms were favorably validated by comparing the corrected posterior segment OCT images to a reference non-optical imaging technique (MRI). These results demonstrated that the standard OCT image is flatter than the true shape of the posterior segment. Although these distortion-correction methods are outside the scope of the work presented here, they complement the motivation of this study; the corrected (more curved) OCT images would therefore have a greater error when calculating the axial thickness. Hence, the presented methods to calculate thickness become more relevant.

2.1 Data set and instrumentation

The data set used to test the proposed thickness calculation routines consisted of spectral domain OCT images from 43 young adult subjects with normal vision and ocular health, aged from 18 to 29 years (mean age 21.1 ± 2.5 years). Approval from the Queensland University of Technology human research ethics committee was obtained prior to commencement of the study, and all participants provided written informed consent to participate.

Each subject had spectral domain OCT chorio-retinal images of their right eye captured using the commercially available Heidelberg Spectralis instrument (Heidelberg Engineering, Heidelberg, Germany). For OCT imaging, the Heidelberg Spectralis uses a super-luminescent diode of central wavelength 870 nm, which provides an axial resolution of 3.9 µm and transversal resolution of 14 µm, with a scanning speed of 40,000 A-scans per second. For each subject, a series of volumetric OCT scans were collected from three different but overlapping retinal locations, including the central foveal location, 15° nasal and 15° temporal to the fovea. The instrument’s internal fixation target was moved off-axis to facilitate the capture of the 15° nasal and temporal volumetric scans. Each volumetric OCT scan covered a 30° by 25° retinal region and consisted of 31 horizontal B scan images (1536 A-scans per B-scan), each separated vertically by approximately 240 µm, which allowed retinal and choroidal thickness to be assessed across approximately a 60° by 25° region centered on the fovea. Following the manufacturer’s recommendation, all B-scans included for analysis had an image quality higher than 25dB (mean for all OCT images was 33.0 ± 2.9 dB).

All OCT images were collected using the Enhanced Depth Imaging mode, that improves the visibility of the choroid [47]. Additionally, the instrument utilizes a confocal scanning laser ophthalmoscope (SLO) to automatically track the eye in real-time to facilitate B-Scan frame averaging to improve the signal to noise ratio in the OCT images. This eye tracking function was active during the examination to ensure that each OCT image was the average of 30 B-scans. The SLO provides a high resolution en-face image of the retina (1536x1536 pixels, frame rate 5 Hz), which was used for the montaging of the scans captured at different retinal locations.

To allow objective inter-subject and between-group comparisons of thickness maps, an anatomical standardization [48] was performed. The two-step procedure was used in order to scale the OCT data to account for the influence of axial length and refractive error upon the transverse image scaling, and inter-subject variations in disc-fovea separation. Initially, the transverse scale of each individual subject’s OCT data was adjusted based upon the calculated position of the eye’s second nodal point using our previously described methods [14]. The distance between the center of the optic disc and the center of the fovea was also calculated for each subject from this scaled data. The mean optic disc-fovea distance was 4.52 ± 0.34 mm (mean disc-fovea angle was 5.7 ± 2.9°). To account for these between subject variations in the position of the disc and the fovea, additional scaling and rotation of the images was performed to ensure that the center of the fovea and the center of the disc were in the same relative positions for each subject, using an anatomical standardization approach. This additional scaling ensured that the relative locations of the major anatomical landmarks of the posterior segment (i.e. the disc and the fovea) remained constant between subjects, which allowed the data to be compared reliably between subjects with a variety of refractive errors.

2.2 Overview of wide-field thickness maps and segmentation methods

Following data collection, all OCT images were analyzed using custom developed algorithms to segment and montage the data across the 60° by 25° retinal region for each subject. Automated segmentation methods based upon graph-search theory [10, 21, 23] were used to extract the three layers of interest (the ILM, RPE and CSI) in each image. An experienced masked observer, checked the integrity of the automated segmentation of each of the boundaries of interest, and manually corrected any segmentation errors. The position of the optic nerve head boundary, (corresponding to the termination of Bruch’s membrane/the opening of Bruch’s membrane) was also manually marked by a second experienced masked observer (Fig. 1). Using the corrected layer data, three retinal thickness volume maps and three choroidal thickness volume maps were derived for each of the acquired scans (central, nasal and temporal).

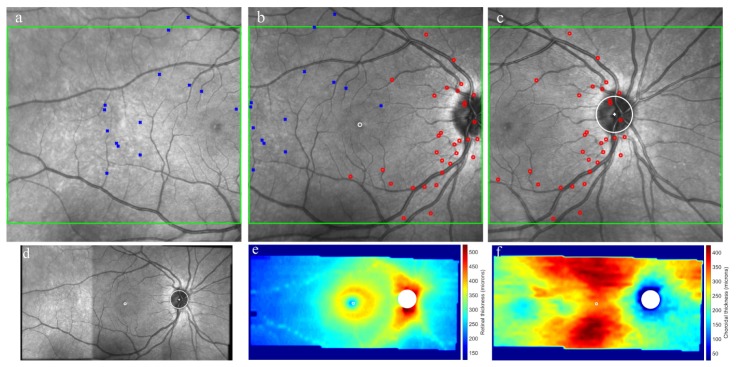
The three 3D OCT scans were acquired at different but overlapping locations of the posterior segment of the eye (i.e. foveal, nasal and temporal retina). The proposed scheme to combine the data from the three scans uses some aspects introduced by Brown and Lowe [49] in their image stitching algorithm. Other methods of OCT image montaging using the en-face image of the eye have also been proposed [36, 37, 50]. Using the SLO image, which provides a high resolution en-face image of the retina, the data from the three SLO images were aligned and combined into a single wide-field en-face retinal image. Common features in the overlapping portions of the SLO images (e.g. retinal blood vessels) were initially identified using an automated image processing procedure based upon an invariant feature based approach, specifically the Scale Invariant Feature Transform (SIFT) [51]. Figure 2(a)-2(c) presents a representative example of the three acquired SLO images (i.e. nasal, central, temporal), with a number of the corresponding SIFT features used to match overlapping regions of the images. The algorithm was used to find geometrically consistent feature matches with a Random Sample Consensus (RANSAC) scheme to solve for the homography between pairs of images. This RANSAC scheme helps to identify outliers and estimate the homography model. This provides a method to align and then blend together the three SLO images, using multi-band blending methods to ensure a smooth transition between images and create a single wide-field SLO retinal image. The multi-band blending technique, proposed by Burt and Adelson [52], blends low frequencies over a large spatial range and high frequencies over a short range. Since the OCT B-scans are precisely registered to the en-face retinal SLO images, the transformation used to combine the three en-face images into a single wide-field fundus image, is then applied to the OCT thickness data in order to create wide-field retinal and choroidal thickness maps, covering approximately a 60° by 25° retinal region. Figure 2(d)-2(f) presents data, including the wide-field fundus en-face image and its corresponding retinal and choroidal thickness maps.

Fig. 2.

Example of a wide-field montage data analysis. SLO images (FOV 30° x 30°) from the spectral domain OCT captured at different retinal locations (a-temporal, b-central and c-nasal). The green box indicates the area covered by the OCT scans (FOV 30° x 25°), while the marks (blue square, red circles) show common features in the overlapping portions of the SLO images identified using the SIFT approach. The bottom row presents the resulting blended/registered data for the en-face SLO image (FOV 60° by 30°) (d) as well as its corresponding retinal thickness map (e) and choroidal thickness map (FOV 60° x 25°) (f). The thickness was calculated using the axial method.

2.3 Thickness calculations

Thickness is a measurement of the distance between two points within opposite layers (or surfaces if volumetric data are considered). The methods here are described with respect to layers, since they are applied to two dimensional data (i.e. B-scans), however, extension of these methods to volumetric data is straight forward. Although the layers between which the tissue thickness measures are derived are well-defined and unambiguous, in OCT imaging of the eye, a specific point on one layer does not have a clearly defined corresponding/associated point in the other layer. Thus, here we consider methods for uncoupled layer thickness measures that do not have a priori point associations between the two layers.

The methods used to calculate thickness are described below. For practical reasons all the images are rescaled into 1 to 1 scale (micron), as this simplifies the coding of the algorithm.

Axial. This is the standard method used in most current studies and commercial instruments. Conceptually it is very simple and measures the distance between the two layers vertically, along the columns of the B-scan (i.e., A-scan). Given that this is the most common method used by current clinical instruments, in this work the axial method is used as a reference metric to allow comparison with the other proposed metrics.

Minimum distance (shortest distance). Requires a simple search approach method to solve the minimum distance between a specific point in the layer to the opposite layer located the shortest distance away. The inner most layer (closer to the top of the B-scan) is taken as the starting point while the outer layer represents the finishing point. This concept has been used in the past for OCT images of glaucoma subjects using manual analysis (i.e. software calipers) [38, 53] as well as automated methods [54]. The minimum distance was calculated as the minimum Euclidean distance.

Minimum distance averaged. The minimum distance can be asymmetric, thus the thickness may not be the same when the starting and finishing layers are interchanged. To compensate for this, the minimum distance is calculated twice (one from the inner to outer layer and vice versa), then the two thickness values are averaged along each A-scan location [43].

Normal along a reference layer. Taking one of the layers as a reference, the thickness is calculated as the intersection of the two layers along the specified layer’s normal. The RPE is taken as the reference layer and used to calculate the normal to this surface. The RPE marks the transition between the retina and choroid, and in subjects free of ocular pathology, is typically a smooth, well-defined layer. This layer is used in the calculation of both thicknesses (i.e. retina and choroid) and serves well as a reference layer. This method has been proposed in other studies using manual software calipers [39, 40] as well as automated analysis [41].

Normal along an averaged layer. When none of the layers are suitable as a reference layer for the calculation of the normal, a nested layer can be used. This could be the case in eyes with pathology, such as changes in RPE regularity due to drusen [55]. The procedure first creates a nested layer as the averaged position of the inner and outer layers. This nested layer normal provides a constraint for finding the corresponding point on the opposite surface that is less prone to producing outliers [43]. Taking the nested surface as a reference, the thickness is calculated as the intersection along the normal to this layer.

Laplace. Initially proposed by Jones [42] to map cortical thickness of the brain using MRI, this method has also been used to map rodent OCT retinal thickness [56]. Laplace’s equation enables a mathematical description of the continuity of any physical field of forces and has been applied to gravitation, mechanics, electrodynamics, thermodynamics etc. Geometrically, Laplace’s equation can be generalized to describe any set of nested surfaces (“equipotential surfaces”), which may transform smoothly and continuously their topology in space. To obey Laplace’s equation one has to assume a certain “conservation law” that each small region on the initial surface has a corresponding region on the transformed “equipotential surface” characterized by zero net energy flowing through those regions. Following the concept of Jones et al [42], distances between centers of those pairs of small regions will determine the mapping of thickness. In the case of mapping retinal layers, such an approach is reasonable since cells in each layer are connected to each other creating a set of topologically separate “equipotential surfaces”.

Mathematically Laplace’s equation has the following mathematical form:

$${\nabla }^2\psi =\frac{{\partial }^2\psi }{\partial x^2}+\frac{{\partial }^2\psi }{\partial y^2}=0$$

Laplace’s equation is used to solve the potential between the two surfaces, by setting each of them with different potential. The thickness is defined as the length of the line of flow between the two surfaces. Interestingly these lines have desirable properties: they are orthogonal to each surface, do not intersect, and are nominally parallel. A number of computational methods are available to solve Laplace’s equation; here the Jacobi method is used. Thus, the Laplacian equation is solved iteratively throughout the entire data set, while keeping the boundaries fixed. The equation takes the form of

$${\psi }_{i+1}(\mathrm{x},\mathrm{y})=\left[{\psi }_i(\mathrm{x}+\Delta \mathrm{x},\mathrm{y})+{\psi }_i(\mathrm{x}-\Delta \mathrm{x},\mathrm{y})+{\psi }_i(\mathrm{x},\mathrm{y}+\Delta y)+{\psi }_i(\mathrm{x},\mathrm{y}-\Delta y)\right]/4$$

Where ${\psi }_i(\mathrm{x},\mathrm{y})$is the value at x,y in the ith iteration. Convergence is measured by the total field energy over all the pixels.

$${\epsilon }_i={{\displaystyle \sum \left({\left(\Delta {\psi }_i/\Delta x\right)}^2+{\left(\Delta {\psi }_i/\Delta y\right)}^2\right)}}^{1/2}$$

When the ratio $\left({\epsilon }_i-{\epsilon }_{i+1}\right)/{\epsilon }_i$ becomes smaller than a predefined threshold (10⁻⁵ in our simulations), iterations stop. The gradient, ψ, uses a simple two point difference. Finally streamlines are computed at every pixel by integrating the tangent vector field using Euler’s method. It is important to note that while most of the considered metrics are based upon relatively simple concepts with no physical basis, the Laplace thickness is based on a physical model.

3. Results and discussion

3.1 Validation of the montage techniques

To validate the automated procedure used to align and blend the SLO images, each of the SLO image-pairs was manually analyzed to identify landmarks (generally retinal blood vessel bifurcations) within each of the overlapping regions for SLO image-pairs. Eight landmarks per overlapping region were identified, 16 in total per subject considering both overlapping regions (temporal-central and central-nasal). These manually marked points (on the original SLO image) were then transformed using the transformation derived from the automated analysis of the SLO images, and the Euclidian distances between coupled points was calculated. Figure 3 presents an example of the aligned and blended SLO images, together with the landmarks manually identified by the observer. Similar to this example, the blended data for all subjects showed a smooth transition between overlapping SLO images with good continuity of the vasculature in the overlapping regions, thus exhibiting good qualitative alignment overall. The mean and standard deviation of the error (between the location of the corresponding manually marked landmarks in the wide-field aligned and blended SLO image) over all landmarks and subjects also showed a good agreement (4.31 ± 2.56 pixels, 25.8 ± 15.3 microns). With no statistically significant difference (p>0.05) observed between the aligned regions (temporal-central 4.81 ± 1.83 pixels, 28.8 ± 10.9 microns; central-nasal 4.63 ± 2.68 pixels, 27.7 ± 16.0 microns).

Fig. 3.

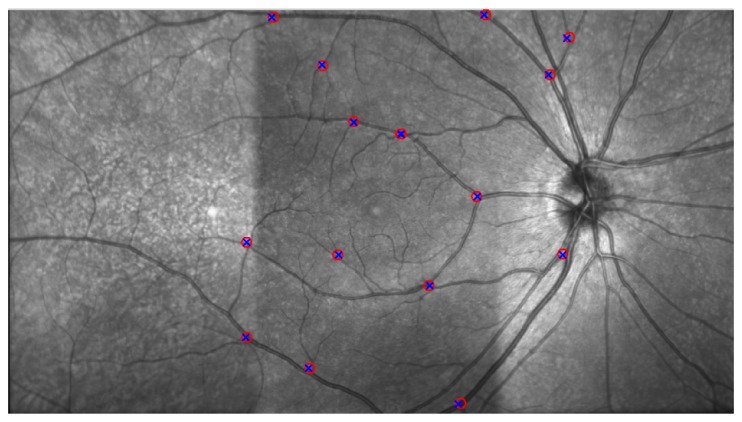
A representative example of an aligned and blended SLO image, formed by three overlapping images. A smooth transition of the retinal vasculature can be observed, along with good alignment of the manually selected points used to validate the automatic procedure. Eight landmarks per overlapping region were identified in each of the SLO image-pairs (circle, cross), 16 in total per subject considering both overlapping regions (temporal-central and central-nasal).

3.2 Example B-scan: application on tilted B-scans

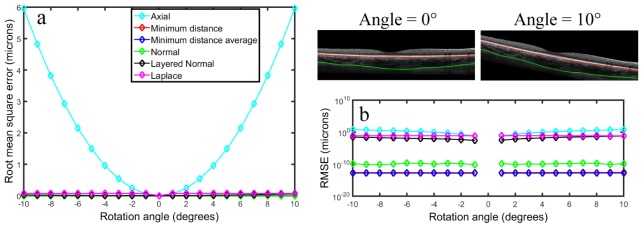
To systematically examine the effects of image tilt upon each of the thickness metrics, a single B-scan image from a representative subject was analyzed multiple times using each of the thickness metrics after being sequentially tilted (around the center of the image) through +/−10 degrees in 1 degree increments. This simulation (the rotation of the B-scan image) aims to replicate a scan acquired under suboptimal conditions. For each degree of image tilt, the choroidal thickness was calculated across the B-scan and the root mean square error (RMSE) between the original thickness (no tilt) and the tilted image was calculated. Figure 4 illustrates the effect of image tilt on the choroidal thickness calculation. A similar effect was observed for the retinal thickness. The axial thickness metric is substantially affected by image tilt, however, thickness values calculated using the other metrics, do not show an obvious bias due to image tilt, with all RMSE <0.08 microns. The error in the axial thickness associated with image tilt has been highlighted by other researchers [26–28], which emphasizes the need to capture B-scans which are relatively flat, however, this may not be possible during wide-field imaging of the eye’s posterior segment, due to the natural curvature of the retina, which is relatively flat centrally but more curved in peripheral regions.

Fig. 4.

Root mean square error (RMSE) calculated as the difference between the choroidal thickness at the rotated angle and the no tilt image for the different metrics considered in this study (a) and the log version of the same graph (b). A representative example of the original B-scan (0 degree angle) and its tilted version (10 degree angle) is also provided.

3.3 Comparison of axial versus proposed methods

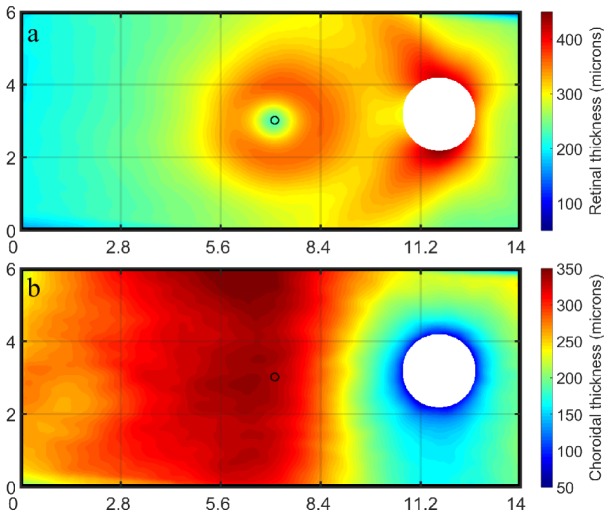
To assess the performance of the different metrics while calculating thickness in OCT images, the segmentation data were used to extract wide-field retinal and choroidal thickness maps. As described above, an anatomical standardization approach was applied to reduce the potential confounding influence of between subject variability in the position of retinal landmarks [48,57]. Figure 5 presents the group mean thickness maps for all subjects calculated using the axial thickness method. Taking this thickness metric as a reference, the difference between the axial method and each of the proposed metrics (i.e. axial – alternative metric) was calculated across the entire thickness map for all subjects. Thus negative difference values indicate an underestimation of tissue thickness by the axial method compared to the alternative metric, while positive values indicate an overestimation. Figure 6 and Fig. 7 present the results for the retinal and the choroidal thickness data respectively. For these two plots, the group mean difference is presented in the left column and the corresponding significance map is presented in the right column for each method. The significance map presents the p-values from a two-tailed paired t-test performed on the difference at each data point, and is divided into three bins, non-significant (p>0.05), significant (0.05< p >0.00001) and highly significant differences (p<0.00001).

Fig. 5.

Group mean (n = 43) retinal thickness map (a) and choroidal thickness map (b) using the axial thickness metric. The optic nerve head corresponding to the maximum size of the group has been masked from the image. The central circle indicates the foveal location. The x and y axes are in mm.

Fig. 6.

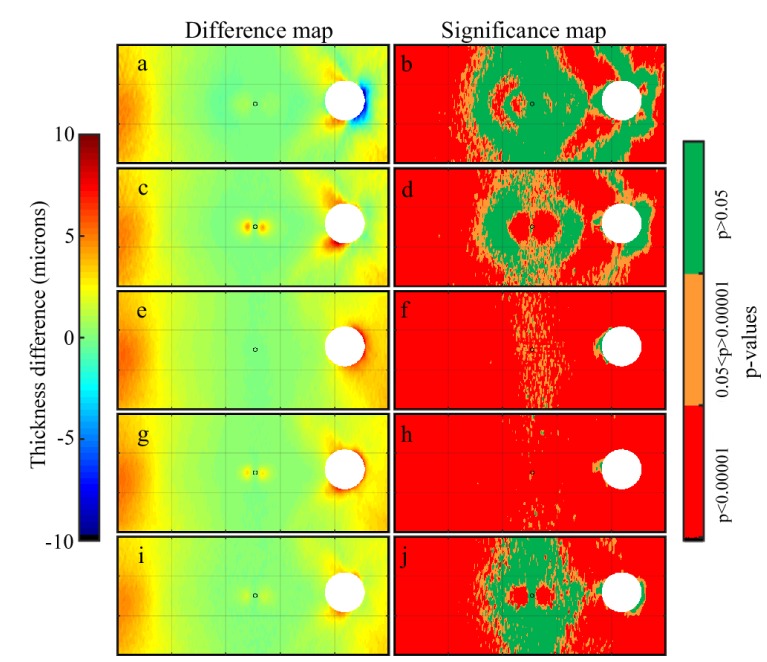
Group mean retinal thickness difference maps (left) and significance maps (right) (n = 43) for the considered alternative thickness metrics, including the (a-b) normal, (c-d) layered normal, (e-f) minimum distance, (g-h) minimum distance averaged, (i-j) Laplace. For reference, the central fovea is marked with a circle while the optic nerve head (ONH) is masked from the analysis, given that no thickness data can be extracted within this region. The size of the ONH in the figure corresponds to the maximum ONH size of all subjects. Negative difference values indicate an underestimation of tissue thickness by the axial method compared to the alternative metric, while positive values indicate an overestimation. P-values in the significance map are from a two-tailed paired t-test performed on the difference at each data point.

Fig. 7.

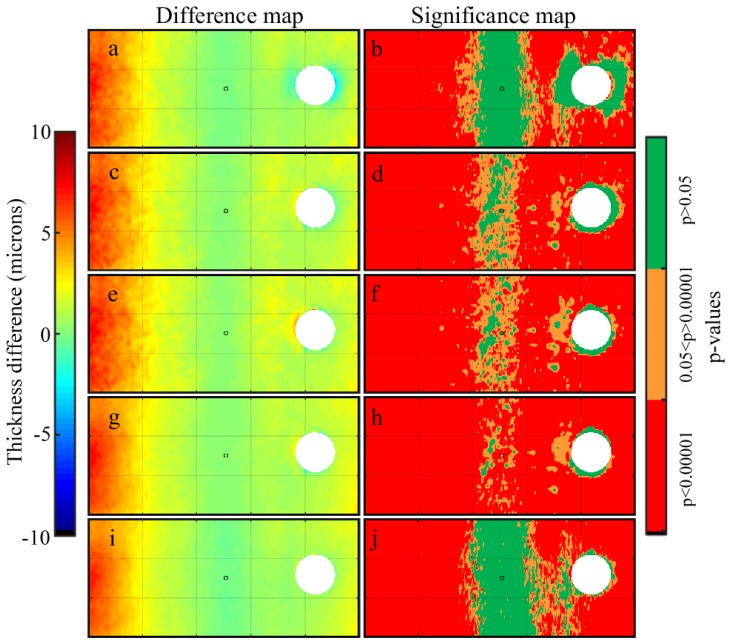
Group mean choroidal thickness difference maps (left) and significance maps (right) (n = 43) for the considered alternative thickness metrics, including the (a-b) normal, (c-d) layered normal, (e-f) minimum distance, (g-h) minimum distance averaged, (i-j) Laplace. For reference, the central fovea is marked with a circle while the optic nerve head (ONH) is masked from the analysis, given that no thickness data can be extracted within this region. The size of the ONH in the figure corresponds to the maximum ONH size of all subjects. Negative difference values indicate an underestimation of tissue thickness by the axial method compared to the alternative metric, while positive values indicate an overestimation. P-values in the significance map are from a two-tailed paired t-test performed on the difference at each data point.

Overall, the mean differences tend to be smaller at the foveal centre and increase towards the periphery. This positive difference in the periphery can be appreciated in all the alternative methods, which indicates that the axial thickness approach tends to overestimate the tissue thickness in these regions. For both the retinal and choroidal maps considered in this study, the mean difference values ranged up to 10 microns.

3.4 Effect of refractive error on the thickness metrics

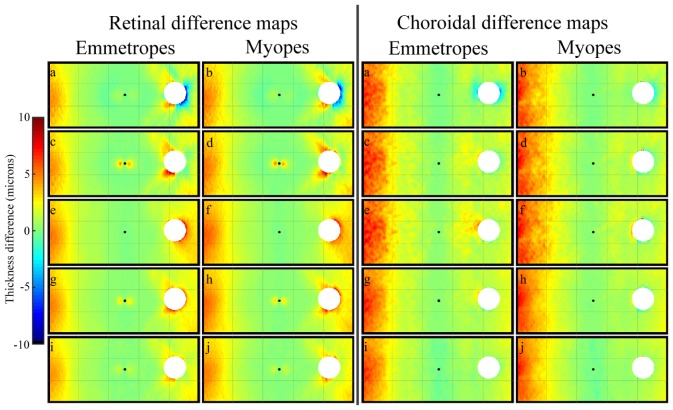
To assess the effect of refractive error on the thickness metrics, the subjects were classified based upon the non-cycloplegic spherical equivalent refraction (SER) of their right eye as being either myopic (SER≤ −0.75 D; n = 24; mean SER −3.11 ± 2.06 D; mean cylinder −0.38 ± 0.45 D) or emmetropic (SER between −0.50 D and + 1.00 D; n = 19; mean SER + 0.26 ± 0.44 D; mean cylinder −0.25 ± 0.31 D). For these two refractive groups the percentage area over the entire map containing highly significant thickness differences (p<0.00001) compared to the axial metric were calculated. Table 1 presents this percentage for the retina and choroid in myopes and emmetropes for each of the different thickness metrics. For all alternative metrics, the myopes had larger percentages of highly significant differences, for both the retina and the choroid. Differences in retinal shape between myopes and emmetropes have been previously reported [58], and this is the most likely explanation for the larger differences in comparison to the axial thickness metric observed in the myopic subjects. Additionally, the choroid maps were also typically found to exhibit larger areas of significant difference compared to the retinal maps. To further examine the effects of refractive error, the mean thickness difference maps (i.e., axial minus proposed metrics) for myopes and emmetropes were investigated separately for the retina as well as the choroid (Fig. 8). Although slightly larger differences were observed in the myopes, in general the distribution and magnitude of differences was similar between the two groups, which strengthens the idea that these results are not substantially biased by the difference in the anatomical features associated with refractive error.

Table 1. Percentage of the map with highly statistically significant differences (p<0.00001) between the axial thickness map and the alternative method for both retinal and choroidal maps and myopic and emmetropic subjects.

	Retina		Choroid
Axial versus	Emmetropes	Myopes	Emmetropes	Myopes
Normal	6.35	23.07	16.22	27.08
Layered Normal	10.58	33.72	25.51	33.76
Minimum distance	30.52	62.36	30.46	37.44
Minimum distance average	41.77	71.29	48.67	58.41
Laplace	27.54	43.79	30.32	44.13

Fig. 8.

Group mean retinal (left subplots) and choroidal thickness difference maps (right subplots). Each group presents maps for emmetropes (left) and myopes (right) for the considered alternative thickness metrics, including the (a-b) normal, (c-d) layered normal, (e-f) minimum distance, (g-h) minimum distance averaged, (i-j) Laplace. For reference, the central fovea is marked with a circle while the optic nerve head (ONH) is masked from the analysis, given that no thickness data can be extracted within this region. The size of the ONH in the figure corresponds to the maximum ONH size of all subjects. Negative difference values indicate an underestimation of tissue thickness by the axial method compared to the alternative metric, while positive values indicate an overestimation.

4. Conclusions

Current axial thickness calculations provide a straightforward, computationally efficient way to extract thickness values from OCT images. However, as demonstrated in this paper, this thickness metric can be biased under certain conditions that should be considered. Our findings indicate that both image tilt and the shape (i.e. curvature) of the posterior segment appear to bias axial thickness calculations. These unwanted effects become more significant when imaging in the periphery of the posterior segment, since apparent tilt and curvature of the retina are more prominent. Thus, alternative approaches to estimate tissue thickness are of interest in ophthalmic applications. Although the effects of image tilt on axial thickness measures have been demonstrated previously [26–28], our current paper provides the first systematic investigation of five alternative metrics for quantifying tissue thickness in OCT images of the posterior eye.

Overall, the results of the current study have shown that while errors in thickness calculations are typically of small magnitude (<10 microns), they are highly statistically significant, and should therefore be taken into consideration, particularly for some research applications. Errors associated with axial thickness metrics are likely to increase when images are not acquired under optimal conditions (i.e. tilted B-scans) and when imaging larger, or more peripheral regions of the posterior segment using wide-field scanning methodologies [29, 30, 35, 36]. Our results show that the error, defined as the difference between the axial and the other alternative thickness metrics, systematically increases with increasing eccentricity from the foveal center, most likely due to the geometry of the eye. This may also be significant when imaging small animal eyes [56] or the posterior segment of eyes with different geometries (i.e. myopic versus emmetropic eyes) [58]. Although the results presented in this paper are restricted to the posterior segment of the human eye, the methods could also be applied to OCT thickness estimations of the anterior segment. Given that the curvature of the anterior segment (e.g. the cornea) is typically steeper than the posterior segment, the alternative metrics presented may prove useful in future work examining anterior segment thicknesses. A limitation of the results presented here is that we have analyzed standard OCT images (i.e., uncorrected from optical distortions). Although this is common practice for most clinical studies, the posterior segment in standard OCT images has been shown to be flatter than published values for the normal eye [46]. Thus, full distortion corrected OCT images should incur a greater axial thickness error than those presented here. Future work combining OCT image correction and the proposed thickness metrics should provide a more accurate estimate of the true tissue thickness.

Additionally, a scheme to blend OCT data, using the SLO en-face image, has been presented and evaluated. Although the introduction of long-range OCT light sources and OCT systems capable of panoramic imaging [30, 59] may reduce the need for such a scheme, current instruments can only scan a limited region of the posterior segment. Therefore, this technique, which provides an automated algorithm to image (and quantify) a wider area of the posterior segment, is clinically relevant and could be used to increase our knowledge of retinal and choroidal morphology, beyond the central macular region typically imaged.

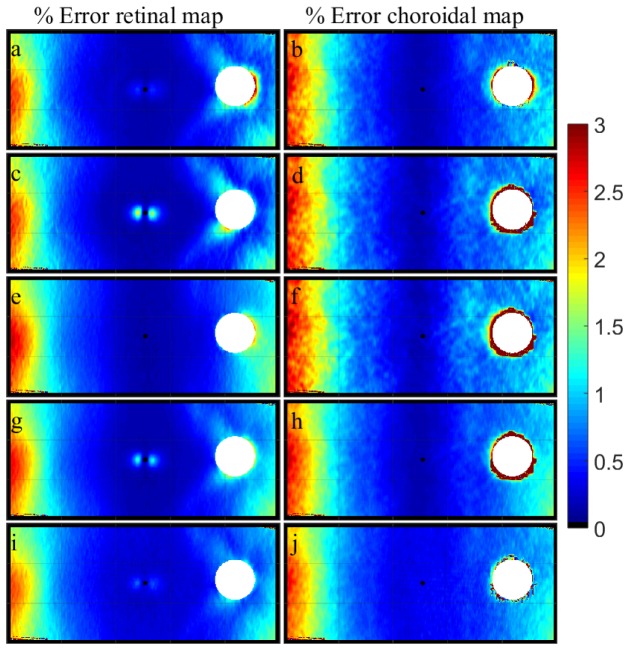
Comparing the results across the wide-field posterior segment image, all the alternative thickness metrics provided comparable results and similar trends (i.e. the axial thickness calculation tends to overestimate the tissue thickness). However, it is important to note that the peripheral OCT images were captured while the eye was turned to fixate the non-central target (ensuring the measured area was relatively flat with respect to the instrument reference plane), which minimizes the error associated with the axial metric. Thus, scans acquired using single-shot wide-field scanning methodologies may yield larger errors. Previous publications [31, 60] have discussed the implications of the overestimation of thickness calculations using axial methods, and estimated this error to be ~1.5% for choroidal thickness estimates over a 6 mm wide region [60] and ~4% error for a wider 60 degree field [31]. For comparative purposes the percentage error maps for our axial thickness data and each of the proposed metric were also calculated (Fig. 9). Values of up to 3% error were obtained in the most peripheral region of the retinal and choroidal thickness maps (60° x 25°).

Fig. 9.

Group mean retinal (left) and choroidal (right) percentage thickness error maps (n = 43) for the considered alternative thickness metrics, including the (a-b) normal, (c-d) layered normal, (e-f) minimum distance, (g-h) minimum distance averaged, (i-j) Laplace. For reference, the central fovea is marked with a circle while the optic nerve head (ONH) is masked from the analysis, given that no thickness data can be extracted within this region. The size of the ONH in the figure corresponds to the maximum ONH size of all subjects.

Although the errors in thickness measures were most prominent in the periphery, retinal thickness errors in regions close to foveal center were also observed with some of the proposed metrics (most obviously in the layered normal and the minimum distance averaged methods). These errors are most likely due to the curvature of the foveal pit, which appears to have biased the thickness measures of the proposed alternative metrics. Since these small errors were not evident with all of the proposed metrics, they appear to be an artefact associated with these proposed metrics rather than an overestimation of the true thickness by the axial method.

The normal and the layered normal thickness metric provide an intuitive way to compute the thickness, but since these approaches rely on a reference surface to obtain the normal to the layer, the method may present issues if this reference layer is not smooth and homogeneous in its curvature. For example, it can result in an apparent outlier around the ONH, given that the RPE tends to bend in this region, and also at the foveal center when the reference layer involves the more sharply curved ILM boundary. It should also be noted that our current data set involved only normal, healthy subjects. Therefore, for certain pathologies (such as macular drusen) in which the RPE contour is altered and shows disruption in its normally smooth curvature, metrics based on a normal to this layer are likely to provide misleading values. Similarly, the minimum distance metrics, which have also been used in the past to quantify OCT thickness data [38, 53, 54], can experience problems. This metric provides the closest points on the opposing layer, however, it loses unique point association between the two layers (i.e. consecutive thickness values along the tissue can have the same finish point), and can also yield thickness measures that appear to be too small compared to the other metrics in certain regions (e.g. at the foveal centre and close to the optic nerve head boundary).

Although computationally more complex, the Laplace method represents an interesting approach, since it is based on a physically meaningful model. This model has been extensively used to map the thickness of brain tissue with MRI [42], and has the potential to be useful in OCT imaging. Unlike the other proposed models, the lines traced to obtain the thickness values have desirable properties (orthogonal to each surface, do not intersect, and are nominally parallel). Since its initial introduction in MRI data [3], the Laplace thickness method has been investigated to improve a number of aspects such as computational [61], volumetric aspects of the computation [62] or issues related to boundary conditions [63]. Adaptation of these strategies for the calculation of OCT tissue thickness is likely to also benefit the accurate and reliable estimation of the tissue thickness.

In summary, this study demonstrates that the traditional axial method of thickness calculation can be influenced by factors such as image tilt and curvature in OCT images of the retina and choroid. In the central retina, thickness differences were of small magnitude, and unlikely to be of clinical significance. However, the magnitude of error increased in more peripheral regions of the retina and choroid. Although further research is needed to examine the performance of the proposed thickness metrics in cases of ocular pathology, the alternative thickness metrics should be considered, particularly in wide-field OCT imaging applications.