Abstract
Retinal hemodynamics is important for early diagnosis and precise monitoring in retinal vascular diseases. We propose a novel method for measuring absolute retinal blood flow in vivo using the combined techniques of optical coherence tomography (OCT) angiography and Doppler OCT. Doppler values can be corrected by Doppler angles extracted from OCT angiography images. A three-dimensional (3D) segmentation algorithm based on dynamic programming was developed to extract the 3D boundaries of optic disc vessels, and Doppler angles were calculated from 3D vessel geometry. The accuracy of blood flow from the Doppler OCT was validated using a flow phantom. The feasibility of the method was tested on a subject in vivo. The pulsatile retinal blood flow and the parameters for retinal hemodynamics were successfully obtained.
OCIS codes: (100.2960) Image analysis, (100.6890) Three-dimensional image processing, (170.4500) Optical coherence tomography, (170.4460) Ophthalmic optics and devices
1. Introduction
Currently, serious retinal disorders, such as glaucoma, diabetic retinopathy, and age-related macular degeneration, are the leading cause of irreversible blindness around the world [1]. To better understand the pathophysiology of early disorders, one essential measurement is retinal blood flow. Retinal blood flow is also an important clinical parameter to monitor disease progression and assess treatment [2–4]. In the past, a variety of techniques have been used for imaging ophthalmic vessels, such as fluorescein angiography, laser Doppler flowmetry [5], and ultrasound Doppler imaging [6]. However measurement of the absolute blood flow is still a challenge because of its pulsatile nature.
Doppler optical coherence tomography (OCT) enables the imaging of retinal blood velocity in human eyes [7, 8]. The principle of Doppler OCT is based on measuring the Doppler shift caused by the moving blood cells relative to the OCT probing light. For this method, there are two key parameters for the measurement of absolute retinal blood flow: Doppler shift and Doppler angle. Improvements in Fourier domain OCT imaging speed have enables the easy measurement of Doppler shifts within the vessels. However, the Doppler shift only represents the flow component along the probing light beam. The Doppler angle, which is defined as the angle of the probing light beam with respect to the flow vector, is also required to calculate the absolute blood flow. Several techniques have been developed to measure the Doppler angle. Several investigators proposed a method using a bi-directional OCT system that can illuminate the sample from two angles [9–11]. These systems can measure absolute blood flow regardless of the incidence angle. However it requires modification of the hardware, which may not be easy to incorporate in existing commercial OCT instruments already in clinics. Another approach uses double scans with different radii to extract the Doppler angle [12, 13], which requires careful estimation of the vessel center. An angle-independent method was also proposed by using en face images [14]. However, this method requires a high-speed swept-source OCT system, and the measured flow in the blood vessels is restricted to a relatively high speed.
Currently, increasing acquisition speed of Fourier domain OCT allows volumetric imaging of the in vivo retina. The Doppler angle can be extracted from volumetric data directly. Recently, a three-dimensional (3D) segmentation method based only on the intensity of the image was proposed for reconstruction of blood vessels centered at the macular region [15]. However the contrast between the static tissue and blood vessels based on intensity image was low. The absence of good contrast made it difficult to determine the boundaries of the vessels. Thus new techniques are required to distinguish blood vessels from static tissue for 3D reconstruction of the retinal vessels. Some investigators proposed methods that use the volumetric data of Doppler OCT to obtain the vessel orientation [16, 17]. However the contrast of the blood vessels in Doppler OCT is not high with low flow velocities or with large Doppler angles. Compared with Doppler OCT for measuring flow velocity, OCT angiography methods map the microvascular networks without providing information on flow velocity [18–23]. This method is less sensitive to the Doppler angle, and therefore it is suitable for imaging the microvasculature of the fundus [24]. It also provides good contrast of retinal vessels in the optic disc [21]. Thus OCT angiography may be an ideal tool for 3D reconstruction of retinal vessels to yield the vessel orientation.
In this paper, we present a new method for measuring absolute retinal blood flow in human eyes using the combined techniques of OCT angiography and Doppler OCT. We used the intensity-based Doppler variance (IBDV) method to perform OCT angiography, and we developed a 3D segmentation method to extract 3D boundaries of the retinal vessels and obtain Doppler angles. The combined techniques enabled us to measure in vivo pulsatile retinal blood flow in the optic disc with angle correction. We were then able to evaluate the parameters of retinal hemodynamics, including peak systolic velocity, average velocity, end diastolic velocity, pulsatility index (PI), and resistance index (RI).
2. Methods
2.1 Spectral domain optical coherence tomography
In this study, a custom-built spectral domain OCT (SD-OCT) system was used to acquire fundus images and data of the optic disc area. A similar system for imaging the posterior segment of the eye was described previously [25]. Briefly, a superluminescent diode (BLM2-D; SuperLum Diodes Ltd., Moscow, Russia) with a center wavelength of 850 nm and a bandwidth of 100 nm was used as the light source. In this system, a charge-coupled device camera (AViiva EM4; E2v Technologies, Chelmsford, England), with a line rate scan of up to 70,000 A-lines per second, was used to record the interference signal. In this study, to balance the system sensitivity and acquisition time, the acquisition rate was set at 50 kHz. Assuming a refractive index of 1.38 [26], the axial resolution was 3.1 μm, and the image range of depth was 1.98 mm at the retina. The signal to noise ratio of the system was 110 dB near zero imaging depth at the acquisition rate of 50 kHz. The sample arm power was 0.8 mW, which was consistent with safe ocular exposure limits set by the American National Standards Institute. A 6 dB sensitivity roll-off from 0.05 mm imaging depth to1.0 mm imaging depth was measured.
Custom-built OCT data acquisition and processing software was developed, and real-time preview of the acquired data was achieved with the help of a graphics processing unit accelerated computing technique. For raster scans, each set of 3D measurements was composed of 128 slices of 400 A-lines over a 4.0 × 4.0 mm area. Each slice was composed of eight sequential B-scans at the same position [27]. The total acquisition time for the 3D volumetric data was approximately 8.0 seconds.
For circular scans, each frame was composed of 2,048 A-lines with a 2-mm diameter, which acquired almost 20 frames during one cardiac cycle (75 beats per minute). The image speed was fast enough to acquire the pulsatility of the blood flow. Each circular scan was composed of 150 frames and the corresponding acquisition time was approximately 6.0 seconds. Thus at a low heart rate (60 beats per minute), the flow data for at least 5 cardiac cycles was covered. The subject was asked to fixate on an internal target during image acquisition.
2.2 OCT angiography and three-dimensional segmentation of blood vessels
The intensity-based Doppler variance method [20, 27] was used to visualize the retinal vasculature. The data was acquired by raster scan at the optic disc area as described (Section 2.1). The variance value () was calculated by sequential B-scans at the same position, which achieved a high time difference () [27]
| (1) |
where was the number of the depth points that were averaged and was the number of B-scans at the same position. In this application, the was set at two and the was set at eight. denotes the amplitude value that was extracted from the complex OCT data.
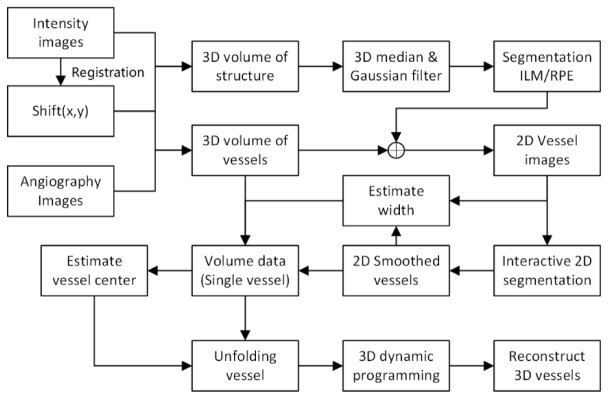
Before segmenting vessels of the optic disc area, motion artifacts due to heartbeat and respiration were corrected [28]. A subpixel registration algorithm [29] was used to align sequential slices based on intensity images. Corrections for lateral and axial movements, ∆x and ∆z respectively, between sequential slices were also applied in the OCT angiography images. The two-dimensional (2D) locations of retinal vessels were first extracted based on en face views of an OCT angiography image. Based on previous work [27], a 3D expansion of a dynamic programming method was then modified and improved to segment the cylindrical shape of the retinal vessels with the help of 2D structural geometry of the vessel. Figure 1 outlines the core steps of the vessel segmentation algorithm for the optic disc area. The method can be summarized in four steps as follows:
Fig. 1.
Flow diagram for three-dimensional segmentation of retinal blood vessels. ILM, inner limiting membrane; RPE, retinal pigment epithelium; 3D, three dimensional; 2D, two dimensional.
-
(1)
3D segmentation of inner limiting membrane (ILM) layer: the ILM, which is the first layer of the retina, was segmented to improve the quality of the en face views of OCT angiography images as previously described [27]. Briefly, the method transformed the boundary detection problem to an optimization problem that searched for an optimal path. Before segmentation, a 3D median filter was applied to the volumetric data. Then the initial location of the ILM was determined from the A-scan profile. Finally, the location of the ILM layer was refined by using a 3D expansion of a dynamic programming method [27].
-
(2)
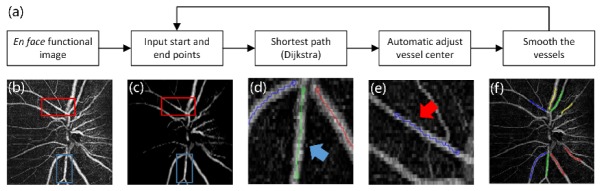
2D geometry structure extraction of retinal vessels: Fig. 2(a) shows the flow diagram of 2D geometry structure extraction. Before segmenting the retinal vessels, a median filter was applied to en face views of OCT angiography images with a window size of pixels (Fig. 2(b)). Thus the signals for smaller vessels were attenuated while the signals for larger vessels were preserved (Fig. 2(c)). A manual graphical user interface was developed to identify the start and end points for each vessel. These points were usually defined as locations of crossovers or bifurcations. Then a graph-based segmentation algorithm was used to detect the location of the target vessels [30]. The final shortest path of each vessel was detected by using Dijkstra’s algorithm [31]. Compared with the dynamic programming method, the computational complexity for Dijkstra’s algorithm was greater, but this algorithm had the advantage of detecting the boundaries that were almost perpendicular to the image (Fig. 2(d)). Figure 2(f) shows the segmented result of the retinal vessels.
Fig. 2.
2D geometry structure extraction of retinal vessels. (a) Flow diagram of interactive 2D segmentation. (b) En face view of retinal vessels in the optic disc area. (c) The filtered image of retinal vessels in the optic disc area. (d) and (e) Illustration of segment results at the start and end points. (f) 2D geometric structure of the vessels.
-
(3)
Volumetric data extraction for single vessels: The vessels in the optic disk area were divided into different segments and represented with different colors (Fig. 2(f)). Thus, the 3D data set for a single vessel could be extracted based on the 2D geometric structure. The vessel width was first estimated based on the en face view of the angiography image. The vectors that were perpendicular to the vessel direction were calculated, and the data of the 2D images were resampled along the vectors (Fig. 3(a)). Then the summed data along the direction of flow in the vessel and width were estimated by obtaining the full width at half maximum of the summed profile (Fig. 3(b)). In the cross-sectional view (depth direction) of the angiography image along direction of flow (Fig. 3(c)), the upper and lower boundaries were detected with a 2D-based dynamic programming method [32], and depth information was obtained by averaging the two boundaries, thus generating a preliminary estimation of the vessel center.
Fig. 3.
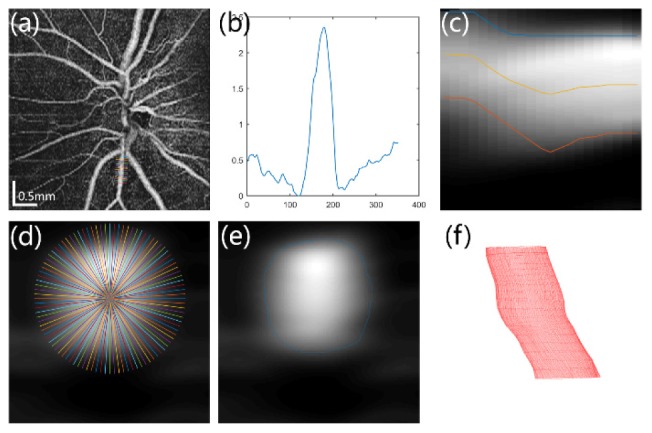
Diagram of 3D boundary detection for a retinal vessel. (a, b) Estimate of vessel diameter. (c) Estimate of vessel depth. (d) Illustration of resample and “unfolding” of 3D data set for retinal vessel. (e) Cross-section view of boundary detection results. (f) 3D visualization of vessel morphology.
-
(4)
3D boundary detection for retinal vessels: to apply the 3D segmentation algorithm, the extracted volumetric data of the vessel were required to be warped-around the boundary of the vessel. In the plane perpendicular to the vessel direction, the preliminary vessel center was considered as the origin. Figure 3(d) illustrates the method for unfolding the vessel boundary into a terrain-like surface. We then applied a 3D expansion of a dynamic programming method to the resampled 3D data set to obtain the boundaries of the retinal vessels. These steps yielded a cross-sectional view of boundary detection (Fig. 3(e)) and 3D visualization of vessel boundaries (Fig. 3(f)). Finally, manual inspection and a few minor corrections were still required, especially near crossover or bifurcation regions. A graphical user interface-based program was developed to accelerate the process. The final vessel center was determined by ellipse-fitting of vessel boundaries on the plane that was perpendicular to vessel direction. The 3D vessel direction was obtained by calculating the tangent of the vessel center line.
2.3 Doppler OCT and angle correction
Phase resolved Doppler OCT obtains the Doppler shift by calculating phase differences between sequential A-scans. The phase difference () can be expressed as [33, 34]:
| (2) |
where was the complex signal at depth on the A-scan. was the number of the depth points that were averaged, and was the average number of A-lines. For Doppler OCT, was set at 4 and was set at 1 to balance axial and lateral resolution. Motion artifacts [28] will also induce small phase shifts despite the use of a high-speed camera. An averaged shifted histogram method was used to estimate the bulk motion Doppler shift to compensate for axial eye movement [35].
Phase change is proportional to the velocity of the moving sample. The velocity along the incident beam direction () can be written as [33]:
| (3) |
where was the central wavelength of the OCT system, was the refractive index of the human retina, and was the time difference between adjacent A-lines. Combined with the Doppler angle (), which was extracted from OCT angiography images (Section 2.2). The absolute velocity of the blood () was calculated as:
| (4) |
3. Doppler validation
3.1 Experiment setup
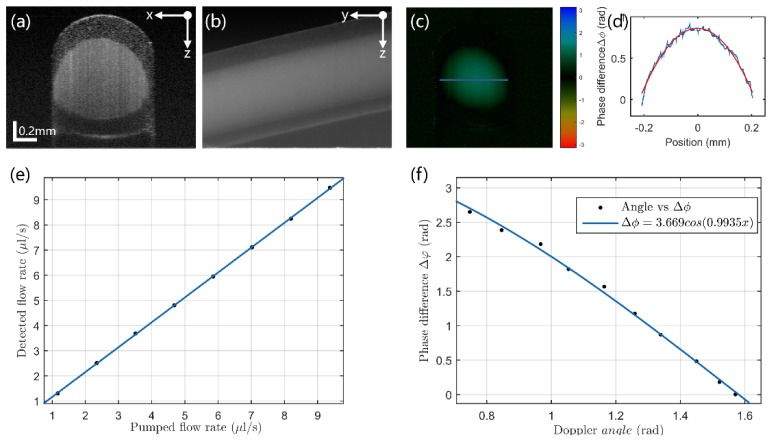
The accuracy of the Doppler OCT method was tested on a flow phantom (Fig. 4(a)). The blood flow was simulated by a milk phantom moving in a transparent tube with an inner diameter of 800 μm. For better penetration, the milk phantom was diluted with 20% water to achieve a refractive index of 1.34. The flow was controlled by a syringe pump, and the tube was mounted on a rotational stage. For each measurement, the raster and repeat scans were performed sequentially. In the raster scan, the direction of the flow was obtained. Figure 4(b) shows the lateral projection of the flow phantom ( plane) at a Doppler angle of 77.4°. Each repeat scan was composed of 100 frames, and the scan was set perpendicular to the tube ( direction). Figure 4(a) and 4(c) show cross-sectional views of the OCT intensity image and Doppler OCT image. Figure 4(d) shows the phase difference profile that was marked by the blue line passing though the center of the tube in Fig. 4(c). The phase difference at the center of the tube () was obtained by using a parabolic fitting. According to Poiseuille's law, the volumetric flow rate () was calculated as follows [36]:
| (5) |
where was the refractive index of the flow phantom, and was the diameter of the tube.
Fig. 4.
Validation of Doppler OCT. (a) OCT intensity image of the flow phantom at a Doppler angle of 77.4°. (b) Lateral projection of flow phantom at a Doppler angle of 77.4°. (c) Doppler OCT image corresponding to the intensity image in (a). (d) The blue line is the phase difference profile that is marked by the blue line in (c), and the red line is the result of parabolic fitting. (e) Comparison between pumped flow and detected flow with the fixed Doppler angle. (f) Validation of relationship between Doppler angle and phase difference with fixed pumped flow.
3.2 Doppler OCT flow phantom results
We first verified the accuracy of flow measurements with the fixed Doppler angle. The pump speed was increased linearly from 0.57 mm/min to 4.55 mm/min while keeping the Doppler angle constant. A total of 8 measurements, corresponding from 1.17 μl/s to 9.37 μl/s, was conducted. In addition, we also verified the correlation between Doppler angle and phase difference. The angle between the phantom flow and the light beam was decreased almost linearly from 89.9° to 42.8° while the pump speed was fixed at 1.71 mm/s. A total of 10 measurements was collected.
There was an excellent correlation between the nominal pump flow rate as set by the syringe pump and the detected flow rate (Fig. 4(e)). The average deviation between the nominal flow rate and the detected rate was less than 0.12 μl/s. According to Eqs. (3) and (4), the Doppler angle and phase difference followed a cosine function. The measured data was well-fitted by a cosine function, with a correlation coefficient () of 0.99 (Fig. 4(f)). A slight variation may have been associated with phase stability of the SD-OCT system. Nevertheless, the Doppler OCT system accurately measured the flow rates in a tube, and the Doppler angle was accurately corrected by extracting the direction of the tube.
4. In vivo imaging of retinal vessels in the optic disc
4.1 Participant and experiments
The left eye of a healthy subject was enrolled to demonstrate the feasibility of the method. This study was approved by the Institutional Review Board for Human Research of Wenzhou Medical University. The subject, who provided informed consent, was treated according to tenets of the Declaration of Helsinki.
Each measurement was composed of the two consecutive scan modes, raster and circular, described in Section 2.1. The raster scan data was used to obtain the morphology of the retinal vessels, and the pulsatile retinal blood flow was acquired from the circular scan data. The subject was asked to sit in front of the OCT probe with chin and forehead against the rest and fixate on a target during the acquisition. In addition, three repeat measurements were performed sequentially within 15 minutes to test the repeatability of the method. The subject was also asked to hold his head position steady during one of the three measurements, and the position of optic disc was aligned between each measurement.
After the OCT angiography and Doppler OCT images were obtained from each measurement, the positions of the two modality images were registered together (Fig. 5). Eight major vessels (4 arteries and 4 veins) were chosen to obtain the pulsatility of blood flow. The location of the circular scan corresponding to the OCT angiography image is indicated by the blue circular line in Fig. 5. The locations of measurement points for blood flow (Fig. 5, short red lines) were determined by finding the intersections between the measured vessels and the circular scan. For each cardiac cycle, peak systolic velocity () and end diastolic velocity () were measured. The average velocity () was defined as: . In addition, the PI was defined as , and the RI was defined as .
Fig. 5.
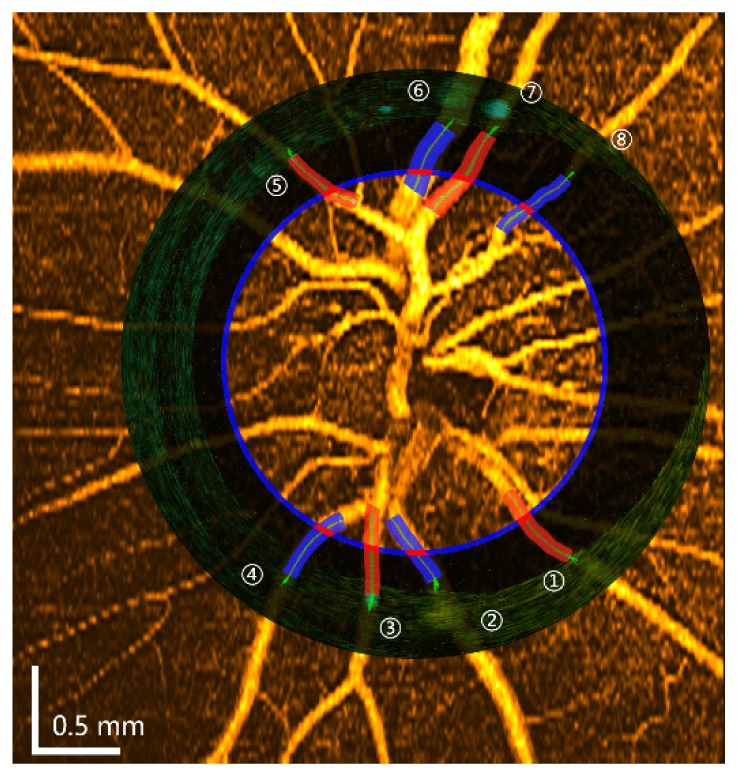
Registration between OCT angiography and Doppler OCT. The blue circular line indicates the circular scan position corresponding to the en face view of the OCT angiography image. The circular view of the Doppler image was merged with the angiography image. Eight major vessels were selected, and the locations of the measured vessels were indicated by short red lines. The boundaries of the measured vessels were also overlaid on the angiography image, and the green lines indicate the center of each vessel. The red color indicates arteries and blue color indicates veins.
4.2 OCT angiography and 3D segmentation of retinal vessels
OCT angiography was performed on raster scan data, and most of the large vessels were covered within an area of 4.0 × 4.0 mm. The morphology of the retinal vessels in the optic disc was obtained by the IBDV method. Figure 6(a) shows an en face view of the intensity image at the optic disc at 250 μm below the ILM layer boundary. Figure 6(d) shows the corresponding en face view of the OCT angiography image. Compared with the intensity image, the microvascular network of the retina at the optic disc can be visualized in OCT angiography images. Although the major retinal vessels were also visualized in the intensity image (Fig. 7(a)), OCT angiography (Fig. 7(b)) provided clearer boundaries of the vessels, and smaller vessels could also be visualized (Fig. 6(d)). The IBDV method provide high sensitive contrast to vessels that are nearly perpendicular to the probing beam [34]. Therefore, compared to the 3D reconstruction method based on the intensity image [15] or the Doppler OCT image [17], the OCT angiography method provides a more suitable technique for 3D segmentation and reconstruction of the retinal vessels. The 3D volume rendering of the retinal vessels in the optic disc is shown in Fig. 6(b). The 3D morphology of the retinal vessels was clearly visualized.
Fig. 6.
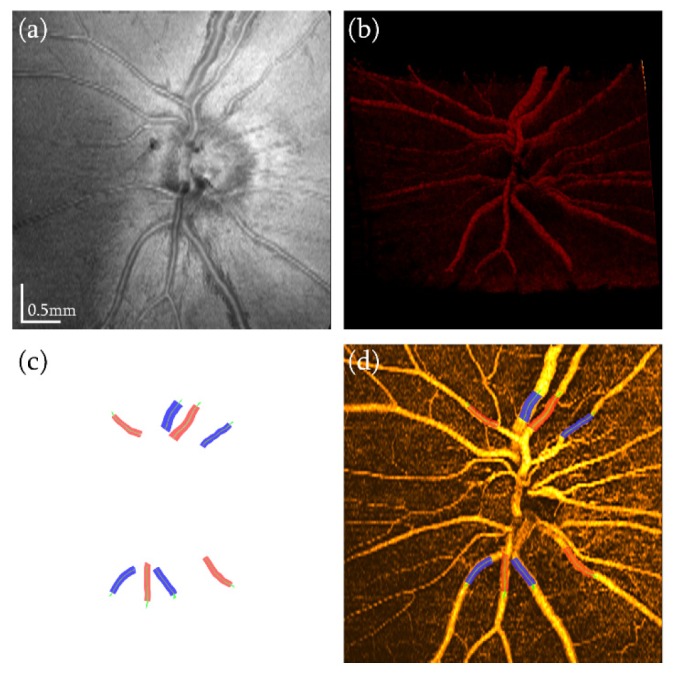
OCT angiography and three-dimensional segmentation of retinal vessels on the optic disc. (a) En face view of the intensity image and the OCT angiography image. (b) Rendered 3D volume of OCT angiography. (c) 3D reconstruction of the selected vessels. The green lines indicate the center of each vessel. The red color indicates arteries and blue color indicates veins. (d) OCT angiography image overlayed with boundaries of the reconstructed vessels.
Fig. 7.
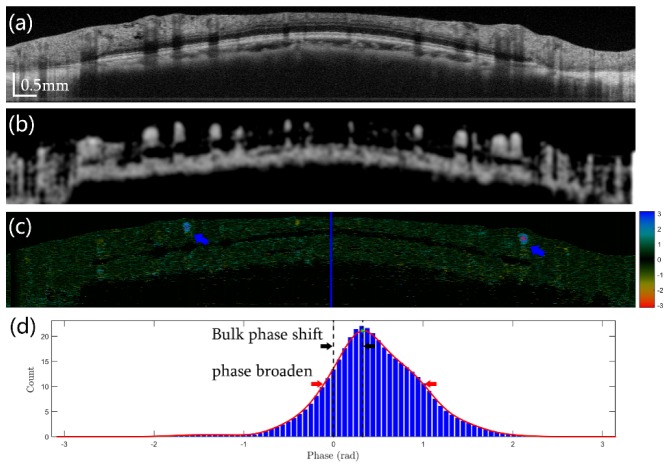
Comparison between OCT angiography and Doppler OCT. (a) Intensity image of optic disk area with circular scan. (b) OCT angiography image and (c) Doppler image in which two vessels required phase unwrapping (blue arrows). (d) Averaged shifted histogram of the A-scan marked by the blue line in (c). The black arrows indicate bulk phase shift and red arrows indicate phase noise of the in vivo retina.
The boundaries of the eight retinal vessels identified in Fig. 5 were also successfully segmented. Figure 6(c) shows the 3D reconstruction of the eight vessels. The red color indicates artery and blue color indicates vein. The basic idea of OCT angiography was to separate moving objects from static tissue. Any changes in light scattering properties within the light beam can generate a signal for OCT angiography. Capillaries with an average diameter of 6~9 μm can still be visualized despite the fact that the lateral resolution is around 20 μm in the OCT system [18, 20, 21, 37]. However the limited lateral resolution could cause the diameter of small vessels to appear slightly larger in OCT angiography images. In this study, we focused on the hemodynamics of relative large vessels, i.e., those that were larger than 50 μm in diameter. The estimated diameters of these larger vessels is not significantly affected by the 20-µm lateral resolution of the OCT angiography images. The boundary of the larger vessels can still be accurately estimated by applying a correction factor. In addition, the uniform expansion of the boundary for vessels does not introduce any obvious errors in the estimation of the vessel center.
Shadowing artifacts [21, 27, 38] may also cause detection errors for retinal vessels. This effect is obvious in highly reflective layers such as the retinal pigment epithelium (RPE) layer (Fig. 7(b)). However the RPE layer can be excluded because of the low reflectivity of the outer nuclear layer (ONL) layer. In addition, we adjusted the parameters in the 3D dynamic programming method to maintain the round shape of the boundary compared with structure segmentation [27]. Finally, we corrected a few minor errors by manual inspection. Figure 6(d) shows that the en face view of the OCT angiography image and the boundaries of the reconstructed vessels overlap closely.
The centers of the vessels were obtained by ellipse fitting of the vessel boundaries, and the Doppler angles were obtained by calculating the direction of the center lines. The centers and directions of the vessels are indicated by the green lines in Fig. 6(c). The local vessel gradient was calculated from the continuous center line of the vessel. Compared with extracting vessel orientation by using two cross-sectional Doppler images with different radii [12, 13], this method has the advantage of accurate estimation of the Doppler angle. The vessel orientation can also be obtained from the 3D data set of Doppler OCT [16, 17]. However, the pulsatile nature of the blood flow limits the angle measurement, especially at the end of the diastolic phase. In OCT angiography, the contrast of the blood vessels is not obviously affected by changes of blood flow, which may be more suitable for extracting the velocity vector.
4.3 Velocity measurements
Doppler OCT was performed on the circular scans (Fig. 7(a)), and pulsatile flow was analyzed in eight vessels (Fig. 7(b), 7(c)). Figure 7(d) shows the averaged histogram of one A-line scan derived from twenty bins and eight histograms [35]. The bulk motion Doppler shift is marked by black arrows in Fig. 7(d). Figure 7(c) shows the cross-sectional view of the Doppler OCT image with bulk motion Doppler shift by using the averaged shifted histogram method. The phase difference was marked by colors in Fig. 7(c). The blue color indicates outbound blood flow and the yellow-red color indicates inbound blood flow. An unwrapping method was also applied when the phase difference at the center of the vessel was significantly different (≥1.5 rad) from the averaged phase difference (Fig. 7(c)).
The red arrows in Fig. 7(d) show that the phase noise of the in vivo retina was 1.20 rad, which was similar to previously reported values [35, 39]. This phase noise was significantly larger than that from a mirror (0.03 rad) in same SD-OCT system. The low in vivo retinal signal and eye motion may have been the cause of an increased phase noise. The phase noise was reduced by averaging pixels within the vessel:
| (6) |
where is the phase noise and is the number of pixels for averaging. The diameters of the major vessels were larger than 50 μm, which corresponded to an ellipse of pixels. The average phase noise () was reduced to 0.1 rad. The phase noise was further reduced by high oversampling of the vessels, which increases the averaging number . However, this will also increase the sampling interval between frames for the target vessel. Hence it was necessary to obtain a balance between Doppler OCT sensitivity and sampling interval to achieve the most accurate velocity measurements.
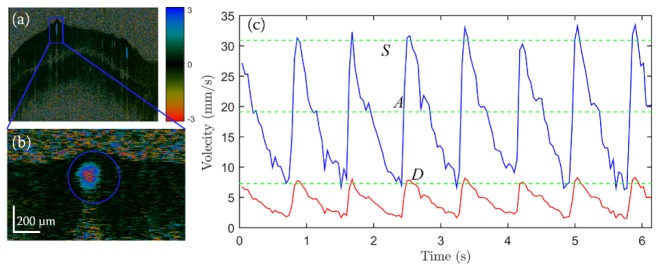
The pulsatile retinal blood flow was imaged by Doppler OCT, and absolute retinal blood flow was obtained by using the Doppler angle that was extracted from the 3D reconstruction of each blood vessel. Figure 8 shows the pulsatile velocity profile of vessel 3 (see Fig. 5) within a time span of ~6 s. The red profile presents the velocity profile before Doppler angle correction, and the blue profile was the corresponding velocity after correction. There was a slight velocity variance between the sequential cardiac cycles. This was probably due to the highly dynamic nature of blood flow. Averaging over several cardiac cycles helps to obtain stable measurements of velocity. The average time interval from diastolic phase to systolic phase was 0.16 s. The sampling rate for pulsatile measurement of blood flow required more than 13 frames per second. In this study, the frame rate for the Doppler scan was 24 frames per second, which is enough for measuring pulsatile blood flow. The green dashed lines from top to bottom denoted peak systolic velocity, averaged velocity and end diastolic velocity, respectively.
Fig. 8.
Pulsatile flow of a retinal vessel. (a) Doppler OCT image for a circular scan of the optic disc. (b) Enlarged Doppler OCT image of the selected vessel marked by the blue rectangle in (a). (c) Pulsatile velocity profile of the selected vessel within a time span of ~6 s. Red profile, velocity before Doppler angle correction; blue profile, corresponding velocity after correction. Green dashed lines: top, peak systolic velocity (S); middle, average velocity (A), bottom, end diastolic velocity (D).
Table 1 shows blood flow measurements of eight retinal vessels. For all of the vessels except numbers 5 and 6, the velocity could be repeatedly measured. The variation for peak systolic velocity among three repeated measurements was smaller than 8.24 mm/s. The variation for end diastolic velocity was smaller than 2.61 mm/s. The measured average velocity in the arteries and veins was consistent with previously reported values [11–13]. The failure in flow measurements for vessels 5 and 6 occurred because the Doppler angle was close to 90 degrees. Subtle measurement errors due to large Doppler angles can lead to significant deviations in velocity estimation. Large Doppler angles also include small phase differences which can degrade measurement accuracy due to phase noise in the system. The PI and RI, which are usually obtained from Doppler ultrasound, can evaluate the elasticity index that is a parameter of blood flow [40, 41] and can also be repeatedly measured [39]. Compared to absolute velocity measurement, PI and RI measurements are more consistent because they are independent of the Doppler angles.
Table 1. Blood flow measurements of retinal vesselsa.
| Vessel No. |
S (mm/s) |
A (mm/s) |
D (mm/s) |
PI | RI |
Artery/Vein (A/V) |
|---|---|---|---|---|---|---|
| 1 | 23.81 ± 8.24 | 13.57 ± 1.77 | 3.32 ± 0.07 | 1.50 ± 0.01 | 0.86 ± 0.00 | A |
| 2 | 8.59 ± 2.00 | 5.79 ± 0.19 | 2.99 ± 0.60 | 0.95 ± 0.09 | 0.63 ± 0.02 | V |
| 3 | 32.20 ± 0.83 | 19.59 ± 0.20 | 6.99 ± 0.22 | 1.29 ± 0.00 | 0.78 ± 0.00 | A |
| 4 | 5.68 ± 1.15 | 3.48 ± 0.45 | 1.27 ± 0.67 | 1.29 ± 0.13 | 0.77 ± 0.02 | V |
| 5 | 25.33 ± 25.74 | 13.99 ± 5.39 | 3.87 ± 4.38 | 1.54 ± 0.12 | 0.84 ± 0.01 | A |
| 6 | N/A | N/A | N/A | N/A | NA | V |
| 7 | 50.20 ± 6.57 | 30.53 ± 2.22 | 10.87 ± 0.20 | 1.29 ± 0.00 | 0.78 ± 0.00 | A |
| 8 | 5.97 ± 0.45 | 3.43 ± 0.28 | 0.88 ± 0.16 | 1.51 ± 0.03 | 0.86 ± 0.00 | V |
aS, peak systolic velocity; A, average velocity; D, end diastolic velocity; PI, pulsatility index; RI, resistance index; N/A, not applicable; rates expressed as means ± standard deviations.
Although the morphology of vessels can be reconstructed from OCT angiography images with a large Doppler angle, there are still challenges in absolute flow measurements because of subtle phase differences caused by the Doppler effect when the vessel is nearly perpendicular to the probing beam. One solution is to ask the subject to fixate on a different target between each measurement. For most of the major vessels, the pulsatility of the blood flow can be measured when the Doppler angle is away from the perpendicular by more than 3 degrees. Another limitation of this method is that there is still slight movement between the raster scan and the circular scan. This requires manual registration between the OCT angiography images and the Doppler OCT images (Fig. 5). This may cause some errors in the estimated location of the measurement points in OCT angiography images. This problem could potentially be solved by adding an eye tracking system with a fundus camera. The lateral motion can be corrected with a phase correlation algorithm that calculates the relative translational offset from fundus images [42].
5. Conclusions
In this study, we proposed a method for the measurement of absolute blood flow at the optic disc area by combining OCT angiography with Doppler OCT. The 3D morphology of retinal vessels in the optic disc was visualized by using an intensity-based Doppler variance method. A 3D segmentation method based on an expansion of dynamic programming was used to extract the 3D boundaries of retinal vessels. Doppler angles were extracted from the vessel boundaries, and the absolute retinal blood flow was obtained by applying an angle correction. The accuracy of Doppler OCT and the relationship with the Doppler angle was validated on a flow phantom. The validated methodology was then used to measure pulsatile retinal blood flow in the optic disc of a subject. The parameters for retinal hemodynamics were successfully measured repeatedly among the major retinal vessels. The pulsatile nature of the blood flow and absolute velocity can be obtained by this method without modification of the hardware. It can easily be incorporated into existing commercial OCT instruments already in clinics. This method has potential for earlier diagnosis and more precise monitoring in retinal vascular diseases.
Acknowledgments
We acknowledge support from the National Major Equipment Program of China (2012YQ12008004 to Lu), the National Nature Science Foundation of China (Grant No. 81170869 and 81570880 to Lu, Grant No. 81400441 to Shen), and the Zhejiang Provincial Natural Science Foundation of China (LY14H180007). Dr. Chen has a financial interest in OCT Medical, Inc., which, however, did not provide support for this work. We thank Dr. Britt Bromberg of Xenofile Editing (www.XenofileEditing.com) for providing editing services for this manuscript.
References and links
- 1.Pascolini D., Mariotti S. P., “Global estimates of visual impairment: 2010,” Br. J. Ophthalmol. 96(5), 614–618 (2012). 10.1136/bjophthalmol-2011-300539 [DOI] [PubMed] [Google Scholar]
- 2.Flammer J., Orgül S., Costa V. P., Orzalesi N., Krieglstein G. K., Serra L. M., Renard J.-P., Stefánsson E., “The impact of ocular blood flow in glaucoma,” Prog. Retin. Eye Res. 21(4), 359–393 (2002). 10.1016/S1350-9462(02)00008-3 [DOI] [PubMed] [Google Scholar]
- 3.Katsi V. K., Marketou M. E., Vrachatis D. A., Manolis A. J., Nihoyannopoulos P., Tousoulis D., Vardas P. E., Kallikazaros I., “Essential hypertension in the pathogenesis of age-related macular degeneration: a review of the current evidence,” J. Hypertens. 33(12), 2382–2388 (2015). 10.1097/HJH.0000000000000766 [DOI] [PubMed] [Google Scholar]
- 4.Gracner T., “Ocular blood flow velocity determined by color Doppler imaging in diabetic retinopathy,” Ophthalmologica 218(4), 237–242 (2004). 10.1159/000078613 [DOI] [PubMed] [Google Scholar]
- 5.Petrig B. L., Riva C. E., “Retinal laser Doppler velocimetry: toward its computer-assisted clinical use,” Appl. Opt. 27(6), 1126–1134 (1988). 10.1364/AO.27.001126 [DOI] [PubMed] [Google Scholar]
- 6.Williamson T. H., Harris A., “Color Doppler ultrasound imaging of the eye and orbit,” Surv. Ophthalmol. 40(4), 255–267 (1996). 10.1016/S0039-6257(96)82001-7 [DOI] [PubMed] [Google Scholar]
- 7.Chen Z., Milner T. E., Dave D., Nelson J. S., “Optical Doppler tomographic imaging of fluid flow velocity in highly scattering media,” Opt. Lett. 22(1), 64–66 (1997). 10.1364/OL.22.000064 [DOI] [PubMed] [Google Scholar]
- 8.Rao B., Yu L., Chiang H. K., Zacharias L. C., Kurtz R. M., Kuppermann B. D., Chen Z., “Imaging pulsatile retinal blood flow in human eye,” J. Biomed. Opt. 13(4), 040505 (2008). 10.1117/1.2967986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Davé D. P., Milner T. E., “Doppler-angle measurement in highly scattering media,” Opt. Lett. 25(20), 1523–1525 (2000). 10.1364/OL.25.001523 [DOI] [PubMed] [Google Scholar]
- 10.Werkmeister R. M., Dragostinoff N., Pircher M., Götzinger E., Hitzenberger C. K., Leitgeb R. A., Schmetterer L., “Bidirectional Doppler Fourier-domain optical coherence tomography for measurement of absolute flow velocities in human retinal vessels,” Opt. Lett. 33(24), 2967–2969 (2008). 10.1364/OL.33.002967 [DOI] [PubMed] [Google Scholar]
- 11.Blatter C., Coquoz S., Grajciar B., Singh A. S. G., Bonesi M., Werkmeister R. M., Schmetterer L., Leitgeb R. A., “Dove prism based rotating dual beam bidirectional Doppler OCT,” Biomed. Opt. Express 4(7), 1188–1203 (2013). 10.1364/BOE.4.001188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang Y., Bower B. A., Izatt J. A., Tan O., Huang D., “In vivo total retinal blood flow measurement by Fourier domain Doppler optical coherence tomography,” J. Biomed. Opt. 12(4), 041215 (2007). 10.1117/1.2772871 [DOI] [PubMed] [Google Scholar]
- 13.Dai C., Liu X., Zhang H. F., Puliafito C. A., Jiao S., “Absolute retinal Blood Flow Measurement With a Dual-Beam Doppler Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 54(13), 7998–8003 (2013). 10.1167/iovs.13-12318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Baumann B., Potsaid B., Kraus M. F., Liu J. J., Huang D., Hornegger J., Cable A. E., Duker J. S., Fujimoto J. G., “Total retinal blood flow measurement with ultrahigh speed swept source/Fourier domain OCT,” Biomed. Opt. Express 2(6), 1539–1552 (2011). 10.1364/BOE.2.001539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Guimarães P., Rodrigues P., Celorico D., Serranho P., Bernardes R., “Three-dimensional segmentation and reconstruction of the retinal vasculature from spectral-domain optical coherence tomography,” J. Biomed. Opt. 20(1), 016006 (2015). 10.1117/1.JBO.20.1.016006 [DOI] [PubMed] [Google Scholar]
- 16.Makita S., Fabritius T., Yasuno Y., “Quantitative retinal-blood flow measurement with three-dimensional vessel geometry determination using ultrahigh-resolution Doppler optical coherence angiography,” Opt. Lett. 33(8), 836–838 (2008). 10.1364/OL.33.000836 [DOI] [PubMed] [Google Scholar]
- 17.Michaely R., Bachmann A. H., Villiger M. L., Blatter C., Lasser T., Leitgeb R. A., “Vectorial reconstruction of retinal blood flow in three dimensions measured with high resolution resonant Doppler Fourier domain optical coherence tomography,” J. Biomed. Opt. 12(4), 041213 (2007). 10.1117/1.2771553 [DOI] [PubMed] [Google Scholar]
- 18.Mariampillai A., Standish B. A., Moriyama E. H., Khurana M., Munce N. R., Leung M. K., Jiang J., Cable A., Wilson B. C., Vitkin I. A., Yang V. X., “Speckle variance detection of microvasculature using swept-source optical coherence tomography,” Opt. Lett. 33(13), 1530–1532 (2008). 10.1364/OL.33.001530 [DOI] [PubMed] [Google Scholar]
- 19.Enfield J., Jonathan E., Leahy M., “In vivo imaging of the microcirculation of the volar forearm using correlation mapping optical coherence tomography (cmOCT),” Biomed. Opt. Express 2(5), 1184–1193 (2011). 10.1364/BOE.2.001184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liu G., Chou L., Jia W., Qi W., Choi B., Chen Z., “Intensity-based modified Doppler variance algorithm: application to phase instable and phase stable optical coherence tomography systems,” Opt. Express 19(12), 11429–11440 (2011). 10.1364/OE.19.011429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yasuno Y., Hong Y., Makita S., Yamanari M., Akiba M., Miura M., Yatagai T., “In vivo high-contrast imaging of deep posterior eye by 1- um swept source optical coherence tomography and scattering optical coherence angiography,” Opt. Express 15(10), 6121–6139 (2007). 10.1364/OE.15.006121 [DOI] [PubMed] [Google Scholar]
- 23.Wang R. K., Jacques S. L., Ma Z., Hurst S., Hanson S. R., Gruber A., “Three dimensional optical angiography,” Opt. Express 15(7), 4083–4097 (2007). 10.1364/OE.15.004083 [DOI] [PubMed] [Google Scholar]
- 24.Nagiel A., Sadda S. R., Sarraf D., “A promising future for optical coherence tomography angiography,” JAMA Ophthalmol. 133(6), 629–630 (2015). 10.1001/jamaophthalmol.2015.0668 [DOI] [PubMed] [Google Scholar]
- 25.Wang Y., Jiang H., Shen M., Lam B. L., DeBuc D. C., Ye Y., Li M., Tao A., Shao Y., Wang J., “Quantitative analysis of the intraretinal layers and optic nerve head using ultra-high resolution optical coherence tomography,” J. Biomed. Opt. 17(6), 066013 (2012). 10.1117/1.JBO.17.6.066013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Nassif N., Cense B., Park B. H., Yun S. H., Chen T. C., Bouma B. E., Tearney G. J., de Boer J. F., “In vivo human retinal imaging by ultrahigh-speed spectral domain optical coherence tomography,” Opt. Lett. 29(5), 480–482 (2004). 10.1364/OL.29.000480 [DOI] [PubMed] [Google Scholar]
- 27.Huang S., Piao Z., Zhu J., Lu F., Chen Z., “In vivo microvascular network imaging of the human retina combined with an automatic three-dimensional segmentation method,” J. Biomed. Opt. 20(7), 076003 (2015). 10.1117/1.JBO.20.7.076003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.de Kinkelder R., Kalkman J., Faber D. J., Schraa O., Kok P. H., Verbraak F. D., van Leeuwen T. G., “Heartbeat-induced axial motion artifacts in optical coherence tomography measurements of the retina,” Invest. Ophthalmol. Vis. Sci. 52(6), 3908–3913 (2011). 10.1167/iovs.10-6738 [DOI] [PubMed] [Google Scholar]
- 29.Guizar-Sicairos M., Thurman S. T., Fienup J. R., “Efficient subpixel image registration algorithms,” Opt. Lett. 33(2), 156–158 (2008). 10.1364/OL.33.000156 [DOI] [PubMed] [Google Scholar]
- 30.Chiu S. J., Li X. T., Nicholas P., Toth C. A., Izatt J. A., Farsiu S., “Automatic segmentation of seven retinal layers in SDOCT images congruent with expert manual segmentation,” Opt. Express 18(18), 19413–19428 (2010). 10.1364/OE.18.019413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cormen T. H., Introduction to algorithms (MIT press, 2009). [Google Scholar]
- 32.Liu X., Shen M., Huang S., Leng L., Zhu D., Lu F., “Repeatability and Reproducibility of Eight Macular Intra-Retinal Layer Thicknesses Determined by an Automated Segmentation Algorithm Using Two SD-OCT Instruments,” PLoS One 9(2), e87996 (2014). 10.1371/journal.pone.0087996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhao Y., Chen Z., Saxer C., Xiang S., de Boer J. F., Nelson J. S., “Phase-resolved optical coherence tomography and optical Doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity,” Opt. Lett. 25(2), 114–116 (2000). 10.1364/OL.25.000114 [DOI] [PubMed] [Google Scholar]
- 34.Liu G., Lin A. J., Tromberg B. J., Chen Z., “A comparison of Doppler optical coherence tomography methods,” Biomed. Opt. Express 3(10), 2669–2680 (2012). 10.1364/BOE.3.002669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14(17), 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 36.Sutera S. P., Skalak R., “The history of Poiseuille’s law,” Annu. Rev. Fluid Mech. 25(1), 1–20 (1993). 10.1146/annurev.fl.25.010193.000245 [DOI] [Google Scholar]
- 37.An L., Shen T. T., Wang R. K., “Using ultrahigh sensitive optical microangiography to achieve comprehensive depth resolved microvasculature mapping for human retina,” J. Biomed. Opt. 16(10), 106013 (2011). 10.1117/1.3642638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Mahmud M. S., Cadotte D. W., Vuong B., Sun C., Luk T. W. H., Mariampillai A., Yang V. X. D., “Review of speckle and phase variance optical coherence tomography to visualize microvascular networks,” J. Biomed. Opt. 18(5), 050901 (2013). 10.1117/1.JBO.18.5.050901 [DOI] [PubMed] [Google Scholar]
- 39.Yu L., Chen Z., “Doppler variance imaging for three-dimensional retina and choroid angiography,” J. Biomed. Opt. 15(1), 016029 (2010). 10.1117/1.3302806 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bellner J., Romner B., Reinstrup P., Kristiansson K.-A., Ryding E., Brandt L., “Transcranial Doppler sonography pulsatility index (PI) reflects intracranial pressure (ICP),” Surg. Neurol. 62(1), 45–51 (2004). 10.1016/j.surneu.2003.12.007 [DOI] [PubMed] [Google Scholar]
- 41.Radermacher J., Mengel M., Ellis S., Stuht S., Hiss M., Schwarz A., Eisenberger U., Burg M., Luft F. C., Gwinner W., Haller H., “The renal arterial resistance index and renal allograft survival,” N. Engl. J. Med. 349(2), 115–124 (2003). 10.1056/NEJMoa022602 [DOI] [PubMed] [Google Scholar]
- 42.Stone H. S., Orchard M. T., Chang E. C., Martucci S. A., “A fast direct Fourier-based algorithm for subpixel registration of images,” IEEE Trans. Geosci. Remote Sens. 39(10), 2235–2243 (2001). 10.1109/36.957286 [DOI] [Google Scholar]