A 32-Channel Combined RF and B₀ Shim Array for 3T Brain Imaging

Abstract

Purpose

We add user-controllable direct currents (DC) to the individual elements of a 32-channel radio-frequency (RF) receive array to provide B₀ shimming ability while preserving the array’s reception sensitivity and parallel imaging performance.

Methods

Shim performance using constrained DC current (±2.5A) is simulated for brain arrays ranging from 8 to 128 elements. A 32-channel 3-tesla brain array is realized using inductive chokes to bridge the tuning capacitors on each RF loop. The RF and B₀ shimming performance is assessed in bench and imaging measurements.

Results

The addition of DC currents to the 32-channel RF array is achieved with minimal disruption of the RF performance and/or negative side effects such as conductor heating or mechanical torques. The shimming results agree well with simulations and show performance superior to third-order spherical harmonic (SH) shimming. Imaging tests show the ability to reduce the standard frontal lobe susceptibility-induced fields and improve echo planar imaging geometric distortion. The simulation of 64- and 128-channel brain arrays suggest that even further shimming improvement is possible (equivalent to up to 6th-order SH shim coils).

Conclusion

Including user-controlled shim currents on the loops of a conventional highly parallel brain array coil is feasible with modest current levels and produces improved B₀ shimming performance over standard second-order SH shimming.

INTRODUCTION

In vivo B₀ inhomogeneity remains an obstacle to many scientific and clinical applications of MRI. Off-resonance increases line widths and complicates differentiation of chemical species in NMR spectroscopy. Similarly, B₀ inhomogeneity prevents effective fat saturation and water–fat separation (1). During radio-frequency (RF) excitation, off-resonance reduces the effectiveness of many types of RF pulses (2). Finally, in echo train methods such as echo planar imaging (EPI), field inhomogeneity shortens T₂*, leading to image blurring in the phase encode direction as well as geometric distortion from phase accrual during the echo spacing period (3). Signal void artifacts occur in regions of poor B₀ homogeneity in gradient-echo imaging due to through-slice dephasing of the signal. These effects in EPI (and the related image blurring effect in spiral imaging) constrain the use of fMRI and diffusion in important brain regions with poor B₀ homogeneity such as the orbital–frontal cortex, inferior temporal lobes, brainstem, and spinal cord. Whereas parallel imaging methods (4) lower the effective echo spacing in EPI, and thus reduce the distortion proportionally, they do not fully mitigate it (5). Thus, any B₀ shimming solution must retain access to state-of-the-art parallel imaging factors so that both mitigation methods can be brought to bear.

B₀ shimming of local susceptibility fields is challenging because the field perturbations are subject-dependent and localized in space, rendering them difficult to cancel with low-order polynomials. This requires a shim coil set containing high spatial-frequency components. Given such a coil array, an improved shim can almost always be created by optimizing the currents on a slice-by-slice basis, which requires the ability to dynamically update the shim currents during the sequence. Dynamic shimming imposes additional requirements on the shim amplifiers, such as high voltage compliance if the coil inductance is large—and eddy-current preemphasis and/or shielding coils if the shim conductors are near the metallic bore of the scanner.

The most common shimming approach uses sets of spherical harmonic (SH) shim coils up to second order (6), which are independently driven either statically (7) or dynamically (8,9). Whereas third- to fifth-order shim insert coils might be of benefit, particularly at ultrahigh field (10), their disadvantages include high inductance, decreasing efficiency at higher orders, and expensive shim current supplies. Moreover, SH shim coils also induce both short- and long-lived eddy currents that necessitate the use of preemphasis on dynamic shimming waveforms (11).

The limitations of SH shim coils have motivated the recent introduction of single-coil (12) and multicoil (MC) (13,14) shimming systems consisting of independently driven loop coils arrayed close to the body. The spatially nonorthogonal basis set of fields generated by the coil array has been shown to improve shimming of the mouse brain (13) and human brain (14), as compared with third-order SH insert coils. Benefits of MC shim arrays include their low inductance, minimal induced eddy currents, low-cost current supplies, and high efficiency for generating ΔB₀ in the body. Recent simulations indicate that MC shims generate SH fields with equivalent or greater efficiency than conventional SH coil geometries, showing an efficiency gain of 50% at the second order and 100% at the third order, where efficiency is defined as Hz per ampere per meter of wire used (15).

In the initial realization of MC shims for the human brain at 7 tesla (T), 48 coils each with 100 turns of wire (supplied with up to ±1 A [ampere]) were arrayed on a cylinder in circular bands toward the top and bottom of the head (14), leaving a 10-cm gap in the middle for an encircling array of eight transmit–receive RF coils. In such a design, the shim coils consume valuable space near the RF array, constraining the placement of additional RF coil elements. Conversely, the presence of the encircling RF coils prevents the placement of shim loops freely around the perimeter of the head. This raises the question of how to best integrate RF and MC shim arrays. Both types of arrays function the most efficiently when their elements are placed as close to the body as possible. Moreover, both arrays benefit from incorporating large numbers of elements to provide maximum degrees of freedom. These analogous design guidelines, as outlined in Table 1, put the two array systems in sharp conflict over the space immediately adjacent to the body.

Table 1.

Synergies Between RF Receive Arrays and Multi-Coil Shim Arrays

Design Principle	Benefit for RF Receive Array	Benefit for MC Shim Array
Place loops as close to body  as possible.	Increase B1− sensitivity and SNR.	Generate ΔB0 shim field in body with  high efficiency.
Use as many coils/degrees  of freedom as practical.	Improve parallel imaging performance.	Cancel higher-order B0 inhomogeneity.

MC, multicoil; RF, radio frequency; SNR, signal-to-noise ratio.

A recently proposed solution to this “real estate” problem is to integrate RF reception and B₀ shimming functions into the same conducting loop. Single-channel prototypes have been demonstrated at 3T (16,17) and 7T (18) using inductive chokes to bridge shim current into the RF loop and across tuning capacitors. In initial experiments, the coils demonstrated the ability to generate shim fields while simultaneously receiving RF signals (and, optionally, during RF transmission as well (16,17)) with signal-to-nose (SNR) equivalent to an RF-only coil element (18). When the loops are placed 1 to 2 cm away from the head, B₀ offsets of several hundred Hz/A are generated in regions of the brain and surrounding sinuses (18).

The goal of the present work is to determine, first by simulation and then by building a 32-channel 3T brain array, whether single-turn MC shim arrays can reproduce the performance of multi-turn arrays when shimming efficiency is optimized by moving the loops as close to the body as possible, and to assess the impact of the modifications on the RF performance of the array. To this end, we use a close-fitting helmet for the substrate of the combined RF-shim array, as is commonly used for RF-only arrays (19). To help compensate for the lower inductance of the single-turn loops, we increase the current maximum from ±1 A to ±2.5 A per coil.

The present work builds on early results shown in abstract form for our 32-channel RF-shim array (20). In parallel with this work, another group has also recently demonstrated the feasibility of a 3T combined RF-shim array, with 32 RF channels and 16 shim channels driven in symmetric pairs by 8 direct currents (DC) shim supplies (21,22).

We use simulations to assess B₀ shimming performance as a function of number of array coil elements, expanding on previously published simulation results (17,18). Performance is evaluated using both a simulated shim of an acquired ΔB₀ brain field map, as well as principal component analysis (PCA) to estimate the number of independent spatial eigenmodes contained in each set of ΔB₀ shim fields. Additionally, single-channel combined RF-shim loops for 3T and 7T are compared, and the outlook for RF-shim arrays at 7T is briefly discussed. We then describe the fabrication and testing of a 32-channel RF-shim array for a clinical 3T human scanner. The array is used to compensate in vivo B₀ homogeneity and reduce distortion in high-resolution EPI as compared with conventional second-order shims.

METHODS

Simulations

Simulations are performed on 50 slices of a gradient-recalled echo-based field map acquired on a healthy volunteer using the 3T Siemens Magnetom Skyra scanner (Siemens AG, Healthcare Sector, Erlangen, Germany) after applying the system’s second-order SH global shimming (100 × 100 × 50 matrix, 240 × 240 × 100 mm field of vision [FOV]). The field map, ΔB₀ (x,y,z), is calculated as a signed field offset map relative to the average B₀ field. Five RF-shim brain array coil geometries are simulated (8, 32, 48, 64, and 128 channels) as single-turn loops tiled on the surface of a helmet in a “soccer ball” pattern with critical overlap nearest-neighbor decoupling (19). For comparison, the 100-turn 48-channel cylindrical shim array described in (14) is also simulated. The ΔB₀ field map for each coil is obtained using Biot-Savart (Ripplon Software Inc; New Westminster, BC, Canada) calculation software (23) and retaining the z-component. As a benchmark, the ΔB₀ maps are also shimmed using SH basis sets ranging from the third to sixth order. The ΔB₀ standard deviation (SD) (σ_B0) is computed on a slice-wise and whole-volume basis for each array.

Optimal currents for each coil element are calculated as those needed to minimize the least-squares deviation of the total field (ΔB₀(x,y,z) + shim coil created field) in the brain region on both a global whole-brain (50 slices) and slice-optimized basis (1-cm slabs centered on slice of interest). Constrained optimization is performed using the MATLAB function “fmincon” (Mathworks, Natick, MA), with the current amplitude in each coil limited to less than ±2.5 A. The spherical harmonic field amplitudes are unconstrained.

Following Breuer’s analysis of receive arrays (24), we perform PCA on the shim array fields. For an array with N_c loop elements, the three-dimensional (3D) coil ΔB_o field maps are vectorized and used to populate the rows of a N_c × N coil sensitivity matrix, C, for a coil array size N_c, with N voxels over the entire ROI. This matrix is then used to form a square N_c × N_c covariance matrix, R = C C^T. The eigenvalues for R are calculated and sorted. The cumulative sum of eigenvalues is plotted against the number of coil principal components. A threshold of 80% is chosen as an arbitrary cutoff to capture the majority of the meaningful (significant energy) orthogonal spatial modes.

Hardware

The proof-of-concept experimental RF-shim array is based upon a functioning 32-channel 3T RF receive array that we previously built (25) for the Siemens Skyra scanner (Magnetom; Skyra, Tim 4G, dual density signal transfer, Siemens AG). The 32-channel brain array is built on a close-fitting plastic (acrylonitrile butadiene styrene) helmet created using a rapid prototyping 3D printer (Dimension SST 1200es, Dimension, Inc., Eden Prairie, MN). Coil loops with a diameter of 9.5 cm made of AWG16 solid wire are arrayed in a hexagonal–pentagonal pattern, with critical overlap to decouple neighboring elements. Other details of the RF coil are given in (25).

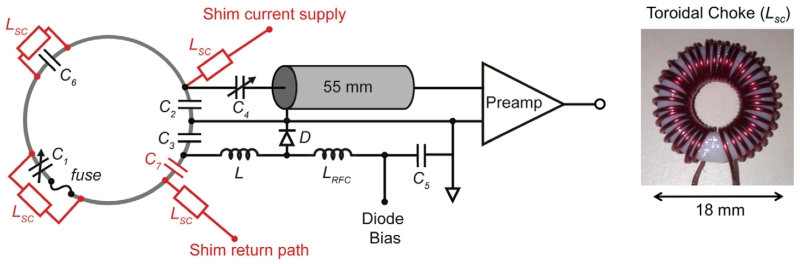
All wires and components in the shimming subsystem are designed to carry at least 5 A of current without over-heating. DC shim current is brought to each loop via twisted pair AWG18 copper wires. Each coil uses its own ground return path. Inductive chokes are used to block RF from leaking onto the twisted pair, as well as to bridge shim current across the two distributed RF tuning capacitors and the RF safety fuse in each element (Fig. 1). Due to space constraints, the two eye loops are joined as a single shim coil, resulting in only 31 independent shim channels. The initial and completed coil arrays along with DC feed wires are shown in Figure 2.

FIG. 1.

Diagram of RF-shim coil element (9.5-cm diameter) with conventional RF components shown in black. The components in red add shimming functionality to the coil. Toroidal chokes (inset photo at right) pass shim current in and out of the loop and bridge the distributed RF capacitors and safety fuse. A blocking capacitor, C₇, is added near one of the feed points to contain the shim current within the loop. As in a conventional receive coil, detuning is achieved when inductor L forms a parallel LC blocking circuit with capacitor C₃ when the PIN diode D is turned on. Capacitor C₄ transforms the coil impedance to 50 Ω. (Values: C₁ = 32 pF, C₂ = C₃ = 33 pF, C₄ = 11 pF, C₅ = C₇ = 1 nF, C₆ = 27 pF, L = 48 nH, L_RFC = 3.3 μH, L_SC = 1 μH). RF, radio frequency.

FIG. 2.

Top and bottom halves of coil before and after conversion to a combined RF-shim array. Four toroidal inductive chokes are used on each element to block RF from the shim current path and/or to bridge tuning capacitors. Care is taken to route DC lines at least 2 cm from the RF preamps to prevent feedback oscillations. For the final 25 cm before reaching the loops, chokes and LC trap circuits are used on the twisted pair to suppress RF pickup during transmission. Digitally programmable shim supply boards (right-most column) provide DC current up to ±2.5 A per channel. The output op amps are mounted to heat sinks with in-laid piping for optional water cooling. DC, direct current; RF, radio frequency.

The wires pass out of the central region, where strong RF transmit fields are generated by the body coil, in a flat tray containing the 25 cm of DC twisted pair nearest the helmet. High-impedance blocking elements are placed along each wire at intervals of 20 cm or less to prevent the wires from picking up transmitted RF (causing heating and reducing the body coil efficiency). Alternating between chokes and resonant inductor-capacitor (LC) trap circuits along the length of each wire minimizes coupling between the connected elements of each type, which could shift their resonant frequencies and reduce the traps’ RF blocking efficiency. For the twisted-pair DC lines on the helmet, care must taken to route the wires at least 2 cm away from the RF preamplifier inputs or outputs in order to prevent oscillations arising from feedback between the preamp output and input ports.

A self-shielding toroidal choke geometry (Fig. 1) is chosen to prevent gradient switching and transmitted RF from inducing voltage across the choke, potentially disrupting shim currents or causing heating. 3D-printed toroidal substrates measuring 18-mm wide are wound with 35 turns of AWG22 copper wire to provide an inductance of approximately 1.0 μH, corresponding to a reactance of ~775 Ω at the scanner frequency of 123.25 MHz.

Shim currents are supplied using a low-cost (~$100), in-house constructed class-AB amplifier circuit based on TI-OPA549 (Texas Instruments, Dallas, TX) high-current operational amplifiers (op amps) in a push–pull configuration operating at 7.5 volts (Fig. 3). The voltage across a 0.1 Ω current sense resistor is used in the feedback loop to maintain a true constant current output proportional to the control input voltage. The current output is set using an on-board LTC1592 (Linear Technologies, Milpitas, CA) 16-bit digital-to-analog converter (DAC). The DAC output and feedback loop voltages are summed to zero at the input of an OPA228 op amp such that changes in the DAC output will cause compensating changes in the current output. The DAC is controlled using serial peripheral interface (SPI) digital signals from a Microchip MCP 2210 USB-to-SPI converter (Microchip Technology, Westborough, MA) that is in turn controlled using driver software on a personal computer.

FIG. 3.

Schematic for in-house, low-cost, digitally programmable shim supply circuit boards. The boards use paired OPA549 high-current op amps controlled by current feedback from a 0.1 Ω current sense resistor on the output. The summing point op amp feedback loop can be operated in two modes: 1) a resistor for zero bandwidth and unconditional stability, and 2) a capacitor that sets an appropriate bandwidth to permit gradient-induced voltage compensation without allowing oscillations.

Because the voltage drop across the cables, chokes, and shim coil is relatively small (~1 V), most of the power is dissipated in the OPA549 ICs. For this reason, the OPA549s are mounted to Lytron aluminum cold plates with embedded copper piping (Lytron, Woburn, MA) to allow optional watercooling (Fig. 3). The 7.5-volt supply value is chosen as low as possible to minimize power dissipation. The shim supply assembly with all 31 boards is placed in the scanner room 2.5 meters behind where the coil sits on the patient table. Digital control signals are delivered via fiber optic cables. To assess the significance of induced voltage, a test 9.5-cm diameter sniffer coil is connected to an oscilloscope and placed in various positions and orientations in the bore while an EPI sequence plays on the scanner. Thermal safety evaluation includes bench-testing of individual chokes carrying 3A DC and the entire coil array with 1A DC in each channel.

Experiments

SNR is assessed in two ways. First, the unloaded-to-loaded quality factor ratio (Q-ratio) is obtained for individual 3T test loops by using a lightly coupled double probe to measure S₂₁ on a network analyzer. To measure loaded Q, the coil is placed 2 cm from the side of a saline-filled head-and-torso phantom (The Phantom Laboratory, Salem, NY) with permittivity of ~77 (ϵ/ϵ₀) and conductivity of 1.5 S/m (0.9% NaCl by mass). The Q-ratio is measured for conventional RF-only loops and for RF-shim loops, with chokes added to bridge RF-tuning capacitors and with a DC-blocking capacitor added (Supp. Fig. S1). The effect of adding twisted pair to supply current to the loop is also measured. To investigate the impact of using different numbers of chokes, the test is repeated on loops with varying numbers of distributed tuning capacitors. For comparison, loops tuned for 7T imaging (297 MHz) are also tested.

Second, SNR maps (26) for the 32-channel array coil are acquired on the 3T scanner using the head-and-torso phantom before and after conversion to a combined RF-shim array. For comparison, an SNR map is also acquired with a geometrically similar 32-channel commercial head coil (Siemens Healthcare, Erlangen, Germany). Dimensions of the two coils are shown in Supporting Figure S2. A proton density weighted gradient echo sequence is used (sagittal, repetition time [TR]/echo time [TE]/flip angle [FA]: 30 ms/6 ms/30°, matrix: 256 × 256, FOV: 220 × 220 mm, slice thickness = 7 mm, bandwidth [BW] = 200 Hz/pixel number of averages [NA] = 1). Noise covariance information is acquired using the same sequence but with the RF transmission disabled.

Calibration ΔB₀ field maps (in Hz) are obtained with 300 mA of current flowing through one coil at a time. Maps are acquired on a 20-cm diameter water-filled balloon phantom with a double-echo gradient echo sequence (transverse, TE: [5, 7.46] ms, TR: 630 ms, FA: 50°, matrix: 100 × 100 × 62, FOV: 240 × 240 × 124 mm, slice thickness = 2 mm). Field mapping scan duration is 2 minutes per shim channel—or slightly over 1 hour for the entire array. The background inhomogeneity in the balloon phantom (zero shim current) is also mapped and subtracted from the coil B₀ maps. After the full set of B₀ basis function maps are acquired, the versatility of the array is tested by generating ΔB₀ fields approximating first- and second-order spherical harmonics.

Before imaging humans, the detuned coil array is subjected to the safety tests described by Keil et al. (25). Eight healthy volunteers are recruited to test the ability of the shim array to compensate B₀ inhomogeneity in the brain. Subjects are consented and the study is conducted in accordance with the Massachusetts General Hospital Institutional Review Board. Scans are performed in the head-first supine position using the scanner body coil for RF transmit and the combined RF-shim array coil for RF receive. The scanner’s second-order SH shims are calculated and applied using the system’s standard field mapping shimming procedure. Then, the dual-echo gradient echo sequence is acquired. A 3D brain mask is created by processing magnitude images using the FMRIB Software Library (FSL) (27) Brain Extraction tool (28). The FSL Prelude tool (29) is used to perform 3D phase unwrapping over the masked brain region, and the phase difference is converted to a Δfrequency map in units of Hertz.

The utility of the MC shim array is tested using high-resolution EPI sequences with long readout trains that are prone to geometric distortion caused by B₀ inhomogeneity. Acquisition parameters are: transverse, TE/TR: 65/18940 ms; FA = 90 deg.; matrix: [240 × 240 × 62]; FOV: 240 × 240 mm; slice thickness: 2 mm; BW: 1190 Hz/pixel; echo spacing: 1.11 ms; NA = 1; 6/8 partial Fourier undersampling. Scans are run in both blip-up (posterior–anterior) and blip-down (anterior–posterior) modes to compare the overlap between the two distorted images with and without the MC shims applied. Baseline field mapping and EPI scans are performed with the scanner’s second-order SH shims applied on a global basis. The slice-optimized matrix shim is then calculated to optimally compensate off-resonance in a 1-cm slab of interest using at most ±2.5 A per coil. After MC shimming, the residual field variation is measured using a second B₀ field map. Finally, the EPI protocol is rerun to assess the impact of MC shimming on geometric distortion.

RESULTS

Figure 4 compares simulated shimming performance of the six array geometries and SH shimming up to sixth order. The residual field variation is shown in three representative slices with pronounced frontal and/or temporal lobe off-resonance. As expected, the residual off-resonance diminishes as the number of shim channels is increased due to the greater number of degrees of freedom provided by larger arrays. The 32-channel shim array performance is comparable to third-order global shimming and fourth-order slice-optimized shimming. At 128 channels, the shim array is comparable to the SH basis up to the fifth or sixth order, removing the majority of frontal lobe B₀ inhomogeneity (60% overall decrease in σ_B0 for slice optimized shimming), except for slices very close to the sinus cavity. Marked improvements in temporal lobe off-resonance are also achieved. Histograms of the simulated off-resonant frequencies that are present in each field map are shown in Supporting Figure S3.

FIG. 4.

Simulated shimming performance is compared for six shim array geometries and spherical harmonics up to sixth order using a reference ΔB₀ brain field map acquired at 3T (50 slices, 2 mm thickness). Three representative slices are shown for both global (50-slice) and slice-optimized shimming. For RF-shim helmet arrays, performance improves with array size, with a 32-channel approaching the performance of a fourth-order spherical harmonic basis set. With 128 channels, the RF-shim array rivals fifth- to sixth-order spherical harmonics, providing enough degrees of freedom to mitigate all but the most severe deep sinus B₀ inhomogeneity. The 48-channel cylindrical array outperforms the 48-channel RF-shim array, particularly for global shimming, likely due to the cylindrical array’s greater symmetry and more uniform coverage around the head.

The PCA analysis of coil B₀ field maps, plotted in Figure 5, illustrates how many independent degrees of freedom of substantial efficiency are present in each simulated coil array. The number of eigenmodes in the SH basis up to sixth order are shown for comparison. Consistent with results in (24) showing that 8-channel RF receive arrays can achieve undersampling factors up to rate 3 (over all three dimensions combined); the PCA on B₀ shows that an 8-channel shim array has approximately 3 independent degrees of freedom for canceling B₀ inhomogeneity.

FIG. 5.

The cumulative sum of coil array eigenvalues is plotted against the number of principal components in each array’s ΔB₀ field maps over 50 slices. Plots are normalized to 100% of the total eigenvalue energy. An 80% threshold provides an indication of how many independent degrees of freedom are contained in the ΔB₀ fields generated by the set of coils in each array. The size of the spherical harmonic basis up to the sixth order is indicated for reference. The 128-channel RF-shim array is comparable to a sixth-order spherical harmonic basis set consistent with the simulations in Figure 4. PCA = principal component analysis; RF, radio frequency.

The combined RF-shim coil passes all standard safety tests, including RF power absorption, gradient eddy current heating, and RF heating trials. Additionally, when the shim current of 2.5 A is switched on in the magnet bore, no movement of coil components, chokes, or twisted pair due to torques is observed (the worst-case static torque on a loop is ~40 mN-m).

Each shim channel presents a DC resistance of ~0.4 ohm and an inductance of ~10 μH. The chokes and DC twisted pair in the shimming subsystem are compatible with normal operation of the RF receive array, including PIN diode detuning, critical overlap neighbor decoupling, and preamplifier decoupling. The addition of chokes causes a modest shift in the resonant frequency of the coil that decreases as the number of distributed tuning capacitors grows (Supp. Fig. S1).

The addition of 1-μH toroidal chokes to the resonant RF loop causes an approximately 10% to 13% reduction in the Q-ratio at 3T (Supp. Fig. S1). At 7T, the addition of 0.35 μH toroidal chokes reduces the Q-ratio by between 3% and 18%, depending on the exact coil topology. Due to the finite impedance of the chokes, fluctuations in the Q-ratio and coil tuning were initially observed when the twisted pair was moved or handled. These interactions were largely eliminated by adding 1,000 pF bypass capacitors connecting the node where the twisted pair meets the chokes to the virtual ground between the split drive-point capacitors, C₂ and C₃ (Supp. Fig. S1).

The reduction in 3T Q-ratio is borne out in the SNR maps (Fig. 6) acquired on the 3T scanner using the head- and-torso phantom. The maps show a moderate SNR loss after the introduction of chokes and twisted pair on the converted RF-shim array: 5% at the center of the head, 23% in a narrow peripheral ROI, and 12% over the whole slice. Despite the SNR loss after conversion to a combined RF-shim array, the prototype coil still performs at the level of the geometrically similar 32-channel commercial head coil (Fig. 6).

FIG. 6.

SNR and interelement coil coupling are compared for the 32-channel RF-shim array before and after conversion, as well as for a size-matched 32-channel commercial receive coil (see Supporting Figure S2). Sagittal SNR maps show a modest loss after the 32-channel RF array is converted into a combined RF-shim array, with the greatest impact at the periphery. However, the array still provides equivalent SNR to the commercial coil. The coil correlation matrix shows that interelement coupling is not degraded by the added shimming hardware. RF, radio frequency; SNR, signal-to-noise ratio.

The largest induced voltage measured during gradient switching by the 9.5-cm sniffer coil during an EPI sequence (slew rate = 170 mT/m/ms) is 0.3 volts peak to peak. In EPI images acquired using the RF-shim array, no artifacts are observed due to perturbation of the shim currents by gradient-induced voltages in the loops.

In bench-testing, a test choke carrying 3 A DC heats by 8 °C over 5 minutes and then reaches thermal equilibrium, growing just slightly warm to the touch. When the entire shim array is tested with 1 A flowing in all channels for 20 minutes, no temperature rise is detectable on the helmet surface or directly on the choke, wire, and loop conductors. The heat sinks, by contrast, reach 70 °C in some locations, indicating the need for water cooling if the shim array is to be operated at full capacity for the duration of typical clinical MRI scan. However, for the current amplitudes and time scales of our initial experiments, water cooling of the heat sinks did not prove necessary.

Figure 7 shows the field pattern generated by eight representative loops. The single elements produce standard surface-coil like patterns with 200 Hz or more of frequency shift per ampere near the edge of the FOV. Figure 7 also shows linear combinations of currents chosen to generate several first- and second-order SH patterns within the balloon phantom. The fidelity of the field is not constant across the entire imaging volume, as illustrated for the Z2 harmonic, which degrades toward the bottom of the brain where there are fewer coil elements to support it. But we confirm that shim coils arrayed on the surface of a helmet substrate can be used to model (and thus substitute for) low-order SH fields, as demonstrated previously in (30) for a cylindrical arrangement of coils.

FIG. 7.

ΔB₀ field maps measured in balloon phantom (a) generated by 300 mA current in eight representative coils encircling the midplane of the brain. The independent spatial profiles of the coils are well suited to forming target fields for shimming. (b) Linear combinations of the coil profiles are used to model first- and second-order harmonics: X gradient and Y gradient (25 Hz/cm); and XY, X2-Y2, and Z2 shims (7 Hz/cm²). The Z2 shim degrades toward the bottom of the helmet, where there are fewer coils to support the field.

Early in vivo slice-optimized brain shimming results are presented in Figure 8. In each case, initial field maps acquired with the scanner’s second-order SH shims applied are compared to predicted and measured MC shims. The MC shims provide a 30% to 50% improvement in the SD of ΔB₀ for the five slices shown, along with a corresponding reduction in EPI geometric distortion.

FIG. 8.

Five brain slices in two volunteers are shimmed by optimizing shim currents for a 1-cm slab around the slice of interest. Slice-optimized shimming reduces the standard deviation of ΔB₀ within each by between 30% and 50%, as compared with the global second-order shimming. Close agreement is obtained between predicted and acquired shimmed ΔB₀ maps. High-resolution EPI scans show markedly less distortion when MC shims are applied, largely bringing features such as the ventricles back into alignment, as indicated by the orange lines. Residual inhomogeneity in the anterior-most edge of the brain distorts the edge of the image, highlighting the need to combine MC shimming with parallel imaging approaches (e.g. generalized autocalibrating partially parallel acquisitions) for practical high-resolution EPI scanning. The total current used to shim each slice, starting from the top row, is [5.0, 6.4, 10.1, 7.1, 8.5] amps. EPI parameters are 1-mm in-plane, 2-mm slice, TE/TR = 65/18,940 ms, 6/8 partial Fourier, bandwidth = 1190 Hz/pix, NA = 1, echo spacing = 1.11 ms, undersampling factor R = 1.

Using a dual-core 2.8 GHz i7 processor, computation time to obtain the optimal 31 shim current values is ~30 seconds for a 50-slice global shim and ~1 to 3 seconds for a slice-optimized shim.

DISCUSSION

In the brain-shimming simulations (Fig. 4 and Supp. Fig. S2) and PCA analysis of the coil B₀ fields (Fig. 5), shim performance improves as expected with increasing array size. PCA provides a tool for quickly evaluating different coil geometries to trade off between optimal parallel imaging performance and optimal shim performance. These two design metrics are provided by the PCA of an array’s RF B₁⁻ and ΔB₀ fields, respectively.

The 48-channel cylindrical multiturn shim array outperforms the 48-channel RF-shim helmet, particularly for global shimming, perhaps owing to the cylindrical array’s greater symmetry and more uniform coverage around the head. However, we feel that this comparison does not undermine the motivation for integrating the RF coils with the shim loops. The 48-channel array of 100-turn loops presented in (14), although efficient for B₀ shimming, would likely be impractical in the presence of a massively parallel receive array such as that used in the present paper. The placement of the loops would interfere with the electrical performance of the RF loops arrayed on the surface of the helmet and could also pose mechanical problems for cabling, and so forth. The elements could also shield and adversely impact transmit coil performance. In (14), only 8-channel RF transmit/receive coils were used, nested in the gap between the shim coils; and already the shim coils cause a 15% to 20% reduction in SNR of the array.

Although the 32-channel prototype RF-shim array shows some SNR loss after conversion from RF-only to RF-shim array (Fig. 6), its sensitivity remains comparable to a commercial 32-channel helmet array, making the prototype suitable for clinical and neuroscientific applications. In future investigations, the underlying source of the SNR loss will be sought and, if possible, eliminated. Uncombined coil SNR maps (not shown) reveal a greater sensitivity loss for some array elements than for others, suggesting that factors in the SNR loss may be localized and correctable. Contributions to SNR loss could include the resistance of the chokes in the RF coil circuit, losses in the DC twisted pair from RF that leaks through the chokes or that couples directly to the twisted pair, and routing of the twisted pair too close to RF preamplifier inputs and outputs. In future work, the twisted pair will be routed straight outward perpendicular to the helmet surface and then out of the bore along the z-axis, maximizing distance from the preamplifiers. In addition, bypass capacitors will be added (Supp. Fig. S1) to reduce RF leakage.

Previously published SNR maps comparing a single-element 7T RF-shim coil to a conventional RF coil show no detectable difference in SNR (18). This led to the hypothesis that chokes in 7T loops may have little impact on SNR due to the fact that 7T coils are typically body-noise dominated. The Q-ratio measurements in Supp. Fig. S1, however, do show a modest negative impact from the addition of the chokes. Whereas Q-ratios provide an approximate metric of coil performance, an SNR map comparison between RF-only and RF-shim coils should be performed in the array environment before a conclusion can be drawn about the impact of adding shim components on a 7T RF array, a measurement that we reserve for future work.

The 0.3 V peak-to-peak detected by the sniffer coil during EPI gradient switching is considerably less than the maximum output voltage of the shim supplies (~6 V). Correspondingly, no image artifacts from shim current perturbation are observed. This demonstrates one of the advantages of using single-turn shim loops rather than multiturn loops; magnetic flux scales linearly with the number of turns in the coil. A problem with large odd-order spherical harmonic shim coils is that the coupling can be quite large between the odd-order gradients, which are a first-order SH, and the third-order shim SH coil. The induced voltage can exceed 100 V, requiring a shim amplifier with 100 V output to maintain a steady current. This makes the shim amplifiers considerably more expensive and illustrates a positive practical aspect of our approach (small, single-turn, close to the head loops). The induced voltages are small enough that simple, low-cost op-amps can be used as the primary shim driver (as also shown previously in Ref. 14).

In initial testing, the shim supplies were configured with a high bandwidth to permit the feedback loop to compensate voltages induced by gradient switching in real time. However, this topology was prone to occasional oscillations, disrupting experiments and producing an audible tone in the magnet bore. With a small change to the summing op amp feedback loop (Fig. 3), the supplies operate in a very low (essentially zero) bandwidth mode that is unconditionally stable. Comparing images acquired in the two modes, no artifacts are introduced due to perturbations of the shim currents, suggesting that even with low bandwidth supplies the voltages induced by gradient switching in small, single-turn loops are too small to cause harmful disruption of the shim currents.

While single-turn shim coils do not provide enough B₀ field strength to replace conventional gradient coils, they may offer a useful way to generate supplementary spatial-encoding fields (30) (Fig. 7). For instance, higher-order fields have been proposed as additional degrees of freedom for improving RF parallel transmit performance (31,32), and a variety of spatial encoding methods exploit linear combinations of first-order and higher-order fields for phase encoding and readout (33–36).

In the experimental in vivo shimming shown in Figure 8, slice-optimized shims required 5 A to 10 A total current, well within the design specification for the shim array. The relatively small current amplitudes required for slice-optimized shimming underscore the high efficiency that is achieved when the coils are placed as close to the body as possible.

After MC shims are applied, good agreement is obtained between the predicted and acquired field maps. Calibration field mapping of coil ΔB₀ fields is performed once and used for all subsequent experiments. Because the coil housing is designed to always slide into the same position on the patient table, the coils generate reproducible ΔB₀ fields from one experiment to the next.

As Figure 4 illustrates, shim performance improves markedly as the array size grows and the elements become smaller and more densely patterned around the body. By contrast, the amount of available current does not impose a practical limitation on the experimental performance of the 32-channel array; only minor improvements are obtained by increasing the current limit from 1 A to 2.5 A per channel. We therefore consider 2.5 A adequate to show proof of concept for a combined RF-shim array, even though the OPA549 devices can supply up to 8 A and the coil wiring and chokes are designed to handle 4 A with minimal heating. We expect to take fuller advantage of this available current at higher fields (e.g., 7T) or by using denser arrays of small coils that benefit from higher current limits in simulations.

Slice-optimized MC shimming mitigates geometric distortion in high-resolution EPI scans (Fig. 8), bringing severely distorted features such as the ventricles and cortical convolutions back into closer alignment with the gradient echo anatomic image. Improved agreement is also seen between blip-up and blip-down EPI scans of the same slice. Some distortion remains in the shimmed images, particularly at the extreme anterior edge of the brain. This occurs when 1) ΔB₀ varies too steeply at the edge of the brain to be compensated by the 31-channel array, or 2) the edge of the brain “gets in the way” and is over-corrected as the optimizer attempts to shim the frontal lobe hotspot.

For slices in the temporal lobe region, ΔB₀ varies too sharply above the ear canals to be adequately compensated by the 31-channel MC shim array. Experimental fields maps in this region show moderately decreased σ_B0 over the whole slice, but only marginal improvement above the ear canals (see Supp. Fig. S4), consistent with simulations in Figure 4. Overall, the temporal region is challenging to shim and demonstrates the need for even larger arrays of shim coils to compensate high-frequency spatial variation in B₀.

Although MC shimming does not eliminate all geometric distortion in the images, we emphasize that with its long effective echo spacing period of 1.11 ms, the 1-mm EPI scans represent an extreme test of shim performance. In practice, high-resolution EPI typically employs parallel imaging methods such as generalized autocalibrating partially parallel acquisitions (5) to reduce the effective echo spacing. RF-shim arrays promise to improve image quality in these acquisitions by reducing the need for parallel imaging and its attendant SNR penalty, while still permitting access to these methods when they are deemed necessary.

The implementation of real-time dynamic shimming is synergistic with the RF-shim array’s low coil element inductance and minimal coupling to the gradients and cryostat. Although only static shim settings are used in the present work, the MC shim array appears well suited to dynamic shimming applications. In bench-testing, the shim supply boards are able to drive shim coils from 0 A to 2.5 A in as little as 20 μs.

Although it was demonstrated for the brain, RF-shim arrays could be applied to other body regions such as the cervical spine, breast, and abdomen. They additionally provide a promising tool for 7T imaging, where B₀ inhomogeneity is more severe. In future designs, elements may be positioned with an eye toward trading off parallel imaging and shim performance, with priority accorded to one or the other metric depending on the application. An additional degree of freedom is the use of irregular element shapes, which show improved accuracy and efficiency for generating low-order ΔB₀ fields in recent MC shim array simulations (37).

CONCLUSION

A proof-of-concept combined RF-shim array is shown with 32 channels of RF loops and 31 channels of shim loops. Used as a MC shim array, the array significantly reduces B₀ inhomogeneity and EPI geometric distortion in the brain compared to second-order SH shimming, with minimal disruption of the RF performance or side effects such as coil heating or mechanical torques.

Whereas integrating shim components into the array brings a modest SNR penalty, the array’s parallel imaging performance and interelement decoupling are preserved, and some of this SNR penalty might be avoided with improved wiring design. MC arrays model higher-order field shapes with high efficiency, provided that the coils are brought sufficiently close to the body. By combining shim coils and RF coils into a single shared conductor on a close-fitting helmet, it is possible to reduce the number of turns to a single loop and still achieve adequate ΔB₀ offset in the brain to compensate B₀ inhomogeneity with less than ±2.5 A per channel. Simulated and experimental results demonstrate that shim performance of such an array is limited primarily by the number of channels used, rather than by practical limits on the current in each channel.