Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 1;6:22232. doi: 10.1038/srep22232

Low internal pressure in femtoliter water capillary bridges reduces evaporation rates

Kun Cho 1, In Gyu Hwang 1, Yeseul Kim 1, Su Jin Lim 1, Jun Lim 2, Joon Heon Kim 3, Bopil Gim 4, Byung Mook Weon 1,a
PMCID: PMC4772007  PMID: 26928329

Abstract

Capillary bridges are usually formed by a small liquid volume in a confined space between two solid surfaces. They can have a lower internal pressure than the surrounding pressure for volumes of the order of femtoliters. Femtoliter capillary bridges with relatively rapid evaporation rates are difficult to explore experimentally. To understand in detail the evaporation of femtoliter capillary bridges, we present a feasible experimental method to directly visualize how water bridges evaporate between a microsphere and a flat substrate in still air using transmission X-ray microscopy. Precise measurements of evaporation rates for water bridges show that lower water pressure than surrounding pressure can significantly decrease evaporation through the suppression of vapor diffusion. This finding provides insight into the evaporation of ultrasmall capillary bridges.

Liquid capillary bridges are ubiquitous in microscopic or nanoscopic confinement. In general, capillary bridges are thermodynamically formed through capillary condensation, which is quantified by the Kelvin equation. They are also hydrodynamically formed during the evaporation process in a confined location between two surfaces. In this work, we visualized evaporating water capillary bridges between a microsphere and a flat solid surface with X-ray microscopy. Microscopic capillary bridges have attracted much attention because they exhibit interesting kinetics1, showing either capillarity-induced condensation or evaporation, which impacts many processes such as ink deposition, spray drying, evaporative lithography, and fluid dynamics in powders2. Capillary forces exerted by Laplace pressure in capillary bridges play essential roles in the bonding of microscale or nanoscale objects3. Particularly, in several natural and industrial situations, water bridges frequently appear and mediate physical phenomena: for instance, adhesion between grains4,5, suspension rheology6,7, sand friction8, capillary interactions3,9, adhesion between soft substrates10, and particle indentation into tissues11. The formation and interpretation of capillary bridges are significant operations in atomic force microscopy12,13. Furthermore, liquid bridges at nanoscale contacts14 usually cause capillarity-induced negative pressure inside the bridges15,16,17. For instance, negative pressure in liquid capillary bridges can reach −160 MPa for a very small volume around the AFM tip radius (e.g., ~10 nm)17. Negative pressure inside nanoscale liquid bridges can modify classical phase transitions according to the scale18, including the evaporation kinetics19. Evaporation of femtoliter (1 fL = 1 μm3) sessile droplets that have positive internal pressure larger than 1 atm has been studied experimentally20,21,22 and numerically23. (See a recent review24.) Recent studies20,24 suggest that the evaporation kinetics of ultrasmall volumes with internal pressure larger than 1 atm can deviate from macroscopic laws for droplet evaporation25,26,27. Detailed understanding of the rapid evaporation process in femtoliter water drops is important for controlling evaporation kinetics in femtoliter chemistry, where stable femtoliter containers are under development for chemical and biochemical analysis28,29. The influence of internal pressure lower than 1 atm on the evaporation kinetics of femtoliter capillary bridges remains unclear. There is a lack of experiment-based understanding on the detailed evaporation kinetics of femtoliter capillary bridges with negative pressure, with the exception of a few numerical studies19,30. High-resolution visualization of liquid surface profiles is necessary to figure out the unique dynamic features of capillary bridges31,32. A technique applicable to microscale or nanoscale objects that can provide direct, real space, and real-time visualization is still required to precisely quantify the evaporation kinetics of capillary bridges for ultrasmall liquids.

In this paper, we present a feasible experimental method to directly quantify the evaporation kinetics of water capillary bridges surrounding a microsphere on a flat solid surface by precisely tracking the water surface profiles with transmission X-ray microscopy, as demonstrated and illustrated in Figs 1 and 2. This imaging technique enables us to evaluate the evaporation rate of a femtoliter water bridge. Particularly, we find that internal pressure lower than 1 atm inside the bridge can significantly reduce the evaporation rates.

Figure 1. Visualizing capillary bridges.

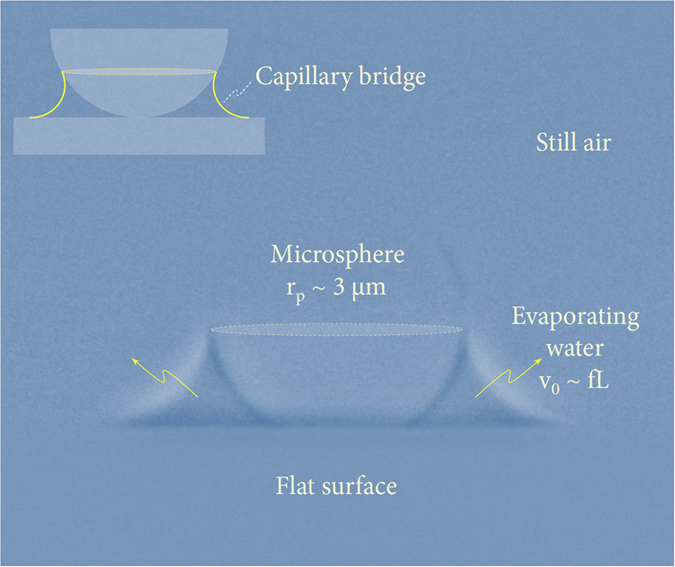
Figure 1

Open in a new tab

Clear visualization of a water capillary bridge between a microsphere on a flat solid surface, taken by high-resolution transmission X-ray microscopy. A water film that is thicker than the microsphere diameter gradually evaporates in still air in the early stages and eventually evolves into a circular capillary bridge surrounding a microsphere with a radius rp ~ 3 μm on a flat substrate at late stages. The water bridge has a small volume of ~100 fL taken from an image at 0.12 seconds prior to complete evaporation in the final image (see Supplementary Movies 1 and 2).

Figure 2. X-ray microscopic observations.

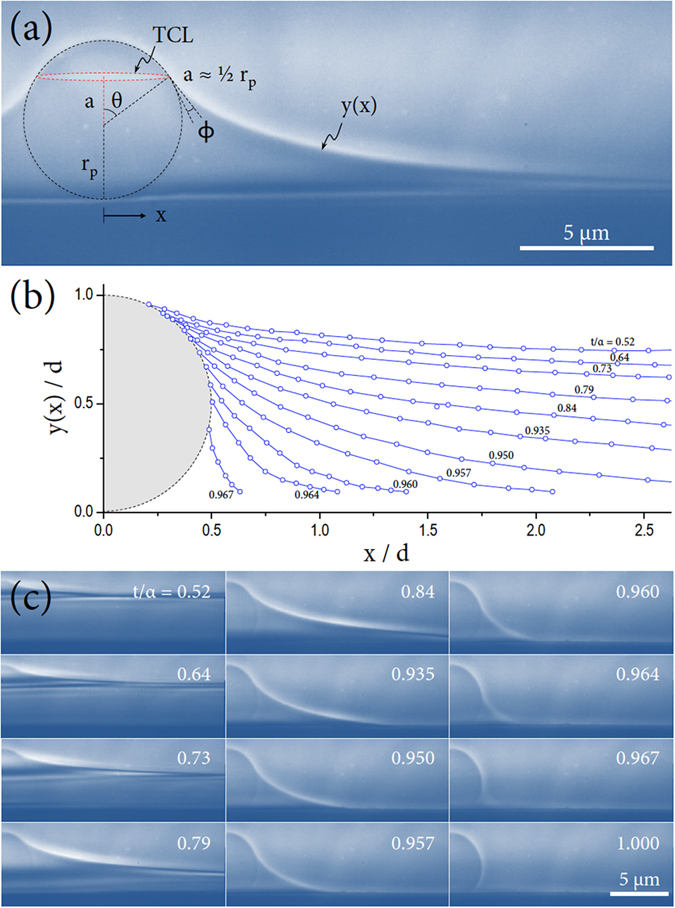
Figure 2

Open in a new tab

(a) A representative image for the surface profiles of an evaporating water film surrounding a single microsphere on a flat surface, taken by high-resolution transmission X-ray microscopy, shows clear boundaries among air, water, particle, and substrate. Particularly, this image shows the moment when the water surface was pinned on the particle surface at a condition, a ≈ ½ rp, where the length a, given by a = rp cosθ, is related to the water film height h = rp + a. The water contact angle ϕ is associated with a dynamic force balance at the three-phase contact line (TCL) for the particle, water, and air11. (b) The water surface profile y(x) with position x, normalized by the particle diameter d = 2rp, were precisely measured by X-ray microscopy. The profiles moved downward during evaporation. Here the profile intervals were arbitrarily chosen to guide the eye. (c) The real sequential images for (b) (see Supplementary Movie 3).

Results

Precise quantitative analyses for changes in meniscus profiles and volumes of water capillary bridges were performed. We observed the two evaporation stages and measured the evaporation rates at the final stages.

Pinning-Depinning Transition

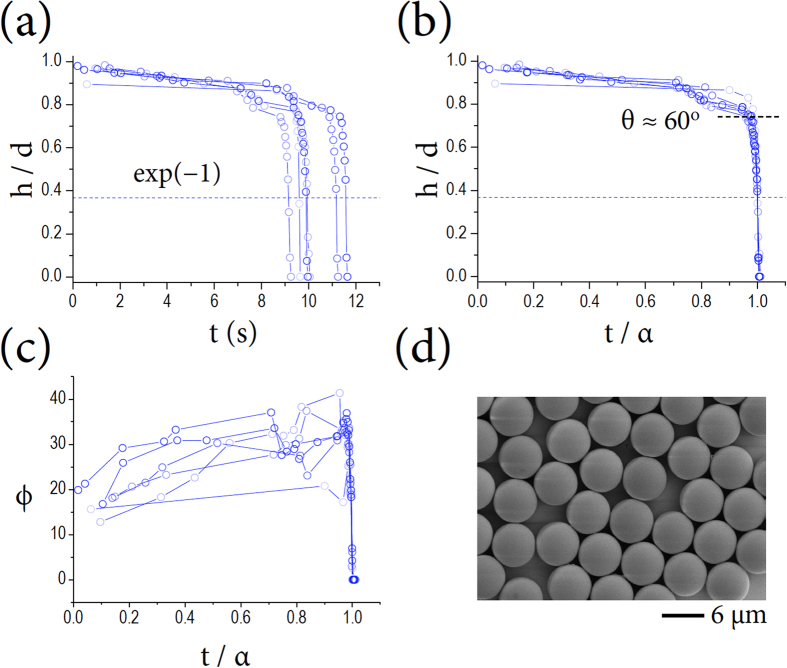
Thanks to the accurate tracking of water surface profiles, we are able to observe two distinct stages in the evaporation dynamics of the water film surrounding a single microsphere. As demonstrated in Fig. 3(a), the water film height h, which is normalized by the particle diameter d, changes with time as the water film initially gets pinned and then quickly depinned during evaporation. The sudden-death-like event from pinning to depinning occurs at the late stages close to the final evaporation time for each event. To analyze this behavior, we utilize a standard method that involves rescaling time by the characteristic time α, taken at h/d = exp (−1) for each curve. The characteristic time is usually adopted to measure the lifetime of a decay curve, enabling us to reconcile the different final evaporation times for each event. Such rescaling in Fig. 3(b) reveals that the first pinning stage appears up to t/α ~ 0.96, corresponding to θ ~ 60o, which is interestingly equivalent to a ≈ ½ rp in Fig. 2(a). In addition, the second depinning stage emerges for a very short time: the main sudden change occurs around t ~ α. On the other hand, the water contact angle ϕ defined from the three-phase contact line for water-air-particle interfaces increases at the pinning stage, t < α, as the height of the water surface is gradually decreased by pinning at the three-phase contact line and quickly decreases to zero at the depinning stage, around t ~ α, as demonstrated in Fig. 3(c). The abrupt decrease of the contact angle at the final stage is due to the depinning process and the hydrophilicity of the functionalized microspheres. The origin of pinning might be related to the heterogeneity of the particle surface or the non-equilibrium state of the water bridge due to evaporation. The microspheres used here are almost monodispersed, rp = 3.0 ± 0.03 μm, as demonstrated by the SEM image in Fig. 3(d), hence, our experiments were robustly repeatable. At the final stage, the water contact angle is almost zero and the small volume liquid meniscus is catenoidal. This meniscus belongs to a capillary bridge between a sphere and a flat surface, which is a three-dimensional object, and its cross-sectional image looks circular. As a result, the water bridge approximately becomes a catenoidal capillary bridge that has a circular radius R.

Figure 3. Two evaporation stages.

Figure 3

Open in a new tab

(a) The water film height, normalized by each particle diameter, is initially pinned and then quickly depinned by evaporation. This behavior can be analyzed by rescaling time according to the characteristic time α, taken at h/d = exp(−1). (b) The first pinning stage appears up to t/α ~ 0.96, corresponding to θ ~ 60o, equivalent to a ≈ ½ rp. The second depinning stage emerges for a very short time around t ~ α. (c) The water contact angle ϕ increases during the pinning stage and quickly decreases up to zero during the depinning stage, indicating that the water bridge becomes catenoidal. (d) The microspheres used here are monodispersed, rp = 3.0 ± 0.03 μm (a standard deviation from 24 datasets), as demonstrated by the SEM image.

Evaporation Rates

Precise measurements of time-dependent small volumes for water catenoidal capillary bridges at the depinning stage provide quantitative information about the evaporation kinetics for femtoliter capillary bridges. As shown in Fig. 4, during the final evaporation stage for water capillary bridges, the water volumes gradually decrease with time from the characteristic volumes v0 ~ 240 fL that approximate the volume at t ~ α. Here, we modify a general evaporation equation for a spherical cap model20,24 to describe the evaporation equation for a catenoidal capillary bridge. The water volume changes at a given moment for capillary bridges may be expressed as

Figure 4. Evaporation rates at the final stages.

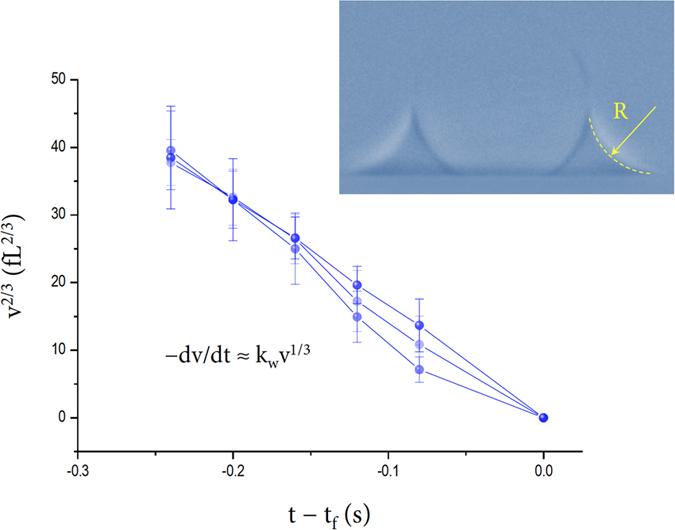
Figure 4

Open in a new tab

Evaporation dynamics of water capillary bridges whose volumes gradually decrease with time from characteristic volumes of v0 ~ 240 fL. The volume changes are described as v2/3 = v02/3 – (⅔) kwt and v → 0 as t → tf, where kw is a constant and is experimentally set as ~ 248 fL2/3/s for water. The evaporation rate expression of −dv/dt = kwv1/3 is similar to the sessile drop evaporation law20,24, but the evaporation rate for a bridge is slower than that for a hemisphere sessile drop with identical surface area. The error bars were determined by the repetition of measurements for each sample.

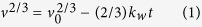graphic file with name srep22232-m1.jpg

where kw is an experimental constant that does not depend on time and is evaluated as ~248 fL2/3/s for water. The measured kw value can be used to evaluate how much a calibrated capillary bridge evaporation deviates from a typical sessile drop evaporation. This v2/3 versus t relation is natural in sessile drop evaporation20,24 and v → 0 as t → tf (the complete evaporation time). The evaporation rate is then determined by differentiating the above Eq. (1) as

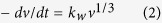graphic file with name srep22232-m2.jpg

The evaporation rate would be proportional to the circular radius R of the water bridge at the final stage of evaporation (Fig. 4). (R can be measured during ~0.12s prior to tf).

Discussion

We identified the existence of two evaporation stages for a water film surrounding a microsphere, as demonstrated in Fig. 3(b). This behavior is similar to the wetting-drying transition36. The pinning of a water film on the surface of a microsphere would be attributed to the surface heterogeneities of the microsphere, which would affect the dynamic wetting behavior37,44,45 and therefore, the consequential evaporation kinetics. The two-stage evaporation dynamics is known2,42 but direct visualization of the two stages and the effect of low internal pressure on the evaporation rate are studied in this work.

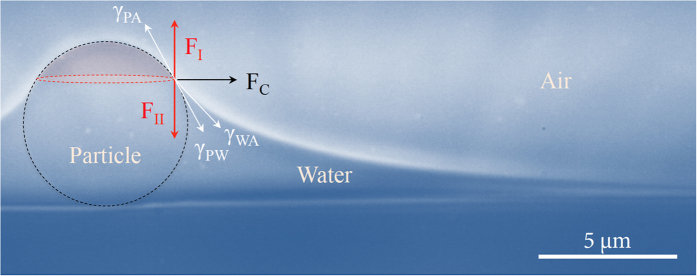
Figure 5 illustrates the pinning-depinning critical condition at the TCL: the vertical force components would be balanced as (γPA − γPW) sinθ = γWA sin(θ − ϕ) for the interfacial tensions (γ) among the particle (P), air (A), and water (W). This situation can be valid only if the upper part of the TCL is dry, which would be possible during the first pinning stage. Taking γPA − γPW ≈ 46 mN/m and γWA = 72 mN/m for polystyrene, air, and water46, the vertical force balance leads to the pinning condition for ϕ ≈ 26.4o at θ = 60o (equivalently a ≈ ½ rp), which is consistent with our observation ϕ ≈ 30o in Fig. 3(c). A recent simulation work reported the same condition a ≈ ½ rp for pinning at similar conditions47.

Figure 5. Vertical force balance for contact line pinning.

Figure 5

Open in a new tab

The vertical force components, FI and FII, is balanced where interfacial tensions (γ) exist among the particle (P), air (A), and water (W). The upper part of the TCL is dry during the pinning stage. The horizontal force component FC contributes to the capillary attraction.

At the depinning stage around t ~ α, the water bridges are catenoidal, as demonstrated in Fig. 4 (the inset) and supported by the almost zero water contact angle ϕ in Fig. 3(c). The R dependence of the evaporation rate for a water capillary bridge is similar to the empirical evaporation law for microscopic sessile drops 24,25,26,27. This scaling suggests that the evaporation rate is proportional to the perimeter of the droplet. The –dv/dt ∝  R scaling would be related to the vapor diffusion mechanism, which can be described as dv/dt ∝ R2D(dc/dR), where D is the diffusivity of the vapor, c is the concentration of the vapor24,26, and R2 originates from the surface area of the bridge.

Despite the different geometry, consideration of the evaporation rate between a bridge and a hemisphere sessile drop with an identical surface area is useful. The surface area of the water bridge is estimated to be ~100 μm2 for v0 ~ 240 fL and is equivalent to the surface area of a hemisphere sessile drop with a radius ~4.0 μm. The measured evaporation rate of 1.5 pL/s at v0 ~ 240 fL in Fig. 4 is much smaller than the estimate of 8.9 pL/s for a 4.0-μm-radius hemisphere sessile drop, based on the Hu-Larson evaporation equation27 -dm/dt = πRD (1 - H)cv (0.27θ2 + 1.30) (where H is the relative humidity, cv the saturated water vapor concentration, and θ the contact angle) calculated by adopting normal conditions for water at room temperature and 33.5% relative humidity. The Kelvin equation enables us to estimate the relative vapor pressure, which is given as ~0.9998 and is thus negligible for our case (by using material constants for water14,15,16,17,18). This consideration suggests that femtoliter catenoidal capillary bridges can have lower internal pressure than 1 atm and thus exhibit slower evaporation rates than sessile drops with identical surface areas.

The slow evaporation rate for the catenoidal water bridge is attributed to the lower internal pressure of the bridge. The pressure inside the bridge pw is estimated to be 0.6 atm for v0 ~ 240 fL, and 1.2 atm for the equivalent-surface-area hemisphere drop. (The estimation model of pw was adapted from refs. 17,18). Here slow evaporation from the water bridge is plausible through suppression of the vapor diffusion from 0.6 to 1.0 atm (to the surrounding pressure), compared with the evaporation from 1.2 to 1.0 atm for the hemisphere sessile drop. This estimation implies that lower liquid pressure than the surrounding atmospheric pressure would cause a significant reduction in the evaporation rate at femtoliter scales, as qualitatively suggested1,31.

Our experiment shows that lower or negative internal pressure may cause a decrease in the evaporation rate. Other factors could also play a role in the reduction of the capillary evaporation rate. For example, the geometry of a sessile droplet can increase the evaporation rate at the edge48. There may be the possibility of a geometric effect in which the vapor diffusion is hindered by the microsphere and the flat substrate. The catenoidal capillary bridge shape would be important for reducing the evaporation rate. After the liquid molecule enters the area just above the liquid-vapor interface and moves around, if it moves in the direction normal to the interface, it may have a greater likelihood of diffusing into vapor. However, when it moves in other directions, it would be more likely to be captured by the liquid since the liquid surface is curved instead of flat. On the other hand, at very late stages (t − tf ≈ 0), the competition between capillary pressure and disjoining pressure might have a significant effect on the evaporation kinetics: disjoining forces significantly dominate capillary forces in ultra-thin films19,49,50. Consequently, the quantitative evaporation kinetics for capillary bridge evaporation is quite predictable to engineers. Additionally, the presence of low or negative liquid pressure, pw < 1.0 atm, at femtoliter scales can suppress vapor diffusion from the bridge surface to the atmosphere.

Finally, we emphasize the feasibility of transmission X-ray microscopy for exploring in detail the evaporation kinetics of femtoliter water capillary bridges. The meniscus could be extracted from X-ray microscopy and Image Pro-Plus software. This technique could provide a high spatial resolution of 46 nm, which is enough for direct visualization of capillary bridge evaporation in still air between a microsphere and a flat solid surface. Better resolution from X-ray microscopy is expected and thus further useful study is promising for hydrodynamics study on capillary bridges. Detailed information on the evaporation kinetics of capillary bridges in microscopic or nanoscopic confinement would be useful in many natural and industrial situations. At femtoliter scales, capillary bridges are well known to have lower internal pressure than the ambient surrounding pressure. Our finding shows that lower internal pressure than the surrounding pressure can significantly decrease evaporation through the suppression of vapor diffusion. This finding provides a clue for better understanding of the evaporation of ultrasmall capillary bridges.

Methods

X-ray microscopy is a promising in-situ technique in soft matter research33. We utilize the full-field transmission X-ray microscopy at the 7C X-ray Nano Imaging (XNI) beamline established at the Pohang Light Source II34. This beamline is dedicated primarily to full-field imaging of the internal structures of biological and material samples. The beamline provides 46 nm resolution with a 32.7 × 15.3 μm2 field of view. A focused hard X-ray beam with 6.717 keV photon energy from a synchrotron source and a high speed camera (pco. dimax S4; 25 fps, 2016 × 944 pixels) were used to acquire real-time evaporation dynamics. Then 6.0-μm-diameter polystyrene (Catalog No. 07312-5, Polysciences, Inc.) microspheres suspended in pure water were used for evaporation experiments. The polystyrene in the core of the microspheres was intrinsically hydrophobic, and we used anionic sulfate functionalized polystyrene microspheres that are hydrophilic and stably suspended in water. A droplet of the microsphere suspension was gently placed on the top of a flat solid surface made of borosilicate glass tubes (GC-1, Narishige Co., Japan) with outer diameter and thickness of 1.0 and 0.2 mm, respectively. X-ray microscopy was used to obtain sequential side-view images for the evaporation process of the microsphere suspension on the flat solid surface. The detailed principle and the setup of X-ray microscopy can be seen in refs. 33,34. X-ray imaging technique is an elegant in-situ visualization method for clear differentiation of water, air, and particle interfaces.

Representative evidence is provided in Fig. 1 to demonstrate clear visualization of the water capillary bridge between a microsphere on a flat solid surface, obtained with high-resolution transmission X-ray microscopy. A water film that is thicker than the microsphere diameter gradually evaporates in still air at the early stages and eventually evolves into a catenoidal capillary bridge surrounding a polystyrene microsphere with a radius rp ~ 3 μm on a flat glass substrate at late stages (Fig. 1). The water bridge has a small volume of ~100 fL taken from an image at 0.12 seconds prior to complete evaporation in the final image.

Images were processed with Image Pro-Plus (version 6.0, Media Cybernetics, Inc.). A representative image in Fig. 2(a) shows clear boundaries among air, water, particle, and substrate. Particularly, this image shows the moment when the water surface is pinned on the particle surface at the condition of a ≈ ½ rp, where the length a is given by a = rp cos θ and the water film height can be rewritten as h = rp + a. The angle at the interfaces of the particle, water, and air at the contact point is defined as the water contact angle ϕ. This angle is associated with a dynamic force balance among the interfacial tensions of the particle, water, and air11,35,36. The water contact angle was actually measured from X-ray sequential images by taking the dynamic contact angle between the tangent lines for particle-water and air-water interfaces at the three-phase contact line (TCL) during the evaporation process, as illustrated in Fig. 2(a). The water surface profile y(x), which is described with an exponential function and normalized by the particle diameter d = 2rp, were precisely measured throughout imaging analysis by X-ray microscopy, as shown in Fig. 2(b). The water surface profiles moved downward during evaporation.

The axisymmetric meniscus profiles were modeled with an exponential function for the middle stages and a catenoidal shape38 at the final stages, t/α > 0.96, instead of the exact complicated expression39,40. At the final stages of evaporation, the profile was fitted with a circular function for which the coefficient of determination was over 0.99997. The mathematics of the geometry of capillary bridges has been studied in detail analytically41−43. Precise quantitative analysis for the volume changes of water capillary bridges with time is available.

Additional Information

How to cite this article: Cho, K. et al. Low internal pressure in femtoliter water capillary bridges reduces evaporation rates. Sci. Rep. 6, 22232; doi: 10.1038/srep22232 (2016).

Supplementary Material

Supplementary Information
srep22232-s1.doc (29.5KB, doc)
Supplementary Movie 1
Download video file (1.5MB, mov)
Supplementary Movie 2
Download video file (1.5MB, mov)
Supplementary Movie 3
Download video file (1.8MB, mov)

Acknowledgments

We thank the APCTP for its hospitality. This work (NRF-2013R1A22A04008115) was supported by the Mid-career Researcher Program through an NRF grant funded by the MEST (Korea) and by Sungkyun Research Fund, Sungkyunkwan University, 2014. This research was also funded by the Ministry of Science, ICT and Future Planning (2009–0082580) and by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry and Education, Science and Technology (NRF-2012R1A6A3A04039257). This research was supported by MSIP and PAL, Korea.

Footnotes

Author Contributions B.M.W. designed and supervised the research. K.C., I.G.H., Y.K. and S.J.L. conducted the X-ray imaging experiments. J.L. maintained the X-ray Nano Imaging beamline. J.H.K. prepared the samples. K.C., J.H.K. and B.G. analyzed the imaging data. All authors discussed the results and wrote the manuscript.

References

  1. Maeda N., Israelachvili J. N. & Kohonen M. M. Evaporation and instabilities of microscopic capillary bridges. Proc. Natl. Acad. Sci. USA 100, 803–808 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Neeson M. J., Dagastine R. R., Chan D. Y. C. & Tabor R. F. Evaporation of a capillary bridge between a particle and a surface. Soft Matter 10, 8489−8499 (2014). [DOI] [PubMed] [Google Scholar]
  3. Kralchevsky P. A. & Denkov N. D. Capillary forces and structuring in layers of colloid particles. Curr. Opin. Colloid Interface Sci. 6, 383−401 (2001). [Google Scholar]
  4. Kudrolli A. Granular matter: sticky sand. Nat. Mater. 7, 174−175 (2008). [DOI] [PubMed] [Google Scholar]
  5. Scheel M. et al. Morphological clues to wet granular pile stability. Nat. Mater. 7, 189−193 (2008). [DOI] [PubMed] [Google Scholar]
  6. Koos E. & Willenbacher N. Capillary force in suspension rheology. Science 331, 897−900 (2011). [DOI] [PubMed] [Google Scholar]
  7. Domenech T. & Velankar S. S. On the rheology of pendular gels and morphological developments in paste-like ternary systems based on capillary attraction. Soft Matter 11, 1500−1516 (2015). [DOI] [PubMed] [Google Scholar]
  8. Fall A. et al. Sliding friction on wet and dry sand. Phys. Rev. Lett. 112, 175502 (2014). [DOI] [PubMed] [Google Scholar]
  9. Di Leonardo R., Sanlimbeni F. & Ruocco G. Very-long-range nature of capillary interactions in liquid films. Phys. Rev. Lett. 100, 106103 (2008). [DOI] [PubMed] [Google Scholar]
  10. Wexler J. S., Heard T. M. & Stone H. A. Capillary bridges between soft substrates. Phys. Rev. Lett. 112, 066102 (2014). [DOI] [PubMed] [Google Scholar]
  11. Mijailovich S. M., Kojic M. & Tsuda A. Particle-induced indentation of the alveolar epithelium caused by surface tension forces. J. Appl. Physiol. 109, 1179−1194 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kim J., Won D., Sung B. & Jhe W. Observation of universal solidification in the elongated water nanomeniscus. J. Phys. Chem. Lett. 5, 797−742 (2014). [DOI] [PubMed] [Google Scholar]
  13. Yang L., Tu Y. & Fang H. Modeling the rupture of a capillary liquid bridge between a sphere and plane. Soft Matter 6, 6178−6182 (2010). [Google Scholar]
  14. Sirghi L., Szoszkiewicz R. & Riedo E. Volume of a nanoscale water bridge. Langmuir 22, 1093−1098 (2006). [DOI] [PubMed] [Google Scholar]
  15. van Honschoten J. W., Brunets N. & Tas N. R. Capillarity at the nanoscale. Chem. Soc. Rev. 39, 1096−1114 (2009). [DOI] [PubMed] [Google Scholar]
  16. Tas N. R., Mela P., Kramer T., Berenschot J. W. & van den Berg A. Capillarity induced negative pressure of water plugs in nanochannels. Nano Lett. 3, 1537−1540 (2003). [Google Scholar]
  17. Yang S. H., Nosonovsky M., Zhang H. & Chung K.-H. Nanoscale water capillary bridges under deeply negative pressure. Chem. Phys. Lett. 451, 88−92 (2008). [Google Scholar]
  18. Nosonovsky M. & Bhushan B. Phase behavior of capillary bridges: towards nanoscale water phase diagram. Phys. Chem. Chem. Phys. 10, 2137−2144 (2008). [DOI] [PubMed] [Google Scholar]
  19. Maroo S. C. & Chung J. N. Negative pressure characteristics of an evaporating meniscus at nanoscale. Nanoscale Res. Lett. 6, 72 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Arcamone J., Dujardin E., Rius G., Pérez-Murano F. & Ondarçuhu T. Evaporation of femtoliter sessile droplets monitored with nanomechanical mass sensors. J. Phys. Chem. B 111, 13020−13027 (2007). [DOI] [PubMed] [Google Scholar]
  21. Talbot E. L., Berson A., Brown P. S. & Bain C. D. Evaporation of picoliter droplets on surfaces with a range of wettabilities and thermal conductivities. Phys. Rev. E 85, 061604 (2012). [DOI] [PubMed] [Google Scholar]
  22. Prasad A., Lin A. T.-H., Rao V. R. & Seshia A. A. Monitoraing sessile droplet evaporation on a microme-chanical device. Analyst 139, 5538−5546 (2014). [DOI] [PubMed] [Google Scholar]
  23. Zhang J., Leroy F. & Müller-Plathe F. Influence of contact-line curvature on the evaporation of nanodroplets from solid substrates. Phys. Rev. Lett. 113, 046101 (2014). [DOI] [PubMed] [Google Scholar]
  24. Erbil H. Y. Evaporation of pure liquid sessile and spherical suspended drops: a review. Adv. Colloid Interface Sci. 170, 67−86 (2012). [DOI] [PubMed] [Google Scholar]
  25. Picknett R. G. & Bexon R. The evaporation of sessile or pendant drops in still air. J. Colloid Interface Sci. 61, 336−350 (1977). [Google Scholar]
  26. Birdi K. S., Vu D. T. & Winter A. A study of the evaporation rates of small water drops placed on a solid surface. J. Phys. Chem. 93, 3702−3702 (1989). [Google Scholar]
  27. Hu H. & Larson R. G. Evaporation of a sessile droplet on a substrate. J. Phys. Chem. B 106, 1334−1344 (2002). [Google Scholar]
  28. Chiu D. T., Lorenz R. M. & Jeffries G. D. M. Droplets for ultrasmall-volume analysis. Anal. Chem. 81, 5111−5118 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gorris H. H. & Walt D. R. Analytical chemistry on the femtoliter scale. Angew. Chem. Int. Ed. 49, 3880−3895 (2010). [DOI] [PubMed] [Google Scholar]
  30. Ranjan R., Murthy J. Y. & Garimella S. V. A microscale model for thin-film evaporation in capillary wick structures. Int. J. Heat Mass Transfer 54, 169−179 (2011). [Google Scholar]
  31. Contreras-Naranjo J. & Ugaz V. M. A Nanometer-scale resolution interference-based probe of interfacial phenomena between microscopic objects and surfaces. Nat. Commun. 4, 2865 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Hennequin Y. et al. Optical detection and sizing of single nanoparticles using continuous wetting films. ACS Nano 7, 7601−7609 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Weon B. M., Lee J. S., Kim J. T., Pyo J. & Je J. H. Colloidal wettability probed with X-ray microscopy. Curr. Opin. Colloid Interface Sci. 17, 388−395 (2012). [Google Scholar]
  34. Lim J., Kim H. & Park S. Y. Hard X-ray nanotomography beamline 7C XNI at PLS-II. J. Synchrotron Radiat. 21, 827−831 (2014). [DOI] [PubMed] [Google Scholar]
  35. Nutt C. W. Froth Floation: The adhesion of solid particles to flat interfaces and bubble. Chem. Eng. Sci. 12, 133−141 (1960). [Google Scholar]
  36. Aveyard R. & Clint H. Particle wettability and line tension. J. Chem. Soc. Faraday Trans. 92, 85−89 (1996). [Google Scholar]
  37. Pagonabarraga I. Adsorbed colloids relax slowly. Nat. Mater. 11, 99−100 (2012). [DOI] [PubMed] [Google Scholar]
  38. Wang F. & Lu J. Evaporation induced wrinkling of graphene oxide at the nanoparticle interface. Nanoscale 7, 919−923 (2015). [DOI] [PubMed] [Google Scholar]
  39. Hu D. L. & Bush J. W. M. Meniscus-climbing insects. Nature 437, 733−736 (2005). [DOI] [PubMed] [Google Scholar]
  40. Chan T. S., Gueudre T. & Snoeijer J. H. Maximum speed of dewetting on a fiber. Phys. Fluids 23, 112103 (2011). [Google Scholar]
  41. Princen H. M. Surface and Colloid Science (Wiley-Interscience, New York, edited by Matejevic E. Vol. 2, pp. 254 (1969). [Google Scholar]
  42. Orr F. M., Scriven L. E. & Rivas A. P. Pendular rings between solids: meniscus properties and capillary force. J. Fluid Mech. 67, 723−742 (1975). [Google Scholar]
  43. van Honschoten J. W., Tas N. R. & Elwenspoek M. The profile of a capillary liquid bridge between solid surfaces. Am. J. Phys. 78, 277−286 (2009). [Google Scholar]
  44. Kaz D. M., McGorty R., Mani M., Brenner M. P. & Manoharan V. N. Physical ageing of the contact line on colloidal particles at liquid interfaces. Nat. Mater. 11, 138−142 (2012). [DOI] [PubMed] [Google Scholar]
  45. Manoharan V. N. Colloids at interfaces: Pinned down. Nat. Mater. 14, 869−870 (2015). [DOI] [PubMed] [Google Scholar]
  46. Sickert M., Rondelez F. & Stone H. A. Single-particle Brownian dynamics for characterizing the rheology of fluid Langmuir mono-layers. Europhys. Lett. 79, 66005 (2007). [Google Scholar]
  47. Fujita M., Koike O. & Yamaguchi Y. Direct simulation of drying colloidal suspension on substrate using immersed free surface model. J. Computational Phys. 281, 421−448 (2015). [Google Scholar]
  48. Deegan R. D. et al. Contact line deposits in an evaporating drop. Phys. Rev. E 62, 756−765 (2000). [DOI] [PubMed] [Google Scholar]
  49. Butt H.-J. & Kappl M. Normal capillary force. Adv. Colloid Interface Sci. 146, 48−60 (2009). [DOI] [PubMed] [Google Scholar]
  50. Willett C. D., Adams M. J., Johnson S. A. & Seville J. P. K. Capillary bridges between two spherical bodies. Langmuir 16, 9396−9405 (2000). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep22232-s1.doc (29.5KB, doc)
Supplementary Movie 1
Download video file (1.5MB, mov)
Supplementary Movie 2
Download video file (1.5MB, mov)
Supplementary Movie 3
Download video file (1.8MB, mov)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES