Mapping nucleosome positions using DNase-seq

Abstract

Although deoxyribonuclease I (DNase I) was used to probe the structure of the nucleosome in the 1960s and 1970s, in the current high-throughput sequencing era, DNase I has mainly been used to study genomic regions devoid of nucleosomes. Here, we reveal for the first time that DNase I can be used to precisely map the (translational) positions of in vivo nucleosomes genome-wide. Specifically, exploiting a distinctive DNase I cleavage profile within nucleosome-associated DNA—including a signature 10.3 base pair oscillation that corresponds to accessibility of the minor groove as DNA winds around the nucleosome—we develop a Bayes-factor–based method that can be used to map nucleosome positions along the genome. Compared to methods that require genetically modified histones, our DNase-based approach is easily applied in any organism, which we demonstrate by producing maps in yeast and human. Compared to micrococcal nuclease (MNase)-based methods that map nucleosomes based on cuts in linker regions, we utilize DNase I cuts both outside and within nucleosomal DNA; the oscillatory nature of the DNase I cleavage profile within nucleosomal DNA enables us to identify translational positioning details not apparent in MNase digestion of linker DNA. Because the oscillatory pattern corresponds to nucleosome rotational positioning, it also reveals the rotational context of transcription factor (TF) binding sites. We show that potential binding sites within nucleosome-associated DNA are often centered preferentially on an exposed major or minor groove. This preferential localization may modulate TF interaction with nucleosome-associated DNA as TFs search for binding sites.

The majority of a eukaryotic genome is wrapped around histone octamers, forming nucleosomes, the basic DNA-packaging units of chromatin (Kornberg and Lorch 1999). Recent studies have revealed many general positioning properties of nucleosomes. For example, the barrier model states that +1 nucleosomes (the first nucleosomes downstream from a transcription start site [TSS]) have relatively fixed positions across a homogeneous cell population and function as a barrier for phasing nucleosomes further downstream, resulting in increasingly fuzzier positions as their distances from the +1 nucleosomes increase (Mavrich et al. 2008; Schones et al. 2008). Other nucleosome positioning properties include a nucleosome free region (NFR) within most promoter regions (Bai and Morozov 2010), as well as canonically positioned nucleosomes downstream from TSSs (Mavrich et al. 2008; Jiang and Pugh 2009b; Radman-Livaja and Rando 2010) and around replication origins (Eaton et al. 2010; Méchali 2010).

The precise positioning of nucleosomes affects a variety of biological processes that require access to the underlying genomic DNA, including transcription (Li et al. 2007), DNA replication (Ehrenhofer-Murray 2004; Dorn and Cook 2011), and the binding of other regulatory proteins (Li et al. 2005; Narlikar et al. 2007; Koerber et al. 2009). Both computational models (Raveh-Sadka et al. 2009; Wasson and Hartemink 2009) and experimental data (Martinez-Campa et al. 2004; Mao et al. 2011) have shown that small shifts in nucleosome positioning can have a profound impact on these processes.

To map nucleosome positions genome-wide, a few different experimental protocols have been developed, including FAIRE-seq (Nagy et al. 2003), ATAC-seq (Buenrostro et al. 2013), and ChIP-based methods (for example, Albert et al. 2007 and Lee et al. 2007), but the workhorse of the field has been digestion with micrococcal nuclease (MNase). MNase-digested genome fragments were originally hybridized to microarrays (Yuan et al. 2005) but have more recently been sequenced (MNase-seq) (Field et al. 2008; Mavrich et al. 2008; Jiang and Pugh 2009a; Henikoff et al. 2011). These studies have revealed key features of nucleosome positioning genome-wide, though the inherent sequence specificity of the MNase enzyme (Hörz and Altenburger 1981) has led to some mild controversy regarding the fine-scale interpretation of the results (Chung et al. 2010; Allan et al. 2012). Partly in response to this concern, Brogaard et al. (2012) developed a method of chemical cleavage that obviates the need for MNase and can determine nucleosome positions with high precision. However, this method requires genetically engineering native histones, making it harder to apply across organisms than methods using nuclease digestion.

Deoxyribonuclease I (DNase I) was used to probe the structure of an individual nucleosome before its exact details were known (Noll 1974). The oscillatory cleavage patterns of DNase I along the nucleosome core particle were studied extensively during that period (Lutter 1978, 1979; Prunell et al. 1979; Simpson and Stafford 1983). However, in recent years, DNase I has only been widely used to identify DNase hypersensitive sites (DHS), which tend to be open chromatin regulatory regions like promoters, silencers, and enhancers (Crawford et al. 2006; Boyle et al. 2008; Hesselberth et al. 2009; Song et al. 2011). DNase I digestion followed by sequencing (DNase-seq) has been employed in multiple large-scale genomics efforts, including the ENCODE Project (The ENCODE Project Consortium 2007, 2011; Neph et al. 2012; Thurman et al. 2012). As a result, we now have high volumes of DNase-seq data, but to date, these data have largely been analyzed to locate and study DHSs—regions devoid of nucleosomes—rather than used to explore the vast majority of the genome that is nucleosome-associated.

In this study, we show that DNase-seq data sets also contain substantial information about nucleosome translational positioning and that existing DNase-seq data can be used to infer nucleosome positions with high accuracy. To accomplish this, we first describe and characterize the distinctive DNase I cleavage profile on nucleosome-associated DNA. The features of this profile include an overall quadratic shape, an oscillatory cleavage rate, and a surprising asymmetry of the cleavage of each strand as it winds along the nucleosome. We show that these features can be built into a Bayes-factor–based nucleosome scoring method to achieve high sensitivity and specificity in distinguishing nucleosomal and nonnucleosomal genomic regions. Applying this method, we generate the first genome-wide nucleosome maps based on DNase-seq data for both yeast and human. We show that the resulting maps are highly concordant with previous maps (Brogaard et al. 2012; Gaffney et al. 2012). Canonical nucleosome positioning properties, including highly phased nucleosome arrays around TSSs and replication origins, are clearly reflected in our DNase-based maps. The spatial relationships we observe between nucleosomes and bound transcription factors (TFs) are also in strong accord with previous reports. Our method thus adds a nucleosome positioning capability to the widely used DNase-seq protocol, improving its time and cost efficiency by enabling it to map both DHSs and nucleosome positions at the same time.

In comparison with other work, several recent studies have noted a similar oscillatory cleavage pattern of DNase I in high-throughput DNase-seq data (Boyle et al. 2008; Gaffney et al. 2012; Winter et al. 2013; Vierstra et al. 2014). However, none of them utilized this pattern to map genome-wide nucleosome positions. Winter et al. (2013) used an oscillatory pattern to identify regions called “DNase I annotated regions of nucleosome stability” (DARNS), which are not individual nucleosome positions but rather genomic regions representing typically small portions of nucleosomes that maintain their rotational phasing. Vierstra et al. (2014) use DNase I to identify “nucleosome architecture” around TF binding sites, but their method requires paired-end sequencing and relies on the size of reads to distinguish nucleosome-associated fragments from those within DHSs. More importantly, their method is designed to map the positions of nucleosomes adjacent to DHSs and not to position nucleosomes genome-wide.

An important feature of our approach is that we exploit the DNase I cuts both within and outside nucleosomes, leveraging all available information to identify nucleosome positions, while MNase-based methods primarily rely on MNase cleaving the genome at linker regions. This enables us to identify the well-known 10.3 base pair (bp) nucleosome translational position offsets (Gaffney et al. 2012) that MNase is not able to identify. Peaks and troughs in the oscillatory cleavage pattern of DNase correspond to accessibility of the DNA minor and major groove along the nucleosome. They therefore reveal the rotational positioning of nucleosomes, i.e., the orientation of DNA major and minor grooves relative to the histone surface. The nucleosome rotational setting at potential TF binding sites has been shown to modulate the binding of TFs (Li and Wrange 1995; Sekiya et al. 2009; Cui and Zhurkin 2014). Using this pattern, we systematically study the rotational context of TF motif matches for 21 yeast TFs and five human TFs. We observe that TF motif matches within nucleosome-associated DNA are often located in a manner that aligns consistently with either the minor or major groove. This preferential localization may exist to regulate the ability of TFs to search for their binding sites along the genome.

Results

In the sections that follow, we first collect DNase-seq data in yeast, use the data to develop our model, and then apply our model to produce a genome-wide nucleosome map for the yeast genome. After validating the quality of our DNase-based map, we consider the required sequencing depth needed to achieve similar quality in larger genomes like human. We then pool data from a collection of existing human DNase-seq data sets and use the pooled data to produce a nucleosome map for the human genome.

DNase cleavage shows a distinctive oscillatory profile along the nucleosome

We used DNase I to digest chromatin from asynchronous wild-type yeast cells growing in rich medium. To explore the DNase I cleavage profile that arises within nucleosomes, we first identified the 2000 most strongly positioned nucleosomes in the yeast genome, ranked according to their nucleosome center position (NCP) score-to-noise ratios, as determined by Brogaard et al. (2012). For those 2000 nucleosomes, we calculated the average number of DNase-seq reads (transformed by an inverse hyperbolic sine function) that mapped to each position of each strand within the nucleosome (see Methods). We show the resulting cleavage profile in Figure 1A. To ensure the robustness of our results, we repeated this same analysis using DNase-seq data from yeast published by Hesselberth et al. (2009); the Hesselberth DNase-seq data exhibit the same profile we observe in our own data (Supplemental Fig. 1).

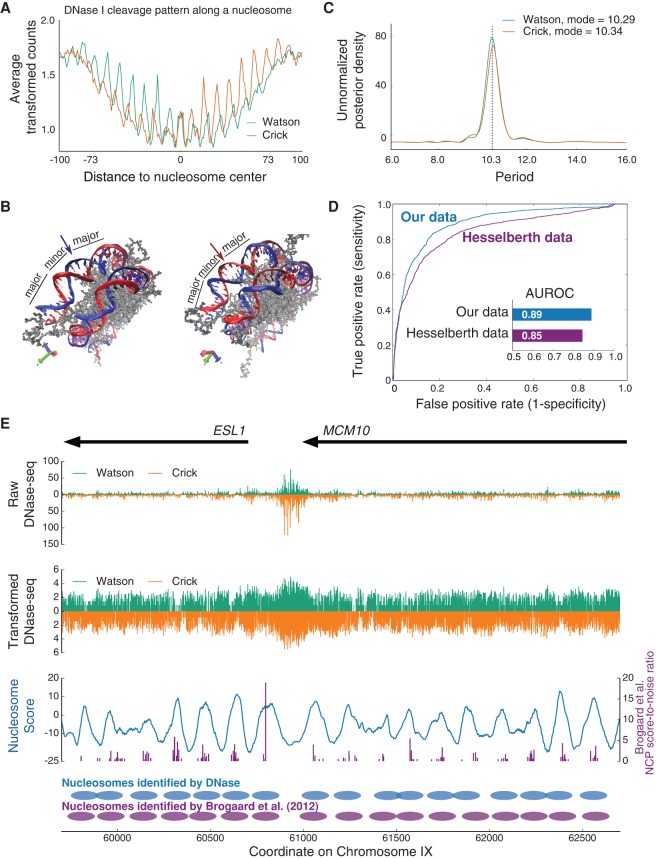
Figure 1.

(A) Strand-specific cleavage profile of DNase I along the nucleosome, computed by averaging DNase-seq counts (transformed by the inverse hyperbolic sine function) within the 2000 most strongly positioned nucleosome sites in the yeast genome. (B) Crystal structure of a nucleosome shown from two angles (image created using Protein Data Bank entry 1AOI [Luger et al. 1997]). The strand that faces outward as the minor groove is differentially accessible on opposite sides of the nucleosome dyad. The two positions labeled with arrows have the same relative distance to the dyad. (Left) The blue strand faces outward and is more exposed to digestion at this position, while the red strand faces inward and is less exposed. (Right) The red strand is now the one that faces outward, while the blue strand faces inward. In other words, on opposite sides of the nucleosome dyad, each strand is exposed differently as the minor groove becomes accessible (more exposed upstream of the dyad and less exposed downstream from the dyad). (C) Posterior density of the period of oscillation, as determined by Bayesian harmonic regression. The most probable period a posteriori for each of the two different strands is ∼10.3 bp. (D) Classification ROC for 10-fold cross-validation on both our data (blue) and the data of Hesselberth et al. (2009) (purple). All test cases from the ten folds were combined to draw an overall ROC for each data set. The areas under the two ROCs are computed and presented as a bar chart (inset). (E) Example genomic region from yeast Chromosome IX in which nucleosome positions are mapped using our moving window nucleosome scoring approach. (Top) Raw DNase-seq counts in this region. Note that DNase-seq analysis has traditionally focused only on finding and exploring DHS regions, such as the one that corresponds to the strong peak of signal just to the left of coordinate 61,000 (promoter of ESL1). (Middle) Transforming the raw DNase-seq counts using an inverse hyperbolic sine function allows clearer (but still weak) patterns to be seen in nucleosome-associated DNA. (Bottom) Smoothed moving window nucleosome score on this region (blue), in comparison with the NCP score-to-noise ratios from Brogaard et al. (2012) (purple). Nucleosome positions mapped by a greedy algorithm applied to our nucleosome scores, and for comparison the NCP score-to-noise ratios, are shown beneath the nucleosome score curve.

In the cleavage profile, we see an overall quadratic shape, indicating that DNA nearer the nucleosome dyad is better protected from DNase I cleavage than DNA nearer the edge of the nucleosome. This is most likely due to dynamic nucleosome wrapping and unwrapping (DNA breathing) (Li and Widom 2004; Li et al. 2005). Overlaid on this quadratic shape, we also observe a signature oscillatory cleavage pattern, which has been previously well-established (Noll 1974; Boyle et al. 2008; Winter et al. 2013). Since DNase I binds within the minor groove, it can more easily nick nucleosomal DNA when the minor groove is exposed. A harmonic regression analysis shows that the period of this oscillation is ∼10.3 bp for our data (Fig. 1C) and 10.4 bp for the data of Hesselberth and colleagues (Supplemental Fig. 2), values that agree with earlier studies and with the periodic exposure of the minor groove along the nucleosome. Comparing the cleavage profiles for the two different strands, we see a 2- to 3-bp offset in the periodic patterns. This is likely due to the fact that DNase I nicks one strand at a time in the presence of Mg²⁺, and the active site of this nicking activity is not quite centered in the enzyme (Suck et al. 1988), resulting in a 2- to 3-bp offset between nicks on opposite strands (Cousins et al. 2004; Boyle et al. 2008).

We note two other interesting and important features in the cleavage profile. First, for each strand, the rate of cleavage is asymmetric across the nucleosome dyad. Specifically, the oscillatory pattern is strong upstream of the dyad (on the 5′ side) but is markedly dampened downstream (on the 3′ side). Second, however, the cleavage profiles of the two strands are almost exact mirror images of each other, as would be expected (Supplemental Fig. 3). We believe the within-strand asymmetry across the dyad arises from the way DNase I can interact with each strand, given the specific three-dimensional structure of nucleosome-associated DNA. From the crystal structure of the nucleosome (Fig. 1B; Luger et al. 1997), we see that upstream (5′) of the dyad, the minor groove of each strand faces outward from the histone octamer, but downstream (3′) from the dyad, access to the minor groove is somewhat impeded by the previous wrap of the DNA around the histone octamer. This asymmetry was first observed and explained by Lutter (1978), who reasoned (before the structure of the nucleosome was determined) that the asymmetry along each strand is the direct consequence of DNA wrapping around the histone core in a left-hand manner.

It is known that nucleosomes exhibit weak periodic sequence preferences that enable them to wrap DNA more effectively (Satchwell et al. 1986; Segal et al. 2006). These weak sequence preferences are thus correlated with the periodic exposure of the minor groove along the DNA, leading an alternative explanation of the oscillatory cleavage pattern: that it instead arises from periodic sequence patterns across large stretches of the genome coupled with sequence bias in the cleavage preferences of DNase I. To explore this possibility, we took DNase-seq data generated from naked yeast DNA, entirely devoid of nucleosomes, and repeated our analysis with this data set (collected by Hesselberth et al. 2009; results shown in Supplemental Fig. 1). The oscillatory pattern of the DNase cleavage profile is completely absent in this data set, so we rule out the possibility that it arises from DNase I sequence bias acting on periodic sequence patterns. We therefore conclude it is best explained by the periodic exposure of the minor groove that occurs along nucleosome-associated DNA.

Distinctive DNase cleavage profile allows nucleosome positions to be distinguished from nonnucleosome positions

We hypothesized that the quadratic, oscillatory, and within-strand–asymmetric DNase I cleavage profile would be very informative for identifying nucleosome positions along the genome. To test this hypothesis, we first explored the possibility of utilizing the profile to distinguish nucleosomal from nonnucleosomal genomic positions in a classification setting. We built major features of the profile into a Bayes-factor–based nucleosome scoring method (see Methods). We used 147-bp windows centered on the top 2000 nucleosome center positions from Brogaard et al. (2012) as the true positive set. We used 147-bp windows centered on a set of 2000 locations selected uniformly at random from the genome as the true negative set. To assess classification performance, we carried out a 10-fold cross-validation in which both the nucleosomal and nonnucleosomal windows were randomly split into 10 equal partitions. Model parameters were trained on nine of the partitions using an empirical Bayes approach, and each model so trained was then used to classify windows from the remaining partition as being nucleosomal or nonnucleosomal. All of the test cases from across the ten folds were combined to compute a receiver operating characteristic (ROC) curve; area under the ROC (AUROC) was used to assess classification performance (Fig. 1D). Our classifier achieves a good combination of sensitivity and specificity in distinguishing nucleosomal from nonnucleosomal windows (out-of-sample AUROC on our data is 0.89, and for comparison, 0.85 on Hesselberth data). The data we publish here provide mildly better discriminatory power compared to the Hesselberth data, particularly on less well-positioned nucleosomes (the two ROCs in Fig. 1D overlap at first, but then diverge beyond a false positive rate around 5%). This difference might be because the Hesselberth data have a lower sequencing depth and/or because our data exhibit a less noisy nucleosomal cleavage profile (Supplemental Fig. 1). In the following sections, we only present results using our data (parallel analyses conducted with Hesselberth data exhibit the same general properties).

Distinctive DNase cleavage profile allows nucleosome positions to be mapped genome-wide

Encouraged by the classification performance of our nucleosome score calculated from the DNase I cleavage profile, we investigated whether we could exploit the same score to map nucleosome positions genome-wide. We trained model parameters using all of the nucleosomes in the top 2000 set above and then calculated a nucleosome score at every position along the genome, using a moving 147-bp window. Figure 1E shows an example region from Chromosome IX in yeast, where we plot the raw and transformed DNase-seq counts, and then the smoothed moving window nucleosome score computed from these data. The figure also compares our smoothed nucleosome score with the NCP score-to-noise ratios reported by Brogaard et al. (2012). The peaks of our Bayes-factor–based nucleosome score accord well with NCP score-to-noise ratio peaks, even when the DNase-seq data seem visually to exhibit only a weak positioning signal. This shows the power of using a Bayesian method that not only integrates a weak signal across multiple genomic positions, but also integrates out uncertainty in model parameters.

We then used a greedy algorithm (see Methods) to select nucleosome center positions across the genome and thereby compute a genome-wide nucleosome map, derived entirely from DNase-seq data (Fig. 1E, bottom panel). To explore the validity of this map, using the chemical-cleavage map from Brogaard et al. (2012) as a reference, we calculated the nucleosome center-to-center distances from our nucleosomes to those of the reference (see Methods). We also counted the number of nucleosomes shared between our map and the reference map (true positives), as well as the number of nucleosomes in the reference that do not overlap ones in our map (false negatives) and the number of nucleosomes in our map that do not overlap ones in the reference (false positives). As a comparison, we performed the same calculations for an MNase-seq–based nucleosome map from Jiang and Pugh (2009a); note that we used their “consensus set,” which itself is compiled as a consensus of four separate MNase-seq data sets (Field et al. 2008; Mavrich et al. 2008; Shivaswamy et al. 2008; Jiang and Pugh 2009a).

Figure 2A shows a density estimation of the center-to-center distances between the different maps. Overall, our DNase-seq–based map achieved a precision similar to the consensus MNase-seq–based map. However, a notable 10.3-bp fluctuation is apparent in the distances between the reference and the map based on DNase-seq. This indicates that if a DNase-based nucleosome center does not coincide with a reference nucleosome center, it is far more likely to be a multiple of 10.3 bp away from it. Many have reported that nucleosomes exhibit this translational positioning offset property, in which a nucleosome is likely to position itself at “rotationally in-phase” positions that are multiples of 10.3 bp away from each other (Albert et al. 2007; Brogaard et al. 2012; Gaffney et al. 2012; Winter et al. 2013). We believe that our DNase-seq–based approach identifies genuine nucleosome centers, and where the map does not perfectly coincide with the reference, the differences appear to represent translational offsets with respect to reference nucleosome centers. In contrast, the MNase-seq–based map is not able to identify the precise translational offsets associated with alternative nucleosome positions. Furthermore, our DNase-seq–based map has both a higher sensitivity and specificity than the MNase-seq–based map (Fig. 2B), even when the latter is compiled as the consensus of multiple data sets (each individual data set performs worse than the consensus; see Supplemental Figs. 4, 5). The superior ability of our approach to produce an accurate nucleosome map is most likely due to the fact that it uses DNase I cuts both within and outside the nucleosome. The oscillatory cut information can be maintained even at fuzzy nucleosomes because of the stability of nucleosome rotational positioning (Gaffney et al. 2012; Winter et al. 2013). However, MNase-seq methods rely primarily on the digestion signals from within nucleosome linkers, which are weaker when nucleosomes are not well positioned.

Figure 2.

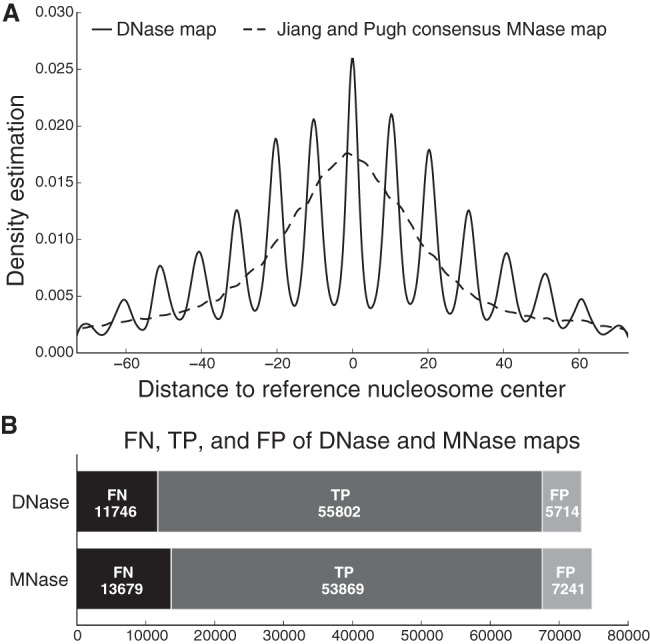
(A) Distribution of center-to-center distances between our DNase-seq–based nucleosome map and the Brogaard reference map (solid curve), and between the consensus MNase-seq–based nucleosome map and the Brogaard reference map (dashed curve). (B) The number of true positives (TP), false negatives (FN), and false positives (FP) of our DNase-seq–based nucleosome map and the consensus MNase-seq–based nucleosome map, in each case using the Brogaard nucleosome map as a reference (gold standard).

DNase-seq–based map recapitulates known features of nucleosome positioning

We next sought to ensure that our DNase-seq–based nucleosome map recapitulates well-known features of nucleosome positioning genome-wide. Specifically, we computed composite nucleosome positioning patterns around TSSs, ARS consensus sequences (ACSs) that mark origins of replication, and TF binding sites, and confirmed that they are essentially identical to previous reports that map nucleosomes by other methods (Fig. 3).

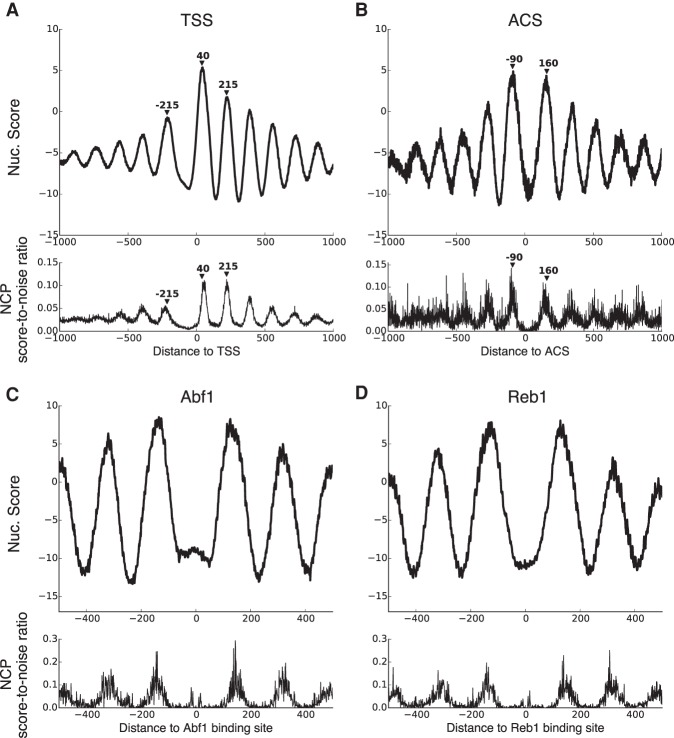
Figure 3.

Median nucleosome score around all mRNA TSSs (A), around ACS sites at all origins of replication (B), and around all binding sites of Abf1 (C) and Reb1 (D) across the yeast genome. TSS coordinates are taken from Rhee and Pugh (2012), ACS coordinates are taken from Eaton et al. (2010), and TF binding site coordinates are taken from MacIsaac et al. (2006). For comparison, the bottom of each panel shows the average NCP score-to-noise ratios from Brogaard et al. (2012) at corresponding positions.

Around the TSS (Fig. 3A), we see that the +1 nucleosome is the most strongly positioned, while subsequent downstream nucleosomes become progressively weaker as one moves further into the gene body (consistent with the barrier model). We also observe a strong depletion of nucleosomes immediately upstream of the TSS, in a location called the nucleosome free region (NFR). The spacing of nucleosomes upstream of the NFR is somewhat less regular and again becomes progressively weaker as one moves further upstream. These patterns all agree with previous reports (for example, Mavrich et al. 2008 and Brogaard et al. 2012). Similarly, we observe strong and regular nucleosome positioning around replication origins (Fig. 3B). According to previous reports that map nucleosomes with MNase (Eaton et al. 2010), the ACS site is known to be closer to the upstream nucleosome, with the upstream and downstream nucleosome centers at –90 and 160 bp relative to the origin, respectively, and our results accord well with this observation. Both of these composite nucleosome score patterns can also be seen at individual genomic loci (Supplemental Fig. 6).

Figure 3, C and D, shows median nucleosome scores around Abf1 and Reb1 binding sites. Abf1 and Reb1 can both act as barriers for nucleosome positioning, and we see regularly positioned nucleosome arrays both upstream and downstream of their binding sites, in close correspondence with the scores from Brogaard et al. (2012). Note that in both our DNase-seq–based map and the Brogaard map, we observe weak nucleosome center signals very close to the TF binding sites. Although it is possible that some of these TFs are bound to nucleosome-associated DNA, it seems more likely that the binding of a TF and the binding of a nucleosome at overlapping genomic locations are mutually exclusive events in each individual cell, but that the data represent a mixture of different binding configurations across the population of cells in the assay. Again, the composite score patterns can also be seen at individual genomic loci (Supplemental Fig. 7).

Sequencing depth influences DNase-seq–based mapping of nucleosomes

We have demonstrated we can use DNase-seq data to accurately map nucleosome positions genome-wide in yeast. Yeast has a relatively small genome that can be easily sequenced to high depth. We were interested to explore how well our approach might scale to larger genomes, so we started by evaluating how sequencing depth influenced the performance of our method in the classification setting. To this end, we uniformly subsampled 80%, 60%, 40%, 20%, 5%, and 1% of our DNase-seq data and performed the same classification as in section “Distinctive DNase cleavage profile allows nucleosome positions to be distinguished from nonnucleosome positions” on those subsampled data sets. Figure 4 shows the classification performance as a function of the subsample percentage. Since our DNase-seq counts scale with the number of reads rather than the number of sequenced nucleotides, the ratio of the number of reads to the overall size of the genome (reads/nt) is the appropriate measure of sequencing depth for our purposes. The full data set we report here consists of 83,053,784 reads across the yeast genome, which corresponds to 6.9 reads per genomic nucleotide. As Figure 4 indicates, a sequencing depth of 1.4 reads/nt (corresponding to a 20% subsample) still achieves a good classification performance (AUROC > 0.85). However, further subsampling of the data starts to decrease the performance more dramatically.

Figure 4.

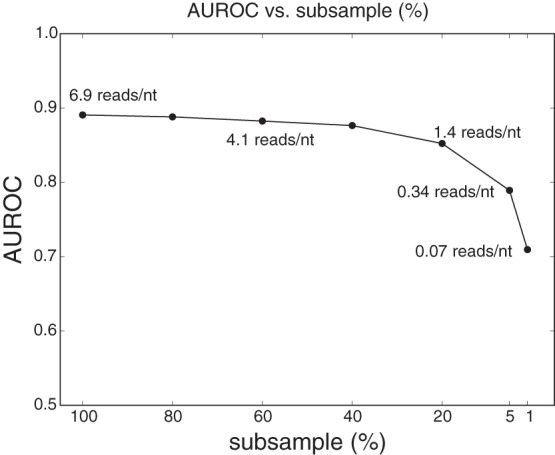
Classification performance (AUROC) as a function of data subsampling percentage. Sequencing depths (measured in reads/nt) corresponding to the subsample percentages are displayed next to the curve.

Most currently available human DNase-seq data sets have sequencing depths around 0.05 reads/nt (Boyle et al. 2008; Degner et al. 2012; Winter et al. 2013). However, certain data sets, for example Degner et al. (2012), have multiple replicates from the same cell type that can be pooled together to increase the overall sequencing depth. In the following section, we use the data from Degner et al. (2012) to demonstrate the application of our method across the human genome.

Mapping nucleosome positions in the human genome

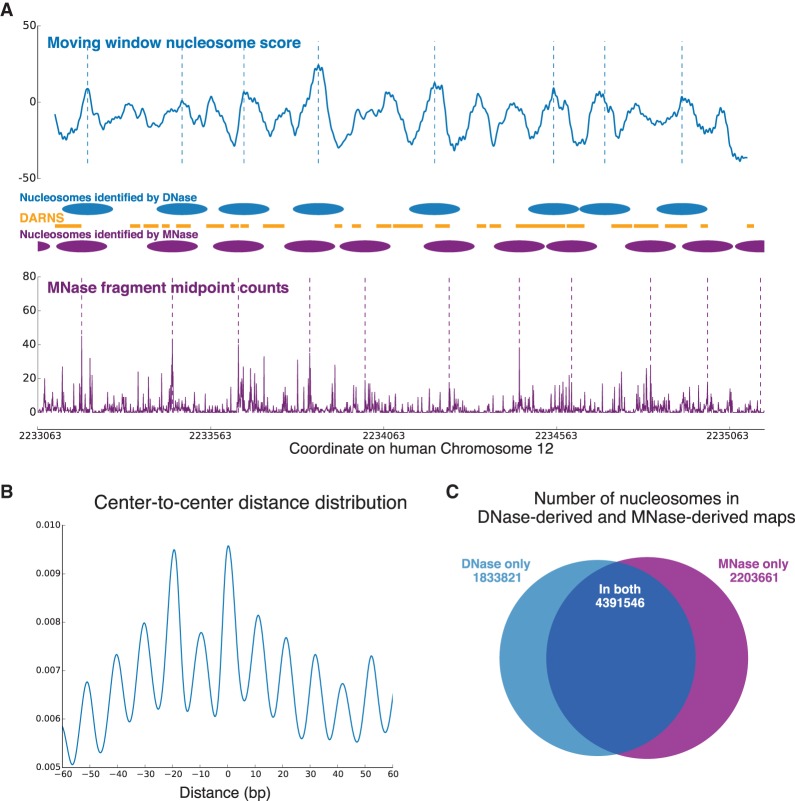
Degner et al. (2012) performed DNase I sequencing in 70 Yoruba lymphoblastoid cell lines. We pooled all their DNase-seq data sets together (overall sequencing depth ∼0.9 reads/nt) and applied our method to this combined human data set. We used the model parameters trained on our yeast DNase-seq data, so we did not require any prior knowledge about human nucleosome positioning for training. We compared our results to those derived from the MNase-seq data reported by Gaffney et al. (2012) (paired-end MNase-seq on lymphoblastoid cell lines derived from seven Yoruba individuals). Figure 5A shows the comparison in one example region from Chromosome 12. As before, we used a greedy algorithm to identify nucleosome centers from both our nucleosome score and the paired-end MNase-seq fragment middle point counts of Gaffney et al. (2012). Figure 5A also compares DARNS from Winter et al. (2013) with nucleosomes identified from DNase-seq and MNase-seq. DARNS are regions over which nucleosomes maintain their rotational positioning, and by design, usually represent only part of a nucleosome (Supplemental Fig. 8 shows the length distribution of all DARNS across the genome, as reported by Winter et al. 2013).

Figure 5.

(A) Comparison of DNase-seq–identified nucleosomes and MNase-seq–identified nucleosomes in human Chromosome 12 (intronic region of CACNA1C). Nucleosome centers are identified by the same greedy algorithm on our nucleosome score curve and on the MNase-seq fragment middle point counts, respectively. Nucleosomes identified from the two types of data overlap significantly, especially considering the large noise in the MNase-seq data. The middle panel also shows the DARNS from Winter et al. (2013), which likely represent portions of phased nucleosomes. (B) Distribution of center-to-center distances between our DNase-seq–based nucleosome map and the MNase-seq–based map of Gaffney et al. (2012). (C) The number of nucleosomes shared between the DNase-seq and MNase-seq maps, as well as the number of nucleosomes that appear in only one of the maps.

To compare the MNase-seq and DNase-seq nucleosome maps more globally, we calculated the center-to-center distances between nucleosome centers identified by these two methods. The low sequencing depth of the human DNase-seq data meant that large stretches of the genome had almost no cuts. For efficiency, these regions were not processed, and all comparisons below are on those regions where sufficient DNase-seq depth was present to identify nucleosomes. Figure 5B shows the distribution of these center-to-center distances, and we observe that when predicted center positions do not coincide, they are more likely to be translational offsets of each other that are rotationally in phase (multiples of 10.3 bp away from each other). In Figure 5C, we display numbers of overlapping and nonoverlapping nucleosomes between the two maps, calculated the same way as in Figure 2B. More than 70% of the nucleosomes identified from DNase-seq data overlap with nucleosomes identified from MNase-seq data. We see that we are able to identify nucleosome positions with good precision (but as mentioned above, with low recall; we expect the recall would improve markedly with greater sequencing depth, as was the case in the yeast genome).

Additional genome-wide nucleosome positioning features, including canonically positioned nucleosomes around TSSs and TF binding sites, are also recapitulated by our DNase-seq–derived nucleosome map (Supplemental Fig. 9). Finally, using MNase-seq–identified nucleosome centers as an approximate ground truth, we were able to compute a DNase I cleavage profile in human and see an oscillation profile largely similar to the one we observed in yeast using the more precise nucleosome centers of Brogaard et al. (2012) (Supplemental Fig. 10).

TF motif matches within nucleosomal DNA are often located preferentially on major or minor groove

The oscillatory DNase I cleavage pattern provides information about nucleosome rotational positioning (the orientation of the major and minor grooves of DNA with respect to the histone surface as it wraps around the histone core). Nucleosome rotational positioning has been shown to be able to regulate the binding of TFs to sites along the DNA (Li and Wrange 1995; Sekiya et al. 2009; Cui and Zhurkin 2014). Here, we used the oscillatory pattern (detrended, see Methods) to examine nucleosome rotational positioning at the centers of TF motif matches of 21 yeast TFs that bind DNA directly in rich medium (Gordân et al. 2009) and five human TFs with well-defined motifs that have been shown to be pioneer factors (Sherwood et al. 2014).

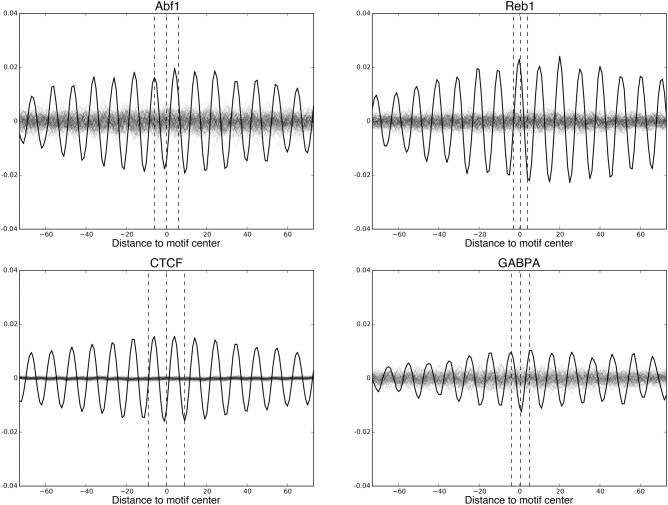
For a TF with N motif matches, we calculated the average nucleosome-associated oscillation around these N motif matches; as a control, we calculated the average oscillation around N randomly selected genomic sites (we call these “motif oscillation” and “random oscillation,” respectively; see Methods for more details). The peaks and troughs of the oscillation correspond to the minor and major grooves of nucleosomal DNA, respectively. Since randomly selected genomic sites are equally likely to lie anywhere along a helical twist of DNA, their oscillatory peaks and troughs should largely cancel, resulting in a low-amplitude oscillation. However, the motif oscillations of many TFs have significantly higher amplitude than random oscillations (Fig. 6 shows four examples: Abf1 and Reb1 in yeast, and CTCF and GABPA in human). This indicates that TF motif matches seem to locate preferentially with respect to the rotational phasing of the DNA along the nucleosome.

Figure 6.

Average oscillations around motif matches of Abf1 and Reb1 in yeast, and CTCF and GABPA in human (“motif oscillations,” black). “Random oscillations” (gray) are average oscillations around randomly chosen genomic sites. One hundred random oscillations are calculated and shown for each TF. Dashed lines indicate the boundaries and centers of the TF motifs. For many TFs, including those shown here, their “motif oscillation” has a significantly higher amplitude than their corresponding “random oscillations,” indicating their TF motif matches locate preferentially with respect to the rotational phasing of the DNA along the nucleosome.

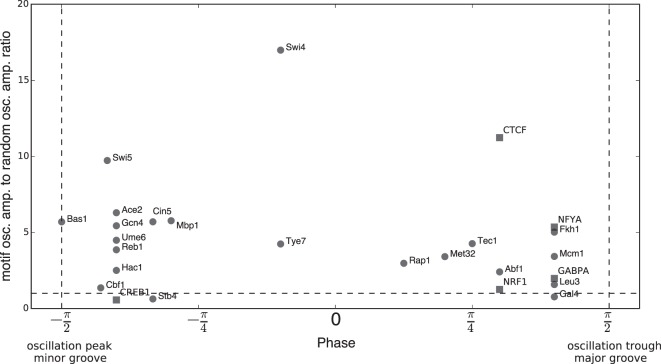
We then placed these 26 TF motifs along a scale from minor-groove–associated to major-groove–associated according to the distance between the motif center and the nearest peak or trough (Fig. 7). Notably, most TF motif matches are strongly enriched to be centered close to either the major or the minor groove. A similar calculation on randomly generated GC- or AT-rich motifs suggests that such preferential localization may at least partly be due to the coincidence between motif sequence composition and nucleosome sequence preference at DNA major and minor grooves (Supplemental Fig. 11; Satchwell et al. 1986; Segal et al. 2006). Regardless of the reason, this result indicates that nucleosome rotational positioning is tightly coupled with the sequence preferences of many TFs.

Figure 7.

Most TF motifs are centered near either the major or minor groove. Twenty-one yeast TFs are shown as circular dots. Five human TFs are shown as square dots. For each TF, the distance between its motif center and the nearest peak of its motif oscillation is calculated and converted to an “oscillation phase” within [−π/2, π/2]: If the motif center is located at the peak of the composite oscillation and thus tends to be centered on an exposed minor groove, its phase is −π/2; conversely, if the motif center is located at a trough and thus centered on a major groove, its phase is π/2. The y-axis shows the ratio between each TF's motif oscillation amplitude and the amplitude of random oscillations. This is a measure of the significance of the preferential localization. Most TFs have a phase ≥ π/4 or ≤ −π/4 and a ratio >3, indicating that they are significantly associated with the major or minor groove, respectively.

Discussion

To date, DNase-seq data have primarily been used to discover DHSs, but here we develop a Bayes-factor–based method that uses DNase-seq data to map nucleosome positions and can do so along the whole genome. DNase I cleavage of nucleosomal DNA produces a distinctive within-strand–asymmetric oscillatory profile reflective of the nucleosome structure rather than the sequence bias of DNase I. We modeled this profile and used a Bayes factor as a nucleosome score to build a highly sensitive and specific nucleosome position classifier. This same nucleosome score allowed us to derive a genome-wide nucleosome map in yeast, with similar precision to maps based on MNase digestion but greater accuracy, exhibiting fewer false positives and false negatives. Our method explicitly models the oscillatory DNase cutting pattern within nucleosomal DNA, which is often maintained even at fuzzy nucleosomes because of their rotational positioning stability. This enables us to identify nucleosome translational positioning offsets that other methods cannot. Our maps recapitulate canonical associations between nucleosome positions and other genomic features, such as TSSs, ACSs, and TF binding sites.

Genomic data are in general quite noisy. This is evident in the visually weak nucleosome positioning signals shown in Figure 1E. Still, our method is able to effectively extract a nucleosome positioning signal from this noisy data by combining the following modeling strategies: (1) data for all base pairs across the entire nucleosome window are jointly modeled to leverage all relevant information; (2) the nucleosome-structure–specific oscillatory pattern is incorporated in our model, increasing its specificity; (3) the use of strand-specific data further increases the specificity of the model, although the two genomic strands are modeled to share a mirror-symmetric profile, reducing the number of parameters; (4) data are transformed using a log-like inverse hyperbolic sine function to decrease their variance; and (5) we adopt a Bayesian approach to integrate out remaining uncertainty in the model parameters. This last point is particularly important when modeling noisy data.

Our method is also applicable to other organisms, which we demonstrated by applying it to human DNase-seq data to produce a map of nucleosome positions in human. Owing to the lower sequencing depth, large stretches of the genome have insufficient reads to make any determination of nucleosome position, so we filtered these regions out, resulting in lower recall. However, in regions where the number of reads is sufficient, we have good accuracy, based on the analyses in sections “Sequencing depth influences DNase-seq–based mapping of nucleosomes” and “Mapping nucleosome positions in the human genome.” The alignment with nucleosome positions determined from the MNase-seq data of Gaffney et al. (2012) is reasonable, considering the low DNase-seq sequencing depth, the variability of nucleosome positions across human cell lines (Radman-Livaja and Rando 2010), the use of a model trained on yeast data, and the fact that Gaffney et al. (2012) studied seven cell lines, while the DNase-seq data from Degner et al. (2012) are derived from 70 cell lines.

The oscillatory pattern utilized by our method reveals important insights about minor and major groove accessibility of nucleosome-associated DNA. Many studies have shown that nucleosome rotational positioning can regulate the binding of TFs to sites along the DNA (Li and Wrange 1995; Sekiya et al. 2009; Cui and Zhurkin 2014), and we observed that for many TFs, their motif matches within nucleosomes tend to center near either the major or minor groove of DNA. We expect several factors are coupled together, including the sequence preferences of TFs, the sequence preferences of nucleosomes as they contact major and minor grooves of DNA, and the structural exposure of major and minor grooves along the nucleosome. Such coupling may contribute to the complex regulation of TF binding when TFs and nucleosomes compete with each other for binding sites. For example, certain TFs that are able to bind their target sites inside a nucleosome may act as pioneer factors to open chromatin and facilitate the binding of other TFs.

The method we develop here adds a nucleosome mapping capability to the already widely used DNase-seq protocol, a standard tool for studying genomic regulatory elements in many organisms, including those in the ENCODE and modENCODE projects. Since nucleosome structure is well conserved across eukaryotic species, our method is readily applicable to any DNase-seq data set with sufficient sequencing depth, as we demonstrated using human DNase-seq data. The previous work of Winter et al. (2013) showed that DNase-seq has the ability to identify nucleosome rotational positioning, and numerous other studies have shown that DNase-seq can be used to identify and study DHSs, as well as TF binding sites (Luo and Hartemink 2013). Those results, together with our results here, show that DNase-seq is a highly time- and cost-efficient protocol that is able to map both DHSs and nucleosome positions simultaneously. Our method provides a basis for mining additional insights about nucleosome binding from already available DNase-seq data sets, as well as future ones. The method can also be incorporated into a more general framework for inferring a whole-genome protein–DNA interaction landscape (Zhong et al. 2014), which includes the binding of both nucleosomes and transcription factors.

Methods

DNase-seq data

The DNase-seq data generated in this study were derived from a W303 strain of yeast, grown asynchronously in rich medium. Protocols for nucleus isolation, DNase I digestion, and sequencing library preparation were adapted from Henikoff et al. (2011) and Song and Crawford (2010), with minor changes (see Supplemental Material for details). Reads generated by the sequencer were 50 bp each, but only the first 20 bp of each read is genomic DNA because of the MmeI digestion step in the protocol. So, only the first 20 bp were used when aligning reads to the genome.

The DNase-seq raw reads from Hesselberth et al. (2009) were obtained from the Sequence Read Archive (SRA, http://www.ncbi.nlm.nih.gov/sra), with accession numbers SRX002990 (in vivo) and SRX003233 (in vitro).

Raw reads from the above yeast data sets were mapped to the June 2008 build of the Saccharomyces cerevisiae genome using Bowtie (Langmead et al. 2009). Only uniquely mapped reads were retained for further analysis. We counted the number of reads that map to each genomic location (only the 5′ end of a read is counted, not its full length).

Human DNase-seq data were collected by Degner et al. (2012). We obtained the mapped reads made available from http://eqtl.uchicago.edu/dsQTL_data/MAPPED_READS/. All of their DNase-seq data were pooled to increase sequencing depth.

In both yeast and human data, the read count at each genomic coordinate was transformed using an inverse hyperbolic sine function (asinh):

$$\mathrm{asinh}(\theta )=\ln (\theta +\sqrt{1+{\theta }^2}).$$

This transformation has been used by others in modeling genomic read counts (Hoffman et al. 2012). It is quite similar to a log transformation: Like a log transformation, it reduces both the variance in the data and the influence of large outliers, but unlike a log transformation, it handles zero values gracefully.

Nucleosomal positions and nonnucleosomal positions

The 2000 nucleosome centers with the highest NCP score-to-noise ratios, as reported by Brogaard et al. (2012), were selected as bona fide nucleosome centers. Genomic windows around those nucleosome centers were used for training our models. They were also used as positive examples in the binary classification task.

To create negative examples for the classification task, we uniformly randomly selected 2000 genomic windows as nonnucleosomal positions. Note that whenever a genomic window of size 147 bp is called nucleosomal in this paper, it means a nucleosome dyad is positioned at the exact center of that window. So, although nucleosomes cover a large portion of the genome, most genomic positions will not be nucleosome centers. Therefore, our random genomic windows are reasonable approximations of nonnucleosomal windows (error rate <1/147).

Note that the nucleosomal and nonnucleosomal positions defined here are for yeast. We did not require bona fide nucleosome centers in human because we used parameters trained in yeast when applying our model to human data.

DNase I cleavage profile on nucleosomal DNA

To calculate the cleavage profile of DNase I on nucleosomal DNA, we extracted the asinh-transformed counts of the 147-bp windows around each of the 2000 nucleosome centers identified above. The count vectors were stacked to form two matrices of size 2000 × 147, one for each strand. The column averages of the two matrices are called DNase I cleavage profiles and are visualized in Figure 1A.

To isolate the oscillatory pattern from the overall quadratic trend, we computed a detrended pattern by smoothing the cleavage profile shown in Figure 1A using LOWESS (Cleveland 1979). We then subtracted the smoothed version from the original cleavage profile. We call the resultant 147-bp series the detrended oscillation pattern.

Bayesian harmonic regression analysis

We used harmonic regression to analyze the oscillatory cleavage pattern of DNase I on nucleosomal DNA. We describe the method briefly here; for more details, see Prado and West (2010).

For a given strand, we denote its detrended oscillation pattern as

$$z_{-73},z_{-72},\dots ,z_0,\dots ,z_{72},z_{73}.$$

This series is then modeled using linear regression:

$$\begin{array}{l}{z}_t=A\times \cos (\omega t)+B\times \sin (\omega t)+{\epsilon }_t{\epsilon }_t\sim N(0,{\sigma }^2)\\ \mathrm{\forall }t\in [-73,-72,\dots ,0,\dots ,72,73].\end{array}$$

Note that for mathematical convenience, we parameterize the model using ω, the oscillation frequency of the series, even though the parameter we are interested in estimating is the period, which is 2π/ω. We can rewrite the linear regression in matrix form:

$$\mathit{Z}=\mathit{F}\beta +\epsilon ,$$

where F is the design matrix and β (A B)^T. For a given ω value, we can calculate the maximum likelihood estimate for β as

$$\hat{\beta }={({\mathit{F}}^{\mathit{T}}\mathit{F})}^{-1}{\mathit{F}}^{\mathit{T}}\mathit{Z}.$$

By assuming a reference prior, p(β, σ|ω) ∝ σ⁻¹, we can calculate the (unnormalized) posterior of ω as

$$p(\omega |\mathit{Z})\propto {|{\mathit{F}}^{\mathit{T}}\mathit{F}|}^{-1/2}\{1-{\hat{\beta }}^{\mathit{T}}{\mathit{F}}^{\mathit{T}}\mathit{F}\hat{\beta }/({\mathit{Z}}^{\mathit{T}}\mathit{Z}){\}}^{(2-T)/2}p(\omega ),$$

where T is the total number of data points in Z. If we assume a uniform prior for the frequency parameter, we can use the above expression along with a change of variables to calculate the unnormalized posterior density of the period (as shown in Fig. 1C) and can use that density to identify the posterior mode of the period.

Bayes-factor–based nucleosome score

Likelihoods and Bayes factor computation

Given a genomic window of size 147 bp, we wish to assess how likely it is that a nucleosome is centered at this window. We therefore define two statistical models: a nucleosome model and a background (nonnucleosome) model. We describe the likelihood functions for the two models in the following paragraphs.

Denote the strand-specific asinh-transformed DNase-seq counts within a 147-bp window as

$$\begin{array}{rl}& \text{Forward}\text{strand}\mathit{X}=x_{-73},x_{-72},\dots ,x_0,\dots ,x_{72},x_{73},\\ & \text{Reverse}\text{strand}\mathit{Y}=y_{-73},y_{-72},\dots ,y_0,\dots ,y_{72},y_{73}.\end{array}$$

We model the data using normal distributions, with variance proportional to the mean:

$$x_t\sim N({\mu }_t^{(x)},k\times {\mu }_t^{(x)})y_t\sim N({\mu }_t^{(y)},k\times {\mu }_t^{(y)})k>0.$$

The mean-variance relationship is intrinsic to the data (see Supplemental Fig. 12).

For the nucleosome model, we parameterize the mean curve as

$${\mu }_t^{(x)}={\mu }_{-t}^{(y)}=e^a+e^b\times t^2+z_t,$$

where t is the nucleosome base-pair index, z_t is the observed, detrended oscillation pattern described in section “DNase I cleavage profile on nucleosomal DNA,” and a and b are parameters that describe the baseline level of cleavage and the curvature of the curve, respectively. This parameterization captures the main features shown in Figure 1A. The likelihood for this nucleosome model is therefore:

$$\begin{array}{rl}& L_n(a,b,k|\mathit{X},\mathit{Y})\\ & =\prod _{t=-73}^{73}{\left(2\pi k\right(e^a+e^b\times t^2+z_t\left)\right)}^{-\frac{1}{2}}\exp \left(-\frac{{(x_t-e^a-e^b\times t^2-z_t)}^2}{2k(e^a+e^b\times t^2+z_t)}\right)\\ & \times \left(2\pi k\right(e^a+e^b\times t^2+z_{-t}){)}^{-\frac{1}{2}}\exp \left(-\frac{{(y_t-e^a-e^b\times t^2-z_{-t})}^2}{2k(e^a+e^b\times t^2+z_{-t})}\right).\end{array}$$

For the background model, we parameterize the mean curve as a flat line:

$${\mu }_t^{\left(x\right)}={\mu }_{-t}^{\left(y\right)}=e^a.$$

This follows from the observation that, when averaged over a large number of randomly selected 147-bp genomic windows, DNase-seq cleavage profiles are essentially flat, modulo random sampling noise (see Supplemental Fig. 13). The likelihood for the background model is thus:

$$\begin{array}{rl}{L}_r(a,k|\mathit{X},\mathit{Y})=& \prod _{t=-73}^{73}{\left(2\pi k{e}^a\right)}^{-\frac{1}{2}}\exp \left(-\frac{{(x_t-e^a)}^2}{2k{e}^a}\right)\\ & \times {\left(2\pi k{e}^a\right)}^{-\frac{1}{2}}\exp \left(-\frac{{(y_t-e^a)}^2}{2k{e}^a}\right).\end{array}$$

The likelihood ratio between the nucleosome model and the background model is a measure of how likely the genomic window is to be a nucleosomal window and could therefore be used as a nucleosome score. However, individual windows exhibit a significant amount of variation in the DNase-seq data (as with any genomic data). So we instead calculate a Bayes factor that is able to integrate out the uncertainties of the model parameters:

$$BF=\frac{{\int }_a{L}_n(a,\hat{b},\hat{k}|\mathit{X},\mathit{Y}\left)p_n\right(a)da}{{\int }_a{L}_r(a,\hat{k}|\mathit{X},\mathit{Y}\left)p_r\right(a)da}.$$

Here, we take the uncertainty in the baseline cleavage level into account by integrating out a in both likelihood functions. The prior distribution for a in both likelihood functions is normal, with mean and variance hyperparameters determined using an empirical Bayes approach (see next section); other parameters are kept fixed at their maximum likelihood estimates (MLE) (see next section). We evaluated our approach in comparison with a few alternative approaches and chose it because of its high accuracy and low computational cost (see section “Alternative approaches for computing nucleosome scores” and Supplemental Fig. 14).

Prior distributions and MLE of model parameters

To determine the prior distributions needed to calculate Bayes factors, we adopted an empirical Bayes approach (Carlin and Louis 1997). For each of the 2000 nucleosomal positions, we computed the MLE of a, b, and k in our likelihood function (1):

$${\hat{a}}_i,{\hat{b}}_i,{\hat{k}}_i\mathrm{\forall }i\in \{1,2,\dots ,2000\}.$$

To determine the prior distribution for a in the nucleosome model, all 2000 â_is were used to fit a normal distribution through maximum likelihood estimation. The prior distribution for a in the background model was determined similarly, but using background data windows. Any parameters that were not integrated out were fixed at their MLE values, these being calculated by pooling the 2000 nucleosomal (or background) data windows together.

Alternative approaches for computing nucleosome scores

Our approach (listed as Approach 4 below) was evaluated and selected from the following alternative approaches for computing nucleosome scores, reflecting different levels of model complexity:

1. The mean curve for the nucleosome model is parameterized as e^a + e^b × t² (without the oscillatory pattern), and the nucleosome score is simply the likelihood ratio between the nucleosome model and the background model (no Bayes factor).

2. Similar to Approach 1, but the nucleosome score is a Bayes factor in which the level parameters a of both likelihood functions are integrated out.

3. Similar to Approach 2, but the curvature parameter b of the nucleosome model is also integrated out.

4. Similar to Approach 2, but the oscillatory pattern series (z_t) is added to the mean curve of the nucleosome model.

5. Similar to Approach 3, but the oscillatory pattern series (z_t) is added to the mean curve of the nucleosome model.

Approach 1 has the lowest computational cost because it does not require numerical integration; conversely, Approaches 3 and 5 have the highest computational cost because they require numerical integration in two dimensions. The performance of different approaches in distinguishing nucleosomal from nonnucleosomal windows (as measured by AUROC) is shown in Supplemental Figure 14. Based on these results, we conclude that the simple likelihood ratio (Approach 1) performs significantly worse than all of the Bayes-factor–based approaches (Approaches 2–5). Among the Bayes-factor–based approaches, those that integrate out both a and b do not perform markedly better than those that integrate out only a, despite requiring significantly more computation time. Therefore, we decided to use an approach that only integrates out a. Finally, adding the oscillation pattern z_t provides better performance, and this improved performance arises without incurring additional computation time, so we included it in our final approach: Approach 4.

Mapping nucleosome positions with a greedy algorithm

We wanted to produce a genome-wide map of nucleosome positions, given the moving window nucleosome scores across the genome. To identify the nucleosome centers that would comprise our map, we used the following greedy algorithm, which is quite similar to the one used by Brogaard et al. (2012):

1. Rank the series of nucleosome scores in descending order.

2. The genomic position corresponding to the highest nucleosome score is called a nucleosome center.

3. The nucleosome scores in the 117-bp window centered on the position identified in the previous step are removed from the series. We chose 117 bp instead of 147 bp to allow some overlap between two selected nucleosomes; this can partially mitigate the greediness of the algorithm. We confirmed that the result shown in Figure 2B is largely unchanged for parameter values between 97 bp and 127 bp (see Supplemental Fig. 15).

4. Repeat all of the above steps until no nucleosome score greater than zero remains in the series.

Applying this algorithm to the whole genome or separately for each chromosome gives identical results, so we did the latter when computing our genome-wide nucleosome position map (to reduce memory usage).

Comparing pairs of nucleosome maps

To compare a given nucleosome map with a reference nucleosome map, we calculated three quantities: the number of nucleosomes shared between the two maps (true positives), the number of nucleosomes that only appear in the reference map (false negatives) and the number of nucleosomes that only appear in the given nucleosome map (false positives). If two nucleosome centers on the two different maps were <73 bp away from each other, they were said to overlap and thus be shared between the two maps; otherwise, they were either false negatives or false positives. The total number of true positives, false negatives, and false positives were computed and reported. In addition, for all nucleosomes shared between two maps, we calculated the center-to-center distances between corresponding shared nucleosomes. We used kernel density estimation (with a kernel bandwidth of 1 bp) to visualize the distribution of these distances, as shown in Figures 2A and 5B.

Identifying TF motif matches with motif scanning

We used TF motifs from MacIsaac et al. (2006) for yeast TFs and from the JASPAR database (Mathelier et al. 2014) for human TFs. We confirmed that the yeast TFs used in this paper have similar motifs when they are computed from in vitro PBM data (Gordân et al. 2011). We defined candidate binding sites by scanning a position weight matrix (PWM) across the genome, using a permissive threshold on the PWM score (the log-likelihood ratio of seeing a motif-width DNA sequence under the PWM model versus under a fourth-order Markov background sequence model), greater than four.

Calculating nucleosome-associated oscillation around TF motif matches and random genomic sites

We first computed a “nucleosome-associated oscillation series” for the entire genome by applying our 147-bp detrended oscillation pattern to the 147 positions associated with every called nucleosome along the genome. With this in hand, we then evaluated whether the locations of each TF's motif matches tended to align themselves consistently with this series. For a given TF with N motif matches, we examined a 147-bp window centered on each motif match, and averaged the values of the nucleosome-associated oscillation series within those N windows to obtain the “motif oscillation.” As a control, we randomly selected N genomic sites and carried out the same calculation to obtain a “random oscillation.” To assess the significance of the amplitude of a TF's motif oscillation within its motif match (i.e., the amplitude inside the dashed lines of Fig. 6), we computed 100 random oscillations for that TF and calculated their average amplitude. The ratio between the amplitude of the motif oscillation and the average amplitude of 100 random oscillations was used as a measure of how significantly the motif oscillation deviates from a random oscillation.

Data access

The DNase-seq data generated in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; http://www.ncbi.nlm.nih.gov/geo/) under accession number GSE69651. Our computational tools have been released as a Python package called NucID (Nucleosome Identification using DNase), available in the Supplemental Material, as well as on GitHub at https://harteminklab.github.io/NucID/. Pre-computed tracks of genome-wide nucleosome scores are available at http://trackhub.genome.duke.edu/harteminklab/NucID/. Links to all of these resources are also available from a single location on the web at http://www.cs.duke.edu/~amink/software/.