Skip to main content
NCBI home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 1;6:21786. doi: 10.1038/srep21786

Interfacial Properties of Monolayer and Bilayer MoS2 Contacts with Metals: Beyond the Energy Band Calculations

Hongxia Zhong 1,*, Ruge Quhe 1,3,*, Yangyang Wang 1,5, Zeyuan Ni 1, Meng Ye 1, Zhigang Song 1, Yuanyuan Pan 1, Jinbo Yang 1,2, Li Yang 4, Ming Lei 3, Junjie Shi 1,a, Jing Lu 1,2,b
PMCID: PMC4772071  PMID: 26928583

Abstract

Although many prototype devices based on two-dimensional (2D) MoS2 have been fabricated and wafer scale growth of 2D MoS2 has been realized, the fundamental nature of 2D MoS2-metal contacts has not been well understood yet. We provide a comprehensive ab initio study of the interfacial properties of a series of monolayer (ML) and bilayer (BL) MoS2-metal contacts (metal = Sc, Ti, Ag, Pt, Ni, and Au). A comparison between the calculated and observed Schottky barrier heights (SBHs) suggests that many-electron effects are strongly suppressed in channel 2D MoS2 due to a charge transfer. The extensively adopted energy band calculation scheme fails to reproduce the observed SBHs in 2D MoS2-Sc interface. By contrast, an ab initio quantum transport device simulation better reproduces the observed SBH in 2D MoS2-Sc interface and highlights the importance of a higher level theoretical approach beyond the energy band calculation in the interface study. BL MoS2-metal contacts generally have a reduced SBH than ML MoS2-metal contacts due to the interlayer coupling and thus have a higher electron injection efficiency.

Owing to their excellent properties, two-dimensional (2D) molybdenum disulfide MoS2 has attracted much recent attention1,2,3,4,5,6. A variety of prototype devices based on 2D MoS2 have been fabricated, such as field-effect transistors (FETs)7,8,9, inverters10, fully integrated circuits11, sensors12, photoelectronic devices13, phototransistors14,15, spintronic devices16, and valleytronic devices17,18. Very recently, wafer-scale high performance 2D MoS2 FETs have been fabricated in batch mode, paving the way towards atomically thin integrated circuitry19. Among 2D MoS2, monolayer (ML) and bilayer (BL) MoS2 attract the most attention2,3,5,6,7,8,9,10,11,12,13,14,15,16,17,18. They show quite interesting differences and make up a pair of complementary materials: (1) ML MoS2 has a larger direct band gap, while BL MoS2 possesses a smaller indirect band gap due to the strong interlayer coupling. Correspondingly, photoluminescence is dramatically enhanced in ML MoS26,20. (2) ML MoS2 is inversion asymmetric and serves as an ideal valley Hall insulator (VHI)1. By contrast, inversion symmetric BL MoS2 is not a VHI, but it can be transformed into a VHI with a tunable valley magnetic moment by a vertical electric field, which destroys the inversion symmetry5. (3) Zeeman-like spin splitting is nearly intact by a vertical electric field in ML MoS2 but it becomes tunable in BL MoS2 because top and bottom MoS2 feel different electric potentials16.

In a real device, semiconducting 2D MoS2 needs a contact with metal electrodes, and a Schottky barrier is often formed in semiconductor-metal interface, which impedes the carrier transport. The formation of low-resistance metal contacts is the biggest challenge that masks the intrinsic exceptional electronic properties of 2D MoS2, and many efforts have been made to study 2D MoS2-metal contact so as to reduce the Schottky barrier height (SBH)21,22,23. The SBH of a 2D MoS2-metal contact depends on the work function of metal and the layer number of MoS2. Lower work function metal and more MoS2 layer number favor a smaller SBH. For example, there is a significant SBH between Ti and ML MoS224,25; by contrast, Ti forms an Ohmic contact with BL MoS2 at room temperature and a Schottky contact with a small SBH of ~0.065 eV at a low temperature11,26. Although there are several energy band calculations based on single particle density functional theory (DFT) to examine ML MoS2-metal interfaces22,23,25,27,28, a comprehensive energy band calculation for BL MoS2-metal interfaces is still lacking at present.

There are two open issues concerning this validity of the DFT energy band approach to treat the SBH of a transistor. Because the SBH at the metal-semiconductor interfaces depends on the difference between the Fermi level (Ef) of the metal and the band edge positions of the semiconductor, the band edge positions of the semiconductor must be accurately determined29,30. It is well known that the common LDA and GGA fail to do so. From a theoretical point of view, the accurate band edge positions should be the quasiparticle energy, which can be obtained from first-principles many-electron Green function approach within the GW approximation, where electron-electron correlation effects are treated properly13,31,32,33,34,35,36,37,38. The first open issue concerning the DFT energy band scheme to evaluate SBH is whether the many-electron effects should be included.

The second open issue is the way of the energy band calculation in treating the SBH of a transistor. There are two possible interfaces to form Schottky barrier in a MoS2 transistor23,39: one is the source/drain interface (B) between the contacted MoS2 and the metal surface in the vertical direction if the interaction between MoS2 and metal is weak, and the other is source/drain-channel (D) interface between the contacted MoS2 and channel MoS2 in the lateral direction if a metallization has taken place between MoS2 and metal. The energy band calculation treats the source and the channel independently and ignores the coupling between the source and the channel, which may lead to the Fermi level pinning and change the SBH.

In this Article, we provide a theoretical study of the interfacial properties of ML and BL MoS2 on several commonly used metals (Sc, Ti, Ag, Pt, Ni, and Au)8,21 at different levels. A comparison between the observed and calculated SBH in ML and BL MoS2-Ti interfaces suggests that GW correction to the band edge positions of 2D MoS2 is strongly depressed in a device because of a charge transfer. More importantly, we find that the energy band calculation is unable to reproduce the observed SBHs in 2D MoS2-Sc and -Pt interfaces. This failure prompts us to perform direct an ab initio quantum transport device simulation, and we find the SBHs in 2D MoS2-Sc and -Pt interfaces can be better reproduced in latter calculation. SBH is found to be reduced from ML MoS2-metal interfaces to BL MoS2-metal interfaces in different level calculations.

Methodology

We use six layers of metal atoms (Ni, Ag, Pt, and Au in (111) orientation and Sc and Ti in (0001) orientation) to model the metal surface and construct a supercell with ML and BL MoS2 adsorbed on one side of the metal surface. BL MoS2 takes AB stacking mode (with a D3d point group symmetry) in our model. The calculated in-plane lattice constant a = 3.166 Å, which is in good agreement with the experimental value 3.160 Å40. The MoS2 1 × 1 unit cell is adjusted to the 1 × 1 unit cells of Sc and Ti(0001) faces, and the MoS2 Inline graphic × Inline graphic unit cell is adjusted to 2 × 2 unit cells 27. The lattice constant mismatches with respect to that of MoS2 are 1.2~9.1%. A vacuum buffer space of at least 15 Ǻ is set to ensure decoupling between neighboring slabs. MoS2 mainly interacts with the topmost three layers metal atoms22, so cell shape and the bottom three layers of metal atoms are fixed.

The geometry optimization and electronic properties of the periodic structures are performed using the projector augmented wave (PAW) method implemented in the Vienna ab initio simulation package (VASP) code41,42. The generalized gradient approximation (GGA) functional to the exchange-correction functional, of the Perdew–Wang 91 (PW91) form43 with vdW corrections (VDW-DFT)44, and the PAW pseudopotential are adopted42. The cut off energy is set to 500 eV after convergence tests. An equivalent Monkhorst-Pack k-points grid45 of 25 × 25 × 1 for a MoS2 unit cell is chosen for supercell relaxations and 30 × 30 × 1 for property calculations. In our current calculations, the total energy is converged to less than 10−5 eV. Dipole corrections in the z direction are used in all calculations. The maximum force is less than 0.02 eV/Å during optimization. We employ the GW band gap calculated by Louie’s group36 and experimental band gap center (BGC)46 to analyze the SBH, because the values do not change much in different groups37,47,48.

Two-probe model is established to study the interface properties in a FET configuration. The devices are constructed of ~60 Å ML/BL MoS2 in the channel region along the transport direction and ML/BL MoS2-Sc (Pt) interfaces in the electrode region. The electrode is consisted of 6 Sc (Pt) layers with ML/BL MoS2 adsorbed on the Sc (0001) (Pt(111)) surface and a ~15 Ǻ vacuum buffer space. The supercell of the electrode region contains 1 × 1 unit cell of MoS2 and Sc (0001) surface in for Sc electrode and Inline graphic × Inline graphic unit cell of MoS2 and 2 × 2 unit cells of Pt(111) surface for Pt electrode. The transport properties of the FET are calculated by the DFT coupled with the nonequilibrium Green’s function (NEGF) method, as implemented in the ATK 11.8 package49,50. We employ the single-zeta plus polarization (SZP) basis set during the device simulation. A test using higher double-zeta plus polarization (DZP) basis set is also performed. In consistent with previous DFT calculations, GGA of PW91 form to the exchange-correlation functional is used through the device simulations. The Monkhorst-Pack k-point meshes for the central region and electrodes are sampled with 1 × 50 × 1 and 50 × 50 × 1 separately. The temperature is set to 300 K. The Neumann condition is used on the boundaries of the direction vertical to the MoS2 plane. On the surfaces connecting the electrodes and the central region, we employ Dirichlet boundary condition to ensure the charge neutrality in the source and the drain region. The transmission coefficient T(E) is given by T(E) = G(E)ΓL(E)G†(E)ΓR(E), where G(E) and G†(E) are the retarded and advanced Green functions, and the broadening function ΓL/R(E) describes the level broadening due to left/right electrode and is obtained from the electrode self-energies ΓL/R(E) = i(ΣL/R −Σ†L/R)). The electrode self-energies can be viewed as an effective Hamiltonian describing the interaction between device and lead.

Results and Discussion

Geometry and stability of ML and BL MoS2-metal interfaces

After optimizing the structures from 6 initial configurations in an interface with 1 ×1 MoS2 unit cell and 3 initial configurations in an interface with Inline graphic MoS2 unit cell, we obtain the most stable configurations of the ML MoS2-metal interfaces, as shown in Fig. 1. The initial configurations of BL MoS2-metal interfaces are constructed on the basis of the most stable ML MoS2-metal interfaces. On Sc(0001), the Mo atoms in the primitive cell sit above the top metal atom layer, and the S atoms sit above the second MoS2 metal atom layer metal atom; on Ti(0001), the Mo atoms in the primitive cell still sit above the top metal atom layer, but the S atoms sit above the centers of triangles. On Ni and Pt(111), the three Mo atoms in the supercell sit above the fcc hollow, hcp hollow, and top sites, respectively. In the cases of Ag and Au(111), the Mo atoms are all above the centers of the triangles formed by the fcc, hcp, and top sites. The calculated key parameters of ML and BL MoS2-metal interfaces studied in this work are summarized in Table 1. When ML and BL MoS2 are in contact with metals, the equilibrium distances dS-M range from 1.557~3.405 Å, increasing in the order of Ti < Sc < Ni < Pt < Ag < Au. The binding energies Eb have a reversal order, i.e., Ti > Sc > Ni > Pt > Ag > Au, since a smaller dS-M generally causes a larger binding energy. Ti and Sc have a strong adhesion with ML/BL MoS2 (Eb = 1.181~1.848 eV per surface sulfur atom), Ni, Pt, and Ag have a medium adhesion (Eb = 0.503~0.830 eV per surface sulfur atom), and Au has a weak adhesion (Eb = 0.307~0.354 eV per surface sulfur atom). ML and BL MoS2-metal contacts nearly share the same dS-M and Eb. The binding of MoS2 to metal surfaces22,27 is considerably stronger than that of graphene to metal surfaces, with the binding energy of 0.027~0.327 eV per carbon atom51. Such a difference is reasonable because MoS2 is chemically more reactive than graphene. We note that previous DFT calculations indicate that the Eb of ML MoS2 on Ir, Pd, and Ru surfaces ranges from 0.62~0.82 eV per surface sulfur atom27.

Figure 1. Interfacial structures of the most stable configuration for ML MoS2 on metal surfaces.

Figure 1

Open in a new tab

(a) Side and (b) top views of ML MoS2 on Sc(0001) surface. (c) Top view of MoS2 on Ti(0001) surface. (d) Side and (e) top views of ML MoS2 on Ni and Pt(111) surfaces. (f) Top view of MoS2 on Ag and Au(111) surfaces. dS-M is the equilibrium distance between the metal surface and the bottom layer MoS2. The rhombi plotted in black line shows the unit cell for each structure.

Table 1. Calculated interfacial properties of ML and BL MoS2 on metal surfaces.

Metal Mismatch WM(eV) ML MoS2 BL MoS2
dS-M(Å) Eb(eV) W(eV) ΔEf(eV) Φv(eV) ΦL(eV) dS-M(Å) Eb(eV) W(eV) ΔEf(eV) Φv(eV) ΦL(eV)
Sc3.308(Å) 4.485% 3.593 1.786 1.181 4.369 −0.881 0.000 0.000 1.783 1.182 4.306 −0.944 0.000 0.000
            0.000 (0.539)GW         0.000 (0.000)GW
1.290%       4.19     0.000     4.300 −0.950   0.000
              (0.362)GW           (0.000)GW
Ti2.951(Å) 6.791% 4.427 1.557 1.812 4.597 −0.653 0.000 0.187 1.560 1.848 4.616 −0.634 0.000 0.096
              (0.3–0.35)b         — (0.065) d
            (0.000)a (0.33)c         — (0.276)GW
            — (0.731)GW         0.000 –
2.990%       4.626   0.000 0.216     4.681     0.161
              (0.796)GW           (0.341)GW
Ag5.778(Å) 5.367% 4.489 2.961 0.503 4.662 −0.588 0.212 0.000 2.917 0.547 4.763 −0.487 0.138 0.000
Ni4.984(Å) 9.112% 5.222 2.094 0.830 5.001 −0.249 0.633 0.000 2.097 0.729 5.102 −0.148 0.612 0.000
Au5.768(Å) 5.185% 5.226 3.405 0.307 5.173 −0.077 0.763 0.000 3.325 0.354 5.187 −0.063 0.667 0.000
            (0.88)e (0.000)e         — —
Pt5.549(Å) 1.191% 5.755 2.476 0.570 5.444 0.194 0.520 0.000 2.438 0.634 5.476 0.226 0.345 0.000
            (0.770)f              
Open in a new tab

The experimental cell parameters of the surface unit cells shown in Fig. 1 for various metals are given under the metals. The corresponding lattice mismatches are given. The equilibrium distance dS-M is the averaged distance between the surface S atoms of MoS2 and the relaxed positions of the topmost metal layer in the z direction. Eb is the binding energy per surface S atom between MoS2 and a given surface. WM and W are the calculated work functions for clean metal surface and metal surface adsorbed by MoS2, respectively. Φv and ΦL are the vertical and lateral SBH at the DFT level, respectively, of a MoS2 transistor (see Fig. 7(c)); the SBH obtained in other DFT calculations, the GW-corrected SBHs, and the measured SBH are given below them in parenthesis for comparison. ΔEf is the Fermi level shift of 2D MoS2. The corresponding values for Sc and Ti surfaces in small mismatch are also given. Caution must be taken for the data of ML and BL MoS2-Ni contacts due to the large lattice mistmach (9.1%) limited by the computational resource.

aDFT values from refs. 22,39.

bExperimental value23.

cDFT value from ref. 23,39.

dExperimental value at a low temperature in ref. 26.

eDFT value from ref. 28.

fThe SBH for ML MoS2-Pt is hole SBH and the DFT value from ref. 28.

Electronic structure of ML and BL MoS2-metal interfaces

The electronic structures of free-standing ML MoS2 and the interfacial systems are presented in Fig. 2. Free-standing ML MoS2 has a direct band gap of 1.68 eV, consistent with the reported PBE value of 1.67 eV52. The band structures of ML MoS2-metal contacts are classified into three categories in terms of the hybridization degree of ML MoS2 on metals. The band structure of ML MoS2 is identifiable clearly for MoS2 on Au surface (weak hybridization), as a result of weak charge-transfer interaction and dispersion interaction between ML MoS2 and Au surface. The band structure of ML MoS2 is destroyed seriously (strong hybridization) by Sc and Ti surfaces and is destroyed but still identifiable (medium hybridization) by Ni, Pt, and Ag surfaces, because the outmost electrons of the five metals except Ag are d electrons, which strongly hybridize with the states near the Fermi level Ef of ML MoS2. For the sake of comparison, the electronic structures of free-standing BL MoS2 and BL MoS2-metal interfaces are also shown in Fig. 3, with a smaller indirect band gap of 1.46 eV for free-standing BL MoS2. The band hybridization degree is similar from ML to BL MoS2 and can be also divisible into the same three categories. The hybridization degree of ML/BL MoS2 on metals is consistent with its binding energy: The higher the binding energy is, the higher the hybridization degree is.

Figure 2. Band structures of ML MoS2 on Sc, Ti, Ni, Pt, Ag, and Au surfaces by the DFT method, respectively.

Figure 2

Open in a new tab

The Fermi level is at zero energy. Gray line: metal surface bands; red line: bands of MoS2. The line width is proportional to the weight. Blue line: the positions of CBM and VBM of MoS2 after the GW-BGC correction. The labels Maj/Min indicate the majority-spin and minority-spin bands of MoS2 on Ni surface. The band structure of free-standing ML MoS2 calculated in a primitive unit cell and a 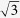Inline graphic × Inline graphic supercell are provided for comparison.

Figure 3. Band structures of BL MoS2 on Sc, Ti, Ni, Pt, Ag, and Au surfaces by the DFT method, respectively.

Figure 3

Open in a new tab

The Fermi level is at zero energy. The gray (red) line denotes metal surface (BL MoS2) bands. The line width is proportional to the weight. Blue line: the positions of CBM and VBM of MoS2 at the GW-BGC scheme. The labels Maj/Min indicate the majority-spin and minority-spin bands of BL MoS2 on Ni surface. The band structure of free-standing BL MoS2 calculated in a primitive unit cell and a Inline graphic × Inline graphic supercell are provided for comparison.

In order to have a deep understanding of the hybridization in Figs 2 and 3, we further calculate the partial density of states (PDOS) on Mo and S orbitals for ML and BL MoS2-metal contacts as shown in Figs 4 and 5. Upon making a contact with Sc and Ti, a large amount of Mo and S states are extended into the original band gap of ML/BL MoS2 due to metallization. In the MoS2-Sc system, the contribution of S 3sp and Mo 4d states dominate Ef, which is associated with a strong S-Sc mixing. Ef is dominated by Mo 4d states, with the other states playing a minor role in the MoS2-Ti system. Mo and S states also appear in the original MoS2 band gap due to orbital overlap between MoS2 and metal. There is no Mo and S state in the original MoS2 band gap in MoS2-Au system, indicating that MoS2 preserves the semiconducting nature on Au surface.

Figure 4. Partial density of states (PDOS) (DOS on specified atoms and orbitals, for example, Mo-d (d-orbital on Mo)) of ML MoS2 on Sc, Ti, Ni, Pt, Ag, and Au surfaces at the DFT level.

Figure 4

Open in a new tab

The Fermi level is at zero energy. The PDOS of free-standing ML MoS2 calculated in a primitive unit cell and a Inline graphic×Inline graphic supercell is provided for comparison.

Figure 5. PDOS of BL MoS2 on Sc, Ti, Ni, Pt, Ag, and Au surfaces at the DFT level.

Figure 5

Open in a new tab

The Fermi level is at zero energy. The PDOS of free-standing BL MoS2 calculated in a primitive unit cell and a Inline graphic × Inline graphic supercell are provided for comparison.

Large charge carrier density at the source/drain interface B indicates a strong overlap of electron orbitals and sufficient injection of electron into the MoS2 layer22. The electron densities averaged in planes parallel to the interface ρl of the investigated six ML MoS2-metal contacts are displayed in Fig. 6. We can see from Fig. 6 that ρl at the strong bonding interfaces (Sc, Ti, Ni, and Pt) is higher than that at the weak bonding interfaces (Ag and Au), a difference compared with the PDOS analysis in Fig. 4. This difference implies that the chemisorption interface has a larger possibility to achieve a lower contact resistance.

Figure 6. Electronic structure at the interface between ML MoS2 and metal at the DFT level.

Figure 6

Open in a new tab

<ρl> is the average value in planes parallel to the interface of MoS2-metal. Inline graphic is the average electrostatic potential in planes normal to the MoS2-metal interface. The dot lines indicate the location of the sulfur layer and the metal layers at the interface. The higher the ρlat the interface is, the higher the electron injection is.

Many-electron effects

The accurate SBH at a metal-semiconductor interface depends on the absolute band-edge positions of the semiconductor. Because the DFT method seriously underestimates the band gap of a semiconductor, the inclusion of the GW correction is also necessary to obtain a correct band gap and absolute band-edge positions of a freestanding (or undoped) semiconductor. If the band gap center (BGC) or Fermi level Ef or work function and the GW corrected band gap (Inline graphic) of the semiconductor are available, the absolute energies at the conduction band maximum (CBM) and the valence band minimum (VBM) can be obtained via the relation:

graphic file with name srep21786-m7.jpg
graphic file with name srep21786-m8.jpg

Unfortunately, in many cases, the BGC of a semiconductor is unavailable. A common solution29,30 is to assume that the BGC at the DFT level is unchanged after the GW correction (named GW-BGC approximation). Figure 7(a,b) illustrate the GW correction to the absolute band positions for freestanding ML and BL MoS2 in BGC approximation. Based on the GW-BGC scheme, the calculated ionization potential (IP = 5.45 eV) and electron affinity (χ = 4.22 eV) of bulk MoS2, compared with values of 5.33 and 4.45 eV at the DFT level29, are in good agreement with the experimental values (IP = 5.47 ± 0.15 eV and χ = 4.07 ± 0.35 eV)53. Actually, Yang et al.54 found that the absolute band-edge energies for ML dichalcogenides given by the direct GW method and the GW-BGC scheme are quite similar. Therefore, the GW-BGC approximation is a good approximation for our studied MoS2 systems.

Figure 7.

Figure 7

Open in a new tab

Schematic illustration of the absolute band positions with respect to the vacuum level at both DFT and GW levels for ML (a) and BL (b) MoS2, respectively. (c) Schematic cross-sectional view of a typical metal contact to 2D MoS2. A, C, and E denote the three regions while B and D are the two interfaces separating them. Blue and red arrows show the pathway (A → B → C → D→ E) of electron injection from contact metal (A) to the MoS2 channel (E). Inset figure shows the typical topology of a MoS2 FET. (d–m) Ten band diagrams of (c) at the DFT level, depending on the type of metals and MoS2 layer number. TB denotes the tunneling transmission barrier. Examples are provided at the bottom (top) of each diagram. EFm and ECh denote the Fermi level of the absorbed system and the band gap center of channel MoS2, respectively. Red arrows indicate the direction of electron or hole flow. The cause of the band bending is given in the main text.

The GW corrections to the band gap of free-standing ML (Inline graphic = 2.84 eV) and BL (Inline graphic = 1.82 eV) MoS2 are available36,37. In our calculations for the SBH at the vertical direction, we take the GW-BGC approximation to determine the absolute band edge positions. In our calculations for the SBH at the lateral direction, we determine the GW-corrected absolute band position by taking the experimental work function (5.25 eV46) of free-standing BL MoS2 (namely channel BL MoS2) as the BGC and further assume free-standing ML and BL MoS2 share identical BGC. The calculated work function of free-standing BL MoS2 at the DFT level is 5.04 eV, which is 0.21 eV slightly smaller than its experimental value. The calculated work function of free-standing ML MoS2 at the DFT level is merely 0.08 eV larger than the calculated one of free-standing BL MoS2.

Schottky barrier at ML and BL MoS2-metal interfaces

The vertical n-type (or p-type) Schottky barrier for the medium (Ag, Pt, and Ni) and weak (Au) bonding cases can be obtained from the difference between Ef and the identifiable CBM (or VBM) of ML/BL MoS2 of the interfacial system, which are shown in the same band structures. By contrast, a strong band hybridization has taken place for ML/BL MoS2 on Sc and Ti surfaces, resulting in metallization of ML/BL MoS2 and absence of vertical Schottky barrier for the four contacts. It has been proved that for the semiconductor fully under metal (namely, in the electrode region), the many-electron effects are greatly depressed if a charge transfer takes place38,55; as a result, the KS band edge positions and band gap are a good approximation. Therefore, we only consider many-electron effects for the band structure of the semiconductor in the channel of a device in the case that a metallization takes place between metal and underneath 2D MoS2. Namely, only as calculating the lateral SBH of 2D MoS2-Sc and -Ti contacts, we consider many-electron effects. We obtain electron SBH at the DFT level of Inline graphic = 0.212 and 0.633 eV for ML MoS2-Ag and Ni contacts, respectively, from the difference between Ef and the identifiable CBM of ML MoS2 shown in the same band structure (Fig. 2). Similarly, we obtain hole SBH of Inline graphic = 0.520 eV for ML MoS2-Pt contact from the difference between Ef and the identifiable VBM of ML MoS2. While for ML MoS2-Au contact, Ef is nearly in the middle of the band gap; Therefore, ML MoS2-Au contact has a midgap Schottky barrier, and this is consistent with the experiment56.

Lateral Schottky barrier ΦL is determined by the energy difference between Ef of the interfacial system and the CBM (n-type) or VBM (p-type) of channel ML MoS2. ML MoS2 forms an Ohmic contact with Sc in the lateral direction at the DFT level since Ef of the interfacial system is higher than the Inline graphic of channel MoS2. However, there is a large lateral SBH at the GW level, with Inline graphic = 0.539 eV. There is a lateral n-type Schottky barrier for Ti contacts at both the DFT and GW levels, with smaller Inline graphic = 0.216 and larger Inline graphic = 0.796 eV. The DFT SBHs of ML MoS2-metal interfaces are in good agreement with the previous DFT calculations (see Table 1). For example, the lateral DFT SBH for ML MoS2-Ti interface is 0.33 eV calculated by Banerjee et al.23,39. There is some uncertainty in identifying the metallization. However, even if we identify a metallization for ML MoS2 under Ag, Pt, and Ni, the values of the resulting lateral SBHs are close to those of the vertical SBHs.

The vertical Ohmic contact feature remains on Sc and Ti surfaces from ML to BL MoS2, because the strong band hybridization remains. From ML to BL MoS2, ΦV in MoS2-Au contact is significantly decreased by 0.096 eV at the DFT level as a result of the reduction of the band gap (0.220 eV). The vertical SBHs for Ag, Pt, and Ni contacts are slightly decreased by 0.074, 0.175, and 0.021 eV, respectively, at the DFT level from ML to BL MoS2. The reduced SBH from ML to BL MoS2 is in good agreement with the experiment21. BL MoS2 still forms an Ohmic contact with Sc in the lateral direction.

Since the lattice mismatches are large for the Sc-MoS2 (4.485%) and Ti-MoS2 (6.791%) interfaces in the above study, we further enlarge the supercell to reduce the lattice mismatch. The Inline graphic unit cell of MoS2 is adjusted to the 2Inline graphic × 2Inline graphic unit cells of Sc(0001) surface, with the lattice mismatch decreased to 1.29%. The 2Inline graphic ×2Inline graphic unit cell of MoS2 is adjusted to Inline graphic unit cells of Ti(0001) surface, with the lattice mismatch decreased to 2.99%. Compared with the large mismatch configuration, the small mismatch ones do not change the contact type and just slightly increase Inline graphicfrom 0.187 (0.096) to 0.216 (0.161) eV for ML (BL) MoS2-Ti contact, which is closer to a DFT value of 0.33 eV of Banerjee et al.23,39 based on a larger ML MoS2-Ti interfacial supercell containing 6 Mo and 12 S atoms per unit cell in the contact region.

The experimentally extracted SBHs of ML and BL MoS2-Ti contact are 0.3~0.3523 and 0.065 eV26, respectively, which are in agreement with our calculated values of 0.216 and 0.161 eV at the DFT level but apparently deviate from the corresponding values with many-body effect correction (0.796 and 0.341 eV, respectively). Such a comparison suggests that many-electron effects have been greatly depressed by the charge transfer between channel MoS2 and the electrodes, which significantly screens the electron-electron Coulomb interaction and validates sing-electron approximation. In other word, the transport gap of ML MoS2 is determined by the DFT band gap rather than the quasiparticle band gap.

In a recent work, the SBH and the transport gap of phosphorene have been measured57. Phosphorene is p-type doped by Ni electrodes, and the transport gaps of ML and few layer phosphorene with Ni electrodes are in good agreement with the DFT band gaps at the GGA level. For example, the transport gap of ML and BL phosphorene are 0.98 ± 0.4 and 0.71 ± 0.4 eV57, respectively, and the corresponding band gaps are 0.91 and 0.6 eV at the DFT level58, while the quasiparticle band gaps are 2.0 and 1.3 eV59. Therefore, the suppressed many-electron effects can be expanded to a general device if 2D channel semiconductor is doped by electrodes, and correspondingly the transport gap depends on the DFT band gap instead of the quasiparticle band gap.

In our above calculations, we adapt the lattice constant of MoS2 to that of metal surfaces as the match way in ref. 27 in view of the fact that the bulk metal electrode is more robust than ML and BL MoS2. We note that the lattice constant of MoS2 is fixed in ref. 28. In order to explore the effects of the match way on the work function of MoS2-metal interface, we give the work function of interfacial systems in the case of fixing MoS2 lattices in Table S1. The work function of the system with Ti surface adjusted to MoS2 is 0.205 eV smaller than that of the system with BL MoS2 adjusted to Ti surface; consequently, the lateral SBH disappears. Such a result is in consistent with the experimental SBH of 0.065 eV for BL MoS2-Ti contact26. There is nearly no difference in work function between these two strained method for BL MoS2-Sc and ML MoS2-Ti contacts.

Tunneling barrier at ML and BL MoS2-metal interfaces

In order to complete the analysis of contacts, we further investigate the electrostatic potential at the ML MoS2-metal interfaces and show the results in Fig. 6. The tunneling barrier ∆V here is defined as the potential energy above the Fermi energy between the MoS2 and metal surfaces, indicated by the black rectangular, and the tunneling width wB is defined as the full width at half maximum of the ∆V. As shown in Fig. 6 and Table 2, the ∆V values at the strong hybridization interfaces (Sc, Ti, Ni, and Pt) are significantly lower and the wB values are significantly narrower than those at the weak ones (Ag and Au). A lower barrier height and a narrower width at a semiconductor-metal interface mean a higher electron injection efficiency. We estimate the tunneling probabilities TB from metal to MoS2 using a square potential barrier model as:

Table 2. Tunneling barrier height ΔV, width w B, and probabilities (T B) through the ML (BL) MoS2-metal interfaces.

Metal ML MoS2
 BL MoS2
ΔV wB TB ΔV wB TB
(eV) (Å) (%) (eV) (Å) (%)
Sc 0.000 0.000 100 0.000 0.000 100
Ti 0.000 0.000 100 0.000 0.000 100
Ag 3.003 0.916 19.68 2.911 0.904 20.61
Ni 0.785 0.327 74.33 0.822 0.336 73.20
Au 4.697 1.374 4.74 4.585 1.356 5.11
Pt 1.810 0.458 53.21 1.871 0.517 48.47
Open in a new tab
graphic file with name srep21786-m24.jpg

where m is the effective mass of a free electron and ħ is the Plank’s constant. The TB values are thus estimated to be 100, 100, 74.33, 53.21, 19.68, and 4.74% for Sc, Ti, Ni, Pt, Ag, and Au contacts, respectively (see Table 2). Apparently, Sc and Ti contacts have perfect transmission. The tunneling properties of the tunneling barrier at the BL MoS2-metal interfaces are also summarized in Table 2. Compared with the case of ML MoS2 contact metals, there is little change in the tunneling properties for BL MoS2, indicating that the tunneling properties are insensitive to the MoS2 layer number.

In the light of Schottky barrier and tunneling barrier, the nature of MoS2- metal contacts can be classified into five types. Sc can form high quality contact interface with ML and BL MoS2 with zero tunneling barrier and zero Schottky barrier, leading to Ohmic contact (Fig. 7(d)). Although the metallization of ML MoS2 with Ti eliminates the Schottky barrier at the interface B, the injected electrons from the metal still confront a n-type Schottky barrier at the interface D, leading to Type 1 in Fig. 7(e). The nature of BL MoS2-Ti contacts also belong to Type 1. It is noteworthy that the tunneling barrier vanishes in Type 1 contact due to the metallization at interface B. Unlike the case in Type 1, there is a tunneling barrier at the interface B in Types 2 and 3 contacts. Only p-type Schottky barrier is formed in ML and BL MoS2-Pt contacts (Type 3, Fig. 7(g)). In Type 4 contact (ML and BL MoS2-Au), Schottky barrier and tunneling barrier are formed at the interface B, and SBH is zero at the interface D because of the lack of orbital overlaps.

Fermi level line-up

Our calculated Inline graphic of ML MoS2 on all investigated metal surfaces are listed in Fig. 8(a), in which the GW results for Sc and Ti contacts are also provided for comparison. For Sc contacts, the Inline graphic obtained by transport calculations is also presented, which will be discussed later in the transport properties. The CBM of Sc, Ti, Ag, Au, and Ni-ML MoS2 systems are closer to the Fermi levels than the VBM, leading to the n-type contact. While the VBM of Pt-ML MoS2 absorbed system is closer to the Fermi levels and form p-type contact. The n-type characteristic of ML MoS2 on Sc, Ti, Ag, Au, and Ni surfaces has been observed experimentally8,21,24, and the p-type characteristic on Pt surface is calculated in other DFT calculation28. Therefore, ML MoS2 p−n junction can be fabricated by using Sc, Ti, Ag, Au, or Ni to contact one end of ML MoS2 and Pt to contact the other end of it. The ML MoS2 p−n junction can be used to develop optoelectronics or valley-optoelectronics technology60. Comparing the Inline graphic at the DFT and GW levels for Sc and Ti contacts, we find that the doping type is unchanged.

Figure 8.

Figure 8

Open in a new tab

SBHs of (a) ML and (b) BL MoS2 on the six metal surfaces. Inline graphic denotes n type SB for electrons, while Inline graphic represents p type SB for holes.

The calculated Inline graphic of BL MoS2 on the six metal surfaces are listed in Fig. 8(b), in which the GW results for Sc and Ti contacts are also provided for comparison. Compared with Fig. 8(a), the GW correction to the band gap of BL MoS2 is less significant because many-body effect is reduced with the increasing size in the vertical direction. BL MoS2 FET is also p-type doped by Pt contact and n-type doped by the other five contacts. Consistently, the experiments have found n-type characteristic of BL MoS2 on Ti and Au surfaces11,26.

The Fermi level shift ΔEf is defined as the difference between the interfacial systems and free-standing 2D MoS2 work functions when the band hybridization occurs at the interfaces (Sc, Ti, Ni, Pt, and Ag contacts). ΔEf is defined as ΔEf = Emid – Ef for the interface without band hybridization (for Au contact), where Emid is the midpoint of the identifiable band gap of MoS2. Negative (positive) ΔEf means n-type (p-type) doping of 2D MoS2. The doping types determined from ΔEf are in agreement with those determined from Figs 8 and 9. ΔEf as a function of the difference between the clean metal (WM) and ML (BL) MoS2 work functions (Inline graphic) is shown in Fig. S1 (2). The cross point from n- to p-type doping is WM – Inline graphic = 0.21 (0.13) eV for ML (BL) case. The ΔEf has a nearly linear dependence with the WM –Inline graphicwith a slope of 0.64 in both ML and BL MoS2-metal contacts, approximately equal to the previously reported theoretical value of 0.71 in ML MoS2-metal contacts28. Notably, ΔEf is insensitive to the MoS2 layer number, leading to the same linear relation between ΔEf and work function. Note that the slope close to 0 indicates a strong Fermi level pinning, and we therefore observe a partial Fermi level pinning picture once more when the six metals contact ML MoS2. The partial Fermi level pinning is a synergic result of the metal work function modification and the interface gap states formation in the studied interface systems28.

Figure 9.

Figure 9

Open in a new tab

(a) Transmission spectra of the ML and BL MoS2 transistors with Sc electrodes. In Model I, the lattice constant of MoS2 is adjusted to that of Sc, while in Model II the lattice constant of Sc is adjusted to that of MoS2. (b,c) Local density of states (LDOS) in color coding for the ML MoS2 transistors in Models I and II, respectively. The red line indicates the boundary of ML MoS2-Sc and the free-standing ML MoS2, and the yellow dashed line indicates the Fermi level.

Quantum Transport Simulation

We note that the experiment reported that few layer (3–18 layers) MoS2-Sc contact still has a very small SBH of 0.03 eV21. ML and BL MoS2 should have a larger SBH due to the enhanced band gaps compared with few layer MoS2 and this is inconsistent with the predicted Ohmic contact for Sc electrode (Ef of Sc electrode is above the CBM of channel ML/BL MoS2 by 0.22/0.21 eV) in the above dual interface model calculation. In the dual interface model, one determines the SBH indirectly by calculating the work functions of MoS2 under metal and channel MoS2 separately. In a real device, there is possible complex coupling between MoS2 under metal and channel MoS2 (namely Fermi level pinning). A direct and better theoretical approach to determine the SBH of a FET is to calculate the transport property of the device by using the DFT method coupled with NEGF.

In our quantum transport simulations, the device is constructed of ML/BL MoS2 in the channel region and ML/BL MoS2-Sc interfaces in the electrode region. The lattice constant of the ML/BL MoS2 should be carefully chosen, as it directly affects the size of the band gap and thus transport properties. In a real device, the lattice constant of the ML/BL MoS2 in the central region is close to that of free-standing ML/BL MoS2, while in the electrode region the lattice constant of the ML/BL MoS2 should be adapted to that of corresponding bulk metals supercell. In order to capture this feature, we consider two extreme cases in the transport calculations: in Model I, the lattice constant of ML/BL MoS2 in the device is adapted to that of Sc surface, and in Model II, the lattice constant of Sc surface is adapted to that of ML/BL MoS2. One could expect that the transport properties of the real device should be between the two cases.

The transmission spectra of ML and BL MoS2 transistors using the two models calculated with SZP basis set are provided in Fig. 9(a), respectively. A test shows that a larger DZP basis set gives a quite close SBH. The transmission spectra of ML MoS2 transistors give transport gaps of 0.92 eV in Model I and 1.67 eV in Model II, and the latter value is quite close to the band gap (1.68 eV) of free-standing ML MoS2. The Fermi level Ef is slightly below the CBM in both two models, showing a n-type Schottky barrier between ML MoS2 and Sc electrode in the devices. The values of the electron SBH are read as 0.040 eV and 0.260 eV in Models I and II, respectively. As the real system is between the two extreme cases, we estimate the SBH in the real ML MoS2 transistor with Sc electrodes to be around 0.150 eV by roughly averaging the values of the two cases. As the number of MoS2 layers increases, its band gap decreases. Our transport simulations also show a reduction (~0.09 eV in Model I and 0.56 eV in Model II, respectively) of the transport gap of BL MoS2 compared to that of ML. The average value of SBH in the BL MoS2 with Sc contact over the two models is estimated to 0.185 eV in the transport simulation. Therefore, increasing the lay number of MoS2 not always leads to a decrease in SBH although it often does.

The local density of states (LDOS) versus the coordinate along the transport direction of ML MoS2 transistors using the two models calculated with SZP basis set are provided in Fig. 9(b,c). It is apparent from the LDOS that the conduction band is bent downward due to an electron transfer from Sc to channel ML MoS2 where no impurity states exist. Such a downward bending is different from a common band upward bending in a metal-n type semiconductor interface where donor states exist and electrons are transferred from semiconductor to metal. In accordance with the value calculated from the transmission spectra, the LDOS also shows an average n-type SBH of 0.15 eV for ML MoS2-Sc interface. Taken together, unlike the DFT energy band analysis, which gives an artificial Ohmic contact, the quantum transport simulations give a n-type Schottky contact for ML and BL MoS2 Sc-interfaces with electron SBH of 0.150 and 0.185 eV, respectively, which are qualitatively in agreement with the experiment21, where 3–18 layer MoS2 Sc-interface has a small electron SBH of 0.03 eV.

The failure of the energy band analysis in predicting MoS2-Sc contact comes from the ignorance of the coupling between MoS2 under Sc and channel MoS2 because we calculate the electronic properties of the electrode and the channel region separately during deriving the lateral SBH. This coupling makes the Ohmic contact difficult to occur because the Fermi level is pinned below the CBM of MoS2. Therefore, caution must be taken for any lateral Ohmic contact predicted by the energy band analysis, and a further quantum transport calculation is necessary to obtain a more reliable interface. Actually, the Ohmic contact in ML phosphorene-Pd contact derived from the energy band analysis also turns out to be artificial in terms of the quantum transport simulations61.

If the SBH appears in the vertical direction, the coupling between metal and MoS2 has been taken into account in the energy band calculations because the metal and semiconductor parts are treated a whole. In this case, it appears that the quantum transport simulation will give similar SBH. We calculate the transport properties of ML and BL MoS2 with Pt electrodes. As the lattice mismatch between MoS2 and Pt supercell is small (~1.2%), we only consider Model I in which the lattice constant of ML/BL MoS2 is adapted to that of Pt supercell. As shown in Fig. S1, transport gaps of 1.34 and 1.03 eV are observed for ML and BL MoS2-Pt interfaces in the transmission spectra. The Fermi level in BL MoS2-Pt contact is apparently closer to the VBM, having a hole SBH of 0.32 eV, which is in indeed good agreement with the one (0.345 eV) from the energy band analysis. It appears that the coupling between Pt and BL MoS2 has been taken into account in the energy band calculations. It is notable that the energy band analysis and the quantum transport simulations also give similar p-type SBHs for ML WSe2-Pt interface (0.28 and 0.34 eV, respectively)62. However, the Fermi level of ML MoS2-Pt contact is located nearly in the middle of the transport gap (slightly closer to the CBM of ML MoS2), showing a midgap SBH. This is not in consistent with the energy band analysis, which favors a p doping of ML MoS2 with a hole SBH of 0.520 eV. The story becomes more complicated as the experimental observations show electron SBH of ~0.23 eV for 3–8 layers MoS2-Pt interface21. The origin of the controversy among the energy band analysis, quantum transport simulations, and experiments remains unclear and more studies on the MoS2-Pt system are desirable. It is interesting to mention that, in the MoS2-Pd system, both n- and p-doped characteristics of MoS2 have been reported63,64,65. It is well known that Pt has a larger work function than Pd (6.1 eV vs 5.6 eV)51, and generally Pt can induce p doping more easily. It appears that the possibility of p doping of ML and BL MoS2 by Pt contact cannot be excluded completely.

Discussions

There are four types of commonly used band gap for a 2D semiconductor: transport gap, quasiparticle gap (dominated by electron-electron correlation), optical gap (dominated by strong exciton effects), and DFT gap (single electron approximation). Taking ML/BL phosphorene as an example, the four band gaps are: 0.98/0.7157, 2.0/1.358, 1.30/0.70 , and 0.91/0.60 eV59. Apparently, the DFT band gap and optical gap are the closest to the transport gap because the 2D channel semiconductor is doped by carrier. In addition to doping by electrode, the 2D semiconductor channel is also subject to electrostatic doping by gate. This is another cause why many-electron effects are strongly depressed of the 2D channel semiconductor. However, the transport gaps are still about 10% slightly larger than their respective DFT gaps in phosphorene66, suggestive of the existence of weak many-electron effects with about 10% correction in doped phosphorene, which is one order of magnitude smaller than that in intrinsic phosphorene. Actually, the band gap of a heavily doped silicene is 0.34 and 0.38 eV at the DFT and GW level, respectively, consistent with a correction of about 10% upon the inclusion of the many-body effects38. From a physical point of view, the transport gap of a 2D semiconductor should equal to the quasipartical band gap of heavily doped system, which is slightly larger than the DFT band gap. Figure 10 illustrates the size relation of these common band gaps. Hence, a small correction (increase by about 10%) to the DFT CBM and VBM appears to be required to obtain the accurate CBM and VBM positions of a doped 2D semiconductor and thus get the accurate SBH at the interface.

Figure 10. A schematic diagram for the size relation of the five common band gaps of a 2D semiconductor.

Figure 10

Open in a new tab

Conclusion

In summary, we provide the first comparative study of the interfacial properties of monolayer and bilayer MoS2 on Sc, Ti, Ag, Pt, Ni, and Au surfaces by using different theoretical approaches. A comparison between the calculated and observed Schottky barrier heights suggests that many-electron effects are strongly depressed but do not vanish and the transport gap of a device depends on the DFT-GGA band gap (a minor correction is still needed) rather than the quasiparticle band gap. Such a depression of many-electron effects can be applied to a general metal-2D semiconductor interface. In generally, the Schottky barrier heights are decreased from ML MoS2-metal interfaces to BL MoS2-metal interfaces due to the interlayer coupling, implying that BL MoS2 with a higher electron injection efficiency is probably more suitable for a transistor than ML MoS2 given the same gate controllability. Most strikingly, we find that DFT energy band calculations are unable to reproduce the experimental Schottky barrier heights in some cases and give incorrect Ohmic contact prediction because the Fermi level pinning has not been fully taken into account. In the interface study between other 2D material and metal, such a shortcoming remains. To solve such a problem, a higher level ab initio quantum transport calculation based on a two-probe model is desired.

Additional Information

How to cite this article: Zhong, H. et al. Interfacial Properties of Monolayer and Bilayer MoS2 Contacts with Metals: Beyond the Energy Band Calculations. Sci. Rep. 6, 21786; doi: 10.1038/srep21786 (2016).

Supplementary Material

Supplementary Information
srep21786-s1.pdf (175KB, pdf)

Acknowledgments

This work was supported by the National Natural Science Foundation of China (No. 11274016/11474012), the National Basic Research Program of China (No. 2013CB932604/2012CB619304), and the National Science Foundation Grant (1207141).

Footnotes

Author Contributions The idea was conceived by J.L. The DFT electronic band calculation was performed by H.Z. and the device simulation was performed by R.Q. and M.Y. The data analyses were performed by J.L., H.Z., R.Q., J.S., L.Y., J.Y., Z.N., Y.W., M.Y., M.L., Z.S. and Y.P. This manuscript was written by H.Z., R.Q. and J.L. All authors contributed to the preparation of this manuscript.

References

  1. Mak K. F., McGill K. L., Park J. & McEuen P. L.. The valley Hall effect in MoS2 transistors. Science 344, 1489–1492 (2014). [DOI] [PubMed] [Google Scholar]
  2. Yin X. et al. Edge nonlinear optics on a MoS2 atomic monolayer. Science 344, 488–490 (2014). [DOI] [PubMed] [Google Scholar]
  3. Stajic J.. Using the valleys in monolayer MoS2. Science 344, 1476–1478 (2014). [Google Scholar]
  4. Lee C.-H. et al. Atomically thin p–n junctions with van der Waals heterointerfaces. Nature Nanotech. 150, 676–681 (2014). [DOI] [PubMed] [Google Scholar]
  5. Wu S. et al. Electrical tuning of valley magnetic moment through symmetry control in bilayer MoS2. Nature Phys. 9, 149–153 (2013). [Google Scholar]
  6. Mak K. F., Lee C., Hone J., Shan J. & Heinz T. F.. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010). [DOI] [PubMed] [Google Scholar]
  7. Baugher B. W. H., Churchill H. O. H., Yang Y. & Jarillo-Herrero P.. Intrinsic electronic transport properties of high-quality monolayer and bilayer MoS2. Nano Lett. 13, 4212–4216 (2013). [DOI] [PubMed] [Google Scholar]
  8. Radisavljevic B., Radenovic A., Brivio J., Giacometti V. & Kis A.. Single-layer MoS2 transistors. Nature Nanotech. 6, 147–150 (2011). [DOI] [PubMed] [Google Scholar]
  9. Sarkar D. et al. MoS2 field-effect transistor for next-generation label-free biosensors. ACS Nano 8, 3992–4003 (2014). [DOI] [PubMed] [Google Scholar]
  10. Radisavljevic B., Whitwick M. B. & Kis A.. Integrated circuits and logic operations based on single-layer MoS2. ACS Nano 5, 9934–9938 (2011). [DOI] [PubMed] [Google Scholar]
  11. Wang H. et al. Integrated circuits based on bilayer MoS2 transistors. Nano Lett. 12, 4674–4680 (2012). [DOI] [PubMed] [Google Scholar]
  12. Perkins F. K. et al. Chemical vapor sensing with monolayer MoS2. Nano Lett. 13, 668–673 (2013). [DOI] [PubMed] [Google Scholar]
  13. Sundaram R. S. et al. Electroluminescence in single layer MoS2. Nano Lett. 13, 1416−1421 (2013). [DOI] [PubMed] [Google Scholar]
  14. Yin Z. et al. Single-layer MoS2 phototransistors. ACS Nano 6, 74–80 (2012). [DOI] [PubMed] [Google Scholar]
  15. Lopez-Sanchez O., Lembke D., Kayci M., Radenovic A. & Kis A.. Ultrasensitive photodetectors based on monolayer MoS2. Nature Nanotech. 8, 497–501 (2013). [DOI] [PubMed] [Google Scholar]
  16. Yuan H. et al. Zeeman-type spin splitting controlled by an electric field. Nature Phys. 9, 563–569 (2013). [Google Scholar]
  17. Zeng H., Dai J., Yao W., Xiao D. & Cui X.. Valley polarization in MoS2 monolayers by optical pumping. Nature Nanotech. 7, 490–493 (2012). [DOI] [PubMed] [Google Scholar]
  18. Mak K. F., He K., Shan J. & Heinz T. F.. Control of valley polarization in monolayer MoS2 by optical helicity. Nature Nanotech. 7, 494–498 (2012). [DOI] [PubMed] [Google Scholar]
  19. Cui X. et al. Multi-terminal transport measurements of MoS2 using a van der Waals heterostructure device platform. Nature Nanotech. 10, 534–520 (2015). [DOI] [PubMed] [Google Scholar]
  20. Splendiani A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010). [DOI] [PubMed] [Google Scholar]
  21. Das S., Chen H.-Y., Penumatcha A. V. & Appenzeller J.. High performance multilayer MoS2 transistors with scandium contacts. Nano Lett. 13, 100–105 (2013). [DOI] [PubMed] [Google Scholar]
  22. Popov I., Seifert G. & Tománek D.. Designing electrical contacts to MoS2 monolayers: a computational study. Phys. Rev. Lett. 108, 156802 (2012). [DOI] [PubMed] [Google Scholar]
  23. Kang J., Liu W., Sarkar D., Jena D. & Banerjee K.. Computational study of metal contacts to monolayer transition-metal dichalcogenide semiconductors. Phys. Rev. X 4, 031005 (2014). [Google Scholar]
  24. Amani M. et al. Electrical performance of monolayer MoS2 field-effect transistors prepared by chemical vapor deposition. Appl. Phys. Lett. 102, 193107 (2013). [Google Scholar]
  25. Liu W. et al. High-Performance Few-Layer-MoS2 Field-Effect-Transistor with Record Low Contact-Resistance. IEEE International Electron Devices Meeting 499–502 (2013). [Google Scholar]
  26. Qiu H. et al. Electrical characterization of back-gated bi-layer MoS2 field-effect transistors and the effect of ambient on their performances. Appl. Phys. Lett. 100, 123104 (2012). [Google Scholar]
  27. Chen W., Santos E. J. G., Zhu W., Kaxiras E. & Zhang Z.. Tuning the electronic and chemical properties of monolayer MoS2 adsorbed on transition metal substrates. Nano Lett. 13, 509–514 (2013). [DOI] [PubMed] [Google Scholar]
  28. Gong C., Colombo L., Wallace R. M. & Cho K.. The unusual mechanism of partial Fermi level pinning at metal–MoS2 interfaces. Nano Lett. 14, 1714–1720 (2014). [DOI] [PubMed] [Google Scholar]
  29. Jiang H.. Electronic band structures of molybdenum and tungsten dichalcogenides by the GW approach. J. Phys. Chem. C 116, 7664–7671 (2012). [Google Scholar]
  30. Toroker M. C. et al. First principles scheme to evaluate band edge positions in potential transition metal oxide photocatalysts and photoelectrodes. Phys. Chem. Chem. Phys. 13, 16644 (2011). [DOI] [PubMed] [Google Scholar]
  31. Wirtz L., Marini A. & Rubio A.. Excitons in boron nitride nanotubes: dimensionality effects. Phys. Rev. Lett. 96, 126104 (2006). [DOI] [PubMed] [Google Scholar]
  32. Park C.-H., Spataru C. D. & Louie S. G.. Excitons and many-electron effects in the optical response of single-walled boron nitride nanotubes. Phys. Rev. Lett. 96, 126105 (2006). [DOI] [PubMed] [Google Scholar]
  33. Yang L., Park C.-H., Son Y.-W., Cohen M. L. & Louie S. G.. Quasiparticle energies and band gaps in graphene nanoribbons. Phys. Rev. Lett. 99, 186801 (2007). [DOI] [PubMed] [Google Scholar]
  34. Yang L., Deslippe J., Park C.-H., Cohen M. L. & Louie S. G.. Excitonic effects on the optical response of graphene and bilayer graphene. Phys. Rev. Lett. 103, 186802 (2009). [DOI] [PubMed] [Google Scholar]
  35. Fei R. et al. Enhanced many-body effects in one-dimensional linear atomic chains. Phys. Status Solidi B 8, 1636–1643 (2013). [Google Scholar]
  36. Qiu D. Y., da Jornada F. H. & Louie S. G.. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013). [DOI] [PubMed] [Google Scholar]
  37. He J., Hummer K. & Franchini C.. Stacking effects on the electronic and optical properties of bilayer transition metal dichalcogenides MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B 89, 075409 (2014). [Google Scholar]
  38. Quhe R. et al. Tunable and sizable band gap in silicene by surface adsorption. Sci. Rep, doi: 10.1038/srep00853, 2, 853 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kang J., Liu W. & Banerjee K.. High-performance MoS2 transistors with low-resistance molybdenum contacts. Appl. Phys. Lett. 104, 093106 (2014). [Google Scholar]
  40. Reshak A. H. & Auluck S.. Calculated optical properties of 2H-MoS2 intercalated with lithium. Phys. Rev. B 68, 125101 (2003). [Google Scholar]
  41. Kresse G. & Furthmüller J.. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996). [DOI] [PubMed] [Google Scholar]
  42. Kresse G. & Joubert D.. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999). [Google Scholar]
  43. Perdew J. P. & Wang Y.. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244–13249 (1992). [DOI] [PubMed] [Google Scholar]
  44. Ortmann F., Bechstedt F. & Schmidt W. G.. Semiempirical van der Waals correction to the density functional description of solids and molecular structures. Phys. Rev. B 73, 205101 (2006). [Google Scholar]
  45. Monkhorst H. J. & Pack J.. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976). [Google Scholar]
  46. Li Y., Xu C.-Y., Zhang B.-Y. & Zhen L.. Work function modulation of bilayer MoS2 nanoflake by backgate electric field effect. Appl. Phys. Lett. 103, 033122 (2013). [Google Scholar]
  47. Ramasubramaniam A.. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012). [Google Scholar]
  48. Cheiwchanchamnangij T. & Lambrecht Walter R. L.. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 85, 205302 (2012). [Google Scholar]
  49. Smith D. R., Schultz S., Markoš P. & Soukoulis C. M.. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 65, 195104 (2002). [Google Scholar]
  50. Soler J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condense. Mat. 14, 2745 (2002). [Google Scholar]
  51. Khomyakov P. A. et al. First-principles study of the interaction and charge transfer between graphene and metals. Phys. Rev. B 79, 195425 (2009). [Google Scholar]
  52. Ding Y. et al. First principles study of structural, vibrational and electronic properties of graphene-like MX2 (M=Mo, Nb, W, Ta; X=S, Se, Te) monolayers. Physica B 406, 2254–2260 (2011). [Google Scholar]
  53. Schlaf R., Lang O., Pettenkofer C. & Jaegermann W.. Band lineup of layered semiconductor heterointerfaces prepared by van der Waals epitaxy: Charge transfer correction term for the electron affinity rule. J. Appl. Phys. 85, 2732–2753 (1999). [Google Scholar]
  54. Liang Y., Huang S., Soklaski R. & Yang L.. Quasiparticle band-edge energy and band offsets of monolayer of molybdenum and tungsten chalcogenides. Appl. Phys. Lett. 103, 042106 (2013). [Google Scholar]
  55. Neaton J. B., Hybertsen M. S. & Louie S. G.. Renormalization of molecular electronic levels at metal-molecule interfaces. Phys. Rev. Lett. 97, 216405 (2006). [DOI] [PubMed] [Google Scholar]
  56. Fang H. et al. Degenerate n-doping of few-layer transition metal dichalcogenides by potassium. Nano Lett. 13, 1991–1995 (2013). [DOI] [PubMed] [Google Scholar]
  57. Das S. et al. Tunable transport gap in phosphorene. Nano Lett. 14, 5733–5739 (2014). [DOI] [PubMed] [Google Scholar]
  58. Tran V., Soklaski R., Liang Y. & Yang L.. Layer-controlled band gap and anisotropic excitons in few-layer black phosphorus. Phys. Rev. B 89, 235319 (2014). [Google Scholar]
  59. Qiao J., Kong X., Hu Z. X., Yang F. & Ji W.. High-mobility transport anisotropy and linear dichroism in few-layer black phosphorus. Nat. Commun. 5, 4475 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zhang Y. J., Oka T., Suzuki R., Ye J. T. & Iwasa Y.. Electrically switchable chiral light-emitting transistor. Science 344, 725–728 (2014). [DOI] [PubMed] [Google Scholar]
  61. Pan Y. et al. Monolayer Phosphorene-Metal Interfaces. arXiv preprint arXiv. 1507, 02420 (2015). [Google Scholar]
  62. Wang Y. et al. Does p-type ohmic contact exist in WSe2-metal interfaces? Nanoscale 8, 1179–1191 (2016). [DOI] [PubMed] [Google Scholar]
  63. Kaushik N. et al. Schottky barrier heights for Au and Pd contacts to MoS2. Appl. Phys. Lett. 105, 113505 (2014). [Google Scholar]
  64. Das S., Prakash A., Salazar R. & Appenzeller J.. Toward low-power electronics: tunneling phenomena in transition metal dichalcogenides. ACS Nano 8, 1681–1689 (2014). [DOI] [PubMed] [Google Scholar]
  65. Fontana M. et al. Electron-hole transport and photovoltaic effect in gated MoS2 Schottky junctions. Sci. Rep, doi: 10.1038/srep01634, 3, 1634 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Wang X. et al. Highly anisotropic and robust excitons in monolayer black phosphorus. Nature Nanotech. 10, 517–521 (2015). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep21786-s1.pdf (175KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES