Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 1;6:22264. doi: 10.1038/srep22264

Metabolic Trade-offs in Yeast are Caused by F1F0-ATP synthase

Avlant Nilsson 1, Jens Nielsen 1,2,a
PMCID: PMC4772093  PMID: 26928598

Abstract

Intermediary metabolism provides living cells with free energy and precursor metabolites required for synthesizing proteins, lipids, RNA and other cellular constituents, and it is highly conserved among living species. Only a fraction of cellular protein can, however, be allocated to enzymes of intermediary metabolism and consequently metabolic trade-offs may take place. One such trade-off, aerobic fermentation, occurs in both yeast (the Crabtree effect) and cancer cells (the Warburg effect) and has been a scientific challenge for decades. Here we show, using flux balance analysis combined with in vitro measured enzyme specific activities, that fermentation is more catalytically efficient than respiration, i.e. it produces more ATP per protein mass. And that the switch to fermentation at high growth rates therefore is a consequence of a high ATP production rate, provided by a limited pool of enzymes. The catalytic efficiency is also higher for cells grown on glucose compared to galactose and ethanol, which may explain the observed differences in their growth rates. The enzyme F1F0-ATP synthase (Complex V) was found to have flux control over respiration in the model, and since it is evolutionary conserved, we expect the trade-off to occur in organisms from all kingdoms of life.

To generate energy, yeast can use both the, oxygen consuming, respiratory pathways and the, ethanol producing, fermentative pathways. The respiratory pathway generates 10 times more ATP per glucose molecule, and has a fivefold higher biomass yield1. It is therefore somewhat counterintuitive that yeast makes use of the fermentative pathway even in the presence of oxygen, i.e. the Crabtree effect2, when it grows fast. Similar examples of aerobic low yield metabolism occur in other microbes, e.g. E. coli3, and in human4, e.g. lactate production in cancer, muscle and red blood cells. The underlying biological motivation for this is still under debate, and it is not predicted by standard metabolic models5. But it has been hypothesized that fermentation has a higher catalytic efficiency than respiration, i.e. that more energy is produced per mass of enzyme6.

Many microorganisms and mammalian cells use glucose as their preferred carbon source, but can still utilize a range of alternative carbon sources. Catabolism of galactose through the Leloir pathway only involves a few additional enzymatic steps, but the growth rate is much lower1. Over-expression of the enzymes of the Leloir surprisingly decreased the growth rate even further7. This has been attributed to the physiological burden on the cell from the transcription and translation of additional enzymes8. Yeast cells grown on glucose in batch culture9 first deplete the glucose whilst producing ethanol. They then undergo a diauxic shift, where their protein composition is remodeled, and continue to growth on ethanol, at a lower rate.

To understand these observations, we turned to the hypothesis that cells are constrained by the allocation of protein mass. This hypothesis has gained recent attention through the description of the cell as a self-replicating system6,10, where different cellular processes, e.g. metabolism, biosynthesis, ribosomes, membrane transport, compete for a finite protein pool in order to maximize growth. The proteome of E. coli, has been found to cluster in to such biologically distinct sectors, with positive or negative relations to the growth rate11. The protein pool becomes limiting, since each enzyme has a characteristic mass 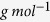Inline graphic and effective rate 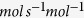Inline graphic, with a resulting mass efficiency, i.e. the enzymes specific activity 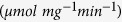Inline graphic. This has also been studied from the perspective of molecular crowding12, where the total amount of enzyme is limited by the solvent capacity of the cytosol. But since the solvent capacity is shown to be near invariant13, this is similar to a limited protein pool.

An extension of flux balance analysis12,14 has been developed to handle this catalytic dimension of metabolism. These models use the specific activities of the enzymes to either estimate their volume, constrained by a limited solvent capacity12, or more directly by estimating their share of mass in the total protein pool14. The method has been successful in predicting the maximum growth rate of E. coli on different carbon sources14. And it also has the potential to explain aerobic low yield metabolism, since genome scale models with randomly sampled data predict this in their best fit, in both E. coli12 and S. cerevisiae3. This was also the predicted outcome in a genome scale model of human, using in vitro enzyme activity for 15% of the reactions and the median for the remaining15. In this study we reduce the scope to intermediary metabolism of S. cerevisiae to avoid the use of simulated data and ensure complete in vitro enzyme data coverage.

In S. cerevisiae the size of the protein pool depends on the growth rate, and varies between 40–60% of the dry weight2,16. The remaining mass is allocated to RNA 6–12%, glycogen 0–8% and the cell wall of polysaccharides 10–25%16,17. A large share of the protein pool is taken by enzymes involved in protein synthesis, e.g. the ribosomes, and they are responsible for most of the changes in protein mass (Supplementary Figure S1). Measurements of the growth rate dependent changes in biomass composition show that S. cerevisiae can increase its protein content (g per g cell dry weight) by decreasing the glycogen reserves16. It can also increase the protein content by increasing the cell size, since this increases the protein rich cytosol at the expense of the cell wall, by shifting the ratio of surface to volume (Supplementary Figure S2). Increasing cell size, however, has a trade-off, as it may reduce the substrate uptake, by the decreased the surface to mass ratio (Supplementary Figure S2). As the growth rate increases, so does the requirement of energy and precursor metabolites generated in the intermediary metabolism, but due to the increasing requirement for ribosomes this has to be provided using a constant or even shrinking pool of protein mass allocated to the enzymes involved in intermediary metabolism (Supplementary Figure S1), and this becomes a challenging optimization problem.

Results

The Model Predicts the Crabtree Effect

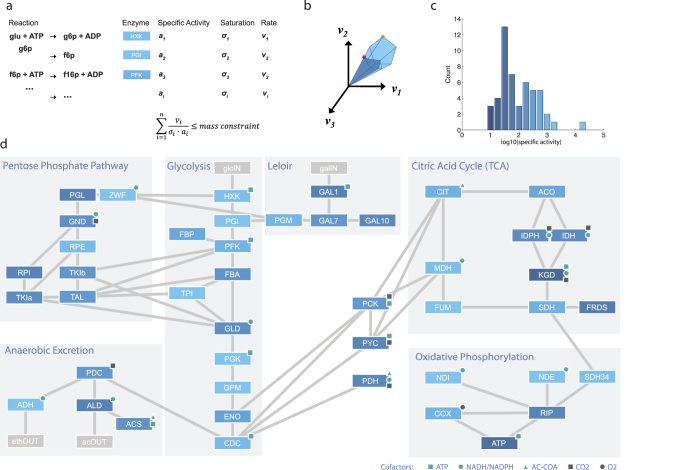
To study the effects of protein efficiency, we implemented a stoichiometric model of the intermediary metabolism (Fig. 1), including a biomass equation. We then collected the in vitro specific activities 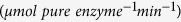Inline graphic, for all of the enzymes in the model (Supplementary Table S1). This allowed us to estimate the mass of each enzyme required to support metabolic flux. We then used proteomics data from literature18 to calculate the fraction of protein mass in intermediary metabolism (200 mg/g protein). Together with a typical protein content of S. cerevisiae of approximately 50%2, the mass of protein covered by the model was estimated to 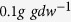Inline graphic, and we constrained the model to this value.

Figure 1. The model of intermediary metabolism.

Figure 1

Open in a new tab

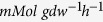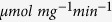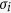(a), Each enzyme, i, may carry a flux, vi, Inline graphic and operates with an activity, Inline graphic, where a is the maximum specific activity of the enzyme Inline graphic and Inline graphic is a saturation factor. The sum of mass is constrained. (b) The constraint shrinks the subspace of feasible fluxes, which may result in a different optimal solution. (c) Histogram of log10 transformed specific activity values from the model 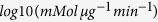Inline graphic. (d) Enzymes are connected if they share a metabolite, and are colored according to their specific activity (c).

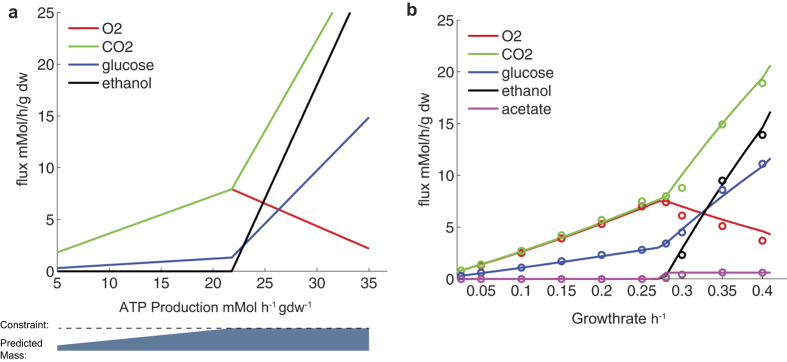
We observed that fermentation requires less protein per produced ATP than oxidative phosphorylation (Supplementary Table S2). Together with the mass constraint, this leads to a critical ATP production rate, after which fermentation gradually replaces respiration (Fig. 2a). Since biomass production depends on ATP, this translates into a critical growth rate at which ethanol production is onset, the key characteristics of the Crabtree effect. This is consistent with the observation that the critical growth rate is lowered when the ATP expenditure is increased19. It is also consistent with the inverse correlation between the critical growth rate and the nitrogen content of the medium20, since nitrogen starvation should reward protein efficiency. An increased protein efficiency should also decrease the amount of ribosomes required for growth. This may explain that the Crabtree effect is promoted by phosphor limitation21, since ribosomal RNA is the main sink for phosphor at high growth rates.

Figure 2. The exchange fluxes of metabolites depend on the ATP production rate (a) and growth rate (b).

Figure 2

Open in a new tab

Simulations were run with the objective to minimize substrate utilization at increasing production rates. At low rates the protein mass is not limiting, as illustrated by the predicted mass bar. At a critical rate the fluxes become large enough for the constraint to come in to effect, and a switch in metabolic strategy occurs. Fermentation gradually replaces the less mass efficient oxidative phosphorylation, with increasing rates, as this is the most substrate efficient strategy consistent with the mass constraint. Experimental data2 Inline graphic is overlaid the model predictions (−).

We used the model to simulate yeast metabolism in a chemostat operated at different dilution rates (equal to the specific growth rate), and found good agreement with experimental values (Fig. 2b). To better fit the experimental data, the ATP expenditure was adjusted to follow the experimentally determined levels (See Supplementary Figure S3 for the steps of the fitting process and the growth rate dependence of the ATP expenditure). The observed variations in ATP expenditure may be explained by shifts in the biomass composition, e.g. in the experimental setting2 the protein level was observed to increase from 40% to 53% below the critical growth rate, and then decrease again to 46%.

Chemostat experiments have shown that yeast produces acetate at high growth rates2. The model correctly predicted the critical growth rate at which this occurs, and that the rate of acetate production stabilizes. The flux was initially over predicted, 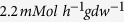Inline graphic compared to 0.6, which is in better agreement with experiments in batch culture, where rates up to 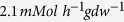Inline graphic are observed22. To avoid an incorrect carbon sink we put an upper bound on the acetate production at the experimentally observed level. We then used the model to investigate the underlying mechanism behind the acetate production, and found that it was related to anabolic reduction power, NADPH. As fermentation replaces respiration, NADPH production by the pentose phosphate pathway (PPP) is replaced by the acetate producing aldehyde dehydrogenase (ALD6), because the cell needs a sink for carbon from glycolysis. This shift is confirmed by C13 labeling experiments23.

F1F0-ATP Synthase Causes the Crabtree Effect

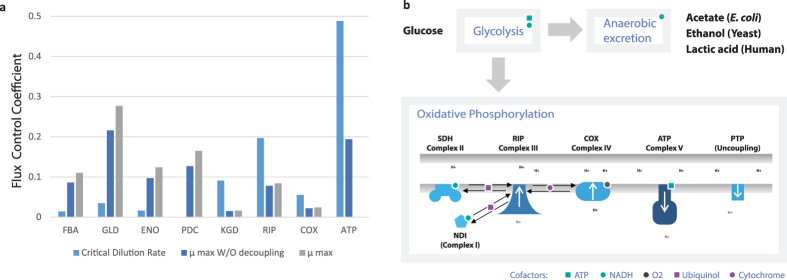
To gain mechanistic insight into the Crabtree effect we investigated how the critical and maximum growth rates depend on the specific activity parameter of each enzyme (Fig. 3a). The enzymes with high flux, but low specific activity, exerted most control. The critical growth rate was mainly controlled by enzymes from oxidative phosphorylation, most noteworthy F1F0-ATP synthase contributed with almost half of the flux control. Several enzymes shared control over the maximum growth rate, with the common denominator that they could not be bypassed using the fermentative growth strategy.

Figure 3.

Figure 3

Open in a new tab

(a) Flux control coefficients (FCC) quantify the relation between enzyme activity and the predicted growth. The critical growth rate is dominated by enzymes from oxidative phosphorylation, and the maximum growth rate by enzymes from glycolysis. Figure shows enzymes for which 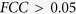Inline graphic, a full list is also available (Supplementary Table S3). (b) A branch point between oxidative phosphorylation and anaerobic excretion is present in several organisms, with organism specific fermentation products. The rate of ATP formation by F1F0-ATP synthase (complex V) is given by the proton motive force. This force can be uncoupled using the permeability transition pore (PTP) which allows Complex I–IV to use oxygen as an electron acceptor unconstrained by the low activity of Complex V.

Because of the high flux control of F1F0-ATP synthase, we expect that the cell regulates the amount of this enzyme tightly. Above the critical rate this is necessary, since it is the predicted decrease in F1F0-ATP synthase that allows more protein mass to be allocated to the glycolytic and fermentative enzymes. Proteomics of the mitochondria show that the relative abundance of proteins within the mitochondria is independent of respiratory or fermentative conditions24, F1F0-ATP should therefore be proportional to the mitochondrial content. Microscopy analysis reveals that mitochondria increases three fold in volume, when respiring on glycerol compared to fermenting on glucose25. Experimental studies of respiratory capacity show that yeast adjusts the amount of mitochondria to match the growth rate dependent ATP synthesis rate26. Mitochondria has also been shown to increases as a response to increased ATP expenditure due to the addition of Benzoic acid, and can cover up to 26% of the cell volume27.

We investigated the robustness of the Crabtree prediction by withholding each enzyme from the mass constraint in turn. F1F0-ATP synthase was the only enzyme that single-handedly changed the result. To verify the parameter value, we used the fact that F1F0-ATP synthase is evolutionary conserved28, and searched the literature for F1F0-ATP synthase activity measurements from other organisms (Supplementary Table S4). The electrochemical gradient, i.e. the proton motive force (PMF), is the most influential factor in determining the activity of the enzyme. At cellular levels of PMF, 180–220 mV29, the specific activity from 10 different experiments was found to be 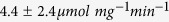Inline graphic, which is comparable to 5.6 used in the model. We also noticed that the turnover number of F1F0-ATP synthase in yeast30, 120 s−1, was almost twice as high as the median turn over number in the model, 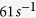Inline graphic, but that its specific activity was one of the lowest, due to its molecular mass being more than 10 times higher than the median, 640 kDa compared 55 kDa (Supplementary Table S1).

The evolutionary preservation of F1F0-ATP synthase likely explains the universality of low yield metabolism. A challenge to this are the Crabtree negative yeasts, e.g. K. marxianus31 that only produces low amounts of ethanol even at as high growth rates as 0.5 h−1. This might be explained by their high protein content31, up to 72%, compared with only about 46% in S. cerevisiae2, since the Crabtree effect is only predicted to occur if protein is limiting. The protein content of the two organisms are similar up to the critical growth rate after which they diverge (Supplementary Figure S1). Although the respiring K. marxianus grows faster than S. cerevisiae, it still grows slower than the fermenting S. kluyveri, 0.63 h−1 31.

Implications For Oxidative Phosphorylation

A major difference between oxidative phosphorylation in S. cerevisiae and most other organisms is that the large hydrogen pumping protein complex, Complex I, 1000 kDa32, is replaced by a single enzyme NDI, 56 kDa33. NDI does not contribute to the proton gradient, and has a 40 times higher specific activity compared to its human counterpart32,34. Complex I’s contribution to a high ATP yield on glucose makes it important for organisms surviving conditions of glucose starvation, e.g. many filamentous fungi and humans. But it likely limits the ATP production rate for fast growing organisms, since it is better to allocate the mass to F1F0-ATP synthase according to our analysis of flux control. A similar phenomenon occurs in E. coli at high growth rates, where the proton pumping Complex I is replaced by a non pumping variant35.

When producing ATP under fermentative conditions, the NADH formed by glycolysis is balanced with the consumption from alcohol dehydrogenase (ADH). However, when the cell is growing, some of the carbon is diverted to biomass and there is a net production of NADH36. This can be resolved by producing glycerol or through oxidative phosphorylation. Since F1F0-ATP synthase limits the flux through oxidative phosphorylation, we investigated the effect of adding an uncoupling reaction to the model, allowing it to bypass F1F0-ATP synthase and release the proton gradient (Fig. 3b). Such uncoupling has been observed in isolated yeast mitochondria37 and takes place in yeast through the permeability transition pore (PTP), which has recently been identified as an uncoupled state of F1F0-ATP synthase38. The addition of the uncoupling reaction increased the predicted maximum growth rate by 4%, the ethanol production rate by 30%, and decreased the biomass yield by 15%. This type of low yield growth is observed in batch cultures, and is likely triggered by the presence of high glucose concentrations. Together with the formation of additional fermentation products and increased ATP expenditure it may explain the 80% higher biomass yield observed in chemostats at the same specific growth rate (Supplementary Table S5). This is consistent with the observation that the proton gradient, 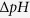Inline graphic, between cytosol and mitochondria is 0.3 in batch cultures and 0.5 when respiring in glucose limited chemostats39.

Prediction of Enzyme Abundances

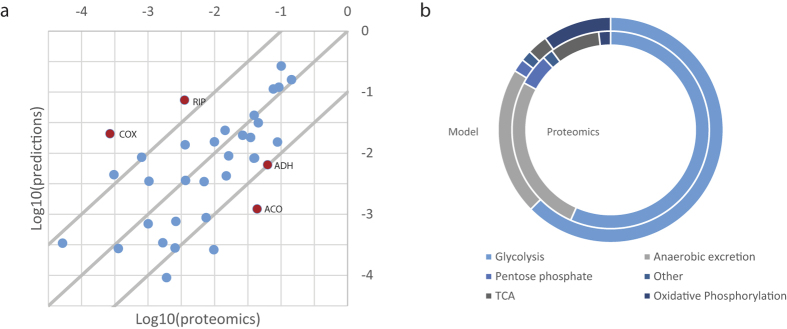
The model assumes that all enzymes operate at 0.5 of their maximum specific activity. This assumption is based on the observation that most glycolytic enzymes are half saturated in E. coli40, and on the trade-off between low metabolite concentrations and high enzyme saturation41. This is expected to be incorrect for almost all enzymes, since each saturation factor will depend on allosteric regulation, phosphorylation state, internal metabolite concentrations and in some cases on strong backwards fluxes due to thermodynamics. We confirmed this suspicion by comparing the predicted protein mass to proteomics data from literature (Fig. 4). For the individual enzymes the predictions were not very accurate (Fig. 4a), although most predictions lie within an order of magnitude of the protein abundance measurements. On the level of pathways these errors however appear to cancel out (Fig. 4b).

Figure 4. Comparison of the protein mass ratios predicted by the model and from proteomics abundances18,59 multiplied with tabulated masses33.

Figure 4

Open in a new tab

(a) A Log10-Log10 plot of the data shows that most predictions lie within an order of magnitude of the proteomics measurements. Miss matches are highlighted in the cases where either the predicted or proteomics values are of significant magnitude, 1% (−2 on the log scale) of the mass or higher. For 10 reactions no flux was predicted and therefore no protein abundance, this corresponded to 6% of the proteomics data. Non log transformed data can be found in Supplementary Table S6. (b) the distribution of mass between pathways.

One of the more striking under predictions occurred for alcohol dehydrogenase (ADH), this is likely due to product inhibition in the batch culture (Fig. 4a). Aconitate hydratase (ACO) was also strongly unpredicted, possibly because the backwards reaction is thermodynamically favored42. Two enzyme complexes from OXPHOS (RIP and COX) were in contrast over predicted by the model. This could be related to detection problems for membrane bound complexes, but could also be an additional indication that the electron transport chain is uncoupled under batch conditions.

The Model Predicts Substrate Dependent Maximum Growth Rates

Distinct metabolic pathways are utilized for growth on different substrates, e.g. glucose, galactose, acetate and ethanol. Using the model we predicted the maximum specific growth rates (Fig. 5) and found them to be in good agreement with experimentally determined rates1. The Crabtree effect is predicted to occur for growth on both glucose and galactose. The lower efficiency and predicted growth rate for galactose is due to the burden of the additional and relatively inefficient enzymes of the Leloir pathway (Fig. 1d). These enzymes are especially burdensome during fermentation where the glycolytic flux is increased. The shift to fermentation is therefore predicted to occur over a shorter range of growth rates. We also noticed that the model predicts the production of acetate when growing on ethanol at high rates, which is normally observed towards the end of experiments in batch culture9.

Figure 5. The simulated protein efficiency for growth of biomass on different carbon sources, and the predicted maximum growth rates.

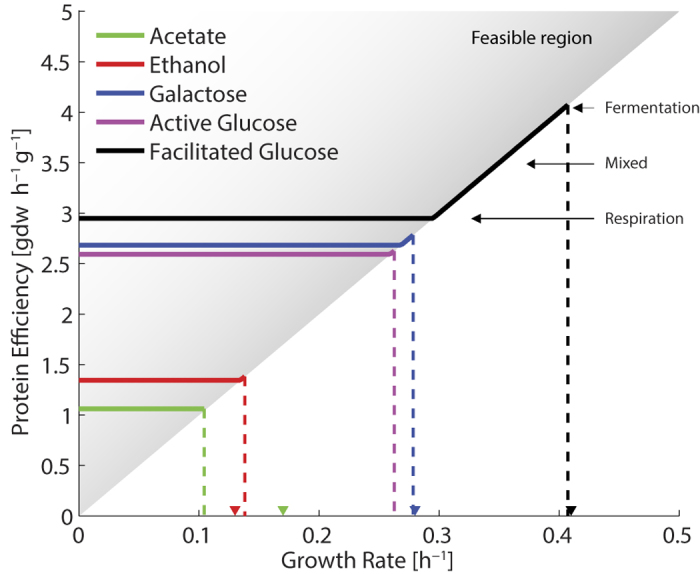
Figure 5

Open in a new tab

Increasing growth rates require more efficient protein, assuming a fixed enzyme pool 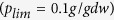Inline graphic, resulting in the feasible region 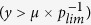Inline graphic. The enzymes involved in the utilization of ethanol and acetate have low calculated efficiency, and therefore the maximum growth rate is predicted to be low. For glucose and galactose the gradual shift towards fermentation at high growth rates increases the protein efficiency and thereby the predicted maximum growth rate. Predicted rates are compared with experimentally observed growth rates1 (▾), acetate 0.11 (0.17), ethanol 0.14 (0.13), galactose 0.28 (0.28) and glucose 0.41 (0.41) h−1.

The model correctly predicts a significantly lower growth on ethanol and acetate compared with glucose. And the lower efficiency for these substrates is caused by a higher degree of respiration and thereby ATP generated through F1F0-ATP synthase, according to our analysis of flux control (Supplementary Table S3). The model however failed to predict their internal order. This might be a consequence of inconsistent substrate concentrations in the experiment1, but may also be related to the model underestimating the mass allocated to ADH (Fig. 4). The total amount of mass that can be allocated to intermediary metabolism might also be underestimated at these low growth rates, since the ribosome content is growth rate dependent (Supplementary Figure S1).

We investigated the effect of active glucose transport by adding a transport reaction for glucose requiring 1 mol ATP per mol glucose. This had only a a minor effect under respiratory conditions, the ATP produced per mass decreased by 6%. But for fermentation it reduced the efficiency by 50%, since the net production of ATP decreased to 1 ATP per glucose, which made it a less viable growth strategy than respiration. This may explain the dominance of glucose transporters using facilitated diffusion in yeast43.

Discussion

Metabolic modeling of metabolic trade-offs has a long history. It was early suggested that a limitation in respiratory capacity could explain the shift ethanol production, when the uptake of glucose increased44. Using the cybernetics approach, the overflow metabolism in E. coli was linked to a limitation in respiration or the production of NADH by the TCA cycle45. These limitations were later given a biophysical motivation, by macromolecular crowding12 or enzyme mass allocation14. The experimentally determined specific activity values, used in this study, point towards a limitation in respiration, as fermentation appears to be a more protein efficient strategy. This result could be expected based on chemostat studies2, where the ratio of ATP production per total cell protein increases by 40% between respiration at growth rate 0.25 h−1, and fermentation at growth rate 0.4 h−1, due to the simultaneous increase in ATP production (Supplementary Figure S3) and decrees in protein content (Supplementary Figure S1). From flux analysis perspective this is however not the expected outcome, since the sum of fluxes (often used as a proxy for enzyme usage46) in contrast is 70% higher for ATP production by fermentation, compared to respiration (Supplementary Table S2). It is only by weighting the sum of fluxes with the specific activities that fermentation becomes more efficient, illustrating the value of using experimentally determined parameters. By making enzyme allocation a part of the flux cone (Fig. 1b), we get a rational for the mixture between respiration and fermentation observed at intermediate growth rates 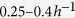Inline graphic (Fig. 2b). These are otherwise considered elemental flux modes, and optimality would suggest using one or the other47.

The perspective of optimal enzyme allocation is challenged by experiments showing that cells keep substantial amounts of enzymes available also in conditions that do not strictly require them48 and that fluxes through glycolytic enzymes appear to be regulated on a post transcriptional level49. This may be understood as an adaptive strategy, where the cell is prepared to quickly respond to changes in environmental conditions48. And after prolonged selection in a glucose limited chemostat, there is indeed a significant decrease in glycolytic activity50. An additional glycolytic capacity is compatible with the present study, since less efficient protein allocations are within the feasible region at sub maximum growth rates (Fig. 5). A study of the growth rate dependence of glycolytic enzymes in the laboratory strain CEN.PK51 show that they in general decrease as the critical growth rate is approached, and then increase again towards the maximum rate. For the industrial strain, investigated in the same study, there was no such trend and the fermentative capacity was consistently higher. The glycolytic capacity might also be influenced by growth rate dependent differences in intracellular metabolite concentrations. Systematically lower concentrations would decrease the saturation of each enzyme, and call for increased enzyme abundances. This illustrates that the saturation factor, σ, assumed to be 0.5 for all enzymes, is a simplification. A more refined model would have a unique, condition dependent, saturation factor for each enzyme, as has recently been suggested47. Experimental fitting of such saturation parameters would however be a challenge and the increase in number of parameters might result in over fitting.

The predicted maximum growth rate and critical growth rate depend linearly on the protein constraint, 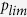Inline graphic and saturation factor σ since FBA is a linear equation system. They are also proportional to the ATP production, since it is the main cause of flux and thereby the predicted enzyme abundances. In the current formulation where σ is assumed to be the same for all enzymes, 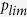Inline graphic and σ can be replaced by a single variable. Although this is a free variable from mathematical perspective, the usage of proteomics data and reasoning about general enzyme saturation levels confines it to a limited range. For σ the upper bound is 1 corresponding to the scenario where all enzymes are at constant maximum saturation. There is no corresponding lower bound, but from an evolutionary point of view it would be wasteful for it to be much lower than 0.5, since kinetic parameters can be adjusted on evolutionary timescales, within their physical limitations, to fit the needs of the organism. As has been shown in a cross-species analysis52. The 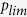Inline graphic depends both on the relative protein abundances between different subsystems, and on the total protein content of the cell. The total content is relatively similar in the cases where 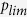Inline graphic is in effect, 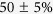Inline graphic. The proteomics data used to estimate the fraction, 20%, that goes in to intermediary metabolism is generated for cells grown on glucose in batch condition, and might not necessarily be valid for other conditions. These conditions are however relatively similar to chemostats at high dilution rates, and the functions of the remaining subsystems should be necessary also under other conditions. Protein synthesis is the most abundant subsystem 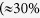Inline graphic of the mass) and its abundance increases with growth rate (Supplementary Figure S1), as it has been shown to do in E. coli53. This means that 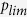Inline graphic might be increasingly underestimated at lower growth rates. This effect should however be limited, since a substantial share of the protein pool is allocated to protein synthesis also at low growth rates (Supplementary Figure S1). Although protein synthesis takes a large share of the protein pool in S. cerevisiae, this share, and there by its relative importance, is much lower than in E. 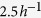coli53, due to the significantly lower maximum specific growth rate Inline graphic compared to Inline graphic.

The experimentally determined specific activity values are an additional source of uncertainty. The error is normally reported to be small within the experiment, but searching the enzyme database BRENDA54, it is not uncommon to find that experimental values differ between labs by a factor of 2 or more. To test the effect of different saturation levels and experimental noise we ran the simulation 5 000 times with randomly perturbed specific activity values. The sensitivity analysis shows that the predictions of the Crabtree effect and maximum growth rate are robust (Supplementary Figure S4). This is a consequence of the specific activity values having a logarithmic distribution (Fig. 1c), where large perturbations are required to disrupt the internal order.

We here present a stoichiometric model of intermediary metabolism, augmented with in vitro enzyme activity data, that quantitatively predicts the Crabtree effect as well as the maximum growth rate on different carbon sources. The taken approach has obvious advantages over standard FBA, that predicts neither, and over kinetic models, due to its comparatively low complexity. Using the model we identified F1F0-ATP synthase as a key flux controlling enzyme for respiratory metabolism in yeast, which provides new insight into the evolutionary advantage of the Crabtree effect. Given the strong predictive power of the model, together with its simplicity we project that this approach has great potential for studying also other parts of metabolism, e.g. amino acid biosynthesis that involves reactions in both cytoplasm and mitochondria. But also for the field of metabolic engineering where it may be used to evaluate the impact of introducing a synthetic pathway that has to compete for the total protein pool.

Methods

Model formulation

A stoichiometric model is, briefly, a sparse matrix where the rows correspond to metabolites and the columns to reactions. In this formulation biomass is defined as the pool of metabolites that are required for growth and these are gathered using an artificial biomass reaction. The model is transformed into a linear optimization problem using the principles of flux balance analysis (FBA)55. FBA investigates flux distributions that fulfill the constraint of homeostasis, i.e. steady state metabolite concentrations. The model assumes that the cell will chose the flux distribution that maximizes growth for a given substrate uptake rate46, or equivalently minimizes substrate uptake for a given growth rate55.

A stoichiometric model of intermediary metabolism, iAN50, was implemented based on the genome scale iFF708 model55 and a model of yeast intermediary metabolism from the RAVEN toolbox56. The model included glycolysis, the pentose phosphate pathway, anaerobic excretion, citric acid cycle (TCA), oxidative phosphorylation, and uptake pathways for galactose, ethanol and acetate. The galactose uptake reactions from the iFF708 model were corrected using the KEGG database57. The drain of metabolites from intermediary metabolism to the biomass equation were estimated using the iFF708 model. A simulation minimizing glucose uptake was run in the iFF708 model. The directionality of all the fluxes was fixed, and the simulation was run again allowing free uptake of all the metabolites found in iAN50 but disallowing glucose uptake. These free uptake fluxes were minimized and taken as the drain of metabolites on iAN50 for the biomass equation. Setting this as the biomass equation ensured that the fluxes were the same for the corresponding reactions in iAN50 and iFF708 model. In addition the equation was made modular so that biomass constituents, e.g. protein, RNA and DNA could be optimized one by one.

In extension to standard FBA, the total enzyme mass was estimated and constrained to the biologically observed level, using an approach equivalent to one taken before12,14. Briefly, for each reaction the mass of the enzymes required was estimated by dividing the predicted flux 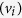Inline graphic with the maximum in vitro activity 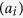Inline graphic and a saturation factor 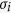Inline graphic. 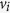In this simulation Inline graphic was fixed to 0.5 for all reactions. To ensure that all Inline graphic were positive, each reversible reaction was split in to two irreversible reactions in each direction. The in vitro activities where collected from literature, and all though most of the studies were found using the enzyme database BRENDA54, the individual publications were investigated and the values taken directly from the source (Supplementary Table S1). The problem formulation is given in Equation 1. Where 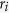Inline graphic are reactions 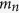Inline graphic are metabolites forming the stoichiometric matrix S. A flux vector v is predicted that fulfills the constraints given by the upper, ub, and lower bounds, lb. An optimization using a vector of objectives, c, that normally contains only zeros, apart from for the biomass or substrate reactions.

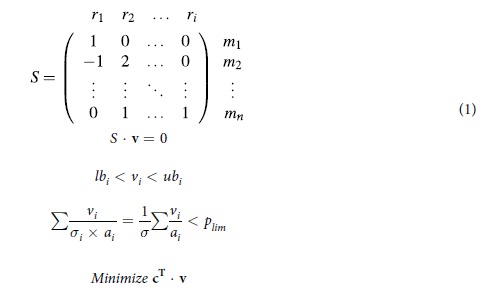graphic file with name srep22264-m28.jpg

For the visualization of the model (Fig. 1), the co factor metabolites ATP, ADP, NAD, NADH, NADP, NADPH, acetyl-CoA, -CoA, were removed from the stoichiometric matrix S and an adjacency matrix was constructed by considering all reactions sharing a metabolite as adjacent. The network was visualized using Cytoscape58 and the specific activities of the enzymes were mapped to intensities using the normalized, log transformed, specific activity.

Analysis of Proteomics

The reference enzyme mass distribution was calculated from proteomics data from literature. The proteomics data18 was measured in the mid exponential phase of cells grown on yeast nitrogen base (YNB) liquid medium. The cells were auxotroph for lysine and arginine and the medium supplemented with lysine and arginine. The relative protein abundances were taken from the protein abundance database PaxDb59, these abundances were multiplied with tabulated enzyme masses from UniProt33. The mass of protein covered by the model, including isozymes, relative to the total protein pool, was calculated as described above. This resulted in an estimated 20% of the protein pool being covered by the model. Together with a typical protein content of S. cerevisiae of approximately 50%2, the mass of protein covered by the model was estimated to 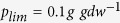Inline graphic. The protein mass covered by protein, amino acid and nucleotide synthesis was calculated using the same method. The respective cellular functions were identified using KEGG57 and Uniprot33.

Simulations

The metabolic requirements for ATP production (Fig. 2a), were predicted by incrementally increasing the ATP production and minimizing glucose uptake for each chosen rate. Similarly, for growth (Fig. 2b), the specific growth rate was incrementally increased. To avoid an over prediction of acetate the upper bound on excretion was set to the biologically observed2 maximum level, 0.6 mMol/gdw/h (Supplementary Figure 3). In addition, the growth related ATP maintenance drain was varied with the growth rate to fit the experimentally2 observed levels (Supplementary Figure S3). 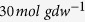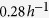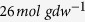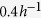The level was increased linearly from 21 to Inline graphic between the growth rates 0.01 and Inline graphic and then linearly decreased to Inline graphic until Inline graphic(Supplementary Figure S3). The experimental levels were calculated from exchange fluxes as a sum of contributions from oxygen uptake and fermentation products, 2.75 mole ATP per mole O2 uptake and 1 mole ATP per mole fermentation product. The fitting of the ATP expenditure was inspired by the shifts in cellular protein content that followed a similar trend.

For the prediction of carbon source dependent maximum growth rates (Fig. 5), chemostat experiments were performed in silico with different carbon sources as described above. The protein efficiency was calculated by dividing the estimated protein with the growth rate, at each point.

For the simulation of growth in batch (Supplementary table S5), the growth rate was maximized, with unlimited glucose uptake rate. Simulations where run with and without the addition of an uncoupling reaction, allowing free movement of protons from the inter membrane space to the matrix. The acetate and glycerol excretion was fixed to the experimentally determined levels and the growth related ATP was set to 35 mMol/gdw/h while the protein content was set to 40% in the biomass equation. The fluxes from the batch experiment were used for the protein abundance prediction (Fig. 4).

Calculation of Flux Control Coefficients

The Flux Control Coefficients 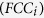Inline graphic, are similar to the ones calculated using Metabolic Control Analysis (MCA). The difference being that the protein abundance determines activity in MCA, and here activity is determined directly by the specific activity parameter. Each specific activity value, 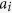Inline graphic, was perturbed by a factor of 1.001 (Eq. 2). The change in predicted growth rate was calculated by comparing the maximum growth rate in the perturbed state 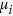Inline graphic to the non perturbed state μ (Eq. 2). The maximum possible value for a 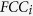Inline graphic is 1, reflecting a situation where a single enzyme exerts all flux control over the growth rate. To calculate the critical growth rate, the production of ethanol and acetate was constrained to 0. Two objectives were investigated, Biomass production and ATP production. In the case of biomass production on glucose the simulation was run with and without uncoupling.

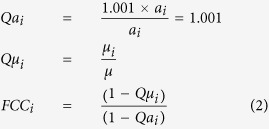graphic file with name srep22264-m41.jpg

Estimation of in vivo specific activity of F1F0-ATP synthase

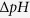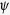For each study (Supplementary Table S4) the PMF was calculated from the reported Inline graphic and Inline graphic values. The experimental values that were close to 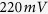Inline graphic where recorded together with the maximum value found in the study. The experimental turnover values, s−1, were converted to specific activity, using the molecular mass of F1F0-ATP synthase in yeast.

Sensitivity analysis and Robustness test

The robustness of the model was investigated by randomly perturbing the specific activity parameters to a degree controlled by a perturbation factor, I. For each simulation each specific activity value, 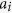Inline graphic, was perturbed by a random value 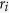Inline graphic as follows 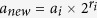Inline graphic, where r was sampled from a uniform distribution on the interval −I to I.

The robustness was further investigated by setting the specific activity to infinity for each enzyme in turn and determining whether ethanol production was still predicted.

Additional Information

How to cite this article: Nilsson, A. and Nielsen, J. Metabolic Trade-offs in Yeast are caused by F1F0-ATP synthase. Sci. Rep. 6, 22264; doi: 10.1038/srep22264 (2016).

Supplementary Material

Supplementary Information
srep22264-s1.pdf (330.9KB, pdf)

Acknowledgments

This work was financed by the Knut and Alice Wallenberg Foundation and the Novo Nordisk Foundation. We thank Dr. Eduard Kerkhoven, Dr. Petri-Jaan Lahtvee, Amir Feizi, Antonio Marras and Benjamín Sánchez for valuable comments.

Footnotes

Author Contributions A.N. constructed the model and performed the simulations. J.N. conceived the project. A.N. and J.N. wrote the manuscript.

References

  1. Van Dijken J. P. et al. An interlaboratory comparison of physiological and genetic properties of four Saccharomyces cerevisiae strains. Enzyme Microb. Technol. 26, 706–714 (2000). [DOI] [PubMed] [Google Scholar]
  2. van Hoek P., van Dijken J. P. & Pronk J. T. Effect of specific growth rate on fermentative capacity of baker’s yeast. Appl. Environ. Microbiol. 64, 4226–4233 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. van Hoek M. J. & Merks R. M. Redox balance is key to explaining full vs. partial switching to low-yield metabolism. BMC Syst. Biol. 6, 22 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Vazquez A. & Oltvai Z. N. Molecular crowding defines a common origin for the warburg effect in proliferating cells and the lactate threshold in muscle physiology. PLoS One 6, e19538 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Famili I., Forster J., Nielsen J. & Palsson B. O. Saccharomyces cerevisiae phenotypes can be predicted by using constraint-based analysis of a genome-scale reconstructed metabolic network. Proc. Natl. Acad. Sci. USA 100, 13134–13139 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Molenaar D., van Berlo R., de Ridder D. & Teusink B. Shifts in growth strategies reflect tradeoffs in cellular economics. 25, 323 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. de Jongh W. A. et al. The roles of galactitol, galactose-1-phosphate, and phosphoglucomutase in galactose-induced toxicity in Saccharomyces cerevisiae. Biotechnol. Bioeng. 101, 317–326 (2008). URL http://dx.doi.org/10.1002/bit.21890. [DOI] [PubMed] [Google Scholar]
  8. Ostergaard S., Olsson L., Johnston M. & Nielsen J. Increasing galactose consumption by Saccharomyces cerevisiae through metabolic engineering of the GAL gene regulatory network. Nat Biotech 18, 1283–1286 (2000). URL http://dx.doi.org/10.1038/82400. [DOI] [PubMed] [Google Scholar]
  9. Larsson C., Lidén G., Blomberg A. & Niklasson C. Monitoring and control of batch and Fedbatch Cultures of Saccharomyces cerevisiae by Calorimetry. Pure Appl. Chem. 65, 1933–1937 (1993). [Google Scholar]
  10. Berkhout J. et al. How biochemical constraints of cellular growth shape evolutionary adaptations in metabolism. Genetics 194, 505–512 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hui S. et al. Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol. Syst. Biol. 11, 784 (2015). URL http://dx.doi.org/10.15252/msb.20145697. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Beg Q. K. et al. Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc. Natl. Acad. Sci. USA 104, 12663–12668 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Zhou Y. et al. Carbon catabolite repression correlates with the maintenance of near invariant molecular crowding in proliferating E. coli cells. BMC Syst. Biol. 7, 138 (2013). URL http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3924228/. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Adadi R., Volkmer B., Milo R., Heinemann M. & Shlomi T. Prediction of Microbial Growth Rate versus Biomass Yield by a Metabolic Network with Kinetic Parameters. PLoS Comput. Biol. 8, e1002575 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Shlomi T., Benyamini T., Gottlieb E., Sharan R. & Ruppin E. Genome-scale metabolic modeling elucidates the role of proliferative adaptation in causing the warburg effect. PLoS Comput. Biol. 7, e1002018 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Nissen T. L., Schulze U., Nielsen J. & Villadsen J. Flux distributions in anaerobic, glucose-limited continuous cultures of Saccharomyces cerevisiae. Microbiology 143 Pt 1, 203–218 (1997). [DOI] [PubMed] [Google Scholar]
  17. Aguilar-Uscanga B. & François J. M. A study of the yeast cell wall composition and structure in response to growth conditions and mode of cultivation. Lett. Appl. Microbiol. 37, 268–274 (2003). URL http://dx.doi.org/10.1046/j.1472-765X.2003.01394.x. [DOI] [PubMed] [Google Scholar]
  18. de Godoy L. M. F. et al. Comprehensive mass-spectrometry-based proteome quantification of haploid versus diploid yeast. Nature 455, 1251–1254 (2008). URL http://dx.doi.org/10.1038/nature07341. [DOI] [PubMed] [Google Scholar]
  19. Postma E., Verduyn C., Scheffers W. A. & Van Dijken J. P. Enzymic analysis of the crabtree effect in glucose-limited chemostat cultures of Saccharomyces cerevisiae. Appl. Environ. Microbiol. 55, 468–477 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Larsson C., Von Stockar U., Marison I. & Gustafsson L. Growth and metabolism of Saccharomyces cerevisiae in chemostat cultures under carbon-, nitrogen-, or carbon- and nitrogen-limiting conditions. J. Bacteriol. 175, 4809–4816 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Boer V. M., Crutchfield C. A., Bradley P. H., Botstein D. & Rabinowitz J. D. Growth-limiting intracellular metabolites in yeast growing under diverse nutrient limitations. Mol. Biol. Cell 21, 198–211 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Heyland J., Fu J. & Blank L. M. Correlation between TCA cycle flux and glucose uptake rate during respiro-fermentative growth of Saccharomyces cerevisiae. Microbiology 155, 3827–3837 (2009). [DOI] [PubMed] [Google Scholar]
  23. Frick O. & Wittmann C. Characterization of the metabolic shift between oxidative and fermentative growth in Saccharomyces cerevisiae by comparative 13C flux analysis. Microb. Cell Fact. 4, 30 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Ohlmeier S., Kastaniotis A. J., Hiltunen J. K. & Bergmann U. The Yeast Mitochondrial Proteome, a Study of Fermentative and Respiratory Growth. J. Biol. Chem. 279, 3956–3979 (2004). [DOI] [PubMed] [Google Scholar]
  25. Egner A., Jakobs S. & Hell S. W. Fast 100-nm resolution three-dimensional microscope reveals structural plasticity of mitochondria in live yeast. Proc. Natl. Acad. Sci. USA 99, 3370–3375 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Dejean L., Beauvoit B., Guérin B. & Rigoulet M. Growth of the yeast Saccharomyces cerevisiae on a non-fermentable substrate: Control of energetic yield by the amount of mitochondria. Biochim. Biophys. Acta – Bioenerg. 1457, 45–56 (2000). [DOI] [PubMed] [Google Scholar]
  27. Verduyn C., Postma E., Scheffers W. a. & Van Dijken J. P. Effect of benzoic acid on metabolic fluxes in yeasts: A continuous-culture study on the regulation of respiration and alcoholic fermentation. Yeast 8, 501–517 (1992). [DOI] [PubMed] [Google Scholar]
  28. Yoshida M., Muneyuki E. & Hisabori T. ATP synthase-a marvellous rotary engine of the cell. Nat. Rev. Mol. Cell Biol. 2, 669–677 (2001). [DOI] [PubMed] [Google Scholar]
  29. Perry S. W., Norman J. P., Barbieri J., Brown E. B. & Gelbard H. A. Mitochondrial membrane potential probes and the proton gradient: A practical usage guide. Biotechniques 50, 98–115 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Förster K. et al. Proton transport coupled ATP synthesis by the purified yeast H+-ATP synthase in proteoliposomes. Biochim. Biophys. Acta-Bioenerg. 1797, 1828–1837 (2010). [DOI] [PubMed] [Google Scholar]
  31. Fonseca G. G., Gombert A. K., Heinzle E. & Wittmann C. Physiology of the yeast Kluyveromyces marxianus during batch and chemostat cultures with glucose as the sole carbon source. FEMS Yeast Res. 7, 422–435 (2007). [DOI] [PubMed] [Google Scholar]
  32. Andreani A. et al. Effects of new ubiquinone-imidazo[2,1-b]thiazoles on mitochondrial complex I (NADH-ubiquinone reductase) and on mitochondrial permeability transition pore. Bioorg. Med. Chem. 12, 5525–5532 (2004). [DOI] [PubMed] [Google Scholar]
  33. UNIPROT. Activities at the Universal Protein Resource (UniProt). Nucleic Acids Res. 42, D191–8 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. de Vries S. & Grivell L. A. Purification and characterization of a rotenone-insensitive NADH: Q6 oxidoreductase from mitochondria of Saccharomyces cerevisiae. Eur. J. Biochem. 176, 377–384 (1988). URL http://dx.doi.org/10.1111/j.1432-1033.1988.tb14292.x. [DOI] [PubMed] [Google Scholar]
  35. Peebo K. et al. Proteome reallocation in Escherichia coli with increasing specific growth rate. Mol. Biosyst. 11, 1184–93 (2015). URL http://dx.doi.org/10.1039/C4MB00721B. [DOI] [PubMed] [Google Scholar]
  36. van Dijken J. P. & Scheffers W. A. Redox balances in the metabolism of sugars by yeasts. FEMS Microbiol. Lett. 32, 199–224 (1986). [Google Scholar]
  37. Mourier A., Devin A. & Rigoulet M. Active proton leak in mitochondria: A new way to regulate substrate oxidation. Biochim. Biophys. Acta - Bioenerg. 1797, 255–261 (2010). [DOI] [PubMed] [Google Scholar]
  38. Bernardi P. The mitochondrial permeability transition pore: A mystery solved? Front. Physiol. 4, 95 (2013). URL http://dx.doi.org/10.3389/fphys.2013.00095. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Orij R., Postmus J., Ter Beek A., Brul S. & Smits G. J. In vivo measurement of cytosolic and mitochondrial pH using a pH-sensitive GFP derivative in Saccharomyces cerevisiae reveals a relation between intracellular pH and growth. Microbiology 155, 268–278 (2009). [DOI] [PubMed] [Google Scholar]
  40. Bennett B. D. et al. Absolute metabolite concentrations and implied enzyme active site occupancy in Escherichia coli. Nat. Chem. Biol. 5, 593–599 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Tepper N. et al. Steady-State Metabolite Concentrations Reflect a Balance between Maximizing Enzyme Efficiency and Minimizing Total Metabolite Load. PLoS One 8, e75370 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Blair J. M. Magnesium and the Aconitase Equilibrium: Determination of Apparent Stability Constants of Magnesium Substrate Complexes from Equilibrium Data. Eur. J. Biochem. 8, 287–291 (1969). URL http://dx.doi.org/10.1111/j.1432-1033.1969.tb00526.x. [DOI] [PubMed] [Google Scholar]
  43. Maier A., Völker B., Boles E. & Fuhrmann G. F. Characterisation of glucose transport in Saccharomyces cerevisiae with plasma membrane vesicles (countertransport) and intact cells (initial uptake) with single Hxt1, Hxt2, Hxt3, Hxt4, Hxt6, Hxt7 or Gal2 transporters. FEMS Yeast Res. 2, 539–550 (2002). [DOI] [PubMed] [Google Scholar]
  44. Sonnleitner B. & Käppeli O. Growth of Saccharomyces cerevisiae is controlled by its limited respiratory capacity: Formulation and verification of a hypothesis. Biotechnol. Bioeng. 28, 927–937 (1986). [DOI] [PubMed] [Google Scholar]
  45. Majewski R. A. & Domach M. M. Simple constrained-optimization view of acetate overflow in E. coli. Biotechnol. Bioeng. 35, 732–738 (1990). [DOI] [PubMed] [Google Scholar]
  46. Lewis N. E. et al. Omic data from evolved E. coli are consistent with computed optimal growth from genome-scale models. Mol. Syst. Biol. 6, 390 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Müller S., Regensburger G. & Steuer R. Resource allocation in metabolic networks: kinetic optimization and approximations by FBA. Biochem. Soc. Trans. 43, 1195–1200 (2015). [DOI] [PubMed] [Google Scholar]
  48. Costenoble R. et al. Comprehensive quantitative analysis of central carbon and amino-acid metabolism in Saccharomyces cerevisiae under multiple conditions by targeted proteomics. Mol. Syst. Biol. 7, 464 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Daran-Lapujade P. et al. The fluxes through glycolytic enzymes in Saccharomyces cerevisiae are predominantly regulated at posttranscriptional levels. Proc. Natl. Acad. Sci. USA 104, 15753–15758 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Jansen M. L. A. et al. Prolonged selection in aerobic, glucose-limited chemostat cultures of Saccharomyces cerevisiae causes a partial loss of glycolytic capacity. Microbiology 151, 1657–1669 (2005). [DOI] [PubMed] [Google Scholar]
  51. Van Hoek P., Van Dijken J. P. & Pronk J. T. Regulation of fermentative capacity and levels of glycolytic enzymes in chemostat cultures of Saccharomyces cerevisiae. Enzyme Microb. Technol. 26, 724–736 (2000). [DOI] [PubMed] [Google Scholar]
  52. Savir Y., Noor E., Milo R. & Tlusty T. Cross-species analysis traces adaptation of Rubisco toward optimality in a low-dimensional landscape. Proc. Natl. Acad. Sci. USA 107, 3475–3480 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Scott M., Mateescu E. M., Zhang Z. & Hwa T. Interdependence of Cell Growth Origins and Consequences. Science (80-). 330, 1099–1102 (2010). [DOI] [PubMed] [Google Scholar]
  54. Schomburg I. et al. BRENDA in 2013: integrated reactions, kinetic data, enzyme function data, improved disease classification: new options and contents in BRENDA. Nucleic Acids Res. 41, D764–72 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Förster J., Famili I., Fu P., Palsson B. Ø. & Nielsen J. Genome-scale reconstruction of the Saccharomyces cerevisiae metabolic network. Genome Res. 13, 244–253 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Agren R. et al. The RAVEN Toolbox and Its Use for Generating a Genome-scale Metabolic Model for Penicillium chrysogenum. PLoS Comput. Biol. 9, e1002980 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Ogata H. et al. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 27, 29–34 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Cline M. S. et al. Integration of biological networks and gene expression data using Cytoscape. Nat. Protoc. 2, 2366–2382 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Wang M. et al. PaxDb, a Database of Protein Abundance Averages Across All Three Domains of Life. Mol. Cell. Proteomics 11, 492–500 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep22264-s1.pdf (330.9KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES