Mechanical Forces and Growth in Animal Tissues

Abstract

Mechanical forces shape biological tissues. They are the effectors of the developmental programs that orchestrate morphogenesis. A lot of effort has been devoted to understanding morphogenetic processes in mechanical terms. In this review, we focus on the interplay between tissue mechanics and growth. We first describe how tissue mechanics affects growth, by influencing the orientation of cell divisions and the signaling pathways that control the rate of volume increase and proliferation. We then address how the mechanical state of a tissue is affected by the patterns of growth. The forward and reverse interactions between growth and mechanics must be investigated in an integrative way if we want to understand how tissues grow and shape themselves. To illustrate this point, we describe examples in which growth homeostasis is achieved by feedback mechanisms that use mechanical forces.

Mechanical forces affect the way cells of a tissue grow in volume and in number. Likewise, the growth of a tissue can affect its mechanical state by inducing stresses that have important consequences for morphogenesis.

An essential feature of developing tissues is their ability to pattern a field of cells into distinct regions with different properties—be it the expression of genes that commit cells to a specific fate, the regulation of the cytoskeleton, or the level of proliferation, to name a few examples. Tissue patterning is controlled by biochemical pathways that specify cell identity based on signals produced and exchanged by cells in the tissue. Such signals may be working at short or long range. A classic example of long-range signaling is achieved by so-called morphogens that form a concentration gradient of activity. Morphogens are widespread in animals and control cell fate and tissue growth (reviewed in Wartlick et al. 2011).

How cells read these instructions is still debated. Cells may measure the local concentration, spatial, or even temporal variations (reviewed in Day and Lawrence 2000; Wartlick and González-Gaitán 2011; Restrepo et al. 2014). A morphogen can be a transcription factor in a fertilized egg, such as Drosophila bicoid (reviewed in Porcher and Dostatni 2010), but more often it is a secreted factor, such as TGF-β, Wingless, or Sonic hedgehog (reviewed in McDowell and Gurdon 1999; Baena-Lopez et al. 2012; Kicheva et al. 2012). Importantly, morphogens not only pattern tissues, but also promote their growth (Wartlick and González-Gaitán 2011; Baena-Lopez et al. 2012). For many years, the prevailing view regarding the control of size and shape of tissues was a strict biochemical control by morphogens. Genetic networks define the localized expression of morphogens, which spread from their source to instruct cell growth and proliferation. Most of our efforts to understand morphogenesis have thus concentrated on the signaling pathways responsible for pattern formation, and the “form-generating function” of morphogens is, thus, purely biochemical. In this context, it is unclear how the shape and size of a tissue arises in mechanical terms. It is important also to consider that cells must cope with the mechanical constraints that are inherent to all tissues. These mechanical constraints restrict what the cells can do in response to morphogens. Mechanical forces make cells move or change shape. They are the final effectors of morphogenesis.

Our understanding of how forces interact with patterning signals has considerably improved over the last few years. Which cellular processes fuel the emergence of forces and how the forces that are generated then shape tissues at the multicellular level has recently been intensely investigated. These investigations, fostered by improvement in live-imaging technology (Mavrakis et al. 2010; Supatto et al. 2011; Keller 2013), showed how the synergy between cytoskeletal elements and adhesion complexes give rise to morphogenetic processes, such as Drosophila gastrulation and metamorphosis (Bertet et al. 2004; Zallen and Wieschaus 2004; Aigouy et al. 2010; Bosveld et al. 2012), zebrafish gastrulation (Behrndt et al. 2012; Maître et al. 2012), or chick neural-tube closure (Nishimura et al. 2012).

In this review, we address how tissue mechanics may impact morphogenesis in the context of growing tissues and, conversely, how patterns of growth can affect tissue mechanics. As we discuss below, the developmental mechanics of growing tissues is less well understood than nongrowing ones. The first reason for this is technical. It is difficult to observe growing tissues. The second reason is more conceptual. There is something specific about the mechanics of growing bodies—new material is added from within—that makes it difficult to apprehend. The theory of elasticity of growing media is very recent (Rodriguez et al. 1994) compared with that of nongrowing ones, which dates back to the 19th century (reviewed by Todhunter 2014). First, we address how mechanical forces can affect the way a tissue grows, altering both volume increase and proliferation. Second, we address the reverse interactions and discuss how the patterns of growth and proliferation of tissues are an integral part of their mechanics, and thereby contribute to their morphogenesis. In our concluding remarks, we stress how one should integrate both these forward and reverse interactions to understand how tissues shape themselves.

THE IMPACT OF TISSUE MECHANICS ON GROWTH

Within a tissue, each cell is embedded in a mechanical environment, and is constantly experiencing forces from its neighbors and the extracellular matrix (ECM). Each cell also participates in the local force balance, either passively, by imposing a viscoelastic resistance to external force, or actively, via the constitutive tension of its cytoskeleton, associated with the contractile activity of the motor protein myosin II. In this section, we discuss how these different aspects of tissue mechanics impact on growth. By growth, we refer here to the collective effects of volume increase and proliferation. Growth is generally associated with cell divisions; it is, thus, an oriented process and we will treat both the cellular processes that orient cell divisions and the pathways that underlie mass increase.

Growth Orientation

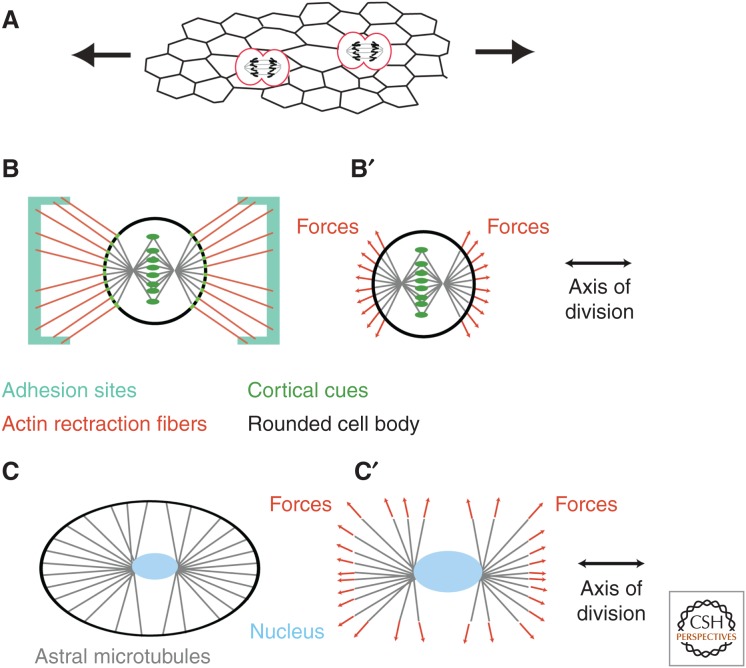
When the distribution of forces exerted on a cell is anisotropic, the cell deviates from its isotropic rest shape. This mechanical asymmetry can polarize the orientation of cell and tissue growth via the orientation of cell divisions. Indeed, as mechanical stress stretches cells, it can polarize the axis along which they divide (Fig. 1A). There is an important body of literature, dating back to the work of Hertwig in the 19th century, that relates the orientation of divisions to the main geometrical axis of cells (for a historical perspective, see Minc and Piel 2012).

Figure 1.

Orienting cell divisions. (A) The existence of external forces in a tissue induces internal stresses that deform cells. This deformation may then orient cells divisions. (B) In cells adhering to a substrate, experiments on isolated cells cultured on patterned substrates have shown that the rounded cell body may keep the memory of its adherent geometry through actin-rich retraction fibers, which pull on the cell cortex. (B′) Somehow, the pulling forces are transmitted to the astral microtubules, which results in orienting the mitotic spindle. (C) Observations of unperturbed embryos, as well as recent experiments in confined geometries, have highlighted how cells sense their shape to orient the mitotic spindle. (C′) The shape of cells can be sensed by astral microtubules, which extend to the cell cortex and generate a global torque and force to orient the centrosomes and nucleus, or spindle, depending on whether the alignment occurs before or after nuclear envelope breakdown.

Micropatterning approaches allow cells to be cultured with a controlled geometry. Investigations on cells cultured on patterns of ECM showed that force distribution more than cell geometry is an essential component of spindle alignment with the main axis of cells. Cells round up during division, leading to an apparent loss of the geometrical information born in the initially polarized shape. However, in cells cultured on geometric patterns of adhesion, actomyosin-rich retraction fibers connect the rounded cortex to adhesion sites (Fig. 1B). The net force of these fibers on the rounded cortex orients the spindle (Théry et al. 2007) in a way that is sensitive to the geometry of adhesion more than the actual shape of the cell (Théry et al. 2005) and to external forces via a putative mechanosensitive reinforcement (Fig. 1B′) (Fink et al. 2011). The link between retraction fibers and the spindle seem to be provided by subcortical actin structures that exert a pulling force on astral microtubules (Fink et al. 2011).

In vivo observations have linked mechanical stress to altered cell shape and spindle alignment in Drosophila wings (Aigouy et al. 2010; LeGoff et al. 2013) and in zebrafish epiboly (Campinho et al. 2013), supporting the findings that cell shape and topology play an important role for spindle orientation (Gibson et al. 2011). Minc et al. (2011) altered the geometry of early sea urchin embryos and observed that cell shape dictates the spindle orientation. It seems to be the geometry of the cell, not the direct mechanical stress via intercellular adhesion or coupling to the ECM that orients the spindle (Fig. 1C). A role for astral microtubule sensing the geometry of the cell has been proposed. These microtubules attach to the cell cortex at the periphery and exert a pulling force on the centrosome, thus orienting the nucleus of the cell about to divide. One way the cell can sense its geometry is if the pulling force of a microtubule increases with increasing length.

Whether cells orient their spindle by sensing their shape or of cell/ECM tensions is still an open question. In vivo approaches suffer from the difficulty to measure strains and stresses in a living organism (see below), whereas single-cell culture approaches have yet to show that retraction fibers are a universal feature of tissues in vivo.

Rate of Growth

Mechanical forces can also affect the rate at which cells grow. More than 30 years ago, Folkman and Moscona (1978) found a correlation between the size and shape of cells and proliferation. Attaching cells to substrates of varying adhesiveness, they could control the shape of cells. They found that the larger the cells, the larger their rate of division. This result has been confirmed by more specific tuning of cell size and shape using microprinting techniques (Singhvi et al. 1994; Chen et al. 1997). In these studies, which pioneered microprinting technology in cell biology, cell shape/size was tuned separately from interactions with the ECM. For example, a cell could be forced to adopt a small adherent size, while still maintaining a high adhesiveness and cell–ECM interactions. They showed that it is the size of cells, not necessarily interactions with ECM, that promotes cell growth.

Forcing individual cultured cells to specific shapes may seem unphysiological. But the impact of mechanics on growth was also shown in more natural environments. In tissues, cells are mechanically connected to the ECM via integrin-mediated adhesion. A striking demonstration of mechanical control over proliferation came from 3D cultures of mammary epithelial cells (MEC) in which cells organize into 3D epithelial tubes or spheres known as acini. These acini grow to a larger extent when grown on a stiff ECM (Paszek et al. 2005). Cells not only “sense” forces from the ECM, they also “sense” forces coming from their neighbors via cadherin-mediated adhesion sites. When epithelial cells are grown in vitro at sufficiently high density, they create a confluent monolayer of cells that are mechanically interconnected at adherens junctions. In these connected cells, the actomyosin cortex underlying adherens junctions is constitutively contractile, which leads to the emergence of mechanical stress in the tissue. Nelson et al. grew such epithelial monolayers in different geometrical patterns. Cells at different positions of the pattern—for example, a corner of a square versus its center—experience a different distribution of forces from their neighbors, leading to a spatial pattern of mechanical stress (Nelson et al. 2005). They found a systematic correlation between proliferation and mechanical stress—stretched regions proliferated more than unstretched ones.

Mechanical Pathways

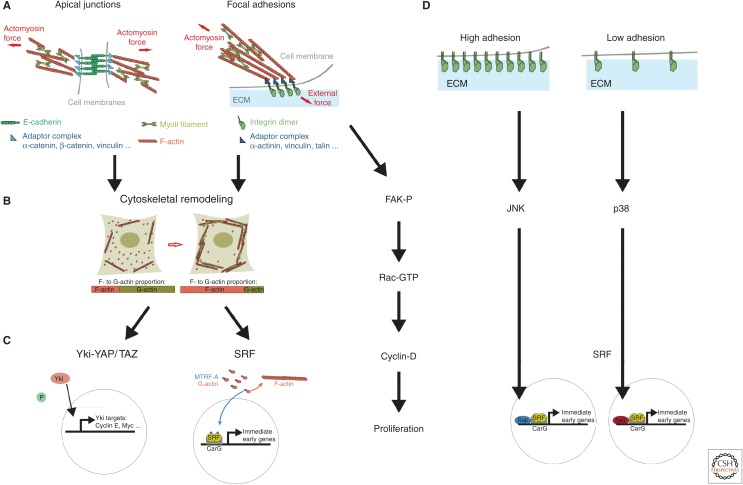
It, therefore, seems that cells are mechanosensitive; they can probe their mechanical environment. What are the molecular pathways underlying mechanosensation and its effect on cell growth and proliferation? Several biochemical pathways mediate the link between forces and growth, and they share the following property. The first relay of a mechanical signal is cytoskeletal reorganization (Fig. 2A,B). Cells can sense forces exerted by the ECM through the mechanosensitive activation of focal adhesion sites (for a review, see Roca-Cusachs et al. 2012), which leads to an increase of the local actomyosin contractility. This provides a way to sense the stiffness of the ECM. A basal contractile activity of the actomyosin connected to focal adhesions leads to a constant mechanical tug of war with the ECM, providing cells with a way to “feel” the compliance of their environment. Whether probing a force exerted by neighbors and transmitted by the ECM, or just ECM stiffness itself, cytoskeletal remodeling is a central relay of mechanical signaling. At the molecular level, force sensing at focal adhesions has been shown to rely on vinculin/talin interactions (del Rio et al. 2009) and p130Cas (Sawada et al. 2006). Sensing of forces is also at play at adherens junctions. E-cadherin-based adhesion connects the tensile cortices of adjacent cells (Maître et al. 2012). This is performed through direct interactions between the actomyosin cortex and E-cadherin complexes (Cavey et al. 2008; le Duc et al. 2010; Smutny et al. 2010; Borghi et al. 2012). One can expect that forces control the cytoskeleton at adherens junctions. The reason for this is that mechanical forces play an active role in maturation of cadherin complexes (le Duc et al. 2010; Liu et al. 2010; Buckley et al. 2014), which are organizers of actomyosin assembly (Verma et al. 2012), and control Rho signaling, a regulator of the cytoskeleton (Wildenberg et al. 2006; Yamada and Nelson 2007; Ratheesh et al. 2012). Putative molecular transducer of forces are α-catenin (Yonemura et al. 2010) and vinculin (le Duc et al. 2010; Yonemura et al. 2010). Evidence for a molecular sensor of forces at adherens junction was recently found in the Drosophila wing primordium (Rauskolb et al. 2014). The Ajuba LIM protein Jub seems to relay mechanical information from α-catenin to downstream signaling (see below).

Figure 2.

Mechanical signaling and tissue growth. (A) Force generation and force transmission occur at apical adherens junctions (left) and basal focal adhesion sites (right). At apical junctions, the contractile actomyosin cortices of two neighboring cells are mechanically coupled via the E-cadherin adhesion complex. The adaptor complex, which links E-cadherin to the cortex, includes proteins, such as vinculin, which is mechanosensitive. At basal sites of adhesion, force balance between the contractile actomyosin and the ECM is sensed at sites of focal adhesion, which involves integrin dimers and associated proteins coupling to actin filaments. (B) Force sensation is then converted into a structural reorganization of the actin cytoskeleton, increased external force promoting polymerized actin. (C) The polymerized state of the actin cytoskeleton is then sensed by the transcription activators YAP/TAZ-Yki, a downstream component from the Hippo pathway– or myocardin-related transcription factor (MRTF)-A, a component of the serum response factor (SRF) pathway, which both shuttle to the nucleus to promote growth. (D) Mechanical signaling can also affect growth in the absence of cytoskeletal reorganization. Force sensation at focal adhesions leads to the phosphorylation of the focal adhesion kinase (FAK), which induces expression of cyclin D. The SRF pathway has also been proposed to sense the level of adhesion with the ECM in an actin-independent way, via Jun amino-terminal kinase (JNK) and p38. Also involved in this regulation and shown on the figure are the SRF cofactors (Sap and Net) at the SRF-binding consensus element (CArG).

Downstream from mechanical signaling are transcription factors that drive expression of genes controlling cell growth and proliferation (Fig. 2C). One of the strongest candidates for a link between mechanics and the regulation of growth is the mammalian transcriptional coactivator YAP/TAZ—ortholog of the gene Yorkie (Yki) in Drosophila. The canonical pathway upstream of YAP/TAZ-Yki is the Hippo tumor-suppressor pathway, which promotes phosphorylation of YAP/TAZ-Yki leading to its retention in the cell cytosol and degradation. In Drosophila, loss of Hippo signaling translocates Yki to the nucleus, where its transcriptional activity induces the expression of genes controlling growth and proliferation, such as the cell-cycle regulator cyclin E (Tapon et al. 2002), the cell-death inhibitor Diap1 (Wu et al. 2003), the cell-growth promoter dMyc (Neto-Silva et al. 2010; Ziosi et al. 2010), and the bantam microRNA (Nolo et al. 2006; Thompson and Cohen 2006).

Evidence for a role of Yap/TAZ in mechanotransduction came from MEC and mouse embryonic fibroblasts grown on stiff ECM, or forced to adopt a stretched geometry. Both treatments induced translocation of YAP/TAZ to the nucleus (Dupont et al. 2011; Wada et al. 2011). Interestingly, this effect can, in some instances, be independent of Hippo signaling but requires cytoskeletal stiffening via RhoA activity (Dupont et al. 2011). Complementary investigation in Drosophila showed how increasing the level of polymerized actin—a treatment reminiscent of the cytoskeletal reorganization in stretched cells—induces Yki activation and an overgrowth phenotype (Fernández et al. 2011; Sansores-Garcia et al. 2011). A recent report showed that modulation of cytoskeletal tension by alterations of myosin II activity also resulted in wing growth phenotype (Rauskolb et al. 2014). Increased tension also resulted in Yki activation to promote growth. These findings altogether suggested a link between YAP/TAZ-Yki mechanics and proliferation. The pieces of the puzzle were reassembled in the context of contact inhibition of proliferation (CIP) of human MEC. Aragona et al. (2013) showed how CIP, which corresponds to a slowing down of proliferation as cell density increases in a culture, is dependent on both a reduced stretching of cells by their environment, and an increased severing of F-actin. Using tissue-engineering approaches and drug treatments, they delineated the hierarchy of the YAP/TAZ mechanical pathway. Cell stretching first controls tension of the cytoskeleton by a reduction of F-actin capping/severing activity. This then promotes translocation of YAP/TAZ to the nucleus and transcriptional activity to induce growth. In the context of CIP, this explains how increased cell density leads to growth arrest (Aragona et al. 2013). Interestingly, Aragona and colleagues observed this hierarchy between mechanics, the cytoskeleton and YAP/TAZ both when the stress came from cell–ECM interactions (playing with ECM stiffness and stretch) and when it was intercellular forces at apical junctions that activated YAP/TAZ. How is information relayed from cytoskeletal tension to Yki activity? In Drosophila wings, Rauskolb et al. (2014) have recently shown that the Ajuba LIM protein Jub negatively regulates Warts—a protein kinase and core component of the Hippo pathway—in a tension-dependent manner. This results in increased Yki activity and promotes growth when cells are stretched. Yin et al. (2013) also showed how actin remodeling modulates the Hippo core components via the upstream regulator Merlin-NF2. These two studies contrast with the work on MEC cells, in which YAP/TAZ activation by tension is independent of LATS, the ortholog of Warts (Dupont et al. 2011). Mouse fibroblast and epithelial cells do transduce mechanical signals through LATS (Wada et al. 2011). Further studies will thus need to address the exact mechanism by which forces control Yki-YAP/TAZ activity in different systems. Note that a role for cadherin-based adhesion directly regulating the Hippo pathway, not via mechanics and the cytoskeleton, to control YAP/TAZ-mediated proliferation has also been reported (Kim et al. 2011).

Another mechanical pathway that may control growth is that which controls activity of serum response factor (SRF). SRF is a transcription factor implicated in the regulation of many immediate early genes, providing control over the cytoskeleton, adhesion, and proliferation. SRF activity is regulated by two signaling pathways: one involves actin dynamics and is Rho-dependent, and the other is Ras dependent (for a review, see Posern and Treisman 2006). In the Rho-dependent branch, the myocardin-related transcription factor (MRTF)-A (also known as MAL or MLK1), binds to G-actin. Formation of F-actin, at the expense of the G-actin pool, frees MRTF-A, which then translocates to the nucleus and activates SRF transcriptional activity (Miralles et al. 2003). This provides a means for mechanical stimulations to induce transcriptional activity via the cytoskeleton (Fig. 2B,C). In human lung fibroblasts, increased matrix stiffness leads to actin polymerization, and subsequent translocation of MRTF/MAL/MLK1 to the nucleus to promote SRF activation (Huang et al. 2012). Human epidermal stem cells grown on micropatterned islands differentiate at a higher frequency when forced to adopt a rounded, constrained geometry. This differentiation is the result of changes in the actin cytoskeleton, which promote SRF activation via MRTF/MAL/MLK1 (Connelly et al. 2010). During Drosophila oogenesis, the invasive movement of border cells requires MAL-D to promote strengthening of the cytoskeleton (Somogyi and Rørth 2004). There, MAL-D seems to be activated by cell stretching on initiation of movement. Although not addressed in these investigations, SRF might mediate a mechanical effect on growth and proliferation because this pathway is known to modulate proliferation (Miano 2003).

Not all putative mechanosensitive pathways rely on actin dynamics (Fig. 2D). Wozniak et al. identified the Ras-dependent branch of SRF, which does not rely on actin dynamics, as another mechanosensitive pathway (Wozniak et al. 2012). On conditions of high adhesion with the ECM, JNK promotes transcription of SRF target genes, leading to enhanced proliferation. On low adhesion, p38 activity leads to the inhibition of SRF target genes, and subsequent reduction of proliferation. Focal adhesion kinase (FAK) transmits readout of matrix stiffness at the level of integrin-mediated focal adhesion. Although force sensing involves actomyosin as described above, FAK signaling is directly converted into changes in the level of cyclin D1 in MEC and vascular smooth muscle cells, without passing through the cytoskeletal remodeling relay (Klein et al. 2009).

Target of Mechanical Signal: Growth or Cell Cycle?

The cell-cycle machinery is not a clock that cycles with a fixed period. The final readout that dictates the phase of the cycle is Cdk activity (Coudreuse and Nurse 2010), which is modulated by cyclins. A lot of variability in the rate of cell-cycle progression occurs during the G₁ phase, which follows cytokinesis, precedes the S phase of genome duplication, and is a time for sensing of external factors (Massagué 2004). It is during this phase that cells “compute” whether they commit to replicate the genome and divide. To do so, cells first go through the R (for “restriction”) checkpoint, which assesses levels of growth factors (Pardee 1974), and is associated with levels of cyclin D. Cells that fail to pass this checkpoint go into a quiescent G₀ phase. Cells also check for sufficient levels of nutrients via the TOR pathway, which has been shown to regulate S-phase entry of mammalian cells (Fingar et al. 2004). Sensing of mechanical signals seems also to occur during G₁ as FAK mechanosensing acts on cyclin D (Klein et al. 2009), while YAP/TAZ-Yki acts on cyclin E (Huang et al. 2005)—these cyclins are known to act on the G₁/S transition. It is unclear whether mechanical signals promote proliferation only, or also concurrently promote cell growth. In the case of YAP/TAZ-Yki, it was shown in Drosophila that Yki promotes the expression of cyclin E, in addition to the oncogene dMyc, which drives cell growth (Neto-Silva et al. 2010; Ziosi et al. 2010). Mechanical signals, when interpreted by the YAZ/TAZ-Yki pathway, therefore potentially promote a balanced growth in which cell divisions and cell growth are in phase, leading to a doubling of the volume of a cell from its birth to the moment it divides. This balance between cell growth and cell division is important for tissue mechanics. As we discuss in the next section, growth and cell divisions may have contrasting mechanical effects.

In a more general context, the question of balance between cell growth and the cell cycle is of prime importance for tissue mechanics. Although it is generally assumed that growth and cycling are balanced, this situation is not systematic. In Drosophila, for example, different tissues behave differently. In the early embryo and in the pupal thorax, cells divide without growth (O’Farrell et al. 2004; Bosveld et al. 2012). Absence of growth during the first divisions of early development (cleavage) is a general feature shared by invertebrates and vertebrates (Gilbert 2010). Primordia of the adult Drosophila tissues (imaginal discs) show different behaviors early in and throughout development. At early stages, cell-cycle progression is blocked but cells grow, leading to an increase in cell volume (Madhavan and Schneiderman 1977). Later on, different tissues resume cell division at different times. In the precursors of the abdomen, the histoblast nest cells first cycle faster than they grow because they have accumulated cyclin E in prior larval stages (Ninov et al. 2007). But as the pool of cyclin E is depleted, cell division and growth become balanced (Ninov et al. 2007). In the precursor of the wing and thorax—the wing imaginal disc—cells maintain a rough growth balance during the third instar of larval development, but they stop growing at pupal stage, although they continue to divide. When growth and cell division are balanced in the Drosophila wing, this is not because of the cell cycle controlling cell growth, as it was shown that blocking cell cycle does not affect cell growth (Neufeld et al. 1998). Reciprocally, growth reduction by dMyc loss-of-function mutations does slow down the cell cycle, which supports the hypothesis of a hierarchy, with growth controlling the cell cycle (Johnston et al. 1999). In cultured mammalian cells, careful quantifications have shown that cell size influences the cell cycle in a direct way, although the mechanism is still elusive (Tzur et al. 2009). Delineating a growth/cycle hierarchy in tissues will require similar careful measurements, yet to be performed in vivo.

Measuring and Perturbing Growth and Mechanics of Tissues in Vivo

One of the main challenges that mechanobiology faces today is to understand tissue growth and mechanics in vivo. So far, most studies that have addressed the control of growth by mechanical forces were performed in vitro, often on isolated cells. These cultures sometimes mimic some properties of actual organs, such as the shape-generating acini (Paszek et al. 2005). Nevertheless, addressing these questions in vivo is a necessity for future investigations. Imaging technology has improved a lot recently, allowing in vivo imaging of early development of Drosophila, zebrafish, chicken, and mouse (reviewed in Supatto et al. 2011; Keller 2013). However, mass increase proceeds after early embryonic stages, once the organism has often become motile and is, therefore, hard to observe under a microscope. Because growing tissues are harder systems to work on, fewer tools were developed to quantify forces and deformations on them than on early embryos.

New methodologies are arising to circumvent these difficulties. The deformations associated with growth in Drosophila imaginal tissues can be quantified using a chronic imaging approach (Heemskerk et al. 2014). Force inference via image analysis of cell junctions allows one to measure patterns of mechanical stress, even when the tissue cannot be accessed mechanically (Chiou et al. 2012; Ishihara and Sugimura 2012; Ishihara et al. 2013). Force sensors based on deformable liquid droplets could also be a method of choice provided they can be delivered in vivo (Campàs et al. 2014). In this case, the use of magnetic fluids could be a means to also perturb the tissue mechanically in vivo (Desprat et al. 2008), something that has traditionally been performed on explants (Wiebe and Brodland 2005; Luu et al. 2011; Schluck et al. 2013). At a molecular level, tension sensor modules allow the imaging of forces imposed on cells via adhesion complexes (Grashoff et al. 2010; Borghi et al. 2012). With these new methods in hand, we can expect to put our knowledge of single-cell mechanobiology in the context of organismal development in the foreseeable future.

HOW TISSUE GROWTH IMPACTS MECHANICS

So far, we have addressed how tissue mechanics impacts growth. But reverse interactions also exist. Patterns of growth and proliferation are an integral part of tissue mechanics, leading to the generation of stresses that are important for morphogenesis

Stress Generation and Stress Dissipation in a Proliferating Tissue

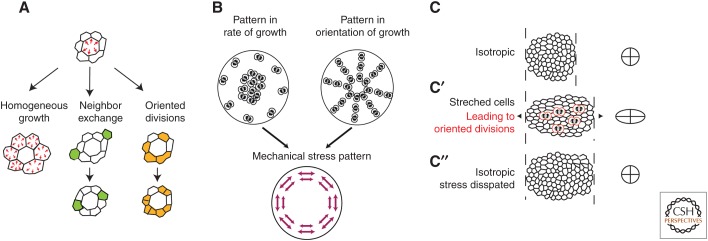
Cell growth is associated with an increase in cell mass and, hence, cell volume. Tissue connectedness around the cell and its associated tissue elasticity resists this volume increase. As a result, the growing cell experiences an increase in pressure, and the surrounding tissue experiences a stretch (Fig. 3A, top). Several mechanisms are able to relax these stresses. First, growth of other cells can compensate for the locally created stress by stretching the previously compressed cells (Fig. 3A, left). Second, neighboring cells may exchange neighbors in a way that dissipates the pressure increase (by increasing the number of direct neighbors of the growing cell (Fig. 3A, center). Likewise, cell divisions may introduce a reorganization of the tissue that reduces the stress (Fig. 3A, right). This is the long-axis rule discussed above.

Figure 3.

How cell growth impacts on tissue mechanics. (A) If a cell grows (red arrows) more than its neighbors, a mechanical stress is generated that results in increased pressure in the growing cell and the stretching of its neighbors (top). The stress disappears when the neighbors also grow until growth is spatially homogeneous (left). Other mechanisms that can dissipate the mechanical stress are cell exchange (see the green cells in the middle), and oriented divisions along the axis of stress (see the orange cells on the right). (B) Patterns of growth, such as growth heterogeneities or polarized growth, induce mechanical stresses in a tissue. Regional differences in tissue growth (left) may lead to mechanical stress in the tissue. Here, growth was symbolized by cell division, but it is indeed the volume increase that matters, not cell divisions. If more growth proceeds in the center of the tissue, and provided tissue is sufficiently elastic to prevent stress dissipation, this will result in a stretch of the periphery of the tissue. Oriented cell division (right) can lead to similar patterns of mechanical stress, provided they are accompanied by volume increase. (C) In a tissue with no preferred direction, cells are isotropic, and the average fit to an ellipse yields a circle (right). (C′) An external uniaxial mechanical stress (which may originate from neighboring regions) deforms cells along its axis (right: average fit to an ellipse is elongated). This stretch promotes orientation of cell divisions (red dividing cells on the schematic). (C″) As a result of the polarized growth, cells will at least partially lose their stretch (averaged fit to an ellipse is a circle). Thus, oriented cell divisions contribute to the dissipation of the mechanical stress that was imposed on the tissue.

This schematic view of a single growing cell holds at the tissue scale. Growth inhomogeneity generates mechanical stress in a tissue, whereas topological rearrangements, such as cell exchange and division, tend to dissipate stress (Fig. 3B,C). In support of this, overgrowing clones in the Drosophila wing precursor have been shown to generate mechanical stress in their vicinity (LeGoff et al. 2013; Mao et al. 2013). During zebrafish epiboly, cell divisions participate in a reduction of mechanical stress in the enveloping cell layer that spreads over the yolk cell (Campinho et al. 2013).

For patterns of growth to generate mechanical stress, the orientation of growth may be as important as the rate of growth (Fig. 3B). Patterns of polarized growth are an integral part of many morphogenetic processes. In vertebrate limb formation, cell divisions are oriented along the A/P axis in the lateral plate mesoderm, and gradually shift to an orientation perpendicular to it in the limb bud (Wyngaarden et al. 2010). In the Drosophila wing, the Fat/Dachsous planar polarity pathway orients cell divisions in a proximodistal orientation (Baena-Lopez et al. 2005). Dachs, an atypical myosin downstream from Fat/Dachsous, which is polarized in the wing pouch (Mao et al. 2006; Schwank et al. 2011; Ambegaonkar et al. 2012), may be the driver of this polarity (Mao et al. 2011). There is still no formal demonstration of a tissue in which growth orientation acts as stress generator, but their contribution to tissue mechanics should be considered further, as polarized growth is a recurring process to shape tissues.

Why is it that the orientation of cell divisions can lead to the dissipation of stress in the context of the long-axis rule and not in the context of polarized growth? During each cell division, the tissue is locally reorganized because division is intrinsically anisotropic (i.e., it is defined by a principal axis). Consequently, an anisotropic mechanical stress is locally generated. The cell division may or may not be associated with growth, which accounts for an isotropic stress (a pressure, see above). If a cell has been stretched by an external stress (a stress external to the tissue or just the balance of forces coming from the cell neighbors), the long-axis rule will orient the cell division such that the local stress created by the division opposes and reduces the preexisting stress around the dividing cell. It may locally cancel it, or even overcompensate and, thus, create a new stress. But at the scale of the tissue, the effect is gradual. The macroscopic external stress will slowly reduce as more divisions along the cells-long axis accumulate. The external stress will decay and divisions will stop being oriented along its axis as cells become isotropic (Fig. 3C). Note that this accounts only for the effect of the orientation of divisions. If these divisions are associated with growth, the pressures generated may still lead to macroscopic stresses (see above). In contrast, if the axis of division is set by external polarity cues, such as the planar polarity pathway irrespective of local stresses and cell shape, the local stress created by the division will not cancel the preexisting stress around the dividing cell. As more divisions accumulate, their local stress may add up and generate a macroscopic stress at the level of the tissue. Both mechanisms of cell division orientation (long axis and polarity cues) may be at play within a given tissue (LeGoff et al. 2013; Mao et al. 2013).

Overall, it seems that growth and proliferation can have contrasting effects on tissue mechanics, leading either to the buildup or to the dissipation of mechanical stress. The mechanical state of a tissue will depend on the respective rate of elastic stress accumulation (e.g., by cell division) and its dissipation by cell rearrangements associated with cell division. The existence of nonlinear effects caused by feedback mechanisms makes it hard to predict specific outcomes. Analytical and numerical models are, therefore, necessary to make the connection between cell behavior and tissue-scale mechanics. There is an extensive literature from the theory of complex fluids, which is relevant to this subject. Looking at a tissue in a coarse-grained fashion, one may describe it as a material with elastic, viscous, or plastic behavior. However, because cells consume ATP to generate mechanical work, the tissue should be viewed as active matter. In the past 10 years, the theoretical study of active materials has been the subject of intense activity (for a review, see Marchetti et al. 2013). Initially developed to model the mechanics of the cytoskeleton, active fluid models have also been successfully applied to the mechanics of growing tissues in which each cell division contributes to the generation of an anisotropic active stress. Such approaches have been used to address how cell divisions drive stress dissipation in a tissue (Ranft et al. 2010) and how polarized growth leads to the generation of viscous stress (Bittig et al. 2008; Blanch-Mercader and Casademunt 2014).

Making Three-Dimensional (3D) Shapes from Growth-Induced Mechanical Instabilities

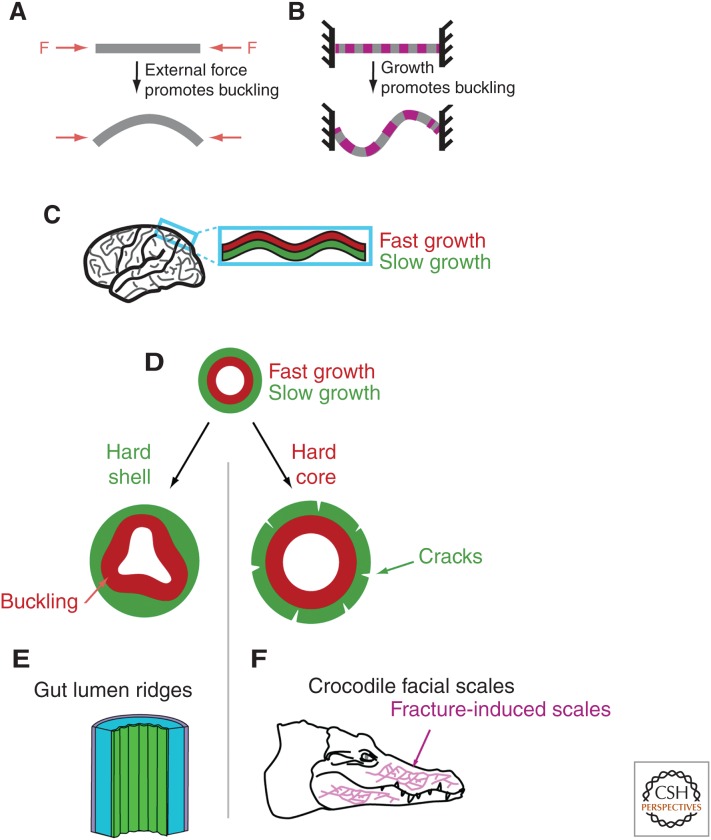
We have discussed how growth, and more specifically regional differences in growth, can induce the accumulation of mechanical stress within tissues. We illustrate with a few examples how this can give rise to 3D shapes. Of particular interest is the buckling instability, when a compressive stress above a certain threshold suddenly folds a sheet- or rod-like structure (Fig. 4A).

Figure 4.

Making 3D shapes. (A) If an elastic rod or sheet is subjected to compressive forces, the rod will buckle above a certain threshold. (B) Buckling may also proceed in the absence of an external force when the structure grows, provided it is constrained at its ends. (C) Folds of the mammalian cortex have been proposed to stem from a buckling instability in which the fast growth of the external layer of the cortex is constrained by the slower growth of another layer below it. (D–F) Apposition of tissues with different growth rates may give rise to very different 3D structures depending on the boundary conditions. To illustrate this, we consider a fast-growing layer surrounded by a slow-growing layer. If the surrounding layer is rigid and makes a hard shell (left), buckling may proceed in the fast-growing inner layer. Such a mechanism has been proposed to initiate gut lumen ridges (E). If it is the fast-growing layer that is the strongest and makes a hard core (right), then the external layer will be deformed and may even crack. This has been proposed to drive the formation of facial scales of crocodiles (F).

In principle, a growing cell monolayer, although being two dimensional, can buckle in the third dimension under the mechanical compression generated by its growth and some constraint of size limitation (Fig. 4B) (Drasdo 2000). The constraint may come, for example, from surrounding tissues that do not grow as fast. The physical principles of such shape-generating instabilities have been well investigated theoretically (Drasdo 2000; Dervaux and Ben Amar 2008; Hannezo et al. 2014). Further theoretical work (Hannezo et al. 2011; Ben Amar and Jia 2013), as well as a combination of theory and experiments (Shyer et al. 2013), have shown how buckling could promote the formation of villi in the mammalian gut. Growth of the luminal endoderm, constrained by the surrounding muscles, leads to circumferential compression and subsequent bucking of the endoderm, yielding previllous structures (Fig. 4D, left). The differential growth of the gut tube and the attached mesenteric sheet has also been shown to drive the 3D looping of the gut in a variety of species (Savin et al. 2011). The mechanical model for gut looping explains the different gut geometries across species from mere differences of tissue-geometric and elastic properties, as well as rate of growth. Cortical layers of the human brain constitute another complex folded structure. Richman et al. proposed, 40 years ago, that buckling instabilities associated with differential growth of the inner and outer cortical layers could generate the folds (Fig. 4C) (Richman et al. 1975). Although alternative models exist, the buckling model seems supported, at least partially, by experiments (Bayly et al. 2014).

The almost opposite mechanical situation to buckling seems to happen in the facial skin of the crocodile (Fig. 4E). In the course of embryonic development, the skin that enwraps the rapidly growing facial bones of crocodiles grows more slowly than the skull. The skin is consequently stretched and eventually cracks under the mechanical stress, because crocodile skin lacks flexibility. These cracks have been shown to give rise to the facial scales on the adult skin (Milinkovitch et al. 2013). Both the gut lumen ridges and the crocodile facial scales arise from the mechanical interactions of a fast-growing core and a slow-growing surface. The different outputs (inner buckling or outer cracking) depend on which layer (inner or outer) is mechanically dominant (Fig. 4D–F). Simple mechanics can lead to a great variety of morphological outputs.

CONCLUSIONS: INTEGRATING FORWARD AND REVERSE INTERACTION BETWEEN GROWTH AND TISSUE MECHANICS

As explained above, cells do not passively follow upstream biochemical signals because they are embedded in a mechanical environment, which influences how they divide (orientation and frequency) and grow. Growth and proliferation also strongly influence the mechanical properties of tissue. It then seems clear that growth and tissue mechanics cannot be studied in isolation. The reciprocal interactions between growth and tissue mechanics are an important part of what shapes growing tissues. A general rule of thumb of how mechanics influence growth is that the more cells are compressed, the slower they grow. Conversely, when regional differences of growth exist in a tissue, it is the fast-growing regions that are compressed and the slow-growing ones that are stretched. It then seems that the aforementioned reciprocal interactions result in a negative feedback on growth, such that regional differences of growth tend to vanish. On the basis of this, several models proposed that it is a mechanical feedback that ensures homogeneous growth of the Drosophila wing primordium despite the sharp, spatially restricted distribution of morphogens (Shraiman 2005; Aegerter-Wilmsen et al. 2007; Hufnagel et al. 2007). Recently, Eisenhoffer et al. (2012) showed how mechanical constraints orchestrate homeostasis of tissue growth in zebrafish and cultures of MDCK cells. They observed a strong increase in delamination of nonapoptotic cells in regions of overcrowding, both in vitro and in vivo. This delamination is triggered by mechanical signals relayed by the stretch-activated channel piezo. Disruption of mechanosensation by morpholino knockdown of piezo leads to the formation of an epithelial cell mass in the tail fin of zebrafish, demonstrating how this mechanism ensures tissue integrity by locally expelling cells from overcrowded regions. A concurrent study found that overcrowding also leads to nonapoptotic cell delamination in the Drosophila pupal thorax (Mariani et al. 2012). These investigations addressed how mechanics can feed back on growth at the tissue scale via cell delamination. Future work needs to address whether mechanical feedback can also act on cell growth and cell cycle in vivo, as single-cell measurements suggest (see above). Although the intricate relationship between growth and mechanics has long been theorized to drive tissue homeostasis in animal tissues, we are now at a turning point where we can start to address it experimentally. This endeavor will require a tight interplay between modeling, imaging, and quantitative measurements on growing tissues, as well as genetic perturbation of the signaling pathways that control growth.