Eighth Grade Algebra Course Placement and Student Motivation for Mathematics

Abstract

This study uses student panel data to examine the association between Algebra placement and student motivation for mathematics. Changes in achievement goals, expectancy, and task value for students in eighth grade Algebra are compared with those of peers placed in lower-level mathematics courses (N = 3,306). In our sample, students placed in Algebra reported an increase in performance-avoidance goals as well as decreases in academic self-efficacy and task value. These relations were attenuated for students who had high mathematics achievement prior to Algebra placement. Whereas all students reported an overall decline in performance-approach goals over the course of eighth grade, previously high-achieving students reported an increase in these goals. Lastly, previously high-achieving students reported an increase in mastery goals. These findings suggest that while previously high-achieving students may benefit motivationally from eighth grade Algebra placement, placing previously average- and low-performing students in Algebra can potentially undermine their motivation for mathematics.

Driven by concerns about workforce readiness, global competitiveness, and equity in access, the United States has participated in a decades-long push to accelerate mathematics instruction (see Balfanz, Legters, & Jordan, 2004; National Research Council, 2011; Oakes, 2005). Much of the effort towards this has been through universal access to Algebra during middle school—most commonly, by eighth grade (Simzar & Domina, 2013). Students who fail to master Algebra in eighth or ninth grade face a blocked pathway to advanced mathematics and participation in science, technology, engineering, and math (STEM) career opportunities (Attewall & Domina, 2008; Long, Conger, & Iatorola, 2012). Thus, progress towards the goals of reaching universal access to Algebra has changed the math-taking experiences of many students.

There is a need for greater retention in advanced mathematics despite efforts towards universal Algebra placement. High school students typically opt out of advanced mathematics courses after fulfilling courses required to graduate high school (Meece, 2006). Thus, participation in advanced mathematics is ultimately a function of access and student choice. A strong predictor of choice is student motivation (Martin, Anderson, Bobis, Way, & Vellar, 2012), and research has yet to determine the relation between changing Algebra policies (any policy that guides the placement of students into Algebra courses) and students’ motivation for mathematics. Recent studies raise questions about the educational effectiveness of enrolling larger proportions of students in Algebra courses, suggesting that eighth grade Algebra enrollment may have unintended negative consequences such as lower mathematics test score growth for students who enter the course with relatively low mathematics skills (Clotfelter, Ladd, & Vigdor, 2012; Domina, 2014; Loveless, 2008). We hypothesize that declining student motivation in mathematics may help to explain these disappointing findings.

This case study uses the increasing eighth grade Algebra enrollment trends in an urban California school district to examine the relation between eighth grade Algebra course placement and students’ motivation for mathematics. Specifically, we investigate motivational changes for students selected into eighth grade Algebra and for eighth grade peers enrolled in other lower-level math courses, typically Pre-Algebra, hereafter collectively referenced as general mathematics courses. Using two waves of motivation survey data, we estimate motivational changes for students between the fall and spring of eighth grade. Our research questions are as follow: (1) To what extent does motivation for math change for eighth grade Algebra students compared with eighth grade peers enrolled in general mathematics courses? and (2) Do these motivational changes vary by mathematics achievement prior to Algebra course placement?

Review of Changes in Algebra Policy

In the 1980s and 1990s, the California Department of Education issued repeated calls to enroll all middle school students in advanced mathematics courses, namely Algebra, to increase progress towards universal eighth grade Algebra enrollment (Domina, McEachin, Penner, & Penner, 2014). In 1999, the state’s school accountability law attached incentives to this call, and in 2008, the state’s Board of Education voted to make Algebra examinations the sole “test of record” for eighth grade mathematics (Domina et al., 2014). This vote mandated that students demonstrate proficiency in Algebra by the end of eighth grade to fulfill accountability expectations under the No Child Left Behind Act and California’s Public Schools Accountability Act (Rosin, Barondess, & Leichty, 2009). Though a universal Algebra policy was never fully implemented in California, the proportion of eighth graders in California enrolled in Algebra more than tripled between 1999 and 2008, rising from 16 to 51 percent (Rosin et al., 2009). California has since emerged as a national leader in efforts towards increased eighth grade Algebra enrollment and as such, serves as a paradigmatic example of Algebra efforts nationwide (Domina, Penner, Penner, & Conley, 2014). Currently, more eighth grade students take Algebra than any other math class (Domina, 2014). Though California’s adoption of the Common Core State Standards—which recommends Pre-Algebra content at the eighth grade level—may slow movement towards universal Algebra policies, the state’s leading policy-makers argue that universal eighth grade Algebra policies should remain a priority (Wurman & Evers, 2010).

Effort towards universal eighth grade Algebra enrollment is backed by research that points to positive correlations between early Algebra course taking—for example, taking Algebra in eighth grade rather than ninth—and equity in access to mathematic curricula, achievement, and educational attainment (Filer & Chang, 2008; Gamoran & Hannigan, 2000; Kurlaender, Reardon, & Jackson, 2008). Observational data indicate that students who enroll in eighth grade Algebra score higher on skills tests, show more rapid test score growth, and reach higher levels of educational attainment than their peers who enroll in less rigorous eighth grade math courses (Gamoran & Hannigan 2000; Gamoran, Porter, Smithson, & White, 1997). However, these findings are based on observational data and are thus subject to considerable selection bias. Studies that have made progress towards estimating less biased effects of Algebra course taking in experimental or quasi-experimental settings report mixed results (for a review, see Stein et al., 2011). A review of related research claimed that universal Algebra policies did not lead to achievement gains without supports for struggling students, such as extended learning time for Algebra instruction (Stein et al., 2011).

More recently, analyses utilizing course placement changes in North Carolina indicated that the initiative to expand eighth grade Algebra had negative effects on student achievement, especially for students who come into eighth grade Algebra courses with relatively weak mathematics skills (Clotfelter, Ladd, & Vigdor, 2012). Quasi-experimental evaluations of California’s Algebra-for-all policy suggest that increases in the eighth grade Algebra enrollment rates corresponded with declining mathematics achievement (Williams et al., 2011). Evaluations of Chicago’s mandated universal Algebra policy found that failure rates increased, grades declined, test scores did not improve, and students were no more likely to enroll in college (Allensworth, Nomi, Montgomery, & Lee, 2009). Loveless (2013) examined variation in state enrollment patterns to see if rising enrollments in advanced eighth-grade math courses were correlated with achievement gains on the National Assessment of Educational Program (NAEP) and found that states with rising percentages of eighth graders taking Algebra, or other more advanced courses such as Geometry, were no more likely to raise their NAEP scores from 2005-2011 than states with declining percentages of eighth graders in those courses. Loveless (2013) also found that increased enrollments in Algebra I and Pre-Algebra were associated with decreases in mean achievement gains. These findings collectively highlight unintended negative consequences of increased Algebra enrollment trends.

Motivation for Mathematics

Students' motivation for mathematics may be a potential mechanism through which Algebra course placement undermines student achievement. We hypothesize that changes in student motivation may account for some of these unintended negative consequences. Motivational beliefs are psychological mechanisms that influence students’ motivation to exert effort on learning tasks (Wigfield & Cambria, 2010; Wigfield & Eccles, 2000). We adopted two widely-used frameworks for studying motivational beliefs in academic contexts—achievement goal theory and expectancy-value theory. Achievement goal theory explains why a learner engages in specific achievement-related behaviors (Kaplan, Middleton, Urdan, & Midgley, 2002), whereas expectancy-value theory predicts which activities individuals choose to engage (Wigfield & Eccles, 2000). These motivation theories, therefore, include complementary elements that help to explain both students’ achievement in math class as well as their choice to take or opt out of future math classes. Recent studies have found that operating under a perspective that examines both achievement goal and expectancy-value constructs, rather than just one or the other, delivered a more complete understanding of mechanisms contributing to change in motivation (Conley, 2012; Senko & Hulleman, 2013).

Achievement goal theory includes mastery, performance-approach, and performance-avoidance goals (Dweck & Elliot, 1983). Students with mastery goals tend to focus on developing competence and are more likely to persist in learning activities, have greater interest in their classes, and seek help (Harackiewicz, Barron, & Elliot, 1998; Harackiewicz, Barron, Tauer, Carter, & Elliot, 2000; Karabenick, 2003). Students with performance-approach goals focus on demonstrating competence, which is linked to positive associations with achievement and academic efficacy (Harackiewicz, Barron, Pintrich, Elliot, & Thrash, 2002; Pajares, Britner, & Valiante, 2000). Performance-approach goals, however, have also been found to be associated with reduced help-seeking behavior, increased anxiety, cheating, self-handicapping, low self-efficacy, reduced metacognitive strategy use, and maladaptive responses to conflict (Anderman, Griesinger, & Westerfield, 1998; Elliot & McGregor, 1999; Karabenick, 2003; Murdock, Miller, & Kohlhardt, 2004; Skaalvik, 1997). One explanation for the mixed outcomes related to performance-approach goals may be that their impact is influenced by the adoption of other concurrent goals. For example, there is evidence that performance approach goals are associated with adaptive patterns of learning when mastery goals are also espoused (Midgley, Kaplan, & Middleton, 2001). Lastly, students with performance-avoidance goals maintain goals of avoiding appearing incompetent. These goals are typically associated with procrastination, withdrawal of effort, low performance outcomes, high anxiety, disorganized study habits, help-avoidance, self-handicapping, low achievement, and low interest (e.g., Elliot & Church, 1997; Elliot, McGregor, & Gable, 1999; Middleton & Midgley, 1997; Midgley & Urdan, 2001; Skaalvik, 1997; Urdan, 2004; Wolters, 2004). In all, these goals negatively correlate with performance outcomes (Hulleman et al. 2010).

In the expectancy-value model of achievement, expectancy for success is defined as students’ belief about how well they will do on an upcoming task, whereas task value is the degree to which a student believes that the academic task is worth pursuing (Eccles et al., 1983; Wigfield & Eccles, 2000; Wigfield, Tonks, & Eccles, 2004). Task value is influenced by interest (the student’s enjoyment from doing a task), attainment (the personal importance of performing well on the task), utility (how the task relates to students’ current or future plans), and cost (the anticipated effort needed to complete the task). In mathematics specifically, findings show that an individual’s expectancy for success and valuing of mathematics predict their performance in mathematics and their choices of whether to continue studying math (Wigfield & Eccles, 2000). Students’ expectancies for success are assessed as competence beliefs in the present study and are referenced as self-efficacy hereafter.¹

Hypotheses

Student motivation is influenced by the fit between the academic task and their current competence level (Eccles & Roeser, 2011). If students are placed in a course before they are able to competently perform at the level required by the course, their motivation may suffer. We expect that students placed in eighth grade Algebra who performed at a low level on their seventh grade mathematics assessment will experience a mismatch between their current educational experiences and competence levels. These students may not have the necessary prior knowledge to meet the demands of Algebra; and as a result, we expect their feelings of math efficacy to decline (H1). Because expectancy beliefs relate positively to subjective task value (Eccles & Wigfield, 1995) we expect their subjective task value for mathematics to also decline (H2). The opposite is expected for students who are placed in eighth grade Algebra and performed at a high level on their seventh grade mathematics assessment. These students are expected to enter the course with the prerequisite skills necessary to engage successfully in algebraic learning tasks and thus, bolster their efficacy and task value (H3).

In terms of achievement goals, mastery goals are associated with positive perceptions of academic ability and self-efficacy (Meece, Blumenfeld, & Hoyle; 1988, Midgley et al. 1998; Wolters, 2004). Specifically, students with high-perceived competence are inclined to adopt mastery and performance-approach goals (Elliot, 1999), whereas those with low perceived competence tend to adopt performance-avoidance goals (Skaalvik, 1997). Thus, we expect that previously low-achieving students placed in Algebra will experience an increase in performance-avoidance goals and a decrease in mastery and performance-approach goals (H4) with the opposite holding for previously high-achieving students placed in eighth grade Algebra (H5).

Method

Participants

Data are from the California Motivation Project-Mathematics (CAMP-Math). CAMP-Math is a part of the larger Math and Science Partnership—Motivation Assessment Program (MSP-MAP) funded by the National Science Foundation (NSF) that studies the role of motivation-related beliefs of students in mathematics and science courses. Our sample is a portion of students drawn from seven middle schools that are a part of a large urban unified school district in California. Students were included in the analysis if the student: (1) was in eighth grade in either the 2004-05 or 2005-06 school year, (2) had a valid mathematics California Standards Test (CST) score in the spring of their seventh grade year, (3) took the General Mathematics, Algebra, or Geometry CST in the spring of their eighth grade year, and (4) had valid covariate and motivational measures for the fall and spring motivational surveys given during their eighth grade year. Using the type of CST exam students took in the spring of their eighth grade year as a proxy for course enrollment, we started with a sample of 4,229 students who were in eighth grade General Math, Algebra, or Geometry in either 2004-05 or 2005-06 and had valid math scores in the spring of their seventh grade year. After using listwise deletion to filter by valid covariate and motivational measures, we were left with 3,306 students, which is approximately 78% of the total sample.

Table 1 provides a summary of the full and study samples used in our analyses. T-tests between the final sample and the eliminated sample with missing data revealed that the two groups differed significantly in the proportion of Hispanic students and Vietnamese students, prior math CST scaled scores, the proportion of previously high-achieving and low-achieving students. The two groups differed significantly on mastery goals, self-efficacy, and task value in the fall of eighth grade and on performance-approach goals, performance-avoidance goals, and self-efficacy in the spring of eighth grade. The missing data and the above noted differences between the final sample and the eliminated sample suggest that results may therefore not be generalizable to the full district population. The differences, however, are small in magnitude.

Table 1.

Descriptive statistics for full (N=4,229 students) and study samples (N=3,306 students)

	Full sample			Study sample
	obs.	mean/ %	SD	obs.	mean/ %	SD	p-value of difference
Gender
Male	2,051	48.5%		1,593	48.2%		0.48
Race/ethnicity
White	423	10.0%		331	10.0%		0.96
Hispanic	2,888	68.3%		2,226	67.3%		0.01*
Vietnamese	571	13.5%		470	14.2%		0.01*
Other	351	8.30%		281	8.50%		0.38
Free/reduced lunch (NSLP) and English Learner (EL) status
NSLP status	3,180	75.2%		2,474	74.8%		0.15
EL status	2,051	48.5%		1,587	48.0%		0.33
Prior math achievement (CST scaled score)
7th grade	4,229	337	60.6	3,306	341	60.7	0.00***
Prior math achievement bins
High achievement	1,594	37.7%		1,302	39.4%		0.00***
Average achievement	1,362	32.2%		1081	32.7%		0.10
Low achievement	1,273	30.1%		922	27.9%		0.00***
8th grade motivational measures, Fall
Mastery	3,500	3.71	0.92	3,089	3.73	0.91	0.00***
Performance approach	3,522	2.49	1.06	3,101	2.50	1.06	0.18
Performance avoid	3,560	2.44	1.01	3,083	2.43	1.01	0.12
Self-efficacy	3,525	3.32	0.89	3,103	3.34	0.87	0.01**
Task value	3,531	3.44	0.64	3,108	3.46	0.64	0.00***
8th grade motivational measures, Spring
Mastery	3,602	3.50	1.00	3,273	3.50	1.00	0.25
Performance approach	3,630	2.21	0.99	3,297	2.18	0.98	0.00***
Performance avoid	3,619	1.94	0.91	3,289	1.91	0.98	0.00***
Self-efficacy	3,636	3.23	0.94	3,302	3.24	0.90	0.02*
Task value	3,636	3.31	0.66	3,303	3.31	0.66	0.46

Note. Motivation scales = 1 – 5; Math scale score range = 150 – 600, 150-256 = Far Below Basic, 257-299 = Below Basic, 300-349 = Basic, 350-413 = Proficient, 414-600 = Advanced; Free/reduced lunch (NSLP) and English Learner (EL) status scale = 0-1 (1 = yes, 0 = no). Prior achievement bins: high achievement = Proficient or Advanced; average achievement = Basic; low achievement = Below Basic or Far Below Basic.

Lastly, listwise deletion of students’ missing motivational measures resulted in a slightly different sample size for each of the motivational beliefs measured; however, adjusted sample sizes do not differ significantly on any of the variables from the study sample used in our analyses. The remaining sample was fairly evenly split by gender (1,593 males and 1,713 females) with an average age of 13.6 years (SD=0.64) for students in the spring of eighth grade. Our analyses included Hispanic (67%), Vietnamese (14%), and White (10%) students. Other ethnic groups comprised approximately 9% of the sample and were pooled to create an “Other” ethnic category of reference. Students in the Geometry group accounted for approximately 3% of the total sample and were left out of the reported results.

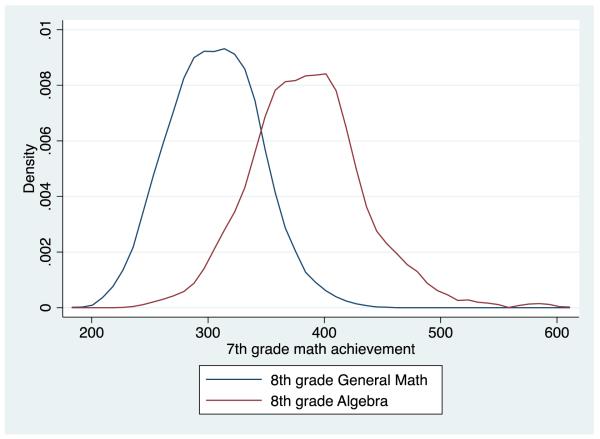
Figure 1 illustrates students’ seventh grade mathematics achievement by eighth grade math course placement. In our sample, approximately 38% of eighth grade students were enrolled in Algebra at the time of data collection, indicating that selection factors were present. A percentage closer to 100%—otherwise known as universal Algebra course placement—would have indicated less of a presence of selection factors. Table 2 provides descriptive statistics and associated p-values demonstrating statistically significant differences between the eighth grade general mathematics and Algebra groups. At the time of data collection students were still selected into Algebra based on variables that may have included teacher recommendation and/or parent request. The selection factors present across schools varied by school and a school fixed effects, used in the analyses, aims to help control for this variation by addressing biases that arise from the non-random assignment of students to schools.² Despite the selection factors present at the time of data collection, the district was amidst progressively moving towards universal eighth grade Algebra policy by relaxing selection policies into Algebra, which is highlighted by the overlap in prior achievement distributions at the time of data collection (Figure 1). The overlap illustrates that there were students placed in Algebra who had prior achievement levels that were equal to or lower than peers enrolled in general mathematics courses.

Figure 1.

Eighth Grade Math Course Placement by Prior Mathematics Achievement

Kernel density graph illustrating the distribution of prior math achievement (seventh grade CST math score) by eighth grade math course placement (N=3,306 students). Eighth grade math course placement is indicated by the California Standardized Test (CST) exam taken by student in the spring of eighth grade. CST math scale score range = 150 – 600, 150-256 = Far Below Basic, 257-299 = Below Basic, 300-349 = Basic, 350-413 = Proficient, 414-600 = Advanced.

Table 2.

Descriptive statistics for study sample by eighth grade course placement (N=3,306 students)

	General Mathematics			Algebra
	obs.	mean/%	SD	obs.	mean/%	SD	p-value of difference
n	1,940	58.70%		1,259	38.10%		0.00***
Gender
Male	1,007	51.90%		542	43.10%		0.00***
Race/ethnicity
White	169	8.70%		157	12.50%		0.00***
Hispanic	1,525	78.60%		685	54.40%		0.00***
Vietnamese	111	5.70%		279	22.20%		0.00***
Other	136	7.00%		137	10.90%		0.00***
Free/reduced lunch (NSLP) and English Learner (EL) status
NSLP status	1,525	78.60%		875	69.50%		0.00***
EL status	1,193	61.50%		380	30.20%		0.00***
Prior math achievement (CST scaled score)
7th grade	1,940	306	38.7	1,259	385	48.7	0.00***
Prior (7th grade) math achievement bins
High achievement	221	11.40%		973	77.50%		0.00***
Average achievement	839	43.20%		242	19.30%		0.00***
Low achievement	882	45.40%		40	3.20%		0.00***
8th grade motivational dimensions, Fall
Mastery	1,796	3.65	0.92	1,196	3.85	0.88	0.00***
Performance approach	1,807	2.55	1.07	1,198	2.43	1.05	0.00***
Performance avoidance	1,802	2.53	1.01	1,180	2.3	0.99	0.00***
Self-Efficacy	1,808	3.19	0.86	1,198	3.56	0.85	0.00***
Task value	1,811	3.38	0.61	1,199	3.57	0.66	0.00***
8th grade motivational dimensions, Spring
Mastery	1,915	3.39	1.02	1,251	3.63	0.96	0.00***
Performance approach	1,933	2.2	0.99	1,256	2.13	0.95	0.05
Performance avoidance	1,926	1.93	0.9	1,255	1.89	0.89	0.24
Self-Efficacy	1,936	3.14	0.94	1,258	3.35	0.94	0.00***
Task value	1,937	3.26	0.64	1,258	3.37	0.69	0.00***

Notes. Motivation scales = 1 – 5; Math scale score range = 150 – 600, 150-256 = Far Below Basic, 257-299 = Below Basic, 300-349 = Basic, 350-413 = Proficient, 414-600 = Advanced. Prior achievement bins: high achievement = Proficient or Advanced; average achievement = Basic; low achievement = Below Basic or Far Below Basic.

Outcome Measures

Student motivation data were collected via surveys administered during the fall (approximately four weeks after the start of the school year) and spring (approximately four week before the end of the school year) for two consecutive academic years, 2004-05 and 2005-06.³ All students in class on the day the surveys were administered were invited to participate, with less than 1% opting out. Student achievement and demographic data were simultaneously collected from the district annual testing records.

Achievement goals

Student reported achievement goals were measured using three scales from the Patterns of Adaptive Learning Survey (PALS; Midgley et al., 2000; Midgley et al., 1998). All items were assessed using a 5-point Likert scale ranging from 1 (not at all true for me) to 5 (very true for me). Mastery goals were assessed using items that focused on learning and understanding—e.g., “My goal in math is to learn as much as I can.” Performance-approach goals were assessed using items that focused on demonstrating ability and outperforming others—e.g., “My goal in math is to look smarter than other students.” Lastly, performance-avoidance goals were assessed using items that focused on not appearing incompetent—e.g., “My goal in math is to avoid looking like I can’t do my work.” Achievement goal scales were anchored in the middle and at the endpoints—Not at all true for me, Somewhat true for me, Very true for me. A complete list of items, standardized factor loadings, and internal consistencies of the scales, ranging from acceptable to good, are provided in Table 3.

Table 3.

Standardized factor loadings of student survey items for achievement goal, self-efficacy, and task value structure

Student survey items	λ	R 2
Mastery goal structure (5 items, α = .81)
Learning a lot of new things is what is important to me in math.	0.73	0.46
One of my main goals in math is to improve my skills.	0.73	0.47
My main goal in math is to learn as much as I can.	0.76	0.42
Really understanding my math work is important to me.	0.73	0.47
Learning new skills in math is one of my goals.	0.83	0.32
Performance-approach goal structure (5 items, α = .83)
In math, doing better than other students is important to me.	0.64	0.59
My goal in math is to look smarter than other students.	0.75	0.43
One of my goals is to show others that math is easy for me.	0.70	0.51
It’s important to me that others think I am good at doing math.	0.68	0.54
My goal in math is to do better than other students.	0.79	0.38
Performance-avoid goal structure (5 items, α = .79)
My goal is to keep others from thinking that I’m not smart in math.	0.60	0.64
It’s important to me that I don’t look stupid in math class.	0.64	0.59
An important reason I do my math work is so that I don’t embarrass  myself.	0.58	0.67
I do my math work so that my teacher doesn’t think I know less than  others.	0.67	0.55
My goal in math is to avoid looking like I can’t do my work.	0.71	0.50
Academic self-efficacy for math (4 items, α = .85)
How certain are you that you can learn everything taught in math?	0.65	0.58
How sure are you that you can do even the most difficult homework  problems in math?	0.76	0.42
How confident are you that you can do all the work in math class,  if you don’t give up?	0.72	0.48
How confident are you that you can do even the hardest work in your  math class?	0.75	0.44
Task value (4 items, α = .85)
Interest Value (6 items, α = .87)
How much do you like doing math?	0.88	0.23
I like math.	0.86	0.26
Math is exciting to me.	0.92	0.15
I am fascinated by math.	0.94	0.13
I enjoy doing math.	0.88	0.23
I enjoy the subject of math.	0.88	0.23
Utility Value (4 items, α = .79)
How useful is learning math for what you want to do after you   graduate and go to work?	0.86	0.26
Math will be useful for me later in life.	0.81	0.35
Math concepts are valuable because they will help me in the   future.	0.56	0.69
Being good at math will be important when I get a job or go to   college.	0.64	0.59
Attainment Value (6 items, α = .84)
Being someone who is good at math is important to me.	0.67	0.55
I feel that, to me, being good at solving problem which involve   math   or reasoning mathematically is (not at all to very important).	0.63	0.60
	0.72	0.48
Being good at math is an important part of who I am.	0.76	0.43
It is important for me to be someone who is good at solving   problems that involve math.	0.78	0.39
It is important to be to be a person who reasons mathematically.	0.68	0.53
Thinking mathematically is an important part of who I am.
Cost Value (2 items, α = .72)
I have to give up a lot to do well in math.	0.82	0.32
Success in math requires that I give up other activities I enjoy.	0.67	0.55

Note. The range for scale reliability is reported for all four waves of motivation surveys included in the analyses. All standardized factor loadings are significant at p < .001. Results come from the full sample of 4,229 students. Chi-square = 3,883, df = 601, p < .001; CFI = 0.95; TLI = 0.95; RMSEA = 0.04; SRMR = .04.

Source: Midgley et al. (2000).

Self-efficacy

Students’ beliefs in their abilities were measured with the Academic Efficacy scale from PALS (Midgley et al., 2000). Self-efficacy assessed students’ judgments about their ability and confidence to perform adequately in math—e.g., “How sure are you that you can do even the most difficult math work?” All items were assessed using a 5-point Likert scale. Items were anchored at the endpoints and in the middle using wording that paralleled the wording of the stem—e.g., Not at all sure, Somewhat sure, Very sure. As seen in Table 3, the standardized factor loadings for students’ self-efficacy ranged from 0.65 to 0.75 and the internal consistency was good.

Subjective task value

Value was assessed with four scales adapted from the work of Eccles, Wigfield, Blumenfeld and their colleagues (Eccles & Wigfield, 1995; Eccles et al., 1993; Wigfield, Eccles, Yoon, Harold, Arbreton, Freedman-Doan, & Blumenfeld, 1997). Four subscales assessing students’ interest, utility, attainment, and cost were supported by confirmatory factor analysis, χ²(548) = 6,492.06, goodness-of-fit index = .94, and root-mean-square error of approximation = .043 (Conley, 2012). Interest was assessed using items that focused on students’ attraction to, liking for, and enjoyment of math—e.g., “I find math very interesting.” Utility was assessed using items that focused on students’ beliefs about the usefulness of math as an area of study—e.g., “Math is useful to me for things I do outside of school.” Attainment was assessed using items that focused on students’ judgments about the importance of math for their sense of who they are—e.g., “Thinking mathematically is an important part of who I am.” Cost was assessed using items that focused on students’ judgments about the amount of time and effort required to be successful in math—e.g., “Success in math requires that I give up other activities I enjoy.” All items were assessed using a 5-point Likert scale. All but two items were anchored in the middle and at the endpoints with the anchors: Not at all true for me, Somewhat true for me, Very true for me. The mean of the mean of each of the four value scales (utility, interest, attainment, and the reverse of cost) is used as an overall measure of task value, a practice commonly used when assessing task values in adolescents (Eccles, O’Neil, & Wigfield, 2005). The standardized factor loadings and internal consistencies for these constructs ranged from acceptable to good and are detailed in Table 3.

Predictor Measures

Eighth grade course placement

The change in students’ motivation specific to eighth grade course placement was estimated using an Algebra course dummy variable in regression analyses. Course placement was determined by which CST exam students took in the spring of eighth grade. Each middle school operated under a specific set of labeled courses making grouping across specific course placement difficult. For example, some schools enrolled students into either yearlong Algebra 1 or Pre-Algebra, while others enrolled students into either yearlong Algebra (i.e., Algebra 1P) or a two-year Algebra sequence (i.e., Algebra 1A and Algebra 1B). Students in Pre-Algebra or Algebra 1A were essentially exposed to a year of Pre-Algebra curriculum and were designated to take the General Mathematics CST in the spring of eighth grade. Students enrolled in Algebra 1 or Algebra 1P took the Algebra CST.

The CST exams cover the specific curriculum taught and were therefore used as a measure of course placement. Our study sample portrayed general alignment between the course and exam taken. Approximately 99% of the students in our study sample with valid course name data (N = 3,175 students) took the CST exam that aligned with the course they were enrolled in. Regression analyses were re-run using course names as identifiers for students placed in either Algebra or lower-level math courses and returned nearly identical results to the ones presented in the present study. This check for robustness confirms the reliability of using the CST as a proxy for course placement.

Control variables

Student-level covariates included in our analyses included race/ethnicity, gender, seventh grade standardized state math scores, free/reduced lunch status (used as a proxy for socioeconomic status), and English Learner (EL) status. Gender was a dummy variable, coded 1 for male and 0 for female. Ethnic categories were Hispanic, White, Vietnamese, and Other. Participation in the National School Lunch Program (NSLP) was coded 1 for yes and 0 for no. EL status was a dummy variable coded 1 for EL and 0 for non-EL. Lastly a cohort dummy was used to adjust for differences between students in the 2004-05 and 2005-06 cohorts.

Model

The conceptual model views motivation as a product of past levels of motivation and other determinants such as prior achievement, English language fluency, socioeconomic status, gender, and ethnicity. Using a lagged motivation model helps to control for omitted variable bias and with prior motivation controlled, the analysis amounts to a study of changes in motivation across the 1-year period (NICHD ECCRN & Duncan, 2003). Specifically, a primary goal of our analysis is to investigate the relation of eighth grade Algebra course placement and changes in students’ motivation over the course of eighth grade. For that reason, we assess changes in students’ motivational beliefs from the fall of eighth grade to the spring of eighth grade using measurements of students’ beliefs collected from students while they were enrolled in the course of interest. Thus, motivation of student i at the end of period t can be expressed as:

$${\mathit{Mot}}_{\mathit{it}}={\beta }_0+{\beta }_1{\mathit{Mot}}_{\mathit{it}-1}+{\beta }_2{\mathit{Ach}}_{\mathit{it}-1}+{\beta }_3{\mathit{Alg}}_{\mathit{it}}+\sum \begin{array}{c}R\hfill \\ j=1\hfill \end{array}{\beta }_j{}^{\mathrm{x}}\mathrm{X}_{\mathit{jit}-1}+{F\delta }_{s\left(i,s\right)}+e_{i,c}$$ (1)

In (1), Mot is a variable that represents each of the five measures examined in this study: mastery, performance-approach, performance-avoidance, self-efficacy, and task value. Mot_it and Mot_it−1 is student i’s motivational response at the fall and spring of eighth grade, respectively. Ach_it−1 is student i’s prior math achievement at time t−1 (seventh grade CST standardized score). Alg_it is a dummy variable for students placed in eighth grade Algebra and β₃ is the coefficient estimating the association of Algebra enrollment on student motivation in comparison with peers enrolled in general mathematics courses. X’s are characteristics such as gender, ethnicity, EL status, cohort, and NSLP status. Time-invariant school characteristics δs(i, s) were controlled with school fixed effects using Stata’s xtreg command (StataCorp, 2011), which helps to address biases that arise from the non-random assignment of students to schools (Carnoy, Kilpatrick, Schmidt, & Shavelson, 2007). This adjustment ensures that the estimated links among motivation, achievement, and course placement are based on within school variation in dependent and independent variables by considering each student’s deviation from the mean value of the variable of interest among students who share the same school. Observations of students who share a classroom are not independent of one another; thus, we cluster standard errors on classroom identification to account for the non-random assignment of students into classrooms. Multilevel modeling using Stata’s xtmixed command (StataCorp, 2011) and specifying school identification at Level 3 and classroom identification at Level 2 returned similar results, thus including a school fixed effect and a clustered standard error on classroom identification was deemed sufficient to account for the nested nature of our data. Lastly, to allow for comparability across the different units of measurement, the regression analysis was based on standardized achievement and motivation variables.

The second model used in our analyses is a moderated model, which uses an interaction between the Algebra course placement dummy and whether the student had high prior achievement (scored as Proficient or Advanced on the seventh grade CST math assessment) or low prior achievement (scored as Below Basic or Far Below Basic on the seventh grade CST math assessment).⁴ Here, motivation of student i at the end of period t can be expressed as:

$${\mathit{Mot}}_{\mathit{it}}={\beta }_0+{\beta }_1{\mathit{Mot}}_{\mathit{it}-1}+{\beta }_2{\mathit{Alg}}_{\mathit{it}}+{\beta }_3{\mathit{Alg}}_{\mathit{it}}\times {\mathit{HighAch}}_{\mathit{it}-1}+{\beta }_4{\mathit{Alg}}_{\mathit{it}}\times {\mathit{LowAch}}_{\mathit{it}-1}+\sum \begin{array}{c}R\hfill \\ j=1\hfill \end{array}{\beta }_j{}^{\mathrm{x}}\mathrm{X}_{\mathit{jit}-1}+{F\delta }_{s\left(i,s\right)}+e_{i,c}$$ (2)

In (2), we are interested in whether the association between eighth grade Algebra and motivation is different for different levels of prior achievement. A significant coefficient (β₃ or β₄) would indicate that students who had high prior achievement or low prior achievement experience changes in motivation that differ from the main association (β₂) experienced by students performing at the Basic level (referred to as average achieving students). For simplicity purposes results are discussed in terms of high-achieving students (students who scored at the Proficient or Advanced level on their seventh grade math CST) and low-achieving students (students who performed at the Below Basic or Far Below Basic level on their seventh grade math CST).

Results

Table 4 presents descriptive information on the motivation measures for prior (seventh grade) achievement bins by eighth grade mathematics course placement. In the fall of eighth grade, students in Algebra who had average prior achievement reported significantly higher mastery goals (p < 0.01) than peers in general mathematics courses. Descriptive trends in Table 4 show that the difference in mastery goals between general math and Algebra students are even larger for low prior achievers than for average prior achievers in the fall, but those trends are not statistical significant as a result of the smaller sample size for the low prior achievement group. Further previously high-achieving students in Algebra reported significantly higher mastery goals (p < 0.05), lower performance-avoidance goals (p < 0.05), and higher task value (p < 0.01) than peers in general mathematics courses. By the spring of eighth grade, previously average-performing students in Algebra report significantly lower self-efficacy (p < 0.001) and previously high-achieving students in Algebra report significantly higher mastery (p < 0.001) and task value (p < 0.01) than peers in general mathematics courses. In all, previously average-performing students in Algebra do not differ significantly on most motivational measures with the exception that these students begin Algebra with significantly higher mastery goals than peers in general math courses in the fall of eighth grade and differ significantly only on self-efficacy by the spring of eighth grade. By the spring, students in eighth grade Algebra have significantly lower self-efficacy than previously average-performing peers in general mathematics courses. Lastly, students across eighth grade math courses do not differ significantly in performance-avoidance goals with the exception that previously high-achieving students in Algebra begin with significantly lower performance-avoidance goals in the fall of eighth grade—in either the fall or spring of eighth grade, regardless of prior achievement.

Table 4.

Descriptive information on motivation measures for prior (7^th grade) achievement bins by eighth grade math course placement (N=3,306 students)

	General Math		Algebra
	mean	SD	mean	SD	p-value of difference
Motivational measures, Fall–Low prior achievement
Mastery	3.66	0.91	3.85	0.88	0.57
Performance approach	2.64	1.07	2.45	1.13	0.28
Performance avoidance	2.64	1.00	2.45	0.85	0.26
Self-Efficacy	3.05	0.86	2.94	0.89	0.43
Task value	3.33	0.59	3.24	0.67	0.37
Motivational measures, Fall–Average prior achievement
Mastery	3.72	0.92	3.81	0.88	0.01**
Performance approach	2.47	1.06	2.51	1.06	0.64
Performance avoidance	2.43	1.05	2.35	1.00	0.17
Self-Efficacy	3.59	0.79	3.31	0.84	0.14
Task value	3.47	0.60	3.50	0.63	0.04
Motivational measures, Fall–High prior achievement
Mastery	3.62	0.93	3.86	0.88	0.03*
Performance approach	2.47	1.06	2.41	1.04	0.44
Performance avoidance	2.46	1.00	2.28	1.00	0.04*
Self-Efficacy	3.22	0.85	3.65	0.83	0.33
Task value	3.40	0.63	3.61	0.66	0.01**
Motivational measures, Spring–Low prior achievement
Mastery	3.41	1.01	3.56	0.83	0.38
Performance approach	2.28	1.02	2.21	0.91	0.65
Performance avoidance	2.03	0.94	2.09	0.86	0.66
Self-Efficacy	2.97	0.92	2.83	0.93	0.34
Task value	3.23	0.61	3.13	0.74	0.27
Motivational measures, Spring–Average prior achievement
Mastery	3.42	1.05	3.49	0.94	0.09
Performance approach	2.10	0.94	2.11	0.94	0.77
Performance avoidance	1.87	0.91	1.96	0.91	0.05
Self-Efficacy	3.50	0.84	3.02	0.86	0.00**
Task value	3.28	0.66	3.22	0.66	0.17
Motivational measures, Spring–High prior achievement
Mastery	3.36	1.03	3.67	0.96	0.00**
Performance approach	2.14	0.97	2.13	0.96	0.61
Performance avoidance	1.84	0.85	1.87	0.89	0.99
Self-Efficacy	3.24	0.94	3.46	0.93	0.57
Task value	3.29	0.66	3.42	0.69	0.01**

Notes. Motivation scales = 1 – 5; Prior achievement bins: high prior achievement = Proficient or Advanced (math scale score range = 350-600); average prior achievement = Basic (math scale score range = 300-349); low prior achievement = Below Basic or Far Below Basic (math scale score range = 150-299).

^*p < 0.05,

^**p < 0.01,

^***p < 0.001

Achievement Goal Changes

Table 5 shows both the main associations and moderated model estimates of the relation between Algebra course placement and changes in students’ achievement goals. Models 1, 2, and 3 show the main associations, indicating that on average, students enrolled in Algebra reported a significant increase in performance-avoidance goals. Specifically, Model 3 shows that students in Algebra reported a .13 standard deviation (hereafter σ) increase in performance-avoidance goals as compared with peers enrolled in general mathematics courses.⁵

Table 5.

Standardized regression coefficients predicting students' achievement goals (N=3,306 students)

Dependent variable = students’ spring, 8th grade achievement goals
	Panel A. Direct Associations			Panel B. Moderated Associations
	(1)	(2)	(3)	(4)	(5)	(6)
	Mastery	Performance Approach	Performance Avoid	Mastery	Performance Approach	Performance Avoid
Algebra	0.03 (0.05)	−0.05 (0.05)	0.13 * (0.05)	0.02 (0.05)	−0.06 (0.06)	0.09 (0.06)
High prior achievement X Algebra				0.10 * (0.04)	0.09 * (0.04)	−0.02 (0.04)
Low prior achievement X Algebra				0.03 (0.13)	0.02 (0.14)	−0.18 (0.15)
Controls
Prior math achievement	0.07** (0.03)	0.01 (0.03)	−0.05 (0.02)
High prior math achievement				0.04 (0.05)	−0.04 (0.05)	0.04 (0.06)
Low prior math achievement				−0.02 (0.04)	0.04 (0.04)	0.11* (0.04)
Hispanic	0.05 (0.06)	−0.01 (0.05)	−0.09 (0.06)	0.04 (0.06)	−0.01 (0.05)	−0.10 (0.06)
Vietnamese	0.10 (0.07)	0.15* (0.07)	0.05 (0.07)	0.10 (0.07)	0.14* (0.07)	0.04 (0.07)
Other	0.15 (0.08)	−0.00 (0.06)	−0.13 (0.07)	0.15 (0.08)	−0.01 (0.06)	−0.13 (0.07)
English Learner	0.11** (0.04)	0.04 (0.03)	0.04 (0.03)	0.10** (0.04)	0.04 (0.03)	0.04 (0.03)
Free/reduced lunch	−0.02 (0.04)	0.03 (0.03)	0.02 (0.04)	−0.01 (0.04)	0.03 (0.03)	0.02 (0.04)
Male	−0.12*** (0.03)	0.05 (0.03)	0.11** (0.03)	−0.12*** (0.03)	0.05 (0.03)	0.11** (0.03)
Cohort dummy	0.03 (0.04)	0.10** (0.04)	−0.19*** (0.04)	0.03 (0.04)	0.10** (0.04)	−0.19*** (0.04)
Mastery, fall	0.54*** (0.02)			0.54*** (0.02)
Performance approach, fall		0.61*** (0.02)			0.61*** (0.02)
Performance avoid, fall			0.41*** (0.02)			0.41*** (0.02)
Constant	0.63*** (0.12)	0.04 (0.14)	−0.32 (0.35)	0.62*** (0.12)	0.03 (0.13)	−0.35 (0.35)
R 2	0.335	0.378	0.186	0.335	0.380	0.187
N	3062	3093	3068	3062	3093	3068

Note. Standard errors in parentheses; time-invariant school characteristics are controlled in the analysis with school “fixed effects”, which amounts to including dummy variables for all but one school (using Stata’s xtreg command). Fixed effects estimates are based on within-school variation in dependent and independent variables. Algebra is in reference to the base category consisting of eighth grade students enrolled in General Mathematics. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP) participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.001.

Models 4, 5, and 6 show the association between Algebra course placement and changes in students’ achievement goals as moderated by students’ prior (seventh grade) achievement group. In Model 4, the regression coefficient associated with the Alg_it predictor, 0.02, is the association between eighth grade Algebra course placement and students’ mastery goals for students that had an average prior math achievement (e.g., scored Basic on the seventh grade math CST) score. The significant coefficient associated with the interaction term HighAch_it−1 × Alg_it, .10, however, shows that the association between Algebra course placement and students’ mastery goals is moderated by whether or not students’ had high prior math achievement. Students in Algebra who had high prior math achievement were associated with a .12σ (0.10 + 0.02 = 0.12) increase in mastery goals relative to previously high achieving peers in General Mathematics courses.

In Model 5, the regression coefficient associated with the Alg_it predictor, −0.06, represents the association between eighth grade Algebra course placement and students’ performance-approach goals for students who had average math achievement prior to Algebra course placement. The significant coefficient associated with the interaction term HighAch_it−1 × Alg_it, .09, shows that the association between students’ performance-approach goals and Algebra course placement is moderated by whether or not students’ had high prior math achievement. Specifically, previously high-achieving students in Algebra reported a .03σ (−0.06 + 0.09 = 0.03) increase in performance approach goals as compared with high achieving peers in General Mathematics courses.

Expectancy and Value Changes

Table 6 shows the main associations and moderated model estimates of Algebra course placement and changes in students’ expectancy and value beliefs. Model 1 shows that students in Algebra reported a significant decrease (.26σ) in their sense of efficacy as compared with their peers in general mathematics courses. Model 2 also shows that students in Algebra, on average, reported a significantly greater decline (.14σ) in their task value than their peers in general mathematics courses.

Table 6.

Standardized regression coefficients predicting students’ efficacy and value (N=3,306)

Dependent variable = students’ spring, 8th grade self-efficacy and value
	Panel 1. Direct Associations		Panel B. Moderated Associations
	(1)	(2)	(3)	(4)
	Self-Efficacy	Task Value	Self-Efficacy	Task Value
Algebra	−0.26*** (0.04)	−0.14** (0.05)	−0.31*** (0.05)	−0.18*** (0.05)
High prior achievement X Algebra			0.26*** (0.03)	0.17*** (0.04)
Low prior achievement X Algebra			−0.11 (0.10)	−0.04 (0.11)
Controls
Prior math achievement	0.20*** (0.02)	0.09*** (0.02)
High prior math achievement			0.02 (0.04)	−0.00 (0.05)
Low prior math achievement			−0.20*** (0.04)	−0.04 (0.04)
Hispanic	−0.05 (0.06)	0.01 (0.06)	−0.04 (0.06)	0.01 (0.06)
Vietnamese	−0.01 (0.07)	0.08 (0.07)	−0.01 (0.07)	0.06 (0.07)
Other	0.04 (0.08)	0.08 (0.07)	0.04 (0.08)	0.08 (0.07)
English Learner	0.07 (0.04)	0.12*** (0.03)	0.06 (0.04)	0.12*** (0.03)
Free/reduced lunch	−0.04 (0.04)	0.02 (0.03)	−0.04 (0.04)	0.02 (0.03)
Male	0.05 (0.03)	−0.12*** (0.03)	0.05 (0.03)	−0.12*** (0.03)
Cohort dummy	0.02 (0.04)	0.08* (0.04)	0.02 (0.04)	0.07 (0.04)
Self-efficacy, fall	0.53*** (0.02)		0.53*** (0.02)
Task value, fall		0.61*** (0.01)		0.61*** (0.02)
Constant	0.79*** (0.16)	0.48*** (0.08)	0.83*** (0.14)	0.49*** (0.09)
R 2	0.354	0.409	0.355	0.411
N	3,100	3,106	3,100	3,106

Note. Standard errors in parentheses; time-invariant school characteristics are controlled in the analysis with school “fixed effects”, which amounts to including dummy variables for all but one school (using Stata’s xtreg command). Fixed effects estimates are based on within-school variation in dependent and independent variables. Algebra is in reference to the base category consisting of eighth grade students enrolled in General Mathematics. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP) participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.001.

Models 3 and 4 show the moderated association of Algebra course placement and students’ academic self-efficacy and task value. In Model 3, the regression coefficient associated with the Alg_it predictor, −.31, is the association between eighth grade Algebra and students’ efficacy for previously average-achieving students. These students reported a significantly greater decline (.31σ) in their sense of efficacy than their peers in general mathematics courses. The significant coefficient associated with the interaction term HighAch_it−1 × Alg_it, .26, shows that the association between eighth grade Algebra and students’ efficacy is moderated by whether or not students’ had high prior math achievement. Students with high achievement prior to eighth grade Algebra course placement reported a .05σ (−0.31 + 0.26 = −0.05) decline in self-efficacy as compared with previously high achieving peers in General Mathematics courses.

In Model 4, the regression coefficient associated with the Alg_it predictor (−.18) is the association between eighth grade Algebra and students’ task value for previously average-achieving students placed in eighth grade Algebra. These students experienced a statistically significant .18σ decrease in task value beliefs as compared with their peers in general mathematics courses. The significant coefficient associated with the interaction term HighAch_it−1 × Alg_it, .17, shows that the association between eighth grade Algebra and students’ task value is moderated by whether or not students’ had high prior math achievement. Specifically, students with high prior achievement experienced a −.01σ (−0.18 + 0.17 = −0.01) decline in task value as compared with previously high-achieving performing peers in General Mathematics courses. The decline in task value that is associated with students placed in eighth grade Algebra is almost entirely attenuated for students with high prior achievement in seventh grade.

Testing the robustness of self-efficacy results. The finding that Algebra course placement relates with declines in student self-efficacy is in accordance with the big-fish-little-pond effect (BFLPE) model, which posits that students compare their own academic ability with the abilities of their classmates and use this comparison as a basis for forming their own academic self-concept beliefs (Marsh, 1987). In essence, students attending schools where the average ability levels of other students is high will have lower academic self-concepts compared to equally able students attending school where the average ability is low. Extending this theory to hypothesize at the classroom level, the deleterious changes in students’ expectancy beliefs presented in Table 6 may be in part due to equally able students lowering their academic self-concept beliefs after comparing themselves to more able students. Drawing on Eccles et al.’s (1983) expectancy-value framework to characterize students’ math self-concept beliefs, we examine a test of robustness to determine whether students’ relative standing among peers in middle school math classrooms accounts for a significant amount of change in efficacy beliefs over the course of eighth grade, regardless of Algebra course placement. Appendix B presents the extended analyses incorporating both the individual (e.g., student) and group level (class-average ability) to assess the contextual effects of group level ability on student beliefs. Findings indicate that students placed in eighth grade Algebra experience a significant decline in self-efficacy relative to peers placed in general mathematics courses, net of the class average predicting this change. This finding indicates that while the BFLPE may partially (and insignificantly) explain the decline in self-efficacy found amongst students placed in Algebra, it does not explain the full relation between Algebra course placement and self-efficacy. After controlling for class average, students placed in Algebra experience a significant decline in self-efficacy relative to peers placed in general mathematics classes, suggesting our results indicating Algebra course placement, regardless of changes in relative class standing, is associated with significant declines in academic self-efficacy.

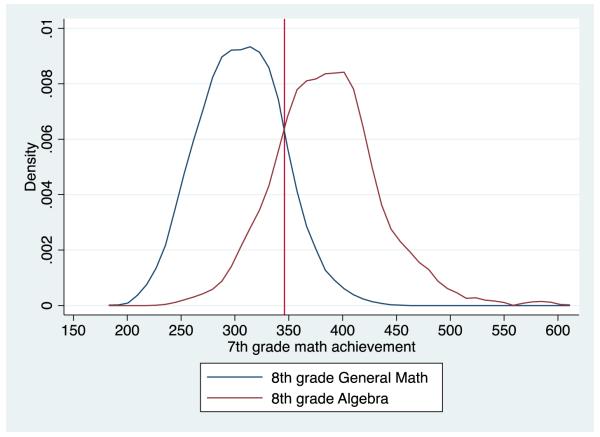
Testing the robustness of results using a reduced sample of students in the overlapping portions of the achievement distribution. A constrained analysis utilizing an area of common support, as shown in the achievement distribution illustrated in Figure 1, was conducted as a robustness check of the main results reported. The constrained analyses using a sub-sample of students representing the overlapping portions of the achievement distribution shown in Figure 1—students in General Math with a prior (7^th grade) CST score of 346 or higher and students in Algebra with a prior (7^th grade) CST score of 346 or lower—improves the comparability of General Math and Algebra track students. Descriptive information and results are presented in Appendix C. Table 1b presents descriptive information for the sub-sample of 529 students used in analysis and t-tests showed minimal differences between the sub-sample and study sample presented in Table 1. Table 6d presents regression coefficients predicting students’ achievement goals, expectancy, and value. Results show coefficients predicting students’ achievement goals in the same direction as reported above, though not statistically significant. Results show coefficients predicting statistically significant decreases in self-efficacy and task value for students in Algebra relative to peers in General Math courses, findings in line with the reported results above.

Discussion

To our knowledge, this is the first study to reveal information about the association between Algebra course placement and changes in students’ motivation. All research to date examining the effects, influences, and associations of Algebra course placement on student outcomes has focused largely on student cognitive and achievement outcomes (for a review, see Stein et al., 2011; Domina, 2014). There is a need for research that examines outcomes such as student motivation given its influence on cognitive and achievement outcomes.

The current study examines changes in achievement goals, self-efficacy, and task value for students placed in eighth grade Algebra relative to peers placed in lower-level eighth grade general mathematics courses. Students placed in Algebra reported decreases in both self-efficacy and task value as compared with peers placed in general mathematics course, a finding that is partially in agreement with our hypotheses (H1 and H2), which predicted a change in this direction for previously low achieving students placed in Algebra. Thus, we accept these hypotheses and determine that previously average performing students also experience a decline in self-efficacy and task value. Contrary to our hypothesis (H3) previously high achieving students did not experience an increase in self-efficacy and task value—however, these declines were attenuated for previously high-achieving students placed in Algebra. Partially in line with our hypothesis (H5) students in Algebra reported higher performance-avoidance goals relative to peers in eighth grade general mathematics courses. However, our hypotheses that this would occur only for low achieving student was not supported. Contrary to our hypothesis, the association with performance-avoidance goals was not moderated by prior math achievement, such that students with high prior achievement were not less likely to report higher performance-avoidance goals than students with average or low prior achievement. Therefore, we partially accept this hypothesis and determine that all students in our study sample experienced an increase in performance-avoid goals. Lastly, in line with our hypothesis (H6), previously high-achieving students placed in Algebra reported experiencing higher mastery goals and performance-approach goals relative to previously average- and low-achieving peers placed in Algebra. However, previously high achieving students did not demonstrate a decrease in these goals, as expected.

These findings, taken together, characterize an overall decline in students’ motivation for mathematics for previously average- and low-performing students placed in eighth grade Algebra. This is a concern given that increases in mastery goal orientations, expectations of success (efficacy), and task value are related to higher achievement, educational attainment, effort, and engagement (Rosen, Glennie, Dalton, & Bozick, 2010). Further, mastery goals, self-efficacy, and task value beliefs associate positively with standardized math achievement outcomes for students in our study sample (Appendix D), suggesting that the declines in these motivational beliefs may be associated with declines on students’ proximal achievement outcomes in mathematics. Given that our results are correlational, the direction of causality cannot be determined however. Previous research on motivation and achievement suggest a bidirectional relation in which changes in goals and changes in achievement are reciprocally linked (Zimmerman, 1989; Zimmerman, 2011). Although the CST scores did not come until after students already reported their spring motivation it can be argued that the achievement in the classroom prior to the CST could have been impacted by student motivation and that students’ CST scores serve as an indicator of student math achievement during the school year.

Students’ decline in task value beliefs are of particular concern given that the importance (value) that students give to a domain (e.g., math, science, and English) early in their academic careers relates significantly to the number of classes that students take in that domain in high school (Durik, Vida, & Eccles, 2006; Simpkins, Davis-Kean, & Eccles, 2006). Declines in students’ task value for mathematics may partially explain the lack of retention in advanced math courses. The cultivation of efficacy and value beliefs is critical to students’ success in Algebra and subsequent decisions to pursue advanced mathematical learning. The deterioration of these beliefs may hinder the growth of a STEM workforce.

In terms of achievement goals, students in eighth grade Algebra have relatively higher performance-avoidance goals—goals that have robust empirical links to negative learning and achievement outcomes (for review, see Hulleman, Schrager, Bogmann, Harackierwicz, 2010). Lastly, previously high-achieving students placed in eighth grade Algebra have relatively higher mastery and performance-approach goals than previously average- or low-achieving achieving peers in Algebra as well as peers placed in general mathematics courses. There has been support that performance-approach goals can be adaptive when mastery goals are also high (Harackiewicz et al., 2002; Midgley et al., 2001).⁶

Multiple Interpretations of Results and Instructional Implications

Several interpretations are possible for our results. The motivational declines may have resulted from students being placed in Algebra without adequate preparation. An alternative explanation is that the negative motivational associations of taking Algebra that previously low- and average-achieving students reported may have less to do with the Algebra specifically but more to do with the instructional quality. Though our dataset does not include instructional quality, another research team that also found negative effects of early exposure to Algebra explored the possibility that the district’s need for additional teaching support for Algebra courses caused it to place less qualified teachers in those classrooms (Clotfelter, Ladd, & Vigdor, 2012). The authors, however, found that weaker teacher credentials did not explain the association between Algebra placement and lower achievement, suggesting that the decline may not be a result of the difference in teacher quality.

Beyond teacher credentials, the measure of instructional quality takes into account a host of other variables. In a five-year study with high school students at different schools, Boaler and Staples (2008) found that social awareness and cultural sensitivity are critical factors for influencing student participation and academic success. Their primary case study was based on a school that successfully placed students, of significant ethnic and economic diversity, in mixed-ability math courses. More students in this school took advanced high school math courses and reported intending to continue taking math in college when compared with better-prepared students in schools with more traditional learning environments. Findings showed student success was linked to classes that valued multiple dimensions of math, such as through a task that had an open set of requirements that provided students several ways to contribute and succeed. The team also found that classrooms that developed a culture of having students justify their answers were also more successful academically. Future research can focus on instructional differences in eighth grade mathematics classrooms and examine how they impact student motivation to inform educators on how programmatic changes can attenuate adolescent motivational decline in Algebra classes.

To ameliorate declines in students’ motivation for students placed in eighth grade Algebra, policy makers, administrators, and educators can consider implementing teaching practices that include multidimensional activities and student justification. Creating a classroom climate in which help seeking and justification is encouraged has consequences for the entire class and can especially benefit the increasingly heterogeneous Algebra classes as they become less selective. The change in group composition of math ability levels that results from the push for Algebra for all has implications for motivation. For example, high achieving secondary school students reported lower collective efficacy of the group’s abilities than self-efficacy of one’s personal abilities when group processes were of low quality (Cheng, Lam, & Chan, 2008). However, when group processes were of high quality, both low and high achievers reported higher collective efficacy than self-efficacy. Group dynamics while learning therefore can impact student motivation, and in ongoing research, we are exploring whether the greater difference in ability levels in Algebra could potentially be part of the explanation for the motivational declines within students. Lastly, there has been evidence that extended learning time in Algebra boosts achievement and readiness for course content (e.g., Kemple, Herlihy, & Smith; 2005; Nomi & Allensworth, 2009), thus offering extended learning time for previously average- and low-performing students might also remediate student experiences in Algebra.

Policy Implications

The newly-adopted Common Core State Standards recommends Pre-Algebra in eighth grade and Algebra in ninth grade, which may lead to the eventual deceleration of eighth grade Algebra trends. In the meantime, discussion regarding Algebra policies can consider refocused goals and transition from maintaining an objective for a de-tracked, universal mathematics curriculum to goals of preparing all students in all tracks to participate, and succeed in, Algebra early enough to afford them the opportunity to reach higher-level mathematics. Further, the de-tracking goals these policies set out to accomplish in the first place have not been met as new course placement norms have gradually occurred. Since taking Algebra in the eighth grade became the new normal, gifted students began taking Algebra in seventh grade (Loveless, 2013). For example, in California, 8.1% (nearly 38,000 students) took the Algebra end of the course exam in 2012. Essentially, striving for a curriculum for all has merely shifted up the timeline of when students take Algebra. Instead, while amidst the current state of accelerated enrollment in the course, schools can consider working towards incorporating students’ Algebra readiness into their Algebra course placement policies. Progress towards this, and ultimately, away from universal course placement policies, can improve students’ experiences in Algebra and evade motivational decline in mathematics.

Advantages and Limitations of Study Logistics

The district represented by our study sample serves a population of minority students of primarily Hispanic and Vietnamese origins, almost half of which are English language learners, and most of which are socioeconomically disadvantaged. Lack of STEM engagement is particularly problematic for these underrepresented minority students. Hispanics make up 17% of the U.S. population, are our fastest growing ethnic group, and are the most likely group to drop out of the STEM pipeline before reaching and after enrolling in college (Chapman, Laird, & KewalRamani, 2010). Further, Vietnamese educational attainment is among the lowest of Asian Americans with 72% graduating from high school and only 27% finishing college (Asian American Center for Advancing Justice, 2011). As such, our unique study sample offers information that can be used to more accurately consider the potential motivational consequences of intensifying middle school mathematics curriculum for these understudied student populations.

The district from which our sample was taken shows eighth grade Algebra enrollment trends similar to those found nationwide (Domina et al., 2014), enrolling more than 36% of eighth grade students in Algebra or higher in 2004-05 and increasing enrollment each year to reach over 84% of eighth grade students in Algebra or higher in 2007-08; however, the lack of a universal policy does not allow for a causal analysis of effects on student motivation. Rather the findings presented here are associational and can be used to deliver information of the potential direction of effects that universal course placement policy can have on student motivation. Further, our study uses CST scores as the sole measure of achievement but research has suggested that standardized exams on the math portion can include cultural and linguistic barriers that impact English language learners (Boaler & Staples, 2008). Given the large percentage of English language learners in our sample, this is a potential limitation in using standardized test scores to measure math achievement.

Conclusion

Findings from this study suggest that eighth grade universal Algebra placement may not be the panacea for increasing the on-flow and retention in the STEM pipeline and that instead, interventions are needed towards preparing all students to succeed in Algebra rather than mandating them in. Evidence from this study suggests that placing low-performing students in mathematics courses for which they may not be ready can lead to reduced self-efficacy and task value in mathematics and heightened performance-avoidance goals. These changes occurring at the developmentally sensitive time of early adolescence can contribute to the downward spiraling trend between students and their motivation towards mathematics (Gottfried, Fleming, & Gottfried, 2001). Because of Algebra’s foundational place as a gatekeeper to advanced math and science learning, these adverse motivational consequences can cripple students’ before they can climb up the STEM ladder, essentially blocking the pathways that universal Algebra policy had aimed to remedy in the first place. Future directions must work to pair course placement policies and resources for students who may need these adjustments to succeed. Further, there is a need for research to connect these efforts to achievement and student motivational outcomes. These efforts can subsequently remediate adolescent motivational decline, particularly in mathematics, which will ultimately improve student access and choice to persist in mathematics and its related career paths.

Appendix A. Analyses Using a Continuous Prior Math Achievement X Algebra Course Placement Interaction

Table 5b.

Standardized regression coefficients predicting students’ achievement goals (N=3,306 students)

Dependent variable = students’ spring, 8th grade achievement goals
	Panel A. Direct Associations			Panel B. Moderated Associations
	(1)	(2)	(3)	(4)	(5)	(6)
	Mastery	Performance Approach	Performance Avoid	Mastery	Performance Approach	Performance Avoid
Algebra	0.03 (0.05)	−0.05 (0.05)	0.13* (0.05)	0.03 (0.05)	−0.06 (0.05)	0.12* (0.05)
Algebra X Prior math achievement				0.08 (0.05)	0.10* (0.04)	0.04 (0.05)
Controls
Prior math achievement	0.07** (0.03)	0.01 (0.03)	−0.04 (0.02)	0.04 (0.04)	−0.04 (0.03)	−0.06 (0.04)
Hispanic	0.04 (0.06)	−0.01 (0.05)	−0.09 (0.06)	0.04 (0.06)	−0.01 (0.05)	−0.09 (0.06)
Vietnamese	0.10 (0.07)	0.15* (0.07)	0.05 (0.07)	0.09 (0.07)	0.14* (0.07)	0.05 (0.07)
Other	0.15 (0.08)	−0.00 (0.06)	−0.13 (0.07)	0.15 (0.08)	−0.01 (0.06)	−0.13 (0.07)
English Learner	0.11** (0.04)	0.04 (0.03)	0.04 (0.03)	0.10** (0.04)	0.04 (0.03)	0.04 (0.03)
Free/reduced lunch	−0.02 (0.04)	0.03 (0.03)	0.02 (0.05)	−0.02 (0.04)	0.03 (0.03)	0.02 (0.05)
Male	−0.11*** (0.03)	0.05 (0.03)	0.11** (0.03)	−0.11*** (0.03)	0.05 (0.03)	0.11** (0.03)
Cohort dummy	0.03 (0.04)	0.10** (0.04)	−0.19*** (0.04)	0.03 (0.04)	0.10* (0.04)	−0.19*** (0.04)
Mastery, fall	0.55*** (0.02)			0.54*** (0.02)
Performance approach, fall		0.61*** (0.02)			0.61*** (0.02)
Performance avoid, fall			0.41*** (0.02)			0.41*** (0.02)
Constant	0.64*** (0.12)	0.04 (0.13)	−0.31 (0.35)	0.63*** (0.12)	0.03 (0.13)	−0.31 (0.36)
R2	0.335	0.379	0.186	0.336	0.380	0.187
N	3,061	3,092	3,065	3,061	3,092	3,065

Note. Standard errors in parentheses; time-invariant school characteristics are controlled in the analysis with school “fixed effects”, which amounts to including dummy variables for all but one school (using Stata’s xtreg command). Fixed effects estimates are based on within-school variation in dependent and independent variables. Algebra is in reference to the base category consisting of eighth grade students enrolled in general mathematics courses. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP) participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.001

Table 6b.

Standardized regression coefficients predicting students’ efficacy and value (N=3,306)

Dependent variable = students’ spring, 8th grade self-efficacy and value
	Panel 1. Direct Associations		Panel B. Moderated Associations
	(1)	(2)	(3)	(4)
	Self-Efficacy	Task Value	Self-Efficacy	Task Value
Algebra	−0.26*** (0.04)	−0.14** (0.05)	−0.27*** (0.04)	−0.16*** (0.04)
Algebra X Prior math achievement			0.09* (0.04)	0.13** (0.04)
Controls
Prior math achievement	0.20*** (0.02)	0.09*** (0.03)	0.16*** (0.03)	0.03 (0.03)
Hispanic	−0.05 (0.06)	0.01 (0.06)	−0.05 (0.06)	0.01 (0.06)
Vietnamese	−0.01 (0.07)	0.07 (0.07)	−0.02 (0.07)	0.06 (0.07)
Other	0.04 (0.08)	0.08 (0.07)	0.03 (0.08)	0.07 (0.07)
English Learner	0.07 (0.04)	0.12*** (0.03)	0.07 (0.04)	0.12*** (0.03)
Free/reduced lunch	−0.04 (0.04)	0.02 (0.03)	−0.04 (0.04)	0.02 (0.03)
Male	0.05 (0.03)	−0.11*** (0.03)	0.05 (0.03)	−0.11*** (0.03)
Cohort dummy	0.02 (0.04)	0.08* (0.04)	0.02 (0.04)	0.07 (0.04)
Self-efficacy, fall	0.53*** (0.02)		0.53*** (0.02)
Task value, fall		0.61*** (0.02)		0.61*** (0.02)
Constant	0.79*** (0.16)	0.48*** (0.08)	0.78*** (0.15)	0.48*** (0.09)
R2	0.353	0.408	0.354	0.410
N	3,099	3,105	3,099	3,105

Note. Standard errors in parentheses; time-invariant school characteristics are controlled in the analysis with school “fixed effects”, which amounts to including dummy variables for all but one school (using Stata’s xtreg command). Fixed effects estimates are based on within-school variation in dependent and independent variables. Algebra is in reference to the base category consisting of eighth grade students enrolled in general mathematics courses. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP) participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.001

Appendix B. Big-Fish-Little Pond Effect Robustness Check for Self-Efficacy Results

Table 6c.

Standardized regression coefficients predicting students’ self-efficacy in the spring of 8^th grade (N=3,306 students)

Dependent variable = self-efficacy, Spring of 8th grade
	(1)	(2)	(3)
Class average	−0.15*** (0.03)		−0.09 (0.05)
Algebra		−0.26*** (0.04)	−0.15* (0.07)
Controls
Self-efficacy, fall of 8th grade	0.53*** (0.02)	0.53*** (0.02)	0.53*** (0.02)
Prior math achievement (7th grade)	0.22*** (0.02)	0.20*** (0.02)	0.22*** (0.02)
Male	0.05 (0.03)	0.05 (0.03)	0.05 (0.03)
Hispanic	−0.05 (0.06)	−0.04 (0.06)	−0.05 (0.06)
Vietnamese	0.00 (0.07)	−0.01 (0.07)	−0.01 (0.07)
Other	0.05 (0.08)	0.04 (0.08)	0.05 (0.08)
Free/reduced lunch status	−0.04 (0.04)	−0.04 (0.04)	−0.04 (0.04)
English Learner status	0.07 (0.04)	0.07 (0.04)	0.07 (0.04)
Cohort dummy	0.01 (0.04)	0.02 (0.04)	0.02 (0.04)
Geometry		−0.17 (0.10)	0.02 (0.15)
Constant	0.95*** (0.14)	0.78*** (0.16)	0.78*** (0.15)
R2	0.35	0.35	0.36
Observations	3,095	3,095	3,095

Note. Standard errors in parentheses; time-invariant school characteristics are controlled in the analysis with school “fixed effects”, which amounts to including dummy variables for all but one school (using Stata’s xtreg command). Algebra indicates student math course placement in 8^th grade and is in reference to the base category consisting of eighth grade students enrolled in general mathematics courses. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP) participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.00

Appendix C. Constrained Analysis to Check for Robustness of Results

Figure 1b.

Eighth Grade Math Course Placement by Prior Mathematics Achievement with Reference Line

Kernel density graph illustrating the distribution of prior math achievement (seventh grade CST math score) by eighth grade math course placement (N=3,306 students). Eighth grade math course placement is indicated by the California Standardized Test (CST) exam taken by student in the spring of eighth grade. CST math scale score range = 150 – 600, 150-256 = Far Below Basic, 257-299 = Below Basic, 300-349 = Basic, 350-413 = Proficient, 414-600 = Advanced. Reference line indicated at X=346 (prior CST score of 346).

Table 1b.

Descriptive statistics for overlap only sample (N=529 students)

	obs.	mean/%	SD	Min.	Max.	P-value of difference from study sample (N=3,306 students)
Gender
Male	268	50.7%	0.50	0.00	1.00	0.20
Race/ethnicity
Hispanic	364	68.8%	0.46	0.00	1.00	0.45
White	60	11.3%	0.32	0.00	1.00	0.23
Viet	67	12.7%	0.33	0.00	1.00	0.27
Other	38	7.2%	0.26	0.00	1.00	0.25
Free/reduced lunch (NSLP) and English Learner (EL) status
NSLP status	400	75.6%	0.43	0.00	1.00	0.63
EL status	232	43.9%	0.50	0.00	1.00	0.03*
Prior math achievement (CST scaled score)
7th grade	529	345	30.5	243	445	0.05*
8th grade motivational measures, Fall
Mastery	500	3.75	0.93	1.00	5.00	0.74
Performance approach	502	2.49	1.08	1.00	5.00	0.81
Performance avoid	490	2.37	1.01	1.00	5.00	0.15
Self-efficacy	503	3.38	0.86	1.00	5.00	0.32
Task value	503	3.46	0.63	1.23	5.00	0.94
8th grade motivational measures, Spring
Mastery	526	3.43	1.02	1.00	5.00	0.09
Performance approach	527	2.12	0.96	1.00	5.00	0.13
Performance avoid	529	1.90	0.91	1.00	5.00	0.69
Self-efficacy	527	3.25	0.92	1.00	5.00	0.90
Task value	529	3.25	0.68	1.42	4.92	0.02*
8th grade math course
General Math	273	0.52	0.50	0.00	1.00	0.00***
Algebra	256	0.48	0.50	0.00	1.00	0.00***

Note. Motivation scales = 1 – 5; Math scale score range = 150 – 600, 150-256 = Far Below Basic, 257-299 = Below Basic, 300-349 = Basic, 350-413 = Proficient, 414-600 = Advanced; Free/reduced lunch (NSLP) and English Learner (EL) status scale = 0-1 (1 = yes, 0 = no). Prior achievement bins: high achievement = Proficient or Advanced; average achievement = Basic; low achievement = Below Basic or Far Below Basic.

Table 6d.

Standardized regression coefficients predicting students’ achievement goals, efficacy, and value (N=529 students)

Dependent variable = students’ spring, 8th grade achievement goals, efficacy, and value
	(1)	(2)	(3)	(4)	(5)
	Mastery	Performance Approach	Performance Avoid	Self- Efficacy	Task Value
Algebra	0.05 (0.10)	−0.15 (0.10)	0.16 (0.13)	−0.58*** (0.12)	−0.41*** (0.11)
Controls
Prior math achievement	0.05 (0.12)	−0.10 (0.11)	−0.05 (0.14)	−0.15 (0.13)	−0.19 (0.11)
Hispanic	−0.00 (0.10)	−0.17 (0.12)	0.05 (0.14)	−0.02 (0.12)	−0.17 (0.11)
Vietnamese	0.07 (0.14)	−0.07 (0.16)	0.04 (0.17)	−0.02 (0.15)	−0.06 (0.14)
Other	0.24 (0.16)	0.04 (0.17)	0.02 (0.19)	0.27 (0.16)	0.08 (0.14)
English Learner	0.03 (0.08)	0.06 (0.08)	−0.05 (0.09)	0.12 (0.09)	0.13 (0.09)
Free/reduced lunch	−0.16 (0.10)	0.05 (0.09)	0.04 (0.11)	−0.08 (0.09)	−0.05 (0.09)
Male	−0.10 (0.08)	0.04 (0.07)	0.09 (0.09)	−0.00 (0.08)	−0.16* (0.08)
Cohort dummy	−0.06 (0.08)	0.10 (0.07)	−0.09 (0.10)	−0.02 (0.08)	0.05 (0.09)
Mastery, fall	0.60*** (0.04)
Performance approach, fall		0.62*** (0.04)
Performance avoid, fall			0.38*** (0.05)
Self-efficacy, fall				0.49*** (0.03)
Task value, fall					0.68*** (0.03)
Constant	0.02 (0.15)	0.02 (0.16)	−0.24 (0.19)	0.34* (0.16)	0.36 (0.15)
R2	0.37	0.41	0.16	0.34	0.46
N	498	500	490	501	503

Note. Standard errors in parentheses; time-invariant school characteristics are controlled in the analysis with school “fixed effects”, which amounts to including dummy variables for all but one school (using Stata’s xtreg command). Fixed effects estimates are based on within-school variation in dependent and independent variables. Algebra is in reference to the base category consisting of eighth grade students enrolled in General Mathematics. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP)participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.001.

Appendix D. Extended Analyses: Relations between Motivation Constructs on Achievement

A natural question that arises from the results of this study asks how students’ changes in achievement goals, expectancy, and value associate with subsequent achievement in mathematics in eighth grade. Thus, a follow up analysis was conducted to highlight the importance of our findings. A simple change model using change in students’ motivation as a predictor for mathematics achievement revealed that changes in students’ mastery goals, self-efficacy, and task value significantly predict achievement in mathematics. Table 7 presents standardized regression results for students’ achievement goals, expectancy, and value predicting students’ mathematics achievement in eighth grade. With all variables standardized, these coefficients represent a measure of effect size. Model 1 indicates that students who experience a 1σ increase in mastery goals from the fall of eighth grade to the spring of eighth grade have, on average, a 0.02σ higher mathematics achievement relative to peers who did not experience a change in their mastery goals over the course of eighth grade. This finding is in line with Keys, Conley, Duncan, and Domina’s (2012) study, which used CAMP-Math data to determine that mastery goal orientations in seventh and eighth grade students consistently and significantly predicted math achievement. Models 2 and 3 indicate that a change in students’ performance goals (both approach and avoidance) do not significantly predict a change in mathematics achievement. Model 4 indicates that students who experience a 1σ increase in self-efficacy have, on average, a 0.07σ higher mathematics achievement and Model 5 indicates that students who experience a 1σ increase in task value beliefs have, on average, a 0.06σ higher mathematics achievement. Conversely, a 1σ decrease in students’ mastery goals, self-efficacy, or task value results in a 0.02σ, 0.07σ, or 0.06σ decrease in mathematics achievement by the spring of eighth grade, respectively. In application to our study these findings show that, though the effects are small, student level declines in self-efficacy and task value for students placed in eighth grade Algebra may be concerning as they relate to lowered achievement levels in mathematics.

Extended Analyses

The conceptual model of achievement that guides our empirical analysis view mathematics achievement as a product of past levels of student motivation and other determinants. Suppose we have two waves of motivational data (1 and 2) and that the achievement of student i at the end of wave 2 can be expressed as:

$${\mathit{Ach}}_{2i}={\beta }_0+{\beta }_1\Delta {\mathit{Mot}}_i+\sum \begin{array}{c}R\hfill \\ j=1\hfill \end{array}{\beta }_j{}^{\mathrm{x}}\mathrm{X}_{\mathit{jit}-1}+e_{2i}$$ (1)

In (1), Δ Mot_i is the change in students’ motivation for each of the five constructs measured (mastery, performance approach, performance avoidance, self-efficacy, and task value) over the course of eighth grade. To calculate students’ change in motivation we subtract a students’ motivation at wave 1 (in the fall of eighth grade) from students’ motivation at wave 2 (in the spring of eighth grade). X’s are other determinants of achievement such as students’ prior mathematics achievement, eighth grade course placement, gender, ethnicity, EL status, NSLP status, and a classroom fixed effects using Stata’s xtreg command (StataCorp, 2011). In this simple change model we interpret β₁ as relating the change in students’ motivation from wave 1 to wave 2 to achievement at wave 2. Table 5 presents the regression results for goal orientations, expectancy, and value predicting mathematics achievement.

Table 7.

Simple change model with standardized regression coefficients predicting students’ 8^th grade mathematics achievement (N=3,306 students)

Dependent variable = 8th grade math achievement
	(1)	(2)	(3)	(4)	(5)
Δ Mastery	0.02* (0.01)
Δ Performance approach		0.02 (0.01)
Δ Performance avoidance			−0.02 (0.01)
Δ Self-efficacy				0.07*** (0.01)
Δ Task value					0.06*** (0.01)
Controls
Algebra	−0.54*** (0.12)	−0.54*** (0.12)	−0.53*** (0.10)	−0.55*** (0.12)	−0.55*** (0.12)
Prior achievement	0.77*** (0.02)	0.78*** (0.02)	0.76*** (0.02)	0.77*** (0.02)	0.77*** (0.02)
Hispanic	−0.01 (0.04)	−0.00 (0.04)	−0.02 (0.04)	−0.00 (0.04)	−0.01 (0.04)
Vietnamese	0.25*** (0.05)	0.24*** (0.05)	0.27*** (0.05)	0.24*** (0.05)	0.24*** (0.05)
Other	0.10 (0.06)	0.11 (0.05)	0.11* (0.05)	0.10 (0.05)	0.10 (0.05)
English Learner (EL)	−0.00 (0.03)	−0.00 (0.03)	−0.02 (0.03)	−0.00 (0.03)	−0.00 (0.03)
Free/reduced lunch (NSLP)	−0.00 (0.03)	−0.00 (0.03)	0.00 (0.03)	0.00 (0.03)	−0.00 (0.03)
Male	−0.00 (0.02)	−0.00 (0.02)	0.02 (0.02)	−0.00 (0.02)	0.00 (0.02)
Constant	0.19** (0.06)	0.19** (0.06)	0.19** (0.06)	0.19** (0.06)	0.19** (0.06)
R2	0.41	0.41	0.43	0.42	0.42
N	3,059	3,089	3,064	3,096	3,102

Note. Standard errors in parentheses; time-invariant classroom characteristics are controlled in the analysis with classroom “fixed effects”, which amounts to including dummy variables for all but one classroom (using Stata’s xtreg command). Fixed effects estimates are based on within-classroom variation in dependent and independent variables. Algebra and Geometry are in reference to the base category consisting of eighth grade students enrolled in general mathematics courses. Controls are in reference to White, Female, English Only (EO), and non National School Lunch Program (NSLP) participants.

^*p < 0.05,

^**p < 0.01,

^***p < 0.001