Reverberation of excitation in neuronal networks interconnected through voltage-gated gap junction channels

Voltage-dependent gap junction gating contributes to reverberation in neuronal circuits.

Abstract

We combined Hodgkin–Huxley equations and gating models of gap junction (GJ) channels to simulate the spread of excitation in two-dimensional networks composed of neurons interconnected by voltage-gated GJs. Each GJ channel contains two fast and slow gates, each exhibiting current–voltage (I-V) rectification and gating properties that depend on transjunctional voltage (V_j). The data obtained show how junctional conductance (g_j), which is necessary for synchronization of the neuronal network, depends on its size and the intrinsic firing rate of neurons. A phase shift between action potentials (APs) of neighboring neurons creates bipolar, short-lasting V_j spikes of approximately ±100 mV that induce V_j gating, leading to a small decay of g_j, which can accumulate into larger decays during bursting activity of neurons. We show that I-V rectification of GJs in local regions of the two-dimensional network of neurons can lead to unidirectional AP transfer and consequently to reverberation of excitation. This reverberation can be initiated by a single electrical pulse and terminated by a low-amplitude pulse applied in a specific window of reverberation cycle. Thus, the model accounts for the influence of dynamically modulatable electrical synapses in shaping the function of a neuronal network and the formation of reverberation, which, as proposed earlier, may be important for the development of short-term memory and its consolidation into long-term memory.

INTRODUCTION

In models describing synchronization of neuronal networks or the spread of excitation in excitable structures, cell-to-cell communication through gap junction (GJ) channels composed of the connexin (Cx) protein was typically defined as having constant conductance (see online database of models that contain GJs at https://senselab.med.yale.edu/ModelDB/ModelList.cshtml?id=114107&describe=yes&celldescr=&). It is well established that GJ communication (GJC) exhibits changes caused by gating by voltage and chemical reagents as well as current–voltage (I-V) rectification; however, neither of these properties were accounted for during simulations of networks formed of neurons, cardiomyocytes, or other types of excitable cells. GJC plays an important role in the propagation of excitation in the heart, communication between neurons, metabolic exchange between cells in most organs and tissues, including the lens (which lacks blood circulation), and organ formation during development or regulation of cell proliferation (Bukauskas and Verselis, 2004; González et al., 2007).

Electrical synapses between mammalian neurons are preferentially composed of Cx36, which is commonly expressed by neurons throughout the central nervous system (Connors and Long, 2004; Söhl et al., 2005). Many roles for electrical synapses have been documented, such as metabolic communication, synchronization of neuronal networks, and memory formation (Bennett and Zukin, 2004; Bissiere et al., 2011). Also, electrical synapses rectify and cause asymmetry of signal transfer (Furshpan and Potter, 1959; Auerbach and Bennett, 1969; Phelan et al., 2008; Rash et al., 2013). Modulation of electrical synapses can occur by different factors, including phosphorylation (Ouyang et al., 2005; Cachope et al., 2007; Alev et al., 2008), changes in pH (González-Nieto et al., 2008), intracellular concentration of divalent cations (Palacios-Prado et al., 2013, 2014), and activity-dependent long-term depression (Haas et al., 2011).

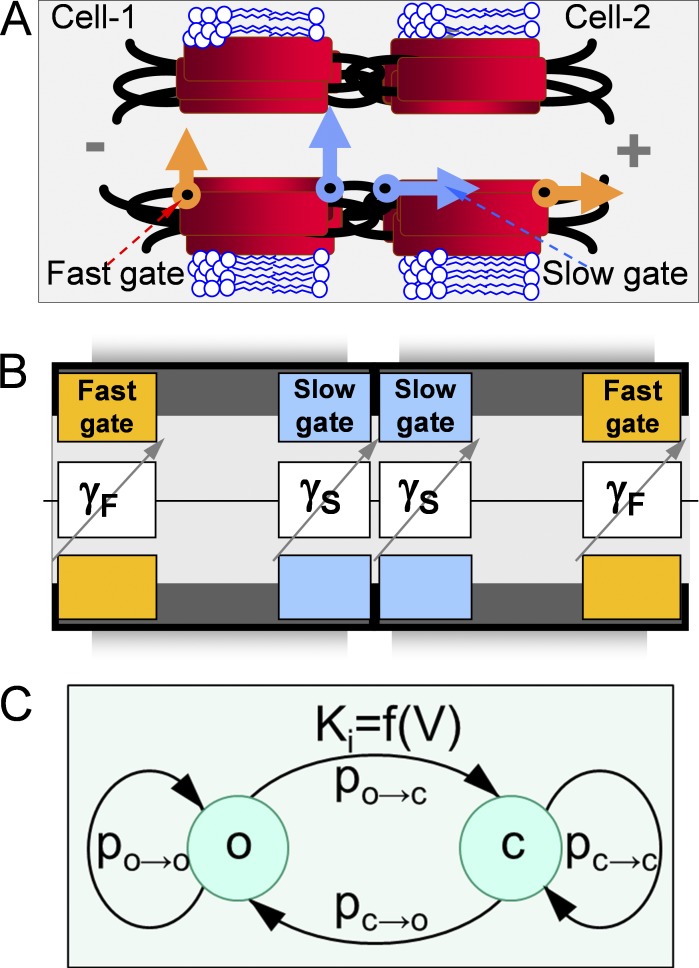
A property that appears to be common to all 21 members of the Cx family is the sensitivity of junctional conductance (g_j) to transjunctional voltage (V_j). Single-channel studies have shown that V_j causes channels to close to a subconductance (residual) state with fast gating transitions (<1 ms; Bukauskas and Weingart, 1994; Moreno et al., 1994). It was shown that V_j as well as chemical uncouplers can also induce gating transitions to the fully closed state and that these transitions are slow, >10 ms (Bukauskas and Weingart, 1994; Bukauskas and Peracchia, 1997). Gating to different levels via distinct fast and slow gating transitions led to the suggestion that there are two distinct V_j-sensitive gates, termed fast and slow (or loop gating) mechanisms (Bukauskas and Verselis, 2004). Earlier, gating properties of GJ channels were described by using the Boltzmann function (Harris et al., 1981), which assumes that GJ channels have two states: open and fully closed. It was presumed that each hemichannel of the GJ channel gates only when the apposed (or docked) hemichannel (aHC) is open and that all V_j falls on the gated hemichannel, whereas in fact V_j falls on both hemichannels and they can gate at the same time. Furthermore, there were several attempts to describe V_j gating of GJs with a multistate approach, which provided more detailed descriptions of gating processes (Vogel and Weingart, 1998; Ramanan et al., 1999; Chen-Izu et al., 2001). The discovery of fast and slow gates (Fig. 1, A and B) motivated us to develop stochastic 4- and 16-state models of GJ channel gating (Paulauskas et al., 2009, 2012).

Figure 1.

GJ channels contain fast and slow gating mechanisms. (A) Schematic of the GJ channel illustrating fast gates (orange) that close the channel partially to the so-called residual state and the slow gates (blue) that close the channel fully. (B) Schematic of the GJ channel is combined with the principal electrical scheme composed of four variable resistances in series attributed to the fast (γ_F) and slow (γ_S) gates. (C) A schematic of possible transitions of the gate, which has open (o) and closed (c) states.

However, all previous models were adopted to study GJC between two individual cells. Here, we present a model describing a 2-D network of neurons, each exhibiting excitability according to Hodgkin–Huxley (H-H) formalism and interconnected through a 16-state model of GJ channel gating (16SM). We demonstrate that during the spread of excitation, a delay between action potentials (APs) creates a bipolar V_j spike of approximately ±100 mV, causing relatively small decay of g_j, which can accumulate into significant g_j decays during bursting activity of neurons. Also, we demonstrate that very low g_j allows for synchronization of a network composed of neurons exhibiting different intrinsic firing frequencies. Furthermore, we show that a relatively small heterogeneity in I-V rectification of GJs creates conditions for unidirectional AP propagation, leading to reverberation of excitation, which, as proposed (Lorente de Nó, 1933; Hebb, 1950; Tegnér et al., 2002; Constantinidis and Wang, 2004; Wang et al., 2004, 2011), can serve as a form of short-term memory and can mediate consolidation of short-term memory into long-term memory.

MATERIALS AND METHODS

Model of the neuronal network

We linked up to several hundred cells into a 2-D cluster, each exhibiting excitability described using H-H equations (Hodgkin and Huxley, 1952). Each cell in the cluster communicated with neighboring cells through GJs. Junctional current (I_j) and g_j were simulated using stochastic 16SM (S16SM) and Markov chain 16SM (MC16SM). We used the sets of 16SM parameters, which are presented in Tables 1 and 2. All models were implemented in MATLAB.

Table 1.

Set of parameters of MC16SM used for simulation of multicellular networks

Gate/Parameter	A	V0	γopen	γclosed	Ropen	Rclosed	Pt	Π
	mV−1	mV	pS	pS	mV	mV
Fast gate	0.15	40	24	3	10,000	10,000	0.00005	−1
Slow gate	0.15	40	24	0	10,000	-	0.00005	−1

The set of parameters of an MC16SM used for simulation of multicellular networks interconnected through electrical synapses formed of GJ channels resembling Cx36 and to assemble Figs. 3 B, 4 (E–G), 5, 6, 7, and 8. In search of minimum g_j necessary for synchronization and signal transfer of APs in 1-D and 2-D clusters of neurons (g_j,min-synch and g_j,min-transf; Fig. 5), we varied the number of GJ channels forming electrical synapses.

Table 2.

Set of parameters of S16SM and MC16SM used for simulation of multicellular networks

Gate/Parameter	A	V0	γopen	γclosed	Ropen	Rclosed	Pt	Π
	mV−1	mV	pS	pS	mV	mV
Fast gate	0.15	10	120	10	10,000	10,000	0.00005	−1
Slow gate	0.15	10	120	0	10,000	-	0.00005	−1

The set of parameters of an S16SM and an MC16SM used for simulation of multicellular networks interconnected through electrical synapses formed of GJ channels resembling Cx45 and to assemble Figs. 2, 3 (C and D), and 4 (B–D, F, and G).

H-H model

We have modified the original H-H model (Hodgkin and Huxley, 1952) by adding I_j, described by the following system of ordinary differential equations:

$$\{\begin{array}{l}{I}_m=I_{\mathit{ext}}+C_m\frac{d{V}_m}{\mathit{dt}}+g_K{n}^4\left(V_m-V_K\right)+g_{\mathit{Na}}{m}^{3}h\left(V_m-V_{\mathit{Na}}\right)+g_l\left(V_m-V_l\right)+I_j;\\ \frac{\mathit{dn}}{\mathit{dt}}={\alpha }_n\left(V_m\right)·\left(1-n\right)-{\beta }_n\left(V_m\right)·n;\\ \frac{\mathit{dm}}{\mathit{dt}}={\alpha }_m\left(V_m\right)·\left(1-m\right)-{\beta }_m\left(V_m\right)·m;\\ \frac{\mathit{dh}}{\mathit{dt}}={\alpha }_h\left(V_m\right)·\left(1-h\right)-{\beta }_h\left(V_m\right)·h.\end{array}$$

Here, I_m is the transmembrane current per unit area, I_ext is external stimulus current, V_m is membrane potential, and C_m is the membrane capacitance per unit area; V_K, V_Na, and V_l are the potassium, sodium, and leak reversal potentials, respectively; g_K, g_Na, and g_l are the maximum values of potassium, sodium, and leak conductances per unit area, respectively; n, m, and h are variables (0 ≤ n, m, h ≤ 1) associated with potassium channel activation, sodium channel activation, and sodium channel inactivation, respectively; and α_i and β_i are rate constants for the respective ion channels.

The membrane capacity C_m was chosen as 1 µF/cm². The corrected values of reversal potentials were chosen as V_K = −12, V_Na = 115, and V_l = 10.6 mV, whereas conductances were chosen as g_K = 36, g_Na = 120, and g_l = 0.3 mS/cm² (Hodgkin and Huxley, 1952). The functions α_i and β_i were as follows:

$${\alpha }_n\left(V_m\right)=\frac{0.1-0.01·V_m}{e^{\left(1-0.1·V_m\right)}-1};$$

$${\alpha }_m\left(V_m\right)=\frac{2.5-0.1·V_m}{e^{\left(2.5-0.1·V_m\right)}-1};$$

$${\alpha }_h\left(V_m\right)=0.07·e^{\left(-\frac{V_m}{20}\right)};$$

$${\beta }_n\left(V_m\right)=0.125·e^{\left(-\frac{V_m}{80}\right)};$$

$${\beta }_m\left(V_m\right)=4·e^{\left(-\frac{V_m}{18}\right)};$$

$${\beta }_h\left(V_m\right)=\frac{1}{e^{\left(3-0.1·V_m\right)}+1}.$$

We used Euler’s method for the numerical solution of H-H model equations, which was implemented in MATLAB. A time step of 0.01 ms was used in most numerical experiments.

S16SM

In an S16SM (Paulauskas et al., 2012), each of four gates is characterized by gating properties and the unitary conductance of the open (o) and closed (c) states (Fig. 1 C). We have used an S16SM approach to describe the operation of each gate, allowing a simulation of I_j and g_j changes over time. This model is available online at http://connexons.aecom.yu.edu/Applet.htm, and its application in analyzing gating of GJs under normal and pathologic conditions was reported in Palacios-Prado et al. (2009, 2010) and Skeberdis et al. (2011).

In general, the model defines the probability of an individual gate to remain in the same state or to change its state for any given discrete time interval (Δt) and V_j. Closing one gate changes voltage across the other three gates in series, which will affect their probability of changing the state over the next Δt. The transition probabilities between open and closed states p_o→c and p_c→o or probabilities to remain in the same state (p_o→o and p_c→c) are given by

$$p_{o\to c}(K,P_t)=\frac{P_t·K}{1+K},$$

$$p_{o\to o}(K,P_t)=1-p_{o\to c}(K,P_t),$$

$$p_{c\to o}(K,P_t)=\frac{P_t}{1+K},$$

and

$$p_{c\to c}(K,P_t)=1-p_{c\to o}(K,P_t),$$

where P_t adjusts probability of transitions during a discrete time interval, Δt, to equilibrate simulated and experimental times (Paulauskas et al., 2009, 2012). K is the equilibrium constant of slow/fast gate, determined as follows: $K_{S/F,o\leftrightarrow c}=e^{A_{S/F}\left(-\Pi ·V_{S/F}-V_{S/F,o}\right)}$ (Chen-Izu et al., 2001). Here, A_S/F characterizes sensitivity to voltage, V_S/F,o is voltage at which K_S,o↔c or K_S,o↔res is equal to 1, and Π is a gating polarity (+1 or −1). V_S/F is voltage across fast/slow gate.

There is a solid body of evidence demonstrating I-V rectification of open and residual states of the GJ channel and an unapposed hemichannel (DeVries and Schwartz, 1992; Trexler et al., 1996; Oh et al., 1999; Bukauskas et al., 2002a; Kronengold et al., 2003; Valiunas et al., 2004; Tong and Ebihara, 2006; Rackauskas et al., 2007). We assumed that γ_S,open, γ_F,open, and γ_F,res rectify in accordance with the exponential function as proposed in Vogel and Weingart (1998): ${\gamma }_{F,\mathit{open}}={\gamma }_{F,\mathit{open},0}·e^{V_F/R_{F,\mathit{open}}},$ ${\gamma }_{F,\mathit{open}}={\gamma }_{F,\mathit{open},0}·e^{V_F/R_{F,\mathit{open}}},$ ${\gamma }_{F,\mathit{res}}={\gamma }_{F,\mathit{res},0}·e^{V_F/R_{F,\mathit{res}}},$ ${\gamma }_{F,\mathit{res}}={\gamma }_{F,\mathit{res},0}·e^{V_F/R_{F,\mathit{res}}},$ ${\gamma }_{S,\mathit{open}}={\gamma }_{S,\mathit{open},0}·e^{V_S/R_{S,\mathit{open}}},$ and ${\gamma }_{S,\mathit{open}}={\gamma }_{S,\mathit{open},0}·e^{V_S/R_{S,\mathit{open}}},$ where γ_F,open,0 and γ_F,res,0 are γ_F,open at V_F = 0, whereas γ_s,open,0 is γ_F,open at V_S = 0. R_F,open, R_F,res, and R_S,open are rectification coefficients of the open/residual states and fast/slow gates, respectively.

Rectification of γ_F,open, γ_F,res, and γ_S,open does not allow for the evaluation of V_F and V_S in one step and necessitates the use of an iterative procedure to estimate the conductance of the GJ channel. In brief, initially we know the states of each gate, which allows for the estimation of V_F and V_S without accounting for rectification:

$$V_{F,A}=\frac{V_j·{\gamma }_j}{{\gamma }_{F,A}},$$

$$V_{S,A}=\frac{V_j·{\gamma }_j}{{\gamma }_{S,A}},$$

$$V_{S,B}=\frac{V_j·{\gamma }_j}{{\gamma }_{S,B}},$$

and

$$V_{F,B}=\frac{V_j·{\gamma }_j}{{\gamma }_{F,B}}.$$

Then, we recalculate conductances of gates accounting for rectification and reevaluate a new set of V_F and V_S. We repeat the last cycle and at the nth iterative step evaluate conductance of the GJ channel (γ_j,n) as well as the difference, Δγ_j,n = γ_j,n − γ_j,n−1 for convergence testing. The value of γ_j,n is given by

$${\gamma }_{j,n}=\frac{1}{\left(\frac{1}{{\gamma }_{\text{F,A}}}+\frac{1}{{\gamma }_{\text{S,A}}}+\frac{1}{{\gamma }_{\text{S,B}}}+\frac{1}{{\gamma }_{\text{F,B}}}\right)}.$$

The iterative procedure is stopped once the tolerance criterion Δγ_j,n < (γ_j,n−1/1000) is reached. The final values of V_F and V_S allow for the evaluation of possible changes in the state of each gate, as well as estimation of voltages across all four gates, the sum of which should be equal to V_j, i.e., V_j = V_F,A + V_S,A + V_F,B + V_S,B.

This information is transferred to the next discrete time interval and the process is repeated. In >99% of calculations, the number of iterations was four to seven. Once the effect of I-V rectification on the unitary conductance of each GJ channel γ_j,i of the electrical synapse composed of m channels is evaluated, then g_j is estimated from

$$g_j={\displaystyle \sum _{i=1}^m{\gamma }_{j,i}}.$$

MC16SM

To accelerate the simulation and reduce noise, we developed an MC16SM by transforming an S16SM. Instead of evaluating gating of each individual GJ channel, we calculated changes over time of averaged probabilities for each of four gates to be open or closed depending on V_j by using a Markov chain approach. Earlier, we used stationary/steady-state probabilities of Markov chain to model GJ voltage gating (Sakalauskaite et al., 2011; Snipas et al., 2015). However, a steady-state approach is not suitable in this case, because modeling of neuronal networks requires evaluation of dynamic changes in g_j. Thus, we used transitive rather than steady-state probabilities. In doing so, we used a recursive relation, pⁿ = pⁿ⁻¹ · P, to calculate the transitive probability vector pⁿ at a discrete time moment, t_n, for each of 16 states, where P denotes the transition probability matrix of a discrete-time Markov chain. Each state s_j can be expressed as a 4-tuple, s_j = (s_F,A; s_S,A; s_S,B; s_F,B), where each component denotes the state—open (o) or closed (c)—of the respective gate in the GJ channel. Thus, the model consists of 16 states, which can be numbered in lexicographical order as follows: s₁ = (o;o;o;o); s₂ = (o;o;o;c); s₃ = (o;o;c;o); s₄ = (o;o;c;c); s₅ = (o;c;o;o); s₆ = (o;c;o;c); s₇ = (o;c;c;o); s₈ = (o;c;c;c); s₉ = (c;o;o;o); s₁₀ = (c;o;o;c); s₁₁ = (c;o;c;o); s₁₂ = (c;o;c;c); s₁₃ = (c;c;o;o); s₁₄ = (c;c;o;c); s₁₅ = (c;c;c;o); and s₁₆ = (c;c;c;c).

The transition probabilities among 16 states can be expressed by using the same transition probabilities p_o→c and p_c→o of singular o↔c transitions, as in S16SM. For example, transition probability from s₄ = (o,o,c,c) to s₆ = (o,c,o,c), which we denote as p_oocc→ococ, can be estimated as follows: p_oocc→ococ = (1 − p_o→c) · p_o→c · p_c→o · (1 − p_c→o).

Thus, all basic parameters of the model necessary for building a transition probability matrix P are the same as in the S16SM model, and the same equations are used to estimate K, evaluate I-V rectification, and calculate γ_j. However, because voltage across each gate depends on the state s_j, i.e., V_F = V_F(s_j) and V_S = V_S(s_j), then γ_j must also be evaluated at each state, i.e., γ_j = γ_j(s_j). Once the transition probability matrix P is formed and the probability vector pⁿ is estimated, then the expected value of junctional conductance g_j is estimated as

$$g_j={\displaystyle \sum _i{p}_i·\gamma \left(s_i\right)}.$$

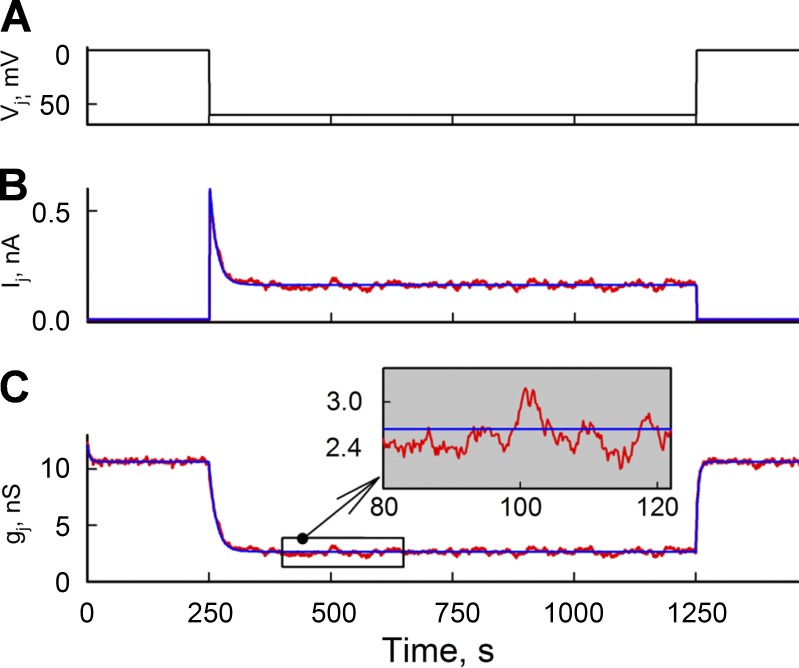
Fig. 2 shows I_j (B) and g_j (C) traces generated in response to a V_j step of −60 mV (A) using an S16SM (red traces) and an MC16SM (blue traces).

Figure 2.

Comparison of I_j and g_j time plots simulated using an S16SM and an MC16SM. (A) V_j step of −60 mV applied to one cell of the cell pair. Both cells were voltage clamped. (B) I_j time plots obtained simulating a junction composed of 500 channels using an S16SM (red) and an MC16SM (blue). (C) g_j time plots obtained from the ratio I_j/V_j. g_j values evaluated using MC16SM (blue) reflect averaged changes of g_j values obtained using S16SM (red) and are virtually free of noise (inset).

Online supplemental material

Fig. S1 supplements Fig. 4 C. Fig. S2 supplements Fig. 5. Figs. S3–S6 are snapshots of Fig. 8 and Videos 1–4 and provide explanations of conditions under which these videos were recorded. A more detailed description of 16SM is presented in the supplemental materials and methods. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201511488/DC1.

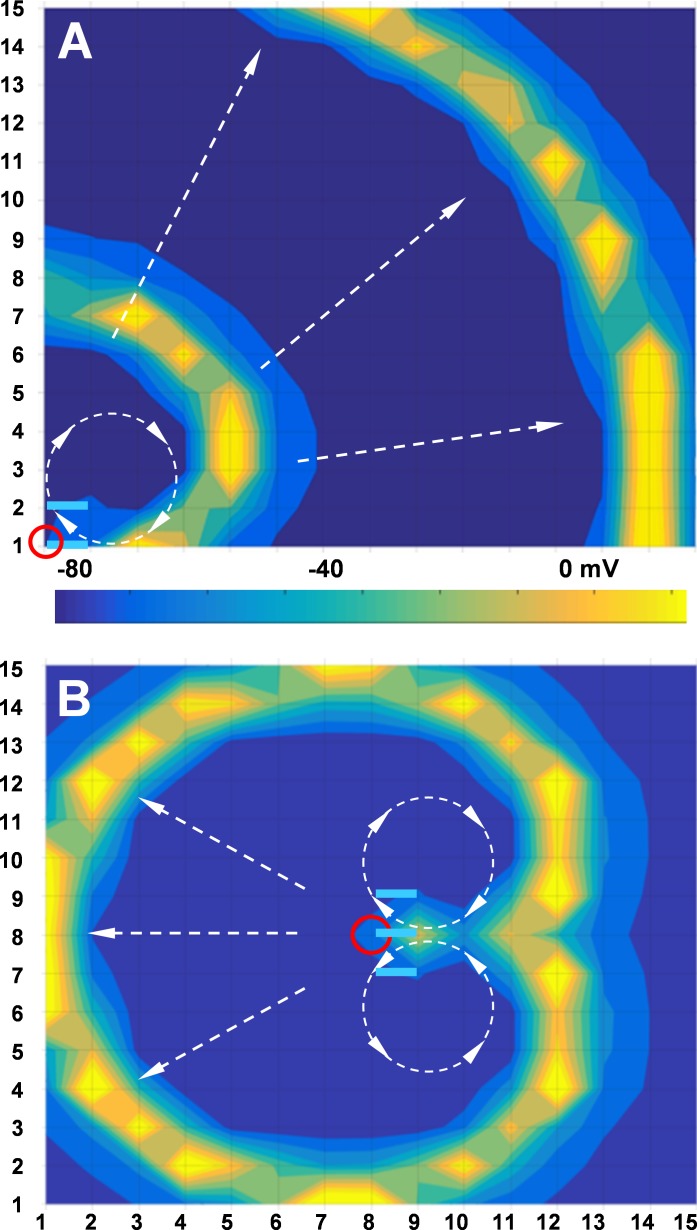
Figure 8.

Reverberations of excitation in a 15 × 15 cluster of neurons caused by a single stimulus. In A and B, stimulus was applied to cell 1/1 and cell 8/8 (red circles), respectively. I-V–rectifying junctions are shown by light blue segments. Colored bar is calibrated for transmembrane potential.

RESULTS

Physiology of fast and slow gates

The demonstration of fast and slow gates (Bukauskas and Verselis, 2004) required consideration of four gates in series, which resulted in the development of an S16SM of gating (Paulauskas et al., 2012). The initial hypothesis of fast and slow gating mechanisms was based on recordings of de novo GJ channel formation observed after providing two patched insect cells (Aedes albopictus, clone C6/36) in contact (Bukauskas and Weingart, 1993, 1994). Based on these data, it was concluded that each hemichannel of the GJ channel possesses a fast gate controlled by V_j that closes the channel from the open state with conductance γ_j,_o to a substate or residual state with conductance γ_j,_res and a slow gate that operates between an open state with conductance γ_S,open and a fully closed state with conductance γ_S,closed = 0 (Fig. 1 A; Bukauskas and Weingart, 1994). Furthermore, gating of GJs to the substate were reported in mammalian cells expressing different Cx isoforms (Moreno et al., 1994; Veenstra et al., 1994; Bukauskas et al., 1995; Bukauskas and Peracchia, 1997).

Furthermore, there is a solid body of evidence demonstrating I-V rectification of open and residual states of the single GJ channel (Bukauskas et al., 2002a; Rackauskas et al., 2007) and undocked/unapposed hemichannels (DeVries and Schwartz, 1992; Trexler et al., 1996; Oh et al., 1999; Kronengold et al., 2003; Valiunas et al., 2004; Tong and Ebihara, 2006). I-V rectification of gates is typically reflected in the nonlinear instantaneous g_j (g_j,inst) dependence on V_j measured at the very beginning of applied V_j steps when V_j gating is not yet activated. Homotypic GJ channels, which exhibit oppositely oriented near-exponential relationships of γ_F,open or γ_S,open over V_j in aHCs, demonstrate a relatively small g_j,inst dependence on V_j, as shown in Fig. 7 of Paulauskas et al. (2009). However, if cells express different Cx isoforms and form heterotypic GJ channels or are exposed to asymmetric conditions in ionic composition or phosphorylation, which can differently affect I-V rectification of fast and/or slow gates residing in aHCs, then an asymmetry of I-V rectification of GJ channels can be well expressed, causing unidirectional signal transfer and reverberation of excitation in neuronal networks, as we demonstrate later in Figs. 7 and 8.

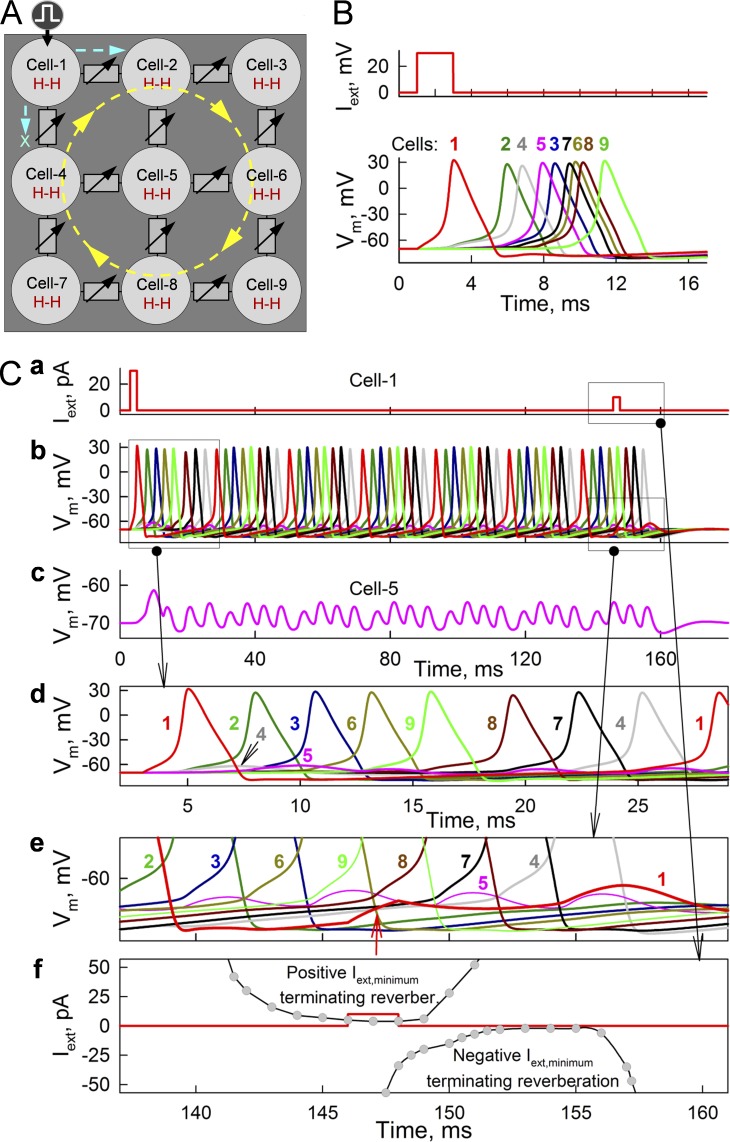
Figure 7.

Formation of reverberation of excitation in a cluster of nine neurons connected through GJs modulatable by an MC16SM. (B) Spread of APs from stimulated cell 1 through all cells shown in A. g_j values of GJs varied randomly from 0.175 to 0.2 nS and did not exhibit I-V rectification. (C) Initiation and termination of reverberation of excitation (b) by a single stimulus applied to cell 1 at 2 and 146 ms, respectively (a). Cell 5 is located at the core of reverberation and exhibits only electrotonic depolarizations not transforming into APs (c). The first stimulus caused AP, which spreads to cell 2 but not to cell 4 (d). Reverberation of excitation was stopped by the second pulse, which caused depolarization of ∼3 mV in the middle of cell 1 cycle (red arrow in e) and prevented reexcitation of cell 1 by cell 4. (f) Summarized data demonstrating time windows during which positive and negative I_{ext,cell 1} pulses of minimal amplitude were able to terminate reverberation of excitation.

Simulation of signal transfer through electrical synapses

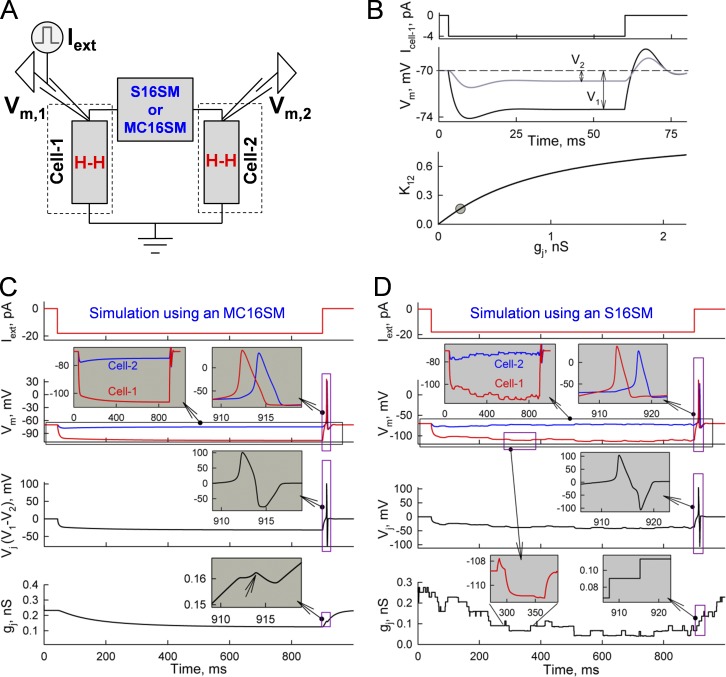
Studies of electrical cell–cell coupling in brain slices are most often performed by injecting a pulse of constant hyperpolarizing current into one cell and measuring the electrotonic response in a neighboring cell. Initially, we simulated electrotonic signal transfer between two cells connected through soma-somatic junctions (Fig. 3 A). Cell 1 was injected with an external current (I_ext) under current clamp conditions, and the changes in transmembrane voltages were estimated in cell 1 (V_m,1) and cell 2 (V_m,2). Fig. 3 B shows that at g_j = 0.2 nS, electrotonic responses in cell 1 (V₁) and cell 2 (V₂) reached steady states after ∼30 ms. The ratio between V₂ and V₁ is named as a coupling coefficient, K₁₂ = V₂/V₁. The bottom plot in Fig. 3 A shows the K₁₂–g_j relationship simulated for soma-somatic GJs; the gray circle shows averaged K₁₂ (∼0.15) and g_j (∼0.2 nS) values measured in rat cerebellar cortex basket cells (Alcami and Marty, 2013). However, for dendro-dendritic GJs located relatively distantly from somas (more than ∼100 µm), an influence of axial resistance of the dendrites (R_d in Fig. S1 B and supplemental materials and methods) should be accounted for. Our preliminary data demonstrate that g_j values are increasingly undervalued with an increase in the distance of electrical synapse from somas of communicating neurons (unpublished data).

Figure 3.

Simulation of cell–cell coupling through soma-somatic GJs. (A) The scheme illustrates two cells, each exhibiting an excitability described by H-H formalism and communicating through GJs operating according with an S16SM or an MC16SM. The left electrode was used to inject current (I_ext) under current clamp mode and measure transmembrane voltage in cell 1 (V_m,1). The right electrode was used to record transmembrane voltage in cell 2 (V_m,2). (B) Electrotonic responses evoked in cell 1 (V₁) and cell 2 (V₂) by an I_ext step of −4 pA. Simulations were performed using an MC16SM. (C) Simulation of changes in V_m,1, V_m,2, and g_j caused by gating of GJs formed of the Cx exhibiting properties similar to Cx45, in response to an I_ext step of −18 pA. Simulation was performed using an MC16SM. The left inset in the V_m time plot shows that before reaching a steady state, V_m,1 increases and V_m,2 decays, resulting in an increase of V_j and V_j gating. Phase differences between APs arising at the end of the I_ext step caused a bipolar V_j spike (inset in V_j time plot) and, consequently, a small decay of g_j (inset in g_j time plot) caused by V_j gating. (D) Simulation as in A, but performed using an S16SM instead of an MC16SM and assuming that the junction contains 10 GJ channels.

In testing whether the strength of electrical synapses can cause gating, we initially assumed that cells are connected through the relatively highly V_j-sensitive Cx45, which, like Cx36, is expressed in neurons, but to a lesser degree (von Maltzahn et al., 2004; Chapman et al., 2013). Fig. 3 C shows that an I_ext of −18 pA caused changes in V_m,1 and V_m,2, resulting in a V_j of ∼30 mV; simulation was performed using MC16SM. The g_j trace demonstrates that g_j decayed, and it took ∼600 ms to reach a steady state at ∼50% of the initial g_j. With the decrease in g_j, V_m,1 increased and V_m,2 decreased (Fig. 3 C, left inset in V_m time plot), thus causing V_j to rise, which accelerated a decay in g_j. Furthermore, after an I_ext step, the AP developed in cell 1 and was transmitted to cell 2 with a ∼2-ms delay that generated a bipolar V_j pulse (Fig. 3 C, inset on V_j time plot), resulting in a small decrease in g_j (arrow in the inset of g_j time plot). Assuming that GJs are formed of the less V_j-sensitive Cx36 (V_F,o and V_S,o were 40 mV instead of 10 mV for Cx45; Bukauskas et al., 2002b; González et al., 2007; Marandykina et al., 2013), then the g_j decrease was ∼10-fold lower (unpublished data). Gating parameters of Cx36 and Cx45 are shown in Tables 1 and 2.

Fig. 3 D shows data simulated using S16SM instead of MC16SM; parameters of gates were the same as in Fig. 3 C. It was assumed that the electrical synapse contained 10 GJ channels with a single-channel conductance of 25 pS. This revealed stepwise rather than smooth changes in g_j. It is notable that the unitary stepwise changes in g_j resulted in slow changes in V_m,1 and V_m,2 (Fig. 3 D, left inset in g_j time plot).

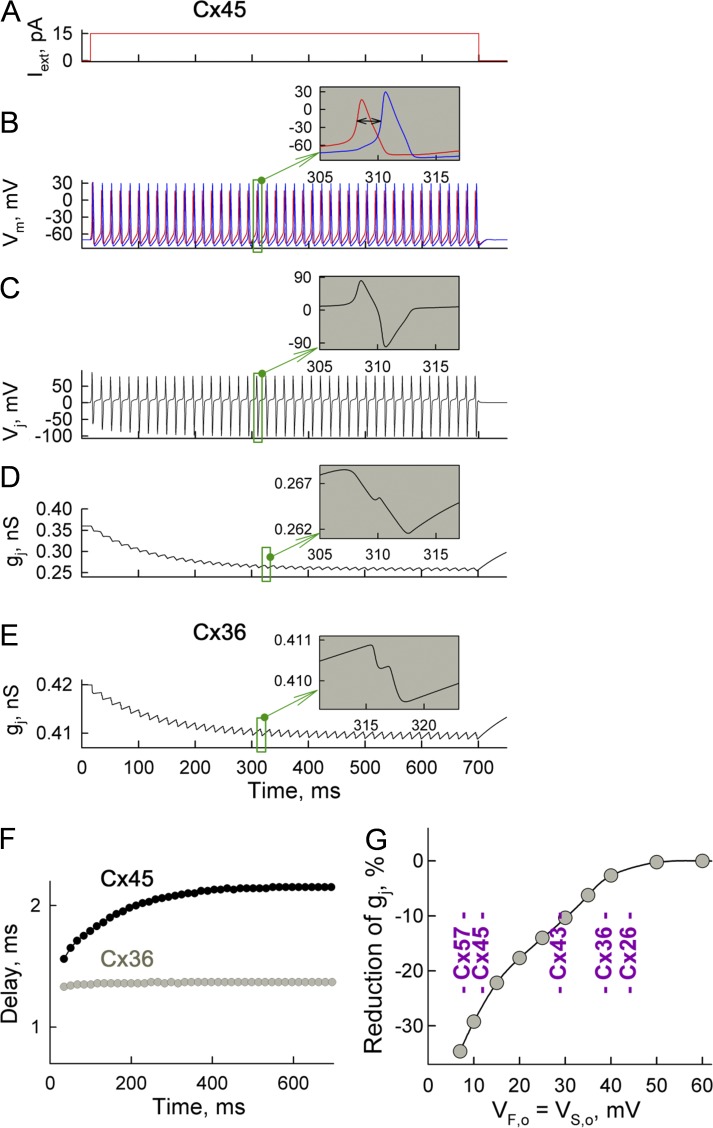
To assess the extent to which the V_j values that develop during spiking activity can affect g_j, we exposed cell 1 of the cell pair to I_ext of +15 pA (Fig. 4 A), which caused a burst of APs at 63 Hz in cell 1 (Fig. 4 B, red trace). Then, excitation was transferred to cell 2 (Fig. 4 B, blue trace) with a ∼2-ms delay (Fig. 4 B, inset, ↔). In this simulation, V_F,o = V_S,o = 10 mV, which roughly corresponds to Cx45. Fig. 4 C shows repeated V_j values arising mainly during the phase shift between APs in neighboring cells, which we term V_j,AP. The amplitude of the V_j,AP spike can reach approximately ±100 mV, which caused a ∼2% decrease in g_j (Fig. 4 D, inset on g_j trace). During bursting activity of neurons, small reductions in g_j accumulate, giving a ∼28% decrease in g_j at the steady state (Fig. 4 D). However, Fig. S1 A (see also supplemental materials and methods) shows that at higher g_j values (2 instead of 0.36 nS), the phase shift between APs in neighboring cells decreases, resulting in substantially shorter and smaller-amplitude V_j,AP spikes. Consequently, this caused a ∼30% smaller drop in g_j than that shown in Fig. 4 D.

Figure 4.

Changes of GJC in the pair of neurons exhibiting bursting activity. (A–D) Demonstration of changes in V_m, V_j, and g_j over time for GJs formed of hypothetical Cx45 in response to an I_ext step of 15 pA. (B) Burst of APs evoked in cell 1 (red) and then transferred to cell 2 (blue). Inset shows that the delay between APs was ∼2 ms. (C) Transjunctional voltage was defined as V_j = V_{m,cell 1} − V_{m,cell 2}; inset shows bipolar V_j spikes arising because of a phase difference between APs. (D) Decay of g_j during the I_ext step. (E) Decay of g_j of GJs formed of connexin exhibiting gating properties resembling those of Cx36. (F) Delay of AP transfer from cell 1 to cell 2 increased by ∼38% in cells expressing Cx45 and at a much smaller level for cells expressing Cx36. (G) Predicted reduction in g_j during I_ext steps of 15 pA in the cell pair expressing various Cx isoforms. All simulations were performed using an MC16SM.

At V_F,o = V_S,o = 40 mV, which resembles Cx36 properties, a decrease in g_j during one V_j,AP spike was ∼0.35%, which accumulated during bursting activity, resulting in a ∼2.5% decrease in g_j (Fig. 4 E). Fig. 4 F shows that a greater decrease of g_j in cells expressing Cx45 correlates with a larger delay of AP transfer than in Cx36-expressing cells. Fig. 4 G shows how the reduction of g_j depends on V_F,o and V_S,o, which roughly replicate gating of different Cxs at I_ext = +15 pA (squares; spiking activity is present). Thus, g_j can decrease ∼30% in highly V_j-sensitive Cx45 or Cx57, whereas for less V_j-sensitive Cxs, e.g., Cx36 or Cx26, the decrease in g_j was much smaller. Even though electrical synapses are formed preferentially of Cx36 GJs exhibiting low V_j sensitivity under normal conditions, their sensitivity to V_j increases significantly when intracellular Mg²⁺ ([Mg²⁺]_i) is elevated to 5 mM (Palacios-Prado et al., 2013), which would lead to larger reductions in g_j during bursting activity of neurons. Also, a robust increase in sensitivity to V_j was demonstrated for Cx45 and Cx57 during acidification (Palacios-Prado et al., 2009). Hence, the decrease in g_j that occurs during bursting activity depends not only on Cx type but also on the surrounding conditions influencing the functional state of the cell.

To examine whether V_j,AP spikes and changes in g_j are different for dendro-dendritic junctions, we simulated the cell pair with a principal electrical scheme as shown in Fig. S1 B and the supplemental materials and methods. Parameters of fast and slow gates as well as the value of g_j were identical to those of the soma-somatic junction. Fig. S1 C shows that V_j,AP spikes obtained for soma-somatic (red) and dendro-dendritic (green) junctions are similar in amplitude and duration, whereas both cause g_j decay similar to that shown in Fig. 4 D.

Role of electrical synapses in synchrony of neuronal networks

Synchronization of neuronal networks can be achieved through chemical (Brunel and Hakim, 1999; Juang and Liang, 2014) as well as electrical (Hormuzdi et al., 2004) synapses. It is known that neurons coupled through electrical synapses can exhibit synchronous spiking activity while being separated by several hundred micrometers (Alcami and Marty, 2013). Otherwise, it is well established that electrical cell–cell coupling between neurons is relatively weak. In neuronal networks connected through dendro-dendritic GJs, g_j values are <1 nS (∼0.13 nS in Vervaeke et al. [2010], 0.02–0.2 nS in Venance et al. [2004], and 0.13–1.0 nS in Devor and Yarom [2002]). Higher values of g_j were reported for soma-somatic junctions (mean ∼2.1 nS between low-threshold spiking thalamocortical neurons in Gibson et al. [1999] and ∼6 nS in clusters of mesencephalic trigeminal nucleus neurons in Curti et al. [2012]). Relatively small g_j values of electrical synapses are most likely caused by a very small single-channel conductance of Cx36 GJ channels (∼6 pS; Moreno et al., 2005) and the small size of junctional plaques (JPs; Rash et al., 2013).

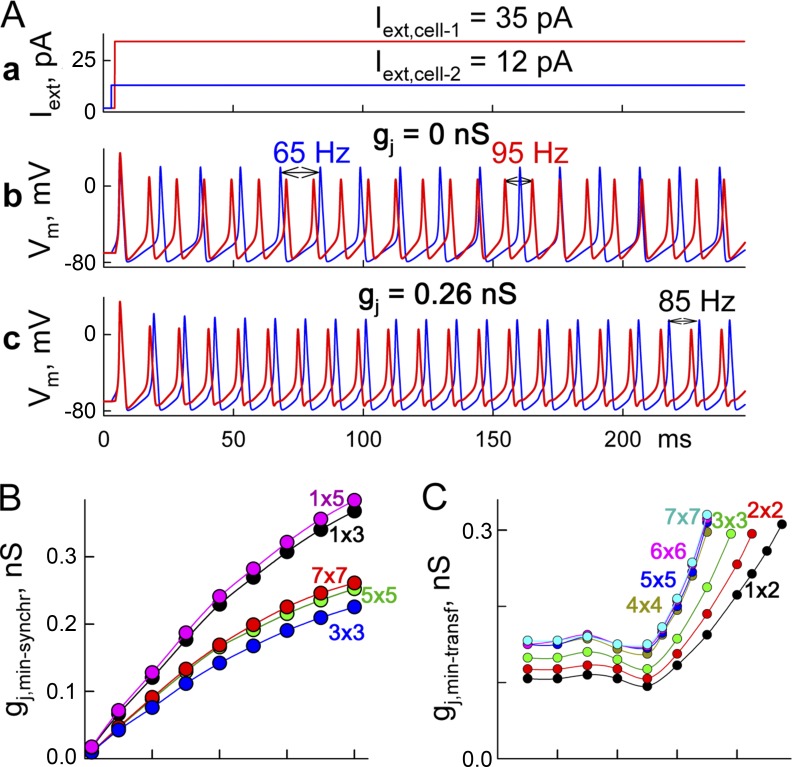
We examined a minimum g_j required to achieve phase synchronization/lock in a cluster of two or more cells (g_j,min-synchr), each of which exhibits spontaneous activity but differs in firing rates. Fig. 5 A (b) shows that at g_j = 0, cell 1 exposed to I_ext of 35 pA exhibited APs at 95 Hz, and cell 2 exposed to I_ext of 12 pA exhibited APs at 65 Hz. When g_j was increased and reached 0.26 nS, cells exhibited phase-locked oscillations (Fig. 5 A, c) at an intermediate frequency of 85 Hz. Fig. 5 A (a) shows g_j,min-synchr dependence on the maximum difference in firing rates (ΔFR) among cells in the 2-D clusters; random distributions of firing rates were created by using different I_ext values. For each 2-D cluster consisting of n × n cells, five different numerical experiments were performed. Parameters of an MC16SM were selected assuming that GJs are formed of Cx36 (Table 1). The central cell of the cluster was exposed to the highest I_ext value, whereas values between minimum and maximum I_ext and assignments to other cells were selected randomly. Fig. 5 B shows that g_j,min-synchr approaches zero at small ΔFR and increases as ΔFR rises. It also demonstrates that averaged values of g_j,min-synchr tend to be higher for bigger clusters but approach steady state at the cluster size of ∼7 × 7. Also, g_j,min-synchr values of 1-D or cable-like (1 × n) clusters were at least ∼30% higher than those of 2-D clusters.

Figure 5.

Synchronization of neuronal clusters. (A and B) Minimum values of g_j necessary for synchronization of neuronal networks (g_j,min-synchr). (A) Repeated APs in cell 1 (red) and cell 2 (blue; b and c) evoked by long depolarizing current pulses shown in a. At g_j = 0, cells exhibited repeated spiking activity at 65 and 95 Hz (b) and g_j = 0.26 nS (c). (B) Summarized data of g_j,min-synchr values in 1-D and 2-D clusters of different sizes depending on differences in their firing rates of neurons, ΔFR. (C) Summary of the minimum g_j necessary for AP transfer between neurons (g_j,min-transf) depending on frequency of APs caused by repeated 2-ms-long I_ext steps of 30 pA. Values of g_j,min-transf were evaluated in the cell pair (1 × 2) and 2-D clusters ranging from 2 × 2 to 7 × 7.

At g_j = 0, if cell 1 of the cell pair is exposed to 2-ms-long depolarizing pulses of 30 pA at 70 Hz, then it exhibits regular firing activity while other cells remain silent. When g_j was increased and reached 0.1625 nS, cell 2 responded with an AP to every AP in cell 1. Summary of Fig. 5 C shows that the minimum g_j necessary for one-to-one AP transfer (g_j,min-transf) in the cell pair increases with rising frequency of I_ext pulses. Also, the values of g_j,min-transf increased as the size of the 2-D cluster increased from 2 × 2 to 7 × 7. In all experiments, the cell exposed to repeated stimulation was located maximally close to the center of the cluster. There was a clear convergence to a steady state when the size of the cluster reached 4 × 4. Furthermore, there is well-expressed decay of a cutoff of frequency from ∼95 Hz for the cell pair to ∼70 Hz for 4 × 4 to 7 × 7 clusters with an increase in size of the cluster. Also, at ∼50 Hz, there is a well-expressed minimum of g_j,min-synchr for all sizes of clusters, which is most likely related to the enhanced amplitude (∼8%) of APs initiated at the period of excitation of 20 ms.

To evaluate how V_j gating affects synchronization of neuronal networks, we examined a network interconnected through (a) constant resistors, (b) GJs formed of low-V_j-sensitivity Cx36, and (c) GJs interconnected through high-V_j-sensitivity Cx45. Fig. S2 shows that the difference in g_min,synch between Cx36 and the constant resistors is negligible (<2%). However, for Cx45, g_min,synch was more than two times higher. We expect that a similar increase in g_min,synch can occur for Cx36 under intracellular hypermagnesemia (Palacios-Prado et al., 2013, 2014), which increases V_j-sensitive gating of Cx36.

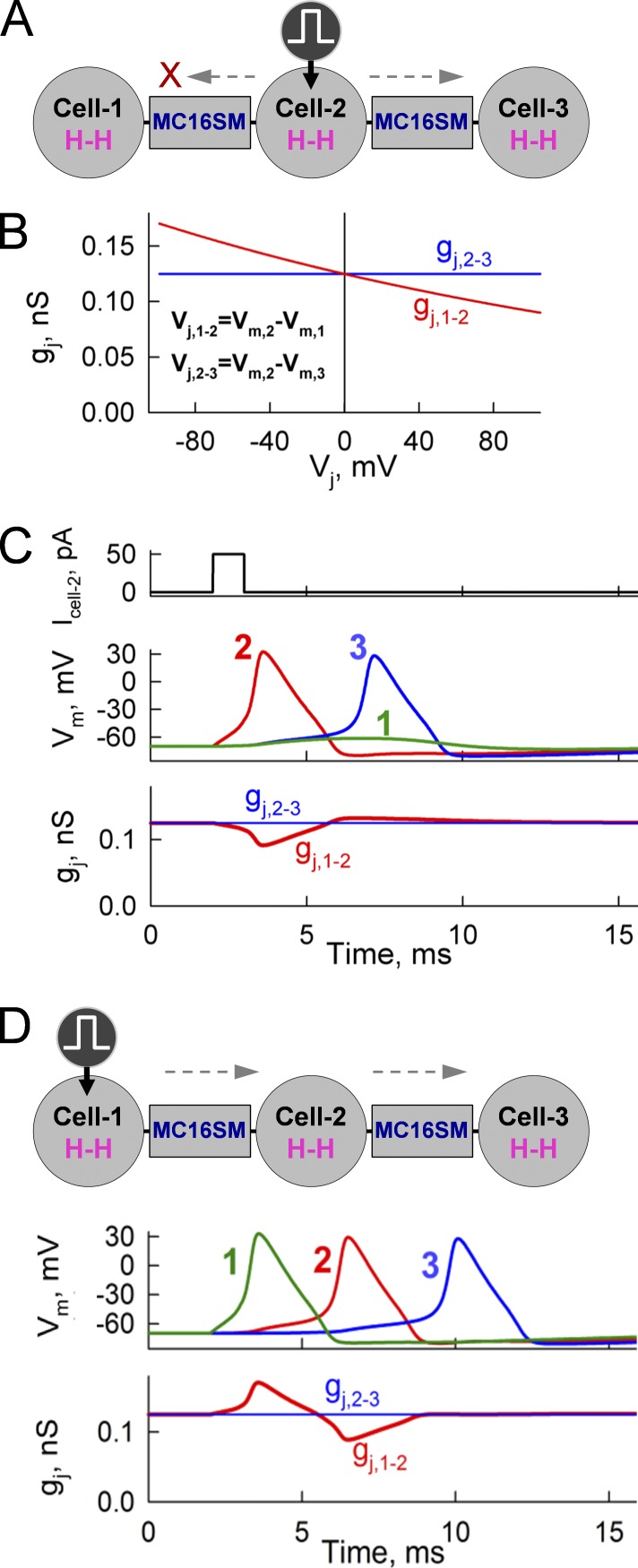
Unidirectional AP transfer between cells connected through GJs exhibiting I-V rectification

Cells, despite well-expressed homeostasis, differ in pH, electrolytic balance, phosphorylation, etc., which may cause an asymmetry in cell-to-cell signaling. Asymmetry in GJC was observed in approximately one third of cases between striatal output neurons (Venance et al., 2004) and between neurons in the inferior olive nucleus (Devor and Yarom, 2002). Recently, we reported that asymmetry in [Mg²⁺]_i leads to rectification of g_j,inst (Palacios-Prado et al., 2014). To explore how I-V rectification can affect signal transfer between cells, we simulated AP transfer in three linearly arranged cells connected through an MC16SM (Fig. 6 A). We assumed that the junction between cells 1 and 2 exhibited well-expressed I-V rectification as shown in the red g_j,1-2–V_j plot (Fig. 6 B), whereas the junction between cells 2 and 3 was not rectifying (blue g_j,2-3 line); I-V rectification coefficients of GJs were equal to 150 and 10,000 mV, respectively. Cell 2 was excited by a 50-pA pulse 1 ms in duration. This caused an AP in cell 2 (Fig. 6 C). Difference in V_m between cells 1 and 2 resulted in short-lasting V_j with an amplitude reaching ∼100 mV. The orientation of I-V rectification was such that at positivity on the cell 2 side, g_j,1-2 decreased (red trace), causing a block of AP transfer to cell 1 (green V_m trace), whereas excitations were transferred to cell 3. Stimulation of cell 1 (Fig. 6 D) induced an AP during which cell 1 became more positive than cell 2 and, because of I-V rectification and oppositely oriented V_j, g_j,1-2 increased, which facilitated AP transfer to cell 2 and onto cell 3. Thus, relatively weak I-V rectification of GJs can lead to unidirectional signal transfer between neurons.

Figure 6.

Unidirectional signal transfer in a cluster of three cells through electrical synapses exhibiting I-V rectification. (A) Schematic of the cells with stimulation of cell 2. (B) g_j–V_j plot exhibiting rectification of GJs between cells 1 and 2 and no rectification of GJs between cells 2 and 3. (C) Stimulation of cell 2–initiated AP that spread to cell 2, but not to cell 1, because of reduced g_j,1-2. (D) Stimulation of cell 1–initiated AP that increased g_j,1-2 because of I-V rectification, therefore facilitating AP transfer to cells 2 and 3.

Reverberation of excitation in a cluster of cells connected through electrical synapses

It is well established that unidirectional signal transfer or an interruption/brake of the wave of excitation can initiate reverberation or reentry, causing heart fibrillation (Davidenko et al., 1995). Here, we present data demonstrating formation of reverberation in a cluster of nine neurons connected through electrical synapses (Fig. 7). Assuming that GJs do not exhibit I-V rectification and g_j values of electrical synapses are distributed randomly in a range of 0.175–0.2 nS, then an AP evoked in cell 1 spreads through the cluster and terminates (Fig. 7 B). When I-V rectification was ascribed between cells 1 and 4 and between cells 2 and 5, leaving other GJs lacking rectification, then an I_ext pulse of 25 pA (Fig. 7 C, a) initiated an AP in cell 1 that was transmitted to cell 2, but not to cell 4 (Fig. 7 C, d). Consequently, the excitation spread along the yellow circle (Fig. 7 A). After reexcitation of cell 1, the process repeated many times. Interestingly, cell 5 exhibited only low-amplitude electrotonic depolarizations (Fig. 7 C, c), which is typically observed at the core of spiral waves (Davidenko et al., 1992). Reverberation was stopped by a second pulse of 10 pA (Fig. 7 C, a), causing a depolarization of ∼3 mV (Fig. 7 C, e, red arrow) and preventing reexcitation of cell 1. To examine how termination of reverberation depends on the amplitude and timing of I_ext, we applied the second pulse at different phases in the reverberation cycle. Gray circles and curves show time windows (Fig. 7 C, f) during which reverberation was stopped using positive or negative I_ext pulses. Thus, termination of reverberation requires relatively low levels of excitatory or inhibitory currents locked to a specific phase of reverberation cycle. Once initiated, reverberation does not need inhomogeneity of I-V rectification to continue.

Reverberation of excitation in a 15 × 15 cluster is shown in Fig. 8 (see Fig. S3 and Video 1). A single stimulus applied to cell 1/1 (Fig. 8 A, red circle) caused reverberation of excitation, with its core (Fig. 8 A, dashed circle) identical to that in Fig. 7. During this simulation, it was assumed that all junctions exhibited identical g_j, but only two junctions shown by light-blue segments exhibited an asymmetry of I-V rectification equal to that shown in Fig. 6 B. Colored isopotential areas (see calibration bar for transmembrane potential) show the spread of excitation (dashed arrows) across the cluster. A stimulus applied to cell 8/8 (Fig. 8 B, red circle) caused formation of two endless reverberation circles spreading across the cluster. In this experiment, it was assumed that junctions indicated by light-blue segments exhibited I-V rectification (see Fig. S4 and Video 2). Cells located in the center of the reverberation core (Fig. 8, A [cell 2/2] and B [cells 9/9 and 7/9]) exhibited low-amplitude electrotonic responses similar to those shown in Fig. 7 C (c), whereas all other cells in the cluster generated ordinary APs. To examine whether the spread of excitation in a 15 × 15 cluster is affected by boundary conditions, we wrapped the cluster on a virtual torus by connecting all cells in column 1 with cells in column 15 and all cells in row 1 with cells in row 15. Reverberation was initiated by a single stimulus applied to cell 4/8 (red circle); I-V–rectifying junctions are indicated by light-blue segments. Fig. S5 and Video 3 show a returning excitation wave that spreads from right to left and collides with the wave spreading from the reverberation core. These data show that for clusters of ∼15 × 15 and larger, the boundary conditions do not noticeably affect the spread of excitation and formation of reverberation. Our data also show that reverberation can be initiated independently whether the region of I-V rectification is located in the corner of the cluster or more centrally. However, as shown in Fig. S6 and Video 4, the presence of multiple I-V rectification inhomogeneities can cause local deformations of spreading spiral waves when passing these regions. Larger regions of I-V inhomogeneity might break down the front of excitation, leading to formation of a new reverberator (not shown), as was demonstrated in computational model of cardiac arrhythmias (Casaleggio et al., 2014).

DISCUSSION

In all reported models describing synchronization or phase-locked activity of neuronal networks, as well as the spread of excitation in various excitable structures, GJC is defined as constant. However, it is well established that fast and slow gates of GJ channels are modulated by voltage, chemical uncouplers, and coupling-promoting reagents. These changes occur in a timescale from hundreds of milliseconds to minutes. Furthermore, GJ channels exhibit I-V rectification, which changes the single-channel conductance instantaneously. Hence, the regulation of GJ channels is highly complex, and an influence of V_j gating as well as I-V rectification should be accounted for, especially during high spiking activity of neuronal networks. We acknowledge that 2-D models present a simplified architecture of neuronal networks; however, it was reported that a 2-D lattice describing a network of basket cells is physiologically adequate (Alcami and Marty, 2013). The 2-D lattice is also extensively used to model the tissues of cardiomyocytes (Pertsov et al., 1993; Casaleggio et al., 2014) or in numerical modeling of epileptic seizures (Volman et al., 2011).

In neuronal networks, V_j can change dynamically because of a phase shift between APs in neighboring cells, which we name V_j,AP. One of our major goals was to find whether V_j,APs that last only a few milliseconds can influence GJC through V_j gating and how such influence depends on the Cx isoform. The spikes of V_j,APs, despite their brevity, are high in amplitude (>100 mV) and potentially influence open probability of fast and/or slow gates because of V_j gating and single-channel conductance caused by I-V rectification. Indeed, data shown in Fig. 4 D demonstrate that for Cx45, a single V_j,AP can cause ∼2% decay in g_j. During bursting activity of neurons, small g_j decays accumulate, leading to significant decays of g_j, as is shown in Fig. 4 D.

Although mammalian electrical synapses are preferentially composed of Cx36 GJs with low sensitivity to V_j under normal conditions, their sensitivity to V_j can increase significantly at enhanced [Mg²⁺]_i (Palacios-Prado and Bukauskas, 2012; Palacios-Prado et al., 2014). This suggests that synchronization of neuronal networks may be reduced under ischemic/stroke conditions when an ATP deficit leads to an increase in [Mg²⁺]_i. An even stronger rise in sensitivity to V_j is demonstrated for Cx45 and Cx57 during acidification (Palacios-Prado and Bukauskas, 2009; Palacios-Prado et al., 2010). Because Cx45 is mostly expressed in the inferior olive (Van Der Giessen et al., 2006), whose role in coordination and control of movement is well established, our data predict that g_j in this structure should be affected by activity of neurons more than in most other structures that preferentially express Cx36. Because Cx36 is resistant to spike-induced depression (Fig. 4 E) and acidification (González-Nieto et al., 2008), synchronization of neuronal networks during paroxysmal activity or ischemia can be maintained. This may explain why Cx36 predominates over Cx45 and other Cxs in neurons of mammalian brains.

Electrical synapses are expressed in a majority of mammalian brain regions. Along with chemical synapses, they facilitate synchronous or phase-locked activity of neuronal networks. Direct GJC between neurons in hippocampus, neocortex, amygdala–hippocampus–cortical axis, and other areas of the mammalian brain is well established, and knowledge on the regions expressing Cx36 has expanded extensively over the last decade because of application of better antibodies and imaging technologies with enhanced resolution (Bennett and Zukin, 2004; Connors and Long, 2004; Hormuzdi et al., 2004; Saraga et al., 2006; Bissiere et al., 2011). Electrical synapses, by forming dendro-dendritic junctions, participate in synchronizing activity of neuronal networks (Hestrin and Galarreta, 2005) spatially separated by several hundred micrometers (Fukuda and Kosaka, 2000; Saraga et al., 2006). In the somatosensory cortex, synchrony is found among inhibitory interneurons at separations of up to 400 µm (Fukuda, 2007), whereas in the primary visual cortex, this distance was from 500 to 800 µm. In the prefrontal cortex, synchronized firing during working-memory tasks appeared to be within 500 µm (Bissiere et al., 2011).

Synchronization of electrically coupled oscillators was examined theoretically in multicellular networks, and it was shown that relatively low g_j can be sufficient to synchronize or phase-lock oscillatory activity of neurons exhibiting different oscillatory activities (Saraga et al., 2006). In different regions of the brain, electrical cell–cell coupling between neurons connected through dendro-dendritic GJs is relatively weak and constitutes ∼0.13–1.0 nS (Devor and Yarom, 2002; Venance et al., 2004; Vervaeke et al., 2010). Such GJC satisfies the conditions necessary for AP transfer between neurons, but it is only a few fold higher than g_j,min-transf, which is in the range of ∼0.1–0.3 nS and varies depending on the firing rate of pacemaker cells (Fig. 5 C). However, such GJC is >10-fold stronger than the g_j necessary for synchronization neurons if their intrinsic oscillatory activity is contiguous (Fig. 5 B).

It is evident that electrical synapses with a conductance of >10 nS would bypass function of chemical synapses and compromise information processing in neuronal networks. Presumably, this is one of reasons that electrical synapses are formed preferentially of Cx36, which exhibits the smallest single-channel conductance among all members of the Cx family (Moreno et al., 2005); <1% of Cx36 GJ channels clustered in junctional plaques are functional under normal conditions (Curti et al., 2012; Marandykina et al., 2013). An increase in open probability of Cx36 GJs during intracellular hypomagnesemia (Palacios-Prado and Bukauskas, 2012; Palacios-Prado et al., 2014), inhibition of arachidonic acid synthesis, or weak acidification (González-Nieto et al., 2008) can strengthen electrical synapses, thus resulting in hypersynchronization, which is linked to development epileptic seizures (Carlen et al., 2000; Gajda et al., 2003).

Data shown in Fig. 6 demonstrate that relatively weak rectification of GJ channels can change g_j instantaneously during short-lasting V_j,AP that can lead to unidirectional signal transfer and consequently to reverberation of excitation (Figs. 7 and 8). Thus, I-V rectification can very quickly reshape the functional state of a neuronal network in response to dynamic changes of bursting activity and initiate self-sustained reverberation. Furthermore, it was proposed that I-V rectification of GJs is defined by an asymmetry of fixed charges, assumed to be charged amino acids, inside the channel pore, and described using the Poisson–Nernst–Plank equation (Oh et al., 1999). Recently, we demonstrated a Mg²⁺-dependent plasticity of electrical synapses between neurons in the mesencephalic trigeminal nucleus (Palacios-Prado et al., 2013) and in the thalamic reticular nucleus (Palacios-Prado et al., 2013, 2014). Also, we showed a novel form of I-V rectification in Cx36 that depends on Mg²⁺ binding within the pore (Palacios-Prado et al., 2013, 2014). It was assumed that a domain of extracellular loop 1, containing D47 residue, forms a Mg²⁺-binding/interaction site, which at higher [Mg²⁺]_i (∼5 mM) creates an exponential I-V rectification, which is oriented in the opposite direction than I-V rectification caused by fixed charges. Superposition of these two forms of I-V rectification results in a hyperbolic I_j,inst-V_j relationship measured uniquely in Cx36 GJ channels (Palacios-Prado et al., 2014). In addition, it was shown that at low [Mg²⁺]_i (∼10 µM) in both cells, the I_j,inst-V_j relationship becomes linear, whereas transjunctional asymmetry in [Mg²⁺]_i can cause an exponential I_j,inst-V_j relationship. This is caused by a presence of I-V rectification in the hemichannel exposed to 5 mM [Mg²⁺]_i and absence of I-V rectification in the hemichannel exposed to 0.01 mM [Mg²⁺]_i. The I-V rectification in electrical synapses has been proposed to affect the dynamic output of neuronal networks, and therefore this novel Mg²⁺-dependent I-V rectification could explain the switching between firing states and changes in the output of neuronal networks during different metabolic states when [Mg²⁺]_i is strongly affected (Gutierrez and Marder, 2013).

We demonstrate that reverberation of excitation in a multicellular network of neurons interconnected only through electrical synapses and inhomogeneities of I-V rectification can be initiated and terminated by a single excitation of only one cell. Previously, Lorente de Nó (1933) proposed the concept of the continuous reverberation of excitations in the circuit formed from several neurons to explain the vestibulo-ocular reflex. This allows for the generation of a burst of APs in response to a single excitation and was viewed as a mechanism for the active maintenance of working memory. However, this hypothesis is not listed in the latest views on the mechanisms of short- and long-term memories preferentially related to molecular, structural, and functional changes of chemical synapses (Kandel et al., 2014; Bailey et al., 2015). Later, Lorente de Nó’s idea was extended in theoretical studies demonstrating a possibility for reverberation of excitation in neuronal networks interconnected with chemical synapses (Tegnér et al., 2002; Constantinidis and Wang, 2004; Wang et al., 2004, 2011). However, there are no studies demonstrating, either experimentally or theoretically, an involvement of electrical synapses in the realization of reverberation in mammalian brain. On the other hand, reverberation of excitation was demonstrated in crayfish between segmented giant axons connected exclusively through electrical synapses (Watanabe and Grundfest, 1961). The role of reverberation of excitation in memory mechanisms was expanded by the proposal (Hebb, 1950) that memory consolidation in neuronal networks includes two basic mechanisms, post-acquisition reverberation of excitation and structural synaptic plasticity (Ribeiro and Nicolelis, 2004). It was proposed that reverberations in neuronal circuits consistently increased during “slow-wave” sleep phase, which was related to consolidation of short-term memory into long-term memory. Reverberation decreased during wakefulness, which suggests that sensory input might suppress reverberations. All studies relating the role of reverberation in short-term memory and its consolidation into long-term memory are based on circuits in which neurons are connected through chemical synapses (Tegnér et al., 2002; Constantinidis and Wang, 2004; Ribeiro and Nicolelis, 2004; Wang et al., 2004, 2011). Our data show that reverberation of excitation can also form in circuits interconnected through electrical instead of chemical synapses and plays a specific role in a complex mechanisms of memory. In such networks, reverberation can also be terminated by low-amplitude phase locked external stimulation (Fig. 7 C, f), resembling activation of sensory signals during a waking period. We expect that reverberation can also exist in circuits consolidating electrical and chemical synapses, in which the presence of even a single chemical synapse in a chain of neurons connected through electrical synapses can trigger unidirectional signal transfer and consequently reverberation of excitation.

Data presented in Fig. 7 show that the center of reverberation core cells did not exhibit APs but instead displayed multiple low-amplitude depolarizations that appeared to be electrotonic responses from APs in neighboring cells. Such behavior is characteristic only for reverberation and cannot be observed during the high frequency caused by enhanced automaticity. Also, low-amplitude depolarizations are a hallmark of spiral wave dynamics (Davidenko et al., 1992), which have been associated with cardiac arrhythmias (Pertsov et al., 1993). It has been detected that epileptic seizures may also manifest as recurrent spiral waves in cat neocortex (Stacey, 2012). Interestingly, a termination of reverberation requires relatively low levels of excitatory or inhibitory current, whereas active windows are locked to specific phases of the reverberation cycle (Fig. 7 C, f). Again, such a property applies only to reverberation of excitation and not to enhanced automaticity, which cannot be terminated by phase-locked stimulation. Both these criteria can serve to differentiate reverberation from enhanced automaticity in the experiment.

The role of GJs in the structural synaptic plasticity is less known; however, several studies suggest a link between GJ activity and memory consolidation via the process of phosphorylation. Cx phosphorylation can influence GJC in cell cultures (Márquez-Rosado et al., 2012) and hippocampus (Nakai et al., 2014). Indeed, phosphorylation/dephosphorylation could combine both necessary conditions of Hebb’s hypothesis, synaptic plasticity and reverberation of excitation, into a single theoretical mechanism: changes caused by Cx phosphorylation/dephosphorylation can increase I-V rectification, which allows unidirectional signal transfer between cells and, consequentially, enables reverberation of excitation.