Multiple cytosolic calcium buffers in posterior pituitary nerve terminals

Researchers have measured the ability of nerve terminals to buffer Ca²⁺ entering in response to electrical activity to better understand plasticity of hormone release.

Abstract

Cytosolic Ca²⁺ buffers bind to a large fraction of Ca²⁺ as it enters a cell, shaping Ca²⁺ signals both spatially and temporally. In this way, cytosolic Ca²⁺ buffers regulate excitation-secretion coupling and short-term plasticity of release. The posterior pituitary is composed of peptidergic nerve terminals, which release oxytocin and vasopressin in response to Ca²⁺ entry. Secretion of these hormones exhibits a complex dependence on the frequency and pattern of electrical activity, and the role of cytosolic Ca²⁺ buffers in controlling pituitary Ca²⁺ signaling is poorly understood. Here, cytosolic Ca²⁺ buffers were studied with two-photon imaging in patch-clamped nerve terminals of the rat posterior pituitary. Fluorescence of the Ca²⁺ indicator fluo-8 revealed stepwise increases in free Ca²⁺ after a series of brief depolarizing pulses in rapid succession. These Ca²⁺ increments grew larger as free Ca²⁺ rose to saturate the cytosolic buffers and reduce the availability of Ca²⁺ binding sites. These titration data revealed two endogenous buffers. All nerve terminals contained a buffer with a K_d of 1.5–4.7 µM, and approximately half contained an additional higher-affinity buffer with a K_d of 340 nM. Western blots identified calretinin and calbindin D28K in the posterior pituitary, and their in vitro binding properties correspond well with our fluorometric analysis. The high-affinity buffer washed out, but at a rate much slower than expected from diffusion; washout of the low-affinity buffer could not be detected. This work has revealed the functional impact of cytosolic Ca²⁺ buffers in situ in nerve terminals at a new level of detail. The saturation of these cytosolic buffers will amplify Ca²⁺ signals and may contribute to use-dependent facilitation of release. A difference in the buffer compositions of oxytocin and vasopressin nerve terminals could contribute to the differences in release plasticity of these two hormones.

INTRODUCTION

Excitable cells, such as endocrine cells and neurons, use a sophisticated Ca²⁺ handling apparatus to control cellular Ca²⁺ and modulate the impact of Ca²⁺ signals. Cytosolic Ca²⁺ buffers are critical components of this apparatus. These proteins bind to ∼99% of Ca²⁺ within a few milliseconds of entry (Neher, 1995) and control the availability of Ca²⁺ for diverse signaling functions. In nerve terminals, action potentials open voltage-gated Ca²⁺ channels to provide the Ca²⁺ that triggers neurotransmitter release. Ca²⁺ buffers in nerve terminals play a major role in determining the magnitude and time course of Ca²⁺ signals and their ultimate efficacy in triggering release (Heinemann et al., 1994; Augustine, 2001; Schneggenburger and Neher, 2005). Depending on their rate of binding, Ca²⁺ buffers spatially restrict the rise in [Ca²⁺]_Free to a region around the site of entry that can be as small as ∼100 nm (Naraghi and Neher, 1997; Neher, 1998; Wang and Augustine, 2014). In rapid processes such as Ca²⁺-triggered exocytosis, cytosolic Ca²⁺ buffers create a complex scenario in which the effect of a Ca²⁺ signal in triggering release depends on cytosolic buffer properties and the spatial relations between the sources of Ca²⁺ and sites of action.

In the posterior pituitary, Ca²⁺ entry triggers the release of the peptide hormones oxytocin and vasopressin from distinct populations of nerve terminals. Secretion is driven by action potentials arriving from the hypothalamus, and the amount of secretion per action potential increases with the frequency and pattern of activity. The dependence of release on activity differs for the two hormones (Poulain and Wakerley, 1982; Gainer et al., 1986). Cytosolic Ca²⁺ buffers can contribute to the use-dependent facilitation of release because as Ca²⁺ binding sites saturate the rise in cytosolic free Ca²⁺ per action potential will increase (Klingauf and Neher, 1997; Blatow et al., 2003; Matveev et al., 2004). The cytosol of posterior pituitary nerve terminals has considerable Ca²⁺ buffering capacity (Stuenkel, 1994), but the concentrations and affinities of its Ca²⁺ binding proteins are unknown. As a result, it is not presently possible to estimate how these Ca²⁺ buffers could influence the facilitation of release.

Most of our present knowledge of cytosolic Ca²⁺ buffers in situ stems from use of a method introduced by Neher and Augustine (1992), which yields an estimate of the endogenous Ca²⁺ buffering capacity, κ_e, defined as the ratio Δ[Ca²⁺]_Total/Δ[Ca²⁺]_Free in the absence of exogenous Ca²⁺ chelators and fluorescent Ca²⁺ probes. This approach has been applied to many cell types, yielding κ_e values in the range of 40–200, with a few anomalous values near 1,000 (Neher, 1995). Although this method has enjoyed widespread use, the quantity κ_e is of limited value. As [Ca²⁺]_Free rises, Ca²⁺ binding sites saturate and κ_e declines. A measurement of a single value for κ_e therefore provides very limited insight into systems where [Ca²⁺]_Free is dynamically regulated over an appreciable range. The assessment of endogenous Ca²⁺ buffer saturation requires the measurement of changes in buffering as [Ca²⁺] rises. Few studies have attempted to analyze saturable Ca²⁺ binding sites in situ and estimate their K_d and concentration. In cardiac myocytes, Ca²⁺ buffer saturation permitted the estimation of a concentration and K_d (Berlin et al., 1994). In the axons of dentate gyrus granule cells, increasing [Ca²⁺]_Free from ∼70 nM to ∼1 µM reduced κ_e from ∼200 to <25 (Jackson and Redman, 2003). Interpreting this concentration dependence of κ_e in terms of the saturation of a binding site indicated that the endogenous buffer had a K_d of 500 nM and concentration of 130 µM. Therefore, evaluating κ_e over a range of [Ca²⁺]_Free can be used to characterize Ca²⁺ buffers in situ. However, this requires separating the buffering by the dye from the buffering by endogenous Ca²⁺ binding molecules, and dye buffering can often exceed that of the cytosol. We have developed a robust method for the analysis of in situ titration of Ca²⁺ binding sites. In posterior pituitary nerve terminals this method resolved binding to the different buffering species and enabled us to estimate the K_d of the Ca²⁺ dye fluo-8 in situ (McMahon and Jackson, 2014). Here we used in situ titration to investigate the cytosolic Ca²⁺ buffers of these nerve terminals. We resolved two endogenous Ca²⁺ buffering species, estimated their K_d and concentration, and assessed their mobility. A biochemical analysis revealed calbindin D28K and calretinin, and the in vitro properties of these Ca²⁺ binding proteins, are consistent with the in situ properties measured here. These endogenous Ca²⁺ buffers will determine the effectiveness of Ca²⁺ as a trigger of secretion, and their saturation in physiologic ranges of Ca²⁺ has the capacity to facilitate release during repetitive activity.

MATERIALS AND METHODS

Posterior pituitary slice preparation

Methods follow previous work from this laboratory (McMahon and Jackson, 2014). Male Sprague-Dawley rats (age 6–9 wk) were anesthetized with isoflurane and decapitated following procedures approved by the Animal Care and Use Committee at the University of Wisconsin. The posterior pituitary was removed and immediately placed in ice-cold artificial cerebrospinal fluid consisting of 125 mM NaCl, 4 mM KCl, 1.25 mM NaH₂PO₄, 26 mM NaHC0₃, 2 mM CaCl₂, and 1 mM MgCl₂ bubbled with 95% O₂/5% CO₂. Acute slices (70 µm) were cut with a VT1200S vibratome (Leica). Slices were stored in artificial cerebrospinal fluid at room temperature until use; all experiments were performed within 4 h.

Electrophysiologic recordings

The posterior pituitary consists primarily of peptidergic nerve terminals with a mean diameter of ∼3 µm and a significant population of larger nerve terminals with diameters >10 µm (Nordmann, 1977). In the present study, we patch clamped large nerve terminals with diameters of 5–15 µm at or near the surface of a slice, located under visual guidance with laser scanning gradient contrast microscopy (Dodt and Zieglgänsberger, 1994; Mainen et al., 1999). Patch-clamp recordings from the larger nerve terminals of this preparation provide estimates of capacitance generally consistent with this size (Bielefeldt et al., 1992; Hsu and Jackson, 1996). Recordings in the whole-terminal configuration were obtained with an Axopatch 200B amplifier and digitized with a Digidata 1322A interface (Molecular Devices). Experimental control and data acquisition were performed with pClamp8 software (Molecular Devices). Slices were perfused with a recording solution consisting of 121 mM NaCl, 4 mM CsCl, 10 mM CaCl₂, 1 mM MgCl₂, 20 mM tetraethylammonium chloride, 2 mM 4-aminopyridine, 10 mM glucose, 0.003 mM tetrodotoxin, and 10 mM HEPES, pH 7.3. Recordings were performed with an internal patch pipette solution consisting of 130 mM CsCl, 10 mM Na phosphocreatine, 15 mM tetraethylammonium chloride, 4 mM Mg-ATP, 0.3 mM GTP, and 10 mM HEPES, pH 7.3. These solutions were designed to block voltage-gated Na⁺ and K⁺ channels to isolate Ca²⁺ current (I_Ca; Branchaw et al., 1997). In addition, the internal solution contained 50 or 100 µM of the Ca²⁺ indicator fluo-8 (Teflabs). Patch pipettes fabricated from borosilicate glass capillaries (King Precision Glass) had resistances of 2–5 MΩ when filled with internal solution. Leak current was corrected with a p/4 subtraction protocol. Data from nerve terminals in which I_Ca displayed prominent notches or humps suggestive of poor space clamp were discarded.

Western blotting

Frontal cortex, anterior pituitary, and posterior pituitary from 3-mo-old Sprague Dawley rats were homogenized separately with a Dounce homogenizer in 300 µl of lysis buffer (50 mM Tris-HCl, pH 8.0, 150 mM NaCl, and 1% IGEPAL CA-630; I8896; Sigma-Aldrich), with protease inhibitor cocktail (P8340; Sigma-Aldrich) and 1 mM PMSF. The homogenates were sonicated for 5 min on ice and centrifuged at 16,000 g for 20 min in 4°C to collect the supernatant. Protein concentrations were determined by BCA assay and adjusted to 1 µg/µl for all samples. A 15-µl aliquot of each sample was resolved on 15% SDS-PAGE gel, transferred to nitrocellulose membranes, and probed with rabbit anti-calbindin D28K (1:1,000, ab108404; Abcam), rabbit anti-calretinin (1:500, ab92341; Abcam), and rabbit anti-parvalbumin (1:1,000, ab11427; Abcam) antibodies, followed by secondary horse radish peroxidase conjugated antibody, and developed with enhanced chemiluminescence (Pierce Chemicals). The same membrane was then stripped with stripping buffer (1.5% glycine, 0.1% SDS, and 1% Tween 20, pH 2.2) for 15 min at room temperature, probed with mouse anti-actin (1:2,000; Abcam), goat anti-oxytocin (1:1,000, EB09854; Everest), or guinea pig anti–growth hormone antibodies (1:2,000). The experiments were repeated twice.

Ca²⁺ imaging and two-photon microscopy

Fluorescence images were acquired on a Prairie Ultima two-photon microscope (Bruker) using galvanometer-based scanning. A Chameleon Ti-sapphire laser (Coherent), tuned to 920 nm, delivered <100-fs pulses at ∼80 MHz. Epifluorescent light was collected with a 60×, 0.9 NA water-immersion objective, and transfluorescent light was collected with a 1.4 NA oil-immersion condenser. Collected light was filtered with 525/70-nm bandpass filters and detected with photomultiplier tubes. We used the high dynamic range, visible emission Ca²⁺ indicator fluo-8. At equilibrium, the fluorescence of such a dye is related to [Ca²⁺]_Free by the following equation (Maravall et al., 2000):

$${\left[{\text{Ca}}^{2+}\right]}_{\text{Free}}=K_{\text{d}}\frac{F-\frac{1}{R_f}}{1-F},$$ (1)

where F = f/f_max is the ratio of measured fluorescence to maximal fluorescence when the indicator is saturated with Ca²⁺; R_f = f_max/f_min is the dynamic range of the indicator. For fluo-8 we estimated an in vitro value for R_f of ∼150 from measurements in 10 mM EGTA and 10 mM CaCl₂. The manufacturer states that R_f > 200 , and for values as large as this uncertainties in its magnitude introduce errors in estimates in [Ca²⁺]_Free that are well below the measurement error of f (Maravall et al., 2000). For K_d of fluo-8, we used 390 nM as determined in posterior pituitary nerve terminal cytosol by in situ titration (McMahon and Jackson, 2014). This value equals that determined in vitro.

Dye loading after the establishment of a whole-terminal recording was monitored in real time by resting fluorescence, which stabilized within ∼30–60 s of break-in. Data were collected only after fluorescence had reached this plateau. We have routinely observed that the indicator dye remains in nerve terminals for up to an hour after the termination of a recording, suggesting minimal dye loss by axonal diffusion or leakage. We therefore assumed that the intracellular dye concentration equals that in the pipette.

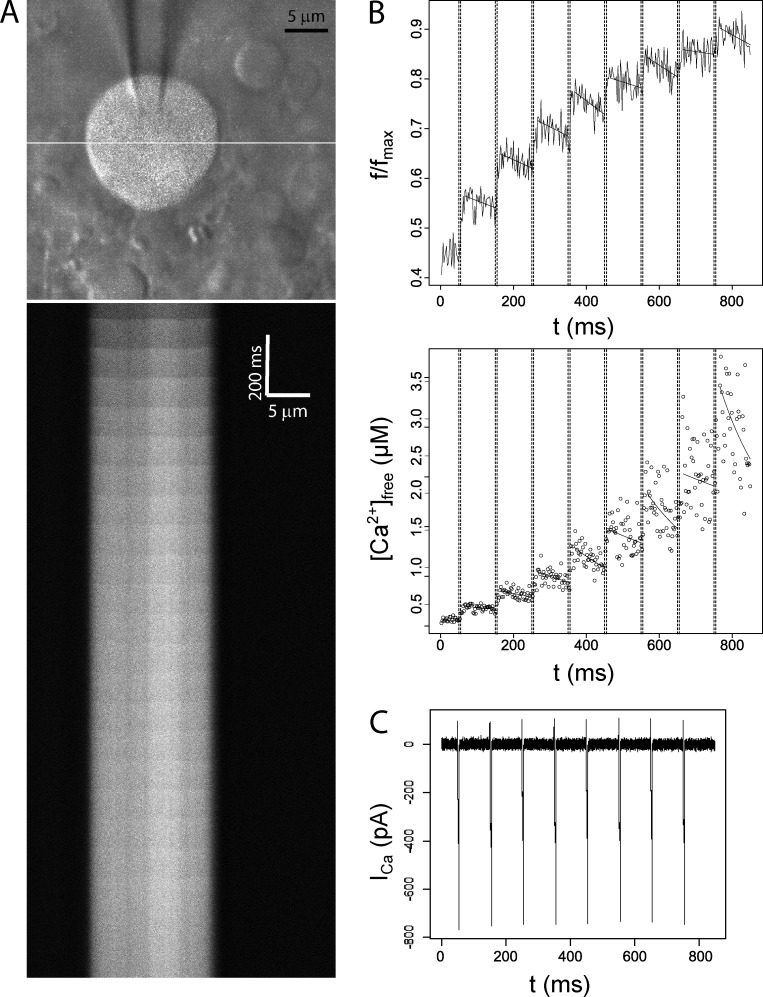
We acquired fluorescence in line-scan mode at 1 kHz while applying trains of 10–20 voltage steps of 5 ms at 100-ms intervals. This protocol serves as an effective stimulus for Ca²⁺ entry into pituitary nerve terminals (Jackson et al., 1991; Branchaw et al., 1997) and also approximates physiologic electrical activity of the neurohypophysis (Poulain and Wakerley, 1982). Fig. 1 illustrates a typical experiment. A nerve terminal was loaded with fluo-8, and fluorescence was scanned along the white line indicated in Fig. 1 A (top). Fig. 1 A (bottom) presents fluorescence versus distance along this line at 1-ms intervals over the course of a train of 20 voltage steps (10 Hz) from −80 to 10 mV. Each voltage step opened voltage-gated Ca²⁺ channels to produce I_Ca (Fig. 1 C), and fluorescence averaged over the scanned line segment increased in parallel (Fig. 1 B, top). Line scans revealed spatial gradients that collapsed within a few milliseconds, as can be seen in the delayed rise of the fluorescence signal near the center of the nerve terminal (Fig. 2 B). These spatial gradients were generally small compared with the total fluorescence (Fig. 2 C), and after collapse of the gradient, [Ca²⁺]_Free was taken to be spatially uniform. The extrusion of Ca²⁺ is sufficiently slow, that for many nerve terminals, spatially averaged fluorescence in the intervals between voltage steps remained approximately constant over the brief 100-ms interval between pulses, with no statistically significant time dependence. For these nerve terminals, the mean fluorescence over the interval was used for both the initial fluorescence, F_Initial, of the next pulse, and the final fluorescence, F_Final, of the preceding pulse. For other experiments, such as that presented in Fig. 1 B (top), a decline in fluorescence between pulses could be seen. The amount of extrusion was small and the time dependence of F could be well approximated by a linear fit. F_Initial and F_Final were estimated from these fits, as illustrated in Fig. 1 B (top).

Figure 1.

Fluorescence, calcium concentration, and calcium current in a fluo-8–loaded nerve terminal. (A, top) Overlay of two-photon fluorescence and gradient contrast images of a patch-clamped nerve terminal containing 50 µM fluo-8. The white line indicates the path for line scanning. (A, bottom) Line scan data show fluorescence as a function of position (x axis) and time (y axis). Fluorescence increases were evoked by a train of 20 voltage steps (5 ms, 10 Hz, from −80 to 10 mV). (B, top) Background-subtracted fluorescence within the terminal was averaged over the scanned line and plotted versus time for the first eight pulses of the train. Dashed lines indicate the time at which the voltage was stepped to 10 mV. The stimulus-evoked increase in f/f_max (F) was initially robust but decreased as the dye saturated. Solid lines after each pulse indicate a linear fit to the fluorescence used to estimate F_Final immediately after and F_Initial immediately before a pulse. (B, bottom) [Ca²⁺]_Free was calculated from F with Eq. 1. Stimulus-evoked Δ[Ca²⁺]_Free was initially modest but increased as Ca²⁺ buffers saturated. The curves in the bottom of B were computed from the linear fits to fluorescence displayed in the top of B. (C) I_Ca during the train of voltage steps.

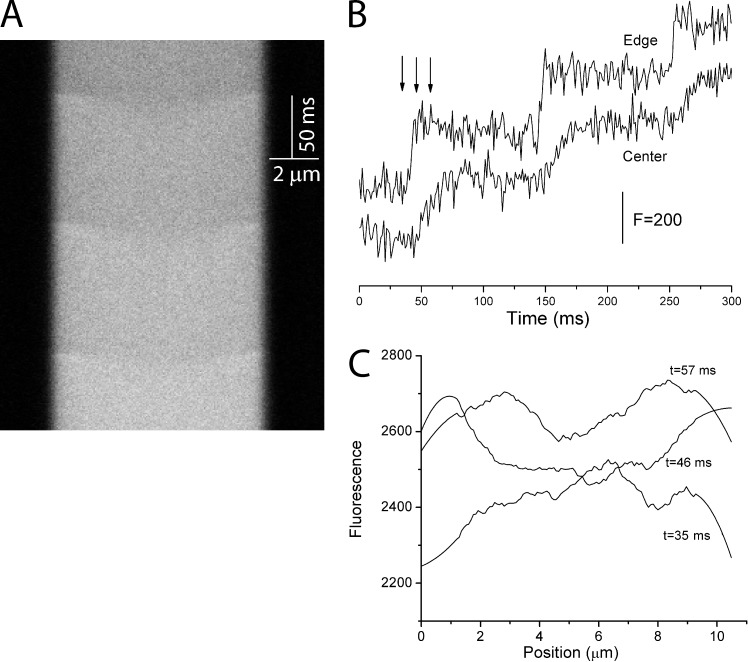
Figure 2.

Spatial calcium gradients form and collapse rapidly. (A) Line scan data as in Fig. 1 A (top) show fluorescence as a function of position and time but with an expanded time axis to show three of the steps from a train of 20 (5 ms, 10 Hz, from −80 to 10 mV). Fluo-8 concentration was 100 µM. (B) Plots of fluorescence versus time for 1.6-µm-wide segments near the nerve terminal edge and in the center. The three arrows indicate the time points used for C. (C) Plots of fluorescence versus position at the indicated times corresponding to the arrows in B. The scan at 35 ms was taken just before the first voltage pulse of the train. The scan at 46 ms was taken just after that voltage step and illustrates the delay in the fluorescence rise near center. The scan at 57 ms shows that the gradient has nearly collapsed. These plots were smoothed using a 30-point Savitzky–Golay filter in Origin.

Toward the end of a stimulus train, fluorescence reached a plateau, which reflected saturation of the dye rather than a [Ca²⁺]_Free steady state (McMahon and Jackson, 2014). We take this limiting value as f_max and use it to determine F (=f/f_max) in the calculation of [Ca²⁺]_Free with Eq. 1. Data from nerve terminals where ΔF for the final stimulus pulse was >1.5% of f_max were discarded on the grounds that f_max may be underestimated. Analysis with a more stringent condition (a cutoff of 0.5% or 1.0%) produced similar results, indicating that the analysis was not sensitive to the precise value of this cutoff. Because of uncertainty in [Ca²⁺]_Free as f approaches f_max (Eq. 1), measurements within two standard errors of f_max were excluded from the model fitting procedure.

Ca²⁺ buffering model

Simultaneous recordings of F and I_Ca provide measurement of [Ca²⁺]_Free and the amount of Ca²⁺ that enters, respectively. With a series of pulses as in Fig. 1, each pulse provides a point in a 3D space with the values of prepulse [Ca²⁺]_Free,Initial, postpulse [Ca²⁺]_Free,Final, and stimulus evoked change in total cytosolic Ca²⁺ concentration, Δ[Ca²⁺]_Total. These quantities are interrelated through the binding equilibriums of Ca²⁺ binding sites; therefore, fitting these data to a model for the titration of Ca²⁺ binding sites can provide estimates of cytosolic buffer properties (McMahon and Jackson, 2014). Using equilibrium binding expressions for Δ[Ca²⁺]_Total in terms of [Ca²⁺]_Free,Initial and [Ca²⁺]_Free,Final, denoted here as Ca₁ and Ca₂, respectively, the relevant measured quantities in a nerve terminal containing fluo-8 and two endogenous buffers are related by the following expression (McMahon and Jackson, 2014):

$$\begin{array}{l}\Delta {\left[{\text{Ca}}^{2+}\right]}_{\text{Total}}=\left({\text{Ca}}_2-{\text{Ca}}_1\right)+\left[D\right]\left(\frac{{\text{Ca}}_2}{K_{\text{d,dye}}+{\text{Ca}}_2}-\frac{{\text{Ca}}_1}{K_{\text{d,dye}}+{\text{Ca}}_1}\right)+\\ \left[B_{e1}\right]\left(\frac{{\text{Ca}}_2}{K_{\text{d},e1}+{\text{Ca}}_2}-\frac{{\text{Ca}}_1}{K_{\text{d},e1}+{\text{Ca}}_1}\right)+\left[B_{e2}\right]\left(\frac{{\text{Ca}}_2}{K_{\text{d},e2}+{\text{Ca}}_2}-\frac{{\text{Ca}}_1}{K_{\text{d},e2}+{\text{Ca}}_1}\right),\end{array}$$ (2)

where [D] is dye concentration and Ca₁ and Ca₂ are calculated from F using Eq. 1. We obtain Δ[Ca²⁺]_Total by integrating I_Ca and dividing by terminal volume measured from 3D reconstruction of fluorescence photosections. This volume was multiplied by the fraction that was accessible, and this quantity was treated as a free parameter during the model fitting process. The terms on the right in Eq. 2 represent the change in [Ca²⁺]_Free, the change in Ca²⁺ dye complex, and the changes in complexes of Ca²⁺ with two cytosolic buffers. Note that the free parameters relating to endogenous buffers are all in the final two terms. Trains of 10–20 stimuli were applied 10 times at 20-s intervals to yield large 3D datasets with ∼200 points for fitting to Eq. 2. Dropping the final term, e2, provided a model with one cytosolic buffer. To model buffer washout with time, we extended Eq. 2 by multiplying the terms for e1 and/or e2 by an exponential decay factor.

The Ca²⁺ buffering capacity of Ca²⁺ binding species i can be calculated as a function of [Ca²⁺]_Free with the following equation (Neher and Augustine, 1992):

$${\kappa }_i=\frac{K_{\text{d},i}{\left[B\right]}_i}{{\left(K_{\text{d},i}+{\left[{\text{Ca}}^{2+}\right]}_{\text{Free}}\right)}^2}.$$ (3)

This equation provides a convenient means of presenting data and for summing the contributions of multiple species.

Data analysis and computational details

Data analysis and model fitting were performed in the statistical computing environment R (R Development Core Team). Results are presented as mean ± SE. The Ca²⁺ buffering models were fitted by a total least squares procedure, which accounts for errors in the three independent variables measured experimentally. For fits to Eq. 2, [Ca²⁺]_Free was expressed in terms of F so that we fitted to data with normally distributed errors. The data were fitted to two competing models with either one or two endogenous buffers by a custom stochastic gradient descent algorithm, which has been extensively tested and validated with simulated datasets (McMahon and Jackson, 2014). Fits were evaluated with the f test (threshold: P = 0.01), and data were discarded when the P values for any parameter were not significant at the P = 0.01 level (using P = 0.1 or 0.05 for either the f test or parameter significance produced similar results). The computer program Origin 8.0 (OriginLab) was used for some plots and smoothing.

RESULTS

Endogenous buffer saturation

Large posterior pituitary nerve terminals were patch clamped in the whole-terminal configuration using patch pipettes containing the Ca²⁺ indicator fluo-8 (Fig. 1 A, top), and two-photon imaging enabled us to measure Ca²⁺. Once dye loading was complete (within 30–60 s of break-in), imaging experiments commenced. Voltage steps opened Ca²⁺ channels to elicit Ca²⁺ entry, and applying a series of voltage steps in rapid succession provided a titration curve of the Ca²⁺ binding molecules in the nerve terminal, including both the Ca²⁺ dye and endogenous cytosolic Ca²⁺ buffers. Averaging fluorescence over the scanned line and plotting the spatial mean versus time showed that the fluorescence changes were nearly synchronous with the simultaneously recorded Ca²⁺ current (I_Ca; Fig. 1 B, top). With a series of voltage steps, these fluorescence changes became smaller until they were barely visible. In contrast, the changes in [Ca²⁺]_Free computed from these fluorescence changes (Eq. 1, see Materials and methods) grew larger (Fig. 1 B, bottom), even as the Ca²⁺ entry per pulse, determined from I_Ca, remained relatively constant (Fig. 1 C). This indicates that Ca²⁺ binding sites within the nerve terminals saturate with increasing [Ca²⁺]_Free.

The nearly horizontal boundaries in the line scans in Fig. 1 A (bottom) indicated that Ca²⁺ equilibrated through diffusion and binding within a few milliseconds during and immediately after each voltage step. To illustrate the spatial gradients and their collapse more clearly, a line scan from another nerve terminal focused on the first three voltage steps (Fig. 2). With this timescale, the line scan illustrates the transient spatial gradients more clearly as sags in the boundaries at each voltage pulse (Fig. 2 A). The time course of fluorescence near the edge of the nerve terminal showed rapid increases that began at the start of each voltage pulse and ended when the 5-ms voltage pulse ended (Fig. 2 B). In contrast, the fluorescence at the center increased more slowly with a slight delay. A plot of fluorescence versus position shows roughly uniform fluorescence immediately before the first step (t = 35 ms; Fig. 2 C). A spatial gradient was seen ∼5 ms after the first step (t = 46 ms), and fluorescence became uniform ∼10 ms later (t = 57 ms). Therefore, the spatial and temporal characteristics of the fluorescence changes indicate that the continued increases in spatially averaged fluorescence and [Ca²⁺]_Free immediately after the end of each pulse (Fig. 1 B) reflect spatial equilibration rather than a rapid Ca²⁺-induced Ca²⁺ release. This is consistent with the lack of effects of ryanodine and thapsigargin in pituitary nerve terminals (Stuenkel, 1994). These results indicate that binding sites relevant to our titration analysis equilibrate rapidly in space and time and validate our use of a model based on equilibrium binding (Eq. 2). The spatial gradient during a voltage step decays rapidly, and even at its greatest (t = 46 ms; Fig. 2 C), fluorescence varies by <10%. This justifies our use of spatially averaged fluorescence in the calculation of [Ca²⁺]_Free in Eq. 1.

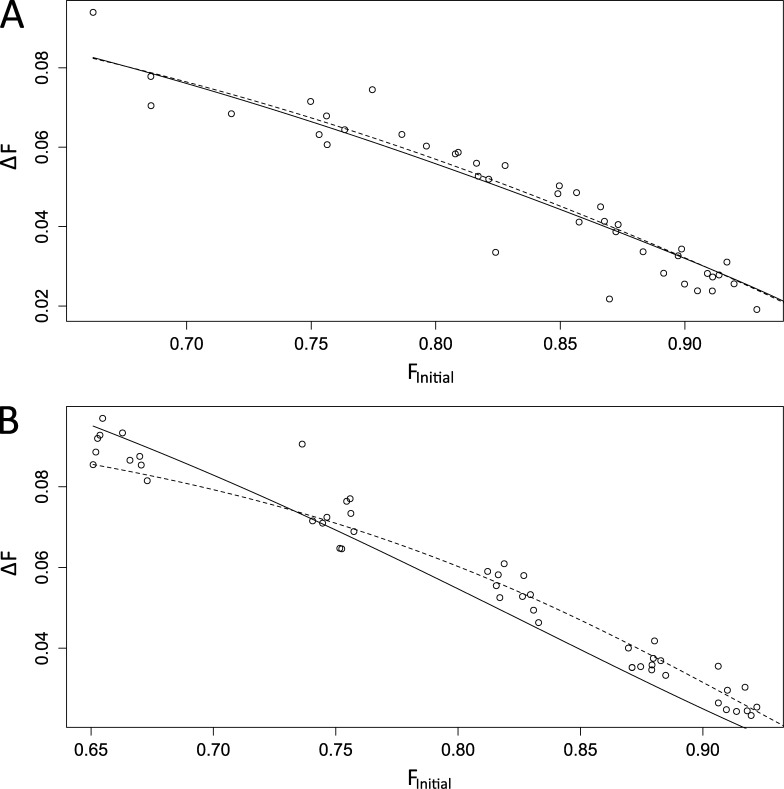
Data of the form presented in Figs. 1 and 2 provided measurements of the Ca²⁺ concentration before a step, [Ca²⁺]_Free,Initial, the Ca²⁺ concentration after a step, [Ca²⁺]_Free,Final, and the change in total Ca²⁺ concentration during a step, Δ[Ca²⁺]_Total (determined by integrating I_Ca). At equilibrium these quantities will satisfy Eq. 2 (see Materials and methods), and this expression provides a framework for assessing Ca²⁺ binding interactions with the indicator dye and endogenous buffers. The rapid collapse of spatial gradients seen in Fig. 2 indicates that the equilibrium among the relevant Ca²⁺ binding sites is reached rapidly. The decays between steps indicate that Ca²⁺ removal during the interpulse intervals is too slow to be relevant to these binding equilibriums. Fitting our [Ca²⁺]_Free and I_Ca measurements to this model yielded the concentrations and K_d values of the endogenous buffers. These fits involving three experimental quantities can be displayed with 3D plots, but this form of display is difficult to evaluate visually (McMahon and Jackson, 2014). However, I_Ca, and therefore Δ[Ca²⁺]_Total, usually remained relatively constant over the course of an experiment (Fig. 1 C). This reduces the dimensionality of the experiment from three to two, and makes it easier to view results. Plots of ΔF versus F_Initial illustrate the quality of fits, and plotting F rather than [Ca²⁺]_Free preserves the homoscedasticity of errors, i.e., it gives uniform scatter over the range of values plotted. Fig. 3 A displays data from a nerve terminal where including only one endogenous buffer in Eq. 2 produced a satisfactory fit. Fits to one- and two-buffer models both fell within the scatter of data, yielding visually identical and statistically indistinguishable fits. Fig. 3 B displays another dataset where a two-buffer model (dashed curve) provided a better fit; the one-buffer fit clearly fell outside the scatter of data points, whereas the two-buffer fit fell within this scatter and satisfied our goodness-of-fit criterion.

Figure 3.

Model fits are displayed for plots of F_Initial and ΔF. In general, Δ[Ca²⁺]_Total (obtained from I_Ca) displayed little variation (∼10–20%) during the stimulus train, whereas ΔF could change by an order of magnitude. In this plot, we fixed Δ[Ca²⁺]_Total to its mean value and plotted ΔF versus F_Initial. Solid lines indicate best fits of Eq. 2 with a single endogenous buffer; dashed lines show the fit with two endogenous buffers. (A) The one-buffer model provided a satisfactory fit to this dataset. Small deviations of the model from the data were not significant. (B) The one-buffer model failed to fit the data from this nerve terminal, but the two-buffer model provided a satisfactory fit.

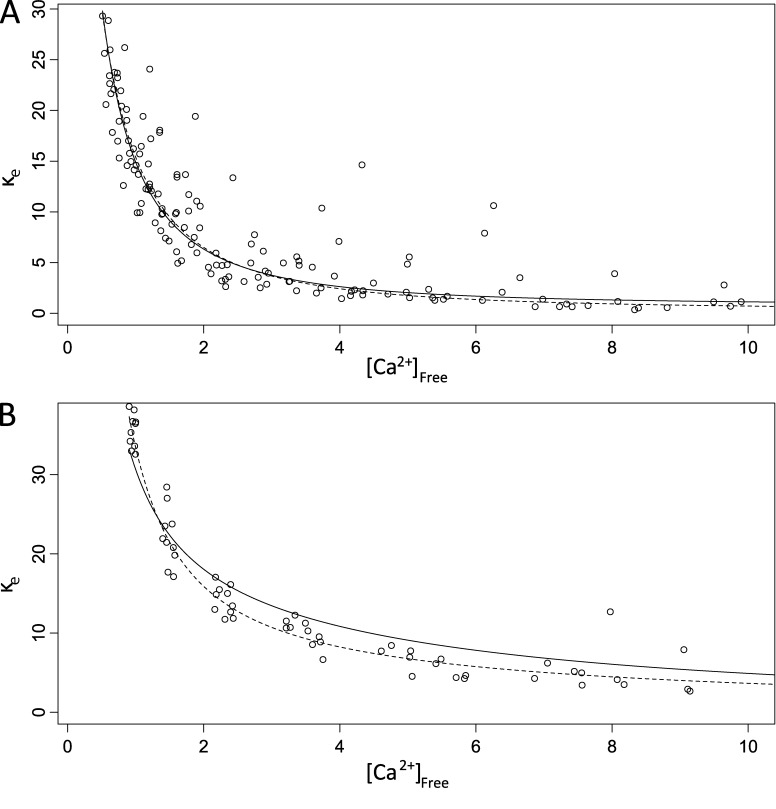
To illustrate the saturation of endogenous buffers, we calculated the total endogenous Ca²⁺ buffer capacity, κ_e, as Δ[Ca²⁺]_Total/Δ[Ca²⁺]_Free minus the dye buffering capacity computed from Eq. 3. These plots show that κ_e declined as [Ca²⁺]_Free rose (Fig. 4) and provide another visual assessment of the model fits that has the added benefit of displaying the saturation of buffers (at the expense of nonuniform scatter). These plots also permit a comparison of one-buffer and two-buffer fits, where a one-buffer curve was calculated from a single term of Eq. 3 with K_d and [B] from the fit, and a two-buffer curve was calculated as the sum of two such terms. The data in Fig. 4 A were well described by a one-buffer model, and the two-buffer fit was indistinguishable (dashed line). In Fig. 4 B the two-buffer model described the decline in κ_e over a wide range of [Ca²⁺]_Free, whereas the one-buffer model clearly deviated from the data.

Figure 4.

Buffer capacity declines as free calcium concentration rises. (A) Plots of endogenous buffer capacity (κ_e) versus [Ca²⁺]_Free for a nerve terminal well fitted by a single endogenous buffer (Eq. 2 with e1 only, as in Fig. 3 A but from a different nerve terminal). The curves were calculated from one or two terms of the form of Eq. 3 with the parameters from the fits. (B) A nerve terminal with two endogenous buffer components (Eq. 2 with both e1 and e2; same nerve terminal as in Fig. 3 B). Solid black curves show the model fit with a single endogenous buffer; dashed curves show a model fit with two endogenous buffers. For A, adding a second buffer provided no improvement, and the fits were indistinguishable. For B, the two-buffer model provided a clear improvement. The single-buffer fit (A) yielded K_d,e1 = 1.5 µM and [B_e1] = 114 µM. The two-buffer fit (B) yielded K_d,e1 = 0.293 µM, [B_e1] = 33 µM, K_d,e2 = 9 µM, and [B_e2] = 60 µM.

Approximately half our datasets (8 of 17 nerve terminals) were well described by a model containing a single endogenous buffer (as in Figs. 3 A and 4 A), whereas in the other nine nerve terminals a model with two endogenous buffers provided a significant improvement and gave a satisfactory fit (Figs. 3 B and 4 B). Table 1 presents the mean values and standard errors for the concentrations and K_d values of the endogenous buffers determined from these fits, the fraction of excluded volume (a free parameter of the model determined during the fitting), and resting [Ca²⁺]_Free ([Ca²⁺]_Free,0, determined with Eq. 1 from the resting fluorescence). All nerve terminals examined contained a low-affinity buffer. In the one-buffer dataset we found K_d = 1.5 µM and binding site concentration of 170 µM. In the two-buffer dataset we found K_d = 4.7 µM and concentration of 140 µM for the low-affinity buffer. For the high-affinity buffer of this group we found K_d = 0.385 µM and concentration of 340 µM. The mean accessible volume fraction of the single-buffer nerve terminals was slightly higher than that of the two-buffer nerve terminals, but this difference was not statistically significant; the [Ca²⁺]_Free,0 values were essentially the same.

Table 1.

Buffer and nerve terminal properties

Terminals	Kd,e1	BT,e1	Kd,e2	BT,e2	VA	[Ca2+]Free,0	n
	µM	µM	µM	µM		µM
One buffer	1.5 ± 0.2	170 ± 46	-	-	0.52 ± 0.10	0.607 ± 0.13	8
Two buffer	0.38 ± 0.08	340 ± 110	4.7 ± 0.8	140 ± 40	0.38 ± 0.05	0.570 ± 0.09	9

Properties of endogenous Ca²⁺ buffers in nerve terminals with one or two species. K_d and B_T are the dissociation constant and total concentration of endogenous buffers, respectively (Eq. 2). V_A is the fraction of total cellular volume accessible to Ca²⁺; [Ca²⁺]_Free,0 is the resting Ca²⁺ concentration computed from resting F with Eq. 1.

At these resting [Ca²⁺]_Free,0 levels, the one-buffer nerve terminals have a κ_e value of 57 (Eq. 3). The two-buffer nerve terminals have a total κ_e of 167, which breaks down to 24 for the low-affinity buffer and 143 for the high-affinity buffer. This suggests that the high-affinity buffer, when present, will have a major impact on Ca²⁺ rises near rest.

Detection of Ca²⁺ binding proteins

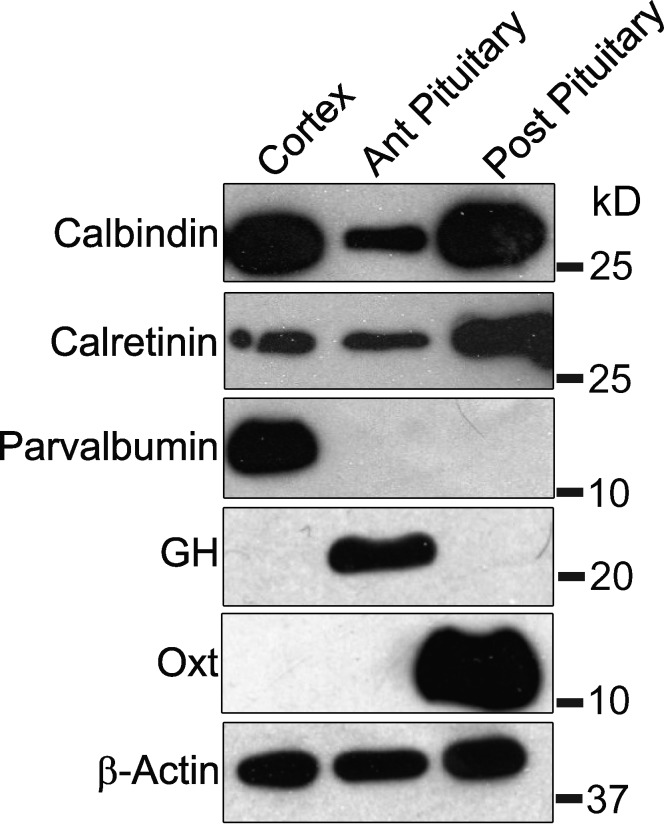
The nervous system has three major cytosolic Ca²⁺ buffer proteins, calbindin D28K, calretinin, and parvalbumin (Schwaller, 2010). To assess their expression in the posterior pituitary we performed Western blots of these proteins along with blots for markers of the anterior and posterior lobes of the pituitary. The frontal cortex, which expresses all three Ca²⁺ binding proteins, was used as a positive control. Both the anterior and posterior pituitary expressed calretinin and calbindin D28K but not parvalbumin (Fig. 5). The signals for both were especially strong in the posterior pituitary. (The slightly weaker band for calretinin in the cortex resembles data available from the manufacturer and does not indicate a low level.) These results suggest that the posterior pituitary has higher levels of calretinin than the cortex, whereas the anterior pituitary has lower levels. (Samples in each lane contained the same total protein, and similar β-actin levels were observed). Pituitary hormones were used as markers and showed the expected pattern of expression, with growth hormone detected in the anterior pituitary and oxytocin detected in the posterior pituitary. We detected no parvalbumin in either the anterior or posterior pituitary, in sharp contrast with the strong signal in the cortex. This experiment demonstrated that the posterior pituitary expresses calbindin D28K and calretinin, but not parvalbumin. Therefore, these two proteins are likely to serve as the endogenous Ca²⁺ buffers observed in our imaging experiments.

Figure 5.

Western blots show the expression levels of three Ca²⁺-binding proteins in the frontal cortex, anterior pituitary, and posterior pituitary. Calbindin D28K is more abundant in the frontal cortex and posterior (Post) pituitary than the anterior (Ant) pituitary; calretinin is especially abundant in the posterior pituitary; parvalbumin is only seen in the frontal cortex. The anterior pituitary hormone, growth hormone (GH), and posterior pituitary hormone, oxytocin (Oxt), serve as markers and illustrate complete separation of the two structures during dissection. 15 µg of total protein was loaded for all samples, as verified by similar levels of β-actin. For each sample, the corresponding protein standard is indicated as the number at right.

Buffer mobility and washout

Endogenous Ca²⁺ buffers can be categorized as either fixed or mobile, and this distinction has major functional consequences: mobile buffers accelerate diffusion, and immobile buffers retard diffusion (Sala and Hernández-Cruz, 1990; Zhou and Neher, 1993; Delvendahl et al., 2015). We explored buffer mobility by evaluating the decrease in Ca²⁺ buffering over time caused by washout during whole-terminal patch-clamp recordings. For this analysis we first focused on recordings from 15 nerve terminals that remained stable for ≥10 min and compared the buffering capacity determined shortly after break-in with the buffering capacity determined 10 min later. This group included some experiments for which fits to Eq. 2 failed and did not include those nerve terminals yielding satisfactory fits to Eq. 2 (Figs. 3 and 4) that lasted <10 min. To determine κ_e for this group of 15 without fitting to Eq. 2, we used a model-independent method in which Δ[Ca²⁺]_Total was divided by Δ[Ca²⁺]_Free, and the dye buffering capacity, κ_d, was calculated from Eq. 3 (κ_e in Fig. 4 was calculated this way as well). κ_e determined in this way declined by 37%, and the exponential decay time calculated from the 0- and 10-min time points was 1,300 ± 210 s. There was no significant difference between the decline in κ_e between one-buffer and two-buffer nerve terminals. However, the 15 terminals used in this comparison included only three one-buffer nerve terminals. For reasons that are unclear, recordings from one-buffer terminals appeared to be less stable.

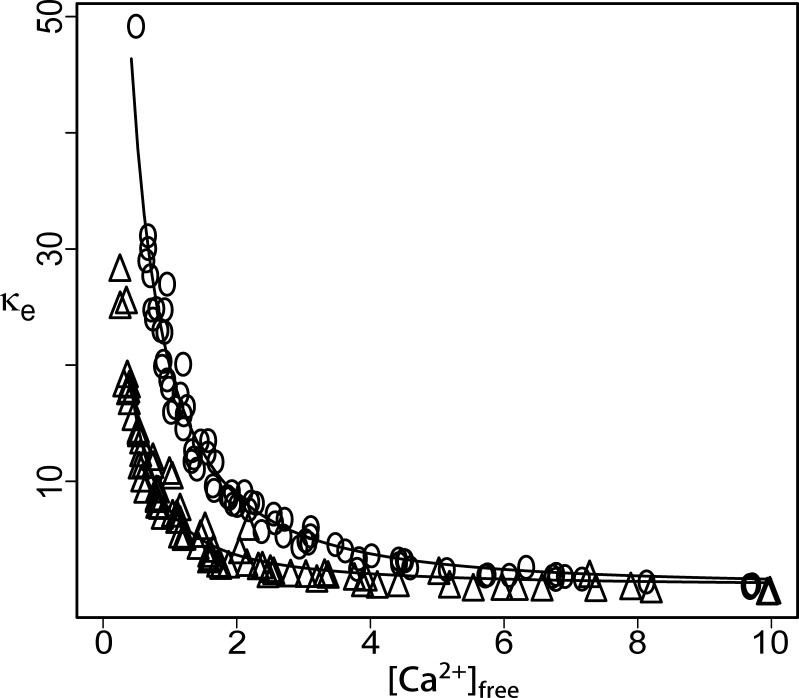
Fig. 6 presents an especially clear example of buffer washout from a nerve terminal. κ_e, determined as just described above and for Fig. 4 (from Δ[Ca²⁺]_Total, Δ[Ca²⁺]_Free, and κ_d), was plotted versus [Ca²⁺]_Free. The plot from data obtained ∼10 min after break-in (Fig. 6, open triangles) fell well below the earlier plot obtained from the first train of pulses applied shortly after fluorescence stabilization (∼30 s after break-in; Fig. 6, open circles). This difference was observed over the entire range of [Ca²⁺]_Free. Although the fractional change in κ_e appears greater at high [Ca²⁺]_Free, analysis described in the next paragraph supports a general conclusion of washout of the high-affinity component, with no statistically significant loss of the low-affinity component.

Figure 6.

Endogenous Ca²⁺ buffering capacity (κ_e) is reduced during the ∼10 min of whole-cell recording. Open circles show κ_e shortly after break in. After 10 min of dialysis (open triangles), a significant fraction of the endogenous buffering capacity was lost. Smooth curves show the model fits from trains collected at the relevant time points.

We also evaluated buffer washout using a modification of the model represented by Eq. 2. We multiplied the concentration of buffer species e1, [B_e1], by an exponential decay factor of the form e^−t/τ. t represents time after break-in, and τ represents the time constant of washout of buffer species e1. This model was then fitted to data from 20 trains of voltage steps collected over 5–6 min of recording. This fit involved varying the parameters of Eq. 2, as well as τ. None of the eight single-buffer nerve terminals (Table 1, top row) showed a statistically significant decay in buffering capacity; 1/τ (the rate of buffer washout) was indistinguishable from zero in all cases. Of the nine two-buffer nerve terminals (Table 1, bottom row), the fits to four were improved by including the exponential washout factor, whereas fits to the other five showed no improvement. The rate of washout is inversely proportional to cell volume (Pusch and Neher, 1988), and it is noteworthy that the four nerve terminals yielding a significant value for τ had a mean volume of 900 ± 300 µm³, whereas the five two-buffer nerve terminals not yielding a τ value had a mean volume of 1,800 ± 270 µm³. The eight one-buffer nerve terminals, none of which yielded a τ value, also had larger volumes of 1,700 ± 600 µm³.

We also modified our mobile buffer model by multiplying both [B_e1] and [B_e2] of the two buffers of Eq. 2 by the same exponential factor and fitted this version to the data from the eight two-buffer nerve terminals. This enabled us to test the hypothesis that both buffers washed out at the same rate. Bootstrap resampling indicated that in no instance did this model improve the fits compared with a model where only one of the two buffers was mobile. Overall, the results of these fits to extended models with mobile buffers indicate that the high-affinity buffer is mobile and that the low-affinity buffer is not sufficiently mobile to produce detectable washout.

Fits to our extended model with one mobile species yielded properties for the two buffers presented in Table 2. These values are similar to those from the aforementioned two-buffer fits for model fitting with no washout (Table 1, bottom row). The mobile buffer in these experiments declined with a time constant of τ = 243 ± 56 s. To compare τ values across nerve terminals, one must take into account the dependence of washout on cell volume and access resistance (Pusch and Neher, 1988). Taking each τ value and factoring in the values of series resistance and volume from that nerve terminal, Eqs. 17 and 18 from Pusch and Neher (1988) gave a diffusion constant, D = 12 ± 1 µm²/s from the 10-min decline measurements of 15 nerve terminals and 14 ± 3 µm²/s for the four extended model fits where significant washout was seen. (Note that the D values have smaller errors than the τ values because the volumes and access resistances contribute to the variability in τ.) Based on the Stokes–Einstein equation, these D values correspond to apparent molecular weights of 1.3 and 0.9 MD, respectively.

Table 2.

Mobile buffer in two-buffer terminals

Buffer	Kd,e1	BT,e1	Kd,e2	BT,e2	VA	τ	[Ca2+]Free,0	n
	µM	µM	µM	µM		s	µM
Immobile	0.47 ± 0.09	230 ± 90	5.5 ± 1.2	105 ± 8	0.39 ± 0.08	-	0.612 ± 0.08	5
Mobile	0.28 ± 0.14	470 ± 210	3.5 ± 0.7	180 ± 90	0.37 ± 0.06	243 ± 56	0.603 ± 0.11	4

Endogenous Ca²⁺ buffer properties from nerve terminals with two endogenous buffers, where either both components appear to have undetectable mobility (top row) or the higher-affinity buffer has a significantly higher mobility (bottom row). K_d,e1, B_T,e1, K_d,e2, B_T,e2, and τ were determined by fitting to Eq. 2, with the inclusion of an exponential factor multiplying [B_e1] and allowing the time constant to vary. V_A and [Ca²⁺]_Free,0 were as described in Table 1. τ gives the time constant for exponential decay of the concentration of the high-affinity endogenous buffer by diffusion into the patch pipette. For the top row, no washout could be detected. The fitting yielded a value for τ indistinguishable from zero.

DISCUSSION

In this study, we characterized the properties of distinct molecular species that contribute to the complex dynamics of Ca²⁺ signaling in posterior pituitary nerve terminals. The increase in step size of [Ca²⁺]_Free during depolarizing trains (Fig. 1, B [top] and C) served as the critical observation that enabled us to go beyond the standard determination of concentration independent κ_e values. Therefore, we were able to use a saturable titration model to determined K_d and concentration and take the additional step of resolving two endogenous Ca²⁺ binding species. This analysis provided an assessment of cytosolic Ca²⁺ buffer properties directly from a study of their functional impact on cellular Ca²⁺ signals. All nerve terminals contained a relatively immobile low-affinity buffer, and approximately half contained an additional weakly mobile high-affinity buffer. The Ca²⁺ binding proteins present in the cytoplasm of pituitary nerve terminals will determine the action of Ca²⁺ on the secretion apparatus, and their saturation will modify these responses over time during repetitive activity.

Endogenous Ca²⁺ buffers

Our analysis revealed the presence of two endogenous Ca²⁺ buffers, but not in all nerve terminals. Nerve terminals fell into two categories, one with both a high-affinity and low-affinity buffer and another with only a low-affinity buffer. In both populations Ca²⁺ buffering at rest was comparable with that observed in other preparations, with κ_e falling within the range of previous observations of ∼40–200 (Neher, 1995). A previous study of Ca²⁺ buffering in dissociated pituitary nerve terminals determined κ_e to be ∼175 (Stuenkel, 1994). This value is somewhat greater than our estimate of resting κ_e = 124 for two-buffer terminals and substantially greater than our estimate of κ_e = 57 for one-buffer terminals. These differences most likely reflect a lower resting [Ca²⁺]_Free in the experiments of the previous study (Stuenkel, 1994), which would make more Ca²⁺ binding sites available.

Roughly half the pituitary nerve terminals contain high-affinity buffer, with a K_d of 385 nM and concentration of 340 µM. All nerve terminals contain a lower-affinity buffer with a higher K_d of 1.5–4.7 µM and concentration of 140–170 µM (Table 1). Our Western blots revealed the presence of both calretinin and calbindin D28K in the posterior pituitary. The high-affinity component is consistent with the ∼200–500 nM in vitro K_d range for calbindin D28K. The K_d of our one-buffer terminals was the same as the ∼1.5 µM in vitro K_d of calretinin (Schwaller, 2010; Alpár et al., 2012), but the low-affinity component of our two-buffer terminals had a higher K_d of 4.7 µM. Overall, our biochemical detection of calbindin D28K and calretinin (Fig. 5) is consistent with our fluorometric titration results. An earlier and simpler version of this titration method identified a cytosolic buffer in hippocampal granule cell axons with properties close to the known cytosolic buffer of these neurons, calbindin D28K (Jackson and Redman, 2003), and subsequent immunocytochemical analysis confirmed our fluorometric estimate of the concentration of this species (Müller et al., 2005). The concentrations of cytosolic buffer proteins determined here in nerve terminal cytoplasm in Table 1 can be converted to protein concentrations by dividing by four functional Ca²⁺ binding sites for calbindin D28K and five for calretinin (Schwaller, 2010). These multiple binding sites on each protein do not differ widely in affinity, and single-site noncooperative binding models used here adequately approximate their collective impact on the saturation of Ca²⁺ signals.

Although our in situ K_d values are close to published in vitro values, such comparisons must recognize the following: (1) cytosolic Ca²⁺ buffers can have multiple nonequivalent sites and cooperative binding; (2) Mg²⁺ competes with some Ca²⁺ binding sites to varying degrees; and (3) the cytosolic environment can alter affinities, as seen with organic chelators (Thomas et al., 2000; Hagen et al., 2012). Indeed, these considerations underscore the need for studies of cytosolic buffers in situ as conducted here. Our fluorometric analysis is consistent with the absence of parvalbumin in Western blots because parvalbumin has a much lower K_d than the high-affinity component determined here. The rapid equilibration seen in our line scans is also consistent with the absence of parvalbumin because parvalbumin equilibrates slowly (Lee at al., 2000). In any case, at the relatively high resting [Ca²⁺]_Free,0 of pituitary nerve terminals, parvalbumin would be largely saturated.

The nerve terminals of the posterior pituitary are heterogeneous, with half releasing oxytocin and half releasing vasopressin. Our results suggest that cytosolic buffer content is also heterogeneous. Posterior pituitary nerve terminals have also been distinguished on the basis of volume, electrophysiologic properties, and presence of other neuropeptides (Bondy et al., 1989; OuYang et al., 2004). The nerve terminals with only low-affinity buffer had a mean volume of 1,730 ± 570 µm³, compared with 1,390 ± 230 µm³ for terminals with both buffer components; however, this difference was not statistically significant.

In addition to Ca²⁺ binding proteins, cytoplasm contains several other Ca²⁺ binding molecules, including small molecules such as ATP (Baylor and Hollingworth, 1998), Ca²⁺ signaling proteins such as calmodulin, and polar phospholipids. ATP is present at high concentrations and has fast binding kinetics, but its low affinity would make its contribution negligible even at millimolar concentrations (as is readily shown with Eq. 3). Other Ca²⁺ binding molecules, presumably with a range of affinities, could contribute to saturable buffering, and our K_d estimates could reflect some aggregate behavior. Such aggregate effects may account at least in part for the higher K_d of the low-affinity component (Table 1) compared with the in vitro K_d of calretinin.

Buffer mobility

Endogenous Ca²⁺ buffers washed out of nerve terminals during whole-terminal patch clamp recording, but very slowly. Although a previous study of pituitary terminals suggested that κ_e was stable for 5 min (Stuenkel, 1994), the lower bound to the mass of the buffer estimated in that study of 125 kD, determined by the same equations we used (Pusch and Neher, 1988), was well below our estimate of ∼1 MD; therefore, there is no real disagreement. In the present study we were able to observe buffer washout because of longer recording times and more sensitive instrumentation (smaller volumes and lower series resistances may also be significant factors). The expected M^1/3 dependence of the diffusion constant on molecular weight of a globular protein suggests that the washout we observed is ∼3.2-fold slower than that expected for calbindin D28K (28 kD) and calretinin (31 kD). If these proteins were completely free to diffuse, the washout would have been observable in our experiments, especially in nerve terminals with larger volumes. This suggests that posterior pituitary nerve terminals have little if any freely diffusing buffer.

The slow washout indicates that essentially all of the endogenous buffer interacts with cytoskeleton and intracellular membrane to impede diffusion. The factor of approximately three reduction in washout time can most easily be interpreted in terms of a loose tethering in which approximately one third of the protein is free, and the free and bound fractions equilibrate in under ∼1 min. The clear association of washout with the high-affinity component in our extended fits suggests that the high-affinity buffer, presumably calbindin D28K, is more mobile than the low-affinity buffer, presumably calretinin. Reduced mobility is consistent with our failure to detect parvalbumin. This protein has a very low molecular weight (12 kD) and no known binding partners or signaling functions (Schwaller, 2010); therefore, it is not likely to be tethered. Both calbindin D28K and calretinin display significant conformational changes on Ca²⁺ binding and have known binding partners (Schwaller, 2010). Calbindin D28K is immobile in cerebellar axons (Schmidt et al., 2005), and calretinin exhibits anomalously slow diffusion in cerebellar neurons (Arendt et al., 2013). The very slow washout of endogenous buffer in our experiments is consistent with these results. Several secretory cell types have immobile endogenous buffers with much lower affinities than those observed in the present study, but the molecular identity of these Ca²⁺ binding sites has not been established (Xu et al., 1997; Habets and Borst, 2006; Matthews et al., 2013; Delvendahl et al., 2015; Nakamura et al., 2015).

Implications for facilitation

High-frequency electrical stimulation facilitates neurotransmitter release from many nerve terminals (Zucker and Regehr, 2002), including those of the posterior pituitary (Poulain and Wakerley, 1982; Gainer et al., 1986). Theoretical and computational investigations of presynaptic Ca²⁺ suggest that buffering can contribute to this form of short-term plasticity (Klingauf and Neher, 1997; Matveev et al., 2004). Paired-pulse facilitation can be induced at normally nonfacilitating synapses by exogenous chelator (Rozov et al., 2001), and saturation of calbindin D28K underlies paired-pulse facilitation in multipolar bursting cells and mossy fiber terminals (Blatow et al., 2003). The saturation of endogenous Ca²⁺ buffers described here will amplify presynaptic Ca²⁺ signals during repetitive activity and therefore contribute to the frequency-dependent facilitation of release from the posterior pituitary. This mechanism would then be additive with action potential broadening (Gainer et al., 1986; Bourque, 1990; Jackson et al., 1991) and Ca²⁺-dependent nitric oxide synthase-mediated reduction in action potential failure (Klyachko et al., 2001; Zhang et al., 2007).

Calbindin D28K is already partly saturated at [Ca²⁺]_Free,0 and will amplify stimulus-induced Ca²⁺ increases as soon as they start, but calretinin with its higher K_d will have its impact at higher levels of [Ca²⁺]_Free where mitochondrial sequestration also comes into play (Stuenkel, 1994; Kosterin et al., 2005). The heterogeneity of pituitary nerve terminals mentioned earlier in the Discussion includes differences in the frequency dependence and optimal patterns of activity that elicit vasopressin and oxytocin release (Poulain and Wakerley, 1982; Gainer et al., 1986; Cazalis et al., 1987; Bicknell, 1988). If the heterogeneity in Ca²⁺ buffers reported here is associated with neuropeptide content, this could underlie some of the differences in secretion behavior. Two populations of nerve terminals with different cytosolic Ca²⁺ buffers will define distinct ranges of [Ca²⁺]_Free over which buffer saturation will amplify Ca²⁺ signals.