Revised Parameters for the AMOEBA Polarizable Atomic Multipole Water Model

Abstract

A set of improved parameters for the AMOEBA polarizable atomic multipole water model is developed. The protocol uses an automated procedure, ForceBalance, to adjust model parameters to enforce agreement with ab initio-derived results for water clusters and experimentally obtained data for a variety of liquid phase properties across a broad temperature range. The values reported here for the new AMOEBA14 water model represent a substantial improvement over the previous AMOEBA03 model. The new AMOEBA14 water model accurately predicts the temperature of maximum density and qualitatively matches the experimental density curve across temperatures ranging from 249 K to 373 K. Excellent agreement is observed for the AMOEBA14 model in comparison to a variety of experimental properties as a function of temperature, including the 2^nd virial coefficient, enthalpy of vaporization, isothermal compressibility, thermal expansion coefficient and dielectric constant. The viscosity, self-diffusion constant and surface tension are also well reproduced. In comparison to high-level ab initio results for clusters of 2 to 20 water molecules, the AMOEBA14 model yields results similar to the AMOEBA03 and the direct polarization iAMOEBA models. With advances in computing power, calibration data, and optimization techniques, we recommend the use of the AMOEBA14 water model for future studies employing a polarizable water model.

INTRODUCTION

“What does a fish know about the water in which he swims all his life?”

~Albert Einstein (“Self Portrait”, 1936)

“Water is the most extraordinary substance! Practically all its properties are anomalous…”

~Albert Szent-Georgi (“The Living State”, 1972)

Empirical models of water play an important role in the prediction and rationalization of bulk water properties. One of the first water models was proposed by Bernal and Fowler in 1933.¹ Before the advent of digital computers, this simple atomistic model was used to deduce the crystal structure of ice, X-ray diffraction curve for water, and the heat of solution of ions. Water was among the first molecular systems to be simulated at the atomic level via Monte Carlo² and molecular dynamics techniques.³ The ST2 water model, used throughout much of the early computational work, showed simple distributed point charge models could be tailored to reproduce bulk properties.⁴ Elaboration of fixed point charge models led to the development of the widely used TIP3P², TIP4P² and SPC⁵ potentials, as well as the subsequent ST4⁶, TIP5P⁷, SPC/E⁸, TIP4P-Ew⁹ and F3C¹⁰ potentials, among many others. All of these water models have been used as the foundation for development of various biomolecular force fields, therefore, many of the models are still commonly used for explicit solvent calculations on biological systems.

A tremendous variety of specialized water potentials have been proposed for accurate modeling of molecular cluster data and selected bulk properties. These specialized potentials are typically parameterized and calibrated against accurate and reliable ab initio results for small numbers of molecules and include an explicit accounting of electronic polarization. Perhaps the first pair-interaction water model to be systematically constructed from ab initio data was the original MCY model from 1976.¹¹ Early attempts at polarizable models include Vesely’s work with Stockmayer potentials¹² and the polarizable electropole model of Barnes, et al.¹³ Kuwajima and Warshel later incorporated explicit polarization into a modified potential inspired by the MCY work.¹⁴ Other early polarizable potentials were provided by Sprik and Klein,¹⁵ the NEMO method,¹⁶ the POL3 model from Kollman’s group,¹⁷ and Dykstra’s MMC model.¹⁸ While a complete list is far too long to present here, more recent members extending this class would include TTM3-F,¹⁹ SWM4-DP,²⁰ DPP2,²¹ etc. Key features of such water models include the ability to reproduce with high fidelity the electrostatic potential around an isolated water molecule, and the ability of individual molecules to respond to their local environment. Some water potentials, such as TTM3, couple the electrostatic representation to the structure of the molecule as specified by valence terms. While potentials explicitly allowing proton dissociation were proposed over 35 years ago,²² such models are not commonly used in molecular simulation.^23,24

Much of chemistry can be rationalized at the level of partial charge interactions based on electronegativity arguments and inductive effects. To yield an accurate representation of an electrostatic potential usually requires a molecular description beyond simple partial atomic charges.²⁵ While atom-centered charge fitting schemes such as RESP²⁶ are extensively employed to parameterize force fields, the typical result is a relative error of several percent over an envelope close to, but outside of, the van der Waals surface of a polar molecule. One solution to improve upon the partial atomic charge water models is to include polarizability, as in the Atomic Multipole Optimized Energetics for Biomolecular Applications (AMOEBA) force field. The advantages of a polarizable model are evident in heterogeneous systems; for example, water-ion mixtures. Both cations and anions are highly polarizing, and the larger anions in particular are also very polarizable. While it is certainly possible for non-polarizable force fields to provide reasonable bulk phase structural and thermodynamic properties,²⁷ a fully polarizable model should have an advantage in terms of transferability. Ion parameters derived against gas phase ion-water ab initio calculations adapt seamlessly to condensed phase modeling.²⁸

The choice of water potential is often a key first step in construction of a general-purpose molecular force field. Water is a ubiquitous solvent, and the balance of solvent-solvent, solvent-solute and solute-solute interactions often plays a critical role in determining solute behavior. Computation of relative hydration free energies and ligand binding energies is aided by cancellation of errors in force field models. However, accurate calculation of absolute free energies generally requires a fine balance between solvent and solute interactions. Errors in the solvent-solvent potential will systematically recur in all subsequent calculations involving solvent. This explains the fact the most current biomolecular force fields are explicitly or implicitly parameterized for use with a particular water model. For example, recent revision of the Amber non-polarizable force field for use with the TIP4P-Ew water model involved a substantial reworking of the protein parameter values²⁹ or the elimination of the simple mixing rules to combine these force fields by explicitly parameterizing for the solute-solvent interactions themselves³⁰.

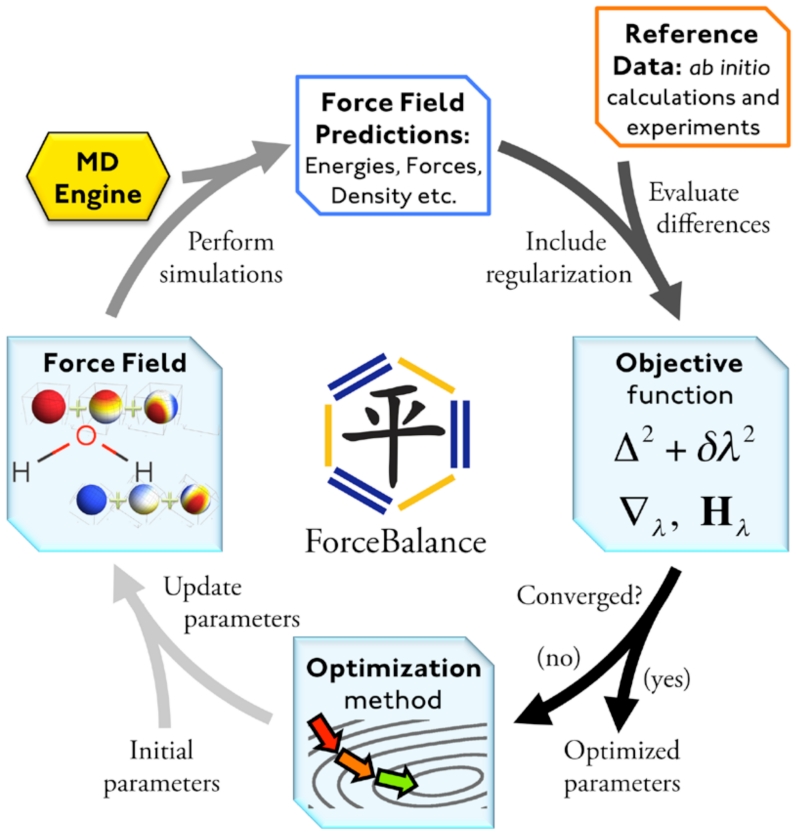
Fitting of model parameters can be carried out manually via a trial and error method, or an automated procedure can be employed. Least squares optimization of force fields first began with the Consistent Force Field proposed by Lifson and Warshel in the 1960s.³¹ Other early efforts extended least squares optimization through use of ab initio calculations³² and application to bulk phase crystal modeling.³³ Recently, force matching techniques have played a major role in development of both atomistic and coarse grained models.^34,35,36 ForceBalance^37,38,39 (Figure 1) extends this prior work in several directions, including the ability to use a larger and more diverse data set which includes experimental liquid phase measurements and ab initio calculations. The overall objective function is expressed as a weighted sum of squared residuals over the experimental and theoretical target data sets. Recently, ForceBalance has been used to derive two new, rigid, fixed partial charge water models, TIP3P-FB and TIP4P-FB.³⁹

Figure 1.

The ForceBalance procedure. Calculation begins with an initial set of parameters (lower left), which is used to generate a force field and perform simulations (upper left). The objective function is a weighted sum of squared differences between the simulation results and the reference data (right), plus a regularization term used to prevent overfitting. The optimization method (bottom) updates the parameters in order to minimize the objective function.

In the present work, we derive a revised set of parameters for the AMOEBA water model using the ForceBalance methodology. The new model, to be referred to as AMOEBA14, represents a significant improvement over the original 2003 AMOEBA water parameterization⁴⁰ (herein referred to as AMOEBA03). The AMOEBA14 model provides a significant improvement in the ability to predict experimental and ab initio data, particularly for a number of liquid properties across a range of temperatures. In addition, we provide some initial results to show the new model is capable of yielding acceptable results of ion-water energetics, which holds promise of compatibility of AMOEBA14 water with the previously determined AMOEBA force fields for organic molecules⁴¹ and for proteins.⁴²

METHODOLOGY

AMOEBA Model

The atomic multipole optimized energetics for biomolecular applications (AMOEBA)⁴⁰ water model in this work has the functional form:

$$E=E_{\mathit{bond}}+E_{\mathit{angle}}+E_{b\theta }+E_{\mathit{vdW}}+E_{\mathit{ele}}^{\mathit{perm}}+E_{\mathit{ele}}^{\mathit{ind}}$$ (1)

The first three terms describe the short-range interactions, including bond stretching, angle bending, and the Urey-Bradley bond-angle cross term. The bond stretching parameters includes anharmonicity up to second order deviations from the ideal bond length

$$E_{\mathit{bond}}=K_b{(b-b_0)}^2\left[1-2.55\left(b-b_0\right)-3.793125{(b-b_0)}^2\right]$$ (2)

and the angle bending function includes up to fourth order deviations from the ideal angle

$$E_{\mathit{angle}}=K_{\theta }{(\theta -{\theta }_0)}^2\left[1-0.014\left(\theta -{\theta }_0\right)+(5.6\times {10}^{-5)}{(\theta -{\theta }_0)}^2-(7.0\times {10}^{-7}){(\theta -{\theta }_0)}^3+(2.2\times {10}^{-8}){(\theta -{\theta }_0)}^4\right]$$ (3)

The Urey-Bradley parameters follow a harmonic functional form

$$U_{\mathit{UB}}=K_{\ell }{(\ell -{\ell }_0)}^2$$ (4)

The remaining three terms in Equation 1 describe the nonbonded van der Waals (vdW) interactions and the electrostatic contributions from both permanent and induced dipoles. The vdW term follows a Halgren buffered 14-7 potential to model the pairwise additive interactions for dispersion at long-range and exchange repulsion at short-range⁴³,

$$E_{\mathit{ij}}^{\mathit{buff}}={\epsilon }_{\mathit{ij}}{\left(\frac{1+\delta }{{\rho }_{\mathit{ij}}+\delta }\right)}^{n-m}\left(\frac{1+\gamma }{{\rho }_{\mathit{ij}}^m+\gamma }-2\right)$$ (5)

and which is less steep than the Lennard-Jones functional form. The nonbonded van der Waals (vdW) parameters we use are n=14, m=7, δ=0.07, γ=0.12, the well depth ε_ij, and ${\rho }_{ij}=\frac{R_{ij}}{R_{ij}^0}$ where R_ij is the i-j separation and $R_{ij}^0$ is the minimum energy distance. Van der Waals parameters are included for both oxygen and hydrogen atoms. The hydrogen reduction factor moves the hydrogen vdW center toward the oxygen along the bond length. For example, a reduction factor of 0.80 would move the hydrogen vdW center 20% of the bond length toward the oxygen.

The permanent electrostatic term includes the atomic monopole, dipole and quadrupole moments for each atom center. The polarization effects within the AMOEBA water model include mutual polarization by mutual induction of the dipoles for each atom. The non-additive definition of the model translates to each atom within the water molecule being a polarizable site and experiencing the mutual polarization. As a consequence of the non-additive mutual definition of the AMOEBA model, a polarization catastrophe would arise if a damping scheme were not introduced; therefore, the polarization parameters for the AMOEBA water model include the polarizability of oxygen and hydrogen and a damping factor related to Thole’s description of damping.⁴⁴ The distribution of the charge (ρ) in AMOEBA has the functional form

$$\rho =\frac{3\alpha }{4\pi }\exp (-{\mathit{au}}^3)$$ (6)

with a representing the damping parameter⁴⁴ controlling how strongly the charge distribution is smeared and u is the distance relating the polarizabilities of atomic sites i and j [u=R_ij/(α_iα_j)^1/6].

For the mutual model, the induced dipole is calculated at each atomic site via

$${\mu }_{i,\alpha }^{\mathit{induc}}={\alpha }_i{E}_{i,\alpha }={\alpha }_i\left(\sum _{\left\{j\right\}}{T}_{\alpha }^{\mathit{ij}}{M}_j+\sum _{\left\{j\right\}}{T}_{\alpha \beta }^{{\mathit{ij}}^{\prime }}{\mu }_{j^{\prime },\beta }^{\mathit{induc}}\right)\text{with}\alpha ,\beta =1,2,3$$ (7)

where α_i is the atom polarizability, E_i,αa represents the electric fields generated by permanent multipoles and induced, M _j = [q_j, μ_j1, μ_j2, μ_j3, …]^T includes the permanent multipole components and $T_{\alpha }^{ij}=[T_{\alpha },T_{\alpha 1},T_{\alpha 2},T_{\alpha 3},\dots ]$ represents the matrix for the interaction of sites i and j where $T_{\alpha }={\nabla }_{\alpha }T=-\frac{R_{\alpha }}{R^3}$ and T_αβ = ▽_αT_β. The summations are carried out over two sets: {j}, all atom sites outside the molecule containing atom site i, and {j’}, all atom sites other than i. The function for the induced dipoles self-consistently reduces to

$${\mu }_{i,\alpha }^{\mathit{induc}}\left(n+1\right)={\mu }_{i,\alpha }^{\mathit{induc}}\left(n\right)+{\alpha }_i\left(\sum _{\left\{j\right\}}{T}_{\alpha \beta }^{{\mathit{ij}}^{\prime }}{\mu }_{j^{\prime },\beta }^{\mathit{induc}}\left(n\right)\right)\text{with}\mathrm{n}=0,1,2,\dots$$ (8)

From this solution, the first term in Equation 8 represents the direct induced dipole for atom i as a result of the electric field generated from the permanent multipoles from neighboring molecules. The second term represents the mutual induced dipole resulting from induced dipoles induced on all other atom sites. The mutual induction calculation is iterated until the induced dipoles are no longer induced by dipoles on all other sites with a tolerance set to 10⁻⁵ D.

For the reparameterization of the AMOEBA functional form, there were 21 tunable parameters included in the optimization: the vdW radius (R) and potential well depth (ε) for oxygen and hydrogen, reduction factor for hydrogen, bond-stretching force constant (Kb) and length (b), angle-bending force constant (K_θ) and magnitude (θ), Urey-Bradley force constant (K_/) and length (/), charge for hydrogen and oxygen, multipoles (dipole, quadrupole) for hydrogen and oxygen, the polarizability for hydrogen and oxygen, and the Thole polarization damping factor.

Simulation Protocol

Initial cycles of ForceBalance used a cubic box with an initial side length 18.65 Å and containing 216 water molecules. Molecular dynamics in the NPT ensemble was performed via a Martyna-Tuckerman-Klein integrator incorporating a Nose-Hoover thermostat and barostat.⁴⁵ Final liquid parameter optimization cycles were also done on 216 waters. Each final simulation was run for four nanoseconds following 400 picoseconds of equilibration. The simulations for the final parameterization employed Langevin dynamics with a multiple timestep velocity Verlet integrator with the Langevin friction force and random force. The Langevin dynamics used a friction coefficient of 1.0 picoseconds⁻¹. These final simulations used a Monte Carlo barostat with a trial frequency of 1 box size change per 25 MD steps. All dynamics simulations were performed with either the TINKER⁴⁶ or OpenMM⁴⁷ modeling software packages. Properties, including the self-diffusion constant, viscosity, dielectric constant, enthalpy of vaporization, heat capacity, isothermal compressibility and 2^nd virial coefficient, were computed by the same methods used for the earlier AMOEBA03 water model.⁴⁰

Calibration Data

The data utilized for fitting the parameters was composed of a combination of experimentally-determined condensed phase properties as well as robust ab initio-derived properties. The condensed phase properties considered were the density, enthalpy of vaporization, isothermal compressibility, isobaric heat capacity, thermal expansion coefficient, and dielectric constant. The temperature and pressure combinations were: 1 atmosphere at temperatures ranging from 249 K to 373 K (32 total), and 298 K at pressures from 1 kilobar to 8 kilobar (8 total). The complete lists of temperatures, pressures, and values for each experimental property are included in the Supplemental Information.

The ab initio reference data included properties for systems ranging in size from the monomer to clusters of 22 water molecules. For the monomer, the charge, dipole, quadrupoles, polarizability, vibrations, and geometry were considered. The ab initio interaction energies and ground state geometries for the ground state dimer, Smith dimer set (10 total),⁴⁸ trimer, tetramer, pentamer, eight hexamers,⁴⁹ two octamers,⁵⁰ five 11-mers,⁵¹ five 16-mers, two 17-mers, and four 20-mers^52,53 were utilized for calibration. In previous work,⁵⁴ over 42000 clusters (ranging from two to 22 water molecules) geometries were obtained from AMOEBA simulations of liquid water for temperatures ranging from 249 K to 373 K. Energies and gradients for the clusters were determined via RI-MP2^55,56/heavy-aug-cc-pVTZ⁵⁷ as implemented in Q-Chem 4.0.⁵⁸ This large compilation of theoretical data was included in the fitting of the AMOEBA water parameters.

ForceBalance

The AMOEBA03 water model was parameterized by hand to fit results from ab initio calculations on gas phase clusters,⁴⁰ and temperature and pressure dependent bulk phase properties.⁵⁹ Here we apply ForceBalance, an automatic optimization method, to parameterize a revised AMOEBA14 model using the expanded data set described in the last section. ForceBalance has previously been applied to the development of a direct polarization variant of AMOEBA, labeled iAMOEBA, which omits the self-consistent calculation of polarization interactions.⁵⁴ One of the goals for iAMOEBA was to accurately describe bulk phase properties; therefore, the condensed phase properties, e.g. density, were given a greater weight than gas phase properties, such as cluster interaction energies. Ideally, the mutual AMOEBA model should be applicable across all system sizes and phases as well. To reflect this goal for the mutual polarization model, each property in the calibration set was initially given an equal weight. This is in contrast to the previous direct polarization water model, where the condensed phase experimental data was weighted more heavily than the gas phase cluster data.

The enthalpy of vaporization measures the water-water interaction strength, while the related property of the density reflects the hydrogen-bonded network structure, both of which have significant temperature (and pressure) dependence. If the enthalpy value is too large or its change with temperature is too steep, then the attraction between the water molecules is too great and the heat capacity would be too high. This would be problematic for not only the homogeneous water system, but in heterogeneous systems where the water-water, water-solute, and solute-solute interactions need to be balanced. For example, a temperature of maximum density (TMD) of a model that is very different than the experimental TMD would likely change the trends in hydrophobic hydration with temperature, since the entropic penalty for cavity formation in the liquid by definition changes with temperature. Therefore, the weighting of the condensed phase properties was adjusted to increase the weights of the enthalpy of vaporization and density in relation to the other condensed phase properties. The whole set of condensed phase properties maintained equal weighting with the gas phase data, but the individual condensed phase properties were assigned different weights with respect to each other.

ForceBalance supports many different optimization algorithms, and the calculation in this work was carried out using the trust-radius Newton-Raphson (or Levenberg-Marquardt^60,61) algorithm with an adaptive trust radius.^62,63 This algorithm requires the first and second derivatives of the objective function in the parameter space, which we derive from the first derivatives of the simulated properties using the Gauss-Newton approximation.

A major challenge in force field parameterization is the significant statistical noise in the objective function from the sampling of properties to be matched to experiment. The parametric derivatives are challenging to evaluate because numerical differentiation requires running multiple simulations and evaluating small differences between statistically noisy estimates. ForceBalance uses thermodynamic fluctuation formulas to calculate accurate parametric derivatives of simulated properties without running expensive multiple simulations.^{38, 64} For instance, the ensemble average of a generic observable A that does not depend explicitly on the force field parameters (for example, the density or an order parameter) can be expressed as follows:

$$\begin{array}{cc}\hfill {\langle A\rangle }_{\lambda }& =\frac{1}{Q\left(\lambda \right)}\int A\left(\mathbf{r},V\right)\exp \left(-\beta \left(E\left(\mathbf{r},V;\lambda \right)+\mathit{PV}\right)\right)d\mathbf{r}\mathit{dV}\hfill \\ \hfill Q\left(\lambda \right)& =\int \exp \left(-\beta \left(E\left(\mathbf{r},V;\lambda \right)\right)+\mathit{PV}\right)d\mathbf{r}\mathit{dV}\hfill \end{array}$$ (9)

where A is the observable, r a given molecular configuration in a periodic simulation cell, l the force field parameter, E the potential energy, β ≡ (k_BT)⁻¹ the inverse temperature, k_B the Boltzmann constant, T the temperature, P the pressure, V the volume, Q the isothermal-isobaric partition function, and the angle brackets with a l subscript represent an ensemble average in the thermodynamic ensemble of the force field parameterized by l. In practice, this integral is evaluated numerically using molecular dynamics or Monte Carlo simulation in the NPT ensemble.

Since the expression for A depends on l only through the potential energy E, we can differentiate Equation 9 analytically:

$$\begin{array}{cc}\hfill \frac{d}{d\lambda }{\langle A\rangle }_{\lambda }& =\frac{1}{Q\left(\lambda \right)}\int A\left(\mathbf{r},V\right)\exp \left(-\beta \left(E\left(\mathbf{r},V;\lambda \right)+\mathit{PV}\right)\right)\left(-\beta \frac{\mathit{dE}\left(\mathbf{r},V\right)}{d\lambda }\right)d\mathbf{r}\mathit{dV}\hfill \\ \hfill & -\frac{1}{Q{\left(\lambda \right)}^2}\frac{\mathit{dQ}}{d\lambda }\int A\left(\mathbf{r},V\right)\exp \left(-\beta \left(E\left(\mathbf{r},V;\lambda \right)+\mathit{PV}\right)\right)d\mathbf{r}\mathit{dV}\hfill \\ \hfill & =-\beta \left({\langle A\frac{\mathit{dE}}{d\lambda }\rangle }_{\lambda }-{\langle A\rangle }_{\lambda }{\langle \frac{\mathit{dE}}{d\lambda }\rangle }_{\lambda }\right)\hfill \end{array}$$ (10)

The potential energy derivative $\langle \frac{dE}{d\lambda }\rangle$ is evaluated by numerically differentiating the potential energies at the sampled structures. Equation 10 provides a way to evaluate the parametric derivative of thermodynamic properties without running additional sampling simulations, though the derivative of any observable always manifests as a higher order correlation function and has a larger statistical error than the observable itself. This equation may be directly applied to obtain derivatives of ensemble-averaged observables with implicit parametric dependence through the thermodynamic ensemble, such as the density ρ. Equation 10 is easily extensible to obtain derivatives of observables with explicit parameter dependence, such as the enthalpy; derivatives for higher-order thermodynamic response properties such as the dielectric constant are obtained using the chain rule.⁵⁴ We omit the calculation of second parametric derivatives for reasons of computational cost and statistical noise, relying instead on the least-squares form of the objective function and the Gauss-Newton approximation to obtain the Hessian.

In order to maximize the efficiency of simulating properties, ForceBalance interfaces with several powerful and complementary technologies. ForceBalance includes interfaces to AMOEBA via the TINKER⁴⁶ modeling software and via OpenMM 6.1,⁴⁷ a graphics processing unit (GPU)-accelerated MD engine. The Work Queue library⁶⁵ allows ForceBalance to parallelize multiple simulations across compute nodes in different physical locations. ForceBalance analyzes the data from finished simulations using the multistate Bennett acceptance ratio estimator (MBAR)⁶⁶ which allows multiple simulations at different thermodynamic phase points to statistically contribute to one another. All of these software packages and methods are freely available on the Web.

The problem of overfitting is treated by regularization via a penalty function, which corresponds to imposing a prior distribution of parameter probabilities in a Bayesian interpretation. The prior widths reflect the expected variations of the parameters during the optimization, which may be chosen heuristically or sampled over in an empirical Bayes approach. Our optimization was regularized using a Gaussian prior specified in Table 1, corresponding to a parabolic penalty function in parameter space centered at the original AMOEBA parameter values with the chosen force constants. Since the various parameters have different physical meanings (e.g. vdW well depth, O-H bond length), each parameter type was assigned its own prior width.

Table 1.

AMOEBA water parameters for the AMOEBA03 and revised AMOEBA14 water models and the prior widths used in the ForceBalance optimization scheme.

Parameter	Units	AMOEBA03	AMOEBA14	Prior Width
O Monopole	e	−0.51966	−0.42616	0.4
O Dipole Z	e bohr	0.14279	0.06251	0.1
O Quadrupole XX	e bohr2	0.37928	0.17576	0.2
O Quadrupole YY	e bohr2	−0.41809	−0.23160	0.2
O Quadrupole ZZ	e bohr2	0.03881	0.05584	0.2
H Monopole	e	0.25983	0.21308	0.4
H Dipole X	e bohr	−0.03859	−0.10117	0.1
H Dipole Z	e bohr	−0.05818	−0.27171	0.1
H Quadrupole XX	e bohr2	−0.03673	0.12283	0.2
H Quadrupole YY	e bohr2	−0.10739	0.08950	0.2
H Quadrupole XZ	e bohr2	−0.00203	−0.06989	0.2
H Quadrupole ZZ	e bohr2	0.14412	−0.21233	0.2
O Polarizability	Å	0.837	0.920	0.1
H Polarizability	Å	0.496	0.539	0.1
Damping Factor	Å	0.39	0.39	none
O vdW Diameter	Å	3.405	3.5791	0.3
O vdW Epsilon	kcal/mol	0.11	0.1512	0.1
H vdW Diameter	Å	2.655	2.1176	0.3
H vdW Epsilon	kcal/mol	0.0135	0.0105	0.1
H vdW Reduction Factor	none	0.91	0.8028	0.1
O-H Bond Length	Å	0.9572	0.9565	0.1
Bond Force Constant	kcal/mol/Å2	556.85a	556.82	50
H-O-H Angle Value	degree	108.5	107.91	5
Angle Force Constant	kcal/mol/rad2	48.7a	48.98	40
H-H Urey-Bradley Length	Å	1.5326a	1.5467	none
Urey-Bradley Force Const.	kcal/mol/Å2	−7.6a	−8.62	25

^aCurrent AMOEBA03 bond angle and Urey-Bradley intramolecular parameters. These values differ from those originally published in Reference 40, and were changed to correct an error in the ordering of the O-H stretch vibrational modes.

We ran the optimization until fluctuations from numerical noise prevented further improvement. The calculation converged to within the statistical error after about 10 nonlinear iterations, though we performed several optimizations with different choices of weights for the reference data and prior widths before arriving at the final answer.

RESULTS AND DISCUSSION

AMOEBA14 Water Parameters

The parameters for the new AMOEBA14 water model, the AMOEBA03 model, and the Gaussian prior widths included in the ForceBalance optimization are reported in Table 1. The prior widths are proportional to the inverse-squared strength of the harmonic penalty for each parameter and reflect the parameter’s intrinsic size and expected variability. It should be noted, the bond force constant, angle force constant, and the Urey-Bradley parameters for AMOEBA03 were modified in 2013 when it was observed the original parameters incorrectly predicted the order of the vibrational frequencies; therefore, the comparison we are making for intramolecular parameters is to those revised parameters. Table 1 shows that the intramolecular parameters for the AMOEBA model remained essentially unchanged from 2003 to 2014.

The damping value of 0.39 was kept fixed during the AMOEBA14 model optimization since the value in the 2003 model was set based on water cluster energies, and this damping value has been tested and employed for the majority of atom classes within the AMOEBA model. For the AMOEBA03 water model, the polarizability parameters for oxygen and hydrogen were those proposed by Thole. While the polarizability values were allowed to fluctuate during the ForceBalance optimization of AMOEBA14, they do not deviate significantly from the AMOEBA03 model.

Repulsion-dispersion parameters (vdW radius and well-depth) were assigned to both the oxygen and hydrogen atom centers. AMOEBA14 has a larger vdW radius and well-depth for oxygen and a smaller vdW radius and well-depth for hydrogen compared to AMOEBA03. The newly proposed reduction factor for hydrogen shifts the hydrogen vdW center toward oxygen by approximately 20% of the O-H bond length. The parameter optimization approached a point of zeroing out the hydrogen vdW site and reducing the model to one repulsion-dispersion site on oxygen, but the final set of parameters include both atoms and the description of the water oxygen is consistent with the description of oxygen in other organic molecules for the AMOEBA model.

The AMOEBA14 water model increases the charge of the oxygen and decreases the charge of the hydrogen in comparison to the AMOEBA03 model. The z-component of the oxygen dipole is less than AMOEBA03 and the x- and z-components of the hydrogen dipole are greater. There are substantial deviations for both the oxygen and hydrogen quadrupole parameters in relation to the AMOEBA03 model. The xx-component of the quadrupole moment tensor decreases by approximately the same magnitude by which the yy-component of the quadrupole increases for oxygen. An increase of the same scale is observed for the xx- and yy-components of the quadrupole moment tensor for hydrogen, but there is a sign change for these hydrogen quadrupole parameters. These changes in the non-bonded interactions reflect improvements in the gas phase and condensed phase properties of water described in the next sections.

AMOEBA14 Fitted Gas Phase Water Properties

Table 2 provides the multipole properties predicted by the AMOEBA14 and AMOEBA03 water models. The AMOEBA14 water parameters predict the dipole of a gas phase water monomer to be 1.808 Debye in comparison to the experimental value of 1.855 Debye. The changes in the atomic quadrupole parameters improve the molecular xx-quadrupole moment compared to experiment, while the yy- and zz-quadrupole moments are nearly unchanged in comparison to the AMOEBA03 model.

Table 2.

Multipole properties predicted by the revised AMOEBA14 and previous AMOEBA03 water models compared to experimental values. Units are Debye, Debye·A, and A²·s⁴·kg⁻¹, respectively.

	AMOEBA03	AMOEBA14	Experiment
Dipole dz	1.771	1.808	1.855a
Quadrupole
Q xx	2.502	2.626	2.630b
Q yy	−2.168	−2.178	−2.500b
Q zz	−0.334	−0.045	−0.130b
Polarizability
α xx	1.672	1.767	1.528c
α yy	1.225	1.308	1.412c
α zz	1.328	1.420	1.468c

^aReference 92.

^bReference 93.

^cReference 94.

As in the original AMOEBA model, the ideal bond angle is larger than the experimental and ab initio values. The three vibrational frequencies of the water monomer are predicted to within 0.3 cm⁻¹ and the ordering of the modes is in agreement with experiment. In Table 3 the AMOEBA water dimer equilibrium structure and interaction energy are compared to experiment and ab initio results. For the equilibrium dimer minimum, the AMOEBA14 model is in somewhat poorer agreement with ab initio values than the earlier AMOEBA03 model. However, averaged over a series of low energy dimer configurations, the AMOEBA14 is as good as or superior to AMOEBA03. As previously noted, ten ab initio dimer interaction energies and geometries were including in the fitting of the model parameters. The root mean squared deviations (RMSDs) for the monomer and dimer geometries were 0.017 and 0.057 Å, respectively.

Table 3.

Dimer equilibrium properties: Dissociation energy (D_e, kcal/mol), O-O distance (_rO-O, Å), α angle (angle between O-O vector and O_donor-H_donor vector, degrees), β angle (angle between O-O vector and plane of acceptor molecule, degrees), total dipole moment (μ_tot, Debye).

Property	AMOEBA03	AMOEBA14	ab Initio	Experiment
De	4.96	4.64	4.98c	5.44±0.7a
r O-O	2.892	2.908	2.907c	2.976b
α	4.18	4.41	4.18c	−1±10b
β	57.2	64.9	55.6d	57±10b
μ tot	2.54	2.20	2.76e	2.643b

^aReference 95.

^bReference 96.

^cReference 97.

^dReference 98.

^eReference 99.

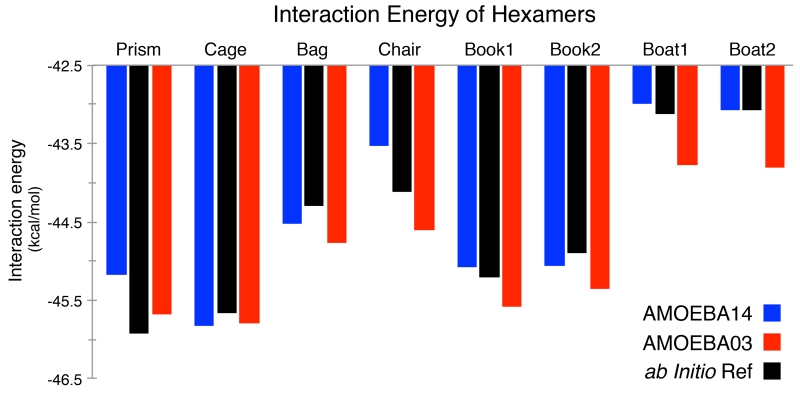
The interaction energies for water clusters, ranging from dimers to clusters of 20 water molecules (see Table 4), were analyzed with the AMOEBA water model. The geometries of the clusters were optimized and the interaction energy determined via AMOEBA. The cluster results are compiled in Table 4. The mean absolute deviation (MAD) for the interaction energy of the smaller clusters (2-8 water molecules) is 0.39 kcal/mol, considered to be within chemical accuracy (i.e., within 1 kcal/mol of experiment). Specific results for the hexamers are shown in Figure 2. The larger clusters (11- to 20-mers) have an MAD of 7.97 kcal/mol for the interaction energy prediction. The discrepancy between the accuracy levels of the AMOEBA water model for the small and large clusters is interesting and would suggest the error of AMOEBA with respect to system size could be systematic. To examine this possibility, the MADs of each of the condensed phase properties (discussed further below) was tabulated in Table 5, and the errors were of the same magnitude as the small clusters.

Table 4.

Cluster binding energies (kcal/mol) with the AMOEBA14 model in comparison to ab initio reference calculations. Mean absolute deviations (MADs) are reported over the small and large cluster categories.

Molecule		Ref.	AMOEBA14	Diff.
Dimers a (Smith)	1	−4.968	−4.65	0.32
	2	−4.453	−4.22	0.24
	3	−4.418	−4.19	0.23
	4	−4.25	−3.54	0.71
	5	−3.998	−3.06	0.94
	6	−3.957	−2.92	1.04
	7	−3.256	−2.49	0.77
	8	−1.3	−1.02	0.28
	9	−3.047	−2.37	0.68
	10	−2.182	−1.96	0.22
	Trimer b	−15.742	−15.38	0.36
	Tetramer b	−27.4	−27.43	−0.03
	Pentamer b	−35.933	−35.78	0.16
Hexamer c	Prism	−45.92	−45.18	0.74
	Cage	−45.67	−45.83	−0.16
	Bag	−44.3	−44.52	−0.22
	CyclicChair	−44.12	−43.53	0.59
	Book A	−45.2	−45.08	0.12
	Book B	−44.9	−45.06	−0.16
	CyclicBoat A	−43.13	−42.99	0.14
	CyclicBoat B	−43.07	−43.07	0.00
Octamer d	S4	−72.7	−72.22	0.48
	D2d	−72.7	−72.24	0.46
11-mer e	434	−105.718	−101.11	4.61
	515	−105.182	−100.99	4.19
	551	−104.92	−100.58	4.34
	443	−104.76	−101.17	3.59
	4412	−103.971	−100.33	3.64
16-mer f	Boat A	−170.8	−160.45	10.35
	Boat B	−170.63	−160.39	10.25
	Anti-boat	−170.54	−160.30	10.25
	ABAB	−171.05	−161.20	9.85
	AABB	−170.51	−160.89	9.62
17-mer f	Sphere	−182.54	−171.53	11.01
	5525	−181.83	−170.42	11.41
20-mer g	Dodecahedron	−200.1	−193.81	6.29
	FusedCubes	−212.1	−205.77	6.33
	FaceSharingPrisms	−215.2	−204.41	10.79
	EdgeSharingPrisms	−218.1	−207.06	11.04
		MAD	Units
Clusters	Dimer to Octamer	0.39	kcal/mol
	11- to 20-mer	7.97	kcal/mol

^aReference 100.

^bReference 40.

^cReference 49.

^dReference 50.

^eReference 51.

^fReference 101.

^gReference 52.

Figure 2.

Energies of water hexamer minima for the AMOEBA03 and AMOEBA14 models compared to reference complete basis set (CBS) ab initio calculations from Reference 49.

Table 5.

Mean absolute deviations (MADs) from experiment of the liquid phase properties calculated by AMOEBA14 across all temperatures (249K to 373K).

Property	MAD	Units
ρ	1.22	kg/m3
ΔHvap	0.43	kJ/mol
α	0.66	10−4/K
κ T	1.31	10−6/bar
Cp	2.28	cal/mol/K
ε(0)	1.51	N/A

In the analysis of the 42000 clusters (~2400 clusters of n water molecules, n=2-22), the potential energies, gradients, net forces, and torques were computed with AMOEBA14 and compared to the ab initio reference data. As a specific example of the results, the root mean squared (RMS) errors for the cluster of 18-mers were 7.8 kJ/mol (10%) for energy, 33.8 kJ/mol/Å (42%) for the gradient, 9.9 kJ/mol/Å (30%) for the net force, and 6.3 kJ/mol/rad (25%) for the torque. The standard deviations for the reference data were 29.2 kJ/mol, 83 kJ/mol/Å, 29 kJ/mol/Å, and 20 kJ/mol/rad, for the energies, gradients, forces, and torques, respectively. Over all of the cluster sizes, the AMOEBA14 model predicted the potential energies to, on average, within 15% of the reference. This accuracy level is surprising when the weighting of the reference data is considered. The bulk clusters were assigned the smallest weights, i.e., fitting the energies and gradients were the lowest priority in the parameter optimization. The robustness of the AMOEBA14 model in comparison to ab initio cluster reference data reaffirms the utility of the model for both gas and bulk phase properties.

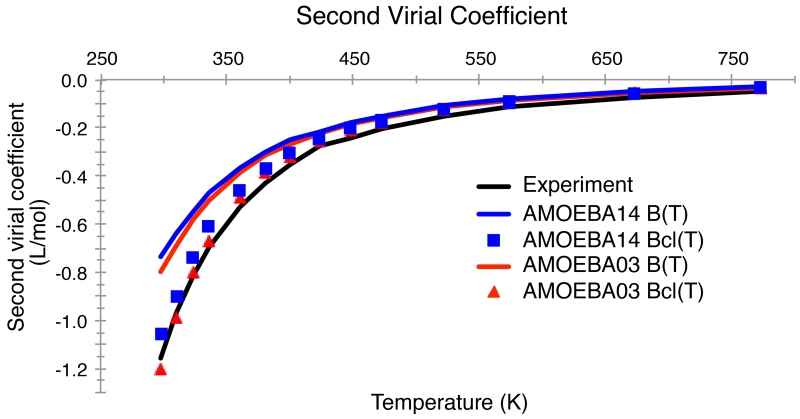
The second virial coefficient of water computed with an empirical potential is a sensitive measure of the accuracy of the Boltzmann-weighted dimer potential energy surface. Following Millot, et al., we computed the classical virial coefficient, as well as first-order translational and rotational quantum corrections.⁶⁷ Some workers have argued that the quantum corrections are unnecessary as they are implicitly incorporated into empirical water potentials.⁶⁸ Others have emphasized the importance of higher-order corrections and experimental error, especially at temperatures below about 325 K.⁶⁹ Figure 3 shows both the classical and first-order corrected second virial coefficients for the AMOEBA03 and AMOEBA14 models. The two models exhibit very similar behavior, and in both cases the uncorrected coefficients are in excellent agreement with experiment. Nonpolarized models intended for use in the bulk phase simulation tend to lie below the experimental second virial curve, especially at low temperature. The iAMOEBA model (not shown) is also somewhat underpolarized, and also yields second virial coefficients that are too negative.

Figure 3.

Second virial coefficient of water as a function of temperature for the AMOEBA03 and AMOEBA14 models for temperatures from 249 K to 373 K and atmospheric pressure (1 atm). The Bcl(T) curves show the classical second virial coefficient, while the B(T) curves have translational and rotational quantum corrections added to the classical results. Experimental values are from References 106 and 107.

In previous work,²⁸ the dependence of the density maximum on the water geometry was explored. The 2003 model adopted an equilibrium angle of 108.5° in the gas phase (“correct” value per ab initio: 104.5°) in order to achieve an average angle of 105.3° in the condensed phase and be in near agreement with experiment at room temperature. With the re-optimized AMOEBA parameters, the equilibrium gas phase angle is 107.8° and the condense phase angle is 105.1°. The average AMOEBA14 H-O-H angle slightly increases (104.9° to 105.4°) as the temperature increases from 249 K to 373 K. While previous theoretical estimates concluded the liquid water should see the angle contract with increasing temperature,⁷⁰ experimental data has reported no relation between angle magnitude and temperature.⁷¹

AMOEBA14 Fitted Condensed Phase Water Properties

In the parameterization of the initial AMOEBA03 water model, only the density and heat of vaporization at room temperature were considered. Within the fitting of the current model, six condensed phase properties were considered at a range of temperatures (249 K to 373 K) and pressures (1 atm to 8 kilobar). For AMOEBA14, the enthalpy of vaporization and density trends with temperature were the focal points in the fit and were given a greater weight in the optimization. All of the thermodynamic data and their trends with respect to temperature are shown in Figures 2-5, while tables with the raw numbers are included in the Supplemental Information.

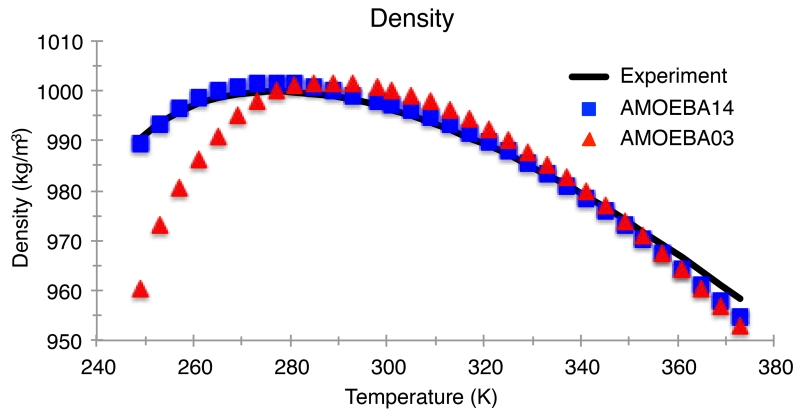
Figure 5.

Density of water for the AMOEBA03 and AMOEBA14 models compared to experiment for temperatures from 249 K to 373 K at atmospheric pressure (1 atm). The temperature of maximum density from experiment and for AMOEBA14 is 277 K. Experimental values are taken from Reference 108.

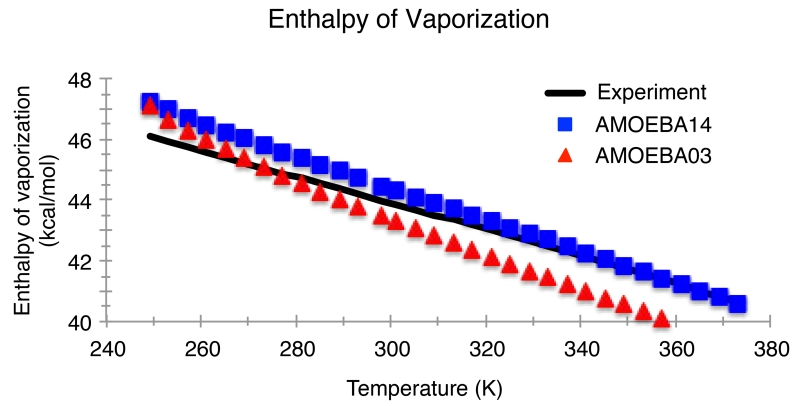
Since AMOEBA03 was specifically fit to the enthalpy of vaporization and the density at room temperature, the initial model agrees with the corresponding experimental values to within statistical error. However, the linear temperature dependence of the enthalpy of vaporization only intersects with the experiment at room temperature. With the AMOEBA14 water model, the enthalpy of vaporization at room temperature differs by only 0.49 kcal/mol over the temperature range examined, and the mean absolute deviation (MAD) of the model was 0.43 kcal/mol compared to 0.65 for AMOEBA03 (Figure 4). The experimental maximum density of 999.972 kg/m³ occurs at 277.15 K and 1.0 atm of pressure. The temperature of maximum density as predicted by the AMOEBA03 model is shifted to higher temperatures by nearly 15 K, and the curve of the temperature dependence is slightly narrower. The new AMOEBA14 water parameters yield a temperature of maximum density in quantitative agreement with experiment and the shape of the curve is in qualitative agreement with experiment. (Figure 5).

Figure 4.

Enthalpy of vaporization of water for temperatures for the AMOEBA03 and AMOEBA14 models and experiment for temperatures from 249 K to 373 K and atmospheric pressure (1 atm). The mean signed deviation is −0.43 kcal/mol. Experimental values are from Reference 102.

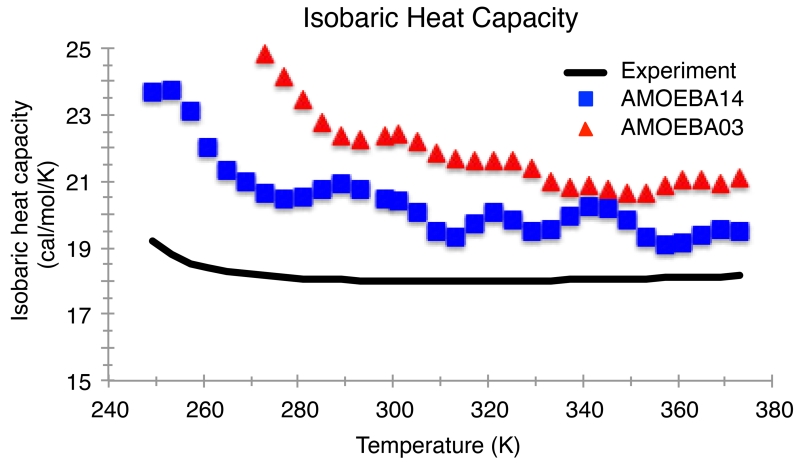
The AMOEBA14 results for the thermodynamic fluctuation properties (heat capacity, isothermal compressibility, and thermal expansion coefficient) are shown in Figures 6-9. Since the temperature dependence of the predicted enthalpy of vaporization has a slightly greater slope than experiment (Figure 4), the calculated heat capacity for AMOEBA14 is greater than experiment by, on average, 2.28 cal/mol/K. AMOEBA14 improves upon the AMOEBA03 model, whose enthalpy of vaporization temperature dependence is much steeper, resulting in much higher heat capacity values. The discrepancy between the AMOEBA14 calculated and experimental heat capacity is due to the approximations within our classical, flexible model, and previous work has estimated the accuracy of the heat capacity determined by AMOEBA to be ±5 cal/mol/K.²⁸ While an overestimation of the heat capacity means an overestimation of the entropy fluctuations, what matters more is that the temperature onset of anomalous fluctuations (i.e. above the normal background) is better described by the AMOEBA14 model relative to AMOEBA03 (Figure 6).⁷²

Figure 6.

Isobaric heat capacity for the AMOEBA03 and AMOEBA14 models compared to experiment for temperatures from 249 K to 373 K at atmospheric pressure (1 atm). Experimental values are taken from Reference 102.

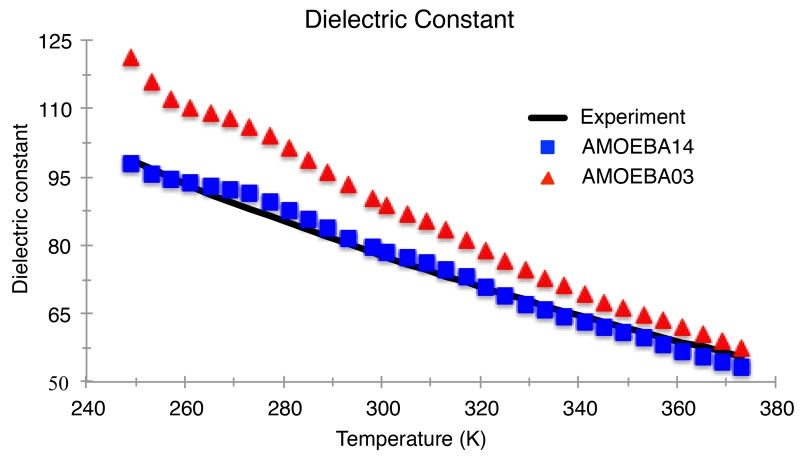
Figure 9.

Dielectric constant for the AMOEBA03 and AMOEBA14 models compared to experiment. For temperatures from 249 K to 373 K at atmospheric pressure (1 atm). Experimental values are taken from Reference 102.

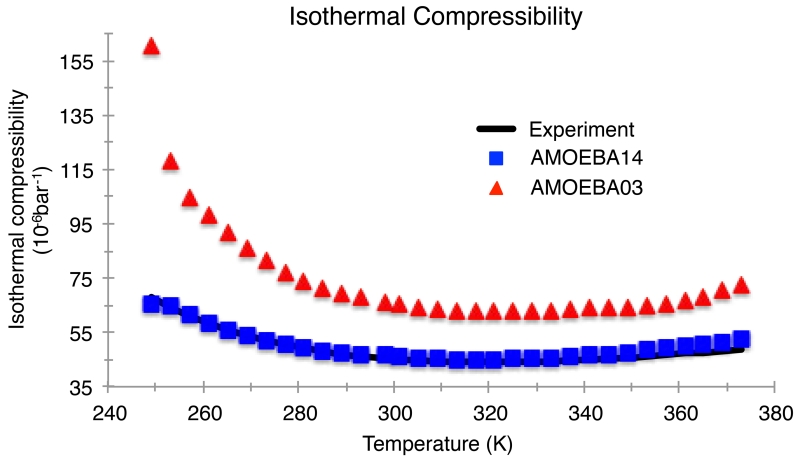
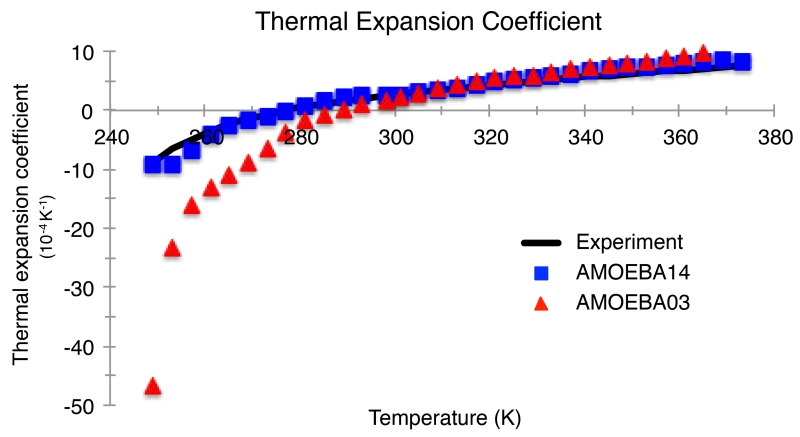
The AMOEBA14 model also shows a drastic improvement in the quantitative value of the isothermal compressibility in comparison to the 2003 model, which overestimates the compressibility by ~30% at ambient conditions. Again, the more important point is that the temperature trends are correct for AMOEBA14, with a compressibility minimum very near the 319K value seen experimentally (Figure 7). AMOEBA14 not surprisingly shows the transition from positive to negative thermal expansion coefficient at the same temperature as experiment, which is to be expected given that the TMDs are the same (Figure 8).

Figure 7.

Isothermal compressibility for the AMOEBA03 and AMOEBA14 models compared to experiment for temperatures from 249 K to 373 K at atmospheric pressure (1 atm). Experimental values taken from Reference 108.

Figure 8.

Thermal expansion coefficient for the AMOEBA03 and AMOEBA14 models compared to experiment for temperatures from 249.15K to 373.15K at atmospheric pressure (1 atm). Experimental values are from Reference 108.

Finally, Figure 9 shows the temperature dependence of the dielectric constant, which is in excellent agreement with experiment, and also agrees well with the AMOEBA03 value of ~80 at room temperature. The excellent reproduction of the dielectric constant for the AMOEBA14 model is due to a good balance within the electrostatic model. Carnie and Patey showed the dipolar correlations are suppressed when the quadrupole interactions increase, thereby decreasing the dielectric constant of the liquid.⁷³ It has been noted⁷⁴ that since the dielectric response arises from both the magnitude as well as the fluctuations of the water dipole, by definition, a good dielectric constant can be achieved by a model with either small dipoles with large fluctuations (corresponding to small quadrupoles < ~1.8 D-Å) or large dipoles with small fluctuations (large quadrupoles > ~2.5 D-Å). It appears, therefore, that the polarization of the AMOEBA models give rise to dipoles that are large enough to overcome the quadrupolar quenching in achieving its excellent dielectric properties.

AMOEBA14 Validation

Radial Distribution Function

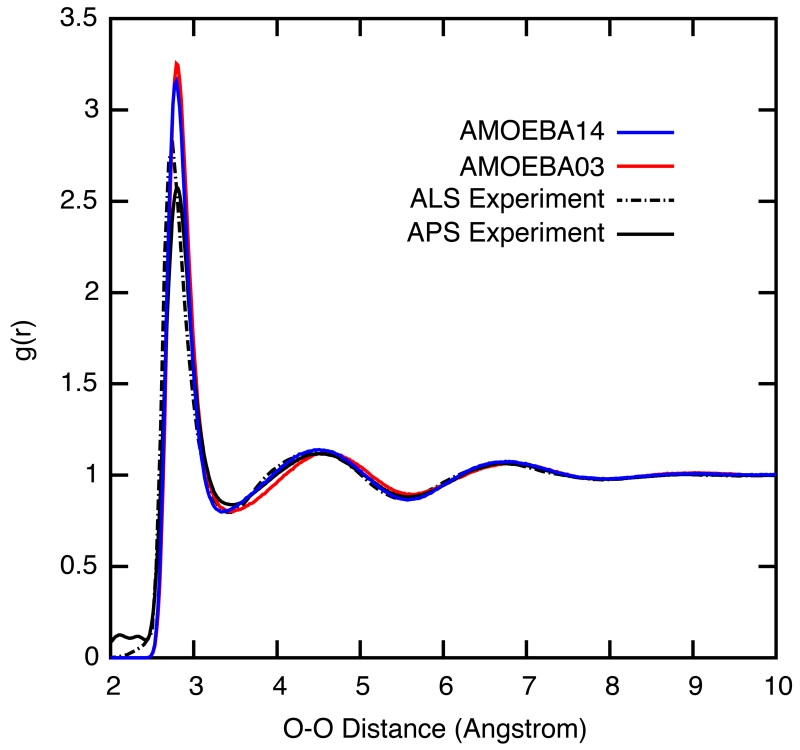
The radial distribution functions (RDFs) can be derived from X-ray scattering and neutron diffraction^75,76 and provide information about the structure of liquid water. Figure 10 shows the oxygen-oxygen RDF curve of the AMOEBA03, AMOEBA14 and iAMOEBA models when compared against the ALS⁷⁷ and more recent APS⁷⁸ experimental estimates of the real space structure derived from the intensity data. The gOH(r) and gHH(r) curves are included in the Supplemental Information. The AMOEBA14 model is in overall good agreement with experiment for the three distributions. The height of the first peak in gOO(r) is approximately 0.4 and 0.6 greater than the ALS and APS X-ray data, respectively, but the location of the peak is at the same oxygen-oxygen distance as experiment. The first and second troughs, as well as the second peak, of the gOO(r) nearly overlap the experimental curve, with deviations of less than 0.1%. A similar level of agreement is seen between the AMOEBA models and experiment for the gOH(r) and gHH(r), and as an effective potential it probably captures, imperfectly, any nuclear quantum effects.

Figure 10.

The water oxygen-oxygen radial distribution functions at 298 K for AMOEBA03, AMOEBA14 and iAMOEBA compared against experimental values from References 77-79.

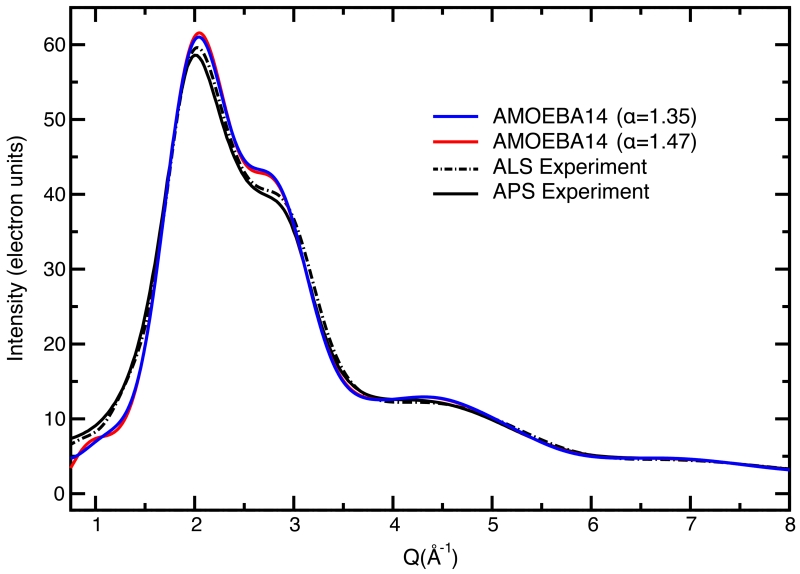
Assuming a model for the condensed phase water electron density based on modified atomic form factors (MAFFs)⁷⁷, we can Fourier transform the radial distribution functions to derive a simulated intensity curve to compare against the ALS⁷¹ and APS⁷⁸ intensity data (Figure 11). Since the RDFs were not included in the calibration data, we performed three optimizations with different molecular polarizability targets (1.35, 1.41 and 1.47 ų) to determine its effect on water structure. The lower bound is based on an earlier ab initio calculation that suggested a reduction in the molecular polarizability in going from gas phase (1.47 ų) to the condensed phase (1.35 ų).⁸⁰ More recent work has evaluated the molecular polarizability in the liquid using a different method, and determined that it was not significantly different from the gas phase value.⁸¹ It is evident from Figure 11 that modifying, within reason, the polarizability, produced no qualitative difference in the RDFs, although other properties may be sensitive to other water properties, although we do not investigate them here. Overall the AMOEBA model intensities fall outside the differences between the ALS and APS experiments, which is likely a result of the larger first peak in the gOO(r) compared to experimental estimates.

Figure 11.

Comparison of the ALS and APS experimental X-ray scattering intensities from References 78 and 79 for liquid water at 1 bar and 298 K with curves simulated with AMOEBA14 models modified to have molecular polarizabilities of α=1.47 ų and α=1.35 ų .

Electrostatic Potential

The general protocol in the development of novel AMOEBA parameters typically optimizes the atomic multipole parameters by fitting to the molecular electrostatic potential generated via a gas phase ab initio molecular orbital calculation.⁴¹ As detailed above, the AMOEBA14 water multipole parameters were allowed to fluctuate in conjunction with the remaining parameters and the monomer electrostatic potential map was not included in the fitting. The TINKER POTENTIAL program was used to compare the electrostatic potential for a single water molecule on a dense, uniform grid of points in a band 1.0 to 2.05 Å from the vdw surface. The average magnitude for the electrostatic potential from an MP2/aug-cc-pVQZ calculation was 6.6851 kcal/mol/e- and the deviations for AMOEBA03 and AMOEBA14 werefound to be −0.0499 and −0.0584. While the AMOEBA14 model was not fit to the ab initio electrostatic potential, the model is clearly effective for gas phase calculations outside of the calibration data.

Transport and Surface Tension Properties at Room Temperature

The viscosity, self-diffusion constant, and the surface tension at room temperature, were computed for the AMOEBA14 model. Viscosity was computed via the Einstein-Helfand relation and using the off-diagonal components of the pressure tensor. The viscosity of AMOEBA14 is 0.900 centipoise (cP) and is in nearly perfect agreement with the experimental measurement of 0.896 cP at 298 K.⁸² Self-diffusion was computed via the Einstein equation via average motion over all molecules across a full MD simulation. The standard self-diffusion coefficient as determined from an NPT simulation with 216 molecules in a periodic box is 1.99×10⁻⁵ cm²/s, which underestimates the experimental self-diffusion coefficient of 2.29×10⁻⁵ cm²/s. Yeh and Hummer have suggested an analytical system-size correction for diffusion coefficients computed via periodic MD simulation.⁸³ Application of their correction increases the AMOEBA14 value to 2.36×10⁻⁵ cm²/s. The surface tension computed via averaging over the diagonal elements of the pressure tensor is γ = 69.21 N/m, and deviates less than 0.5% from the corresponding experimental value determined at 298 K.⁸⁴ All of these properties are summarized in Table 6.

Table 6.

Miscellaneous bulk water properties and ion solvation free energies for the AMOEBA14 water model. All energies are in kcal/mol. Distances are in Å, viscosity in cP, and diffusion is in 10⁻⁵ cm²/s.

Property	Expt	AMOEBA03	AMOEBA14	iAMOEBA
Viscosity	0.896b	1.08	0.900	0.85
Self-Diffusion Constant	2.29c	2.0	1.99	2.54
Size-Corrected Diffusiona	—	2.3	2.36	2.93
Surface Tension (300K)	71.73d	64	—	68.3
Surface Tension (298K)	71.97d	—	69.21	—
Na+ ΔG(Hydration)	−86.8e	−89.9	−91.91	—
Cl− ΔG(Hydration)	−87.2e	−84.6	−89.25	—
Na+-H2O Dimer Distance	2.23f	2.232	2.252	2.47
Na+-H2O Dissociation Energy	−23.6f	−23.53	−23.23	−21.81
Cl−-H2O Dimer Distance	3.103g	3.151	3.147	2.965
Cl−-H2O Dissociation Energy	−15.4g	−15.99	−15.72	−18.11

^aReference 83.

^bReference 82.

^cReference 102.

^dReference 84.

^eReference 103.

^fReference 104.

^gReference 105.

Ion-Water Interactions

It is important to validate the AMOEBA14 water model for not only a homogeneous system, but also a heterogeneous system. The ion-water interaction was examined for the gas phase dimer system and the ion hydration free energy. The ions considered were the sodium cation (r=2.85, ε=0.15, α=0.12) and chloride anion (r=4.20, ε=0.5, α=4.0). Ion hydration free energies were computed via the orthogonal space random walk (OSRW) method.⁸⁵ The binding energies and equilibrium distance for the ion-water dimer and the ion hydration free energies are reported in Table 6. The AMOEBA14 model predictions for the ion-water dimer interaction energies are within 0.5 kcal/mol of experiment, while the ion hydration free energies are slightly overestimated for both the anion and the cation. Since water-ion intermolecular interactions are large and involve significant polarization, it is encouraging that the ion parameters required only minor adjustment from the 2003 values²⁸ for use with AMOEBA14. While much further testing is necessary, this holds promise that AMOEBA parameters for other systems will retain compatibility with the new AMOEBA14 water model.

CONCLUSION

The inclusion of polarizability makes the AMOEBA model preferable over other fixed-charge water models when characterizing water at different state points, for asymmetric environments, and for better transferability. With the advances made in computational modeling over the past decade, the AMOEBA water model was revisited in order to calibrate the parameters against a large, diverse data set. The new AMOEBA water model improves in accuracy over the original model for the prediction of bulk properties over large temperature and pressure ranges, in addition to maintaining reliability for gas phase property determination. By utilizing the ForceBalance methodology to optimize the AMOEBA model, nearly two dozen parameters could be systematically fit to a data set of ab initio calculations and experimental measurements.

The new AMOEBA water model is an improvement over the previous model, since a range of temperatures and pressures, as well as more gas phase and bulk properties, were included in the fitting of the parameters. For the six condensed phase properties in the calibration data set, AMOEBA14 qualitatively matches the experimental curves over the temperature range and the deviations from experiment are generally within a reasonable error margin. The current model exactly matches the experimental temperature of maximum density and the enthalpy of vaporization at room temperature differs by less than 0.5 kcal/mol, with a mean absolute deviation of 0.43 kcal/mol over the temperature range studied. The improvement observed for the bulk phase prediction of the AMOEBA14 model does not come at the expense of the accuracy of the model for gas phase property determination. The AMOEBA14 model has a similar accuracy level as the AMOEBA03 model for the interaction energy of gas phase cluster ranging from dimers to 20-mers. The integrity of the new model parameters holds for properties not included in the calibration data set, as evidenced by the good agreement observed between the experimental radial distribution functions for oxygen-oxygen, oxygen-hydrogen, and hydrogen-hydrogen and those obtained via AMOEBA14.

The development of the new AMOEBA14 parameters is significant for modeling systems solvated in water, where the balance of solvent-solvent, solvent-solute, and solute-solute interactions is crucial for determining solute behavior. Within this work we have demonstrated the accuracy of the AMOEBA14 model for a heterogeneous system, specifically the calculation of ion hydration free energies. Future applications of the model, for example, determining ligand binding affinities, will benefit from the improved definition of the AMOEBA water parameters.

It should be noted, most current generation water models are missing an explicit term to account for charge penetration effects. Such a term is needed to correct for the use of point charges, or point multipoles in the case of AMOEBA, restricted to nuclear positions. A variety of empirical and semi-empirical damping functions have been proposed to treat penetration in the context of both molecular mechanics,^86,87,88 including the AMOEBA benzene dimer,⁸⁹ and QM/MM calculations.^90,91 We plan to explore how charge penetration effects within the AMOEBA model impact the water parameterization. For example, the preliminary indication is inclusion of charge penetration reduces the largest differences between ab initio and AMOEBA dimer energies (see Table 4).

With the improved accuracy of the AMOEBA water model for bulk phase property prediction, we recommend the implementation of our revised parameters for future studies employing a polarizable water model. The model is proven to be transferable between gas phase and bulk phase, as well as in homogeneous and heterogeneous systems.