Abstract
The design space for electrical stimulation of the nervous system is extremely large, and because the response to stimulation is highly non-linear, the selection of stimulation parameters to achieve a desired response is a challenging problem. Computational models of the response of neurons to extracellular stimulation allow analysis of the effects of stimulation parameters on neural excitation and provide an approach to select or design optimal parameters of stimulation. Here, I review the use of computational models to understand the effects of stimulation waveform on the energy efficiency of neural excitation and to design novel stimulation waveforms to increase the efficiency of neural stimulation.
Keywords: neural model, electrical stimulation, deep brain stimulation, energy efficiency, selectivity, optimization
Introduction
Computer-based models of the effects of electrical stimulation on neurons are potentially useful tools for analysis and design of neurostimulation therapies. Computational models provide a means to understand the biophysical mechanisms underlying the effects of extracellular stimulation on neurons (e.g., McNeal 1976, Rattay 1989, Warman et al. 1992, McIntyre et al. 2004) and can be used to predict the effects of variations in stimulation parameters on the neural response to stimulation (Kuncel and Grill 2004). As well, computational models provide the foundation for model-based design of electrode geometries and stimulation parameters intended to improve the ability control the neural response to stimulation. For example, computational models have been used to analyze and design electrode configurations for spinal cord stimulation (Holsheimer et al. 2005, Howell et al. 2014), deep brain stimulation (Butson and McIntyre 2006, Keane et al. 2012, Howell et al. 2015), epidural cortical stimulation (Manola et al. 2005, Wongsarnpigoon and Grill 2012), and peripheral nerve stimulation (Veltink et al. 1989, Choi et al. 2001, Kent and Grill 2013). As well, such computational models can be used to guide the selection or optimization of stimulation parameters.
Two important considerations when selecting or designing stimulation parameters are selectivity and efficiency. Selectivity is the ability to activate the targeted neural elements without activating the non-target neural elements, and the magnitude of the therapeutic effect (efficacy) as well as the type and magnitude of side effects are often determined by the degree of selectivity. For example, short stimulation pulse durations increase the spatial selectivity of stimulation (Grill and Mortimer 1996), thereby increasing the therapeutic window of deep brain stimulation (Rizzone et al. 2001, Reich et al. 2015), and model-based selection of stimulation parameters decreased the side effects from deep brain stimulation (Alberts et al. 2010, Frankemolle et al. 2010). Efficiency is achieving the required level of neural activation or response to achieve clinical efficacy with the minimum amount of stimulation, and the measure of “amount” can be with respect to a number of different but related quantities including stimulation current or voltage amplitude, stimulation charge, stimulation power, and stimulation energy.
Stimulation Waveforms for Neural Stimulation
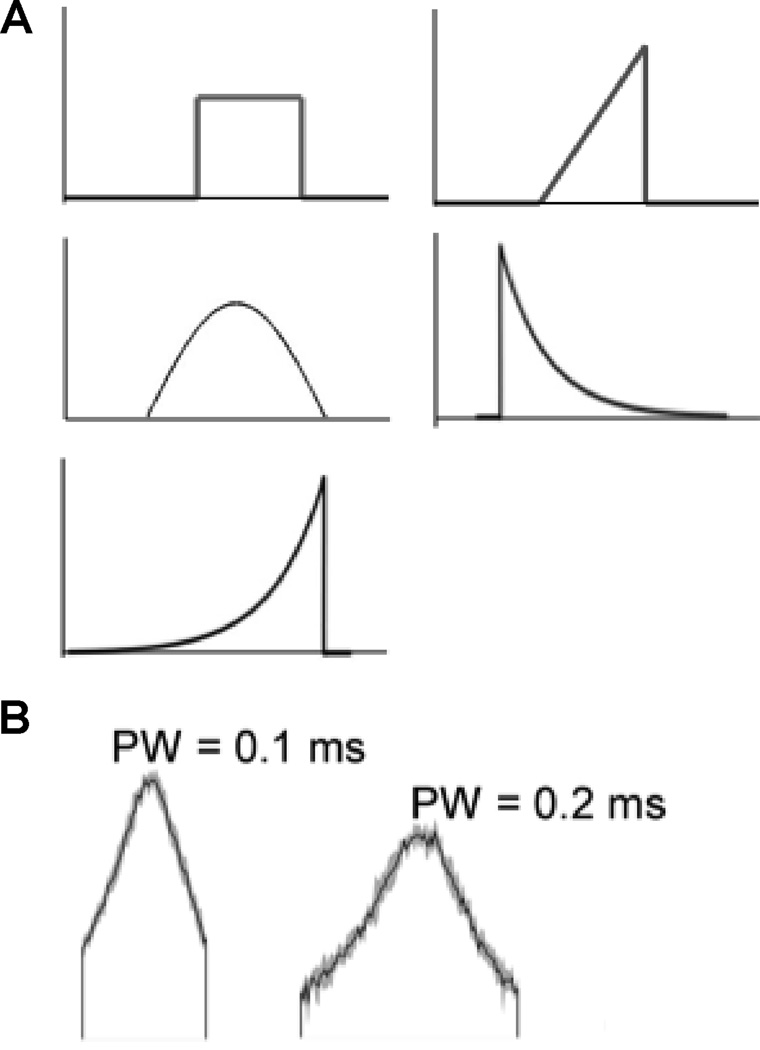
The selectivity and efficiency of neural stimulation are dependent on the choice of the stimulation waveform (Figure 1). When stimulating a peripheral nerve, it is desirable to increase the threshold difference between different diameter nerve fibers (i.e., fiber diameter selectivity). Increasing fiber diameter selectivity increases the ability to grade the magnitude of the evoked response, or, in other words, reduces the gain between stimulation intensity and evoked neural activity, and this is expected to increase efficacy. Fiber diameter selectivity can be increased by minimizing the duration of monophasic rectangular pulses used for stimulation and further increased by adding a second charge-balancing phase to the stimulation pulse (Gorman and Mortimer 1983). Further, it is desirable to increase the threshold difference between nerve fibers lying at different distances from an electrode (i.e., spatial selectivity), for example to control individually the force production in multiple muscles innervated by nerve fibers in different locations within a compound nerve trunk (McNeal and Bowman 1985, Sweeney et al. 1990). As with fiber diameter selectivity, spatial selectivity is increased by short duration rectangular stimulation pulses (Grill and Mortimer 1996), and this increased spatial selectivity may increase the therapeutic window between on-target and off-target activation, thereby increasing efficacy. Cable models of myelinated nerve fibers (McNeal et al. 1976) enabled determination of the underlying biophysical basis for stimulation pulsewidth dependent selectivity. The redistribution of ohmic currents along the axon during stimulation is dependent on the stimulation pulse duration (Warman et al. 1992), and redistribution of these currents during longer duration pulses increases the threshold of nerve fibers closer to the electrode (and larger diameter fibers) and decreases the threshold of nerve fibers further from the electrode (and smaller diameter nerve fibers) (Grill and Mortimer 1996). Thus, short duration pulses increase selectivity relative to long duration pulses by minimizing threshold changes from current redistribution.
Figure 1.
Waveform shapes for electrical stimulation of the nervous system. (A) Conventional waveform shapes defined a priori include short rectangular pulses, ramps, sines, falling exponentials, and rising exponentials. (B) Truncated Gaussian waveforms, at two different durations, determined by optimal design using a genetic algorithm (Wongsarnpigoon and Grill 2010).
The stimulation waveform shape can also be manipulated to increase stimulation selectivity between activation of the targeted neural elements and activation of non-target neural elements, and thereby increase the dynamic range between therapeutic effects and unwanted side effects. For example, sub-threshold pre-pulses, which manipulate the non-linear ionic conductances of the membrane, influence selectivity by altering neuronal excitability in advance of applying a subsequent stimulation pulse (Zimmerman 1968, Sassen and Zimmerman, 1973, Grill and Mortimer, 1995). Sub-threshold depolarizing pre-pulses increase the thresholds of the most excitable axons, enabling selective stimulation of smaller diameter axons or axons lying further from the electrode, which would normally have threshold higher than the larger axons or the axons lying closer to the electrode (Grill and Mortimer, 1997, Deurloo et al. 2001). Such an inversion of the current-distance relationship would be useful, for example, to activate selectively axons positioned deeply in a nerve with the objective of controlling individually the activation of multiple muscles innervated by a common nerve trunk (McNeal and Bowman 1985, Sweeney et al. 1990), or might be able to overcome side effects produced by misplaced electrodes for deep brain stimulation. Sub-threshold pre-pulses also increase the threshold difference between comingled local cells and axons of passage in proximity to the electrode during central nervous system (gray matter) stimulation (McIntyre and Grill 2000). In vivo experiments support that asymmetric but still charge balanced waveforms increase stimulation selectivity between local cells and passing axons as compared to conventional monophasic or symmetric biphasic waveforms (Wang et al. 2012). Increased neural element selectivity is expected to increase clinical efficacy and reduce side effects by minimizing activation of off-target neurons (Kuncel and Grill 2004). Beyond the selectivity of stimulation, by nerve fiber diameter, nerve fiber location, or neural element type, which can determine the therapeutic effects and side effects of stimulation, the selection of stimulation parameters and the shape of the stimulation waveform also influence the efficiency of stimulation.
Efficiency of Stimulation
There are multiple dimensions of stimulation efficiency that are affected by the selection of stimulation parameters and the stimulation waveform shape. The charge delivered during a stimulus pulse (charge efficiency) is an important consideration for tissue damage resulting from neural stimulation (Shannon 1992, Merrill et al. 2005). Although present clinical devices employ comparatively large surface area macroelectrodes, where charge considerations may not limit performance, devices in development employ many much smaller electrodes to shape the spatial distribution of stimulation, for example in deep brain stimulation (Martens et al. 2011, van Dijk et al. 2015). With smaller surface area electrodes, stimulation waveforms that minimize the charge required for neural excitation may enable a larger range of stimulation intensities without exceeding charge density limitations (Shannon 1992, Merrill et al. 2005). The instantaneous power of a stimulus pulse (power efficiency) is important since the maximum power that can be delivered is directly proportional to the size of the battery. Modern clinical devices are typically placed in subcutaneous pockets, where device size may not be primary limitation. However, reducing the size, for example, of deep brain stimulation devices may enable placement of the implanted pulse generator on the skull to avoid lead tunneling and the potential complications of leads running from the skull to the chest. The energy required for stimulation (energy efficiency) determines both the physical size and the lifetime of battery-powered implanted pulse generators, which, when depleted, must be replaced through an expensive and invasive procedure. As demonstrated by Wongsarnpigoon et al. (2010) no single waveform shape is simultaneously charge-, power-, and energy-optimal, and thus the definition of the objective function or the performance criterion is critical to determining the optimal waveform for a particular application.
When considering effects of stimulation parameters or stimulation waveform on measures of efficiency, the effects on efficacy are often not considered. The targeted level of neural activation is typically taken as stimulation of some number of neurons (sometimes only one) that are assumed to be sufficient for clinical efficacy. Alternatively, the activated proportion of a population of modeled neurons as a function of variation in a stimulation parameter (e.g., increasing stimulation current or voltage), can be used to assess efficiency (Foutz and McIntyre 2010, Wongsarnpigoon and Grill 2010), but the relationship between the number of activated neurons and clinical efficacy or side effect generation is likely to be highly non-linear.
The Importance of Energy Efficient Neural Stimulation
The challenge of energy-optimal neural stimulation has practical implications for the battery lifetime for implanted pulse generators (IPGs) powered with primary-cell batteries, recharge interval for IPGs powered with rechargeable batteries, and device size (volume) for all types of IPGs. An example of the importance of energy-optimal neural stimulation is found in one of the most successful clinical applications of neural stimulation – deep brain stimulation (DBS) to treat the symptoms of movement disorders. The primary-cell batteries that power the IPGs used in most applications of DBS last approximately 3–5 years (Ondo et al. 2007). However, this lifetime is substantially shorter than the anticipated duration of required treatment, which, in most cases, is the lifetime of the recipient. Therefore, patients must undergo repeated surgical procedures to replace the battery-depleted IPG, and these procedures obligate patients to incur repeatedly the associated risks including infection (Boviatsis et al. 2010, Bronstein et al. 2011) and misprogramming (Okun et al. 2005). Rechargeable IPGs are an alternative to primary-cell devices and are anticipated to have longer battery lifetimes, although real-world experience is as of yet quite limited. Improved efficiency of stimulation will benefit rechargeable IPGs, as reduced energy requirements will increase the recharge interval and thereby reduce the number of charge-discharge cycles, perhaps improving device lifetimes. Finally, device lifetime is related to the capacity (volume) of the battery, and as the energy efficiency of stimulation is improved, devices with the same lifetime can be made smaller. There are a number of approaches for improving stimulation efficiency including altering the material properties (Cogan, 2008, Merrill et al., 2005) or geometry (Golestanirad et al., 2013, Howell and Grill, 2014, Wei and Grill, 2005) of the electrode. Additionally, and the focus here, efficiency may be improved by modifying the stimulation waveform.
In addition to the very practical implication for IPG energy consumption, analysis and design of energy efficient neural stimulation waveforms is a useful test case to demonstrate computational approaches to analysis and design of neurostimulation therapies – from analytical solutions of linear first-order differential equations through engineering optimization using non-linear representations of the stimulated neurons. The power of model-based design is the opportunity not only to conduct multiple iterations rapidly and at low cost, but as well the opportunity to arrive at optimal solutions. However, it is important to recognize that the utility of such solutions will only be as good as the fidelity of the model use in the optimization process. Here we consider the particular problem of how to select a stimulation waveform to minimize the amount of energy required to evoke an action potential.
Calculation of the Energy Optimal Pulse Duration for Rectangular Pulses
The vast majority of modern neural stimulation devices employ short-duration rectangular pulses, and thus it is important to consider how the parameters of such pulses can be selected so as to minimize the energy required for excitation (Figure 2). The strength duration relationship is a simple model to describe the minimum amplitude rectangular stimulus pulse required to evoke an action potential, called the threshold Ith, as a function of the duration or pulsewidth, PW, of the pulse, and can be described by the following equation (Weiss 1901):
where Irh is the rheobase current, the threshold current for a pulse of infinite duration (in practice, a long PW), and Tch is chronaxie, or PW at which the threshold current is twice Irh. Using this equation we can determine the stimulus pulse duration that minimizes the energy required for stimulation, i.e., the threshold energy.
Figure 2.
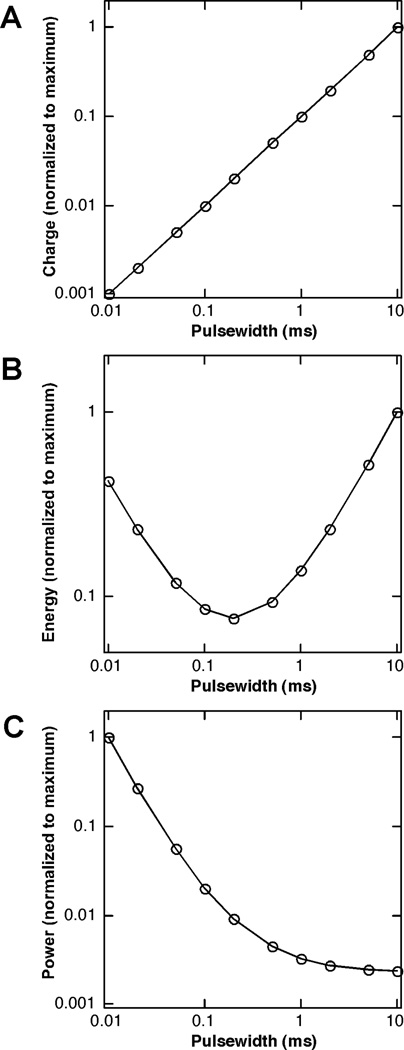
Threshold (A) charge, (B) energy, and (C) power, normalized by their respective maximal values, as a function of the duration of a monophasic rectangular stimulus pulse. Even with this simple waveform, no duration was simultaneously charge-, energy- and power-optimal.
Recall that power is the rate of energy transfer, so energy is the time integral of power:
Assuming a pulse of duration PW and an electrical load of R, and recalling that electrical power is I2R, yields
and substituting in the strength duration relationship to describe the threshold current as a function of the PW
Then to determine the PW that minimizes power, we take the derivative of this expression with respect to PW and set it equal to zero:
Solving this equation yields PW = Tch - that is, the pulsewidth that minimizes energy is equal to the chronaxie (Kroll 1993).
This approach can also be used to determine the PW that minimizes stimulation power and stimulation charge. Stimulation power is proportional to the square of the current, and making use of the strength duration relationship, the threshold power is given by
Thus, the threshold power decreases as PW increases, and long pulsewidths should be used to be power efficient. The threshold charge is the product of the threshold current and the pulse duration, and making use of the strength duration relationship, the threshold charge is given by
Thus, the threshold charge decreases as PW decreases, and short pulsewidths should be used to be charge efficient. Collectively, these results (Figure 2) reveal that stimulation is most energy-efficient with PW = Tch, most power-efficient with long PW, and most charge efficient with short PW, thereby indicating that no single pulse duration is simultaneously energy-, power-, and charge-optimal (Wonsarnpigoon et al. 2010), and the optimal pulsewidth will be determined by consideration of the performance requirements of a particular application.
The Rising Exponential as an Energy Optimal Waveform Shape
One waveform shape in particular—the rising exponential—was concluded to be energy-optimal across multiple studies. Offner (1946) sought to determine the stimulation waveform shape that minimized the power required for stimulation, on the assumption that neural damage was determined by generated heat, which is turn was proportional to stimulation power. Similarly, using analytical and numerical optimization, Kajimoto et al. (2004) concluded that a rising exponential was the energy-optimal waveform shape, and Fishler (2000) and Jezernik and Morari (2005) reached the same conclusion.
However, these results were all obtained using a linear (passive) model of the neural membrane. While a linear approximation may be useful for estimating subthreshold responses (Warman et al. 1992), this model does not account for accommodation - the increase in threshold during extended subthreshold stimulation that appears to be a ubiquitous property of excitable cells. Indeed, Offner (1946) recognized and acknowledged this limitation, and restricted his conclusion that the exponentially rising pulse was the most power efficient waveform to the case when accommodation was ignored. When non-linear (active) models of the neural membrane, which include the membrane ionic conductances responsible for accommodation, are considered, the rising exponential is not be the optimal stimulation waveform shape to minimize the energy required for stimulation (Wongsarnpigoon et al. 2010). The apparent efficiency gains of long-duration rising exponential pulses, as compared to rectangular pulses, were an artifact of the long-duration rising exponential pulses being essentially identical short-duration rising exponential pulses preceded by close-to-zero amplitude “tails” of differing durations (Wongsarnpigoon et al. 2010). Importantly, these results illustrate that the energy required for stimulation is indeed dependent on the shape of the stimulation waveform, and highlight the importance of using an appropriately complex model to analyze the effects of waveform shape on neural excitation.
Effect of Stimulation Waveform Shape of Energy Efficiency of Stimulation
There are a number of evaluations of the effects of stimulation waveform shape on the energy efficiency of neural stimulation, and these analyses were accomplished using appropriately complex non-linear models of the neural elements (nerve fibers or local projection neurons). Sahin and Tie (2007) employed a non-linear model of a mammalian nerve fibers (Sweeney et al. 1987) to determine the energy required to generate an action potential (threshold energy) as a function of pulse duration across a multitude of monophasic waveform shapes including conventional rectangular pulses, ascending and descending linear ramps, ascending and descending exponentials, a Gaussian, and a single half-cycle of a sinusoid. They concluded that the Gaussian-shaped waveform required the minimum energy for stimulation, followed closely by the sine, and that the rising and decaying exponential waveforms required the greatest energy for stimulation. Further, the pulse duration at which the different waveforms achieved minimum energy varied across the waveform shapes, but in all cases corresponded to the chronaxie.
We analyzed the charge, power, and energy required to excite a population of model mammalian axons, represented with the MRG model of a peripheral nerve fiber (McIntyre et al. 2002), with monophasic rectangular, ramp, and exponential waveforms and then validated these findings with in vivo experimental measurements (Wongsarnpigoon et al. 2010). The results revealed that no single waveform was simultaneously energy-, charge-, and power-optimal, and thus the definition of the performance metric or objective function is critical to determining the optimal waveform for a particular application. Although, the differences between the minimum threshold energies across waveforms were relatively small, energy thresholds were strongly dependent on pulse duration.
Foutz and McIntyre (2010) compared activation of non-linear models of passing axons or local projection neurons using a point source representation (Zhang and Grill 2010) or a model of a clinical deep brain stimulation electrode across a range of monophasic stimulation waveform shapes including: conventional rectangular pulses, centered triangular pulse, ascending and descending linear ramps, ascending and descending exponentials, a Gaussian, and a sine. Similar to Sahin and Tie (2007), they found that with intracellular stimulation, the Gaussian and sinusoidal waveforms minimized threshold energy, and that the centered ramp produced excitation with energy comparable to the Gaussian waveform. In subsequent experimental measurements of peripheral nerve stimulation thresholds (Foutz et al. 2012), they demonstrated that the centered triangular waveform required less energy than rectangular waveforms for very short duration pulses. The trends from models of intracellular activation of neural elements were preserved for extracellular stimulation – with similar results with both point source and realistic DBS electrodes. However, the pulse durations at which energy optimal stimulation was achieved were longer with the DBS electrode, as compared to the point source, and were longer when considering activation of the passing axons, as compared to the local cells. These results highlight the importance of the spatial distribution of the potentials along the neural elements (as determined by the electrode geometry and electrical properties of the tissue), as well as the membrane (excitation) properties of the elements themselves, in determining the effects of changes in stimulation waveform on threshold and energy efficiency.
One of the collective limitations of these approaches was the assumption that the stimulation waveform shapes were monophasic. For chronic neural stimulation biphasic waveforms are important to reverse the charge deposited on the electrode-electrolyte interface during the stimulation pulse to avoid potentially harmful irreversible electrochemical reactions (Merrill et al. 2005). The second phase of the stimulus, however, can quench the excitation produced by the primary phase thereby increasing the current (and energy) thresholds for stimulation, although this effect can be mitigated with an interphase delay (van den Honert and Mortimer 1979, Gorman and Mortimer 1983). As well, the phase durations and interphase spacing can be manipulated to reduce the energy required for initiation of action potentials as well as to reduce the energy required for entrainment of neurons exhibiting intrinsic bursting activity (Hofmann et al. 2011), as might be important in the efficacy of deep brain stimulation (Grill et al. 2004). Thus, although the consideration of only monophasic stimuli was a limitation of these studies, appropriate design of the charge recovery phase(s) of the waveform provides another opportunity to improve performance.
Another important consideration is the electrical circuitry required to generate the stimulation waveform. If a complex circuit is required to generate an energy optimal stimulation waveform shape, then any energy savings resulting from the waveform design may be lost by the energy requirements of the circuit used to generate the waveform. Further, optimization of the circuit topology in concert with the stimulation waveform shape may be another approach to enhance further the efficiency of stimulation (Foutz et al. 2012, Lee et al. 2015).
Optimized Pulse Shapes for Stimulation
In the analyses reviewed above, the stimulation waveforms were from a restricted set of conventional shapes selected a priori. However, there is no reason to assume that the energy optimal waveform shape lies within this realm, and therefore a number of studies were conducted to determine or design the optimal stimulation waveform shape.
We used an optimization approach termed a genetic algorithm to determine the waveform shape that minimized the energy required to generate an action potential across a broad range of pulse durations (Wongsarnpigoon and Grill 2010). A genetic algorithm operates analogously to biological evolution; in the optimization the candidate stimulation waveforms were the “organisms” and the cost function to be minimized was the threshold energy, subject to the constraint that the waveform generated an action potential in a single model mammalian axon. As the genetic algorithm progressed through iterations (generations), the waveforms became increasingly energy efficient and converged upon an energy-optimal shape that resembled a truncated Gaussian (Figure 1). Subsequent evaluations in a population of model mammalian axons, as well as in vivo measurements of peripheral nerve excitation thresholds, indicated that the optimized waveforms were more energy efficient than rectangular pulses of the same duration, but the overall energy savings were modest. Interestingly, the energy optimal waveforms that resulted when a charge balancing (anodic) pulse either preceded or followed the primary cathodic phase had shapes that were dependent on the phase order as well as the relative durations of the cathodic and anodic phases (Wongsarnpigoon and Grill 2010).
Forger et al. (2011) employed the calculus of variations to identify a waveform shape that minimized the r.m.s. current required to generate an action potential in a Hodgkin-Huxley (HH) model neuron. The resulting polyphasic stimulus resulted in a 40 % reduction in r.m.s. current as compared to a rectangular stimulus. The hyperpolarizing portion of the stimulus that preceded the large amplitude depolarizing phase removed resting inactivation of the sodium channel (Clay et al. 2012), reminiscent of a hyperpolarizing pre-pulse (Grill and Mortimer 1995). If constrained to its monophasic primary phase, the resulting optimized waveform resembled the Gaussian waveforms identified in earlier analyses as reducing the energy required for stimulation (Sahin and Tie 2007 Foutz et al. 2010, Wongsarnpigoon and Grill 2010). Importantly, Forger et al. obtained a remarkably similar waveform using spike triggered averaging of stochastic perturbations delivered to actual squid axons, both demonstrating the utility of model-based design, and highlighting a novel in vitro approach to waveform design.
Similarly, Tahayori and Dokos (2012) coupled a single compartment model of the neural membrane incorporating the Hodgkin Huxley dynamics from the squid axon to a gradient descent algorithm to minimize the total charge required to generate an action potential with arbitrary waveform shapes of fixed durations and amplitudes. The resulting waveform contained a sharp rise to a peak, followed by a decay to zero, and followed by a slow increase until the end of the pulse. The contribution of this second phase to excitation is not clear. They employed a penalty term to generate a smoothly varying waveform, but relaxation of this requirement resulted in a substantial reduction in the threshold charge, illustrating the risks of imposing a priori requirements on shape when trying to determine optimal waveform shapes.
Krouchev et al. (2014) used the Least Action Principle and a space clamped patch of neuronal membrane to determine the optimal trajectory of transmembrane potential and subsequently, for a given model, determine the energy optimal stimulation current to drive the transmembrane potential along that trajectory. Again, the resulting optimal current waveforms were approximately Gaussian in shape, reinforcing the findings of earlier studies that fortuitously selected this shape a priori or arrived at this shape via optimization.
Conclusion
The parameter space for electrical stimulation of the nervous system is extremely large, and the design and selection of stimulation parameters to achieve a desired response is a challenging problem. Computational models of the neural response to stimulation provide an approach to select or design optimal parameters for neurotherapeutic devices. The selection and design of stimulation waveforms that reduce the energy required for excitation has practical implications for IPG energy consumption, and was a useful demonstration case of computational approaches to analysis and design of neurostimulation therapies.
Energy optimal waveform shapes yielded comparatively small gains in efficiency, and clinical devices continue to use short duration rectangular stimulation pulses. Importantly, model-based analysis revealed that energy thresholds were strongly dependent on pulse duration, and energy-optimal durations were waveform specific. No single waveform shape or duration was simultaneously energy-, charge-, and power-optimal, and thus the performance requirement of specific applications of neurostimulation need to be defined for the design process. As well, most analyses focused exclusively on efficiency, and simultaneous consideration of stimulation selectivity may yield waveforms that increase clinical efficacy by increasing activation of targeted neural elements and reducing the activation of non-target neural elements. Finally, the results highlight the importance of using an appropriately complex model to analyze the effects of waveform on neural excitation, as prior simplified models yielded suboptimal results, and optimal stimulation waveform parameters were dependent on the electrode geometry and electrical properties of the tissue (i.e., the spatial distribution of extracellular potentials along the neurons).
Acknowledgments
Preparation of the this material was supported by the National Institutes of through grants R01 NS040894, R01 NS079312, and R01 NS050514.
Bibliography
- Alberts JL, Hallahan K, Thota A, Noecker AM, Vitek JL, McIntyre CC. Reducing cognitive-motor declines associated with bilateral subthalamic deep brain stimulation through computational modelling in a Parkinson's disease patient. J Neurol Neurosurg Psychiatry. 2010;81:1170–1172. doi: 10.1136/jnnp.2008.160093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boviatsis EJ, Stavrinou LC, Themistocleous M, Kouyialis AT, Sakas DE. Surgical and hardware complications of deep brain stimulation. A seven-year experience and review of the literature. Acta Neurochir (Wien) 2010;152:2053–2062. doi: 10.1007/s00701-010-0749-8. [DOI] [PubMed] [Google Scholar]
- Bronstein JM, Tagliati M, Alterman RL, Lozano AM, Volkmann J, Stefani A, Horak FB, Okun MS, Foote KD, Krack P, Pahwa R, Henderson JM, Hariz MI, Bakay RA, Rezai A, Marks WJ, Jr, Moro E, Vitek JL, Weaver FM, Gross RE, Delong MR. Deep brain stimulation for parkinson disease: an expert consensus and review of key issues. Arch Neurol. 2011;68:165–171. doi: 10.1001/archneurol.2010.260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butson CR, McIntyre CC. Role of electrode design on the volume of tissue activated during deep brain stimulation. J Neural Eng. 2006;3:1–8. doi: 10.1088/1741-2560/3/1/001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi AQ, Cavanaugh JK, Durand DM. Selectivity of multiple-contact nerve cuff electrodes: a simulation analysis. IEEE Trans Biomed Eng. 2001;48:165–172. doi: 10.1109/10.909637. [DOI] [PubMed] [Google Scholar]
- Clay JR, Forger DB, Paydarfar D. Ionic mechanism underlying optimal stimuli for neuronal excitation: role of Na+ channel inactivation. PLoS One. 2012;7:e45983. doi: 10.1371/journal.pone.0045983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cogan SF. Neural stimulation and recording electrodes. Annu Rev Biomed Eng. 2008;10:275–309. doi: 10.1146/annurev.bioeng.10.061807.160518. [DOI] [PubMed] [Google Scholar]
- Deurloo KE, Holsheimer J, Bergveld P. The effect of subthreshold prepulses on the recruitment order in a nerve trunk analyzed in a simple and a realistic volume conductor model. Biol Cybern. 2001;85:281–291. doi: 10.1007/s004220100253. [DOI] [PubMed] [Google Scholar]
- Fishler MG. Theoretical predications of the optimal monophasic and biphasic defibtillation waveshapes. IEEE Trans Biomed Eng. 2000;47:59–67. doi: 10.1109/10.817620. [DOI] [PubMed] [Google Scholar]
- Forger DB, Paydarfar D, Clay JR. Optimal stimulus shapes for neuronal excitation. PLoS Comput Biol. 2011;7(7):e1002089. doi: 10.1371/journal.pcbi.1002089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foutz TJ, Ackermann DM, Jr, Kilgore KL, McIntyre CC. Energy efficient neural stimulation: coupling circuit design and membrane biophysics. PLoS One. 2012;7:e51901. doi: 10.1371/journal.pone.0051901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foutz TJ, McIntyre CC. Evaluation of novel stimulus waveforms for deep brain stimulation. J Neural Eng. 2010;7:066008. doi: 10.1088/1741-2560/7/6/066008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankemolle AM, Wu J, Noecker AM, Voelcker-Rehage C, Ho JC, Vitek JL, McIntyre CC, Alberts JL. Reversing cognitive-motor impairments in Parkinson's disease patients using a computational modelling approach to deep brain stimulation programming. Brain. 2010;133:746–761. doi: 10.1093/brain/awp315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golestanirad L, Pollo C, Graham SJ. Analysis of fractal electrodes for efficient neural stimulation. 35th Annual International Conference of the IEEE EMBS. 2013;2013:791–794. doi: 10.1109/EMBC.2013.6609619. [DOI] [PubMed] [Google Scholar]
- Gorman PH, Mortimer JT. The effect of stimulus parameters on the recruitment characteristics of direct nerve stimulation. IEEE Trans Biomed Eng. 1983;30:407–414. doi: 10.1109/tbme.1983.325041. [DOI] [PubMed] [Google Scholar]
- Grill WM, Mortimer JT. Stimulus waveforms for selective neural stimulation. IEEE Engineering in Medicine and Biology. 1995;14:375–385. [Google Scholar]
- Grill WM, Mortimer JT. The effect of stimulus pulse duration on selectivity of neural stimulation. IEEE Transactions on Biomedical Engineering. 1996;43:161–166. doi: 10.1109/10.481985. [DOI] [PubMed] [Google Scholar]
- Grill WM, Mortimer JT. Inversion of the current distance relationship by transient depolarization. IEEE Transactions on Biomedical Engineering. 1997;44:1–9. doi: 10.1109/10.553708. [DOI] [PubMed] [Google Scholar]
- Grill WM, Snyder AN, Miocinovic S. Deep brain stimulation creates an informational lesion of the stimulated nucleus. NeuroReport. 2004;15:1137–1140. doi: 10.1097/00001756-200405190-00011. [DOI] [PubMed] [Google Scholar]
- Hofmann L, Ebert M, Tass PA, Hauptmann C. Modified pulse shapes for effective neural stimulation. Front Neuroeng. 2011;4(9):1–10. doi: 10.3389/fneng.2011.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holsheimer J, Struijk JJ, Tas NR. Effects of electrode geometry and combination on nerve fibre selectivity in spinal cord stimulation. Med Biol Eng Comput. 1995;33:676–682. doi: 10.1007/BF02510785. [DOI] [PubMed] [Google Scholar]
- Howell B, Grill WM. Evaluation of high-perimeter electrode designs for deep brain stimulation. J Neural Eng. 2014;11:046026. doi: 10.1088/1741-2560/11/4/046026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell B, Lad SP, Grill WM. Evaluation of intradural stimulation efficiency and selectivity in a computational model of spinal cord stimulation. PLoS One. 2014;9:e114938. doi: 10.1371/journal.pone.0114938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell B, Huynh B, Grill WM. Design and in vivo evaluation of more efficient and selective deep brain stimulation electrodes. J Neural Eng. 2015;12:046030. doi: 10.1088/1741-2560/12/4/046030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jezernik S, Morari M. Energy-optimal electrical excitation of nerve fibers. IEEE Trans Biomed Eng. 2005;52:740–743. doi: 10.1109/TBME.2005.844050. [DOI] [PubMed] [Google Scholar]
- Kajimoto H, Kawakami N, Tachi S. Optimal design method for selective nerve stimulation. Electronics and Communications in Japan, Part 3. 2004;87:62–72. [Google Scholar]
- Keane M, Deyo S, Abosch A, Bajwa JA, Johnson MD. Improved spatial targeting with directionally segmented deep brain stimulation leads for treating essential tremor. J Neural Eng. 2012;9:046005. doi: 10.1088/1741-2560/9/4/046005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent AR, Grill WM. Model-based analysis and design of nerve cuff electrodes for restoring bladder function by selective stimulation of the pudendal nerve. J Neural Eng. 2013;10:036010. doi: 10.1088/1741-2560/10/3/036010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroll MW. A minimal model of the monophasic defibrillation pulse. Pacing Clin Electrophysiol. 1993;16:769–777. doi: 10.1111/j.1540-8159.1993.tb01657.x. [DOI] [PubMed] [Google Scholar]
- Krouchev NI, Danner SM, Vinet A, Rattay F, Sawan M. Energy-optimal electrical-stimulation pulses shaped by the Least-Action Principle. PLoS One. 2014;9(3):e90480. doi: 10.1371/journal.pone.0090480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuncel AM, Grill WM. Selection of stimulus parameters for deep brain stimulation. Clinical Neurophysiology. 2004;115:2431–2441. doi: 10.1016/j.clinph.2004.05.031. [DOI] [PubMed] [Google Scholar]
- Lee H-M, Kwon KY, Li W, Howell B, Grill WM, Ghovanloo M. A power-efficient switched-capacitor stimulating system for electrical/optical deep-brain stimulation. IEEE Journal of Solid-State Circuits. 2015;50:360–374. [Google Scholar]
- Manola L, Roelofsen BH, Holsheimer J, Marani E, Geelen J. Modelling motor cortex stimulation for chronic pain control: electrical potential field, activating functions and responses of simple nerve fibre models. Med Biol Eng Comput. 2005;43:335–343. doi: 10.1007/BF02345810. [DOI] [PubMed] [Google Scholar]
- Martens HC, Toader E, Decré MM, Anderson DJ, Vetter R, Kipke DR, Baker KB, Johnson MD, Vitek JL. Spatial steering of deep brain stimulation volumes using a novel lead design. Clin Neurophysiol. 2011;122:558–566. doi: 10.1016/j.clinph.2010.07.026. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM. Selective microstimulation of central nervous system neurons. Annals of Biomedical Engineering. 2000;38:219–233. doi: 10.1114/1.262. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM, Sherman DL, Thakor NV. Cellular effects of deep brain stimulation: model-based analysis of activation and inhibition. J Neurophysiol. 2004;91:1457–1469. doi: 10.1152/jn.00989.2003. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. Journal of Neurophysiology. 2002;87:995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans Biomed Eng. 1976;23:329–337. doi: 10.1109/tbme.1976.324593. [DOI] [PubMed] [Google Scholar]
- McNeal DR, Bowman BR. Selective activation of muscles using peripheral nerve electrodes. Med Biol Eng Comput. 1985;23:249–253. doi: 10.1007/BF02446866. [DOI] [PubMed] [Google Scholar]
- Merrill DR, Bikson M, Jefferys JG. Electrical stimulation of excitable tissue: design of efficacious and safe protocols. J Neurosci Meth. 2005;141:171–198. doi: 10.1016/j.jneumeth.2004.10.020. [DOI] [PubMed] [Google Scholar]
- Offner F. Stimulation with minimum power. J Neurophysiol. 1946;9:387–390. doi: 10.1152/jn.1946.9.5.387. [DOI] [PubMed] [Google Scholar]
- Okun MS, Tagliati M, Pourfar M, Fernandez HH, Rodriguez RL, Alterman RL, Foote KD. Management of referred deep brain stimulation failures: a retrospective analysis from 2 movement disorders centers. Arch Neurol. 2005;62:1250–1255. doi: 10.1001/archneur.62.8.noc40425. [DOI] [PubMed] [Google Scholar]
- Ondo WG, Meilak C, Vuong KD. Predictors of battery life for the Activa Soletra 7426 Neurostimulator. Parkinsonism Relat Disord. 2007;13:240–242. doi: 10.1016/j.parkreldis.2006.11.002. [DOI] [PubMed] [Google Scholar]
- Rattay F. Analysis of models for extracellular fiber stimulation. IEEE Trans Biomed Eng. 1989;36:676–682. doi: 10.1109/10.32099. [DOI] [PubMed] [Google Scholar]
- Reich MM, Steigerwald F, Sawalhe AD, Reese R, Gunalan K, Johannes S, Nickl R, Matthies C, McIntyre CC, Volkmann J. Short pulse width widens the therapeutic window of subthalamic neurostimulation. Ann Clin Transl Neurol. 2015;2:427–432. doi: 10.1002/acn3.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzone M, Lanotte M, Bergamasco B, Tavella A, Torre E, Faccani G, Melcarne A, Lopiano L. Deep brain stimulation of the subthalamic nucleus in Parkinson's disease: effects of variation in stimulation parameters. J Neurol Neurosurg Psychiatry. 2001;71:215–219. doi: 10.1136/jnnp.71.2.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahin M, Tie Y. Non-rectangular waveforms for neural stimulation with practical electrodes. J Neural Eng. 2007;4:227–233. doi: 10.1088/1741-2560/4/3/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sassen M, Zimmermann M. Differential blocking of myelinated nerve fibers by transient depolarization. Plügers Archiv. 1973;341:179–195. doi: 10.1007/BF00592788. [DOI] [PubMed] [Google Scholar]
- Shannon RV. A model of safe levels for electrical stimulation. IEEE Trans Biomed Eng. 1992;39:424–426. doi: 10.1109/10.126616. [DOI] [PubMed] [Google Scholar]
- Sweeney JD, Ksienski DA, Mortimer JT. A nerve cuff technique for selective excitation of peripheral nerve trunk regions. IEEE Trans Biomed Eng. 1990;37:706–715. doi: 10.1109/10.55681. [DOI] [PubMed] [Google Scholar]
- Sweeney JD, Mortimer JT, Durand D. Modeling of mammalian myelianted nerve for functional neuromuscular stimulation. 9th Annual Conference of the IEEE Engineering in Medicine and Biology Society. 1987;1987:1577–1578. [Google Scholar]
- Tahayori B, Dokos S. Optimal stimulus current waveshape for a Hodgkin-Huxley model neuron. Conf Proc IEEE Eng Med Biol Soc. 2012;2012:4627–4630. doi: 10.1109/EMBC.2012.6346998. [DOI] [PubMed] [Google Scholar]
- van den Honert C, Mortimer JT. The response of the myelinated nerve fiber to short duration biphasic stimulating currents. Ann Biomed Eng. 1979;7:117–125. doi: 10.1007/BF02363130. [DOI] [PubMed] [Google Scholar]
- van Dijk KJ, Verhagen R, Chaturvedi A, McIntyre CC, Bour LJ, Heida C, Veltink PH. A novel lead design enables selective deep brain stimulation of neural populations in the subthalamic region. J Neural Eng. 2015;12(4):046003. doi: 10.1088/1741-2560/12/4/046003. [DOI] [PubMed] [Google Scholar]
- Veltink PH, van Veen BK, Struijk JJ, Holsheimer J, Boom HB. A modeling study of nerve fascicle stimulation. IEEE Trans Biomed Eng. 1989;36:683–692. doi: 10.1109/10.32100. [DOI] [PubMed] [Google Scholar]
- Wang Q, Millard DC, Zheng HJ, Stanley GB. Voltage-sensitive dye imaging reveals improved topographic activation of cortex in response to manipulation of thalamic microstimulation parameters. J Neural Eng. 2012;9:026008. doi: 10.1088/1741-2560/9/2/026008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warman EN, Grill WM, Durand D. Modeling the effects of electric fields on nerve fibers: determination of excitation thresholds. IEEE Trans Biomed Eng. 1992;39:1244–1254. doi: 10.1109/10.184700. [DOI] [PubMed] [Google Scholar]
- Wei XF, Grill WM. Current density distributions, field distributions and impedance analysis of segmented deep brain stimulation electrodes. J Neural Eng. 2005;2:139–147. doi: 10.1088/1741-2560/2/4/010. [DOI] [PubMed] [Google Scholar]
- Weiss G. Sur la possibilite de render comparables entre eux les appareils servant a l’excitation electrique. Arch Ital Biol. 1901;35:413–446. (as cited in Bostock H, J Physiol, 1983; 341: 59–74) [Google Scholar]
- Wongsarnpigoon A, Grill WM. Energy-efficient waveform shapes for neural stimulation revealed with a genetic algorithm. J Neural Eng. 2010;7(4):046009. doi: 10.1088/1741-2560/7/4/046009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wongsarnpigoon A, Grill WM. Computer-based model of epidural motor cortex stimulation: effects of electrode position and geometry on activation of cortical neurons. Clin Neurophysiol. 2012;123:160–172. doi: 10.1016/j.clinph.2011.06.005. [DOI] [PubMed] [Google Scholar]
- Wongsarnpigoon A, Woock JP, Grill WM. Efficiency analysis of waveform shape for electrical excitation of nerve fibers. IEEE Trans Neural Syst Rehabil Eng. 2010;18:319–328. doi: 10.1109/TNSRE.2010.2047610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang T, Grill WM. Modeling deep brain stimulation: Point source approximation vs. realistic representation of the electrode. Journal of Neural Engineering. 2010;7:066009, 11. doi: 10.1088/1741-2560/7/6/066009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zimmermann M. Selective activation of c-fibers. Plügers Archiv. 1968;301:329–333. doi: 10.1007/BF00362643. [DOI] [PubMed] [Google Scholar]