Assessment of Scientific Reasoning: the Effects of Task Context, Data, and Design on Student Reasoning in Control of Variables

Abstract

Scientific reasoning is an important component under the cognitive strand of the 21st century skills and is highly emphasized in the new science education standards. This study focuses on the assessment of student reasoning in control of variables (COV), which is a core sub-skill of scientific reasoning. The main research question is to investigate the extent to which the existence of experimental data in questions impacts student reasoning and performance. This study also explores the effects of task contexts on student reasoning as well as students’ abilities to distinguish between testability and causal influences of variables in COV experiments. Data were collected with students from both USA and China. Students received randomly one of two test versions, one with experimental data and one without. The results show that students from both populations (1) perform better when experimental data are not provided, (2) perform better in physics contexts than in real-life contexts, and (3) students have a tendency to equate non-influential variables to non-testable variables. In addition, based on the analysis of both quantitative and qualitative data, a possible progression of developmental levels of student reasoning in control of variables is proposed, which can be used to inform future development of assessment and instruction.

1. Introduction

As science continues to be fundamental to modern society, there is a growing need to educate on the process of science along with science content. That is, within science courses there is greater emphasis on the general reasoning skills necessary for open-ended scientific inquiry (Bybee & Fuchs, 2006). This is reflected in the Framework for K-12 Science Education (NRC, 2012), the basis for the Next Generation Science Standards (NGSS), which clearly lay out the scientific processes and skills that students are expected to learn at different grade levels. For example, students as young as middle school are expected to learn how to analyze evidence and data, design and conduct experiments, and think critically and logically in making connections between data and explanations. These skills, often broadly labeled as scientific reasoning skills, include the ability to systematically explore a problem, formulate and test hypotheses, control and manipulate variables, and evaluate experimental outcomes (Bao et al., 2009; Zimmerman, 2007).

Physics courses provide ample opportunities to teach scientific reasoning (Boudreaux, Shaffer, Heron, & McDermott, 2008), and the American Association of Physics Teachers has identified goals for physics education that reflect this idea; including experience in designing investigations, developing skills necessary in analyzing experimental results at various levels of sophistication, mastering physics concepts, understanding the basis of knowledge in physics, and developing collaborative learning skills (AAPT, 1998). To better achieve these goals, an increasing number of inquiry-based physics curricula have been designed with the focus on helping students learn both science content and scientific reasoning skills. A non-exhaustive list of such courses includes Physics by Inquiry (McDermott & Shaffer, 1996), RealTime Physics (Sokoloff, Thornton, & Laws 2004), ISLE (Etkina & Heuvelen, 2007), Modeling Instruction (Wells, Hestenes, & Swackhamer, 1995), and SCALE-UP (Student-Centered Activities for Large Enrollment Undergraduate Programs) (Beichner, 1999). A common emphasis of these reformed curricula is to engage students in a constructive inquiry learning process, which has been shown to have a positive impact on advancing students’ problem solving abilities, improving conceptual understanding, and reducing failure rates in physics courses. Most importantly, the inquiry-based learning environment offers students more opportunities to develop reasoning skills; opportunities otherwise unavailable in traditionally taught courses (Beichner & Saul, 2003; Etkina & Van Heuvelen, 2007).

Among the different components of scientific reasoning, control of variables (COV) is a core reasoning skill, which is broadly defined as the ability to scientifically manipulate experimental settings when data is collected to test a hypothesis. In such manipulations, certain variables are kept constant while others are changed. In teaching and learning, both the recognition of the need for such controls and the ability to identify and construct well controlled conditions are the targets of assessment and instruction.

The COV ability has been extensively researched in the literature (Chen & Klahr, 1999; Kuhn, 2007; Kuhn & Dean, 2005; Lazonder & Kamp, 2012; Penner & Klahr, 1996; Toth, Klahr, & Chen, 2000). COV is an important ability needed in almost all phases of scientific inquiry such as variable identification, hypothesis forming and testing, experimental design and evaluation, data analysis, and decision making. The existing research reveals a rich progressive spectrum of sub skills under the generally defined COV ability; from the ability to identify simple configurations of COV conditions to the more complex multi-variable controls and causal inferences from experimental evidence.

For example, in research involving elementary students, Chen and Klahr engaged students in simple experiments involving only a few variables (Chen & Klahr, 1999). Students in second through fourth grade were presented with a pair of pictures and asked to identify whether they showed a valid or invalid experiment to determine the effect of a particular variable. The researchers found that elementary students as young as second grade were not only capable of learning how to identify COV experiments, but also were able to transfer their COV knowledge when the learning task and the transfer task were the same. In studies of third and fourth graders, Klahr and Nigam found that students were able to design unconfounded experiments and make appropriate inferences after direct instruction, although performance wasn’t always consistent. (Klahr & Dunbar, 1988)

More complex tasks were used in the studies by Penner and Klahr (1996), in which middle school students were presented with multiple variables in different contexts such as those involving ramps, springs, and sinking objects. For the context involving sinking objects, Penner and Klahr (1996) probed student understanding of multi-variable influence by asking what combination of variables would produce the fastest sinking object. They found that younger children (age 10 years) were more likely to design experiments which demonstrated the correctness of their own personal beliefs; whereas older students (12 and 14 years old) were more likely to design unconfounded experiments and tended to view experiments as a means of testing hypotheses.

The work of Kuhn focused on higher-end skills regarding students’ abilities in deriving multi-variable causal relations (Kuhn, 2007). In one study, fourth-graders used computer software to run experiments related to earthquakes (and ocean voyages). The context of this study enabled more variables to be included than in the previously mentioned studies. In addition, within this study students were asked to determine whether each variable was causal, non-causal, or indeterminate. A number of findings were observed: students were better able to identify a causal variable rather than a non-causal variable. Students did not always realize that one can test something even if it does not influence the result. In addition, although students could progress in learning COV skills, they continued to struggle when handling multivariable causality. For example, students sometimes described what they thought would be the cause of an outcome using descriptors that did not match their experimental results. There were also cases in which students described a certain material as being necessary even though it was not mentioned during experimentation. Kuhn concluded that students could correctly design experiments but did not have a good method for handling multivariable causality (Kuhn, 2007).

More recent work by Boudreaux et al. involves the study of COV abilities of college students and in-service teachers, in which they identified three distinct COV abilities at progressing levels of complexity (Boudreaux et al., 2008). The first and simplest level was the ability to design experimental trials. Students were given a scenario with a specific set of variables and were asked to design an experiment that could test whether a particular variable influenced the outcome and explain their reasoning. The second level was the ability to interpret results when the experimental design and data warranted a conclusion. Students were presented with a table of different trials and data from an experiment and asked whether a given variable influenced the behavior of the system. The trials contain both well-controlled and confounded cases and the data also show both influential and non-influential relations. The third and most difficult level was the ability to interpret results when the experimental design and data did not warrant a conclusion. In this case, students were provided with a table of various trials and data that didn’t represent a well-controlled COV experiment, and students were asked whether a given variable was influential. Through this study, Boudreaux et al. (2008) found that college students and in-service teachers had difficulty with COV skills at all levels. They concluded that students and teachers typically understand that it is important to control variables but often encounter difficulties in implementing the appropriate COV strategies to interpret experimental results. They also found that it was more difficult for students to interpret data involving an inconclusive relation than with a conclusive one.

A synthesis of the findings from the literature reveals possible developmental stages of COV skills from simple control of a few variables to complex multivariable controls and causal analysis. The structure of the complexity appears to come from several categories of factors including the number of involved variables, the structure and context of the task, the type of embedded relations (conclusive or inconclusive), and the control forms (testable and non-testable); most of which have also been well documented in the literature (e.g., Chen & Klahr, 1999; Kuhn et al., 1988; Lazonder & Kamp, 2012; Wilhelm & Beishuizen, 2003). Table 1 provides a consolidated list of COV skills that have been studied in the existing literature, with suggested developmental levels of these skills.

Table 1.

Suggested developmental levels of COV skills from the literature

Lower-end skills	Identifying or recognizing a COV situation Identifying an unconfounded COV experiment to test a variable
Intermediate skills	Deciding whether an experimental design involving multiple variables (>2) is a valid COV test of multiple selected variables (>1) Inferring from COV experimental results and designs that a variable, among several, is causally related to the outcome
Higher-end skills	Inferring from COV experimental results and designs that a variable is testable in the design when it is non-causal Being able to reason through experiments, data, and hypotheses by analyzing, manipulating, and synthesizing an integrated network of multivariate causal relations for hypothesis testing and modification

Unfortunately, the existing research cannot provide a clear metric of the entire set of COV skills in terms of their developmental levels. This is because only subsets of these skills were researched in individual studies which makes it difficult to pull together a holistic picture. The purpose of our study, therefore, is to build on this work and probe the related skills in a single study, allowing us to more accurately map out the relative difficulties of the different skills and investigate how the difficulty of COV tasks is affected by task format, context, and relations among variables. Specifically, our study aimed to (1) identify at finer grain sizes common student difficulties and reasoning patterns in COV under the influence of question context and difficulty and (2) develop a practical assessment tool for evaluating student abilities in COV at a finer-grain size. Both are important as the study outcomes may advance our understanding of student abilities in COV which is a fundamental scientific reasoning element central to inquiry-based learning. As a result, researchers and teachers can gain insight into typical patterns of student reasoning at different developmental stages which in turn can better inform instruction and related assessments.

2. Research design

2.1. Research goals

As a means of identifying at finer grain sizes common student difficulties and reasoning patterns in COV, the assessment questions used in this study were designed to investigate three areas of research: (1) the extent to which the existence of experimental data in the questions impacts student reasoning and test performance; (2) whether physics vs. real-life contexts influence student reasoning; and (3) students’ ability to distinguish between testability and casual influences of variables in COV experimental settings.

As described earlier, Boudreaux et al. (2008) identified several common difficulties related to college student abilities in COV. In their studies, students were provided two physics scenarios similar to questions 2 and 3 in Figure 1 and asked if the data presented could be used to test whether or not a variable influences the result. In their original design, both the trial conditions and experimental results were always provided to students together and were generally referred to as “data”. There are two possible issues with their design worth further exploration.

Fig. 1.

Test B questions which are designed to include experimental data. Question 1 poses a COV situation involving a real-life context. Questions 2 and 3 are situated in physics contexts and are based on the tasks used in Boudreaux et al. (2008). Test A questions (not shown) are identical except that the last row of experimental data in the table were removed.

One is the undistinguished use of the term “data” in the questions. In a COV experiment, the trial conditions and experimental results (data) are two separate entities that warrant individual treatments. To determine if a design is a well-controlled COV experiment or not, the trial conditions alone are enough. The experimental data is needed only when causal relations among variables are to be determined. In Boudreaux et al. (2008), the trial conditions and results were treated as a single body of experiment data and students were always prompted to consider the entire given data (both conditions and results) in their reasoning. This makes it difficult to isolate if students’ reasoning were based on the trial conditions, the experimental results, or both. In addition, students may be prompted to think that the experimental results would play a role in determining if a design is a well-controlled COV experiment or not, which is in fact not true.

The other issue is the use of the word “influence” in the questions. Although the question setting and statement are likely clear to an expert who understands that the question probes the testability of variables and asks whether a relation can be tested based on the trial conditions regardless of the nature of the relation, novices may be distracted by the word “influence” and may interpret the meaning of the question as if it is asking for the validity of a causal relation. This is evident in the results reported by Boudreaux et al. (2008), which suggests that students have a tendency to intertwine causal mechanisms (influential relations) with testability in COV settings. Students seem to equate, either explicitly or implicitly, a non-influential variable to a non-testable variable. When given non-testable conditions, it was reported that half of the students failed to provide the correct response (non-testable) and most of these students stated that “the data indicate that mass does not affect (or influence) the number of swings” (Boudreaux et al., 2008), which is an example of conflating non-influential with non-testable. Therefore, the use of the word “influence” may confound students’ interpretation of the question and compromise the assessment capacity in distinguishing between testability and influence of variables.

In light of this, the questions used in this study make clear distinctions between trial conditions and experimental data as well as between testability and influence. As such, it seemed appropriate to modify the two questions used by Boudreaux et al. (2008) for use in this study such that (1) the questions no longer contain the word “influence”, and (2) additional versions of the questions provide only trial conditions without the experimental data. In this way, the questions more clearly measure the two threads of COV skills which are: (1) to determine whether or not selected variables are testable under a given experimental design and (2) when testable, to determine if selected variables are influential to the experimental outcomes.

By separating trial conditions from experimental data, the nature of the questions becomes different. For questions without experimental data, students only need to reason through trial conditions, which correspond to measuring the lower level COV skills such as recognizing or identifying unconfounded COV conditions (see Table 1). With experimental data included, students may be drawn into reasoning through possible causal relations between variables and experimental outcomes in addition to the COV trial conditions. In such cases, students are engaged in coordinating evidence with hypotheses in a multivariable COV setting that involves a network of possible causal relations. Therefore, these questions are considered to assess higher level reasoning skills similar to those studied by Klahr & Dunbar (1988) and Kuhn & Dean (2005).

2.2. The design of the assessment questions

To address the research question regarding whether the presence of experimental data impacts student reasoning, the trial conditions and experimental data need to be separated in the assessment. To do so, we created two versions of the tests, Test A and B, which were identical except that the questions on Test A included only trial conditions while questions on Test B included both trial conditions and experimental data. Fig. 1 displays the questions for Test B. Test A is identical except that the last row of data in the table for each question was removed. Table 2 gives a summary of the contexts and measures of the questions used in this study.

Table 2.

Information about items for both Test A and Test B. Note that experimental data was not provided on Test A but was provided on Test B.

Item	Context	Posed Question	Correct Answer
Fishing	Real-life	Can a named variable be tested?	Named variable can be tested
Spring	Physics	Which variables can be tested?	Two variables can be tested; one is influential, the other is not.
Pendulum	Physics	Which variables can be tested?	No variables can be tested

This method of question design enables multi-level measurement of COV abilities because when data are not provided, the test questions probe student reasoning in recognizing unconfounded COV designs. Therefore, Test A primarily assess lower-end COV skills shown in Table 1. On the other hand, when data are provided, students may be engaged in coordinating multiple causal relations in a multivariable COV setting. As a result, Test B is considered to assess higher level reasoning skills listed in Table 1. By comparing students’ performance on Test A and B, the effects of experimental data on student reasoning can be determined.

The second goal of this study is to investigate how question context influences student reasoning. Among the three questions shown in Fig. 1, the first question is designed with a real-life context of fishing activities. The second and third questions are designed with physics contexts concerning oscillations of mass-spring and pendulum systems. By comparing students’ responses and explanations to these questions, the effects of physics vs. real life contexts on student reasoning can be evaluated.

The third goal of this study is to investigate students’ ability to distinguish between testability and causal influences of variables in COV experimental settings. This part of the measurement is implemented in the spring question (see Fig. 1), which involves two testable variables (i.e. unstretched spring length and distance pulled back at release). In Test B, where data are provided, one of these variables is influential (influences the experiment outcome) while the other is not. By contrasting students’ responses and explanations to the questions in two versions, student ability to distinguish between testability and causal influences of variables in COV experimental settings can be determined.

The questions used in Test A and Test B have a mixed format including both multiple choice multiple response form and an open response field for students’ explanations. In this way, students’ written explanations can be analyzed to probe further details of student reasoning, such as how students react to the existence of experimental data in a question, the sets of variables considered by students in different contexts (physics versus real-life), and influential and non-influential variables in the spring question.

In summary, because the testability of variables is solely determined by the experimental design without the need for experimental data, Test A and B constitute two stages of measurement of this particular reasoning ability. Without experimental data (Test A), the tasks measure students’ ability in recognizing COV conditions, which leads to the decision of the testability of variables in a given experiment. With experimental data (Test B), the tasks assess whether students can distinguish between testability and the influence of variables. In other words, Test B measures if students can resist the tendency to evaluate the plausibility of the possible causal relations rather than the testability of such relations in a given experimental setting. It is therefore reasonable to hypothesize that tasks not showing experimental data are easier (measuring basic COV skills) than those providing data (measuring more advanced COV reasoning).

Further, the questions used in this study allow multiple answers, in which both influential and non-influential relations are embedded. Therefore, the questions can measure advanced level skills in COV reasoning on multiple variables and relations. The design allows the measurement of a more complete set of skills ranging from lower-end skills such as identifying a COV trial condition, to intermediate skills such as identifying a causal variable, and to higher-end skills such as identifying a testable but non-causal variable in multi-variable conditions. The data collected from this study will allow quantitative determination of the relative difficulty levels of the targeted skills.

3. Data collection

In order to provide greater credibility to the research outcomes, two populations of students were studied; one from China and one from the USA. The Chinese population included 314 high school students in tenth grade (with an average age of 16). The US population included 189 college freshmen enrolled in an algebra-based introductory physics course in a university. On the level of physics content knowledge involved, both populations are at a similar level (Bao et al., 2009). The Chinese students used test versions written in Chinese and the US students used English versions. The tests were translated and evaluated by a group of 6 physics faculty who are fluent in both languages to ensure a consistent language presentation.

In the collection of data, versions of Test A and Test B were alternately stacked one after the other and handed out to students during class. In this way, students randomly received one of the two test versions. Students were given 15 minutes to complete the test, which appeared to be enough time to finish all three questions. Classroom observations suggest that most students took less than 10 minutes to complete the test.

4. Results

4.1. Results for effect of experimental data on student performance and reasoning

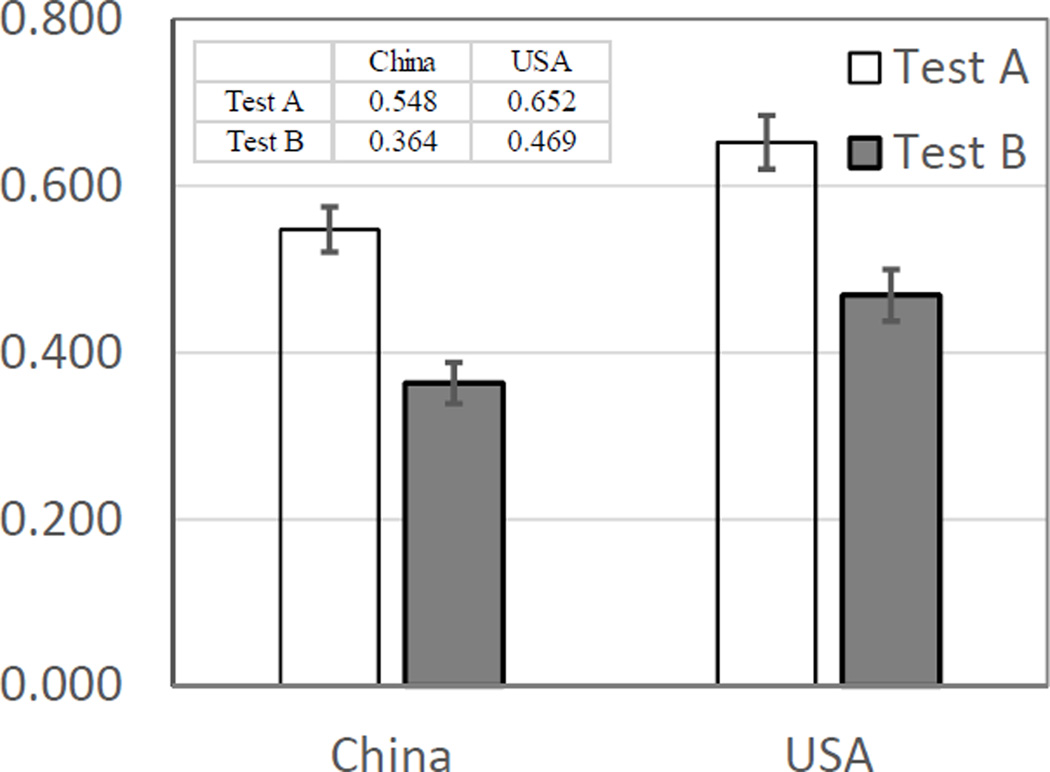
The first research goal examines the difference in student performance on questions without (Test A) and with (Test B) experimental data. The scores from all three questions of each test were summed to determine the main effect between the test versions. The results are plotted in Fig. 2, which shows a similar pattern for both US and Chinese populations: the average score of test A (data not given) is significantly higher than the average score of test B (data given) (USA t(187)=4.104, p=0.000, effect size=0.595; China t(304)=5.028, p=0.000, effect size=0.573). The differences between test A and test B scores are nearly identical for the two different populations (China 18.4% and USA 18.3%). Note that the US students are college freshmen and are at least 2–3 years older than the tenth grade Chinese students. The population differences are reflected in variations of the overall average scores, which show a 10.5% difference between the US and Chinese students. Analysis using two-way ANOVA confirms the t-test results revealing two main effects, one from test version, F(1, 495)=52.250, p=0.000 and one from population, F(1, 495)=8.665, p=0.003. Between test and population, there is no interaction, F(1, 495)=0.066, p=0.797, indicating that both populations behave similarly regarding their score differences on the two versions of tests.

Fig. 2.

Mean scores on Test A (data not given) and Test B (data given). The error bars represent the standard errors (approximately ±0.03 for both populations).

The results here show that students perform better on COV tasks when experimental data are not provided. This result is consistent with the literature, which distinguished two levels of reasoning skills: (1) identifying a properly designed COV experiment (a low-end skill) and (2) coordinating results with experimental designs (an intermediate to high-end skill) (see Table 1) (Kuhn, 2007).

For the free-response explanations collected in this study, when data were absent (Test A), 94% of students’ written explanations explicitly mentioned the terms of “controlled” and “changed variables” in answering the questions and focused on the conditions of variables being changed or held constant in their reasoning. For example, one student stated in response to the spring question, “The mass of the bob, which does not change in all three trials, can’t be tested to see whether it affects the outcome or not. However, both the remaining two variables are changing, so they can be tested.” Another student had a similar comment on the pendulum question, stating that “Every pair of two experiments does not satisfy the rule that only one variable varies while the other variables keep constant. So they cannot be tested.”

In contrast, when experimental data were given (Test B), 59% of the students did not appear to treat the questions as COV design cases. Rather, their written responses indicated that they tended to go back and forth between the data and the experimental designs, trying to coordinate the two to determine if the variable was influential. For example, one student explained, “If both the mass of the bob and the distance the bob is pulled from its balanced position at the time of release are the same, and the un-stretched lengths of the spring are different, then the number of oscillations that occur in 10 seconds also vary, so the un-stretched length of the spring affects the number of oscillations.” Another student noted, “When the length of the string is kept the same, the number of swings varies with changes in the mass of the ball and the angle at release.” Meanwhile, 41% of the students still demonstrated the use of the desired COV strategies in their written explanations, which is less than half of the number of students with correct reasoning in Test A.

4.2. Results for question context on student performance and reasoning

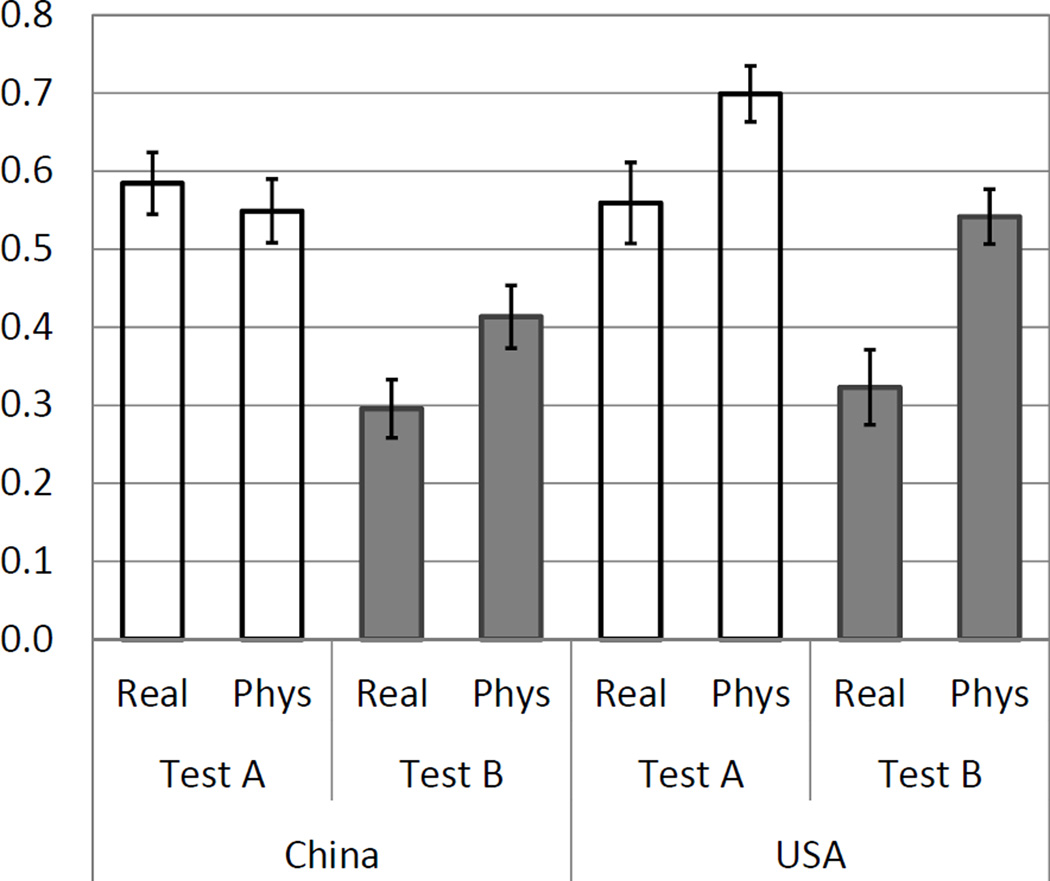
The second aim of this study was to investigate the effects of physics vs. real-life contexts on student performance and reasoning in COV settings. Fig. 3 shows student performances in real-life and physics scenarios. The real-life context results are mean scores for question 1 (fishing) and the physics context results are the mean scores for questions 2 and 3 combined (spring and pendulum). The same general trend continues to be observed in that students perform better on Test A (no data) than on Test B (with data) in both the physics and real-life contexts. However, within each test version and across the different populations, there are obvious variations.

Fig. 3.

Mean scores of US and Chinese students on physics and real-life problems in Test A (data not given) and Test B (data given). The error bars reflect the standard errors.

For the Chinese students, question context didn’t impact student performance on Test A (no data), t(306)=0.631, p=0.529, effect size=0.072, but the effect is statistically significant on Test B (with data), t(294)=2.146, p=0.033, effect size=0.248. For the US students, the effects of question context is statistically significant on both tests: Test A, t(164)=2.218, p=0.028, effect size=0.324, and Test B, t(174)=3.674, p=0.000, effect size=0.528.

Obviously, the results are multi-faceted with three main variables (Test version, Context, and Population), which may also interact. To obtain a more complete picture of the possible effects and interactions, the data was analyzed using a three-way ANOVA as shown in Table 3. The results show that each of the three variables has a statistically significant effect on student performance, with the Test version having the largest impact and Population having the least. Among the possible interactions, Test vs. Context and Context vs. Population are both statistically significant. On the other hand, interactions of Test vs. Population and all three variables together are not significant. This shows that both populations have similar performance patterns on the two versions of the test and the similarity is maintained when all three variables are considered together.

Table 3.

Results of 3-factor ANOVA (compacted listing). The significance is evaluated with the p-value where p<0.05 is generally considered to be statistically significant.

Variables and Interactions	F	p-value
Test (A vs. B)	52.250	0.000
Context (Real vs. Physics)	13.829	0.000
Population (USA vs. China)	8.665	0.003
Test * Context	4.901	0.027
Test * Population	0.066	0.797
Context * Population	6.932	0.009
Test * Context * Population	0.664	0.415

4.3. Results for embedded relations on student performance and reasoning

The third goal of this study looks at reasoning involving not only the variables but also the relations among the variables. In COV experiments, variables can be testable or non-testable, as well as influential or non-influential. This study looks specifically at students’ ability to distinguish between testability and casual influences of variables in COV experimental settings, which is measured with the spring question on Test B.

Among the three variables involved in the spring question, two variables (un-stretched length and distance pulled from equilibrium) are testable, and the third variable (mass) is not. Of the two testable variables, one variable (un-stretched length) is influential and the other is not. Using a multiple-answer design with one correct and two partially correct choices, three levels of reasoning skills can be tested in the spring question alone. The lowest level involves recognizing that mass is not a testable variable. Students who do not chose choice “c” are considered to succeed on this basic COV skill level. The second skill level is defined as when students are able to correctly recognize the influential variable (un-stretched length) as testable but miss the non-influential variable that is also testable (i.e., choosing “a” but not “b”), which reflects the incorrect reasoning of equating non-testable with non-influential. At the third and highest level, students are able to correctly recognize all testable variables (choice “d”) regardless of whether they are influential or not.

To more clearly show the mapping between students’ answers and the corresponding skills, Table 4 summarizes students’ responses from both populations on selected answer choices. The skills are ordered based on the presumed levels from lower to higher end. The data show the percentages of responses for the corresponding choices as well as the statistical significances in p-values of different comparisons. Answers to the fishing and pendulum questions are provided as supplemental data for the results shown in Fig. 3.

Table 4.

Students’ response data from both US and Chinese populations on the correct and partially correct choices used to determine students’ COV skill levels. In each table cell, the top value provides the percentage of students that answered with the corresponding choice. The numbers under the percentage (when applicable) are the two-tailed p-values from t-tests of comparisons between different test versions or populations. The p-values are labeled with two letters, where AB stands for a comparison between Test A and Test B and CU stands for a comparison between Chinese and US students. Typically, p<0.050 is considered statistically significant.

COV Skills	Questions (Choice)	China		USA
		Test A (no data)	Test B (with data)	Test A (no data)	Test B (with data)
Deciding if a variable is testable when it is testable	Fishing (a, correct)	58% AB: 0.000 CU: 0.751	30% CU: 0.706	56% AB: 0.001	32%
Deciding if any of several variables are testable when all are non-testable and some are influential (in Test B only).	Pendulum (h, correct)	55% AB: 0.121 CU: 0.019	46% CU: 0.276	70% AB: 0.017	53%
Being able to decide if one of several variables is testable when it is testable and influential (only in Test B)	Spring (a, partially correct)	3% AB: 0.000 CU: 0.608	26% CU: 0.007	4% AB: 0.017	13%
Being able to decide if one of several variables is testable when it is testable but non-influential (only in Test B)	Spring (b, partially correct)	5% AB: 1.000 CU: 0.190	5% CU: 0.051	10% AB: 0.537	13%
Being able to decide if any of several variables are testable when some are influential and some are non-influential (only in Test B)	Spring (d, correct)	54% AB: 0.002 CU: 0.012	36% CU: 0.003	70% AB: 0.036	55%

For the spring question, two variables (un-stretched length and distance pulled from equilibrium) are testable and the variable, un-stretched length, is influential (measured in Test B only). On this question, choice “d” is the correct answer and significant differences between student performance on Test A and B were observed for both populations. Students’ selections on partially correct answers (choice “a” in particular) were also significantly different between the two versions of the tests. This shows that providing experimental data (or not) in the questions has significant effect on student reasoning regarding testability and influence of COV variables.

5. Discussion

5.1. Effects of experimental data on student performance and reasoning

Identifying or designing a simple COV experiment is a basic skill that young students have been shown to have learned (Chen & Klahr, 1999; Dean & Kuhn, 2007; Klahr & Nigam, 2004). Our results support this as students performed better on COV tasks when outcome data were not provided. This result is also consistent with the literature which suggests considerable difference between identifying a properly designed COV experiment (a low-end skill by our definition) and coordinating results within an experiment (an intermediate to high-end skill) (see Table 1). That is, when the question did not include data and asked whether the experiment was a valid COV experiment, students were observed to pay attention to only those variables which changed and those which did not. This outcome was evident from students’ free-response explanations on Test A in which it was observed that 94% of the students clearly attended to features of the variables being changed or held constant across trials and discussed these features in their reasoning. Although students still gave incorrect answers in dealing with simple COV designs, it was evident that students were targeting the proper set of variables and conditions. Therefore, questions on identifying COV designs without the interference of experimental data appear to be good measures targeting low-end COV skills.

On the other hand, when students were shown experimental data (Test B) and asked if the experiment was valid, students no longer treated the questions as simple COV design cases. Rather, their written responses indicated that they tended to go back and forth between the data and the experimental designs, trying to coordinate the two to determine if the variable was influential. Students appeared to attend to the experimental data and use the data in their reasoning, which caused them to consider the casual relations between variables and experimental data rather than the COV design of the experiment. Of the students who took Test B (data given), 59% demonstrated this reasoning in their written responses while 41% incorporated the desired COV strategies in their reasoning. This is less than half the number of students with correct reasoning taking Test A.

Synthesizing the results, it appears that when experimental data were provided (such as those in Test B), students seemed to have a higher tendency to include the data in their reasoning. The experimental data presented in the questions tended to distract students into thinking about the possible causal relations (influence) associated with the variables instead of the testability of the variables. Based on the literature and the results from this study, a student may be considered to be at a higher skill level if he/she can resist the distraction from thinking about experimental data and still engage in correct COV reasoning. In these cases, students need to integrate COV into more advanced situations to coordinate both variables and potential causal relations. This level of skill was also studied by Kuhn, in which students were asked to determine the causal nature of multiple variables by using COV experimentation methods (Kuhn, 2007). In Kuhn’s study, COV strategies served as the basic set of skills that supported the more advanced multivariable causal reasoning.

It is also worth noting that the technique of providing distracters is similar to what has already been widely used in concept tests, such as the Force Concept Inventory (FCI), which provides answer options specifically targeting students’ common misconceptions (Hestenes et al., 1992). A student who does well on the FCI is one who is able to resist the tempting answers and think through the problem using physics reasoning.

Based on the data analysis and existing literature, the question designs used in this study seem to work well in probing and distinguishing the basic and advanced levels of COV reasoning in terms of the testability and influence of variables. That is, Test A provides the simpler tasks of identifying proper COV experiments, while Test B uses COV as a context to assess more complicated reasoning supported by the basic COV skills.

5.2. Effects of question context on student performance and reasoning

In comparing the effects of physics vs. real-life contexts on student performance and reasoning in COV settings, the effects of question context were found to be larger with the US students than with the Chinese students as shown in Fig. 3 and Table 4. In addition, comparing the two test versions across both populations, the effects of question context were found to be larger with Test B than with Test A. Regardless, students in general perform better with physics contexts than with real-life contexts. To explore possible causes of the effects of the context, students’ written responses were analyzed, which revealed different patterns of reasoning when dealing with the real-life scenario vs. the physics scenarios.

One factor that emerged is that the real-life context often triggered a wide variety of real-world knowledge, which may have biased student reasoning. In such cases, a student may hold on to his/her beliefs, ignoring what the question is actually asking about (Caramazza, McCloskey, & Green, 1981). For example, many students included belief statements in their explanations such as “the thin fish hook works best”, ignoring the experimental conditions. Boudreaux et al. (2008) reported similar results, which were described as “a failure to distinguish between expectations (beliefs) and evidence”. On the other hand, when dealing with physics contexts, students often have limited prior knowledge, and the knowledge that students do have is more likely to be learned through formal education which is less tied to their real world experiences. Therefore, with fewer possible biases from real-life belief systems, students may be better able to use their COV reasoning skills to answer the question.

Another factor that appears to influence reasoning when faced with a real-life scenario is the tendency for students to consider additional variables other than those given in the problem. For example, in students’ written explanations for the fishing question, one student discussed several additional variables including the type of fish, cleverness of fish, water flow, fish’s fear of hooks, difficulty in baiting the hook, and the physical properties of the hook. Note that the only variables provided were hook size, fisherman’s location, and length of fishing rod; and that students were instructed to ignore other possible variables. It is evident that a familiar real-life context can trigger students into considering a rich set of variables that are commonly associated with a context based on life experience. A total of 17 additional variables (other than those provided in the question) were named by students in the written responses to the fishing question. This can be contrasted with the physics context questions, in which only a total of 5 additional variables were mentioned (mainly material properties and/or air resistance).

Furthermore, students’ considerations of additional variables may be affected by the open-endedness of a question. Compared to a real-life situation, a physics context is often pre-processed by instructors to have extraneous information removed, and therefore is more “cleanly” constrained and close-ended. For example, students learn through formal education that certain variables, such as color, do not matter in a physics question on mechanics. In this sense, contextual variables are pre-processed in a way that is consistent with physics domain knowledge, thereby filtering the variables to present a cleaner, more confined question context. This is often desired by instructors in order to prevent students from departing from the intended problem-solving trajectories. A real-life context problem, on the other hand, is naturally more open-ended. The variables are either not pre-processed or are pre-processed in a wide variety of ways depending on the individual’s personal experiences. Therefore, a richer set of possibilities (variables) exist that a student may feel compelled to consider. This makes a real-life task much less confined than a physics problem and students often have available more diverse sets of variables to manipulate.

The explanation of open-endedness is similar to what Hammer et al. (2004) refer to as cognitive framing. Framing is a pre-established way, developed from life experiences, that an individual interprets a specific situation. In Hammer et al.’s words, a frame is a “set of expectations” and rules of operation that a student will use when solving a problem which affects how the student handles that problem. This framing idea applies well to our own observations in this study. In a real-life context, a student’s frame is built with real world experiences, which often loosely involve many extra variables that can make their way into the student’s explanations. In a physics context, students are accustomed to using formally structured (and confined) physics methods, so the diversity of possible thoughts is greatly reduced. Typically, physics classes train students to use only the variables given in the problem, which confines the task but also gradually habituates students into a “plug-and-chug” type of problem-solving method limiting their abilities in open-ended imaginations and explorations.

Based on both quantitative and qualitative data, the question context (real-life vs. physics) does impact students’ reasoning (reflected in the number and types of variables students call upon). This analysis suggests that prior knowledge and the open-endedness of a question may play an important role leading to the effects of context on reasoning; however, pinpointing such causal relations is beyond the scope of this study and warrants further research.

5.3. Effects of embedded relations on student performance and reasoning

The testability and influence of variables are two important aspects of COV experiments. As discussed earlier, students appear to have difficulty in distinguishing between testability and influence, and they often equate non-influential variables with non-testable variables. This difficulty is explicitly measured in the question designs of this study as it is considered as an important identifier separating low-end and high-end COV skills.

From the results in Table 4, looking more closely at the partially correct answers (choices “a” and “b”) for the spring question, many more students chose the influential variable (choice “a”) as the only testable variable on Test B (data given) than on Test A (no data). This result suggests that students can better identify a testable variable when experimental data are not provided; that is, when students are not distracted into considering causal influential relations. The students who picked only choice “a” were at the second level of COV skills tested in this question, which corresponds to equating non-influential variables as non-testable. This outcome confirmed our hypothesis about students’ difficulty in distinguishing between testability and influence. It further shows that the designs of the two versions of the spring questions provide a means to quantitatively measure this unique difficulty.

The results from Table 4 also show that about 1/3 of the Chinese students and half of the US students achieved the highest level of COV skills tested in this question; these students were able to engage in correct COV reasoning with complicated multi-variable conditions that included both influential and non-influential relations.

To further investigate students’ reasoning regarding testability and influence, the written responses to the spring question in Test B were analyzed. The results show that some students explicitly used the variable that was not influential as the reason not to choose the variable as being testable. For example, one student stated: “The number of oscillations has nothing to do with the distance the bob is pulled from its balanced position at the time of release.” This student appeared to know that the distance the bob is pulled from its balanced position does not influence the outcome, which led the student to determine this variable to be non-testable without using the information of the experimental conditions given in the question. From the analysis of the qualitative explanations, 21% of the students showed similar reasoning and chose the variable that was influential (choice “a”) as the only testable variable. On the other hand, nearly all students who picked the correct answer (choice “d”) used the correct reasoning and identified testable variables as testable regardless of whether they were influential or non-influential.

Synthesizing the results, it is obvious that embedding more complicated relations among variables in a task will make the task more difficult for students and can reveal a series of developmental levels of COV skills. As a result, it is practical to purposefully integrate relations of varied complexity into tasks as a means to assess multiple levels of reasoning skills. Regarding the assessment designs, some of the finer level reasoning patterns such as conflating the influence with testability would be difficult to measure if only one of the two test versions were to be used. This is because student difficulties would appear as a general mistake in COV reasoning rather than as a unique level of reasoning. By using both Test A and Test B, this reasoning is better able to be revealed by contrasting the results from both tests (see spring question choice “a”). As a result, this new test design provides a useful assessment strategy in measuring student reasoning at finer grain sizes. The results from this study can also inform teachers on designing effective learning activities in which the inclusion of experimental data or not can be used to manipulate the difficulty levels of the activities, as well as a means of training different levels of student ability in reasoning.

6. Conclusion

COV is a core component of scientific reasoning. Current research tends to address broad definitions of COV, but it is necessary to identify COV skills at smaller grain sizes particularly for the purposes of designing and evaluating instruction. This study tested an assessment method designed to make finer-grained measurements using two versions of questions with nearly identical contexts except that the experimental data in the tasks were provided in one version but not the other. The questions were also designed to study the effects of question context (real life vs. physics) and embedded relations on students’ reasoning.

Results from this study show that students (1) perform better when no experimental data are provided, (2) perform better in physics contexts than in real-life contexts, and (3) have a tendency to equate non-influential variables to non-testable variables. Combining the existing literature and the results of this study, a possible progression of developmental stages of student reasoning in control of variables can be summarized as shown in Table 5. Although these progression levels have been ordered based on the assessment results discussed in this paper, due to the limited scope of this study, this work represents an early stage outcome. Subsequently, it can lead to a range of future research that more fully maps out the progression of cognitive skills associated with student reasoning in COV from novices to experts.

Table 5.

A proposed progression levels of COV skills tested in this study along with the test version and item, with which the skills are measured.

COV Skill	Test B Spring	Test Version and Item
Deciding if a variable is testable when it is testable (without data)	Low-end	Test A Fishing
Deciding if a set of variables are testable when none is testable (without data)	Low-end	Test A Pendulum
Deciding if an experimental design involving multiple testable and non-testable variables (>2) is a valid COV experiment (without data)	Low-end to Intermediate	Test A Spring
Deciding if a variable is testable when it is not testable (with data)	Low-end to Intermediate	Test B Pendulum
Deciding if a variable is testable when it is testable and influential (with data)	Intermediate	Test B Spring
Deciding if one of several variables is testable when it is testable but non-influential (with data)	Intermediate to High-end	Test B Spring
Deciding if any of several variables are testable when some are influential and some are non-influential (with experimental data)	High-end	Test B Spring

In addition, the assessment design implemented in this study was shown to be effective in probing finer details of student reasoning in COV. In particular, the results suggest that whether or not experimental data are provided actually triggers different thought processes in students. When experimental data were not given, students were able to focus on the conditions of the COV settings and were more likely to identify the correct testable variables. When experimental data were given, students seemed to have a high tendency to include the data in their reasoning, which distracted students into thinking about the possible causal relations (influence) associated with the variables instead of the testability of the variables. The design used in this study enables the measurement to distinguish students on a range of skill levels, which can be used to quantitatively determine the developmental stages of student reasoning in COV and beyond.

The results of this study are important for the development and evaluation of curriculum that targets student reasoning abilities. The COV skills are almost universally involved in all hands-on inquiry learning activities. In the literature, student reasoning in COV settings is often defined as a general umbrella category that lacks explicit subcomponents and progression scales. This makes the measurement and training of COV reasoning difficult as instruction and curriculum are not well informed regarding specific targets and treatments. The results from this study will help establish the structural components and progression levels of the many aspects of COV reasoning, which can be used to guide the development and implementation of curriculum and assessment. In addition, the method of including experimental data (or not) provides a practical strategy for teachers to design classroom activities and labs that involve COV experiments. This study also enriches the literature and motivates further research on the development and assessment of COV skills.

Highlights.

• The introduction, discussion and conclusion sections were rewritten to address the reviewers’ concerns.

• The introduction includes a more clear definition of COV

• The discussion and conclusion include broad impacts to teaching and learning

• The results and discussion sections were carefully rewritten to better separate out the two.

• The qualitative and quantitative data were presented separately and were later synthesized in the discussion.