Redistribution of inhaled hyperpolarized ³He gas during breath-hold differs by asthma severity

Abstract

The purpose of this work was to quantify the redistribution of ventilation-weighted signal in the lungs of asthmatic subjects during a breath-hold using high temporal-spatial resolution hyperpolarized (HP) He-3 MRI. HP He-3 MRI was used to obtain time-resolved, volumetric images of lung ventilation during breath-hold in 39 human subjects classified as either healthy/nondiseased (n = 14), mild-to-moderate asthmatic (n = 17), or severely asthmatic (n = 8). Signals were normalized to a standard lung volume, so that voxels within the lung from all 39 subjects could be analyzed as a group to increase statistical power and enable semiautomated classification of voxels into 1 of 5 ventilation level categories (ranging from defect to hyperintense). End-inspiratory ventilation distribution and temporal rates of mean signal change for each of the five ventilation categories were compared using ANOVA. Time rates of signal change were hypothesized to represent underlying gas redistribution processes, potentially influenced by disease. We found that mild-to-moderate asthmatic subjects showed the greatest rate of signal change, even though those with severe asthma had the greatest end-inspiration ventilation heterogeneity. The observed results support the existence of local differences in airway resistances associated with the different obstructive patterns in the lungs for severe vs. mild-to-moderate asthmatic subjects.

asthma is an obstructive lung disease that afflicts millions of people across the globe. Although pulmonary function tests are a very useful tool for investigating asthma, they only provide whole lung measurements and are not sensitive to the assessment of anatomically regional disease heterogeneity that exists in asthma. Regional evaluation of lung structure can be performed using computerized tomography (CT); however, CT is less well suited for assessment of regional function. Chest CT also uses ionizing radiation, making longitudinal studies in certain populations difficult to perform (6). Nuclear scintigraphy can provide functional imaging, depicting changes in gas distribution within the lungs during inhalation and exhalation, but suffers from low spatial resolution (25). Furthermore, it is often limited to two-dimensional (2D) projection images in the clinic (4).

Functional images of ventilation using hyperpolarized helium-3 (HP He-3) magnetic resonance imaging (MRI) have been used extensively in studies of subjects with a variety of lung diseases, including asthma (1). Most HP He-3 clinical research studies acquire a “static” set of 2D or 3D images covering the lung volume during a single-breath-hold maneuver. Images of this type have been used to identify regions of ventilation defect, a binary measure of regions of the lung, which appear unventilated by a single bolus inhalation of HP He-3 gas. Studies have shown that the extent of these ventilation defects is correlated with degree of asthma severity (7).

However, conventional breath-hold imaging is unable to detect temporal dynamics of gas distribution in the lungs. Ventilation is known to be a dynamic process involving the constant movement of gas within and between the airspaces. The rates of gas wash-in and wash-out are of great interest, especially in obstructive diseases, such as asthma and COPD. Previous work has demonstrated the feasibility of dynamic 2D (27) and 3D HP He-3 MRI (13, 14) to identify regions of gas trapping. However, it is technically challenging to develop robust quantitative metrics of regional variations in gas wash-in and wash-out because of respiratory motion during a multiple breath protocol (15). However, dynamic changes in the HP He-3 gas signals during a breath-hold where motion can be effectively considered negligible may have potential functional significance.

Several factors can affect signal changes of HP He-3 gas during a breath-hold maneuver, including diffusive (passive) redistribution through partially obstructed airways or collateral pathways (3, 17, 28), as well as pendelluft (active convectively driven flow) (21). Additionally, differences in the regional partial pressures of oxygen will result in different T₁ relaxation rates (9, 10), where T₁ is the longitudinal magnetization relaxation time constant. In this work, we quantify signal changes over the course of a 7.5-s breath-hold using a simple linear fit. We show that signal changes are representative of underlying physical and physiological processes and that the rate of signal change, defined as the slope of the fitted line, varies with degree of asthma severity.

Theory

We considered an inhalation maneuver as the input to the functionally dynamic system (that is, the lungs), with a functional response characterized by the temporally dependent spatial distribution of inhaled HP He-3 gas. We assumed that the gas distribution at end-inhalation is in a nonequilibrium state that is spatially heterogeneous, and over time (during a breath hold), it trends toward a more homogeneous pattern at equilibrium. The changes in gas distribution during the breath-hold might be driven by local variations in pressure or lung compliance, or possibly by regional differences in oxygen partial pressure. The “rate” of relaxation would be dependent on how far the regional pressures differ from equilibrium. In other words, the initial (end-inspiration) spatial distribution of the inhaled gas will directly correlate with the rate of signal wash-in or wash-out, depending on whether the region was initially ventilated below or above equilibrium levels. Furthermore, we hypothesized that the rate at which this “relaxation” occurs is affected by physiology associated with differing degrees of asthma disease severity.

In this work, we tested this hypothesis by acquiring dynamic time series of HP He-3 MRI volumes using the method described by Holmes et al. (14). We modeled the average signal time course of lung voxels grouped together according to their end-inspiration level of ventilation as a simple linear function, describing the rate of change within each ventilation level group. We then compare these rates in subjects from the severe asthma research program (SARP) with different degrees of asthma severity.

MATERIALS AND METHODS

MR imaging of dynamic He-3 ventilation was performed on a 1.5 T MRI scanner (GE HealthCare, Waukesha, WI) in 39 human subjects, classified as either healthy/nondiseased (n = 14) or asthmatic (n = 25). Asthmatic subjects were then subclassified by disease severity as either mild-to-moderate (n = 17) or severe (n = 8). Additional selected demographic and spirometric information for this cohort is presented in Table 1. These subjects are part of the ongoing SARP study (26), and the severity classifications were determined on the basis of the American Thoracic Society Workshop on Refractory Asthma (2). Subjects with severe asthma were those requiring maintenance with high-dose inhaled corticosteroid or systemic corticosteroid, plus meeting at least two of seven minor criteria relating to treatment intensity and asthma instability. Those subjects with an asthma diagnosis, but not meeting the criteria for severe asthma, were designated as having mild-moderate asthma.

Table 1.

Cohort demographic and spirometric information

Asthma Severity Group	Group Size (Male/Female)	Agea, yr	FEV1 %predb	FVC %predb	FEV1/FVC %predb
Healthy	14 (6/8)	19–30 (22.5 ± 3.7)	103.9 ± 10.8	103.9 ± 7.6	100.1 ± 6.5
Mild-to-moderate	17 (5/12)	18–46 (25.1 ± 7.6)	93.2 ± 16.0	98.0 ± 13.0	95.8 ± 12.4
Severe	8 (3/5)	24–69 (44.4 ± 12.7)	67.8 ± 24.9	81.5 ± 15.4	81.0 ± 15.4

^aData are presented as range, followed by means ± SD.

^bData are presented as means ± SD.

FEV1, forced exhalation volume in 1 s; FVC, forced vital capacity.

Subjects were evaluated using spirometry and plethysmography prior to imaging, as previously described (24). Specifically, lung volume measurements were acquired in a constant-volume body plethysmograph (Jaeger Masterscreen; VIASYS Healthcare, Yorba Linda, CA) using the Boyle's law method. After reaching a stable end-expiratory volume in four sequential breaths, a pant rate of <1 Hz was used during brief mouthpiece occlusion, after which subjects exhaled maximally to residual volume (RV) and then inhaled maximally to total lung capacity (TLC). Spirometry (Jaeger; VIASYS Healthcare) was also performed by each subject, according to American Thoracic Society/European Respiratory Society guidelines (18). The forced exhalation volume in 1 s (FEV₁) was recorded as the best value obtained in three separate measurements and is reported as the percent of the predicted value (FEV₁%pred) (12). Plethysmography was performed within 1–2 wk before imaging.

Helium-3 gas was hyperpolarized using a prototype commercial polarizer (GE Healthcare, Durham, NC), yielding polarizations levels of ∼28%. The HP He-3 was mixed with N₂ to yield a 4.5-mM concentration of polarized spins in a total volume equal to 14% of the subject's TLC. Subjects were coached prior to gas delivery to perform a dynamic respiratory procedure consisting of gas inhalation, a breath-hold period at end-inspiration, a forced exhalation, and finally, a period of tidal breathing. Only the breath-hold period, which was maintained for no less than 7.5 s, was analyzed for this work, although other periods of the maneuver were utilized for postprocessing the data as described below.

Dynamic MRI data were acquired using an excite/receive radiofrequency coil tuned to the helium frequency (∼48 MHz at 1.5 T) and a 3D multiecho vastly undersampled isotropic projection acquisition (ME-VIPR) pulse sequence with 8 half-echoes per repetition, as previously described (13, 14). Notably, this acquisition provides k-space coverage yielding a nominal isotropic spatial resolution of 3.3 mm, or 128 equally spaced points within a 42-cm field of view, and ∼660 unique half-echoes sampled each second. Dynamic proton images were acquired with the system body coil prior to the HP He-3 ventilation scan during an identically coached respiratory maneuver. This was used as practice for the HP He-3 acquisition, and subsequently used to aid the delineation of the thoracic cavity in the breath-hold portion of the HP He-3 data.

He-3 ventilation images were reconstructed using I-HYPR (19), as described by Holmes et al. (14). Volumetric temporal frames were reconstructed at a rate of two unique frames per second (0.5-s resolution) at 3.3-mm isotropic resolution. Analysis was performed on the first 7.5 s of the breath-hold period in each subject, with dynamics represented by a 15 volume time series. The first frame was manually selected to coincide with the end-inspiration time point, specified as the last time point at which total signal increased following gas inhalation, or equivalently the first point postinhalation at which total signal did not subsequently increase.

Image postprocessing.

Image reconstruction was performed using custom code written in C, while data processing and analysis were performed using custom code written for MatLab (MathWorks, Natick, MA).

The loss of helium-3 spin polarization due to T₁ relaxation and RF irradiation (with flip angle α) over the course of acquisition was corrected voxel-wise by modeling the signal decay directly from the breath-hold portion of the acquired image data series, according to

$$S\left(t\right)=S\left(0\right){\left({\cos }^{110}\left(\alpha \right){\mathrm{e}}^{-\frac{1}{{\mathrm{T}}_1}}\right)}^{\mathrm{t}}$$ (1)

where the signal (i.e., longitudinal magnetization with relaxation time constant T₁) at time t (in seconds), S(t), is proportional to the total signal at time t = 0, S(0). The value of 110 in the exponent of the cosine term represents the data acquisition rate of 110 RF excitations (projection acquisitions) per second. Signal values in the 15 image frames acquired within the same breath-hold, each separated by Δt = 0.5 s, are used to estimate the exponential decay (combination of flip angle and T₁ effects). This estimate is then used to eliminate the decay term from Eq. 1 in each voxel (i.e., by dividing it out at each time point). Figure 1 illustrates this process.

Fig. 1.

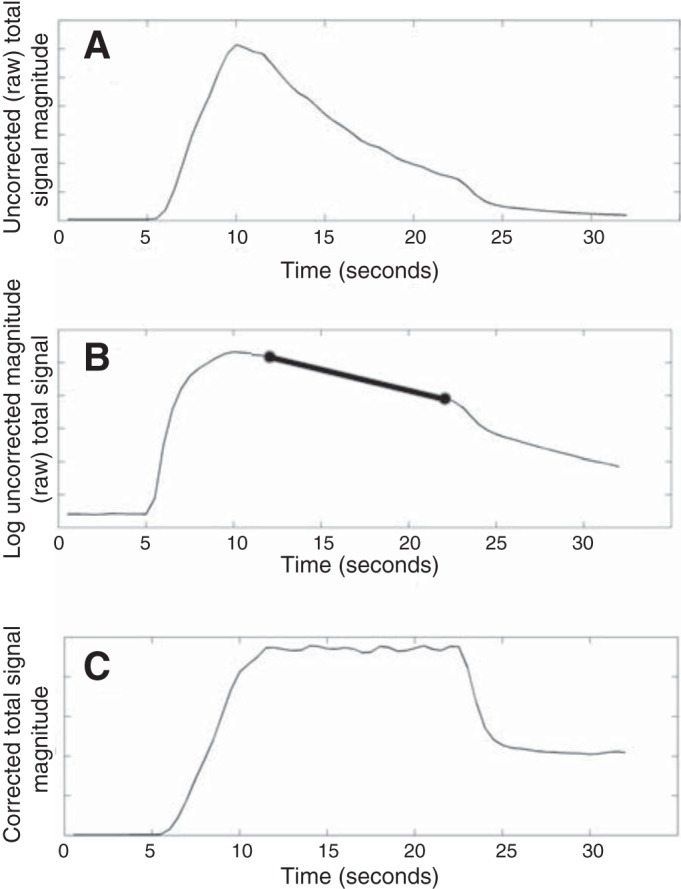
A: raw, uncorrected “total signal” within the lung boundary over time. B: logarithm of the signal in A. The slope of the linear portion of the time series in B is related to the exponential decay rate of the raw signal. The thick black line in B is the line segment used to estimate the slope of this linear trend. C: time course of the total signal within the lung after correcting for the exponential decay term computed from (B). The inhalation, breath-hold, and exhalation periods are now clear.

This procedure simultaneously corrects for the global mean decay rate (i.e., over entire lung) related to both RF irradiation and longitudinal (T₁) relaxation. Because of the association between the latter process and possible variations in the regional oxygen partial pressure (Po₂), more thorough analysis is warranted, since this regional error in the decay correction could potentially bias our results. Local regions that experience slower or faster T₁ decay rates (compared to the global mean) will be overcorrected or undercorrected, respectively, using the global method in Fig. 1. Thus, signal in these regions could potentially appear to “wash-in” or “wash-out,” respectively, due to such regional errors in the correction. Bias could, therefore, result from correlations between the regional T₁ relaxation rate (due to local Po₂, for example) and how well ventilated a region is immediately following inhalation. This correlation is unlikely to be zero, and we desire to assess the relative magnitude of such errors. Therefore, we consider the scenarios for the extremes of the physiological range below.

In the presence of oxygen, T₁ of helium nuclei is inversely proportional to the Po₂:

$${\mathrm{T}}_1=\frac{1.951\times {10}^3}{\mathrm{P}{\mathrm{o}}_2}\sec ,$$ (2)

with Po₂ in units of Torr (9). Using 40–100 Torr as a reasonable expected physiological range of Po₂ values spanning nonventilated to well-ventilated alveoli, assuming regional perfusion is not matched (23), the corresponding range of T₁ values would be between 19.5 s (at 100 Torr) and 48.8 s (at 40 Torr). This constrains the difference between the true and the estimated decay rates, and, thus, the correction error. If the global average were at the extreme high end of the range (Po₂ = 100 Torr), locally obstructed regions (Po₂ = 40 Torr) would be maximally overcorrected by around 3% per second, and ∼26% over the course of 7.5. Alternatively, if the global average were ∼40 Torr (almost entirely obstructed and only possible under acute exacerbation), regions at the high end of 100 Torr would be maximally undercorrected over the course of 7.5 s by a smaller factor, about 20%. The consequences of these potential sources of bias on the interpretation of our results will be further addressed in the discussion to follow.

HP He-3 images were masked to eliminate voxels outside the boundary of the lung and within the largest airways. Operating under the assumption that motion is negligible during the breath-hold, a single mask volume per subject was generated and applied to all images in the time series. The masking process is shown in Fig. 2. A 3D resolution-matched proton image, acquired as described above, was reconstructed from the breath-hold phase of the dynamic maneuver and used in conjunction with the helium images to achieve acceptable segmentations. Lung segmentations from proton data were generated using level sets, specifically an active contour method, which identifies object boundaries (in this case, the lung) through stepwise curve evolution, and was found to handle cases of poorer image quality well (5, 20). The segmented lung mask was registered through an affine transformation to masks generated from the helium images themselves. These helium segmentations were generated by first smoothing the 3D volumes with a Gaussian kernel (σ = 2 voxels, or ∼6.5 mm), and then thresholding at 8% of the maximum signal level. Finally, remaining background noise was removed by eliminating connected regions with less than 1,000 voxels. Each of the final registered masks were then verified and adjusted manually if necessary. The large airways were then extracted using a region-growing algorithm (22), with an initial seed in the trachea. This method exploits the elevated contrast between airways and lung parenchyma during and immediately following the inhalation maneuver by adding points to the segmented region that are “connected to” the seed (i.e., share a voxel edge) and have signal level no lower than 75% of the signal within the seed. In cases in which this contrast was less dramatic (in which lung parenchyma was nearly as bright as the large airways), the algorithm was reseeded until at least a segment of the airways past the 2nd branch point was removed. Large airway segmentations were then visually inspected for accuracy, ensuring no regions of parenchyma were erroneously removed.

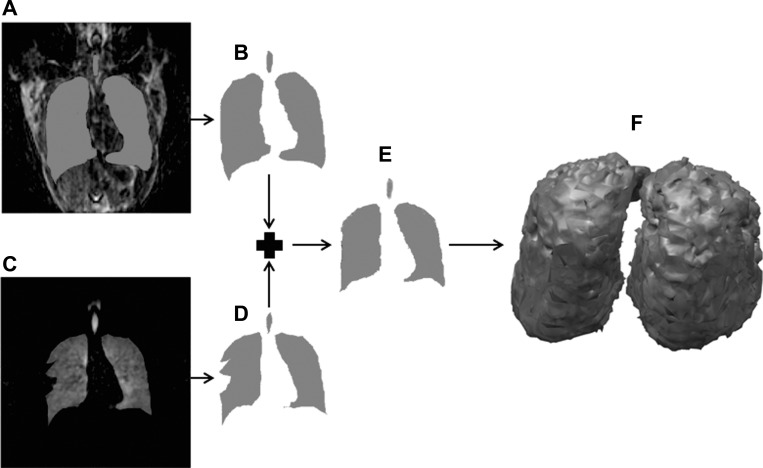
Fig. 2.

In a 26-yr-old mild-to-moderate asthmatic subject, a three-dimensional (3D) resolution-matched proton image was acquired. A: coronal slice reformat of a proton acquisition overlaid with the lung segmentation. B: extracted lung segmentation from the slice in A. C: matched coronal slice reformation of a helium acquisition overlaid with the lung segmentation. Note the mismatch between the helium acquisition and the mask at the defect region. D: extracted lung segmentation from the slice in C. Note that although parts A–D were done in 3D, they are shown here in two dimensions for clarity. E: final mask generated by combining the proton segmentations (B) and helium segmentations (D) using an affine transformation of the proton mask to the helium mask, with additional editing by hand done when necessary. F: 3D rendering of the final mask after removing the trachea and large airways.

Following segmentation, lung voxel values were normalized in each subject to eliminate intersubject variations in HP He-3 signal intensities. Although initial HP He-3 concentration was kept consistent across subjects, polarization levels at the onset of breath-hold will vary on a scan-to-scan basis due to small differences in flip angle (i.e., subject coil loading) or the time elapsed during gas inhalation by the subject, leading to varying amount of RF irradiation prior to achieving breath-hold. Thus, each voxel was first converted to units of percentage of total inhaled gas volume, and then renormalized to a standard lung volume, chosen as 5 liters. These two steps were accomplished using Eq. 3:

$$v_n^{\mathrm{\prime }}=\frac{5000v_n}{{\left(0.328\right)}^3\ast N{\displaystyle {\sum }_{i=0}^{N-1}{v}_i}}$$ (3)

where N is the number of voxels within the segmented volume, v_n and v_n^′ are raw and normalized signal intensities, respectively, and 5,000 and (0.328)³ represent the volumes of the “standard” lung and each individual reconstructed voxel in milliliters, respectively. Intuitively, the normalization expressed by Eq. 3 can be thought of as (normalized voxel signal) = (voxel % of total lung signal)/(lung volume/5 liters).

Data Analysis

Spin density analysis.

Voxels were classified into 1 of 5 different “ventilation levels”, ranging from “nonventilated” defect regions (level 1) to “hyperintense” regions (level 5) using k-means clustering (16), allowing for group-wise clustering and analysis. Because signals were normalized to a standard lung volume, all voxels within the lung from all 39 subjects could be pooled and clustered as a whole, rather than performing the classification on each subject individually. This reduced variability and bias due to variation in polarization and lung volume that would modulate end-inspiratory signal intensities.

ANOVA was performed to investigate differences between nondiseased, mild-to-moderate, and severe asthmatic groups for ventilation defect percentage (level 1 classification), and more generally for the percent of lung classified within each of the five different ventilation classifications.

Dynamic analysis.

The voxel classifications for the five end-inspiration spin density levels were then projected through time onto each of the 15 time points (7.5 s, total) within each subject, such that the classification was identical throughout the breath-hold. Each 3D volumetric time course was then reduced to the mean voxel intensities within each ventilation classification level, i.e., five values per time point. A linear regression model was fit to the mean voxel intensities through time for each of the five ventilation levels. An ANOVA test was used to determine significant differences between the slopes of the fitted lines for each ventilation level in each subject. The slopes of the fitted lines will be referred to as the “rate of change” within a ventilation level.

RESULTS

Spin Density Analysis

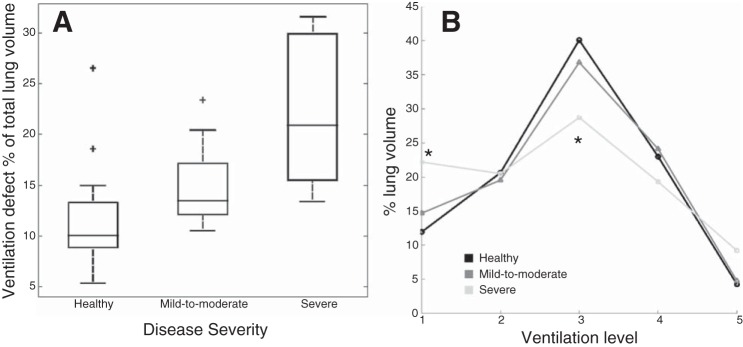
Figure 3 shows box-plots of the percent of the lung classified by the automated k-means classification as “nonventilated” (ventilation level 1). Ventilation defect percentage increased with disease severity, and the severe group (21.6% ± 7.5%, mean ± SD) was significantly higher than both healthy (12.3% ± 5.3%) and mild-to-moderate (14.7% ± 3.7%) groups (P < 0.001). This corroborates previous findings (8). Since ventilation level membership as a percentage of total lung volume (percentages across all five ventilation classifications must sum to 100%), it should be obvious that a relatively higher percentage at one level must be compensated for by a reduction in the percentage represented by those remaining. The way in which the severe asthmatic subjects “compensate” for this elevated percentage of lung in ventilation level 1 is shown in Fig. 3B, which shows plots of all five ventilation classes as a percentage of total lung volume in each severity group. Interestingly, relative to the healthy and mild-to-moderate groups, severe asthmatic subjects showed a statistically significant reduction in the percentage of lung classified at the median level 3 (P < 0.001, means ± SD: healthy = 39.7% ± 6.8%, mild-to-moderate = 36.8% ± 4.1%, and severe = 29.4% ± 6.1%), which could be interpreted to represent the “normal” level of ventilation, since it contains the “equilibrium” normalized signal value (at equilibrium, following a breath-hold of effectively infinite length, gas would be identically distributed throughout the lung and every single voxel would have this normalized signal intensity).

Fig. 3.

A: box plots of ventilation defect volume (i.e., percent of total lung volume classified at level 1, or “defective”) in the three disease severity categories. Plus signs indicate outliers. The severe group has significantly (P < 0.01) elevated ventilation defect percentage compared with the other two groups. B: chart of the percentage of total lung classified within each of the five ventilation levels for all three severity groups. The “flatter” distribution of the severe asthmatic group is indicative of a more heterogeneous pattern of ventilation. *P < 0.01, percentage of lung volume classified as level 1 and 3 are significantly higher and lower, respectively, in the severe group compared with the other two groups.

Dynamic Analysis

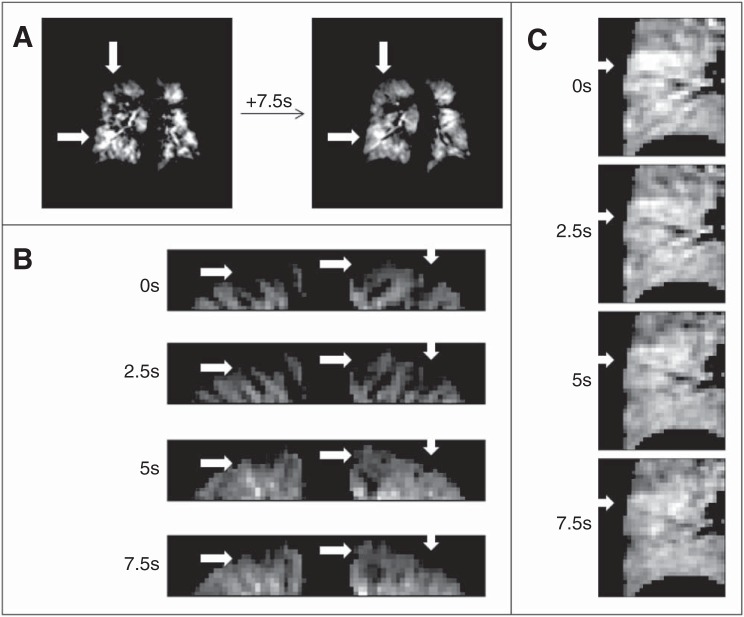
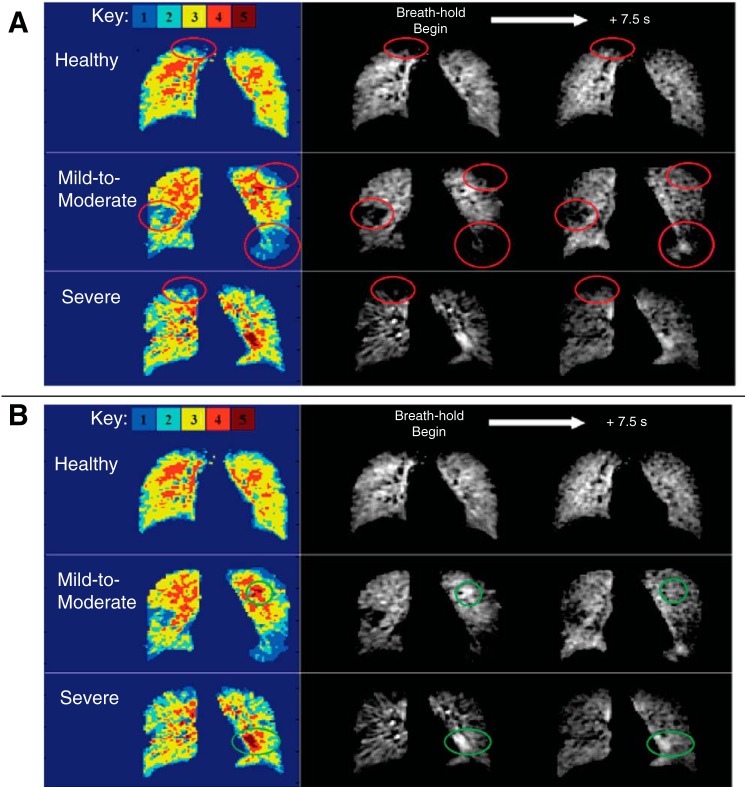
Qualitative evaluation of delayed filling and wash-out is demonstrated by regions of both delayed filling and delayed wash-out in three different coronal reformats from three different subjects in Fig. 4 (white arrows). First, a full coronal slice reformat is shown from the end-inspiration time point and the same slice 7.5 s later, from a subject with severe asthma (Fig. 4A). The top arrow shows an initially unventilated region, which has filled to a large degree 7.5 s later, while the arrow at bottom-left shows an initially hyperintense region that has partially washed out after the 7.5 s of breath-hold. Figures 4, B and C show zoomed portions of coronal reformatted images from two subjects, both with mild to moderate asthma at four different, equally spaced time points over the course of the 7.5-s breath-hold. Figure 5 shows similar delayed wash-in and wash-out phenomena in coronal slices chosen from three different subjects, one each from the healthy, mild-to-moderate, and severe asthmatic groups, along with the color-coded maps of initial ventilation classification in the same coronal slices.

Fig. 4.

In a 67-yr-old female severe asthmatic subject, qualitative evaluation of delayed filling and wash-out is demonstrated by regions of both delayed filling and delayed wash-out in three different coronal reformats from three different subjects. A: regions of filling and washout for the first and last time points postinhalation. B: apical portions of the lung shown depict many regions of delayed filling, with a few regions of interest highlighted by arrows. C: large region in the lower right lung, highlighted by an arrow, is initially hyperintense and shows a delayed washing out of the signal over 7.5 s.

Fig. 5.

In a healthy (female, 21 yr old), mild-to-moderate asthmatic (male, 36 yr old), and severe asthmatic (male, 45 yr old) subject, similar delayed wash-in and wash-out phenomena are shown. Color-coded maps indicate initial ventilation classification in the displayed coronal slices. A: regions of interest are circled, highlighting areas of initially poor ventilation (level 1 or 2), which fill to varying degrees following 7.5 s of breath-hold. B: same slices from the same subjects, instead highlighting regions of initial hyperintensity (level 5) that alternatively wash out to varying degrees following breath-hold.

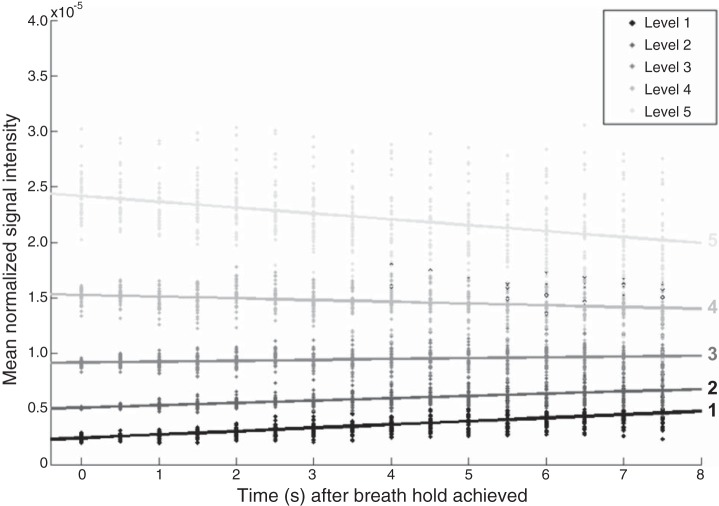
The rates of change between different ventilation categories are shown in Fig. 6. The estimated slopes of each line are 2.35 × 10⁻⁷, 1.60 × 10⁻⁷, 6.22 × 10⁻⁸, −9.99 × 10⁻⁸, and −3.59 × 10⁻⁷ for ventilation levels 1, 2, 3, 4, and 5, respectively, with the SE for each equal to 1.42 × 10⁻⁸ (note the standard errors are the same since the slope at each level was estimated from the entire population using an ANOVA model). Each of the five computed lines have significantly different slopes (P < 0.01), and, thus, the rate of signal change over the 7.5 s breath-hold is dependent on the initial ventilation level. More specifically, voxels that are initially underventilated (levels 1 and 2) show positive rates of change, or a wash-in effect, while hyperintense regions (levels 4 and 5) show the opposite, or a wash-out effect. Furthermore, the rate of wash-in is highest in the least ventilated regions, while the rate of wash-out is highest in the most hyperintense regions.

Fig. 6.

Scatterplot of the mean normalized voxel intensity within each of the five ventilation level classifications in all 39 subjects (entire population) at each point in time (every 0.5 s). Plotted lines show the linear regression fit within each of the ventilation levels over time. The slopes of the fitted lines (2.35 × 10⁻⁷, 1.60 × 10⁻⁷, 6.22 × 10⁻⁸, −9.99 × 10⁻⁸, and −3.59 × 10⁻⁷ for ventilation levels 1, 2, 3, 4, and 5, respectively) are each significantly different from all others (P < 0.01).

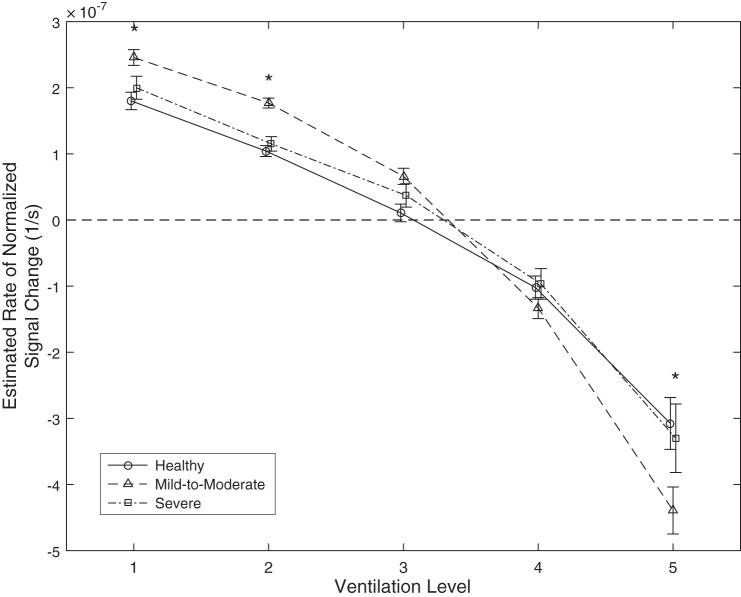
Figure 7 shows the results separately for subjects within each of the three asthma severity groups. First, the same pattern is apparent, i.e., initially poorly ventilated regions have a positive slope/rate of change (wash-in) and hyper-intense regions have a negative rate of change (wash-out). Additionally, mild-to-moderate asthmatic subjects have an increased absolute rate of change in all five ventilation levels compared with both healthy and severe disease groups that reaches statistical significance for level 1 (P < 0.05, mean ± SE: healthy = 1.80 × 10⁻⁷ ± 0.11 × 10⁻⁷, mild-to-moderate = 2.46 × 10⁻⁷ ± 0.12 × 10⁻⁷, and severe = 2.00 × 10⁻⁷ ± 0.17 × 10⁻⁷), level 2 (P < .001, means ± SE: healthy = 1.04 × 10⁻⁷ ± 0.08 × 10⁻⁷, mild-to-moderate = 1.78 × 10⁻⁷ ± 0.08 × 10⁻⁷, and severe = 1.15 × 10⁻⁷ ± 0.11 × 10⁻⁷) and level 5 (P < 0.01, means ± SE: healthy = −3.08 × 10⁻⁷ ± 0.39 × 10⁻⁷, mild-to-moderate = −4.39 × 10⁻⁷ ± 0.36 × 10⁻⁷, and severe = −3.30 × 10⁻⁷ ± 0.52 × 10⁻⁷). Healthy subjects and severe asthmatic subjects show very similar patterns in their rates of signal change and are not significantly different at any level of initial ventilation.

Fig. 7.

Chart showing the estimated rate of signal change over time (y-axis) within each of the five initial ventilation levels (x-axis) in the healthy, mild-to-moderate, and severe groups with solid, dashed, and dash-dotted lines, respectively. Asterisks indicate statistically significant differences (significance of at least P < 0.05) between the rate of signal change in the mild-to-moderate group and both of the other groups.

DISCUSSION

Patterns of hyperpolarized He-3 gas signal distribution were shown to change dynamically within a breath-hold. The qualitative pattern observed showed areas of low and high signal intensity trend toward a more homogenous pattern over the course of a breath-hold in all subjects, regardless of disease severity. However, the rate at which the voxel signals trended toward a more homogeneous pattern differed by asthma severity. The fastest rate of change was seen in those with mild-to-moderate asthma, while healthy and severely asthmatic subjects showed relatively slow, statistically equivalent, rates of change, despite the fact severe asthma subjects presented with the greatest overall spatial heterogeneity in ventilation upon breath-hold initiation at end-inhalation.

As shown previously (1, 6, 7), severe asthmatic subjects showed a spatially more heterogeneous pattern of regional ventilation at end-inhalation compared with both healthy and mild-to-moderate asthma groups. Specifically, greater ventilation defect percentage (level 1) was selectively offset by lower percentage in the median ventilation level (level 3) for severe asthmatic subjects compared with healthy subjects and mild-to-moderate asthmatic subjects (Fig. 3B). A more uniform class membership indicates a pattern of varying signal intensity throughout a larger percentage of the lungs and, therefore, greater heterogeneity in severe asthmatic subjects. Healthy and mild-to-moderate asthmatic subjects showed a more peaked class membership at level 3, the median signal class, indicating more homogenous patterns of regional ventilation that were nearly identical for the two groups.

The interpretation of the observed differences in rate of signal change relies on the statistical model used for the parameter estimation: a useful model that 1) accurately and sensitively captures the underlying physiological processes in the estimated parameters, and given this, is satisfied, and 2) yields meaningful insight into connecting the parameterization (and parameter estimates) with the nature of the underlying physiology. With this in mind, minimization of both the number of estimated parameters and the required model assumptions strongly influenced choice of the model to avoid overfitting, avoid introducing bias unnecessarily, and minimize variability in parameter estimates (or rather maximize confidence in their accuracy). A first-order kinetic model and a first-order polynomial (linear) model were both considered, since each superficially meets these basic requirements (two estimated parameters, similarly minimal assumptions). To further evaluate each, we roughly consider the physiological processes driving gas redistribution during breath-hold as belonging to either a “fast” or “slow” regime. A fast process evolves over shorter time scales than the breath-hold (≤7.5 s), and a slow process reaches equilibrium much more slowly. Redistributive mixing over small spatial scales (either passively or actively driven by latent local pressure gradients following inspiration) occurs in the “fast” regime, while diffusive redistribution over large distances (over the entire lung at the limit) occurs in the “slow” regime. Ultimately, the signal we aim to model (i.e., global average time course within each ventilation level) is a summation over all of the processes, both fast and slow. Because the slow regime processes involve mixing over large spatial scales (mixing of two or more large regions), a large number of voxels are involved in each. This leads to significant global coherence and, subsequently, a large contribution to the global average time course. The slowest, most coherent redistribution, has a very long rate constant relative to the breath-hold duration. Root mean square distance traveled (x_rms) for freely diffusing HP He-3 (diffusion coefficient = 0.88 cm²/s) is only ∼3.6 cm during the breath-hold, and is, in fact, much lower (x_rms = ∼0.5 cm, diffusion coefficient = 0.02 cm²/s), assuming previously published estimates of apparent long-range diffusion coefficients of HP He-3 (28). Thus, these processes will very likely be well approximated using a linear model over the breath-hold duration, and first-order kinetic rate constant estimates may be less accurate, given that a large amount of the time course evolution remains unsampled. Alternatively, fast regime processes are unlikely to be as globally coherent, resulting in a “smearing” of many processes governed by a pseudo-continuous range of rate constants. It is reasonable to expect that this manifestation of the fast processes will also appear linear to a reasonable approximation. Even if this assertion is overly optimistic, this effect layered on top of the slow regime signal will very likely be problematic for a first-order kinetic model. If it is captured at all, it can be expected to manifest in the rate constant estimate unpredictably and perhaps inconsistently. In all, the linear model was deemed a superior choice since it clearly was superior with respect to the first condition described above. Thus, we can be very confident in stating that the observed patterns in the estimated rates of signal change are representative of patterns in the physiology driving signal changes during the breath-hold. However, a somewhat abstract connection between the linear model and the nature of the underlying physiology makes assertion of the precise mechanism(s) driving the signal changes somewhat tentative.

A portion of the gas redistribution could be due to simple diffusive exchange between airspaces that are initially ventilated with varying concentrations of HP He-3 (3, 28). A portion could also be associated with either collateral ventilation with different wash-in rates or pendelluft, i.e., regional volume shifts during the breath-hold due to local lung compliance or resistance differences, possibly resulting from different patterns of obstructive disease severity (11). One previous study (17) has investigated this phenomenon in 2D, in which case the authors attributed the observed signal changes over time to collateral ventilation. In this light, the observed differences in the rate of change in mild-to-moderate vs. severe asthmatic subjects may be inferred to reflect differences in gas flow associated with disease-related differences in dynamic functional physiological response to inhalation and subsequent breath-hold.

The act of inhalation causes lowered intrapleural pressures that leads to airflow into the airways and alveoli. Assuming breath-hold is sustained, these intrapleural pressures stabilize by definition. In the case of asthma, inflamed or narrowed airways are expected to remain collapsed or partly obstructed at higher lung volumes, especially for the small non-cartilagenous airways. This obstructive pattern likely leads to the more spatially heterogeneous pattern of ventilation observed immediately postinhalation in asthmatic vs. healthy subjects. As for severe vs. mild-to-moderate asthma, we hypothesize that the spatially heterogeneous obstruction in severe disease is more “stable”, in that it responds very little to functional ventilation dynamics. Thus, it is less conducive to conditions that drive pendelluft compared with the more transient, or functionally responsive, causes of spatial ventilation heterogeneity in milder cases. Airway closures at functional residual capacity (FRC), more prevalent in severe asthma, will only lead to pendelluft if an adjacent branch is open and the closed airway reopens at or prior to breath-hold, such that the volumes/pressures in adjacent branches are sufficiently different to drive it. In contrast, the mild-to-moderate asthmatic subjects have less airway closure at FRC, so spatial heterogeneities are created mainly by branch differences in time constants, which will create pendelluft more readily.

The principal limitation of the current study is that the global decay correction depends on the combination of RF and T₁ effects, the latter of which is potentially influenced by mismatches in the ventilation/perfusion (V/Q) ratio that may mask gas flow and local redistribution. The assumption of global spin density invariance (analogous to mass balance) during breath hold is only valid if the breath hold is properly maintained. Loss of breath-hold is straightforward to detect in practice, and these data can be discarded on a case by case basis. However, temporal spin density invariance will not necessarily hold on a local or even regional level; in fact, we hypothesize that it does not hold by asserting that there are differential rates of signal change locally. Thus, although it is safe to assume that the estimated global decay is, in fact, RF and T₁ related, this may not be the case locally.

Another limitation of the study is that ages are not well matched between disease severity groups (Table 1). Specifically, the severe asthma group was approximately twice as old as the other two groups. Since age-matched data were unavailable for this study (lack of older mild-to-moderate subjects), it is difficult to be certain whether the differences between mild-to-moderate and severe asthma phenotypes are a result of aging, advancement of disease, or a combination of both. A prospective study of age-matched populations, and longitudinal data on these younger, mild-to-moderate asthmatic subjects to determine whether phenotypic progression matches their clinical progression, would be interesting and would aid the inference as to whether the different phenotype is disease related, or related simply to natural aging.

The spatial variation in the RF excitation flip angle has the potential to induce errors in the estimated rate of signal change. The experimental value of flip angle was ∼1.5°, but can easily vary as much as ±10% over the volume of interest. However, we do not expect regional flip angle variations to bias our results since variations in RF power should be uncorrelated with initial degree of ventilation; both poorly and well-ventilated regions should be affected equally. It is, therefore, possible to limit the physiological mechanism(s) driving the observed changes in signal intensity to two main factors. First, there were regional differences in the partial pressure of oxygen (additional details in materials and methods), which is paramagnetic and shortens T₁ relaxation rates (9). Second, there may be regional differences in local lung compliance and/or airway resistance that dampen or delay gas flow as a result of obstructive disease, i.e., pendelluft (21).

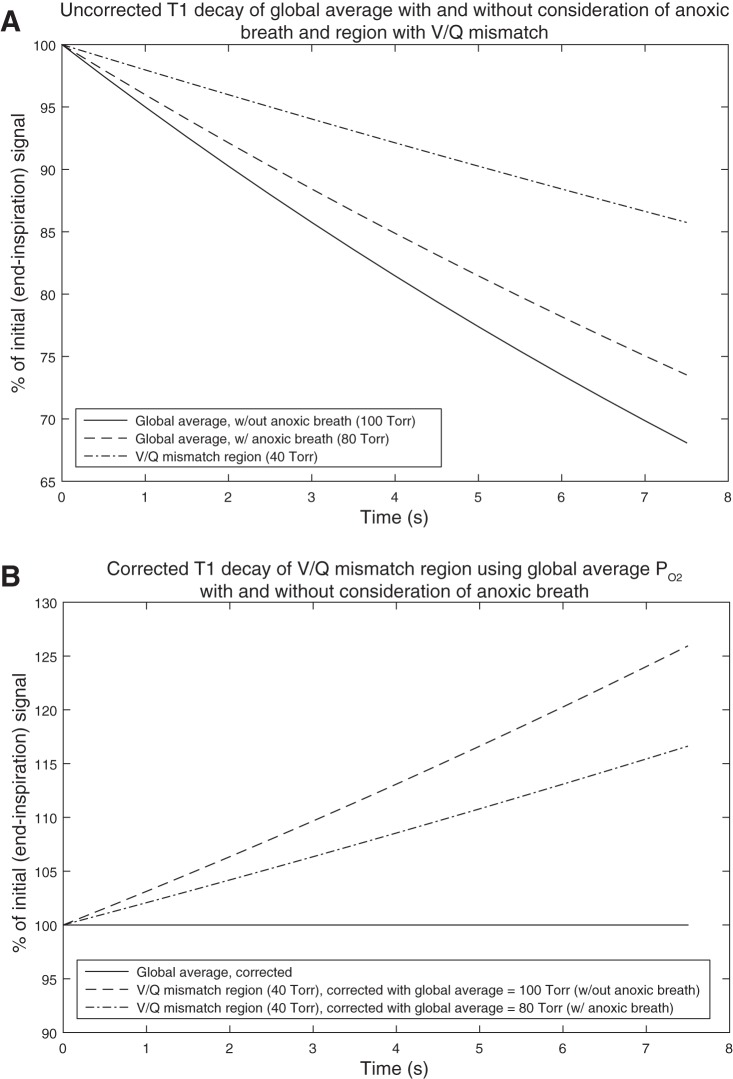
In materials and methods, we explored expected errors related to T₁ relaxation corrections in the worst possible cases. It is important to note that these two worst-case scenarios are mutually exclusive; either the global average is near 100 Torr, and a local defect is at 40 Torr or the global average is 40 Torr, and a local ventilated region is at 100 Torr, but never both simultaneously. Given these possible extreme examples, this has two important implications. First, the largest magnitude of the bias introduced is on the order of 25% and would be insufficient to explain the nearly 100% relative signal changes that we see in regions of ventilation level 1 (i.e., ventilation defect). Second, bias at the levels observed could not be introduced in both regions of potentially extreme Po₂ levels simultaneously (Fig. 6, regions of ventilation levels 1 and 5). A more reasonable assumption is that global average Po₂ is somewhere between 40 and 100 Torr, and regions at both extremes of ventilation are undercorrrected or overcorrected, but to a much less severe degree than for this worst case. Third, it is worth noting that the inhalation of HP He-3 gas is anoxic (HP He-3 mixed with N₂ to a volume equal to 14% of TLC). This will reduce global Po₂ to a level lower than expected following normal inhalation of a similar volume of room air. The expected amount of reduction will be dependent on the difference between FRC and TLC, as well as the “normal” global Po₂. Assuming a “normal” global Po₂ of 100 Torr, TLC of 7 liters (thus, HP He-3 dose volume of ∼1 liter), and FRC of 4 liters, the global average Po₂ would be reduced to 80 Torr, considering the anoxic breath. The effect this will have on the Po₂ related T₁ correction error is illustrated in Fig. 8. Figure 8A shows the uncorrected T₁ decay related to Po₂ of the global average with and without consideration of the anoxic breath, as well as a region of V/Q mismatch. Note that the lower the Po₂, the less severe the rate of decay. Figure 8B then shows the result of correcting the V/Q mismatched region for Po₂-related T₁ decay using the global average with and without considering the anoxic breath. The dashed line in Fig. 8B shows the “worst case” scenario that we have discussed previously, where a region with Po₂ of 40 Torr is corrected using the global average of 100 Torr (results in ∼25% error over 7.5 s). When the global average is reduced to 80 Torr due to the anoxic breath, the “worst case” error is reduced to ∼16% over the 7.5 s breath-hold, shown by the dashed-dotted line in Fig. 8B. Consequently, the fact that the HP He-3 dose is anoxic makes Po₂-related T₁ decay correction error, even less of a factor in this analysis.

Fig. 8.

A: uncorrected T₁ decay related to Po₂ of the global average with and without consideration of the anoxic breath of hyperpolarized (HP) He-3, as well as a region of ventilation/perfusion (V/Q) mismatch (with Po₂ = 40 Torr). Global average Po₂ = 80 Torr for the case of the anoxic breath is computed assuming “normal/steady-state” global average Po₂ = 100 Torr, total lung capacity (TLC) = 7 liters functional residual capacity (FRC) = 4 liters, and HP He-3 dose volume = 1 liter (∼14% of 7 liters). B: result of correcting the V/Q mismatched region for Po₂-related T₁ decay using the global average with and without considering the anoxic breath. The global average is “perfectly corrected” (i.e., no correction error) in this case, clearly, since it is used to correct itself.

While it is likely that regional differences in partial oxygen pressure can and do explain some of the signal changes observed and reported in this work, the degree to which they do so is insufficient to explain the magnitude of the signal changes, especially in the case of delayed filling of ventilation defects. Furthermore, if these regional differences are truly the source of a significant portion of the observed signal change, the underlying physiological mechanism responsible for these observed differences remains of great interest. Taken overall, the dominant signal changes are most likely related to gas redistribution during breath-hold, most likely resulting from different patterns of obstructive disease severity.

Differentiating the portion of the signal change associated with T1 and RF decay sources from those related to regional spin density redistribution over time clearly requires a more sophisticated acquisition and physiological model.

In conclusion, we demonstrate that over the course of a breath-hold, voxel signals trend toward a more homogenous pattern of ventilation in all subjects, regardless of disease severity. We further provide evidence to demonstrate a significant difference in the rate at which signal of inhaled He-3 gas mixed with nitrogen evolves during a breath-hold and by asthma severity. Interestingly, mild-to-moderate asthmatic subjects showed the greatest rate of signal change despite severe asthmatic subjects having the greatest initial level of ventilation heterogeneity based on ventilation defect analysis. We argue that the analysis in this work strongly suggests that these differences relate to obstructive disease physiology between these groups.

GRANTS

This study was supported by grants from the National Institutes of Health- (NIH) National Heart, Lung, and Blood Institute (NHLBI): NIH-NHLBI R01-HL-080412, NIH-NHLBI R01-HL-069116, NIH-NHLBI U10-HL-109168; The Hartwell Foundation; and the Department of Radiology, School of Medicine and Public Health, University of Wisconsin (UW)-Madison. Grant support was also provided by a NIH/National Cancer Institute 5 T32 CA009206 Radiological Sciences Training Grant, Department of Medical Physics, School of Medicine and Public Health, UW-Madison, as well as NIH Grants UL1TR000427 and KL2TR000428.

DISCLOSURES

S.B.F. receives grant support from GE Healthcare.

AUTHOR CONTRIBUTIONS

Author contributions: A.D.H. analyzed data; A.D.H., R.L.S., S.K.N., and S.B.F. interpreted results of experiments; A.D.H. prepared figures; A.D.H. drafted manuscript; A.D.H., R.V.C., R.L.S., N.N.J., S.K.N., and S.B.F. edited and revised manuscript; A.D.H. and S.B.F. approved final version of manuscript; R.V.C. and S.B.F. performed experiments; N.N.J., S.K.N., and S.B.F. conception and design of research.