Modeling changes in glucose and glycerol rates of appearance when true basal rates of appearance cannot be readily determined

Abstract

Advancing diabetes care requires accurate physiological assessments. Hyperinsulinemic clamps with stable isotope tracers can simultaneously measure insulin's ability to suppress lipolysis and hepatic glucose release. Traditionally, these methods require an assessment of basal glucose and glycerol rate of appearance (R_a). Basal R_a is challenging to measure in insulin-dependent diabetes, where exogenous insulin required to maintain normoglycemia can raise peripheral insulin concentrations sufficiently to suppress basal R_a. Thus we identified two alternative statistical approaches to describe changes in glucose and glycerol R_a that are less reliant on basal assessments. Sixteen youths (4 type 1 diabetic, 4 type 2 diabetic, 4 lean controls, and 4 obese nondiabetic) underwent a four-phase (“basal” and 10, 16, and 80 mU·m²·min⁻¹) hyperinsulinemic euglycemic clamp with glucose and glycerol tracers. Glucose and glycerol R_a were calculated per phase. A statistical method, the standard two-stage (STS) algorithm, was applied to the individual log insulin vs. R_a curves to calculate a single predicted R_a value. A population-based mixed-effects model (MEM) compared the group average R_a with log insulin curves and described individual deviations from group means and was used to calculate individual predicted R_a. Both models were applied to the participant data, and predicted R_as at the mean insulin concentration per phase (10 for glycerol, 16 for glucose) were calculated, with good agreement between observed and predicted values. In our data set, the MEM was better able to detect group differences. Both STS and MEM can model lipolysis and endogenous glucose release in insulin-dependent states when basal R_a cannot be accurately measured.

diabetes is one of the leading causes of morbidity and mortality today, and rates of diabetes diagnosis are continuing to increase (15, 24). There are now many therapeutic options for reducing hyperglycemia in diabetes, but all currently fall short of normal physiological insulin secretion. The full biological effects of several diabetes medications remain incompletely understood, and the need for development of additional medications persists (5). Hyperglycemia in diabetes is due to inadequate insulin secretion combined with peripheral insulin resistance (IR) and persistent endogenous glucose release, primarily from the liver (8). Being able to measure each of these contributions to hyperglycemia is critical to understanding physiological effects of varied therapeutic options. Additionally, the interactions between glucose and lipid metabolism are complex, with adipose IR being another prominent abnormality characteristic of diabetes; thus simultaneous measurement of lipid and glucose metabolism can be useful (2, 20, 27).

The gold standard for assessing multitissue insulin sensitivity is a multiphase hyperinsulinemic euglycemic clamp coupled with isotopic tracers. The endogenous glucose rate of appearance (R_a) is calculated with a glucose tracer, most commonly the stable isotope [6,6-²H₂]glucose (9, 32). Typically, comparisons between the fasting glucose R_a and then a subsequent decrease in glucose R_a in response to increasing concentrations of insulin are utilized to express hepatic insulin sensitivity. Similarly, the decrease in lipolysis response to increasing concentrations of insulin (i.e., adipose insulin sensitivity) can be assessed via changes in free fatty acid (FFA) concentrations or glycerol R_a. However, a glycerol tracer is thought to be superior, as glycerol is not subject to intracellular and extracellular recycling (16). Finally, peripheral glucose uptake as measured by glucose infusion rate or glucose rate of disappearance (R_d) during hyperinsulinemia is used as a measure of muscle insulin sensitivity.

In adults without diabetes, the insulin concentration required to decrease endogenous glucose R_a is three- to fourfold greater than fasting insulin levels but is well below the threshold needed to cause near-maximal peripheral glucose uptake (4). The insulin concentration typically required to decrease peripheral lipolysis is even lower than that needed to lower glucose R_a (5). Thus, to simultaneously measure insulin-mediated decreases in lipolysis and glucose R_a and increases in peripheral glucose uptake, a basal period followed by phases of increasing doses of insulin in a stepwise fashion is required. This study design allows for full characterization of the three major tissues involved in whole body responses to insulin.

There are several ways to express dynamic changes in R_a when data are collected from a single or multiphase clamp. Methods in current use rely on measures that collapse the multiple measurements of insulin and R_a during the clamp into a summary measurement that can then be compared across individuals or groups. For example, the typical expression of responsiveness of glucose or glycerol R_a to the suppressive effects of insulin is to divide the R_a during the appropriate clamp phase by the basal R_a, which is typically expressed as “percent suppression of basal” (6). To account for serum insulin concentrations during each phase of the clamp, an additional correction can be done during each phase. The half-maximal inhibitory concentration (IC₅₀) required for insulin to decrease 50% of the basal R_a can then be calculated from the slope and expressed as the IC₅₀ (4). However, both of these methods require an accurate measure of basal R_a. Alternatively, since persistent glucose or glycerol R_a during extreme hyperinsulinemia is known to be abnormal, a lack of complete R_a suppression can be interpreted as IR. However, the latter approach may fail to detect subtle differences between groups.

Stable glucose concentrations are a requirement prior to and during clamp measurements. In people who are dependent on continuous exogenous insulin, glucose control prior to studies can be challenging, and the “basal” time period becomes artificial due to the requirement for exogenous insulin administration. In settings of severe IR, the insulin concentrations required to control glycemia are often greater than the insulin concentrations known to suppress lipolysis or even endogenous glucose release. Assessment of basal fasting metabolism requires a physiologically normal hormonal milieu. Thus, in patients with either type 1 or type 2 diabetes, the “basal fasting” insulin concentration is in excess of the norm for individuals without diabetes, and these states are too dissimilar for comparison or modeling. In these cases, it is difficult to determine a true basal R_a, violating the assumptions of conventionally used calculations. The goal of this study was thus to identify and compare statistical methods to express the responsiveness of endogenous glucose and glycerol R_a to the effects of insulin that are not dependent on the single measurement of basal R_a.

The goal of this article is to describe the three approaches to R_a assessment when the assumptions of a true basal state are violated [simple vs. standard two-stage (STS) vs. mixed-effects model (MEM)] and to compare the performance of all three methods on human clamp data from varied patient populations, including volunteers with diabetes, using standard statistical criteria (the −2 log likelihood).

METHODS

Participants.

Sixteen participants 12–18 yr of age were recruited from pediatric clinics at the Children's Hospital Colorado and the Barbara Davis Center for Childhood Diabetes for a prospective cross-sectional study. Participants included four nonobese control youths (3 females, 1 male; BMI percentile = 61 ± 30th percentile, Hb A_1c = 5.3 ± 0.2%, Tanner stage 4.8 ± 0.5), four nonobese youths with type 1 diabetes (T1D; 2 males and 2 females; BMI percentile = 86 ± 12th percentile, Hb A_1c = 9.1 ± 2.1%, Tanner stage 4.8 ± 0.5), four obese youths without diabetes (2 males, 2 females; BMI percentile = 98 ± 1st percentile, Hb A_1c = 5.4 ± 0.05%, Tanner stage 4.3 ± 0.5), and four obese youths with type 2 diabetes (T2D; 2 males and 2 females; BMI percentile = 96 ± 4.2 percentile, Hb A_1c = 8.8 ± 2.7%, Tanner stage 5 ± 0). To reduce variability in measurements of insulin sensitivity, all participants were untrained (defined as ≤3 h/wk of exercise, verified by standardized 3-day activity recall and by 7-day accelerometer recording; Actigraph, Pensacola, FL), had achieved Tanner stage 4 or above in puberty (as assessed by physical exam by a pediatric endocrinologist, K. J. Nadeau or M. Cree-Green), and were not prescribed medications known to effect IR, blood pressure, or lipids. This study was approved by the University of Colorado Anschutz Medical Campus Institutional Review Board. Parental informed consent and participant assent were obtained from all participants ≤18 yr old, and participant consent was obtained from those aged 18 yr.

Study design.

Participants underwent a screening visit to determine eligibility and an overnight inpatient stay prior to a multistage hyperinsulinemic euglycemic clamp. Volunteers consumed an isocaloric diet (55% carbohydrate, 15% protein, and 30% fat) for 3 days prior to admission, and all participants were free of acute illness, with no strenuous exercise for the 3 days prior.

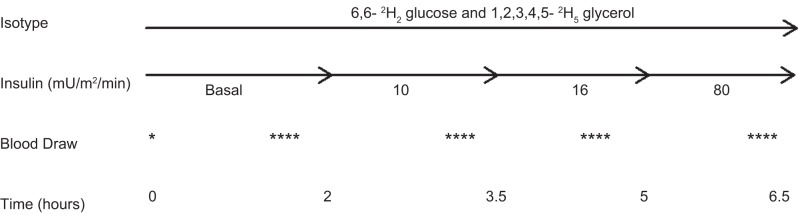
In participants with diabetes, subcutaneous insulin was replaced with an overnight intravenous insulin infusion to normalize blood sugar levels (goal of 100 mg/dl), with the last dose of long-acting insulin given 24 h prior to admission. A 6.5-h, four-phase hyperinsulinemic euglycemic clamp (basal and 10, 16, and 80 mU·m²·min⁻¹ insulin) was performed, fasting in the morning to measure insulin sensitivity, with a 2-h basal phase and three insulin phases of 1.5 h each, similar to our previously described methods (Fig. 1) (22). Insulin doses of 10, 16, and 80 mU·m²·min⁻¹ were selected on the basis of our (22, 23) and others' (12) previous experiences with the high insulin requirements in pubertal youth. In a nondiabetic adolescent, the dose of 10 mU·m²·min⁻¹ will suppresses lipolysis with a minimal influence on endogenous glucose release, the dose of 16 mU·m²·min⁻¹ will suppresses endogenous glucose release, and the dose of 80 mU·m²·min⁻¹ will induce near-maximal insulin-stimulated glucose uptake as a measure of peripheral insulin sensitivity (4, 16, 33). Twenty percent dextrose (spiked with [6,6-²H₂]glucose to maintain stable enrichment of plasma glucose) was infused concurrently to maintain blood glucose at ∼95 mg/dl, based on samples drawn every 5 min from an arterialized hand vein, and run on a bedside Yellow Springs Instrument glucose analyzer, as described previously (4, 22, 23). Steady state was defined as a stable blood glucose of 95 ± 5 mg/dl over the last 30 min of each phase.

Fig. 1.

The tracer infusion protocol is shown. There are 4 phases: a 2-h ”basal“ phase and 10-, 16-, and 80-h phases that are each 1.5 h long. Blood is drawn is at baseline and then 4 times at the end of each phase.

Tracer infusion protocol.

Baseline blood samples (background isotopic enrichment of glucose and glycerol and concentrations of glucose, insulin, glycerol, FFA, and C-peptide) were obtained at ∼6 AM, after which constant infusions of glucose and glycerol stable isotope tracers were started. A primed (4.5 mg/kg) constant (0.03 mg·kg⁻¹·min⁻¹) infusion of [6,6-²H₂]glucose (Isotec, Miamisville, IA) was paired with a primed (1.6 μmol/kg) constant (0.11 μmol·kg⁻¹·min⁻¹) infusion of [²H₅]glycerol (Isotec) (29). Two hours were allowed for the tracers to reach steady state for the basal phase. During the last 30 min of each of the four phases, four samples, each 10 min apart, were drawn for glucose, glycerol, FFA, and insulin concentrations as well as for glucose and glycerol tracer enrichments (14). The mean concentration of glucose, insulin, FFA, and glycerol per period was calculated from all values in the time period.

Sample analysis.

Analysis of [²H₅]glycerol and [6,6-²H₂]glucose were done using a modification of the negative ion chemical ionization gas chromatography-mass spectrometry as described (3, 4, 14). Serum glucose concentrations were determined on the Yellow Springs Instrument glucose analyzer, as described above. Serum insulin was analyzed with radioimmunoassay (Millipore, Billerica, MA); plasma glycerol (R-Biopharm, Marshall, MI) and FFA (Wako Chemicals, Richmond, VA) were determined enzymatically, and C-peptide was determined via chemiluminescent immunoassay (DiaSorin, Stillwater, MN).

Tracer calculations.

All isotopic enrichment measurements were corrected for background enrichments. Glycerol and glucose R_a over the last 30 min of each phase of the insulin clamp were calculated for every 10-min interval using the Steele non-steady-state equation modified for stable tracers (28, 31). We also accounted for the “spiked” glucose in the 20% dextrose infusions, as described by Finegood et al. (13).

Simple approach.

The mean R_a was calculated for each phase of the clamp. The mean glycerol R_a at the 10 mu·m²·min⁻¹ phase is representative of adipose insulin sensitivity with this approach. The mean glucose R_a at the 16 mu·m²·min⁻¹ phase is representative of hepatic insulin sensitivity, assuming that renal glucose R_a remains stable.

STS algorithm.

For each individual, the measured mean glucose R_a from each phase of the clamp was plotted against the log of the measured insulin concentration from the respective phase. Multiple types of curves were fit to the data, and a quadratic curve was selected for all participants, as this provided the best fit of the data for each individual (r² range from 0.75 to 0.97 for glucose and 0.82 to 0.99 for glycerol). The parameter estimates for each individual were obtained, and they were compared between groups using multivariate ANOVA. To determine the predicted glucose R_a, the quadratic equation of the line for each individual was solved with the group median insulin concentration for the 16 mU·m²·min⁻¹ stage. The same process was performed with the glycerol data, but with the 10 mU·m²·min⁻¹ stage group mean insulin.

Mixed-effects models.

Insulin, glucose R_a, and glycerol R_a were not distributed normally, and thus they were log-transformed prior to analysis. Negative glucose R_a values were observed; therefore, a constant was added prior to log transformation (and subtracted off after back transformation).

The relationship between insulin (independent variable) and Ra (dependent variable) over time was compared between groups by fitting a series of polynomial and nonlinear mixed-effects models. The three models considered were 1) the linear random coefficients model Y_ijk = (β_0k + μ_0i) + (β_1k + μ_1i)X_ijk + ε_ijk, 2) the quadratic random coefficients model Y_ijk = (β_0k + μ_0i) + (β_1k + μ_1i)X_ijk + β_2kX_ijk² + ε_ijk, and 3) the exponential random coefficients model Y_ijk = (β_0k + μ_0i) + X_ijk^{(β_1k + μ_1i)} + ε_ijk.

Y_ijk represents the transformed R_a measurements, with i indexing individuals, j indexing time points, and k indexing groups (T1D, T2D, control, and obese). β, μ, and ε represent fixed effects, random effects, and random error, respectively. The shape of the quadratic curve is governed both by β₁ and β₂. In our example, β₁ is the rate of change in R_a when insulin is equal to zero, and β₂ describes the steepness and direction of the curve (a positive value of β₂ means the curve opens upward, and a negative value means the curve opens downward). In the quadratic model, the sensitivity of R_a to insulin will depend on the absolute value of insulin. Separate models were fit to 1) the controls and participants with T1D and 2) the controls and participants with T2D, resulting in four sets of models (pairwise combinations of the glycerol R_a and glucose R_a outcomes and the two combinations of participant groups). All models were fit using PROC NLMIXED, SAS version 9.4. The model with the lowest −2LL (−2 lower limits) was chosen as the final model form. Group differences were tested by fitting the model without a group effect; the difference in the −2LL for the models with and without the group effect was compared with a chi-squared distribution with degrees of freedom equal to the difference in the number of parameters fit. Predicted values of R_a were calculated from the final model using the estimates of the fixed and random effects and the median insulin per group (phase 10 mU·m²·min⁻¹ for glycerol R_a and phase 16 mU·m²·min⁻¹ for glucose R_a).

RESULTS

Metabolite concentrations during the clamp.

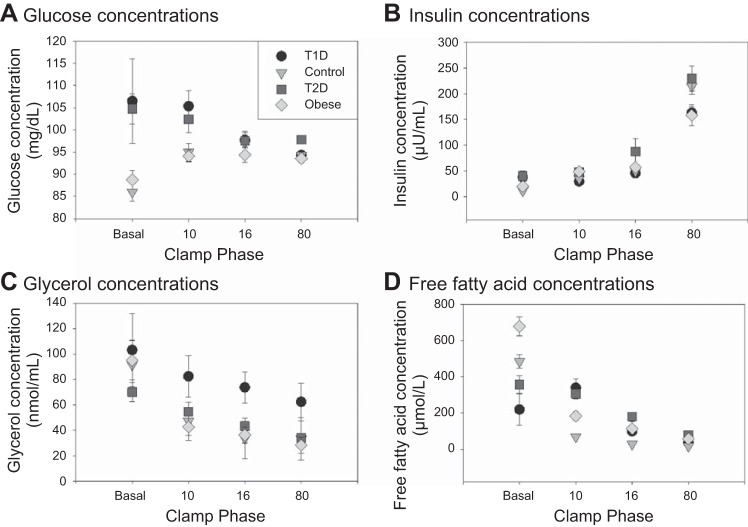
Serum glucose, insulin, glycerol, and FFA concentrations by group per clamp phase are shown in Fig. 2. Volunteers with diabetes had higher blood sugars during the basal phase and the 10 mU·m²·min⁻¹ phase (Fig. 2A). Glucose concentrations were the same thereafter between groups (during the 16 and 80 mU·m²·min⁻¹ phases). Insulin concentrations were also higher in the groups with diabetes during the basal and 10 mU·m²·min⁻¹ phases but similar for the remainder of the clamp (Fig. 2B). Glycerol concentrations were higher in T1D during all phases and lower in T2D during the basal and 10 mU·m²·min⁻¹ phases and then higher in the 16 and 80 mU·m²·min⁻¹ phases (Fig. 2C). FFAs were as anticipated, with close to full suppression at the 10 mU·m²·min⁻¹ phase only in the nondiabetic groups. During the basal phase, FFAs were lowest in youths with diabetes due to suppression from overnight insulin administration. FFAs remained unchanged in T2D during the 10 mU·m²·min⁻¹ phase but rose in T1D due to a lower insulin infusion rate relative to what was needed for overnight glucose control. FFAs then decreased in T1D and T2D during the 80 mU·m²·min⁻¹ phases (Fig. 2D). Additionally, C-peptide was measured in the basal phase and, as predictedm was low in T1D (0.3 ± 0.4 ng/ml) and higher in the obese nondiabetic (2.4 ± 0.4) and T2D groups (3.1 ± 0.7) compared with lean controls (1.4 ± 0.2).

Fig. 2.

Serum metabolite concentrations, including glucose, insulin, glycerol, and free fatty acid concentrations during each phase of the clamp for each group of participants. T1D, type 1 diabetes; T2D, type 2 diabetes.

Simple method results.

Measured glucose and glycerol R_a are shown in Fig. 3. As anticipated, the glucose R_a during the basal phase and 10 mU·m²·min⁻¹ phase was similar between groups, as this dose of insulin was chosen to not impact glucose R_a (Fig. 3A). During the 16 mU·m²·min⁻¹ phase there was an expected dramatic drop in glucose R_a in the controls, with minimal change in participants with diabetes. Using the “simple method,” glucose R_a at the 16 mU·m²·min⁻¹ phase could be utilized as a primary end point. The values for each group were 0.37 ± 0.08 (lean control), 0.70 ± 0.49 (obese nondiabetic), 1.33 ± 0.10 (T1D) and 1.31 ± 0.07 mU·m²·min⁻¹ (T2D). All groups had a relatively suppressed glucose R_a during the highest dose of insulin infusion, although the diabetic groups were not as suppressed as the nondiabetic groups.

Fig. 3.

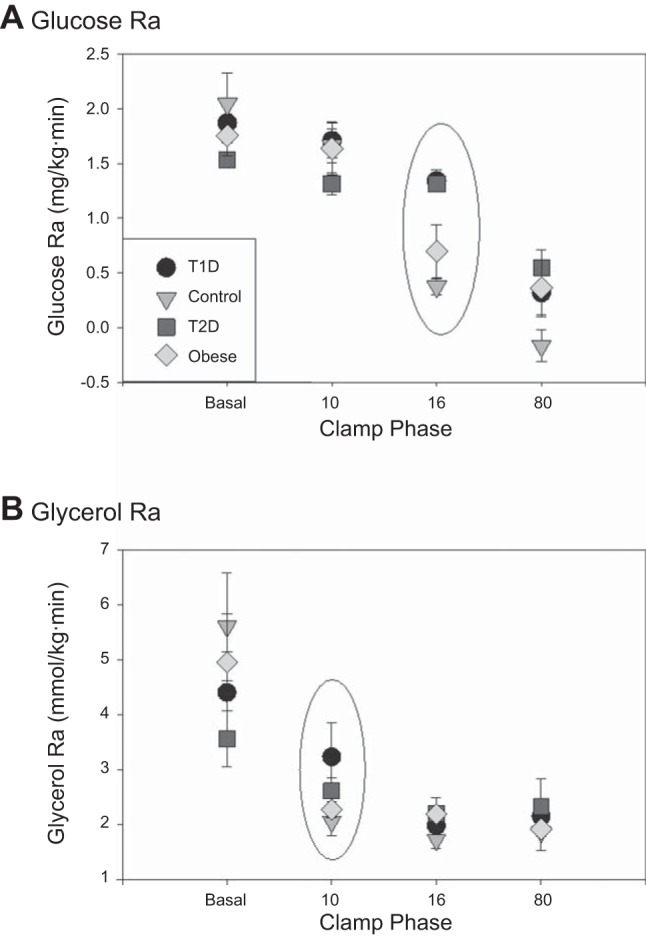
A: calculated glucose rate of appearance (R_a) by the simple method. Glucose R_a during the 16 phase (circled) is representative of the hepatic insulin dose. B: calculated glycerol R_a by the simple method. Glycerol R_a during the 10 phase (circled) is representative of the adipose insulin dose.

As shown in Fig. 3B, glycerol R_a is higher in controls during the basal phase and then drops as expected during the 10 mU·m²·min⁻¹ phase, whereas glycerol R_a does not drop significantly in the diabetic groups until the second stage. Again, using the simple method, glycerol R_a at the 10 mU·m²·min⁻¹ phase can be utilized as a primary glycerol endpoint. The values for each group were 2.05 ± 0.26 (lean control), 2.27 ± 0.14 (obese nondiabetic), 3.23 ± 0.63 (T1D), and 2.61 ± 0.23 mmol·kg⁻¹·min⁻¹ (T2D). All four groups had a suppressed glycerol R_a during the 80 mU·m²·min⁻¹ phase, showing the importance of lower doses of insulin to detect group differences in glycerol R_a.

STS and MEM methods: primary results.

Predicted R_a values for both STS and MEM were calculated using the median insulin concentrations from the groups during the 10 mU·m²·min⁻¹ phase for glycerol R_a (38 IU/dl) and the 16 mU·m²·min⁻¹ phase for glucose R_a (51 IU/dl) and are shown in Table 1 compared with the simple model R_a for each participant. For all six sets of MEM (glycerol R_a T1D and control, glycerol R_a T2D and lean control, glycerol R_a lean and obese nondiabetic, glucose R_a T1D and lean control, and glucose R_a T2D and nondiabetic glucose R_a lean and obese nondiabetic), the quadratic random effects model was selected as the best-fitting model using −2LL (Table 2). For the glucose R_a models comparing the lean nondiabetic and T1D groups and the nondiabetic and T2D groups, all random effects were estimated to be zero, indicating that there was no significant variability in the outcome above that which was explained by group. Consequently, each individual in the group has the same predicted R_a. This was not the case with the model comparing the lean control and obese nondiabetic groups.

Table 1.

Actual vs. STS-predicted vs. MEM-predicted glucose and glycerol R_a

	Glucose Ra, mg·kg−1·min−1					Glycerol Ra, mmol·kg−1·min−1
Participant	Simple method phase 16	STS predicted	MEM for control and T1D groups	MEM for control and T2D groups	MEM for control and obese groups	Simple method (10 phase)	STS predicted	MEM for control and T1D groups	MEM for control and T2D groups	MEM for control and obese groups
Control 1	0.50	0.96	0.74	0.74	0.83	2.18	2.24	2.18	2.21	2.17
Control 2	0.20	0.09	0.74	0.74	0.61	2.61	2.29	2.35	1.76	2.33
Control 3	0.27	0.66	0.74	0.74	0.69	2.08	1.66	1.79	2.34	1.79
Control 4	0.54	0.10	0.74	0.74	0.88	1.36	1.49	1.43	1.42	1.44
T1D 1	1.62	1.35	1.68			2.05	2.68	1.81
T1D 2	1.31	2.07	1.68			2.86	3.59	2.89
T1D 3	1.13	1.05	1.68			3.02	1.73	2.35
T1D 4	1.29	1.56	1.68			5.01	3.64	2.84
T2D 1	1.46	1.53		1.39		3.16	2.58		3.29
T2D 2	1.41	1.15		1.39		2.05	2.47		2.44
T2D 3	1.16	1.19		1.39		2.44	3.13		2.57
T2D 4	1.24	1.03		1.39		2.82	5.00		3.55
Obese 1	1.37	1.65			1.38	1.91	2.05			2.32
Obese 2	0.60	2.25			1.13	2.35	2.77			2.59
Obese 3	0.59	1.15			1.14	2.21	3.41			2.85
Obese 4	0.21	0.71			0.86	2.59	3.24			2.78
Control mean	0.38 ± 0.17	0.45 ± 0.43	0.74 ± 0	0.74 ± 0	0.75 ± 0.12	2.05 ± 0.52	1.92 ± 0.40	1.94 ± 0.41	1.93 ± 0.43	2.13 ± 0.26
T1D mean	1.34 ± 0.20	1.51 ± 0.43	1.68 ± 0			3.24 ± 1.26	2.91 ± 0.90	2.48 ± 0.50
T2D mean	1.32 ± 0.14	1.22 ± 0.21		1.39 ± 0		2.61 ± 0.48	3.29 ± 1.17		2.96 ± 0.54
Obese mean	0.70 ± 0.49	1.44 ± 0.66			1.13 ± 0.21	2.27 ± 0.14	2.87 ± 0.60			3.15 ± 0.66

Values are means ± SE. STS, standard two-stage; MEM, mixed-effects model; R_a, glucose rate of appearance; T1D, type 1 diabetes; T2D, type 2 diabetes. Predicted glucose and glycerol R_a were calculated per participant using the median insulin for the appropriate phase (10 phase for glycerol and 16 phase for glucose). The median insulin concentrations were 38 IU/ml for the 10 phase and 51 IU/ml for the 16 phase.

Table 2.

−2LL values of mixed-effects models

Comparison (Model)	−2LL
	Glucose Ra
T1D vs. control
Linear	−45.1
Quadratic	−52.8
Exponential	−40.6
T2D vs. control
Linear	−54.7
Quadratic	−55.5
Exponential	−51.3
Obese nondiabetic vs. control
Linear	−45.1
Quadratic	−45.2
Exponential	−41.2
	Glycerol Ra
T1D vs. control
Linear	27.7
Quadratic	6.8
Exponential	16.6
T2D vs. control
Linear	18.8
Quadratic	−7
Exponential	4.1
Obese nondiabetic vs. control
Linear	20.9
Quadratic	−6
Exponential	1.9

−2LL, −2 lower limits.

Comparisons between the simple method, SMS, and MEM.

Comparisons of observed and predicted means and SD for both glycerol and glucose R_a for each group from all methods are shown in Fig. 4. For glucose R_a, predicted values for MEM were higher than observed values or predicted values from STS. The predicted values from STS were more variable than from MEM or the observed values. For glycerol R_a, predicted values from both MEM and STS for T1D were lower than observed, and predicted values for T2D were higher than observed. Predicted values for STS were again more variable than MEM; however, the observed values were generally more variable than predicted.

Fig. 4.

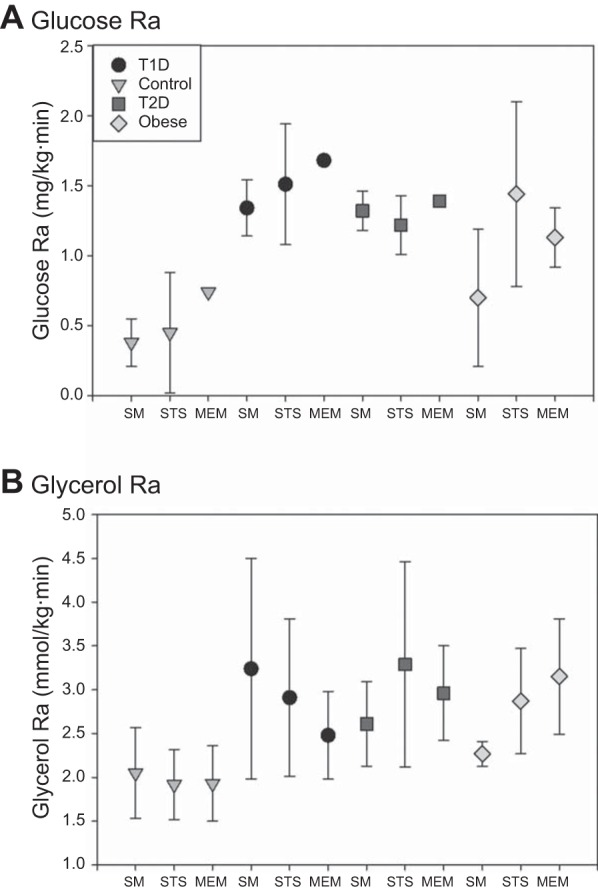
A: glucose R_a for each participant type, calculated with the simple method, i.e., “observed,” and the standard two-stage (STS) and mixed-effects model (MEM) methods. B: glycerol R_a for each participant type, calculated with the simple method, i.e., observed, and the STS and MEM method.

Parameter estimates.

Mean group parameter estimates for glucose R_a for the STS and MEM are shown in Table 3. The parameter estimates from the STS models were more variable across individuals, particularly for the T2D group. The P value for group was significant for all of the diabetes groups' MEMs, except for the model comparing glycerol R_a in the lean control and the T1D participants. There was no difference for either glucose or glycerol MEM between the lean and obese nondiabetic groups. For the STS models, the only P value for group that was significant was the comparison of glucose R_a in the control and T2D participants.

Table 3.

Model parameters from quadratic MEM and quadratic STS models

Group	β0	β1	β2	P Value for Group Comparison
	Glucose Ra
MEM for control and T1D groups
Lean control	2.24 ± 0.36	−0.27 ± 0.19	−0.01 ± 0.02	0.0044
T1D	−0.39 ± 0.84	1.10 ± 0.43	−0.15 ± 0.05
MEM for control and T2D groups
Lean control	2.24 ± 0.34	−0.27 ± 0.18	−0.01 ± 0.02	0.0037
T2D	0.92 ± 1.24	0.33 ± 0.56	−0.05 ± 0.06
MEM for control and obese groups
Lean control	2.20 ± 0.37	−0.24 ± 0.20	0.00 ± 0.03	0.5519
Obese nondiabetic	1.85 ± 0.76	−0.05 ± 0.39	−0.02 ± 0.05
STS models
Lean control	0.40 ± 0.35	−2.36 ± 2.38	3.32 ± 3.34
Type 1 diabetes	−2.21 ± 2.78	6.57 ± 9.97	−3.27 ± 8.55	0.1204*
Type 2 diabetes	−2.98 ± 7.62	11.17 ± 30.50	−9.15 ± 29.88	0.0875**
Obese nondiabetic	−0.16 ± 0.63	−0.77 ± 2.00	3.23 ± 1.99	0.0579***
	Glycerol Ra
MEM for control and T1D groups
Lean control	5.95 ± 0.76	−2.42 ± 0.40	0.26 ± 0.05	0.2308
T1D	8.66 ± 2.01	−3.59 ± 1.01	0.40 ± 0.12
MEM for control and T2D groups
Lean control	5.99 ± 0.58	−2.44 ± 0.31	0.27 ± 0.04	0.0194
T2D	2.62 ± 2.19	−0.58 ± 0.99	0.04 ± 0.11
MEM for control and obese groups
Lean control	5.95 ± 0.63	−2.42 ± 0.33	0.26 ± 0.04	0.1165
Obese nondiabetic	6.73 ± 1.29	−2.55 ± 0.65	0.27 ± 0.08
STS models
Lean control	4.52 ± 1.90	−17.77 ± 7.14	18.70 ± 6.78
T1D	8.76 ± 4.89	−33.46 ± 16.82	33.90 ± 13.69	0.0903*
T2D	9.09 ± 11.62	−36.80 ± 44.27	38.75 ± 41.53	0.2888**
Obese nondiabetic	6.63 ± 4.25	−26.32 ± 16.73	27.91 ± 16.29	0.1698***

Values are estimated means ± SE. P values for quadratic MEM are from likelihood ratio test. P values for quadratic STS models are from multivariate ANOVA.

^*P value for T1D vs. control;

^**P value for T2D vs. control;

^***P value for obese vs. control.

MEM comparison between groups.

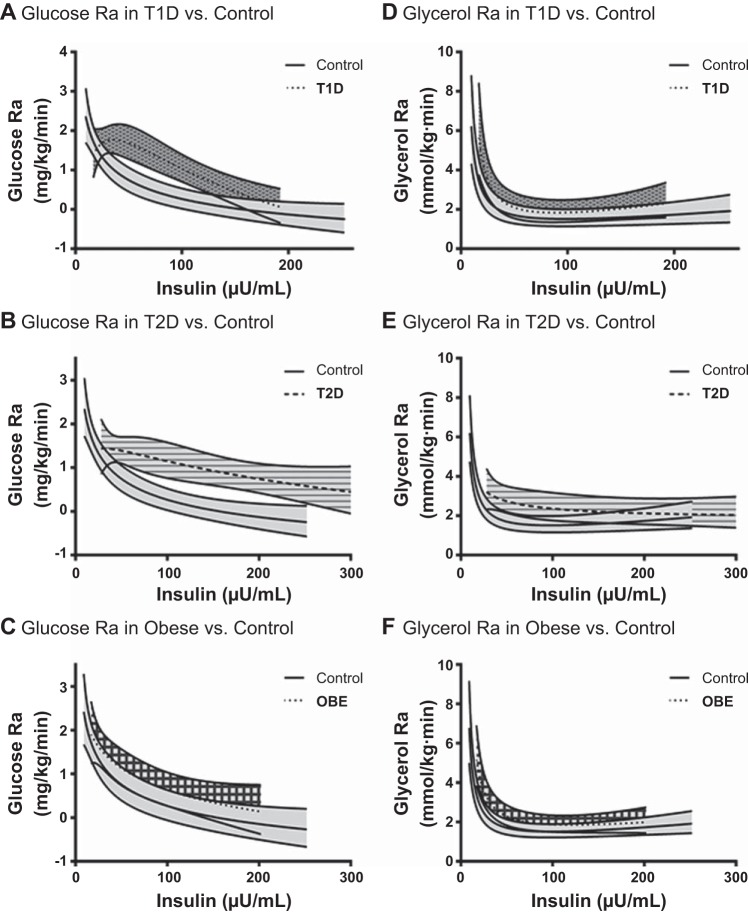
Figure 5 shows predicted R_a [and 95% confidence intervals (CIs)] vs. insulin derived from the MEM. Predicted glucose R_a was higher in T1D and T2D compared with either control group and did not reach zero in the diabetic participants. Glycerol R_a was also higher in T1D and T2D compared with both control groups. The curves for glycerol R_a in the T1D and control groups overlapped more than the curves for the T2D and control groups. Although the 95% CIs for glycerol R_a in the T2D and control groups overlap, the P value for the comparison was significant, resulting from the fact that the CIs in the figure were calculated using approximate standard errors obtained from the delta method. The curves do not extend beyond the values of insulin that were observed in our study, because extrapolation in polynomial models such as the quadratic can result in extreme behavior. Therefore, we would not recommend biological interpretation of the extrapolated curves. There was no difference in the glucose or glycerol R_a between the two nondiabetic groups.

Fig. 5.

Predicted rates of appearance with 95% confidence intervals for each participant group for both glucose and glycerol tracers are shown. OBE, obese.

DISCUSSION

There has been a recent increase in interest in describing the presence and potential clinical implications of IR individuals with T1D in addition to continued interest in IR in T2D (5). However, because of the inherent insulin requirements to achieve normoglycemia, assessments of IR in people with diabetes can be challenging, particularly when tissue-specific measurements are needed. We have described three separate methods to describe tissue-specific measurements of adipose and hepatic IR. The first method is to simply present the R_a during the specific insulin infusion rate (simple method), which excludes basal data and has been described previously (4, 19). The second method (STS) is to calculate the predicted R_a at a set insulin concentration based on the relationship between measured R_a and insulin concentrations at multiple time points, including the basal phase, and is independent of time. The final method (MEM) is a statistical method to compare the entirety of the insulin-R_a response curve, again including the basal phase. The use of these three methods allows for a more descriptive and comprehensive assessment of tissue-specific insulin sensitivity, especially when a basal R_a may not be accurate.

The determination of a basal R_a in participants with diabetes is problematic due to the intertwined role of insulin and glucose in suppressing endogenous production. Glucose concentration per se may have a direct effect of both peripheral glucose uptake and endogenous glucose release (8, 18, 26, 33). Higher glucose infusion rates have been shown to suppress glucose R_a in healthy controls during a somatostatin clamp with an artificially fixed low insulin and glucagon concentration; of noteis that these glucose infusions have resulted in serum blood glucose concentrations of 120–140 mg/dl (33). Alternatively, others have found that glucose has no role in suppressing endogenous R_a in participants with diabetes, and in fact a 50 mg/dl increase in serum glucose concentrations even nonsignificantly increased calculated glucose R_a (21, 30). We have found that hyperglycemia may have differential effects on hepatic glucose production relating to the individual's underlying glucose exposure; for example, controlled hyperglycemia in participants with elevated fasting glucose prior to a clamp did not suppress glucose R_a relative to nondiabetic groups with normal fasting glucose during hyperinsulinemia (25). The investigator must then make a choice to either give minimal additional insulin in the basal period to avoid suppressing lipolysis and hepatic glucose release and suffer from variable glucose concentrations or, alternatively, control the serum glucose concentrations at the expense of increased insulin concentrations, which may suppress lipolysis and hepatic glucose release.

There are several existing methods to quantify changes in endogenous glucose R_a that may not be ideal in volunteers with diabetes. The two most common methods include calculating a percent suppression of R_a from the basal rate of R_a or calculating the insulin concentration required to suppress 50% of the basal R_a (8). The IC₅₀ method attempts to correct for variable insulin concentrations, as the log of the insulin concentration is plotted against the insulin concentration for each phase, similar to our methods (4). However, rather than describing the line, the IC₅₀ utilizes the curve of the line to solve for the insulin concentration at 50% of the basal R_a. This final step, and reliance on the basal R_a, is thus why the IC₅₀ is not accurate when the basal R_a is not true. DeFronzo et al. (8) have also utilized a hepatic insulin resistance scale, which is the product of the basal glucose R_a and fasting insulin, but this approach does not describe dynamic changes measured with the multistep clamp (1).

The first approach to addressing the basal assessment problem we present in this article is the commonly used method of simply presenting an R_a during a specific insulin infusion rate, which we will term the “simple method” (4, 19). However, a single value is limited in its ability to describe a dynamic process. Therefore, we developed two additional approaches to take into account the multiple measurements of R_a and insulin collected during a clamp. Our second approach used a technique often referred to as the STS algorithm (7), in which individual estimates of model parameters are obtained and the parameter estimates are compared between groups. STS has been applied to a variety of settings in which repeated measurements on an individual are available, and for a time this was considered the traditional approach to analyze estimates of insulin sensitivity from the glucose minimal model (17). There are two major disadvantages to the STS approach, however: 1) the individual parameter estimates are treated as if they were known, although some are less precise than others (7), which can result in bias; and 2) there are situations in which individual parameter estimates cannot be obtained (e.g., missing data for a participant results in too few data points to perform nonlinear regression, or the regression algorithm gets stuck in a local minimum) (17). Therefore, we also applied a third approach based on MEM, which represents a population-based approach to making inferences about model parameters. MEM have been utilized previously in the glucose minimal model (10, 11, 17) as well as the disposition index (10, 11). MEMs are so named because they simultaneously allow inference about fixed effects characterizing the population and random effects that allow for individual departures from the population mean. MEMs utilize information from the population in the calculation of individual parameter estimates and account for uncertainty in the individual estimates.

The STS models produced predicted values for the nondiabetic controls and T1D participants with good agreement with the measured R_a at the clamp phase of interest, i.e., the “simple method (10 mU·m²·min⁻¹ for glycerol R_a and 16 mU·m²·min⁻¹ for glucose R_a), as shown in Table 1. However, the predicted glycerol R_a in the group with T2D was higher than that measured at the 10 mU·m²·min⁻¹ phase. Both the glycerol concentrations and basal R_a indicate that there is already partial suppression of lipolysis present during these phases. Predicted glucose R_a values from the MEM models were higher than those observed in lean controls and T1D, but the predicted glucose R_a values in T2D were close to those observed, as were the predicted glycerol R_a values in all four groups.

The STS model provides a way to utilize the entire curve over multiple insulin doses, including the basal phase, and yet has a single final output of the predicted R_a for the purposes of comparisons between groups with a simple t-test and can be included in correlational and regression analysis. Furthermore, the output of either glucose or glycerol R_a is an end point that is readily interpretable with traditional units of mg·kg⁻¹·min⁻¹ or mmol·kg⁻¹·min⁻¹. Similar to the STS models, the MEM compares the entire curve describing the relationship of R_a and insulin concentrations but has the added benefit of using information from all participants to make inference about the population mean trajectory and the within-individual covariance structure. MEM could be used to answer scientific questions of interest regarding the population mean or the individual participant trajectories and can be extended to include covariates of interest. The STS models are computationally simpler; however, they can produce biased results due to the fact that they do not take the uncertainty inherent in the individual parameter estimation into account (7). For the group comparisons performed here, the results of the MEM and STS models were concordant only in the case of the comparison of glycerol R_a in T1D and lean controls. Given the potential bias in the STS method, we prefer the MEM for analysis of data in cohorts of participants with diabetes. Of note, although some between-group comparisons were not significant in the data set to which we applied the three methods, this is not surprising given the small sample size. The purpose of this study was to demonstrate how these models could be used, not to make biological conclusions about the actual data for the different types of participants. Therefore, future work should include comparisons of the two methods utilizing simulated data sets where the truth is known to more fully understand the relative behavior of the methods and application of these methods to larger data sets to investigate the relationship between insulin and R_a in participants with diabetes.

In this example with a four-phase clamp, we found that the quadratic models were the best fit for our data. The exponential model is a natural choice for modeling these data, since exponential functions have asymptotic behavior that can describe the suppressive effects of insulin on R_a. However, in our small example data set, the exponential model did not result in a better fit to the data compared with the quadratic model. Furthermore, this model was the best for the four groups as a whole, whereas a linear fit may have been best for the T2D group individually. However, to compare the groups, they all must be fit with the same type of model so that the parameter values can be compared. We are recommending not that the quadratic model be applied in all situations but rather a general model-fitting approach. If there are fewer than four data points available for each participant, then a quadratic or exponential model will likely not be supported by the data, and a linear model will be required. This would be the case in a two-phase clamp, and for a three-phase clamp the data would need to be fit with multiple models to determine the best fit for the experiment.

In conclusion, we have presented new applications of existing statistical models that can be utilized to describe and compare dynamic changes in glucose and glycerol R_a when a true fasting endogenous basal R_a cannot be reliably determined. These methods are useful and necessary when studying individuals with diabetes, who require exogenous insulin overnight.

GRANTS

K. J. Nadeau was supported by Grants JDRF5-2008-291 and ADA 7-11-CD-08. M. Cree-Green was supported by Grant T32-DK-063687, a Pediatric Endocrine Society Fellowship grant, and Grant BIRCWH K12-HD-057022. This research was also supported by Adult CTRC National Institutes of Health (NIH) Grant M01-RR-00051, Pediatric CTRC NIH Grant 5-MO1-RR-00069, and NIH/NCRR Colorado CTSI Grant UL1-RR025780.

DISCLOSURES

The authors have nothing to disclose.

AUTHOR CONTRIBUTIONS

M.C.G., L.P., B.C.B, and K.J.N. conception and design of research; M.C.G., L.P., B.C.B., and K.J.N. performed experiments; M.C.G. and L.P. analyzed data; M.C.G., L.P., B.C.B., and K.J.N. interpreted results of experiments; M.C.G. and L.P. prepared figures; M.C.G. and L.P. drafted manuscript; M.C.G., L.P., B.C.B., and K.J.N. edited and revised manuscript; M.C.G., L.P., B.C.B., and K.J.N approved final version of manuscript.