Bolus arrival time and its effect on tissue characterization with dynamic contrast-enhanced magnetic resonance imaging

Abstract.

Matching the bolus arrival time (BAT) of the arterial input function (AIF) and tissue residue function (TRF) is necessary for accurate pharmacokinetic (PK) modeling of dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI). We investigated the sensitivity of volume transfer constant ($K^{\mathrm{trans}}$) and extravascular extracellular volume fraction ($v_{\mathrm{e}}$) to BAT and compared the results of four automatic BAT measurement methods in characterization of prostate and breast cancers. Variation in delay between AIF and TRF resulted in a monotonous change trend of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ values. The results of automatic BAT estimators for clinical data were all comparable except for one BAT estimation method. Our results indicate that inaccuracies in BAT measurement can lead to variability among DCE-MRI PK model parameters, diminish the quality of model fit, and produce fewer valid voxels in a region of interest. Although the selection of the BAT method did not affect the direction of change in the treatment assessment cohort, we suggest that BAT measurement methods must be used consistently in the course of longitudinal studies to control measurement variability.

1. Introduction

Microvasculature characteristics of the cancerous tissues, such as vascular permeability, cellularity, and metabolism, are actively being investigated as potential biomarkers for monitoring cancer progression and evaluating treatment response, especially in tumor tissues with rapid angiogenesis^1–4 primarily because of the earlier response time of these biomarkers to the treatment compared with that of the more routine standard of care metrics, such as monitoring tumor size changes. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is a minimally invasive imaging technique based on the hemodynamic response of the tissue to the intravenous injection of contrast agent (CA) that has the potential for microvasculature characterization of normal and cancerous tissues.⁵ Pharmacokinetic (PK) compartmental models, such as Tofts model (TM), are widely used for DCE-MRI data analysis to extract quantitative parameters relating to the tissue hemodynamics and vasculature, such as volume transfer constant ($K^{\mathrm{trans}}$) and the extravascular extracellular space (EES) fraction ($v_{\mathrm{e}}$).^6,7

One of the challenges in reliable and reproducible quantification from DCE-MRI is its well-recognized dependence on the acquisition and analysis approaches.⁸ Although the true microvasculature characteristics are independent of the imaging conditions (e.g., MRI scanner platform, data acquisition details, bolus dose), several studies suggest that accuracy and reproducibility of PK parameters are sensitive to the processing techniques.^8–13 The knowledge of CA concentration uptake in the arterial input function (AIF) is required in order to fit the PK mathematical models to the tissue residual function (TRF). The process of PK fitting requires bolus flight time delay correction, i.e., aligning the bolus arrival time (BAT) of the AIF and TRF curves. It was demonstrated that the error in estimation of the delay between AIF and TRF can have a large effect on the accuracy of parameter estimation.^14,15 With the exception of the methods that are not sensitive to the bolus arrival delay,^16,17 correction for such a delay is otherwise necessary.¹⁸ This correction can be done by adding the delay as a free parameter to the PK analysis optimization procedure at the expense of making the fitting process more complex.^19,20 There is evidence that PK models that have fewer parameters result in improved robustness and stability of the fit²¹ and that exclusion of BAT from the fitting problem reduces the model’s degrees of freedom and improves the accuracy of the estimates and the stability of the model.²² Alternatively, delay correction can be performed directly as a step preceding the PK analysis. In this paper, we focus on the latter class of optimization approaches where the delay correction is done prior to the PK modeling. Such approaches are commonly used in the quantitative analysis of DCE-MRI, as evident from numerous publications. Nevertheless, while direct optimization approaches are commonly used and it is well known based on simulations that accurate delay correction is critical for the accurate analysis, the effects of errors in delay correction have not been investigated in clinical data or digital phantoms.

Performed outside the optimization procedure, delay correction relies on the measurement of the BAT in AIF and TRF. Bolus delay correction can be performed manually by visually identifying the arrival of bolus, but in practice, this is feasible only for ROI-based analysis and may affect repeatability of the analysis. BAT measurement has been studied extensively in hemodynamic characterization of vessels,^23,24 but less so in a DCE-MRI PK modeling field. It should be noted that detection of BAT in TRF signals is more challenging than in arteries (e.g., AIF) due to the differences in the uptake profiles that depend on tissue properties and, in some cases, broad concentration time curves with slight slopes in washout time regions following onset of the enhancement. Several approaches for automatic estimation of BAT have been proposed.^25–29 Huisman et al.²⁵ developed a three-component model for prostate with BAT as a parameter estimated by fitting a curve that focuses on the most probable slope. In Ref. 26, ${\mathrm{BAT}}_{\mathrm{TRF}}$ was calculated using the concentration time curve of the entire region of interest (ROI) and measuring the BAT from the intersection of the lines joining a predetermined number of adjacent points and then using the same BAT for all of the voxels within the same ROI. Automatic detection of BAT, based on fitting piecewise linear functions to the concentration curve, has been proposed by Cheong et al.²⁷ with a two-segment linear model and by Singh et al.²⁹ with a three-piece linear model.

Studies have shown that inaccurate estimation of BAT can lead to uncertainty in the PK estimates.^20,30 Although the importance of accurate compensation for BAT has been recognized, there has not, to the best of our knowledge, been a systematic investigation of the sensitivity of the PK modeling to this parameter, or comparison of BAT estimation approaches in characterization of tissue microvasculature. In this study, we do not aim to introduce or improve approaches to BAT estimation or delay correction. Instead, we quantify the effects of variations in AIF delay correction on PK parameters and compare four previously published approaches for automatic estimation of BAT in DCE-MRI data: two regression-based piecewise linear modeling methods and two heuristic gradient-based methods. We investigated the effect of BAT on $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ and the $R^2$ quality of fit in TM. The experiments were conducted on both synthetic and clinical DCE-MRI data. The patient images were collected in men with diagnosed prostate cancer (PCa) and in women with diagnosed breast cancer (BCa). The DCE-MRI analysis software tools used in this study are open-source and publicly available for use by other groups and for facilitating reproducibility of our results.

2. Materials and Methods

The evaluation consisted of two main components. First, we investigated the sensitivity of the estimated TM parameters to the delay between AIF and TRF. Then we applied four automatic approaches for BAT estimation on clinical DCE-MRI images to evaluate their consistency and compared the model parameters and quality of the fit that resulted from each of the methods. Experiments were conducted on a DCE-MRI digital reference object (DRO) and on the clinical datasets obtained for PCa and BCa patients.

2.1. Dynamic Contrast-Enhanced Magnetic Resonance Imaging Data

2.1.1. Digital reference object

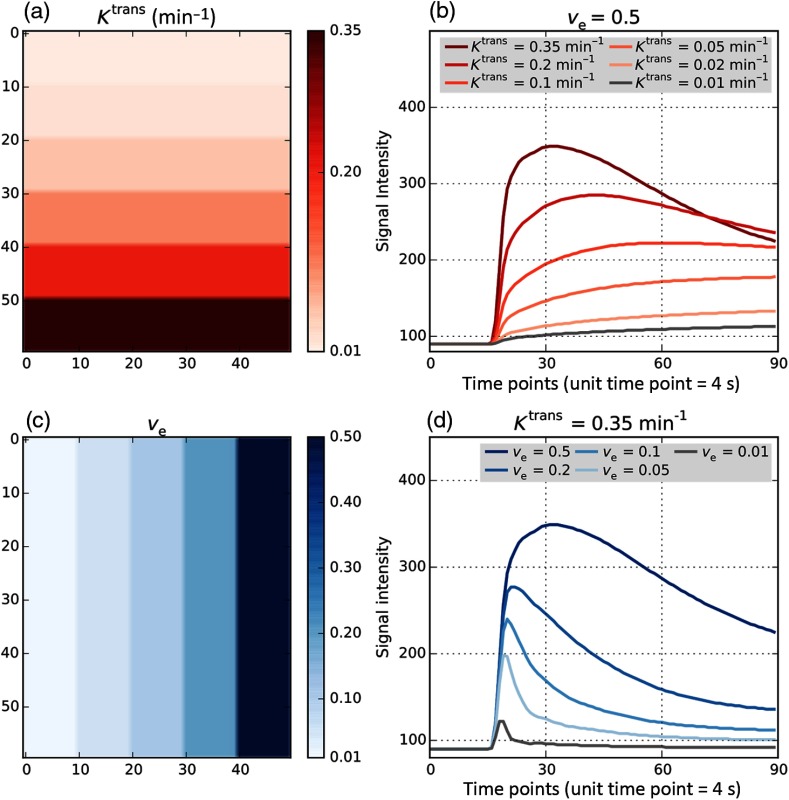
A simulated DCE-MRI phantom with known PK parameter values was used as a reference for testing the accuracy of PK modeling estimates. We used the DCE-MRI DRO version 8, developed by Quantitative Imaging Biomarker Alliance (QIBA) and Duke University of Medicine (Durham, North Carolina).³¹ The DRO phantom (QIBA_v8_Tofts_4s_0s) is a single slice image with 30 square patches covering different combinations of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ values, as shown in Fig. 1. Each pixel contains the signal intensity of the time course data generated using TM sampled with a 4 s temporal resolution, with a patch of $10\times 10\text{pixels}$ for each combination of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ parameters of TM. As illustrated in Fig. 1, the 30 combinations included six $K^{\mathrm{trans}}$ values (0.01, 0.02, 0.05, 0.1, 0.2, and $0.35{\min }^{-1}$) and five $v_{\mathrm{e}}$ values (0.01, 0.05, 0.1, 0.2, and 0.5). The DRO was created using the following parameters: flip angle 30 deg, repetition time $(\mathrm{TR})=5\mathrm{ms}$, the native (precontrast) value of $T_1$ ($T_{10}$) was assumed to be 1000 ms in tissue and 1440 ms in blood. The DRO simulates image acquisition for 360 s with the injection of bolus occurring after 1 min. For MR modeling of the contrast uptake, blood hematocrit was assumed to be 45% and the relaxivity of the gadolinium CA at 1.5 T was assumed to be $0.0045{\mathrm{mmol}}^{-1}{\mathrm{ms}}^{-1}$.³² The AIF ROI was included as a separate image patch in the same image volume.

Fig. 1.

QIBA DCE-MRI digital reference object (DRO) image. DRO v.8 consists of 30 $10\times 10\text{pixel}$ patches with different combinations of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$. Total time of imaging is 6 min, which results in 90 timepoints for the 4 s temporal resolution. (a) $K^{\mathrm{trans}}$ distribution over the phantom, increasing from top to bottom from 0.01 to $0.35{\min }^{-1}$. (b) Simulated MRI intensity signal time courses corresponding to the rightmost column of the DRO with fixed $v_{\mathrm{e}}=0.5$ and varying $K^{\mathrm{trans}}$ values 0.01, 0.02, 0.05, 0.1, 0.2, and $0.35{\min }^{-1}$. (c) $v_{\mathrm{e}}$ distribution over the DRO increasing from left to right. (d) MRI intensity signal time courses for the bottom row of the DRO with fixed $K^{\mathrm{trans}}=0.35{\min }^{-1}$ and $v_{\mathrm{e}}$ values 0.01, 0.05, 0.1, 0.2, and 0.5.

2.1.2. Prostate cancer

PCa MRI images were acquired through a HIPAA compliant study that was approved by the Institutional Review Board (IRB) at Brigham and Women’s Hospital, Boston, Massachusetts. Informed written consent was obtained from the patients participating in the study. MRI data of a total of nine patients with histologically confirmed PCa were collected and analyzed. MR images were acquired on a GE Signa HDx 3.0 T magnet (GE Healthcare, Waukesha, Wisconsin) using a combination of an eight-channel abdominal array and endorectal coil (Medrad, Pittsburgh, Pennsylvania). A set of multiparametric MR sequences, including $T_1$- and $T_2$-weighted imaging, diffusion weighted imaging, and DCE-MRI was performed for each patient.³³ The datasets were previously released in Ref. 13 and are available, by request, from the Quantitative Imaging Network QIN-PROSTATE collection^13,34 of The Cancer Imaging Archive (TCIA)³⁵ in Digital Imaging and Communications in Medicine (DICOM) format.

DCE-MRI images were acquired with a three-dimensional (3-D) spoiled gradient recalled (SPGR) sequence with $\mathrm{TR}/\mathrm{TE}/\alpha =3.6\mathrm{ms}/1.3\mathrm{ms}/15\mathrm{deg}$, $\mathrm{FOV}=26{\mathrm{cm}}^2$, covering the full gland with an image voxel size of $1\times 1\times 6{\mathrm{mm}}^3$. Temporal resolution for acquiring DCE MRI frames was $\sim 5\mathrm{s}$. Gadopentetate dimeglumine (Magnevist, Berlex Laboratories, Wayne, New Jersey) CA was injected intravenously using a syringe pump ($0.15\mathrm{mmol}/\mathrm{kg}$) at the rate of $3\mathrm{ml}/\mathrm{s}$ followed by 20 ml saline flush at the same rate. Imaging protocol included five baseline scans prior to the bolus injection. $T_1$-weighted images were acquired with an SPGR echo sequence with $\mathrm{TR}/\mathrm{TE}/\alpha =385\mathrm{ms}/6.2\mathrm{ms}/65\mathrm{deg}$ over a $16\text{-}{\mathrm{cm}}^2$ field of view (FOV). An abdominal radiologist with more than 10 years of experience interpreting prostate MRIs used the free and open-source software platform 3D Slicer software³⁶ to contour tumor region of interest (TROI) localization. ROI contouring was aided by the pathology report of the prostatectomy and/or biopsy specimen and concomitant MR findings for PCa. The AIF curve was acquired by contouring an ROI from the left femoral artery and averaging the concentration curves for the ROI voxels. The prostate gland was segmented manually on each slice of each image volume.

2.1.3. Breast cancer

Breast DCE-MRI data were acquired on patients ($N=10$) with locally advanced breast cancer, who received preoperative neoadjuvant chemotherapy (NACT) in an IRB approved, HIPPA compliant study at Oregon Health and Science University (OHSU), one of the QIN centers. DCE-MRI images were collected at the pre-NACT first visit (V1) and following the first cycle of the NACT second visit (V2). Breast MR images were acquired using a Siemens 3T system with a body coil transmitter and a four-channel bilateral phased array breast coil receiver. DCE-MRI acquisition parameters included 10-deg flip angle, $2.9/6.2\mathrm{ms}$ echo time/repetition time (TE/TR), a parallel imaging acceleration factor of two, 30 to 34 cm FOV, $320\times 320$ inplane matrix size, and 1.4-mm slice thickness. According to Ref. ³⁷, the total acquisition time was $\sim 10\min$ for 32 to 34 image volume sets of 112 to 120 slices, each with 18- to 20-s temporal resolution. The time of injection of CA (HP-DO3A) [ProHance] IV ($0.1\mathrm{mmol}/\mathrm{kg}$ at $2\mathrm{ml}/\mathrm{s}$) was set to start following acquisition of two baseline image volumes using a programmable power injector and followed by a 20-ml saline flush. A population-averaged AIF was provided for all of the 20 datasets. The AIF was generated by averaging AIF measured in a population cohort that was imaged with the same CA injection protocol (dose, injection rate, and injection site—antecubital vein).³⁷ The OHSU MRI datasets were accompanied by the breast TROIs on post-CA multislice images covering the enhancing tumor component. The imaging data are available publicly in the TCIA QIN breast DCE-MRI collection.³⁸ TROIs, annotations, and parameters that are important for DCE analysis can be accessed from the QIN DCE-MRI analysis challenge website.³⁹

2.2. Data Processing

2.2.1. Pharmacokinetic analysis

DCE-MRI images were processed using an inhouse prototype implementation of PK analysis software using Python 2.7⁴⁰ and SimpleITK.⁴¹ The PK analysis tool is publicly available at the Quantitative Image Informatics for Cancer Research (QIICR) website.⁴² PK modeling based on TM consists of two steps: (1) MR signal to concentration signal conversion and (2) fitting the concentration curve to the TM. $T_1$ can be measured from the spoiled gradient echo sequence [Eq. (1)] using the measured Signal $S$ in presence of Gd, relaxed signal ($S_0$) and the MRI sequence parameters TR and flip angle (θ). According to the MR model, $T_1$ is reduced in the presence of the concentration agent, which can be modeled by Eq. (2), where $T_{10}$ is the $T_1$ of the tissue before CA injection, and $r_1$ is the CA relaxivity.

$$S=S_0\frac{(1-e^{-\frac{TR}{T_1}})\sin \theta }{1-e^{-\frac{TR}{T_1}}\cos \theta },$$ (1)

$$\frac{1}{T_1}=\frac{1}{T_{10}}+r_{1}C.$$ (2)

TM models the flow of CA across the endothelium into the EES. In the second step, the concentration curve is fitted to the TM to find the model parameters transfer constant $K^{\mathrm{trans}}$, fractional volume of EES $v_{\mathrm{e}}$ [Eqs. (3) and (4)]. We chose the two-parameter model without explicit plasma volume fraction term because of the instability in PK analysis and model fitting at the temporal resolution of the clinical data ($>5\mathrm{s}$):

$$C_t(t)=K^{\mathrm{trans}}\underset{0}{\overset{t}{\int }}{C}_{\mathrm{p}}(\tau )e^{-\frac{K^{\mathrm{trans}}}{v_{\mathrm{e}}}(t-\tau )\mathrm{d}\tau },$$ (3)

$$C_{\mathrm{p}}=\frac{C_{\mathrm{b}}}{1-\mathrm{Hct}},$$ (4)

where $C_{\mathrm{b}}$ is the blood concentration, which can be determined from the blood signal using Eqs. (1) and (2). $C_{\mathrm{p}}$ is the plasma concentration, which can be measured from $C_{\mathrm{b}}$ and blood hematocrit (Hct). $C_{\mathrm{t}}$ or TRF is the concentration of CA at the tissue. Different approaches can be used for constructing AIF, such as direct measurement from a feeding artery or population-averaged function.⁴³

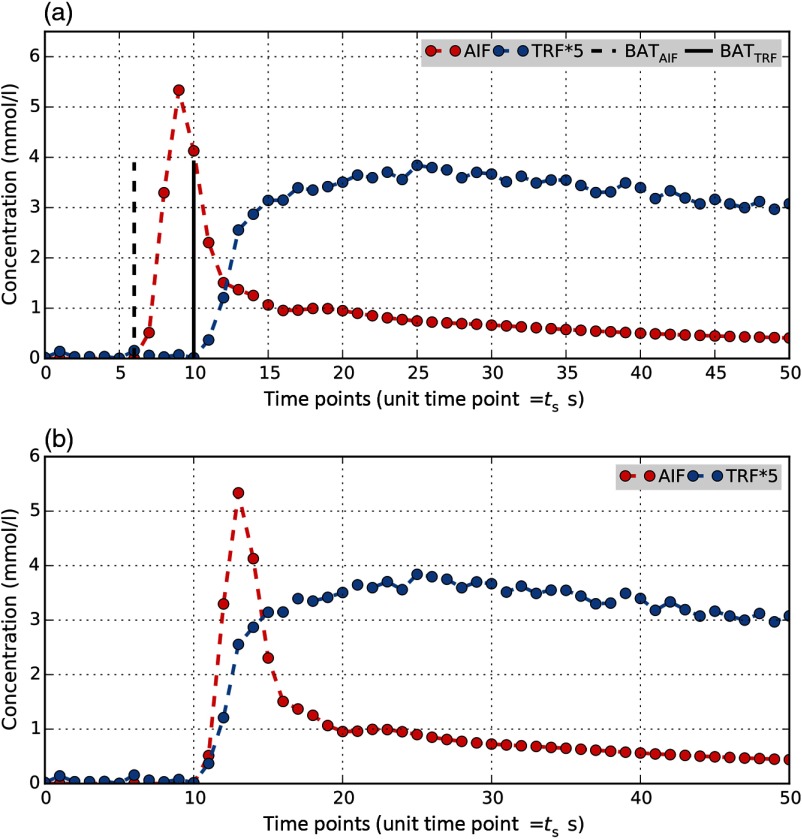
Prior to modeling, delay correction must be applied at every voxel to match the CA arrival times of AIF and TRF. This requires measurement of BAT for AIF (${\mathrm{BAT}}_{\mathrm{AIF}}$) and TRF (${\mathrm{BAT}}_{\mathrm{TRF}}$). The discrete AIF signal is shifted in time to match BATs and compensate for the delay. Figure 2 illustrates the process of delay correction for a selected TRF voxel and an AIF. In this study, we only considered BATs aligned with the temporal sampling of the data which means we shifted signals in steps equal to the sampling time of the DCE-MRI acquisition ($t_{\mathrm{s}}$).

Fig. 2.

Illustration of delay correction in a single voxel prior to PK analysis. A delay between arrival time of contrast agent in the AIF and TRF of an arbitrary voxel is visible in (a), which must be corrected before fitting the curves with TM. The DCE-MRI data has a sampling time $t_{\mathrm{s}}$ s. BAT for AIF (BAT_AIF) was measured as the timepoint 6 ($6t_{\mathrm{s}}\mathrm{s}$) and as timepoint 10 ($10t_{\mathrm{s}}\mathrm{s}$) for BAT_TRF. (b) Delay correction was performed by shifting the discrete AIF signal 4 timepoints forward in time to align with TRF. Zero padding was applied to the left of the AIF signal. The tail portion of the AIF was truncated to match the size of the shifted AIF and TRF.

The Levenberg–Marquardt least squares optimization algorithm was used⁴⁴ to fit the TRF concentration curves to the TM. We used the coefficient of determination, $R^2$, as the measure for assessing the quality of model fits. A perfect fit would results in an $R^2$ value of 1. Given the dataset with $n$ values $[y_1,\dots ,y_i,\dots ,y_n]$, each corresponding to a modeled value of $[{\hat{y}}_1,\dots ,{\hat{y}}_i,\dots ,{\hat{y}}_n]$ with mean $\stackrel{-}{y}$, $R^2$ is defined as

$$R^2=1-\frac{S{S}_{\mathrm{res}}}{S{S}_{\mathrm{tot}}};S{S}_{\mathrm{tot}}=\sum _i{(y_i-\overline{y})}^2;S{S}_{\mathrm{res}}=\sum _i{({\hat{y}}_i-y_i)}^2.$$ (5)

2.2.2. Automatic Bolus Arrival Time Estimation Methods

Our evaluation considered four approaches that operate on time courses of individual voxels of DCE-MRI images for automatic estimation of BAT. The first two methods use regression models to approximate the concentration time course with linear piecewise continuous functions. The linear–linear (LL) model proposed by Cheong et al.²⁷ approximates the curve with two linear components: baseline concentration and the contrast uptake region. The piecewise-linear (PL) model by Singh et al.²⁹ uses three linear components to approximate the baseline, uptake, and washout regions of the curve. In both methods, BAT is set as the point separating the first two linear components. The other two methods we considered are heuristics that attempt direct detection of BAT based on signal gradient changes. The first of these two methods is implemented in GE OncoQuant research software (GE Global Research, Niskayuna, New York) (further referred to as the OQ method); the second, the peak gradient (PG) method is available in the 3D Slicer PkModeling extension.⁴⁵

The regression-based methods, LL and PL, solve the least squares problem by iterating a range of timepoints and fitting the models to the concentration curves. The BAT is obtained from the fit that results in the smallest mean squared error. The LL model²⁷ is a two-piece linear model [Eq. (6)] in which ${\beta }_0$ is the precontrast concentration, ${\beta }_1$ is the slope of concentration curve during the bolus uptake, and $ϵ[i]$ is the error. BAT is estimated as the time $t[k]$ corresponding to the connecting point of the two straight lines. The search area for $t[k]$ in this method lies in the range of $[0,p]$ in which $p$ is the index of maximum value in the concentration time course array:

$$C(t[i])=\{\begin{array}{c}{\beta }_0+ϵ[i]t[i]\le t[k]\\ {\beta }_0+{\beta }_1(t[i]-t[k])+ϵ[i]t[i]>t[k]\end{array}.$$ (6)

The PL model²⁹ has two breaking points and is composed of three connecting straight lines [Eq. (7)]. The first separation point $t[k]$ is considered the BAT. Assuming that the number of points in the curve is $n$, in order to find the best fit, $k$ is iterated from 0 to $n-2$ and $j$ is iterated from $k$ to $n-1$, and for each set of $j$ and $k$, the best fit is calculated by minimization of the sum of squared errors. The values of $k$ and $j$ that make for the smallest sum of the squared errors are chosen as the optimum solution of curve fitting. The original method proposed by Singh et al.²⁹ uses a binary search method in the neighborhood of $t[k]$ to increase the precision of BAT estimation beyond the sampling interval. In this study, to be consistent with the other three methods, we only considered the integer values (BATs at sampling intervals):

$$C(t[i])=\{\begin{array}{c}{\beta }_{0}t[i]\le t[k]\\ {\beta }_0+{\beta }_1(t[i]-t[k])t[k]<t[i]\le t[j]\\ {\beta }_0+{\beta }_1(t[j]-t[k])+{\beta }_2(t[i]-t[j])t[i]>t[j]\end{array}.$$ (7)

The OQ method uses the gradient values of the signal, bolus concentration levels, and AIF information in determination of BAT. First, the concentration curve is transformed into the logarithmic domain so that BAT computation is more reliable due to noise suppression. Concentration values $<0.001\mathrm{mmol}/\mathrm{l}$ are set to zero. Then the peak timepoint for either the AIF curve (if available) or the global curve (the cuve corresponding to the average of all voxels in the image volume) is measured. This time index becomes the starting point of the backward search for BAT for a given curve. If the prior estimate from the global curve or AIF is not available, then the entire curve is considered for searching to the method determines where the curve changes direction from steep descent to gradual flat roll-off from the point of backward search point. For this, the curve derivative is calculated allowing for determining the transition from high to low region (i.e., the kick-point of BAT). This is done by detecting the zero crossings of the curve differential so that both the roll up and roll down will give zero crossings in the derivative of the curve. By looking at the direction in which the crossing occurs, an upcrossing (desired target) and a down crossing are distinguished from one another. Finally, an upcrossing point closest to the initial guess point is used in a final BAT after accounting for index shift during the differentiation process.

Finally, the PG method finds BAT by measuring the point with the highest gradient and searching backward until the signal is DC plus noise.

2.3. Experimental Design

2.3.1. Sensitivity of pharmokinetic parameters to the arrival delay

Underestimation or overestimation of ${\mathrm{BAT}}_{\mathrm{AIF}}$ and ${\mathrm{BAT}}_{\mathrm{TRF}}$ leads to inaccuracies in delay correction. We hypothesize that these inaccuracies can potentially lead to variability in the estimated PK modeling parameters, including $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$. To quantify such an effect, we designed simulations to investigate the effect of the delay between AIF and TRF on the estimation of PK parameters. These experiments utilized DCE-MRI image data of the DRO, and PCa and BCa patients’ datasets. For DRO and PCa images, AIF was determined directly from the image and ${\mathrm{BAT}}_{\mathrm{AIF}}$ was manually assigned. In BCa data, population averaged AIF and ${\mathrm{BAT}}_{\mathrm{AIF}}$ were provided. For each image dataset, ${\mathrm{BAT}}_{\mathrm{AIF}}$ remained constant while ${\mathrm{BAT}}_{\mathrm{TRF}}$ was shifted around ${\mathrm{BAT}}_{\mathrm{AIF}}$. Experiments were conducted by applying different delay times between AIF and TRF (${\mathrm{BAT}}_{\mathrm{AIF}}-{\mathrm{BAT}}_{\mathrm{TRF}}$) in the interval from $-3t_{\mathrm{s}}$ to $+3t_{\mathrm{s}}$ in $t_{\mathrm{s}}$ increments. Even though the negative delay (${\mathrm{BAT}}_{\mathrm{TRF}}<{\mathrm{BAT}}_{\mathrm{AIF}}$) is not physiologically possible, it was included in order to characterize the effect of ${\mathrm{BAT}}_{\mathrm{TRF}}$ underestimation or ${\mathrm{BAT}}_{\mathrm{AIF}}$ overestimation, which could occur in automatic estimation of BAT. For each of the seven experiments, PK parameters, $K^{\mathrm{trans}}$, $v_{\mathrm{e}}$, and goodness of fit $R^2$ were calculated. For DRO the percent errors relative to the ground truth were measured. It should be noted that the true value of the delay time is unknown for a given tissue since only integer shifts were considered if systematic errors as large as $\pm t_{\mathrm{s}}$ were present in the calculations.

2.3.2. Region of interest-based tissue characterization of patient data

In order to study the effect of BAT measurement choice and delay correction on the results of DCE-MRI tissue characterization with TM, we compared PK metrics acquired using four different approaches for BAT estimation: LL, PL, OQ, and PG, including ROI-based tissue characterization of 29 patient datasets (9 PCa patients and 10 BCa patients pre- and postNACT). For PCa DCE-MRI analysis, image-based patient specific AIFs were used. ${\mathrm{BAT}}_{\mathrm{AIF}}$ were determined automatically using the investigated BAT approaches applied to visual inspection of the patient specific AIF signal curves. In the BCa dataset, both models AIF and ${\mathrm{BAT}}_{\mathrm{AIF}}$ were supplied. Although the model AIF was population averaged, thus its BAT and number of points were defined based on the acquisition details for individual studies.

${\mathrm{BAT}}_{\mathrm{TRF}}$ was estimated for every tissue voxel inside the delineated ROIs using the four automatic methods described above. Following the delay correction, TRF was fitted to the TM and $K^{\mathrm{trans}}$, $v_{\mathrm{e}}$, and $R^2$ goodness of fit were measured four times with differently measured ${\mathrm{BAT}}_{\mathrm{TRF}}$ estimates. To ensure using only the acceptable fit in ROI-based analyses and measurements, we considered well-fitted voxels as those with estimates that met the following criteria:

$$0<K^{\mathrm{trans}}\le 5;0<v_{\mathrm{e}}\le 1;0.75\le R^2;{\mathrm{BAT}}_{\mathrm{AIF}}\le {\mathrm{BAT}}_{\mathrm{TRF}}<{\mathrm{BAT}}_{\mathrm{AIF}}+\tau .$$ (8)

In Eq. (8), $\tau$ is the upper threshold for acceptable BAT values. The last criterion puts an acceptable bound on the measured ${\mathrm{BAT}}_{\mathrm{TRF}}$ to remove the tissue voxels with underestimated ${\mathrm{BAT}}_{\mathrm{TRF}}$ values (those that are less than ${\mathrm{BAT}}_{\mathrm{AIF}}$, which is physiologically impossible) and discarding the overestimated outliers, which are lying outside the acceptable delay time.

3. Results

Results of ROI-based tissue characterization are presented separately for PCa and BCa patients in the following order: first, we evaluate the performance of each automatic BAT estimation method based on the percentage of voxels satisfying Eq. (8); next, we summarize the differences in the BAT measurements in the form of $\text{mean}\pm \text{standard deviation}$ for each patient study on the predefined ROIs; finally, we present the results of ROI-based tissue characterization in the form of PK parameters measured with different BAT estimators. For BCa patients, the effect of the BAT estimation approach on therapy response assessment is presented as $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ percentage changes were measured for each BAT estimation approach. Percent changes of parameter $P$ within the TROI between the two visits are defined as $(P_{\text{V}1}-P_{\mathrm{V}2})/P_{\mathrm{V}1}*100$.

3.1. Sensitivity of Pharmokinetic Parameters to the Arrival Delay

3.1.1. Digital reference object study

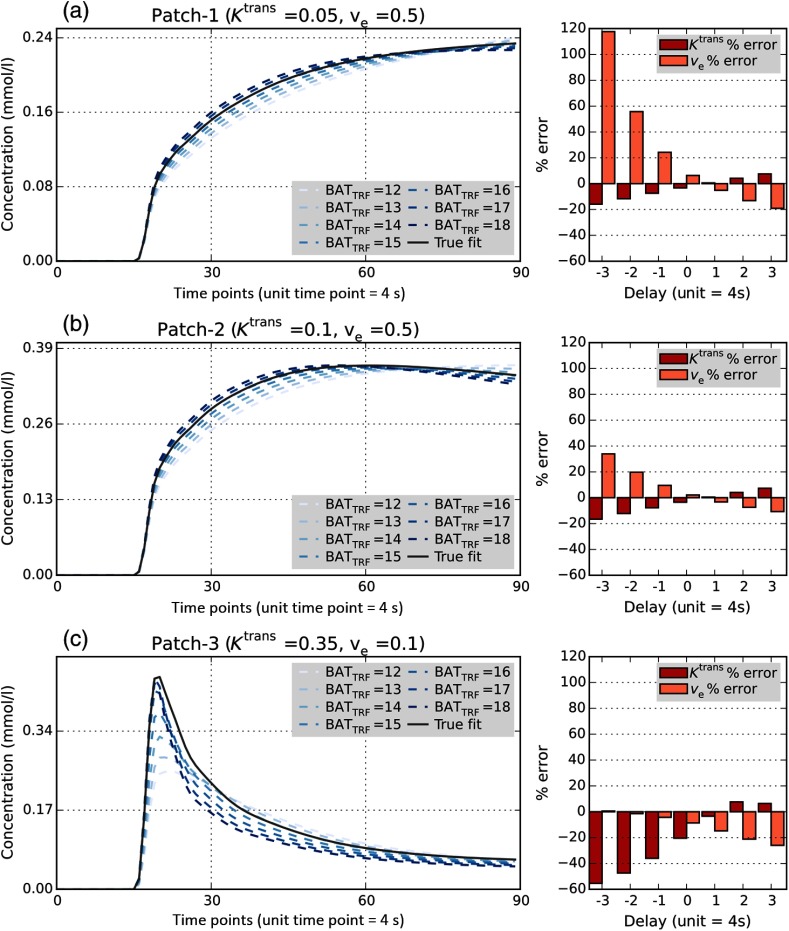
Figure 3 shows the results of PK modeling with ${\mathrm{BAT}}_{\mathrm{AIF}}=60\mathrm{s}$ and different ${\mathrm{BAT}}_{\mathrm{TRF}}$ values for the three representative parameter combinations (pixel patches) of the DRO. We observed that delay between AIF and TRF leads to the deviation of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ from their true values, which is reflected as perturbations in the fitted curves relative to the curve corresponding to the ground truth parameter values.

Fig. 3.

Sensitivity of DRO PK analysis to the arrival delay. Results of PK modeling with varying delays between AIF and TRF curves for three pixel patches of the DRO with known $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ combinations: results including fitted curves to the TM with different delay for (a) $K^{\mathrm{trans}}=0.05$, $v_{\mathrm{e}}=0.5$, (b) $K^{\mathrm{trans}}=0.1$, $v_{\mathrm{e}}=0.5$ and (c) $K^{\mathrm{trans}}=0.35$, $v_{\mathrm{e}}=0.1$. Gray solid line in concentration curves corresponds to the true value of the DRO at the specific voxel and the colored dotted curves are the fits calculated with delay values in the range of $[-3:+3]$. The bar plots on the right of the concentration curves illustrate variations in $K^{\mathrm{trans}}$ percent error and $v_{\mathrm{e}}$ percent error among the 7 values of delay.

We observed that change in the approximate prescribed location of ${\mathrm{BAT}}_{\mathrm{TRF}}$ in either direction leads to increasing error in the estimated values of the PK parameters. Goodness of the model fit, as measured by $R^2$, also diminishes with the deviation of the ${\mathrm{BAT}}_{\mathrm{TRF}}$ from the expected value that corresponds to the start of the contrast uptake at the phantom “tissue” pixels (see Fig. 4).

Fig. 4.

AIF and TRF curves in vicinity of arrival time and $R^2$ variations in response to delay changes. (a) Concentration curves around bolus arrival for the DRO AIF (red dotted line) and the corresponding TRF curves (solid lines) for the three selected patches in Fig. 3. BAT_AIF timepoint was measured as 16 by LL method and as 15 by the other three methods. ${\mathrm{BAT}}_{\mathrm{TRF}}$ timepoint was set to 12, 13, 14, 15, 16, 17, and 18 in separate experiments to simulate delays in the range of $-3$ to $+3$ timepoints. (b) $R^2$ of the model fits, corresponding to different ${\mathrm{BAT}}_{\mathrm{TRF}}$ timepoints for selected patches; goodness of fit is dramatically reduced when the prescribed BAT value deviates significantly from the true ${\mathrm{BAT}}_{\mathrm{TRF}}$.

We conducted a set of tests similar to the phantom experiments, investigating the effect of delay between AIF and TRF on patient data PK modeling. Unlike in the phantom experiments, we could not evaluate percent error due to the lack of ground truth, but could observe general trends of change and the goodness of fit. Figures 5 and 6 illustrate the results of delay variations on PCa patient number #2 and BCa patient number #16 on visit 1, respectively. We observed that, consistent with the DRO experiments, there is a trend for monotonous increase/decrease of the values of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$, while the $R^2$ peaks at a patient specific timepoint. This pattern was also observed in the DRO sensitivity test (Fig. 4). For PCa patient #2, $R^2$ boxplots have a peak mean showing the best goodness of fit at $\text{delay}=+2t_{\mathrm{s}}$ (Fig. 5). Figure 5(a) shows that the visibly apparent uptake of the contrast in the tissue ROI occurs at approximately timepoint 9, which would require a delay correction of 2 time steps. The same pattern of change in $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ due to ${\mathrm{BAT}}_{\mathrm{TRF}}$ deviation was observed in the BCa patient in Fig. 6 and the other PCa and BCa patients used in our analysis.

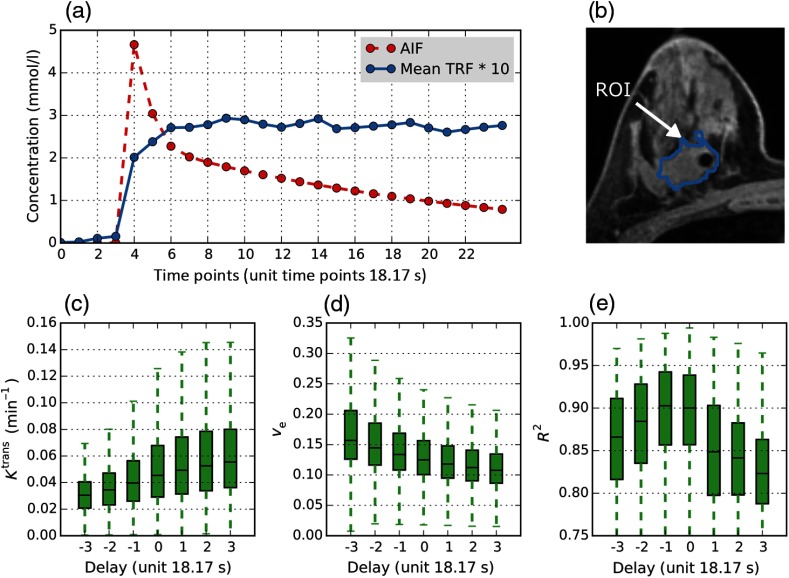
Fig. 5.

Sensitivity of PCa DCE-MRI PK analysis to the bolus arrival delay. PK parameters’ sensitivity within the TROI to the choice of ${\mathrm{BAT}}_{\mathrm{TRF}}$ for PCa patient #2. BAT_AIF was measured automatically from the AIF concentration curve and the BAT_AIF index was set manually in seven consecutive tests. (a) Illustration of the measured AIF from image (red dotted line), the mean (blue solid line) ± maximum/minimum (light blue solid area) for 104 TRF concentration curves in the tumor tissue ROI. (b) 2-D axial image showing delineated ROIs for AIF and tissue ROI on DCE-MRI image (the tissue ROI continues in two adjacent axial planes). (c–e) boxplots of (c) $K^{\mathrm{trans}}$, (d) $v_{\mathrm{e}}$ and (e) $R^2$ at different delay timepoints (timepoint unit: DCE-MRI $\text{sampling rate}=4.4\mathrm{s}$).

Fig. 6.

Sensitivity of BCa DCE-MRI PK analysis to delay between AIF and TRF: patient #16, visit1. ${\mathrm{BAT}}_{\mathrm{A}\mathrm{I}\mathrm{F}}$ was provided as population averaged: (a) Illustration of concentration curves for population averaged AIF (red dotted line), the mean (blue solid line) for 5147 TRF curves in the TROI. (b) 2-D axial image showing delineated tissue ROI on DCE-MRI image. (c–e) boxplots of (c) $K^{\mathrm{trans}}$, (d) $v_{\mathrm{e}}$, and (e) $R^2$ at different BAT_TRF timepoints with the same BAT_AIF (timepoint unit: DCE-MRI $\text{sampling rate}=18.17\mathrm{s}$).

3.2. Region of Interest-Based Tissue Characterization of Patient Data

3.2.1. Prostate cancer

For every DCE-MRI volume of the nine PCa patients, AIF was defined as the mean signal over the femoral artery ROI defined manually. The volumes of segmented regions (tumor and whole gland) for each patient case are shown in Table 1.

Table 1.

The volumes of two sets of ROI delineated for prostate cancer patients’ DCE-MRI datasets: tumor and whole prostate gland ($N=9$).

Patient	#01	#02	#10	#11	#12	#14	#15	#17	#23
Tumor volume (cc)	1.38	0.64	1.18	0.45	0.36	0.35	0.22	0.53	0.65
Gland volume (cc)	93.93	92.51	55.27	74.52	111.62	73.53	83.82	42.28	84.65

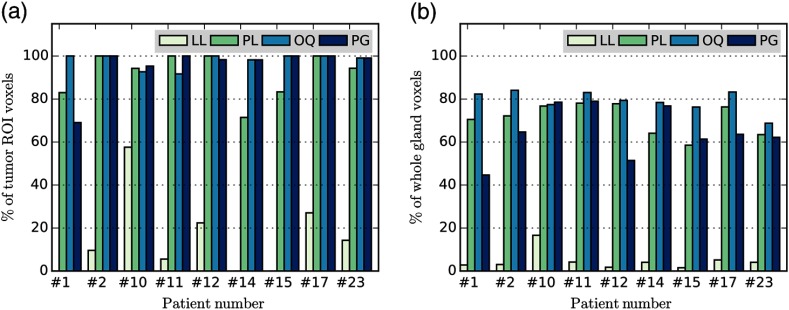
${\mathrm{BAT}}_{\mathrm{AIF}}$ for each case was calculated using LL, PL, OQ, and PG methods. For all of the patients, there was agreement between the results of ${\mathrm{BAT}}_{\mathrm{AIF}}$ among all LL, PL, OQ, and PG methods except for three for patients: #10, #11, and #23 using OQ (Table 2). ${\mathrm{BAT}}_{\mathrm{TRF}}$ was measured for every voxel on the whole gland and TROIs using the four automatic methods under evaluation. TM was fitted to the TRF concentration curve and PK metrics were measured using the ${\mathrm{BAT}}_{\mathrm{TRF}}$ values estimated by each of the methods for every voxel inside the ROI. Valid voxels for tissue characterization were identified by determining those voxels that satisfy the constraints in Eq. (8) with $\tau ={\mathrm{BAT}}_{\mathrm{AIF}}+20t_{\mathrm{s}}$. Percentage of the voxels satisfying the validity criteria for the tumor and the whole gland ROIs are summarized in Fig. 7. On average, the use of individual BAT estimation methods resulted in the following $\text{mean}\pm \text{standard deviation}$ percentage of well-fitted voxels in the TROI: LL: $15.17\pm 17.66\%$, PL: $91.81\pm 9.69\%$, OQ: $97.96\pm 3.16\%$, PG: $95.54\pm 9.47\%$. For the whole gland, the numbers were lower: LL: $4.81\pm 4.33\%$, PL: $70.85\pm 6.82\%$, OQ: $79.20\pm 4.55\%$, PG: $64.67\pm 11.24\%$. In summary, there is a significant variability in the number of valid voxels in comparing different BAT approaches. The LL method appears to result in the largest number of failed voxels that either had unrealistic values of BAT or estimated PK parameters, or led to exceedingly poor model fits.

Table 2.

Values of BAT_AIF and BAT_TRF timepoints for the PCa patient data sets. The BAT_TRF values were averaged for the suspected tumor and whole gland ROIs using different BAT estimation methods. The results of BAT_AIF measurements were identical for LL, PL, and PG methods for all the patients. The results of BAT_TRF timepoints include only valid voxels satisfying Eq. (8) conditions with $\tau ={\mathrm{BAT}}_{\mathrm{AIF}}+20\mathrm{ts}$.

Patient	#01	#02	#10	#11	#12	#14	#15	#17	#23
${\mathrm{BAT}}_{\mathrm{AIF}}$ time point
LL,PL, and PG	6	7	6	6	7	6	6	6	6
OQ	6	7	5	5	7	6	6	6	7
Tumor ROI ${\mathrm{BAT}}_{\mathrm{TRF}}$ time points ($\text{mean}\pm \text{standard deviation}$)
LL	N/A	$7.50\pm 0.53$	$6.56\pm 0.55$	$6.00\pm 0.00$	$7.77\pm 0.60$	N/A	N/A	$6.13\pm 0.34$	$7.00\pm 0.00$
PL	$7.05\pm 0.80$	$8.35\pm 0.64$	$7.07\pm 0.34$	$6.74\pm 0.47$	$8.93\pm 0.26$	$6.40\pm 0.50$	$6.23\pm 0.43$	$7.12\pm 0.32$	$7.74\pm 0.44$
OQ	$7.46\pm 0.91$	$8.15\pm 0.44$	$6.77\pm 0.42$	$6.24\pm 0.47$	$8.12\pm 0.77$	$7.04\pm 0.69$	$6.56\pm 0.61$	$6.84\pm 0.37$	$7.17\pm 0.38$
PG	$8.18\pm 1.48$	$8.46\pm 0.52$	$7.01\pm 0.17$	$6.60\pm 0.52$	$8.68\pm 0.54$	$7.25\pm 0.58$	$6.86\pm 0.68$	$6.94\pm 0.24$	$7.79\pm 0.41$
Whole gland ROI ${\mathrm{BAT}}_{\mathrm{TRF}}$ time points ($\text{mean}\pm \text{standard deviation}$)
LL	$7.29\pm 2.24$	$8.30\pm 1.64$	$7.09\pm 0.94$	$6.76\pm 1.01$	$9.53\pm 3.33$	$7.02\pm 2.56$	$7.77\pm 2.56$	$6.99\pm 2.12$	$7.60\pm 1.18$
PL	$7.57\pm 1.50$	$8.71\pm 1.52$	$7.54\pm 0.98$	$6.94\pm 1.13$	$9.25\pm 1.80$	$6.84\pm 1.26$	$7.26\pm 1.32$	$7.40\pm 1.43$	$7.94\pm 1.31$
OQ	$7.60\pm 1.74$	$8.93\pm 1.93$	$7.25\pm 1.04$	$6.96\pm 1.52$	$9.45\pm 2.77$	$7.12\pm 1.19$	$7.50\pm 1.91$	$7.29\pm 1.14$	$8.28\pm 2.22$
PG	$9.32\pm 4.45$	$9.59\pm 2.71$	$7.89\pm 2.10$	$7.69\pm 2.53$	$11.29\pm 4.66$	$7.96\pm 2.70$	$8.48\pm 3.26$	$8.06\pm 3.11$	$9.11\pm 3.60$

Fig. 7.

Percent of voxels with good fit and feasible ${\mathrm{BAT}}_{\mathrm{TRF}}$ range in PCa patients. PK modeling was performed voxel-wise using ${\mathrm{BAT}}_{\mathrm{TRF}}$ measured by four methods: LL, PL, OQ and PG. The plots show the voxels in which the fit satisfied Eq. (8) with $\tau ={\mathrm{BAT}}_{\text{AIF}}+20\mathrm{ts}$ for two groups of ROIs: (a) tumor and (b) whole prostate gland. LL appeared to result in the largest number of the voxels that did not meet the validity criteria, whereas considerable variability in the number of such voxels was observed among the remaining BAT estimation methods. Note that in the case of patients 1, 14, and 15, the LL method did not result in valid voxels within the TROI.

Different methods for the TROIs are summarized in Table 2 (the reported values are only for valid voxels). In summary, the variation in the estimated ${\mathrm{BAT}}_{\mathrm{TRF}}$ values appears to be rather small in relation to the temporal resolution of the acquisition (difference between means is less than 2 s).

Figure 8 shows an illustrative example of the ${\mathrm{BAT}}_{\mathrm{TRF}}$ variability among different methods for PCa patient #11.

Fig. 8.

Illustration of variations in ${\mathrm{BAT}}_{\mathrm{TRF}}$ in four BAT estimation methods. Axial plane views of one of the slices of the ${\mathrm{BAT}}_{\mathrm{TRF}}$ timepoint map measured using four automatic estimation methods for PCa patient # 11: measured over TROI: (a) LL, (b) PL, (c) OQ, (d) PG and whole prostate gland (e) LL, (f) PL, (g) OQ, and (h) PG. The green solid line shows the boundaries of delineated ROI. The transparent parts of the BAT_TRF map inside the ROI are voxels that did not meet Eq. (8) conditions. (i,j,k,l) Histograms of the number of voxels assigned a specific ${\mathrm{BAT}}_{\mathrm{TRF}}$ timepoint over the whole prostate gland ROI in four methods. It should be noted that for patient #11, BAT_AIF was measured as timepoint 6; hence, the voxels below timepoint 6 are discarded in analysis.

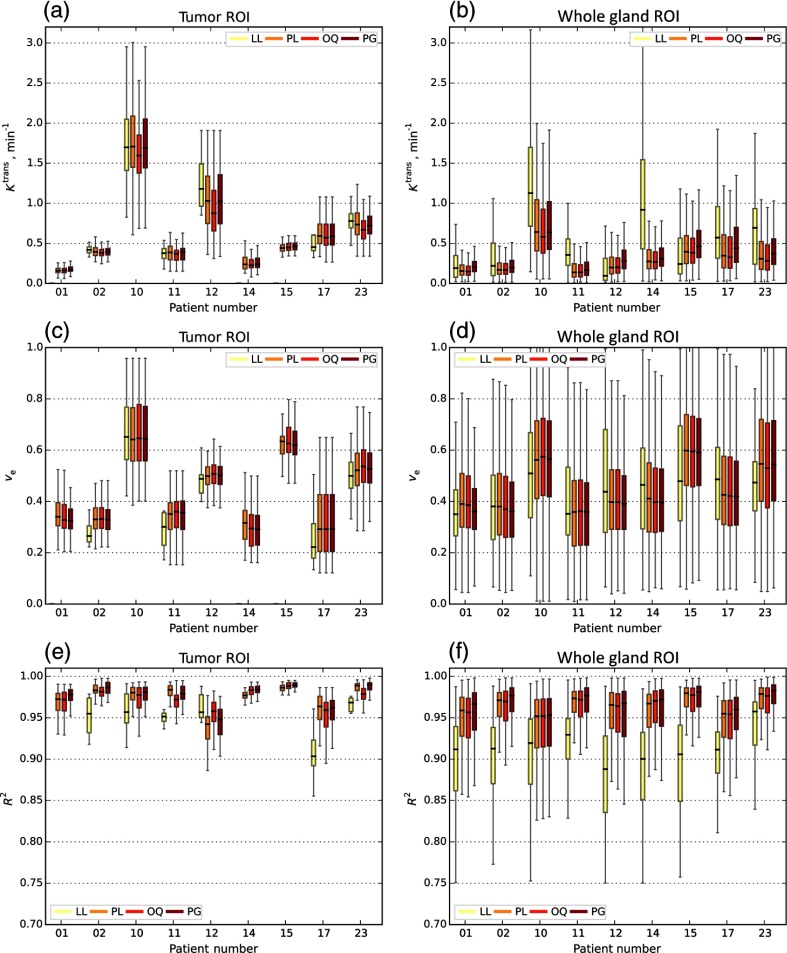
Finally, given the set of valid voxels for each of the BAT estimation approaches, we measured the effect of the BAT method on the estimated parameter values and the goodness of fit. Figure 9 shows the boxplots of $K^{\mathrm{trans}}$, $v_{\mathrm{e}}$, and $R^2$ for each of the patients over the valid voxels of the tumor and prostate whole gland ROIs with ${\mathrm{BAT}}_{\mathrm{TRF}}$ calculated by LL, PL, OQ, and PG methods. Except for the LL method, the results were rather consistent over the TROI. At the same time, significant heterogeneity in the estimated BAT values was observed when considering the whole gland.

Fig. 9.

$K^{\mathrm{trans}}$, $v_{\mathrm{e}}$, and $R^2$ boxplots of nine PCa patients calculated by different BAT estimation methods. The boxplots including (a,b) $K^{\mathrm{trans}}$, (c,d) $v_{\mathrm{e}}$, and (e,f) $R^2$ measured on two different ROIs using four automatic methods: LL, PL, OQ, and PG. Plots corresponds to the delineated tumor tissue (a,c,e) and whole gland (b,d,f) ROIs. BAT estimators were compared in modeling the tissue’s physiological characteristics with the TM. Only voxels satisfying Eq. (8) with $\tau ={\mathrm{BAT}}_{\mathrm{AIF}}+20t_{\mathrm{s}}$ are included. For TROIs of patients #1, #14 and #15, there are no LL plots as none of the voxels met Eq. (8) criteria.

3.2.2. Breast cancer

In BCa patients, AIF was prescribed as population averaged AIF; therefore, calculation of ${\mathrm{BAT}}_{\mathrm{AIF}}$ was not required. ${\mathrm{BAT}}_{\mathrm{TRF}}$ was measured using four automatic methods on the segmented TROIs for both visits of 10 BCa patients. The volumes of segmented TROI for each patient in both visits are shown in Table 3.

Table 3.

Breast cancer tumor segmentations ROI volumes for visit 1 (V1) and visit 2 (V2).

Patient	#1	#5	#6	#8	#10	#12	#13	#14	#15	#16
V1 tumor volume (cc)	20.05	3.39	1.17	66.46	5.82	12.1	1.48	5.6	4.77	7.21
V2 tumor volume (cc)	14.13	1.56	2.18	39.94	2.79	4.27	0.95	3.77	14.81	2.32

Using the estimated ${\mathrm{BAT}}_{\mathrm{TRF}}$ of the four methods, TM fitting was performed on the TROIs of the DCE-MRI volumes and PK metrics were calculated for each visit. Since AIF was not patient specific, we could not use the ${\mathrm{BAT}}_{\mathrm{AIF}}$ as a lower bound to eliminate voxels with incorrect ${\mathrm{BAT}}_{\mathrm{TRF}}$ times [the last criterion of Eq. (8)]. However, according to the acquisition information, we knew that the first bolus injection occurred after taking two baseline images, so we chose the lower bound for valid BAT values as the second time point and the upper bound as the seventh time point: (${2t}_{\mathrm{s}}\le {\mathrm{BAT}}_{\mathrm{TRF}}\le {7t}_{\mathrm{s}}$). Figure 10 shows the percent of valid voxels identified using the modified constraints for both visits. On average, the use of individual BAT estimation methods resulted in the following $\text{mean}\pm \mathrm{SD}$ number of valid voxels for visit 1. ROIs were LL: $31.61\pm 9.73\%$, PL: $72.70\pm 12.11\%$, OQ: $77.02\pm 11.55\%$, PG: $73.32\pm 12.47\%$; ROIs for visit 2 were LL: $13.88\pm 9.96\%$, PL: $54.03\pm 14.16\%$, OQ: $60.53\pm 12.62\%$, PG: $50.00\pm 20.40\%$.

Fig. 10.

Percent of valid voxels in the TROI that satisfy the conditions in Eq. (8) with ${2t}_{\mathrm{s}}\le {\mathrm{BAT}}_{\mathrm{TRF}}\le {7t}_{\mathrm{s}}$ for BCa patients. (a) Visit 1 and (b) visit 2. Similar to the results observed for the prostate data, LL leads to the largest number of invalid voxels. However, the differences among the rest of the BAT methods considered were more prominent than those of the PCa dataset.

Summary statistics for the estimated BAT corresponding to valid voxels are shown in Table 4.

Table 4.

Values of mean BAT_TRF (obtained with LL, PL, OQ, and PG methods) for BCa cases for two visits. The results of BATTRF include only valid voxels [meeting Eq. (8) constraints with ${2t}_{\mathrm{s}}\le {\mathrm{BAT}}_{\mathrm{TRF}}\le {7t}_{\mathrm{s}}$].

${\mathrm{BAT}}_{\mathrm{TRF}}$ time points ($\text{mean}\pm \text{standard deviation}$)
Patient	#1	#5	#6	#8	#10	#12	#13	#14	#15	#16
Visit 1
LL	$1.66\pm 0.66$	$1.90\pm 0.57$	$1.97\pm 0.75$	$1.85\pm 0.87$	$1.73\pm 0.70$	$1.67\pm 0.70$	$1.57\pm 0.55$	$1.93\pm 0.70$	$1.62\pm 0.59$	$1.84\pm 0.80$
PL	$2.00\pm 0.55$	$2.34\pm 0.63$	$2.44\pm 0.67$	$2.44\pm 0.78$	$2.53\pm 0.70$	$2.47\pm 0.71$	$2.31\pm 0.65$	$2.49\pm 0.66$	$2.31\pm 0.71$	$2.61\pm 0.58$
OQ	$2.04\pm 0.24$	$2.75\pm 0.43$	$2.52\pm 0.53$	$2.51\pm 0.56$	$2.58\pm 0.65$	$2.65\pm 0.62$	$2.69\pm 0.46$	$2.67\pm 0.51$	$2.66\pm 0.48$	$2.59\pm 0.50$
PG	$2.07\pm 0.38$	$2.98\pm 0.16$	$2.82\pm 0.46$	$2.76\pm 0.50$	$2.88\pm 0.69$	$2.95\pm 0.72$	$2.94\pm 0.27$	$2.96\pm 0.31$	$2.91\pm 0.29$	$2.93\pm 0.37$
Visit 2
LL	$1.63\pm 0.49$	$1.56\pm 1.01$	$1.87\pm 1.14$	$2.08\pm 1.17$	$1.56\pm 0.77$	$1.83\pm 0.77$	$1.47\pm 0.71$	$1.79\pm 0.78$	$2.95\pm 1.69$	$1.31\pm 0.47$
PL	$1.90\pm 0.45$	$1.87\pm 0.51$	$2.56\pm 1.20$	$2.44\pm 1.02$	$2.38\pm 0.79$	$2.37\pm 1.02$	$2.30\pm 0.65$	$2.31\pm 0.79$	$2.53\pm 1.15$	$2.00\pm 0.63$
OQ	$2.01\pm 0.14$	$2.00\pm 0.72$	$2.57\pm 0.64$	$2.42\pm 0.63$	$2.54\pm 0.53$	$2.40\pm 0.60$	$2.57\pm 0.50$	$2.32\pm 0.54$	$2.63\pm 0.80$	$2.23\pm 0.66$
PG	$2.05\pm 0.35$	$2.49\pm 0.50$	$2.86\pm 0.86$	$2.63\pm 0.76$	$2.84\pm 0.46$	$2.70\pm 0.88$	$2.84\pm 0.38$	$2.59\pm 0.64$	$2.83\pm 0.85$	$2.59\pm 0.52$

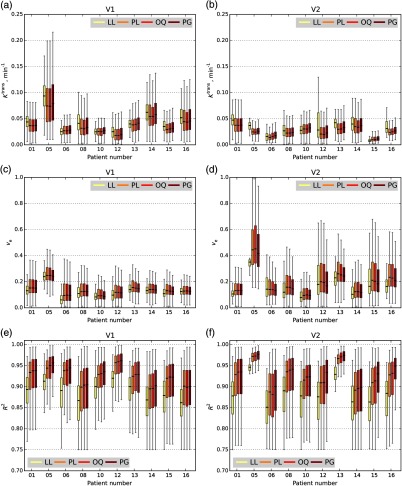
Larger variability across the methods than that in the prostate dataset was observed. We also noted increased variability of the estimated BAT across voxels for a given method, especially for PG.

Again as with the PCa analysis, only valid voxels for each of the BAT estimation methods were included to measure $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ values and the goodness of fit. Figure 11 depicts the boxplots of $K^{\mathrm{trans}}$, $v_{\mathrm{e}}$, and $R^2$ for each of the patients over the valid voxels for visit 1 and visit 2 TROIs using ${\mathrm{BAT}}_{\mathrm{TRF}}$ calculated by LL, PL, OQ, and PG methods. When we apply the validity constraints in Eq. (8) to the data, we observed relatively good agreement for $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ (Fig. 11). However, the selection of the BAT detection technique had a very strong effect on the number of voxels that met the validity constraints, as shown in Fig. 10. For example, for visit 2 BCa patient #6, the percentage of valid voxels was %8.61, %35.46, %49.06, and %30.46 for LL, PL, OQ, and PG, respectively.

Fig. 11.

Boxplots of $K^{\mathrm{trans}}$, $v_{\mathrm{e}}$, and $R^2$ of 10 BCa patients calculated by different BAT methods. The boxplots, including (a,b) $K^{\mathrm{trans}}$, (c,d) $v_{\mathrm{e}}$, and (e,f) $R^2$ measured on two different visits; ROIs using four automatic BAT estimation methods. ROIs corresponds to the visit 1 (a,c,e) and visit 2 (b,d,f). Four different automatic BAT estimation methods (LL, PL, OQ, and PG) are compared in modeling the tissue with TM. Only voxels satisfying Eq. (8) with ${2t}_{\mathrm{s}}\le {\mathrm{BAT}}_{\mathrm{TRF}}\le {7t}_{\mathrm{s}}$ are included.

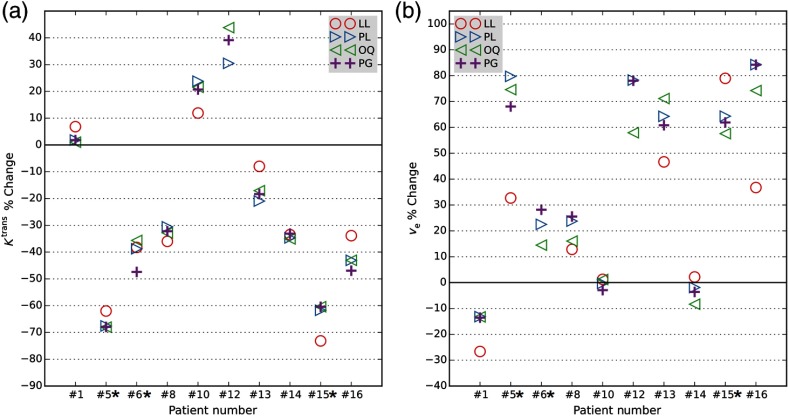
$K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ percent changes between visit 1 and visit 2 were measured on valid voxels as a potential surrogate marker of tumor treatment response using different estimated ${\mathrm{BAT}}_{\mathrm{TRF}}$ values (Fig. 12). Based on the tumor resection pathology reviews and pre-NACT biopsy specimens, patients #5, #6, and #15 achieved pathology-based complete response (pCR) following NACT. The remaining patients were non-pCR.

Fig. 12.

Comparison, in breast cancer patients, of (a) $K^{\mathrm{trans}}$ and (b) $v_{\mathrm{e}}$ percentage changes acquired with different BAT estimation methods. Scatter plot of percentage change of the mean tumor $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ from visit 1 (pre-NACT) to visit 2 (following the first cycle of NACT) in 10 BCa patients based on each of four automatic BAT estimation methods (LL, PL, OQ, and PG). Percent changes measured by including only those voxels in the ROI that satisfy Eq. (8) with ${2t}_{\mathrm{s}}\le {\mathrm{BAT}}_{\mathrm{TRF}}\le {7t}_{\mathrm{s}}$. Tumor resection pathology reviews indicated that only patients #5, #6, and #15 achieved pCR following NACT (marked with asterisks). $K^{\mathrm{trans}}$ percent change for patient 12 with method LL was $+102.72\%$ (not shown).

4. Discussion

It was our goal to investigate the effect of AIF delay correction and BAT measurement on PK parameters. To achieve this goal, we conducted phantom studies and evaluated the effect of the BAT estimation method on the results of PCa and BCa tissue characterization. Our results indicate that $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ of a single TRF curve can vary quite dramatically due to even minor perturbations of the ${\mathrm{BAT}}_{\mathrm{TRF}}$. However, the extent of variations in PK estimates depends on tissue characteristics, CA uptake profile, DCE-MRI acquisition parameters, and the sampling time in particular. The DRO phantom variations in delay between AIF and TRF resulted in errors in estimation of $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$, with deviations from the true values. The extent of error depends on the $K^{\mathrm{trans}}$ and $v_{\mathrm{e}}$ combination (tissue properties). The results show a systematic relationship between the BAT estimation error and the values of the PK parameters: underestimation of ${\mathrm{BAT}}_{\mathrm{TRF}}$ results in under-rating of $K^{\mathrm{trans}}$ and over-rating of $v_{\mathrm{e}}$; overestimation of ${\mathrm{BAT}}_{\mathrm{TRF}}$ results in over-rating of $K^{\mathrm{trans}}$ and underrating of $v_{\mathrm{e}}$. This pattern was observed in DRO, PCa, and BCa datasets. Although the exact BAT was not known for either DRO or patient data, we observed better quality of model fit when the estimated BAT was in agreement with the visually observed bolus arrival.

Automatic BAT detection must be accurate, reliable, and reproducible in order to be adopted in clinical practice. We compared four automatic BAT estimation algorithms on a clinical dataset of PCa and BCa DCE-MRI. With the exception of the LL method, which resulted in a low number of valid voxels, the other three methods—PL, OQ, and PG—yielded an acceptable performance but with differences in the percentage of valid voxels. However, due to the small size of TROIs and homogeneity of the uptake across the ROI voxels, the results of the mean of ${\mathrm{BAT}}_{\mathrm{TRF}}$ were comparable across the three PL, OQ, and PG methods. However, for the whole prostate gland ROIs, variation in number of valid voxels and mean of ${\mathrm{BAT}}_{\mathrm{TRF}}$ was higher than TROIs. For all of the PCa and BCa patients, the results of the OQ method were superior in terms of the number of well-fitted voxels. The finding of poorer fit within the whole gland may be related to the known heterogeneity of perfusion within the entire prostate gland compared to the relative homogeneity within the peripheral zone (where these tumors were located). It has been shown that peak enhancement from baseline significantly differs in glandular-ductal tissue versus stromal/low ductal tissues.⁴⁶

For BCa patients, despite the variations in ${\mathrm{BAT}}_{\mathrm{TRF}}$ measurements by different estimators, in all patients there was agreement by all four methods in the direction of $K^{\mathrm{trans}}$ percent change in the ROI statistics between the baseline and followup longitudinal DCE-MRI images. There were a small number of valid voxels for visit 2 (after NACT). It is possible that this may be due to overall decrease in vascularity with treatment, decreasing the availability of valid voxels.

In this study, we distinguished ${\mathrm{BAT}}_{\mathrm{TRF}}$ from ${\mathrm{BAT}}_{\mathrm{AIF}}$ due to their differences in characteristics and contributions to the PK analysis results. Due to the high uptake slope of the AIF curve proximate to the time instance of the CA injection, it is usually less challenging for the automatic methods to detect ${\mathrm{BAT}}_{\mathrm{AIF}}$ compared to detection of ${\mathrm{BAT}}_{\mathrm{TRF}}$ in which cases in which CA uptake is performed more slowly. However, it should be emphasized that accurate measurement of ${\mathrm{BAT}}_{\mathrm{AIF}}$ is critical as it has a direct effect on measurement of PK metrics.

Except for the two segment linear model (LL), the results of the three other automatic BAT estimation methods were comparable to each other. Although the PL method showed good accuracy, it was significantly slower than the other methods due to the large search region for two parameters for each voxel concentration curve. The PG method tended to fall in local maxima, which could lead to overestimation of BAT values. Applying upper threshold for removing the overestimated outliers from the analysis made the ROI averaged results in the same range as the other methods. One strong advantage of the OQ compared to the other methods was the use of AIF prior knowledge in detection of ${\mathrm{BAT}}_{\mathrm{AIF}}$. A practical complication of using the OQ approach is that no open source implementation of this method is available. We used implementation of this method from a commercial prototype software. Although the LL method was not intended for use in TRF, nevertheless, after keeping the valid voxels, it gives comparable results in BCa dataset.

The adopted voxel analysis methodology of keeping only well-fitted curves in the ROI-based PK analysis showed improvements in reproducibility of the PK estimates in the four methods. Voxels with lack of contrast uptake (e.g., necrotic cells) were, after applying the criteria, also filtered out of the analysis. It is, therefore, possible that some voxels were classified as invalid due to poor fits that were caused by issues unrelated to ${\mathrm{BAT}}_{\mathrm{TRF}}$ methodology. We recognize that there are a multitude of factors that can affect TM, as investigated by Gill et al.⁴⁷

The study had limitations. Only BAT timepoints that were aligned with temporal sampling of the data were used, which will introduce errors as large as $\pm \text{half of the sampling time}$. Only four automatic methods for estimation of BAT were compared. Indeed, more accurate methods of BAT estimation may lead to more accurately estimated PK parameters. The true value of the BAT was unknown, so there was no gold standard to assess the accuracy of the methods.

There are numerous sources that can lead to inaccuracies in estimating PK parameters. Our goal was to focus on one specific parameter. The point of this manuscript was to quantify inaccuracies resulted from independent incorrect BAT estimation, which is used subsequently to estimate PK parameter. It was not our goal to improve accuracy of PK modeling by attempting to reduce various sources of inaccuracies. Therefore, the other parts of our implementation are intentionally kept fixed and follow the methodology commonly implemented in other tools. In previous works,^13,43,48 we have also systematically quantified some of the other important considerations such as the choice of AIF and intrinsic $T_1$ value of the tissue.

In this study, we did not include the plasma volume fraction term (${\nu }_{\mathrm{p}}$) in our PK model. The rationale for using TM without ${\nu }_{\mathrm{p}}$ is that the model is widely accepted and used in the community as a practical solution. Both TM and the extended Tofts model (ETM)⁷ are standard tools for analysis of DCE-MRI images. A recent article surveying and comparing the DCE MRI quantitative analysis tools used by the participants of the NCI QIN³⁷ showed that majority of the software tools used implemented the two parameters TM. TM is also the model suggested by the DCE MRI quantification profile developed by the QIBA of the Radiological Society of North America.⁴⁹

We believe the considerations above justify the use of the standard TM as the benchmark for evaluating the effect of BAT methods. Since ETM models account for plasma fraction in the voxel, BAT delay correction is likely to have an even bigger impact in ETM models, but this exploration is outside the scope of this study.

In conclusion, we observed that BAT choice and AIF delay correction can significantly affect characterization of tissue microvasculature using TM. Depending on the choice of the BAT technique, the majority of the tumor voxels may be considered invalid or unsuitable for analysis due to either biologically unrealistic BAT value (less than the BAT of the AIF), biologically unrealistic values of the estimated model parameters, or poor fit of the model. In the situations where temporal resolution is large and no significant variation in bolus arrival delay is expected across the ROI, constant BAT can be prescribed manually. However, in the cases where per-voxel estimation of BAT is required, we show that the choice of certain BAT approaches may lead to inability of the TM to characterize the majority of voxels within the region or may not cover the areas of tumor that are of particular interest.

The findings of this study can be used to motivate novel PK analysis and BAT search strategies. As an example, one strategy could be to search over a range of delay corrections to identify the one that improves $R^2$ and the number of valid voxels. Another approach could be to perform BAT estimation that expects the neighboring voxels to have similar BAT—all of the methods we investigated in this study operate independently on individual voxels.

We expect that this study will contribute to improved reproducibility of DCE MRI analysis by making the researchers aware of the effect of the BAT detection method on the result and motivate future development of robust and improved BAT detection techniques.

Biographies

Alireza Mehrtash is a research associate in the Radiology Department at Brigham and Women's Hospital, Harvard Medical School. He received his BS and MS in electrical engineering from Ferdowsi University of Mashhad, Iran. He also studied medical imaging at KTH Royal Institute of Technology, Stockholm, Sweden. He is currently a PhD candicate in electrical and computer engineering (ECE) at the University of British Columbia.

Sandeep N. Gupta is the manager of the Biomedical Image Analysis Lab at GE Global Research, leading advanced image analysis algorithm development for quantification of biomedical imaging data. His expertise is in quantitative image analysis, multiparametric and multidimensional image analysis and processing, and image based biomarkers. He has developed several algorithms and tools for quantification of medical imaging data, and published more than 30 peer-reviewed journal papers, 75 scientific abstracts, and has 7 patents issued.

Dattesh Shanbhag is a senior engineer at Medical Image Analysis Laboratory, GE Global Research, Bangalore. He completed his PhD in biomedical engineering at the University of Virginia, USA. His research focus at GE is on development of MRI analysis algorithms for improved quantification. He has played a key role in development of GenIQ, an application for processing of DCE-MRI data, and published over 20 articles in peer-reviewed journals and conferences and has 5 patents issued.

James V. Miller is a principal scientist in the Clinical Systems and Signal Processing organization at GE Global Research, where he develops methods and systems to detect and measure disease in support of clinical decision making. He is also active in open source medical imaging platforms, including the Insight Toolkit (ITK) and the 3D slicer.

Tina Kapur is the executive director of image guided therapy in the Department of Radiology at Brigham and Women's Hospital and Harvard Medical School. She has numerous publications in medical image segmentation and is the holder of several issued U.S. and international patents in the field of surgical navigation. She received her PhD in electrical engineering and computer science from Massachusetts Institute of Technology in 1999.

Fiona M. Fennessy is an associate professor of radiology at Harvard Medical School. She has significant clinical expertise in imaging in oncology with particular emphasis on MR imaging of prostate cancer and gynecological malignancies. She is the fellowship program director of the Cancer Imaging Program (CIP) at Dana Farber Cancer Institute. She is also principal investigator on the NIH R25 CA089017 Multidisciplinary Training in Image Guided Therapy award.

Ron Kikinis is a professor of radiology, part-time, at Harvard Medical School, as well as the founding director of the Surgical Planning Laboratory and the Robert Greenes distinguished director of biomedical informatics, in the Department of Radiology at Brigham and Women's Hospital. He is also the director of Fraunhofer MEVIS and an honorary professor of medical image computing at the University of Bremen, Germany.

Andriy Fedorov completed his undergraduate studies at the Ternopol Institute of Computer Information Technologies, Ukraine. He received his MS in 2003 and PhD in 2009 in computer science from the College of William and Mary. He is currently an assistant professor of radiology at Harvard Medical School and a research fellow at Brigham and Women’s Hospital. His research interests are at the intersection of imaging informatics, open source software, medical image computing, reproducible science, and cancer research.