A genomic selection component analysis characterizes migration-selection balance within a hybrid Mimulus population

Abstract

The genetic differentiation of populations in response to local selection pressures has long been studied by evolutionary biologists, but key details about the process remain obscure. How rapidly can local adaptation evolve, how extensive is the process across the genome, and how strong are the opposing forces of natural selection and gene flow? Here, we combine direct measurement of survival and reproduction with whole-genome genotyping of a plant species (Mimulus guttatus) that has recently invaded a novel habitat (the Quarry population). We renovate the classic selection component method to accommodate genomic data and observe selection at SNPs throughout the genome. SNPs showing viability selection in Quarry exhibit elevated divergence from neighboring populations relative to neutral SNPs. We also find that non-significant SNPs exhibit a subtle, but still significant, change in allele frequency towards neighboring populations, a predicted effect of gene flow. Given that the Quarry population is most probably only 30–40 generations old, the alleles conferring local advantage are almost certainly older than the population itself. Thus, local adaptation owes to the recruitment of standing genetic variation.

INTRODUCTION

Nearly all species exhibit spatial genetic structure. When dispersal is limited and/or local selection is sufficiently strong, local populations become genetically distinctive across the geographic range of species (Clausen et al. 1940). In these circumstances, migrant individuals will introduce divergent haplotypes into a population, a phenomenon often dubbed ‘admixture.’ Admixture is a central focus of study of anthropology where genetic data is used to infer the history of human dispersal (Elhaik et al. 2014) and also in the search for genes causing disease (Patterson et al. 2004). For evolutionary biologists, admixed or hybrid populations illustrate the tension between the diversifying forces of natural selection and genetic drift and the homogenizing force of gene flow (Barton and Hewitt 1989).

Gene flow of maladaptive alleles into a population can generate substantial variance in fitness. The genomic consequences of migration-selection balance depend on the basis and extent of local adaptation. If local adaptation owes to few loci, we expect minimal gene flow at those loci and at closely linked polymorphisms, but effective homogenization elsewhere in the genome (Wu 2001; Nosil et al. 2009; Feder et al. 2012; Renaut et al. 2013). If many loci are targets of local selection, then gene flow may be reduced across the entire genome, although this depends on the strength of selection (Barton and Bengtsson 1986). Even if many loci contribute to local advantage, introgression will occur unless the fitness of F₁ hybrids is very low. Many studies of migration-selection balance have attempted to infer the process from static genetic patterns, mainly allele frequency divergence among populations as a function of genomic position (Bierne et al. 2013). However, mechanisms are most incisively identified by directly measuring the processes that cause and maintain divergence.

As antecedent to direct study, we renovate the classic selection component technique (Christiansen and Frydenberg 1973) to accommodate genomic data (Andolfatto et al. 2011; Hohenlohe et al. 2012). A selection component analysis (SCA) combines the essential features of the field observational study of selection (Lande and Arnold 1983) with a mating system estimation experiment (Ritland and Jain 1981). As in the former, one surveys a collection of individual through their lifetimes, scoring survival and measuring reproductive success. In a phenotypic selection study, fitness components are correlated to trait values. Here, we predict fitness components from individual genotypes at Single Nucleotide Polymorphisms (SNPs) across the genome. The second component of the data is typical of mating system estimation: From each female that successfully reproduces, we genotype a random set of progeny. Combined with genotype information from the known parent (the mother), we can probabilistically infer the paternal contribution to the offspring generation. This enables tests of selection through differential male success without having to measure the reproductive success of individual males, which is often impossible.

After developing the relevant theory, we apply SCA to field data collected from the Quarry population of Mimulus guttatus. Over a single complete generation, we measure allele frequency change at SNPs dispersed across the genome. Viability selection is estimated from genetic differences between plants that progress to flower and those that do not. The second signal in the data – the difference in allele frequency between flowering plants (parents) and the population composed of their progeny – can owe to numerous evolutionary forces. Fecundity and/or sexual selection within the parental generation can effect a change within the population of successful gametes, as can gametic selection through either male or female function. There is also opportunity for selection between zygote and genotyped offspring (e.g. seed abortion or differential germination). Finally, gene flow via immigrant pollen can change allele frequency, a consequence that is likely to be subtle at any one locus but important genome-wide.

The Quarry population (Oregon, U.S.A.) was chosen for study as ecologically and genetic divergent population of Mimulus guttatus. The population occupies a rock quarry that was initiated in the 1960s, but fell into disuse in the early 1980s. The population of annual plants occupying the basin is thus likely about 30–40 generations old, yet is clearly differentiated in morphology and phenology. Most populations in this area, including the Iron Mountain (IM) and Browder Ridge (BR) populations that we contrast to Quarry, are ‘fast-progressors.’ Plants have a limited time in which to bolt (after snow clears from the location), mature and flower, before the area dries completely and all plants die of desiccation (often only 8–10 weeks). In most years at IM and BR, surviving plants can produce only a single flower before desiccating (Mojica et al. 2012). The water supplied to Quarry sustains over a longer time interval, effectively lengthening the growing season. As a consequence, Quarry plants are substantially larger as adults and produce more flowers than do neighboring populations.

The phenotypic divergence of Quarry suggests local adaptation. Supporting this hypothesis, the genomic SCA reveals allele frequency change consistent with conflicting effects of selection and gene flow. To interpret the direction of allele frequency change, we conducted pooled population sampling of Quarry, IM, and BR with subsequent sequencing of each sample (Pool-Seq (Schlotterer et al. 2014)). With these data, we compare estimates of selection within Quarry to the observed divergence in allele frequency between local M. guttatus populations at the same SNPs. The viability selection evident at hundreds of SNPs within Quarry is usually increasing differentiation from IM and BR. Estimates of allele frequencies in the pollen pool from the SCA indicate a genome-wide ‘pull’ of Quarry allele frequencies toward those of neighboring populations, consistent with an effect of gene flow. While local adaptation is known to be prevalent in nature, these data provide a dynamic, genome-wide view of the process.

THEORY

The SCA, as described by Christiansen and Frydenberg (1973), is a likelihood based technique to measure life-stage specific episodes of natural selection. Depending on the particular sampling scheme, the method estimates and distinguishes viability selection (the differential survival of zygotes to adulthood), sexual selection (differential mating success), fecundity selection (differential offspring production by reproductive individuals), and gametic selection (segregation distortion in heterozygotes when producing successful gametes). The relevant data is a random samples of genotypes from each of several different population cohorts such as adult males, adult females that fail to reproduce, adult females that succesfully reproduce, and the offspring of these successful females. Given certain conditions, the counts of genotypes in each cohort can be expressed as multinomial probabilities with the relevant parameters contingent on the presence or absence of each selective process. Assuming a selective process to be absent reduces the number of parameters forming a ‘sub-set model’ that is naturally evaluated by likelihood ratio tests.

Here, we derive likelihoods suitable for a SCA of genomic data. Genomic data adds an additional layer of uncertainty in that individual genotypes are estimated but not known. Christiansen and Frydenberg 1973 assumed genotypes are estimated without error and were thus able to pool across individuals within each cohort (e.g. reproductive females) and derive probabilities for the resultant counts. With uncertain genotype calls, it is necessary to retain the family structure of the data and consider parents and offspring (within families) jointly. The exact nature of uncertainty and hence the appropriate model depends on the genotyping method. Chip-based genotyping methods (Tang et al. 1999) may require a different treatment than the RADseq markers we consider in this study. In the latter case, the data for an individual at a polymorphic SNP is a finite set of sequence reads, with each read scored as R if it matches the reference genome or A (Alternate), if not. After accounting for various sources of error, the read counts for an individual yield a likelihood for each possible underlying genotype (RR, RA, or AA for a diploid locus). These likelihoods, denoted L_RR, L_RA, and L_AA in the equations below, are the inputs to a genomic SCA.

SCA are contingent on how a population is sampled (Christiansen and Frydenberg 1973). Here, we consider a monoecious population subject to structured sampling. The parental portion of the data consists of n_S individuals that survive to reproduce (in our case, successfully progress to flowering) and n_D individuals that die before reproducing (plants that fail to flower). If based on a random sample of the entire population, n_S /(n_S + n_D) estimates ω, the mean viability.However, it is often advantageous to sample in such a way to enrich the less abundant type. In many species, only a small fraction of zygotes survive to reproduce and a random sample will thus be dominated by inviables. This limits power to detect differences in genotype frequencies between viable and inviable (because estimation error associated with the smaller group will obscure differences) and yields few individuals to subsequently test for selection through differential reproductive success. With structured sampling, the investigator determines n_F and n_NF, but then additional information is required to estimate ω (see below). The second component of the data is a sample of genotypes from the progeny of reproductive individuals. Since the population is monoecious, individuals that survive can reproduce through both male and female function. However, it is typically only possible to directly assign offspring to the female parent.

Likelihoods

We here derive likelihoods for a diploid SNP with two alleles, R and A. As in mating system estimation models (Ritland and Jain 1981; Koelling et al. 2012), the log-likelihood (ln L) is a simple sum across families:

$$\mathrm{l}\mathrm{n}L=\sum _{i=1}^{n_D}\mathrm{l}\mathrm{n}(\mathrm{P}\mathrm{r}ob[U_i])+\sum _{j=1}^{n_S}\mathrm{l}\mathrm{n}(\mathrm{P}\mathrm{r}ob[U_j,u_{jk}])$$ (1)

where U_i is the genomic data for the i’th dead individual, U_j is the data for the j’th survivor, u_jk is the data for the k’th offspring of that parent j (u_jk is a series of data sets with k ranging from 1 to nj, the number of genotyped offspring in the family), and Pr[*] denotes a probability statement. Parents and offspring are considered jointly in the latter term, because with uncertain calls, the relative likelihoods of the possible parental genotypes are at least potentially informed by the genotype data of progeny.

For the D individuals, families consist of a single individual:

$$\mathrm{P}\mathrm{r}ob[U_i]={\mathrm{X}}_{\mathrm{R}\mathrm{R}}{\mathrm{L}}_{\mathrm{R}\mathrm{R}[\mathrm{i}]}+{\mathrm{X}}_{\mathrm{R}\mathrm{A}}{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{i}]}+{\mathrm{X}}_{\mathrm{A}\mathrm{A}}{\mathrm{L}}_{\mathrm{A}\mathrm{A}[\mathrm{i}]}$$ (2)

where L_RR[i] is the likelihood of the data if the individual has genotype RR and X_RR is the frequency of RR among D individuals. The second and third terms contain the corresponding terms for RA and AA genotypes. Here, the L terms are implied by the sequence data while the X are model parameters with the constraint that X_RR = 1 - X_RA - X_AA. For S families,

$$\mathrm{P}\mathrm{r}ob[U_j,u_{jk}]=Y_{\mathrm{R}\mathrm{R}}{\mathrm{L}}_{\mathrm{R}\mathrm{R}[\mathrm{j}]}\text{Prob}[u_{jk}|\mathrm{R}\mathrm{R}]+Y_{\mathrm{R}\mathrm{A}}{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j}]}\text{Prob}[u_{jk}|\mathrm{R}\mathrm{A}]+Y_{\mathrm{A}\mathrm{A}}{\mathrm{L}}_{\mathrm{A}\mathrm{A}[\mathrm{j}]}\text{Prob}[u_{jk}|\mathrm{A}\mathrm{A}]$$ (3)

where Y_g is the frequency of genotype g among survivors. Pr[u_jk|MG] is the probability of obtaining the observed offspring data given maternal genotype MG.

We now assume that the population is outcrossing (see DISCUSSION), but allow multiple sires per maternal family. We also assume discrete, non-overlapping generations. The offspring conditional likelihoods, Pr[u_jk |MG], depend on how many different sires fathered the collection of offspring in u_jk. For the n_jz full-siblings within one sub-family of mother j,

$$\text{Prob}[u_{jk}|\mathrm{R}\mathrm{R}]=\prod _{k=1}^{n_{jz}}({\mathrm{Z}}_{\mathrm{R}\mathrm{R}}{\mathrm{L}}_{\mathrm{R}\mathrm{R}[\mathrm{j},\mathrm{k}]}+{\mathrm{Z}}_{\mathrm{R}\mathrm{A}}({\mathrm{L}}_{\mathrm{R}\mathrm{R}[\mathrm{j},\mathrm{k}]}+{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]})/2+{\mathrm{Z}}_{\mathrm{A}\mathrm{A}}{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]})\text{Prob}[u_{jk}|\mathrm{R}\mathrm{A}]=\prod _{k=1}^{n_{jz}}({\mathrm{Z}}_{\mathrm{R}\mathrm{R}}({\mathrm{L}}_{\mathrm{R}\mathrm{R}[\mathrm{j},\mathrm{k}]}+{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]})/2+{\mathrm{Z}}_{\mathrm{R}\mathrm{A}}({\mathrm{L}}_{\mathrm{R}\mathrm{R}[\mathrm{j},\mathrm{k}]}+2{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]}+{\mathrm{L}}_{\mathrm{A}\mathrm{A}[\mathrm{j},\mathrm{k}]})/4+{\mathrm{Z}}_{\mathrm{A}\mathrm{A}}({\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]}+{\mathrm{L}}_{\mathrm{A}\mathrm{A}[\mathrm{j},\mathrm{k}]})/2)\text{Prob}[u_{jk}|\mathrm{A}\mathrm{A}]=\prod _{k=1}^{n_{jz}}({\mathrm{Z}}_{\mathrm{R}\mathrm{R}}{\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]}+{\mathrm{Z}}_{\mathrm{R}\mathrm{A}}({\mathrm{L}}_{\mathrm{R}\mathrm{A}[\mathrm{j},\mathrm{k}]}+{\mathrm{L}}_{\mathrm{A}\mathrm{A}[\mathrm{j},\mathrm{k}]})/2+{\mathrm{Z}}_{\mathrm{A}\mathrm{A}}{\mathrm{L}}_{\mathrm{A}\mathrm{A}[\mathrm{j},\mathrm{k}]})$$ (4)

where L_{g [j,k]} is the likelihood of the offspring data if it has genotype g and Z_g is the frequency of genotype g among sires in the population. Within each maternal family, we take a product across all full sib families, assuming that sires unrelated. The implementation of eqs (4) requires that we can allocate progeny within a maternal family to distinct sub-families consisting of full sibs. Estimating parentage is the purview of mating system estimation methods, e.g. (Ritland 2002). Here, whole genome genotyping provides a great advantage; comparing siblings at thousands of SNPs allows a much finer estimation of relative similarity than afforded by genotyping at a few markers. Our method for assignment of offspring to full sib families is described below (METHODS).

Equations 1–4 are based on Mendelian inheritance and are neutral with respect to evolutionary processes. We distinguish four evolutionary models (0, 1, 2, and 3) as special cases by expressing the genotype frequencies (X, Y, and Z) in terms of evolutionary parameters (Table 1, equation 5 below). All models share the assumption of Hardy-Weinberg frequencies in the zygote population with q equal to the frequency of the reference base. The most elaborate model (model 3) has six parameters: q, S_RR (survival of RR individuals), S_RA, S_AA, Z_RR, and Z_RA. The quantities in the likelihood equations above are functions of these parameters:

$${\mathrm{X}}_{\mathrm{R}\mathrm{R}}=(1-{\mathrm{S}}_{\mathrm{R}\mathrm{R}}){\mathrm{q}}^2/(1-\omega ){\mathrm{Y}}_{\mathrm{R}\mathrm{R}}={\mathrm{S}}_{\mathrm{R}\mathrm{R}}{\mathrm{q}}^2/\omega$$ (5)

$${\mathrm{X}}_{\mathrm{R}\mathrm{A}}=(1-{\mathrm{S}}_{\mathrm{R}\mathrm{A}})2(1-\mathrm{q})\mathrm{q}/(1-\omega ){\mathrm{Y}}_{\mathrm{R}\mathrm{A}}={\mathrm{S}}_{\mathrm{R}\mathrm{A}}2(1-\mathrm{q})\mathrm{q}/\omega$$

$${\mathrm{X}}_{\mathrm{A}\mathrm{A}}=(1-{\mathrm{S}}_{\mathrm{A}\mathrm{A}}){(1-\mathrm{q})}^2/(1-\omega ){\mathrm{Y}}_{\mathrm{A}\mathrm{A}}={\mathrm{S}}_{\mathrm{A}\mathrm{A}}{(1-\mathrm{q})}^2/\omega$$

where ω = q² S_RR + 2(1−q)qS_RA + (1 − q)² S_AA and Z_AA = 1 - Z_RR - Z_RA.

Table 1.

Summary of the four SCA models fit.

Model	Description	Parameter Constraints
0	No viability selection Male allele frequency constrained	SRR = SRA = SAA Z terms determined by q and S terms
1	No viability selection Male allele frequency unconstrained	SRR = SRA = SAA Z terms not determined by q and S terms
2	Viability selection allowed Male allele frequency constrained	SRR ≠ SRA ≠ SAA Z terms determined by q and S terms
3	Viability selection allowed Male allele frequency unconstrained	SRR ≠ SRA ≠ SAA Z terms not determined by q and S terms

Tests compare a model that allows a process to a model that eliminates that process via parameter constraints (Table 1). For example, Model 2 eliminates viability selection (S_RR = S_RA = S_AA), but does not constrain genotype frequencies among sires. Model 3 allows viability selection (S_RR ≠S_RA ≠ S_AA), but does not constrain sires. Thus, the likelihood ratio statistic, Δ₃₂ = 2(L₃−L₂), provides a test for viability selection (L_k is the maximum log-likelihood of model k). Given that model 3 has two more free parameters than model 2, we compare Δ₃₂ to the chi-square (χ²) distribution with 2 degrees of freedom (df) to test for viability selection. Model 1 allows viability selection but constrains genotype frequencies among sires to equal those among all reproductive individuals: Z_RR = Y_RR and Z_RA = Y_RA This eliminates two free parameters from model 3, and as a consequence, ∆₃₁ = 2(L₃−L₁), is also compared to a χ²-distribution with 2 df. In principle, one could test for viability selection by comparing Model 2 to Model 0 and test for male allele frequency deviation by comparing Model 1 to Model 0. By choosing Δ₃₁ and Δ₃₂ as test statistics, we essentially allow process A when testing for process B, and vice versus. We find this method to be more conservative, e.g. fewer significant tests with Δ₃₂ than with Δ₂₀, but more robust because the operation of one process will not interfere with assessment of the other.

We call Δ₃₁ the q_M / q_S test because it tests for a difference in allele frequency between successful male gametes and all reproductive individuals. A significant q_M / q_S test could reflect fecundity selection or sexual selection, but importantly, it does not distinguish clearly between selection through male and female function. q_S, the allele frequency among all reproducing individuals (calculated as Y_RR + Y_RA/2) is comprised of both males and females, whereas q_M (Z_RR + Z_RA/2) estimates allele frequency among successful male gametes. However, q_M ≠ q_S does not imply that q_M differs from q_F, the allele frequency among successful female gametes. q_F = q_S if any differential fecundity through female function (among survivors) is unrelated to genotype. One can distinguish q_F from q_S if data is available on the total female reproductive success of individuals. Generalizing the likelihood model to accommodate fecundity data is straightforward (J.K. Kelly, unpublished), as it is to treat dioecious species (Christiansen and Frydenberg 1973). Finally, q_M may differ from q_S without any selection if there is gene flow into the population through immigrant males (or pollen in our study).

With structured sampling, the investigator determines n_S and n_D As a consequence, the model of eq (1) is not fully identifiable with regard to the survival parameters. In other words, different combinations of S_RR, S_RA, and S_AA may yield equally good model fits because genotype frequencies within cohorts (the X and Y terms of eqs (5)) depend only on the relative values of these quantities. For this reason, we include data from a fully random survey of the population. These individuals are not genotyped but simple counts inform the composite quantity ω within equations (5). Letting N_S be the observed number surviving to reproduce and N_D be the number that die before reproducing in this survey,

$$\mathrm{l}\mathrm{n}{L}_{\mathit{\text{survey}}}=N_S\mathrm{l}\mathrm{n}(\omega )+N_D\mathrm{l}\mathrm{n}(1-\omega )$$ (6)

The overall likelihood becomes ln L + ln L_survey and maximizing this quantity allows the survival parameters to be distinguished.

METHODS

Field sampling and progeny testing

The three populations under study are located in the central Oregon cascades: Quarry (44.3454243 N, −122.1362023 W; Elevation ~1200 meters), IM (44.402217 N, −122.153317 W; Elevation ~1400 meters), and BR (44.373238 N, −122.130675 W; Elevation ~1200 meters). BR is approximately 3.2 km north of Quarry and IM is 6.5 km north/northwest of Quarry. These populations have overlapping flowering phenologies, but neither BR nor IM is likely to be the immediate source of migrants (via seed or pollen) to Quarry. However, IM and BR are phenologically similar to the many other fast-progressing Mimulus populations surrounding Quarry. We adopted a spatially explicit scheme, sampling S and D individuals in approximately equal frequency at Quarry. We established four main transects spanning the primary area of occupation within the Quarry, each 10 meters in length. At regular intervals (~1 meter), we laid sub-transects perpendicular to the main transect and established six points along each sub-transects. At each point, we marked two individuals closest to the point. The first was a plant that we anticipated would successfully progress to flowering (S group) and one we anticipated would fail to reach flowering (Dgroup). Designation of these plants was confirmed at final sampling when we collected whole plant tissue and seed; plants had completely senesced ensuring appropriate classification as S or D. Our viability sampling is likely incomplete because the D group excludes plants that failed to germinate and seedlings that died prior to our initial survey. We germinated and grew 4 progeny from the first or second fruit of each of these plants in the University of Kansas greenhouse. We harvested dried leaf and calyx tissue from field collected parental plants and young leaves from greenhouse germinated progeny for subsequent DNA extraction (Holeski et al. 2014). To determine the overall proportion of the population that survived to flower, we surveyed a random set of 1000 seedlings marked early in the season at the BR location. 700 of these plants eventually flowered. We use these as estimates for N_S and N_D (eq. 6) within Quarry (see Discussion).

Library preparation and sequencing of Quarry plants

We generated genomic libraries for genotyping using Multiplexed-Shotgun-Genotyping (MSG) (Andolfatto et al. 2011), a form of RADseq (Miller et al. 2007) that uses restriction enzymes to reduce genomic representation to homologous loci that are flanked by restriction cut sites. We digested genomic DNA from each plant using the restriction enzyme AseI (NEB Biolabs). Each DNA sample was ligated to one of 48 distinct bar-coded adaptors, each containing a unique 6 bp barcode. Each set of these 48 uniquely bar-coded samples is then pooled independently to create a sub-library. After PCR, we size-selected our library for 250–300bp fragments using a Pippin Prep (http://www.sagescience.com/products/pippin-prep/). We then performed PCR reactions at 14–18 cycles using Phusion High-Fidelity PCR Master Mix (NEB Biolabs) and primers that bind to common regions in the adaptors. The larger number of cycles was used when the input quantity of DNA was low, which was more frequently the case with field collected tissue. In the PCR step, each sub-library was combined with one of 24 distinct Illumina indices allowing 24×48=1152 samples to be combined in a single Illumina lane. To remove primer dimers, we did two rounds of AMPure XP bead cleanup (Beckman Coulter, Inc) using a 0.8 bead volume to sample ratio. A single combined library was constructed containing both parents and offspring by pooling the cleaned sub-libraries based on their molar concentration. We sequenced the library in two lanes of an Illumina Rapid Run (paired end 150bp reads) and then again in one High Output lane (100bp paired end sequencing). We included a 10% phiX spike-in for all lanes to provide additional sequence complexity.

We demultiplexed the fastq files from the sequencing into sample specific sequence files. We processed reads with Scythe (https://github.com/vsbuffalo/scythe/) to remove adaptor contamination and Sickle (https://github.com/najoshi/sickle/) to trim low quality sequence. Using BWA with default parameter values (Li and Durbin 2009), we mapped the processed reads, one sample at a time, to the v2 draft of the Mimulus guttatus genome (http://www.phytozome.net/) after masking repetitive regions. Following read mapping, MSG data from 326 parents and 707 offspring were considered simultaneously to identify SNPs and call genotypes using the UnifiedGenotyper algorithm in the Genome Analysis ToolKit (GATK; (McKenna et al. 2010)). We filtered the SNPs present in the Variant Call File produced by GATK in two stages using custom python scripts. In the first stage, we reduced the dataset to only those SNPs where (1) two bases segregated, (2) at least 50 parents and 50 progeny had calls, (3) the (initial) estimated allele frequency within both parents and offspring was in the range of 0.05–0.95, (4) the GATK Haplotype score was less than 13, (5) the mapping quality score was at least 30, and (6) the average read coverage per plant was at least 1 and at most 100. When more than one SNP was identified within a RAD marker (the 150 bp sequence flanking a restriction enzyme cut site), we thinned the data to a single polymorphism by choosing the SNP with the most genotyped individuals. After analyzing Quarry sequences from the Pool-seq experiment (described below) and conducting an initial run of the SCA, we imposed two additional filters. We required that SNPs from the MSG dataset were also ascertained in the Quarry Pool-seq dataset with a total read count of 1–300. Extremely high read count SNPs were excluded because they appear to be cases where gene duplicates are being mapped (incorrectly) to a single location in the reference genome. Second, we required SNPs to be polymorphic in the final dataset (after all filters were imposed). This final SNP set, consisting of 15,658 polymorphisms, is presented as Supplemental Table 1.

Genotype inference at RADseq markers

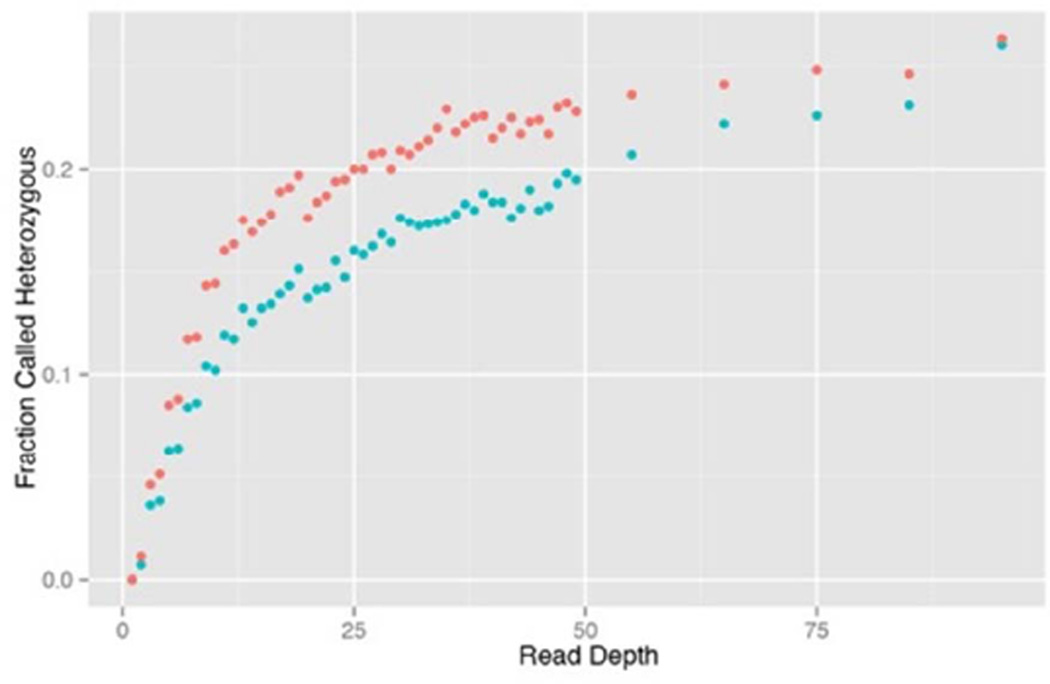
We calculated posterior probabilities (Q_RR, Q_RA, Q_AA) for genotypes of each plant at each SNP using the GATK genotype likelihoods combined with the estimated allele frequency. We used Hardy-Weinberg proportions as the genotype priors. This revealed an unexpected relationship between read depth and heterozygosity (Figure 1). Heterozygotes are under-called in samples with low to intermediate read depths. We hypothesize this to be a consequence of PCR amplification bias during library construction, which has been previously shown to cause under-calling of heterozygotes by variant calling programs (Heinrich et al. 2012). Ideally, each allele of a heterozygous individual would be equally represented in the library such that subsequent random sampling of reads during sequencing corresponds to a binomial process with p = 0.5. However, when the amount or quality of input DNA is low, random differential amplification of the two alleles of a heterozygote can substantially skew library allele frequency away from 0.5. As a consequence, sequencing of heterozygous loci is far more likely to produce skewed outcomes. To illustrate, consider a sample with four reads with one base and none with the other. The binomial predicts the 4/0 outcome (or 0/4) from heterozygotes only 12.5% of the time, but this may be far more likely if one allele predominates in the library following PCR amplification. The magnitude of PCR bias (really, it is more overdispersion than bias if either allele is equally likely to predominate) depends on the number of distinct sequences of each allele in the sample prior to PCR amplification (Heinrich et al. 2012). For the present study, this is unknown and likely to be highly variable, contingent on the amount and quality of DNA extracted from the original sample. However, the more severe under-calling of heterozygotes for dry samples (parents collected in the field after dessicating) than for wet sample (progeny grown in greenhouse providing fresh tissue) is expected given the lower amount and quality of DNA from the former. Unfortunately, the bioinformatic step of removing PCR duplicates (Xu et al. 2012) cannot be applied to MSG RADseq data. It may be possible to remove PCR duplicates with RAD methods that involve sequencing of a randomly sheared DNA fragment, e.g. (Davey et al. 2011). Andrews et al. (2014) review the differences among RADseq methods.

Figure 1.

The fraction of calls where the heterozygote had the highest likelihood (taken directly from GATK) is depicted as a function of read depth, distinguishing DNA extracted from Wet tissue (blue) and Dry tissue (orange).

We address PCR bias by evaluating the entire dataset (simultaneously) to estimating τ_k, the probability that a true heterozygote yields both alleles in a sample of k reads from an individual. In the absence of PCR bias, τ₁ = 0, τ₂ = 1/2, τ₃ = 3/4, and so on. Our method is based on two assumptions: (1) the population is near Hardy-Weinberg genotype proportions for most loci and (2) that true heterozygosity is unrelated to read depth at a SNP. Given these assumptions, it is straightforward to write the likelihood of the entire dataset (observed genotypes for all individuals at all SNPs) in terms of SNP specific allele frequencies and τ_k values over the range of observed read depths (1–250 in our case). We estimate the parameters by maximizing the likelihood (Appendix 1), obtaining a distinct set of τ_k values for parental DNA samples (dry tissue from both S and D adults) and progeny DNA samples (wet tissue). Estimates are presented in Supplemental Table 2. Our procedure also allows allele frequency at a SNP to differ between generations. As expected, τ_k → 1 as read count increases for both Wet and Dry samples. We use updated genotype likelihoods for all subsequent calculations. In cases where the original genotype likelihoods favor a homozygote (L_RR > L_RA or L_AA > L_RA), we update the heterozygote likelihood using L_RA‘ = (1–τ_k)/2 (the probability that a heterozygote looks like a homozygote is 1–τ_k, but we assume it is equally likely to appear RR or AA). The favored homozygote always remains most likely, but the strength of evidence against heterozygotes is reduced with small to moderate k. Importantly, when we recalculate heterozygosity (across plants and SNPs) using updated likelihoods, the association between heterozygosity and read depth is eliminated (Supplemental Figure 1).

Heterozygosity, genetic distance, and full sib assignment

The genotype matrix that emerges from this analysis has three genotypic posterior probabilities (Q_RR, Q_RA, Q_AA) specified for each plant and SNP. Basic population genetic statistics can be calculated from these probabilistic genotype calls. For example, the total heterozygosity of a plant is a simple sum of Q_RA across all called SNPs. The standardized Multi-Locus Heterozygosity, sMLH (Coltman et al. 1999; Hoffman et al. 2014), is the ratio of this sum to the total expected heterozygosity given the SNPs called for this plant (the sum of 2q(1-q) across called SNPs). For these calculations, we estimated q separately for parents and offspring at each SNP.

To estimate genetic distances between plants, we distilled the three posterior probabilities into a genotype score: T = 2Q_RR + Q_RA + (0)Q_AA. T is a SNP specific estimate for the number of R alleles carried by the plant. We calculated the simple Euclidian distance between plants across all SNPs for these scores using the “daisy” function in the R package “cluster” (Maechler et al. 2013; Team 2013). A second application based on the scores was to distinguish full-sibs from half-sibs within progeny sets. Consider two plants from the same maternal plant with scores T₁ and T₂. The expected difference between T₁ and T₂ depends on the maternal genotype, on whether the progeny were sired by the same or different plants, and on the genotype(s) of the sire(s). If the maternal plant is RR or AA, then the expected (absolute) difference between T₁ and T₂ is q(1-q) for full-sibs and 2q(1-q) for half sibs, assuming that males are randomly sampled from a population in Hardy-Weinberg proportions. If the maternal plant is heterozygous, then the expected difference is (1+q(1-q))/2 between full sibs and ½ + q(1-q) between half sibs, respectively.

For each pair of plants within each maternal family, we calculated the absolute difference in scores for each SNP where both plants had calls and then summed these across SNPs. To obtain a standardized difference for the pair, we divided this observed sum, by a sum of expected differences. For the latter, we consider the maternal genotype at each scored SNP and calculate the expected full-sib difference, (Q_RR + Q_AA)q(1-q) + Q_RA (1+q(1-q))/2, and the expected half-sib difference, (Q_RR + Q_AA)2q(1-q) + Q_RA (1/2+q(1-q)). Across sib-contrasts, divergence relative to full-sib expectation ≈ 1.41 divergence relative to half-sib expectation (Supplemental Figure 2). We thus used only the full-sib distance with a threshold of 1.21 (distances greater than threshold diagnosed as half-sibs). Given the matrix of pair-wise distances within each maternal family, we performed average euclidean distance hierarchical clustering as implemented in the R function “hclust”.

Linkage Disequilibrium and STRUCTURE analysis

For STRUCTURE and estimation of linkage disequilibria (LD), we consider only parental plants and then thinned the entire genotype matrix to include only high confidence calls (SNPs where one of the three possible genotypes has a posterior probability greater than 0.90). This reduced matrix contains 300 plants scored at 11751 loci, albeit with a large amount of missing data. Using STRUCTURE v2.3.4 (http://pritchardlab.stanford.edu/structure.html), we ran 10 replicate MCMC simulation chains for each value of K (the hypothesized number of ancestral populations) with K ranging from 1 to 4. Each chain consisted of 100,000 steps following a 100,000 step burn-in. The estimates for individual plant admixture proportions were extracted from the K = 2 replicate with the highest average log-likelihood.

Estimating LD is hindered by the fact that our genotyping method does not provide haplotype information except at the smallest genomic scale (within read pairs). To estimate LD between loci in the absence of phase information, we calculate the covariance of T scores (as defined above) between SNPs (Hill 1974; Rogers and Huff 2009). We calculated r² as a standardized measured of LD (Hill and Robertson 1968): r² = D² / (q1(1-q1)q2(1-q2)) where D is the estimated linkage disequilibrium, q₁ is the frequency of the minor allele at SNP 1 and q₂ the corresponding value for SNP 2. To consider a SNP pair for LD, we required at least 20 parental plants to be called at each SNP and for q₁ and q₂ to be at least 0.2. These constraints insure that high estimated r² is very unlikely between SNPs that are in linkage equilibrium. We used randomization to establish the null (linkage equilibrium) distribution of r², permuting genotypes across samples but preserving observed sample sizes, genotype frequencies, and the missing data pattern.

Genomic SCA

Using the updated likelihoods for each SNP, we estimated models 0–3 (see THEORY). Models were fit sequentially with L₀ estimated first. We used the resultant estimates for q and S as parameter starting points in the numerical search for L₁ and L₂. We calculated likelihoods and optimized for each model using programs written in Python (available upon request). Likelihoods were maximized using the BFGS bounded optimization routine available in SciPy (http://www.scipy.org/). The optimization for L₃ was initiated from two different start points using the parameter estimates of L₁ and L₂, respectively. These two runs nearly always converged to the same maximum for L₃. We calculated p-values for each likelihood ratio statistic (∆₃₁ and ∆₃₂) using the chi-square probability calculator of Minitab14^©. Finally, given the full set of p-values for each test statistic, we applied a False Discovery Rate (Benjamini and Hochberg 1995) of 0.10 to declare genome-wide significance (q-values are reported for all SNPs in Supplemental Table 1).

Pooled population samples and F_ST calculations

We collected 200 plants from IM, BR, and Quarry in 2013 (distinct from the sampling of Quarry plants described above). DNA was extracted from each plant and quantified. We then combined DNA samples within each population in equal molar ratios. We constructed TruSeq Illumina libraries for each pooled population sample at the KU Genomics Core facility. The indexed libraries were pooled for subsequent sequencing in three High-Output lanes of the Illumina HiSeq 2500 instrument (PE 100). Prior to read mapping, we trimmed low-quality ends using Sickle and Scythe (as described above for the MSG data). Using BWA, we mapped the processed read pairs, to the masked v2 draft of the M. guttatus genome. After mapping, we removed PCR duplicates with Picard tools (http://picard.sourceforge.net). The mapped reads from each population were then considered simultaneously with the RADseq data to identify SNPs and call genotypes in GATK. The median depth of coverage was 47 for BR, 57 for IM, and 67 for Quarry. Given that these counts are far below the actual number of alleles sampled from each population into our libraries (400) and that we eliminated PCR duplicates, we treat each read as an independently sampled allele from the population. Our estimate for population allele frequency at a SNP is just the count of reference alleles divided by the total depth at the SNP. We estimate F_ST as the among population variance relative to the total variance when scoring individual reads as binary variables (0 if reference, 1 if alternate). Given this scoring, the one-way ANOVA provides an unbiased estimate for the within and among group variance, properly accounting for sampling error.

RESULTS

Heterozygosity and Admixture

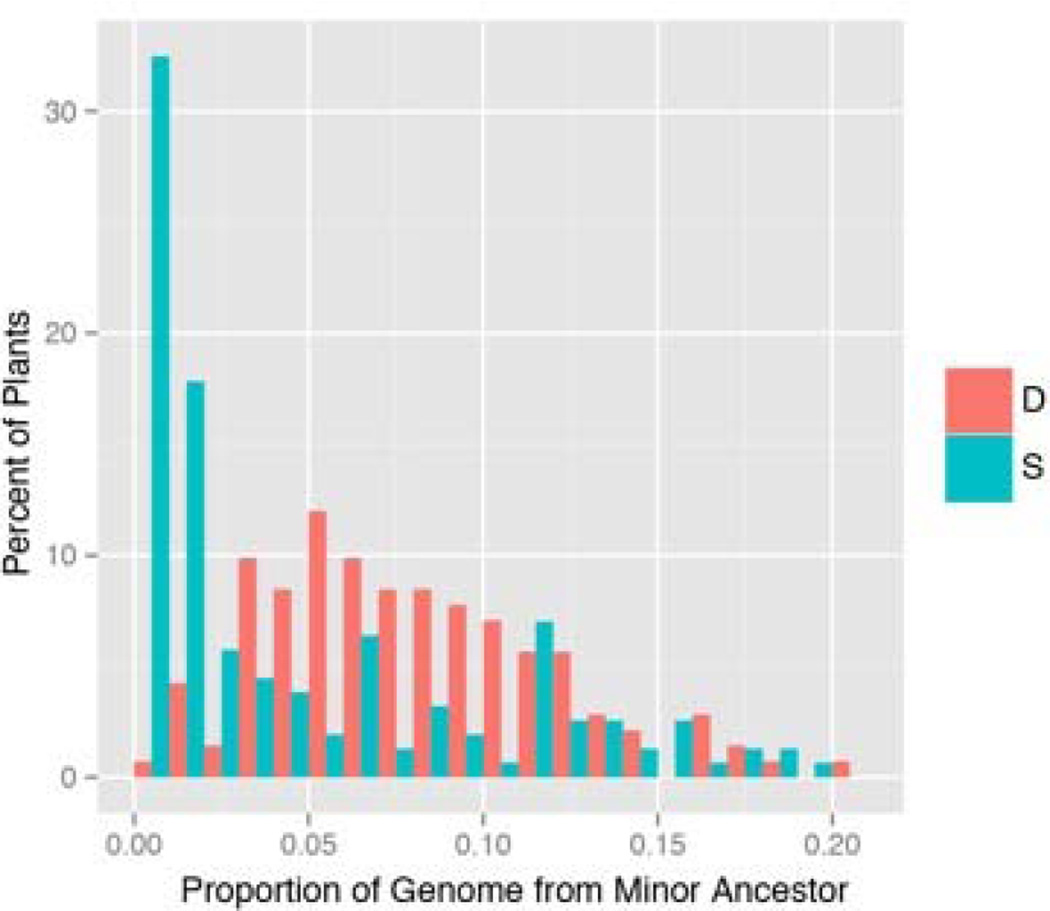
The mean standardized Multi-Locus Heterozygosity, sMLH (Coltman et al. 1999; Hoffman et al. 2014), is 0.99 for progeny (n = 707, SD = 0.06) and 0.95 for adults (n = 325, SD = 0.16). sMLH equals 1 for an outbred plant within a randomly mating population and the distributions for both parents and offspring are centered on 1 (Supplemental Figure 3). However, a minority parental plants appear to be at least partly inbred: mean sMLH of S plants is 1.00 (n = 159, SD = 0.12), while the D mean is 0.89 (n = 166, SD = 0.18), a highly significant difference (F₁, ₃₂₃ = 45.3, p < 0.0001). Genetic evidence of two different types suggest that Quarry is an admixed population. STRUCTURE (Pritchard et al. 2000) estimates that plants are mosaics of two different ancestral populations with one predominant (Figure 2). The average log-likelihood across replicate simulations is much higher for K = 2 (−294,656) than K = 1 (−314,453), but then declines as the postulated number of ancestral populations (K) increases (Supplemental Table 3). The mean percentage of the genome from the minor population was only 4.9% among plants that survived to flower, but 7.9% among D plants, a highly significant difference (Figure 2; F_1,298 = 25.7, p < 0.0001).

Figure 2.

The estimated admixture of parental plants is reported as a percentage ancestry of minor population within S (blue) and D (orange) plants.

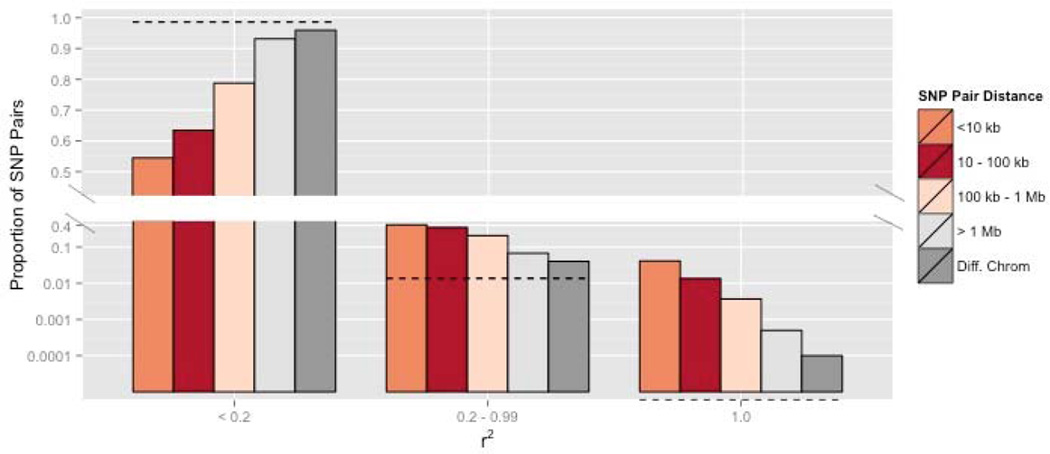
Linkage Disequilibria (LD) between SNPs provides a second, distinct, signature of admixture. Our genotyping method provides limited information about haplotypes (see METHODS), but we still find that LD is substantially elevated within Quarry (Figure 3). SNP pairs exhibiting strong association (estimated r² ≥ 0.2) are much more frequent than predicted by linkage equilibrium at distances of 10s to 100s of kilobases (bars exceed dotted line in right portion of Figure 3). Most striking, SNPs separated by millions of bases on a chromosome, and even across chromosomes, often exhibit high, and occasionally perfect (r² = 1), association. Pairwise comparisons between parental individuals indicate a relationship between genomic similarity and survivorship: S individuals are more similar to each other (on average) than to D individuals. D individuals were most dissimilar to other D plants (Supplemental Figure 4). Pairwise comparisons among siblings within the progeny generation indicate that maternal families are a mixture of full sibs and half sibs. Given four progeny genotyped per family, we inferred a single sire for 36 maternal families, two sires for 73 families, three for 57 families and four sires for 26 families.

Figure 3.

The frequency distribution for r² between SNPs within chromosomes is presented for Quarry parents. Here, we limit contrasts to SNP pairs separated by at least 1000 bp. The dotted line is the expected proportion of r² estimates in the specified range for sites in linkage equilibrium (established by permutation). The dotted line is set at 0.0 for r² = 1 because it was never observed in the permutated data.

Selection on SNPs within Quarry

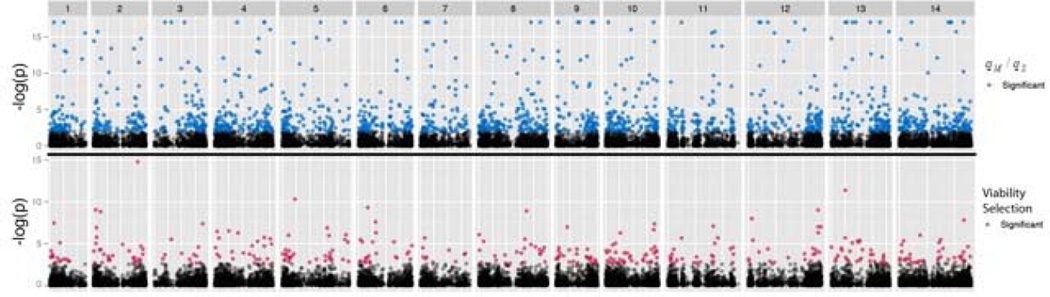
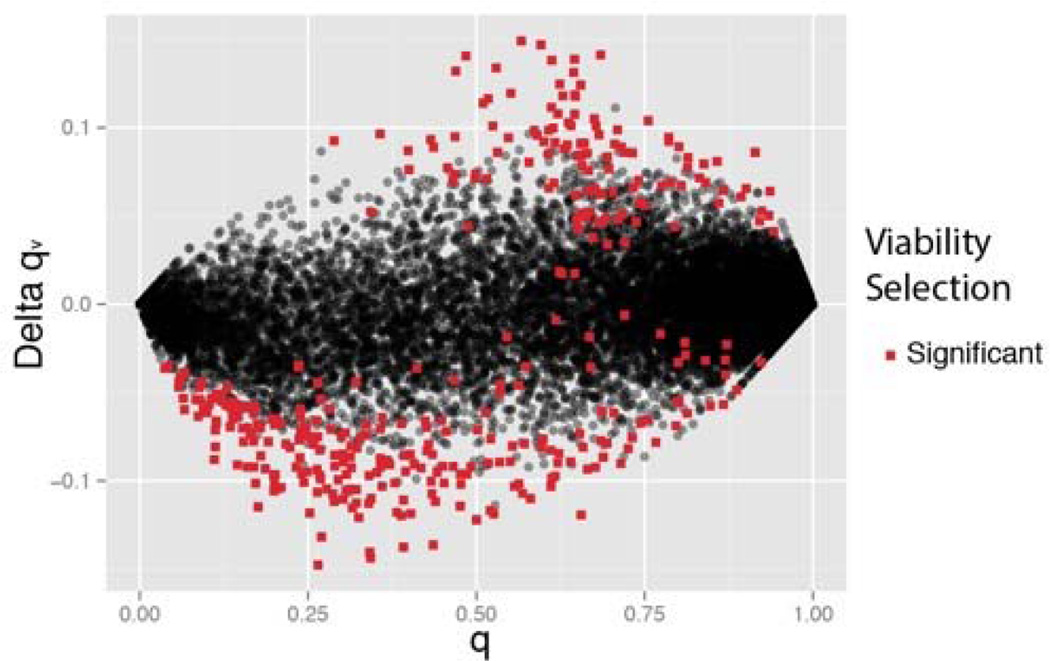
In total, 367 SNPs exhibited a significant difference (genome-wide) in genotypic frequencies between S and D plants (∆₃₂), indicative of viability selection. 1733 SNPs proved genome-wide significant for q_M / q_S (i.e. do genotype frequencies among successful males differ from that among all flowering plants?; ∆₃₁). Figure 4 illustrates the locations of sig/ns SNPs for both ∆₃₁ and ∆₃₂ across the 14 chromosomes. To characterize allele frequency change owing to the different components of selection, we calculate ∆q_v = q_S – q as the predicted change owing to viability selection (Table 2A). Mean ∆qv is near zero among ns SNPs, but substantially negative among significant SNPs where the more common allele is favored nearly two thirds of the time (Figure 5). A small number of significant SNPs have point estimates for genotype survivals suggesting over/under dominance (these SNPs have small ∆qv in Figure 5). A more compelling trend involves intermediacy of allele frequency: q was between 0.1 and 0.9 for 94% of viability-sig SNPs, but only 57% of ns SNPs which may reflect that ∆qv should be proportional to q(1-q).

Figure 4.

Significance of tests is reported as –Log10(p) for each SNP for viability selection (lower panel) and q_M / q_S (upper panel). The partitions demark chromosomes and color distinguishes genome-wide FDR < 0.1 (red/blue) from FDR > 0.1 (black).

Table 2.

The predicted differences in allele frequency are reported owing to (A) viability selection or (B) evident in the q_M / q_S test. In (A), SNPs are parsed by significance (sig/ns) for ∆₃₂, while by ∆₃₁ in (B).

	n	Mean ∆q	SE
(A) Viability selection
ns SNPs	15291	−0.003	0.0002
sig SNPs	367	−0.024	0.004
(B) qM / qS test
ns SNPs	13925	0.014	0.001
sig SNPs	1733	0.025	0.007

Figure 5.

The predicted change in allele frequency owing to viability selection as a function of initial frequency for significant (red) and non-significant (black) SNPs.

Let ∆q_MS denote the estimated difference in the frequency of the reference base between successful male gametes (q_M) and the frequency in all flowering plants (q_S). Across all SNPs, the average Δq_MS is substantially positive: mean = 0.015, SE = 0.001. Parsing these SNPs according to q_M / q_S test significance, we find mean Δq_MS is positive among significant and non-significant SNPs (Table 2B). 163 of 367 SNPs significant for viability selection were also significant for q_M / q_S. Among these, there is a slight negative association between Δqv and Δq_MS (r = −0.17, p < 0.03). This is consistent with antagonistic selection, but the evidence is not strong. A negative correlation is built into this contrast because q_S is estimated with error and it contributes positively to Δqv but negatively to Δq_MS.

Selection within Quarry in relation to differentiation from neighboring populations

In total, over 9.8 million SNPs and insertion/deletions were ascertained in the pooled population samples. However, the overwhelming majority of these SNPs are outside the MSG-RAD loci analyzed for selection, and we thus thinned the data to SNPs in the SCA. Among these, there is a high correlation (r = 0.84) of allele frequency estimates between MSG and pooled-genomic samples from Quarry. The frequency of the reference base is typically lower in the Quarry pooled sample (mean = 0.74) than in the IM (mean q = 0.84) or BR (mean q = 0.82). The high frequency of the reference base in IM is expected. The reference genome is based on a single inbred line from IM.

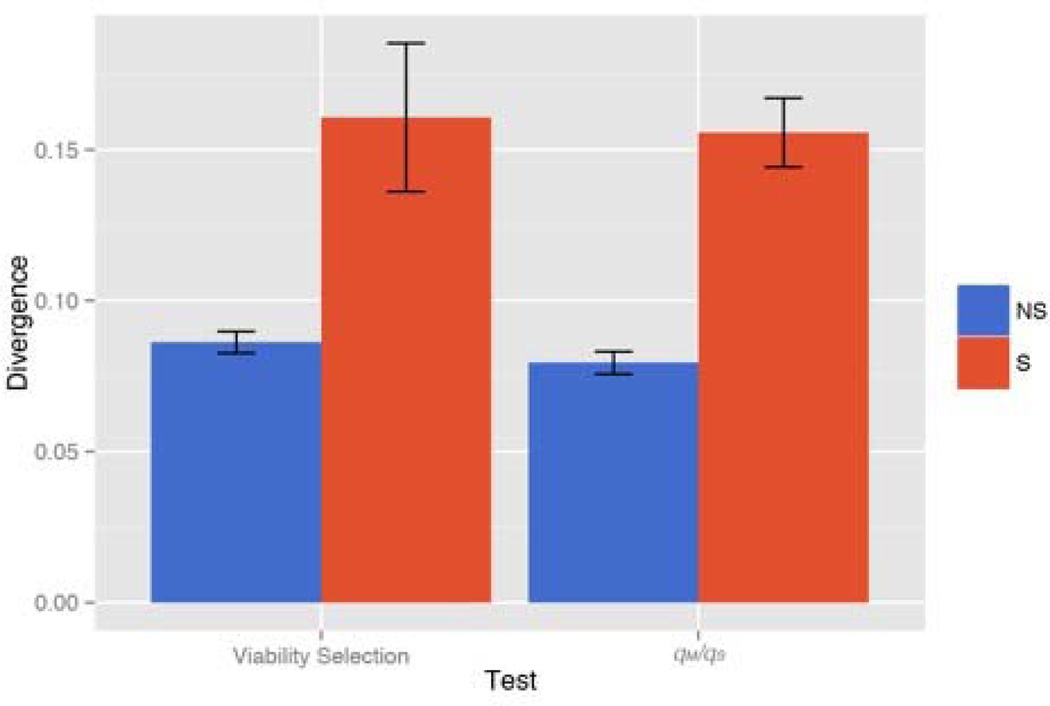
We estimate divergence of Quarry from and IM and BR in two different ways, F_ST between populations (Wright 1951) and the simple difference in alternative base frequency between Quarry and IM/BR (data from these populations combined). The average pairwise F_ST for IM vs Quarry is 0.132 (SE=0.001) and 0.124 (0.001) for BR vs Quarry. Divergence between BR and IM is much lower: F_st = 0.065 (0.001). F_ST for contrasts of Quarry to IM and BR is significantly higher at SNPs under selection than for non-significant SNPs (Supplemental Table 4). Moreover, there is a strong directionality to differentiation in terms of the frequency of the reference base. The alternative base is generally more common in Quarry than in IM or BR (means reported above), but this inflation is much greater at SNPs significant for viability selection (left side of Figure 6) and at SNPs significant for q_M/q_S.

Figure 6.

Divergence is measured as the difference in alternative based frequency between Quarry and pooled sample of IM and BR. The mean divergence is report for SNPs that are ns (blue) and sig (orange) for viability selection (left) and q_M/q_S right).

DISCUSSION

The selection component method (SCA) was developed to characterize the different ways that natural selection can act throughout the life cycle of an organism. Sampling and subsequent genotyping of a population that includes mother-offspring combinations can estimate the change in allele frequency owing to viability selection, sexual selection, and fecundity selection (Christiansen and Frydenberg 1973). While SCA has been employed in a few systems (Prout 1965; Watt 1977; Clark and Feldman 1981; Heath et al. 1988; Barbadilla et al. 1994), applications have been limited by logistical constraints. In particular, large sample sizes are required to demonstrate that reasonable per-locus selection coefficients are significantly non-zero. In a sufficiently large experiment, the effort and cost of genotyping parents and offspring at more than a few loci has, until recently, been prohibitive. Genomic methods make this problem much less severe. While incorporating genomic data into SCA does present substantial challenges, it also has the potential to address previously intractable questions.

The products of an SCA depend on the sampling design, as well as the features of the organism under study. Equations 1–6 describe a minimal design, in which a monecious population is sampled prior to viability selection, survivorship to reproduction is noted, and then a sample of offspring is collected from each reproductive female. The data is genotypes in three sets: (1) individuals that failed to reproduce, (2) individuals that survived to reproduce, at least through female function, and (3) progeny of those individuals. Contrasts between these sets address two hypotheses. First, genotype frequencies should not differ between (1) and (2) if there is no viability selection. The null hypothesis for the contrast between (2) and (3), what we call the q_M/q_S test, is that allele frequency among all survivors (q_S) equals that among successful male gametes (q_M). There are multiple possible causes for a significant q_M/q_S test. General fertility selection (e.g. some flowering plants are more fecund than others through both male and female function) or male-specific selection (some flowering plants are more effective at outcross siring distinct from the number of seed set) could generate a difference between q_M and q_S. Gametic selection through pollen competition or meiotic drive could create a difference even if the number of progeny sired is equivalent across males. Also, because q_M is inferred from the male contribution to offspring, there is opportunity for selection between the formation of zygotes and the genotyping of progeny. Finally, a significant q_M/q_S test could reflect migration.Immigration of male gametes into a population could alter q_M without any differential performance of resident sires.

The extension of the method to dioecious species is accomplished by parsing category (2) into adult males and reproductive females (Christiansen and Frydenberg 1973). More nuanced tests can be made by adding measures of individual reproductive success. If the total number of offspring of each female is recorded and the likelihood model elaborated to accommodate these counts, allele frequency among successful female gametes (q_F) can be predicted. Tests involving q_F can more clearly delineate female fecundity selection (is q_F different from q_S?) from other causes of a significant q_M/q_S test. For example, an important question in hermaphroditic organisms is the extent to which selection through male function is distinct from selection through female function (Delph and Ashman 2006; Arnold 1994). At a single locus, this is equivalent to asking if q_F is different from q_M. Like the q_M/q_S test, the q_M/q_F test can be accomplished without having to identify specific male parents; the latter necessary when the intention is to determine how particular phenotypes affect male reproductive success.

Genotype inference is an important aspect of SCA based on genomic data. The genotype of an individual at a locus is a set of probabilities (e.g. L_RR, L_RA, and L_AA), not a fixed value. In our experiment, genotype uncertainty owes to having low sequence read numbers at many RAD loci in many individuals (and also due to PCR bias as discussed below). However, uncertainty is not specific to RADseq. Alternative methods such as low-level, whole-genome sequencing will also yield imperfect estimates of individual genotypes. In fact, equations 1–6 are entirely suitable to data where most individuals have only one or two reads at most SNPs. A single high quality read substantially informs likelihood calculations. Consider an individual with a single G read at a SNP that is A/G polymorphic. We may not know if the individual is GG or AG, but it is very unlikely to be AA. Moreover, if this individual is offspring to a mother that is GG (or strongly indicated to be GG), there is a very high likelihood that the male parent contributed the A allele (thus informing q_M estimation in the entire population). In principle, one could sequence individual DNA samples to sufficient depth (more problematically, sufficiently high depth across all samples) to eliminate genotype uncertainty. However, even where this is possible, it is not likely the best allocation of effort. Each read added to a locus informs the likelihood to a lesser and lesser extent. Expanding the number of individuals that are sampled from the population, even if genotypes are encumbered with uncertainty, will provide greater power to estimate allele frequency change.

In the next section, we describe how data from a minimal SCA design can be synthesized with other analyses to address a particular problem, migration-selection balance within an admixed population. In isolation, the SCA yields an abundance of significant tests, but the secondary analyses provide essential context. The STRUCTURE and Linkage Disequilibria analyses are based on the data of the SCA (SNPs in RAD loci), but retain the multi-locus genotype information of individuals. These results indicate that the SNP-specific Δq from the SCA are not likely independent outcomes. The second set of analyses, based on distinct genomic data (Pooled population sequencing of Quarry and neighboring populations), provide a basis for interpreting the magnitude and direction of Δq in relation to the hypothesized processes of local selection and countervailing gene flow.

Migration-selection balance

A basic population genetic principal is that natural selection should target specific loci, while gene flow affects the entire genome (Lewontin and Krakauer 1973). This is the conceptual basis for the F_ST outlier tests that have been extensively applied in genome scans of many species (Beaumont and Nichols 1996; Cruickshank and Hahn 2014). Consistent with this view, we find a genome-wide effect of gene flow (Table 2, Δq_MS for non-significant SNPs). However, selective effects are not confined to a few loci, which are often termed ‘genomic islands’ in the F_ST outlier literature. Instead, selective effects are quite broadly dispersed, affecting SNPs within each region of each chromosome (Figure 4). Few of these SNPs are likely to be the specific targets of selection, but instead reflect allele frequency change owing to hitch-hiking (Maynard Smith and Haigh 1974). Less than 1% of the M. guttatus genome is contained within the RADseq loci surveyed for selection. However, owing to linkage and admixture, these SNPs are associated with other polymorphisms thousands, perhaps millions, of bases away (Figure 3).

A diversity of selective processes are likely at work in the Quarry population, but multiple lines of evidence indicate a major role for migration-selection balance. STRUCTURE suggests that Quarry plants are genetic mosaics of two different ancestral populations, and we find that survival to flowering is lower in plants with a higher genomic proportion of the minor ancestor (Figure 2). This is predicted with local selection if we interpret the major population as the locally adapted type and the minor population as an aggregate of immigrant genotypes. Consistent with this interpretation, survivors (S plants) are genomically more similar to each other than they are to plants that failed to flower (D plants) or D plants are to each other (Supplemental Figure 4). The dominant ‘type’ of a locally adapted population is expected to be more genetically homogenous than the immigrant population given that the latter is derived from many different locations.

In the SCA, there is a tendency for viability selection to increase the frequency of the alternative base (Table 2). The Pool-Seq data indicate that the reference base has higher average frequency in the neighboring IM and BR populations and thus the net effect of viability selection is to increase divergence of Quarry. Most importantly, Figure 6 suggests a history of divergent selection at the SNPs exhibiting viability selection during 2013. They are nearly twice as divergent (in terms of alternative base frequency) as non-significant SNPs. The same trend is observed when we measure divergence with F_st (Supplemental Table 4). Of course, viability selection did not always favor the alternative base, about 1/3 of significant Δq_v were positive. Among these, we observe that selection is nearly always favoring the more common allele (upper right quadrant of Figure 5). This same tendency is observed for significantly negative Δq_v (lower left quadrant of Figure 5), although to a lesser extent. Regardless of whether the reference or alternative base happens to be locally advantageous, migration-selection balance models predict that the locally favorable allele will be the more locally frequent at equilibrium (Wright 1931).

There were substantially more SNPs significant for q_M / q_S than for viability selection, but interpretation is less clear for these. The most basic observation is the positive mean Δq_MS across all SNPs. We interpret this most likely as genome-wide effect of gene flow through pollen contributed from neighboring populations where the frequency of the reference base is, on average, substantially higher. The transects of our survey spanned the central portion of Quarry where water persists farthest into the summer, but there are many additional small groups of monkeyflowers within 10m of the main population. These patches occur in faster drying areas and so their phenology more closely resembles plants in IM and BR. The difficulty for interpreting significance of SCA for Δq_MS is that, with migration, q_M differs from q_S even in the absence of selection. For example, if gene flow increases allele frequency at a SNP, then we are much more likely to detect subsequent fecundity or sexual selection if it increases allele frequency (pushing q_M further away from q_S) than if it decreases allele frequency (erasing the effect of gene flow). Unfortunately, we cannot easily ‘factor out’ the effects gene flow. The predicted change owing to migration is proportional to the difference in allele frequency between populations (Wright 1931) and this difference certainly varies among SNPs. Perhaps not coincidentally, q_M/q_S is much more likely to be significant at SNPs that show elevated divergence of between Quarry and IM/BR (right side of Figure 6).

Caveats

The SCA models (equations 3–5) assume random mating. This is a noteworthy assumption given that M guttatus self-fertilizes to varying degrees in nature (Awadalla and Ritland 1997; Koelling et al. 2012) and because admixture, which is an evident feature of Quarry (Figures 2–3), can generate deviations from Hardy-Weinberg proportions owing to the Wahlund effect (Crow and Kimura 1970). Our genotype inference method assumes approximate Hardy-Weinberg proportions, but the implementation of this method does not strongly constrain individual values for the standardized Multi-Locus Heterozygosity (sMLH = 1 for a fully outbred individual). Both generations (S and D parents as well as progeny) exhibit distributions for sMLH centered on 1, but there is a slightly lower mean among parents (0.95 instead of 0.99) and greater variability. Perhaps more importantly, this limited variation in sMLH among parents is associated with survivorship. Average heterozygosity was slightly less in plants that failed flower than those that succeeded. Similar heterozygosity-fitness correlations have been noted in many natural populations (Hoffman et al. 2014).

A second issue is whether genotype inference, specifically the method to account for PCR bias (Appendix 1), might induce error in estimation or hypothesis testing from the SCA. Two sorts of error must be considered, false positives (selection is inferred when the SNP is unaffected by selection/linkage or gene flow) and false negatives (non-significant tests for SNPs exhibiting real allele frequency change). False negatives will always be a difficulty for SCA given finite sample sizes and small, but still important, allele frequency changes. The most likely effect our updating of heterozygote likelihoods is to increase false negatives because it essentially weakens genotype calls. The initial likelihoods from GATK often strongly favor one homozygote at intermediate read depths. The updated likelihoods invariably still favor that homozygote, but the strength of evidence against the heterozygote is reduced. The necessity of this procedure is evident if one attempts to calculate likelihoods for parent-offspring combinations using unmodified genotype likelihoods. An abundance of “impossible genotypes” result at SNPs where the maternal plant is strongly called as one homozygote, but an offspring is strongly called as the alternative homozygote. This is not a common event, but it happens with most parent-offspring contrasts somewhere in the genome (although at different SNPs for different parent-offspring contrasts).

We also conducted a series of tests to determine if SCA-significant SNPs were associated with “low quality” genotype calls. As a measure of confidence, we used the difference in likelihood between the most likely genotype at a SNP and the second most likely (highest value = 1 when the alternative genotypes have relative likelihoods near zero). We find that the average confidence in genotype calls is higher at SNPs significant for viability selection and/or q_M / q_S than at non-significant SNPs, and this is true of both parental (D and S plants) and offspring genotypes (Supplemental Table 1). This is expected if the likelihood machinery is working properly, power should increase as genotype uncertainty decreases. Finally, the inclusion of extrinsic data provides important corroboration. If significance in the SCA were due to some unrecognized bias in genotype inference at RAD loci, there is no reason for the same SNPs to exhibit elevated divergence among populations (the latter inference based on completely different data obtained through Pool-seq).

All that said, PCR bias is an impediment to SCA and future studies should endeavor to reduce it as much as possible. Some genotyping methods allow removal of PCR duplicates prior to subsequent analyses (Andrews et al. 2014). Technical replicates – multiple independent library preps and amplifications from each sampled individual – should also reduce the undercalling of heterozygotes. Technical replicates require a sufficient amount input DNA (which was not available from the S and D plants of this study) and there is a cost in term of effort and expense. However, the gain in terms of precision may outweigh the cost for many experiments.

A third issue is our use of an extrinsic survey of the BR population to estimate overall viability in Quarry. If one starts with a random sample of the population, and lets survivorship of this random sample determine the number of S and D individuals, then the extrinsic survey is unnecessary. We used a structured sampling scheme, anticipating that survivorship would be much lower than it turned out to be. Structured sampling is easily accommodated by SCA with an independent survey to calibrate survivorship (eqn 6). In our study, the independent survey was conducted at a neighboring population. We think overall survivorship was similar in Quarry to BR (P. Monnahan, unpublished observation), but it may have been slightly lower or higher. To evaluate the consequences of this, we re-ran the entire SCA on all SNPs assuming lower (600/1000) and higher (800/1000) survivorship in the survey. The results (full output as Supplemental Tables 5–6) are only incrementally different. For viability selection (367 significant SNPs with 70% survival), the number significant (using same threshold as Figure 4) increases to 401 if survivorship is 60%, but declines slightly to 363 if survivorship is 80%. For q_M / q_S (1733 significant in Figure 4), slightly fewer are significant with 60% survival (1718), slightly more with 80% survival (1752).

The genetic basis for local adaptation

The geographic range of most species is much greater than the dispersal capabilities of individual organisms, allowing local populations to become genetically distinctive. This most basic of evolutionary processes – the balance between selection and migration – has been a focus of study throughout the history of evolutionary biology, but advances in genomic technology now afford an unprecedented view of the dynamic. In a reciprocal transplant experiment using synthetic recombinant populations of Boechera stricta, Anderson et al. 2014 estimated substantial selection coefficients on marker loci across the genome, particularly for viability. Experimental evidence of selection within a generation was also noted for stick insect ecotypes upon being transferred to a novel host (Gompert et al. 2014). This experiment was extended to observe genome-wide allele frequency divergence across generations and how this relates to observed genomic divergence between ecotypes (Soria-Carrasco et al. 2014). Parallel to our synthesis of SCA with Poolseq data (Figure 6), divergent regions between ecotypes of the stick insect were observed to change in the predicted direction when ecotypes were transplanted to a novel host. These studies are similar to ours in that local selection has been shown to affect hundreds to thousands of loci throughout the genome. Strong LD is present in the transplant studies owing to the nature of the starting populations (Recombinant Inbred Lines derived from a cross between divergent populations of Boechera, the divergent populations themselves for the stick insects). In contrast, Quarry represents a natural experiment in which extensive LD owes to admixture and limited recombination since the population was founded.

Figure 4 suggests a highly polygenic basis to local adaptation, but owing to long-range and potentially idiosyncratic LD (Figure 3), it is impossible to estimate how many loci are involved. Certainly, the many significant SNPs evident in our survey are not likely themselves to be effectors of fitness, but instead illustrate the genome-wide effects that selection imposes through hitch-hiking within an admixed population. The current selective dynamic seems to be maintained via migration of maladaptive alleles from nearby, ecologically distant populations. However, gene flow must have originally played a beneficial role for the establishment of this population. Given the young age of the population (30–40 generations), the alleles under selection are older than the population itself indicating that its current locally adapted state is due to the recruitment of standing genetic variation. We do not know the ancestral source of the dominant genotype in Figure 2, or even if the source was a single population. Perennial populations/species within the M. guttatus species complex do exhibit phenotypic similarities to Quarry plants, particularly larger vegetative size at time of first flower. Regardless of ancestry, it is notable that in less than 40 generations, the role of migration has reversed from furnishing the genetic variation that allows local adaptation, to continually reintroducing maladapted alleles.

Appendix 1: A maximum likelihood method to estimate heterozygote likelihoods

The initial variant calling for an individual at a SNP yield a likelihood for each possible genotype, L_RR, L_RA and L_AA, respectively. We code this as 0 if L_RR is maximal, 1 if L_RA is maximal, and 2 if L_AA is maximal and accompany this score with the observed read depth. The log-likelihood for a SNP (indexed by i) that is scored in n individuals (indexed by j) is $\sum _{j=1}^n\mathrm{l}\mathrm{n}(z_{ij})$, where

• z_ij = q_i² + q_i (1 − q_i)(1 − τ_k) if s = 0

• z_ij = 2q_i (1 − q_i)τ_k if s = 1

• z_ij = (1 − q_i)² + q_i(1 − q_i)(1 − τ_k) if s = 2

Here, s is the observed score for a particular individual/SNP and k is the associated read depth.The overall log-likelihood is the sum of $\sum _{j=1}^n\mathrm{l}\mathrm{n}(z_{ij})$ across all SNPs in the dataset. For a given set of τ_k the maximum likelihood for q_i depends only on the data from SNP i (we are ignoring linkage disequilibria for this analysis). In contrast, maximizing the likelihood for τ_k requires that we consider all SNPs simultaneously. For this reason, we first maximized τ_k based on an initial set of estimates for q_i. Then, using the updated τ_k, we proceeded through all SNPs, one at a time, maximizing $\sum _{j=1}^n\mathrm{l}\mathrm{n}(z_{ij})$ with respect to q_i. This process was repeated until convergence. Likelihoods were maximized using the BFGS bounded optimization routine available in SciPy (http://www,scipy,.org/). The code—written in Python—is available upon request.