HIV Treatment and Prevention: A Simple Model to Determine Optimal Investment

1. Introduction

In 2012, an estimated 35 million people were living with human immunodeficiency virus (HIV) worldwide and 2.3 million new infections occurred.¹ Both antiretroviral therapy (ART) and prevention are important HIV control measures. However, HIV control resources are limited. Striking the right balance between treatment and prevention can maximize health benefits in the most cost-effective manner.

ART for HIV-infected individuals is effective at both reducing infectivity and slowing disease progression.^2–4 However, ART is expensive and requires access to medical care.⁵ Hence even in developed countries, a significant fraction of people eligible for ART do not receive it.^{6, 7} Moreover, it is estimated that worldwide, for every person newly enrolled in ART in 2010, two new infections occurred, indicating that more prevention efforts may be needed.⁶ Many HIV prevention methods are available and in use. Costs and effectiveness of the programs vary widely, from condom distribution, which may cost less than $4 per person per year but have limited effectiveness,⁸ to daily preexposure prophylaxis (PrEP) with antiretroviral drugs, which may be highly effective at preventing disease acquisition but costs more than $10,000 per person per year in the United States (US).^{9, 10}

Determining the appropriate investment of a limited budget in a portfolio of HIV treatment and prevention programs is complicated by several factors. First, the HIV epidemic grows nonlinearly, so preventing one infection today could lead to many infections averted in the future. Second, treatment and prevention programs may have overlapping benefits, since the same infection cannot be prevented twice. Individuals targeted by a prevention program may also reap the indirect benefits of a treatment program. Finally, programs may exhibit economies or diseconomies of scale as they are scaled up; thus, for example, twice the investment in prevention may not yield twice the reduction in risk.

This paper develops a simple framework for determining the optimal mix of treatment and prevention programs for HIV. The goal is to maximize health benefits, either quality-adjusted life years (QALYs) gained or HIV infections averted (an indirect measure of health benefits), subject to investment constraints. Most previous research on the cost-effectiveness of HIV control measures has focused on the cost-effectiveness of treatment or prevention only,^11–13 and studies of HIV resource allocation decisions have often focused only on HIV prevention programs.^14–18 We consider investment in both. Prior studies that have directly compared treatment and prevention have used simulation models to assess program effectiveness,^19–26 often ignoring their costs. We aim to provide a simple method of evaluating investment in treatment and prevention portfolios that is accessible to decision makers.

We simplify the resource allocation problem by approximating health benefits and costs with linear functions. Often, models that assume linearity of HIV intervention benefits do not capture epidemic effects or do so incompletely.^{11, 27–31} Our linear estimate of health effects accounts for both primary health benefits accruing to individuals who receive prevention or treatment as well as secondary health benefits accruing to other individuals who thereby avoid infection. Other studies have approximated epidemic effects similarly;^{32, 33} we expand on this by using the estimates as inputs to the resource allocation problem. Additionally, unlike many prior resource allocation models, we allow for subadditivity of program benefits and diseconomies of scale in program costs.

In Section 2 we formulate and solve our model, starting with a linear formulation and then expanding it to include overlap of treatment and prevention benefits and diseconomies of scale. In Section 3 we present methods for estimating model parameters. We illustrate our results in Section 4 with the examples of ART and two prevention programs – PrEP and community-based education – in men who have sex with men (MSM) in the US. We conclude with discussion in Section 5.

2. Model Formulation

We consider a population of adults including both HIV-infected and uninfected individuals. We assume the status quo includes baseline levels of treatment and prevention. We consider the decision of allocating funds between scaling up treatment for eligible infected individuals and implementing incremental prevention programs for uninfected individuals over a period of T years (n-1 prevention programs are available). We define x₁ as the number of incremental people starting ART due to the scale up and x_i (i = 2, …, n) as the number of uninfected people reached by prevention program i over T years. We denote overall program implementation by x = (x₁, x₂, …, x_n). We assume that programs are implemented early in the time horizon, and individuals remain on ART for their lifetime and receive prevention for T years. We assume that there is a minimum acceptable level of investment in each program, $x_i^{\mathit{\text{min}}}$, and a maximum feasible level of program implementation, $x_i^{\mathit{\text{max}}}$; thus, $0\le x_i^{\mathit{\text{min}}}\le x_i^{\mathit{\text{max}}}(i=1,\dots ,n)$. Table 1 shows all model notation.

Table 1.

Model notation

Variable	Description
T	Time horizon for program implementation, years
x1	Number of incremental people starting ART over T years due to scale up; $0\le x_1^{\mathit{\text{min}}}\le x_1\le x_1^{\mathit{\text{max}}}$
xi	Number of uninfected people reached by prevention program i (i = 2, …, n) over T years; $0\le x_i^{\mathit{\text{min}}}\le x_i\le x_i^{\mathit{\text{max}}}$
x	Number of people starting ART and reached by prevention programs; (x1, x2, …, xn-1, xn)
Q(x)	Net present number of QALYs gained from the implementation of x
IA(x)	Net present number of HIV infections averted from the implementation of x
a1	Net present number of QALYs gained per person starting ART; a1 > 0
ai	Net present number of QALYs gained per person reached by prevention program i; ai > 0
b1	Net present number of infections averted per person starting ART; b1 > 0
bi	Net present number of infections averted per person reached by prevention program i; bi > 0
qtx	Net present number of QALYs a treated individual gains from receiving ART
qIA	Net present number of QALYs an individual gains from avoiding infection
σT	Chance that a person acquires HIV in T years
εtx	Efficacy of ART in reducing sexual infectivity in infected individuals
εi	Efficacy of prevention intervention i in reducing the chance of HIV acquisition
C(x)	Net present healthcare costs in the modeled population with the implementation of x
B	Budget for HIV spending in the modeled population
C1	Net present cost of starting one additional person on ART
Ci	Net present cost of reaching one uninfected person with prevention program i for T years
sIA	Net present savings from averting an HIV infection
c1	Net present lifetime costs of ART for one person
ci	Net present cost of prevention program i for one person for T years
δQ(x)	Magnitude of overlap in QALYs gained by the implementation of x
δIA(x)	Magnitude of overlap in infections averted by the implementation of x
kQ	Overlap constant for QALYs gained; kQ > 0
kIA	Overlap constant for infections averted; kIA > 0
λ1(x1)	Average cost above baseline per person receiving ART at program coverage of x1; assumed to be nonnegative, nondecreasing, and linear
λi(xi)	Average cost above baseline per person in prevention program i at coverage of xi; assumed to be nonnegative, nondecreasing, and linear
αi	Slope of the λi(xi) function
βi	Intercept of the λi(xi) function
r	Annual discount rate for costs and health benefits
D	Cumulative discount factor for a T-year time horizon

Note: ART = antiretroviral therapy; QALY = quality-adjusted life year

We seek to maximize net present QALYs gained, Q(x), or HIV infections averted, IA(x), from the implementation of x. These terms can be written as

$$Q(\mathbf{x})={\int }_0^T{e}^{-rt}[(\mathrm{Q}\mathrm{A}\mathrm{L}\mathrm{Y}\mathrm{s}\text{experienced at time}t|\mathbf{x})-(\mathrm{Q}\mathrm{A}\mathrm{L}\mathrm{Y}\mathrm{s}\text{experienced at time}t|\mathbf{0})]dt$$

and

$$IA(\mathbf{x})={\int }_0^T{e}^{-rt}[(\text{New infections at time}t|\mathbf{0})-(\text{New infections at time}t|\mathbf{x})]dt$$

where 0 is no incremental investment in any programs and r is the discount factor. QALYs gained is a standardized health outcome measure which is particularly appropriate for comparing treatment and prevention interventions³⁴ but many decision makers also consider HIV infections averted^{14–17, 35}, so we also include that objective.

2.1 Linear Resource Allocation Problem

We define a₁ as the estimated net present number of QALYs gained per person starting ART and a_i (i = 2, …, n) as the net present number of QALYs gained per person reached by prevention program i. We assume that these values include an estimate of the direct QALY benefit to each person reached by the programs plus an estimate of the indirect QALY benefit for persons who avoid infection as a result. We similarly define b₁ and b_i as the estimated net present number of (direct and indirect) infections averted per person starting ART and per person reached by prevention program i, respectively. We describe in Section 3 how these parameters can be estimated from empirical data.

Assuming no overlap in program benefits (that is, health benefits from simultaneous program implementation equal the sum of health benefits from each program implemented alone), we can write the following objective functions:

$$Q(\mathbf{x})\cong {\sum }_{i=1}^n{a}_i{x}_i$$

$$IA(\mathbf{x})\cong {\sum }_{i=1}^n{b}_i{x}_i$$

We constrain our objective functions with a budget B such that C(x) = B, where C(x) denotes the incremental costs in the modeled population with the implementation of x. Specifically, we consider the incremental costs of treatment and prevention programs, discounted to the present at annual rate r; this accounts for the cost of the intervention itself and the savings in medical care from improved health and reduced disease transmission.

In the simplest form of the problem, we model costs linearly. We define C₁ as the net present cost of starting one additional person on ART (for life) and C_i (i = 2, …, n) as the net present cost of reaching one uninfected person with prevention program i for T years. Then total cost can be written as $C(\mathbf{x})={\sum }_{i=1}^n{C}_i{x}_i$. We assume that all C_i are positive, since a program that is costless or cost-saving would always be implemented at the maximum feasible level.

The resource allocation problem can be written as

• P1
  $${\text{max}}_{x}Q(\mathbf{x})={\sum }_{i=1}^n{a}_i{x}_i{\text{or max}}_{x}IA(\mathbf{x})={\sum }_{i=1}^n{b}_i{x}_i$$

  $$s.t.{\sum }_{i=1}^n{C}_i{x}_i=B$$

  $$x_i^{\mathit{\text{min}}}\le x_i\le x_i^{\mathit{\text{max}}},i=1,\dots ,n$$

P1 has a linear objective function and a linear budget constraint, so the optimal solution is a “greedy” solution (that is, funds are allocated sequentially to programs in increasing order of their cost-to-benefit ratio until all funds are spent).³⁶ Specifically, for maximizing QALYs, it is optimal to invest in $x_i^{\mathit{\text{min}}}$ for all programs, and then invest any remaining budget as follows: invest up to $x_i^{\mathit{\text{max}}}$ for the program with the smallest cost-to-benefit ratio, C_i/a_i (ties can be broken arbitrarily); if budget remains, repeat the process for the program with the next smallest C_i/a_i; and continue until all budget is spent. This makes intuitive sense: it is optimal to invest in the programs that have the lowest ratio of costs to benefits. The results are similar when maximizing infections averted, but the comparison is between the ratios C_i/b_i.

We note that our problem is a resource allocation problem, not a cost-effectiveness analysis, so the cost-to-benefit ratios described here should not be confused with incremental cost-effectiveness ratios. We analyze the optimal allocation of resources among programs given a fixed budget constraint and assuming independence of intervention effects. (As we will describe in the following section, we capture potential dependence between program effects with an overlap multiplier (Problem P2 below).) Our analysis determines the optimal level of investment scale up in a given program, which is different from analyzing the cost-effectiveness of one program incremental to another; instead, the goal is to spend a fixed budget in the most effective manner possible. The cost-to-benefit ratios C_i/b_i are specific to the intervention considered, and do not depend on the other interventions under consideration.

2.2 Resource Allocation Problem with Overlap

Problem P1 assumes that benefits of treatment and prevention programs are purely additive. In practice the health benefits of simultaneously implemented programs can be less than the sum of the benefits of each program if implemented alone. For example, the number of HIV infections averted from a prevention program will be less when many eligible infected individuals receive ART than when few receive ART. This is because the average infectivity of infected individuals will be lower when many individuals receive ART, thus decreasing the baseline risk faced by uninfected individuals. A number of studies of concurrent prevention and treatment programs have observed this phenomenon.^{19, 25, 26, 31, 37}

We denote the magnitude of overlap in QALYs gained and infections averted by the implementation of x as δ_q(x) and δ_IA(x), respectively. With this, we rewrite the resource allocation problem as:

• P2
  $${\text{max}}_{x}Q(\mathbf{x})={\sum }_{i=1}^n{a}_i{x}_i-{\delta }_Q(\mathbf{x}){\text{or max}}_{x}IA(\mathbf{x})={\sum }_{i=1}^n{b}_i{x}_i-{\delta }_{IA}(\mathbf{x})$$

  $$s.t.{\sum }_{i=1}^n{C}_i{x}_i=B$$

  $$x_i^{\mathit{\text{min}}}\le x_i\le x_i^{\mathit{\text{max}}},i=1,\dots ,n$$

We assume that δ_Q(0) = 0 and δ_IA(0) = 0, and that these functions are increasing in x_i. We describe in Section 3 how these functions can be estimated. If δ_Q(x) and δ_IA(x) are concave in x, then the objective function is convex. In this case, a boundary solution is optimal, and the same rules apply for optimally investing as in P1. If δ_Q(x) and δ_IA(x) are convex in x, then the objective function is concave and the optimal solution can be determined from first-order conditions.³⁸ For other forms of δ_Q(x) and δ_IA(x), an analytical solution may be difficult to attain, but the problem can be solved numerically using standard methods.³⁸

One reasonable form for the overlap function is a Cobb-Douglas function. For example, for the case of ART and one prevention program, these functions are given by δ_Q(x) = k_Qx₁x₂ and δ_IA(x) = k_IAx₁x₂, where k_Q and k_IA are nonnegative constants. These functions account for increasing overlap as a function of each program’s implementation, captured in the term x₁x₂. If either x₁ or x₂ is zero, then δ_Q(x) and δ_IA(x) are zero, since overlap is only relevant when both programs are implemented. The Cobb-Douglas functions are neither convex nor concave. If these overlap functions are used, the problem can be solved numerically (see Appendix).

2.3 Resource Allocation Problem with Overlap and Increasing Marginal Costs

We further build on the resource allocation problem by considering increasing marginal costs with program scale up (that is, diseconomies of scale). For example, costs per person reached can increase with scale up if individuals reached first are the easiest (cheapest) to reach, or if individuals reached with scale up are less adherent and require more investment to achieve behavior change.^{37, 39} Increasing marginal costs can also serve as a proxy for diminishing returns in program effectiveness as a function of program scale up.⁴⁰ While secondary transmission benefits can lead to substantial numbers of infections averted at low program coverage, it is likely that the growth of health benefits slows as coverage increases and benefits approach their maximum level. This has been observed, for example, for PrEP for HIV prevention in MSM.¹⁰ As with overlap in health benefits, increasing marginal costs (or diminishing returns) may have little impact until program coverage is high.

We denote by λ_i(x_i) the incremental average cost per person for treatment or prevention at program coverage x_i (above cost C_i(x_i)). We assume that λ_i(x_i) is a nonnegative, nondecreasing linear function,^{39, 41, 42} given by λ_i(x_i)=α_i x_i − β_i. Thus, the incremental cost is incurred when coverage exceeds a threshold level β_i/ α_i. The cost function is now

$$C_i(x_i)=\{\begin{array}{cc}\hfill C_i{x}_i,\hfill & \hfill x_i^{\mathit{\text{min}}}\le x_i\le \frac{{\beta }_i}{{\alpha }_i}\hfill \\ \hfill C_i{x}_i+({\alpha }_i{x}_i-{\beta }_i)x_i,\hfill & \hfill \frac{{\beta }_i}{{\alpha }_i}\le x_i\le x_i^{\mathit{\text{max}}}\hfill \end{array}$$

where the terms C_i are as defined in the previous section.

With this modification, the resource allocation problem becomes

• P3
  $${\text{max}}_{x}Q(\mathbf{x})={\sum }_{i=1}^n{a}_i{x}_i-{\delta }_Q{\text{or max}}_{x}IA(\mathbf{x})={\sum }_{i=1}^n{b}_i{x}_i-{\delta }_{IA}(\mathbf{x})$$

  $$s.t.{\sum }_{i=1}^n{C}_i(x_i)=B$$

  $$x_i^{\mathit{\text{min}}}\le x_i\le x_i^{\mathit{\text{max}}},i=1,\dots ,n$$

Since the budget constraint is piecewise, there are n×n cases to consider and, as before, the form of δ_Q(x) and δ_IA(x) affects the analytical tractability. The problem can be solved numerically, and some specific cases can be solved analytically.

We describe in the Appendix how to find the optimal solution to the resource allocation problems P2 and P3 for the special case of ART and one prevention program, with overlap given by Cobb-Douglas functions.

2.4 Evaluating Cost-Effectiveness

Models of HIV resource allocation typically assume a fixed budget to be allocated to maximize health impact,^{14–18, 35, 43} making the implicit assumption that any programs that are invested in will be incrementally cost-effective and that any minimum constraints on investment ($x_i^{\mathit{\text{min}}}$ in our formulation) are appropriate. If there are no lower or upper limits on investment in any intervention, then the budget will always be spent and our framework will determine the set of investments that maximizes health benefit. In this case, there is a single dominant solution (same cost, equal or greater health benefit compared to all other possible investments) whose cost-effectiveness compared to the status quo can be readily determined.

When there are limits on investment in some or all interventions, then further analysis is needed to determine the efficiency and cost-effectiveness of alternative portfolios. In this case, one could solve the resource allocation problem separately for all possible combinations of interventions and then examine the cost-effectiveness plane to determine the incremental cost-effectiveness of various investments. We provide an example in Section 4.

3. Parameter Estimation

Since the model is intended to provide decision makers with a simple method of determining the optimal allocation of resources between treatment and prevention, it is important that planners can easily estimate model inputs. We now provide a set of simple rules for estimating key model parameters, summarized in Table 2. We define a discount factor $D={\sum }_{t=1}^T\frac{1}{{(1+r)}^t}$ that we use in calculating net present values of costs and health benefits.

Table 2.

Parameter estimation guidelines^*

Health Benefit Parameters
Discount factor: $D={\sum }_{t=1}^T\frac{1}{{(1+r)}^t}$   Treatment: a1 ≅ qtx + qIA(b1/D)   Prevention: ai ≅ qIA(σTεi + (bi/D)), i = 2, …, n
Estimation Guidelines
qtx	Net present number of QALYs a treated individual gains from receiving ART; estimates available in literature or can be estimated from existing models
qIA	Net present number of QALYs an individual gains from avoiding infection; estimates available in literature or can be estimated from existing models
σT	Chance that a person acquires HIV in T years   Stable epidemic: ${\sigma }_T\cong 1-{(\frac{\#\text{uninfected at end of year}}{\#\text{uninfected at start of year}})}^T$   Growing epidemic: ${\sigma }_T\cong \frac{1-{(\frac{\#\text{uninfected at end of year}j}{\#\text{uninfected at start of year}j})}^T+1-{(\frac{\#\text{uninfected at end of year}k}{\#\text{uninfected at start of year}k})}^T}{2}$
εtx	Efficacy of ART in reducing sexual infectivity in infected individuals; estimates available in literature
εi	Efficacy of prevention intervention i in reducing the chance of HIV acquisition; estimates available in literature
b1	Net present number of infections averted per person starting ART   Stable epidemic: $b_1\cong (\frac{\#\text{new infections per year}}{\#\text{untreated}+(1-{\epsilon }_{tx})\times \#\text{treated}}-\frac{\#\text{new infections per year}\times (1-{\epsilon }_{tx})}{\#\text{untreated}+(1-{\epsilon }_{tx})\times \#\text{treated}})\times D$   Growing epidemic: $b_1\cong \left[\right(\begin{array}{c}\hfill \frac{\#\text{new infections in year}j}{\#\text{untreated in year}j+(1-{\epsilon }_{tx})\times \#\text{treated in year}j}\hfill \\ \hfill +\frac{\#\text{new infections in year}k}{\#\text{untreated in year}k+(1-{\epsilon }_{tx})\times \#\text{treated in year}k}\hfill \end{array})-(\begin{array}{c}\hfill \frac{\#\text{new infections in year}j\times (1-{\epsilon }_{tx})}{\#\text{untreated in year}j+(1-{\epsilon }_{tx})\times \#\text{treated in year}j}\hfill \\ \hfill +\frac{\#\text{new infections in year}k\times (1-{\epsilon }_{tx})}{\#\text{untreated in year}k+(1-{\epsilon }_{tx})\times \#\text{treated in year}k}\hfill \end{array}\left)\right]\times \frac{1}{2}D$
bi	Net present number of infections averted per person starting prevention program i   Stable epidemic: $b_i\cong {\sigma }_T{\epsilon }_i(\frac{\#\text{new infections per year}}{\#\text{infected at start of year}})\times D$   Growing epidemic: $b_i\cong {\sigma }_T{\epsilon }_i\left(\text{min}\right((\frac{\#\text{new infections in year}j}{\#\text{infected at start of year}j}),(\frac{\#\text{new infections in year}k}{\#\text{infected at start of year}k})\left)\right)\times D$
Cost Parameters
Discount factor: $D={\sum }_{t=1}^T\frac{1}{{(1+r)}^t}$   Treatment: C1 ≅ c1 − sIA(b1/D)   Prevention: Ci ≅ ci − sIA(σTεi + (bi/D)), i= 2, …, n
Estimation Guidelines
c1	Difference in discounted lifetime healthcare costs for an infected individual receiving ART and an infected individual who never receives ART; estimates available in literature
ci	Net present cost of prevention program i for one person for T years; estimates available in literature or can be calculated based on program components
sIA	Difference in discounted lifetime healthcare costs for an infected individual and an uninfected individual; estimates available in literature

Note: ART = antiretroviral therapy; QALY = quality-adjusted life year

^*A number of simplifying assumptions are made in creating the parameter estimates. QALY gains from treatment (a₁) are estimated as the direct QALY gains to the individual being treated plus estimated secondary QALY gains accruing from other individuals in the population who thereby avoid infection. The net present QALY gains from prevention (a_i) are estimated as the direct QALY gains when the individual avoids infection plus estimated secondary QALY gains when other individuals thereby avoid infection. The chance a person acquires HIV in T years (σ_T) is a cumulative probability calculated without conditioning on whether the individual survives previous periods. The net present number of infections averted per person starting ART (b₁) is calculated as the difference in the number of infections caused per year by untreated individuals versus treated individuals, multiplied by the length of the time horizon and the discount factor. The net present number of infections averted per person starting prevention program i (b_i) is calculated assuming an average rate of new infections per year, multiplied by the annual chance a person acquires HIV infection, the efficacy of the prevention program, the length of the time horizon, and the discount factor. The net present per person cost of treatment (C₁) is calculated as the cost of treatment for the person who enrolls in treatment minus an estimate of averted treatment costs from individuals who thereby avoid infection. The net present per person cost of a prevention program (C_i) is calculated as the cost of the program minus an estimate of averted treatment costs from an individual who avoids infection and other individuals who thereby avoid infection.

3.1 Estimation of Health Benefits Parameters

QALY parameters (a_i)

The number of net present QALYs gained per person from ART, a₁, can be calculated as the sum of the (net present) QALYs a treated individual gains from receiving ART, q_tx, and the (net present) QALYs gained from infections averted as a result of that individual receiving ART. The QALYs gained from infections averted depend on the net present QALY gain to an individual from avoiding infection, q_IA, and the number of infections averted, b₁. Thus a₁ ≅ q_tx + q_IA(b₁/D). Estimates for q_tx and q_IA can be obtained from the available literature or estimated from existing disease models; we discuss how to estimate b₁ below.

The number of net present QALYs gained per person from prevention program i, a_i, is a function of both the individual’s decreased chance of becoming infected and infections averted because of the epidemic effects from decreased incidence, b_i. We model the individual’s decreased chance of becoming infected as σ_Tε_i, where σ_T is the average chance a person acquires HIV in T years and ε_i is the efficacy of prevention intervention i in reducing the chance of HIV acquisition. This leads to a_i ≅ q_IA(σ_Tε_i + (b_i/D)). An estimate for ε_i can be obtained from the literature.

The method of estimating σ_T, the average chance that a person acquires HIV in T years, depends on the characteristics of the epidemic. For a stable epidemic, such as that in the overall population of MSM in the US, σ_T can be calculated based on the fairly stable yearly incidence. The chance of not acquiring HIV infection in one year can be calculated as the number of uninfected people at the end of the year divided by the number uninfected at the start of the year. The chance of acquiring HIV within T years can then be calculated as 1 – (chance of not acquiring HIV in 1 year)^T. For a rapidly growing epidemic, the calculation of σ_T must take into account the growth in incidence over time. In this case we can calculate σ_T using incidence estimates from two time points in the epidemic. This could be an estimate from past years’ data, a current estimate, or a projection for the future, depending on what data is available to the decision maker. The overall σ_T can be estimated as the average of the σ_T for the low and high incidence time points, with each σ_T calculated using the methodology described above.

Infections averted parameters (b_i)

The net present number of infections averted per person from treatment or prevention, b₁ or b_i, also depends on the characteristics of the epidemic. For a stable epidemic, to estimate b₁ we first estimate the number of new infections each year caused by treated versus untreated infected individuals. We assume this does not change over time in a stable epidemic. We estimate the number of HIV-infected individuals in the population who are currently receiving ART, based on available data. We then calculate the number of new infections caused by untreated individuals using the assumption that treated individuals’ contribution to incidence is reduced by the efficacy of ART in reducing infectivity, ε_tx. The number of infections caused by an untreated individual in one year is then calculated as:

$$\frac{\#\text{new infections per year}}{\#\text{untreated}+(1-{\epsilon }_{tx})\times \#\text{treated}}$$

and the number of infections caused by a treated individual in one year would be this reduced by a factor of (1− ε_tx). We multiply these numbers by the discount factor D to estimate the net present number of new infections caused in T years. Then, the difference between the number caused by an untreated individual and the number caused by a treated individual is b₁. For a rapidly growing epidemic, the methodology for estimating b₁ is similar, but we use incidence estimates from two time points, as we do for calculating σ_T. We calculate the number of infections caused by an untreated individual and a treated individual, as described above, in the low incidence year and in the high incidence year, and then use the average of those to calculate the net present number of new infections caused in T years by each type of individual. As before, the difference is b₁.

We estimate b_i for prevention program i by multiplying an individual’s reduction in the chance of acquiring infection (σ_Tε_i, as described above) by the net present number of infections he would cause over T years if he became infected. In a stable epidemic, the net present number of infections caused per infected person over T years is the number of annual new infections divided by the total number of infected people at the start of the year, multiplied by the discount factor:

$$\frac{\#\text{new infections per year}}{\#\text{infected at start of year}}\times D.$$

In a rapidly growing epidemic, we calculate the number of infections caused per person per year for two time points in the epidemic. To be conservative, since prevention programs may exhibit diminishing returns,^{10, 40, 44, 45} we use the smaller of the two estimates to calculate b_i.

3.2 Estimation of Cost Parameters (C_i)

We now provide simple rules for estimating the net present cost of starting (and maintaining) one additional person on ART, C₁, and the net present cost of reaching one uninfected person with prevention program i for T years, C_i. Each parameter is a function of the cost of either ART or prevention for one person, as well as the savings from infections averted as a result of the person receiving ART or prevention. We define the net present savings from averting an HIV infection as s_IA. This is the difference in discounted lifetime healthcare costs for an infected individual and an uninfected individual; an estimate for s_IA can be obtained from the literature. For treatment, we assume that once an individual starts ART, he remains on treatment for the rest of his life. We estimate the net present lifetime costs of treatment as c₁. This is the difference in discounted lifetime healthcare costs for an infected individual receiving ART and an infected individual who never receives treatment; this parameter can be estimated from the literature. We then calculate C₁ as C₁ ≅ c₁ − s_IA(b₁/D).

Similarly, we define c_i as the discounted cost of prevention program i for one person for T years. This can either be obtained from the literature or calculated based on the costs of each component of the prevention program and the number of people reached by the program. In estimating C_i, we additionally factor in the savings in healthcare costs from a lower chance of each individual becoming HIV infected, σ_Tε_i, and infections averted because of epidemic effects, b_i. This leads to C_i ≅ c_i − s_IA(σ_Tε_i + (b_i/D)).

3.3 Estimation of Overlap Functions (δ_q(x) and δ_IA(x))

In the Appendix we outline methods for estimating k_Q and k_IA for the two-program problem with Cobb-Douglas production functions. These estimates are based on program effectiveness, average incidence, time horizon T, and initial size of the susceptible population. For the case of n programs, one approach to estimating overlap is to estimate the pairwise overlap between each pair of programs, using a method such as that described in the Appendix, and then include the corresponding overlap factors whenever investment in two or more programs is made. We illustrate this approach in Section 4.

In practice, overlap factors will generally be very small relative to the health benefits a_i and b_i and only noticeable when program implementation is high. Hence, it may be reasonable to ignore overlap when solving for the optimal treatment and prevention mix if implementation levels are relatively low. For the examples in Section 4, inclusion of overlap does not change the optimal solution.

4. Examples: Treatment and Prevention for MSM in the US

We illustrate our models with the two-program examples of ART and two types of prevention for MSM in the US: PrEP and community-based education (CBE), as well as a three-program example that considers all three interventions. MSM account for 56–61% of estimated new HIV infections in the US^{46, 47} and are an important group to reach with HIV control measures. Preexposure prophylaxis with daily antiretroviral drugs (ARVs) reduced HIV acquisition by 44% among MSM in the iPrEx study.⁹ However, PrEP is very costly, so it is important to examine investment in PrEP compared to investment in ART. Previous studies have assessed the cost-effectiveness of PrEP compared to no PrEP for MSM in the US but have not compared it with investment in ART.^{10, 27, 48} Community-based education, conversely, is a fairly low cost intervention aimed at reducing HIV risk behaviors. One such program, the Mpowerment Project, was found to modestly reduce the prevalence and frequency of unprotected anal intercourse in young MSM.⁴⁹ A previous study found the Mpowerment Project was cost-effective compared to no intervention, but did not compare it with investment in ART.⁵⁰

We estimated parameter values for ART, PrEP, and CBE (Table 3) using the guidelines described in Section 3. Where necessary, we drew values from the literature or estimated them using a previously published model of the HIV epidemic in MSM in the US.¹⁰ We examined the general adult MSM population of approximately 4.3 million men.^{51, 52} We estimated 12.3% HIV prevalence in this population. Annual incidence is fairly stable at 0.8%.^{47, 51–54} We considered a time horizon of 20 years of program implementation and discounted costs, QALYs, and infections averted at 3% annually.³⁴ We considered a total budget of $10 billion, estimated as 50% of the US federal budget for domestic HIV prevention.⁵⁵ We assumed 50,000 ≤ x₁ ≤400,000 and 10,000 ≤ x_i ≤ 3,000,000; these are lower and upper limits on the number of people receiving ART and prevention program i, respectively. We assumed that a non-zero minimum investment was required for prevention program i because various factors, such as ethical and societal considerations, are involved in setting investment priorities.

Table 3.

Key parameter values for numerical examples of antiretroviral therapy (ART) and prevention for MSM (comprising either preexposure prophylaxis (PrEP) or community-based education (CBE))

Parameter	PrEP and ART	CBE and ART	Source
Time Horizon
Time horizon for program implementation, years, T	20	20	Assumed
Program Constraints
Minimum acceptable ART scale up level, $x_1^{\mathit{\text{min}}}$	50,000	50,000	Assumed
Maximum feasible ART scale up level, $x_1^{\mathit{\text{max}}}$	400,000	400,000	Assumed
Minimum acceptable prevention implementation level, $x_2^{\mathit{\text{min}}}$	10,000	10,000	Assumed
Maximum feasible prevention implementation level, $x_2^{\mathit{\text{max}}}$	3,000,000	3,000,000	Assumed
Health Benefits
Net present QALYs gained per person starting ART, a1	15.53	15.53	Calculated (see Section 3.1)
Net present QALYs gained per person reached by prevention program, a2	1.24	0.222	Calculated (see Section 3.1)
Net present infections averted per person starting ART, b1	0.873	0.873	Calculated47, 51, 53 (see Section 3.1)
Net present infections averted per person reached by prevention program, b2	0.054	0.010	Calculated9, 47, 49, 51, 53 (see Section 3.1)
Net present QALYs gained from receiving ART, qtx	5	5	10
Net present QALYs gained from avoiding infection, qIA	9	9	10, 62
Chance of acquiring HIV in T years, σT	14.6%	14.6%	Calculated47, 51, 52 (see Section 3.1)
ART efficacy in reducing sexual infectivity, εtx	90%	90%	3, 63–65
Prevention efficacy in reducing the chance of HIV acquisition, ε2	44%	8%	9, 49
Costs
Budget for HIV spending, B	$10 billion	$10 billion	Estimated55
Net present cost of starting one person on ART, C1	$118,100	$118,100	Calculated (see Section 3.2)
Net present cost of reaching one person with prevention program for T years, C2	$140,393	$272	Calculated (see Section 3.2)
Net present savings from averting an HIV infection, sIA	$70,000	$70,000	10, 62
Net present lifetime cost of ART for one person, c1	$200,000	$200,000	10
Net present cost of prevention program for one person for T years, c2	$150,000	$2,000	Calculated10, 50 (see Section 3.2)
Overlap constant* for QALYs gained, kQ	1.44E-06	2.62E-07	Calculated (see Appendix)
Overlap constant* for infections averted, kIA	1.51E-07	2.75E-08	Calculated (see Appendix)
Cost of ART above baseline, λ1(x1)	0	0	Assumed
Cost of prevention above baseline, λ2(x2)	.05x2−300 for x2>6,000	.01x2−200 for x2>20,000	Estimated39, 42
Discount rate for costs, QALYs and new infections, r	3%	3%	34

Note: ART = antiretroviral therapy; PrEP = preexposure prophylaxis; CBE = community-based education; QALY = quality-adjusted life year

^*Assumes overlap functions of the form δ_Q(x) = k_Qx₁x₂ and δ_IA(x) = k_IAx₁x₂.

4.1 PrEP and ART

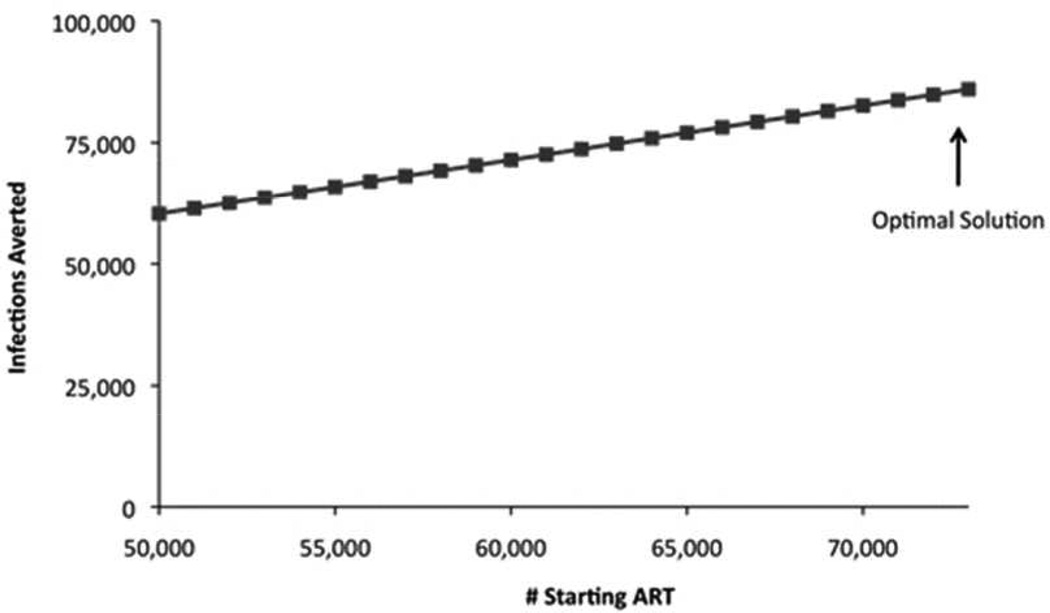
When considering the two-program problem of ART versus PrEP, for both P1 (which assumes linear costs and no intervention overlap) and P2 (which includes overlap in program effects), the optimal solution is to spend the minimum amount required on PrEP (x₂=10,000 people receiving PrEP) and invest the remaining budget in ART scale up (x₁=72,786 incremental people receiving ART). This is the case regardless of whether the objective is to maximize QALYs gained or infections averted. This is intuitive because the per person benefits from ART are greater than those from PrEP, and the per person costs are less. This allocation results in approximately 1,142,000 QALYs gained and 64,000 HIV infections averted over 20 years (Figure 1).

Figure 1.

Linear estimates of health benefits from investments in ART and PrEP for MSM in the US. Estimated health benefits for each level of implementation of x1, the incremental number of people receiving ART, are plotted for P2. Any budget remaining after x1 is implemented is invested in x2, PrEP. Only feasible values of x1 are considered (e.g., from x_1^min=50,000 to the level of x1 achievable at x_2^min). Figure 1a shows QALYs gained, Figure 1b shows infections averted. ART = antiretroviral therapy; PrEP = preexposure prophylaxis; QALY = quality-adjusted life year.

We also considered the case of diminishing returns for PrEP (problem P3). We estimated that the per person cost of PrEP increases for each person receiving PrEP once x₂ reaches 6,000. The costs of ART remain linear. However, because $x_2^{\mathit{\text{min}}}>\mathrm{6,000}$, the marginal cost of PrEP is increasing. The optimal investment decision remains the same as for the case of linear costs of PrEP: implement $x_2^{\mathit{\text{min}}}$ (10,000 people receiving PrEP) and invest the remaining budget in ART. Since implementing $x_2^{\text{min}}$ costs more with nonlinear costs, it is only feasible to implement up to x₁=72,769 incremental people receiving ART. The numbers of QALYs gained and infections averted are just slightly lower than in P1 and P2 but within the rounding of our reporting.

4.2 Community-Based Education and ART

Community-based education is a much lower-cost intervention than PrEP, with a lower cost-to-health-benefit ratio than ART. In the two-program problem, for both P1 (linear costs and no intervention overlap) and P2 (which includes overlap in program effects), the optimal solution is to invest the maximum amount in CBE and invest the remaining budget in ART scale up. In this example, there is budget remaining after investing in $x_2^{\mathit{\text{max}}}$ people reached by CBE, leading to the optimal solution of x₁=77,754 incremental people receiving ART and x₂=3,000,000 people reached by CBE. This is the case regardless of whether the objective is to maximize QALYs gained or infections averted. This allocation results in approximately 1,873,000 QALYs gained and 97,000 HIV infections averted over 20 years.

For a community-based intervention, costs may be higher than in the base case for certain cities and subgroups of MSM. Hence, we considered the case of increasing marginal costs for CBE (problem P3). We estimated that the per person cost of CBE increases once x₂ reaches 20,000. The costs of ART remain linear, but the costs of CBE are linear or quadratic, depending on the level of implementation. The QALY maximizing solution is x₁=84,184 incremental people receiving ART and x₂=72,549 people reached by CBE, with approximately 1.3 million QALYs gained. The solution that averts maximal infections is x₁=84,446 incremental people receiving ART and x₂=48,397 people reached by CBE, with approximately 74,000 HIV infections averted.

4.3 PrEP, Community-Based Education and ART

We also considered the three-program example of ART versus PrEP versus CBE. For P1, with the base case parameter values, the optimal solution is to spend the minimum amount required on PrEP (x₂=10,000 people receiving PrEP), the maximum possible on CBE (x₃=3,000,000 people receiving CBE) and invest the remaining budget in ART scale up (x₁=65,877 incremental people receiving ART). This is the case regardless of whether the objective is to maximize QALYs gained or infections averted. This results in approximately 1,701,000 QALYs gained and 88,000 HIV infections averted over 20 years. To apply problem framework P2, we approximate overlap in the three-program problem as the sum of the overlap between ART and PrEP and between ART and CBE. The optimal solution remains unchanged, but the resulting QALYs gained and infections averted are slightly lower due the effects of overlap (approximately 1,648,000 QALYs gained and approximately 83,000 HIV infections averted over 20 years). As is intuitive, the health outcomes when all three programs are considered fall between those attained in the two-program examples, but they are more similar to those attained by investment in ART and CBE, since most investment is allocated to CBE. When all three programs are considered, health benefits are diminished because of the constraint on minimum investment in PrEP, which is a less efficient intervention than CBE and ART; if there is no such constraint, no money is invested in PrEP and the optimal solution is the same as for the case of ART and CBE.

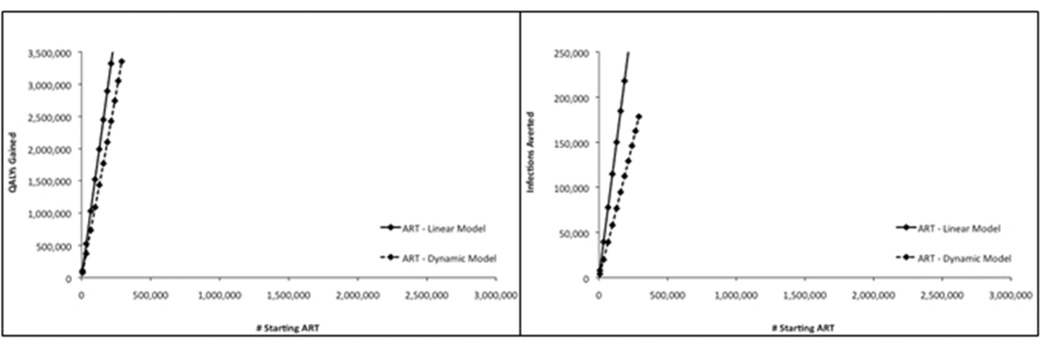
4.4 Comparison of Results with Dynamic Model Results

To assess the accuracy of our models, we compared the health benefits we estimated using P1 with those from a previously published dynamic model of HIV in MSM in the US.¹⁰ Figure 2 shows QALYs gained and infections averted as estimated by each method for varying levels of investment in ART, PrEP, and CBE. The results from the two models are fairly similar, suggesting that the assumption of linearity in our simple model is reasonable. The optimal solution of investing maximally in ART before investing in PrEP and investing in CBE before investing in ART is consistent between the two models. Where there are differences between the simple and dynamic models (for ART, the linear model accurately estimates QALYs but overestimates infections averted; for CBE and PrEP, the linear model accurately estimates infections averted but overestimates QALYs), the relative scale of ART, PrEP, and CBE benefits is still consistent between the two models, indicating that the simple model is likely “good enough” for informing resource allocation decisions.

Figure 2.

Estimated health benefits from investment in antiretroviral therapy (ART, Figure 2a), preexposure prophylaxis (PrEP, Figure 2b), and community-based education (CBE, Figure 2c) for MSM in the US calculated by a linear model (P1; solid lines) and a dynamic model (dashed lines). Estimated health benefits are plotted for separate ART, PrEP, and CBE programs as determined by the linear model in this study (P1) and a previously published dynamic model. Figure 2a shows QALYs gained and infections averted for ART, Figure 2b shows QALYs gained and infections averted for PrEP, and Figure 2c shows QALYS gained and infections averted for CBE. ART = antiretroviral therapy; CBE = community-based education; PrEP = preexposure prophylaxis; QALY = quality-adjusted life year.

4.5 Cost-Effectiveness Analysis

The above examples have considered various combinations of the three interventions and with constraints on levels of investment. Figure 3 shows net present costs and QALYs for the optimal portfolio corresponding to each possible combination of interventions, and assuming the upper and lower limits on investment as described above. We assumed that at most 3 million people could be reached by CBE, so when investing in just CBE, only $816 million is spent. For all other sets of interventions, the entire $10 billion budget is spent.

Figure 3.

Estimated net present costs and QALYs over a 20-year time horizon from investment in all possible combinations of ART, PrEP, and CBE for MSM in the US calculated by a linear model (P1). Upper and lower limits on investment in each intervention are as described in the text. ART = antiretroviral therapy; CBE = community-based education; PrEP = preexposure prophylaxis; QALY = quality-adjusted life year; ICER = incremental cost-effectiveness ratio.

We can use the information in Figure 3 to ask the question: given the set of interventions considered in a portfolio, is the corresponding optimal investment cost-effective compared to the status quo? The least cost-effective portfolio occurs when only PrEP is considered ($113,600/QALY gained compared to the status quo). The most cost-effective portfolio occurs CBE is considered ($1200/QALY gained compared to the status quo). All other portfolios have incremental cost-effectiveness ratios (ICERs, compared to the status quo) that fall between these two values.

We can also ask the question: what combinations of interventions lie on the efficient frontier, and what is their ICER compared to the next least costly alternative on the efficient frontier? For our example, the portfolio of CBE only and the portfolio of CBE and ART lie on the efficient frontier. Adding ART to a portfolio that includes CBE costs $7600/QALY gained. For this example, then, a decision maker could conclude that it is most cost-effective to invest just in CBE but is also cost-effective to invest in ART and CBE, and that portfolios that include PrEP or do not include CBE would be dominated by other alternatives.

4.6 Sensitivity Analysis

In sensitivity analysis, we assessed how several key factors – the efficacy of the prevention program, the time horizon of program implementation, and the nature of the epidemic in the modeled population – affect the results. Table 4 shows parameter values for the ART and PrEP scenarios examined. For simplicity, we assumed linear program costs.

Table 4.

Key parameter values for sensitivity analysis of numerical example of antiretroviral therapy (ART) and preexposure prophylaxis (PrEP) for MSM

Parameter	High PrEP Efficacy	Shorter Time Horizon	Rapidly Growing Epidemic	Source
Time Horizon
Time horizon for program implementation, years, T	20	5	20	Assumed
Program Constraints
Minimum acceptable ART scale up level, $x_1^{\mathit{\text{min}}}$	50,000	10,000	10,000	Assumed
Maximum feasible ART scale up level, $x_1^{\mathit{\text{max}}}$	400,000	100,000	100,000	Assumed
Minimum acceptable PrEP implementation level, $x_2^{\mathit{\text{min}}}$	10,000	2,000	1,000	Assumed
Maximum feasible PrEP implementation level, $x_2^{\mathit{\text{max}}}$	3,000,000	1,000,000	500,000	Assumed
Health Benefits
Net present QALYs gained per person starting ART, a1	15.53	7.64	28.94	Calculated
Net present QALYs gained per person starting PrEP, a2	2.04	0.199	2.91	Calculated
Net present infections averted per person starting ART, b1	0.873	0.269	1.98	Calculated47, 51, 53
Net present infections averted per person starting PrEP, b2	0.089	0.004	0.160	Calculated9, 47, 49, 51, 53
Net present QALYs gained from receiving ART, qtx	5	5	5	10
Net present QALYs gained from avoiding infection, qIA	9	9	9	10, 62
Chance of acquiring HIV in T years, σT	14.6%	3.9%	24.5%	Calculated47, 51, 52
ART efficacy in reducing sexual infectivity, εtx	90%	90%	90%	3, 63, 64
PrEP efficacy in reducing the chance of HIV acquisition, ε2	73%	44%	44%	9
Costs
Budget for HIV spending, B	$10 billion	$2.5 billion	$5 billion	Estimated55
Net present cost of starting one person on ART, C1	$118,100	$179,490	$13,800	Calculated
Net present cost of starting one person on PrEP for T years, C2	$134,139	$44,449	$127,404	Calculated
Net present savings from averting an HIV infection, sIA	$70,000	$70,000	$70,000	10, 62
Net present lifetime cost of ART for one person, c1	$200,000	$200,000	$200,000	10
Net present cost of PrEP for one person for T years, c2	$150,000	$46,000	$150,000	Calculated10
Overlap constant* for QALYs gained, kQ	2.39E-06	3.80E-07	2.32E-05	Calculated (see Appendix)
Overlap constant* for infections averted, kIA	2.51E-07	3.54E-08	2.13E-06	Calculated (see Appendix)
Discount rate for costs, QALYs and new infections, r	3%	3%	3%	34

Note: ART = antiretroviral therapy; PrEP = preexposure prophylaxis; QALY = quality-adjusted life year

^*Assumes overlap functions of the form δ_Q(x) = k_Qx₁x₂ and δ_IA(x) = k_IAx₁x₂.

In the iPrEx study, PrEP reduced HIV incidence by 73% in patients who reported or exhibited high adherence to the daily regimen.⁹ With this higher efficacy (versus 44% assumed in the base case), the number of QALYs gained and infections averted per person receiving PrEP increases, and the net present per person cost of PrEP decreases. However, ART is still a more efficient investment than PrEP and it is still optimal to spend the minimum amount on PrEP and invest the remaining budget in ART. Since the net per person cost of PrEP is lower, there is more budget remaining after investing in $x_2^{\mathit{\text{min}}}$ so x₁ is higher than in the base case, with 73,316 incremental people receiving ART. Studies of PrEP among heterosexuals^56–59 and injection drug users⁶⁰ have found reductions in risk of HIV acquisition ranging from 0% to 75%. For any of these efficacy levels, if achieved among MSM, our analysis shows that ART is a more efficient investment than PrEP.

The base case assumed that CBE reduces risky behavior by 8%. If CBE reduces risky behavior by only 4% or less, when the objective is to maximize infections averted, it becomes optimal to invest more than the minimum amount in ART scale up. The optimal solution is to invest $x_2^{\mathit{\text{min}}}$ in CBE and invest all remaining budget in ART scale up, for 84,616 incremental people receiving ART. When maximizing QALYs gained, it only becomes optimal to invest more than the minimum amount in ART scale up when CBE reduces risky behavior by less than 1%.

In the base case we considered a 20-year time horizon for PrEP use and ART scale up. Decision makers may prefer a shorter time horizon, since they are often concerned with short-term budgets rather than long-term expenditures. Accordingly, we examined a 5-year time horizon. Again, the optimal solution is to spend the minimum amount on PrEP and invest the remaining budget in ART scale up (x₁=13,433 incremental people receiving ART). However, shortening the time horizon leads to a greater decrease in the health benefits of PrEP, a₂ and b₂, than in the benefits of ART, a₁ and b₁ (Figure 4). This is because treatment yields an immediate benefit, both in the QALY gain to the individual receiving treatment and in the protection conferred to others. The benefits of PrEP are more dependent on epidemic effects accumulating over time, while ART confers immediate protection to all partners of treated individuals.

Figure 4.

Estimate of QALYs gained (Figure 4a) and HIV infections averted (Figure 4b) for ART and PrEP for MSM in the US as a function of time horizon of program implementation. Estimated per person health benefits (a1, a2, b1, b2) are plotted for ART and PrEP as a function of the time horizon of program implementation. The percentage of the benefits from 20-year implementation is noted for T=5. Figure 4a shows QALYs gained (a1, a2), Figure 4b shows infections averted (b1, b2). ART = antiretroviral therapy; PrEP = preexposure prophylaxis; QALY = quality-adjusted life year.

The same trend can be seen with the comparison of ART and CBE. Shortening the time horizon to 5 years (versus 20 years in the base case) leads to a greater decrease in benefits from CBE than from ART. As before, the optimal solution is to invest only the minimum amount in ART scale up and to invest all remaining funds in CBE. However, in this case there is budget remaining after investing the maximum possible in CBE, leading to the optimal solution of x₁=12,889 incremental people receiving ART and x₂=1,000,000 reached by CBE.

The base case considered the general MSM population in the US, which has a fairly stable HIV epidemic. A rapidly growing epidemic presents very different conditions for disease control. In sensitivity analysis we considered an epidemic with prevalence growing from 5% to 18% over 20 years, and with incidence growing from 0.7% to 2.2% during this same period. This could be similar to the epidemic in some subgroups of MSM, such as young African American MSM.^{46, 47} When we solve our model for ART and PrEP in this type of epidemic, the optimal solution is again to spend the minimum amount on PrEP and invest the remaining budget in ART scale up. With our assumed budget and minimum acceptable levels of program implementation, there is excess budget after implementing up to $x_1^{\mathit{\text{max}}}$ (x₁=100,000 incremental people receiving ART), so x₂=28,414 people receive PrEP. In this scenario, the ratio of PrEP health benefits, a₂ and b₂, to ART benefits, a₁ and b₁, is greater than in the base case. This is because prevention is relatively more important in a rapidly growing epidemic, where incidence is high and there are many potential infections to prevent. The same result is seen for CBE, but the greater number of infections averted per person in the rapidly growing epidemic leads to the program being cost-saving. In sensitivity analysis we did not consider the case of a diminishing epidemic, as there is less need and urgency for treatment and prevention investment.

As shown by these examples, the optimal balance of treatment and prevention depends heavily on the cost of the interventions. For PrEP, a very expensive preventive intervention, it is always optimal to invest only the minimum required amount in PrEP (if any) and spend the remaining budget on scaling up ART. Even with very high PrEP efficacy, the high cost of PrEP precludes it from being a better value investment than ART. Similarly, CBE is a low-cost intervention, and it is optimal to invest in CBE before ART scale up unless CBE effectiveness is extremely low.

5. Discussion

Treatment scale up and prevention programs are both important in combating the HIV epidemic. Our model provides a simple yet accurate framework for determining the optimal mix of program investment.

Our analysis demonstrates that HIV budgets are often best spent on the program that offers the greatest “bang for the buck.” This is an intuitive finding, which is supplemented by the simple methods we outline for estimating the health benefits and costs of treatment and prevention programs. Decision makers could easily solve our model in a spreadsheet after collecting and estimating model inputs. The inputs, such as HIV incidence, prevalence, baseline ART use, and per person cost of prevention, are less extensive than for a dynamic model and draw from data to which public health decision makers would typically have access. Additionally, for the example analyses we carried out, the inclusion of program overlap did not change the optimal resource allocation, suggesting that good solutions can be obtained without estimating possible program overlap effects, as long as program coverage is not extremely high.

We illustrated our model with the example of ART, PrEP and CBE in MSM in the US. We saw that it is always better to invest in ART scale up rather than PrEP, because ART has a better ratio of health benefits to costs. Even with high PrEP efficacy or in a rapidly growing epidemic, factors that could tip the scales toward prevention, PrEP is a much less efficient use of resources than is ART scale up. This adds interesting context to the debate on PrEP use, especially given the ethical considerations of using ARVs for uninfected individuals when many infected individuals still need treatment.⁶¹ Community-based education is a much less costly intervention. With linear costs, it is best to invest as much as possible in such a program before investing in treatment scale up, but if the program has increasing marginal costs, a mix of investment in ART scale up and prevention may be optimal.

We consider the objectives of maximizing QALYs gained and HIV infections averted. For our example analyses, the choice of objective function did not change the optimal resource allocation. In other cases, particularly when the potential portfolio includes both prevention and treatment programs, the two objective functions may yield different solutions. Then QALYs gained may be the most appropriate objective to consider, as it comprehensively captures benefits of both treatment and prevention.³⁴

Our analysis has several limitations. Our framework accounts for net present costs of treatment and prevention and their future impact on the HIV epidemic. However, decision makers may think in terms of shorter time horizons and prefer to budget accordingly. Additionally, similar to most existing HIV resource allocation models, we have framed our problem as one of allocating a given budget among a predefined set of interventions, subject to upper and lower limits on investment in each intervention. To determine the most efficient set of interventions to invest in, one must compare the costs and health benefits for each possible set of interventions. If desired, one can also use the framework to determine the diminution in health benefits (if any) arising from minimum required levels of investment in interventions. Such analysis is straightforward using our framework.

We approximate diminishing returns with nonlinear cost functions. Incorporating diminishing returns in the objective functions in addition to the cost functions could lead to a more accurate estimate of program effects. This would be a straightforward extension of the model but would affect analytical tractability. Additionally, we approximate dynamic effects with a static model. For the example problem of HIV control among MSM in the US, we showed that the resource allocation results from our static model (invest first in CBE, then ART, then PrEP) matched the results obtained using a more comprehensive dynamic model. For a very rapidly growing epidemic or when high levels of intervention coverage are considered, the static model may be a less accurate approximation of the epidemic dynamics and may overestimate health effects of interventions. The overestimation occurs because of diminishing epidemic returns as interventions are scaled up (the same infection cannot be prevented twice); such dynamic effects are not captured by the linear model. In such a case, use of a more complex dynamic model may be appropriate.

We designed our model to be applicable across different settings and for many types of HIV prevention programs. Although we developed it with the intention of comparing treatment and prevention programs, it could also be used to compare only prevention programs. Just as the basic structure facilitates comparing treatment to various types of prevention programs, one could estimate inputs for various prevention programs and solve for the optimal investment accordingly. Public health officials regularly must make decisions about how to allocate resources for HIV prevention, and our simple model could assist them in such decisions.

The simplicity of our model design also allows it to be used for different types of HIV epidemics (different growth rates or a different population). While populations targeted for HIV control are heterogeneous, with varied risk behaviors and mixing patterns, our model is intended to consolidate those factors into the model inputs, resulting in greater ease of use than with complex dynamic models. A decision maker who wishes to address different risk groups separately could utilize the model separately for each group (with appropriately estimated parameters), assuming the groups are independent.

HIV is a persistent burden in the US and worldwide, and only limited resources are available to control the epidemic. Public health decision makers need simple tools that help determine the optimal balance of investment in treatment and prevention. Our model can provide a simple yet accurate basis for determining optimal investment.

APPENDIX

Optimality Conditions for the Case of an ART Program, One Prevention Program, a Cobb-Douglas Overlap Function, and Increasing Marginal Costs

Consider the case of ART and one prevention program, with cost functions given by

$$C_i(x_i)=\{\begin{array}{cc}\hfill C_i{x}_i,\hfill & \hfill x_i^{\mathit{\text{min}}}\le x_i\le \frac{{\beta }_i}{{\alpha }_i}\hfill \\ \hfill C_i{x}_i+({\alpha }_i{x}_i-{\beta }_i)x_i,\hfill & \hfill \frac{{\beta }_i}{{\alpha }_i}\le x_i\le x_i^{\mathit{\text{max}}}\hfill \end{array}$$

and overlap functions given by δ_Q(x) = k_Qx₁x₂ and δ_IA(x) = k_IAx₁x₂, where k_Q and k_IA are nonnegative constants. The resource allocation problem P3 is then:

$${\text{max}}_{x_1,x_2}Q(x_1,x_2)=a_1{x}_1+a_2{x}_2-k_Q{x}_1{x}_2$$

or

$${\text{max}}_{x_1,x_2}IA(x_1,x_2)=b_1{x}_1+b_2{x}_2-k_{IA}{x}_1{x}_2$$

$$s.t.C_1(x_1)+C_2(x_2)=B$$

$$x_1^{\mathit{\text{min}}}\le x_1\le x_1^{\mathit{\text{max}}}$$

$$x_2^{\mathit{\text{min}}}\le x_2\le x_2^{\mathit{\text{max}}}$$

Since the budget constraint is piecewise, we have four cases to consider:

$$(1)x_1\le \frac{{\beta }_1}{{\alpha }_1},x_2\le \frac{{\beta }_2}{{\alpha }_2};(2)x_1\le \frac{{\beta }_1}{{\alpha }_1},x_2>\frac{{\beta }_2}{{\alpha }_2};(3)x_1>\frac{{\beta }_1}{{\alpha }_1},x_2\le \frac{{\beta }_2}{{\alpha }_2};(4)x_1>\frac{{\beta }_1}{{\alpha }_1},x_2>\frac{{\beta }_2}{{\alpha }_2}.$$

To solve this problem, we determine which cases are feasible based on the lower and upper limits for x₁ and x₂. We then compare the optimal solutions for each feasible case.

In Case 1, the budget constraint is linear since x₁ and x₂ are small enough that diminishing returns do not yet take effect. Therefore Case 1 is simply P2. When we rearrange the budget constraint to obtain x₂ as a function of x₁ and substitute this into the objective functions, Q(x₁, x₂) and IA(x₁, x₂) are strictly convex functions. We can show that $\frac{d^{2}Q(x_1)}{d{x}_1^2}=2k_Q\frac{C_1}{C_2}$ and $\frac{d^{2}IA(x_1)}{d{x}_1^2}=2k_{IA}\frac{C_1}{C_2}$, which are strictly greater than zero when overlap is present, since k_Q > 0 and k_IA > 0. Thus, the optimal solution is a boundary solution, as for P1. The same rules for optimally investing apply as in P1.

For Case 2, the budget constraint is C₁x₁ + C₂x₂ + (α₂x₂ − β₂)x₂ = B. We solve this for x₁ as a function of x₂: $x_1=\frac{B-C_2{x}_2-({\alpha }_2{x}_2-{\beta }_2)x_2}{C_1}$. We then substitute to obtain an objective function of one variable. Our optimization problem becomes

$$\underset{x_2}{\text{max}}Q(x_2)=a_1\frac{B-C_2{x}_2-({\alpha }_2{x}_2-{\beta }_2)x_2}{C_1}+a_2{x}_2-k_Q{x}_2\frac{B-C_2{x}_2-({\alpha }_2{x}_2-{\beta }_2)x_2}{C_1}$$

or

$$\underset{x_2}{\text{max}}IA(x_2)=b_1\frac{B-C_2{x}_2-({\alpha }_2{x}_2-{\beta }_2)x_2}{C_1}+b_2{x}_2-k_{IA}{x}_2\frac{B-C_2{x}_2-({\alpha }_2{x}_2-{\beta }_2)x_2}{C_1}$$

$$s.t.\text{max}(x_2^{\mathit{\text{min}}},\frac{{\beta }_2}{{\alpha }_2})\le x_2\le \text{min}(x_2^{\mathit{\text{max}}},x_2^{\mathit{\text{bound}}})$$

where $x_2^{\mathit{\text{bound}}}$ is the nonnegative minimum of $\frac{{\beta }_2-C_2\pm \sqrt{{(C_2-{\beta }_2)}^2-4{\alpha }_2(C_1{x}_1^{\mathit{\text{min}}}-B)}}{2{\alpha }_2}$. The objective function is cubic, so its convexity depends on x₂. For example, for maximizing QALYs gained, the objective function is strictly convex when $x_2>\frac{1}{3}(\frac{a_1}{k_Q}-\frac{C_2-b_2}{{\alpha }_2})$. Because of the nature of the objective function, rather than determining whether the function is convex or concave in the feasible range of x₂ for Case 2, for simplicity we check the optimality of all feasible boundary and interior solutions to determine which solution is optimal. We evaluate the objective function at the following solutions $(x_1^{*},x_2^{*})$:

Solution type	$x_1^{*}$	$x_2^{*}$
Lower boundary	$\text{min}(x_1^{\mathit{\text{max}}},\frac{B-C_2{x}_2^{*}-({\alpha }_2{x}_2^{*}-{\beta }_2)x_2^{*}}{C_1})$	$\text{max}(x_2^{\mathit{\text{min}}},\frac{{\beta }_2}{{\alpha }_2})$
Upper boundary	$\text{min}(x_1^{\mathit{\text{max}}},\frac{B-C_2{x}_2^{*}-({\alpha }_2{x}_2^{*}-{\beta }_2)x_2^{*}}{C_1})$	$\text{min}(x_2^{\mathit{\text{max}}},x_2^{\mathit{\text{bound}}})$
Interior	$\text{min}(x_1^{\mathit{\text{max}}},\frac{B-C_2{x}_2^{*}-({\alpha }_2{x}_2^{*}-{\beta }_2)x_2^{*}}{C_1})$	$\mathrm{m}in(x_2^{\mathit{\text{int}}})$
Interior	$\text{min}(x_1^{\mathit{\text{max}}},\frac{B-C_2{x}_2^{*}-({\alpha }_2{x}_2^{*}-{\beta }_2)x_2^{*}}{C_1})$	$\text{max}(x_2^{\mathit{\text{int}}})$

where

$$x_2^{\mathit{\text{int}}}=\frac{-(k_Q{C}_2-k_Q{\beta }_2-a_1{\alpha }_2)\pm \sqrt{{(k_Q{C}_2-k_Q{\beta }_2)}^2+k_Q{\alpha }_2[3(k_{Q}B-a_2{C}_1)+a_1(C_2-{\beta }_2)]+a_1^2{\alpha }_1^2}}{3k_Q{\alpha }_2}$$

or

$$x_2^{\mathit{\text{int}}}=\frac{-(k_{IA}{C}_2-k_{IA}{\beta }_2-b_1{\alpha }_2)\pm \sqrt{{(k_{IA}{C}_2-k_{IA}{\beta }_2)}^2+k_{IA}{\alpha }_2[3(k_{IA}B-b_2{C}_1)+b_1(C_2-{\beta }_2)]+b_1^2{\alpha }_1^2}}{3k_{IA}{\alpha }_2}$$

and the feasibility of both values of $x_2^{\mathit{\text{int}}}$ would need to be confirmed.

Case 3 is very similar to Case 2, but the budget constraint is quadratic in x₁ rather than x₂: C₁x₁ + (α₁x₁ − β₁)x₁ + C₂x₂ = B. We follow the same steps in solving the problem as in Case 2. We first solve the budget constraint for x₂ as a function of x₁: $x_2=\frac{B-C_1{x}_1-({\alpha }_1{x}_1-{\beta }_1)x_1}{C_2}$. We substitute to obtain an objective function of one variable, and our optimization problem becomes

$$\underset{x_1}{\text{max}}Q(x_1)=a_2\frac{B-C_1{x}_1-({\alpha }_1{x}_1-{\beta }_1)x_1}{C_2}+a_1{x}_1-k_Q{x}_1\frac{B-C_1{x}_1-({\alpha }_1{x}_1-{\beta }_1)x_1}{C_2}$$

or

$$\underset{x_1}{\text{max}}IA(x_1)=b_2\frac{B-C_1{x}_1-({\alpha }_1{x}_1-{\beta }_1)x_1}{C_2}+b_1{x}_1-k_{IA}{x}_1\frac{B-C_1{x}_1-({\alpha }_1{x}_1-{\beta }_1)x_1}{C_2}$$

$$s.t.\text{max}(x_1^{\mathit{\text{min}}},\frac{{\beta }_1}{{\alpha }_1})\le x_1\le \text{min}(x_1^{\mathit{\text{max}}},x_1^{\mathit{\text{bound}}})$$

where $x_1^{\mathit{\text{bound}}}$ is the nonnegative minimum of $\frac{{\beta }_1-C_1\pm \sqrt{{(C_1-{\beta }_1)}^2-4{\alpha }_1(C_2{x}_2^{\mathit{\text{min}}}-B)}}{2{\alpha }_1}$. The convexity of the objective function depends on x₁ because it is cubic. For example, for maximizing QALYs gained it is strictly convex when $x_1>\frac{1}{3}(\frac{a_2}{k_Q}-\frac{C_1-b_1}{{\alpha }_1})$. Just as with Case 2, we evaluate the objective function for the feasible boundary and interior solutions $(x_1^{*},x_2^{*})$ to determine which solution is optimal. The solutions we check are as follows:

Solution type	$x_1^{*}$	$x_2^{*}$
Lower boundary	$\text{max}(x_1^{\mathit{\text{min}}},\frac{{\beta }_1}{{\alpha }_1})$	$\text{min}(x_2^{\mathit{\text{max}}},\frac{B-C_1{x}_1^{*}-({\alpha }_1{x}_1^{*}-{\beta }_1)x_1^{*}}{C_2})$
Upper boundary	$\text{min}(x_1^{\mathit{\text{max}}},x_1^{\mathit{\text{bound}}})$	$\text{min}(x_2^{\mathit{\text{max}}},\frac{B-C_1{x}_1^{*}-({\alpha }_1{x}_1^{*}-{\beta }_1)x_1^{*}}{C_2})$
Interior	$\mathrm{m}in(x_1^{\mathit{\text{int}}})$	$\text{min}(x_2^{\mathit{\text{max}}},\frac{B-C_1{x}_1^{*}-({\alpha }_1{x}_1^{*}-{\beta }_1)x_1^{*}}{C_2})$
Interior	$\text{max}(x_1^{\mathit{\text{int}}})$	$\text{min}(x_2^{\mathit{\text{max}}},\frac{B-C_1{x}_1^{*}-({\alpha }_1{x}_1^{*}-{\beta }_1)x_1^{*}}{C_2})$

where the term $x_1^{\mathit{\text{bound}}}$ is the nonnegative minimum of $\frac{{\beta }_1-C_1\pm \sqrt{{(C_1-{\beta }_1)}^2-4{\alpha }_1(C_2{x}_2^{\mathit{\text{min}}}-B)}}{2{\alpha }_1}$ and

$$x_1^{\mathit{\text{int}}}=\frac{-(k_Q{C}_1-k_Q{\beta }_1-a_2{\alpha }_1)\pm \sqrt{{(k_Q{C}_1-k_Q{\beta }_1-a_2{\alpha }_1)}^2-3k_Q{\alpha }_1(a_1{C}_2-a_2(C_1-{\beta }_1)-k_{Q}B)}}{3k_Q{\alpha }_1}$$

or

$$x_1^{\mathit{\text{int}}}=\frac{-(k_{IA}{C}_1-k_{IA}{\beta }_1-b_2{\alpha }_1)\pm \sqrt{{(k_{IA}{C}_1-k_{IA}{\beta }_1-b_2{\alpha }_1)}^2-3k_{IA}{\alpha }_1(b_1{C}_2-b_2(C_1-{\beta }_1)-k_{IA}B)}}{3k_{IA}{\alpha }_1}$$

and the feasibility of both values of $x_1^{\mathit{\text{int}}}$ must be confirmed.

For Case 4, the budget constraint is quadratic in both in x₁ and x₂: C₁x₁ + (α₁x₁ − β₁)x₁ + C₂x₂ + (α₂x₂ − β₂)x₂ = B. This constraint is strictly convex:

$$\frac{d^{2}C}{d{x}_1^2}=2{\alpha }_1>0$$

$$\frac{d^{2}C}{d{x}_2^2}=2{\alpha }_2>0$$

$$\frac{d^{2}C}{d{x}_1^2}\frac{d^{2}C}{d{x}_2^2}-{\left[\frac{d^{2}C}{d{x}_{1}d{x}_2}\right]}^2=4{\alpha }_1{\alpha }_2>0$$

The objective function, Q(x₁, x₂) = a₁x₁ + a₂x₂ − k_Qx₁x₂ or IA(x₁, x₂) = b₁x₁ + b₂x₂ − k_IAx₁x₂, is neither convex nor concave:

$$\frac{d^{2}Q}{d{x}_1^2}=0$$

$$\frac{d^{2}Q}{d{x}_2^2}=0$$

$$\frac{d^{2}Q}{d{x}_1^2}\frac{d^{2}Q}{d{x}_2^2}-{\left[\frac{d^{2}Q}{d{x}_{1}d{x}_2}\right]}^2=-{(k_Q)}^2<0$$

and

$$\frac{d^{2}IA}{d{x}_1^2}=0$$

$$\frac{d^{2}IA}{d{x}_2^2}=0$$

$$\frac{d^{2}IA}{d{x}_1^2}\frac{d^{2}IA}{d{x}_2^2}-{\left[\frac{d^{2}IA}{d{x}_{1}d{x}_2}\right]}^2=-{(k_{IA})}^2<0$$

Thus this is a general case of constrained optimization, and we must use the first-order conditions to solve it. We determine the first-order conditions and solve for interior solutions, and then we test the optimality of feasible boundary and interior solutions $(x_1^{*},x_2^{*})$. The solutions we check are as follows:

Solution type	$x_1^{*}$	$x_2^{*}$
Lower boundary, x1	$\text{max}(x_1^{\mathit{\text{min}}},\frac{{\beta }_1}{{\alpha }_1})$	$\text{min}(x_2^{\mathit{\text{max}}},x_2^{\mathit{\text{bound}}})$
Lower boundary, x2	$\text{min}(x_1^{\mathit{\text{max}}},x_1^{\mathit{\text{bound}}})$	$\text{max}(x_2^{\mathit{\text{min}}},\frac{{\beta }_2}{{\alpha }_2})$
Interior	Numerically solve for $(x_1^{*},x_2^{*})$: $-2k_Q{\alpha }_1{(x_1^{*})}^2+(2a_2{\alpha }_1+k_Q({\beta }_1-C_1))x_1^{*}+a_2(C_1-{\beta }_1)$ $=-2k_Q{\alpha }_2{(x_2^{*})}^2+(2a_1{\alpha }_2+k_Q({\beta }_2-C_2))x_2^{*}+a_1(C_2-{\beta }_2)$ or $-2k_{IA}{\alpha }_1{(x_1^{*})}^2+(2b_2{\alpha }_1+k_{IA}({\beta }_1-C_1))x_1^{*}+b_2(C_1-{\beta }_1)$ $=-2k_{IA}{\alpha }_2{(x_2^{*})}^2+(2b_1{\alpha }_2+k_{IA}({\beta }_2-C_2))x_2^{*}+b_1(C_2-{\beta }_2)$ $x_2^{*}=\frac{{\beta }_2-C_2\pm \sqrt{{(C_2-{\beta }_2)}^2-4{\alpha }_2[{\alpha }_1{(x_1^{*})}^2+(C_1-{\beta }_1)x_1^{*}-B]}}{2{\alpha }_2}$

where the term $x_1^{\mathit{\text{bound}}}$ is the nonnegative minimum of $\frac{{\beta }_1-C_1\pm \sqrt{{(C_1-{\beta }_1)}^2-4{\alpha }_1[{\alpha }_2{(x_2^{\mathit{\text{min}}})}^2+(C_2-{\beta }_2)x_2^{\mathit{\text{min}}}-B]}}{2{\alpha }_1}$ and $x_2^{\mathit{\text{bound}}}$ is the nonnegative minimum of $\frac{{\beta }_2-C_2\pm \sqrt{{(C_2-{\beta }_2)}^2-4{\alpha }_2[{\alpha }_1{(x_1^{\mathit{\text{min}}})}^2+(C_1-{\beta }_1)x_1^{\mathit{\text{min}}}-B]}}{2{\alpha }_2}$.

Estimation of Overlap Factors for the Example of ART, PrEP, and CBE in the US

We used simulation results from a dynamic model of treatment and prevention among MSM in the US¹⁰ to develop estimation methods for k_Q and k_IA. We determined that the constants k_Q and k_IA depend on HIV incidence in the population, efficacy of treatment and prevention in terms of a₁ and b₁ and ε_i, time horizon T, and the initial size of the susceptible population, for $k_Q=\frac{(\text{average incidence})\times a_1\times {\epsilon }_i\times (33.5)\mathit{\text{ln}}(T)}{(\#\text{initially susceptible})}$ and $k_{IA}=\frac{(\text{average incidence})\times b_1\times {\epsilon }_i\times (3t-(7570)(\text{average incidence})+188)}{(\#\text{initially susceptible})}$. Overlap is inversely proportional to the initial size of the susceptible population. This is intuitive: when the susceptible population is large, treatment and prevention programs will be spread among many people, whereas when the susceptible population is small, both programs are trying to protect the same people. Overlap increases with a₁ and b₁ and ε_i, which is also intuitive because the magnitude of the overlap depends on the magnitude of health benefits from each intervention. QALYs gained are slightly less affected by overlap than are infections averted, since some fraction of the QALYs gained are due to benefits to the individuals being treated, and those QALYs are not affected by concurrent implementation of a prevention program.

When solving the two-program case of P2, we assume the budget would always be fully utilized. One can imagine that if k_Q or k_IA were large enough, the objective function would begin to decrease at some threshold of x₁ and x₂ and so health benefits would be greater if implementation did not go beyond that point. However, because k_Q and k_IA are likely to be very small relative to a_i and b_i, we assume that increasing x₁ and x₂ always yields positive health outcomes, and thus the budget constraint would always be binding.