Abstract
In this work, we develop a Bayesian approach to perform selection of predictors that are linked within a network. We achieve this by combining a sparse regression model relating the predictors to a response variable with a graphical model describing conditional dependencies among the predictors. The proposed method is well-suited for genomic applications since it allows the identification of pathways of functionally related genes or proteins which impact an outcome of interest. In contrast to previous approaches for network-guided variable selection, we infer the network among predictors using a Gaussian graphical model and do not assume that network information is available a priori. We demonstrate that our method outperforms existing methods in identifying network-structured predictors in simulation settings, and illustrate our proposed model with an application to inference of proteins relevant to glioblastoma survival.
Keywords: Bayesian variable selection, Gaussian graphical model, protein network, linear model
1. Introduction
In this work, we address the problem of identifying predictors that are both relevant to a response variable of interest and functionally related to one another. In the context of genomic studies, the mechanism for an effect on an outcome such as a quantitative phenotype or disease risk is typically a coordinated change within a pathway, and the impact of a single gene may not be strong. In this setting, our proposed inference method can highlight pathways or regulatory networks which impact the response. To uncover these relationships, we develop a Bayesian modeling approach which favors selection of variables that are not only relevant to the outcome of interest but also linked within a conditional dependence network. Unlike previous approaches which incorporate network information into variable selection, we do not assume that the graph relating the predictors is known. Instead, we develop a joint model to learn both the set of relevant predictors and estimate a graphical model describing their interdependence.
There is increasing evidence from genome-wide association studies that complex traits are governed by a large number of genomic variants with small effects, making them difficult to detect in the absence of very large sample sizes [4, 5, 6]. Importantly, however, genes do not act in isolation: instead, they affect phenotypes indirectly through complex molecular networks. One of the primary motivations for incorporating network information into regression modeling is that coordinated weak effects are often grouped into pathways [7], so accounting for the relationships among the predictors has the potential to increase power to detect true associations. Although there are many databases which provide information on biochemical relationships under normal conditions, the available reference networks may be incomplete or inappropriate for the experimental condition or set of subjects under study. Rather than assuming that a relevant prior network is available, it is therefore of interest to infer one directly from the data at hand. Learning networks from high-throughput data relies on the assumption that genes, proteins, or metabolites which have similar patterns of abundance are likely to have an underlying biological relationship. Although the inferred connections are based on correlations rather than direct experimental observation, approaches for network reconstruction based on these assumptions have been shown to be accurate in learning regulatory or functional pathways [1]. In particular, co-expression networks derived from microarray data have been shown to correspond quite well to known functional organization across all categories of genes [2], and it has been demonstrated that correlation-based methods perform well in recovering protein signaling networks from flow cytometry data [3].
A number of recent papers use a known network describing the relationships among predictors to inform variable selection. Li and Li [8, 9] propose a regularized regression approach, combining a lasso penalty to encourage sparsity with a penalty based on the graph Laplacian to encourage smoothness of the coefficients with respect to a graph. Pan et al. [10] develop a single penalty using the weighted Lγ norm of the coefficients of neighboring nodes which more strongly encourages grouped variable selection. Huang et al. [11] combine a minimax concave penalty with a quadratic Laplacian penalty to achieve consistency in variable selection. Most recently, Kim et al. [12] propose a penalty structure which encourages the selection of neighboring nodes but avoids the assumption that their coefficients should be similar.
In the Bayesian framework, Li and Zhang [13] and Stingo and Vannucci [14] incorporate a graph structure in the Markov random field (MRF) prior on indicators of variable selection, encouraging the joint selection of predictors with known relationships. Stingo et al. [15] and Peng et al. [16] propose selection of both known pathways and genes within them, using previously established pathway membership information and the network structure within each pathway to guide the selection. Hill et al. [17] develop an empirical Bayes approach which incorporates existing pathway information through priors that reflect a preference for the selection of variables from within a certain number of pathways or with a certain average pairwise distance within a pathway. Zhou and Zheng [18] develop a Bayesian analogue to the penalized regression approaches using the graph Laplacian, with an extension to allow uncertainty over the sign of edges in the graph.
In contrast to the above approaches which use a graph relating the variables as an input to a variable selection procedure, we are interested in both identifying the relevant variables and learning the network among them. Previous attempts at this problem include Dobra [19], which proposes estimating a network among relevant predictors by first performing a stochastic search in the regression setting to identify sets of predictors with high posterior probability, then applying a Bayesian model averaging approach to estimate a dependency network given these results. Liu et al. [20] propose a Bayesian regularization method which uses an extended version of the graph Laplacian as the precision matrix for a multivariate normal prior on the coefficients. They infer relationships among these coefficients by thresholding their estimated correlations. Our proposed method differs from these approaches in that our network is based on a Gaussian graphical model among the predictors, which provides a sparse and interpretable representation of the conditional dependencies found in the data. This is very different from a network among the coefficients, which provides information on which predictors have a similar effect on the response but not on relationships among the predictors themselves. Since we rely on a Gaussian graphical model to infer the network among predictors, the predictors should be reasonably normal. This assumption is quite common and is appropriate for many biological data types: in particular, RNA, protein and metabolite levels are typically normalized as a part of the standard data processing pipeline. Our model also accommodates the inclusion of non-normal fixed covariates such as age and gender.
Our modeling approach allows inference of both the relevant variables and the network structure linking them. Importantly, our method does not require that a network structure among the predictors is known a priori. Instead, we simultaneously infer a sparse network among the predictors and perform variable selection using this network as guidance by incorporating it into a prior favoring selection of connected variables. The proposed approach not only offers good performance in terms of selection and prediction, but also provides insight into the relationships among important variables and allows the identification of related predictors which jointly impact the response. In addition, since we take a Bayesian approach to the problem of joint variable and graphical model selection, we are able to fully account for uncertainty over both the selection of variables and of the graph. This is particularly important in the context of graphical model selection since in most applications uncertainty over the graph structure is large. In contrast, stagewise estimation with graph selection as the first step following by variable selection taking the inferred graph as fixed fails to account for this uncertainty. We find that in selecting proteins relevant to glioblastoma survival, the proposed joint method not only improves prediction accuracy, but also identifies several interacting proteins which are missed using standard Bayesian variable selection.
The remainder of the paper is organized as follows. In Section 2, we first provide background on variable selection and graphical models, then specify the details of the proposed model. In Section 3, we discuss posterior inference including the Markov chain Monte Carlo (MCMC) sampling approach and selection of the variables and edges. In Section 4, we assess the performance of the proposed method via simulation studies. In Section 5, we apply the proposed method to identify a set of network-related proteins which impact glioblastoma survival. Finally, we conclude with a discussion in Section 6.
2. Methods
2.1. Variable selection and graphical models
The goal of variable selection is to identify the subset of predictors which are truly relevant to a given outcome. Selecting a sparse model can help reduce noise in estimation and produce more interpretable results, particularly when the true underlying model is sparse. This is often the case when dealing with high-throughput biological data such as gene or protein expression, where typically only a small number of markers out of many thousands assayed are believed to be associated to a disease outcome. Traditional methods for variable selection include forward, backward, and stepwise selection. More recently, penalized methods based on the lasso [21], which places an L1 penalty on the regression coefficients to achieve sparsity, have become popular. In the Bayesian framework, stochastic search variable selection [22] is a widely used variable selection approach for linear regression. In this method, latent indicators are used to represent variable inclusion, and the prior on the coefficient for a given variable is a mixture density with a “spike” at 0 if the variable is not included and a diffuse “slab” if the variable is included.
When dealing with related variables, we may be interested in inferring the dependencies among them. An undirected graph, or Markov random field, is represented by G = (V, E) where V is a set of vertices and E is a set of edges such that the edge (i, j) ∈ E if and only if (j, i) ∈ E. Undirected graphical models, which use a graph structure to represent conditional dependencies among variables, have the property that there is no edge between the vertices representing two variables if and only if the variables are independent after conditioning on all other variables in the data set. In the context of multivariate normal data, graphical models are known as Gaussian graphical models (GGMs) or covariance selection models [23]. In this setting, the graph structure G implies constraints on the precision matrix Ω, the inverse of the covariance matrix Σ. Specifically, the entry ωij = 0 if and only if the edge (i, j) is missing from the graph G, meaning that variables i and j are conditionally independent. Since graphical model estimation corresponds to estimation of a sparse version of Ω, regularization methods are a natural approach. In particular, the graphical lasso [24, 25, 26], which imposes an L1 penalty on the sum of the absolute values of the entries of Ω, is a popular method for achieving the desired sparsity in estimation of Ω.
In the Bayesian framework, the G-Wishart [27, 28] is the conjugate prior for Ω constrained by an arbitrary graph G. Even when the graph structure is known, sampling from this distribution poses computational difficulties since both the prior and posterior normalizing constants are intractable. Recent proposals addressing the challenge of G-Wishart sampling include Dobra et al. [29], Wang and Li [30] and Lenkoski [31]. Despite improvements in efficiency, the scalability of these methods is still limited. The Bayesian graphical lasso [32], proposed as the Bayesian analogue of the frequentist graphical lasso, uses shrinkage priors to allow more efficient model fitting. However, it does not model the graph structure directly and therefore only allows graph inference through some form of thresholding on the posterior precision matrix. In previous work, we have utilized both type of priors, taking advantage of the Bayesian graphical lasso to integrate relevant prior information when inferring metabolic networks [33] and the G-Wishart when inferring multiple graphical models across related sample groups [34]. Here we adopt the recent approach of Wang [35] which avoids some of the computational issues of G-Wishart sampling (in particular, the need to approximate the normalizing constant) but still allows inference directly on the graph structure through a prior that combines a continuous spike-and-slab prior on entries of the precision matrix with binary latent indicators of edge inclusion. This approach allows scaling to several hundred variables, while previous methods based on G-Wishart sampling were limited to a few dozen.
2.2. Proposed joint model
Let yi represent the observed response variable and Xi represent the observed vector of p predictors for the ith subject, where i = 1,…, n. The Xi correspond to a potentially large set of related predictors, such as gene or protein abundances, of which we are interested in both identifying an explanatory subset and understanding their interrelation. In our modeling approach, we consider both the response Yn×1 and the predictors Xn×p to be random variables, so our likelihood is the joint distribution f(Y, X). Because we assume Y to be a function of X, we can factor the joint distribution into the conditional distribution of Y given X and the marginal distribution of X
| (1) |
We then define f(Y|X) as a linear regression model and f(X) as a multivariate normal distribution. In the model for Y|X, we include a set of m additional covariates Zi which are not subject to selection. These may correspond to clinical variables such as age or gender. We write the conditional distribution of y given X as
| (2) |
where α0 is the intercept term, αm×1 and βp×1 represent the respective effects of Z and X, the εi are iid errors, and τ2 is the error variance. Although the y in equation (2) represents a continuous outcome, the model can be extended in a straightforward manner to allow binary, multinomial, or survival responses, as discussed in Section 2.7 and in the Supplement. The distribution of the predictors X, which are assumed to be centered, is
| (3) |
where Ω = Σ−1 is the precision matrix of the multivariate normal distribution.
2.3. Prior on coefficients β
We consider the jth variable to be included in the model if its coefficient βj ≠ 0. The problem of variable selection therefore corresponds to the problem of inferring which βs are nonzero. We follow the stochastic search variable selection approach [22] in formulating a prior on the coefficients β1,…, βp which allows sparse inference. To summarize the inclusion of predictors in the model, we introduce a vector of latent indicator variables γ. The prior for βj conditional on γj is a mixture of a normal density and a Dirac delta function δ0, which can be written as
| (4) |
where hβ > 0 is a fixed hyperparameter. Following the recommendation in Sha et al. [36] and Stingo et al. [15], hβ should be set to a value within the range of the variability of X. This type of mixture prior is known as a spike-and-slab prior.
2.4. Graph selection prior on Ω and G
The goal of the graph selection prior is to allow inference of a network among the predictors X. We take advantage of recent improvements in the scalability of Bayesian graphical model inference, as mentioned in Section 2.1, to infer a network among all predictors, avoiding the need for a separate variable screening step. Here we follow the proposal of Wang [35] in using a hierarchical prior which relies on latent binary indicators for edge inclusion. Specifically, let gij ∈ {0,1} represent the presence of edge (i,j) in the graph G, where i < j. The prior distribution on the precision matrix Ω from equation (3) combines an exponential prior on the diagonal entries with a mixture of normals on the off-diagonal entries of to allow the entries for selected edges to have a larger variance than that of non-selected edges:
| (5) |
where {C(G, ν0, ν1, λ)} is the normalizing constant, ν0 > 0 is small, ν1 > 0 is large, λ > 0, and I{Ω∈M+} is an indicator function which restricts the prior to the space of symmetric positive definite matrices. By choosing ν0 to be small, we ensure that ωij will be close to 0 for non-selected edges. For selected edges, a large value of ν1 allows ωij to have more substantial magnitude. In the second level of the hierarchy, we place a prior on the edge inclusion indicators gij:
| (6) |
where C(ν0, ν1, λ, π) is a normalizing constant and π reflects the prior probability of edge inclusion. The parameters ν0, ν1, λ and π are all taken to be fixed. Guidance on the selection of these parameters is provided in Wang [35], which reports that values of νo ≥ 0.01 and ν1 ≤ 10 result in good convergence and mixing for standardized data. Wang [35] recommends the choice of λ = 1 but finds that the results are relatively insensitive to this choice, and suggests that 2/(p − 1) is a sensible setting for π. In addition, Wang [35] provides performance measurements under a variety of parameter combinations. Since these hyperparameters have an impact under our model not only on the selection of edges, but also indirectly on the selection of variables, we provide sensitivity analysis for π in the Supplement. We find that the number of selected variables is not strongly sensitive to this choice.
2.5. Prior linking variable selection indicators γ to selection of the graph G
The standard prior in the Bayesian literature for the variable selection indicators γ is an independent Bernoulli
where λ is the prior probability of variable inclusion. Instead of an independent prior, we propose a prior that allows us to tie the selection of variables to the presence of edges relating them in the graph. To accomplish this, we rely on a Markov random field (MRF) prior favoring the inclusion of variables which are linked to other variables in the network. MRF priors have been utilized in the variable selection context by Li and Zhang [13] and Stingo and Vannucci [14]. However, unlike these authors, who assume that the structure of the network among predictors is known, we incorporate inference of the network structure. We express the prior for γ conditional on G as
| (7) |
where a and b are scalar hyperparameters and G is an adjacency matrix representation of the graph. In this formulation, the parameter a affects the probability of variable inclusion, with smaller values corresponding to sparser models. The parameter b determines how strongly the probability of inclusion for a variable is affected by the inclusion of its neighbors in the graph. As noted in Li and Zhang [13], increasing values of b may lead to a phase transition in which the number of included variables rises sharply. For guidance on choosing a value of b which corresponds to a sparse model, see Section 3.1 of Li and Zhang [13].
To summarize, our prior linking variable and edge selection reflects a preference for the inclusion of connected predictors in the model by incorporating a Markov random field on the variable selection indicators which utilizes the estimated network among predictors. The proposed model is therefore appropriate for data sets where the predictors which affect the outcome of interest are in fact connected through a network. As discussed in Section 1, this is the case for a broad range of biological settings where there is an interest in associating gene, protein, or metabolite levels to complex traits or disease risk.
2.6. Conjugate priors for error variance τ2, intercept α0, and coefficients of fixed covariates α
For the prior on the error variance τ2 in equation (2), we use the standard conjugate prior
| (8) |
where IG is the inverse-gamma density, and a0 > 0 and b0 > 0 are fixed hyperparameters. For the prior on the intercept α0, we use the standard conjugate prior
| (9) |
where h0 is a fixed hyperparameter. For the prior on the coefficient vector α in equation (2), which represents the effects of additional covariates which are not subject to selection, we use the standard conjugate prior
| (10) |
where 0 is the prior mean, Im represents the m × m identity matrix, and hα > 0 is a fixed hyperparameter. As in the choice of hβ, we follow Sha et al. [36] and Stingo et al. [15] in recommending that hα should be set within the range of the variability of Z, and h0 should be fixed to a large value so that the prior on the intercept is vague.
2.7. Extension to survival response
To accommodate survival outcomes, we use an accelerated failure time (AFT) model as in Sha, Tadesse and Vannucci [37]. Let ti represent the time to event for subject i and ci represent the censoring time. We observe times as well as censoring indicators δi = I{ti ≤ ci}. We then estimate augmented failure times yi where
| (11) |
We assume that the latent variables follow the linear model given in equation (2), and retain the prior specification as given for the standard linear model.
3. Posterior inference
The joint posterior distribution for the set of all parameters γ = {α,β, τ2, γ, Ω, G} is proportional to the product of the likelihood and the prior distributions
| (12) |
Since this joint distribution is not tractable, Markov chain Monte Carlo (MCMC) simulations are required to obtain a posterior sample of the parameters. However, this sampling may be difficult because the joint posterior space is quite complex and includes many dependent parameters. In particular, updates to the variable selection indicators γ require dimension changes for β. By integrating out some parameters and focusing on the remaining set, we can both simplify the sampler and reduce the number of iterations needed to obtain a satisfactory posterior sample of the parameters of interest. Specifically, for both the linear and AFT models, we integrate out the parameters α0, α, β and τ2 to obtain a multivariate t-distribution for Y with degrees of freedom 2a0, mean 0, and scale . The joint posterior for the simplified model is then
| (13) |
3.1. MCMC sampling
In the MCMC sampling scheme, we include steps to update the variable selection indicators γ conditional on the current graph, to update the graph G and precision matrix Ω, and to sample the latent variables if we are in the probit or AFT setting. A brief outline of the sampling scheme is given below. At the top level, the sampler follows a Metropolis-Hastings within Gibbs approach. For a full description, see the Supplement.
Update variable selection indicators γ. At each iteration, we propose either adding or removing a variable. We then accept or reject the proposed move using a Metropolis-Hastings approach, conditional on the currently selected graph.
Update the graph G and precision matrix Ω. In this step, we sample new values for the graph G and precision matrix Ω using the block Gibbs sampler proposed in Wang [35].
Update the latent variables Y for the probit or AFT models. For the probit model, this entails sampling the latent variables from a truncated multivariate normal distribution conditional on the current set of included variables. For the AFT model, we sample the augmented failure times from a truncated multivariate t-distribution.
Beginning from an arbitrary set of initial values, we iterate until we have obtained a representative sample from the posterior distribution. Samples from the burn-in period, which are affected by the initial conditions, are discarded, and the remaining samples are used as the basis for inference.
3.2. Variable selection and prediction
Since the search space of possible sets of variables is quite large, any particular model may only be encountered a limited number of times during the MCMC sampling. For this reason, we focus on the marginal posterior probabilities of inclusion (PPIs) to perform variable selection rather than the maximum a posteriori (MAP) model, which is the single model with highest posterior probability. The PPI for a variable is the proportion of MCMC iterations after the burn-in where it is included. In order to make the final model selection, a threshold is typically imposed on the PPIs. Here we use the median model, which corresponds to a threshold of 0.5. Barbieri and Berger [38] demonstrate that the median model is the optimal predictive model in the context of linear regression when the predictor matrix X satisfies the condition that X′X is diagonal, outperforming the single model with the highest posterior probability.
To perform prediction, we follow an approach similar to that given in Section 8 of [39]. Specifically, given a future set of covariates Zf and Xf, we predict Ŷ as the MCMC average
| (14) |
where T is the total number of MCMC iterations. The intercept α̂0 and coefficient vectors α̂ and β̂(t) are estimated as
| (15) |
where γ(t) is the vector of variable selection indicators from the tth MCMC iteration.
3.3. Graph selection
As the number of possible graphs is even larger than the number of possible combinations of variables, we adopt a similar approach for graph selection as for variable selection. Namely, rather than selecting the most frequently encountered graph, we select the edges marginally by including all edges with posterior probability of inclusion (PPI) greater than 0.5. This estimate is a common approach for graph selection and has been shown to perform well in practice [34, 35].
4. Simulation study
4.1. Performance comparison
In this simulation, we compare our proposed method to other variable selection methods in a regression setting with network-related predictors. We simulate the data following the setting given in Li and Li [8], but with reduced scale to allow computational tractability. In this scenario, the predictors correspond to clusters of genes consisting of a transcription factor and the genes it regulates. A subset of these regulatory pathways contribute to the outcome variable. Li and Li [8] include 4 variants on this model which allow effects of differing direction and magnitude. Specifically, in Model 1, genes within the same cluster have effects with the same sign. In Model 2, genes within the same cluster may have effects with opposite signs. Models 3 and 4 follow the same sign pattern but the effects have smaller magnitude.
In the simulation given here, we include 40 transcription factors, each of which regulates 5 genes. This corresponds to a graph with a total of 200 edges where nodes are grouped into 40 modules. The first 4 groups of transcription factors and the genes they regulate have nonzero coefficients following the same pattern as in Li and Li [8]. The complete coefficient vectors for each model are given in Table 1. Across all models, the number of true predictors is ptrue = 24 out of a total of p = 240. The expression levels X are generated from a multivariate normal with mean 0 and covariance Σ, where Σ is defined so that the variance of the expression level for each transcription factor is 1, and the correlation of the expression level of a transcription factor to the expression level of each gene it regulates is 0.7. The error variance is set to . The response variable y is generated from the linear model y = Xβ + ε where . The resulting signal-to-noise ratio (SNR) for models 1, 2, 3, and 4 are 12.5,4.7, 7.0, and 4.5, respectively. For both the training and test data, X and Y were centered.
Table 1. Coefficient values for each of the 4 simulation models described in Section 4.1.
| Model | β | |
|---|---|---|
|
| ||
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
For each of the four models, 100 training samples were used for parameter estimation, and 100 test samples were used to evaluate prediction. Variable selection and prediction were performed using the lasso [21], elastic net [40], network-constrained regularization [8], stochastic search variable selection [22] and the proposed joint graph and variable selection method. The first three models were fit using the Matlab software Glmnet available from http://web.stanford.edu/∼hastie/glmnet_matlab/. The penalty parameters were chosen via grid search to minimize 10-fold cross-validation error on the training data.
For both Bayesian methods, the parameter hβ, which determines the prior variance of the non-zero βs in equation (4), was set to the variance of the nonzero βs divided by . Since the data were centered, the intercept term α0 was assumed to be 0. As discussed by Smith [41], this is equivalent to a non-informative prior with h0 → ∞ in equation (9). The shape and scale parameters of the inverse gamma prior on τ2 given in equation (8) were set to a0 = 2 and . This choice of hyperparameters leads to a prior mean for the error variance of , corresponding to a value of 25.5 in Models 1 and 2 and a value of 17.9 in Models 3 and 4. The effect of varying b0, which corresponds to varying the mean of the inverse gamma prior, is examined in the sensitivity analysis provided in the Supplement. For the stochastic search Bayesian variable selection, the prior probability of edge inclusion was set to the true value of ptrue/p = 0.1. For the joint variable and graph selection model, we need to specify the parameters for the graph selection prior given in equations (5) and (6). Following the recommendations in Wang [35], we set ν0 = 0.1, ν1 = 10, λ = 1, and π = 2/(p − 1). We must also specify parameters for the Markov random field prior given in equation (7). We set the hyperparameter a, which controls the overall sparsity of variable selection, to -2.75, and the hyperparameter b, which affects the prior probability of inclusion for connected variables, to 0.5. When b = 0 or the graph G contains no edges, the setting for a results in a prior probability of variable inclusion around 0.06. The nonzero value of b combined with a non-empty graph will act to increase this. An analysis of the sensitivity of the variable selection to a and b is reported in the Supplement.
In running the MCMC for the Bayesian methods, the initial value for the vector of variable selection indicators γ was chosen to be 0. For the joint graph and variable selection method, the initial value for Ω was set to Ip. For both methods, we allowed 5,000 iterations of burn-in, which were discarded, followed by 5,000 iterations used as the basis for inference. Variable and edge selection were based on the criterion that the posterior probability of inclusion was greater than 0.5.
The 5 methods were compared on the basis of sensitivity (the true positive rate of variable selection), specificity (1 - the false positive rate of variable selection), the Matthews correlation coefficient (MCC) (a combined measure of the overall variable selection accuracy), the area under the ROC curve (AUC), and mean squared prediction error (PMSE). Since the number of true positives and true negatives are very different, sensitivity and specificity provide an imperfect view of variable selection accuracy. For this reason, we include the MCC, a single balanced metric summarizing classification performance which accounts for the differing numbers of true positives vs. true negatives. To assess the performance of variable selection across a range of model sizes, we also provide the AUC. Let TP represent the number of true positives (correctly identified variables), TN the number of true negatives (correctly rejected variables), FP the number of false positives (noise variables selected), and FN the number of false negatives (incorrectly rejected variables). We can then define the sensitivity, specificity, and MCC as
Estimation of the AUC requires computing sensitivity and specificity for varying levels of sparsity. For the regularization methods, the AUC was obtained by varying the L1 penalty parameter. For the elastic net and network-constrained regularization approaches, which require selection of a second penalty parameter, this parameter was chosen by performing 10-fold cross validation at each level of the L1 penalty parameter. The AUC for the Bayesian methods was obtained by varying the selection threshold for the posterior probabilities of variable inclusion. Finally, mean squared prediction error is defined as
where n is the number of observations in the test data, Ŷ is the predicted value of Y for the test data, and Ytest is the true value of Y in the test data set. The resulting values are given in Table 2.
Table 2.
Results of the simulation study for each of the 4 models described in Section 4.1 in terms of sensitivity, specificity, Matthews correlation coefficient (MCC), area under the ROC curve (AUC), and mean squared error of prediction (PMSE), given as an average across 50 simulations with standard errors in parentheses. The methods compared are the lasso, elastic net (Enet), network-constrained regularization (Li Li), stochastic search Bayesian variable selection (BVS), and the proposed joint graph and variable selection method (Joint).
| Model 1 | Model 2 | Model 3 | Model 4 | ||
|---|---|---|---|---|---|
|
| |||||
| Sensitivity | Lasso | 0.798 (0.012) | 0.544 (0.012) | 0.510 (0.010) | 0.423 (0.013) |
| Enet | 0.857 (0.013) | 0.594 (0.012) | 0.573 (0.014) | 0.464 (0.014) | |
| Li Li | 0.850 (0.014) | 0.565 (0.011) | 0.555 (0.017) | 0.462 (0.017) | |
| BVS | 0.367 (0.012) | 0.286 (0.009) | 0.222 (0.007) | 0.205 (0.005) | |
| Joint | 0.433 (0.014) | 0.320 (0.010) | 0.241 (0.006) | 0.230 (0.007) | |
|
| |||||
| Specificity | Lasso | 0.928 (0.004) | 0.916 (0.007) | 0.929 (0.006) | 0.931 (0.006) |
| Enet | 0.911 (0.005) | 0.879 (0.009) | 0.911 (0.006) | 0.918 (0.006) | |
| Li Li | 0.825 (0.023) | 0.877 (0.013) | 0.886 (0.016) | 0.898 (0.014) | |
| BVS | 0.998 (0.001) | 0.993 (0.001) | 0.997 (0.001) | 0.996 (4.8e-4) | |
| Joint | 0.999 (3.6e-4) | 0.996 (0.001) | 0.998 (4.4e-4) | 0.997 (0.001) | |
|
| |||||
| MCC | Lasso | 0.627 (0.012) | 0.430 (0.014) | 0.435 (0.014) | 0.370 (0.018) |
| Enet | 0.628 (0.013) | 0.397 (0.013) | 0.439 (0.014) | 0.370 (0.016) | |
| Li Li | 0.522 (0.020) | 0.388 (0.016) | 0.401 (0.015) | 0.344 (0.017) | |
| BVS | 0.565 (0.012) | 0.457 (0.011) | 0.425 (0.008) | 0.391 (0.007) | |
| Joint | 0.624 (0.011) | 0.513 (0.010) | 0.450 (0.008) | 0.429 (0.008) | |
|
| |||||
| AUC | Lasso | 0.883 (0.007) | 0.751 (0.008) | 0.738 (0.008) | 0.682 (0.008) |
| Enet | 0.922 (0.006) | 0.780 (0.005) | 0.777 (0.008) | 0.722 (0.009) | |
| Li Li | 0.920 (0.007) | 0.768 (0.006) | 0.772 (0.009) | 0.710 (0.008) | |
| BVS | 0.889 (0.006) | 0.795 (0.007) | 0.778 (0.006) | 0.731 (0.009) | |
| Joint | 0.923 (0.005) | 0.852 (0.007) | 0.848 (0.006) | 0.810 (0.007) | |
|
| |||||
| PMSE | Lasso | 40.6 (0.93) | 46.6 (1.17) | 24.0 (0.56) | 25.4 (0.64) |
| Enet | 40.3 (0.95) | 46.9 (1.23) | 24.5 (0.57) | 25.8 (0.67) | |
| Li Li | 42.9 (1.16) | 47.6 (1.29) | 25.0 (0.77) | 26.3 (0.81) | |
| BVS | 41.7 (0.83) | 44.7 (1.22) | 22.3 (0.49) | 23.7 (0.56) | |
| Joint | 39.0 (0.80) | 41.5 (1.06) | 21.8 (0.44) | 22.8 (0.54) | |
Based on this summary, we see that although the regularization methods (Lasso, Enet, and Li Li) tend to have good sensitivity, the proposed joint Bayesian method has much better specificity. The poor specificity of the regularization methods makes sense in the light of previous work demonstrating that selection of the regularization parameter using cross-validation is optimal with respect to prediction, but tends to result in the inclusion of too many noise predictors [24]. We therefore experimented with using a fixed penalty parameter of 1.4 for the lasso, which was chosen to achieve specificity more similar to that of the Bayesian methods, with the caveat that such a fixed choice for the penalty parameter is only possible in the context of a simulation study. Unsurprisingly, we found that a stronger penalty improves specificity, but degrades prediction. For example, in Model 1, fixing the penalty parameter to 1.4 improves specificity to 0.989, but worsens the PMSE to 47.7, much higher than when using parameters chosen using cross-validation, possibly due to overshrinkage of the coefficients when using the stronger penalty. As compared to standard Bayesian variable selection, the joint approach improves sensitivity due to greater ability to detect small effects acting within pathways, and also offers small improvements in specificity. To assess the tradeoff between sensitivity and specificity, we rely on both the MCC, which provides a single measure to assess variable selection accuracy conditional on model selection, and the AUC, which provides a summary of the trade-off between sensitivity and specificity across a range of model sizes. The proposed joint method is either best or very close to best on these metrics across all models, and also achieves the lowest PMSE across the methods compared.
Although our primary focus in comparison of methods is accuracy of variable selection, we found that the accuracy of graph structure learning for the proposed joint model was quite high across all simulation settings, with an average true positive rate for edge detection of 0.998 and average false positive rate of 3.6e-4. Since there are p · (p − 1)/2 – 200 missing edges in the graph, the corresponds to an average of 10.3 false positive edge selections.
In this section, we have demonstrated that when the network structure is relevant to the set of predictors influencing the outcome, the proposed joint model outperforms standard Bayesian variable selection in terms of both selection and prediction accuracy. We also provide a comparison in the Supplement demonstrating that when the predictors are independent, the two methods perform similarly along these metrics, so that while there is no advantage to applying the joint model to non-network related predictors, it does not degrade performance.
5. Case study
In this section, we utilize the proposed method to examine the impact of protein levels on glioblastoma survival. Specifically, we obtained protein measurements for glioblastoma patients assayed via reverse phase protein arrays (RPPA) from The Cancer Proteome Atlas (TCPA) [42]. This data is available online at http://app1.bioinformatics.mdanderson.org/tcpa/design/basic/index.html. The data set includes quantifications for 187 proteins for 215 subjects. For 212 of these subjects, we were able to obtain clinical data including age, sex and survival times, from The Cancer Genome Atlas (TCGA), available online at http://cancergenome.nih.gov. For 159 subjects, the number of days to death was recorded, while the remaining survival events are right-censored, so the reported times correspond to days to last contact. This data set is a logical setting for the application of our proposed joint graph and variable selection method since proteins typically interact within signaling pathways, and the entire pathway, rather than a single protein, can influence disease progression. Although there is a large amount of reference information on protein interactions from databases such as KEGG, these data represent different (typically healthy) conditions, which may not be relevant to the population of glioblastoma patients.
To model this data, we follow the accelerated failure time (AFT) model discussed in Section 2.7, using standardized data with age and sex as fixed covariates. In order to assess performance, we split the data into a training set of size ntrain = 175 and test set of size ntest = 37. We chose to use an uneven split with more subjects in the training set than the test set to allow better model selection given the complexity of the problem. We compare two inference approaches: standard Bayesian variable selection and the proposed joint variable and network selection method. We do not include a comparison to the regularized methods as the Glmnet software does not implement the AFT model. In addition, we do not assume that relevant prior network information is available, as is required for the method of Li and Li.
Both Bayesian methods require the choice of prior hyperparameters. Following the guidance in Sections 2.3 and 2.6, we use hα = hβ = 1 since the data are standardized, and h0 = 1 × 106. To compensate for the somewhat weaker signal vs. in the simulated data, for standard Bayesian variable selection we use a prior probability of variable inclusion of 0.2, and for the joint method, we set the parameter α to -1.75. This corresponds to a prior probability of variable selection of around 0.15 when either b = 0 or we have an empty graph. We set b to 0.5 as in the simulation, which has the effect of increasing the prior probability of variable inclusion given that the variable is connected in the graph.
As is commonly seen in real biological data, the degree of correlation among the protein measurements is quite high, in contrast to the simulation setting, in which most variables were truly independent. Since it is biologically likely that most proteins only interact with a limited number of other proteins, we increase the prior parameters ν0 and ν1 vs. the setting used in simulation in order to achieve a reasonably sparse graph. This adjustment allows us to focus on the strongest connections which are best supported by the data. Specifically, we set v0 to 0.6 and v1 to 360. Although these values are larger than those used in the simulation study, they are still within the range recommended by Wang [35] as providing good mixing and convergence. We retain the settings λ = 1 and π = 2/(p − 1) used in the simulation section.
For both variable selection approaches, we carried out MCMC simulations on the training data, performing 10,000 iterations burn-in followed by 10,000 iterations as the basis for inference. We then used these results to predict log survival times for the test data following the general idea of equations (14) and (15), modified to use the MCMC estimate of the latent value Y and to include the fixed covariates and intercept. The predicted survival times were evaluated on the basis of two metrics: the integrated Brier score [43] and the concordance index [44]. The integrated Brier score (IBS) measures the gap between the true and estimated survival curves, making scores closer to 0 the best. We compute the Brier score at time t as
| (16) |
where is the observed (possibly censored) time for subject i, Ĝ is the Kaplan-Meier estimate of the censoring distribution for subjects i = 1,…, ntest, and Ŝi(t) is the probability of subject i being alive at time t based on the survivor function estimated following Sha, Tadesse and Vannucci [37]. The integrated Brier score is simply the integral of the Brier score from time 0 to the maximum survival time :
| (17) |
where tmax is the maximum survival time in the test data set. Our second metric, the concordance index (C-index), measures the proportion of pairs of subjects with observed survival times where the predictions are concordant with the truth in terms of which subject survived longer. Scores close to 1 are therefore best for this metric. The C-index is computed as
| (18) |
where t̂i and t̂j are the predicted survival times for subjects i and j, Φ is the set of pairs (i, j) such that and δj = 1, and |Φ| is the number of such pairs. For more discussion on the evaluation of survival models, see Hielscher et al. [45].
Using standard Bayesian variable selection, three proteins were identified as relevant to survival: Bcl-2, paxillin, and rictor-pT1135. The “p” suffix denotes phosphorylation at the given site. The proportion of selected variables is quite a bit lower than the prior probability of variable inclusion, suggesting that the signal in the data is fairly weak. Using the joint model, six proteins were selected: beta-catenin, c-Met-pY1235, CD20, Chk2-pT68, heregulin, and rictor-pT1135. Although the joint method had more proteins with high posterior probability (> 0.5), the two methods had a very similar number of proteins with posterior probability > 0.2 (18 for standard Bayesian variable selection vs. 17 for the joint method), suggesting that the prior calibration was reasonable. The proposed joint model performed better in terms of prediction using both metrics, suggesting that the larger number of discoveries may reflect improved power. It achieved a lower IBS of 0.12 vs. 0.14 for standard Bayesian variable selection, and a greater C-index of 0.77, in contrast to 0.74 for standard Bayesian variable selection. While this improvement provides some validation of the proposed method, it's difficult to assess its significance. In this context, where the sample size is limited and independent training sets are not available, it's not possible to obtain valid estimates of the prediction error. The results from the joint method also provide insight into coordinated effects of network-related proteins. The posterior selected graph among all proteins includes 230 edges, corresponding to an average node degree of around 2.5. Among the 6 selected proteins, 4 were linked to each other through the line graph Chk2-pT68 – c-Met-pY1235 – CD20 – heregulin. Figure 1, which was produced using the Rgraphviz package [46], shows the selected predictors in the context of the full network inferred. Of the two proteins with no edges to other selected variables, rictor-pT1135 was also chosen using standard Bayesian variable selection, indicating that it may exert a strong influence independent of network effects. The additional proteins identified by the joint model appear to be meaningful. CD20, for example, has previously been discovered as a prognostic factor for leukemia and ovarian cancer [47, 48]. The inferred connections seem plausible as well. For example, Chk2, which is part of the DNA damage response pathway, is involved in the activation of transcription factors which regulate c-Met [49], and both Chk2 and c-Met have been implicated in glioblastoma survival [50, 51].
Figure 1.
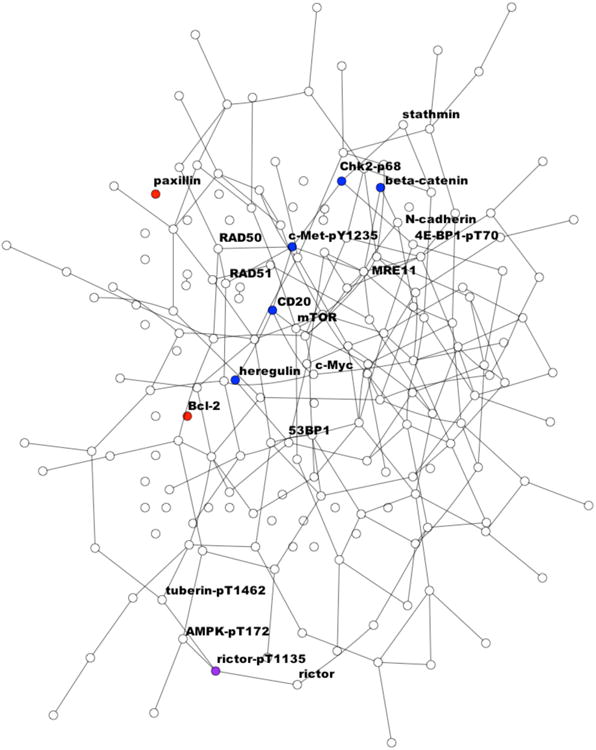
Inferred network for the glioblastoma case study given in Section 5. The graph includes 230 connections among the 187 proteins under study. Proteins selected by the joint model only are marked in blue, proteins selected by standard Bayesian variable selection are marked in red, and proteins selected under both are marked in purple. Labels are provided for all selected proteins and their neighbors in the graph.
6. Conclusion
In this work, we have developed a novel modeling strategy to simultaneously select network-structured variables and learn the network relating them. Our approach is fully Bayesian, and therefore allows us to account for uncertainty over both the variable and graph selections. Through simulations, we have demonstrated that this approach can achieve improved selection and prediction accuracy over competing variable selection methods. We have illustrated this method with an application to identify proteins and their interactions which impact glioblastoma survival. The proposed method is well-suited to other biological applications where genes, proteins or metabolites exert coordinated effects within pathways, and can accommodate outcomes which are continuous, binary, multinomial, or survival.
We have found our method to provide satisfactory results in settings with around 200 to 300 preselected markers. As more computationally efficient approaches for Bayesian estimation of Gaussian graphical models are developed, these can easily be merged into our framework, enabling the analysis of a much larger number of predictors. Although we have chosen to model protein interactions via undirected networks in this paper, a similar approach can be taken when the interactions between predictors are better represented by other types of networks such as directed networks or chain graphs. Additional future developments will include the extension of our approach to more complex models, such semi-parametric regression and more flexible models for time-to-event endpoints. Finally, we would like to consider modificiations to accommodate non-normal predictors. Under the proposed model, some deviation from Gaussianity is acceptable: for example, we found that the joint model performed similarly to other methods in terms of variable selection accuracy and prediction when the predictors were drawn from a multivariate t-distribution with scale matrix Σ and 5 degrees of freedom. For data which are strongly non-normal, however, alternative approaches for network inference would be of interest. In particular, although there has been some work done on robust Gaussian graphical models in the frequentist literature [52, 53], there has been little work in the Bayesian framework. The only proposed Bayesian approach [54], while more robust to outliers than the model developed here, has significant disadvantages in that it is much more computationally expensive and requires restrictive assumptions on the graph structure. Developing a more scalable and flexible approach for robust graphical modeling would therefore be of interest in future work.
Software
The Matlab implementations of the linear, probit, and AFT models have been made available on the author's website. For the simulation in Section 4, which includes 240 predictor variables, it takes about 2 hours to run 10,000 MCMC iterations in Matlab Release 2012b. The IBS and C-index, which were used to measure prediction performance under the AFT model in Section 5, were computed using the Matlab code provided as supporting information to Chekouo et al. [55].
Supplementary Material
Acknowledgments
Christine Peterson's research has been funded by the NIH/NCI T32 Pre-Doctoral Training Program in Biostatistics for Cancer Research (NIH Grant NCI T32 CA096520), by a training fellowship from the Keck Center of the Gulf Coast Consortia, on the NLM Training Program in Biomedical Informatics, National Library of Medicine (NLM) T15LM007093, by a postdoctoral fellowship from the Center for Computational, Evolutionary and Human Genomics (CEHG) at Stanford University, and by NIH grant MH101782. Francesco Stingo is partially supported by a Cancer Center Support Grant (NCI Grant P30 CA016672). Marina Vannucci's research is partially funded by NIH/NHLBI P01-HL082798.
References
- 1.Markowetz F, Spang R. Inferring cellular networks – a review. BMC Bioinformatics. 2007;8(Suppl 6):S5. doi: 10.1186/1471-2105-8-S6-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wolfe CJ, Kohane IS, Butte AJ. Systematic survey reveals general applicability of “guilt-by-association” within gene coexpression networks. BMC Bioinformatics. 2005;6(1):227. doi: 10.1186/1471-2105-6-227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Werhli AV, Grzegorczyk M, Husmeier D. Comparative evaluation of reverse engineering gene regulatory networks with relevance networks, graphical gaussian models and bayesian networks. Bioinformatics. 2006;22(20):2523–2531. doi: 10.1093/bioinformatics/btl391. [DOI] [PubMed] [Google Scholar]
- 4.Purcell SM, Wray NR, Stone JL, Visscher PM, O'Donovan MC, Sullivan PF, Sklar P, et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460(7256):748–752. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Teslovich TM, Musunuru K, Smith AV, Edmondson AC, Stylianou IM, Koseki M, Pirruccello JP, et al. Biological, clinical and population relevance of 95 loci for blood lipids. Nature. 2010;466(7307):707–713. doi: 10.1038/nature09270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Allen HL, Estrada K, Lettre G, Berndt SI, Weedon MN, Rivadeneira F, Willer CJ, et al. Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature. 2010;467(7317):832–838. doi: 10.1038/nature09410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Subramanian A, Tamayo P, Mootha VK, Mukherjee S, Ebert BL, Gillette MA, Paulovich A, Pomeroy SL, Golub T, Lander ES, Mesirov JP. Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proceedings of the National Academy of Sciences. 2005;102(43):15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li C, Li H. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics. 2008;24(9):1175–1182. doi: 10.1093/bioinformatics/btn081. [DOI] [PubMed] [Google Scholar]
- 9.Li C, Li H. Variable selection and regression analysis for graph-structured covariates with an application to genomics. Annals of Applied Statistics. 2010;4(3):1498–1516. doi: 10.1214/10-AOAS332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pan W, Xie B, Shen X. Incorporating predictor network in penalized regression with application to microarray data. Biometrics. 2010;66(2):474–484. doi: 10.1111/j.1541-0420.2009.01296.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang J, Ma S, Li H, Zhang C. The sparse Laplacian shrinkage estimator for high-dimensional regression. Annals of Statistics. 2011;39(4):2021–2046. doi: 10.1214/11-aos897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim S, Pan W, Shen X. Network-based penalized regression with application to genomic data. Biometrics. 2013;69(3):582–593. doi: 10.1111/biom.12035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li F, Zhang NR. Bayesian variable selection in structured high-dimensional covariate spaces with applications in genomics. Journal of the American Statistical Association. 2010;105(491):1202–1214. doi: 10.1198/jasa.2010.tm08177. [DOI] [Google Scholar]
- 14.Stingo FC, Vannucci M. Variable selection for discriminant analysis with Markov random field priors for the analysis of microarray data. Bioinformatics. 2011;27(4):495–501. doi: 10.1093/bioinformatics/btq690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Stingo FC, Chen YA, Tadesse MG, Vannucci M. Incorporating biological information into linear models: a Bayesian approach to the selection of pathways and genes. Annals of Applied Statistics. 2011;5(3):1978–2002. doi: 10.1214/11-AOAS463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Peng B, Zhu D, Ander BP, Zhang X, Xue F, Sharp FR, Yang X. An integrative framework for Bayesian variable selection with informative priors for identifying genes and pathways. PloS One. 2013;8(7):e67672. doi: 10.1371/journal.pone.0067672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hill SM, Neve RM, Bayani N, Kuo W, Ziyad S, Spellman PT, Gray JW, Mukherjee S. Integrating biological knowledge into variable selection: an empirical Bayes approach with an application in cancer biology. BMC Bioinformatics. 2012;13:94. doi: 10.1186/1471-2105-13-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhou H, Zheng T. Bayesian hierarchical graph-structured model for pathway analysis using gene expression data. Statistical Applications in Genetics and Molecular Biology. 2013;12(3):393–412. doi: 10.1515/sagmb-2013-0011. [DOI] [PubMed] [Google Scholar]
- 19.Dobra A. Variable selection and dependency networks for genomewide data. Biostatistics. 2009;10(4):621–639. doi: 10.1093/biostatistics/kxp018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liu F, Chakraborty S, Li F, Liu Y, Lozano AC. Bayesian regularization via graph Laplacian. Bayesian Analysis. 2014;9(2):449–474. doi: 10.1214/14-BA860. [DOI] [Google Scholar]
- 21.Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1996;58(1):267–288. [Google Scholar]
- 22.George EI, McCulloch RE. Approaches for Bayesian variable selection. Statistica Sinica. 1997;7(2):339–374. [Google Scholar]
- 23.Dempster A. Covariance selection. Biometrics. 1972;28(1):157–175. [Google Scholar]
- 24.Meinshausen N, Bühlmann P. High-dimensional graphs and variable selection with the lasso. Annals of Statistics. 2006;34(3):1436–1462. doi: 10.1214/009053606000000281. [DOI] [Google Scholar]
- 25.Yuan M, Lin Y. Model selection and estimation in the Gaussian graphical model. Biometrika. 2007;94(1):19–35. doi: 10.1093/biomet/asm018. [DOI] [Google Scholar]
- 26.Friedman J, Hastie T, Tibshirani R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008;9(3):432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Roverato A. Hyper inverse Wishart distribution for non-decomposable graphs and its application to Bayesian inference for Gaussian graphical models. Scandinavian Journal of Statistics. 2002;29(3):391–411. doi: 10.1111/1467-9469.00297. [DOI] [Google Scholar]
- 28.Atay-Kayis A, Massam H. A Monte Carlo method for computing the marginal likelihood in nondecomposable Gaussian graphical models. Biometrika. 2005;92(2):317–335. doi: 10.1093/biomet/92.2.317. [DOI] [Google Scholar]
- 29.Dobra A, Lenkoski A, Rodriguez A. Bayesian inference for general Gaussian graphical models with application to multivariate lattice data. Journal of the American Statistical Association. 2011;106(496):1418–1433. doi: 10.1198/jasa.2011.tm10465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wang H, Li S. Efficient Gaussian graphical model determination under G-Wishart prior distributions. Electronic Journal of Statistics. 2012;6:168–198. doi: 10.1214/12-EJS669. [DOI] [Google Scholar]
- 31.Lenkoski A. A direct sampler for G-Wishart variates. Stat. 2013;2(1):119–128. doi: 10.1002/sta4.23. [DOI] [Google Scholar]
- 32.Wang H. Bayesian graphical lasso models and efficient posterior computation. Bayesian Analysis. 2012;7(4):867–886. doi: 10.1214/12-BA729. [DOI] [Google Scholar]
- 33.Peterson C, Vannucci M, Karakas C, Choi W, Ma L, Maletić-Savatić M. Inferring metabolic networks using the Bayesian adaptive graphical lasso with informative priors. Statistics and its Interface. 2013;6(4):547–558. doi: 10.4310/SII.2013.v6.n4.a12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peterson C, Stingo FC, Vannucci M. Bayesian inference of multiple Gaussian graphical models. Journal of the American Statistical Association. 2015;110(509):159–174. doi: 10.1080/01621459.2014.896806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Wang H. Scaling it up: stochastic search structure learning in graphical models. Bayesian Analysis. 2015;10(2):351–377. doi: 10.1214/14-BA916. [DOI] [Google Scholar]
- 36.Sha N, Vannucci M, Tadesse MG, Brown PJ, Dragoni I, Davies N, Roberts TC, Contestabile A, Salmon M, Buckley C, Falciani F. Bayesian variable selection in multinomial probit models to identify molecular signatures of disease stage. Biometrics. 2004;60:812–819. doi: 10.1111/j.0006-341X.2004.00233.x. [DOI] [PubMed] [Google Scholar]
- 37.Sha N, Tadesse MG, Vannucci M. Bayesian variable selection for the analysis of microarray data with censored outcomes. Bioinformatics. 2006;22(18):2262–2268. doi: 10.1093/bioinformatics/btl362. [DOI] [PubMed] [Google Scholar]
- 38.Barbieri M, Berger J. Optimal predictive model selection. Annals of Statistics. 2004;32(3):870–897. doi: 10.1214/009053604000000238. [DOI] [Google Scholar]
- 39.Brown PJ, Vannucci M, Fearn T. Multivariate Bayesian variable selection and prediction. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1998;60(3):627–641. doi: 10.1111/1467-9868.00144. [DOI] [Google Scholar]
- 40.Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2005;67(2):301–320. [Google Scholar]
- 41.Smith AF. A general Bayesian linear model. Journal of the Royal Statistical Society: Series B (Methodological) 1973;35(1):67–75. [Google Scholar]
- 42.Li J, Lu Y, Akbani R, Ju Z, Roebuck PL, Liu W, Yang J, Broom BM, Verhaak RG, Kane DW, et al. TCPA: a resource for cancer functional proteomics data. Nature Methods. 2013;10(11):1046–1047. doi: 10.1038/nmeth.2650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Graf E, Schmoor C, Sauerbrei W, Schumacher M. Assessment and comparison of prognostic classification schemes for survival data. Statistics in Medicine. 1999;18(17-18):2529–2545. doi: 10.1002/(sici)1097-0258(19990915/30)18:17/18<2529::aid-sim274>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 44.Harrell FE. Springer Series in Statistics. Springer; New York: 2001. Regression modeling strategies: with applications to linear models, logistic regression, and survival analysis. [Google Scholar]
- 45.Hielscher T, Zucknick M, Werft W, Benner A. On the prognostic value of survival models with application to gene expression signatures. Statistics in Medicine. 2008;29(7-8):818–829. doi: 10.1002/sim.3768. [DOI] [PubMed] [Google Scholar]
- 46.Gentry J, Long L, Gentleman R, Falcon S, Hahne F, Sarkar D, Hansen KD. Rgraphviz: provides plotting capabilities for R graph objects. R package version 2.6.0 [Google Scholar]
- 47.Thomas DA, O'Brien S, Jorgensen JL, Cortes J, Faderl S, Garcia-Manero G, Verstovsek S, Koller C, Pierce S, Huh Y, et al. Prognostic significance of CD20 expression in adults with de novo precursor B-lineage acute lymphoblastic leukemia. Blood. 2009;113(25):6330–6337. doi: 10.1182/blood-2008-04-151860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Milne K, Köbel M, Kalloger SE, Barnes RO, Gao D, Gilks CB, Watson PH, Nelson BH. Systematic analysis of immune infiltrates in high-grade serous ovarian cancer reveals CD20, FoxP3 and TIA-1 as positive prognostic factors. PLoS One. 2009;4:e6412. doi: 10.1371/journal.pone.0006412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Rivera M, Sukhdeo K, Yu JS. Ionizing radiation in glioblastoma initiating cells. Frontiers in Oncology. 2013;3:1–6. doi: 10.3389/fonc.2013.00074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Squatrito M, Brennan CW, Helmy K, Huse JT, Petrini JH, Holland EC. Loss of ATM/Chk2/p53 pathway components accelerates tumor development and contributes to radiation resistance in gliomas. Cancer Cell. 2010;18(6):619–629. doi: 10.1016/j.ccr.2010.10.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kong D, Song S, Kim D, Joo KM, Yoo J, Koh JS, Dong SM, Suh Y, Lee J, Park K, et al. Prognostic significance of c-Met expression in glioblastomas. Cancer. 2009;115(1):140–148. doi: 10.1002/cncr.23972. [DOI] [PubMed] [Google Scholar]
- 52.Finegold M, Drton M. Robust graphical modeling of gene networks using classical and alternative t-distributions. The Annals of Applied Statistics. 2011;5(2A):1057–1080. doi: 10.1214/10-AOAS410. [DOI] [Google Scholar]
- 53.Sun H, Li H. Robust Gaussian graphical modeling via l1 penalization. Biometrics. 2012;68(4):1197–1206. doi: 10.1111/j.1541-0420.2012.01785.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Finegold M, Drton M. Robust Bayesian graphical modeling using Dirichlet t-distributions. Bayesian Analysis. 2014;9(3):521–550. doi: 10.1214/13-BA856. [DOI] [Google Scholar]
- 55.Chekouo T, Stingo FC, Doecke JD, Do K. miRNA-target gene regulatory networks: a Bayesian integrative approach to biomarker selection with application to kidney cancer. Biometrics. 2015 doi: 10.1111/biom.12266. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


