Cryo-EM Data Are Superior to Contact and Interface Information in Integrative Modeling

Abstract

Protein-protein interactions carry out a large variety of essential cellular processes. Cryo-electron microscopy (cryo-EM) is a powerful technique for the modeling of protein-protein interactions at a wide range of resolutions, and recent developments have caused a revolution in the field. At low resolution, cryo-EM maps can drive integrative modeling of the interaction, assembling existing structures into the map. Other experimental techniques can provide information on the interface or on the contacts between the monomers in the complex. This inevitably raises the question regarding which type of data is best suited to drive integrative modeling approaches. Systematic comparison of the prediction accuracy and specificity of the different integrative modeling paradigms is unavailable to date. Here, we compare EM-driven, interface-driven, and contact-driven integrative modeling paradigms. Models were generated for the protein docking benchmark using the ATTRACT docking engine and evaluated using the CAPRI two-star criterion. At 20 Å resolution, EM-driven modeling achieved a success rate of 100%, outperforming the other paradigms even with perfect interface and contact information. Therefore, even very low resolution cryo-EM data is superior in predicting heterodimeric and heterotrimeric protein assemblies. Our study demonstrates that a force field is not necessary, cryo-EM data alone is sufficient to accurately guide the monomers into place. The resulting rigid models successfully identify regions of conformational change, opening up perspectives for targeted flexible remodeling.

Introduction

Protein-protein interactions are involved in many important cellular processes. Atomic structural knowledge on the interfaces of protein-protein complexes is needed for better understanding how these biological systems work, how they are regulated, and how they might be modulated by small molecules or mutations. However, for many complexes, high-resolution structure determination by x-ray crystallography or NMR is highly challenging, especially for large protein assemblies. Recently, the advent of direct electron detectors has enabled high-resolution structure determination by cryo-electron microscopy (cryo-EM) (1, 2). However, in many cases, biochemical sample preparation is still a major bottleneck (1), and atomic or near-atomic resolution maps are the exception rather than the rule. More than 70% of cryo-EM maps have a resolution lower than 10 Å (3, 4), and the majority are likely to remain at this resolution range for the foreseeable future (4).

Integrative modeling

Alternatively, atomic models can be built by fitting existing structures into a cryo-EM map. In recent years, many groups have successfully combined low-resolution data with computational methods to solve the structures of large molecular machines like the 26S proteasome (5), the bacterial type II pilus (6), or the nuclear pore complex (7). These approaches are properly classified as “integrative modeling” (8, 9, 10); a complex is modeled by assembling preexisting protein templates (previously solved by x-ray or NMR) by computational optimization, under the constraints of a set of experimental data.

The three most prominent integrative modeling paradigms are shape-driven modeling (e.g., cryo-EM fitting (11, 12), but also modeling using small-angle x-ray scattering (SAXS) data (13, 14, 15)), contact-driven modeling (NMR nuclear Overhauser effects (16), fluorescent resonance energy transfer, and cross-link mass spectrometry (17)), and interface-driven modeling (NMR chemical shift perturbation (18), mutagenesis, limited proteolysis mass spectrometry (19)). In some cases, NMR can also provide information on the relative orientation of molecules (20, 21). Finally, integration of multiple types of experimental data (e.g., (22, 23) and references therein) is possible as well.

The large number of experimental techniques inevitably raises the question regarding which type of data is best suited to drive integrative modeling approaches. Unfortunately, a systematic comparison of the different integrative modeling paradigms is unavailable to date.

Flexibility and conformational change in integrative modeling

Proteins undergo conformational change upon complexation. Computationally taking apart and reassembling a complex structure (bound docking) is useful for testing modeling algorithms, but has little practical value. Therefore, throughout the protein-protein docking field (where many integrative modeling methods originate), the use of unbound forms is the norm. All protein docking methods use a concept of “force field” (either an actual molecular force field, or equivalent geometric and/or stereochemical criteria) to assemble the unbound forms, starting with an initial rigid placement. However, using unbound forms for rigid modeling introduces an amount of structural noise, in the sense that even a perfect rigid placement may contain clashes and may have a considerable root mean-square deviation (RMSD) from the complex structure. This has a considerable negative impact on docking performance, particularly if the conformational change is substantial (24, 25). This cannot be compensated just by improvements in discrimination and scoring, because for large conformational changes, current docking programs cannot produce hits (24). This was recognized by Schneidman-Duhovny et al. (26). In their integrative modeling method, IDOCK, initial rigid-body models are generated using PatchDock (27) with a relaxed force field, considerably enhancing the sampling for cases with larger conformational change. IDOCK then relies on experimental data to select the models that are close to the correct rigid superposition.

Docking methods, after the initial rigid placement, use flexible refinement procedures to deal with conformational change. Likewise, flexible fitting algorithms (28, 29) can model conformational change using EM data. However, it is far from guaranteed that these conformational changes can be modeled accurately. In docking, flexible refinement methods typically make significant improvements in the scoring and the native contacts, modest improvements (up to 1 Å) in the rigid body positioning, but no significant improvements for the individual partners toward their bound forms (30, 31, 32). For EM flexible fitting, the consensus is that flexible fitting is beneficial for high-quality data, but otherwise prone to errors and overfitting (33, 34). Various opinions exist on what qualifies as high-quality data. Volkmann (33) found that flexible fitting only improves upon rigid fitting at resolutions better than 5 Å, whereas Villa and Lasker indicate a resolution limit at around 9 Å (34). In any case, these resolutions are still better than the large majority of cryo-EM maps.

In summary, obtaining a good initial rigid-body placement is crucial for successful integrative modeling of any kind, because subsequent flexible modeling steps cannot be universally relied upon to improve the result significantly. For docking methods, the force fields that are used to place rigid components have difficulties in case of large conformational changes.

Protein docking benchmark

The protein docking benchmark (35) provides an excellent testing ground for comparative evaluation of integrative modeling strategies. It offers a set of nonredundant protein-protein complexes from the Protein Data Bank (PDB) that reflects the diversity of known protein-protein interactions. For all test cases, the complex structure and the structures of its unbound constituents are available, allowing us to create realistic test settings for integrative modeling paradigms. A plethora of methods has been tested separately on the protein docking benchmark, including ab initio docking methods (i.e., without any experimental information) (30, 36, 37, 38, 39, 40, 41, 42, 43), bioinformatic interface predictions (31, 44, 45, 46, 47, 48, 49, 50), docking driven by experimental data such as cross-link data (51), SAXS data (14, 15, 52), ion mobility (13), and cryo-EM maps (26, 53, 54, 55, 56).

Here, we test and compare the three main integrative modeling paradigms on the protein docking benchmark: EM-driven, interface-driven, and contact-driven modeling, focusing on the initial rigid body placement. Synthetic data were created for each case. Additionally, we applied our EM-driven protocol on the modeling of the archaeal 20S proteasome in complex with its regulatory ATPase, where both real cryo-EM data and atomic structure are available (57). EM-driven modeling achieved a success rate of 100%, outperforming both interface-driven and contact-driven modeling. This result is very surprising; cryo-EM data was simulated at only 20 Å resolution, whereas perfect information was used for interfaces and contacts. This shows that cryo-EM maps, even at very low resolution, are superior to other integrative modeling data (in particular, contact data and interface data) for heterodimeric and heterotrimeric protein assemblies.

Materials and Methods

We compared three different integrative modeling strategies by performing three types of docking experiments, driven by synthetic experimental data: docking driven by low-resolution cryo-EM maps (ATTRACT-EM), docking driven by knowledge of the true interface, and docking driven by knowledge of the true contacts.

Generation of cryo-EM data

Synthetic cryo-EM maps were simulated based on the bound complex structure with a very low resolution (20 Å) using Situs (58, 59). Simulated maps were used noise-free or by adding Gaussian noise. Instead of adding noise in Cartesian space (where the frequency depends on the voxel size and the noise kernel), noise was directly added to the structure factors. These were calculated by three-dimensional fast Fourier transform using the fftn routine in NumPy (60). Noise levels were calculated that would result in a targeted Fourier shell correlation (FSC) (typically 0.95) with the noise-free map of the 15–20 Å band. All structure factors of higher resolution were suppressed, whereas structure factors of lower resolution were left unaffected. The structure factors were transformed back to Cartesian space by inverse fast Fourier transform. Noise levels were verified by calculating the FSC curve toward the noise-free map using EMAN2 (61), verifying that the FSC at 20 Å (FSC-20) was indeed the desired level. For the proteasome-PAN complex (57), the experimental map (Electron Microscopy Data Bank (EMDB): 5130) was downsampled to 5 Å using the affine transformation routine from SciPy (http://www.scipy.org/) and filtered to 20 Å resolution with a low-pass Gaussian filter using EMAN2 (61).

To compute structural noise, the unbound forms were superposed onto the bound complex and a 20 Å simulated cryo-EM map was generated using Situs. The FSC-20 value toward the simulated map of the bound complex was computed using EMAN2.

ATTRACT-EM assembly protocol

For EM-fitted modeling, we used our previously presented ATTRACT-EM assembly protocol (55) with some modifications. As before, the protocol aims to maximize the gradient vector matching (GVM) correlation. However, the rigid-body refinement stage using the ATTRACT force field was eliminated, and the complete procedure was driven by the cryo-EM map alone. The Gaussian overlap potential during sampling was eliminated. Instead, during all sampling stages, protein partners were confined to a region of space derived from the cryo-EM density map (atom density mask). For voxels within the mask, a certain number of atoms are allowed, corresponding to the average packing density of protein plus some margin, as in the previous version (55). Outside the mask, the number of allowed atoms is zero. Hence, the mask both confines the proteins to a certain region of space and prevents massive overlap between the protein partners.

As in the previous protocol, sampling was enhanced by subunit exchanges (recombinations) between subunits. Starting from 48,000 random two-body placements, the current ATTRACT-EM protocol consists of four Monte Carlo sampling stages of 250 steps, with in between a scoring stage, consisting of an exhaustive recombination between the top 600 structures in the GVM score, and selection of the 48,000 recombinations with the highest GVM score for the next sampling stage. After the fourth sampling stage, the top 600 is submitted to a refinement, consisting of 20 energy minimization stages. After each minimization stage, the structures were ranked by GVM score, and the top 600 was cloned nine times, and a random displacement was applied to each clone. The resulting 6000 structures were subjected to the next minimization stage. The refinement was performed for a total of six times with a tabu filter, i.e., filtering out structures within 5 Å of the top model of any previous refinement. Finally, a recombination was done between the structures of all refinements and the result of the first Monte Carlo sampling stage, and another four refinements with tabu filter were performed.

The first Monte Carlo sampling stage employed atom density masks with a 10 Å voxel size, 5 Å in all other sampling stages (both Monte Carlo and minimization). When the ATTRACT force field was used, it was added as an additional energy term to all sampling stages.

In all cases, to select the final models, the 10 refinement results (clusters) were sorted by the average GVM structure of the first four structures (similar to HADDOCK). The models were then ranked as follows: rank 1–10, the best structure (i.e., highest score by GVM) of each cluster (rank 1 coming from the best cluster, etc.). Rank 11–20, the second best structure of each cluster, rank 21–30 the third best, and rank 31–40 the fourth best. The rest of the top 100 consisted of structure 5–64 from the best cluster. Structures beyond the top 100 were taken from the rest of the best cluster (exhausting all 600 structures), and then from the second best cluster, etc.

General ATTRACT protocol for interface-driven and contact-driven modeling

For interface- and contact-driven modeling, we used a protocol based on ATTRACT two-body docking as described in (62). The protein structures were converted into the optimized potentials for liquid simulation (OPLS) atom type description (63) with the ATTRACT tool aareduce. For each two-body docking case, 100,000 starting structures were generated with random orientations of the protein partners. In an initial rotational sampling stage, the force field was disabled. Only the restraints were applied and the proteins could orient toward each other with the translational degrees of freedom fixed (64, 65). The rotational sampling phase applied a maximum of 50 minimization steps. Subsequently, the proteins were minimized with respect to their rigid body degrees of freedom (1000 minimization steps) and rescored using OPLS van der Waals, electrostatic and restraint energy with a restraint weight of 0.01. Energy calculations were accelerated using a precalculated grid.

Interface-driven modeling

To test an integrative modeling approach based on experimentally identified interface residues, we used ATTRACT with ambiguous distance restraints based on active and passive residues, following their original specification in the HADDOCK method (64, 65, 66). The active residues on the proteins were derived from the interface residues in the bound complex structure within a cutoff of 5 Å. The minimum distance for the ambiguous distance restraints was set to 2 Å with a force constant of 2.0 kcal/mol/Ų.

Contact-driven modeling

Contacts were taken from the bound complex structures corresponding to all the residue-residue contacts with a distance smaller than 5 Å, resulting in an average of 476 contacts per complex, ranging from 164 to 1378 contacts per complex. These contacts were used as harmonic maximum distance restraints during docking, with a maximum distance of 5 Å and a force constant of 1000 kcal/mol/Ų.

Test set and structure preparation

Integrative modeling was performed on the entire protein docking benchmark 4.0 (35). The benchmark consists of 176 heterodimeric complexes for which the bound and unbound forms are provided, classified according to RMSD between bound and unbound forms as rigid-body, medium, and hard cases. We used a cleaned up version of the benchmark (30), established by the following procedure. Proteins were first aligned with FATCAT (67), and then residues were renumbered in the unbound structures to match the bound forms. Parts in the unbound form that are not present in both bound and unbound form were removed. Point mutations were introduced to resolve minor differences in the protein sequences, if needed. Missing hydrogens and heavy atoms were built with PDB: 2PQR (68, 69) and protonation states were determined by PropKa (70). One complex (PDB: 1N2C) was so massive that our cleanup procedure failed and was removed. In addition, we did not consider the alternative binding modes of PDB: 1OYV and 1QFW, resulting in a test set of 173 complexes.

Since we are performing rigid-body modeling using a rather strict criterion (see below), we looked into all benchmark cases that are fundamentally impossible, where even the best rigid-body superposition would not be good enough. Strictly speaking, not all integrative modeling paradigms predict the same thing. EM-driven (and other shape-driven) modeling predicts global whole-body positions, whereas the other paradigms (interface-driven modeling, contact-driven modeling, and ab initio docking) predict local positions, aligned on the interface regions. Therefore, we performed both whole-body and interface superpositions of the unbound forms onto the bound forms (Table S1 in the Supporting Material), and only kept the 158 cases where both ideal superpositions resulted in a two-star CAPRI solution (Table S1). Of the remaining 15 complexes, 10 were added to the impossible set:

• •PDB: 2VIS and 1GP2 were only one-star in their whole-body superpositions
• •PDB: 1E4K, 2HMI, 1FQ1, 1ATN, and 1DE4 were only one-star in their interface superpositions
• •PDB: 2O3B, 1JMO, and 2I9B were only one-star in both superpositions.

The impossible test set was not taken into account for the comparison between EM-driven, interface-driven, and contact-driven paradigms. However, ATTRACT-EM results on the impossible set were in fact quite good, resulting in a two-star model in 7/10 cases (including PDB: 1GP2 and 2I9B, where perfect whole-body superposition does not work), 3/10 cases at rank #1, and all 10 cases were at least one star.

The other five complexes are properly modeled as three-body complexes. They were identified as such by FATCAT (67), splitting one of the proteins into two parts and aligning each part separately. Any flexible linker connecting the two parts was removed manually, and linker distance restraints between the part (1.4 Å + 3.8 Å for every missing residue) were defined between the parts, similar to Karaca and Bonvin (36). Of the five complexes, PDB: 1IRA and 1F6M are true three-body cases, partitioning the flexible partner results in more or less equal parts (12–23 kDa) and superposing the parts separately onto their bound counterparts led to a great reduction in I-RMSD (from >4 Å to 1.0–1.6 Å). For 1FAK and 1Y64, the I-RMSD reduction is similar, but the flexible partner is split into a large molecule and a small auxiliary binding domain (4.1–6.0 kDa). Therefore, we consider them as pseudo-three-body cases: they were modeled in the same way as the real three-body cases, but during the evaluation, the auxiliary body was ignored and the two full bodies were evaluated as a two-body complex. The fifth three-body complex, 1H1V, even after splitting the flexible partner, remained impossible to model at two-star precision (I-RMSD 2.3 Å), and was therefore not considered at all. Note that all five three-body complexes are part of the three-body benchmark by Karaca and Bonvin, which includes another five complexes from the benchmark 4.0. However, since these other five structures result already in two-star solutions by two-body superposition, we did not consider them as three-body structures.

Evaluation criterion

Models were evaluated against the two-star CAPRI criterion (71). In CAPRI, predictions are evaluated by interface-RMSD (I-RMSD), ligand-RMSD (L-RMSD), and fraction of native contacts (fnat). A CAPRI two-star solution is defined by (I-RMSD ≤ 2.0 Å OR L-RMSD ≤ 5.0 Å) AND fnat ≥ 0.3. For I-RMSD calculation, the backbone atoms of all residues within a cutoff of 10 Å from the protein partner were considered. For L-RMSD calculation, the structure was superimposed on the bound form of the receptor protein and the RMSD of the ligand backbone atoms was evaluated. For fnat calculation, a contact was defined as two residues with a minimum distance of heavy atoms <5 Å (71).

For EM-driven modeling, 100 generated models were considered, and a complex was considered successful if at least one of them fulfilled the CAPRI two-star criterion. For interface-driven and contact-driven modeling, evaluation was performed generously. A complex was considered successful if any of the 100,000 structures fulfilled the two-star criterion, and the two-star fnat threshold was not taken into account.

For pseudo-three-body cases, the auxiliary domain was not considered in the evaluation; the two full bodies were evaluated as a two-body complex against the two-star criterion. For real three-body cases, the L-RMSD is ambiguous and the success criterion was considered simply as I-RMSD < 2.0 Å.

Calculation of clashes

Clashes were defined as intermolecular atomic contacts within 3 Å. Deep clashes were defined as intermolecular contacts within 2 Å involving any atom of the protein core. The protein core was defined as follows: surface dots were determined by placing 100 random dots at 3 Å around every heavy atom and then eliminating all dots within 3 Å of any other atom. Surface atoms were then defined as all atoms with at least one surface dot. The protein core was defined as all atoms with a distance of at least 3.5 Å to the nearest surface atom. Atoms involved in deep clashes with the other core were predicted as undergoing large conformational change, if at least three such atoms were present in the model.

All images of protein models were generated with PyMol (72).

Results

Generation of simulated data and modeling

Experimental techniques that identify interface residues and contacts do not give perfect results; typically, only a fraction of all residues and contacts is identified, and experimental noise may cause some data to be inaccurate. Nevertheless, in this study, we assumed ideal conditions with perfect information on all true contacts (476 contacts per complex on average) and all true interface residues of all complexes in the benchmark. In contrast, we used simulated cryo-EM maps of very low resolution (20 Å). For experimental cryo-EM maps, the relevant noise level can be determined by examining the FSC at the 20 Å level (FSC-20). Visual inspection of FSC curves of experimental cryo-EM maps of 10–15 Å resolution (2, 73, 74, 75, 76) showed them to be nearly free of noise at 20 Å (FSC-20 > 0.95–0.98). As a consequence, noise corresponding to FSC-20 = 0.95 was added to each simulated map. Modeling protocols were run on the ATTRACT docking engine (62, 77, 78). An updated version of the ATTRACT-EM protocol (55) was used for EM-driven modeling, consisting of multiple sampling and scoring stages. In the sampling stages, no force field is applied, but excessive overlaps are prevented by a voxel atom density term (55). In the scoring stages, only the GVM correlation (55) to the cryo-EM map is taken into account. Interface-driven and contact-driven modeling was performed with a standard rigid docking protocol using the OPLS force field (63) together with experimental restraints. We used HADDOCK-style distance restraints (64, 79, 80) for interface-driven and harmonic distance restraints for contact-driven modeling.

Evaluation of modeling results

The CAPRI docking challenge (71) defines a set of criteria for the evaluation of docking models in comparison with a reference structure of the complex. In CAPRI, predictions are evaluated by I-RMSD, L-RMSD, and fnat. Based on these criteria, a model is categorized as zero-star to three-star quality. We consider the CAPRI one-star criterion to be too lenient for integrative modeling. The results of recent CAPRI rounds (32, 81, 82) show that one-star models can typically be obtained by computational methods alone, using little or no experimental information. In contrast, >130 integrative models calculated with HADDOCK (64, 79, 83) with good experimental data have been deposited in the PDB, and as such are held to higher standards than a computational model. In particular, correct intermolecular contacts are essential to predict the effect of mutations, while a two-star model must contain at least 30% of the native contacts, the fnat threshold is only 0.1 (10%) for a one-star model.

We investigated the quality of a perfect rigid superposition of the unbound forms in terms of CAPRI stars (Table S1). Strictly speaking, there is no single perfect superposition across the paradigms. EM-driven (and other shape-driven) modeling predicts global whole-body positions, whereas the other paradigms (interface-driven modeling, contact-driven modeling, and also ab initio docking) predict local positions, aligned on the interface regions. However, for >90% of the benchmark (158/173 cases), both perfect superpositions (local and global) meet the criteria for two-star quality (Table S1). For four additional cases, this is true if the complex is modeled as three bodies. In contrast, for more than half of the benchmark, even perfect superpositions do not result in a model of three-star quality, making it fundamentally impossible to attain by rigid-body modeling. Therefore, we consider the two-star criterion to be most appropriate, and we limit our study to the 162 benchmark cases where a two-star model by rigid modeling is in principle possible.

EM-driven modeling was counted as a success if one of the 100 best scored models was of two-star quality (or better). In contrast, we considered contact-driven or interface-driven modeling a success if a two-star model was present among any of the 100,000 generated models. In this way, we accounted for the fact that most contact/interface-driven modeling methods perform flexible refinement steps, which can significantly improve the scoring. Moreover, as flexible refinement has tiny impacts on I-RMSD or L-RMSD but typically improves fnat (30, 31), we systematically considered fnat as correct for interface/contact-driven models, whereas the fnat criterion was evaluated for EM-driven docking.

Modeling results on the protein benchmark

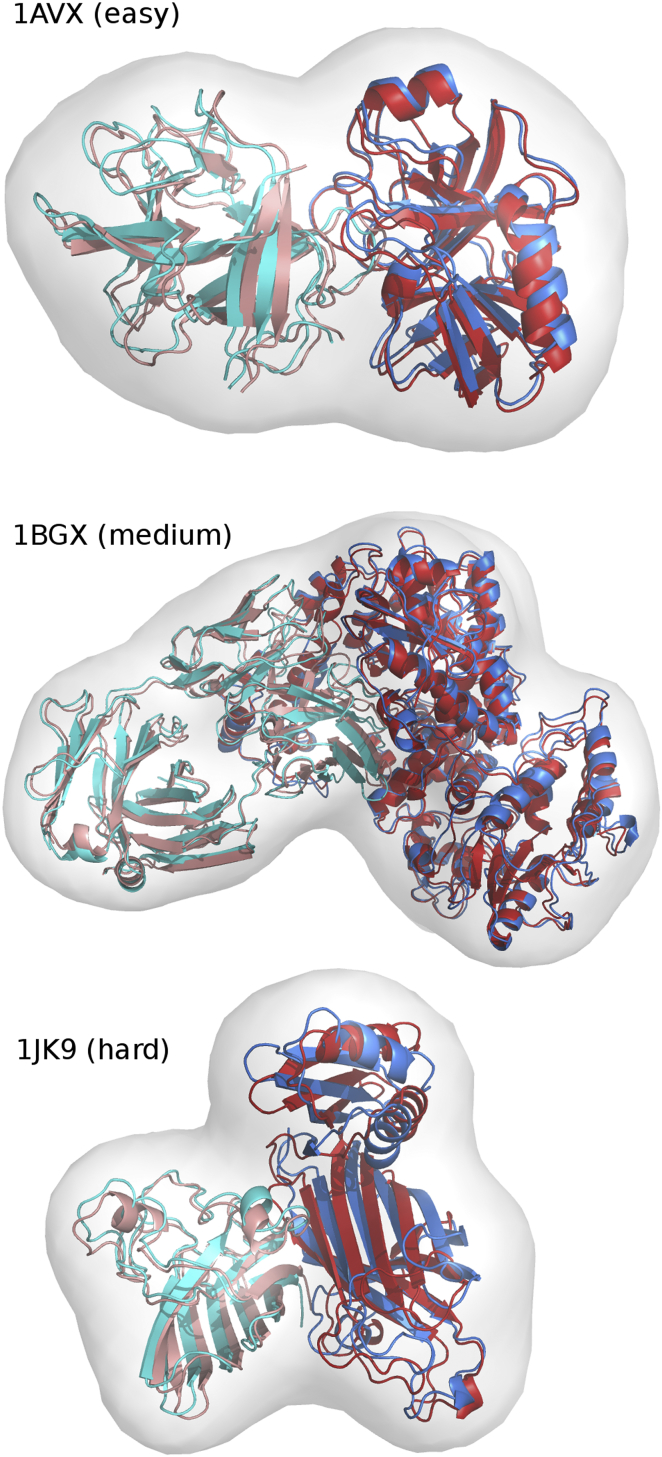
The cryo-EM based integrative modeling approach was successful in all 162 cases of the benchmark. 130 complexes (83%) had a CAPRI two-star model as top ranked solution (including the four three-body cases), and the top 10 contained a two-star model for 95% of the complexes. This demonstrates that our cryo-EM based modeling approach is very robust toward a large diversity of protein-protein interactions, including those that undergo large conformational changes (the hard cases in the benchmark). Many ab initio rigid-body docking methods cannot sample any near-native solutions for hard cases, even when evaluating them only by the CAPRI one-star criterion. Examples of models generated by the cryo-EM protocol are shown in Fig. 1.

Figure 1.

Examples of ATTRACT-EM results on an easy, medium, or hard docking case. For cases PDB: 1AVX, 1BGX, and 1JK9, the structure obtained by ATTRACT-EM protocol (red and pink) are presented superimposed to the bound form of the complex (blue and cyan). The atom density map at 20 Å resolution is represented as a gray surface. To see this figure in color, go online.

The success rate was considerably lower for interface-driven and contact-driven modeling; 75% (122/162) and 89% (144/162) of the complexes, respectively, contained at least one two-star model among all 100,000 generated models. Results were particularly bad for the hard cases of the benchmark, with only 4 and 5 successes out of 15, respectively. These poor achievements for hard cases confirm the low tolerance to conformational changes of these two integrative modeling methods. Moreover, the success rate among all cases plummeted when only the best scoring models were considered, particularly for interface-driven modeling; only six complexes showed a two-star model at rank #1. These results are also representative for the subset of 15 complexes used to test the influence of noise and the force field (see next paragraphs).

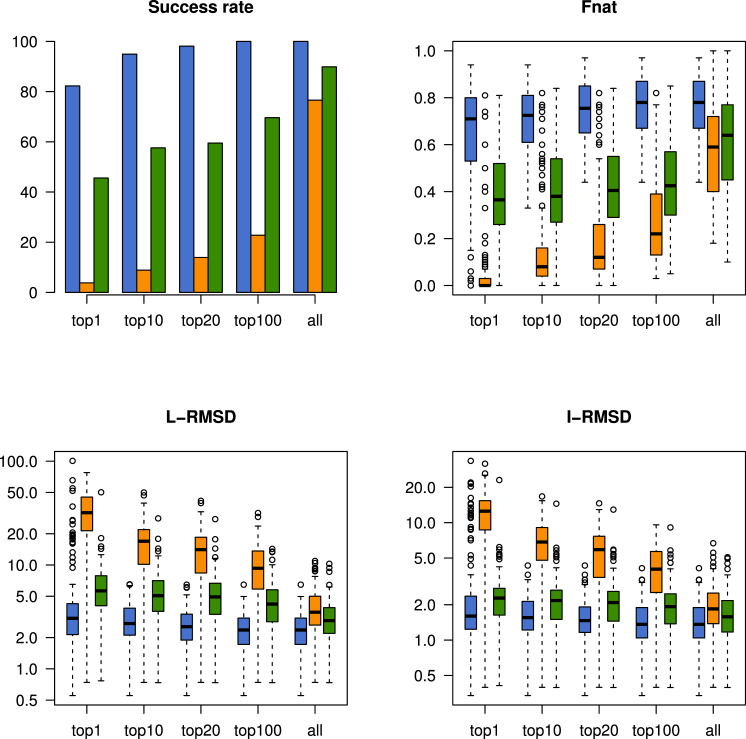
Fig. 2 shows a detailed comparison between EM-driven, interface-driven, and contact-driven docking on all 158 two-body cases, showing that EM-driven docking performs better in all aspects. Statistics for individual complexes are shown in Table S2, showing the superior performance of EM-driven modeling for nearly all complexes. EM-driven docking achieved rigid body superpositions that are typically around 1 Å away from the perfect superposition (Fig. S1).

Figure 2.

Docking results for the different integrative modeling approaches on two-body docking cases. The total success rate in the N top ranked (N in 1, 10, 20, 100, or all) models obtained by contact-driven docking (green), interface-driven docking (orange), or EM-driven docking (blue) were evaluated for all 158 two-body cases, as well as the best L-RMSD, best I-RMSD, and best fnat. For I-RMSD, L-RMSD, and fnat are presented the median best value per case (thick black line), the 0.25 and 0.75 quartiles (box), and the values above or under 1.5 times the interquartile distance (circles). I-RMSD and L-RMSD are presented in logarithmic scale. A docking case was considered successful if at least one CAPRI two-star solution was among the top N ranked models. To see this figure in color, go online.

Overall results are similar for two-body and three-body cases. In particular, our interface-driven protocol for three-body cases (I-RMSD 3.7–5.4 Å) is very similar to the HADDOCK protocol of Karaca and Bonvin (36), who included a flexible refinement and achieved results that are better (I-RMSD 2.8–3.9 Å on the same four cases) but still of only one-star quality. In contrast, EM-driven modeling achieved two-star quality at rank #1 for all four cases. Complete results for the three-body cases are shown in Table S3.

Influence of noise on EM-driven modeling results

We investigated the effect of noise on EM-driven modeling by comparing the previous default noise results (FSC-20 = 0.95) with results obtained with noise-free maps, as well as with higher levels of noise. We observed earlier that since our modeling protocol is stochastic, different results may be obtained by small changes in initial conditions. We reran the protocol twice with noise-free data on the entire benchmark (with different random starting positions), and also repeated it for default noise, for a total of four trials. A detailed comparison of results obtained by ATTRACT-EM protocol on noise-free and noised simulated maps is presented in Table S4. Each trial had a success rate of >95% and every complex succeeded for at least one trial under each noise condition. Therefore, we conclude that there is no significant difference between default noise and noise-free maps. To investigate if higher levels of noise would have a negative effect on the results, a subset of 15 complexes was selected and maps with higher noise levels (FSC-20 = 0.80–0.90) were generated. No significant differences in modeling results were observed (Table S5). For example, the highest noise level of FSC-20 = 0.80 yielded a two-star model at rank #1 for 13/15 complexes, and in the top 10 for all 15, which is identical to the results for default noise.

Note that merely the use of unbound protein forms already presents a source of noise, namely the structural noise resulting from conformational change upon binding. We quantified this noise and found that it accounted for FSC-20 values of ∼0.95 for rigid body cases and ∼0.85 for hard cases (results not shown).

Influence of a force field on results of EM-driven docking

The main difference between the EM-driven and the interface/contact-driven protocols is the usage of a force field to guide the template placement in the latter case. To assess the influence of the force field, we performed EM data-driven modeling where the ATTRACT force field, rather than just the voxel atom density, was used in the sampling stage. This protocol was evaluated on the same 15 cases as above. To our surprise, the modeling in the initial stages converged faster than without force field, even for the hard cases (results not shown). However, the final results were very similar to the results with default noise: at rank #1, 10 cases had a two-star structure and two others had nearly that quality. 14 cases had a two-star in the top 10 and all of them in the top 100 (Table S5). Therefore, using a force field in the sampling stage has little benefit or harm for the final result.

However, we emphasize that only the EM data, not the force field, was used in any of the scoring stages. The best final models, while being correct (two-star quality) and favorable in GVM score, had a force field energy that was favorable only for the rigid and medium cases (ATTRACT score: −8 to −21) and highly unfavorable for the hard cases (ATTRACT score: 200–3762). When the force field energy, rather than the GVM score, was used to score the final models, a two-star structure was at rank #1 for only 7/15 complexes and in the top 10 for 8/15.

Application to an experimental case

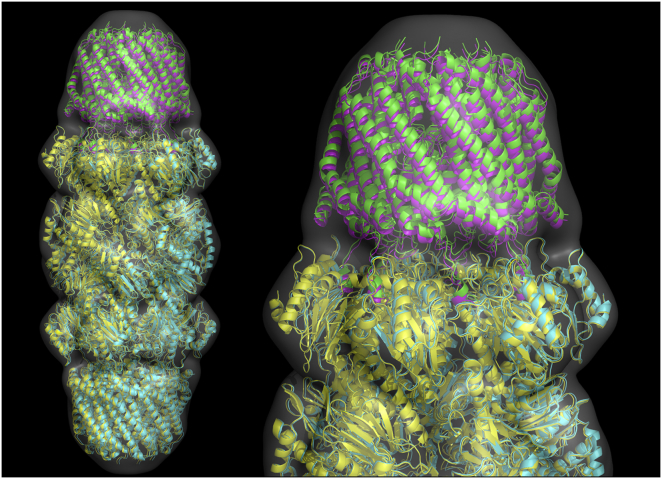
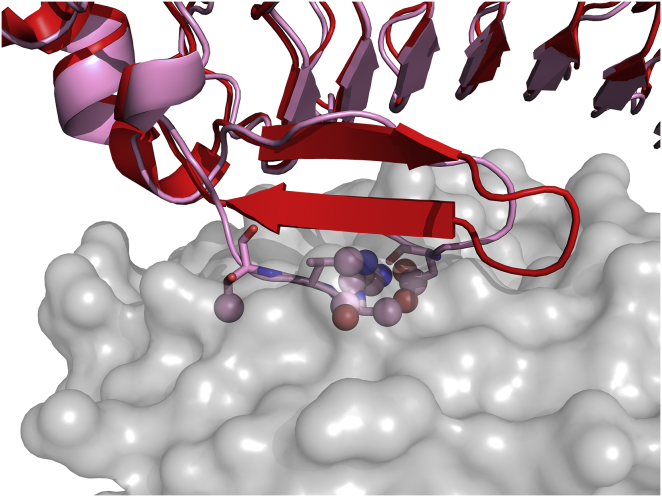
We applied the ATTRACT-EM protocol to an experimental case, the archaeal 20S proteasome in complex with the C-terminus of the archaeal proteasome regulatory ATPase (PAN). This complex has been solved by both cryo-EM (EMD: 5130) and by crystallography (PDB: 3IPM) by the same authors (57). The experimental cryo-EM data (originally at 7.5 Å resolution) was filtered down to 20 Å. We observed that the FSC-20 between the two halves of the data is ∼0.95 (57), but the FSC-20 with a simulated map of PDB: 3IPM is only 0.82. Nevertheless, after modeling a PAN molecule onto the rest of the complex, the rank #1 ATTRACT-EM model had an interface RMSD of 1.1 Å (Fig. 3), and a subangstrom model (I-RMSD 0.77 Å) was obtained at rank #10. This is close to the average precision of ∼1 Å in rigid-body placement for the protein benchmark (Fig. S1). Similar results were obtained for positive control runs based on simulated data of 3IPM with various noise levels (noise-free, default noise, and FSC-20 = 0.82, results not shown). Therefore, we can only conclude that the ATTRACT-EM protocol, using data of 20 Å resolution, is rather robust, and that high-quality rigid placements can be obtained even in the presence of experimental noise.

Figure 3.

ATTRACT-EM results on archaeal 20S proteasome in complex with the C-terminus of the archaeal proteasome regulatory ATPase (PAN). The structures obtained by ATTRACT-EM protocol (yellow and pink) are presented superimposed to the bound form of the complex (green and cyan) (PDB: 3IPM). The experimental electron density map (EMD-5130) was filtered down to 20 Å resolution and is represented as a gray surface. The top ranked model obtained by ATTRACT-EM is in close agreement with the bound complex structure (I-RMSD: 1.1 Å, L-RMSD: 2.4 Å, fnat: 0.77). To see this figure in color, go online.

Comparison to other EM-driven docking strategies

We compared our results with already published results from two other EM-driven docking methods, HADDOCK-EM (56) and IDOCK (26).

IDOCK has been tested with cryo-EM data on a subset of 27 complexes from the protein benchmark. The performance of IDOCK on this subset of complexes was representative of the performance on the whole benchmark set (26). Here, we compared the performance of ATTRACT-EM to the performance of IDOCK with simulated electron density maps. IDOCK obtained two-star success rates of 22%, 55%, and 63% for the top 1, 10, and 100 ranked clusters, respectively. The ATTRACT-EM protocol, which achieved success rates of 83%, 95%, and 100% for the top 1, top 10, and top 100 models on 162 benchmark cases, clearly outperforms the IDOCK approach.

HADDOCK-EM was tested using simulated electron density maps on a subset of 17 complexes from the docking benchmark (56). For 20 Å resolution maps, we compared the best sampled I-RMSD for each case with the corresponding results for ATTRACT-EM (Table S6). For 15 out of the 17 cases, the performance in terms of best sampled I-RMSD was similar (± 0.2 Å, 5 cases) or better (10 cases) for ATTRACT-EM. On average, the I-RMSD of the best sampled ATTRACT-EM model was 0.61 Å lower in I-RMSD than the best sampled HADDOCK model. For the medium and hard docking cases, ATTRACT-EM achieved lower I-RMSD in six out of seven cases, with a 0.1–3.6 Å difference.

Clashes as indicator of flexibility

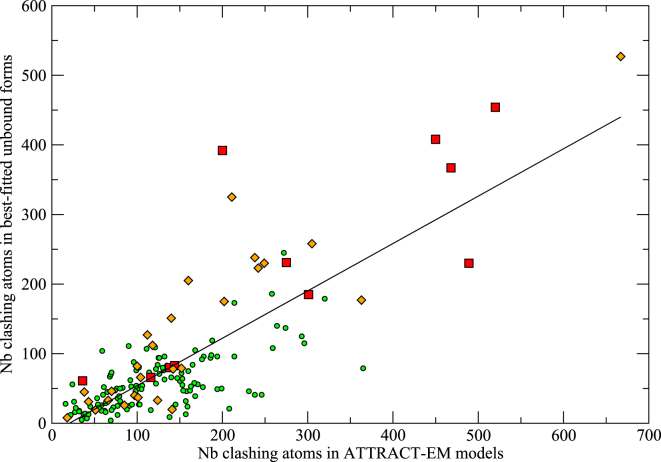
Clashes in high-quality models with accurate rigid placement may be indicative of conformational changes in the interface. We analyzed clashes in the best ranked two-star models from two-body EM-driven modeling, and tested their predictive value. Fig. 4 shows that the overall number of clashes correlates well with the number of clashes in the perfect unbound-bound superposition (linear correlation coefficient 0.80). Therefore, by this simple metric, EM-driven modeling can discriminate between rigid and hard docking cases without prior knowledge. However, since a clash only implies a displacement of one of the atoms (not both), we found that individual clashes are poor predictors of the actual atoms that undergo large conformational change (results not shown). In other words, clashes indicate general conformational change but do not accurately pinpoint the specific atoms with large RMSD. In contrast, we found that atoms that clash with the core of the partner protein (Fig. 5) are indeed more often involved in large conformational change. Such deep clashes were found in 67/158 ATTRACT-EM models, and the deep clashing atoms had a larger conformational change than the average interface atom by a factor 1.8, compared to a factor 2.5 for perfect global rigid superpositions. Together, these results show that the presence of clashes in the ATTRACT-EM models gives useful insight into the bound-unbound flexibility of the partner, which would justify usage of flexible refinement concentrated on the clashing parts.

Figure 4.

Correlation between the number of clashing atoms in the best ATTRACT-EM models and in models obtained by exact superposition of unbound structures on bound complex. Clashes were defined as pairs of atoms within 3.0 Å from each other. The two measurements display a linear correlation coefficient of 0.80. Hard docking cases are indicated as red squares, medium cases as orange diamonds, and rigid docking cases as green circles. To see this figure in color, go online.

Figure 5.

Deep clashes in ATTRACT-EM models indicate high RMSD between bound and unbound structures. On an example case (PDB: 1M10), the bound form of the ligand (red) is superimposed to the best scored ATTRACT-EM model (pink). The unbound receptor is represented as a gray surface. The deep clashing atoms are represented as spheres. To see this figure in color, go online.

Discussion

Integrative modeling approaches have been applied successfully to a variety of large protein assemblies. Many of these hybrid structural models obtained from combining low-resolution experimental data, high-resolution templates, and computational methods have been deposited in the PDB, underlining the important role integrative modeling has acquired in structural biology (10). The large majority of these structures have been modeled either by EM (∼800 structures), using a variety of fitting methods, or by the HADDOCK program (64, 79, 83) (∼130 structures), driven by information on the interface, contacts, and/or relative orientation of the molecules.

Here, we compared cryo-EM with contact or interface information for modeling of heterodimers and heterotrimers from unbound monomers, using simulated data. Our results show an unequivocal superiority of cryo-EM over contact-driven and interface-driven modeling, even at low resolution. This raises the question: to what extent are the conditions in our study fair and general enough to be extended to the general case?

Accounting for flexible refinement

For contact-driven and interface-driven modeling, the initial rigid body stage is typically followed by some kind of flexible refinement. However, we limited the modeling to the rigid stage alone, which may underestimate the success rate for those paradigms. Reflecting this, we have been extremely generous in the evaluation of the results for contact-driven and interface-driven modeling. Since subsequent flexible refinement may improve the scoring, we counted even a single two-star among any of the 100,000 generated structures as a success. Likewise, since flexible refinement may improve the contacts, we did not require the two-star CAPRI native-contacts criterion to be fulfilled. In contrast, for EM-driven modeling, evaluation was strict. We solely counted the top 100 models generated by ATTRACT-EM, imposing the full CAPRI criteria for two-star quality.

In addition, for EM-driven modeling, the simulated cryo-EM data was at very low resolution (20 Å). In contrast, perfect and complete information was used in the contact-driven and interface-driven modeling. In a typical real-case scenario, experimental cryo-EM data would have a better resolution, but experimental contact or interface information would be noisy and incomplete.

Therefore, we see no reason why flexible refinement driven by real-world contact and interface information would do any better than our generous evaluation of idealized rigid modeling results. For EM-based modeling, there is good reason to believe that it would work even better. This is supported by the results on the proteasome-PAN complex, where ∼1 Å rigid placement precision was obtained even when filtering the 7.5 Å map down to 20 Å. Based on this, we conclude that the superiority of cryo-EM data over contact and interface data seems to be real, and not an artifact of rigid modeling.

The influence of noise and conformational change

We found EM-driven modeling to be robust toward noise, both experimental noise in the cryo-EM map and structural noise in the form of conformational change between bound and unbound forms. These results are extremely encouraging and indicate that cryo-EM based integrative modeling strategies should also be applicable when using homology-modeled structures for the protein constituents. Typical homology models are unlikely to have larger conformational change than the hard cases in the docking benchmark (32, 84, 85).

Still, extrapolation of our results to the general case should be made with caution. One reason is that radical conformational changes (e.g., the refolding or flexible rearrangement of entire domains) can pose serious modeling challenges, and also cause artifacts in cryo-EM maps. This does not affect the main conclusion that EM-driven modeling is superior (other modeling paradigms are even more affected by large conformational change) but it would be unjustified to conclude that the ATTRACT-EM protocol is universally successful. In addition, the protein benchmark is not at all representative for complexes solved with cryo-EM. EM has a theoretical lower size limit of around 100 kDa (86), and in practice, difficulties are encountered under 200–300 kDa (1). The protein docking benchmark contains only a handful of complexes above 100 kDa, and only one above 200 kDa. On the one hand, the modeling actually gets easier for larger bodies, because the map provides many more data points per body. Therefore, when it comes to simple dimers and trimers, the protein benchmark is, in fact, a worst case scenario for EM-driven modeling. However, the real challenge will be to maintain the high success rate for EM-driven modeling for real-world cases (hundreds of kDa) where the bodies are as small as in the protein benchmark but much more numerous, presenting a much larger sampling space. Unlike the protein docking benchmark, current benchmarks for multibody modeling (e.g., (54)) are small and do not contain unbound forms. More research is needed to determine if low-resolution cryo-EM data is sufficient for such cases.

The effect of force fields

Integrative modeling programs typically include a force field to balance experimental data against stereochemical correctness and to help discriminate the correct solution in case of ambiguity. In case of distance restraints derived from contact or interface data, this makes perfect sense: the experimental data provide only upper limits to the distances, and lower limits need to be inferred by repulsive forces that prevent the partner from overlapping. This makes force fields necessary. Similarly, all docking programs include force fields in the sense that they heavily penalize clashes; predictions with clashes are normally rejected during CAPRI evaluation.

However, these force fields induce a sensitivity to conformational changes, disqualifying models, which correspond to the best possible rigid-body placement but with clashes due to conformational rearrangements at the interface. This problem is well known in the docking literature (24, 25), and we believe that this is the main reason for the low success rates of medium and hard docking cases in the true interface/contacts-driven docking protocols, as the classification of benchmark cases as medium/hard difficulty is directly related to those conformational changes. Our study shows that the use of a force field can be harmful in this first and crucial rigid-body docking step, by discarding false negative decoys. In contrast, rigid-body fitting into cryo-EM maps does not require any force field. Previously (55), the ATTRACT-EM protocol contained a rigid-body refinement step using the ATTRACT force field, but this step has now been eliminated. By using the cryo-EM data alone to iteratively select models, the ATTRACT-EM protocol allows for a considerable degree of overlap between the protein partners, and is thus barely sensitive to conformational changes at the interface. This explains the success of ATTRACT-EM for the medium and difficult cases of the protein-protein benchmark. We hypothesize that freeing an integrative modeling protocol from usage of a force field, when possible, increases performance in terms of placement of the rigid partners.

Comparison with IDOCK and HADDOCK-EM

Our hypothesis is corroborated by comparison of the performance of ATTRACT-EM with two other published cryo-EM driven integrative modeling methods that avoid clashes. Schneidman-Duhovny et al. (26) presented the IDOCK approach, which consists of rigid-body docking with PatchDock (27), followed by filtering by various experimental data, including cryo-EM, followed by flexible refinement and a scoring function based on both the force field energy and the fit to the experimental data. IDOCK was tested with cryo-EM data on a subset of 27 complexes from the protein benchmark. Comparing the performance of ATTRACT-EM to the performance of IDOCK with simulated electron density maps, our results indicate that ATTRACT-EM clearly outperforms the IDOCK approach. Additionally, for other data sets than cryo-EM (contact information, interface information, and SAXS), the IDOCK results are no better than the models generated by ATTRACT-EM.

Recently, van Zundert et al. (56) added support for cryo-EM maps to the data-driven docking program HADDOCK. The protocol, HADDOCK-EM, starts with a standard docking iteration where the bodies are directed toward predefined regions of space. The docking solutions are then scored and refined with a combination of cryo-EM score, force field energy and, potentially, distance restraints from other experimental data. For the 17 cases on which HADDOCK-EM was tested, ATTRACT-EM performed on average better in terms of lowest I-RMSD. Especially for the medium and hard docking cases, ATTRACT-EM clearly surpassed the performance of the HADDOCK-EM protocol by a significant margin.

Finally, we performed control experiments with ATTRACT-EM where a force field was added during the sampling stages. Although the effects on the sampling were inconclusive, the use of the force field during the final scoring stage discarded many correct models, particularly for the hard docking cases. Therefore, it is crucial not to eliminate any structure that is potentially correct, even though the force field may indicate a very poor energy because of clashes. To some extent, IDOCK already follows this approach, compared to standard PatchDock docking, the force field is relaxed in the initial sampling stage. The ATTRACT-EM protocol goes further: during the sampling stage, structures may clash to a very large degree, and, more importantly, the scoring function consists of the experimental data alone. This is fundamentally different from the paradigm used in IDOCK, HADDOCK-EM, and other methods that first enumerate all structures that are compatible with a force field and filter them based on a weighted sum of force field and experimental data. Rather, we aim to sample the conformational space that agrees best with the cryo-EM data and delegate any use of a force field to a potential flexible refinement stage.

This does mean, however, that ATTRACT-EM models may have a considerable amount of clashes, raising the question of how to interpret these models at the level of individual atomic positions, and if flexible methods should be applied.

Interpretation and flexibility of cryo-EM models

The main risk of introducing flexibility in modeling is overfitting, i.e., driving away from the native structure an unbound form that does actually not undergo significant conformational changes upon binding. In other words, a major challenge of flexible modeling approaches is to decide if and where conformational change is likely to occur, and if and where flexibility should be applied to the model. The presence of clashes in a model is a natural indicator of atomic uncertainty; fixing them by flexible methods may lead to a false sense of atomic precision, whereas in reality, these methods may make the precision worse through overfitting. It is clear why flexible modeling methods are more prone to this than rigid methods. The rigid assembly of a protein complex inside a cryo-EM density map is a problem with six degrees of freedom per monomer, and we show that 20 Å cryo-EM maps provide enough information to solve this problem for 12 (dimer) or 18 (trimer) degrees of freedom. In contrast, the determination of all atomic positions is a problem with three degrees of freedom per atom; even if one takes into account the restrictions imposed by stereochemistry, an immense conformational space remains. To sample this conformational space, 20 Å cryo-EM data is widely considered to be too low in resolution. Therefore, the proper interpretation of a model, in terms of flexibility and atomic precision, is closely related to the quality of the data.

Investigating the most appropriate flexible refinement for ATTRACT-EM models is out of scope of the current study. Still, two perspectives for subsequent flexible refinement can be identified. First, even at low resolution, cryo-EM data can give direct insight into protein flexibility upon complexation. The clashes in the ATTRACT-EM models identify the presence and the location of conformational change, and can identify the atoms for which the conformational change is the largest. These atoms and their vicinities are good targets for subsequent flexible remodeling. Second, although this study performs a head-to-head comparison of cryo-EM data versus contacts and interface data, one could also consider all data together. On the one hand, for the initial rigid modeling, our results strongly suggest that the best strategy is to use the cryo-EM data alone, and use other data only for validation. In contrast, for subsequent flexible remodeling, 20 Å cryo-EM data would be too low in resolution, but interface and contact data (being local, rather than global) could be highly valuable. In summary, one could envision a multistep integrative modeling process where global data (cryo-EM or SAXS) is used to determine the rigid positions, followed by local refinement of the interface using experimental data on contacts or interface residues, validating the rigid models, resolving putative clashes, and remodeling flexible loops. A suitable protocol for such a targeted flexible remodeling could achieve a more accurate definition of the interface, useful for biological interpretation, than rigid modeling alone.

Conclusion

Here, we tested and compared EM-driven, interface-driven, and contact-driven integrative modeling paradigms using the ATTRACT docking engine. At 20 Å resolution, EM-driven modeling achieved a success rate of 100%, outperforming both interface-driven and contact-driven integrative modeling, even with perfect interface and contact information. This performance was robust to experimental noise and conformational change. Our results show that cryo-EM maps, even at very low resolution, are superior to other integrative modeling data in predicting heterodimeric and heterotrimeric protein assemblies. Both contact-driven and interface-driven modeling define distance restraints, and rely on a molecular force field to guide the monomers to the correct positions. Likewise, cryo-EM data have been used either in combination with a force field or to filter docking solutions. Our study demonstrates that a force field is not necessary, cryo-EM data alone is sufficient to guide the monomers into place. The resulting rigid models successfully identify regions of conformational change, opening up perspectives for targeted flexible remodeling.

Author Contributions

S.J.dV. and M.Z. conceived the study. S.J.dV., M.Z., I.C.dB., and C.S. prepared the method development and data preparation. S.J.dV. performed the experiments. S.J.dV., I.C.dB., and C.S. analyzed the experiments. S.J.dV., I.C.dB., and C.S. wrote the article.

Editor: Edward Engelman