Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Mar 3;6:22377. doi: 10.1038/srep22377

Weak antilocalization in Cd3As2 thin films

Bo Zhao 1, Peihong Cheng 2, Haiyang Pan 1, Shuai Zhang 1, Baigeng Wang 1, Guanghou Wang 1, Faxian Xiu 2,a, Fengqi Song 1,b
PMCID: PMC4776113  PMID: 26935029

Abstract

Recently, it has been theoretically predicted that Cd3As2 is a three dimensional Dirac material, a new topological phase discovered after topological insulators, which exhibits a linear energy dispersion in the bulk with massless Dirac fermions. Here, we report on the low-temperature magnetoresistance measurements on a ~50 nm-thick Cd3As2 film. The weak antilocalization under perpendicular magnetic field is discussed based on the two-dimensional Hikami-Larkin-Nagaoka (HLN) theory. The electron-electron interaction is addressed as the source of the dephasing based on the temperature-dependent scaling behavior. The weak antilocalization can be also observed while the magnetic field is parallel to the electric field due to the strong interaction between the different conductance channels in this quasi-two-dimensional film.

Dirac materials, with linear band dispersion in low-energy excitation such as graphene and topological insulators, have been receiving increasing attention owing to the possibility of being a new candidate for next-generation electronic and spintronic devices1,2. Recently, theory predicts that Cd3As2 3 and Na3Bi4 are the three dimensional (3D) Dirac materials, soon after which, they have been experimentally demonstrated by angle-resolved photoemission spectroscopy (ARPES)5,6,7, scanning tunneling microscope (STM)8 and electrical transport measurements9. Remarkably, various novel topological phases, such as Weyl semimetals, topological insulators and topological superconductors can be obtained from 3D Dirac materials by breaking the time reversal symmetry or inversion symmetry10,11. More importantly, electrical transport measurements of Cd3As2 bulk crystals exhibit many novel phenomenona, such as high mobility, giant and linear magnetoresistance (MR), non-trivial quantum oscillations and Landau level splitting under magnetic fields8,9,12,13. Besides, the superconductivity phenomenon has been evidenced on the surface of Cd3As2 crystals. It could be topological superconductors14. Another important phenomenon is the negative MR which confirms the existence of chirality in Weyl fermions that has been observed in Cd3As2 nanowires15 and nanoplates16. And in the systems of Bi0.97Sb0.0317, TaAs18,19, ZrTe520 and Na3Bi21, the chiral anomaly induced negative MR has also been observed.

In low-dimensional structures, studies of electrical transport have revealed several quantum interference (QI) phenomena at low temperature, including weak localization (WL) or weak antilocalization (WAL) and universal conductance fluctuations (UCF). The physical properties of some materials can be determined from these QI phenomena including the temperature dependence of the resistance, Hall effect, and MR. In 2D films, these contributions are logarithmic in temperature and have nontrivial dependence on the magnetic field. In perpendicular and parallel fields, MR always shows different behavior since orbital QI effects are sensitive to field orientation22,23,24. These techniques are well established but continue to be useful in the study of electrical transport in a variety of systems23,24,25. WAL phenomenon is always observed in Dirac materials, such as topological insulators and graphene without inter-valley scattering, as an important consequence of spin-momentum locking and the full suppression of backscattering, resulting in a relative π Berry phase acquired by electrons executing time-reversed paths26,27. Recently, the WAL effect has also been observed in 3D Dirac semimetal Cd3As228,29, 3D Weyl semimetal TaAs18,19 and Bi0.97Sb0.0317. In addition, the WAL effect by theoretical description using the Feynman diagram shows its origin from the inter-valley scattering as described in two-dimensional (2D) Dirac materials such as graphene and topological insulators30.

However, the WAL effect is always absent in 2D films when applied parallel magnetic field due to the suppressed interference in a closed electron path. As an effective tool to investigate the scattering ratio in parallel field, the WAL effect is indispensable. In this work, we study the magnetoresistance of ~50 nm-thick Cd3As2 films. We have found a sharp cusp around 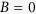Inline graphic which is stable when the magnetic field is perpendicular to the film (B⊥E) or parallel to electric field (B‖E). We take into account 2D HLN formula in the presence of spin-orbit coupling to discuss the WAL effect in B⊥E while we explore the origin of the WAL effect in B‖E, where a negative MR is also observed.

Results and Discussion

Figure. 1 shows the temperature dependence of the resistance 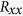Inline graphic of sample CA2. With the temperature decreasing, 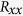Inline graphic shows an increasing behavior over the temperature range which is different from metallic bulk materials. This insulating behavior is also reported in low-dimensional Cd3As2 materials28,29,31 and bulk materials under high pressure32,33. The data can be fitted to the Arrhenius formula of 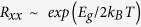Inline graphic at temperatures from 100 K to 200 K, where 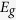Inline graphic is the bandgap, 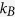Inline graphic is the Boltzmann constant and 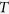Inline graphic is the measurement temperature. We obtain the band gap 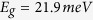Inline graphic, which is reasonable with the value for the Cd3As2 thin film of this thickness3,29. When the temperature reaches <100 K, the resistance deviates from the Arrhenius formula and shows weak temperature dependence below 20 K. The sharp increase below 4 K indicates a contribution from electron-electron scattering in the presence of disorder in the 2D films at low temperatures34,35.

Figure 1. Temperature dependence of the resistance of the Cd3As2 film device CA2.

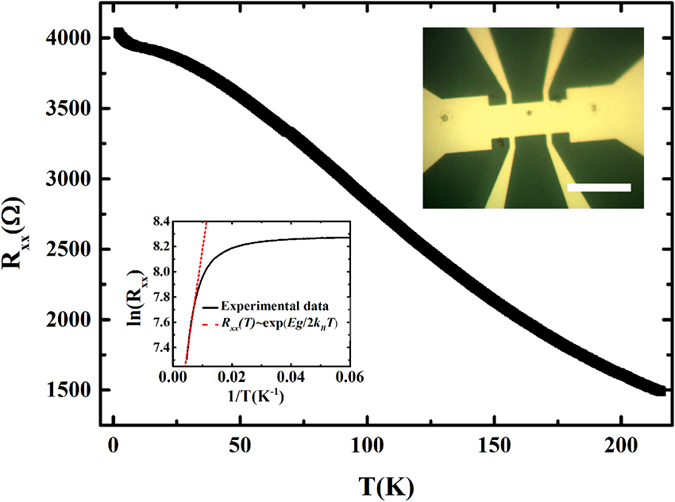
Figure 1

Open in a new tab

The right inset shows its optical image with the scale bar of 50 μm. The left inset shows the Arrhenius fitting of 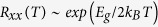Inline graphicwith the result of a 21.9 meV band gap.

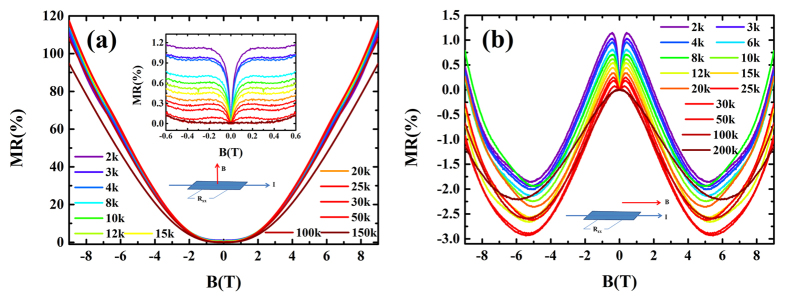
Figure. 2(a,b) show the MR under applied magnetic fields B⊥E and B‖E respectively at various temperatures. The MR defined as:

Figure 2. The MR with the applied magnetic field B⊥E or B||E.

Figure 2

Open in a new tab

Schematic diagram of electrical transport measurements are shown in insert respectively. (a) The magnetoresistance vs magnetic field in B⊥E at various temperatures from 2 K to 150 K. The insert show the sharp cusp at low magnetic field. (b) The magnetoresistance with B‖E at various temperatures from 2 K to 200 K. The WAL effect is also clear around zero fields. With the magnetic field increasing, the MR decreasing shows a negative MR phenomenon with a weak temperature dependent below 150 K. However, it increase with increasing magnetic field when B > 5T.

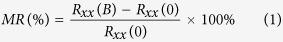graphic file with name srep22377-m9.jpg

For the perpendicular field of 9T, the MR is around 100% with a weak temperature dependent below 150 K. This is different from the giant MR in bulk samples36. Around 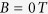Inline graphic, sharp cusps are observed clearly and gradually weaken with increasing temperature. This cusp is ascribed to the quantum interference phenomenon, weak antilocalization, which is also observed in B‖E shown in Fig. 2 (b). However, the MR shows a different behavior in B‖E contrast with that in B⊥E. It decreases with increasing applied magnetic field, showing a negative MR.

Before discussing the magneto-transport properties of the Cd3As2 films, we first investigate their dimensionality. The film can be treated as a 2D system for the thickness t smaller than the appropriate physical length scales. As shown in Table 1, the electronic mean-free path 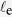Inline graphic for three samples are obtained with the 2D formula 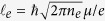Inline graphic, where 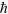Inline graphic is the Planck constant, 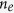Inline graphic is the 2D carrier density obtained from the Hall effect measurement, μ is the carrier mobility extracted from the electronic conductivity formula 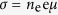Inline graphic. It is clear that the mean-free path 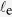Inline graphic is longer than the thickness t = 50 nm for sample CA1 and CA3 and less than the thickness for sample CA2. So the classical diffusive transport is quasi-2D and the treatment before is reasonable. For QI effects, the relevant length scale is the dephasing length Lφ. In nonmagnetic weak disorder systems, the dephasing length is always dominated by inelastic scattering, such as electron-phonon and electron-electron scattering. The electron-phonon scattering with a strong temperature-dependent is always suppressed with decreasing temperature. Thus the Lφ increases with the temperature decreasing. In the measurement temperature from 100 K to 2 K, 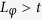Inline graphic (based on the analysis below) indicates a 2D behavior in the QI range. So we restrict our analysis to this quasi-2D limit.

Table 1. Measured and calculated Inline graphic sample parameters.

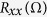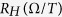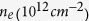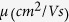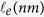Device L(μm) W(μm) Inline graphic Inline graphic Inline graphic Inline graphic Inline graphic
CA1 30 80 416.8 290.36 2.15 2612.4 64
CA2 25 25 4039.8 991.42 0.63 2454.1 32
CA3 4 4 1520.2 377.1 1.66 2480.5 53
Open in a new tab

The device length is the distance between the two measure voltage probes in a four-probe configuration. The values of 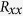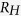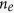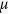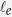Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic are for 2 K. The longitudinal resistance 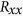Inline graphic, Hall coefficient 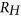Inline graphic obtained from fitting the Hall resistance with linear curve. 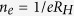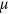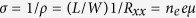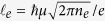The carrier density Inline graphic, the mobility Inline graphic obtained from Inline graphic, the mean-free path Inline graphic.

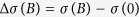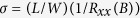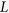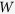In Figs 3 and 4, the magnetoconductivity are treated with Inline graphic at various temperatures, where Inline graphic, Inline graphic and Inline graphic are the length and width of the sample respectively, 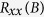Inline graphic is the resistance under applied magnetic field B⊥E or B‖E.

Figure 3. Weak antilocalization effect in applied magnetic field B⊥E.

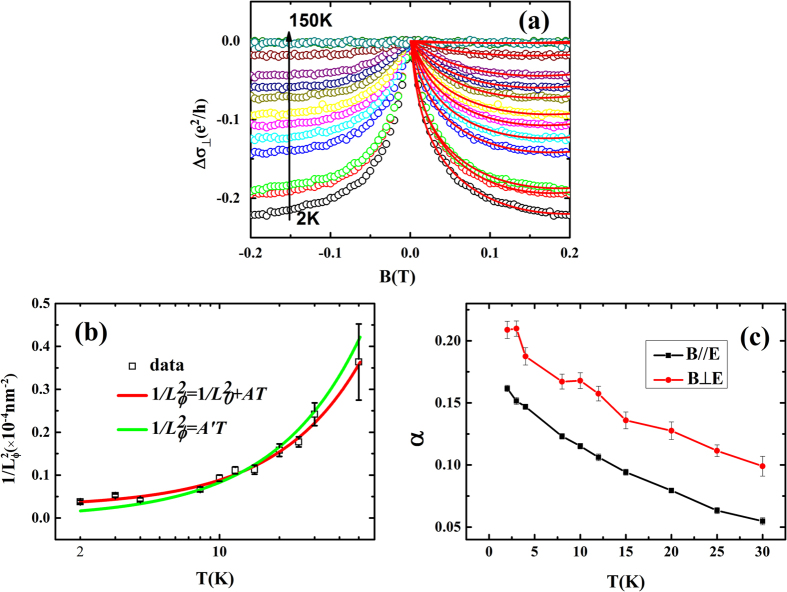
Figure 3

Open in a new tab

(a) The magnetoconductivity of sample CA1 (hole circle) vs magnetic field in B⊥E at temperature from 2 K to 150 K along with fitting (red solid curves) to the Equation 2. (b) The dephasing length vs temperature. (c) Temperature dependent parameter α with B⊥E or B‖E.

Figure 4. Weak antilocalization effect in applied magnetic field B||E.

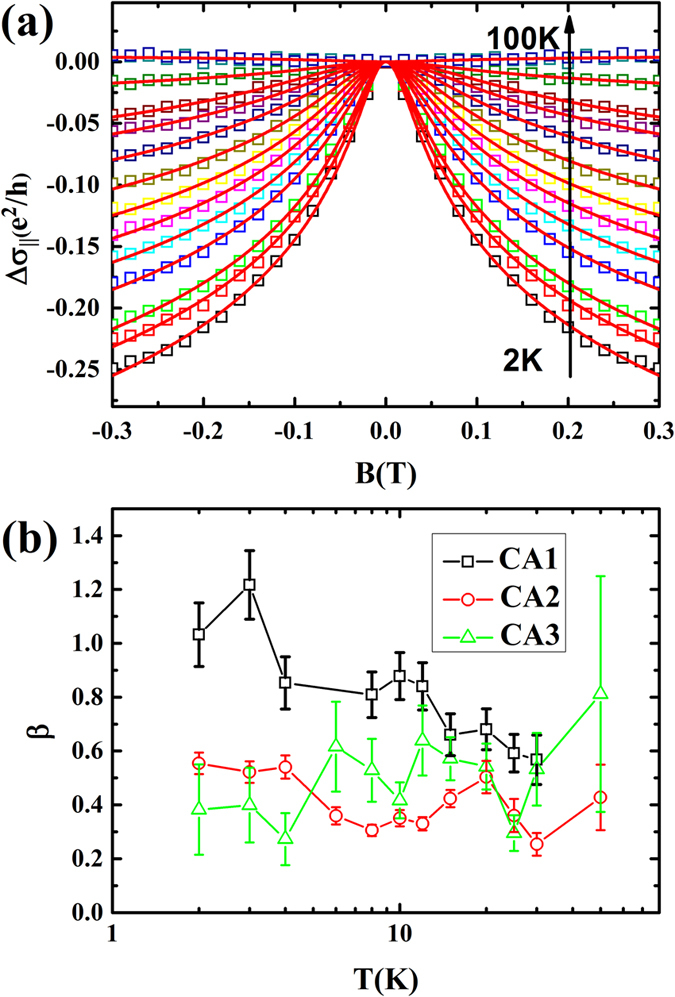
Figure 4

Open in a new tab

(a) The magnetoconductivity of sample CA1 (hole square) vs magnetic field in B‖E at temperature from 2 K to 100 K along with fitting (red solid curves) to the Equation 3. (b) Temperature dependence of β obtained from Equation 3. For sample CA1, the mean free path 64 nm is larger than the film thickness 50 nm.

In 2D systems with an applied perpendicular magnetic field, Hikami, Larkin and Nagaoka (HLN) first described in the presence of spin-orbit coupling for the temperature dependent WAL correction to the conductance37. Besides, the background with parabolic conductance contribution is also considered38. The correction formula can be written as:

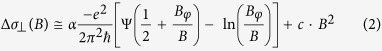graphic file with name srep22377-m23.jpg

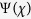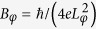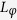where Inline graphic is the digamma function, the characteristic field Inline graphic, and Inline graphic is effective dephasing length. The parameter α takes values of 1/2 and −1 respectively for weak antilocalization and weak localization. The fitting curves for samples CA1 are shown in Fig. 3(a) with red solid curves. The parameter α, shown in Fig. 3(c), with a value of 0.2 at 2 K that is less than it proposed by theory. The temperature dependent of dephasing length 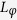Inline graphic is shown in Fig. 3(b). It is clear that the 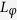Inline graphic decreases from 513 nm to 110 nm with the temperature increasing from 2 K to 100 K. The extracted 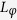Inline graphic values are larger than the thickness of Cd3As2 films, justifying the 2D WAL characteristics in our samples.

The parameter α reflects the number of independent conduction channels in the film26,39. For the 2D electron gas (2DEG) with parabolic dispersion, the magnetoconductivity can transform from WL to WAL (α from −1 to 0.5) as a function of the strength of scattering by spin-orbit impurities. However, for the massless Dirac fermions in 3D topological insulators, the WAL (α = 0.5) always exist for every value of the spin-orbit disorder40. Besides, due to the coexistence of topologically trivial 2DEG and topological surface state, the α < 0.5 is observed in 3D topological insulator41. For the negative magnetoconductivity in 3D Dirac semimetal, the WAL in low field and short-range scattering in high field are also discussed30,42. Recently, the Aharonov-Bohm oscillations have been observed in individual single-crystal Cd3As2 nanowires. It provides transport evidence of the surface state in three-dimensional Dirac semimetals43. So the several independent conduction channels may coexist with each other in this Cd3As2 films with different strength of spin-orbit scattering. It induces α < 0.5.

In the low temperature regime, the dephasing mechanism for 2D system can induce a power-law rule of 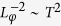Inline graphic due to the electron-phonon scattering and 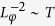Inline graphic because of the quasielastic Nyquist electron-electron scattering process44. Here we proposed the electron-electron interaction and the saturated dephasing mechanism in the Cd3As2 film and it can be fit with the formula 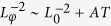Inline graphic44,45, where 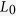Inline graphic represents the zero-temperature dephasing length. It is sensitive to the impurities and surface scattering. The last term 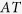Inline graphic is the contribution from electron-electron interaction. As shown in Fig. 3(b), it results in a perfect fitting with the parameter 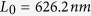Inline graphic. Above all, the electron-electron interaction and the surface scattering or impurities may exist in this film44.

Figure. 4(a) shows the WAL effect of the sample CA1 under B‖E. It clearly displays evident cusp around 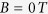Inline graphic with the 2D character confirmed by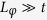Inline graphic. In thin films, Al’tshuler and Aronov (AA) described firstly the quantum corrections to the conductivity when applied magnetic field in the plane of the film46 and a similar suppression of QI phenomenon as in the perpendicular field case. The formula for this correction under B‖E can be written as:24,46

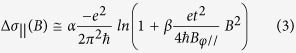graphic file with name srep22377-m38.jpg

where 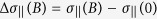Inline graphic. t = 50 nm is the film thickness. The parameter 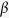Inline graphic is related to the ratio of mean free path and film thickness. The meaning of the parameter α is described before. However, the value of α = 0.16 in B‖E at 2 K is similar to α = 0.2 in E⊥B, and with a similar temperature dependence in Fig. 3(c). So we assume that the dephasing length in B‖E is equal to the one under B⊥E (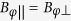Inline graphic)23. Thus, the 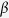Inline graphic vs temperature can be obtained. The 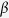Inline graphic of three samples are shown in Fig. 4(b). For CA1, the value of 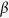Inline graphic is close to 1 at 2 K and decreases to 0.56 when the temperature increases to 30 K. In this sample, the mean free path 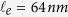Inline graphic is larger than the film thickness. 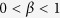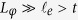So this result shows a good agreement with the value of Inline graphic for Inline graphic in bilayer system, such as double quantum wells and topological insulators films with two separate surface states23,47. 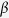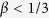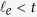For CA2 and CA3, it shows a smaller value Inline graphic than that in CA1, but it also shows a larger value than the theory proposed with Inline graphic for Inline graphic in single layer systems, as shown in Fig. 4 (b).

Although the origin of this obvious WAL effect in this 2D film in B‖E is still a puzzle, a physical origin is proposed to explain this: There are at least two 2D conductance channels contribution in Cd3As2 films. This field introduces an additional phase for the electron which moves in one channel, then tunnels into another channel, moves there, and finally tunnels back and returns to the initial point.

For B‖E, the MC is upturned with increasing field away from WAL effect range. The experimental observation of this crossover is always attributed to the translation from WAL to WL. The weak localization effect due to the QI is always suppressed by thermal average at higher temperatures. However, for the negative MR in B‖E in Fig. 2(b), it is rather robust and survives at higher temperature. The WL also observed in graphene at room temperature48. Besides, this upturn is enhanced in applied magnetic field B‖E. In topological materials, this crossover phenomenon has also been observed at the earliest in 45 nm thick Bi2Se3 films49. It has been attributed to the angle between the spin polarization of surface current and magnetic field direction. Whereas, the Berry phase in this Cd3As2 films is trivial29. Therefore, additional insights will also be required in the future.

Conclusion

In summary, we have measured the resistance and magnetoresistance of Cd3As2 films with thickness of ~50 nm under applied magnetic field B⊥E or B‖E. An insulating temperature dependent resistance with a band gap 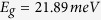Inline graphic is observed in Cd3As2 films. Positive MR sharp cusp around 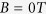Inline graphic under both applied field were measured, which can be satisfactorily described by existing 2D WAL theory. The electron-electron scattering is suggested as a source of the dephasing mechanism in this Cd3As2 film. Under B‖E, the WAL effect is also clearly observed and proposed as the strong coupling between the different conductance channels in this quasi-two-dimensional film. The negative MR is observed in B||E in Cd3As2 films. But the exact origin of this negative MR needs further work.

Methods

The ~50 nm-thick Cd3As2 thin films are grown in a molecular beam epitaxy system. The devices are fabricated with standard Hall bar geometry with a metal mask for sample CA1 and ultra-violet (UV) lithography photoresist as mask for CA2 and CA3. The exposed area is etched with argon plasma. The UV photoresist is cleaned with acetone and deionized water. All measurements were carried out at low temperatures down to 2 K with a magnetic field up to 9T. Standard lock-in amplifiers (Stanford Research 830 and 850) were used to acquire data with the electric current of 1 μA. The parameters of all samples are listed in Table 1.

Additional Information

How to cite this article: Zhao, B. et al. Weak antilocalization in Cd3As2 thin films. Sci. Rep. 6, 22377; doi: 10.1038/srep22377 (2016).

Acknowledgments

We gratefully acknowledge the financial support of the National Key Projects for Basic Research of China (Grant Nos 2013CB922103), the National Natural Science Foundation of China (Grant Nos 91421109, 11522432, 61322407, 11474058), the PAPD project, the Natural Science Foundation of Jiangsu Province (Grant BK20130054), and the Fundamental Research Funds for the Central Universities. We would also like to acknowledge the helpful assistance of the Nanofabrication and Characterization Center at the Physics College of Nanjing University.

Footnotes

Author Contributions B.Z., F.S. and F.X. conceived the work and wrote the paper. B.Z., F.X. and P.C. prepared the samples. B.Z., S.Z., H.P. and F.S. performed the experiments. F.X., B.W., F.S. and G.W. had valuable discussions and edited the manuscript. All authors commented on the manuscript.

References

  1. Kong D. & Cui Y. Opportunities in chemistry and materials science for topological insulators and their nanostructures. Nat. Chem. 3, 845 (2011). [DOI] [PubMed] [Google Scholar]
  2. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011). [Google Scholar]
  3. Wang Z. et al. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B 88, 125427 (2013). [Google Scholar]
  4. Wang Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012). [Google Scholar]
  5. Liu Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 13, 677 (2014). [DOI] [PubMed] [Google Scholar]
  6. Yi H. et al. Evidence of topological surface state in three-dimensional Dirac semimetal Cd3As2. Sci. Rep. 4, 6106 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Borisenko S. et al. Experimental Realization of a Three-Dimensional Dirac Semimetal. Phys. Rev. Letts. 113, 027603 (2014). [DOI] [PubMed] [Google Scholar]
  8. Jeon S. et al. Landau quantization and quasiparticle interference in the three-dimensional Dirac semimetal Cd3As2. Nat. Mater. 13, 851 (2014). [DOI] [PubMed] [Google Scholar]
  9. Narayanan A. et al. Linear Magnetoresistance Caused by Mobility Fluctuations in n-Doped Cd3As2. Phys. Rev. Letts. 114, 117201 (2015). [DOI] [PubMed] [Google Scholar]
  10. Gorbar E. V., Miransky V. A. & Shovkovy I. A. Engineering Weyl nodes in Dirac semimetals by a magnetic field. Phys. Rev. B 88, 165105 (2013). [Google Scholar]
  11. Potter A. C., Kimchi I. & Vishwanath A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nat. Commun. 5, 5161 (2014). [DOI] [PubMed] [Google Scholar]
  12. Cao J. et al. Landau level splitting in Cd3As2 under high magnetic fields. Nat. Commun. 6, 7779 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Zhao Y. et al. Anisotropic Fermi Surface and Quantum Limit Transport in High Mobility Three-Dimensional Dirac Semimetal Cd3As2. Phys. Rev. X 5, 031037 (2015). [Google Scholar]
  14. Wang H. et al. Observation of superconductivity induced by a point contact on 3D Dirac semimetal Cd3As2 crystals. Nature materials 15, 38 (2016). [DOI] [PubMed] [Google Scholar]
  15. Li C. Z. et al. Giant negative magnetoresistance induced by the chiral anomaly in individual Cd3As2 nanowires. Nat. Commun. 6, 10137 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Zhang C. et al. Detection of chiral anomaly and valley transport in Dirac semimetals. arXiv: 1504.07698 (2015).
  17. Kim H.-J. et al. Dirac versus Weyl Fermions in Topological Insulators: Adler-Bell-Jackiw Anomaly in Transport Phenomena. Phys. Rev. Letts. 111, 246603 (2013). [DOI] [PubMed] [Google Scholar]
  18. Zhang C. et al. Observation of the Adler-Bell-Jackiw chiral anomaly in a Weyl semimetal. arXiv: 1503.02630 (2015). [DOI] [PMC free article] [PubMed]
  19. Huang X. et al. Observation of the Chiral-Anomaly-Induced Negative Magnetoresistance in 3D Weyl Semimetal TaAs. Phys. Rev. X 5, 031023 (2015). [Google Scholar]
  20. Li Q. et al. Observation of the chiral magnetic effect in ZrTe5, arXiv: 1412.6543 (2014).
  21. Xiong J. et al. Signature of the chiral anomaly in a Dirac semimetal–a current plume steered by a magnetic field. arXiv: 1503.08179 (2015).
  22. Beenakker C. W. J. & van Houten H. Boundary scattering and weak localization of electrons in a magnetic field. Phys. Rev. B 38, 3232 (1988). [DOI] [PubMed] [Google Scholar]
  23. Lin C. J. et al. Parallel field magnetoresistance in topological insulator thin films. Phys. Rev. B 88, 041307 (2013). [Google Scholar]
  24. Zyuzin A. A., Hook M. D. & Burkov A. A. Parallel magnetic field driven quantum phase transition in a thin topological insulator film. Phys. Rev. B 83, 245428 (2011). [Google Scholar]
  25. Wang H. et al. Crossover between weak antilocalization and weak localization of bulk states in ultrathin Bi2Se3 films. Sci. Rep. 4, 5817 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Lu H.-Z. & Shen S.-Q. Weak localization of bulk channels in topological insulator thin films. Phys. Rev. B 84, 125138 (2011). [Google Scholar]
  27. He H.-T. et al. Impurity Effect on Weak Antilocalization in the Topological InsulatorBi2Te3 Phys. Rev. Letts. 106, 166805 (2011). [DOI] [PubMed] [Google Scholar]
  28. Li H. et al. Negative Magnetoresistance in Dirac Semimetal Cd3As2. arXiv: 1507.06470 (2015). [DOI] [PMC free article] [PubMed]
  29. Liu Y. et al. Gate-tunable quantum oscillations in ambipolar Cd3As2 thin films. NPG Asia Mater. 7, e221 (2015). [Google Scholar]
  30. Lu H.-Z. & Shen S.-Q. Weak antilocalization and localization in disordered and interacting Weyl semimetals. Phys. Rev. B 92, 035203 (2015). [Google Scholar]
  31. Zhang E. et al. Magnetotransport properties of Cd3As2 nanostructures. arXiv: 1503,004222 (2015). [DOI] [PubMed]
  32. Zhang S. et al. Breakdown of three-dimensional Dirac semimetal state in pressurized Cd3As2. Phys. Rev. B 91, 165133 (2015). [Google Scholar]
  33. He L. P. & Li S. Y. Pressure-induced superconductivity in the three-dimensional Dirac semimetal Cd3As2. arXiv: 1502,02509 (2015).
  34. Lin J. & Giordano N. Localization and electron-electron interaction effects in thin Au-Pd films and wires. Phys. Rev. B 35, 545 (1987). [DOI] [PubMed] [Google Scholar]
  35. Wang J. et al. Evidence for electron-electron interaction in topological insulator thin films. Physical Review B 83, 245438 (2011). [Google Scholar]
  36. Liang T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280 (2015). [DOI] [PubMed] [Google Scholar]
  37. Hikami S., Larkin A. I. & Nagaoka Y. Spin-Orbit Interaction and Magnetoresistance in the Two Dimensional Random System. Prog. Theor. Phys. 63, 707 (1980). [Google Scholar]
  38. Burkov A. A. Negative longitudinal magnetoresistance in Dirac and Weyl metals Phys. Rev. B 91, 245157 (2015). [Google Scholar]
  39. Garate I. & Glazman L. Weak localization and antilocalization in topological insulator thin films with coherent bulk-surface coupling. Phys. Rev. B 86, 035422 (2012). [Google Scholar]
  40. Adroguer P., Liu W. E., Culcer D. & Hankiewicz E. M. Conductivity corrections for topological insulators with spin-orbit impurities: Hikami-Larkin-Nagaoka formula revisited. Phys. Rev. B 92, 241402 (2015). [Google Scholar]
  41. Li Z. et al. Experimental evidence and control of the bulk-mediated intersurface coupling in topological insulator Bi2Te2Se nanoribbons. Phys. Rev. B 91, 041401 (2015). [Google Scholar]
  42. Lu H.-Z., Zhang S.-B. & Shen S.-Q. High-field magnetoconductivity of topological semimetals with short-range potential. Phys. Rev. B 92, 045203 (2015). [Google Scholar]
  43. Wang L.-X., Li C.-Z., Yu D.-P. & Liao Z.-M. Aharonov-Bohm oscillations in Dirac semimetal Cd3As2 nanowires arXiv: 1511.07958 (2015). [DOI] [PMC free article] [PubMed]
  44. Lin J. J. & Bird J. P. Recent experimental studies of electron dephasing in metal and semiconductor mesoscopic structures. J. Phys. Condens. Matter 14, R501 (2002). [Google Scholar]
  45. Li Z. et al. Two-dimensional universal conductance fluctuations and the electron-phonon interaction of surface states in Bi2Te2Se microflakes. Sci. Rep. 2, 595 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Al’tshuler B. L. & Aronov A. G. Magnetoresistance of thin films and of wires in a longitudinal magnetic field. JETP Lett. 33, 499 (1981). [Google Scholar]
  47. Raichev O. E. & Vasilopoulos P. Weak-localization corrections to the conductivity of double quantum wells. J. Phys. Condens. Matter 12, 589 (2000). [Google Scholar]
  48. Han J. et al. Room-temperature observations of the weak localization in low-mobility graphene films. J. Appl. Phys. 114, 214502 (2013). [Google Scholar]
  49. Wang J. et al. Anomalous anisotropic magnetoresistance in topological insulator films. Nano Research 5, 739 (2012). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES