Variable priming of a docked synaptic vesicle

Significance

After synaptic vesicles dock at an active zone on the presynaptic plasma membrane of axon terminals, the vesicles become primed for fusion with the membrane, an essential step in synaptic impulse transmission. We used electron tomography to examine nanometer-scale variations in structural relationships of docked vesicles at the simply arranged active zones of frog neuromuscular junctions. The results, together with prior biochemical and electrophysiological concepts, lead to the hypothesis that priming is regulated by variation in force generated by the shortening and lengthening of macromolecules in the common active zone organelle “active zone material” that links docked vesicles to presynaptic membrane components. Knowledge of mechanisms that regulate synaptic transmission is required for understanding how different synapses accomplish their specialized tasks.

Abstract

The priming of a docked synaptic vesicle determines the probability of its membrane (VM) fusing with the presynaptic membrane (PM) when a nerve impulse arrives. To gain insight into the nature of priming, we searched by electron tomography for structural relationships correlated with fusion probability at active zones of axon terminals at frog neuromuscular junctions. For terminals fixed at rest, the contact area between the VM of docked vesicles and PM varied >10-fold with a normal distribution. There was no merging of the membranes. For terminals fixed during repetitive evoked synaptic transmission, the normal distribution of contact areas was shifted to the left, due in part to a decreased number of large contact areas, and there was a subpopulation of large contact areas where the membranes were hemifused, an intermediate preceding complete fusion. Thus, fusion probability of a docked vesicle is related to the extent of its VM–PM contact area. For terminals fixed 1 h after activity, the distribution of contact areas recovered to that at rest, indicating the extent of a VM–PM contact area is dynamic and in equilibrium. The extent of VM–PM contact areas in resting terminals correlated with eccentricity in vesicle shape caused by force toward the PM and with shortness of active zone material macromolecules linking vesicles to PM components, some thought to include Ca²⁺ channels. We propose that priming is a variable continuum of events imposing variable fusion probability on each vesicle and is regulated by force-generating shortening of active zone material macromolecules in dynamic equilibrium.

Synaptic vesicles (SVs) move toward and dock on (are held in contact with) the presynaptic plasma membrane (PM) of a neuron’s axon terminal before fusing with the PM and releasing their neurotransmitter into the synaptic cleft to mediate synaptic transmission (1, 2). Docking is achieved by force-generating interactions of the vesicle membrane (VM) protein synaptobrevin with the PM proteins syntaxin and SNAP25 (3, 4). These interactions, which produce force by forming a coiled coil called the SNARE core complex, are regulated by auxiliary proteins (1, 5–7). Such force on the VM–PM contact site may also play a role in their fusion (8). At typical synapses, docking and fusion take place at structurally specialized regions along the PM called active zones (9, 10). Several lines of evidence suggest that the formation of the SNARE core complex occurs in the macromolecules composing the common active zone organelle, active zone material (AZM) (2, 11–14), which is positioned near Ca²⁺ channels concentrated in the PM at active zones (15–17). Influx of Ca²⁺ through the channels after the arrival of a nerve impulse triggers fusion of the VM of docked SVs with the PM.

Priming is a step in synaptic transmission between the docking of an SV on, and fusion with, the PM and accounts for the observation that relatively few docked SVs fuse with the PM after the arrival of a nerve impulse (18). It has been suggested that priming transitions docked SVs from fusion-incompetent (i.e., having 0% fusion probability) to fusion-competent (i.e., having 100% fusion probability), in a binary way (reviewed in ref. 19). However, as described for frog neuromuscular junctions (20–23), the number of SVs that can fuse with the PM after arrival of an impulse varies greatly with differing concentrations of cytosolic Ca²⁺, indicating that priming is more complex than a simple binary transition. Biochemical and electrophysiological approaches have provided evidence that priming is mediated by interactions between the SNARE proteins and their regulators (7, 12–14, 24) and can involve differences in positioning of docked SVs relative to Ca²⁺ channels (25). Biochemistry has also led to the suggestion that primed SVs may become deprimed (26).

We have previously shown by electron tomography on frog neuromuscular junctions (NMJs) fixed at rest that there are, for docked SVs, variations in the extent of the VM–PM contact area and in the length of the several AZM macromolecules linking the VM to the PM, the so-called ribs, pegs, and pins (2, 27). Here, we examined these, and other, structural variations in the same axon terminals fixed at rest, during repetitive evoked synaptic activity, or after recovery from such activity, with a view toward testing and extending our understanding of the processes that regulate priming. Our findings suggest a model in which all docked SVs are primed to varying degrees by a reversible continuum of AZM-mediated forces on them, and it is the degree of priming at any moment that determines the probability of a docked SV fusing with the PM upon arrival of a nerve impulse.

Results

VM–PM Contact Sites in Terminals Fixed at Rest.

Schematized layouts of relevant active zone components at frog NMJs and planes of reference are in Fig. 1. There are several hundred active zones in the arborization of axon terminals that constitute the presynaptic portion of a frog’s NMJ. Each active zone is ∼1 µm long. On each side of the main body of AZM, there is a row of ∼20 SVs (28). It has been estimated that only 1–2% of the SVs flanking the AZM in a terminal arborization fuse with the PM when an impulse arrives (29). We examined by electron tomography the proximity of the VM to the PM for 103 randomly selected SVs flanking the main body of the AZM in resting terminals fixed with glutaraldehyde and stained with osmium tetroxide at room temperature. The VM of 101 SVs contacted the PM without merging with it, as described below; the VM of the remaining two SVs was ∼10 nm away from the PM. Thus, more than 98% of SVs alongside AZM and next to the PM at active zones were docked. Measurements on resting terminals presented here, unless indicated otherwise, are from the 101 docked SVs and their associated PM and ribs, pegs, and pins and from 230 nearby undocked SVs. All values, unless indicated otherwise, are presented as means ± SD. We used the bootstrap test for comparison of nonparametric data. As discussed elsewhere in Results, measurements on key variables in the chemically fixed and stained resting sample were compared with those in a smaller sample from resting terminals fixed by rapid freezing and stained by osmium tetroxide freeze-substitution. There was no significant difference.

Fig. 1.

Layout of the active zone of resting axon terminals at frog NMJs. (A) Composite map of active zone components viewed in the active zone’s transverse plane. Docked SVs flank a shallow evagination of the PM, which is called the active zone ridge, and the main body of the AZM, which is composed of several logically distinct classes of macromolecules including the ribs and pegs. Pins are a class of AZM macromolecules beyond the AZM’s main body. Pins directly link the VM to the PM. Ribs link the VM to PM via pegs, which are connected to PM macromolecules thought to include Ca²⁺ channels and Ca²⁺-activated K⁺ channels. (B) Three-dimensional arrangement of docked SVs and their associated pins, ribs, pegs, and beams. The docked SVs lie in a row on each flank of the active zone ridge. The several ribs connected to each SV extend in parallel along the slopes of the active zone ridge to terminate on a beam, which runs orthogonal to the ribs and parallel to the median plane of the active zone. The median plane of the active zone extends vertical to the PM and along the long axis at the midline of the active zone ridge. The transverse plane also extends vertical to the PM but orthogonal to the median plane, and the horizontal plane is orthogonal to both the median and transverse planes. The horizontal plane of the active zone is nearly parallel to the plane of the PM beyond the active zone ridge, whereas the median plane of the active zone bisects the long axis of the main body of AZM. A and B are adapted from ref. 2.

Combined thickness of the VM and PM.

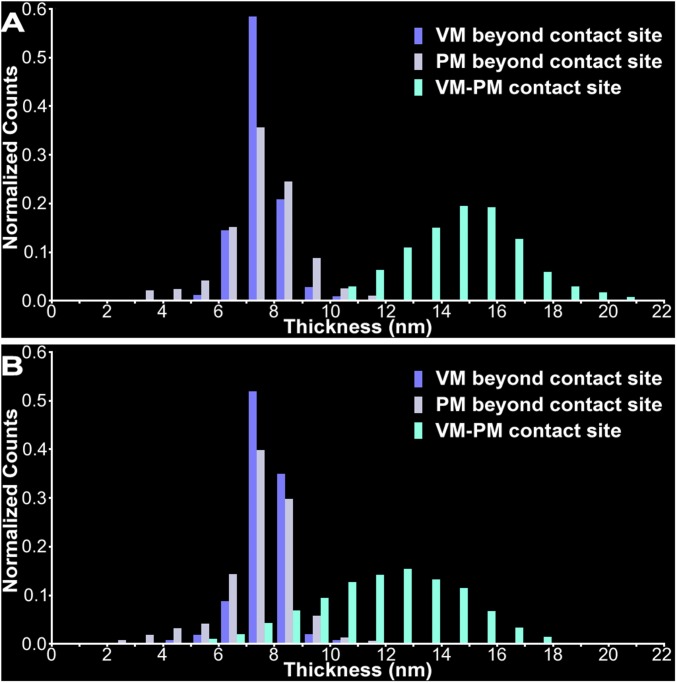
To quantitatively determine the spatial relationship of docked SVs to the PM at VM–PM contact sites, we began by comparing the combined thickness of the VM and PM throughout the contact site to the thickness of each membrane beyond the contact site in 3D surface models of each of the 101 docked SVs and its associated PM (Fig. 2 A–D). The thickness measurements were made using an algorithm for calculating the shortest distances across the membrane between vertices that established the membrane surfaces (Fig. 2 B and C) (30). For the example SV in Fig. 2D, the average thickness of the VM beyond the contact site was 7.4 ± 1.3 nm, whereas the average thickness of the PM beyond the contact site was 7.5 ± 1.5 nm; these dimensions are consistent with membrane thickness measurements made on 2D electron microscope images of cellular membranes in tissue sections (31). The average thickness of the combined VM and PM at the contact site was 15.1 ± 1.4 nm (Fig. 2D), which was not significantly different from the sum of the average thicknesses of the two membranes beyond the contact site (P = 0.72). These thicknesses were representative of those measured across the entire population of docked SVs and their associated PM (Fig. S1). Thus, for docked SVs there was no detectable gap between, or merging of, the two membranes at VM–PM contact sites at the 2- to 3-nm spatial resolution provided by our methods (32).

Fig. 2.

Proximity of the VM to PM at VM–PM contact sites. (A) Virtual slice, 2.3-nm-thick, through the transverse plane of an active zone from a resting terminal. Irregular staining of the VM of the two docked SVs and the PM makes it difficult to visually assess the relationship of the VM and PM at their contact site. (B) Portions of complete surface models of the two docked SVs and the stretch of PM in A. The vertices used to generate the models provide continuous surfaces for the VM and PM while accounting for irregularities in the membrane staining. (C) The contribution to the surface models in B made by the VMs and PM in A. Double-headed arrows indicate variations in the thickness of the surface models of the VMs (blue) and PM (light gray) away from the contact site and variations in the combined thickness of the VM and PM at the contact site (greenish-blue). (D) Frequency distributions of thousands of vertex-to-vertex measurements made across the entire membrane of a docked SV and the PM from complete 3D surface models. The mean thicknesses of the VM and the PM away from the VM–PM contact site are the same (P = 0.98), and the mean combined thickness of the VM–PM contact site is equal to the simulated sum of the mean VM and PM thicknesses away from the contact site (P = 0.72). Thus, there is no gap between or merging of the VM and PM at the contact site. (E) Virtual slice, 2.5-nm-thick, through the transverse plane of an active zone from a terminal fixed during repetitive synaptic activity. (F) Portion of complete surface models of the docked SV and PM in E. The VM–PM contact site is highlighted in greenish-blue. (G) The contribution to the surface models in F made by the VM and PM in E, as described in C. (H) Frequency distributions of vertex-to-vertex measurements made across the entire membrane of the docked SV and the PM from complete 3D surface models. The mean combined thickness of the VM–PM contact site is less than the simulated sum of the mean VM and PM thicknesses away from the contact site (P < 0.05). Thus, the VM and PM at their contact site are merged, which is characteristic of hemifusion. (Scale bars: 50 nm.)

Fig. S1.

Thicknesses of the VMs and PMs at and away from the VM–PM contact sites for populations of docked and hemifused SVs. (A) Frequency distributions of thousands of vertex-to-vertex measurements made for each of the SVs across the irregular thicknesses of the VM and PM away from the contact site and across the combined thickness of the VM and PM at the contact site of 101 docked SVs in resting terminals using surface models of the entire docked SVs and their associated PM. The combined thickness of the VMs and PMs at their contact sites is the sum of the thicknesses of the VMs and PMs beyond their contact sites. (B) Frequency distributions of thicknesses of the VM and PM away from the contact site and the combined thickness of the VM and PM at the contact site of seven hemifused SVs in stimulated terminals. The histograms include all measurements for the VM, PM, and VM–PM contact site.

Extent of VM–PM contact areas.

The VM–PM contact areas in resting terminals, mapped onto surface models of their PM, were roughly oval (Fig. 3A). We measured the extent of the contact area for each of the 101 docked SVs by projecting it onto a best-fit plane (27) and determining the number of pixels within its perimeter (the scale of a pixel typically corresponded to ∼1 nm² in the data). These areas varied 13-fold, from 46 to 630 nm² (330 ± 150 nm²), with a normal frequency distribution [P = 0.93 Kolmogorov–Smirnov (KS) test; Fig. 3C]. The contact areas accounted for 0.5–7% of the total cytosolic surface area of the SVs, which varied only two-fold (6,900–14,000 nm²). There was no significant correlation between the extent of the contact area and the total surface area of a docked SV (P = 0.15, Pearson correlation test).

Fig. 3.

Variation in the extent of the VM–PM contact areas in terminals fixed at rest, during repetitive synaptic activity or 1 h after activity. (A) The VM–PM contact areas for three docked SVs (dark blue) in terminals fixed at rest were projected on surface models of the PM viewed in the horizontal plane. Based on the number of pixels within the perimeter of the contact sites projected onto best-fit planes and the scale of the pixels, the left contact area is 60 nm², the middle contact area is 300 nm², and the right contact area is 600 nm². (B) Projection of a typical VM–PM contact area for a hemifused SV (teal-blue) in a terminal fixed during activity. The contact area is 630 nm². (Scale bar: A and B, 50 nm.) (C) The extents of the VM–PM contact areas of the 101 docked SVs, measured as in A, in terminals fixed at rest vary 13-fold, and the contact areas have a normal frequency distribution across the population (330 ± 150 nm²). (D) The extents of the contact areas of the 74 docked SVs in our sample from terminals fixed during repetitive activity have a normal frequency distribution (230 ± 120 nm²), but the location of the center of the distribution is shifted to the left of that for resting terminals shown in C (P < 0.001; t test) because of a decrease in the fraction of large contact areas and an increase in the fraction of small contact areas. The extent of the contact areas of the 7 SVs exhibiting VM–PM hemifusion in our sample was similar to the large contact areas in resting terminals. (E) The extent of the VM–PM contact areas for the 49 docked SVs in our sample from terminals fixed 1 h after activity had a normal distribution (330 ± 160 nm²), with the location of its center the same as that of resting terminals shown in A (P = 0.76; t test).

VM–PM Contact Sites in Terminals Fixed During Repetitive Evoked Impulse Activity.

Axon terminals were activated by electrical nerve stimulation at 10 Hz for 2 min beginning when the fixative was applied to their muscles; all terminals were fixed within the 2 min (2). We have previously shown that at active zones of terminals prepared in this way and examined by electron tomography there are not only docking sites having SVs in contact with the PM but also docking sites having Ω-shaped undulations in the PM indicative of former docked SVs shortly after their membrane had fused with the PM and formed a pore. Such fused SVs were still connected to AZM macromolecules. Moreover, there were vacated docking sites at which fused SVs had separated from the AZM and flattened into the PM; nearby undocked SVs were in the process of docking (2). Here, we studied the relationship of the VM to the PM at the VM–PM contact sites for 81 SVs.

Combined thickness of the VM and PM.

For ∼90% (74/81) of the VM–PM contact sites, there was no measurable gap between or merging of the VM and PM, as at all contact sites of docked SVs in resting terminals (all P values >0.05). Thus, the SVs forming these contact sites were docked. However, for ∼10% (7/81) of the VM–PM contact sites the combined thickness of the VM and PM was significantly less than the sum of the thicknesses of the two membranes beyond the contact site (Fig. 2 E–H, Fig. S1, and Table S1; all P values <0.05), indicating that the VM and PM had been fixed during the formation of a single bilayer characteristic of hemifusion, an intermediate state of membrane fusion that precedes fusion pore formation (33). VM–PM hemifusion, as assessed visually, has been reported for CNS synapses (34, 35).

Table S1.

Parameters for the contact sites of hemifused SVs with the PM

Hemifused SV no.	Average contact site thickness, nm	Average simulated thickness, nm	P	Contact site area, nm2
1	12.6 ± 2.1	15.7 ± 1.2	0.016	700
2	12.2 ± 2.6	15.8 ± 1.8	0.003	790
3	12.1 ± 2.3	15.8 ± 1.8	0.045	870
4	10.9 ± 2.5	15.9 ± 1.6	0.007	510
5	10.7 ± 2.3	15.6 ± 1.3	0.002	630
6	11.6 ± 2.4	15.4 ± 1.3	0.015	690
7	11.3 ± 2.0	16.1 ± 1.2	0.004	460

P values are derived from comparison (Bootstrap test) of the average contact site thickness and the average thickness of the simulated measurements that are based on the thickness of the SV membrane and PM away from the contact site.

Extent of VM–PM contact areas.

The extents of the VM–PM contact areas of the 74 docked SVs had a normal frequency distribution as in resting terminals, albeit truncated (Fig. 3D). However, the location of the center of the distribution was markedly shifted to the left (P < 0.001, t test). Moreover, the extents of the contact areas for all of the contact sites exhibiting hemifusion were similar to the large contact areas in resting terminals and overlapped with the few large contact areas of docked SVs in the active terminals that had not undergone hemifusion (Fig. 3 B and D and Table S1). These results would be expected if docked SVs having relatively large VM–PM contact areas at rest had preferentially undergone fusion with the PM during synaptic activity and those that had flattened into the PM were replaced at their docking sites by previously undocked SVs having relatively small contact areas, as explained in Discussion.

VM–PM Contact Sites in Terminals Fixed One Hour After Repetitive Evoked Impulse Activity.

All of the 49 SVs in contact with the PM at docking sites in terminals stimulated at 10 Hz for 2 min and fixed 1 h later were docked. Moreover, the extent of the VM–PM contact areas had a normal frequency distribution with the location of its center the same as that of the normal distribution in resting terminals (P = 0.76, t test; Fig. 3E). The recovery of the center of the frequency distribution to its resting location 1 h after synaptic activity indicates that the extent of contact areas of docked SVs is dynamic and in equilibrium, as explained in Discussion.

Variation in SV Eccentricity in Resting Terminals.

To assess whether the variation in extent of the VM–PM contact areas was attributable to the exertion of variable force on docked SVs toward the PM, we measured the eccentricity of the profiles of docked and undocked SVs, which can be affected by force (36), and determined the orientation of the SV's long axis.

When viewed in 3D surface models, both docked and undocked SVs in resting terminals had three orthogonal diameters, characteristic of an ellipsoid; we used these diameters to measure their shape. The three diameters varied from SV to SV, but the average geometric means of the diameters for both populations were similar (docked SVs, 56.0 ± 4.4 nm; undocked SVs, 55.9 ± 4.2 nm). The ellipsoidal shape of SVs was evident in the eccentricity of their profiles in serial virtual slices through them (Fig. 4 A and B). We determined the long diameter of the profiles of SVs in their middle virtual slice in reconstructions of tissue sections that were cut either near the active zones’ transverse plane (the 101 docked SVs and 230 undocked SVs) or horizontal plane (41 docked SVs). This revealed that the long diameter of the docked SVs’ profiles was preferentially oriented to within 45° of the horizontal plane of the active zone and to within 30° of the plane of the PM at the contact site (Fig. 4 A and C). The long diameter was also preferentially oriented nearly orthogonal to the median plane of the active zone (within 45°; Fig. 4 A, B, and D), which parallels the midline of the AZM. On the other hand, the long diameter of the profiles of undocked SVs had no common orientation (Fig. 4 A and C).

Fig. 4.

SV long-diameter orientation and eccentricity in resting terminals. (A) One of a series of virtual slices, 1.7-nm-thick, through a reconstructed section of an active zone cut in the transverse plane showing eccentric profiles of docked and undocked SVs. The long diameter of the profiles in the middle virtual slice through each of the SVs is indicated by the double-headed arrows (docked SVs, black; undocked SVs, dark gray). Red and green bars indicate the median and horizontal active zone planes, respectively. (B) Virtual slice 4-nm-thick through a reconstructed section of an active zone cut in the horizontal plane. A row of docked SV profiles is on each side of the median plane (red bar) of the active zone. Black double-headed arrows indicate the long diameter of the docked SV profiles, determined as described for A. (Scale bar: A and B, 50 nm.) (C) Frequency distributions of the long-diameter orientations for docked (n = 101) and undocked (n = 230) SV profiles measured in the middle virtual slice through each of the SVs from tissue sections cut in the active zones’ transverse plane, as in A. The long diameter of >90% of docked SV profiles is nearly parallel (within 45°) to the horizontal plane of the active zone, whereas the long diameter of the undocked SV profiles has no such common orientation. (D) Frequency distribution of the long-diameter orientations for docked SV profiles (n = 41) measured in the middle virtual slice through each of the SVs from tissue sections cut in the active zone’s horizontal plane, as in B. The long diameter of >90% of docked SV profiles is nearly orthogonal (within 45°) to the median plane of the active zone. (E) Measured in surface models, the average short to long diameter ratio of the 101 docked SVs is significantly less than that for the 230 undocked SVs (*P < 0.01, t test; error bars, SEM). Cartoons contrast the average shapes of undocked and docked SVs based on the ratios of short (vertical double-headed arrow) to long (horizontal double-headed arrow) diameter; for docked SVs, the short diameter is perpendicular to the PM (light gray).

Comparison of the short diameter to the long diameter of docked and undocked SVs, using 3D surface models, showed that this ratio was, on average, 6% less for the docked SVs (P < 0.01, t test) (Fig. 4E). Specifically, the short diameter of the docked SVs was, on average, 9.8 ± 0.38 nm (mean ± SEM) shorter than the long diameter, whereas the short diameter of the undocked SVs was, on average, only 6.1 ± 0.23 nm (mean ± SEM) shorter than the long diameter. Moreover, for 81% of the docked SVs, the short diameter was nearly perpendicular to the PM (within 45°). The short to long diameter ratio for the docked SVs had a normal frequency distribution (P = 0.99, KS test), and it was positively correlated with the extent of the VM–PM contact area (P < 0.02, Pearson correlation test). Thus, not only was the long diameter of docked SVs preferentially oriented nearly parallel to the PM at the contact site and orthogonal to the median plane of the active zone, but also the eccentricity of docked SVs was, on average, greater than that of undocked SVs, and the greater a docked SV’s eccentricity, the larger was the SV’s contact area. These results would be expected if varying amounts of force are exerted on the docked SVs toward the PM and toward the midline of the AZM and that such force regulates both the extent and orientation of the SVs’ eccentricity and the extent of their VM–PM contact area.

Because of the small size of SVs and the irregularity in the general contour of the VM, we could not determine in virtual slices whether a difference in the extent of the contact area was correlated with a deviation in contour of the VM at the contact site. However, the broad extracellular surface of the PM showed no obvious deviation at contact sites in virtual slices and surface models (Figs. 2 A–C, 4A, and 5A), regardless of the extent of the contact area, indicating that a docked SV’s curvature at the site conforms to the flatness of the PM. The absence of deformation at contact sites in freeze-fracture replicas of the PM leads to the same conclusion; see, for example, images in ref. 28.

Fig. 5.

Correlation of the extent of the VM–PM contact area with length and position of ribs, pegs, and pins in resting terminals. (A) Ten-nanometer- thick surface models of a docked SV, its associated PM, a pin, a rib, and a proximal and distal peg viewed in the active zone’s transverse plane (color-coded as in Fig. 1). (B) Surface models of the entire docked SV in A and its associated PM rotated ∼70° around the SV’s axis vertical to the PM. This docked SV was connected to a total of four ribs and four pins; each pin linked the VM directly to the PM, whereas each rib was linked to the PM by proximal and distal pegs as in A. The connection sites of all of the ribs and one pin (seen in this view) on the VM, and the connection sites of the pin and eight pegs on the PM are marked by three-voxel-thick terminal segments of these structures. (C) The connection sites of the ribs, pins, and pegs associated with each of the 101 docked SVs were used to determine, per docked SV, the average length of the proximal segment of the ribs (arrow with solid gold circle), the average length of the pins (arrow with solid copper circle), the average proximities of the rib–VM connection sites and the pin–VM connection sites to the PM (arrows with solid gold square and solid copper square, respectively), and the average distance between the proximal and distal pegs (arrow with solid gold triangle). (D–H) In agreement with the sloped regression lines, the Pearson correlation coefficients (r), and the P values (p) show that from docked SV to docked SV the average length of the proximal segment of the ribs (D), the average length of the pins (E) and the average proximity of the rib–VM connection sites and pin–PM connection sites to the PM (F and H) are negatively correlated with the VM–PM contact area, whereas the average distance between the proximal and distal pegs (G) is positively correlated with the VM–PM contact area. As indicated by the regression lines, the extent of variation for each parameter (D–H) was ∼4 to ∼5 nm.

Variation in the Spatial Relationships of Ribs, Pegs, Pins, and PM Macromolecules in Resting Terminals.

The AZM’s ribs, pegs, and pins connect the VM of each docked SV to the PM, and they are positioned to provide, by shortening, force that could both increase the extent of VM–PM contact area and generate SV eccentricity with the long diameter parallel to the VM–PM contact site and orthogonal to the long axis of the main body of the AZM. Accordingly, we determined whether the number, relationships and/or length of these structures were correlated to the extent of the VM–PM contact area and, by inference, the extent of SV’s long diameter.

The VM of most docked SVs (85 of 101) in our sample was connected to one end of three to four ribs and three to four pins at distinct sites encircling the VM–PM contact area (Fig. 1B; see also ref. 2). The VM of the rest of the docked SVs had four or five connection sites formed by at least two ribs and two pins and having a similar distribution. The rib–VM connection sites were on the SV hemisphere facing the main body of the AZM, whereas the pin–VM connection sites were primarily on the opposite SV hemisphere (Fig. 1). From their connection sites on the VM, the ribs extended at an acute angle to the plane of VM–PM contact site toward their connection sites with pegs (Fig. 5 A–C), which linked them to macromolecules in the PM thought to include Ca²⁺ channels, and the ribs' termination on the orthogonally arranged beams, which parallel the long axis in the main body of AZM (11). The pins also extended at an acute angle to the plane of VM–PM contact site to connect directly to the PM. There was no significant correlation between the extent of a docked SV’s contact area and the number of its rib–VM connection sites (P = 0.18, Spearman rank correlation), the number of its pin–VM connection sites (P = 0.14, Spearman rank correlation), or the total number of its rib– and pin–VM connection sites (P = 0.07, Spearman rank correlation).

The staining along the length of some pins and ribs was discontinuous, but in all cases, the staining of the pin–VM and rib–VM connection sites was readily discernible, as was the staining of pin–PM and peg–PM connection sites (Fig. 5B). Thus, we determined the length of pins, which were nearly straight, by measuring the distance between the pin–VM connection sites and the pin–PM connection sites (Fig. 5C). Ninety-five percent of the ribs had two pegs, one proximal and the other distal to the docked SV; the remainder had only one peg. For ribs having two pegs, we designated the portion of ribs between rib–VM connection sites to proximal peg–PM connection sites as the proximal rib segment. We determined the length of proximal rib segments by measuring the distance between rib–VM connection sites and proximal peg–PM connection sites (Fig. 5C), accepting that the proximal rib segments were nearly straight and that the length of pegs, which was <5 nm, contributed little to the measured distance. We determined the length of rib segments between the rib–VM connection sites and distal peg–PM connection sites in the same way.

For the entire sample, the average pin length was 12.7 ± 2.9 nm, whereas the average length of the proximal segment of the ribs was 16.7 ± 3.2 nm and the average rib length from the rib–VM connection to the distal pegs was 26.3 ± 4.5 nm. The lengths of the proximal rib segments connected to each docked SV varied considerably as did the lengths of the pins (average SD for proximal rib segment lengths, 3.0 nm; average SD for pin lengths, 4.1 nm). However, for each docked SV the average length of the proximal rib segments, which had a normal frequency distribution across the population (P = 0.39, KS test), and of the pins, which also had a normal frequency distribution across the population (P = 0.49, KS test), were negatively correlated with the extent of the VM–PM contact areas (Fig. 5 D and E). Similarly, the average distances of the rib–VM and pin–VM connection sites to the nearest point on the PM (Fig. 5C), which also had normal frequency distributions across the populations (rib–VM, P = 0.80; pin–VM, P = 0.42; KS test), were negatively correlated with the extent of the contact area (Fig. 5 F and H). Thus, the larger a docked SV’s VM–PM contact area and, by inference, the more eccentric its ellipsoid shape, the shorter was the average length of its proximal rib segments and pins and the shorter was the average distance from its rib–VM and pin–VM connection sites to the PM.

By contrast, we detected no correlation between the extent of a docked SV’s contact area and the average distance from its rib–VM connection sites to its distal peg–PM connection sites (P = 0.78, Pearson correlation test). However, the extent of a docked SV’s contact area was positively correlated with the average distance between the proximal peg–PM connection sites and the distal peg–PM connection sites, which ranged from 11 to 24 nm (Fig. 5 C and G) with a normal frequency distribution (P = 0.99, KS test). Based on the regression line in Fig. 5G, the average extent of variation of the proximal to distal peg distance between the smallest and largest contact areas was ∼4 nm. Thus, the positive correlation between the extent of a docked SV’s VM–PM contact area and the average shortness of the proximal rib segments was attributable in part to increased nearness of the proximal pegs to the VM–PM contact site.

Measurements from NMJs Fixed by Rapid Freezing and Stained by Freeze-Substitution.

The above electron tomography was done on frog muscles fixed with an isosmotic solution of phosphate-buffered glutaraldehyde and stained with an isosmotic solution of buffered OsO₄ at room temperature. Because such fixation involves chemical reactions that may require seconds to minutes to occur throughout a tissue, it is widely thought that an alternative method of fixation by rapid freezing, which occurs almost instantaneously, and staining by OsO₄ freeze-substitution presents structures closer to their native state. However, in comparing the two fixation/staining methods, we and others (2, 37–39) have not detected measurable differences in the preservation of certain components of axon terminals. In particular, we have previously reported for frog NMJs that the dimensions of AZM macromolecules and the number and distribution of their connections sites on docked SVs are similar regardless of which fixation/staining method was used (2, 37). Here, we compared our measurements on the spatial relationships of AZM macromolecules, SVs and PM in terminals fixed with glutaraldehyde and stained with OsO₄ at room temperature to measurements on the same parameters in a smaller sample size from a muscle fixed and stained by rapid freezing and freeze-substitution. Again, there was no difference at 2- to 3-nm spatial resolution (Table S2). Based on this and our previous electron tomography studies involving both methods of tissue preparation on multiple muscles (2, 37), fixation and staining by glutaraldehyde and OsO₄ at room temperature offer the advantage that adequate staining of AZM is more reliable from muscle to muscle.

Table S2.

Parameters for SV, PM, and AZM macromolecules

Parameter	Rapid freeze Fixation		Glutaraldehyde fixation		P
	n	Mean ± SD	n	Mean ± SD
VM thickness	14	7.9 ± 0.6 nm	101	7.6 ± 0.49 nm	0.08
PM thickness	4	8.1 ± 0.5 nm	32	7.5 ± 0.58 nm	0.10
VM–PM thickness	14	16.1 ± 1.80 nm	101	16.5 ± 1.4 nm	0.22
VM–PM contact area	14	350 ± 160 nm2	101	330 ± 150 nm2	0.67
Docked SV average diameter	24	54.7 ± 5.40 nm	101	56.0 ± 4.4 nm	0.21
Undocked SV average diameter	31	54.2 ± 3.91 nm	230	55.9 ± 4.2 nm	0.18
Docked SV eccentricity	24	0.84 ± 0.07	101	0.84 ± 0.06	0.98
Undocked SV eccentricity	31	0.89 ± 0.04	230	0.89 ± 0.05	0.30
Proximal rib segment length	35	17.3 ± 5.98 nm	307	16.5 ± 4.3 nm	0.33
Pin length	36	12.2 ± 5.80 nm	325	12.7 ± 4.8 nm	0.58
Rib–VM to PM distance	37	11.2 ± 3.22 nm	323	12.1 ± 3.6 nm	0.14
Pin–VM to PM distance	36	9.91 ± 4.94 nm	325	10.2 ± 4.8 nm	0.73
Proximal peg-to-distal peg distance	35	16.1 ± 3.88 nm	307	16.5 ± 4.0 nm	0.51

Data show SV, PM, and AZM macromolecules in terminals fixed by rapid freezing and stained by freeze-substitution in comparison with the same parameters in terminals fixed with glutaraldehyde and stained at room temperature (RT). n is the no. of measurements. P values are derived from comparison (t tests) of the parameters from the two fixation/staining methods.

Aldehydes have been reported to induce SV fusion with the PM (40). However, we did not find Ω-shaped or other undulations of the PM at any of the >36 active zones in resting terminals examined by electron tomography in this study. Such undulations would be expected if the glutaraldehyde solution we used had induced a significant level of VM–PM fusion. Furthermore, we observed no SV openings (41) in the entire PM at any of more than 200 active zones, including several thousand docked SVs, in our library of frog NMJs examined by conventional electron microscopy in freeze-fracture replicas from muscles fixed with isosmotic solutions of glutaraldehyde (42). The absence of a significant effect of glutaraldehyde fixation on SV fusion with the PM is consistent with our observation that such fixation does not have a measurable effect on the spatial relationships of docked SVs and their associated AZM macromolecules and PM at active zones of the frog’s NMJ compared with those from similar preparations fixed by rapid freezing.

Discussion

We found that at the VM–PM contact site of docked SVs in axon terminals of frog NMJs fixed at rest, there was no discernible gap between, or merging of, the VM and PM. However, the extent of the VM–PM contact area from docked SV to docked SV varied by more than an order of magnitude, even though docked SVs were similar in size. The different extents of contact areas had a normal frequency distribution, indicating they are members of a homogeneous population. Thus, the variation across the population represents different degrees of the same regulatory processes occurring at the different contact sites.

Fixing nerve terminals during synaptic activity, which captures SVs at active zones in various stages of docking on, fusion with, and flattening into the PM (2, 23), provided a way of determining whether the degree of priming of a docked SV for fusing with the PM is dependent on the extent of its VM–PM contact area. Approximately 90% of the SVs contacting the PM at docking sites in terminals treated in this way were docked as were all such SVs in resting terminals. The extent of their contact areas was also normally distributed. If there were no relationship between fusion probability of a docked SV and its contact area, one would expect that the location of the center of the normal distribution would be the same as that in resting terminals. However, it was shifted to the left, such that the fraction of docked SVs having relatively large contact areas in resting terminals had been reduced and the fraction of those having smaller contact areas had been increased. For the remaining ∼10% of the SVs contacting the PM at docking sites, the VM and PM at the contact site were hemifused, an intermediate of membrane fusion that precedes the formation of a fusion pore (33), and the extent of all of the hemifused contact areas was similar to that of the large contact areas measured at rest. The occurrence of hemifusion only at relatively large VM–PM contact areas in our samples demonstrates that docked SVs with large VM–PM contact areas preferentially fuse with the PM during synaptic activity. Accordingly, the leftward shift in the normal distribution of VM–PM contact areas of docked SVs fixed during activity must have been due in part to docked SVs with large contact areas having preferentially fused with, and flattened into, the PM before fixation occurred. The probability of a docked SV fusing with the PM upon arrival of an impulse is determined by its degree of priming. Thus, our results show that processes regulating the extent of the VM–PM contact area of a docked SV must also regulate its degree of priming; the larger a docked SV’s VM–PM contact area the more the docked SV is primed (Fig. 6).

Fig. 6.

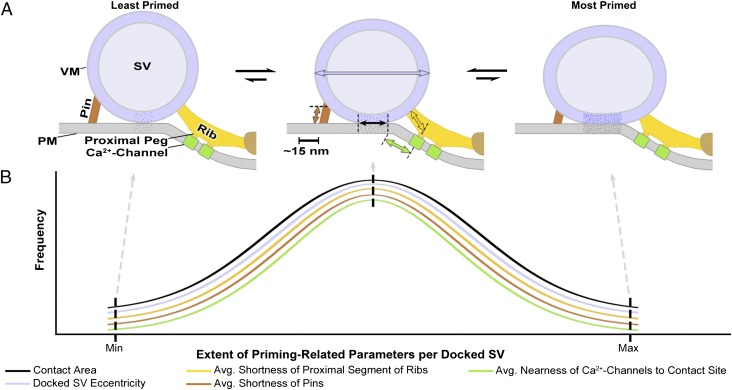
Schematic of the AZM-mediated variable force hypothesis for the priming of docked SVs at frog NMJs. According to the hypothesis, the priming of a docked SV is the progressive destabilization of the VM and PM at their contact site toward fusion threshold and the movement of the SV’s associated Ca²⁺ channels toward the contact site and the SV’s Ca²⁺ sensors involved in impulse-triggered VM–PM fusion. These events result from variable forces generated by the shortening of the multiple pins and proximal rib segments of the AZM that link the VM of each docked SV to components of the PM, including Ca²⁺ channels. The degree of shortening of each pin and proximal rib segment is independent and reversible because of the tightening and loosening, in dynamic equilibrium, of the SNARE core complexes that the pin and proximal rib segments are thought to contain. (A) The sum of the forces generated by the shortening/lengthening of individual pins and proximal rib segments (indicated by copper and gold double-headed arrows) at any moment determines not only the degree of VM and PM destabilization (indicated by stipple density) and the average distance of the Ca²⁺ channels from the contact site (green double-headed arrow) at that moment but also the extent of the contact area (black double-headed arrow) and the eccentricity of the SV’s shape (blue double-headed arrow). (B) Frequency distributions, based on our direct measurements, of the extent of priming-related parameters per docked SV, ranging from minimum to maximum, across the population of docked SVs at a resting NMJ at any given moment. The relatively few docked SVs most primed when a nerve impulse arrives have the highest probability of being among the 1–2% of the docked SVs that fuse with the PM to mediate impulse transmission.

For the stimulated terminals fixed during synaptic activity, the leftward shift in the normal distribution of VM–PM contact areas of docked SVs not only indicates that docked SVs having large VM–PM contact areas had selectively fused with and flattened into the PM, but the shift also indicates that those fused SVs that had flattened into the PM were replaced at their docking sites by SVs that initially formed relatively small VM–PM contact areas. Because the curve was not bimodal or skewed to the left, some of the newly formed VM–PM contact areas must have undergone gradual expansion, which indicates that the processes regulating the extent of a docked SV’s VM–PM contact area are dynamic. In terminals similarly stimulated and allowed to rest for 1 h before fixation, all SVs at docking sites were docked and the location of the center of the normal frequency distribution of their contact areas was the same as in resting terminals. Because the curve was not skewed to the right, the contact areas of newly docked SVs had not only expanded over time but had also variably and randomly contracted to reach equilibrium. According to this likelihood, the dynamic processes that regulate VM–PM contact area/priming of a docked SV are randomly variable, and those docked SVs that have the largest VM–PM contact areas the moment an impulse arrives are most primed for fusing with the PM at that moment (Fig. 6).

In order for the VM of a docked SV to fuse with the PM both the VM and PM must be energetically destabilized at their contact site until they reach fusion threshold; above fusion threshold the lipid bilayers spontaneously undergo a series of rearrangements to form the hemifusion intermediate and ultimately the fusion pore (33). Force is known to drive destabilization of apposed artificial lipid membranes toward fusion threshold (8). We found that the average eccentricity of the docked SVs’ ellipsoid shape in resting terminals was significantly greater than that of undocked SVs. Moreover, the long diameter of the docked SVs ran parallel to the PM and orthogonal to the long axis of the main body of the AZM, which connects them to the PM. Positively correlated with the extent of a docked SV’s eccentricity was the extent of its VM–PM contact area, whereas the curvature of the VM conformed to the flatness of the PM. These findings indicate that force is exerted on docked SVs toward the AZM and toward the PM; the greater the force, the greater is the eccentricity of a docked SV and the larger is the SV’s VM–PM contact area. Thus, we propose that the variable priming of docked SVs for fusion with the PM involves the variable exertion of force on VM–PM contact sites by components of the AZM, so that those docked SVs that are most primed when an impulse arrives are nearest VM–PM fusion threshold (Fig. 6).

The AZM’s ribs, pegs, and pins, which connect the VM to the PM, are appropriately positioned to exert force that brings about the correlated variation in a docked SV’s eccentricity and the extent of its VM–PM contact area. The ribs connected to each docked SV on the hemisphere that faces the main body of the AZM run in parallel toward the midline of the main body. Nearly all ribs are linked to macromolecules in the PM by two pegs, one proximal and the other distal to the docked SV. The pins linked to the opposite SV hemisphere extend to connect directly with the PM. There was no significant correlation between the number of rib/pin connections to a docked SV and the extent of its VM–PM contact area, and the length of the individual proximal rib segments and pins connected to each docked SV varied considerably. However, for each of the docked SVs, the shorter the average length of the proximal rib segments and pins linked to the SV, the nearer were the SV’s rib–VM and pin–VM connection sites to the PM and the greater was the extent of the SV’s VM–PM contact area. Accordingly, we propose that the variable force exerted on a docked SV that accounts for the variation in its eccentricity, in the extent of the SV’s VM–PM contact area and in the degree of the SV’s priming is derived from the average variable shortening and lengthening of its proximal rib segments and pins (Fig. 6).

Electrophysiological experiments made on certain CNS synapses have led to the suggestion that the priming of a SV is dependent in part on changes in its relative proximity to Ca⁺² channels (25). It has also been estimated that just a 5-nm difference in the distance between the Ca⁺² channels and docked SVs at an active zone would have a profound effect on the probability that the Ca⁺² entering the cytosol through the channels upon arrival of a nerve impulse will reach the SV’s Ca⁺² sensors, synaptotagmin, in sufficient concentration to trigger VM–PM fusion (43). The membrane macromolecules to which pegs are linked are thought to include Ca⁺² channels (44–46). We showed that in resting terminals the proximal pegs were on average ∼4 nm closer to docked SVs having the largest VM–PM contact areas than to docked SVs having the smallest VM–PM contact areas. Accordingly, our results raise the possibility that force generated by the shortening of the proximal rib segments contributes to increasing the degree of priming of a docked SV, not only by energetically destabilizing the VM and PM at their contact site toward fusion threshold but also by displacing the proximal pegs and their associated Ca⁺² channels toward the SV’s synaptotagmin (Fig. 6). Force exerted on the Ca²⁺ channels could further influence the degree of priming by increasing the channel’s ion conductance, as has been shown for voltage-dependent K⁺ channels (47).

The SNARE core complex and its auxiliary proteins are thought to be involved in both docking and priming (1, 5–7, 12–14, 24). Because the complexes link the VM to the PM as do the proximal rib segments/pegs and pins, their apparent length [∼14 nm (48)] is similar to the average length of the proximal rib segments/pegs (∼17 nm) and the pins (∼13 nm), and there are no discernible structures in the vicinity of the VM–PM contact site other than proximal rib segments/pegs and pins, it is reasonable to suggest that the SNARE core complex and its auxiliary proteins are components of these structures. Accordingly, whereas the SNARE core complex and its auxiliary proteins would be contained in each pin, the PM’s syntaxin and SNAP25 would reach the proximal rib segments to form the core complex with the SV’s synaptobrevin via the proximal pegs alongside the cytosolic portion of Ca²⁺ channels, which are also thought to occupy the pegs and extend into the ribs (2, 11, 49). Biochemical findings indicate that the SNARE core complex and its auxiliary proteins can be linked to N-type Ca²⁺ channels such as those at active zones of the frog’s NMJ (50). If each pin and proximal rib segment were to have one SNARE core complex there would be six to eight complexes linked to the great majority of docked SVs, which is within the range of complexes per docked SV predicted from biochemistry (51). The coiling of the SNARE proteins to form the SNARE core complex generates force, and it has been suggested that during SV docking such force overcomes the repulsive forces between the lipids of the VM and PM (52) to bring about and maintain the direct contact of the membranes (3, 4). Moreover, several lines of evidence indicate the coiling of an individual SNARE core complex is dynamic and in equilibrium between loose (long) and tight (short) conformations (53–55); repulsive forces between the lipids of the VM and PM may drive uncoiling of the SNARE core complex. The concept of independently and randomly reversing transitions in the coiling of SNARE core complexes in proximal rib segments and pins after docking has been achieved provides an explanation for our observation that it is the average length of these structures that is correlated with the degree of priming of a docked SV.

Although AZM is associated with docked SVs at synapses throughout vertebrate and invertebrate nervous systems, the gross arrangement of AZM relative to the docked SVs is strikingly different (10) from one synaptic type to another within a species and for the same synaptic type between species. However, at all synapses where AZM relationships have been examined by electron tomography, AZM macromolecules link the VM to the PM (2, 11, 12, 14, 27, 37, 56–59). This commonality, together with the high degree of homology of proteins involved in docking and priming at all synapses (60), suggests that our AZM-mediated variable force hypothesis (Fig. 6) for the regulation of priming at the frog’s NMJ may have general applicability.

Materials and Methods

Animal experimentation was approved by Stanford University’s (Animal Use Protocol no. 10505) and Texas A&M University’s (Animal Use Protocol no. 2011-18) administrative panels on laboratory animal care (Institutional Animal Care and Use Committee). Frogs (Rana pipiens, ∼5-cm nose-rump length) were terminally anesthetized (MS-222; Sigma Chemical) and pithed. Paired cutaneous pectoris muscles were used for all observations. The muscles are broad, flat and one to three muscle fibers thick, which favors rapid and uniform fixation and staining. The muscles were prepared for electron tomography according to the methods described in SI Materials and Methods, Tissue Preparation.

Electron Tomography.

We used a total of 91 datasets (36 from terminals fixed at rest with glutaraldehyde; 34 from terminals fixed during evoked impulse activity with glutaraldehyde; 17 from terminals fixed 1 h after evoked impulse activity with glutaraldehyde; 4 from terminals fixed at rest by rapid freezing). The datasets were collected at magnifications ranging from 38,000× to 125,000×, according to the methods in refs. 2, 11, and 37, which are briefly described in SI Materials and Methods, Electron Tomography.

Data Analysis.

Membrane thickness.

For docked SVs, we made thickness measurements on surface models of the VM and the PM away from the VM–PM contact site and of the combined VM–PM at the contact site using an algorithm designed to calculate the shortest distances across the membrane between vertices that established the membrane surfaces, as indicated by the double-headed arrows in Fig. 2 C and G. Specifically, the membrane thickness measurements were made for all vertices of each surface model. Straight lines were drawn from each vertex to each of its neighboring vertices and extended beyond the surface model. Along the direction of each line, and within a cylinder having a radius of 1.5 nm, the distance between the two farthest vertices was measured. The minimum value of the measured distances along the cylinders from a vertex to all of its neighboring vertices was determined as the membrane thickness at the position of that vertex. For each docked SV, there were ∼2,400 intersurface vertex calculations at the contact site between a VM and PM, ∼250,000 for the rest of the VM, and ∼2,000,000 for adjacent portions of PM.

Extent of the VM–PM contact area.

The vertices at the interface of the VM and PM at their contact site were projected onto the best-fit plane along an eigenvector containing the least eigenvalue, which was calculated using the covariance matrix of the vertices’ coordinates (61). The best-fit plane was pixilated, and each pixel was standardized to have the area of one face of a voxel from the reconstruction to maintain scale. The contact area was calculated by counting the number of pixels that contained the projected vertices and converting it to area according to scale. Where the defined surfaces of the VM and PM intersected, they were considered in contact.

SV size, surface area, and eccentricity.

The 3D shape of each SV surface model was determined by measuring three orthogonal diameters along the three eigenvectors. The longest diameter was designated the “long diameter” (d_l), the shortest diameter was designated the “short diameter” (d_s), and the intermediate diameter was designated the “intermediate diameter” (d_i).

To determine the size of each docked and undocked SV in our datasets, d_l, d_i, and d_s were used to calculate a geometric average according to the following equation: $\text{SV}\hspace{0.17em}\text{size}\hspace{0.17em}={\left(d_l{d}_s{d}_i\right)}^{1/3}.$

The surface area (S) of each SV surface model was determined using the formula for the surface area of an ellipsoid according to the following equation:

$$S=\frac{\pi }{2}(d_s^2+d_l{d}_{i}xE\left(x,k\right)+\frac{d_i{d}_s^2}{d_{l}x}F\left(x,k\right)),$$

where $x=\sqrt{\left(1-\frac{d_s^2}{d_l^2}\right)}$, $k=\frac{\sqrt{\left(1-\frac{d_s^2}{d_i^2}\right)}}{x}\hspace{0.17em},$ F(x,k), and E(x,k) were first and second incomplete elliptic integrals. The calculation was carried out using Matlab functions for incomplete elliptic integrals (MathWorks). The ratio of d_s to d_l was used as an indicator of SV eccentricity, as presented in Fig. 4E.

Orientation of SV profile eccentricity.

Using the long diameter of SV profiles in the middle virtual slices through them, we calculated its angular orientation with respect to the active zone’s horizontal and median planes. For docked SVs, we also calculated it with respect to the plane of the VM–PM contact site.

Connection site distances.

The connection sites of the ribs and pins with the VM were defined by the vertices at the rib–VM and pin–VM interfaces in surface models. The connection sites of the pins and pegs with the PM were defined in the same way.

The distance from each rib–VM and pin–VM connection site to the closest point of the PM was determined by measuring the length between each vertex within the connection site to the closest vertex of the PM and averaging the lengths. The distance between each pin’s VM connection site and PM connection site was determined by measuring the length between each vertex within the pin–VM connection site to all of the vertices of the pin–PM connection site, and averaging the lengths. The distance between each rib’s VM connection site and the rib's proximal peg–PM connection site and the distance between each rib’s proximal peg–PM connection site and the rib’s distal peg–PM connection site were determined in the same way.

Statistical analyses.

Two-tailed Student’s t tests, KS tests, Pearson’s product–moment correlations, and Spearman rank correlations were performed with OriginPro software package (OriginLab). The bootstrap test method (62), which was performed with the Interactive Data Language (IDL) software package (Exelis), was used for comparing membrane thicknesses, and is described in SI Materials and Methods, The Bootstrap Test.

Computer Hardware and Software.

For the analyses, a personal computer was used loaded with Windows Vista, IDL version 7, Java 6, EM3D (version 1.3) coded in IDL, and EM3D 2.0 coded in C⁺⁺ and Java.

SI Materials and Methods

Tissue Preparation.

Resting terminals, fixation, and staining at room temperature.

Under a dissecting microscope, 10 mg of tetrodotoxin (Sigma-Aldrich) per mL frog Ringer’s solution [115 mM NaCl, 2 mM KCl, 2.2 mM CaCl₂, 1 mM NaHPO₄⋅H₂O; 220–230 milliosmoles (mOsM), pH 7.2] was injected in situ beneath the muscles for 5 min to inhibit any glutaraldehyde evoked nerve/muscle impulses; 0.8–1% glutaraldehyde (Ted Pella) in Millonig’s phosphate buffer (220–230 mOsM total, pH 7.2) was injected beneath the muscles and dripped onto their superficial surface several times over 15 min. The muscles were removed from the frog, pinned flat in a Sylgard 184-coated (Dow Corning) Petri dish containing 0.8–1% glutaraldehyde in phosphate buffer (220–230 mOsM total, pH 7.2), placed on a shaker for 50 min and washed with phosphate buffer for 45 min on a shaker. The muscles were then further fixed and stained for 1 h in 1% OsO₄ in phosphate buffer (220–230 mOsM total, pH 7.2), washed for 1 h in H₂O, stained 1 h in saturated aqueous uranyl acetate, dehydrated in increasing concentrations of ethanol, and embedded flat in a 1-mm-thick wafer of Eponate 12 (Ted Pella). Osmolarities were determined with an Advanced Micro-Osmometer (Advanced Instruments).

Resting terminals, fixation, and staining by rapid freezing and freeze-substitution.

John Heuser, Department of Cell Biology and Physiology, Washington University, St. Louis, and Thomas Reese, Structural Cell Biology Section, National Institute of Neurological Disorders and Stroke, Bethesda, generously provided us with an araldite embedded block of tissue from a Rana pipiens cutaneous pectoris muscle fixed by quick freezing and stained with OsO₄ by freeze-substitution. Details of the muscle’s preparation are described in ref. 23.

Terminals fixed during evoked impulse activity.

Muscles were pinned out in a Petri dish containing Ringer’s solution, and the cut end of the nerve was drawn into a suction electrode. As described elsewhere (2), stimulation parameters were established by passing single current pulses through the suction electrode while monitoring under a dissecting microscope muscle contractions induced by synaptic transmission. Threshold for contraction of the entire muscle occurred at a current amplitude of ∼1 μA for 1 ms. The Ringer’s solution was then replaced for ∼5 min by Ringer’s solution containing 10⁻⁵ g/mL (+)-tubocurarine chloride hydrate (Sigma-Aldrich) to block muscle contractions. The (+)-tubocurarine–containing Ringer’s solution was replaced by Ringer’s solution containing 0.8–1% glutaraldehyde (220–230 mOsM total; pH 7.2), and nerve stimulation simultaneously began at 10 Hz with a current amplitude 10 times greater than threshold. Stimulation continued for 2 min; we previously observed under a dissecting microscope that in stimulated nerve-muscle preparations not exposed to (+)-tubocurarine, contractions of all muscle fibers ceased after 2 min in the fixative indicating all NMJs were fixed at that time. After stimulation, muscles remained in fixative for 40 min. The muscles were further processed for electron tomography according to the method used for preparing resting terminals fixed and stained at room temperature described above.

Terminals fixed after evoked impulse activity.

Muscles were pretreated with (+)-tubocurarine, as above. The nerve stimulation was the same as above except it was done in Ringer’s solution without fixative. Following the 2 min of activity, the terminals remained in Ringer’s solution for 1 h before processing them for electron tomography according to the method used for preparing resting terminals fixed and stained at room temperature.

Sections.

Thickness of tissue sections varied from ∼50 to 150 nm based on measurements from the reconstructed volumes. Sections were stained for 10 min with saturated uranyl acetate in methanol, rinsed with water, stained again with Reynolds lead citrate for 10 min, and rinsed with water.

Electron Tomography.

Data collection.

We used one of two electron microscopes designed for automatic data acquisition: (i) FEI TF30 Polara electron microscope (FEI Company) equipped with a 2048 × 2048 Tietz TemCam-F224HD CCD (Tietz Video and Imaging Processing Systems); and (ii) FEI Tecnai G2 F20 electron microscope (FEI Company) equipped with a 2048 × 2048 CCD (Gatan). The stage on each microscope was cooled to liquid N₂ temperature to reduce beam damage to the specimen. Datasets consisted of images taken at 1° tilt intervals to ±60° along a single tilt axis or two orthogonal tilt axes.

Reconstruction.

The tilt images were aligned automatically using 5- or 10-nm gold colloid (British Biocell International) deposited on one or both sides of the sections as fiducial markers before data collection. For the datasets used in the current study, the scheme provided an average accuracy of 1.34 ± 0.57 pixels root-mean-square (0.56 ± 0.24 nm root-mean-square). The reconstructions were made by a weighted back-projection method. Both the alignment and reconstruction algorithms are in the unified software package for electron tomography, EM3D (em3d.org) (30). In 5 of the 89 datasets, we used a translation- and rotation-invariant tensor-wavelet transform to enhance the signal-to-noise ratio without significantly affecting the signal (11).

Virtual slices, segmentations, and surface models.

Virtual slices through the reconstructed tissue sections were one-voxel thick, representing 0.29 to 1.2 nm of a tissue section’s thickness. The images of virtual slices in Figs. 2 A and H and 4 A and B were formed by summing multiple virtual slices to the thicknesses that are specified in the figure legends. Structures were segmented from the reconstructions using EM3D to define individual volumes of interest and were rendered to generate 3D surface models, as described in ref 30. The RGB (red, green, and blue) color-code values of surface models are given in ref. 2.

Correction factors.

Some tissue sections showed evidence of shrinkage as a result of electron beam exposure (63). For determining correction factors, we used the serial virtual slices through the reconstructed datasets to measure three orthogonal outer diameters of each SV (d_a, d_b, d_c) with the “measurement tool” in EM3D. Two of the orthogonal diameters (d_a, d_b) were measured on the middle virtual slice through the SV, and one diameter was measured along the z axis (d_c) extending throughout the entire series of virtual slices. The size of each SV was determined by calculating the geometric average of the three orthogonal diameters according to the following equation: $\mathrm{SV}\hspace{0.17em}\mathrm{size}={\left(d_a{d}_b{d}_c\right)}^{1/3}.$

Using the SV size, and assuming that the long diameters of undocked SVs in a dataset are randomly oriented and that the averages of d_a, d_b, and d_c are equivalent, the correction factor for the z axis of each reconstruction was determined by dividing the average d_c of undocked SV profiles in the reconstruction by the average size of all of the SVs in the reconstruction. The z axis correction factor for our datasets ranged from 1.07 to 1.36. We also calculated the correction factor for the xy axis by dividing the average d_a and d_b of the undocked SV profiles by the average size of the SVs in the dataset. The xy axis correction factor for our datasets ranged from 0.86 to 0.97.

When we applied correction factors to measurements of parameters considered here, the effect on all but one, SV eccentricity, was negligible. Thus, except for SV eccentricity, data are presented without correction factors.

The Bootstrap Test.

We compared the distribution of the actual thickness measurements across the VM–PM contact site (T_m) to simulated distributions of the sum of VM and PM thicknesses (T_i). For simulated distributions, we randomly selected vertex-vertex thickness measurements of the VM and added them to randomly selected vertex-vertex thickness measurements of the PM using 2,000 iterations of this calculation. P values were calculated and averaged from 10,000 iterations of simulated distributions according to the following equation:

$$p=\frac{{\displaystyle \sum _i\text{probability}\hspace{0.17em}\text{that}\left|{\overline{T}}_i-T_i\right|\mathrm{\ge }\left|{\overline{T}}_i-{\overline{T}}_m\right|}}{\mathrm{10,000}},i\mathrm{\in }\left[\mathrm{1,10000}\right],$$

where ${\overline{T}}_m$ is the mean of $T_m,$ and where ${\overline{T}}_i$ is the mean of $T_i.$