Titin strain contributes to the Frank–Starling law of the heart by structural rearrangements of both thin- and thick-filament proteins

Significance

The Frank–Starling law of the heart represents a fundamental regulatory mechanism whereby cardiac pump performance is directly modulated by the extent of diastolic ventricular filling on a beat-to-beat basis. It is now well established that sarcomere length (SL)-induced changes in cardiac contractile protein responsiveness to activating calcium ions play a major role in this phenomenon. However, the molecular mechanisms that underlie this SL-sensing property are not known. Here, we show by small-angle X-ray diffraction and fluorescent probe techniques that the giant protein titin likely transmits the length signal to induce structural alterations in both thin- and thick-filament contractile proteins. These findings provide insights into the molecular basis of the Frank–Starling regulatory mechanism.

Abstract

The Frank–Starling mechanism of the heart is due, in part, to modulation of myofilament Ca²⁺ sensitivity by sarcomere length (SL) [length-dependent activation (LDA)]. The molecular mechanism(s) that underlie LDA are unknown. Recent evidence has implicated the giant protein titin in this cellular process, possibly by positioning the myosin head closer to actin. To clarify the role of titin strain in LDA, we isolated myocardium from either WT or homozygous mutant (HM) rats that express a giant splice isoform of titin, and subjected the muscles to stretch from 2.0 to 2.4 μm of SL. Upon stretch, HM compared with WT muscles displayed reduced passive force, twitch force, and myofilament LDA. Time-resolved small-angle X-ray diffraction measurements of WT twitching muscles during diastole revealed stretch-induced increases in the intensity of myosin (M2 and M6) and troponin (Tn3) reflections, as well as a reduction in cross-bridge radial spacing. Independent fluorescent probe analyses in relaxed permeabilized myocytes corroborated these findings. X-ray electron density reconstruction revealed increased mass/ordering in both thick and thin filaments. The SL-dependent changes in structure observed in WT myocardium were absent in HM myocardium. Overall, our results reveal a correlation between titin strain and the Frank–Starling mechanism. The molecular basis underlying this phenomenon appears not to involve interfilament spacing or movement of myosin toward actin but, rather, sarcomere stretch-induced simultaneous structural rearrangements within both thin and thick filaments that correlate with titin strain and myofilament LDA.

The Frank–Starling law of the heart describes a cardiac regulatory control mechanism that operates on a beat-to-beat basis (1). There is a unique relationship between ventricular end-systolic volume and end-systolic pressure that is determined by cardiac contractility. As a result, ventricular stroke volume is directly proportional to the extent of diastolic filling. In conjunction with heart rate and contractility, the Frank–Starling mechanism constitutes a major determinant of cardiac output. Although the Frank–Starling mechanism has been well established for well over a century, the molecular mechanisms underlying this phenomenon are not resolved (1). At the cellular level, an increase in sarcomere length (SL) results in an immediate increase in twitch force development. Existing data, mostly derived from permeabilized isolated myocardium, strongly support the notion that this phenomenon is due to an increase in the Ca²⁺ responsiveness of the cardiac contractile apparatus, a phenomenon termed “myofilament length-dependent activation” (LDA) (1).

The mechanism by which the mechanical strain signal is transduced by the cardiac sarcomere is not known. We have recently demonstrated that LDA develops within a few milliseconds following a change in SL (2), a finding suggestive of a molecular mechanism caused by strain-dependent mechanical rearrangement of contractile proteins. Moreover, although LDA is a general property of striated muscle, it manifests itself to a much greater extent in cardiac muscle compared with slow-twitch skeletal muscle (3). Cardiac LDA has been shown to be modulated by contractile protein phosphorylation (4–7), as well as by cardiac disease-associated mutations within various contractile proteins (6). In addition, evidence has emerged that the passive force originating from the giant elastic sarcomeric protein titin directly acts to modulate myofilament Ca²⁺ responsiveness (8, 9). Of note, the titin molecule spans the entire half-sarcomere from the Z-disk to the center of the thick filament, and is thus well positioned within the contractile apparatus to relay the mechanical SL input signal (8). The mechanisms underlying the impact of titin strain on myofilament LDA, however, are incompletely understood.

A unifying theory has been advanced whereby the distance between the thin and thick filaments constituting the muscle’s sarcomeres is proposed to modulate myofilament Ca²⁺ responsiveness by affecting the probability of cross-bridge formation. Consistent with this notion, analyses of X-ray diffraction patterns obtained from both isolated cardiac and skeletal muscle reveal an inverse relationship between myofilament lattice spacing and SL (10). However, in a multitude of experimental models, we could not find a consistent correlation between myofilament lattice spacing and myofilament Ca²⁺ responsiveness, rendering interfilament spacing a less likely candidate for the molecular mechanism underlying LDA (1). Instead, we obtained experimental evidence suggesting a direct impact of SL on the spread of cooperative activation along the thin filament (11), potentially by modulation of the ordering of myosin heads in relaxed muscle, that is, before electrical activation (12). However, the primary molecular mechanism by which the strain signal is transmitted to the contractile apparatus could not be determined by those studies.

Here, we use a rat model in which a naturally occurring mutation within the splicing factor RBM20 disrupts titin mRNA splicing. One result of this mutation is the cardiac expression of a giant titin isoform in homozygous mutant (HM) animals at all ages (13). The presence of the giant titin isoform in HM myocardium was associated with reduced cardiac passive force upon stretch, as well as a blunted Frank–Starling response and reduced myofilament LDA. Time-resolved small-angle X-ray diffraction revealed stretch-induced conformational structural changes in both thin- and thick-filament contractile proteins during diastole in WT, but not HM, muscles. Our results suggest a prominent contribution of titin strain to the cardiac Frank–Starling mechanism. The mechanism underlying this phenomenon appears not to involve interfilament spacing or movement of myosin heads toward actin in the relaxed muscle but, rather, stretch-induced structural rearrangements in both the thin and thick filaments that is likely directly mediated by titin strain.

Results

Impact on Muscle Function.

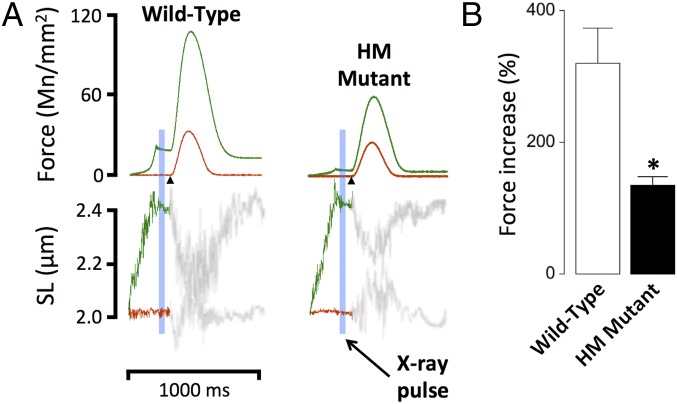
Fig. 1A shows original recordings of twitch force obtained in WT and HM rat myocardium. Muscles were electrically stimulated (Fig. 1A, arrowheads) at either short SL (2.0 μm, red) or following stretch to long SL (2.4 μm, green). Just before electrical stimulation, muscles were exposed to a brief X-ray pulse as indicated by the blue bar (Fig. 1A). This protocol was repeated 30 times every 10th twitch while a CCD-based X-ray detector recorded the 2D X-ray diffraction pattern (Fig. 2). In both WT and HM rat myocardium, stretch induced an increase in both passive and active twitch force, but the increase was significantly blunted in HM muscles. Fig. 1B summarizes the average normalized twitch force increase upon sarcomere stretch. Stretch induced ∼320% of baseline twitch force in WT muscles (Fig. 1B, open bar), compared with ∼134% in HM muscles (Fig. 1B, solid bar), demonstrating that reduced titin strain is associated with a significant blunting of the myocardial Frank–Starling mechanism.

Fig. 1.

Impact of titin length on cardiac muscle function. Cardiac muscles were isolated from WT or HM rats and electrically stimulated (arrowheads). (A) Force and SL recordings; SL in the diastolic phase was either maintained at SL = 2.0 μm (red) or increased transiently to SL = 2.4 μm (green). (B) Average percentage increase of twitch force upon stretch (*P < 0.05 WT vs. HM).

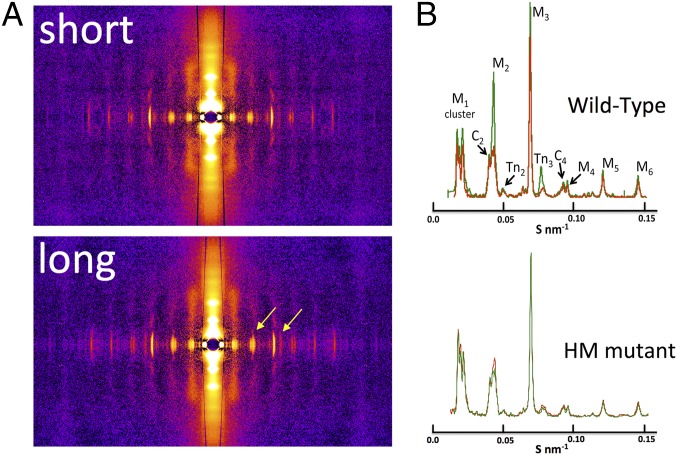
Fig. 2.

Two-dimensional X-ray diffraction and meridional analysis. (A) Representative 2D X-ray diffraction patterns in WT at short and long SL. Stretch-induced distinct alterations in the meridional reflections (yellow arrows) are shown. (B) Average meridional projections at short (red) and long (green) SL. Average intensities and periodicities are summarized in Table S1.

Impact on 2D X-Ray Meridional Reflections.

Fig. 2A shows typical 2D X-ray diffraction patterns recorded at short (Top) and long (Bottom) SL in WT myocardium. The meridional reflections, which run horizontal in Fig. 2A, arise from both thin- and thick-filament proteins, notably myosin (M₁–M₆), troponin (Tn₁–Tn₃), and reflections arising from myosin-binding protein C (Fig. S1). The myosin-binding protein C reflections appear as a series of doublets, possibly the result of interference between the two half-sarcomeres, with each pair (C1, C2, and C4 are visible in our patterns) indexing on an ∼44-nm repeat. Stretch induced an apparent increase in some, but not all, meridional reflections, as indicated by the arrows in Fig. 2A (Bottom). Fig. 2B shows the average meridional projections recorded in WT (Top, n = 11) and HM (Bottom, n = 10) muscles at short (red) and long (green) SL. Although significant changes in sarcomere structure, as reported by the meridional reflections, were observed in WT muscles, no changes were recorded in HM muscles upon stretch. All measured meridional intensities and periodicities obtained from both groups are summarized in Table S1. On average, the intensity of the second order of myosin-binding protein C (C_2,2), the second and sixth orders of myosin (M₂ and M₆), and the third order of troponin (Tn₃) increased significantly in intensity upon stretch in WT, but not HM, muscles. Moreover, upon stretch, the periodicity of the M₂ and M₆ myosin reflection, as well as the Tn₃ reflection, significantly increased in WT muscles, but notably not in HM muscles.

Fig. S1.

Analysis of peak intensities in the M2 cluster. The peaks in the M2 cluster (i.e., those peaks around the expected position of the second-order myosin meridional) were modeled as a series of five Gaussian peaks and fit using the Marquart–Levenberg routine implemented within Fityk. Two of these peaks can be assigned to the C2 doublet of peaks from myosin-binding protein C, with the low-angle peak and the high-angle peak denoted C_2,1 and C_2,2, respectively. One of these peaks is at the expected location of the forbidden second-order myosin meridional reflection M2. The lowest angle peak and the highest angle peak have not been definitively assigned but may be due to higher order reflections of the sarcomere repeat.

Table S1.

Meridional reflections

Reflection	WT				HM
	SL = 2.0 μm spacing, nm	SL = 2.4 μm spacing, nm	ΔSpacing, %	Intensity ratio	SL = 2.0 μm spacing, nm	SL = 2.4 μm spacing, nm	ΔSpacing, %	Intensity ratio
C2,1	23.04 ± 0.03	23.04 ± 0.03	−0.01 ± 0.17	1.28 ± 0.24	23.10 ± 0.02	23.03 ± 0.04	−0.30 ± 0.20	1.13 ± 0.20
C2,2	22.21 ± 0.03	22.16 ± 0.03	−0.15 ± 0.09	1.40 ± 0.11*	22.21 ± 0.04	22.11 ± 0.04	−0.45 ± 0.38	1.37 ± 0.16
M2	21.53 ± 0.01	21.62 ± 0.09	0.28 ± 0.05*	2.46 ± 0.28*	21.42 ± 0.02	21.45 ± 0.04	0.14 ± 0.15	1.34 ± 0.20
Tn2	19.06 ± 0.04	19.05 ± 0.03	−0.05 ± 0.25	0.89 ± 0.12	19.09 ± 0.06	19.12 ± 0.04	0.22 ± 0.37	1.18 ± 0.20
M3	14.30 ± 0.001	14.30 ± 0.001	0.00 ± 0.002	1.14 ± 0.05	14.3 ± 0.01	14.33 ± 0.01	0.21 ± 0.05	1.05 ± 0.14
Tn3	12.84 ± 0.02	12.95 ± 0.02	0.86 ± 0.21*	2.05 ± 0.02*	12.77 ± 0.03	12.82 ± 0.03	0.39 ± 0.31	1.33 ± 0.16
C4	10.94 ± 0.01	10.94 ± 0.01	0.00 ± 0.002	1.12 ± 0.14	11.04 ± 0.02	11.00 ± 0.01	−0.36 ± 0.14	1.23 ± 0.13
M4	10.65 ± 0.01	10.65 ± 0.01	0.00 ± 0.002	1.40 ± 0.23	10.63 ± 0.01	10.63 ± 0.01	0.00 ± 0.07	1.17 ± 0.16
M5	8.56 ± 0.003	8.56 ± 0.002	0.07 ± 0.04	1.05 ± 0.14	8.54 ± 0.01	8.54 ± 0.01	0.00 ± 0.04	1.13 ± 0.18
M6	7.17 ± 0.002	7.18 ± 0.002	0.14 ± 0.03*	1.42 ± 0.12*	7.22 ± 0.004	7.22 ± 0.003	−0.03 ± 0.05	1.35 ± 0.18

Meridional reflections were recorded at short (SL = 2.0 μm) and long (SL = 2.4 μm) SL. Calibrated periodicities were calculated from the position of the peak of the reflection on the meridional projection of the 2D X-ray diffraction pattern. ΔSpacing is the percentage change in periodicity in going from short to long SL, relative to the periodicity recorded at the short SL. Intensity ratio is the ratio of the reflection intensity recorded at the long SL relative to the short SL. C, myosin-binding protein C; M, myosin; Tn, troponin.

^*P < 0.05.

Impact on 2D X-Ray Myosin Layer Lines.

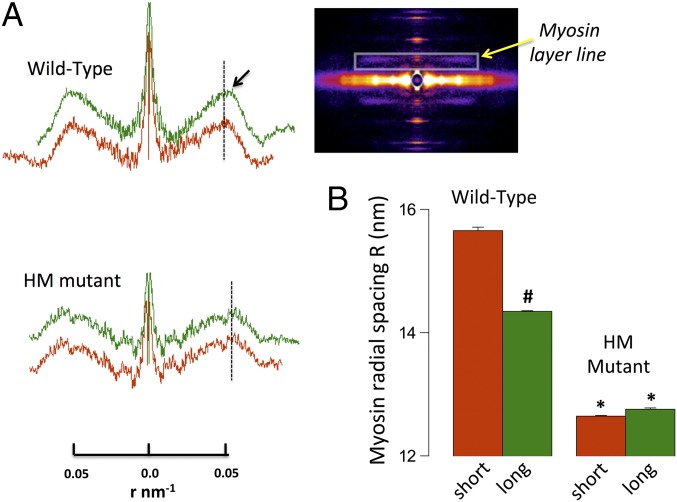
Fig. 3A shows representative first-order myosin layer line projections recorded at short (red) and long (green) SL in WT (Top) and HM (Bottom) muscles. Fig. 3A (Inset) also shows a typical 2D X-ray pattern in which the first myosin layer line is delineated by the rectangle (yellow arrow). The radial position of the center of mass of myosin heads can be estimated directly from the position of first-intensity maxima along the layer line; that is, assuming a three-stranded thick filament with helical symmetry, the peak position of the first myosin layer line should correspond to the first maximum of a J3 Bessel function with the argument 2 • π • r • R, where r is a radial reciprocal lattice coordinate and R is the radius to the center of mass of the myosin heads around the thick filament backbone (14). The radial distances of the myosin head to the thick-filament backbone calculated from these data are summarized in Fig. 3B. Overall, the average radial cross-bridge position was ∼19% further away from the thick filament in WT compared with HM muscles. Moreover, sarcomere stretch in WT muscles positioned the myosin head ∼8% closer to the thick filament, whereas no such movement was recorded in the HM muscles.

Fig. 3.

Myosin layer line analysis. (A) Myosin layer line projections in WT and HM muscle at short and long SL scaled to radial spacing r (in nm⁻¹); the black arrow highlights the smaller radial spacing in the WT upon stretch. (Inset) Myosin layer line position (yellow arrow). (B) Average calculated cross-bridge radial spacing (^#P < 0.05 long vs. short; *P < 0.05 WT vs. HM).

Impact on Equatorial Reflections.

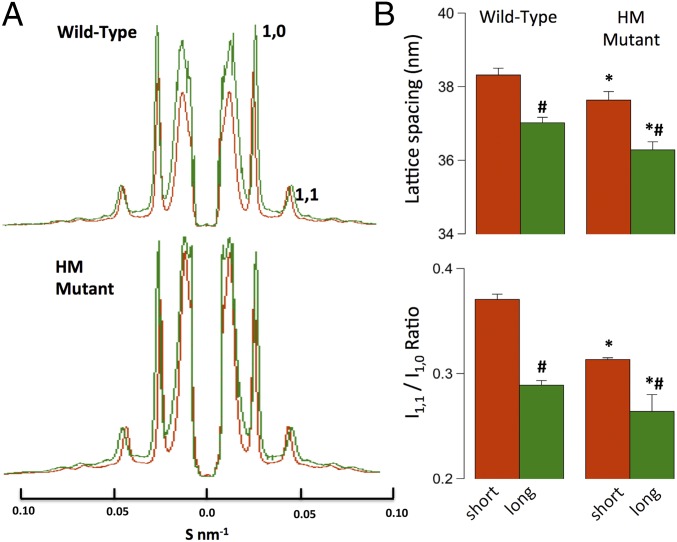
Fig. 4A shows average first-order equatorial projections recorded at short (red) and long (green) SL in WT (Top) and HM (Bottom) muscles. Fig. 4B summarizes the average lattice spacing calculated from these reflections (Top) and the intensity ratio between the 1,1 and 1,0 planes of symmetry (Bottom). Stretch resulted in a reduction in lattice spacing, as reported previously (1), in both groups. Moreover, the average lattice spacing was slightly (∼2%), but significantly, compressed in the HM compared with WT muscles. Likewise, as reported previously (1), the I1,1/I1,0 intensity ratio decreased upon stretch in both muscle groups. Moreover, this ratio was significantly (∼12%) smaller in HM compared with WT muscles. Traditionally, the intensity ratio has been interpreted to indicate mass movement of myosin toward actin (12). However, the current data suggest that interpretation may need to be revisited (see Discussion). Finally, although the functional contractile responses and myofilament length-dependent properties of WT and HM myocardium are very different (see Fig. 1, Fig. S2, and Table S2), the responses of both lattice spacing and intensity ratio upon stretch are quite similar overall, indicating that neither parameter correlates with cardiac LDA, as we have reported previously (1, 12). The average equatorial intensities, normalized to the 1,1 intensity (see Materials and Methods) recorded in both muscle groups are summarized in Table S3.

Fig. 4.

Equatorial analysis. (A) Average equatorial projections scaled to lattice spacing S (in nm⁻¹). (B) Average calculated lattice spacings and first-order intensity ratios (^#P < 0.05 long vs. short; *P < 0.05 WT vs. HM).

Fig. S2.

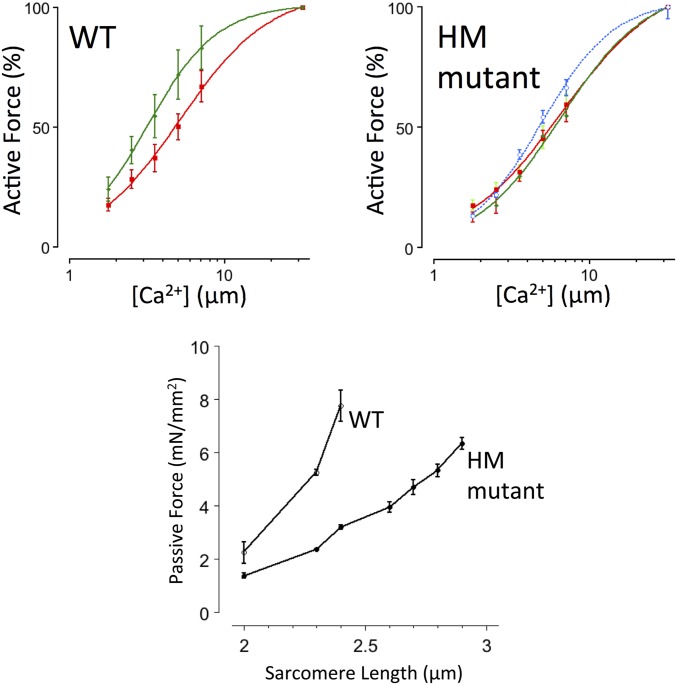
Permeabilized myocyte passive and active force development. Active Ca²⁺-activated force was measured at SL = 2.0 μm (red) and 2.4 μm (green) in WT myocytes, and at SL = 2.0 μm (red), SL = 2.4 μm (green), and SL = 2.9 μm (blue) in HM myocytes; this SL in HM myocytes is where passive force matched the passive force observed in WT myocytes at SL = 2.4 μm. Force was normalized to force measured at maximum [Ca²⁺]. Active force development increased in a cooperative sigmoidal fashion; average fit parameters are summarized in Table S2. (Bottom) Passive force, recorded in the fully relaxed state in the absence of Ca²⁺, as a function of SL. HM myocytes are significantly more compliant than WT myocytes.

Table S2.

Myocyte force-[Ca²⁺] relationships

Parameter	WT		HM
	SL = 2.0 μm	SL = 2.4 μm	SL = 2.0 μm	SL = 2.4 μm	SL = 2.9 μm
Fmax, mN/mm2	10.3 ± 3.7	21.7 ± 3.8*	6.4 ± 2.7	11.0 ± 4.5	17.8 ± 6.0*
EC50, μM	5.77 ± 0.96	3.86 ± 0.81*	5.53 ± 0.43	6.68 ± 0.39	4.99 ± 0.45*
nHill	1.6 ± 0.2	2.2 ± 0.5	1.6 ± 0.1	1.6 ± 0.1	1.8 ± 0.1

Force was measured over a range of [Ca²⁺] in permeabilized myocytes prepared from WT and HM rat hearts (Fig. S2) at SL = 2.0 μm and SL = 2.4 μm in WT myocytes and at SL= −2.0 μm, SL = 2.4 μm, and SL = 2.9 μm in HM myocytes. Passive force in HM myocytes at SL = 2.9 μm was comparable to the passive force recorded in WT myocytes at SL = 2.4 μm (Fig. S2). nHill, an index of cooperativity.

^*P < 0.05, long vs. short SL.

Table S3.

Normalized equatorial reflections

Group	Normalized equatorial intensities
	1,0	1,1	2,0	2,1	3,0
WT
SL = 2.0 μm	2.70 ± 0.04	1	0.05 ± 0.01	0.16 ± 0.01	0.14 ± 0.01
SL = 2.4 μm	3.46 ± 0.05	1	0.08 ± 0.01	0.19 ± 0.01	0.16 ± 0.01
P	0.001		0.04	0.002	0.04
HM
SL = 2.0 μm	3.19 ± 0.01	1	0.04 ± 0.01	0.10 ± 0.02	0.08 ± 0.02
SL = 2.4 μm	3.79 ± 0.25	1	0.04 ± 0.01	0.10 ± 0.02	0.09 ± 0.02
P	0.05		N.S.	N.S.	N.S.

Equatorial reflections were recorded at short (SL = 2.0 μm) and long (SL = 2.4 μm) SL. The intensities of diffraction peals in individual patterns were normalized to the 1,1 reflection intensity; in each individual muscle in either group, the 1,1 reflection intensity did not differ between the short and long SL. HM, homozygous giant titan mutant myocardium; N.S., not significant; P, significance level between short and long SL; WT, WT control myocardium.

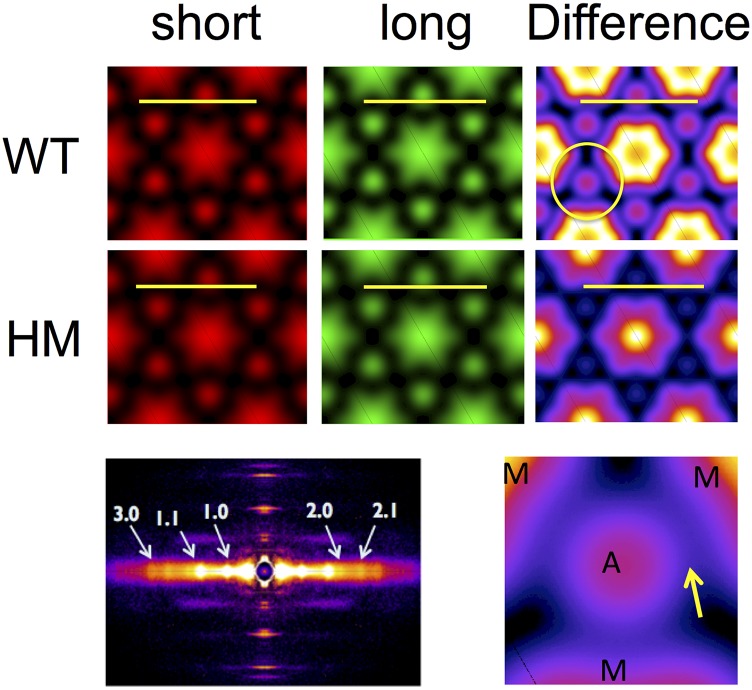
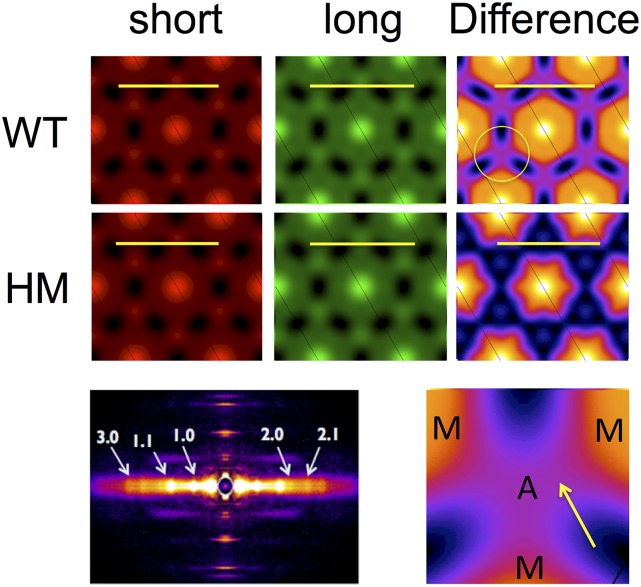
Impact on Electron Density Maps.

By using phase information estimated from sarcomere structural models (15, 16), we reconstructed radial projection electron density (ED) maps from the first five equatorial reflections of the 2D X-ray diffraction pattern (Table S3; note, a typical 2D X-ray pattern obtained from a WT muscle is shown in Fig. 5, Bottom Left). The average ED maps for short (red) and long (green) SL and the difference map between the short and long SL (heat maps; Fig. 5, Right), calculated for the WT and HM muscles, are shown in Fig. 5. In WT muscle, stretch induced a significant (P < 0.01) increase in the ED of both the thick (7%) and thin (6%) filaments, presumably due to an increase in ordering of both thin and thick filaments around their lattice positions, whereas no significant changes were observed in HM muscles. Moreover, upon stretch, an unidentified ED (peak excess density ∼25% of the peak excess thick-filament backbone density) was observed between the thin (A) and thick (M) filaments in WT muscles, as highlighted by the yellow arrow in the magnified difference map in Fig. 5 (Bottom Right). Of note, calculations based on alternative phase assumptions yielded similar relative changes in thick- and thin-filament densities upon stretch: 8% and 6% for thick and thin filaments, respectively, in WT; no significant change in HM; and the appearance of a linking density in WT muscles at long SL that is absent in HM muscle (Fig. S3).

Fig. 5.

ED maps. Average radial projection ED calculated from the first five equatorial reflections. A, thin filament; M, thick filament. (Calibration bar, 50 nm.)

Fig. S3.

Alternative phase ED maps. ED maps were calculated using an alternative phase combination (++−++) as described in SI Materials and Methods. The overall features of these maps are qualitatively similar to the features shown in Fig. 5. However, one feature of these maps is, to our minds, an unrealistically high ED for the thick-filament backbone. When one calculates the ratio of the thick- and thin-filament EDs, however, one gets very similar relative changes as observed with the original phases (main text). Furthermore, bridging density from the thick to thin filaments is still observed in difference maps in WT muscle and not in HM muscle. A, thin filament; M, thick filament. (Calibration bar, 50 nm.)

Impact on Recombinant Troponin C Fluorescence.

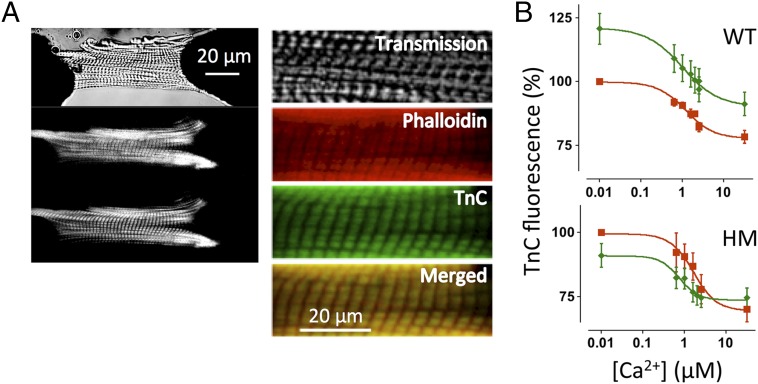
To obtain independent information regarding the structural rearrangement of troponin upon stretch, we used fluorescent probe analysis in chemically permeabilized single myocytes isolated from WT and HM myocardium. Recombinant rat troponin C (TnC) was labeled with the fluorescent probe 5-iodoacetamido-fluorescein (IAF) and partially exchanged for endogenous TnC. In addition, actin was labeled with Alexa-680 phalloidin (Life Technologies, Thermo Scientific) to control for motion artifacts. Fig. 6A shows a typical confocal recording of a mechanically attached myocyte; images are shown for the transmission channel (Top), red phalloidin (Middle), and green TnC (Bottom); magnified false red/green color images are shown (Right), together with the red/green overlay demonstrating colocalization of the labeled TnC with actin. Fig. 6B shows total myocyte TnC fluorescence normalized to the short SL condition as a function of [Ca²⁺]. These data were obtained in the presence of a high concentration of 2,3-butanedione monoxime (50 mM), an agent that blocks strongly bound, force-generating actin–myosin interactions (17). In WT, but not HM, myocytes, stretch induced a significant increase in TnC fluorescence at all [Ca²⁺]. In contrast, increasing [Ca²⁺] induced a sigmoidal decrease in TnC fluorescence, as has been reported previously for fluorescent probes conjugated to this residue on TnC (18). Of note, the apparent Ca²⁺ sensitivity, as indexed by the EC₅₀ parameter, was not affected by sarcomere stretch (Fig. S4); the apparent level of cooperativity, as indexed by the Hill coefficient (19), which was ∼1.0, consistent with biochemical results obtained from isolated TnC or troponin (20), was also not affected. A similar sigmoidal relationship, albeit with a slightly higher Ca²⁺ sensitivity, was observed in the HM myocytes, despite the absence of an impact of stretch in this group. Thus, stretch in WT myocytes induced a conformational rearrangement of troponin, as measured by a florescent probe positioned on TnC, that was distinct from rearrangement of troponin induced by Ca²⁺ ions and that was absent in the HM myocytes.

Fig. 6.

TnC fluorescence in permeabilized myocytes. (A, Left) Attached rat permeabilized cardiac myocyte. Transmitted light image (Top), Alexa-680 phalloidin image (Middle), and TnC-5-iodoacetamido-fluorescein (IAF) image (Bottom) are shown. (A, Right) Expanded scale images also show the red/green merged image. (B) TnC fluorescence-[Ca²⁺] relationships; average EC₅₀ parameters are summarized in Fig. S4.

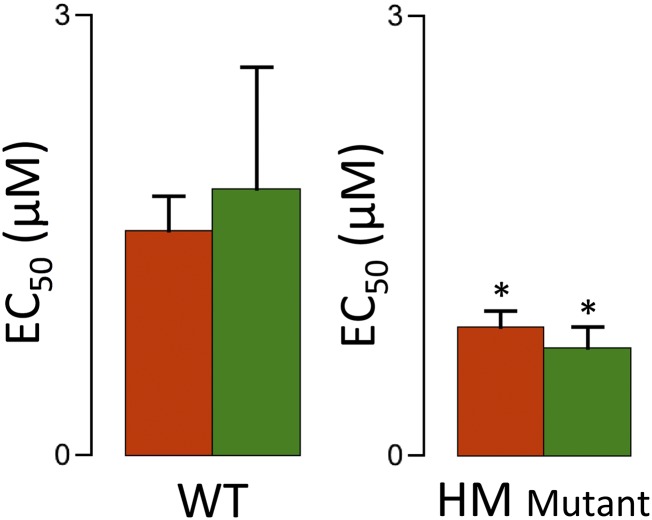
Fig. S4.

TnC fluorescence Ca²⁺ sensitivity. TnC fluorescent data were fit to a modified Hill equation (Fig. 6) at short (red) and long (green) SL in WT and HM permeabilized myocytes, yielding EC₅₀, a parameter that indexes apparent calcium-binding affinity. SL did not affect EC₅₀, whereas the overall EC₅₀ at both lengths was slightly but significantly lower in the HM cells (*P < 0.05).

Discussion

Myofilament Ca²⁺ sensitivity is modulated by SL via an unknown molecular mechanism. Recent evidence has implicated mechanical strain of the giant protein titin in this cellular process (8, 9). Here, we studied isolated cardiac muscle from WT and HM rats expressing a giant titin isoform associated with reduced passive tension, blunted myofilament LDA properties (21), and blunted Frank–Starling responses (9). In WT, X-ray diffraction measurements showed stretch-induced increases in intensity and periodicity of several myosin and troponin reflections, as well as a reduced cross-bridge radius. Moreover, ED reconstruction revealed stretch-induced increased ED at both the thick- and thin-filament positions, and the appearance of an unidentified ED spanning the space between these filaments. The length-dependent changes in structure and function were absent in HM myocardium.

The goal of these studies was to use small-angle X-ray diffraction of intact twitching myocardium from WT and titin mutant rats to investigate the role of changes in sarcomere structure in modulating myofilament LDA. When we initiated these studies, our hypothesis was that analysis of the equator and layer lines would reveal a radially outward movement of myosin heads at longer length indicative of a higher degree of actomyosin interaction in diastole in twitching muscle that we could invoke as part of the molecular explanation for LDA. Our current data conclusively rule out this possibility.

The ratio of the intensities of the 1,1 equatorial reflection to the intensities of the 1,0 reflection, I₁₁/I₁₀, is often used as a measure of the degree of association of cross-bridge mass with the thin filament, usually assumed to be due to a radial shift of mass away from the thick-filament backbone toward the thin filament. Here, we show that the I₁₁/I₁₀ ratio is reduced upon sarcomere stretch in both WT and HM myocardium, contrary to our expectation. Interestingly, the I₁₁/I₁₀ ratio was lower at both SL in HM compared with WT muscles (Fig. 4B), even though, upon stretch, it shows a similar relative change as the change in the WT muscles. Various authors (15, 22) have noted that a decrease in the I_1,1/I_1,0 ratio can be due to a reduced radial ordering of the thin filament relative to the thick filament, such that a decrease in the I_1,1/I_1,0 does not necessarily require radial movement of the cross-bridges, or, alternatively, that it could be due merely to the removal of actin out of the bare zone in the center of the thick filament upon stretch (23). The 2D ED maps calculated from the higher order equatorial data (Fig. 5) indeed show lower density in the thin- and thick-filament positions in HM compared with WT muscles, supporting this notion. The first myosin layer line data can be used to inform on this issue, because they can be more directly interpreted in terms of the radial position of the center of mass of the myosin heads relative to the thick filament. Fig. 3B shows that the radius to the center of the myosin heads at the long SL in WT muscles is smaller than at the short SL, consistent with the I_1,1/I_1,0 ratio data shown in Fig. 4. In HM myocardium, however, although the I_1,1/I_1,0 ratio is reduced upon stretch, the centroids of the layer line maxima are unchanged. Moreover, the calculated cross-bridge radius in the HM myocardium is smaller at both short SL and long SL compared with the cross-bridge radius observed in WT myocardium. One should use caution, therefore, in interpreting the I₁₁/I1₀ ratio parameter solely in terms of radial motion of myosin heads. These results, along with the evidence from ED maps, suggest that a large part of the lower I₁₁/I₁₀ ratio at short SL in both WT and HM myocardium is due to a higher “temperature factor”-type lattice disorder (where the myofilaments occupy a distribution of positions around the expected lattice points), and not to radial movements of myosin heads per se (14). It may also be that the presence of the larger HM titin isoform, and its consequent lower amount of titin-based passive force, reduces the ability of the sarcomere to maintain the myofilaments in the expected lattice positions. Such a phenomenon, by itself, may reduce the probability of productive actomyosin interaction. This hypothesis would be consistent with reported data obtained in animal models, where the presence of a longer than normal isoform of titin in the sarcomere is associated with reduced calcium saturated maximum myofilament force (9, 13, 21, 24), an observation that we confirmed in the present study (Fig. S2 and Table S2). In any case, it is clear that myofilament LDA is not a result of a radial outward movement of myosin heads toward the thin filament upon stretch of the sarcomere in diastole, as we suggested earlier (12).

The M₂ meridional reflection is one of the so-called “forbidden” reflections from the myosin-containing thick filament, because it should not be observed if the thick filament exhibited strict threefold helical symmetry. The existence of forbidden reflections has been attributed to the existence of localized regions on the thick filament with helical tracks containing myosin heads that are distorted from their helical positions. It is premature to attempt a detailed modeling of the structural change upon stretch (and higher titin-based passive tension), but an increase in the M₂ reflection intensity clearly reflects a greater distortion of the helical arrangement of myosin heads, due directly to increased thick-filament strain, or possibly due to interactions between myosin and titin or involvement of myosin-binding protein C.

Stretch induced a significant reduction in the myosin radial spacing in WT, but not HM, muscles. Moreover, in the HM muscles, this parameter was significantly smaller and not affected by stretch (Fig. 3). These results imply that cross-bridges move toward the thick-filament backbone upon diastolic stretch in WT muscles, whereas in HM muscles, cross-bridges are already closer to the thick-filament backbone and, moreover, do not relocate upon stretch. These findings are inconsistent with the notion that myofilament Ca²⁺ sensitivity is regulated by a closer approach of myosin toward actin. The reason why myosin radial spacing is reduced in HM muscles cannot be determined from our study. It is unlikely related to interfilament spacing, because the relative changes in this parameter with changes in SL were similar between the WT and HM muscles (Fig. 4) and, moreover, not correlated to myofilament Ca²⁺ sensitivity at either SL in the HM muscles (Fig. S2 and Table S2).

Stretch of the sarcomere in WT myocardium induced a significant increase in the periodicities of several of the myosin reflections (∼0.1–0.3%), and an even larger increase in the apparent periodicity of the Tn₃ reflection (∼1.0%). Selective and variable stretch-induced lengthening of the periodicity of some, but not all, X-ray reflections may be an indication that this increase in periodicity is not due to a simple elongation of the underlying sarcomere structure. Rather, it is more likely that this phenomenon is the result of a stretch-induced change in the distribution between various structural states sampled in time by myosin and troponin; that is, stretch may cause a reduction in the mobility of these two protein domains. Such a narrowing of the structural substrate distributions could result in both an increase in the reflection intensity and, simultaneously, a change in its apparent periodicity (Table S1). Of note, a recent X-ray diffraction structural study on tetanized frog skeletal muscle (25) revealed a stress-dependent alteration in myosin periodicity, which was interpreted by those investigators to indicate a redistribution of myosin heads from a folded “OFF” conformation toward an extended “ON” conformation.

The structural rearrangement in troponin upon stretch as reported by the fluorescent probe was distinct from and independent of the structural rearrangement induced by Ca²⁺ activation. It is known that Ca²⁺ binding induces an opening of a hydrophobic patch on TnC with affinity toward the switch peptide domain of TnI, ultimately resulting in release of TnI from the actin-binding site, freeing up the myosin site so as to initiate muscle contraction (26). Hence, it appears that the structural rearrangement of troponin upon stretch is different from the structural rearrangement of troponin induced by Ca²⁺ binding to TnC. Of interest, the apparent binding affinity of TnC for Ca²⁺ was not affected by SL, and there was no indication of cooperativity (19) in this process (Fig. 6 and Fig. S4), in contrast to the relationship between active force development and [Ca²⁺] (Fig. S2 and Table S2). The implication of this result is that myofilament LDA and the steep cooperativity of myofilament Ca²⁺ activation for force development must be the result of molecular processes downstream of Ca²⁺ binding to TnC. Of interest, stretch of isolated HM permeabilized myocytes to a far greater SL (2.9 μm), where passive force is comparable to passive force seen in WT myocytes at SL = 2.4 μm, induced increased myofilament calcium sensitivity (Fig. S2 and Table S2). These data support the notion that titin mechanical strain contributes to myofilament LDA; furthermore, they demonstrate that myofilament LDA is indeed operational in HM myocardium, albeit only at an extremely long SL, where passive force starts to develop in these myocytes. It should be noted that such an experiment is not feasible in the intact multicellular preparations used here for X-ray diffraction; presence of extracellular elastic structures in those preparations, such as collagen, would resist stretch to such an extreme SL. Moreover, those extracellular structures would likely bear most of the passive force at such extreme SL, placing most of the mechanical strain external to the cardiac sarcomere (8, 9).

In the present study, we compared WT to HM myocardium that was isolated from a rat strain with a spontaneous mutation in the splicing factor RBM20. Although this mutation prominently affects the splicing of titin, it should be noted that this mutation is also known to regulate the splicing of >50 different cardiac muscle proteins (13), including proteins involved in cardiac calcium homeostasis. However, for the purpose of the present study, which focused on diastolic intact multicellular muscles and permeabilized single myocytes, we assumed that the RBM20 mutation only affects titin length within the cardiac sarcomere.

Changes in troponin structure with changes in SL, as suggested by the X-ray results here, point to a mechanism whereby the titin-based strain transmitted by the putative thick/thin-filament bridging structures directly affects the regulatory apparatus promoting productive actomyosin interaction, and hence more force at longer SL. Such a mechanism is also supported by our fluorescent probe findings (Fig. 6), whereby stretch in WT myocytes induced a conformational rearrangement within troponin that was distinct from the conformational rearrangement induced by Ca²⁺ ions and that was, moreover, absent in HM myocytes. In addition, extensive stretch of HM myocytes to an SL, where passive force matched the passive force recorded in the WT myocyte, induced increased myofilament Ca²⁺ sensitivity (Fig. S2 and Table S2), supporting the notion that myofilament LDA is caused by titin-mediated strain and subsequent structural rearrangements within the relaxed thin and thick filaments. What may constitute the molecular mechanism(s) underlying this phenomenon? Our study clearly eliminates closer positioning of myosin heads toward the thin filament (Fig. 3) and decreased interfilament spacing (Fig. 4). Instead, titin strain may be transmitted directly to the thick filament via interactions within the A-band (8, 27) or, alternatively, via interactions between titin and the thin filament within the I-band (28). However, because we found that the troponin and myosin structures are both strain-dependent, our results require that both molecular mechanisms would have to operate simultaneously upon stretch.

An alternative mechanism may be related to the ED we observed bridging the thick and thin filaments upon stretch in WT myocardium (Fig. 5). Because of the low resolution of the reconstruction (∼13 nm), it is not possible to determine the chemical identity of this bridging structure directly from our data, and caution should be exercised to not overinterpret this density. The bridging density could simply be due to some of the small number of cycling cross-bridges, known to exist even in diastole (29), special “troponin bridges” linking the thick filament directly to the troponin complex (30, 31), or perhaps to myosin-binding protein C. Myosin-binding protein C is emerging as an important regulator of muscle contraction (27, 32–34). Recent evidence indicates that myosin-binding protein C may activate the thin filament via a direct interaction between its N′ domain and actin and/or tropomyosin (35, 36) that may be strain-dependent. Such a mechanism would explain, in part, the prominent myofilament LDA property of the WT cardiac sarcomere, and the blunting of this property in case of low titin strain (8, 9, 37), the absence of myosin-binding protein C (38, 39), or phosphorylation by protein kinase A (4–7). Although it is not possible, at this time, to identify conclusively the conduits for titin-based strain to the myofilaments, it is clear that such conduits are necessary to explain the simultaneous thick- and thin-filament structural rearrangements we observed upon stretch, rearrangements that are clearly correlated with increased myofilament calcium sensitivity. It is also clear from our current results that we can conclusively rule out altered interfilament lattice spacing as well as a closer approach of myosin heads toward actin at longer SL as being responsible for myofilament LDA.

Materials and Methods

Right ventricular trabeculae or small papillary muscles were dissected from WT or HM titin mutant rats and mounted in an experimental chamber equipped with a length controller, force transducer, and real-time SL detector. X-ray diffraction experiments were conducted at the BioCAT beamline 18 ID at the Advanced Photon Source, Argonne National Laboratory. Myocytes were prepared from frozen tissue by mechanical homogenization and attached to microneedles situated on an inverted confocal laser-scanning microscope. Detailed methods are provided in SI Materials and Methods.

All experimental procedures involving live rats were performed according to institutional guidelines concerning the care and use of experimental animals, and the Institutional Animal Care and Use Committee of the Loyola University Stritch School of Medicine approved all protocols.

SI Materials and Methods

Animals, Intact Muscle Preparation, Real-Time SL, and Experimental Protocol.

Homozygous autosomal titin mutant rats (Greaser N2BA-G) and WT rats (Harlan LBNF-1) have been described previously (13, 21). Rats were deeply anesthetized with 50 mg/kg of pentobarbital sodium in combination with 200 units of heparin. Hearts were rapidly excised from the thorax and perfused retrograde with a modified Krebs–Henseleit (KH) solution containing 118.5 mM NaCl, 5 mM KCl, 2 mM NaH₂PO₄, 1.2 mM MgSO₄, 10 mM glucose, 25 mM NaHCO₃, and 0.1 mM CaCl₂, as well as 20 mM 2,3-butanedione monoxime (BDM) to inhibit spontaneous contractions during dissection; pH was adjusted to 7.4 (at 25 °C) by vigorous bubbling with 95%/5% (vol/vol) O₂/CO₂. Intact trabeculae or small papillary muscles (typically about 3–5 mm in length, 50–250 μm in width, and 100–200 μm in thickness) were dissected from the right ventricle and mounted between a force transducer (KG4; Güth Scientific Instruments) and a motor (model 315C; Aurora). Muscles were placed in a 2.5-mm-wide chamber that allowed X-ray light to pass through 12.5-μm Mylar windows with continuous perfusion with the same oxygenated KH solution, but without BDM, at a flow rate of ∼2.5 mL⋅min⁻¹ (40). A cryostat was used to control the temperature to 25 °C by heating the solution just prior to entry into the muscle chamber. SL was continuously monitored (∼4 kHz) using He-Ne laser diffraction, where the first-order diffraction band was captured on a linear CCD-based Field Programmable Gate Array (FPGA) analyzer that outputs calibrated sarcomere length (SL) (PLIN-2605-2; Dexela, Inc.). Following dissection and mounting, muscles were electrically stimulated (field stimulation = 0.5 Hz, 50% above threshold) in the presence of 1 mM [Ca²⁺]. Twitching muscles were maintained at diastolic SL = 2.0 μm throughout the experiment. Muscles experiencing force rundown >20% were discarded. Once stabilized (∼15 min), X-ray patterns were taken from a 10-ms time window just before activation (Fig. 1) every 10th twitch, summing the signal from 30 such time windows, either at the diastolic SL = 2.0 μm or following a ramp stretch to SL = 2.4 μm over 200 ms during diastole for that individual twitch only. That is, muscles were only stretched each 10th twitch when X-ray patterns were recorded during the 10-ms window, 50 ms following the ramp stretch, and otherwise maintained at diastolic SL = 2.0 μm. This protocol ensures a steady contractile state throughout the experiment wherein the influence of the slow force response (41) is eliminated; it also allows for time to recover from radiation damage. Note that the focus in this study was the determination of diastolic sarcomere structure in response to stretch. Hence, the SL laser diffraction conditions were optimized for the measurement of diastolic SL, not systolic SL. For this reason, the SL traces following electrical stimulation shown in Fig. 1 are displayed in light gray to indicate that SL recorded during systole in this study is uncertain.

Small-Angle X-Ray Diffraction.

X-ray diffraction patterns were collected using the small-angle diffraction instrument on the BioCAT beamline 18 ID at the Advanced Photon Source, Argonne National Laboratory (10). X-ray beams were aligned and focused to about 250 × 250 μm at the sample and 150 × 60 μm (horizontal × vertical) at the detector, with a wavelength, λ, of 0.103 nm. The incident flux in the full beam was 10¹³ photons per second, and it was reduced to about 2–4⋅10¹² photons per second by using aluminum attenuators to reduce radiation damage. The distance between the sample chamber and the detector was ∼3.0 m. A high-sensitivity, high spatial resolution CCD detector (PCCD 16080; Aviex) with a 160 × 80-mm active area and 39-μm pixels was used to collect X-ray patterns. Distances in reciprocal space in diffraction patterns were calibrated using the d₀₀₁ diffraction ring from silver behenate at 5.8380 nm. During the X-ray data collection cycle, photons were collected on the CCD detector during the entire cycle, with 10-ms X-ray pulses applied every 10th twitch as described above, after which the detector was read out. Under these conditions, each preparation was exposed to an X-ray dose level of 3–7⋅10⁻² Gy at the two diastolic SL. Background images, recorded in the absence of muscle in the X-ray beam, were subtracted from the images, and the four quadrants of the patterns were rotated, folded, and averaged.

Analysis of the Equatorial X-Ray Pattern.

The equatorial patterns were converted to 1D intensity projections (Fig. 2B) using the program FIT2D (42) on a Linux workstation. FIT2D was also used to measure distances between the 1,0 and 1,1 equatorial peaks on the patterns and converted to d₁₀ lattice spacings using Bragg’s law. Analysis of the intensities of the equatorial reflections followed the procedures of Irving and Millman (15). The intensities of the first five equatorial diffraction spots (1,0; 1,1; 2,0; 2,1; and 3,0) were modeled as Gaussian functions constrained to the positions expected for a hexagonal lattice. Widths were constrained by the function proposed by Yu (43), which takes into account lattice heterogeneity and liquid-like (paracrystalline) disorder. This function was implemented as a user-defined function in the Fityk program (44). The smooth background was removed using the background subtraction tool in Fityk and the function fit to the data using the Marquardt–Levenberg algorithm implemented in Fityk. The ratio of the 1,0 and 1,1 equatorial intensities, I₁₁/I₁₀, was tabulated and used as a measure of shifts of mass from the region of the thick-filament backbones to the region of the thin filament (43, 45, 46). It was observed that the intensity of the 1,1 equatorial reflection did not change appreciably when SL was changed from 2.0 to 2.4 μm. The intensities of reflections in individual patterns therefore were normalized to the intensity of the 1,1 reflection to allow averaging. Averaged intensities were corrected for the Lorentz factor and used to calculate 2D ED maps as described (15); phases assumed were ++−−+ for the 1,0; 1,1; 2,0; 2,1; and 3,0 reflections, respectively (15, 16), for the data shown in Fig. 5; data calculated using the next most likely alternative phases (++−++) are shown in Fig. S3. The minimum intensity in transforms was assumed to be zero, but no other scaling was applied. Note that equatorial reflections past 3,0 were not observed in these patterns, so correction for series truncation was not necessary. Positions of the first maxima on the first myosin layer lines in 2D X-ray diffraction patterns were measured from 1D projections (using FIT2D) parallel to the equator using custom software implemented in the Python language. The smooth background under the layer line was removed using a convex hull algorithm, and the peak position of each side of the layer line was estimated as the centroid of the peak.

Analysis of the Meridional X-Ray Pattern.

One-dimensional intensity traces along the meridian were obtained using FIT2D from the quadrant folded diffraction pattern (discussed above). The diffuse background from amorphous components was removed using a convex hull algorithm implemented in a custom Python program developed in the laboratory of one of the authors (T.C.I., available upon request). Isolated peaks (M3, Tn3, C4, M4, M5, and M6) were integrated as the total intensity above background within the peak. Peaks within the M2 cluster were modeled as a series of Gaussian peaks that were then optimized using the Marquart–Levenberg algorithm implemented in the Fityk analysis program (9) as shown in Fig. S1. Attempts to resolve the individual peaks in the M1 cluster were not successful in resolving the M1 reflection, assumed to be present, and as a consequence, these results were excluded from our analysis.

Permeabilized Myocyte Fluorescent Probes.

We modified our previously published method (47) so as to measure TnC structural rearrangement upon stretch. Briefly, myocytes were harvested from frozen ventricular tissue by mechanical homogenization. A portion of the heart (30–40 mg) was homogenized at 10,000 rpm for 1 s in relaxing solution (PowerGen 700D, Fisher Scientific). Next, the homogenate slurry was filtered through a 70-μm cell strainer, followed by centrifugation at 120 × g for 1 min at 4 °C. The cells were skinned by resuspending the pellet in relaxing solution (97.92 mM KOH, 6.24 mM ATP, 10 mM EGTA, 10 mM Na₂CrP, 47.58 mM K propionate, 100 mM BES, and 6.54 mM MgCl₂) with 1% Triton X-100 added for 10–15 min on a slowly rotating shaker. Thereafter, the Triton X-100 was removed by resuspending the cells two times in relaxing solution after centrifugation at 120 × g for 1 min at 4 °C. After the final centrifugation, resultant permeabilized myocytes were suspended in 1 mL of relaxing solution at 4 °C and kept on ice until use within 8 h. Permeabilized (skinned) myocytes in relaxing solution were placed in a 0.1% BSA-coated, 35-mm culture dish on the stage of an inverted confocal microscope (Zeiss LSM-410). Myocytes to be studied were selected based on a visual scan at 10× magnification, identifying uniformity of the cell and a regular striation pattern. Next, myocytes were attached to two metal microneedles connected to a piezoelectric translator (ThorLabs) and a force transducer (Sensonor 801A; Kronex), and attached to XYZ-stage manipulators. The cell attachment was accomplished using UV-sensitive glue (NOA63; Norland). All measurements were made at a magnification of 40× using a long working distance objective lens. The attached skinned myocyte was perfused with skinned fiber solutions emanating from a closely placed perfusion pipette attached to a custom-designed, computer-controlled syringe perfusion system based on linear actuators (Haydon Kerk Motion Solutions, Inc.). Next, the attached skinned myocyte was exposed to Alexa Fluor-680 phalloidin (1 U/mL for ∼30 min; Life Technologies, Thermo Scientific) so as to label actin, followed by exposure (∼10 min) to 5-iodoacetamido-fluorescein (IAF)-conjugated rat recombinant mutant TnC (rTnC-^35-IAF; 1 μg/mL), both in relaxing solution. For this purpose, the endogenous Cys residue at position 84 was mutated to Ser, followed by expression in Escherichia coli and FPLC purification of the protein as previously described (48). The rTnC was conjugated with IAF at the C35 position using the procedures recommended by the manufacturer (Life Technologies, Thermo Scientific). Confocal images (Fig. 6) of the attached cell were acquired by simultaneously exciting at 488 nm to detect TnC-IAF (500- to 530-nm emission) and at 633 nm to detect Alexa Fluor-680 phalloidin (665-nm long-pass emission). SL was monitored from the transmitted light image using a custom-designed Fast Fourier Transform (FFT) method (Labview; National Instruments) (49) implemented in an FPGA chip (National Instruments). Images were collected at short (SL = 2.0 μm) and long (SL = 2.4 μm) SL. A region of interest was defined that excluded the glued attachments points of the cell, and total IAF background-subtracted fluorescence, normalized to phalloidin fluorescence, recorded in that region was calculated from the images. Cells were continuously perfused with relaxing solution, interspersed with Ca²⁺ activating solutions with varying calcium concentrations (0.01–30 μM) in the presence of 50 mM BDM to inhibit strongly bound, actively cycling cross-bridges (indeed, no force development was recorded). Fluorescent data were normalized to the fluorescence ratio recorded at SL = 2.0 μm at [Ca²⁺] = 0.01 μM. Control experiments in relaxing solution ([Ca²⁺] < 0.01 μM) without added BDM showed similar increases in the TnC-^35-IAF fluorescence ratio in response to stretch in WT myocytes, but not HM myocytes. Data were acquired using custom-designed Labview software (National Instruments) and analyzed offline using Origin Pro-8.0 (OriginLab). Each individual fluorescence ratio-[Ca²⁺] relationship was fit to a modified Hill equation:

$$\mathrm{Fluorescence}\hspace{0.17em}\text{ratio}=\left({\mathrm{F}}_{\max }\mathrm{-}{\mathrm{F}}_{\min }\right)•{\left[{\text{Ca}}^{2+}\right]}^{\mathrm{nH}}/\left(\mathrm{E}{\mathrm{C}}_{50}^{\mathrm{nH}}+{\left[\mathrm{C}{\mathrm{a}}^{2\mathrm{+}}\right]}^{\mathrm{nH}}\right),$$

where F_max is the Ca²⁺ free maximum fluorescence ratio, F_min is the Ca²⁺ saturated minimum fluorescence ratio, nH is the negative of the Hill coefficient, and EC₅₀ is the [Ca²⁺] at which the fluorescence ratio is half-maximal.

In a separate series of experiments, myocytes were mechanically attached as described above, and similarly exposed to a range of Ca²⁺ activating solutions (0.01–30 μM), but in the absence of BDM so as to measure active force development in response to Ca²⁺ activation (note that the myocytes used in this series of experiments were not labeled with fluorescent probes). The force-[Ca²⁺] relationships are shown in Fig. S2, and the average Hill fit parameters are summarized in Table S2.

Statistical Analysis.

All data are represented as mean ± SEM. Statistical analysis, two-tailed paired t tests, was performed using Systat 13 (Systat Software, Inc.). Statistical significance was defined as P < 0.05.

SI Results

The sarcomere in equatorial projection is centrosymmetrical; the only phase possibilities we need consider are 0 radians (+) and Pi radians (−). As detailed in SI Materials and Methods, the calculated ED maps shown in Fig. 5 are based on the equatorial reflections phase combinations ++−−+. Of all the possibilities for the first five equatorial reflections, only the ++−−+ and ++−++ combinations give realistic densities in the positions of thick and thin filaments and lack of spurious features, such as hollow filament cores (15). Although those studies considered data from vertebrate skeletal muscle, at the very low resolution of the calculated ED maps (∼13 nm), any small differences in sarcomeric structure between skeletal and cardiac muscle are very unlikely to affect the phases of the low-order equatorial reflections. The phase combinations used to create Fig. 5, ++−−+, are the phases determined on the basis of modeling studies by others (15), supported by electron microscopic studies (50), and, more recently, another study (16). Other modeling calculations by Yu (43) and Malinchik and Yu (51), however, favor the ++−++ combination. ED maps calculated using these phases are shown in Fig. S3. One feature of these maps is an ED for the thick-filament backbone about twice the ED of the thin filament, which may be unrealistic. Nevertheless, the maps based on this alternative phase combination yield similar relative changes in thick- and thin-filament densities in WT myocardium with stretch, and also show linking density in WT that is absent in HM myocardium (Fig. S3).

Active and passive force measurements were obtained in isolated permeabilized myocytes in a separate series of experiments in which the cells were not labeled with fluorescent probes. Cells in the WT group were studied at SL = 2.0 and SL = 2.4 μm, whereas cells in the HM group were studied at SL = 2.0, SL = 2.4, and SL = 2.9 μm. The data are summarized in Fig. S2 and Table S2. Passive force as a function of SL was significantly lower in HM myocytes compared with WT myocytes at SL ≤ 2.40 μm. However, further stretch of HM myocytes resulted in a passive force at SL = 2.9 μm that was comparable to the passive force in WT myocytes at SL = 2.4 μm. Hence, the entire passive force-SL relationship appears to be shifted rightward toward higher SL in the HM myocytes. Active force development increased in proportion to activator [Ca²⁺] in a cooperative sigmoidal fashion in both WT and HM myocytes. Moreover, increasing SL in WT myocytes to SL = 2.4 μm increased myofilament calcium sensitivity, an indication of robust myofilament LDA. In contrast, HM myocytes failed to increase myofilament calcium sensitivity at SL = 2.4 μm, consistent with previous reports (21). Further stretch of the HM myocytes to SL = 2.9 μm, where passive force approximates the passive force measured in the WT myocytes at SL = 2.4 μm, induced an increase in myofilament Ca²⁺ sensitivity, albeit to a smaller extent than seen in WT myocytes; these data indicate that titin strain modulates myofilament calcium responsiveness in both WT and HM myocardium, but at a much longer SL in the HM myocytes in proportion to titin mechanical strain. Of note, active force development, even at maximum saturating [Ca²⁺], was lower in the HM myocytes than in the WT myocytes, consistent with a previous report (21).