Review, Evaluation, and Discussion of the Challenges of Missing Value Imputation for Mass Spectrometry-Based Label-Free Global Proteomics

Abstract

In this review, we apply selected imputation strategies to label-free liquid chromatography–mass spectrometry (LC–MS) proteomics datasets to evaluate the accuracy with respect to metrics of variance and classification. We evaluate several commonly used imputation approaches for individual merits and discuss the caveats of each approach with respect to the example LC–MS proteomics data. In general, local similarity-based approaches, such as the regularized expectation maximization and least-squares adaptive algorithms, yield the best overall performances with respect to metrics of accuracy and robustness. However, no single algorithm consistently outperforms the remaining approaches, and in some cases, performing classification without imputation sometimes yielded the most accurate classification. Thus, because of the complex mechanisms of missing data in proteomics, which also vary from peptide to protein, no individual method is a single solution for imputation. On the basis of the observations in this review, the goal for imputation in the field of computational proteomics should be to develop new approaches that work generically for this data type and new strategies to guide users in the selection of the best imputation for their dataset and analysis objectives.

Graphical abstract

INTRODUCTION

Global proteomics studies that have the potential for comprehensive protein profiling of a biological sample are commonly performed using label-free liquid chromatography–mass spectrometry (LC–MS).^1–7 Unfortunately, a substantial fraction of data at the peptide level is missing from proteomic datasets in these discovery-based studies, whereas validation studies using targeted methods, but only a few peptides, do not suffer from this issue. This missing information prevents the full, complete, and accurate extraction of quantitative protein and functional information, especially for the tasks of clustering, supervised learning, or protein network inference.^8–10 Thus, one of the major challenges of global proteomic studies is to deal with this missing data appropriately. Because many statistical approaches require complete datasets, there is a large body of statistical literature addressing missing data across diverse fields of science.^11–21 The options are to ignore the missing data and only test observed data, to employ statistical methods that accommodate missing values, or to impute the missing values using simple or more sophisticated models based on assumptions about the underlying structure of the missing data. It is not unusual for LC–MS proteomics datasets to have as much as 50% missing peptide values. The option of ignoring missing values would dramatically reduce the size and completeness of the data and limit the researchers’ ability to infer information about the peptides and proteins.

Parallels between proteomics and microarray-based gene expression analysis exist: proteomics return a matrix of quantitative values for peptides, and microarray-based gene expression analysis returns probe-level transcripts.^22–24 However, important distinctions must be drawn between the two technologies with respect to the missing data. For microarray experiments, the missing values may occur because of various effects including presence of contaminants, scratches, or mechanical spotting problems. Missing data generally comprise less than 5% of the total observed transcript abundances. In contrast, global proteomics datasets typically are missing 20–50% of the total possible peptide values. Moreover, the missing peptide values result from an unknown and complex combination of random and nonrandom processes.^17,25–34 For these reasons, imputation strategies employed for microarray data may or may not be appropriate to impute missing proteomic data. For example, quantitative accuracy depends on chromatographic and instrumental characteristics, such as resolution and scan speed. Biological-based reasons for missing data include amino acid sequence differences between a peptide in the sample and the reference database (for example, posttranslational modifications (PTMs) and splice variants). For example, a PTM in one biological group may result in no identification of data for that peptide in that group because the mass has changed. Finally, a peptide would not be observed if the parent protein is, in fact, not present in a particular sample. The underlying mechanisms by which these data are missing may be independent of the value itself (namely, missing at random, or MAR), or mechanism(s) may be dependent on the data (namely, not missing at random, or NMAR).

To date, a comprehensive review and discussion has not been published covering the impacts of imputation on global LC–MS proteomics. In this review, we first explore the relationship between missing data and peptide intensity. We then apply selected imputation strategies to three label-free LC–MS datasets to evaluate the accuracy with respect to metrics of variance and sample classification. We examine these commonly used imputation approaches (available through existing code) for their individual merits and caveats with respect to LC–MS proteomics data.

IMPUTATION METHODS

Over the past decade, a variety of imputation algorithms have been developed and subsequently discussed in the literature.^{12,14–16,20,27,35–38} In general, these algorithms can be grouped into three categories: (1) imputation by a single-digit replacement, (2) imputation based on local structures in datasets, and (3) imputation based on global structures in datasets. In this review, we evaluated 10 distinct imputation methods; brief descriptions of these methods are given below. All imputation methods except two were available or easily coded with MATLAB (R2012a), from MathWorks, Inc. (Natwick, MA); the others were run using Java code available online and R code available from the authors of the DAnTE software.³⁹ The source codes were downloaded and run locally. Imputation methods used in this review are in Table 1.

Table 1.

Statistical Approaches To Impute Missing Values in Peptide Peak Intensity Datasets

method name	method description	availability	ref
LOD1	Half of the global minimal intensity among peptides
LOD2	Half of the minimal intensity of individual peptide
RTI	Random draw from a truncated normal distribution		Deeb et al.42
KNN	Weighted average intensity of K most similar peptides		Troyanskaya et al.20
LLS	Least-squares estimation of multiple regression based on K most similar peptides	MatLab script http://www.cc.gatech.edu/~hpark/othersoftware_data.php	Kim et al.16
LSA	Weighted average of peptidewise and samplewise estimation with the most correlated peptides	Java http://www.ii.uib.no/~trondb/imputation/	Bo et al.35
MBI	Random selection based on censoring probability from ANOVA model parameters	Code supplied by authors of DanteRhttp://omics.pnl.gov/software/DanteR.php	Karpievitch et al.27
PPCA	The principle components and the missing values are estimated as the model parameters by EM	MatLab script http://lear.inrialpes.fr/~verbeek/software.php.	Tipping et al.37
BPCA	The posterior distribution of the model parameters and the missing values are estimated using a variational Bayes algorithm	MatLab script http://ishiilab.jp/member/oba/tools/BPCAFill.html	Oba et al.36
REM	An iterative process of linear regressions via ridge regression	MatLab script http://www.clidyn.ethz.ch/imputation/index.html	Schneider19

Single-Value Approaches (LOD1, LOD2, RTI)

Single-value imputation refers to replacing missing values by a constant or a randomly selected value. These simple replacement procedures have been shown in microarray-based gene expression analyses to result in low performances when compared with other more advanced approaches;²⁰ however, these approaches may perform well in the presence of largely left-censored missing values and thus are evaluated here. Left-censoring means the values are missing from the low intensity (i.e., left tail) across the full distribution of possible measured intensity values. When data is censored in such a way, it is considered to be NMAR.

One approach to selecting a replacement value for a dataset is to use some minimal observed values estimated as the limit of detection (LOD). Half of the global minimum and half of the peptide minimum are common approaches currently used in the proteomics community to fill in missing values.^40,41 Half of the global minimum is defined as the minimal observed intensity value (not on the log scale) among all peptides (LOD1). The peptide minimum is the lowest intensity value observed for an individual peptide, and half of this value is referred to as LOD2. Random tail imputation (RTI) is based on the assumption that the entire proteomics dataset can be modeled by a single distribution and that the majority of the missing data are left-censored and can be drawn from the tail of the distribution.^42,43 RTI computes the global mean and standard deviation of all observed values within the proteomics dataset, μ and σ, respectively. Peptide intensities are plotted as frequency histograms, and the missing values are then drawn from a truncated normal distribution to obtain values that are within with the left tail of the distribution, N(μ,σ) – k. The parameter k is selected as a maximum value that allows the imputed data to merge into the left tail of the base distribution N(μ,σ) without yielding a bimodal distribution. The parameter selection of k is based on recursive visualization of the imputed data at various values of k using histograms until a suitable value is achieved.

Local Similarity Approaches (KNN, LLS, LSA, REM, and MBI)

Local-similarity-based imputation methods estimate missing values based on the expression profiles of several other peptides with similar peptide intensity profiles in the same dataset. These methods, in general, make the assumption that genes/proteins are regulated dependently and that highly correlated expression behaviors are normally observed with coregulated genes/proteins.⁴⁴ These algorithms tend to follow two basic steps. First, a set of peptides “closest” to the target peptide is chosen. The closeness is usually determined by a measure of similarity (for example, Euclidean distance or correlation). Second, the missing value of a target peptide is imputed by a weighted combination of the neighboring peptides that were selected by the distance metric.

K nearest neighbors (KNN) is an imputation method that directly accounts for the local similarity of the data by identifying similar peptides with similar peak intensity profiles via a distance. KNN was implemented in MATLAB with 10 neighbors per peptide based on Euclidean distance. In some cases, all 10 neighbors had missing values, in which case the algorithm used the next 10 closest neighbors until the missing value could be imputed.

The local least-squares (LLS) imputation is a regression-based estimation method that takes into account the local similarity of the data (in other words, between peptide intensity profiles). Missing values in a target peptide are estimated as a linear combination of K similar peptides, which are determined based on an absolute Pearson correlation coefficient. The appropriate number of neighboring peptide intensities are estimated by the algorithm, and missing values for a target peptide are imputed by multiple regressions based on leastsquares estimation.¹⁶

The least-squares adaptive (LSA) method uses the least-squares principle to estimate missing values. The imputations for the peptides are the weighted averages of several single regression estimates of the same missing values from the most correlated peptides with the target peptide. The estimates for the samples are determined by multiple regressions with missing values replaced by the estimates for the peptides in the intensity matrix. Missing values are subsequently imputed by the weighted average of imputation estimates for the peptides and samples.³⁵

The regularized expectation maximization (REM) algorithm is an iterative process of linear regression of variables (peptide intensities) with missing values on peptides without missing values. Regression coefficients are estimated by ridge regression. A regularized regression parameter in ridge regression is determined by generalized cross-validation by minimizing the expected mean-squared error of imputed values.¹⁹

Model-based imputation (MBI) is an approach that imputes missing values in the context of a protein-specific additive model,²⁶ y_ijkm = Prot_i + Pep_ij + Grp_ijk + error_ijkm, where y_ijkm is the peak intensity of the jth peptide (Pep) associated with the ith protein (Prot) within biological group (Grp) k defined by the experimental design for sample m. The parameters of the model are estimated from the observed data, and random draws from either a truncated normal distribution (if the peptide has high probability of censoring) or from the standard normal distribution based on the observed data form the basis of the imputation.

Global-Structure Approaches (PPCA and BPCA)

Global-structure-based imputation methods apply dimension reduction techniques to decompose the data matrix and then iteratively reconstruct the missing values. Probabilistic principal component analysis (PPCA) is a formulation of PCA with the assumption that the latent variables and the noise are normally distributed. In the PPCA framework, the missing values, together with the principal components, are viewed as the model parameters, which are implemented as the maximum likelihood estimates of the model parameters via an expectation-maximization (EM) algorithm.³⁷ The Bayesian principal component analysis (BPCA) algorithm uses a Bayesian estimation to fit a PPCA model. BPCA consists of three components: principal component regression, Bayesian estimation, and an iterative EM algorithm. The posterior distribution of the model parameters and the missing values are estimated simultaneously by using a variational Bayes algorithm with automatic relevance determination until convergence is reached.³⁷ Missing values are initially imputed by peptide average.³⁶ The BPCA algorithm in MATLAB requires a great deal of central processing unit time to impute missing values for large datasets, such as the human plasma and mouse lung discussed in the next section.

DATASETS

This evaluation was conducted using three LC–MS datasets. The first is a dilution series experiment where the same sample was consistently diluted and therefore the ratio between dilutions is known and can be evaluated after imputation. The second and third datasets are based on real experiments evaluating human plasma and mouse lung tissue. The human plasma dataset has high genotypic and phenotypic heterogeneity within and across experimental groups, and the mouse lung dataset has high genotypic and phenotypic homogeneity within experimental group.

Dilution Series Dataset

A dilution series experiment was conducted to generate a dataset in which known peptide and protein quantitative ratios could be constructed and used to evaluate the level of censoring at low dilutions. This dataset has already been described in detail.⁴⁵ As a summary, this dataset consists of 15 mouse plasma samples, which were subjected to four dilutions such that the total amount of protein was kept constant by supplementing with protein from Shewanella oneidensis. The dilutions consisted of a ratio of (1) 1:0 mouse/S. oneidensis, (2) 1:1 mouse/S. oneidensis, (3) 1:3 mouse/S. oneidensis, and (4) 1:7 mouse/S. oneidensis peptides. Peptide intensity data were transformed to the log₂ scale and filtered first by peptides with insufficient data to construct ratios across all dilutions. Data were normalized as a function of the expected dilution ratio to the largest concentration, yielding expected log₂ ratios between the largest dilution to the remaining three of 1, 2, and 3, respectively. The dilution series dataset required the imputation of 8939 values of the 91 080 possible values representing the matrix of 60 samples by 1518 peptides (namely, only approximately 10% of total possible values). This fraction is relatively low for a typical proteomics dataset because of the requirements of the experiment to retain adequate data for each peptide to perform the ratio calculation over all dilutions. This requirement is also the reason for the low peptide and protein counts for this dataset. However, because of the small size of this dataset, it is the only dataset for which all 10 imputation strategies return results.

Human Plasma

The human plasma dataset is associated with an experiment comparing individuals with normal glucose tolerance (NGT) from type 2 diabetics (T2D). This dataset has been previously described in detail.⁴⁶ As a summary, this dataset consisted of 71 plasma samples evaluated, of which 48 were NGT and 23 were T2D. Retaining only peptides with adequate data for either a quantitative or qualitative comparison between NGT and T2D, the total dataset consisted of 6729 peptides associated with 815 proteins. This dataset had a moderate amount of total missing data in comparison to many proteomics datasets, at approximately 29%.

Mouse Lung

The mouse lung dataset is associated with an experiment comparing in-bred mice for proteome changes in either obesity or exposure to lipopolysaccharide (LPS). This dataset has also been described in detail in previous work.⁴⁷ As a summary, this dataset consisted of 32 lung samples from male C57BL/6 mice, separated into four groups of 8 mice based on two exposures: LPS versus sham control and normal weight versus high-fat-diet-induced obese mice. The total dataset after routine filtering that removes any peptides with inadequate data for statistics consisted of 6295 peptides associated with 1679 proteins. This dataset contained the largest overall global fraction of missing data, approximately 41%.

RESULTS

The algorithms evaluated worked relatively well in general but had several key issues. Although run times are reported for PPCA, under specific parameter settings there were cases where the algorithms failed and had to be readjusted. In particular, PPCA was sensitive to the number of components used in the optimization, and some parameter values yielded an optimization value of infinity and terminated without output. The value of 10 was found to work consistently for all of these datasets and therefore was used for all analyses with PPCA except for classification when more than 10 scores were required. In addition, the MBI R script would not produce the full output (peptides and proteins) of some of the test sets because of a filtering step inherent in the code and therefore could not be compared directly. Given that the MBI code available has not undergone rigorous testing and validation, we evaluated this algorithm only for the dilution series. Lastly, none of our example datasets, except for the dilution series, completed within 1 week using the BPCA algorithm on a standard desktop machine (Intel Xeon CPU Dual processors at 2.4 GHz machine with 12 GB RAM), and BPCA was thus considered to time-out and was also only evaluated in the context of the dilution series. All proteins were estimated using a standard reference-based averaging approach.⁴⁶ This approach selects the peptide that has the least amount of missing data and greatest average intensity in the situation of a tie, scales the peptides to the same mean intensity, and then averages the peptides to a protein-level estimate.

First, the missing data structure of our two general experimental datasets (human plasma and mouse lung) is evaluated to determine if an assumption of left-censoring is appropriate. Second, the dilution series data is used to evaluate the potential of the imputation methods to return a known dilution ratio. Lastly, the human plasma and mouse lung datasets are evaluated for effects of imputation on the separation of the known phenotypes and exposures.

Missing Data Evaluation

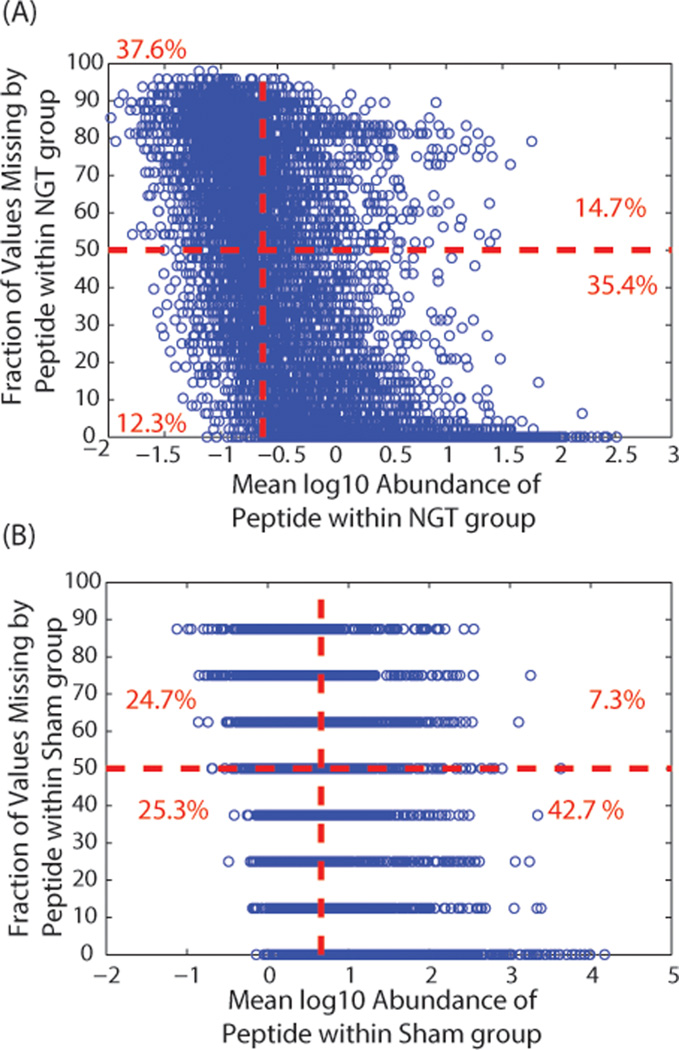
Peptide peak intensity and the amount of missing data have been previously shown to be negatively correlated.^26,27 It has further been conjectured that this is due to left-censoring of the data. Under the assumption that missing data are completely left-censored, only low-abundant peptides should have missing values and the fraction of missing values should increase as the peptide intensity decreases. We evaluate this relationship within only our control groups of the human plasma and mouse lung datasets: NGT (n = 23) and sham control (n = 8), respectively. The negative relationship between missing values and log₁₀ mean intensity within these control groups is illustrated in Figure 1A,B for the human and mouse datasets, respectively. The negative correlation between peptide missing data and intensity is computed as −0.51 for Figure 1A and −0.40 for Figure 1B. However, it is clear that not all peptides of low intensity have large amounts of missing values and likewise not all highly abundant peptides have high coverage.

Figure 1.

Average log₁₀ intensity as measured by peptide peak area in the control group versus fraction of missing values and peptide counts associated with bins corresponding to the fraction of missing data comparing phenotypes and exposures for datasets from (A) human plasma and (B) mouse lung. The control group for the human plasma is the normal glucose tolerant (NGT) samples, and the sham group for the mouse lung is the regular weight mice with no lipopolysaccharide (LPS) exposure. The vertical red line represents median average intensity, and the horizontal red line represents the point that 50% of the values are missing. The red numbers are the fraction of peptides that fall into the four boxes separated by the red lines.

In Figure 1A,B, a horizontal line indicates 50% missing data for an individual peptide across all samples, and a vertical line identifies the mean log₁₀ intensity across all peptides. We observed in the human plasma dataset that, in total, about 27% of the peptides based on these thresholds either have large intensity and large amounts of missing data or low intensity and low amounts of missing data. The mouse lung dataset is from an experiment with much smaller sample sizes, but it has a similar pattern as that of the human plasma dataset. Figure 1 demonstrates that although there is a relationship between peptide intensity and missing values possibly associated with mechanisms, such as limit-of-detection issues, there are many peptides with high mean log₁₀ intensity and large fractions of missing values and conversely low-abundant peptides with very few missing values. Thus, the missing values are a combination of NMAR and MAR data.

The fraction of data missing from each group can be tested against the hypothesis that they are equally missing across groups using a g-test on the total number of missing values.³³ The g-test is a modified chi-square test of independence that determines if the missing data are randomly distributed across experimental groups. For the human plasma dataset, we applied a g-test to each peptide with missing values to determine if the missing values are randomly distributed across the two groups (NGT versus T2D). Only 43% of the missing values could be statistically assigned to a left-censored peptide as defined by a significant g-test result (p-value < 0.05). The second example dataset (mouse lung) had only 19% of the missing values associated with a peptide with a significant g-test result at the same p-value threshold across the four unique groups associated with obesity and LPS exposure. Thus, the mechanisms of missing data are as complex as the experimental platforms and the biology being studied.

Comparison to Expected Ratio (Dilution Experiment)

The dilution series dataset gives us peptides for which an expected ratio is known. For each peptide and protein, the coefficient of variation (CV) of the root-mean-square error (RMSE) was used as a robust metric of deviation of the observed values from the expected values. It is a common approach used in microarray-based gene expression experiments for the evaluation of imputation approaches when the true value is known.²⁰ The RMSE is the square root of the average deviation between predicted and observed values. The CV(RMSE) normalizes the RMSE of each peptide to the observed mean of that peptide to equally weight all peptides and proteins to their average measured intensity, whether high-or low-abundant

$$\mathrm{C}\mathrm{V}(\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_{im})=\frac{1}{3}\sum _{j=1}^3\frac{\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{E}}_{ijm}}{j}=\frac{1}{3}\sum _{j=1}^3\frac{\sqrt{\frac{{\sum }_{k\in \mathrm{M}\mathrm{V}}{(x_{ijkm}-j)}^2}{n_{ij}}}}{j}$$ (1)

The dilution series is designed to have expected log₂ ratios of 1, 2, and 3 between paired samples, where x_ijkm is the log₂ ratio of the base dilution to the jth dilution factor for the ith peptide (or protein) of the kth mouse sample for imputation approach m, where k is included only if that mouse has a missing value (MV). The RMSE is computed only for peptides with missing values (k ∈ MV), and n_ij is the number of missing values for the ith peptide within dilution j.

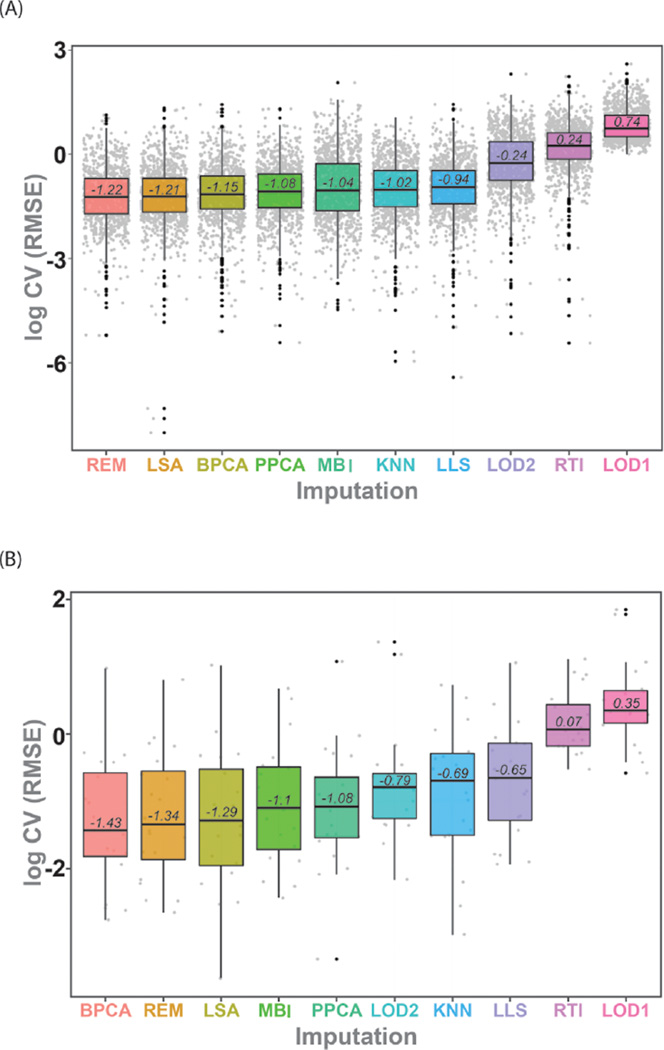
The distribution of log transformed CV(RMSE) values across peptides and proteins for each imputation is given in Figure 2A for peptides and 2B for proteins. The clear increase in CV(RMSE) as a result of blanket imputation (LOD1, LOD2) or random models (RTI) is the most notable observation of Figure 2. The CV(RMSE) values in Figure 2 were compared using a Friedman’s test to account for the blocking factor of peptide or protein. We observed a clear distinction between the imputation approaches, p-value < 2 × 10⁻¹⁰ for both the peptide and protein data, implying a statistically significant difference in at least one of the imputation methods. Posthoc analysis with a Wilcoxon’s signed-rank test with a Bonferroni correction was performed to more clearly evaluate the differences between individual imputation strategies. At the peptide level (Figure 2A), there was no difference among REM, LSA, and BPCA, but they had significantly lower CV(RMSE) than the other approaches. The algorithms PPCA, MBI, KNN, and LLS also were not statistically different from one another and had smaller CV(RMSE) than LOD2, RTI, and LOD1; these last three were all statistically different from one another. At the protein level (Figure 2B), the statistics are based on a smaller sample size since there are many more peptides than proteins and the distinction between imputation algorithms is not as clear. The first seven imputation approaches in Figure 2B are not statistically different from each other with a Bonferroni correction, and LLS is significantly lower than some of the top seven (BPCA, REM, LSA, MBI, PPCA, LOD2, and KNN), but not all. Again, RTI and LOD1 have the highest CV(RMSE) for predicting the expected ratios. For both the peptide and protein level data, the top three imputation approaches are the same, BPCA, REM, and LSA.

Figure 2.

Boxplot of the average log₁₀ CV(RMSE) for the imputed dilution series datasets (Table 1) at the (A) peptide and (B) protein levels. The lower line represents the 25th percentile, the upper line of the box represents the 75th percentile, and the inner line corresponds to the median log₁₀ CV(RMSE).

Classification on Real Experiments (Human Plasma and Mouse Lung Data)

The human plasma and mouse lung datasets were used to provide a LC–MS datasets with peptide variability as would be observed from a typical experiment. Because these two datasets are collected on real samples, we do not have any estimates of the actual values of the missing data. Therefore, they are evaluated by the effect of the imputation on classification of the distinct phenotypes and/or exposures. In particular, for the human diabetes set, we are comparing the NGT to the T2D phenotype, and for the mouse lung dataset, we are comparing the phenotypes of obesity and LPS exposure. A common approach to classification of high-dimensional data is to attain a small number of latent variables, such as those obtained from PCA, and perform classification using a standard algorithm, such as linear discriminant analysis (LDA). A problem in proteomics is that due to missing data conventional PCA cannot be performed with standard methods supplied by statistical computing software because PCA requires complete data, which would require either reducing the dataset to only peptides with complete data or imputation. PCA can be solved using alternate approaches, such as PPCA previously described (under Global Structure Approaches) or using an algorithm called sequential projection pursuit (SPP) via optimization of the objective function defined as variance (sppPCA).^32,37 Thus, two evaluation strategies are employed. First, seven imputation methods were applied to the dataset, and based on the imputed complete data, traditional PCA was completed. The number of latent variables that explained 75% of the variance on average were retained for each of the imputation methods. The second strategy infers the principal component score matrix using optimization routines via PPCA and sppPCA. From these score matrices, the same number of latent variables was extracted as for the imputation methods.

For the two test datasets, a 5-fold cross-validation was performed and applied to the nine methods being evaluated: seven imputation algorithms (KNN, LLS, LOD1, LOD2, LSA, REM, and RTI) followed by the subsequent PCA-LDA and the two direct methods (PPCA and sppPCA) to infer latent variables followed by LDA. The classification accuracy was the number of samples predicted correctly divided by the total number of samples. To evaluate differences between the classification methods, the 5-fold cross-validation procedure was repeated 1000 times to obtain a metric of variance in the classification accuracy.

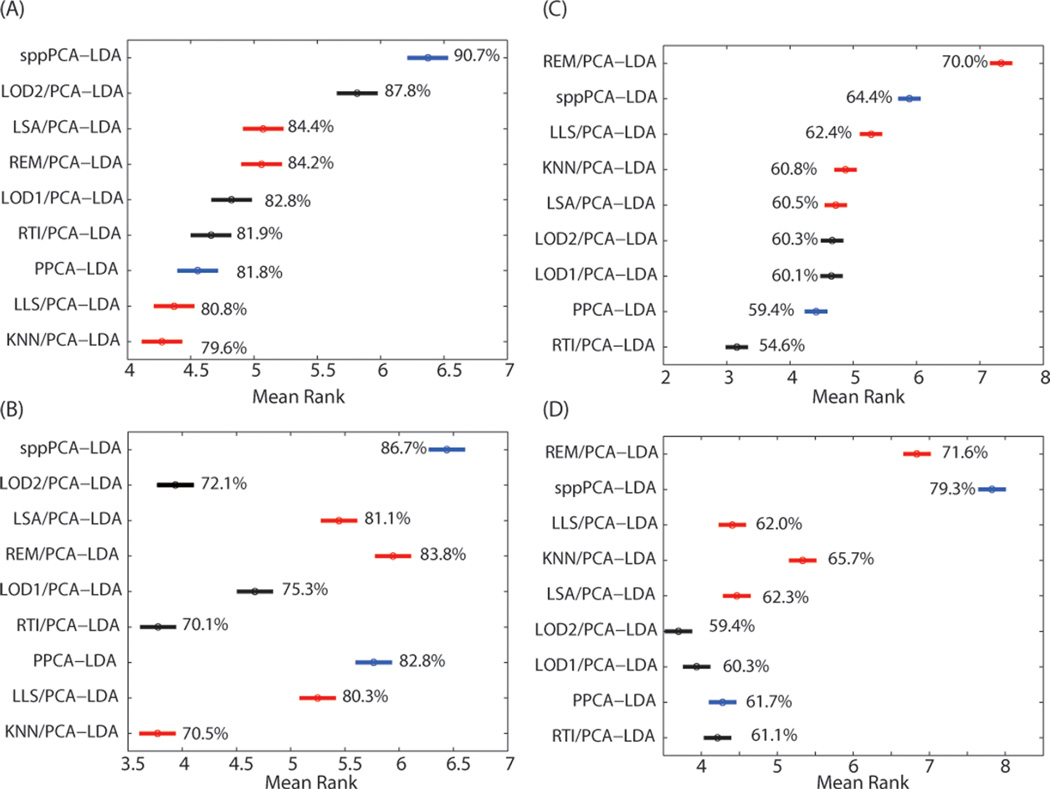
For the mouse lung dataset, 83 495 (46%) of the values across the 201 440 observations associated with the 32 samples and 6295 peptides had to be imputed. The evaluation of the classification accuracy using [Imputation/PCA]-LDA, PPCA-LDA, and SPP-LDA was based on 15 principal components at the peptide level and 14 principal components at the protein level. In particular, each imputation approach yielded classification accuracy for each of the 1000 iterations of 5-fold CV. Using the iterations as a paired blocking factor across imputation algorithms, results from Friedman’s nonparametric statistical test resulted in a significant difference in the imputation methods (p-value < 1 × 10⁻⁵⁰). A Wilcoxon signed-rank test with a Bonferroni multiple test correction was used to analyze all pairwise comparisons and significant differences. Figure 3 shows the confidence intervals of the posthoc test of the imputation algorithms sorted by the peptide-level classification accuracy, where larger ranks correspond to larger classification accuracies. The method sppPCA-LDA performed the best (namely, no imputation and inference of the principal components using SPP optimization prior to classification) at both the peptide (Figure 3A) and protein (Figure 3B) levels.

Figure 3.

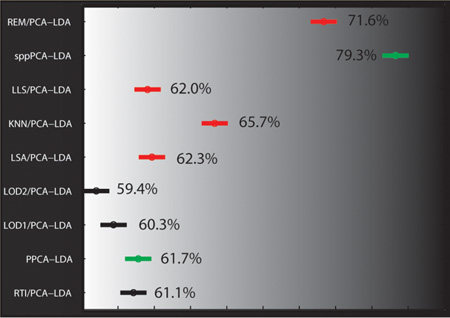
95% confidence intervals of the ranks to compare all imputation algorithms based on classification accuracy for the mouse lung and human plasma data at the peptide level (A, C) and at the protein level (B, D), respectively. Single-value imputation algorithms are colored black, local imputation algorithms are red, and methods that estimate the principal components directly from the data without imputation are blue. Imputation algorithms with no overlap in their confidence intervals are statistically different at α of 0.05, and larger rank is equivalent to larger classification accuracy (shown as percent).

The human plasma dataset consisted of approximately 29% missing data: 138 540 missing values from the 71 samples and 6729 peptides. The imputation of this test dataset was evaluated in a similar manner to the mouse lung data via either [Imputation/PCA]-LDA, PPCA-LDA, and sppPCA-LDA, retaining the top 15 principal components for the peptide data and 17 principal components for the protein data. The same analysis as for the mouse lung dataset was performed, but the classification task was to compare NGT to T2D groups for classification accuracy. The best classification accuracy was returned by REM/PCA-LDA at the peptide level (Figure 3C) and sppPCA-LDA at the protein level (Figure 3D). A Friedman test (blocked on the repeated sampling) followed by a Wilcoxon rank sum posthoc test showed that the classification accuracies were again significantly different across the approaches. In this case, the protein-level results show some similarity in trend to the peptide level, however; REM/PCA-LDA becomes the second most accurate approach, and sppPCA-LDA is the most accurate.

DISCUSSION

Several imputation methods perform relatively well for the evaluation metrics, such as classification accuracy and CV-(RMSE) with the test datasets. Each dataset was imputed at the peptide level and then evaluated for classification accuracy at both the peptide and protein levels. No single imputation algorithm consistently outperformed the others. Each dataset had slightly different algorithms that performed optimally at the peptide and/or protein levels (Figures 2 and 3). Moreover, it is difficult to generalize the performance of the three imputation strategies (naïve, local, global) because of the range of performance. However, in general, the imputation approaches that gave the most accurate classification of the dilution and complete datasets used local similarity, such as REM and LSA. The RTI-, KNN-, and LOD-based algorithms generally produced poor classification accuracy at both the peptide and protein levels, similar to results in microarray. Without in-depth knowledge of the dataset, the best a priori choices for imputation may be REM or LSA.

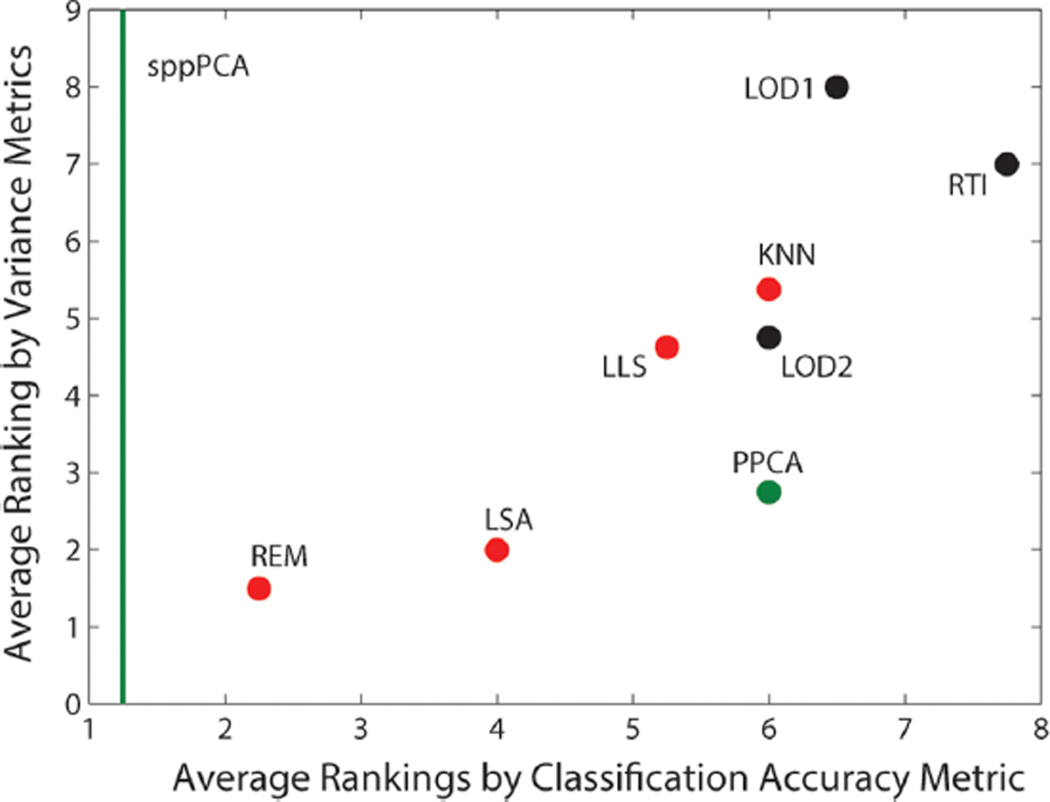
The sppPCA approach is valid only for classification, but given the excellent performance at the peptide and protein levels, further exploration into the value of peptide versus protein level imputation is needed. A valid strategy to proteomic data analysis may be to impute only under necessity and build data mining and analysis tools that do not require imputation. To evaluate these imputation algorithms further, each algorithm was given a rank from 1 to 8 (all imputations except BPCA and MBI), where 1 is the best and 8 is the worst for the CV(RMSE) evaluation for the peptide and protein level evaluation. Likewise, the four classification accuracy evaluations in Figure 3 were also used to rank the algorithms from 1 to 9 (seven imputations and two latent variable prediction methods) and averaged. Figure 4 shows a scatter plot comparing the average ranks based on these two metrics, which are relatively well-correlated (Pearson correlation; R = 0.82). The sppPCA method is represented only as a green line since it does not perform imputation and thus its scale on the y axis is unknown.

Figure 4.

Comparison of each imputation algorithm based on the average rank of imputation algorithms achieved via CV(RMSE) versus the average rank achieved via classification accuracy at the peptide and protein levels. The green line represents the ranking of sppPCA based on classification accuracy since its improvement in variance is unknown given that it does not impute data.

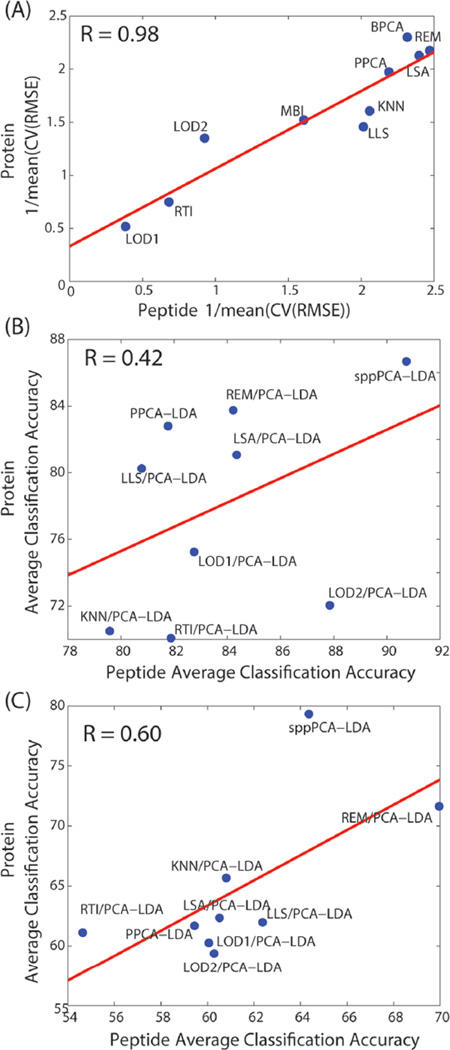
Prior work imputing global transcriptomics data (microarray) found that success of imputation approaches at the probe level with respect to RMSE does not necessarily translate to clustering accuracy at the gene level.²¹ Figure 4 does show some correlation based on ranking between variance metrics and correlation, but we also observed dataset-dependent correlation between accuracy at the peptide and protein levels in Figure 5. The dilution dataset peptide imputation results are highly correlated with the protein results (Figure 5A, R = 0.98). In contrast, the mouse lung peptide imputations have low correlation with the protein results (Figure 5B, R = 0.42), and the human plasma imputation results are moderately correlated (Figure 5C, R = 0.60). The dilution series’ high correlation at the peptide and protein levels is likely because of the simplicity of the experiment. That is, the only changes in expression between groups are based on a dilution and therefore do not reflect the same level of proteoform complexity as that in the mouse lung and human plasma datasets. These later two datasets have diverse proteoforms, such as PTMs and splice variants, for which current global protein quantification methods do not readily account.^46,48

Figure 5.

Comparison of the peptide and protein accuracy metrics for (A) dilution, (B) mouse lung, and (c) human plasma datasets.

CONCLUSIONS

Imputation of missing proteomic data must be performed with caution. Imputation is advantageous for many downstream analyses (e.g., PCA, hierarchical clustering) because imputation enables inclusion of the full dataset. Our evaluation exercises demonstrate that it is not always evident when one imputation strategy would be advantageous versus another. Clearly, selection of the appropriate imputation strategy(ies) will depend upon the data and the goals of the analysis. Progress in development, application, and evaluation of strategies for imputation would be enabled by better understanding of the role and variability of the analytical and data processing processes (e.g., analytical replicates, inference of protein abundances, etc.) responsible for underlying missing data. On the basis of the results here, REM or LSA approaches work the best in general for proteomics. However, it is clear that the field of computational proteomics needs new approaches that work generically for this type of data and new strategies to guide users in the selection of the best imputation for their dataset and analysis objectives. Alternatively, the sppPCA approach is valid only for classification, but given the excellent performance at the peptide and protein levels, further exploration into the value of peptide versus protein level imputation is needed. A valid strategy to proteomic data analysis may be to impute only under necessity and build data mining and analysis tools that do not require imputation.