Abstract
Nucleoside-based cofactors are presumed to have preceded proteins. The Rossmann fold is one of the most ancient and functionally diverse protein folds, and most Rossmann enzymes utilize nucleoside-based cofactors. We analyzed an omnipresent Rossmann ribose-binding interaction: a carboxylate side chain at the tip of the second β-strand (β2-Asp/Glu). We identified a canonical motif, defined by the β2-topology and unique geometry. The latter relates to the interaction being bidentate (both ribose hydroxyls interacting with the carboxylate oxygens), to the angle between the carboxylate and the ribose, and to the ribose’s ring configuration. We found that this canonical motif exhibits hallmarks of divergence rather than convergence. It is uniquely found in Rossmann enzymes that use different cofactors, primarily SAM (S-adenosyl methionine), NAD (nicotinamide adenine dinucleotide), and FAD (flavin adenine dinucleotide). Ribose-carboxylate bidentate interactions in other folds are not only rare but also have a different topology and geometry. We further show that the canonical geometry is not dictated by a physical constraint—geometries found in noncanonical interactions have similar calculated bond energies. Overall, these data indicate the divergence of several major Rossmann-fold enzyme classes, with different cofactors and catalytic chemistries, from a common pre-LUCA (last universal common ancestor) ancestor that possessed the β2-Asp/Glu motif.
The widely distributed Rossmann-fold enzymes share a highly conserved geometry of their ribose binding motif; this geometry is very rarely found in other folds and represents a relic of a common ancestral enzyme.
Author Summary
Common descent is the hallmark of Darwinian evolution. Homology of biological traits, and particularly of protein sequences and structures, serves as an indication for divergence from a common ancestor and a means of assigning phylogenetic relationships. However, because of shared functional demands and chemical-physical constraints, proteins that evolved independently of one another often converge on very similar molecular traits, including structure and sequence. We tested the widely accepted hypothesis of common ancestry of several major enzyme classes, comprising hundreds of different families and using different cofactors and catalytic chemistries. Although they share the same overall architecture—the Rossmann fold—these enzymes show no significant sequence homology across different classes. We describe an analysis based on the omnipresence of a single residue across these classes: an acidic aspartate or glutamate residue that binds ribose, the common denominator of the different cofactors used by these enzymes. We show that Rossmann enzymes possess a unique interaction geometry that represents a fingerprint of common ancestry rather than an outcome of molecular constraint. We thus provide the first systematic test of divergence versus convergence of a highly abundant protein motif and assign common descent in one of the most ancient and functionally diverse protein folds.
Introduction
Nucleoside-based cofactors are widely abundant and are likely to have appeared well before proteins [1–3]. The early protein forms may have therefore evolved to bind and function with nucleoside-based cofactors [4]. However, tracing motifs that relate to the earliest stages of protein-cofactor evolution is a challenge [5]. Omnipresent cofactor-binding motifs, such as the P-loop (phosphate-binding loop or Walker A motif), are considered fingerprints of the earliest precursors of modern proteins [5]. However, in general, abundance of a trait per se (in terms of number of species and their distribution in the tree of life) is not sufficient to indicate common ancestry, as convergence of sequence and structure is a feasible alternative. The more minimal a motif is in terms of the number of amino acids, the more likely it is to be the outcome of convergent evolution—namely, to have evolved independently, along separate lineages, yet ended up with the same molecular solution [6]. In fact, there is ample evidence for convergence, both of structural architectures (folds) and of binding and catalytic motifs. Folds such as β-propellers, for example, have emerged in parallel many times [7–10]. Artificial proteins belonging to the most ancient folds are computationally designed with sequences that bear no relation to natural proteins [8,9]. Omnipresent catalytic motifs such as the Asp/Glu dyads of glycosyl hydrolase and transferases are seen in >50 different folds [11] and with no significant sequence homology beyond the dyad itself. Such motifs have probably emerged independently, and their conserved geometry is due to physicochemical constraints dictated by a shared function. In fact, when it comes to binding and catalytic motifs, convergence is probably as dominant as divergence [12]. Overall, differentiating divergent from convergent evolution remains a crucial, largely unresolved dilemma in evolutionary biology in general and in protein evolution in particular [13–16].
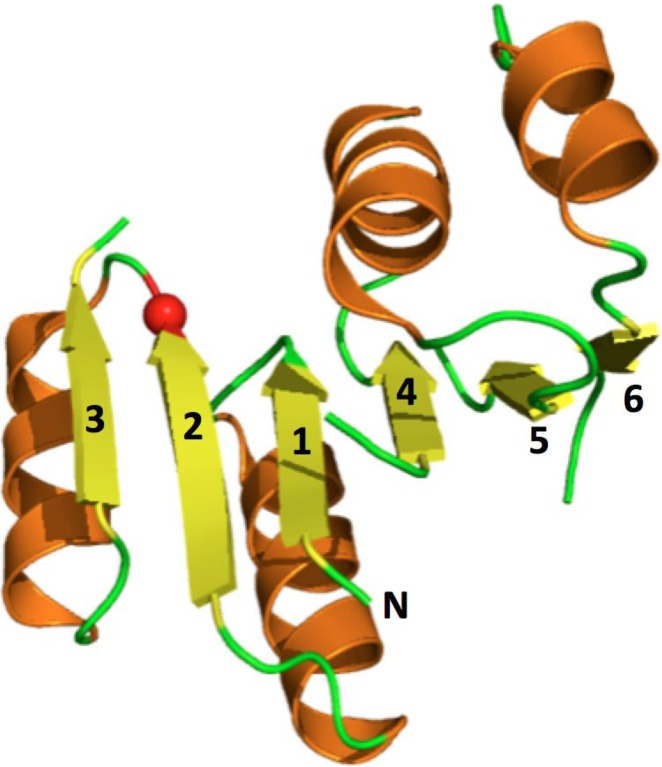
Our study focuses on the Rossmann fold. By virtue of catalyzing >300 different enzymatic reactions [17], the Rossmann fold is one of the most widely occurring protein folds [18–21] and is accordingly well represented in the presumed set of proteins that existed in the last universal common ancestor (LUCA) [20,22,23]. Belonging to the general class of β/α proteins, the Rossmann fold comprises two tandem repeats. Each repeat comprises three consecutive strands forming a parallel pleated sheet and two connecting α-helices [24–26]. The strand order along the core β-sheet is 3-2-1–4-5-6, although modifications of the last strand are often seen (Fig 1). Rossmann-fold enzyme families are also characterized by their use of cofactors [20,27,28] and in particular of nucleoside-containing cofactors that were present in the presumed “RNA world,” prior to the emergence of proteins [1,2]. Rossmann-fold enzymes therefore comprise a clear example of the evolutionary link between cofactors and their utilizing enzymes. Indications for pre-LUCA evolutionary links in the Rossmann fold have been noted that relate to nucleoside binding and the shared fold [19,29]. Shared nucleoside binding motifs have also been described upon the identification of the Rossmann fold and at later stages (e.g., [6,30–39]). Specifically, nicotinamide adenine dinucleotide (NAD)- and flavin adenine dinucleotide (FAD)-utilizing enzymes share a Gly-rich loop that resides between H1 and β1 and interacts with the cofactors’ phosphate moieties [19,40,41], and the hydroxyls of the cofactors’ ribose moiety typically interact with a Glu/Asp at the tip of β2 (β2-Asp/Glu; Fig 1) [42,43]. Sequence homology can obviously be detected between NAD and nicotinamide adenine dinucleotide phosphate (NADP) enzymes and may span over to FAD enzymes, specifically in relation to the above two motifs [44,45]. However, the sequence homology with other Rossmann classes such as S-adenosyl methionine (SAM)-dependent methyltransferases is much less clear [36,44]. The ribose-binding Glu/Asp at the tip of β2 has also been detected in methyltransferases [42,43]. However, the Gly-rich motif is not apparent in SAM-utilizing Rossmann enzymes, possibly because SAM does not contain phosphate groups. Consequently, some sequence-based classifiers, including those using sensitive homology detectors such as CATH (Class Architecture Topology Homologous superfamilies), define these classes as separate superfamilies [46]. However, based amongst other considerations on the shared β2-Asp/Glu motif, other classifiers such as ECOD (Evolutionary Classification of Protein Domains) [30] or Interpro [47] classify all three classes (NAD(P), FAD, and SAM-dependent Rossmann enzymes) in the same homology group [31,32,35,38,39].
Fig 1. Schematic representations of the architecture of the Rossmann fold.
The Rossmann is a β/α fold, namely a consecutive repeat of motifs comprising a β-strand (in yellow), a connecting loop (green), and α-helix (orange). The β-strands form a core β-sheet with the strands in the distinct order of 3-2-1–4-5-6. In effect, the Rossmann fold comprises two consecutive repeats, each comprising three β-strands (3-2-1 and 4-5-6), and two connecting α-helices. Shown in a red sphere is the ribose-binding Asp/Glu residue analyzed here, which resides at the tip of the second β-strand. Note that the Rossmann fold is usually addressed in the wider context, including Rossmann-like, or Rossmanoids, in which the sixth strand is missing, or is modified with additional secondary structural elements (e.g., methyltransferases).
Overall, a common fold [20] and the shared binding motif (the ribose β2-Asp/Glu interaction) are highly suggestive of a common Rossmann ancestor and specifically of common ancestry of NAD-, FAD-, and SAM-utilizing enzymes [30,34,38]. Indeed, these three classes (and a few additional ones addressed below) are all present in the presumed LUCA [48,49]. However, so far, there has been no attempt, to our knowledge, to examine whether these shared features are indeed a hallmark of common descent [39]. Such a systematic analysis is crucial in view of convergence being common and especially because the shared binding motif comprises a single residue.
Results
The Bidentate Ribose-Carboxylate Interaction
We were initially interested in engineering the SAM-binding site of DNA methyltransferases—a Rossmann-fold enzyme superfamily. Our attention was focused on the adenosine group that appears in nearly all of the key enzymatic cofactors. In this context, we were searching for a highly conserved interaction that is critical to adenosine binding and could be modified. However, our analysis indicated that none of the residues that interact with the adenine ring are conserved in all DNA methyltransferases. In contrast, we observed that a Glu residue that interacts with the ribose is entirely conserved. We first observed that the carboxylate-ribose interaction is completely conserved in SAM-dependent methyltransferases, including DNA, RNA, protein, and small molecule methyltransferases. We realized that conservation does not simply concern an active-site Asp/Glu that interacts with SAM [42,43] but primarily relates to a bidentate interaction with the ribose’s 2ʹ and 3ʹ hydroxyls with an unusually narrow distribution of H-bond distances and angles. Distinctly, the interacting Asp/Glu is at the tip of the Rossmann’s second beta strand (β2) (Fig 2A; S1 Fig and S2 Fig). Further, although the β2-Asp/Glu was described as a characteristic of Rossmann NAD dehydrogenases [44], its bidentate nature has not been described as such.
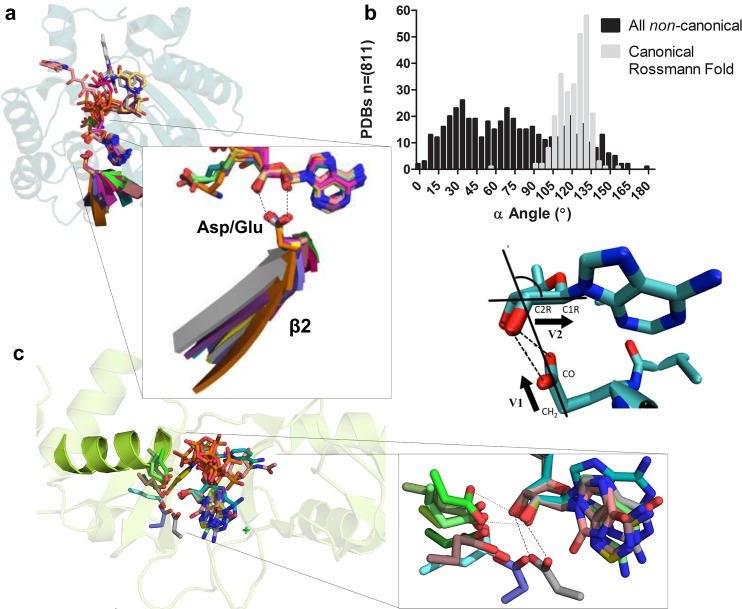
Fig 2. The geometrical and topological features of the canonical Rossmann β2-Asp/Glu motif.
(A) Representative carboxylate-ribose bidentate interactions in Rossmann-fold enzymes. Structures were superpositioned by the ribose moiety of their cofactors. One complete backbone is shown (in cartoon), whilst for others, shown are the bound cofactor, the second β-strand (β2), and the interacting Glu or Asp. PDB (Protein Data Bank) IDs and corresponding cofactors: 1JG2, ADN; 3GVI, ADP; 2HMU, ATP; 2XXB, AMP; 1BWC, FAD; 1V5E, FAD; 1EG2, MTA; 2A14, 2PBF, 2AVD (complete structure), SAM; 2GR2, FAD; 1AHH, NAD; 1GEG, NAD; 1GZ6, NAI. (B) The distribution of the interaction angle (α) in structures of proteins with a ribose bound to an Asp/Glu via a bidentate interaction. α is defined by two vectors: v1, going through the CH2-COO- carbons of the interacting Asp/Glu side chain, and v2, going through the C1-C2 carbons of the ribose ring. Gray bars represent the angles in all Rossmann structures with the canonical motif (n = 263). Black bars represent the angles of all the noncanonical bidentate interactions found in both Rossmann and non-Rossmanns enzymes. The PDB Rossmann structures with canonical and noncanonical interaction and their α angles are listed in S1 Data. (C) Representative noncanonical bidentate interactions in non-Rossmann enzymes. PDBs and the corresponding cofactor: 1HO5, ADN; 2J9L (complete structure; the helix carrying the ribose-binding Asp727 is highlighted), ATP; 3S2U, UD1; 1K9Y, AMP; 2ATV, GDP; 1SIW, GDP; 3TE5, NAI; 1I7L, ATP; 4B45, GSP. These structures are shown individually in S6 Fig.
A wider examination that further included NAD- and FAD-dependent oxidreductases was performed (see Methods and S3 Fig). This analysis confirmed that, as suggested earlier [40,41,50], the ribose-interacting Asp/Glu is also widely spread in these two enzyme classes. However, to our knowledge, the prevalence of this Asp/Glu interaction across NAD/FAD oxidoreductases, as well as SAM-dependent methyltransferases, and the geometrical conservation of the bidentate interaction with the bound ribose have not been previously noted. We therefore defined a new canonical Rossmann motif based on four criteria: (i) a tight, bidentate interaction exists between a carboxylate side chain and the ribose’s 2ʹ and 3ʹ-hydroxyls; (ii) the ribose’s furanose ring conformation is in an envelope form, mainly the E1 and 2E conformations (S4 Fig: see also S1 Text); (iii) the angle the ribose and the interacting carboxylate (hereafter the ribose–carboxylate angle α; defined in Fig 2B) is 90°–140°; and (iv) the interacting Glu/Asp is located at the tip of the β2 strand of the Rossmann fold (Fig 2A).
The Canonical Rossmann Interaction
A systematic analysis identified the above motif features as being unique to the Rossmann fold. All nonredundant PDB structures containing ribose ligands were downloaded (Table 1; n = 2,949; S5 Fig). Of these, ~30% were found to have a carboxylate side chain that is within interacting distance (≤3.4 Å) of both the 2ʹ and 3ʹ hydroxyls of the ribose (n = 811). These structures were then categorized by the angle α (Fig 2B). The secondary structural element to which the interacting Glu/Asp residue belongs was also classified, as well as the fold (using Structural Classification of Proteins [SCOP] and/or CATH annotations). This analysis indicated that the canonical bidentate interaction underlies enzyme families and superfamilies that possess a Rossmann fold. Specifically, the canonical interaction was found in 54% of the structures classified as a Rossmann fold (Table 1). These structures were manually examined, and the order of their β-strands was found to fit the Rossmann-fold topology. Further, ≥96% of the examined Rossmann enzymes have their ribose rings in the 2E or E1 configuration (discussed below). Only 8% of the structures belonging to the Rossmann fold possessed noncanonical interactions—namely, bidentate interactions with α < 90° or > 140° and/or with the interacting Glu/Asp not being located at the tip of a β strand. Conversely, in enzymes belonging to non-Rossmann folds, monodentate or no Asp/Glu interactions are the rule (91%). Further, when bidentate interactions are present in non-Rossmann proteins, they almost never meet the canonical criteria, namely the canonical angle and the interacting Glu/Asp being at the tip of a β-strand. Indeed, amongst non-Rossmann enzymes, only 1.7% exhibit bidentate interactions that meet the canonical criteria versus 6% that exhibit bidentate interactions that do not meet the canonical criteria; Fig 2A–2C, S6 Fig).
Table 1. The occurrence of carboxylate-ribose interactions in all known protein structures with ribose-containing ligands.
| Bidentate Asp/Glu Interactions | Other Interactions | |||
|---|---|---|---|---|
| Canonical | Noncanonical | Monodentate Asp/Glu Interactions | No Glu/Asp Interaction | |
| Rossmann fold (n = 484) | 263 (54%) | 38 (8%) | 66 (14%) | 117 (24%) |
| P-loop nucleoside triphosphatases (NTPases) (n = 210) | 0 (0%) | 2 (1%) | 17 (8%) | 191 (91%) |
| Non-Rossmann folds (n = 901) 1 | 27 15(1.7%) 1 | 52 (6%) | 179 (20%) | 643 (71%) |
| No assigned fold (n = 1,354) 2 | 279 (20%) | 150 (11%) | 249 (18.4%) | 676 (50%) |
| Total (n = 2,949) | 578 | 233 | 511 | 1,627 |
| Methyltransferases 3 (n = 55) | 50 (91%) | n.d. | 0 (0%) | 5 (9%) 4 |
| NAD/FAD-utilizing enzymes 3 (n = 315) | 228 (73%) | n.d. | 22 (7%) | 65 (20%) |
The analysis includes all deposited nonredundant PDB structures circa July 2014, with <2.5 Å resolution and with a ligand containing a ribose with unmodified 2ʹ and 3ʹ hydroxyls (n = 2,739). Fold categories are defined in the Methods.
1 Initially, 27 non-Rossmann PDB structures were identified by the computational search as having a canonical motif. These were manually examined, and consequently eight structures that are clearly Rossmann or Rossmannoids (1DJN, 1GTE, 1PS9, 1I8T, 2C31, 2E5W, 3C6K, and 2DHP) were excluded. It appears that their CATH/SCOP non-Rossmann annotations were derived primarily from additional domains in these structures.
2 Structures for which neither a SCOP nor a CATH category is specified in the PDB (SCOP v.1.75 and CATH_v3.5.0, version date: 20.09.2013 used for this analysis).
3 Superfamily specific statistics for methyltransferases (SCOP families c.66.1 structures bound to SAM) and of NAD/FAD dehydrogenases (SCOP families c.2.1 and c.3.1.5). n.d. = not determined.
4 A profound change in the SAM-binding site was observed in these five structures, whereby a long loop extending from β2 interacts with the ribose hydroxyls.
One notable example showing how unique the canonical motif is to the Rossmann fold is the P-loop nucleoside-triphosphatase (NTPase) fold (CATH annotation 3.40.50.300; SCOP superfamily c.37.1, P-loop containing nucleoside triphosphate hydrolase). This fold also belongs to the class of β/α proteins. Overall, its topology is highly similar to the Rossmann fold, except that the order of strands within its core β-sheet is 2-3-1–4-5-6. Thus, the location of β2, where the canonical Rossmann Asp/Glu ribose-binding residue appears (Fig 1), is shifted relative to the Rossmann topology. We found that none of the structures belonging to the P-loop NTPases superfamily (CATH Family 3.40.50.300; n = 210) contains the canonical carboxylate-ribose interaction. Further, as discussed below, the mode of nucleoside binding in P-loop NTPases differs fundamentally from the one observed in the Rossmann fold.
The Canonical Motif Is a Rossmann-Fold Identifier
Nearly half of the structures (279/578) in our original dataset were found to have the canonical carboxylate-ribose interaction but had no SCOP or CATH category (Table 1). We manually examined all 279 structures and found that 271 of these structures have a Rossmann, or Rossmann-like, topology, as defined above, and with the interacting Glu/Asp located at the tip of β2 (S5 and S6 Tables, S7 Fig). In fact, 108 out of the 279 structures that were not annotated in the CATH version v3.5.0 used to make our dataset are annotated in the current version (v.4.0.0; in which the number of annotated domains is larger by 36%). This “blind test” indicates that the applied criteria are sufficient not only to identify the canonical motif in Rossmann enzymes but also to rigorously identify a Rossmann enzyme merely by the existence of this canonical motif.
The Canonical Motif in NAD Enzymes Is Adenosine Specific
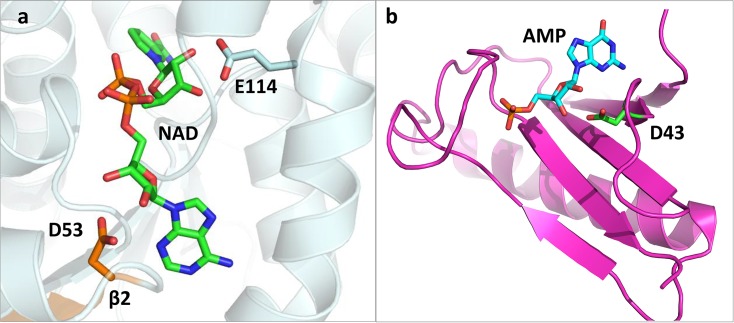
NAD-utilizing enzymes provide another indication for divergence from a common adenosine-binding ancestor. The cofactor NAD contains two riboses, one attached to adenosine and the other to nicotinamide. However, in the 259 available structures of NAD-dependent enzymes, only bidentate carboxylate-ribose interaction was found with the ribose. Among the NAD enzymes annotated as Rossmann, 145 structures out of 155 fit the canonical criteria with respect to the interaction with the adenosine’s ribose (S7 Table). Only four structures possess an additional bidentate interaction with NAD’s nicotinamide ribose. Of these four, two are annotated as Rossmann folds. Both these structures have one canonical interaction at the tip of β2 binding the adenosine ribose, as do the 145 other NAD Rossmann-fold enzymes. The nicotinamide riboses, however, interact with Glu residues located not at the tip of β2, and these bidentate interactions exhibit noncanonical geometries (Fig 3A and S8 Fig). The variability of the ribose-carboxylate angles and topology (Asp/Glu locations other than β2) and the sporadic presence (4/155 indicating appearance in recently evolved lineages) are all consistent with emergence by convergence. In contrast, the prevalence (145/155) and conservation of both geometry and topology of the interaction with the adenosine’s ribose most likely indicates divergence from a primordial ancestor of the Rossmann fold.
Fig 3. Representative noncanonical bidentate interactions in Rossmann and non-Rossmann enzymes.
(A) Zoom-in view of the structure of L-3-hydroxyacyl-CoA dehydrogenase belonging to the Rossmann fold (PDB 1F17). The cofactor, NAD (in green sticks), has its adenosine ribose interacting with D53 located at the tip of β2, with a canonical angle (α = 120°). A second bidentate interaction is observed that is not observed in other Rossmann NAD dehydrogenases, between the nicotinamide ribose and E114 located on H4 and with a noncanonical angle (α = 16°). (B) Zoom-in view of the HIT protein (HINT, histidine triad), a non-Rossmann enzyme in which a carboxylate-ribose bidentate is observed (PDB 3RHN). The cofactor, adenosine monophosphate (AMP), is in cyan sticks. The interacting D43 is at the tip of a β-strand and with a canonical angle (α = 116°). Note, that the β-strand is part of an antiparallel sheet, in oppose to the parallel β-sheet that comprises the Rossmann’s core (Fig 1).
Experimental Examination of the Canonical Interaction
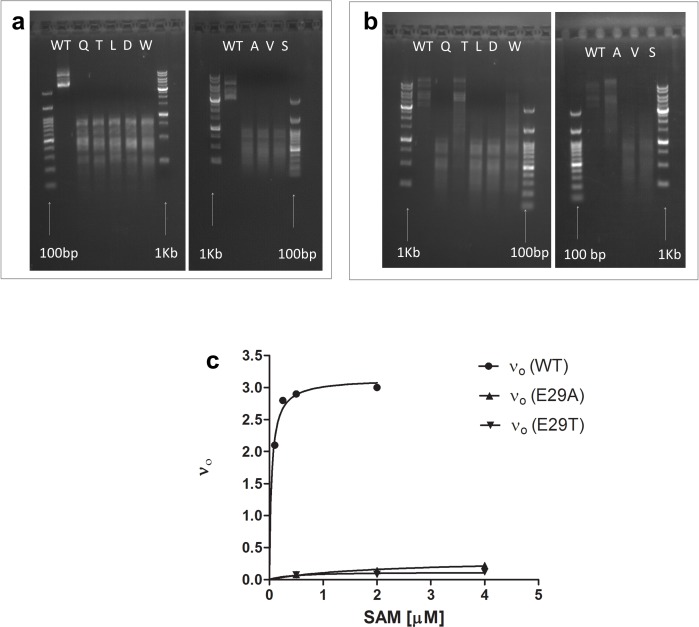
A motif that has been retained for ≥3.7 billion y of evolution is likely to be functionally important. Indeed, the contribution of the Glu/Asp interaction in NAD- and FAD-utilizing enzymes is widely recorded (published data listed in S8 Table) [51,52]. However, we could not find reports describing the experimental examination of its role in SAM-utilizing enzymes. To this end, we examined a typical bacterial mC5 DNA methyltransferase, M.HaeIII, in which Glu29 interacts with the SAM cofactor with the canonical motif geometry (Fig 4), as do nearly all other Rossmann methyltransferases (Table 1). Methylation activity was completely lost upon replacement of Glu29, including conservative replacements such as Gln, or Asp, and dropped by up to 450-fold in terms of k cat /K M in the Glu29Thr and Ala mutants (Fig 4, S8 Table). Overall, it appears that the canonical bidentate interaction have an important contribution to cofactor binding in the three classes of Rossmann enzymes in which it prevails, namely in NAD-, FAD-, and SAM-utilizing enzymes. However, the effects of mutations seemed to differ; for example, in glyceraldehyde-3-phosphate dehydrogenase (GAPDH) (NAD dependent) and sarcosine oxidase (FAD dependent), the conservative D to E mutations reduced k cat /K M by ≤10-fold, whereas in M.HaeIII (SAM dependent), activity was completely lost. Thus, in all three enzymes, relatively conservative exchanges such as D to A or D to N resulted in up to 90-fold losses, yet the loss of activity observed for the SAM-dependent M.HaeIII was generally higher. The contribution of the bidentate interaction to SAM binding is probably higher than in the case of NAD and FAD because in the latter two, the Asp/Glu bidentate interaction is further away from the reaction center.
Fig 4. Experimental examination of the carboxylate-ribose bidentate interaction in DNA methyltransferase M.HaeIII.
(A) The methylation activity by plasmid protection. Plasmids encoding wild-type M.HaeIII and its E29 mutants were transformed to Escherichia coli. Following growth and basal expression of the methyltransferase (no inducer), plasmid DNA was extracted and treated with the restriction enzyme, HaeIII. As can be seen, none of the E29 mutants were capable of methylating its plasmid, as indicated by complete digestion into fragments. The arrows identify the DNA ladders. (B) The assay was repeated with the wild type and the mutants being overexpressed (with inducer). Under these conditions, the assay sensitivity is very high, and variants whose expression or activity is well under 100-fold compared to wild type show 100% protection [53]. (C) Michaelis-Menten curves for wild-type M.HaeIII (WT) and of the E29 mutants exhibiting detectable activity. Time-dependent in vitro methylation assays were performed as described, and initial reaction rates (v 0) were extrapolated from the linear phase in the time-dependent courses of the reaction (raw data are available in S2 Data). Experiments were carried out at 37°C, with WT M.HaeIII at 0.1 μM and the E29 mutants at 8 μM.
The Canonical Geometry: A Local Optimum but Not the Only One
Is the highly conserved geometry of the Rossmann bidentate motif the outcome of chance or of necessity [54]? Namely, does the canonical geometry comprise the most optimal mode of ribose binding, or is it just one out of several options? Evolution of the Rossmann fold and cofactor binding implies that a single solution was selected at the ancestral stage, presumably owing at least in part to its favorable binding energy, and has been conserved ever since. Indeed, a scenario of divergence typically follows from the existence of several possible solutions; in particular, divergence of the bidentate carboxylate interaction geometries would seem to imply that there are multiple such geometries of similar energy. Convergence, on the other hand, is compatible with a scenario whereby the bidentate interaction geometry seen in existing proteins is the only optimal one or even the only possible one.
We can illustrate the above line of reasoning by considering the dihedral angles (ω) of the peptide bonds in proteins. The distribution of ω along >200,000 peptide bonds in known protein structures is narrow, with a clear maximum at planarity (>97% of bonds within ω = 180 ± 10°). This distribution corresponds to a single optimum value of 180° [55]. The planarity of the peptide bond therefore relates to a physical constraint that dictates all protein structures, rather than to a trait that diverged from the very first peptide. Another example mentioned in the introduction is the Asp/Glu dyads seen in glycosydases of many different folds, whereby the intercarboxylate distances are highly conserved within two categories of retaining glycosidases (5.5 Å) and inverting ones (10 Å) [11].
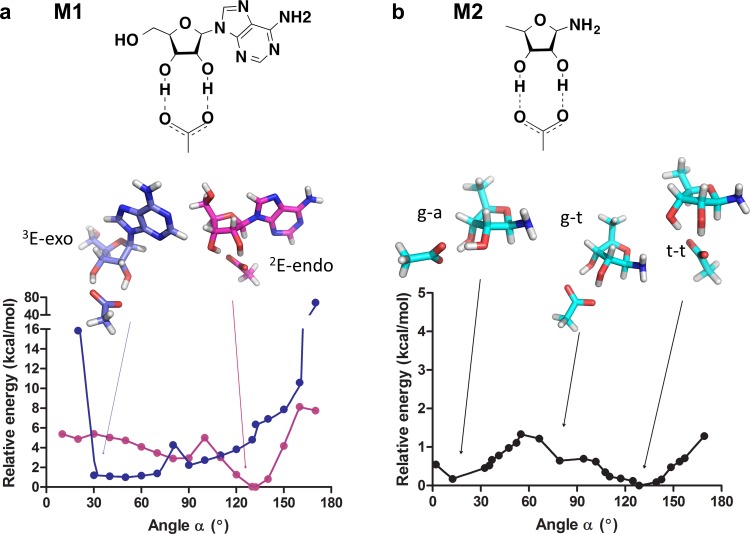
The favorable contribution of the bidentate carboxylate interaction to binding of vicinal-diols (as are the 2ʹ, 3ʹ hydroxyls of ribose) was indicated in small-molecule structures (S9 Fig) and by quantum mechanical calculations [56]. In the present work, we carried out new calculations to examine how energetically favorable is the geometry of the canonical interaction, and specifically how the energy of this interaction changes with the ribose-carboxylate angle (α) and ribose ring configuration. We performed quantum mechanical calculations designed to produce energy profiles of the different furanose configurations of ribose and of the ribose-carboxylate interaction angle (α) [57]. For this purpose, density functional theory electronic structure calculations with the Solvation Model based on Density (SMD) solvation model were used to study the ribose-carboxylate interaction in model systems in which the structures were energy minimized as a function of the ribose-carboxylate angle α (Fig 5; the energy calculations are described in detail in the S1 Text). The quantum mechanical calculations were performed on two models systems, M1 and M2, defined in Fig 5. After conformational searches, we identified the lowest-energy structures of model M2 (dubbed g-a, g-t, and t-t) and those for M1 (dubbed 2E-endo and 3E-exo). The lowest-energy structure obtained for M1 is 2E-endo, and for M2, it is t-t. Both 2E-endo and t-t exhibit a similar endo conformation, with respective α values of 132° and 129° and a similar envelope form for the ribose ring (2E for 2E-endo and E1 for t-t). The relative energy was accordingly plotted against the angle α (Fig 5A for model M1 and Fig 5B for model M2), indicating the lowest-energy structure for each value of α. These plots show that the bidentate interaction presents an angle optimum of ~130°. This optimum clearly overlaps the canonical Rossmann angle (Fig 2B). Further, the vast majority of Rossmann enzymes possess a ribose ring in a 2E or E1 configuration (96% of 263 PDB structures analyzed; see S1 Text) and an endo conformation (100% of 263 structures; see S1 Text), thus matching their modeled counterparts, 2E-endo and t-t.
Fig 5. The potential energy of the bidentate ribose-carboxylate interaction as a function of the interaction angle.
The energies, in kcal/mol, are plotted as a function of the carboxylate-ribose angle α and are relative to the lowest identified energy for each of the models. (A) Structure and energy profile for model M1 indicating the optimized lowest-energy structures, 2E-endo (in magenta) and 3E-exo (in blue). (B) Structure and energy profile for model M2, in which g-a, g-t and t-t are fully optimized structures. Note that the energy plots for the two models are drawn on two different scales (data available in S3 Data).
However, beyond the canonical optimum, the potential energy surface for the carboxylate-bidentate interaction is relatively flat, with several minima. The only angles that appear to be highly disfavored are the edges, i.e., close to 0° and 180°, and these regions are also unoccupied in natural proteins (Fig 2B). Energy minima corresponding to the 3E-exo configuration for M1, and the g-a configuration for M2, are seen in α range of 10°–37° (Fig 5). According to our calculations, the endo configuration is more stable than the exo, by about 1 kcal/mol for model M1 and by only 0.1 kcal/mol for model M2. These differences are relatively small—an energy difference of 0.55 kcal/mol (the average difference for M1 and M2) corresponds to ~2.5-fold difference in affinity. For comparison, as indicated by the effects of mutations of the canonical Asp/Glu, the contribution of this interaction in Rossmann enzymes of different classes differs by well over 10-fold (see the above section and S8 Table).
The model structures that correspond to the alternative energy minima are seen in typical noncanonical interactions (Fig 2C, carboxyl side chains in variable greens). One characteristic example can be seen in Fig 3A, with the angles of the noncanonical interactions being 16°, far off the canonical range (90°–140°) and within the second predicted minimum (Fig 5). This alternative minimum corresponds to an exo disposition and has the ribose ring in the 3E for 3E-exo and in 2E for g-t. This mode is clearly seen in enzyme structures with the interaction angle in the range of 14° to 43° (Fig 2B and Fig 3), whereby the interaction corresponds to an exo configuration and the furanose conformation of the ribose is scattered among several possibilities (see S1 Text). Another example is human phosphoglyceraldehyde kinase where Glu344, located at the tip of β4, not β2, interacts with the ADP ribose in a bidentate manner, with the angle being 57° (S10 Fig).
Overall, the computations indicate that the canonical interaction is an intrinsically favorable mode for binding of ribose. It also corresponds to a furanose ring configuration that is the most energetically favored irrespective of the protein binding pocket and additional interactions, e.g., with the nucleoside’s base. However, the canonical interaction is only one out of at least two, if not more, favorable modes of bonding. Indeed, a wide distribution of interaction angles (Fig 2B) is seen in non-Rossmann ribose-binding proteins and predominantly in noncanonical interactions in Rossmann enzymes.
Discussion
Convergence or Divergence?
The utility of the carboxylate-ribose bidentate interaction, and its appearance in numerous protein families belonging to different folds and binding different cofactors, suggest that it arose independently, i.e., by convergent evolution. This is not surprising in view of the simplicity of this motif—a single carboxylate side chain aligned against the ribose hydroxyls. However, the statistics of occurrence clearly support the hypothesis of divergence. The canonical interaction is >30 times more frequent in Rossmann enzymes (54%) compared to non-Rossmann ones (1.7%). In contrast, the occurrence of noncanonical bidentate interactions in Rossmann and non-Rossmann proteins is nearly identical (8% and 6%, respectively; Table 1). Thus, whilst convergence to the canonical geometry and/or topology did occur, as exemplified in Fig 3B, its frequency of occurrence is not only lower but is also independent of the fold. The distinct features of convergence are apparent, including within Rossmann enzymes.
The distinct geometry of this motif in Rossmann enzymes may also provide a new means for automated classifications, as indicated by our manual examination of the structures with no CATH or SCOP annotations. The presence of an Asp/Glu at the loop connecting the second β-strand and the following helix is insufficient to distinguish between Rossmann from non-Rossmann enzymes (as previously noted [37,39] and also indicated by our data). However, when the carboxylate-ribose angle criterion is added, prediction accuracy increases to 97% (the false positive rate is 8/279).
The ancient origins of the ribose–(Asp/Glu-β2) motif and the claim for divergent evolution are also supported by the role of this motif in the switch of cofactor specificity of dehydrogenases. NADP-dependent dehydrogenases seem to have diverged from NAD-dependent enzymes [58], probably along multiple lineages. NADP differs from NAD in the 3ʹ-hydroxyl of the adenosine ribose being phosphorylated. Thus, binding of NADP is a priori excluded because of the negatively charged Glu/Asp that interacts with the unmodified ribose hydroxyls in NAD dehydrogenases. Indeed, the replacement of the β2-Asp/Glu is a prerequisite for the switch in specificity to NADP (S11 Fig) [59,60]. Thus, loss of the canonical Glu/Asp underlines the evolution of orthogonal, NADP-dependent dehydrogenases.
The existence of alternative ribose-binding modes with binding energies that are similar to that of the canonical Rossmann mode (Fig 5) and the accordingly wide distribution of binding modes of the noncanonical interactions (as reflected by the interaction angle α; Fig 2B) also support the hypothesis that the canonical Rossmann motif is the outcome of common ancestry and not of convergent evolution. Many structural features are the outcome of strict biophysical constraints, namely of one geometry being highly favored (a deep-well potential energy surface). The negative constraints (steric clashes, loss of resonance energy, etc.) are most dominant in dictating deep-well potentials. This is, for example, the case with the planarity of amide bonds [55]. In contrast, the multiminima potential energy surface for the carboxylate-ribose interaction indicates strong constraints acting only at the edges (around 0° and 180°; Fig 5). This suggests that the conservation of the interaction angle in Rossmann enzymes relates to their divergence from a common ancestor in which this angle was dictated by various factors, including but not limited to the favorable ribose-carboxylate interaction.
The Ribose-Binding Rossmann Ancestor
Common ancestry is the hallmark of Darwinian evolution. Our data support the notion of a primordial Rossmann ancestor in which binding of an adenosine-based cofactor was mediated by the ribose-β2-Asp/Glu interaction, alongside the Gly-loop that resides at the tip of the first strand (β1) (Fig 6, S13 Fig) [24,30,36,39]. The Gly-rich motif binds the phosphate groups of NAD/FAD/adenosine-5ʹ-triphosphate (ATP) (typically, GxGxxG) [5,61]. This motif is also recognizable in methyltransferases, although with low sequence identity because, unlike NAD- and FAD-dependent enzymes, their cofactor, SAM, does not contain a phosphate group (Fig 6). The minimal postulated ancestor therefore spans the Rossmann fold's first two strands and the connecting helix (β1-H1-β2) and includes the Gly-rich and ribose-β2-Asp/Glu interaction (Fig 7A) [40,62]. Our analysis supports a postulated pre-LUCA ancestor that underlined the divergence of at least three major enzyme classes: methyltransferases, NAD(P) and FAD oxireductases [29], and the many superfamilies belonging to these two classes, as well as the divergence of other enzyme families using other adenosine-based cofactors such as ATP (Fig 6). The Gly-rich loop and the ribose-β2-Asp/Glu motif was the keystone of this primordial ancestor [40,62]. Such keystone elements may relate to earlier precursors, possibly shorter polypeptides that contained these binding motifs [5,40,41,43,45] and from which the Rossmann ancestor evolved via a series of duplications, recombination, and fusions [63,64].
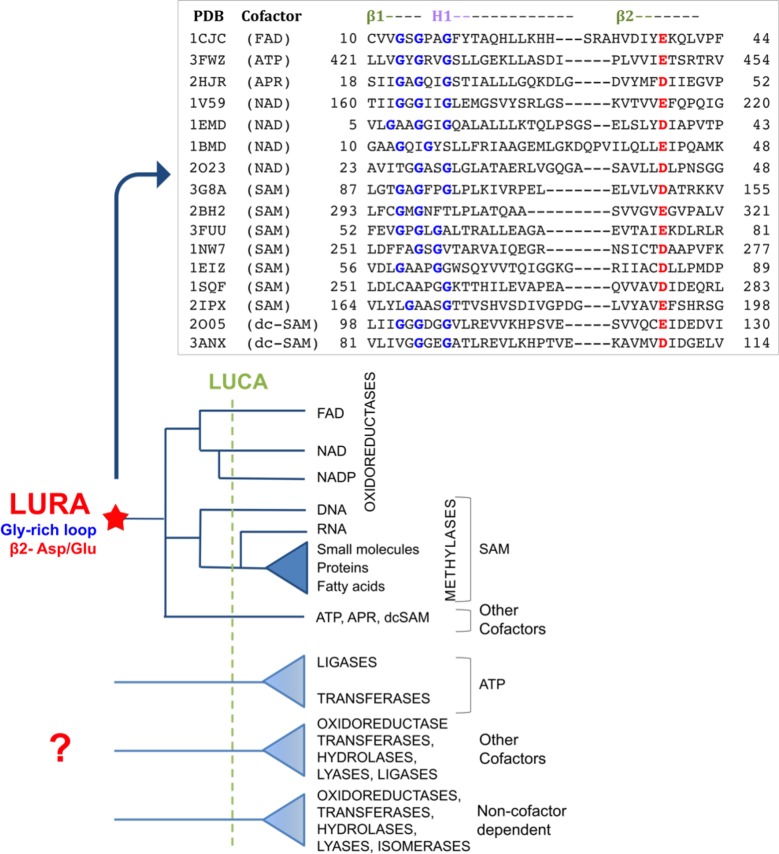
Fig 6. Manual alignment of the β1-H1-β2 segments of representative Rossmann-fold enzymes that possess the canonical motif and a schematic evolutionary tree of the Rossmann fold.
Shown are representatives from the four major classes that seem to have diverged from a common ancestor carrying the β2-Asp/Glu motif (Fig 1). The ribose-binding β2-Asp/Glu is in red. As previously noted [5,33], the motif GxGxxG (in blue) is present in almost all the NAD/FAD enzymes, as well as in enzymes utilizing other phosphate-containing cofactors (ATP, AMP, and adenosine-5-diphosphoribose [APR]). In SAM (or dc-SAM) utilizing enzymes, the Gly-rich motif is blurred as expected for a cofactor that does not contain a phosphate group. The schematic tree originates from a presumed last universal Rossmann ancestor (LURA), and it is based on Enzyme Commission (EC) numbers and CATH classification of LUCA’s enzymes (S1 Table). The star designates the presumed common Rossmann ancestor that includes the ribose-(Asp/Glu-β2) and the Gly-rich motifs.
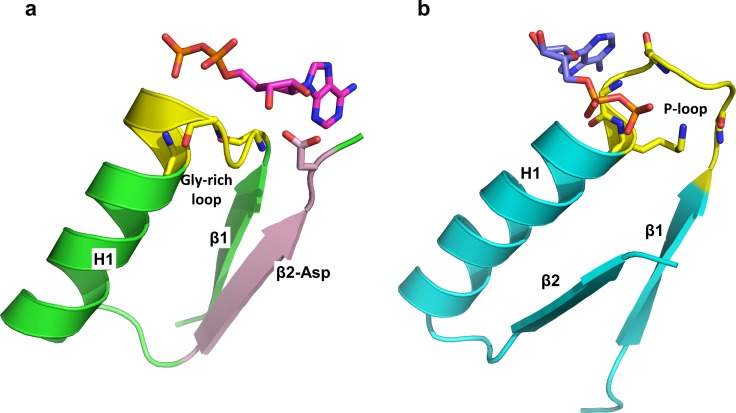
Fig 7. Putative minimal elements underlying the emergence of cofactor-utilizing enzymes.
(A) The β1-α1–β2 segment that contains Gly-rich as well as the canonical β2-Asp/Glu interaction comprises the keystone of Rossmann enzymes [40,62] (taken from an NAD-dependent dehydrogenase, PDB 1LDN; see also S13 Fig). Indicated are the Gly-loop (glycines 27, 29, and 32, in yellow) and the canonical ribose ligating Asp at the tip of β2. (B) The P-loop comprises the keystone of the P-loop containing nucleotide triphosphate hydrolases. Shown is the β1-α1–β2 segment taken from a kinase (PDB 2AXN; in complex with ADP). The P-loop (yellow) stems from the first β-strand (β1) and into the first helix (H1). Note that the adenosine di-phosphate moiety, which is common to both cofactors, is bound in opposite directions (the β1-α1–β2 segments were aligned in the same direction).
Cofactor binding—The keystone
The notion of a cofactor binding as the keystone underlying the emergence of the early proteins [5,44,45] is also supported by another ancient fold with a related topology to the Rossmann fold: the P-loop NTPases. Notable in the P-loop NTPases is the exchange between the second and third strands (β2, β3 strand; Fig 1) [5,65,66]. Indeed, the ribose-β2-Asp/Glu interaction is completely absent in this superfamily/fold (Table 1). Instead, this superfamily is underlined by the P-loop, an omnipresent, ancient phosphate-binding motif that appears in many other superfamilies with different folds [5,66–68]. Like Rossmann enzymes, P-loop NTPases make use of ribose-containing cofactors. However, in these enzymes the P-loop comprises the keystone. Not only is the ribose-β2-Asp/Glu missing in P-loop NTPases, but the nucleoside binding orientation is the opposite of the one observed in the Rossmann fold. Curiously, P-loop NTPases have a second conserved motif, the so-called Walker B motif that often comprises an acidic residue following a stretch of hydrophobic ones [69,70]. The latter form a β-strand, as is the case with the Rossmann β2-Asp/Glu motif. However, the Walker B motif is far less conserved than the Rossmann β2-Asp/Glu motif and typically comprises the third strand of the P-loop NTPase fold. Consequently, in P-loop NTPases, the ribose 2ʹ and 3ʹ hydroxyls typically face the solvent rather than interact with protein residues (Fig 7B). Further, the glycine-rich phosphate-binding motifs of these two rudimentary folds comprise mirror images of one another—GxxGxG in P-loop NTPases versus GxGxxG in NAD-dependent Rossmann fold (Fig 7). Thus, despite >3.7 billion y of evolution, these keystones comprise detectable fingerprints of divergent evolution from pre-LUCA ancestors and of the early emergence and evolution of cofactor-utilizing enzymes.
Methods
Dataset Assembly
For the study of the individual enzyme classes, all structures belonging to SAM-dependent methyltransferases (SCOP category c.66.1), NAD(P)-binding Rossmann-fold domains (c.2.1), and FAD/NAD-linked oxidoreductases (c.3.1.5) were downloaded from SCOP (v.1.75). Redundant structures of the same protein in which the PDB code was the same for the first three letters/digits and the Glu/Asp residue number was identical were removed. Structures with <2.5 Å resolution were further considered, resulting in 55 methyltransferase (c.66.1) and 315 oxidoreductase (c.2.1 and c.3.15) enzyme domains that were assigned as Rossmann by SCOP (a flowchart describing this analysis is available as S3 Fig). For the systematic analysis of all ribose-binding proteins, we first identified 66 ribose-containing ligands (S2 Table) for which ≥10 nonredundant structures are available in the PDB. We excluded ligands that are part of polynucleotides such as RNA or DNA. All PDB structures that have ribose-containing ligands and <2.5 Å resolution were downloaded, and 80% sequence redundancy was removed with cd-hit [71]. The final dataset comprised 2,949 structures (Table 1) comprising 210 P-loop NTPase structures, 2,313 structures containing ligands with one ribose ring, and 426 structures with ligands such as NAD or FAD that contain two riboses (a flowchart describing this analysis is available as S5 Fig). The four structures with NAD ligands and two bidentate interactions were analyzed separately.
Geometry and Topology of Ribose Binding
We calculated the distances, angles, and dihedral angles of atoms of interest using the PDB coordinates and custom Perl-scripts. For all retrieved PDB structures, the first chain in the asymmetric unit containing the cofactor was extracted. A random sample indicated that the variability in the distances and angles between different molecules in the asymmetric unit is low, and hence, an arbitrary choice of the first chain containing the cofactor is representative (S1 Text; average standard deviation for the distance is 0.074 Å, and for α is 2.2°). First, all residues that bind the ribose ligands were determined using CSU, and based on whether there is an Asp/Glu residue in the vicinity of the 2’, and 3’-OH of the ribose (≤4 Å). Then, we further characterized the ribose-Asp/Glu interaction and defined four binding modes: canonical bidentate, noncanonical bidentate, monodentate, or “no Asp/Glu interaction.”
The canonical bidentate interaction was defined by four criteria:
A bidentate interaction indicated by the distances between both oxygens of the interacting carboxyl moiety and the O2 and O3 of the ribose is ≤3.4 Å.
The plane angle (α; calculated as described in S1 Text) is in the range of 90° to 140°.
The interacting Asp/Glu residue is located at the tip of a β-strand. To identify the latter, secondary structure was assigned by dssp (H: alpha helix, E: strand, T: turn, S: bend, L: loop, G: 3/10-helix); the location criterion was defined as met when the interacting Asp/Glu comprised the last position within a strand or the next consecutive residue after a strand. For the initial analysis of individual families (c.66.1, c.2.1 and c.3.1.5), a more stringent threshold was set up for the first criterion whereby at least one of the distances between the hydroxyl 2ʹ-and 3ʹ-oxygens of the ribose was ≤3 Å.
The ribose’s furanose ring conformation is in an envelope form, mainly the E1 and 2E conformations.
Noncanonical bidentate interaction was assigned to structures meeting criterion (i), namely structures with a bidentate interaction yet with the plane angle being <90° or >140° and the interacting Asp/Glu not located at the tip of a β-strand.
Monodentate interactions were assigned to structures with a single putative H-bond interaction between an Asp/Glu carboxylate and either the 2ʹ or the 3ʹ-hydroxyl groups. A more generous cutoff distance of ≤4 Å was taken here than for the bidentate interactions (≤3.4 Å) because the latter, and especially the canonical bidentate interactions, tend to be much tighter (average distance = 2.7 Å; S2B Fig). Finally, no Glu/Asp interaction was ascribed to structures where no carboxylate was found within 4 Å of either the 2ʹ or the 3ʹ-hydroxyl groups of the bound ribose.
Fold Annotation
When available, we retrieved the CATH and SCOP classification for the PDB structures in our dataset. Assignments of Rossmann fold were derived from CATH topology 3.40.50 (CATH_v3.5.0, version date: 20.09.2013, was used for this analysis). However, as explained in the main text, we separately analyzed superfamily 3.40.50.300, the P-loop containing nucleotide triphosphate hydrolases that are usually not considered as Rossmann. For SCOP, categories c.66.1, c.2.1, c.3.1, and c.4.1 were assigned as Rossmann. Including both CATH and SCOP databases significantly increased the fraction of structures with annotated fold (e.g., for structures containing one ribose ligands, the CATH database assigns 207 proteins as Rossmann, and addition of SCOP added another 85). About 46% of structures had neither a CATH nor a SCOP annotation (1,354/2,949). We therefore manually inspected a randomly chosen subset of the structures that possess the canonical interaction. We confirmed these as belonging to the Rossmann fold by identifying the canonical 3-2-1-4-5-6 topology of β-strands, or as Rossmann-like by identifying structures in which the last β strand (β6) is missing (S5 Table).
Role of Glu29 in Methyltransferase M.HaeIII
A variant of M.HaeIII containing four stabilizing mutations and with wild-type-like activity was the starting point for generating the Glu29 mutants [72]. The pASK-IBA3+vector (IBA, ampicillin resistance) plasmid containing the gene for the stabilized M.HaeIII was used as a template for PCR amplification. Mutants in position 29 were constructed by site-directed mutagenesis. The Glu codon was replaced with the Gln codon (CAA), Thr codon (ACC), Leu codon (CTG), Asp codon (GAT), Trp codon (TGG), Ala codon (GCG), Val codon (GTG), or Ser codon (AGC). The mutant encoding plasmids were transformed into E. coli MC1061, [mcrA0 relA1mcrB1 hsdR2 (r-m+; in which DNA methylation is not toxic) bearing the GroEL/ES encoding plasmid pGro7 (chloramphenicol resistance; Takara) to assist the folding of compromised mutants [72]. Transformants were selected by growth in the presence of ampicillin and chloramphenicol. The methyltransferase activity was tested by treatment of the extracted plasmid with the cognate restriction enzyme, HaeIII. The level of plasmid protection by virtue of methylation by M.HaeIII was determined by gel analysis. Bacteria were grown with no inducer or under induction (0.2 μg/ml anhydrotetracycline) and with 0.05% arabinose for induction of GroEL/ES expression. Wild-type M.HaeIII gave full protection even when basally expressed (no inducer). Time-dependent in vitro methylation assays were performed with purified enzyme variants (0.1–8 μM) essentially as described [73], using H3-labeled SAM (0.1–8 μM) and DNA substrate carrying nine methylation GGCC sites per molecule at 2.5 nM.
QM Calculations
We carried out quantum mechanical electronic structure calculations on models M1 and M2 (S1 Text) by using the M06-2X/6-31+G(d,p) [74,75] model chemistry including the effect of aqueous solvent by using the SMD solvation model [76]. All electronic structure calculations were performed with Gaussian09 [77]. We performed an exhaustive conformational search for model M1 (Fig 4A). Starting from the lowest-energy optimized structures obtained with model M1, namely 2E-endo and 3E-exo, we carried out a relaxed potential energy surface scan along the coordinate defined by α (see Fig 5A). In the scan, all degrees of freedom were optimized with the exception of the angle α. This was accomplished by interfacing the Gaussian 09 program49 with a utility program we wrote that allows a constraint on the angle between two vectors. For model M2 (Fig 5B), after carrying out a conformational analysis of the molecule of adenosine and an analysis to find the best conformations that lead to a double hydrogen bond with a molecule of acetate, three fully optimized structures of model M2, denoted as g-t, g-a, and t-t, were found. These structures were taken as initial geometries to explore the potential energy surface (PES). The PES was explored by a combination of successive relaxed energy minimization scans along two angles and a dihedral angle that equals to perform a scan along the angle α (see S1 Text).
Supporting Information
(XLSX)
(XLSX)
(XLSX)
(XLSX)
SAM or SAH cofactors are shown in green sticks, β2 strand of Rossmann fold in orange, and the interacting Asp/Glu with the hydroxyls’ ribose in orange sticks. (A) The catalytic domain of bacterial DNA methylase M.HhaI (PDB 1SKM); (B) human DNA methylase Dnmt3a (PDB 2QRV); (C) human DNA methylase Dnmt1 (PDB 3AV6). (D) An mRNA methylase (PDB 1RI4). (E) An N5-glutamine methylase (PDB 1NV8). (F) Catechol methylase (PDB 3BWM).
(TIF)
(A) Definition of the geometrical parameters. (B) Distribution of the bond lengths between the hydroxyl group of the ribose and the closest oxygen of the carboxylate of the Glu/Asp. (C) Distribution between the angle of the hydroxyl bond of the ribose and the carboxylate. (D) Distribution of the dihedrals of O-C1-C2-C3 and C1-C2-C3-C4. The distribution highlights a distorted envelope 2ʹ endo conformation of the ribose for most of the structures. Data for all PDB entries are provided in S4 Data.
(PNG)
(PNG)
The 2β strand is in orange, the E90 interacting with the hydroxyls of the ribose is shown as an orange stick, and Mg2+ is shown in the green sphere. The electron density map of the ribose is highlighted in blue, showing the 2E-endo conformation of the ring.
(PNG)
(PNG)
PDBs, corresponding cofactor and α angle: (A) 1HO5, ADN (adenosine) (29°); (B) 2J9L, ATP (adenosine-5ʹ-triphosphate) (27°); (C) 3S2U, UD1 (uridine-diphosphate-N-Acetylglucosamine) (19°); (D) 1K9Y, AMP (adenosine monophosphate) (127°); (E) 2ATV, GDP (guanosine-5ʹ-diphosphate) (27°); example of P-loop containing nucleoside triphosphate hydrolases); (F) 1SIW, GDP (137°); (G) 3TE5, NAI (1,4-dihydronicotinamide adenine dinucleotide) (18°); (H) 1I7L, ATP (43°); (I) 4B45 GSP (5ʹ-guanosine-diphosphate-monothiophosphate) (29°).
(PNG)
The basic Rossmann fold is altered primarily by addition of other elements. The β strands belonging to Rossmann are colored differently than the main structure: β1 in blue, β2 in green, β3 in magenta, β4 in orange, and β5 in wheat. The cofactors and the interacting E/D are in sticks. (A) PDB 3UCL binding FAD. The zoom-in view depicts the ribose’s cofactor binding site. (B) PDB 3CGD is constituted by two Rossmann subunits binding NAD and FAD. The zoom-in views depict the two subunits binding the ribose of the corresponding cofactors.
(PNG)
Cartoon structure of L-2-hydroxyisocaproate dehydrogenase (PDB 1HYH). The cofactors are shown in the green sticks; the interacting D45 (canonical) and E110 (noncanonical) are shown as sticks.
(PNG)
Highlighted are the distances between the vicinal diol and the oxygens of the carboxylic acid.
(PNG)
The backbone is shown in the cartoon, the cofactor and residue E344 in sticks, and the Mg2+ in the green sphere. The loop that follows the fourth β-strand (4β) and that carries the bidentate interacting Glu344, as well as the 4β, are shown in pink.
(PNG)
Although these Rossmann-fold enzymes bind different adenosine-containing ligands, Xie and Bourne noted that the adenosine moieties are well aligned, suggesting that these families share a common ancestry. (A) SAM-dependent methyl transferases (PDB 1ZQ9). (B) Carbonyl reductase (PDB 1CYD). (C) Overlapping of the two structures highlights the interaction of E85 (green stick) on 2β tip interacting with SAM’s ribose with the canonical motif and R39 (cyan sticks) on 2β tip interacting with the phosphate moiety of NADP.
(PNG)
Asp34 that stems from the second β-strand (2β) mediates the bidentate interaction with the ribose’s 2ʹ and 3ʹ-hydroxyls.
(PNG)
Among the structures with the canonical motif, a sample of 50 PDB structures was randomly selected. Following standard alignment, with Multiple Sequence Comparison by Log-Expectation (MUSCLE), sequences were grouped by the cofactor. The phosphate-containing cofactors depicted are as follows: ATP, adenosine-5ʹ-triphosphate; AMP, adenosine monophosphate, and APR, adenosine-5-diphosphoribose; FAD, flavin adenine dinucleotide; and NAD, nicotinamide adenine dinucleotide; the non-phosphate-containing cofactors are as follows: SAM, S-adenosylmethionine, and dc-SAM, Adenosylmethioninamine.
(PNG)
(PNG)
(TIF)
(PNG)
The interacting E/D is located on different secondary structure elements and never at the tip of the β2 strand.
(PNG)
(PNG)
(PNG)
Noted are the distances of the interacting E/D at the top of the β2 strand to the ribose hydroxyls. In all these cases, the interacting ribose belongs to the adenosine moiety of these cofactors and not to the nicotinamide (NAD, or NADH—annotated as NAI) or the free ribose (in APR).
(PNG)
(PNG)
(PNG)
(DOCX)
Acknowledgments
We thank Andrei Lupas for valuable insights and for his invaluable note on the relation between our identified motif and the Gly-rich loop of Rossmann enzymes. We thank Igor Berezosvsky, Lei Xie, and Vikram Alba for their insightful comments and Jingjing Zheng, Zoltan Varga, and Maxim Makeev for helpful discussions. We thank Leviel Fluhr for the meticulous manual fold annotation of hundreds of the structures.
Abbreviations
- AMP
adenosine monophosphate
- APR
adenosine-5-diphosphoribose
- ATP
adenosine-5ʹ-triphosphate
- CATH
Class Architecture Topology Homologous superfamilies
- EC
Enzyme Commission
- ECOD
Evolutionary Classification of Protein Domains
- FAD
flavin adenine dinucleotide
- GAPDH
glyceraldehyde-3-phosphate dehydrogenase
- LUCA
last universal common ancestor
- LURA
last universal Rossmann ancestor
- NAD
nicotinamide adenine dinucleotide
- NADP
nicotinamide adenine dinucleotide phosphate
- NTPase
nucleoside triphosphatase
- MUSCLE
Multiple Sequence Comparison by Log-Expectation
- PDB
Protein Data Bank
- PES
potential energy surface
- SAM
S-adenosyl methionine
- SCOP
Structural Classification of Proteins
- SMD
Solvation Model based on Density
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was supported by the Israel Science Foundation (Grant 980/14) and by FEBS Long-Term Fellowship. The above funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Joyce GF. The antiquity of RNA-based evolution. Nature. 2002;418(6894):214–21. 10.1038/418214a . [DOI] [PubMed] [Google Scholar]
- 2. Gilbert W. Origin of Life—the Rna World. Nature. 1986;319(6055):618–. 10.1038/319618a0 . [DOI] [Google Scholar]
- 3. Crick FH. The origin of the genetic code. Journal of molecular biology. 1968;38(3):367–79. . [DOI] [PubMed] [Google Scholar]
- 4. Osadchy M, Kolodny R. Maps of protein structure space reveal a fundamental relationship between protein structure and function. Proceedings of the National Academy of Sciences of the United States of America. 2011;108(30):12301–6. 10.1073/pnas.1102727108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Lupas AN, Ponting CP, Russell RB. On the evolution of protein folds: are similar motifs in different protein folds the result of convergence, insertion, or relics of an ancient peptide world? Journal of structural biology. 2001;134(2–3):191–203. 10.1006/jsbi.2001.4393 . [DOI] [PubMed] [Google Scholar]
- 6. Gherardini PF, Wass MN, Helmer-Citterich M, Sternberg MJ. Convergent evolution of enzyme active sites is not a rare phenomenon. Journal of molecular biology. 2007;372(3):817–45. 10.1016/j.jmb.2007.06.017 . [DOI] [PubMed] [Google Scholar]
- 7. Kopec KO, Lupas AN. beta-Propeller blades as ancestral peptides in protein evolution. PLoS ONE. 2013;8(10):e77074 10.1371/journal.pone.0077074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Koga N, Tatsumi-Koga R, Liu G, Xiao R, Acton TB, Montelione GT, et al. Principles for designing ideal protein structures. Nature. 2012;491(7423):222–7. 10.1038/nature11600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Lin YR, Koga N, Tatsumi-Koga R, Liu G, Clouser AF, Montelione GT, et al. Control over overall shape and size in de novo designed proteins. Proceedings of the National Academy of Sciences of the United States of America. 2015. 10.1073/pnas.1509508112 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Smock GR, Yadid I, Dym O, Clarke J, Tawfik DS. De novo evolutionary emergence of a symmetrical protein is shaped by folding constraints. Cell. 2015;164: 476–486. 10.1016/j.cell.2015.12.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Davies G, Henrissat B. Structures and mechanisms of glycosyl hydrolases. Structure. 1995;3(9):853–9. 10.1016/S0969-2126(01)00220-9 . [DOI] [PubMed] [Google Scholar]
- 12. Todd AE, Orengo CA, Thornton JM. Plasticity of enzyme active sites. Trends in biochemical sciences. 2002;27(8):419–26. . [DOI] [PubMed] [Google Scholar]
- 13. Galperin MY, Koonin EV. Divergence and convergence in enzyme evolution. The Journal of biological chemistry. 2012;287(1):21–8. 10.1074/jbc.R111.241976 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Elias M, Tawfik DS. Divergence and convergence in enzyme evolution: parallel evolution of paraoxonases from quorum-quenching lactonases. The Journal of biological chemistry. 2012;287(1):11–20. 10.1074/jbc.R111.257329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Gould SJ. The structure of evolutionary theory Cambridge, Mass.: Belknap Press of Harvard University Press; 2002. xxii, 1433 p. p. [Google Scholar]
- 16. Farias-Rico JA, Schmidt S, Hocker B. Evolutionary relationship of two ancient protein superfolds. Nat Chem Biol. 2014;10(9):710–5. 10.1038/nchembio.1579 . [DOI] [PubMed] [Google Scholar]
- 17. Toth-Petroczy A, Tawfik DS. The robustness and innovability of protein folds. Current opinion in structural biology. 2014;26C:131–8. 10.1016/j.sbi.2014.06.007 . [DOI] [PubMed] [Google Scholar]
- 18. Edwards H, Abeln S, Deane CM. Exploring fold space preferences of new-born and ancient protein superfamilies. PLoS Comput Biol. 2013;9(11):e1003325 10.1371/journal.pcbi.1003325 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Xie L, Bourne PE. Detecting evolutionary relationships across existing fold space, using sequence order-independent profile-profile alignments. Proceedings of the National Academy of Sciences of the United States of America. 2008;105(14):5441–6. 10.1073/pnas.0704422105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Aravind L, Mazumder R, Vasudevan S, Koonin EV. Trends in protein evolution inferred from sequence and structure analysis. Current opinion in structural biology. 2002;12(3):392–9. . [DOI] [PubMed] [Google Scholar]
- 21. Bukhari SA, Caetano-Anolles G. Origin and evolution of protein fold designs inferred from phylogenomic analysis of CATH domain structures in proteomes. PLoS Comput Biol. 2013;9(3):e1003009 10.1371/journal.pcbi.1003009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Koonin EV. The logic of chance: the nature and origin of biological evolution: FT Press; 2011. [Google Scholar]
- 23. Caetano-Anolles G, Kim HS, Mittenthal JE. The origin of modern metabolic networks inferred from phylogenomic analysis of protein architecture. Proceedings of the National Academy of Sciences of the United States of America. 2007;104(22):9358–63. 10.1073/pnas.0701214104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Rossmann MG, Moras D, Olsen KW. Chemical and biological evolution of nucleotide-binding protein. Nature. 1974;250(463):194–9. . [DOI] [PubMed] [Google Scholar]
- 25. Rao ST, Rossmann MG. Comparison of super-secondary structures in proteins. Journal of molecular biology. 1973;76(2):241–56. . [DOI] [PubMed] [Google Scholar]
- 26. Eventoff W, Rossmann MG. The evolution of dehydrogenases and kinases. CRC critical reviews in biochemistry. 1975;3(2):111–40. . [DOI] [PubMed] [Google Scholar]
- 27. Nath N, Mitchell JB, Caetano-Anolles G. The natural history of biocatalytic mechanisms. PLoS Comput Biol. 2014;10(5):e1003642 10.1371/journal.pcbi.1003642 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Kim KM, Caetano-Anolles G. The proteomic complexity and rise of the primordial ancestor of diversified life. BMC evolutionary biology. 2011;11:140 10.1186/1471-2148-11-140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Aravind L, Koonin EV. SAP—a putative DNA-binding motif involved in chromosomal organization. Trends in biochemical sciences. 2000;25(3):112–4. . [DOI] [PubMed] [Google Scholar]
- 30. Cheng H, Schaeffer RD, Liao Y, Kinch LN, Pei J, Shi S, et al. ECOD: an evolutionary classification of protein domains. PLoS Comput Biol. 2014;10(12):e1003926 10.1371/journal.pcbi.1003926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Fauman EB, Blumenthal RM, Cheng X. Structure and Evolution of Adomet-dependent Methyltransferases In: Publishing WS, editor. S-Adenosylmethionine-Dependent Methyltransferases: Structures and Function; 1999. p. 1–38. [Google Scholar]
- 32. Schubert HL, Blumenthal RM, Cheng X. Many paths to methyltransfer: a chronicle of convergence. Trends in biochemical sciences. 2003;28(6):329–35. 10.1016/S0968-0004(03)00090-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Efimov AV. Structural trees for protein superfamilies. Proteins. 1997;28(2):241–60. . [DOI] [PubMed] [Google Scholar]
- 34. Tran PH, Korszun ZR, Cerritelli S, Springhorn SS, Lacks SA. Crystal structure of the DpnM DNA adenine methyltransferase from the DpnII restriction system of streptococcus pneumoniae bound to S-adenosylmethionine. Structure. 1998;6(12):1563–75. . [DOI] [PubMed] [Google Scholar]
- 35. Lesk AM. NAD-binding domains of dehydrogenases. Current opinion in structural biology. 1995;5(6):775–83. . [DOI] [PubMed] [Google Scholar]
- 36. Panchenko AR, Madej T. Analysis of protein homology by assessing the (dis)similarity in protein loop regions. Proteins. 2004;57(3):539–47. 10.1002/prot.20237 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Djordjevic S, Stock AM. Crystal structure of the chemotaxis receptor methyltransferase CheR suggests a conserved structural motif for binding S-adenosylmethionine. Structure. 1997;5(4):545–58. . [DOI] [PubMed] [Google Scholar]
- 38. Bujnicki JM. Comparison of protein structures reveals monophyletic origin of the AdoMet-dependent methyltransferase family and mechanistic convergence rather than recent differentiation of N4-cytosine and N6-adenine DNA methylation. In Silico Biol. 1999;1(4):175–82. . [PubMed] [Google Scholar]
- 39. Gherardini PF, Ausiello G, Russell RB, Helmer-Citterich M. Modular architecture of nucleotide-binding pockets. Nucleic Acids Res. 2010;38(11):3809–16. 10.1093/nar/gkq090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Wierenga RK, Terpstra P, Hol WG. Prediction of the occurrence of the ADP-binding beta alpha beta-fold in proteins, using an amino acid sequence fingerprint. Journal of molecular biology. 1986;187(1):101–7. . [DOI] [PubMed] [Google Scholar]
- 41. Dym O, Eisenberg D. Sequence-structure analysis of FAD-containing proteins. Protein science: a publication of the Protein Society. 2001;10(9):1712–28. 10.1110/ps.12801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Gana R, Rao S, Huang HZ, Wu C, Vasudevan S. Structural and functional studies of S-adenosyl-L-methionine binding proteins: a ligand-centric approach. Bmc Struct Biol. 2013;13 Artn 6. 10.1186/1472-6807-13-6 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Kozbial PZ, Mushegian AR. Natural history of S-adenosylmethionine-binding proteins. Bmc Struct Biol. 2005;5 Artn 19. 10.1186/1472-6807-5-19 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Goncearenco A, Berezovsky IN. Protein function from its emergence to diversity in contemporary proteins. Phys Biol. 2015;12(4):045002 10.1088/1478-3975/12/4/045002 . [DOI] [PubMed] [Google Scholar]
- 45. Goncearenco A, Berezovsky IN. Prototypes of elementary functional loops unravel evolutionary connections between protein functions. Bioinformatics. 2010;26(18):i497–503. 10.1093/bioinformatics/btq374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Sillitoe I, Lewis TE, Cuff A, Das S, Ashford P, Dawson NL, et al. CATH: comprehensive structural and functional annotations for genome sequences. Nucleic Acids Res. 2015;43(Database issue):D376–81. 10.1093/nar/gku947 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Mitchell A, Chang HY, Daugherty L, Fraser M, Hunter S, Lopez R, et al. The InterPro protein families database: the classification resource after 15 years. Nucleic Acids Res. 2015;43(Database issue):D213–21. 10.1093/nar/gku1243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Ranea JAG, Sillero A, Thornton JM, Orengo CA. Protein superfamily evolution and the last universal common ancestor (LUCA). J Mol Evol. 2006;63(4):513–25. 10.1007/S00239-005-0289-7 . [DOI] [PubMed] [Google Scholar]
- 49. Ma BG, Chen L, Ji HF, Chen ZH, Yang FR, Wang L, et al. Characters of very ancient proteins. Biochem Bioph Res Co. 2008;366(3):607–11. 10.1016/J.Bbrc.2007.12.014 . [DOI] [PubMed] [Google Scholar]
- 50. Buehner M, Ford GC, Moras D, Olsen KW, Rossman MG. D-glyceraldehyde-3-phosphate dehydrogenase: three-dimensional structure and evolutionary significance. Proceedings of the National Academy of Sciences of the United States of America. 1973;70(11):3052–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Clermont S, Corbier C, Mely Y, Gerard D, Wonacott A, Branlant G. Determinants of coenzyme specificity in glyceraldehyde-3-phosphate dehydrogenase: role of the acidic residue in the fingerprint region of the nucleotide binding fold. Biochemistry. 1993;32(38):10178–84. . [DOI] [PubMed] [Google Scholar]
- 52. Nishiya Y, Imanaka T. Analysis of interaction between the Arthrobacter sarcosine oxidase and the coenzyme flavin adenine dinucleotide by site-directed mutagenesis. Appl Environ Microb. 1996;62(7):2405–10. . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Rockah-Shmuel L, Toth-Petroczy A, Sela A, Wurtzel O, Sorek R, Tawfik DS. Correlated occurrence and bypass of frame-shifting insertion-deletions (InDels) to give functional proteins. PLoS Genet. 2013;9(10):e1003882 10.1371/journal.pgen.1003882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Monod J. Chance and necessity; an essay on the natural philosophy of modern biology. 1st American ed. New York,: Knopf; 1971. xiv, 198 p. p.
- 55. Edison AS. Linus Pauling and the planar peptide bond. Nat Struct Biol. 2001;8(3):201–2. 10.1038/84921 . [DOI] [PubMed] [Google Scholar]
- 56. Zhou YX, Rahm M, Wu B, Zhang XL, Ren B, Dong H. H-Bonding Activation in Highly Regioselective Acetylation of Diols. J Org Chem. 2013;78(22):11618–22. 10.1021/Jo402036u . [DOI] [PubMed] [Google Scholar]
- 57. Cramer CJ, Truhlar DG. Correlation and Solvation Effects on Heterocyclic Equilibria in Aqueous-Solution. Journal of the American Chemical Society. 1993;115(19):8810–7. 10.1021/ja00072a039 . [DOI] [Google Scholar]
- 58. Hurley JH, Chen RD, Dean AM. Determinants of cofactor specificity in isocitrate dehydrogenase: Structure of an engineered NADP(+)->NAD(+) specificity-reversal mutant. Biochemistry. 1996;35(18):5670–8. 10.1021/Bi953001q . [DOI] [PubMed] [Google Scholar]
- 59. Dean AM, Golding GB. Protein engineering reveals ancient adaptive replacements in isocitrate dehydrogenase. Proceedings of the National Academy of Sciences of the United States of America. 1997;94(7):3104–9. 10.1073/Pnas.94.7.3104 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Brinkmann-Chen S, Flock T, Cahn JKB, Snow CD, Brustad EM, McIntosh JA, et al. General approach to reversing ketol-acid reductoisomerase cofactor dependence from NADPH to NADH. Proceedings of the National Academy of Sciences of the United States of America. 2013;110(27):10946–51. 10.1073/Pnas.1306073110 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Kleiger G, Eisenberg D. GXXXG and GXXXA motifs stabilize FAD and NAD(P)-binding Rossmann folds through C(alpha)-H… O hydrogen bonds and van der waals interactions. Journal of molecular biology. 2002;323(1):69–76. . [DOI] [PubMed] [Google Scholar]
- 62. Taylor WR, Thornton JM. Recognition of super-secondary structure in proteins. Journal of molecular biology. 1984;173(4):487–512. . [PubMed] [Google Scholar]
- 63. Grishin NV. Fold change in evolution of protein structures. Journal of structural biology. 2001;134(2–3):167–85. 10.1006/jsbi.2001.4335 . [DOI] [PubMed] [Google Scholar]
- 64. Kinch LN, Grishin NV. Evolution of protein structures and functions. Current opinion in structural biology. 2002;12(3):400–8. . [DOI] [PubMed] [Google Scholar]
- 65. Leipe DD, Wolf YI, Koonin EV, Aravind L. Classification and evolution of P-loop GTPases and related ATPases. Journal of molecular biology. 2002;317(1):41–72. 10.1006/jmbi.2001.5378 . [DOI] [PubMed] [Google Scholar]
- 66. Leipe DD, Koonin EV, Aravind L. Evolution and classification of P-loop kinases and related proteins. Journal of molecular biology. 2003;333(4):781–815. . [DOI] [PubMed] [Google Scholar]
- 67. Sobolevsky Y, Trifonov EN. Protein modules conserved since LUCA. J Mol Evol. 2006;63(5):622–34. 10.1007/S00239-005-0190-4 . [DOI] [PubMed] [Google Scholar]
- 68. Saraste M, Sibbald PR, Wittinghofer A. The P-loop—a common motif in ATP- and GTP-binding proteins. Trends in biochemical sciences. 1990;15(11):430–4. . [DOI] [PubMed] [Google Scholar]
- 69. Koonin EV. A common set of conserved motifs in a vast variety of putative nucleic acid-dependent ATPases including MCM proteins involved in the initiation of eukaryotic DNA replication. Nucleic Acids Res. 1993;21(11):2541–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Hanson PI, Whiteheart SW. AAA+ proteins: have engine, will work. Nat Rev Mol Cell Biol. 2005;6(7):519–29. 10.1038/nrm1684 . [DOI] [PubMed] [Google Scholar]
- 71. Huang Y, Niu B, Gao Y, Fu L, Li W. CD-HIT Suite: a web server for clustering and comparing biological sequences. Bioinformatics. 2010;26(5):680–2. 10.1093/bioinformatics/btq003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Rockah-Shmuel L, Tawfik DS. Evolutionary transitions to new DNA methyltransferases through target site expansion and shrinkage. Nucleic Acids Res. 2012;40(22):11627–37. 10.1093/nar/gks944 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Roth M, Jeltsch A. Biotin-avidin microplate assay for the quantitative analysis of enzymatic methylation of DNA by DNA methyltransferases. Biological chemistry. 2000;381(3):269–72. 10.1515/BC.2000.035 . [DOI] [PubMed] [Google Scholar]
- 74. Zhao Y, Truhlar DG. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoretical Chemistry Accounts. 2007;120(1–3):215–41. 10.1007/s00214-007-0310-x [DOI] [Google Scholar]
- 75. Rassolov VA, Ratner MA, Pople JA, Redfern PC, Curtiss LA. 6-31G Basis Set for Third-Row Atoms. Journal of Computational Chemistry. 2001;22(8). [Google Scholar]
- 76. Marenich AV, Cramer CJ, Truhlar DG. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J Phys Chem B. 2009;113(18):6378–96. 10.1021/jp810292n . [DOI] [PubMed] [Google Scholar]
- 77. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 09, Revision D.01 Gaussian, Inc, Wallingford CT: 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(XLSX)
(XLSX)
(XLSX)
(XLSX)
SAM or SAH cofactors are shown in green sticks, β2 strand of Rossmann fold in orange, and the interacting Asp/Glu with the hydroxyls’ ribose in orange sticks. (A) The catalytic domain of bacterial DNA methylase M.HhaI (PDB 1SKM); (B) human DNA methylase Dnmt3a (PDB 2QRV); (C) human DNA methylase Dnmt1 (PDB 3AV6). (D) An mRNA methylase (PDB 1RI4). (E) An N5-glutamine methylase (PDB 1NV8). (F) Catechol methylase (PDB 3BWM).
(TIF)
(A) Definition of the geometrical parameters. (B) Distribution of the bond lengths between the hydroxyl group of the ribose and the closest oxygen of the carboxylate of the Glu/Asp. (C) Distribution between the angle of the hydroxyl bond of the ribose and the carboxylate. (D) Distribution of the dihedrals of O-C1-C2-C3 and C1-C2-C3-C4. The distribution highlights a distorted envelope 2ʹ endo conformation of the ribose for most of the structures. Data for all PDB entries are provided in S4 Data.
(PNG)
(PNG)
The 2β strand is in orange, the E90 interacting with the hydroxyls of the ribose is shown as an orange stick, and Mg2+ is shown in the green sphere. The electron density map of the ribose is highlighted in blue, showing the 2E-endo conformation of the ring.
(PNG)
(PNG)
PDBs, corresponding cofactor and α angle: (A) 1HO5, ADN (adenosine) (29°); (B) 2J9L, ATP (adenosine-5ʹ-triphosphate) (27°); (C) 3S2U, UD1 (uridine-diphosphate-N-Acetylglucosamine) (19°); (D) 1K9Y, AMP (adenosine monophosphate) (127°); (E) 2ATV, GDP (guanosine-5ʹ-diphosphate) (27°); example of P-loop containing nucleoside triphosphate hydrolases); (F) 1SIW, GDP (137°); (G) 3TE5, NAI (1,4-dihydronicotinamide adenine dinucleotide) (18°); (H) 1I7L, ATP (43°); (I) 4B45 GSP (5ʹ-guanosine-diphosphate-monothiophosphate) (29°).
(PNG)
The basic Rossmann fold is altered primarily by addition of other elements. The β strands belonging to Rossmann are colored differently than the main structure: β1 in blue, β2 in green, β3 in magenta, β4 in orange, and β5 in wheat. The cofactors and the interacting E/D are in sticks. (A) PDB 3UCL binding FAD. The zoom-in view depicts the ribose’s cofactor binding site. (B) PDB 3CGD is constituted by two Rossmann subunits binding NAD and FAD. The zoom-in views depict the two subunits binding the ribose of the corresponding cofactors.
(PNG)
Cartoon structure of L-2-hydroxyisocaproate dehydrogenase (PDB 1HYH). The cofactors are shown in the green sticks; the interacting D45 (canonical) and E110 (noncanonical) are shown as sticks.
(PNG)
Highlighted are the distances between the vicinal diol and the oxygens of the carboxylic acid.
(PNG)
The backbone is shown in the cartoon, the cofactor and residue E344 in sticks, and the Mg2+ in the green sphere. The loop that follows the fourth β-strand (4β) and that carries the bidentate interacting Glu344, as well as the 4β, are shown in pink.
(PNG)
Although these Rossmann-fold enzymes bind different adenosine-containing ligands, Xie and Bourne noted that the adenosine moieties are well aligned, suggesting that these families share a common ancestry. (A) SAM-dependent methyl transferases (PDB 1ZQ9). (B) Carbonyl reductase (PDB 1CYD). (C) Overlapping of the two structures highlights the interaction of E85 (green stick) on 2β tip interacting with SAM’s ribose with the canonical motif and R39 (cyan sticks) on 2β tip interacting with the phosphate moiety of NADP.
(PNG)
Asp34 that stems from the second β-strand (2β) mediates the bidentate interaction with the ribose’s 2ʹ and 3ʹ-hydroxyls.
(PNG)
Among the structures with the canonical motif, a sample of 50 PDB structures was randomly selected. Following standard alignment, with Multiple Sequence Comparison by Log-Expectation (MUSCLE), sequences were grouped by the cofactor. The phosphate-containing cofactors depicted are as follows: ATP, adenosine-5ʹ-triphosphate; AMP, adenosine monophosphate, and APR, adenosine-5-diphosphoribose; FAD, flavin adenine dinucleotide; and NAD, nicotinamide adenine dinucleotide; the non-phosphate-containing cofactors are as follows: SAM, S-adenosylmethionine, and dc-SAM, Adenosylmethioninamine.
(PNG)
(PNG)
(TIF)
(PNG)
The interacting E/D is located on different secondary structure elements and never at the tip of the β2 strand.
(PNG)
(PNG)
(PNG)
Noted are the distances of the interacting E/D at the top of the β2 strand to the ribose hydroxyls. In all these cases, the interacting ribose belongs to the adenosine moiety of these cofactors and not to the nicotinamide (NAD, or NADH—annotated as NAI) or the free ribose (in APR).
(PNG)
(PNG)
(PNG)
(DOCX)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.