Computational Studies of Candida Antarctica Lipase B to Test its Capability as a Starting Point to Redesign New Diels-Alderases

Abstract

The design of new biocatalysts is a target that is receiving increasing attention. One of the most popular reactions in this regard is the Diels-Alder cycloaddition due to its applications in organic synthesis and the absence of efficient natural enzymes that catalyze it. In this paper, the possibilities of using the highly promiscuous Candida Antarctica lipase B (CALB) as a protein scaffold to re-design a Diels-Alderase has been explored by means of theoretical quantum mechanics/molecular mechanics (QM/MM) molecular dynamics (MD) simulations. Free energy surfaces have been computed for two reactions in the wild-type and in several mutants with hybrid AM1/MM potentials with corrections at M06-2X/MM level. The study of the counterpart reactions in solution has allowed performing comparative analysis that render interesting conclusion. Since the dienophile anchors very well in the oxyanion hole of all tested protein variants, the slight electronic changes from reactant complex to the transition state suggest that mutations should be focused in favoring the formation of reactive conformations of reactant complex that, in turn, would reduce the energy barrier.

INTRODUCTION

The use of computer-based methods, in combination with protein engineering with evolutionary strategies,¹ appears to be nowadays a promising option to design new biocatalysts. In fact, different goals, apart from increasing or generating activity, have been achieved during the past years, such as altered substrate specificity, improved thermostability, organostability, regioselectivity, enantioselectivity, or the ability to work under mild conditions of temperature and pressure.²

As stressed in recent reviews,^3,4,5 the most popular schemes for the computational assisted design of new enzymes are based on the use of existing protein scaffolds which can be classified as: i) immune-globulins, proteins generated by a mammalian immune system as a reaction to a hapten molecule, a Transition State Analogue (TSA), resembling the Transition State (TS) structure of a chemical reaction;^6,7,8,9,10 ii) a promiscuous protein showing catalytic properties for a secondary reaction that is redesigned to improve or to change this activity;^11,12,13 and iii) a protein without specific catalytic properties that is used as a scaffold to support a design from scratch, or de novo design, of a new activity.^14,15,16,17

Catalytic antibodies (CAs), obtained from the first group of proteins, while showing certain catalytic activity, their efficiency is low compared to that of natural enzymes.¹⁰ As consequence, the use of these proteins in the design process seems to decline in the last years.⁵ In the second group, enzyme promiscuity with respect to different substrates, different catalytic activities or different reaction conditions provides the raw material for the redesign of new properties. The promiscuous activity in natural enzymes can be also enhanced by rational design or directed evolution. And finally, the de novo design of new biocatalysts is based on the knowledge of the TS of the chemical reaction in gas phase and the generation of a minimalist active site to stabilize its charge distribution, known as a ‘theozyme’.¹⁸ Molecular mechanics modeling software^19,20 are used then to search stable protein scaffolds for backbone geometries that allow the catalytic aminoacids and the substrate, in its TS conformation, to be placed without making substantial steric clashes with the protein backbone. In any case, if the new designed protein presents certain level of the desired activity, these computationally design biocatalysts can be improved by the application of in vitro evolution to enhance their stability, expression or activity.^15,21

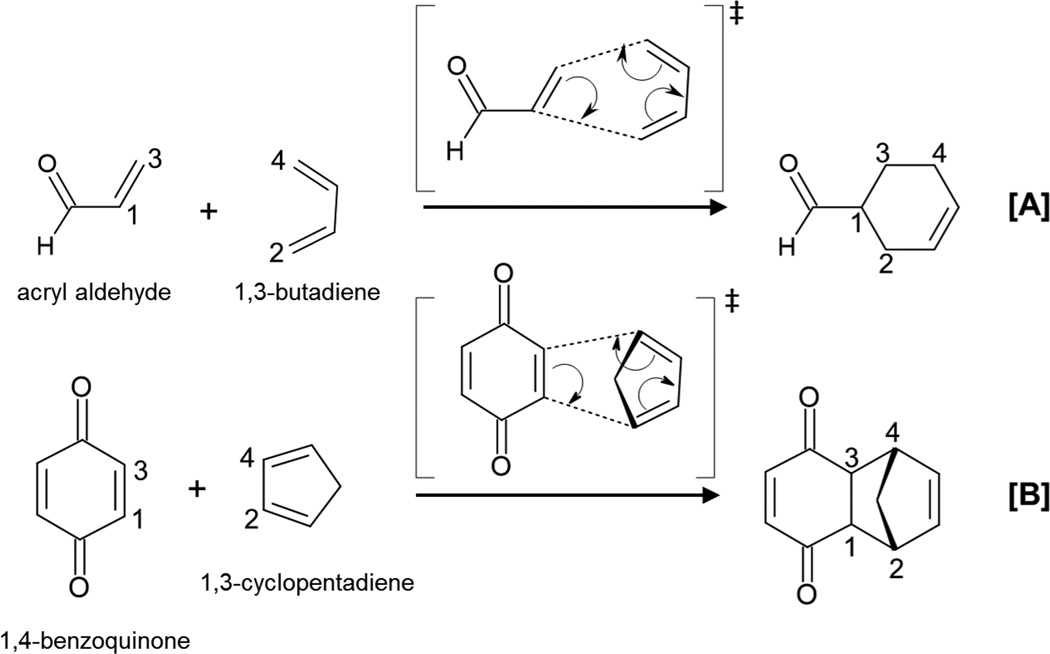
One of the chemical reactions that has received more attention in the design of new enzymes is the Diels-Alder reaction that involves the forming of two carbon-carbon bonds (see Scheme 1). This reaction is a very powerful tool in organic synthesis of cyclic compounds but the number of enzymes catalyzing this cycloaddition reaction, if any, is very low.^22,23,24

Scheme 1.

Representation of Diels-Alder cycloaddition reactions.

High regioselectivity (orto and para isomers are favored with respect to the meta), diastereoselectivity (endo conformers are favored with respect to the exo) and enantioselectivity (the reaction creates up to four new stereocenters) are probably key features that are searched when designing new enzymes catalyzing the addition of a diene with a dienophile.^4,5 The enhanced reaction rate measured in new designed Diels-Alderases has been proposed to be due to a lowering of the entropy of activation by binding the two substrate molecules, also known as “entropy trap”.²⁵ In contrast, a reduction in the activation enthalpy has been also proposed as the origin of catalysis.²⁶ An efficient stereoselective de novo enzyme for normal-electron-demand Diels-Alder reaction was designed by positioning hydrogen bond acceptor and donor species interacting with the diene and dienophile, respectively.¹⁶ This idea was based on frontier molecular orbital (FMO) theory that proposed that narrowing the gap between the highest occupied molecular orbital (HOMO) of the diene and the lowest unoccupied molecular orbital (LUMO) of the dienophile would increase the rate of the reaction.¹⁷

An almost perfect shape complementarity between protein cavity and the substrates in the TS conformation,^27,28 together with hydrogen bond interactions that could be responsible of the control of the relative geometries of the bound substrates and the electronic distribution in the dienophile were suggested as the origin of diels-alderase activity of a designed CA.²⁷ Later, a theoretical study on the germline catalytic antibody and its matured form, based on hybrid QM/MM MD simulations, suggested a complex indirect effect through coupled movements of the backbone of the protein and the substrate in the germline, after mutation.²⁹ These results stress the importance of backbone flexibility in docking studies and in the design of new enzymes. In fact, there are examples where the activity of de novo designed enzymes has been improved by considering backbone flexibility of the protein in the models.^30,31

The use of promiscuous enzymes, and in particular hydrolases, as template to design active site models for versatile reaction targets including Diels-Alder was originally envisioned by Houk and co-workers.³² Ser105Ala CALB was originally proposed by Berglund and co-workers to increase its reaction specificity for Michael additions,³³ who also stressed, as feature of both the natural hydrolytic reaction and the carbon-carbon bond formation, the activation of a carbonyl functionality of the substrate by an oxyanion hole of the enzyme.^34,35,36

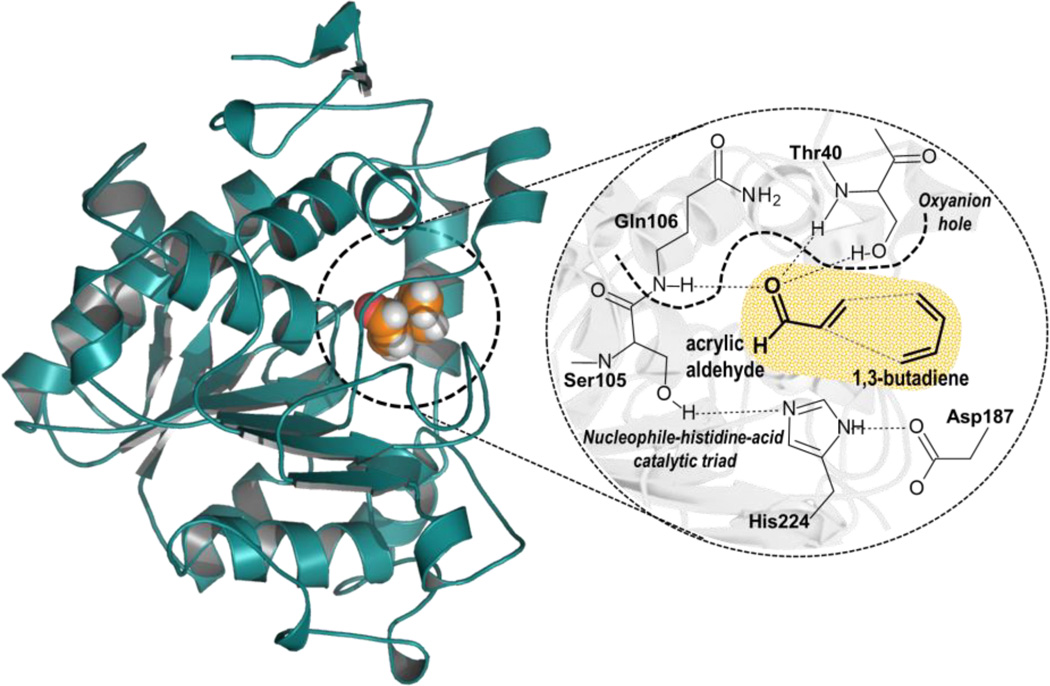
Brinck and co-workers have suggested that an additional mutation, Ile189Ala, to the single Ser105Ala mutation is required for CALB to reach a reasonable performance as Diels-Alderase.³⁷ In their computational approach,^37,38,39,40 a combination of molecular docking, MD simulations and quantum chemical calculations was employed. Comparison of free energy barriers of several variants of CALB, computed as the sum of the free energy difference from the diene-dienophile-protein complex to conformations named as “near attack-conformations” (NAC)⁴¹ plus the energy required to go from the NAC to the TS, computed with cluster models of the active site, were used to predict the most adequate mutations. Recently, a complete picture of the molecular mechanism of CALB as a serine hydrolase has been carried out in our laboratory by means of MD simulations with hybrid QM/MM potentials.⁴² Information derived from the study of the primary reaction allowed determining the key residues involved in the reaction mechanism. In particular, it was confirmed the presence of an oxyanion hole created by the Gln106 and Thr40 residues of the active site, capable of not only anchoring reacting species but stabilizing a negatively charge developed during the reaction. We showed how Ser105 is participating in forming a covalent bond with the substrate and stabilizing the intermediate states. This result suggested that this residue could be replaced by a smaller one that allow larger substrates to access the active site and, simultaneously, avoiding possible competitive reactions. More recently, we have demonstrated the capabilities of CALB as epoxidase.⁴³

In the present paper, we are studying the two Diels-Alder cycloaddition reactions shown in Scheme 1 in solution, in the wild-type CALB and in several CALB mutants. Our target is to test whether CALB can be used as a starting protein scaffold to redesign a Diels-Alderase. In our computational strategy, QM/MM MD simulations are carried out to get free energy surfaces of the chemical step in going from the enzyme-diene-dienophile complex, reactant complex (RC), to the TS. Detailed analysis of the process will provide a deep insight into the behavior of the wild-type and redesigned enzymes. As commented in a previous review, the knowledge of the differences between RC and TS could be used as a guide the design bio-catalysts.⁴⁴

COMPUTATIONAL METHODS

System Setup

The starting coordinates of the wild-type protein were obtained from the CALB PDB entry 1TCA,⁴⁵ which consists of a monomer. The inhibitor employed during crystallization, N-acetyl-D-glucosamine, was replaced by 1,2,3,6-tetrahydro benzaldehyde (the product of the Diels-Alder reaction between acrylic aldehyde and 1,3-butadiene). To assign accurate protonation states to all titratable residues at pH = 7, the pK_a values for these amino acids have been calculated using the empirical PROPKA3 program of Jensen et al.^46,47. Since the total charge of the system was neutral, no counterions were required. After adding the hydrogen atoms to the structure, series of optimization algorithms were applied. In particular, after a series of steepest descent conjugated gradient minimization steps (until a gradient tolerance of 5 kJ·mol⁻¹·Å⁻¹), L-BFGS-B was carried out until completely optimized positions of hydrogen atoms were reached (gradient tolerance of 0.1 kJ·mol⁻¹·Å⁻¹). To avoid a denaturation of the protein structure, all the heavy atoms of the protein and the substrate were restrained by means of a Cartesian harmonic umbrella with a force constant of 1000 kJ·mol⁻¹·Å⁻². Afterward, the system was fully relaxed with the peptide backbone restrained with a lower constant of 100 kJ·mol⁻¹·Å⁻². Finally, the optimized protein was soaked in a box of water molecules (100×80×80 ų). Any water with an oxygen atom lying within 2.8 Å from a heavy atom of the protein was deleted. The remaining water molecules were then relaxed using optimization algorithms. The full system was formed by the protein (4625 atoms), the substrate (18 or 23 atoms, reaction depending) and 20006 solvation water molecules (60018 atoms).

In order to carry out theoretical studies for such large molecular systems hybrid QM/MM potentials were used, where a small part of the system, the substrate molecules, is described by QM while the protein and solvent water molecules are represented by classical force fields. The QM region is shown as the orange-shaded region in Scheme 2.

Scheme 2.

Active Site of Wild Type CALB. Acrylic aldehyde and 1,3-butadiene (in orange) are treated quantum mechanically in all calculations.

During the QM/MM energy optimizations the atoms of the QM region were treated by the AM1 semiempirical Hamiltonian,⁴⁸ and by the M06-2X,⁴⁹ hybrid density functional theory (DFT) methods. AM1 has been shown to predict the wrong endo/exo preference for the Diels-Alder reaction between cyclopropene and butadiene by comparison with high level ab initio calculations.⁵⁰ Nevertheless, the activation energies obtained with the AM1 method was comparable with the value obtained with quadratic configuration interaction with single and double excitations, and triple excitations included via perturbation (QCISD(T)),⁵⁰ and consistent with the experimentally observed rate constant for this reaction.⁵¹ Consequently, while AM1 Hamiltonian appears to be an acceptable method to perform the QM/MM MD simulations, some of the analysis, as the one based on frontier orbitals will be done just with the DFT method. The standard 6-31+G(d,p) basis set was used in the DFT calculations. The protein and water molecules are described using the OPLS-AA⁵² and TIP3P⁵³ force fields, respectively, as implemented in the fDYNAMO library.⁵⁴ Due to the large amount of degrees of freedom, any residue 20 Å apart from any of the atoms of the substrate was kept frozen in the remaining calculations. Cutoffs for the non-bonding interactions are applied using a force switching scheme, within a range radius from 14.5 to 16 Å. After thermalization, QM/MM MD simulations of the system in the NVT ensemble (with the QM region treated at AM1 level) were run during 500 ps at a temperature of 300 K using the Langevin-Verlet algorithm using a time step of 1 fs. According to the time-dependent evolution of the RMSD of those atoms belonging to the protein backbone, the system was considered equilibrated after 250 ps of simulation. In order to study the reaction catalyzed by the CALB mutants, the corresponding residues were replaced on the initial PBD structure and the procedure to set up the system was equivalent to the one carried out to prepare the wild-type CALB complexed with each substrate. The molecular system employed to perform the simulations for the reaction in aqueous solution was prepared by placing the corresponding product of the Diels-Alder reactions in the same pre-equilibrated box of water molecules used for the reaction in the enzymes (100×80×80 ų).

In order to obtain the free energy surfaces, we have generated mono dimensional (1D) and bidimensional (2D) surfaces in terms of potential of mean force (PMF). In the former, the distinguished reaction coordinate was the symmetric combination of distances defining the two C-C forming bonds (d(C1-C2) + d(C3-C4) in Scheme 1), whereas in the 2D PMF, the two mentioned C-C forming bond distances are independently scanned. The procedure to generate the PMFs requires series of MD simulations in which the distinguished reaction coordinates are constrained around particular values with the umbrella sampling procedure.⁵⁵ The values of the variables sampled during the simulations are then pieced together to construct a distribution function using the weighted histogram analysis method (WHAM).⁵⁶ Umbrella force constant of 5000 kJ mol⁻¹·Å⁻², were applied to the distinguished reaction coordinates to allow a perfect overlapping among the windows. 5 ps of relaxation and 10 ps of production in the 2D-PMFs generation (10 and 20 in the 1D-PMFs, respectively), with a time step of 1 fs using the velocity Verlet algorithm⁵⁷ to update the velocities, were run in each window. The PMFs were performed at 300 K, using the NVT ensemble. Structures from previously obtained QM/MM PESs were used as starting points of each window.

In order to reduce the errors associated with the quantum level of theory employed in our QM/MM MD simulations, following the work of Truhlar et al.^58,59,60 a spline under tension^61,62 is used to interpolate this correction term at any value of the reaction coordinates ξ₁ and ξ₂ selected to generate the free energy surfaces. In this way, we obtain a continuous function in a new energy function to obtain corrected PMFs: ^63,64,65

$$E=E_{\mathit{\text{AM}}1/\mathit{\text{MM}}}+S\lfloor \mathrm{\Delta }{E}_{\mathit{\text{LL}}}^{\mathit{\text{HL}}}({\xi }_1,{\xi }_2)\rfloor$$ (1)

where S denotes a two-dimensional spline function, and its argument is a correction term evaluated from the single-point energy difference between a high-level (HL) and a low-level (LL) calculation of the QM subsystem. The AM1 semiempirical Hamiltonian was used as LL method, whereas the M06-2X/6-31+G(d,p) method was selected for the HL energy calculations. In this case, S is adjusted to a grid of 27 × 27 points obtained as HL single energy calculation corrections on geometries optimized at LL. The HL calculations were carried out using the Gaussian09 program.⁶⁶ Obviously, in the case of the corrections on the 1D PMFs, equation (1) appears as a function of just one variable and, in such cases, S was adjusted to a grid of 109 points.

Alchemical Free Energy Perturbation (FEP) methods were used to compute the substrate−protein interaction free energies for the dienophile as described in ref. 67 and 68. Thus, series of QM/MM MD simulations have been carried out in the cavity of the protein and in a box of solvent water molecules, introducing two parameters in the electrostatic and van der Waals QM/MM interaction terms, which were smoothly changed from 1 to 0.

$$E_{\mathit{\text{QM}}/\mathit{\text{MM}}}(\lambda ,\gamma )=\langle \mathrm{\Psi }|{\widehat{H}}_0|\mathrm{\Psi }\rangle +\lambda (\sum \langle \mathrm{\Psi }|\frac{q_{\mathit{\text{MM}}}}{r_{e,\mathit{\text{MM}}}}|\mathrm{\Psi }\rangle +\sum \sum \frac{Z_{\mathit{\text{QM}}}{q}_{\mathit{\text{MM}}}}{r_{\mathit{\text{QM}},\mathit{\text{MM}}}})+\gamma E_{\mathit{\text{QM}}/\mathit{\text{MM}}}^{\mathit{\text{vdW}}}+E_{\mathit{\text{MM}}}$$ (2)

The calculation of the free energy difference of two consecutive windows of the two stages, annihilation of charges and van der Waals parameters, is performed by means of FEP methods, and then the total free energy change is evaluated as the sum of all the windows covering the full transformation from the initial to the final state. In the present study 100 windows have been used to evaluate the electrostatic interaction term, from λ=0 (no electrostatic interaction) to λ=1 (full interaction), which turns into a δλ of 0.01, and the same amount of windows have been used to calculate the van der Waals interaction term, from γ=0 (no electrostatic interaction) to γ=1 (full interaction). In each window a total of 50 ps of QM/MM MD have been performed using the NVT ensemble at the reference temperature of 300 K.

Finally, Kinetic isotope effects (KIE) have been computed for the O¹⁸ isotopic substitutions of the carbonyl oxygen atom of the dienophile, from the TS and the RC localized at DFT/MM level of theory. From the definition of the free energy of a state, G_i, as a function of the molecular potential energy E_i, the total partition function Q_i, and the zero point vibrational energy, ZPE_i,

$$G_i=E_i-RT\text{ln}{Q}_i+{\mathit{\text{ZPE}}}_i$$ (3)

Then, from Eq. 3, and using the Transition State Theory (TST), the ratio between the rate constants corresponding to the light atom “L” and the heavier isotope “H” can be computed as:

$$\mathit{\text{KIE}}=\frac{{\left(\frac{Q_{\mathit{\text{TS}}}}{Q_R}\right)}_L}{{\left(\frac{Q_{\mathit{\text{TS}}}}{Q_R}\right)}_H}{e}^{-\frac{1}{\mathit{\text{RT}}}(\mathrm{\Delta }{\mathit{\text{ZPE}}}_L-\mathrm{\Delta }{\mathit{\text{ZPE}}}_H)}$$ (4)

In Eq. 4, the total partition function, Q, was computed as the product of the translational, rotational, and vibrational partition functions for the isotopologs in RC and TS in the active site of the open and closed loop conformation monomers. The Born-Oppenheimer, rigid-rotor and harmonic oscillator approximations were considered to independently compute the different contributions. Keeping in mind that RC and TS are in a condensed media (the active site of a protein), contribution of translation and rotation to KIEs are negligible. Nevertheless, the full 3N × 3N Hessians have been subjected to a projection procedure to eliminate translational and rotational components, which give rise to small non-zero frequencies, as previously described.⁶⁹ Thus, it has been assumed that the 3N - 6 vibrational degrees of freedom are separable from the 6 translational and rotational degrees of freedom of the substrate. All combinations of 10 structures of RC and the same amount of TS structures were used to obtain averaged values of the secondary O¹⁸ KIEs.

RESULTS AND DISCUSSION

Free energy surfaces: Reaction A

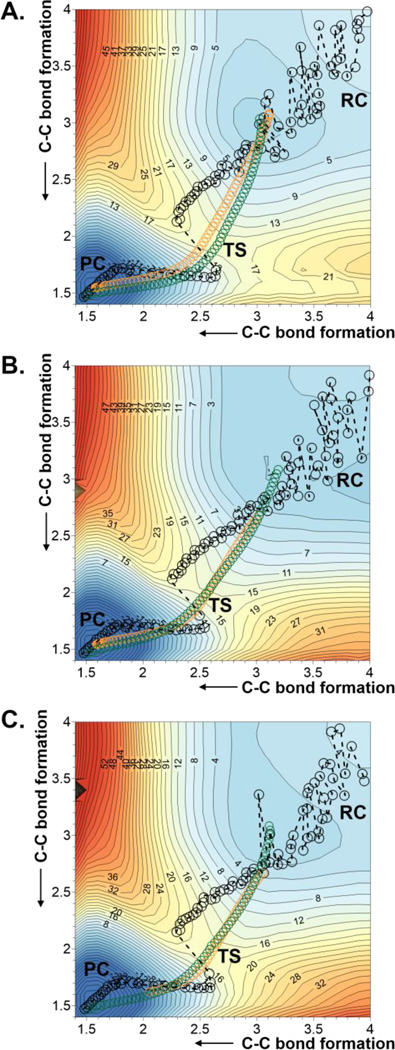
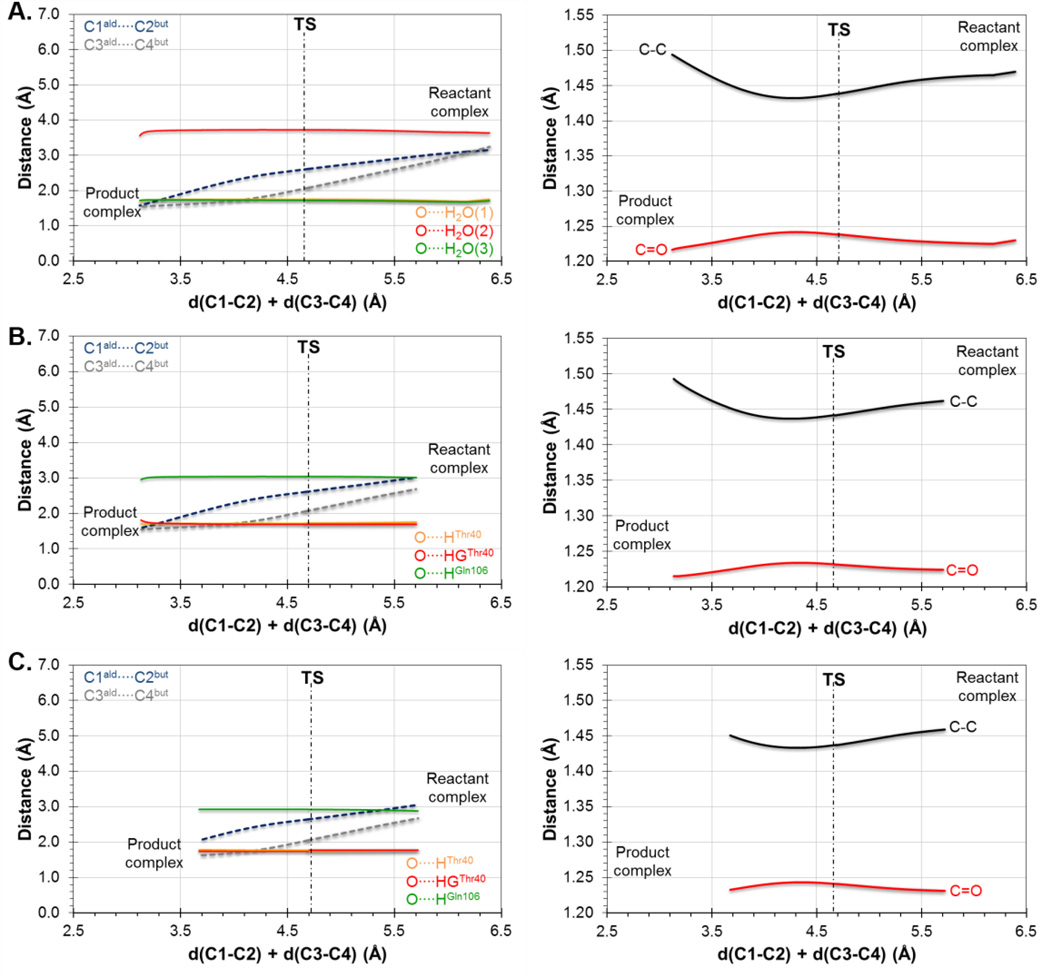
The first step of our study was the Diels-Alder cycloaddition reaction between acrylic aldehyde and 1,3-butadiene (reaction A on Scheme 1), given the relatively small size of both, diene and dienophile. The reaction was carried out in aqueous solution and in the active site of the wild-type and the Ser105Ala mutant of CALB. In order to obtain the free energy surfaces, we first check whether a 1D-PMF, using the symmetric combination of distances defining the two C-C forming bonds as distinguished reaction coordinate, was adequate to describe the process. 1D-PMFs for the reaction in the three environments were generated (see Figure S1 of Supporting Information) and compared with the corresponding 2D-PMF (see Figure 1A, 1B and 1C for the reaction in aqueous solution, wild-type CALB and Ser105Ala CALB, respectively), where both C-C forming bond distances are independently and unequivocally controlled. The projection of the values of the two C-C forming bond distances generated along the 1D-PMFs on the 2D-PMFs (displayed as black circles on free energy surfaces of Figure 1) show how the less computationally demanding 1D-PMF renders a reasonable description of the reaction. Thus, both, 1D- and 2D-PMFs, describe the reaction as a concerted but asynchronous mechanism. Nevertheless, the reaction paths obtained from the 1D PMF are significantly different from the minimum energy paths on the 2D-PMF or the intrinsic reaction coordinate (IRC)⁷⁰ paths, computed at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level from the TS structures optimized at this high level of theory, which almost overlap each other (displayed as green and orange circles on Figure 1, respectively). Despite not being detected in the 1D-PMF profiles (see Figure S1 of Supporting Information), Figure 1 shows the odd description of the reaction around the TS quadratic region when using the 1D-PMF in any of the three environments.

Figure 1.

2D-PMF obtained at AM1/MM level with spline corrections at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level for the Diels Alder cycloaddition reaction between acrylic aldehyde and 1,3-butadiene in (A) aqueous solution; (B) wild-type CALB; and (C) Ser105Ala CALB. Averaged values of the two coordinates obtained along the 1D-PMF are displayed as black circles, green circles correspond to the minimum free energy path, and orange circles to IRC paths computed at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level. Values of isoenergetic curves are in kcal·mol⁻¹ and distances in Å.

Probably associated with this inaccurate description of the TS, the free energy barriers deduced from 1D-PMFs are dramatically different from those derived from the 2D-PMFs (see Table 1). According to the former, the wild-type and the mutated proteins provide an environment that would not reduce the free energy barrier, by comparison with the reaction in aqueous solution. The water molecules would already have a “catalytic” effect, suggesting the significance of the interactions between the dienophile and the water molecules of the solvent. Kong and Evanseck,⁷¹ carried out DFT calculations on this very same acrolein-butadiene Diels-Alder reaction in solution with polarizable continuum models (PCM) and observed a decrease of the activation Gibbs energy of up to 3.4 kcal·mol⁻¹ when including two explicit water molecules hydrogen bond with the carbonyl group of acrolein (in its most stable endo, s-cis conformation). The influence of hydrogen bonding was nevertheless equivalent for the rest of the conformations.⁷¹ More recently, Linder and Brinck⁷² obtained a reduction on the DFT activation enthalpy of 2.4 kcal·mol⁻¹ when including a tiourea molecule to mimic the oxyanion hole of hydrolitic enzymes in their DFT calculations in solution with PCM models. Nevertheless, as pointed out by Brinck and co-workers, Svedendahl and Berglund did not observed any Diels-Alderase activity in CALB wild-type or Ser105Ala mutant.³⁷ In fact, this experimental observation would be in agreement with our predictions derived from our 1D-PMFs which are only qualitatively in agreement with our more accurate 2D-PMFs that provide the same free energy barriers for the reaction in aqueous solution and in the wild-type CALB, 15.5 kcal·mol⁻¹, and just slighter higher barrier in the Ser105Ala CALB mutant; 17.5 kcal·mol⁻¹.

Table 1.

Free energy barriers (ΔG^‡ given in kcal·mol⁻¹) for reaction A and B (see Scheme 1) in water solvent and in active site of different variants of CALB obtained by 1D- and 2D-PMFs computed at AM1/MM level and corrected at M06-2X/6-31+G(d,p) level.

Reaction:		Aqueous solution		CALB mutations:
			Wild-type	Ser105Ala	Ser105Ala; Ile189Ala	Ser105Ala; Ile189Ala: Ile285Ala
A	1D-PMF	23.7	27.6	26.4	-	-
	2D-PMF	15.5	15.5	17.5	-	-
B	1D-PMF	15.7	15.5	11.5	12.9	13.0
	2D-PMF	15.5	11.5	6.5	9.5	9.5

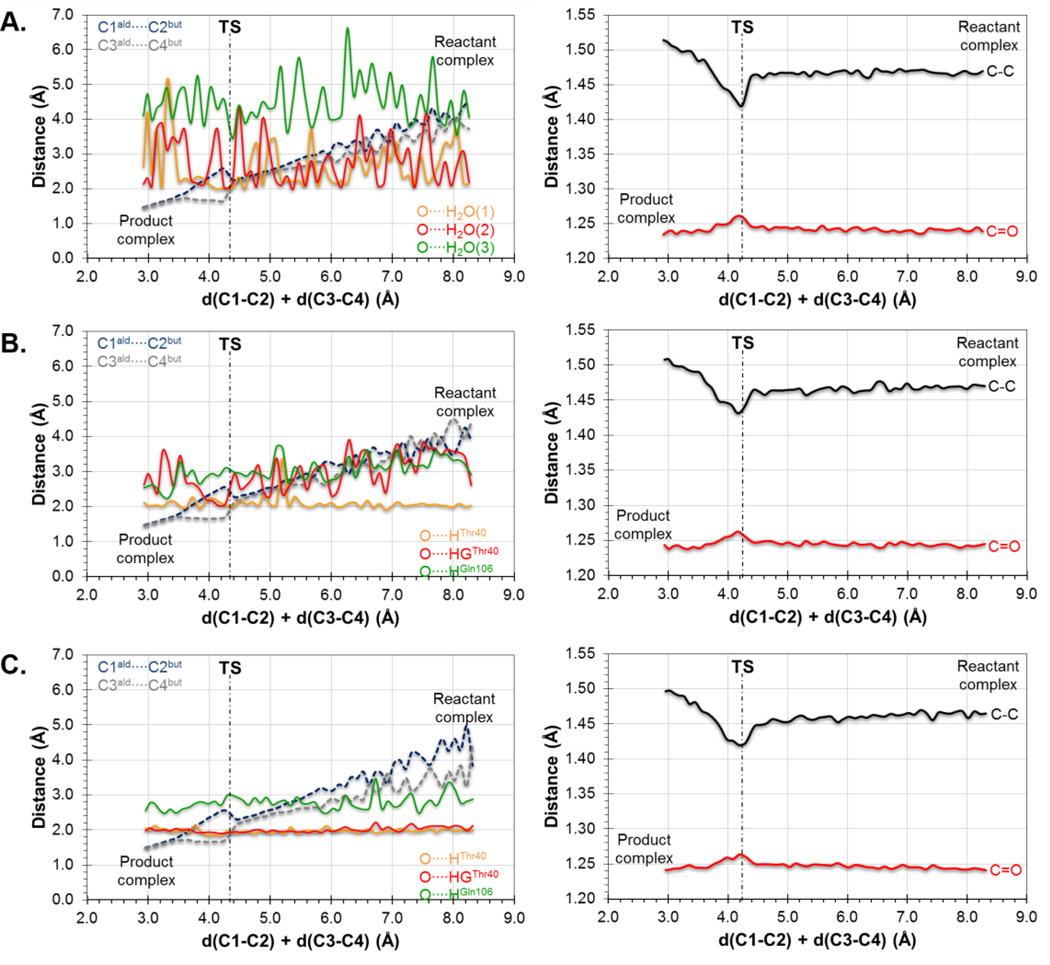
Further insights can be obtained from the analysis of the evolution of key distances along the reaction. In particular, the evolution of the distances defining the two C-C forming bonds and those defining the interaction between the carbonyl oxygen of the dienophile and the oxyanion hole are displayed in Figure 2 and Figure 3, for the results derived from the 1D-PMFs and from the IRCs traced down from M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P TSs located from guess structures selected from the quadratic region of the 2D-PMFs, respectively. Figure 2A shows the results of the reaction in aqueous solution, Figure 2B the reaction in the wild-type CALB and Figure 2C the reaction in Ser105Ala CALB, it is interesting to observe how the two reacting species are progressively approaching to each other from the RC to the TS but, once the system is close to the quadratic region of the TS, the distance defining one of the two C-C forming bonds (C3-C4) is reduced while the other C-C distance (C1-C2) increases (see dashed lines in Figure 2). This relative movement of the diene and dienophile close to the TS, which can be defined as a pivotal movement on the shortest C-C forming bond, appears in the three environments. After the TS dividing surface is crossed, the two distances are reduced until reaching the values of the standard C-C single bond in the products state. The evolution of the distances between the oxygen atom of the carbonyl group of the aldehyde and the two residues defining the oxyanion hole in the mutated protein are stronger than in the wild-type (see Figure 2B and 2C). This effect is more dramatic in the case of the interaction with the hydroxyl group of Thr40, where a strong hydrogen bond seems to be established all along the reaction in the Ser105Ala CALB. This interaction is only well defined in the TS in the case of the wild-type CALB. To a lesser extent, the interaction with Gln106 appears to be also better oriented in the mutant than in the wild-type. In contrast, the distances between the oxygen atom of this carbonyl group and the water molecules, when the reaction takes place in solution, oscillate much more than in the protein environments suggesting a larger entropic penalty (see Figure 2A). The pattern of interactions established between the environment and the carbonyl oxygen on the TS is associated with variations in intra-molecular distances on the dienophile, such as an elongation of the C=O double bond and a shortening of the C-C single bond (see right panels of Figure 2). This could be tested experimentally since measurable normal O¹⁸ 2° KIE values of 1.045 ± 0.009 and 1.042 ± 0.005 on this oxygen atom has been computed in the wild-type CALB and Ser105Ala CALB, which is in agreement with the obtained geometrical description of the process.

Figure 2.

Evolution of inter-molecular (left column) and intra-molecular (right column) key distances along the 1D-PMF of the Diels-Alder cycloaddition reaction between acrylic aldehyde and 1,3-butadiene in (A) aqueous solution, (B) wild-type CALB; and (C) Ser105Ala CALB. Results at AM1/MM level.

Figure 3.

Evolution of inter-molecular (left column) and intra-molecular (right column) key distances along the IRC path from the TSs of the Diels-Alder cycloaddition reaction between acrylic aldehyde and 1,3-butadiene in (A) aqueous solution, (B) wild-type CALB; and (C) Ser105Ala CALB. Results obtained at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level.

When the analysis is done on the basis of the IRC path traced from the TSs located from the 2D-PMFs (see Figure 3) a different picture is obtained, although containing some common features. Thus, the reaction is also described by a non-completely symmetric evolution of the inter-atomic distances of the two C-C forming bonds, although none of them increases around the TS. As observed, this behavior is observed in aqueous solution (Figure 3A) in the wild-type CALB (Figure 3B) and in the Ser105Ala mutant (Figure 3C). It can be also confirmed the interactions between the carbonyl oxygen atom of the dienophile and the residues of the oxyanion hole in both wild-type (Figure 3B) and mutant (Figure 3C), but also with the water molecules when the reaction is studied in solution (Figure 3A). Finally, although more modest, the same behavior noticed on the intra-molecular distances of the dienophile is revealed on right panels of Figure 3. Obviously, some oscillations were observed in Figure 2 since the data were generated from MD simulations, while a continuous behavior is observed in the curves on Figure 3 that are derived from IRCs. These results, that can be considered as more accurate than those presented in Figure 2, would suggest that water molecules of the aqueous environment would be already well oriented in the RC to stabilize the dienophile and small changes would be occurring from RC to TS.

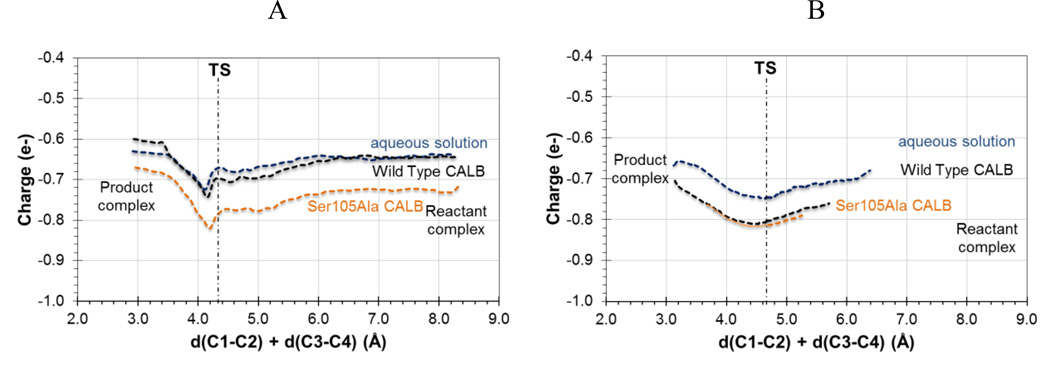
The information derived from Figure 2 and 3 can be complemented by the analysis of charges evolution along the reaction. Figure 4 shows the evolution of charge on the carbonyl oxygen of the dienophile computed at M06-2X/6-31+G(d,p)/MM along the reaction path in aqueous solution, wild-type and Ser105Ala CALB. The curves depicted in Figure 4, either derived from the 1D-PMF (Figure 4A) or from the IRCs (Figure 4B), show how the negative charge on this atom is increasing from RC to the TS, where a maximum is reached. It is evident how the protein environments polarizes this carbonyl group which can contribute to increase the favorable interaction between the residues forming the oxyanion hole and the substrate, as discussed from the geometrical analysis on Figure 2 and 3. The main difference between the results coming from the 1D-PMF and the IRCs is that while the former describes a more significant effect in the case of the Ser105Ala mutant, IRCs suggest that both proteins would equally behave in this regard.

Figure 4.

Evolution of ChelpG charge (in a.u.) on carbonyl oxygen atom of acrylic aldehyde computed at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level along the 1D-PMFs (A) and IRCs (B) of the Diels-Alder reaction path in aqueous solution (in blue), wild-type CALB (in black) and Ser105Ala CALB (in orange) with 1,3-butadiene.

The evolution of the charges on the carbonyl oxygen atom of the dienophile and the interactions established in the oxyanion hole along the reaction profile can be better understood if analyzed in combination with intra-molecular distances such as the distances of the carbonyl bond and the single C-C bond of the acrylic aldehyde (see panels on right column of Figure 2 and 3). Thus, it seems that a charge transfer to the single C-C bond and to the carbonyl oxygen makes in turn the former to be slightly shorter and an elongation of the later. This effect is observed in aqueous solution and in the two proteins, wild-type CALB and Ser105Ala CALB (see Figure 2 and 3). Obviously, the previously discussed intermolecular interactions contribute to this charge transfer that polarizes the carbonyl bond.

A detailed analysis of the TSs demonstrates that all of them appear to be asynchronous and at almost the same values of the reaction coordinate. As observed in Figure 5 and Table 2, the TSs can be considered as very similar not only if the sum of the two C-C forming bond distances are compared (result that was predicted from the maximum of the 1D PMFs on Figure S1) but when focusing into the two distances separately from each other. Cartesian coordinates of the QM atoms of the three TSs located at M06-2X/6-31+G(d,p)//MM level are listed in Table S1 of Supporting Information. Asynchronous TSs for the acrolein-butadiene Diels-Alder reaction were already reported in early ab initio Hartree-Fock studies by Houk and co-workers in gas phase,⁷³ and in the two commented DFT studies based on PCM models.^71,72 Apart from many other theoretical studies, the asynchronicity of the TSs for Diels-Alder reactions involving asymmetrical dienophiles, also experimentally detected by Singleton, Houk and co-workers,⁷⁴ have been rationalized in terms of frontier molecular orbital (FMO) theory.^75,76,77,78 This point will be discussed below.

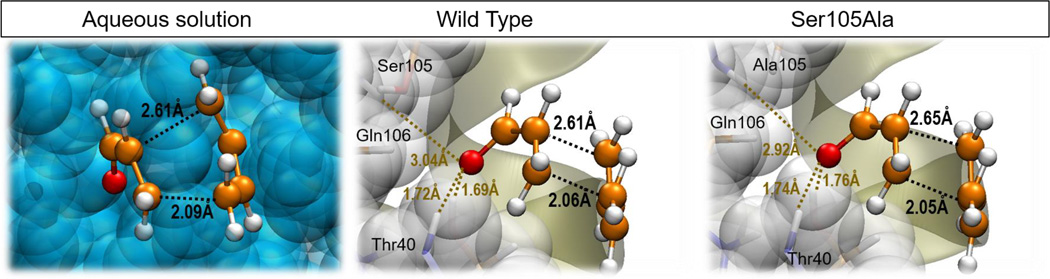
Figure 5.

Optimized TSs structures for the Diels Alder cycloaddition reaction between 1,3-butadiene and acrylic aldehyde in aqueous solution, in the wild-type CALB and in the Ser105Ala CALB. All structures obtained at M06-2X/6-31+G(d,p)/MM level.

Table 2.

Key interatomic distances (in Å) for stationary point structures of Diels Alder reaction A and B (see Scheme 1) in aqueous solution and in the active site of tested variants of CALB obtained at M06-2X/6-31+G(d,p)/MM level of theory.

Reaction A
distances	aqueous solution		distances	Wild-type		Ser105Ala
	RC	TS		RC	TS	RC	TS
C1-C2	3.15	2.61	C1-C2	3.41	2.61	3.55	2.65
C3-C4	3.24	2.09	C3-C4	3.21	2.06	3.28	2.05
Wat1	1.71	1.72	O-HGThr40	1.71	1.69	1.77	1.76
Wat2	1.75	1.75	O-HThr40	1.79	1.72	1.79	1.74
Wat3	3.67	3.76	O-HGln106	2.96	3.04	2.80	2.92

Reaction B
distances	aqueous solution		distances	Wild-type		Ser105Ala		Ser105Ala; Ile189Ala		Ser105Ala; Ile189Ala: Ile285Ala
	RC	TS		RC	TS	RC	TS	RC	TS	RC	TS
C1-C2	2.95	2.28	C1-C2	3.03	2.36	2.93	2.37	2.94	2.37	2.96	2.37
C3-C4	3.01	2.16	C3-C4	3.00	2.20	2.84	2.15	2.88	2.15	2.91	2.16
Wat1	1.79	1.83	O-HGThr40	1.71	1.74	1.78	1.87	1.78	1.84	1.77	1.83
Wat2	2.00	1.99	O-HThr40	1.69	1.68	1.76	1.78	1.75	1.76	1.74	1.76
Wat3	3.30	3.31	O-HGln106	2.73	2.66	2.55	2.58	2.55	2.55	2.57	2.54

When the analysis of the TS structures is done by comparison with the corresponding RC, a good correlation is obtained between the magnitude of the gap in the reaction coordinate and the energy barriers. Thus, it is observed how the difference of the C-C forming bonds distances between the TS and the RC in aqueous solution (0.54 and 1.15 Å) are slightly shorter than in the wild-type CALB (0.80 and 1.15 Å) but significantly shorter than in the Ser105Ala CALB (0.90 and 1.23 Å). The mutant would stabilize a RC where the diene would be not as well docked to the dienophile as occurring in the wild-type, or even in solution. This means, aqueous environment would stabilize more reactive RC conformations (closer to TS) than wild-type or Ser105Ala CALB, what would be reflected in the energy barriers.

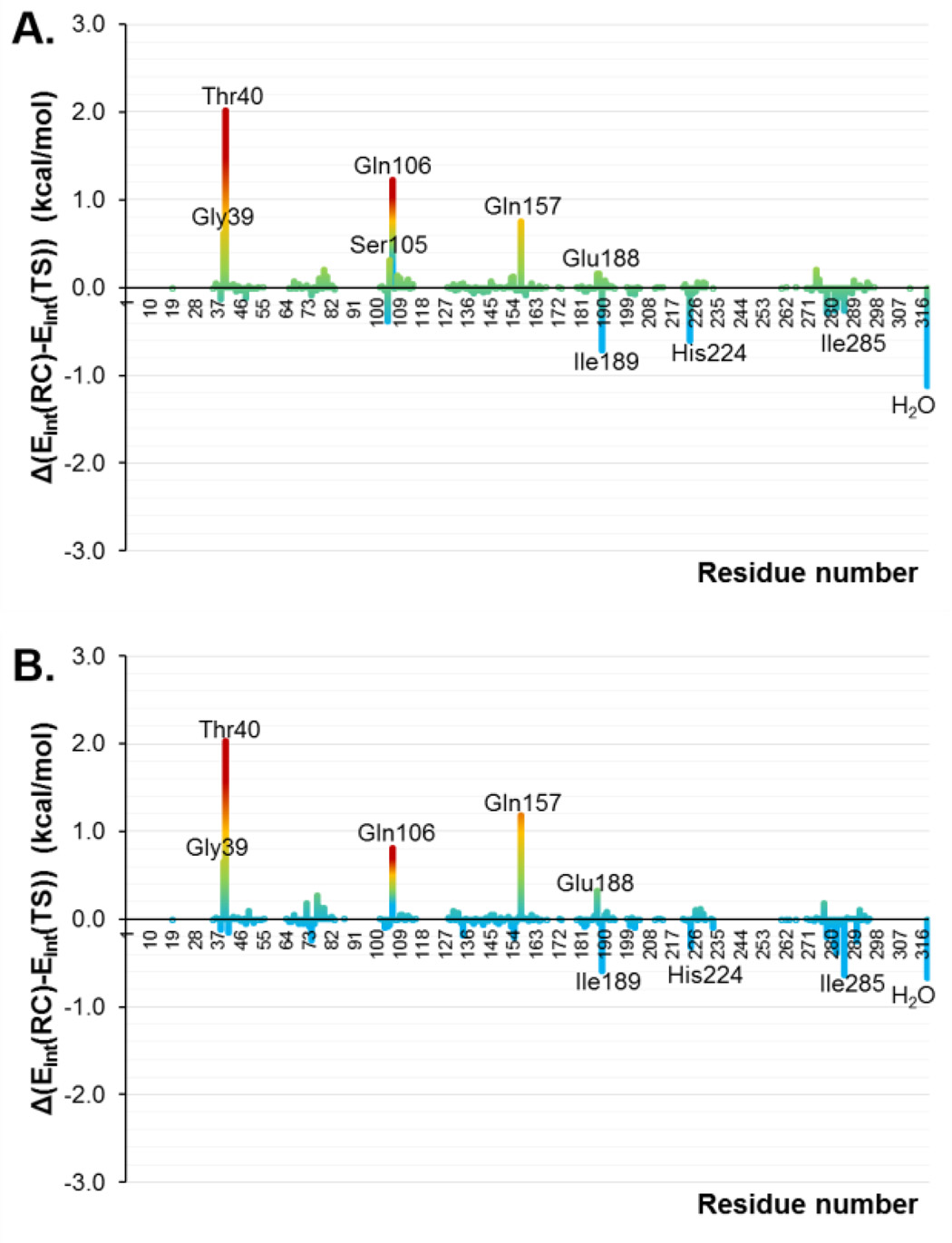
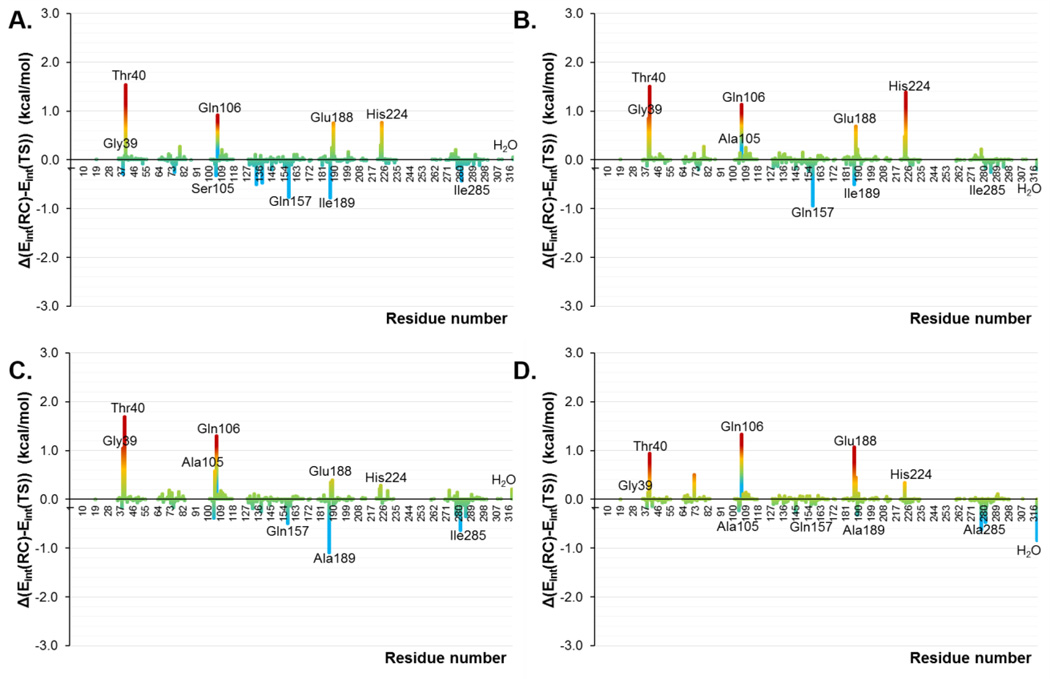
The interaction energies between the substrate and the protein in the TSs and in the RCs, computed by residue, are shown in Figure 6A and 6B as the difference between both states in the wild-type and in the mutant, respectively. Thus, positive values represent stronger interactions in the TS than in RC and, consequently, favorable interactions to reduce the free energy barrier. A list of the most important interaction energies in RC and TS is reported in Table S2 of the Supporting Information. As can be observed, the residues belonging to the oxyanion hole (Thr40 and Gln106) are presenting favorable interactions in both systems. In addition, Gly39, Gln157 and Glu188 also present higher interactions in the TSs than in the RCs. Interestingly, the residue that is mutated by an alanine in position 105, shows positive values in the wild-type and a negligible contribution in the mutant. Nevertheless, we must remember that this mutation was principally done to avoid the enzyme to catalyze its primary reaction. On the other hand, Ile189, His224, Ile285 and the water molecules show unfavorable interactions in both TSs with respect to the RCs. All in all, slight differences are observed between the two enzymes and, in any case, the differences between TSs and RCs interactions in both systems are not dramatic (the largest difference is ca. 2 kcal·mol⁻¹). This result is in agreement with the similar barriers deduced from the 2D PMFs on Figure 1.

Figure 6.

Contributions of individual amino acid residues (ordered along the × axis) computed as average of total QM-MM interaction energy difference between RC and TS in the Diels-Alder reaction between 1,3-butadiene and acrylic aldehyde in wild-type CALB (A) and in the Ser105Ala CALB (B). Averaged values derived from AM1/MM MD simulations. H₂O represents the contribution of bulk water molecules.

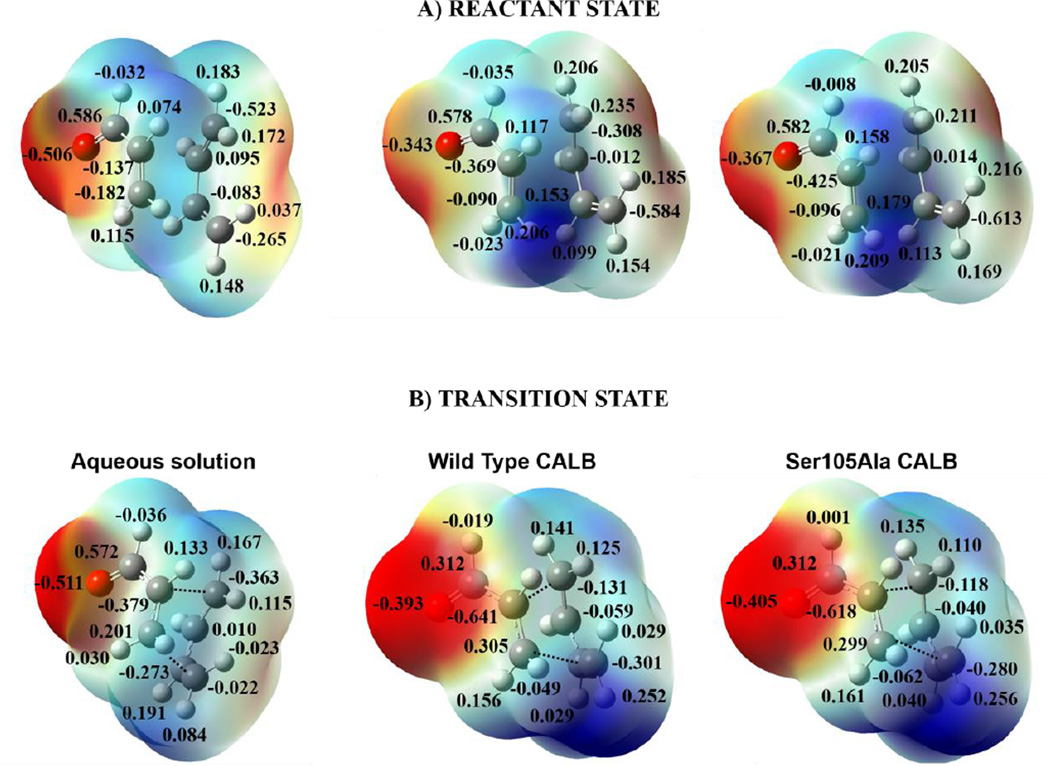
At this point, we can conclude that the interactions between the protein and the substrate can be established not only due to its capability for going inside the protein cavity, but also due to the favorable electronic density distribution of the substrate that allows the interaction with the oxyanion hole. This can be supported by the map of electrostatic potential, MEP, of reactants state and TS that are displayed on Figure 7A and 7B, respectively. Nevertheless, when the reaction takes place in solution, water molecules of the solvent are already oriented in RC, as demonstrated in Figure 3A, and since the MEP of the acrylic aldehyde of TS does not greatly differ from the one obtained in the RC (see Figure 7), the similar barriers computed in solution and in the cavity of the proteins are justified.

Figure 7.

Map of electrostatic potential (MEP) of the RC (A) and of the TS (B), for the Diels-Alder reaction between 1,3-butadiene and acrylic aldehyde in aqueous solution, in the wild-type CALB and in the Ser105Ala CALB. Results obtained at M06-2X/6-31G+(d,p) level with ESP point charges of the environment.

Once the chemical step has been studied, the binding free energies of acrylic aldehyde from aqueous solution to the cavity of the two proteins have been computed. The binding free energy has been estimated by means of alchemical methods, as described in the Computational Methods section, and the results are reported in Table 3. According to the results, the binding of acrylic aldehyde in the two cavities can be considered as a favorable process, more evident in the case of the Ser105Ala mutant. Accordingly, the results also show how the binding affinities are not necessary related with the height of the barrier of the chemical reaction, as expected. Thus, the system that shows the highest affinity (highest binding free energy) of the dienophile by the cavity of the protein (Ser105Ala) is the one that rendered the highest free energy barrier. According to previous analysis, it appears that once a certain affinity of the substrate by the enzyme is reached, the catalytic efficiency would mostly depend on the capability of stabilizing a more reactive conformation of the dienophile-diene-protein RC.

Table 3.

Binding Free Energy (in kcal·mol⁻¹) of acrylic aldehyde from aqueous solution to the oxyanion hole of wild-type and Ser105Als CALB obtained at AM1/MM level.

	wild-type CALB	Ser105Ala CALB
ΔGelec	−4.99	−7.89
ΔGVdW	−6.81	−7.91
ΔGbinding	−3.58	−7.58

Free Energy Surfaces: Reaction B

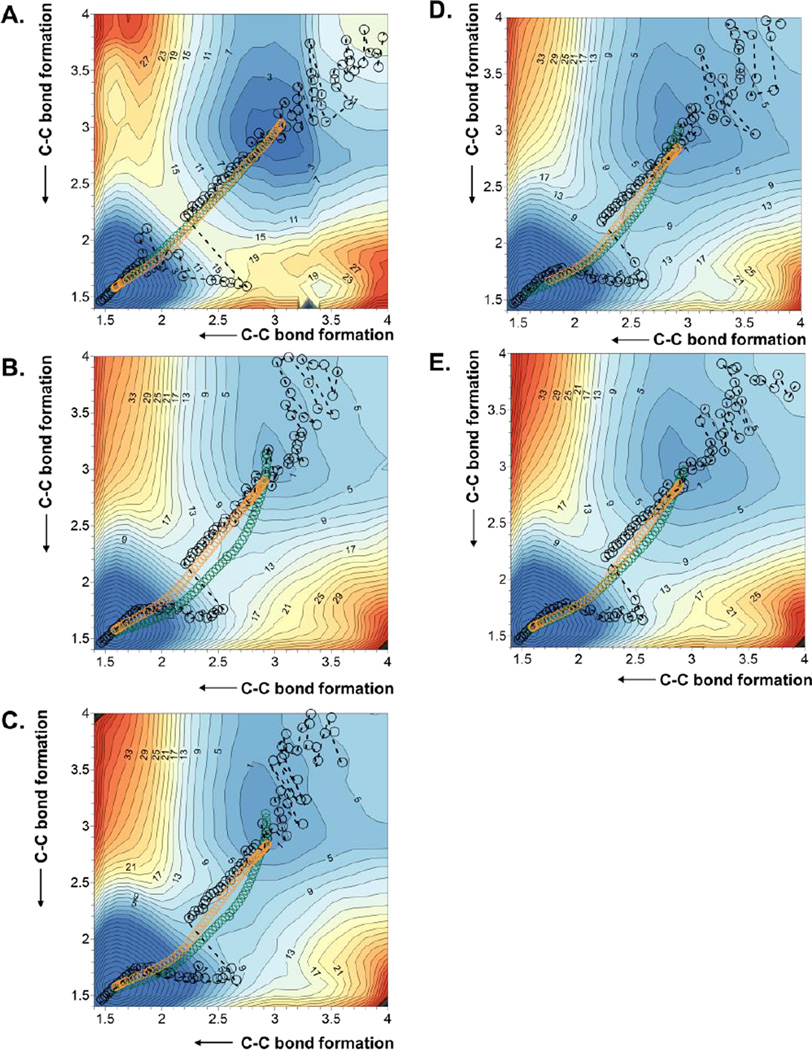
In order to confirm whether the results obtained for reaction A can be extrapolated to other Diels-Alder reactions, the effect of the size of the diene and dienophile in the efficiency of CALB as Diels-Alderase has been tested by exploring the reaction between 1,4-benzoquinone and cyclopentadiene (reaction B in Scheme 1) in the wild-type enzyme and in several mutants. The resulting 1D-PMFs are reported in Figure S2 of Supporting Information, whereas the 2D PMFs are depicted in Figure 8 and the derived free energy barriers listed in Table 1. The bad agreement between the free energy barriers obtained with 1D- and 2D-PMFs when studying reaction A is reproduced in this reaction, which dictates the use of the later to analyze the Diels-Alder reaction. As Figure 8 suggests, this reaction is also described as a concerted but slightly asynchronous process in all tested environments: aqueous solution (Figure 8A), wild-type CALB (Figure 8B), Ser105Ala CALB (Figure 8C), Ser105Ala/Ile189Ala CALB (Figure 8D) and Ser105Ala/Ile189Ala/Ile285Ala CALB (Figure 8E). Again, as occurred in Figure 1, the minimum free energy paths overlap pretty well with the IRCs, which will allow the parallel study between averaged properties, derived from the AM1/MM MD simulations, and the optimizations of single molecules at M06-2X/6-31+G(d,p)/MM level. The reaction paths derived from the 1D-PMFs manifest the same limitations as in reaction A. The located TSs, depicted in Figure 9, are all characterized by significantly different distances of the two C-C forming bonds (see Table 2). Cartesian coordinates of the QM atoms of the TSs, located at M06-2X/6-31+G(d,p)/MM are listed in Table S3 of Supporting Information. A low dependence of the TS asynchronous character with the environment or the particular reaction is shown. Nevertheless, in contrast to the results obtained for reaction A, the free energy barriers of any of the enzymes are lower than the counterpart reaction in solution. As listed in Table 1, the obtained values of free energy barriers are 11.5, 6.5, 9.5 and 9.5 kcal·mol⁻¹ in wild-type, Ser105Ala, Ser105Ala/Ile189Ala and Ser105Ala/Ile189Ala/Ile285Ala, respectively, whereas in solution it is 15.5 kcal·mol⁻¹.

Figure 8.

2D PMF obtained at AM1/MM level with spline corrections at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level for the Diels Alder cycloadition reaction between 1,4-benzoquinone and cyclopentadiene in aqueous solution (A), in the wild-type CALB (B), in the Ser105Ala CALB (C), in the Ser105Ala/Ile189Ala CALB (D) and in the Ser105Ala/Ile189Ala/Ile285Ala CALB (E). Averaged values of the two coordinates obtained along the 1D PMF are displayed as black circles, green circles corresponds to the minimum free energy path, and orange circles corresponds to IRC paths at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level. Values of isoenergetic curves are in kcal·mol⁻¹ and distances in Å

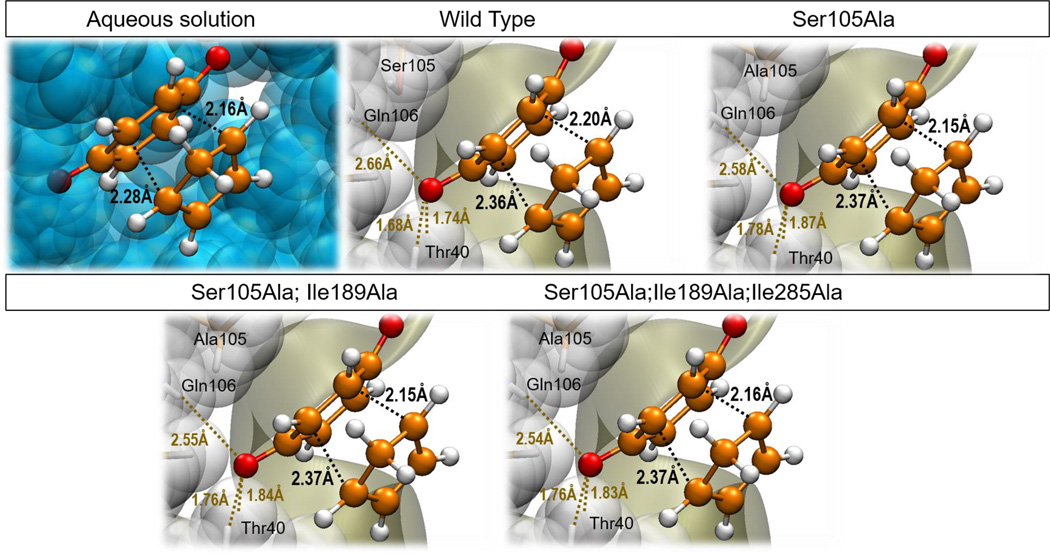
Figure 9.

Optimized TSs, at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level, for the Diels Alder cycloaddition reaction between 1,4-benzoquinone and cyclopentadiene in aqueous solution, in the wild-type CALB, in the Ser105Ala CALB, in the Ser105Ala/Ile189Ala CALB, and in the Ser105Ala/Ile189Ala/Ile285Ala CALB.

According to the obtained free energy barriers, and considering the TST at 300 K, the corresponding catalytic efficiency of these enzymes, defined as k_cat/k_uncat, is 8.4·10², 3.8·10⁶, 2.4·10⁴ and 2.4·10⁴, for the wild-type and the three mutants, respectively. These values are significantly lower than the best value predicted by Brinck and co-workers, 3.1·10⁹, corresponding to the same reaction between benzoquinone and cyclopentadiene in the Ser105Ala/Ile189Ala double mutant.³⁷ Nevertheless, as Brinck and co-workers mentioned in their paper, their values of rate enhancements could be overestimated since the description of the NAC is generous and the contribution to the barrier coming from the formation of NAC could be considered as lower limits.³⁷ On the contrary, our predicted activity is higher than the recently de novo designed enzyme by Hilvert and co-workers for the enantio- and diastereoselective Diels–Alder reaction between 4-carboxybenzyl-trans-1,3-butadiene-1-carbamate and N,N-dimethylacrylamide: 4.63·10².³¹ A note of caution has to be introduce at this point since the catalytic proficiency was defined as [k_cat/(K_diene·K_dienophile)]/k_uncat in the work of Hilvert and co-workers, giving rise to 8.4·10⁷ M⁻¹.

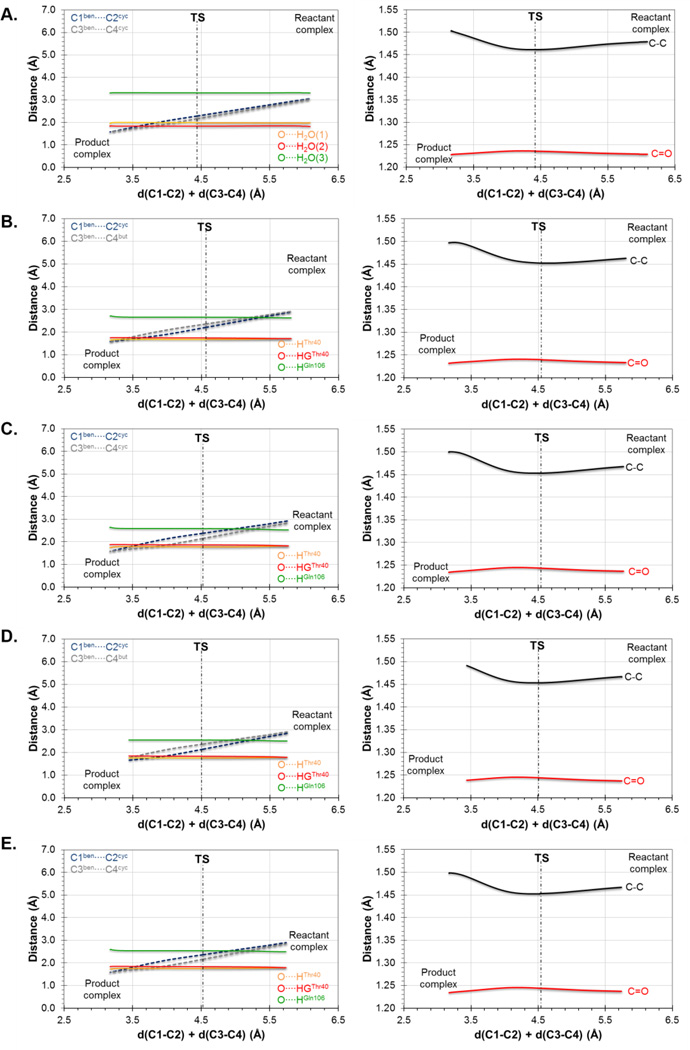
In order to find the origin the catalytic activities of the tested variants of CALB for this Diels-Alder reaction, and following the same protocol as the one carried out for reaction A, key inter- and intra-molecular distances have been monitored along the minimum energy reaction path. The results derived from the IRCs computed at M06-2X/6-31+G(d,p)//OPLS/TIP3P level are displayed in Figure 10: aqueous solution (Figure 10A), wild-type CALB (Figure 10B), Ser105Ala CALB (Figure 10C), Ser105Ala/Ile189Ala CALB (Figure 10D) and Ser105Ala/Ile189Ala/Ile285Ala CALB (Figure 10E). Results deduced from the 1D-PMF are shown in Figure S3 of Supporting Information. All free energy surfaces describe the same picture as the one previously obtained for reaction A: the dienophile, in this case the 1,4-benzoquinone, is properly anchored to the oxyanion hole of the enzyme basically through hydrogen bond interactions with one of the carbonyl oxygen. These interactions are slightly favored in the TS due to the small increase in the charge on this atom from RC to the TS observed in all systems (see Figure S4 of Supporting Information), as occurred in reaction A (see Figure 4). As commented for reaction A, measurable normal O¹⁸ 2° KIE values of 1.025 ± 0.009 on this oxygen atom has been computed in the wild-type CALB, the double and the triple mutant, whereas 1.024 ± 0.005 has been obtained for the Ser105Ala single mutant. These results also suggest the possibility of proving this prediction experimentally.

Figure 10.

Evolution of inter-molecular (left column) and intramolecular (right column) key distances along the IRC path, obtained at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level, from the TSs of the Diels-Alder cycloaddition reaction between 1,4-benzoquinone and cyclopentadiene in aqueous solution (A), in the wild-type CALB (B), in the Ser105Ala CALB (C), in the Ser105Ala/Ile189Ala CALB (D) and in the Ser105Ala/Ile189Ala/Ile285Ala CALB (E).

Nevertheless, the changes in the electronic distribution of the substrate from RC to the TS are not very dramatic, neither, as the similar MEPs in RC and in the TS make clear (see Figure S5 of Supporting Information). These small transformations of the substrate from RC to TS can be also extrapolated to the enzyme. Thus, taking advantage of the fact that there are no covalent bonds between the QM and MM regions of our systems, the contribution of the MM term into the barrier can be identified as the energy required by the protein (or aqueous solution) to be transformed from RC to TS. In all cases, this value was lower, on average, than 1.0 kcal·mol⁻¹ (1.4 kcal·mol⁻¹ in the case of the reaction in aqueous solution). Thus, in order to quantify at some extent this increase in the interactions with the carbonyl group of the dienophile and, in general, with both species of the substrate, the contributions of individual amino acid residues have been computed as average of total QM-MM interaction energy difference between RC and TS. The results are displayed in Figure 11 for the study in the wild-type CALB (Figure 11A), in the Ser105Ala CALB (Figure 11B), in the Ser105Ala/Ile189Ala CALB (Figure 11C) and in the Ser105Ala/Ile189Ala/Ile285Ala CALB (Figure 11D). A list of the interaction energies in RC and TS is reported in Table S4 of the Supporting Information. First of all, and as obtained for reaction A, the residues belonging to the oxyanion hole (Thr40 and Gln106) are presenting stronger interactions in the TSs than in RCs of all systems, being the double mutant the one presenting the largest values. In addition, Gly39, Glu188 and His224 also present higher interactions in the TSs than in the RCs in all systems, despite Gly39 is almost negligible in the wild-type. We must keep in mind that His224 was unfavorable for both systems in reaction A. The new Ala105 now shows positive values in the single and double mutant while it is unfavorable in the case of the triple mutant and for the original Ser105 in the wild-type. On the other hand, no improvement is obtained after mutation of Ile189 and Ile285 that present negative values for all mutants on these two residues. Also, Gln157 shows an unfavorable contribution in all mutants on this reaction while we must keep in mind that it was favorable in the two proteins of reaction A. Finally, it is interesting to note how interactions with the water molecules are favorable only for the double and triple mutants. All in all, and as concluded for the reaction A, slightly differences are observed between the enzymes (which is in agreement with the similar barriers deduced from the 2D PMFs on Figure 8) and, in any case, the difference in the substrate-protein interactions between RC and TS is never larger than 2 kcal·mol⁻¹, for any residue of any systems. In addition, it can be stress that residues that can be favorable for one specific Diels-Alder reaction, it may be less appropriate for others.

Figure 11.

Contributions of individual amino acid residues (ordered along the × axis) computed as average of total QM-MM interaction energy difference between RC and TS in the Diels-Alder reaction between 1,4-benzoquinone and cyclopentadiene in the wild-type CALB (A), in the Ser105Ala CALB (B), in the Ser105Ala/Ile189Ala CALB (C) and in the Ser105Ala/Ile189Ala/Ile285Ala CALB (D). Averaged values derived from AM1/MM MD simulations.

At this point, what could be established as the main source of the computed catalytic effect of the wild-type CALB and the tested mutants would be the capability of these enzymes in stabilizing RC structures closer to the TS than in the case of the reaction in solution. This is achieved by the interactions with the enzyme and it can be monitored if compared the change in the C-C forming bond distances in the two states. Indeed, these changes are 0.67 and 0.85 Å in aqueous solution, while in the enzymes they range between 0.56 and 0.59 Å for one of the C-C bond distances, and between 0.69 and 0.75 Å for the other one, system dependent (see Table 2).

Frontier Molecular Orbitals

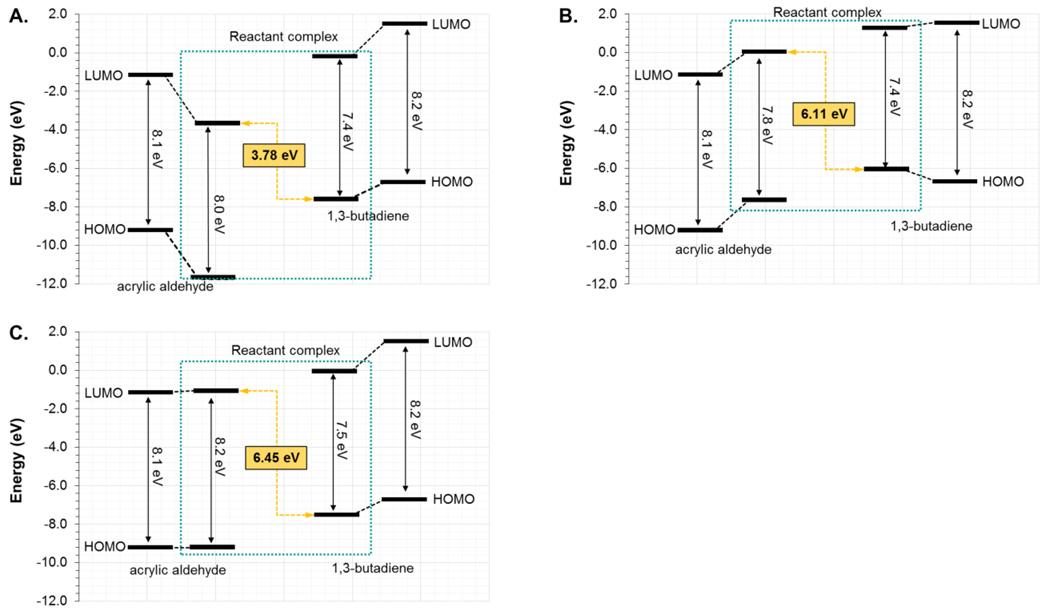
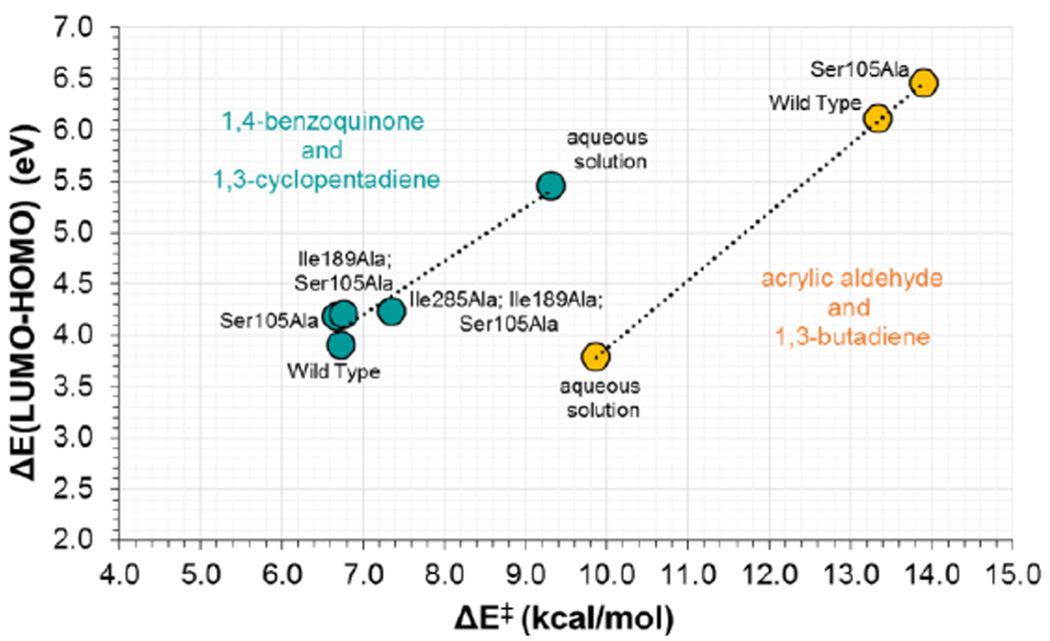
As commented in the Introduction section, another way of explaining the Diels-Alderase activity of a catalyst can be based on the analysis of the frontier orbitals of the dienophile and the diene. The calculation of the HOMO and LUMO of acrylic aldehyde and 1,4-benzoquinone in the RC of the reaction with 1,3-butadiene and cyclopentadiene, respectively, has been performed at M06-2X/6-31G+(d,p)/MM level in the different environments using the CHelpG charges distribution of the protein and water molecules. The results are depicted in Figure 12. For the reaction between acrylic aldehyde and 1,3-butadiene in aqueous solution (Figure 12A), in the wild-type CALB (Figure 12B) and in the Ser105Ala CALB (Figure 12C), it is shown how the energy gap between the LUMO of the dienophile and the HOMO of the diene in the two protein environments (6.1 and 6.5 eV for the wild-type and mutant, respectively) are significantly higher than the value obtained in solution (3.4 eV). The correlation with the energy barriers is in very good agreement, keeping in mind that the free energy barrier in solution (and the potential energy barrier from the single molecule calculations used to generate the FMO) is lower than the energy barriers in the two proteins. It must be kept in mind that this gap can be strongly dependent on the distance between diene and dienophile in the localized complex of reactants state, which has been already analyzed and the correlation with the energetics detected. The same trend is obtained when analyzing the reaction between 1,4-benzoquinone and cyclopentadiene (see Figure S6 of Supporting Information). In this case, the reaction in the different proteins shows smaller HOMO-LUMO gap, in agreement with lower activation energy barriers. A graphical demonstration of this correlation between activation energies and the HOMO-LUMO energy gap in the RC for both Diels-Alder reactions is presented in Figure 13. Thus, the use of frontier orbital analysis to explain the diels-alderase catalytic activity of wild-type or mutants of CALB seems to be valid, at some extent.

Figure 12.

Energy diagram of the HOMO and LUMO of the reactants and RC for the acrylic aldehyde and 1,3-butadiene reaction in aqueous solution (A), in the wild-type CALB (B) and in the Ser105Ala CALB (C). Results obtained at M06-2X/6-31G+(d,p) level using CHelpG charges distribution of the protein and water molecules in the calculations.

Figure 13.

Correlation between HOMO-LUMO energy gap in RC state and activation energies (ΔE^‡, in kcal·mol⁻¹, contains the QM and the QM-MM terms) for the Diels Alder reactions between acrylic aldehyde and 1,3-butadiene reaction (orange points) and between 1,4-benzoquinone and cyclopentadiene (green points), computed from localized structures in different media at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level.

CONCLUSIONS

The possibilities of using the highly promiscuous CALB as a starting point to design a new Diels-Alderase has been studied by means of MD simulations with hybrid AM1/MM potentials with spline corrections at M06-2X/6-31+G(d,p)//OPLS-AA/TIP3P level. Our methodology allows obtaining the free energy profile from the RC to the TS in a realistic complete and fully flexible model of the protein. Two different Diels-Alder cycloaddition reactions, between acrylic aldehyde and 1,3-butadiene and between 1,4-benzoquinone and cyclopentadiene, have been employed as benchmark for the reaction in aqueous solution, in the wild-type enzyme and in several mutants, including the well documented Ser105Ala. A deep insight into the evolution of the geometric and electronic properties of the substrate, as well as the interactions established with the residues of the protein and the FMOs of diene and dienophile has been performed. The results have allowed drawing a complete description of the process and to rationalize the effects of the protein and, in particular, the specific mutations, on enhancing the rate constant. It must be pointed out that this work has been solely focused on the study of the Diels-Alder reaction for the formation of the most stable endo, s-cis conformation. As mentioned in the Introduction, other required features of a potential Diels-Alderase, such as improving its regioselectivity, diastereoselectivity or enantioselectivity, are sometimes even more important.

The first conclusion that can be deduced is the limitations of mono-dimensional 1D-PMF to study processes like the Diels-Alder reaction that involve the simultaneous reducing (or increasing) of two inter-atomic distances (C-C in our case). It appears that a symmetric combination of the two distances can not be used to generate robust free energy profiles. Thus the generation of two-dimensional 2D-PMF is mandatory to get a proper picture of the process.

The results of both reactions describe the studied Diels-Alder reactions as concerted but asynchronous processes with TSs characterized by slightly different distances of the two C-C forming bonds. From the detailed analysis of the process from RC to TS, it has been identified a charge transfer to the oxygen atom of the carbonyl group, present in the two employed dienophiles, through the single C-C bond. Our results confirm how the negative charge on the carbonyl oxygen atom of the dienophile increases when approaching to the TS, where a maximum is reached, what is associated with an elongation of the carbonyl bond. Normal O¹⁸ 2° KIE values on this oxygen atom are obtained for both reactions in the wild-type CALB and in the mutants, in agreement with the obtained geometrical and electronic description of the process and opening the possibility of being corroborated by experimental measurements. The oxyanion hole of the active site is crucial to interact with this oxygen atom and to stabilize the TS. Nevertheless, since the MEP of the substrate does not significantly change from RC to TS, and the carbonyl group is not dramatically polarized, water molecules are also properly oriented to interact with this carbonyl oxygen atom in the initial state. The consequence is a low effect in the relative stabilization of the TS, observed in the proteins and when the reaction is performed in solution. In fact, a lower free energy barrier is observed for the reaction in solution than in the cavity of wild-type or Ser105Ala mutant for the first reaction. Nevertheless, when slightly larger dienophile is employed, the results show that, while the description of the chemical reaction is equivalent to the one deduced from first reaction, it appears that the protein now stabilizes the dinophile-diene RCs in conformations where the diene is better docked to the dienophile: i.e. shorter distances of the two C-C forming bonds. A diminution of these distances in the RC obviously means pushing this structure towards the TS and then a reduction of the energy barriers. The obtained trend on the free energy barriers is also correlated with a proper diminution in the energy gap between the HOMO of the diene and the LUMO of the dienophile, thus describing this effect as not only geometrical but electrostatic in nature.

As a summary, we herein demonstrate that the employed computational methodology is very appropriate to study chemical reactions catalyzed by protein scaffolds and, as it is the case in the present study, can be used to rationalize the effect of mutations on the catalytic activity of the protein. According to the detailed analysis of the Diels-Alder reactions carried out in the present study, the capabilities of the CALB protein to be used as a Diels-Alderase do not directly depend in reducing the energy barrier from RC to TS. No significant electronic and geometrical changes on the substrate take place in this chemical step. The negligible transformations from RC to TS are also extrapolated to the protein, whose contribution to the energy barrier has been estimated as being lower than 1 kcal·mol⁻¹. Instead, efforts must be invested in properly align the two fragments, diene and dienophile, for the bimolecular reaction to take place. Further mutations should be designed focused in improving the formation and stability of the diene-dienophile-protein complex, with special attention to the particular case since residues that can be favorable for one specific Diels-Alder reaction, it may be less appropriate for others.