Integrating molecular dynamics simulations with chemical probing experiments using SHAPE-FIT

Abstract

Integration and calibration of molecular dynamics simulations with experimental data remains a challenging endeavor. We have developed a novel method to integrate chemical probing experiments with molecular simulations of RNA molecules by using a native structure-based model. Selective 2’-hydroxyl acylation by primer extension (SHAPE) characterizes the mobility of each residue in the RNA. Our method, SHAPE-FIT, automatically optimizes the potential parameters of the forcefield according to measured reactivities from SHAPE. The optimized parameter set allows simulations of dynamics highly consistent with SHAPE probing experiments. Such atomistic simulations, thoroughly grounded in experiment, can open a new window on RNA structure-function relations.

1 Introduction

Molecular dynamics simulations enable studies of biomolecules in atomic resolution. Over the past few decades, the predictive capability of this method has improved significantly due to the advances in hardware technologies [1] and novel computational methods [2-4][5]. These advances invite the development of more accurate forcefields for biomolecular simulations. However, the development of highly accurate force field potential functions remains a challenge of molecular simulation. Many studies have been successful in producing dynamics consistent with NMR spectroscopy studies[6-8][9]. In addition to NMR studies the development of nucleotide resolution chemical probing assays in the RNA community presents a new source of experimental data that can be used to benchmark and improve molecular simulation force fields. [10][11]

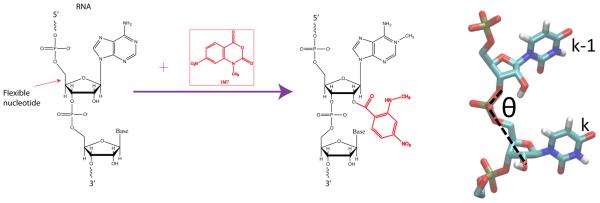
From a biochemical perspective, RNA has the advantage over proteins in being amenable to reverse transcription readout assays, yielding information at nucleotide resolution. These assays were used extensively in ribosome studies to determine the ribosome secondary structure, binding sites and conformational changes[12-14]. The development of in-line probing in the riboswitch community by Breaker and co-workers enabled readout of backbone mobility [10]. Selective 2’-hydroxyl acylation by primer extension (SHAPE) was developed by Weeks and co-workers [11]. This method is a rapid assay capable of backbone mobility readout at nucleotide resolution for a variety of environmental conditions (e.g., magnesium titration). While NMR spectroscopy studies produce superb data sets monitoring RNA mobility, [15][16-25] SHAPE allows one to obtain mobility information in experiments over the course of a few days and also for very large RNA systems (Fig.1). This technique has opened the door to studies using a wide variety of environmental conditions, mutation sequences, and system sizes [26]. This technique is a powerful, widespread method in the RNA community that has produced important experimental datasets for comparison with molecular simulations. Weeks and co-workers have used SHAPE probing to generate three-dimensional structural models of the tRNA based on a three-bead model. Here, we investigated dynamics and calibrate dynamics with chemical probing reactivity measurements [27].

Figure 1.

Detecting nucleotide mobility experimentally and computationally. (a) Schematic for the acylation reaction and the 2'-hydroxyl group of an RNA nucleotide with the SHAPE reagent (NMIA). The acylation reaction is more probable when backbone is mobile and base is unpaired (b) Mobility of the 2'-hydroxyl group is characterized in molecular dynamics simulations using the RMS fluctuations of the angle between the 2'-hydroxyl group, phosphate group, and the 5' oxygen.

From the perspective of RNA molecular simulations, important advances have been made in recent years regarding force field parameters for all-atom explicit solvent molecular dynamics simulations[28, 29]. Few studies have compared RNA simulation with experiment in a detailed manner including a recent PreQ riboswitch study[17, 30-32] and studies of Small Angle X-Ray Scattering [33, 34]. While these studies are essential for improving forcefields, their high computational costs limits their sampling capability and therefore affect the accuracy of the entropic component of the free energy. Specifically, the functional dynamics of many RNA systems occurs on the time scale of hundreds of milliseconds to seconds [35, 36]. While large-scale simulations have produced millisecond simulations of small proteins[37] and microsecond simulations of large systems [38], current computing capabilities prevent all-atom explicit solvent molecular dynamics simulations from accessing the physiological time scales of 100 ms – 1 s.

To improve molecular simulation sampling, structure-based potentials have been used [39-44][45, 46]. This potential is defined by the crystallographic structure and has the advantage of preserving stereochemistry in the crystallographic structure while sampling hundreds of milliseconds. The method allows reproducibly folding and unfolding small to medium size protein and nucleic acid structures hence dramatically improving sampling and therefore the accuracy of the entropic component of the free energy. An additional advantage is that the potential is robust to changes in parameters, enabling calibration to experimental data while leaving the stereochemistry intact.

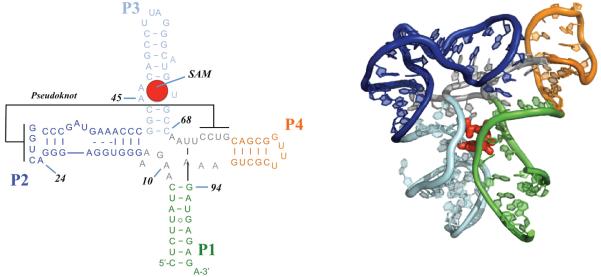
In this paper, we present SHAPE-FIT, a novel technique to automatically calibrate molecular simulations to RNA chemical probing experiments. We demonstrate this method on the T. tengcongensis metF SAM-I riboswitch aptamer domain (Fig. 2), a useful test system that has previously been studied using a variety of experimental and computational techniques. Our method is easily extendable to large RNA systems. The approach can also be combined with explicit water all atom simulations. SHAPE data integrated with molecular simulations improve the forcefield and produce mechanistic studies of RNA systems grounded in experimental data.

Figure 2.

The T. tengcongensis metF SAM-I riboswitch aptamer domain in the off-state. (a) Secondary structure of the aptamer domain with different colors representing secondary structure elements. (b) Tertiary structure of the sequence in the presence of S-adenosylmethionine (SAM) ligand.

2 Materials and Methods

2.1 Computation of SHAPE reactivity

SHAPE reactivity is inversely correlated with the base stability. The acylation reaction rate is higher if the nucleotide is mobile or easily accessible to the probing molecule (Fig.1). However the exact relationship between the SHAPE reactivity and stability is not yet known. To account for the realtionship between the base stability and SHAPE reactivity Deigan et al. [47] proposed a pseudo-energy function. Here, the stability of nucleotide k is given by the relation ΔG(k)=mln(a(k)+1)+n where a(k) is the normalized SHAPE reactivity of nucleotide k, m and n are fitting parameters fitted to m=2.6kcal/mol and n=0.8kcal/mol using Ecoli 16S ribosomal RNA SHAPE data. Here in our study we will use the same pseudo-energy term and the coefficients.

To account for the base stability and backbone mobility we use the fluctuations in the angle between the 2’-hydroxyl group, the phosphate, and the adjacent O5’ group (O2'-P-O5') (see Fig.1). This angle characterizes the mobility of the 2’-hydroxyl atom and is relevant to both SHAPE and in-line probing reaction geometry. Effective stability is characterized by the fluctuations as:

$$\Delta G_{SIM}\left(k\right)=k_{B}T\text{ln}\frac{\langle {{\theta }_k}^2\rangle -{\langle {\theta }_k\rangle }^2}{\sum _{i=1}^N(\langle {{\theta }_i}^2\rangle -{\langle {\theta }_i\rangle }^2)∕N}$$ (1)

Here, the stability of nucleotide k is computed from the fluctuation of this angle where 〈…〉 represents the ensemble average computed from the time series of the simulation trajectory. The value is normalized with the average fluctuation of the RNA chain of length N nucleotides.

Combining the pseudo-energy term above with Eq. 1 we obtain the computed reactivity as:

$$a_{SIM}\left(k\right)=\text{exp}\left(\frac{\Delta G_{SIM}\left(k\right)-n}{m}\right)-1$$ (2)

Note that neither the choice of the order parameter nor the formulation of the stability are unique.

2.2 Optimization of Potential Energy Function

To integrate SHAPE reactivity into the structure-based potential we optimize the native structure-based potential (SBM) [39-44][45, 46] by steepest-descent search in parameter space. The basic function of the previously defined SBM potential (Eq. 3) is a summation of harmonic potentials restraining the bond-lengths, bond-angles and dihedral angles to the native state structure that is given a priori by X-ray or NMR studies:

$$\begin{array}{cc}\hfill & E=\sum _{bonds}{K}_r{(r-r_0)}^2+\sum _{angles}{K}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{dihedrals}{K}_{\varphi }^{\left(n\right)}\left[1-\text{cos}(n\times (\varphi -{\varphi }_0))\right]\hfill \\ \hfill & +\sum _{impropers∕planars}{({\chi }_1-{\chi }_0)}^2+\sum _{i<j-3}\left\{ϵ(i,j)\left[{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{{\sigma }_{ij}}{r_{ij}}\right)}^6\right]+{ϵ}_2(i,j){\left(\frac{{\sigma }_{ij}}{r_{ij}})\right)}^{12}\right\}\hfill \end{array}$$ (3)

The interactions between atoms that are not bonded are represented by a repulsive term that accounts for excluded volume of the polymer and an attractive term is used to account for the native interactions dictated by the structure. Native interactions are defined as contact pairs with a simple cut-off distance of r ≤ r_c = 4 Å for nucleic acids and 6 Å for proteins. We emphasize that while more elaborate definitions for contacts exist [48], the exact contact definition will not significantly affect local dynamics in this study. This choice is more critical for large-scale conformational transitions such as those found in protein folding. The functional form for native contacts is a Lennard-Jones potential where the minimum is set to reproduce the native structure [44]. The barrier height of the dihedral potential $K_{\varphi }^{\left(n\right)}$ and the strength of the non-bonding native interactions between atom pairs $ϵ(i,j)={\left({ϵ}_i{ϵ}_j\right)}^{1∕2}$ assume a uniform weight in such a way that the ratio of the total non-bonded native interaction to the sum of all torsional angle contributions, $\sum ϵ(i,j)∕\sum K_{\varphi }^{\left(n\right)}$ is set to 4.

The results of simulations using the SBM potential (Eq. 3) depend on the choice of the set of parameters $\{\left\{K_r\right\},\left\{K_{\theta }\right\},\left\{K_{\varphi }^{\left(n\right)}\right\},\left\{{\chi }_i\right\},\left\{ϵ\right\},\left\{{ϵ}_2\right\}\}$. Here the most sensitive parameters for dynamics and at the same time the least known parameters to us are torsional angle parameters and non-bonded native interaction terms. For that purpose we search for the parameter space for these set of parameters. Hence our sequence depended parameter space is defined as $\pi =\{\left\{K_{\varphi }^{\left(n\right)}\right\},\left\{ϵ\right\}\}$

Following [49], we search the parameter space to minimize the difference between the experimental and simulation result of the same observable. The target function is defined as the distance between the two data sets:

$$\Psi \left(\pi \right)=1∕N\sum _{k=1}^N{\left[\text{ln}{a_{SIM}}^{\pi }\left(k\right)-\text{ln}{a}_{EXP}\left(k\right)\right]}^2$$ (4)

Here ${a_{SIM}}^{\pi }\left(k\right)$ denotes the computed SHAPE reactivity of nucleotide k with respect to the parameter set π , while a_EXP (k) is the reactivity of the same nucleotide in experiment. We aim to minimize the target function. Typically achieving this goal can be difficult. In some cases, oversimplification of the physical interactions by the potential makes it difficult to find a parameter set that reproduces the experimental data. In other cases, the sought after parameter space becomes too large for an exhaustive search. Here, we tested the functional form of the SBM potential against SHAPE experiments. We reduce the paramter space by focusing only the torsional and native interactions. To effectively search this reduced space we introduced the steepest descent minimization algorithm by iteratively solving the following differential equation (see Eq. 5):

$${\pi }_i={\pi }_{i-1}-\alpha {\nabla }_{\pi }\Psi \left({\pi }_{i-1}\right)$$ (5)

where, π_i is the parameter set in iteration i andα is a scalar that determines the strength of the target function. We note that the choice of α can be optimized to reduce the computational cost [50]. We use constant α at values of 0.01 ≤ α ≤ 0.1 . The iterative procedure is terminated when both ${\Psi }_{\left({\pi }_i\right)}<{\gamma }_1$ and $\mid \Psi \left({\pi }_{i-1}\right)-\Psi \left({\pi }_i\right)\mid <{\gamma }_2$ are satisfied, where γ₁ and γ₂ are preselected positive numbers chosen as 0.2 and 0.05 respectively in our study.

2.3 Molecular Simulations

We studied wild type sequences of the T. tengcongensis met riboswitch aptamer domain (residues 1-101) in two different solution conditions: (i) riboswitch in the presence of cognate ligand S-adenosylmethionine (SAM-I) and (ii) in the absence of the ligand. Because crystallographic structures of these sequences were not available, homology models were constructed using our previously published RNA homology modeling techniques used to model the ribosome [51-53]. Our model of the SAM-bound aptamer was derived directly from the crystallographic structure published by Batey and co-workers [54-56]. To obtain the atomic model of the SAM-I free configuration, we used the Kratky plots published in earlier studies [55].

We performed all-atom simulations of the SAM-I riboswitch aptamer by using structure-based potential [39, 42-44]. Simulations were performed using GROMACS 4.6 suit of programs [57]. We used leap-frog stochastic integrator with an inverse friction coefficient of 1ps with a reference temperature of 77K and a time step of 1fs throughout our simulations. VdW interactions are computed with twin range cut-offs with a cut-off distance of 12 Å. To compute the SHAPE reactivity we simulate each system and compute the ensemble average from the time trace of trajectories. Ideally statistical errors decrease as the length of the simulation increases; however the computational cost also increases. Here, we determine the optimal length of the simulation by computing the average effective stability (Eq. 1) of the RNA chain as a function of simulation length $L,C\left(L\right)=(1∕LN){\int }_0^L{\sum }_{k=1}^N\Delta {G_k}^{SIM}\left(t\right)dt$ and compute the standard error for the observable C. Our analysis indicated that L=5.10⁶ steps gives less than %1 error in the C estimate. Therefore 5.10⁶ steps of simulation length is used to obtain a statistically converged ensemble averages in our study. SHAPE reactivity from simulations is computed using Equations 1-2.

2.4 SHAPE probing experiments

We use SHAPE probing and in-line probing to follow changes in secondary and tertiary structure occurring upon ligand binding [26]. We study these changes for T. tengcongensis metF aptamers. In-line probing measures the ability of more mobile bases to spontaneously cleave [58]. SHAPE probing measures the ability of more mobile bases to react with the 1M7 reagent (Fig. 1). While the methods measure the same basic properties, we have found in-line probing to be less ambiguous in some structures. 1M7 is relatively insensitive to temperature and Mg²⁺ concentration.

2.5 Preparation of RNA systems

Synthetic DNA oligonucleotide (IDT, Coralville, IA) templates were PCR amplified for use as in vitro transcription templates. Transcription reactions were performed using Ampliscribe (EPICENTRE Biotechnologies, Madison, WI) high yield T7 RNA polymerase transcription kits as per instructions.

2.6 SHAPE chemical probing

The aptamer domain RNA was folded at a concentration of 5 nM in 1X HMK buffer (50 mM HEPES-KOH pH 8.0, 2 mM MgCl2, 100 mM KCl) and various concentrations of S-Adenosylmethionine (SAM). 30 μls of 60 mM 1-methyl-7-nitroisatoic anhydride (1M7) in DMSO was added to a 300 μl volume of RNA. The reaction proceeded for 5 minutes at 25 °C and was then precipitated by the addition of 0.1 volumes 3M Na:Acetate pH 6.5, 75 μg glycogen and 3 volumes EtOH. The recovered RNA was then subjected to reverse transcription analysis as described above. Capillary electrophoresis data was integrated by simultaneously fitting Gaussian curves to the whole trace using in-house scripts. The traces were normalized using residues whose reactivity does not change in response to SAM.

2.7 In-line chemical probing

All chemical probing reactions were performed a minimum of three times with and without S-adenosylmethionine. SAM (NEB, Ipswich, MA.) was added to a final concentration of 10 μM. In-line probing was performed as previously described[26] in in-line probing buffer (50 mM Tris-HCl pH 8.3, 20mM MgCl2, 100 mM KCl) with the following modifications: RNAs were unfolded by heating to 90 °C in water for 2 minutes and then crash cooled on ice for 2 minutes followed by addition of buffer with or without SAM. In-line probing reactions were performed at RNA concentrations of 0.3 μM for 40 hrs at 25 °C. Reactions were purified by precipitation with 3 volumes EtOH and 50 μg RNase free glycogen (Ambion) and then analyzed by capillary electrophoresis.

2.8 Analysis of chemical probing reactions

In-line probing and SHAPE probing reactions were analyzed by fluorescently labeling of the RNA on the 3’ terminus. The labeled RNA was then diluted 1-5 μl into 20 μl of formamide, depending on recovery and labeling efficiency, followed by heating to 90 °C for 2 minutes prior to loading on an ABI Prism 310 genetic analyzer (Applied Biosystems) capillary electrophoresis system equipped with a laser induced fluorescence detector. The reactions were electrokinetically injected at 12.5 kVolts for 30 seconds and run in POP-6 polymer (ABI) at 70 °C for 1 hour. Sequencing reactions were performed by transcribing the RNA constructs in the presences of a low level of α-phosphorothioate nucleotides followed by iodine cleavage and capillary electrophoresis.

3 Results

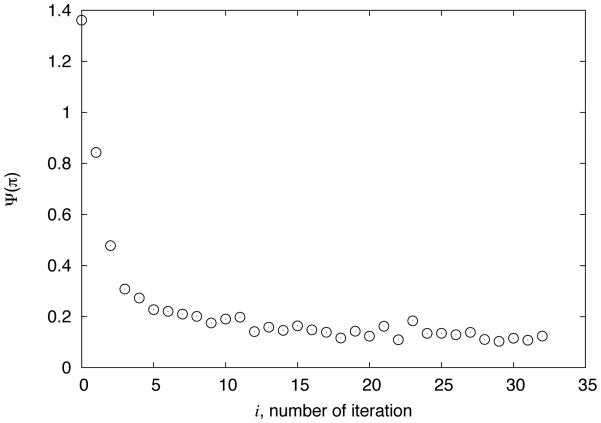
We performed molecular dynamics simulations of the SAM-I riboswitch aptamer wild type sequence in the presence of SAM (Figure 2a-b) with the unmodified potential energy function. Computed SHAPE reactivity is then used to calculate the distance function. We modify the potential as detailed in methods section to minimize the difference between the experimental and computed SHAPE data. Our iterative procedure effectively decreases the target function in each iteration. Figure 3 shows the change in the target function as a function of the number of iterations. The procedure is stopped when a convergence in the distance function is achieved, as there was no more improvement in the target function.

Figure 3.

Evolution of the distance function Ψ(Π ) , quantifying agreement between simulated and measured SHAPE reactivities, as a function of the iteration number.

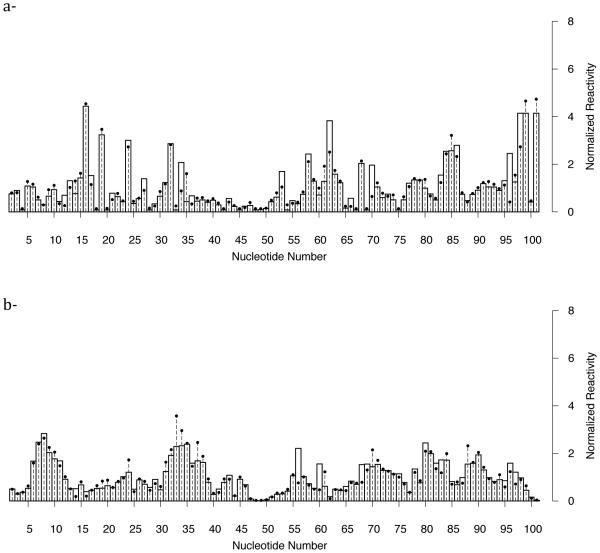
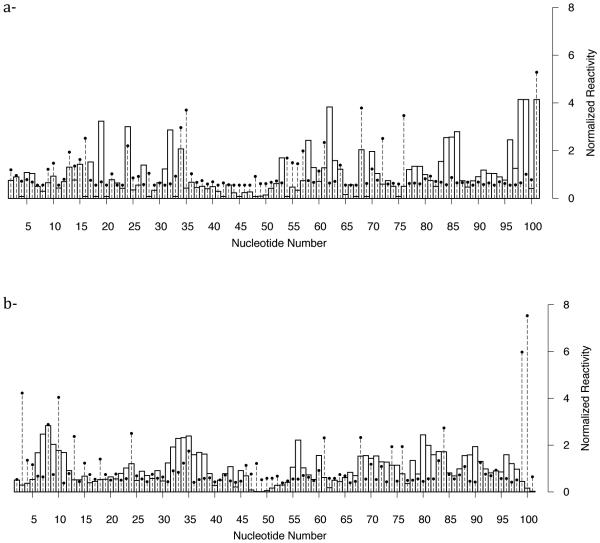
Figure 4a displays the reactivities based on fluctuations from the simulations with the optimized potential and normalized reactivity based on in-line probing experiments. We achieve excellent agreement between simulation and experiment. Comparison of the reactivities with the unmodified potential (see Figure 5a) on the other hand significantly differs from the experiment, showing the success of our automatic procedure. We repeated the optimization procedure for the riboswitch in the absence of SAM-I. Our results are again in agreement (Fig. 4b) with the experiment and the data is quite different with the unmodified simulation results (see Figure 5b). Despite the excellent agreement there are still remaining questions: What is the reason for a nucleotide to show high reactivity while the other do not? What is the difference between liganded and unliganded states that leads to a significant change in the SHAPE spectra? What is the mode of dynamics in the region of high reactivities?

Figure 4.

Comparison between experiment and simulation of SHAPE probing data of SAM-I riboswitch aptamer domain. Dashed horizontal lines with points are normalized activity from SHAPE reactivity measurements. Bars are activities computed from structure-based molecular dynamics simulations after optimization of the potential. Close agreement is achieved after the optimization of the potential (a)- in the presence of SAM and (b)- in the absence of it.

Figure 5.

Comparison between experiment and simulation of SHAPE probing data of SAM-I riboswitch aptamer domain. Dashed horizontal lines with points are normalized activity from SHAPE reactivity measurements. Bars are activities computed from structure-based molecular dynamics simulations before optimization of the potential. (a)- in the presence of SAM and (b)- in the absence of it.

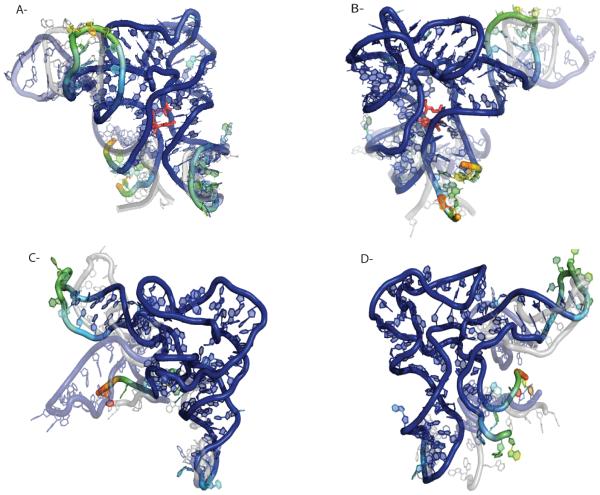
To accurately address the differences in the reactivities and to better understand the changes in mobility between the liganded and unliganded states we used the trajectories from our optimized potentials. Figure 6a-b shows a conformation with bound SAM-I ligand. We report here the most populated conformation in the ensemble color coded according to the SHAPE reactivities. The most populated structure is obtained by clustering the trajectory with RMSD as distance measure. The cluster with the highest weight in the ensemble is the most populated state. We choose the cluster center configuration to be representative for the respective state. We observe that SHAPE reactivity strongly correlates with riboswitch topology. Unpaired regions are, in general, significantly more reactive relative to base paired regions. Regions on the exterior of the molecule tend to be more reactive than those in the core. Simulations that incorporate SHAPE data show the dynamics in highly reactive regions. For example, P1, which is close to the SAM-I ligand remains formed during our simulations yet its high mobility is due to the rotational motion of the domain in solution (see Figure 6a-b). In contrast, P4, another highly reactive domain, goes back and forth towards P2 making contacts with it which results in exposing the buried residues to the solvent in the off state and hence increases the SHAPE reactivity.

Figure 6.

Comparison of SHAPE reactivities of SAM-I riboswitch aptamer domain with and without SAM-I. Residues are colored according to their SHAPE reactivity, blue is unreactive and red is highly reactive. The type of motion in reactive regions are depicted by overlying conformations (partially transparent). (a) Shows the dynamics of riboswitch with bound ligand and (b) is the same molecule rotated by 180 degrees. (c)-(d) show the dynamics of the riboswitch unliganded.

A detailed comparison of the structure and dynamics in the absence of the ligand on the other hand depicts that the P1 domain is now unfolded (Figure 6c-d). The high reactivity in this region is due to the resulting high mobility of the backbone chain as well as due to unpaired nucleotides exposed to the solution. The P4 domain, which also shows high reactivity is now an extended helix. The structure that is dominated in our simulation with optimized potential is similar to that constructed by Lilley and co-workers [59]. Our structure also reveals a lack of pseudo-knot tertiary interactions in the absence of the ligand. The lack of pseudo-knot contacts leads to more extended conformations in the conformational ensemble increasing the radius of gyration by ~10%. This observation is also in accord with previous SAXS studies [55]. Our simulation results are consistent with nucleotide analog interference modification studies (NAIM) and suggest that ligand promotes a global collapse of the aptamer domain by stabilizing tertiary contacts [55].

4 Discussions

We have developed a systematic method to integrate molecular dynamics simulations with chemical probing experiments. The method produces simulated RNA fluctuations consistent with experiment at each nucleotide. The method called SHAPE-FIT hence offers a solution to fine-tune an energy function toward better agreement with experiment with applications in RNA structure and dynamics. While SHAPE probing has been extremely successful in predicting secondary structures and evaluating the mobility of RNA molecules, the exact relation between SHAPE reactivity, nucleotide mobility, and solvent exposure is not entirely understood. The order parameter we choose to monitor has successfully recapitulated the experimental data. Improvements may result from a clearer understanding of the SHAPE reaction. This may be achieved by, for example, via quantum chemical calculations of acylation reaction or understanding of RNA polymerase transcription mechanism.

Here in our study we use the aptamer domain of the SAM-I riboswitch that is designed to fold to a single RNA native state in solution. This may not be the general case for the complete sequence that switches between on and off-states. It may be also difficult to justify a singe native state in many RNA systems as significant populations of alternative folds known to present in solution. Still, native interactions have been found to dominate RNA-folding[60]. A future direction would be to account for multiple native states in our potential. Multiple basin Go models have been successfully applied in protein folding [61, 62]. Application of this model to SHAPE-FIT will be a future direction. Extensions to the method will also include non-native interactions, explicit electrostatic interactions and additional calibration of our model with thermodynamic melting studies.

While our method achieved excellent agreement with experimental data, our use of a local minimization procedure leads to a single solution of the parameter set. One could easily imagine that multiple solutions are possible. These different solutions may lead to different interpretations of the same data. Modeling multiple simultaneous solutions is an opportunity for future research. Another direction is to add multiple experiments to the target function in addition to SHAPE such as SAXS, melting temperatures, etc. This would reduce the parameter space and result in a more robust potential across experimental data sets.

Overall, our method calibrates the structure-based potential to our experimental data, producing simulations consistent with chemical probing experiments. We note that our method is easily scalable to large systems. Thus, mechanistic studies of the folding and function of RNAs using these potentials will be consistent with SHAPE measurements, yielding conclusions grounded in experiment. Accordingly, predictions from such studies have the potential to be more precise. At the same time, these simulations would help interpret SHAPE measurements. Dynamics at each residue can be used for mechanistic interpretation of the SHAPE data as well as providing an atomic level interpretation of the reactivities based on fluctuations. The method has the potential to provide new mechanistic insights into the interplay between structure and dynamics, tightly integrating experiment and atomistic simulation to obtain an atomic level picture of RNA function.