Modeling the Progression of Epithelial Leak Caused by Overdistension

Abstract

Mechanical ventilation is necessary for treatment of the acute respiratory distress syndrome but leads to overdistension of the open regions of the lung and produces further damage. Although we know that the excessive stresses and strains disrupt the alveolar epithelium, we know little about the relationship between epithelial strain and epithelial leak. We have developed a computational model of an epithelial monolayer to simulate leak progression due to overdistension and to explain previous experimental findings in mice with ventilator-induced lung injury. We found a nonlinear threshold-type relationship between leak area and increasing stretch force. After the force required to initiate the leak was reached, the leak area increased at a constant rate with further increases in force. Furthermore, this rate was slower than the rate of increase in force, especially at end-expiration. Parameter manipulation changed only the leak-initiating force; leak area growth followed the same trend once this force was surpassed. These results suggest that there is a particular force (analogous to ventilation tidal volume) that must not be exceeded to avoid damage and that changing cell physical properties adjusts this threshold. This is relevant for the development of new ventilator strategies that avoid inducing further injury to the lung.

INTRODUCTION

Overdistension of the lungs during mechanical ventilation is presumed to be one of the key mechanisms in the production of ventilator-induced lung injury (VILI).^23,24 The damage this causes to the lung tissues is known as volutrauma and is readily avoided in a normal lung simply by keeping tidal volume in the normal range.⁴ However, a significant fraction of the parenchyma can become derecruited in lungs that are already injured, in which case the entire delivered tidal volume is forced into the remaining open fraction.³⁶ This is presumed to overdistend the open regions and cause volutrauma by a mechanism that would appear to be straightforward; excessive strain breaks the normally intact epithelial barrier allowing edematous material that has accumulated in the interstitium to leak into the airspaces. This disrupts surfactant function to increase surface tension and thus cause even greater stresses on the parenchymal tissues. The result is a vicious circle that can spiral out of control.²⁹

Although this scenario might seem rather obvious in general terms, we currently know little about its details. We do have evidence, however, that these details might be somewhat complex; the epithelial leak in a mouse model of VILI appears to be related to tidal volume in a very nonlinear fashion for reasons that remain mechanistically obscure.³⁰ Understanding the details of how epithelial strain leads to epithelial leak is crucial, however, not only for developing ventilator strategies that avoid volutrauma but also for knowing what constraints on strategy are imposed once damage to the epithelial barrier has occurred.

Accordingly, in the present study we developed a computational model of the airway epithelium for the purposes of studying how the initiation of a leak through the epithelial barrier is linked to epithelial strain, and how the leak worsens with increasing strain. We hypothesized that the stress released by the formation of a leak would protect a sheet of epithelial cells from further damage in the presence of increased strain. We used the model to help us establish a mechanistic basis for our previous experimental findings in mice with VILI.³⁰

METHODS

Hexagonal Cell Model

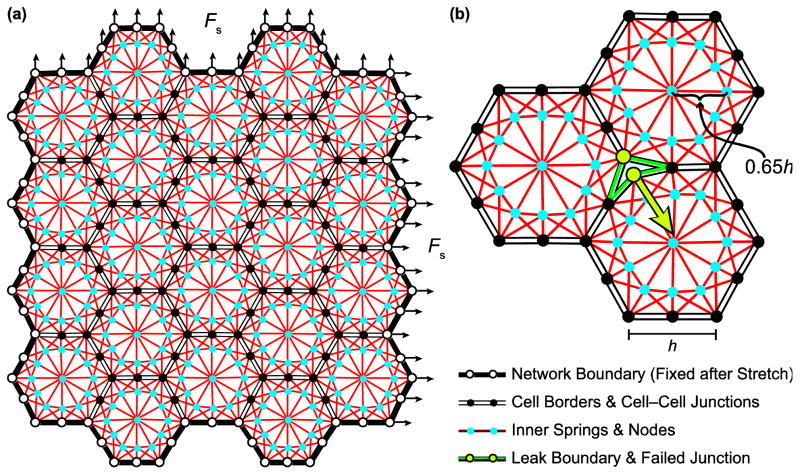
We model an alveolar epithelial cell monolayer as an approximately square two-dimensional assembly of N space-filling hexagonal cells connected together at discrete junction points representing cell–cell junction complexes. The boundary of each cell in its baseline configuration consists of six linear segments, with horizontal segments of length h and diagonal segments of length $h\sqrt{3}/2$ to reduce the vertical dimension so the network is approximately square. Junctions connect three adjacent cells together at each hexagonal corner and connect two adjacent cells midway along each hexagonal edge, as shown in Fig. 1. The internal cytoskeleton of each cell is represented by a network of springs that connect each of the 12 cell–cell junction points on the cell boundary to 3 of the 12 internal nodes located 65% of the distance along the line from the cell center to each cell–cell junction point (Fig. 1). This placement produces a higher density of shorter springs around the hexagon borders, analogous to the submembranous cortical cytoskeleton of alveolar epithelial cells.^13,17 Additionally, this arrangement resulted in the best numerical stability of the model when we solved for its elastic equilibrium configuration over the range of stretch forces we investigated. The node at the cell center connects to each of these 12 internal nodes which themselves are connected to each other to form an internal hexagon. The relationship between force (F) and length (x) of each cytoskeletal spring is linear according to

FIGURE 1.

Configuration of hexagonal network. (a) The outer boundary is fixed after the network is stretched biaxially with force F_s. Each cell contains a network of springs connecting inner nodes to cell–cell junctions. (b) The junctions on the cell borders can separate to form leaks between the cells if the resultant force from the attached springs in one cell exceeds the threshold value for that node.

$$F=k(x-x_0),$$ (1)

where k is a spring constant and x₀ is the resting spring length (90% of the length in the baseline construction of the model). Because the lipid bilayer of the cell membrane must have some finite stiffness, we modeled the boundaries of each cell between adjacent junction points as springs via Eq. 1 with stiffness set to 0.01k. This accounts for the likelihood that the lipid bilayer of the cell membrane is much less stiff than the actin filaments comprising the cytoskeleton. Also, we found this choice of stiffness for the cell membrane to provide numerical stability for the solution of the model’s equilibrium configuration. We note that in this two-dimensional model we are not explicitly accounting for the attachment of the epithelial cell monolayer to its basement membrane substrate, which may imbue the layer with additional mechanical resilience against tearing. However, we can assume in the model that this extra resilience is subsumed in some of the strength of the cell-cell junctions.

Computational Method

We developed custom software based on the finite element method, adapted from our previously described model of airway-parenchymal interdependence,^18–21 that solves a system of force equilibrium equations for a planar spring network.⁴⁰ Each spring was assumed to be a bar element with baseline length x₀. The springs were connected by a hinge at each node to allow free rotation. The spring network was stretched biaxially by applying a force F_s to each of the nodes lying along the right and top boundaries, leaving the left and bottom boundary nodes fixed. Fixing the left and bottom boundary nodes merely establishes a coordinate system fixed to these boundaries to facilitate the simulations, and the actual stretching of the network is uniform and biaxial when the right and upper boundary nodes are moved. Given the applied F_s on the boundary nodes, we solved for the node displacements with the global matrix equation

$$\mathbf{KX}=\mathbf{B},$$ (2)

where K, X, and B are the stiffness, displacement, and force matrices, respectively. The boundary nodes were fixed at their new positions for the rest of the simulation. The elastic equilibrium configuration of the internal spring network was computed using a successive over-relaxation procedure.⁵ For each iteration, the forces at each internal node were computed, multiplied by an adaptively adjusted relaxation factor, and used to solve for the internal node displacements (Eq. 2). This process was repeated until all inner node forces were less than a tolerance value set to 10⁻⁵. At this point, the spring network was assumed to have reached elastic equilibrium.

To form a leak in the network due to the applied F_s, we assigned to each internal cell–cell junction on hexagon borders a force threshold F_t above which it would fail. With the stretched network in its equilibrium configuration after applying F_s to the boundary nodes, we computed the resultant pulling forces at each internal cell–cell junction from the forces in the springs attached to it in each adjacent hexagonal cell. If a node had a pulling force that exceeded its value of F_t, then that node would split into two nodes. This was accomplished by adding an additional node and connecting springs at the location of the failed node and then solving for the new equilibrium configuration of the network using the iterative procedure just described to compute the new pulling forces. This allowed the opposing cells to move apart from each other under the influence of their respective elastic elements, which created a leak between the hexagonal cells as illustrated in Fig. 1b. The leak formation due to F_s was an iterative process in which the node with the largest pulling force greater than its F_t was allowed to fail first while all other nodes remained intact, a new equilibrium configuration was computed, and then the next node with the largest excess force would fail followed by the equilibrium computation, and so on. This process was repeated until no junctions remained with pulling forces greater than their F_t. We counted the number of leaks and computed the total leak area formed by the separated cell edges due to the initially applied F_s at this point in the computation to define the epithelial leak in the stretched state analogous to end-inspiration. To determine the leak at end-expiration, we then incrementally moved the network boundary back to its baseline (pre-stretch) position by computing the new equilibrium configuration of the spring network after each adjustment and calculated the leak area again when this process was complete.

Scaling Parameters

To relate this spring network model to an alveolar epithelial monolayer, consider that the surface area of the epithelium covering each human alveolus is around 220,000 μm^2.37 In our baseline case, we modeled this as an assembly of N = 45 hexagons each with an edge length of h = 1. To achieve the surface area of one alveolus, the dimensional value of the hexagon edge must be 43.4 μm, which served as our reference length scale in the model. We simulated networks with N = 22, 45, 67, 104, 149, 202, and 246 hexagons, yielding dimensional surface areas ranging from 107,659 μm² to 1,203,833 μm² and representing monolayers that cover between half of an alveolus and five and half alveoli. We also simulated 45-cell networks with smaller and larger h values (±10%, ±25%, and ±50%), which reduced or increased the cells sizes (dimensional edge lengths 21.7–65.1 μm) and thus the network surface area (55,053–495,480 μm²).

We computed the epithelial leak for a range of dimensionless stretch force magnitudes, 0.001 ≤ F_s ≤ 0.1, to determine the dependence of the leak area on the stretch applied to the network at both end-inspiration and end-expiration. The maximum F_s corresponds to a strain of 30%, defined as the % change in network area from its initial (unstretched) state. In order to relate the parameters F_s, F_t, and k to dimensional values, we computed a reference force scale f based on Young’s modulus, E, of an alveolar epithelial cell, which has been measured with atomic-force microscopy to be around 1–5 kPa for human A549 cells in a confluent monolayer.^2,15,27 For this model, we assumed E = 1 kPa for the entire spring network. We simulated horizontal stretch of the 45-cell network and used the stress-strain relation E = σ/ε, where σ = f F_s/A_I (the applied force adjusted by the scaling force divided by the initial cross-sectional area over which the force is applied) and ε = ΔL/L₀ (the linear displacement of the network due to the force relative to its initial length), to compute the scaling force f for F_s that yielded E = 1 kPa. In approximating A_I, we assumed the height of the cell monolayer to be 5 μm.³⁶ This resulted in f = 118 nN; thus the simulations covered the range 0.118–11.8 nN. We used a node force threshold F_t = 0.2 for the baseline case, equivalent to 23.6 nN using the force scaling factor. The spring stiffness constant was k = 1 for the baseline case so that a force of 1 generated an extension of 1. Stiffness is a force per length, so the stiffness of the individual springs in the model corresponds to 2.7 nN/μm by dividing the force scale by the length scale. Although it can be helpful to relate the system to dimensional values, we note that it is difficult to translate the values generated by this simplified model to a human system; rather, the utility of the model lies in the interpretation of the behavior in response to the parameters.

We investigated the effects of modifying F_t and k by ±10%, ±25%, and ±50% of their baseline values in the 45-cell model (F_t = 11.8–35.4 nN, E = 0.5–1.5 kPa). To test the effects of inhomogeneity among the cells in the network the value of k for each internal spring was drawn from a normal distribution with mean μ_k = 1 and standard deviation σ_k = 0.05, 0.1, and 0.15. Each junction’s F_t was chosen from a normal distribution with mean μ_Ft = 0.2 and standard deviation σ_Ft = 0.01, 0.02, and 0.03. For the simulations with variation in k and F_t we completed 50 computations for each F_s and report the mean and standard deviation of the results. The same 50 configurations of k and F_t were used to span F_s. All simulations were carried out in MATLAB (MathWorks, Natick, MA) on a regular desktop computer.

RESULTS

Leak Propagation

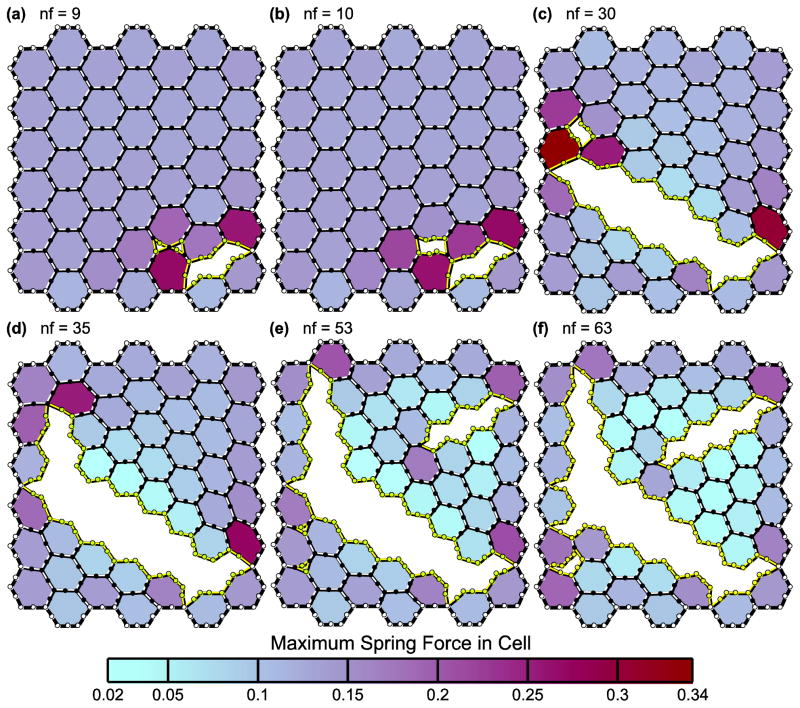
In Fig. 2, we show the 45-cell network subjected to a biaxial stretch force of F_s = 0.07 at several points during the progression of the cell–cell junction failures. Each panel shows the leak after the number of nodes indicated (nf) have failed; 63 nodes in the network failed as a result of the applied F_s (Fig. 2f). The inner springs and nodes are not shown for clarity. Instead, the cells are shaded based on the maximum spring force magnitude within that cell. In this configuration of the model with k = 1, F_t = 0.2, and h = 1, the first node to fail is a corner junction between three cells. Leaks at two corners then coalesce into a single leak when the node between the leaks fails (Fig. 2, a and b). A leak will also grow by adjacent node failures until the outer boundary of the network is reached (Fig. 2, c–e). Because the outer network boundary is not allowed to fail, the sheet of cells cannot completely detach into multiple segments. However, the leak can divide the sheet into sections attached only by the outer boundary. The forces of the internal springs are smaller in the cells bordering the leak because these cells are no longer bounded on one side by other cells and have thus returned close to their original pre-stretched states. Conceptually, the force in a spring is zero if its displacement is zero following Eq. 1. Cell shape thus depends on the spring forces resulting from both the applied F_s and the leak that forms. The final leak area in Fig. 2f relative to the area of the network in its baseline configuration is 0.33. A movie of this leak progression can be found in the Supplementary Material. The behavior of the leak progression in networks with larger N is similar.

FIGURE 2.

Leak progression in the 45-cell network. The panels (a–f) show how the leak caused by the applied stretch force F_s = 0.07 forms. Only one node fails at a time; nf indicates how many nodes have failed in each panel. The shading represents the value of the maximum spring force within each cell. Spring stiffness k = 1, force threshold F_t = 0.2, and cell edge length h = 1.

Behavior with Increasing N and F_s

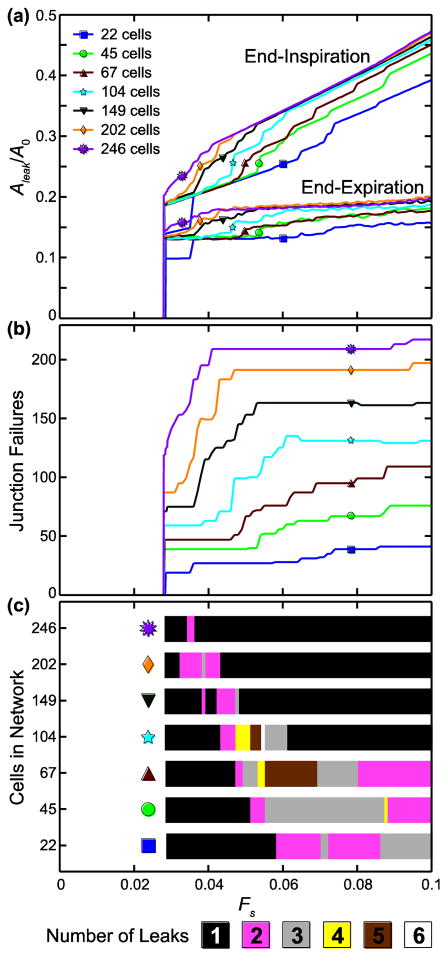
Fig. 3a shows the leak area, A_leak, normalized by the total network area before stretching and junction failure, A₀, for N = 22, 45, 67, 104, 149, 202, and 246 at end-inspiration and end-expiration with increasing F_s (k = 1, F_t = 0.2, h = 1). We see that A_leak/A₀ sharply increases from zero between F_s = 0.028 and F_s = 0.0285. F_s at onset decreases as N increases. After the onset of leak, A_leak/A₀ increases linearly with F_s in the network at end-inspiration, but at end-expiration A_leak/A₀ plateaus at a near-constant value as F_s increases. In both cases, once the leak begins A_leak/A₀ versus F_s appears to converge with increasing N to a solution in which A_leak/A₀ increases with F_s at a constant rate at end-inspiration but maintains a constant value at end-expiration.

FIGURE 3.

Model behavior with increasing stretch force, F_s, and increasing network size. (a) Leak area, A_leak, normalized by the total network area before stretching and cell–cell junction failure, A₀, at end-inspiration and end-expiration. (b) Number of junction failures; note that the number of failures does not continue to increase with F_s. (c) Total number of leaks formed for each stretch force and network size; fewer leaks are formed in the larger networks.

We see in Fig. 3b that the number of failed junctions becomes increasingly constant as F_s increases after leak onset with increasing N, mirroring the constant slope/constant value convergence behavior of A_leak/A₀. The final number of leaks in the network with increasing F_s is shown in Fig. 3c for each N. In general, for most N one large leak forms at lower F_s, additional smaller leaks form as F_s increases, and then the smaller leaks merge with the large leak so that the total number of leaks formed is reduced at higher F_s. As N increases, the highest number of leaks occurs at lower F_s, leaving one large leak at higher F_s.

Sensitivity to Parameters k, F_t, and h

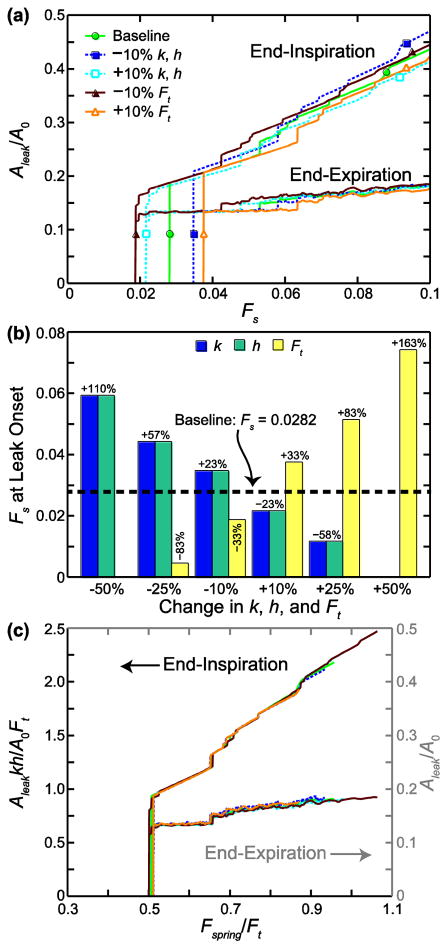
We changed k, F_t, and h by ±10%, ±25%, and ±50% of the baseline values in the 45-cell network; the A_leak/A₀ versus F_s curves for the ±10% cases are shown in Fig. 4a. The curves are the same for k and h because A_leak is scaled by A₀. By Eq. 1, force scales with k for the same displacement, and force scales with displacement for the same k. The spring network acts in a similar way such that changing k or h alters the internal node forces, making them higher or lower with respect to their F_t than they might have been at baseline, and shifts the applied F_s that causes leak. Increasing k or h decreases the minimum F_s that causes leak formation (curve shifts to left), while decreasing k or h shifts the curve to the right. Conversely, increasing F_t increases the minimum F_s that causes leak formation (curve shifts to right), while decreasing F_t shifts the curve to the left. Adjustments of ±25% and ±50% in k, h, and F_t followed the same trend, with larger changes to F_s at leak onset. We note that for a 50% decrease in F_t and a 50% increase in k or h, all values of F_s form a leak (no threshold). F_t has a greater effect on the F_s at leak onset than k and h, as can be seen in Fig. 4b, which shows the change in F_s at leak onset from the baseline case for all parameter changes. We note that in the cases where F_t was decreased or k or h were increased (all of which decrease F_s at leak onset), the leak area at the lowest F_s values makes several jumps instead of just one before increasing more steadily with F_s (Fig. 4a). In this region of leak onset, three or four smaller leaks formed instead of one large leak, as happened in all other cases.

FIGURE 4.

Sensitivity to parameters k (stiffness), h (edge length), and F_t (force threshold) in 45-cell network. (a) Leak area, A_leak, normalized by the total network area before stretching and cell–cell junction failure, A₀, is plotted against the stretch force F_s. (b) Change in F_s at leak onset from the baseline case is shown for ±10%, ±25%, and ±50% changes in k, h, and F_t. For a 50% decrease in F_t and a 50% increase in k or h, all values of F_s formed a leak. (c) All cases are plotted on nondimensional axes, with the end-inspiration curves following the left-hand axis and the end-expiration curves following the right-hand axis. F_spring is the maximum internal spring force in the network before cell–cell junction failures occur.

At end-inspiration A_leak/A₀ is lower relative to the baseline case at a given F_s for increased k, h, and F_t and higher for decreased k, h, and F_t. Stiffer or longer springs increase the spring forces, which makes the network harder to stretch (less area strain) and reduces the area of the leak. At the same time, the increase in spring forces increases node forces, and thus node failure and leak formation, at lower F_s. Increasing (or decreasing) the strength of the junctions also reduces (or increases) the leak area. This behavior can be condensed into a single curve by plotting the results on scaled axes, as shown in Fig. 4c. The horizontal axis is F_spring/F_t, where F_spring is the maximum spring force computed with Eq. 1 after the network is stretched but before node failures, and is dependent on the assigned values of k and h. The left-hand vertical axis is A_leakkh/A₀F_t, which accounts for the change in leak area with adjustment of k, h, and F_t. At end-expiration all curves approach the baseline curve as F_s increases (Fig. 4a). This is plotted in Fig. 4c with the horizontal axis F_spring/F_t but with respect to A_leak/A₀ on the right-hand vertical axis. The parameters k, h, and F_t did not affect A_leak/A₀ at end-expiration.

Inhomogeneous Distributions of k and F_t

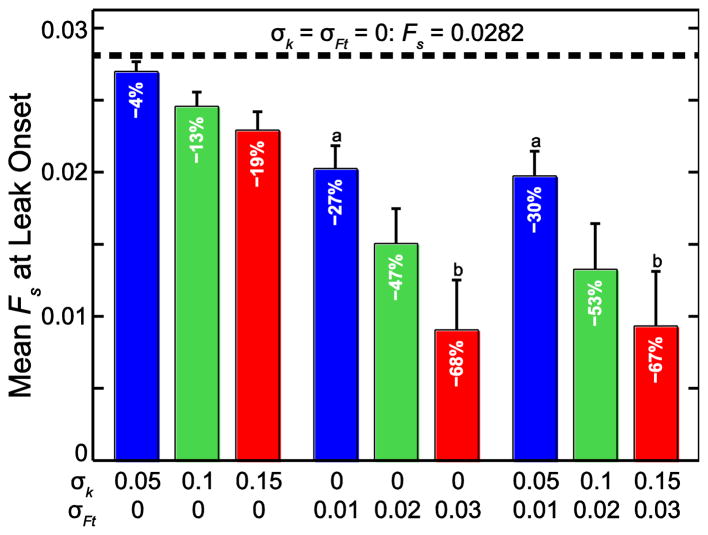
In the 45-cell network, assigning inhomogeneous distributions of k and F_t decreased the minimum F_s at which the leak began compared to the baseline uniform case (F_s = 0.0282). The mean and standard deviation of this value (n = 50) is shown in Fig. 5 for σ_k = 0.05, 0.1, and 0.15 and σ_Ft = 0.01, 0.02, and 0.03 (5%, 10%, and 15% of μ_k and μ_Ft), applied separately and together (μ_k =1, μ_Ft = 0.2, and h = 1 in all cases). Increasing σ_Ft had a larger effect on F_s at leak onset than increasing σ_k, which agrees with the previous result showing that changing F_t has a larger effect on F_s at leak onset than changing k. From a multiple comparison test using one-way ANOVA, all means of F_s at leak onset are significantly different (p ≤ 0.014) from each other and from the baseline case with two exceptions: there is no difference between the cases [σ_k = 0, σ_Ft = 0.01] and [σ_k = 0.05, σ_Ft = 0.01] or between the cases [σ_k = 0, σ_Ft = 0.03] and [σ_k = 0.15, σ_Ft = 0.03].

FIGURE 5.

Stretch force F_s that initiates leak. The uniform case (dotted line) is compared to the cases with increasing variation in k (stiffness) and F_t in the 45-cell network. k and F_t were chosen from normal distributions with μ_k = 1 and σ_k =0.05, 0.1, and 0.15 and μ_Ft = 0.2 and σ_Ft = 0.01, 0.02, 0.03, respectively. Bars represent mean and SD (n = 50). All means significantly different from each other except ^a and ^b (p ≤ 0.01).

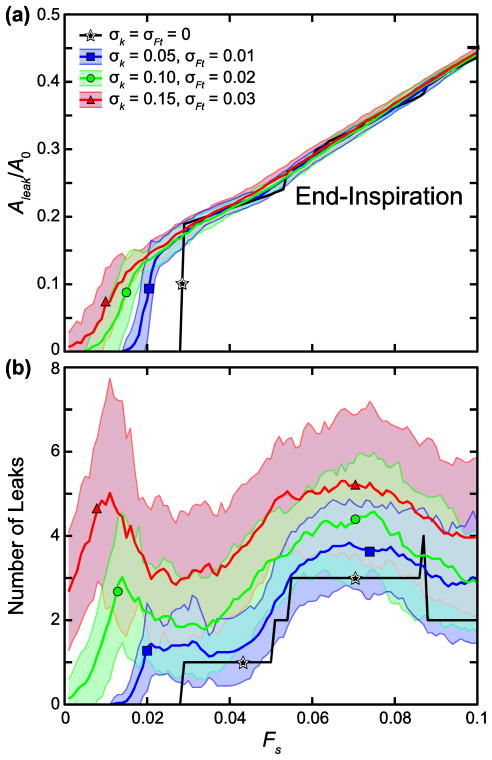
In Fig. 6a, the mean A_leak/A₀ versus F_s curves at end-inspiration with both σ_k and σ_Ft set at 5%, 10%, and 15% of μ_k and μ_Ft, respectively, are shown with their corresponding standard deviation bounds. Increasing parameter variability lowers the threshold for leak initiation and increases the threshold variability, likely because this increases the likelihood that some cell–cell junctions will have very low yield stresses. However, the point at which leak area assumes a linear relationship with F_s is not greatly changed by variability, so variability merely makes the rise from zero to the linear region more gradual. Increasing the degree of variation in F_t and k increases the mean number of leaks that form at leak onset compared to the baseline case computed with uniform F_t and k, as shown in Fig. 6b. This is true at higher values of F_s as well, even though the total leak area is very similar between cases in this region. The inhomogeneity of the parameters thus allows leaks to begin more easily in different regions of the model and to grow independently with less likelihood of eventually coalescing into a smaller number of larger leaks.

FIGURE 6.

Sensitivity to inhomogeneous k (stiffness) and F_t (force threshold) in 45-cell network. (a) Mean leak area, A_leak, normalized by the total network area before stretching and cell–cell junction failure, A₀ and (b) mean number of leaks are plotted with increasing stretch force, F_s. Shading represents standard deviation bounds (n = 50). k and F_t were chosen from normal distributions with μ_k = 1 and σ_k =0.05, 0.1, and 0.15 and μ_Ft = 0.2 and σ_Ft = 0.01, 0.02, 0.03, respectively.

DISCUSSION

We have developed a computational model that can help explain how epithelial strain caused by overdistension during mechanical ventilation leads to epithelial leak and VILI. By applying a stretch force to a sheet of hexagons representing epithelial cells, we modeled the progression of leak between the cells and examined how the leak changed with increased force. We found that if a large enough stretch was applied to the network boundary, a leak transecting the sheet from the outer edges would form. This leak resulted from the coalescence of smaller leaks that started at hexagon corners and then grew progressively due to adjacent node failures (Fig. 2). Increasing the amount of applied stretch revealed a nonlinear relationship between leak and stretch force. Similar threshold behavior has been observed during in vitro cell stretching; for example, Tschumperlin et al. found a nonlinear relationship between cell death and equibiaxial deformation magnitude in 5-day alveolar type II cells, which they suggested were representative of primary culture alveolar type I cells and the alveolar blood-gas barrier.^33,34 In further studies of alveolar epithelial stretch, the Margulies group found that a threshold strain magnitude of 37% change in surface area (corresponding to a tidal volume of 100% total lung capacity) disrupted tight junctions and increased epithelial barrier permeability.^7–9 In vivo, Gajic et al. showed a much greater degree of alveolar cell injury in rats mechanically ventilated with a tidal volume of 40 ml/kg than with a tidal volume of 30 ml/kg.¹⁴

In the baseline case, the model showed initiation of leak with an applied force of 0.0282 resulting in 7.8% area strain (3.8% linear strain). Assuming E = 1 kPa for the network and a linear stress-strain relationship, the stress on the cell sheet causing leak is 38 Pa. We note that E = 1 kPa is the value measured for a single alveolar epithelial cell, not an epithelial cell monolayer. Dassow et al. measured E for a layer of human A549 alveolar epithelial cells to be 40 kPa,¹⁰ which would increase the leak-causing stress to 1.5 kPa. While these values are difficult to interpret because such measurements of alveolar strain and stress during the progression of VILI in humans have not been obtained, a study of lung stress and strain during mechanical ventilation in pigs found surprisingly similar results.²⁶ The investigators showed a threshold of strain that caused leak (as measured by increase in lung weight) that corresponded to a stress of around 10 cm H₂O (980 Pa).

We hypothesized that the stress released by the formation of a leak would protect the sheet of epithelial cells from further damage with increased strain. In support of this hypothesis we found that once the force was large enough for a leak to form, leak area at end-inspiration increased with force in a linear fashion with a positive intercept on the leak area axis (Fig. 3a). In other words, the leak area increased more slowly than the applied force. This effect was even more pronounced at end-expiration where leak area was virtually independent of force after the initial leak-inducing force was exceeded (Fig. 3a). The number of node failures and leaks also did not increase as rapidly as the applied force (Fig. 3, b and c). These relationships held for different values of N, k, F_t, and h and with non-uniform distributions of k and F_t. The springs in cells adjacent to the leak approached their initial length, yielding near-zero or zero force in those springs, while the forces in the cells forming the network boundaries were larger because these outer boundaries were fixed.

The main effect of changing the parameters was the adjustment of the force necessary to initiate the leak (Fig. 4a). Decreasing k and h and increasing F_t increased the amount of force or strain required to cause damage to the cells, which indicates the importance of reducing the stiffness of the cells and strengthening the cell–cell junctions to prevent the onset of injury. Indeed, in vitro studies by Yalcin et al. have shown that “fluidization” of the cytoskeleton reduces injury to the epithelial cells during airway reopening.³⁹ However, reducing k or h also increased the leak area at end-inspiration because less stiff cells are easier to stretch, which leads to a greater strain in the network. Thus, if damage has already occurred, increasing the threshold at which the cell–cell junctions break is more important than reducing k or h. In relation to VILI, this indicates that there is a threshold tidal volume (proportional to the stretch force discussed here) that must not be exceeded during ventilation if further injury to the epithelial barrier is to be prevented. This threshold might vary throughout the injured lung, however, as inhomogeneity increases with derecruitment, which could shrink and lower the range of safe tidal volumes. Importantly, when the plots of leak area versus force are scaled by a non-dimensional parameter, they all coalesce onto single master curves for both end-inspiration and end-expiration (Fig. 4c), which strongly supports the generality of our findings.

The force needed to initiate leak was highly variable in the case of inhomogeneous k and F_t and caused the mean damaging force to be reduced (Fig. 5). However, after the first damaging force was exceeded, the network did not experience a greater amount of damage in terms of increased leak area with larger forces (Fig. 6a), although the total number of leaks varied greatly (Fig. 6b). Increasing inhomogeneity in the distributions of k and F_t decreased the threshold for leak initiation, but decreasing μ_k or increasing μ_Ft will increase this threshold, according to the Fig. 4b. For example, to increase F_s at leak onset with 10% variability in μ_k and μ_Ft, μ_k should be increased by about 25%. Greater change in μ_k and/or μ_Ft is required to achieve this with a greater degree of inhomogeneity in the distributions of k and F_t. Presumably, an intervention that decreases mean cell stiffness, strengthens cell–cell junctions, or reduces the degree of inhomogeneity in these properties in an inhomogeneous lung could raise the force threshold below which no leaks form and thus be protective against VILI.

Leak number also varied over different network sizes (Fig. 3c). In the networks with smaller N, the number of leaks increased with stretch force, but the opposite occurred in larger networks. The converging behavior of the leak area and leak number with increased N suggests that in the case of a sheet with an infinite number of cells, a particular stretch force causes a single leak to form that increases with a constant slope at end-inspiration but remains the same size at end-expiration as the stretch force increases. We note, however, that our model of the epithelial monolayer with a finite number of cells and fixed outer boundary is likely more physiologically representative of an alveolus and the fibrous alveolar duct than an infinite sheet of cells.

The findings from this study are relevant to our previous experimental findings in a mouse model of VILI.³⁰ In those experiments, anesthetized and paralyzed BALB/c mice were mechanically ventilated at high tidal volume and zero positive end-expiratory pressure for up to four hours to induce VILI. We assessed the derecruitability of the lung by measuring the rate at which lung elastance increased during regular (low tidal volume) mechanical ventilation following a recruitment maneuver³ and found that derecruitability accelerated throughout the 4-hour experiment at a rate that increased with the tidal volume used to generate lung injury. This finding was expected and can potentially be explained as the result of plasma proteins leaking into the airspaces through holes in the epithelial barrier to deactivate pulmonary surfactant.²² This corresponds to the predications of the present study that leak will increase with increased force at end-inspiration.

What we have so far been unable to explain, however, is another observation from our previous study,³⁰ which is that the peak airway pressure during the 4-hour period of mechanical ventilation increased only linearly and that the rate of increase was independent of tidal volume. Indeed, it was this result that prompted the present modeling study, and the results suggest an answer. Our model predicts that epithelial leak area at end-expiration remains relatively constant with increasing stretch force (Fig. 4c). Accordingly, flow of edematous fluid into the airspaces would be expected to remain relatively constant with increasing tidal volume because more time is spent near end-expiration, and at end-inspiration the flow would be opposed by the increased alveolar air pressure. Presumably the movement of proteins into the airspaces is enhanced during the increased leak at end-inspiration to explain the increased derecruitability that occurs with more severe lung injury. We recognize that our current computational model addresses only one mechanism of VILI, barrier distribution caused by overdistension leading to volutrauma and barotrauma, and acknowledge that atelectrauma^1,6,16 and biotrauma^12,25,32 also contribute. Our mouse model experiments show that both atelectrauma and volutrauma are necessary in the pathogenesis of VILI, and the results of the present model provide insight into how the two are interrelated.

Although our model predictions of the effects of stretch on leak seem to make sense in terms of our in vivo studies of lung injury, one can imagine that it might be possible to test these predictions in vitro. In fact, numerous studies^{11,28,33,35,38,41} have investigated stretch-induced injury of an alveolar epithelial monolayer. Unfortunately, many of these studies have not visualized the progression of leak or damage during stretch in vitro at strain magnitudes and durations large enough to mimic mechanical ventilation, preventing full characterization of epithelial barrier disruption in VILI. Additionally, the cells are prone to detachment from the membrane being stretched,³⁶ so direct validation in this manner might be problematic.

Accordingly, the predictions of the present study must be viewed in light of the limitations imposed by the various assumptions we made in creating the model. For example, we assume that breaching the epithelium constitutes the crucial step in allowing plasma fluid and proteins to accumulate in the alveolar spaces and thus cause the disruption of surfactant function that leads to the derangements in lung mechanics associated with ARDS. For this to be the case, however, the endothelium must have already been breached in order to allow interstitial accumulation of these blood-derived materials, so presumably a corresponding model could be applied to the breaching of the endothelium. We do not include a mechanism for cell contractility and wound healing in the model because our study was motivated by acute events occurring over an hour or two during the development of VILI in mice. However, modeling VILI over an extended time period would necessitate this addition to the model. We also do not explicitly account for the attachment of the epithelial cells to their basement membrane but instead assume that any mechanical resilience due to this membrane is accounted for in the values of the parameters defining the strengths of the junction nodes and their connecting spring stiffnesses. Similarly, because the model is two-dimensional we do not take the heights of the cells into account and any influence this might have on cell–cell junction strength; again, such strength variations are assumed to be incorporated into the junction strengths in the model. Also, cells might have an elastic impedance to changes in shape necessitated by height change, assuming that their volumes are conserved. The model could, in principle, be extended to include the third dimension (cell height). For example, Suki and Hubmayr³¹ described a multi-layer spring model with epithelial cells sandwiched between a basement membrane and an alveolar surface film; a similar method could be adapted to the hexagonal cell model. However, we do not believe this would change the essential nature of the predictions of leak formation with stretch.

We also considered a model that is purely elastic rather than viscoelastic. This means that leak formation in the model is purely a function of strain and not strain history, which is clearly not the case in reality; VILI generally arises when injurious stretch to the alveolar tissue is applied cyclically over an extended duration of mechanical ventilation. This effect could be included in the model by replacing the cytoskeletal and cell membrane springs with, for example, Kelvin bodies, but solving the model would be computationally much more expensive so as a first step we decided to consider the purely elastic case in the present study. Similarly, we could have, in principle, tiled the monolayer with cells that exhibited different shapes instead of being identical hexagons, and we could have perhaps considered a monolayer geometry that is more representative of an alveolar wall shape than a simple flat square. However, these seem likely to be details that would introduce second order effects at best, and thus would be unlikely to change our overall conclusions. Our sensitivity analyses (Figs. 4–6) and most especially the single normalized master curves we obtained (Fig. 4c) suggest that our model results are robust within these limitations. Finally, we have modeled leak as occurring from a single stretch, whereas in VILI such leak occurs over an extended time period that includes many separate breaths. This could be readily included in the model, however, by making node failure above a threshold occur stochastically so, on average, that many cycles could be required above the threshold before a leak finally occurs.

In summary, we have developed a computational model of a sheet of epithelial cells designed to recapitulate the manner in which leaks appear in the alveolar epithelium when the lung parenchyma is overstretched during mechanical ventilation. The area of the leak develops in a complex manner as a function of stretch, beginning with a sudden yield point where the first leak appears and then progressing slowly as stretch increases, particularly at end-expiration. These model results are compatible with our prior observations³⁰ in overventilated mice in the sense that they might explain why peak airway pressure increased linearly with progressing lung injury at a rate that was virtually independent of tidal volume, while derecruitability increased as a function of parenchymal strain.