Robust Low-dose CT Perfusion Deconvolution via Tensor Total-Variation Regularization

Abstract

Acute brain diseases such as acute strokes and transit ischemic attacks are the leading causes of mortality and morbidity worldwide, responsible for 9% of total death every year. ‘Time is brain’ is a widely accepted concept in acute cerebrovascular disease treatment. Efficient and accurate computational framework for hemodynamic parameters estimation can save critical time for thrombolytic therapy. Meanwhile the high level of accumulated radiation dosage due to continuous image acquisition in CT perfusion (CTP) raised concerns on patient safety and public health. However, low-radiation leads to increased noise and artifacts which require more sophisticated and time-consuming algorithms for robust estimation. In this paper, we focus on developing a robust and efficient framework to accurately estimate the perfusion parameters at low radiation dosage. Specifically, we present a tensor total-variation (TTV) technique which fuses the spatial correlation of the vascular structure and the temporal continuation of the blood signal flow. An efficient algorithm is proposed to find the solution with fast convergence and reduced computational complexity. Extensive evaluations are carried out in terms of sensitivity to noise levels, estimation accuracy, contrast preservation, and performed on digital perfusion phantom estimation, as well as in-vivo clinical subjects. Our framework reduces the necessary radiation dose to only 8% of the original level and outperforms the state-of-art algorithms with peak signal-to-noise ratio improved by 32%. It reduces the oscillation in the residue functions, corrects over-estimation of cerebral blood flow (CBF) and under-estimation of mean transit time (MTT), and maintains the distinction between the deficit and normal regions.

I. Introduction

Computed tomography perfusion (CTP) has important advantages in clinical practice due to its widespread availability, rapid acquisition time, high spatial resolution and few patient contraindications. Brain CTP has been proposed for improving the detection of ischemic stroke and evaluation of the extent and severity of hypoperfusion [1], [2]. Recently, the radiation exposure associated with CTP has raised significant public concerns regarding its potential biologic effects, including hair and skin damage, cataract formation and very small but finite risk of cancer induction [3], [4]. Consensus has been reached that the “as low as reasonably achievable” (ALARA) principle should be executed more consistently. The low-dose protocols are unfortunately leading to higher image noise, which is compensated by using spatial smoothing, reduced matrix reconstruction and/or thick-slices, at the cost of lowering spatial resolution [5], [6].

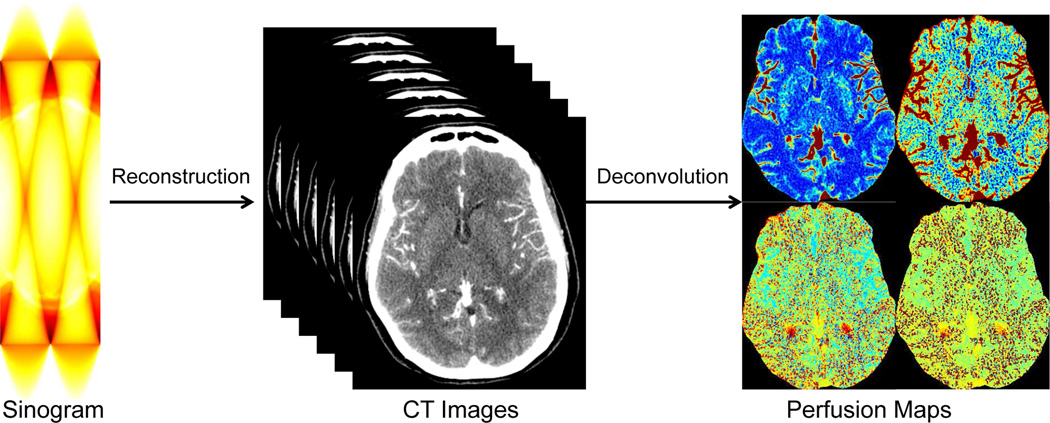
Recent efforts have focused on reducing radiation exposure in CTP while maintaining the spatial resolution and the quantitative accuracy. Various algorithms have been proposed to reduce the noise in the reconstructed CT image series, including the low-pass filtering, edge-preserving filtering such as anisotropic diffusion [7], bilateral filtering [8], non-local means [9], total variation regularization [10], spatio-temporal filtering such as highly constrained back projection (HYPR) [11] and multi-band filtering (MBF). These algorithms attempt to reduce the noise in the reconstructed CT image series (first step in Fig. 1), instead of improving the deconvolution algorithms or the quantification of perfusion maps (second step in Fig. 1). While improving the reconstructed CT images is an important step towards robust and accurate hemodynamics quantification, the deconvolution process itself to quantify the hemodynamic parameter maps is an essential procedure that generates the perfusion maps for disease diagnosis and treatment assessment. A good preprocessing step to reduce the noise combined with an unstable deconvolution algorithm is not good enough for accurate parameter estimation. Thus, perfusion parameter estimation via robust deconvolution is the task we are tackling in this paper.

Fig. 1.

Framework of perfusion map estimation in CT perfusion.

In this work, we propose a new robust deconvolution algorithm to improve the quantification of the perfusion parameter estimation at low-dose by tensor total variation (TTV) regularized optimization. All the previously mentioned noise reduction algorithms for CT image series can complement our model to further reduce the noise and improve the image quality. While previous deconvolution methods have treated each voxel’s concentration signal independently, efforts have been put forward in recent years to take the spatial correlation of the vascular structure and the temporal continuation of the signal flow simultaneously. Spatio-temporal regularization methods to stabilize the residue functions in the deconvolution process have been proposed, including weighted derivative [12], sparse perfusion deconvolution using learned dictionaries [13]–[16], tensor total variation [17], and Bayesian hemodynamic parameter estimation [18] (these methods are reviewed in Section II). However these approaches lack a strong convergence guarantee for the global optimal solution to be reached, which is critical for perfusion quantification in clinical practice.

The purpose of this original research is to develop and evaluate the TTV regularized deconvolution framework for low dose CTP data. The method is retrospectively evaluated in terms of image quality and signal characteristics of low dose brain CTP on both synthetic and clinical data.

The contribution of our work is six-fold: (i) we propose to regularize the impulse residue functions instead of the perfusion parameter maps; (ii) the optimization is performed globally on the entire spatio-temporal data, instead of each patch individually; (iii) total variation regularizer is extended into the four dimensional sequence with distinction between the temporal and spatial dimensions to couple their strength with the optimal coalition; (iv) we provide a globally convergent algorithm with a strong convergence guarantee to solve the convex cost function; (v) there is no need of training data or the learning stage, and (vi) our approach is able to compute all the common perfusion parameters, including cerebral blood flow (CBF), cerebral blood volume (CBV), mean transit time (MTT) and time-to-peak (TTP). Finally we show that our proposed approach reduces the necessary radiation dose to only 8% of the original level and outperforms the state-of-art algorithms with peak signal-to-noise ratio (PSNR) improved by 32%. It also corrects over-estimation of CBF and under-estimation of MTT, and maintains the distinction between the deficit and normal regions.

II. Related work

In this section, we review recent robust deconvolution algorithm for CT or MR perfusion (MRP) [10], [12], [13], [15], [16], [18], [19], with an emphasis on the differences between the previous contributions and our approach.

In [12], a 4-D spatio-temporal data structure is modeled as a piecewise-smooth function with no distinction between the temporal and spatial dimensions. There are two regularization terms: one to penalize the gradient within the homogeneous regions; another to control the weights of the gradient of the edge fields. Though their formulation is inspired by [20], the actual cost function does not have a convergence guarantee. Contrary to their formulation, our proposed approach has the following advantages: (i) the temporal and spatial components are distinguished by assigning different weights and allowing for optimal fusion of their strength; and (ii) it has a convergence guarantee of the convex optimization function.

In [19], the low-dose residue functions are sparsely represented by a linear combination of high-dose residue functions from the repository to remove the noise. The sparsity prior restricts the number of selected candidate residue functions and encourages high-fidelity data restoration. However this approach requires residue functions computed from high-dose perfusion data for learning a dictionary, and the patch-wise sparse representation of the spatio-temporal representations is computational expensive. In contrast, our proposed approach requires no high-quality data for training or learning the dictionary, and performs on the entire 4-D data structure simultaneously with an efficient algorithm and fast convergence rate.

In [13], [15], [16], a patch-wise sparse perfusion deconvolution approach is proposed for low-dose deconvolution. It has two regularization terms: the first one penalizes the error of perfusion map reconstruction from the dictionary patches, the second one penalizes the number of non-zeros in the selection coefficient from the dictionary. The data fidelity term is based on the basic kinetic flow model. Extensions with tissue-specific dictionaries and different perfusion parameters such as blood-brain-barrier permeability are also proposed. However, this line of work needs a training stage on the high-dose data, and the patch-based computation of the perfusion parameters are relatively slow. Each perfusion map also needs to be optimized separately, instead of being computed from one joint model. On the other hand, our proposed approach does not require data and time for training, and the global optimization on the entire 4-D data yields residue functions that can generate all the common perfusion parameter maps in one shot.

In [18], a Bayesian probabilistic framework is proposed to estimate hemodynamic parameters, delays, theoretical residue functions and concentration time curves. Multiple stationary assumptions and new parameters need to be introduced. Moreover the computation of the Bayesian maximum likelihood takes about 10 min on a 256 × 256 × 25 instances. On the contrary, our proposed method does not need complex Bayesian framework and only take less than one minute for computation on a 512 × 512 × 118 spatio-temporal data.

The deconvolution approach proposed in this paper is also distinct from the previous work which uses edge-preserving total variation [10] in low-dose CT reconstruction. [10] focuses on the reconstruction procedure from sinogram to images using inverse Radon transform while our work addresses the deconvolution procedure from image sequences to perfusion maps based on the Indicator dilution theory [21]. Besides this, both the data term and the regularization terms in our paper have substantially different meanings from their definitions. For CT reconstruction, the data term is a projection process, while for deconvolution, it is a spatial-temporal convolution. The TV regularization term is a regularization on 2D CT images for CT reconstruction, while we extended it to 4D tensor regularization involving both the temporal and the spatial correlation information in the deconvolution. To our knowledge, this is the first research proposing tensor total-variation to stabilize the deconvolution process.

III. Materials and methods

A. Data acquisition and preprocessing

Clinical dataset

Retrospective review of consecutive CTP exams in an IRB-approved and HIPAA-compliant clinical trial from August 2007–June 2014 was used. Twelve consecutive patients (10 women, 2 men) admitted to the Weill Cornell Medical College, with mean age (range) of 53 (35–83) years were included. 6 subjects (1–6) had brain deficits caused by aneurysmal subarachnoid hemorrhage (aSAH) or ischemic stroke, and the other 6 subjects (7–12) had normal brain images. CTP was performed with a standard protocol using GE Lightspeed Pro-16 scanners (General Electric Medical Systems, Milwaukee, WI) with cine 4i scanning mode and 60 second acquisition at 1 rotation per second, 0.5 sec per sample, using 80 kVp and 190 mA. Four 5-mm-thick sections with pixel spacing of 0.43 mm between centers of columns and rows were assessed at the level of the third ventricle and the basal ganglia, yielding a spatio-temporal tensor of 512 × 512 × 4 × 118 where there are 4 slices and 119 temporal samples. Approximately 45 mL of nonionic iodinated contrast was administered intravenously at 5 mL/s using a power injector with a 5 second delay. These acquired CTP data at high-dose were considered the reference standard for comparison to lower-dose CTP. For data analysis, vascular pixel elimination was applied by using a previously described method [22], in which the threshold for a vascular pixel was 1.5 times the average CBV of the unaffected hemisphere.

Low-dose simulation

To avoid the unethical repetitive scanning of the same patient at different radiation doses, we follow the practice in [23], [24] to simulate low-dose CT scan by adding spatially correlated statistical noise to the reconstructed CT images (before deconvolution). The tube current-exposure time product (mAs) varies linearly with the radiation dosage level. The dominant source of noise in CT imaging is quantum mottle and it is inversely proportional to the square root of mAs $(1/\sqrt{\mathrm{m}\mathrm{A}\mathrm{s}})$.

The standard deviation of the added noise is computed by

$${\sigma }_a=K·{(\frac{1}{I}-\frac{1}{I_0})}^{\frac{1}{2}}$$ (1)

where I and I₀ are the tube current-exposure time product (mAs) at low-dose and normal dose. K is calibrated on 22 patients and the average value of $K=103.09\mathrm{m}{\mathrm{A}}^{\frac{1}{2}}$. Gaussian noise is convolved with the noise autocorrelation function (ACF) generated from scanned low-dose phantom and scaled to the desired σ_a. For low-dose tube current of 30, 15 and 10 mAs gives the standard deviation σ_a = 17.27, 25.54, 31.73. The noise spectrum of any simulated noise added to any image by this procedure is guaranteed to have the spectral property observed in an actual CT scan of the phantom on the same scanner.

Synthetic dataset

Because the clinical CTP does not have ground truth perfusion parameter values for comparison, we first use synthetic data to evaluate the proposed algorithm. The arterial input function (AIF) is simulated using a gamma-variant function [25] with the analytical form of:

$$c_{\mathit{\text{art}}}(t)=\{\begin{array}{cc}0\hfill & \text{if }t\le t_a\hfill \\ a{(t-t_a)}^b{e}^{-(t-t_a)/c}\hfill & \text{if }t>t_a\hfill \end{array}$$ (2)

where t_a is bolus arrival time to any given region. Generally, a = 1, b = 3, c = 1.5 s, t_a = 0 are used to generate AIF typically obtained for a standard injection scheme. The transpose function h(t) is

$$h(t;\alpha ,\beta )=\frac{1}{{\beta }^{\alpha }\mathrm{\Gamma }(\alpha )}{t}^{\alpha -1}{e}^{-t/\beta }\hspace{1em}\alpha ,\beta >0$$ (3)

We set β = MTT/α to satisfy the central volume theorem [26]. Three types of experiments were performance on synthetic data: residue function recovery, uniform region estimation and contrast preserving.

Digital brain perfusion phantom

To provide a more authentic evaluation of the deconvolution algorithms on brain perfusion data, we use the Digital Brain Perfusion Phantom package¹ provided by Pattern Recognition Lab, FAU Erlangen-Nurnberg, Germany. The package offers data and MATLAB tools to create a realistic digital 4D brain phantom with user-input regions of infarct core and ischemic penumbra in the white and gray matters, as well as the healthy tissue. Since the classical digital CT perfusion phantoms usually consist of homogeneous structures and therefore have a very sparse representation in transformed domains, this digital phantom derived from a human volunteer with additionally created spatial variation allows a more realistic evaluation platform for non-linear regularization of perfusion CT with regions with high intrinsic variability.

B. Computation of perfusion parameters using deconvolution

The computational framework of the perfusion parameters in CTP has been well explained in a review paper by [27]. We briefly introduce the mathematic functionals here and lay the foundation for our proposed algorithm. For a volume under consideration v_voi, let c_art be the local contrast agent concentration at the artery inlet, and c_voi be the average contrast agent concentration in v_voi. ρ_voi is the mean density of the volume v_voi. CBF is defined as the blood volume flow normalized by the mass of the volume v_voi and is typically measured in mL/100g/min. CBV quantifies the blood volume normalized by the mass of v_voi and is typically measured in mL/100g. MTT usually measured in seconds, is defined as the first moment of the probability density function h(t) of the transit times. TTP of the time-concentration curve is the time for the contrast concentration to reach its maximum.

Furthermore, the (dimensionless) residue function R(t) quantifies the relative amount of contrast agent that is still inside the volume v_voi of interest at time t after a contrast agent bolus has entered the volume at the arterial inlet at time t = 0, as

$$R(t)=\{\begin{array}{cc}1-{\int }_0^{t}h(\tau )d\tau \hfill & \text{if }t\ge 0\hfill \\ 0\hfill & \text{if }t<0\hfill \end{array}$$ (4)

Due to the various transit times within the capillary bed, the contrast will leave the volume gradually overtime. According to the indicator-dilution theory, the time attenuation curve (TAC) c_voi can be computed by

$$c_{\mathit{\text{voi}}}(t)=CBF·{\rho }_{\mathit{\text{voi}}}·{\int }_{-\infty }^{\infty }{c}_{\mathit{\text{art}}}(\tau )R(t-\tau )d\tau =CBF·{\rho }_{\mathit{\text{voi}}}·(c_{\mathit{\text{art}}}\otimes R)(t)$$ (5)

where ⊗ denotes the convolution operator. Here the variables c_voi(t) and c_art(t) can be measured and are known, whereas the values of CBF, R(t) and ρ_voi are unknown. To compute the perfusion parameters, an intermediate variable, the flow-scaled residue function K(t) is introduced:

$$K(t)=CBF·{\rho }_{\mathit{\text{voi}}}·R(t)$$ (6)

which is given in units of 1/s. The function c_art(t) is usually replaced by a global arterial input function (AIF) measured in a larger feeding artery in order to achieve a reasonable signal-to-noise ratio (SNR). In brain perfusion imaging, the anterior cerebral artery is often selected. Thus, Eq. (4) can be rewritten as

$$c_{\mathit{\text{voi}}}(t)=(AIF\otimes K)(t)$$ (7)

Hence K(t) can be computed from the measured data AIF(t) and c_voi(t) using a deconvolution method, and the perfusion parameters may be determined as

$$CBF=\frac{1}{{\rho }_{\mathit{\text{voi}}}}·\text{max }(K(t))$$

$$MTT=\frac{1}{\text{max }(K(t))}·{\int }_0^{\infty }K(\tau )d\tau$$ (8)

$$CBV=MTT·CBF=\frac{1}{{\rho }_{\mathit{\text{voi}}}}·{\int }_0^{\infty }K(\tau )d\tau$$

$$TTP=\underset{t}{\text{arg max }}{c}_{\mathit{\text{voi}}}(t)=\underset{t}{\text{arg max}}(AIF\otimes K)(t)$$

Here using max (K(t)) instead of K(0) has particular practical advantages due to bolus delay, defined as the delay time between the contrast arrival at tissue and the artery due to disease or other reasons.

In practice, AIF and c_voi(t) are sampled at discrete time points, t_i = (i − 1) · Δt with i = 1, …, T. Eq. (7) can be discretized as

$$c_{\mathit{\text{voi}}}(t_i)={\int }_0^{\infty }AIF(\tau )K(t-\tau )d\tau \approx \mathrm{\Delta }t\sum _{j=1}^{T}AIF(t_j)K(t_{i-j+1})=\mathrm{\Delta }t\sum _{j=1}^{T}AIF(t_{i-j+1})K(t_j)$$ (9)

Here we assume that the values of AIF(t) can be neglected for t > T. The end of summation index can also be set to i instead of T since K(t) = 0 for t < 0. For a voxel of interest, Eq. (9) can be abbreviated as

$$c=Ak$$ (10)

where Δt and AIF(t_i) are incorporated in the matrix A ∈ ℝ^T×T, c_voi(t_i) and K(t_i) represent the entries in vectors c ∈ ℝ^T and k ∈ ℝ^T. For a volume of interest with N voxels, we have

$$C=AK$$ (11)

where C = [c₁, …, c_N] ∈ ℝ^T×N, K = [k₁, …, k_N] ∈ ℝ^T×N represent the contrast agent concentration and scaled residue function for the N voxels in the volume of interest.

In practice, the causality assumption in Eq. (9), i.e. the voxel signal cannot arrive before the AIF, may not hold. The AIF can lag c_voi(t) by a time delay t_d in practice because the measured AIF is not necessarily the true AIF for that voxel, thus resulting in AIF(t) = c_art(t − t_d). For instance, this lag can happen when the chosen AIF comes from a highly blocked vessel. Thus the calculated R′(t) should be R(t + t_d) to yield c_voi(t) at the voxel. However the causuality assumption in Eq. (9) makes the estimation of R′(t) improper. Circular deconvolution has been introduced to reduce the influence of bolus delay [28], where R′(t) can be represented by time shifting R(t) circularly by t_d.

Specifically, c_art(t) and c_voi(t) are zero-padded to length L, to avoid time aliasing in circular deconvolution, where L ≥ 2T. We denote the zero-padded time series as c̅_art ∈ ℝ^L×1 and c̅_voi ∈ ℝ^L×1. Matrix A is replaced with its block-circulant version A_circ, with the elements (a_circ)_i,j of the block-circulant matrix A_circ ∈ ℝ^L×L defined as in [27] with the form of

$${(a_{\mathit{\text{circ}}})}_{i,j}=\{\begin{array}{cc}{c}_{\mathit{\text{art}}}(t_{i-j+1}),\hfill & \text{for }j\le i\hfill \\ c_{\mathit{\text{art}}}(t_{L+i-j+1}),\hfill & \text{for }j>i\hfill \end{array}$$ (12)

In this paper, we set L = 2T, and Eq. (10) can be replaced by

$$\overline{c}=A_{\mathit{\text{circ}}}\overline{k}$$ (13)

and Eq. (11) can be replaced by

$$\overline{C}=A_{\mathit{\text{circ}}}\overline{K}$$ (14)

where c̅ ∈ ℝ^L×1 and k̅ ∈ ℝ^L×1 are the zero-padded time series of c and k, as

$$\overline{c}={[c_1,c_2,\dots ,c_N,0,0,\dots ,0]}^T$$ (15)

$$\overline{k}={[k_1,k_2,\dots ,k_N,0,0,\dots ,0]}^T$$

Similarly, C̅ ∈ ℝ^L×N and K̅ ∈ ℝ^L×N are the zero-padded time series of C and K. For simplicity, we use C, A and K to represent the block-circulant version in Eq. (14) in the rest of the paper.

C. Tensor total variation regularized deconvolution

The least square solution of Eq. (11) is equivalent to minimizing the squared Euclidean residual norm of the linear system given by Eq. (11) as

$$K_{ls}=\underset{K\in {ℝ}^{T\times N}}{\text{arg min }}({\Vert AK-C\Vert }_2^2)$$ (16)

However, for the ill-conditioned Toeplitz matrix A, the least-square solution K_ls does not represent a suitable solution. A small change in C (e.g. due to projection noise or low-dose scan) can cause a large change in K_ls. Regularization is necessary to avoid the strong oscillation in the solution due to small singular values of matrix A.

Our assumption is that since the voxel dimensions in a typical CTP image are much smaller than tissue structures and changes in perfusion are regional effects rather than single voxel effects. Within extended voxel neighborhoods the perfusion parameters will be constant or of low-variation, while it is also important to identify edges between different regions where tissues undergo perfusion changes, particularly deficit regions. Specifically the pixel spacing of our clinical data is 0.43 mm between the centers of adjacent rows and columns. In comparison, the tissue structure of the white matter and gray matter usually in the range of 10–50 pixels with relatively similar perfusion parameters or residue functions.

We introduce the tensor total variation regularizer to the data fidelity term in Eq. (16) as

$$K_{ttv}=\underset{K\in {ℝ}^{T\times N}}{\text{arg min }}(\frac{1}{2}{\Vert AK-C\Vert }_2^2+{\Vert K\Vert }_{TV})$$ (17)

It is based on the assumption that the piecewise smooth residue functions in CTP should have small total variation. The tensor total variation term is defined as

$${\Vert K\Vert }_{TTV}^{\gamma }=\sum _{i,j,k,t}\sqrt{\sum _{d=1}^4{({\gamma }_d{\nabla }_d\tilde{K})}^2}$$ (18)

where ∇_d is the forward finite difference operator in dimension d, and K̃ ∈ ℝ^{T×N₁×N₂×N₃} is the 4-D volume obtained by reshaping matrix K based on the spatial and temporal dimension sizes. Here N = N₁ × N₂ × N₃ is the total number of voxels in the entire CTP data and T is the time duration of the whole sampling sequence. Note that the computation is performed on the entire spatio-temporal data in one shot, instead of splitting the data into patches. So there is no parameter for the neighborhood size in the TTV regularization. The forward finite difference is computed based on the difference between two adjacent voxels only, just as in the standard TV. Non-local total variation with difference between non-adjacent voxels would be an interesting research direction in the future. The tensor total variation term here uses the forward finite difference operator using L₁ norm. The regularization parameter γ_i, i = t, x, y, z controls the regularization strength for the temporal and spatial dimension. The larger the γ_i, the more smoothing the TV term imposes on the residue function in i^th dimension.

Since the TV term is non-smooth, this problem is difficult to solve. The conjugate gradient (CG) and PDE methods could be used to attack it, but they are very slow and impractical for real CTP images. Motivated by the effective acceleration scheme in Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) [29], we propose an algorithm to efficiently solve the problem in Eq. (17) based on the framework of [29], which uses FISTA for TV regularization.

Algorithm 1.

The framework of TTV algorithm.

Input: Regularization parameters γi, i = t, x, y, z

Output: Flow-scaled residue functions K ∈ ℝT × N1 × N2 × N3.

K0 = 0

t1 = r1 = K0

for n = 1, 2, …, N do Steepest gradient descent $$K_g=r^n+s^{n+1}{A}^T(C-A{r}^n)$$ where $s^{n+1}=\frac{\mathit{\text{vec}}{(Q)}^T\mathit{\text{vec}}(Q)}{\mathit{\text{vec}}{(AQ)}^T\mathit{\text{vec}}(AQ)}$, Q ≡ AT (Arn − C) Proximal map: $$K^n={\text{prox}}_{\gamma }(2{\Vert K\Vert }_{TV})({\mathit{\text{fold}}}_t(K_g))$$ where ${\text{prox}}_{\rho }(g)(x)≔\underset{u}{\text{arg min }}\{g(u)+\frac{1}{2\rho }{\Vert u-x\Vert }^2\}$ Update t, r $$t^{n+1}=(1+\sqrt{1+4{(t^n)}^2})/2$$ $$r^{n+1}=K^n+((t^n-1)/t^{n+1})(K^n-K^{n-1})$$

end for

The proposed scheme include the following well-known important algorithms:

FISTA

FISTA considers minimizing the following problem:

$$\text{min }f(x)+g(x),x\in {ℝ}^p$$ (19)

where f is a smooth convex function with Lipschitz constant L_f and g is a convex function which may be non-smooth. An accelerated scheme is conceived in FISTA to obtain ε-optimal solution in $O(\frac{1}{\sqrt{\epsilon }})$ iterations.

Steepest gradient descent

To find a local minimum of a function, steepest gradient descent takes steps proportional to the negative of the gradient of the function at the current point. An adaptive step size s [30] is used because the ill-conditioned matrix A makes the solution sensitive to the noise in the observation C. In Algiorithm 1, vec(x) means stacking the values in x as a vector.

The proximal map

Given a continuous convex function g(x) and any scalar ρ > 0, the proximal map associated to function g is defined as follows [29]

$${\text{prox}}_{\rho }(g)(x)≔\underset{u}{\text{arg min }}\{g(u)+\frac{1}{2\rho }{\Vert u-x\Vert }^2\}$$ (20)

For the proximal map, we extended the 2-dimensional TV regularizer in [29] to 4-dimensional and adapted the algorithm to tensor total variation regularization. The entire algorithm is shown in Algorithm 1. Since the cost function in Eq. (17) is convex, global optimal solution can be reached using the proposed algorithm.

IV. Experiments

A. Baseline methods

There are four baseline deconvolution methods we compare against: standard truncated singular value decomposition (sSVD) [25], block-circulant truncated SVD (bSVD) [28], Tikhonov regularization [27] and sparse perfusion deconvolution (SPD) [13]. A threshold value λ is empirically chosen as 0.15 (15% of the maximum singular value) to yield optimal performance for SVD-based and Tikhonov algorithms. The first three methods are the most widely used regularized deconvolution methods for CTP, and widely adopted by commercial medical software [31]. SPD is the state-of-art algorithm for low-dose CTP deconvolution. We also further compare with the state-of-art noise reduction method - time-intensity profile similarity (TIPS) bilateral filter [8] - as a preprocessing step before deconvolution. TIPS reduces noise in 4D CTP scans while preserving the time-intensity profiles that are essential for determining the perfusion parameters. The parameters of TIPS filtering are set as recommended in [8], with half width = 5, and the standard deviation = 3 for the spatial dimension and 0.1 for the temporal dimension. We compare with two combinations of TIPS with deconvolution algorithms: TIPS + bSVD and TIPS + TTV, to examine the strength of TIPS in improving the accuracy of perfusion parameters by reducing the noise in preprocessing. We choose these two combinations as typical examples because bSVD is the mostly widely used deconvolution algorithm in commercial software, and TTV is the proposed robust deconvolution algorithm. Thus in total there are seven algorithms to compare with: sSVD, bSVD, TIPS+bSVD, Tikhonov, SPD, TTV and TIPS+TTV, in the following experiments.

B. Implementation details

All algorithms were implemented using MATLAB 2013a (MathWorks Inc, Natick, MA) on a MacBook Pro with Intel Core i7 2.3G Hz Duo CPU and 16GB RAM. One-tail student test is used to determine whether there is significant difference between the evaluation metrics of the comparing algorithms. A α level of .05 is used for all statistical tests to indicate significance.

C. Initialization

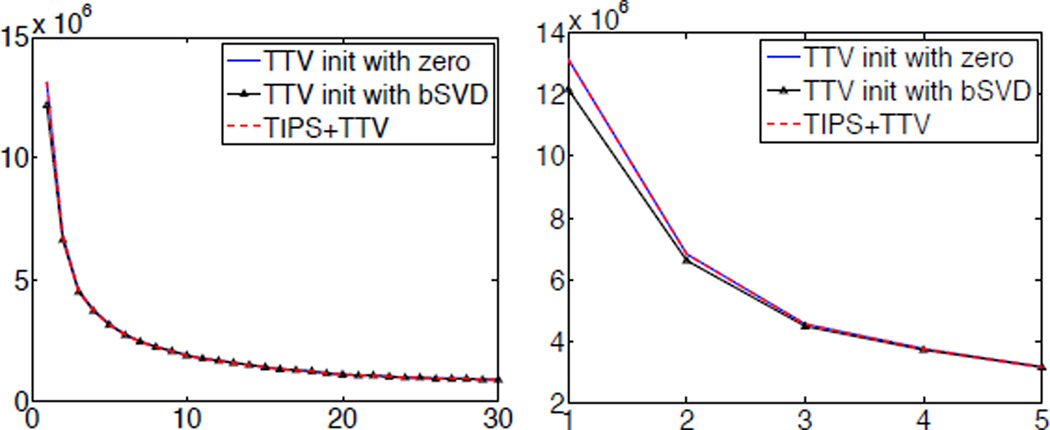
The initialization of the TTV algorithm is important for efficient optimization. Since the TTV algorithm is globally optimal, a good initialization would expedite the process to find the optimal solution. In Algorithm 1, we initialize the TTV algorithm with r¹ = 0 because there is no need to compute any initial solution from existing deconvolution algorithms, and therefore improves the efficiency. We perform an experiment on the digital perfusion brain phantom using TTV algorithm initialized with zero, the solution of bSVD, and TIPS+TTV initialized with zero. Fig. 2 shows the convergence of the cost function of TTV algorithm. It demonstrates that though TTV initialized with the solution of bSVD does have a relatively lower cost to start with, the improvement is minor and by the third iteration, the difference of initialization has disappeared. The plot also shows that TIPS preprocessing does not further improve the optimization to a lower cost. Therefore, initialize r with zero is a practical and efficient option for TTV algorithm.

Fig. 2.

(a) Convergence of cost function over iterations using TTV initialized with zeros, solution of bSVD and TIPS+TTV. (b) Enlarged convergence curve of first five iterations.

D. Evaluation metrics

Three metrics were used to evaluate the image fidelity to the reference: Root mean-squared-error (RMSE), PSNR and Lin’s Concordance Correlation Coefficient (CCC). RMSE evaluates the variability of the estimated low-dose maps compared to the reference. A value close to 0 indicates a smaller difference of data compared to the reference. PSNR reflects the signal-to-noise relationship of the result, and a higher PSNR indicates higher data quality. It is also used in the paper to describe the noise level. Lin’s CCC measures how well a new set of observations reproduce an original set, or the degree to which pairs of observations fall on the 45 line through the origin. Values of ±1 denote perfect concordance and discordance; a value of zero denotes its complete absence. In clinical CTP data, the maximum value in CT data is around 2600 HU, and simulated low-dose of 15 mAs yields σ_a = 25.54, which gives PSNR=40 for the noise level. In the synthetic evaluations, we conducted experiments at much lower PSNRs to highlight the differences between algorithms at even lower radiation.

V. Results

In this section, we describe our experiment design and results on three types of data: synthetic, digital brain phantom, and clinical subjects. The three types of data provide complementary evaluation of the proposed method compared to various baseline methods. The synthetic data gauge the fundamental properties of TTV in residue function recovery, uniform region estimation, contrast preservation, and accuracy at varying perfusion parameter values and noise levels. The digital brain phantom allows for a more authentic evaluation by providing a brain model based on real physiological data and avoiding sparsity by continuously varying perfusion parameters and anatomical structures of MR data. Finally the clinical in-vivo data provides realistic evaluation at varying radiation dosage levels. The subjects with normal brain, aneurysmal subarachnoid hemorrhage (aSAH) and acute stroke also allow the evaluation of diagnosis accuracy based on the perfusion maps computed from the deconvolution algorithms. Overall, the three types of data with the comprehensive experiment designs give a thorough assessment of the proposed method, as compared to the state-of-art. The MATLAB source code will be publicly available at the authors’ webpage².

A. Synthetic Data

Due to the lack of ground truth perfusion parameter values in clinical data, we first evaluate the proposed method on synthetic data.

1) Noise Power Spectrum

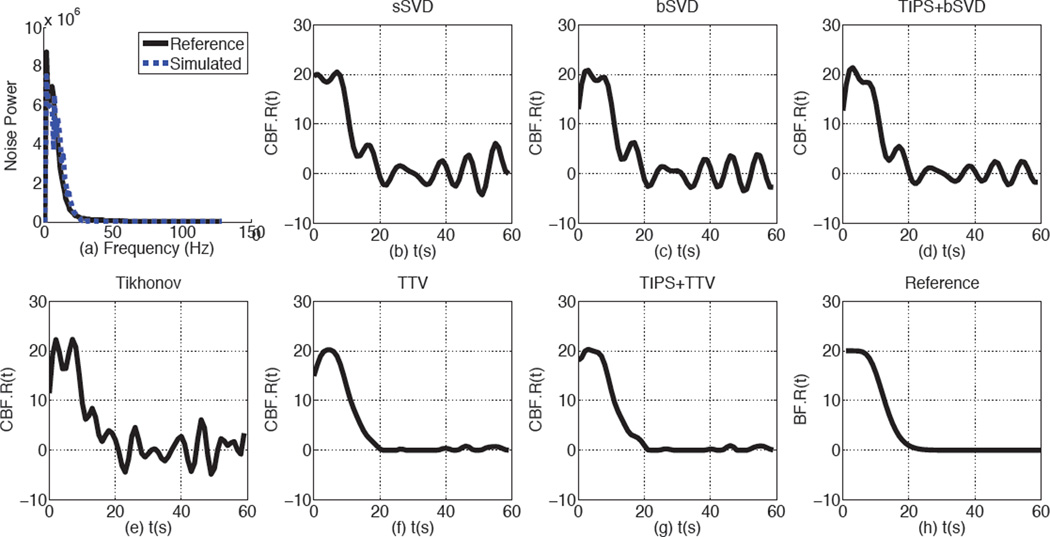
To prove that the simulated noise is comparable to the real noise in the low-dose scans, we generate low-dose phantom by adding correlated Gaussian noise on a CT phantom with a uniform circular region in the background. The noise power spectrum of the simulated and real low-dose phantoms at 10 mA are shown in Fig. 3 (a). From the figure, we could observe that the simulated and real low-dose phantoms have highly comparable noise power spectrum, indicating that the low-dose simulating method adopted in this paper is valid.

Fig. 3.

The Noise power spectrum and the recovered residue functions by baseline methods and TTV. (a) The noise power spectrum is of the scanned phantom image at 10 mAs and simulated statistical correlated Gaussian noise at 10 mA. (b)–(f) The parameters used for residue function recovery are the simulation is CBV = 4 mL/100 g, CBF = 20 mL/100 g/min, PSNR=25. SPD is not included since it optimizes the perfusion maps directly.

2) Residue Function Recovery

We first evaluate the deconvolution methods in residue function recovery. We produce the AIF and residue functions according to Eq. (2) and (4). Then c_voi is generated using Eq. (5), followed by adding correlated Gaussian noise to c_voi to simualted low-dose contrast curve at 10 mA. Finally all the competing algorithms are performed on c_voi and AIF to compare their ability in recovering the ideal residue functions.

The residue function recovered by the baseline methods and TTV are shown in Fig. 3(b–f). The baseline methods show unrealistic oscillation with negative values and elevated peaks, while the residue function recovered by TTV and TIPS+TTV are more in agreement with the reference. Since the maximum value of the residue function is defined as CBF, all the baseline methods over-estimate CBF while TTV-based algorithms has nearly accurate estimation of CBF. Because TTV already has noise removal property, preprocessing with TIPS does not further improve the residue function recovery. On the other hand, even with TIPS preprocessing to remove the noise in the low-dose CTP data, the popular bSVD algorithm still fails to recover the ground truth residue function or the perfusion parameters accurately. This indicates that preprocessing steps of the noisy CTP data can not surrogate a robust deconvolution algorithm to recover the residue functions.

3) Uniform region estimation

Once the residue function are recovered, perfusion parameters CBF, CBV, MTT and TTP can be estimated using Eq. (8). To analyze the perfusion parameter accuracy in the homogeneous region, we first experiment on a small uniform region of 40×40 voxels with the same perfusion characteristics, and compute the mean and standard deviation of the perfusion parameters over this region. We set CBV = 4 mL/100 g, and vary CBF and MTT values or PSNR values to gauge the performance of competing deconvolution algorithms at a wide range of possible conditions. The standard deviation of each algorithm is also computed to judge their stability. Quantitative results are reported to give a detailed comparison using a number of evaluation metrics.

Visual comparison

The ideal variability of the perfusion maps in the uniform region should be zero while the estimated perfusion parameters should be close to ground truth. Fig. 4 shows the estimated perfusion maps of the reference and four methods on the uniform region. While the SVD-based methods (sSVD, bSVD, Tikhonov) behave poorly in recovering the smooth region, TTV yields accurate estimation of the perfusion maps for all four maps. SPD reduces the noise level in estimating CBF and TTP, but is unable to well recover CBV and MTT. It also over-estimate CBF and under-estimate MTT. TIPS preprocessing reduces the noise to certain extent and does improve the perfusion map accuracy and homogeneity when deconvolved with bSVD, yet the noise and artifacts still remain the CBF, MTT and TTP maps. In comparison, TTV not only decreases the noise standard deviation in the estimated perfusion maps, but also restores the accurate quantitative parameters for all maps. TIPS does not further improve the performance of TTV except for TTP, which is more sensitive to noise since it finds the time stamp of the curve peak. The conclusion from this experiment agrees with the residue function recovery result, where TTV performs the best among all deconvolution algorithms, and purely using TIPS for preprocessing could not solve the issues embedded in the deconvolution algorithms.

Fig. 4.

Visual comparison in a uniform region of perfusion parameter (CBF, CBV, MTT, TTP) estimation using baseline methods and TTV. The ideal variation is 0. The reference is the ground truth at CBV = 4 mL/100 g, CBF = 15 mL/100 g/min, MTT = 16 s, TTP = 12 s, PSNR = 15.

Varying perfusion parameters

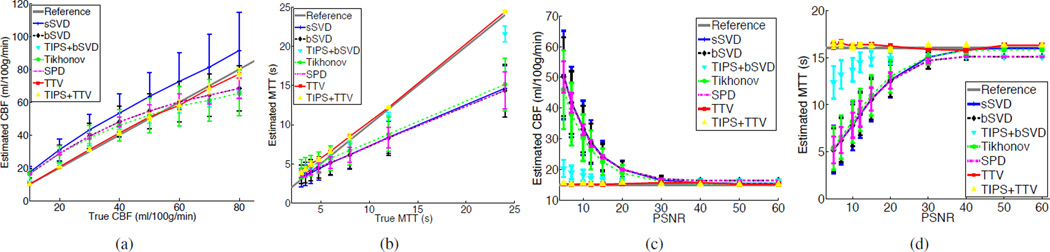
To evaluate the robustness of the deconvolution algorithms at different perfusion parameter values (such as in different tissue types or diseased/healthy regions), we vary the CBF value while keeping CBV the same. Fig. 5 (a)–(b) show the estimated CBF and MTT values at varying CBF values. Obviously, while sSVD tends to over-estimate CBF in all cases, other baseline methods overestimate CBF when CBF is less than 60 mL/100 g/min, and under-estimate CBF when CBF is greater than 60 mL/100 g/min. For MTT, the baseline methods tend to under-estimate MTT. TIPS help to adjust the estimated perfusion parameters to the reference with certain extent, but still deviates from the ground truth. By comparison, TTV has a robust performance in estimating the perfusion parameters at varying CBF values.

Fig. 5.

Comparison of the accuracy in estimating CBF and MTT by sSVD, bSVD, Tikhonov and TTV deconvolution methods. True CBV = 4 mL/100 g. The error bar denotes the standard deviation. (a) Estimated CBF values at different true with PSNR=15. (b) Estimated MTT values at different true MTT with PNSR=15. (c) Estimated CBF values at different PSNRs with true CBF=15 mL/100 g/min. (d) Estimated MTT values at different PSNRs with true MTT = 16 s.

Varying PSNR

To explore the effect of noise levels on the performance of perfusion parameter estimation, we simulate different levels of noise (PSNR varies from 5 to 60) and fix CBF at 15 mL/100 g/min, MTT at 16 s and CBV at 4 mL/100 g. Fig. 5 (c)–(d) show the estimation results. As PSNR decreases, the baseline methods over-estimate CBF and under-estimate MTT. TIPS, as shown in the previous experiments, helps to improve the accuracy to some degree but not perfectly. TTV consistently generates more accurate estimation of CBF than the baseline methods across a broad rage of noise levels. Moreover, while the accuracy of the baseline methods degrades dramatically as the noise level increases, TTV method appears to be remarkably stable.

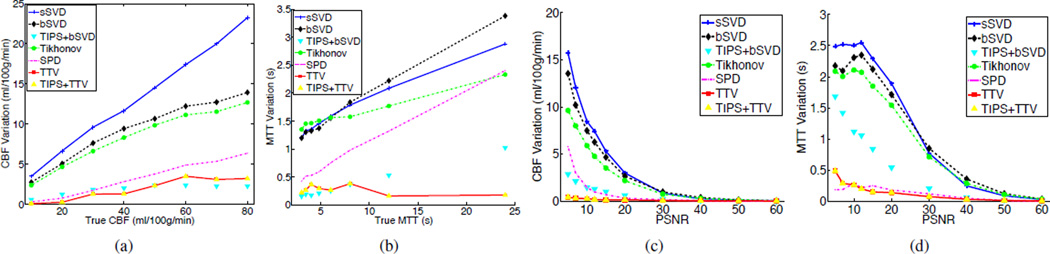
Stability

Stability refers to the standard deviation of the estimated perfusion parameters in repetitive experiments. Stable algorithms is capable of reproducing the same result every time, while unstable algorithms may yield highly distinct output even for the same setup. Thus, stability is a desired property of a robust deconvolution algorithm. As shown in Fig. 6(a)–(b) (where CBF or MTT varies) and Fig. 6 (c)–(d) (where PSNR varies), TTV produces lower CBF and MTT variations than all the baseline algorithms. SPD achieves relatively lower variation, but has lower accuracy of CBF and MTT estimation. TIPS reduces the variation of the bSVD deconvolution algorithm but is less stable compared to TTV. In the meantime, TIPS does not further improve the stability of TTV, which validates the inherent denoising capability of TTV deconvolution algorithm.

Fig. 6.

Comparisons of reducing variations over homogeneous region of (a) CBF at different CBF values with PSNR = 15. (b) MTT at different true MTT values with PSNR = 15. (c) CBF at different PSNR values with true CBF = 15 mL/100 g/min. (d) MTT at different PSNR values with true MTT = 16 s.

Quantitative comparison

To quantitatively compare the accuracy of perfusion parameters in the uniform region, Table I shows RMSE and Lin’s CCC for Fig. 5. CBV is not included because it does not vary. Lin’s CCC are not shown for varying PSNR because the true value for the estimated perfusion parameter does not change and thus Lin’s CCC becomes zero. For CBF and MTT, the most important two perfusion maps for disease diagnosis, TTV-based algorithm significantly outperforms the baseline methods with large margin. In TTP map, sSVD achieves relatively better result when CBF/MTT vary, but the different is small. When PSNR varies, TTV maintains the least RMSE in estimating TTP. An interesting observation is that while the third columns in Table I has higher RMSE than these in the first columns for all baseline methods, TTV has lower RMSE in the third column than in the first column. By observing Fig. 5, it is not difficulty to find that TTV is remarkably robust at different PSNR values, especially at very low PSNR, as shown in Fig. 5(c) and (d). The errors introduced by TTV at different PSNR values are even smaller than those at different true CBF/MTT values. In contrast, the baseline methods either over-estimate CBF or under-estimate MTT at different ground truth CBF/MTT values, but within certain bound, while the error at decreasing PSNR almost increases exponentially. This explains why in Table I TTV reverses the trend in RMSE contrary to the competing methods.

TABLE I.

Average RMSE and Lin’s CCC of the perfusion maps (CBF, MTT and TTP) in a synthetic uniform region of Fig. 5. ‘Estimated’ mean the perfusion parameter to be estimated, ‘varying’ means the varying condition in the evaluation. When the varying parameter is CBF/MTT, the RMSE and Lin’s CCC are averaged over different true CBF/MTT values. When the varying parameter is PSNR, the RMSE is averaged over different PSNR values. The best performance is highlighted in bold font.

Estimated	CBF (mL/100 g/min)			MTT (s)			TTP (s)
Varying	CBF/MTT		PSNR	CBF/MTT		PSNR	CBF/MTT		PSNR
Method/Metric	RMSE	Lin’s CCC	RMSE	RMSE	Lin’s CCC	RMSE	RMSE	Lin’s CCC	RMSE
sSVD	11.69	0.888	36.38	3.60	0.785	10.86	0.47	0.985	2.80
bSVD	7.56	0.931	36.24	3.65	0.772	10.92	0.56	0.977	5.73
TIPS+bSVD	7.04	0.941	4.60	1.08	0.984	3.19	0.57	0.976	0.84
Tikhonov	7.96	0.919	31.57	3.44	0.791	10.64	0.68	0.967	1.98
SPD	7.52	0.931	36.16	3.65	0.773	10.92	5.24	0.977	7.87
TTV	1.60	0.997	0.29	0.71	0.994	0.36	0.52	0.978	0.63
TIPS+TTV	1.60	0.997	0.29	0.71	0.994	0.36	0.52	0.978	0.63

4) Contrast preserving

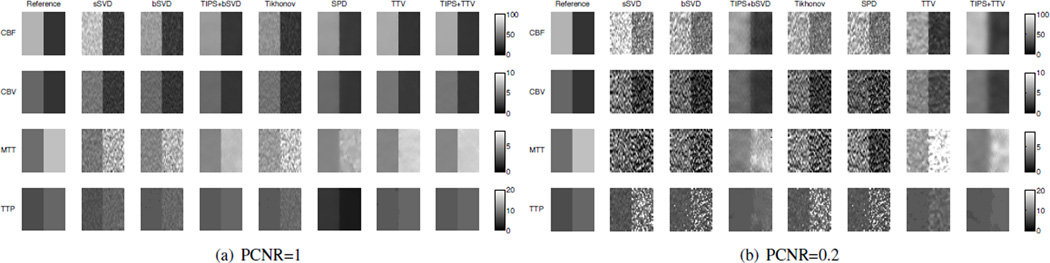
Contrast is an important indicator of how well two neighboring different regions can be distinguished. The contrast of perfusion parameters between the normal and abnormal tissue computed using the deconvolution algorithm from the noisy data should be comparable to that of the noise-free CTP data. To compare the performance of the baseline methods and TTV in preserving contrast, we generate synthetic CTP data spatially containing two 40 × 20 uniform regions with different perfusion characteristic. Peak contrast-to-noise ratio (PCNR) is defined as PCNR = max |I₁ − I₂|/σ, where I₁ and I₂ are the perfusion parameter values of then two images to be compared for contrast. Typical perfusion parameters of the gray matter and the white matter are chosen for the two halves of the region.

Fig. 7 shows the estimated CBF and MTT by the different algorithms when PCNR=1 and 0.2. The corresponding σ=40 and 200.

Fig. 7.

Comparisons of perfusion maps (CBF, CBV, MTT, TTP) estimated by the different deconvolution algorithms in preserving edges between two adjacent regions at PCNR=1 and 0.2. True CBF is 70 and 20 mL/100 g/min on the left and right halves of the region. True CBV is 4 mL/100 g and 2 mL/100 g respectively. True MTT is 3.43 s and 6 s on the left and right halves. True TTP is 6 s and 8 s on two haves. Temporal resolution is 1 sec and total duration of 60 sec.

When PCNR = 1 and the noise level is moderate, SVD-based methods without preprocessing fails to preserve the uniform regions in each half, while the edge is reasonably maintained. SPD performs well in preserving the homogeneous regions in CBF, CBV and TTP but for the most sensitive perfusion map MTT, the noise level is relatively high. TTV performs well on recovering all the perfusion maps while keeping the boundary between the two regions sharp. TIPS preprocessing does help to remove the noise and improve the quality of the perfusion maps significantly when combined with bSVD at this PCNR level, but does not further improve the TTV performance.

When PCNR = 0.2, the story is different. At such a low contrast-to-noise ratio, it is extremely hard to recover the perfusion maps accurately. SVD-based algorithm could hardly preserve the boundary between the two regions, and the noise level is so high that salient information cannot be identified. They also over-estimate CBF and under-estimate MTT when observing the gray-scale color of the maps. SPD reduces the noise level slightly yet the boundary can not be well identified. TIPS removes the noise significantly to recover the perfusion maps, but due to the smoothing in the spatial domain, the boundary of CBF, MTT are blurred. TTV performs favorably compared to all baseline methods in preserving the edges between two adjacent regions in CBF and MTT, as well as accurate estimation of perfusion parameters. Though the variation in the most sensitive map MTT is observable, the boundary is clearly shown. With TIPS, TTV could further reduce the noise level, yet also blur the boundary.

B. Digital brain perfusion phantom

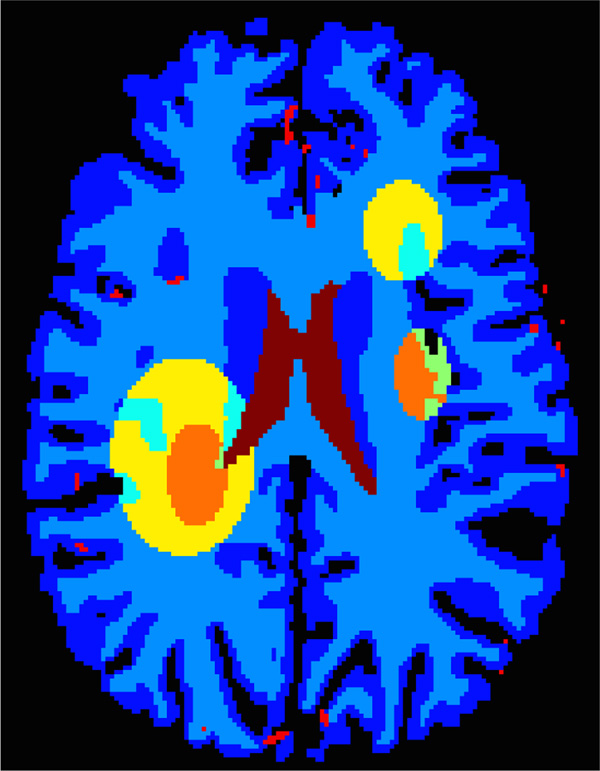
A digital brain perfusion phantom is generated using the MATLAB toolbox. The diseased tissue with reduced or severely reduced blood flow are annotated manually on the digital brain phantom to simulate ischemic penumbra and infarct core in the brain, as shown in Fig. 8. We use the default perfusion parameters in the toolbox for the gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF). TACs are generated by convolving the AIF with residue functions scaled by CBF. All deconvolution or denoising methods are applied to the created digital brain perfusion phantom to compute the residue functions, and then to yield the perfusion parameters including CBF, CBV, MTT and TTP. The visual and quantitative results are compared to evaluate the accuracy and robustness of the competing algorithms.

Fig. 8.

The digital brain perfusion phantom with user-delineated infarct core - severely reduced blood flow (orange) and ischemic penumbra - reduced blood flow (yellow) regions.

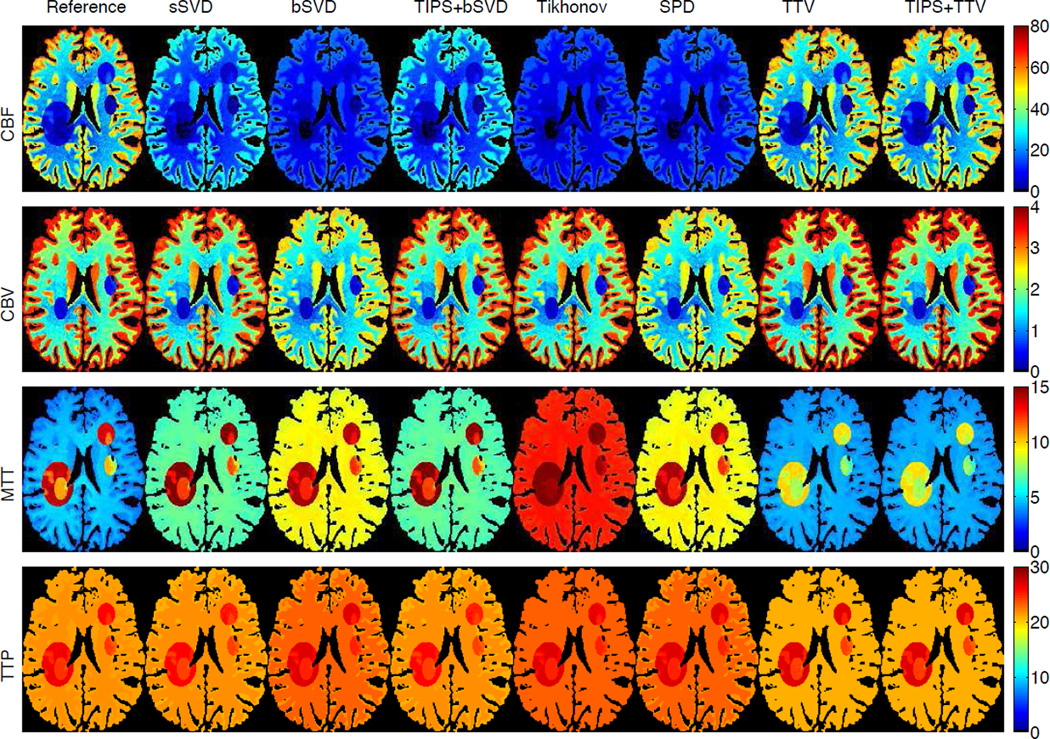
Fig. 9 shows the estimated perfusion maps (CBF, CBV, MTT and TTP) of the digital brain perfusion phantom using the completing methods. The ground truth perfusion maps are provided by the phantom toolbox, so we could compare the estimated maps with the ground truth. Baseline methods under-estimate CBF and over-estimate MTT, while TTV has highly accurate estimation for most of the perfusion maps. Though for MTT, the infarct core and ischemic penumbra are slightly under-estimated, the distinction between the health and reduced blood flow tissue are clear, and the overall MTT map are in better agreement with the reference than the baseline methods. Table II further validates the superiority of TTV algorithm compared to baseline methods for the two most important perfusion maps for clinical diagnosis - CBF and CBV. For MTT and TTP, TTV may not yield the best result for the diseased regions, but the difference with the optimal result is relatively small. It is also noted that TIPS preprocessing helps to boost the performance of bSVD, but may reduce the accuracy for TTV deconvolution by too much smoothing. This further demonstrates the robustness of TTV to noise. The experiments on the digital brain perfusion phantom proves the effectiveness of TTV deconvolution when the perfusion parameters are not sparse in the transformed domain and its capability to recover the anatomical structure and perfusion parameters with high intrinsic variability.

Fig. 9.

Perfusion maps of the digital brain perfusion phantom with infarct core and ischemic penumbra region by annotation. CBF in unit of mL/100 g/min, CBF in mL/100 g, MTT and TTP in sec. (Color image)

TABLE II.

Quantitative evaluation in terms of root mean square error (RMSE) of the perfusion parameters (CBF (mL/100 g/min), CBV (mL/100 g), MTT (s) and TTP (s)) accuracy in the digital brain perfusion phantom using competing deconvolution algorithms in the gray matter (GM), white matter (WM), GM reduced (GMR), GM severely reduced (GMSR), WM reduced (WMR), WM severely reduced (WMSR), and all tissues. The best performance is highlighted with bold font.

	Method	GM	WM	GMR	GMSR	WMR	WMSR	All
CBF	sSVD	24.70	11.02	4.30	1.72	1.78	0.65	17.27
	bSVD	36.29	16.68	4.80	2.35	1.72	0.77	25.52
	TIPS+bSVD	24.73	11.02	4.28	1.72	1.75	0.64	17.29
	Tikh	38.33	17.82	5.49	2.63	1.96	0.88	27.02
	SPD	38.33	17.82	5.49	2.63	1.96	0.88	25.52
	TTV	2.18	0.83	1.71	0.56	0.82	0.23	1.51
	TIPS+TTV	2.21	0.87	1.86	0.62	0.95	0.26	1.55
CBV	sSVD	0.16	0.18	0.57	0.13	0.31	0.07	0.19
	bSVD	0.71	0.43	0.67	0.16	0.36	0.08	0.55
	TIPS+bSVD	0.16	0.18	0.58	0.13	0.31	0.07	0.20
	Tikh	0.13	0.13	0.52	0.10	0.29	0.06	0.16
	SPD	0.13	0.13	0.52	0.10	0.29	0.06	0.55
	TTV	0.11	0.04	0.49	0.08	0.29	0.05	0.13
	TIPS+TTV	0.12	0.04	0.49	0.08	0.29	0.05	0.12
MTT	sSVD	2.81	2.40	1.42	1.78	1.25	1.57	2.48
	bSVD	5.16	4.81	1.47	3.20	0.41	2.02	4.70
	TIPS+bSVD	2.81	2.40	1.36	1.75	1.11	1.52	2.47
	Tikh	8.68	8.11	3.39	5.63	2.12	4.06	7.94
	SPD	8.68	8.11	3.39	5.63	2.12	4.06	4.70
	TTV	0.25	0.28	3.02	1.67	4.04	2.46	1.22
	TIPS+TTV	0.25	0.29	3.08	1.73	4.20	2.55	1.26
TTP	sSVD	0.40	0.38	0.62	0.29	0.60	0.44	0.41
	bSVD	1.20	1.36	0.72	0.81	0.67	0.62	1.24
	TIPS+bSVD	0.40	0.38	0.64	0.29	0.67	0.44	0.42
	Tikh	1.70	1.36	0.74	0.86	0.62	0.65	1.45
	SPD	1.70	1.36	0.74	0.86	0.62	0.65	1.24
	TTV	0.34	0.65	0.18	0.35	0.79	0.41	0.55
	TIPS+TTV	0.34	0.65	0.18	0.37	0.76	0.42	0.55

C. Clinical evaluation

We performed experiments on 12 clinical subjects. Visual comparisons are performed on two subject: one with ischemic stroke and the other with aneurysmal subarachnoid hemorrhage (aSAH). Because repetitive scanning of the same patient under different radiation levels is unethical, low-dose perfusion maps are simulated from the high-dose 190 mAs by adding correlated statistical noise [23]. The maps calculated using bSVD from the 190 mAs high-dose CTP data is regarded as the “gold standard” or reference images in clinical experiments.

1) Visual Comparison

Ischemic stroke

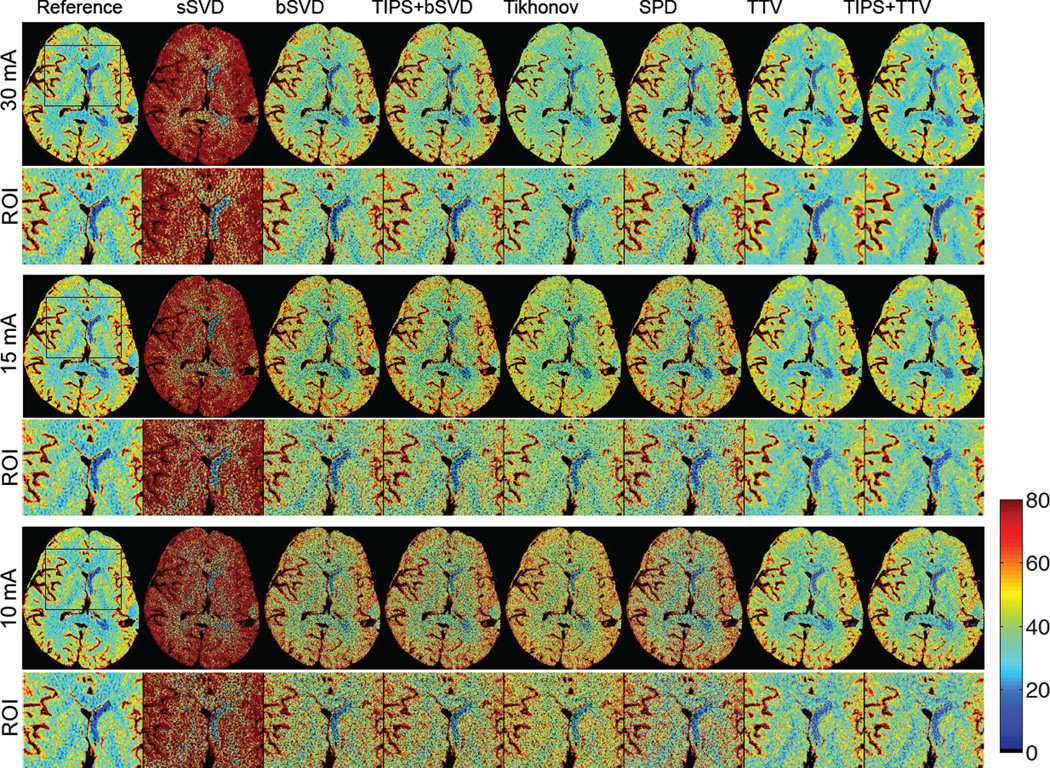
Ischemic stroke is reflected in the CTP map by decreased blood flow in part of the brain area, leading to dysfunction of the brain tissue in that area. Fig. 10 shows CBF maps at reduced tube current-exposure time product (mAs) for a subject with acute stroke in the right middle cerebral artery (MCA) and right posterior cerebral artery (PCA) deep branches (left and right are opposite in the medical image). Fig. 10 displays the CBF maps at 30, 15 and 10 mAs of a subject with ischemic stroke in the right MCA and PCA deep branches. There are significant visual differences between the CBF maps of the different deconvolution methods, where sSVD, bSVD, Tikhonov and SPD overestimate CBF while TTV estimates accurately. With decreased mAs and therefore reduced radiation dosage level, the over-estimation and the increased noise level become more apparent for the baseline algorithms. At all mAs levels, TTV is capable to estimate CBF values at higher accuracy compared to the reference. The ischemic penumbra is in the left of the image with reduced blood flow is more distinguishable from the right hemisphere using TTV deconvolution compared to baseline methods.

Fig. 10.

The CBF (in mL/100 g/min) maps with zoomed ROI regions of a patient with acute stroke (ID 6) calculated using different deconvolution algorithms at tube current of 30, 15 and 10 mAs with normal sampling rate. Baseline methods sSVD, bSVD, Tikhonov and SPD overestimate CBF values, while TTV agrees with the reference. TTP does not help to improve the accuracy. As the tube current decreases and the radiation level reduces, the over-estimation of CBF values using baseline methods becomes more apparent. (Color image)

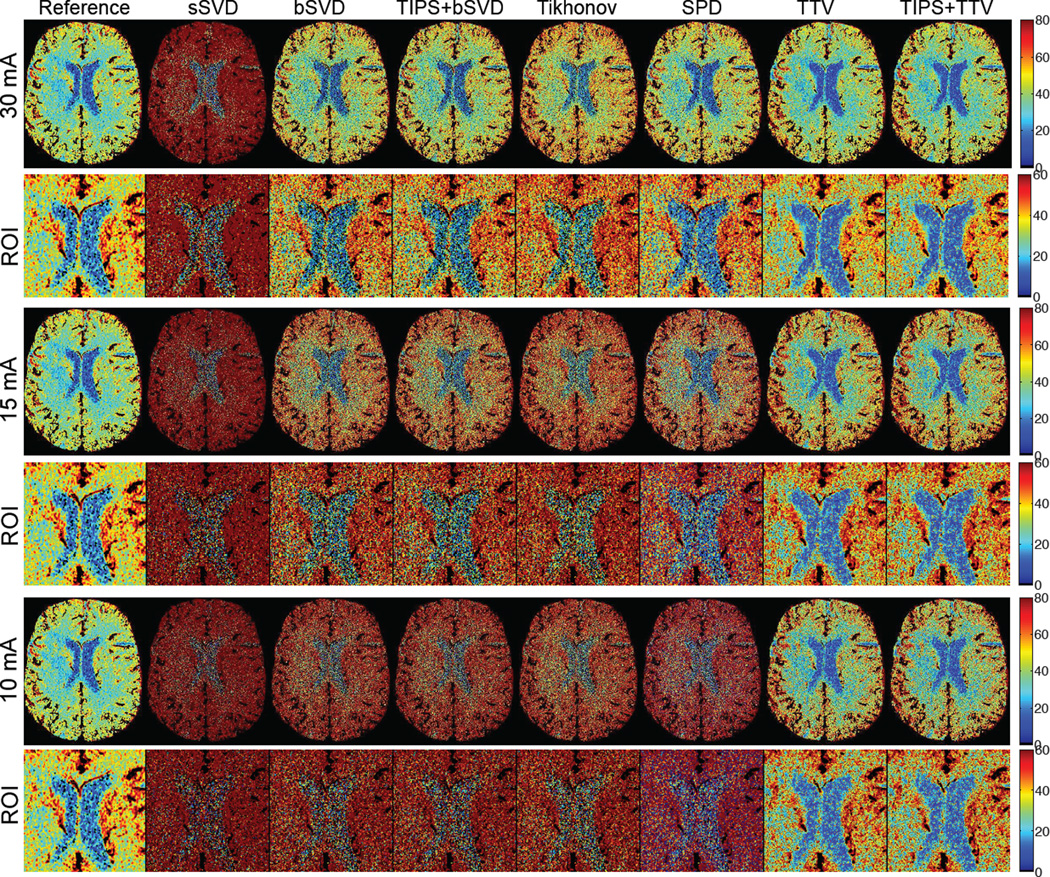
Aneurysmal subarachnoid hemorrhage (aSAH)

aSAH is a severe form of stroke with up to 50% of fetal rate and can lead to severe neurological or cognitive impairment even when diagnosed and treated at an early stage. The imaging of aSAH appears as significantly lower CBF in moderate or severe vasospasm at days 7–9. CBF is the most sensitive perfusion parameter for the diagnosis of cerebral vasospasm, a serious complication of aSAH [32]. Fig. 11 displays the CBF maps at 30, 15 and 10 mAs of a subject with aSAH in the left MCA inferior division. As the tube current-scanning time product in mAs decreases, the baseline methods tend to overestimate CBF with increasing bias, while TTV maintains the data fidelity. The distinction between the white matter, gray matter, cerebrospinal fluid and the arteries are well preserved, and the reduced blood flow on the left MCA (right of the image) is more identifiable, compared to the baseline methods. The noisy and biased estimation in the baseline methods, even with TIPS preprocessing to reduce the noise, can lead to lower diagnosis sensitivity.

Fig. 11.

The CBF (in mL/100 g/min) maps with zoomed ROI regions of a patients (ID 3) calculated using different deconvolution algorithms at tube current of 30, 15 and 10 mAs with normal sampling rate. Baseline methods sSVD, bSVD, Tikhonov and SPD overestimate CBF values, while TTV corresponds with the reference. As the tube current decreases and the radiation level reduces, the over-estimation of CBF values using baseline methods becomes more apparent. (Color image)

2) Quantitative comparison

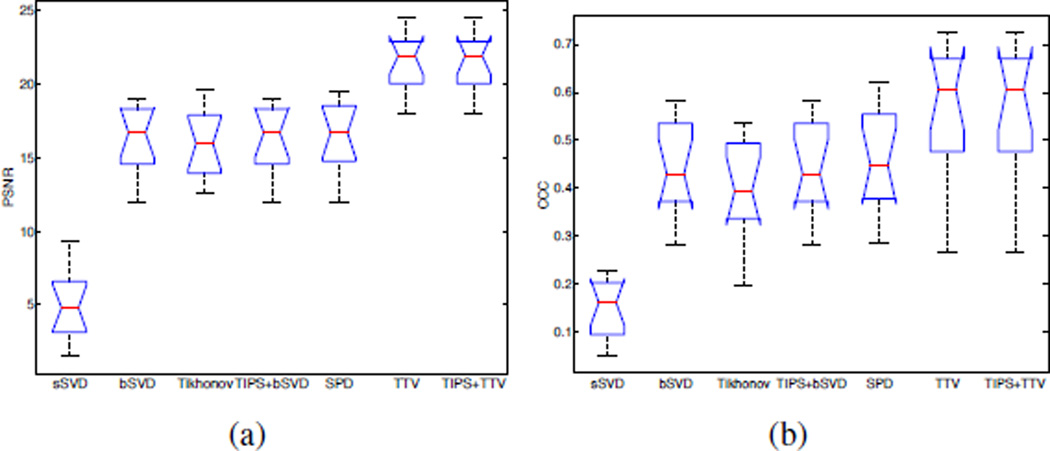
There is significant improvement in image fidelity between the low-dose CBF maps and the high-dose CBF maps by using the TTV algorithm compared to the baseline methods. On average, the PSNR increases by 32%, Lin’s CCC increases by 24% from the best performance by using the baseline methods (Table III, Fig. 12). The quantitative values are computed with the vascular pixel elimination to exclude the influence of high blood flow values in the blood vessels. In Fig. 12, the notch shows the 95% confidence interval for the medians. Since the notches from box plots of TTV-based and the best performance among all the baseline methods (sSVD, bSVD, TIPS+bSVD, Tikhonov, SPD) don’t overlap, we can assume at the (0.05 significance level) that the medians are different. The one-tail student test on the values in Table III also validates that there are statistically significant difference between the PSNR and Lin’s CCC using TTV algorithm compared to the best performance among the baseline methods, with P-value < 0.05.

TABLE III.

Quantitative comparison of seven methods on twelve patients in terms of PSNR and Lins CCC at simulated 15 mAs. Subjects 1–6 have brain deficits due to aneurysmal SAH or ischemic stroke, while subjects 7–12 have normal brain maps. PSNR and Lin’s CCC are computed using the mean value over the whole brain volume with respect to the ground truth (190 mAs using bSVD). The average metrics over all the deficit and/or normal subjects are also computed. The best performance among all methods is highlighted with bold font for each case and the average values. One-tail student test shows the PSNR and CCC of TTV algorithm is statistically significant higher than the best performance in the baseline methods, with P < 0.05

Methods	ID	PSNR	CCC	ID	PSNR	CCC	ID	PSNR	CCC	ID	PSNR	CCC	ID	PSNR	CCC	ID	PSNR	CCC
sSVD	1	2.51	0.074	2	5.02	0.209	3	1.50	0.113	4	3.08	0.116	5	4.57	0.163	6	3.99	0.048
bSVD		14.19	0.306		16.31	0.583		14.93	0.503		12.71	0.407		11.98	0.444		16.37	0.283
Tikhonov		16.03	0.348		16.58	0.537		13.73	0.391		14.15	0.397		12.60	0.432		14.62	0.218
TIPS bSVD		14.19	0.306		16.31	0.583		14.93	0.503		12.71	0.407		11.98	0.444		16.37	0.283
SPD		14.33	0.312		16.33	0.620		15.18	0.517		12.71	0.414		12.00	0.465		16.39	0.284
TTV		20.95	0.664		23.90	0.605		17.94	0.676		19.15	0.609		18.34	0.529		21.60	0.493
TIPS+TTV		20.95	0.664		23.90	0.605		17.94	0.676		19.15	0.609		18.34	0.529		21.60	0.493
sSVD	7	8.17	0.194	8	6.35	0.224	9	6.79	0.159	10	6.08	0.169	11	9.34	0.226	12	3.19	0.07
bSVD		19.05	0.539		16.99	0.377		18.85	0.561		18.06	0.415		18.58	0.531		17.42	0.37
Tikhonov		19.58	0.504		16.64	0.324		19.16	0.502		15.87	0.390		19.34	0.485		13.42	0.20
TIPS bSVD		19.05	0.539		16.99	0.377		18.85	0.561		18.06	0.415		18.58	0.531		17.42	0.37
SPD		19.44	0.559		17.00	0.387		19.17	0.579		18.10	0.428		18.93	0.550		17.46	0.37
TTV		22.03	0.644		24.53	0.403		22.66	0.712		22.44	0.265		23.18	0.727		21.86	0.460
TIPS+TTV		22.03	0.644		24.53	0.403		22.66	0.712		22.44	0.265		23.18	0.727		21.86	0.460

Methods	ID	PSNR	CCC	ID	PSNR	CCC	ID	PSNR	CCC
sSVD	Deficit	3.44	0.120	Normal	6.65	0.174	Average	5.05	0.147
bSVD		14.41	0.421		18.16	0.465		16.29	0.443
Tikhonov		14.62	0.387		17.33	0.400		15.98	0.393
TIPS bSVD		14.41	0.421		18.16	0.465		16.29	0.443
SPD		14.49	0.435		18.35	0.478		16.42	0.457
TTV		20.32	0.596		22.78	0.535		21.55	0.565
TIPS+TTV		20.32	0.596		22.78	0.535		21.55	0.565

Fig. 12.

Comparisons of PSNR and Lin’s CCC on 12 clinical subjects using the competing methods. TTV is our proposed method, and TIPS+TTV is preprocessed with TIPS bilateral filtering. The notch marks the 95% confidence interval for the medians.

D. Computation complexity

For SVD-based algorithms, we need to compute both the singular vectors and the singular values. Therefore the computational complexity is O(NT³) for singular value decomposition on matrix A ∈ ℝ^T×T and N voxels [33]. For TTV, the computation involves mostly matrix and vector multiplication, with the computational complexity of $O({NT}^2/\sqrt{\epsilon })$, where ε is the error bound. When the data matrix and time sequence are large, TTV has lower computational complexity over SVD-based methods.

For computation time, it takes approximately 0.83 s, 2.04 s, 1.35 s, 80.6 s and 25 s to process a clinical dataset of 512 × 512 × 118 by sSVD, bSVD and Tikhonov, SPD and TTV, while TIPS take an additional 20.87 s for preprocessing. The TTV algorithm usually converges within 5–10 iterations. Deconvolution algorithms with less than 1 min processing time is acceptable clinically. In this paper, we use MATLAB implementation of all the algorithms, and TTV needs several iterations while SVD solves the problem in one step. MATLAB is known to be slow in iterations and fast in SVD since it uses lapack. Thus for large dataset in spatial and temporal dimensions, TTV may be more efficient when the number of iterations for TV solver is small.

In terms of trade-off between quality and efficiency, though SVD and Tikhonov based methods are faster, the over-estimation, low spatial resolution, less differentiable tissue types and graining in the perfusion maps generated by these baseline methods for the low-dose data are not acceptable. SPD and TTV have comparable high-quality results for the low-dose recovery, however TTV takes only 30% of the computation time compared to the time for SPD. Moreover, the output of TTV can generate all four perfusion maps at the same time from optimized residue functions, while SPD needs to compute each perfusion map separately.

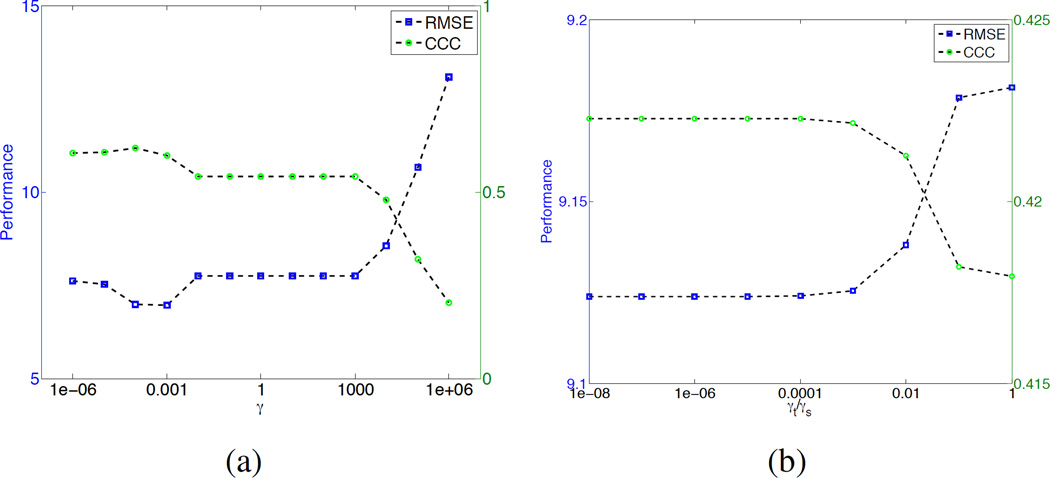
E. Parameters

In the TTV algorithm, there is only a single type of tunable parameter: the TV regularization weight. If the spatial and temporal regularization are treated equally, only one weighting parameter γ needs to be determined. Fig. 13(a) show the RMSE and Lin’s CCC at different γ values. When γ < 10³, RMSE and Lin’s CCC does not change much. The optimal γ is between 10⁻⁴ to 10⁻³.

Fig. 13.

Performace in terms of root-mean-square-error (RMSE) for different parameters (a) γ and (b) ratio γ_t/γ_s.

Since the temporal and the spatial dimensions of the residue impulse functions have different scaling, regularization parameters for t and x, y, z should be different too. We set the spatial γ_s = γ_x,y,z = 10⁻⁴ since the spatial dimensions have similar scaling, and tune the ratio between the temporal weight t and spatial weight γ_s. Fig. 13(b) shows that when the ratio γ_t/γ_s < 10⁻⁴, the performance is stable. Thus we set γ_t = 10⁻⁸ and γ_s = 10⁻⁴ for all experiments.

VI. Discussion

In this study, a novel total variation regularization algorithm to distinctly treat the spatial structural variation and temporal changes is proposed to improve the quantification accuracy of the low-dose CTP perfusion maps. The method is extensively compared with the existing widely used algorithms, including sSVD, bSVD, Tikhonov and SPD, as well as TIPS for preprocessing, on all the common perfusion maps: CBF, CBV, MTT and TTP. Synthetic evaluation with accurate ground truth data is used to validate the effectiveness of the proposed algorithm in terms of residue function recovery, uniform and contrast preserving, sensitivity to blood flow values and noise levels. Digital brain perfusion phantom allows a more authentic validation with ground truth when there are intrinsic structural variability. Finally clinical data with different deficit types using high-dose perfusion maps as the reference image are used to show the visual quality and quantitative accuracy of the perfusion maps at low-dose. In summary, the proposed TTV algorithm is capable of significantly increasing the signal-to-noise ratio in the recovered perfusion maps and residue functions, comparing to the state-of-art deconvolution algorithms.

When the SVD-based algorithms were first introduced in 1996 [25], [34], the perfusion parameters were computed from each tissue voxel independently. It assumes the X-ray radiation and intravenous injection were high enough to generate accurate tissue enhancement curves and AIF for deconvolution. However, SVD-based methods tend to introduce unwanted oscillations [35], [36] and results in overestimation of CBF and underestimation of MTT, especially in low-dose scan setting. The severely distorted residue functions estimated by the baseline methods at simulate 10 mAs tube current in our synthetic evaluation reveal the inherent problem existent in the SVD-based methods: instability. These methods are sensitive to noise in the low-dose environment, and lead to unrealistic oscillations in the residue function, which is the starting point for all perfusion parameter computation.

This instability could be alleviated using the context information in the neighboring tissue voxels with the assumption of a piece-wise smooth model: The residue functions within the extended neighborhood of a tissue voxel will have constant or similar shape, while the changes on the boundary between different regions where tissues undergo perfusion changes should be identified and preserved. The tensor total variation term in the objective function Eq. (17) penalizes large variation of residue functions within the extended neighborhood of the tissue voxels, and adopting the L₁ norm in summing the gradient of all voxels, to avoid the much greater quadratic penalty of L₂ norm at boundaries between different regions. In one word, the spatial and temporal contextual tissue voxels help to robustly estimate the ground truth residue functions while reducing the statistical correlated noise due to the low-dose radiation.

The synthetic evaluations show that the residue functions computed by the baseline methods are unrealistically oscillating, leading to erroneous values of CBF, CBV, MTT and TTP. These baseline methods constantly over-estimate the value of CBF and the errors increase exponentially as PSNR decreases. This misleading over-estimation may cause neglect of infarct core or ischemic penumbra in the patients with acute stroke or other cerebral deficits, resulting in delay in diagnosis and treatment. The large variation in the uniform synthetic region and contrast regions are also caused by the oscillating nature of the results, and introduce misleading information in judging the perfusion condition of the healthy and the ischemic regions.

On the contrary, the proposed TTV method performs comparably to the 190 mAs high-dose results on the 15 mAs low-dose data, which is approximately 8% of the original dose used. The residue functions are stable and have the same shape as the ground truth. Perfusion parameters correlate well with the ground truth, without significant overestimation or under-estimation. The variation in the uniform regions is significantly suppressed, while the edges in the contrast regions are more identifiable.

The clinical evaluations show similar performance comparing the baseline methods and TTV algorithm. While the baseline methods significantly over-estimate CBF values, one of the most important perfusion parameter for stroke diagnosis in recently research [37], TTV yields comparable CBF maps to the reference maps. Moreover, the vascular structure and tissue details are well preserved by the TTV algorithm by removing the noise and maintaining the spatial resolution. Different evaluation metrics and statistical tests further verify the high correlation between the perfusion parameters of the low-dose maps computed by TTV and the reference maps.

There is only one type of parameter γ in the model, which determines the trade-off between data fidelity and TV regularization. Through extensive evaluation, we find that the results are not sensitive to the change of γ in the range of 10⁻⁶ to 10⁻⁴, and the ratio between the temporal and spatial regularization weight in the range of 10⁻⁸ to 10⁻⁴. So we set γ_s = 10⁻⁴ and γ_t = 10⁻⁸ for all the experiments.

While the regularization parameter could be dependent on the temporal and spatial resolution of the data, through our experiments on both the digital perfusion phantom and the clinical data, which have different spatial and temporal resolutions, the same set of regularization parameter work pretty well and robustly estimate the perfusion parameters. Further evaluation on clinical data with varying spatial and temporal resolution would be an interesting analysis for future research.

There are several limitations to our study. First, the validation should be conducted by using larger and more diverse data sets with more samples and disease conditions. Since the aim of our study is to propose a new robust low-dose deconvolution algorithm and validate it preliminarily on synthetic and clinical data, and the improvement on low-dose quantification is significant enough to show the advantage of the proposed method. Second, SVD-based algorithms are used as baseline methods to compare with the proposed TTV. There are other existing methods to post-process the CTP imaging data, including maximum slope (MS), inverse filter (IF) and box-modulated transfer function (bMTF). Further comparison with these post-processing methods should be conducted. But MS, IF and bMTF are not designed for low-dose CTP imaging data, and SVD-based algorithm are the most widely accepted deconvoltuion algorithms in today’s commercial softwares.

In conclusion, we propose a robust low-dose CTP deconvolution algorithm using tensor total variation regularization that significantly improves the quantification accuracy of the perfusion maps in CTP data at a dose level as low as 8% of the original level. In particular, the over-estimation of CBF and under-estimation of MTT, presumably owing to the oscillatory nature of the results produced by the existing methods, is overcome by the total variation regularization in the proposed method. The proposed method could potentially reduce the necessary radiation exposure in clinical practices and significantly improve patient safety in CTP imaging.