Abstract
Purpose
To compare the ordinary monoexponential model with three anomalous relaxation models—the stretched Mittag-Leffler, stretched exponential, and biexponential functions—using both simulated and experimental cartilage relaxation data.
Methods
Monte Carlo simulations were used to examine both the ability of identifying a given model under high signal-to-noise ratio (SNR) conditions and the accuracy and precision of parameter estimates under more modest SNR as would be encountered clinically. Experimental transverse relaxation data were analyzed from normal and enzymatically degraded cartilage samples under high SNR and rapid echo sampling to compare each model.
Results
Both simulation and experimental results showed improvement in signal representation with the anomalous relaxation models. The stretched exponential model consistently showed the lowest mean squared error in experimental data and closely represents the signal decay over multiple decades of the decay time (e.g. 1-10ms, 10-100ms, and >100ms). The stretched exponential parameter αse showed an inverse correlation with biochemically-derived cartilage proteoglycan content.
Conclusion
Experimental results obtained at high field suggest potential application of αse as a measure of matrix integrity. Simulation reflecting more clinical imaging conditions, indicate the ability to robustly estimate αse and distinguish between normal and degraded tissue, highlighting its potential as a biomarker for human studies.
Keywords: spin-spin relaxation, fractional calculus, cartilage, magnetic resonance, multiexponential T2, proteoglycan
Introduction
MRI is increasingly used as a sensitive, noninvasive imaging modality for diagnosis of osteoarthritis (OA). While changes in monoexponential relaxation times have been associated with the degree of cartilage degradation, these parameters exhibit limited specificity to cartilage pathology. For instance, cartilage transverse relaxation time (T2) is modulated by a variety of confounding factors including exercise (1), age (2), gender (3), and hydration (4), limiting its ability to discriminate between normal and diseased tissue. Additionally, monoexponential relaxation times are not specific to particular matrix components, showing correlations with both collagen and proteoglycan content (4).
Improvements in the specificity of relaxation-derived parameters to matrix macromolecules have been shown through the use of alternative relaxation models. For example, multiexponential analysis of T2 relaxation extracts a distribution of exponential relaxation times with components defined by distinct peaks in this distribution. We have previously shown multiexponential T2 relaxation behavior in cartilage (5) and have demonstrated correspondence of specific T2 component fractions to proteoglycan content in normal and degraded cartilage (6). Nonnegative least squares (NNLS) has emerged as a favorable approach for obtaining multiple T2 components from transverse relaxation decay because it requires no a priori assumptions about the number of relaxation components present, and can be used to determine component fractions and relaxation times rather than a single relaxation time produced by monoexponential analysis. However, NNLS also places high demands on signal-to-noise ratio (SNR) and sampling rate of the relaxation decay, posing significant limitations on the applicability of this approach (7,8). These challenges are particularly problematic in the context of MRI studies of cartilage, a thin, anisotropic tissue with short T2.
Recently, we proposed two alternatives to the multiexponential model—the stretched Mittag-Leffler and stretched exponential functions—for describing anomalous relaxation in cartilage (9). Unlike the multiexponential model which assumes, to some extent, fixed water compartments with distinct relaxation times and negligible chemical exchange, these two anomalous relaxation models can incorporate a broad and continuous distribution of relaxation times and can describe processes influenced by multiple length scales and diffusive transport of water through a heterogeneous medium that can modulate transverse relaxation. These additional effects can have a substantive impact on relaxation properties in porous tissue systems like cartilage. In such a system, nuclear spins acquire phase shifts that are influenced by local magnetic fields. Phase shifts accumulated throughout the course the experiment are reflected during acquisition, effectively indicating a type of memory of spin environments in the sample. Our previous work (9) demonstrates that the stretching parameter from these models, the anomalous exponent controlling the extent to which relaxation decay deviates from a monoexponential, is sensitive to the complexity of the material; in particular, this exponent decreases to smaller values with increasing concentration of individual cartilage matrix constituents in solution.
While the need for the identification of alternative transverse relaxation models which closely capture important features of the anomalous T2 signal decay is motivated by the work described above, from the practical standpoint of developing an MRI-based matrix-specific marker for eventual clinical use, these models should: 1) be able to capture relaxation decay features over multiple decades of the decaying signal, 2) provide parameters that are specific to the relevant matrix components affected by disease processes, and 3) permit accurate measurements under clinical imaging conditions, with limited SNR and echo sampling.
In this work we extend our previous study of monoexponential, stretched Mittag-Leffler, and stretched exponential relaxation models (9) to both normal and degraded cartilage. These two models are the focus of the present work, as they require only one additional fitting parameter more than for monoexponential analysis. Additionally, we include analysis using the biexponential model, representing a simplified alternative to multiexponential T2 analysis in cartilage with lower SNR and less stringent acquisition requirements. We examine the ability of discriminating between the decays produced by each model through the use of Monte Carlo simulations using high SNR and high echo sampling rate data. We also use Monte Carlo simulations to establish accuracy and precision estimates for model fit parameters under the in vitro acquisition conditions used for obtaining experimental relaxation data in this work. In addition, we examine the applicability of our results to the eventual clinical setting through simulation of acquisition conditions typically encountered with clinical MRI. Finally, as an extension of our previous work using solutions of matrix components (9), we compare parameters from all four signal models with the biochemically-derived concentration of proteoglycan (i.e. sulfated glycosaminoglycans, sGAG) in normal and enzymatically degraded bovine nasal cartilage (BNC).
Methods
Transverse Relaxation Models
The evolution of transverse magnetization in a uniform sample is classically modeled using the phenomenological Bloch equation:
| (1) |
where transverse magnetization is defined as M⃗xy = Mxx̂ + iMyŷ. The integer-order solution for transverse magnetization in the rotating frame produces the simple monoexponential signal model:
| (2) |
As we have previously described (9), using the Caputo fractional derivative to solve Eq. 1, instead of the ordinary derivative shown above, results in a solution in the form of the stretched Mittag-Leffler (SML) function:
| (3) |
where the stretching parameter α is a constant with values between zero and one, the SML relaxation constant T2,sml has units of milliseconds raised to the α power and Eα is the Mittag-Leffler function defined as:
| (3) |
where Γ is the gamma function.
We have also previously described the stretched exponential (SE) transverse relaxation model (9):
| (5) |
where the units and range of α and the SE relaxation constant T2,se are the same as above for the SML. This expression is also known as the Kohlrausch decay law (10).
Finally, the multiexponential transverse relaxation model consists of a sum of exponential functions:
| (6) |
where wm and T2,m represent the fraction and relaxation time of the mth component, with . Eq. 6 reduces to a biexponential model for M=2.
According to the above Eqs. 2, 3, 5, and 6 for the monoexponential, SML, SE, and biexponential models, respectively, transverse relaxation decay data were fit using the following:
| (7) |
| (8) |
| (9) |
| (10) |
where TE represents the echo time, n represents the number of echoes, and b is a baseline offset term.
Monte Carlo Simulations
Signals were generated using each of the four models under investigation—monoexponential, SML, SE, and biexponential—for both experimental in vitro acquisition conditions encountered in this study and typical clinical imaging acquisition conditions. Average experimentally-derived model parameter values obtained from cartilage under the in vitro conditions used for data acquisition (described below in Cartilage Explant Experiments results section) were used as input values for all simulations. The first set of simulated acquisition conditions was comparable to in vitro experimental conditions in the explant study described below in detail, where the average experimental SNR of 78,000 was used, with TE of 1.2 ms, and 1024 echoes. The second set of simulated acquisition conditions was comparable to that typically encountered on clinical imaging systems, with SNR values of 40 and 100, TE of 8 ms, and 64 echoes. For each signal generated, fits were performed using each of these three models and for each of 200 different realizations of Gaussian noise. For all model comparisons at a given SNR level, a fixed signal amplitude M0 was used. For the in vitro acquisition conditions, mean squared errors (MSEs) were calculated using the time domain signal decays from all fits, and defined as the square root of the sum of squared residuals divided by the number of samples in the decay, serving as a quantitative measure of fit quality. For all simulated conditions, accuracy and precision of derived model parameters was determined. The accuracy of fit parameters is reported in terms of percent error, defined as the difference between the true input simulation value and the average fit value over 200 noise realizations divided by the true input simulation parameter value, all multiplied by 100. Precision is reported in terms of the percent relative standard deviation, defined as the standard deviation of the fit parameter over 200 noise realizations divided by the mean fit value of the parameter, multiplied by 100.
Analysis of Experimental Data
Multi-echo spin echo data were fit using equations 7-10 described above for the monoexponential, SML, SE, and biexponential models, respectively. MSEs were calculated for all fits defined as the square root of the ratio of sum of squared errors to the number of observations. The F-test was used to evaluate if improvements in MSE between the anomalous models and the monoexponential model were statistically significant. Direct comparisons between anomalous models were made using MSE, representing the goodness of fit in this case. All analyses were performed in MATLAB (The MathWorks, Natick, MA).
Cartilage Sample Preparation
BNC plugs (diameter = 8 mm) were excised from the nasal septa of 5-6 month-old calves (Green Village Packing, Green Village, NJ). Each cylindrical plug was cut through the thickness of the septum, that is, the cut was performed laterally based on the original in situ positioning of the cartilage within the animal, using a dermal punch. The membrane covering the in situ lateral surfaces was removed with a scalpel retaining the central volume of the septum. Immediately after harvest, each BNC plug was moistened with Dulbecco's phosphate buffered saline (DPBS) (Invitrogen, Carlsbad, CA, USA) and stored at 4°C. Samples were randomly assigned to control or treatment categories. Treated samples were incubated for up to 24 hrs in 0.1units/ml chondroitinase AC (Ch AC, Seikagaku Corp., Tokyo, Japan) at 37 °C. This enzymatic treatment results in selective depletion of sulfated glycosaminoglycan (sGAG) while having negligible impact on collagen. Samples were washed with DPBS solution after degradation. NMR measurements of degraded samples were acquired immediately after completing the degradation protocol. All samples were subjected to both NMR relaxation analysis and biochemical analysis for sGAG content.
Biochemical Analysis of sGAG Content
Samples were weighed wet and then again after being dried overnight in a vacuum desiccator at room temperature. Dry samples were digested in buffer containing 1mg/ml proteinase k (Sigma-Aldrich, St. Louis MO, USA) and 100 mM ammonium acetate. The 1,9-dimethylmethylene blue assay (DMMB) was used to determine sGAG content (11). Digests were analyzed using a SPECTRAmax 340PC384 spectrometer (Molecular Devices, Sunnyvale, CA, USA), where the absorbance at 525 nm was measured and converted to sGAG content through comparison with chondroitin sulfate C standards (Sigma-Aldrich, ST. Louis, MO, USA).
NMR Measurements
Each BNC sample was placed into a 10 mm diameter NMR tube filled with Fluorinert (Sigma-Aldrich, St. Louis, MO, USA) to maintain sample hydration and eliminate MR signal contamination by the bath solution. Each sample tube was inserted into a vertical 10 mm Helmholtz coil such that the flat circular surfaces of each BNC plug were oriented normal to the main magnetic field, maintaining consistent sample orientation for all samples. NMR measurements were made at 4°C using a 9.4 T vertical bore Bruker DMX NMR spectrometer (Bruker Biospin GmbH, Rheinstetten, Germany). Transverse relaxation decay data were obtained using a Carr-Purcell-Meiboom-Gill (CPMG) pulse sequence. Hard, non-localized excitation and refocusing radiofrequency pulses were used with a rapid digitization of 4 complex-valued samples from the center of each echo, which were combined to form a single complex-valued echo amplitude. Acquisition parameters included TE/TR = 600 μs/10s, 2048 echoes, and NEX = 64. The complex echo amplitudes from the real channel were phased and used for analysis. Odd echoes were discarded, and relaxation decays were truncated at an echo amplitude of 2% of the first echo signal amplitude. Extensive simulations were used to verify that the accuracy and precision of relaxation model fits were not affected by this signal truncation.
Results
Simulations
Table 1 shows average MSEs from the Monte Carlo simulations for each fit model and each input model. Simulation input parameters for each model consisted of average control BNC relaxation parameters. When a monoexponential was used as the input relaxation model to the simulation (top row), both SML and SE models fit equally well, as expected; both models reduce to a monoexponential function when α = 1. Also as expected, biexponential model fits to simulated monoexponential decay data resulted in a degenerate solution showing two components with T2's equal to the simulated monoexponential input value, and thus a comparable MSE to the monoexponential fit. When anomalous relaxation models were simulated using the experimentally derived input parameters (i.e. α values not equal to 1 or two exponentials with different T2 values), the smallest MSEs were obtained from fits using the correct input model. These results show a distinct difference between the anomalous models using parameters derived from cartilage relaxation data and the ability to distinguish between them using high SNR and rapid echo sampling. While simulation results shown in Table 1 were obtained using the average fit values from control samples as the input simulation parameters, comparable results were also obtained using average fit values from degraded samples as simulation input parameters (data not shown) indicating the ability to distinguish between each model under degraded sample conditions.
Table 1. Average MSE values from Monte Carlo simulations using SNR=78,000.
| Average fit MSE | ||||
|---|---|---|---|---|
|
|
||||
| Input model | Monoexponential | Stretched exponential | Stretched Mittag-Leffler | Biexponential |
| Monoexponential | 0.995 | 0.994 | 0.994 | 0.995 |
| Stretched exponential | 517.544 | 0.99 | 286.046 | 57.04 |
| Stretched Mittlag-Leffler | 286.950 | 51.366 | 0.994 | 60.55 |
| Biexponential | 427.328 | 56.947 | 296.514 | 0.996 |
Values represent the average mean squared error (MSE) of each fit model from 200 simulations for a given input model. MSE is defined as , where n is the number of measurements, Ŷl is the predicted value, and Yi is the measured value. Simulation input relaxation parameters were based on the average control BNC values obtained experimentally. 1024 echoes with TE=1.2 ms were used with SNR = 78,000, representing the average SNR obtained from in vitro relaxation decay data of BNC.
Table 2 shows the accuracy and precision of fit parameters for each model using three different SNR levels; in this case, results are only reported using fit models which matched the simulation models. As expected, simulations using high SNR, comparable to the experimental SNR, and in vitro acquisition conditions show errors of less than 0.03%, indicating excellent experimental conditions for accurate estimation of model parameters for comparison with biochemical measures.
Table 2. Accuracy and precision of fit parameters from Monte Carlo simulations.
| Model | Parameter | SNR = 78,000 | SNR = 100 | SNR = 40 | |||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Accuracy (%) | Precision (%) | Accuracy (%) | Precision (%) | Accuracy (%) | Precision (%) | ||
| Mono-exponential | T2 | 3.36e-5 | 7.45e-4 | -0.22 | 1.54 | -1.13 | 3.75 |
|
| |||||||
| Stretched exponential | T2,se | -8.54e-6 | 9.60e-4 | 0.12 | 2.27 | 0.06 | 5.89 |
| αse | -1.20e-4 | 1.37e-3 | 0.38 | 3.03 | 1.66 | 7.93 | |
|
| |||||||
| Stretched Mittag-Leffler | T2,sml | -4.57e-5 | 7.81e-4 | -0.11 | 1.64 | -0.34 | 5.12 |
| αsml | -3.56e-4 | 4.94e-4 | -0.31 | 1.27 | 0.96 | 3.46 | |
|
| |||||||
| Biexponental | w1 | 2.21e-3 | 2.58e-2 | -25.47 | 35.27 | -38.69 | 35.26 |
| T2,1 | 7.14e-4 | 2.43e-2 | -24.89 | 30.41 | -30.29 | 45.25 | |
| T2,2 | 2.87e-4 | 4.17e-3 | -3.25 | 5.36 | -4.12 | 7.29 | |
Each sample condition was simulated with 200 noise realizations. SNR = 78,000 was used, representing the average experimental SNR from in vitro BNC experiments. Two more modest levels, SNR = 100 and SNR = 40, were also simulated representing typical levels for clinical imaging. The average T2, α, and w values derived experimentally from control BNC were used as input values. Decay data for the high SNR condition were simulated using 1024 echoes with TE = 1.2 ms. Decay data using SNR = 100 and 40 were simulated using typical imaging parameters consisting of 64 echoes and TE= 8 ms. Accuracy is defined as fit parameter percent error, which is the difference between the true simulation input parameter and the average fit value over 200 noise realizations, divided by the true input simulation parameter value, all multiplied by 100. Precision is reported as the percent relative standard deviation, which is the standard deviation of fit residuals over 200 noise realizations divided by the mean fit value of the parameter, multiplied by 100.
Results for the more modest SNR conditions displayed in columns 3-6 of Table 2 show accuracy and precision using simulated clinical imaging acquisition parameters and conditions, including lower SNR. For the monoexponential, SE, and SML, the accuracy of each model parameter is within 1% of the true value with the exception of monoexponential T2 and αse, which were within 1.7% for SNR = 40. Precision for monoexponential T2 was slightly better than for the SE and SML relaxation models. The CV of αsml for these modest SNRs was roughly half that of αse. In contrast, the biexponential model showed larger errors at both of these SNR levels. The accuracy and precision of the PG-associated model parameters (i.e. w1 and T2,1) exceeded 25% and 30%, respectively.
Cartilage Explant Experiments
Table 3 shows a ∼40% smaller concentration of sGAG in the enzymatically degraded BNC samples accompanied by a slightly larger (∼2%) water content. Table 4 shows an increase in the monoexponential T2 relaxation from 83 ms to 114 ms consistent with the observed degradation. Similar to the monoexponential result, both T2,se and T2,sml increased with degradation. The αse parameter increased significantly from 0.879 in control samples to 0.943 in degraded samples, consistent with a reduction in matrix macromolecular content and integrity. An increase in αsml was also seen with degradation, although the range of this parameter was substantially smaller than that of αse. Biexponential component fraction w1 showed a non-significant decrease from 15% to 11% with degradation; w1 values in control and degraded cartilage were comparable to the biochemically-derived sGAG by wet weight in Table 3.
Table 3. Biochemical results for control and enzymatically degraded cartilage.
| Sample condition | sGAG (mg/mg w.w.) | Water (mg/mg w.w.) |
|---|---|---|
| Control (n = 4) | 0.161 ± 0.012 | 0.778 ± 0.007 |
| Ch AC (n = 8) | 0.097 ± 0.012 * | 0.794 ± 0.012 ** |
Biochemical results (mean ± SD). Sulfated glycosaminoglycan (sGAG) and percent water are expressed as a fraction of sample wet weight (w.w.). Enzymatic degradation was achieved using chondroitinase AC (Ch AC).
indicates p<0.001, and
indicates p = 0.032.
Table 4. Parameter values from monoexponential, stretched exponential, stretched Mittag-Leffler, and biexponential fits to T2 relaxation data of control and degraded BNC.
| Sample condition | Monoexponential | Stretched exponential | Stretched Mittag-Leffler | Biexponential | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||||||
| T2,mono (ms) | MSE (---) | T2,se (msα) | α (---) | MSE (---) | T2,sml (msα) | α (---) | MSE (---) | w1 (%) | T2,1 (ms) | T2,2 (ms) | MSE (---) | |
| Control (n = 4) | 83 ± 5 | 6.7e-3 | 75 ± 5 | 0.879 ± 0.005 | 2.6e-4 | 79 ± 5 | 0.964 ± 0.001 | 3.1e-3 | 15 ± 1 | 23 ± 1 | 88 ± 5 | 7.1e-4 |
|
| ||||||||||||
| Ch AC (n = 8) | 114 ± 14 * | 2.6e-3 | 109 ± 13 * | 0.943 ± 0.016 * | 5.8e-4 | 111 ± 14 * | 0.977 ± 0.005 * | 1.0e-3 | 11 ± 6 | 49 ± 18 ** | 117 ± 18 ** | 6.8e-4 |
Relaxation fit results (mean ± SD).
indicates p < 0.001, and
indicates p < 0.005.
Both anomalous models resulted in significantly improved fits compared with the monoexponential model based on the F-test, with the stretched exponential model showing the lowest MSE.
MSEs, representing a measure of overall goodness of fit, showed improvements with the anomalous relaxation models over monoexponential fits, with the SE model showing the lowest MSE in control samples. These improvements in MSE were significant for all three anomalous models based on the F-test. In degraded samples, although the SE and biexponential models show comparable MSEs, those of the SE model were consistently smaller. As with control samples, anomalous models exhibited significantly lower MSEs in degraded samples as compared to those found using the monoexponential model.
Figure 1A shows the correlation between monoexponential T2 (T2,mono) and biochemically-derived sGAG content with a coefficient of determination of 0.66 indicating a modest sensitivity to sGAG content. Figure 1B and C show correlations between α for the SE and SML relaxation models and sGAG content, with coefficients of determination of 0.84 and 0.66, respectively. The regression slope is greater in αse than in αsml over the observed range of sGAG content measured in our experiments, indicating a greater sensitivity of the SE as compared to the SML to this matrix component. The y-intercept of both regressions is ∼1 suggesting extrapolation of these fits to a monoexponential relaxation in the limiting case of complete loss of proteoglycan. Figure 1D shows the correlation between the short T2 component fraction w1 and sGAG with a coefficient of determination of 0.84; the small y-intercept of ∼1 and slope of 0.93 suggests a close correspondence between this biexponential component fraction and biochemically-derived sGAG content in these samples.
Figure 1.
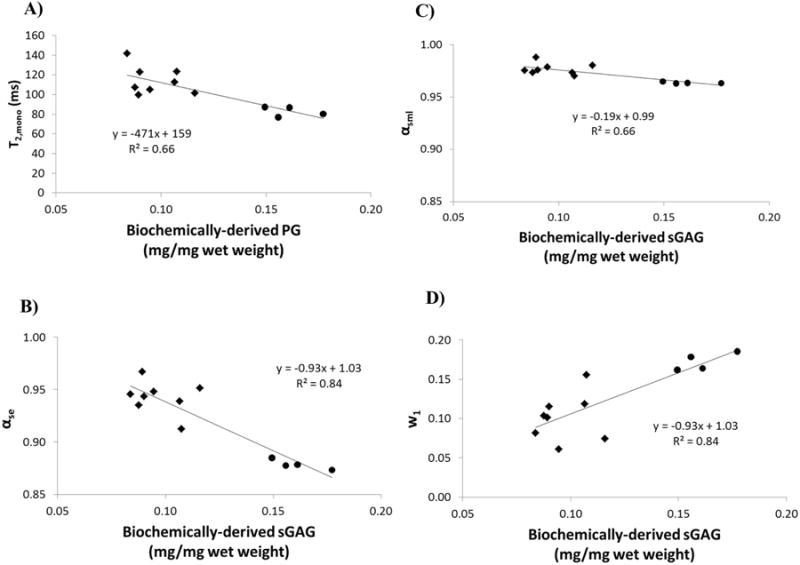
Correlations between relaxation model parameters and biochemically-derived sGAG content from cartilage samples using A) monoexponential T2, B) stretched exponential αse, C) stretched Mittag-Leffler αsml, and D) biexponental fraction w1. Note that the identical scaling of the x- and y-axes in B) and C) shows the substantially larger dynamic range of αse compared with αsml. ● – control samples, ◆ - degraded samples.
Figure 2 shows representative plots of the residuals from control and degraded samples for all four relaxation models. In control samples the improvement in fit using the SE model is substantial, with negligible residuals over three decades of the decay period. In contrast, the monoexponential and SML fits to control BNC data noticeably oscillate about the true signal with deviations commonly on the order of several percent of the total signal. The biexponential fit shows residuals on the order of one percent of the total signal, with similar oscillations around the true signal as observed for the monoexponential and SML fits. Such oscillations in the residuals suggest a non-random source of error in these fits, as confirmed by the Wald-Wolfowitz runs test in each case (12). In degraded samples, the SE shows comparable residuals to the SML and biexponential, although with slightly lower residuals at early echo times in the measured decay. The residuals for the monoexponential fit, as for the control samples, were substantially larger compared with the anomalous relaxation models.
Figure 2.
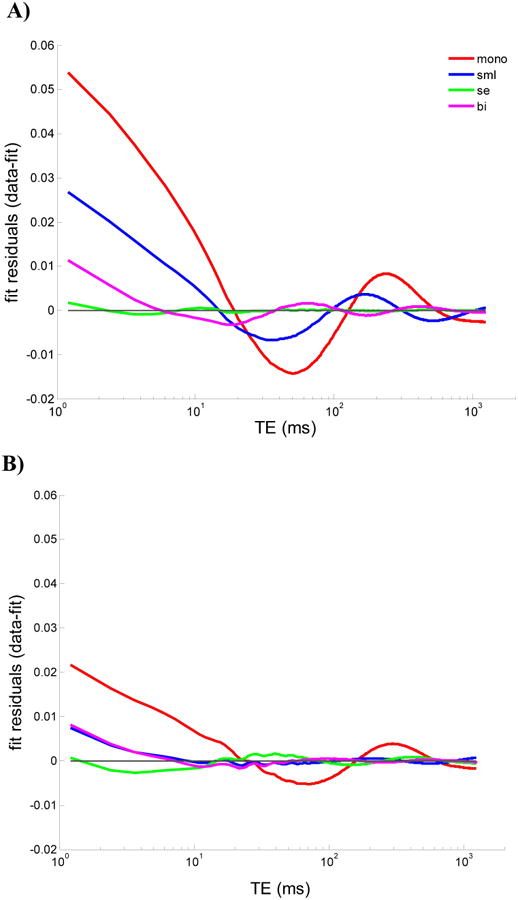
Representative fit residuals using monoexponential, stretched exponential, stretched Mittag-Leffler, and biexponential functions in A) normal and B) degraded samples. The first point of each decay signal was normalized to unity. The fit residual of the stretched exponential is difficult to distinguish from the x-axis for normal samples and is more pronounced in degraded samples showing small oscillations around a fraction of a percent of the total signal. Both SML and biexponential residuals show deviations from the decay at early and intermediate echo times, with larger deviations for the SML in normal cartilage; these two models show comparable residuals within a percent of the total signal in degraded cartilage.
Discussion
It has been established in a variety of tissues that relaxation decay deviates from the standard monoexponential form. One of several approaches to modeling this has been to assume that the transverse decay signal is the sum of the individual exponential decays of relaxing components (13). These decays reflect, for example, the local mobility of protons within water and other mobile molecules. This model may be particularly appropriate for tissues that contain barriers between water micro-environments such as semi-permeable membranes between intracellular and extracellular space, or compartments representing bound or restricted water. However, in porous gel-like tissues such as cartilage, water molecules can diffuse throughout the tissue matrix and experience several different micro-environments over the course of NMR data acquisition, thus complicating the interpretation of pool sizes. Furthermore, numerical inversion of decay data for extracting multiple exponentials is unstable in the presence of noise and requires regularization to stabilize the inversion to obtain apparent pool sizes. However, regularization acts as a type of smoothing and can perturb apparent pool sizes to an extent that is unknown in a given case (7,13,14). Given this and the high SNR requirements for reproducible and accurate numerical inversion using NNLS-based multiexponential analysis (5), substantial challenges for clinical applications to articular cartilage remain using this approach. A simplified alternative to NNLS is to assume a biexponential system, reducing the number of free fitting parameters and relaxing the SNR requirements as compared with NNLS. However, even with this simplification, fits to this model can be unstable with limited SNR and longer echo times as encountered under imaging acquisition conditions.
An alternative approach for describing anomalous transverse relaxation in complex porous systems is through generalization of the Bloch equations using fractional calculus [8]. This approach, which yields the SML, seeks to incorporate attributes of the tissue environment such as nonlocal interactions and memory effects (15,16), microstructural self-similarity, and time-scale or length-scale invariance (17) into the signal model. This is accomplished through the definition of the fractional integral, which incorporates the convolution of a power law in time with the evolution of magnetization over time [9]. This formalism can yield a transverse signal decay that is more rapid than the exponential function for early time and slower for later times. This behavior can be appreciated through the comparison of time-domain signal decays in Figure 3A where the SML decays as a stretched exponential function for smaller arguments of (t/T2) and a power function for larger arguments of (t/T2).
Figure 3.
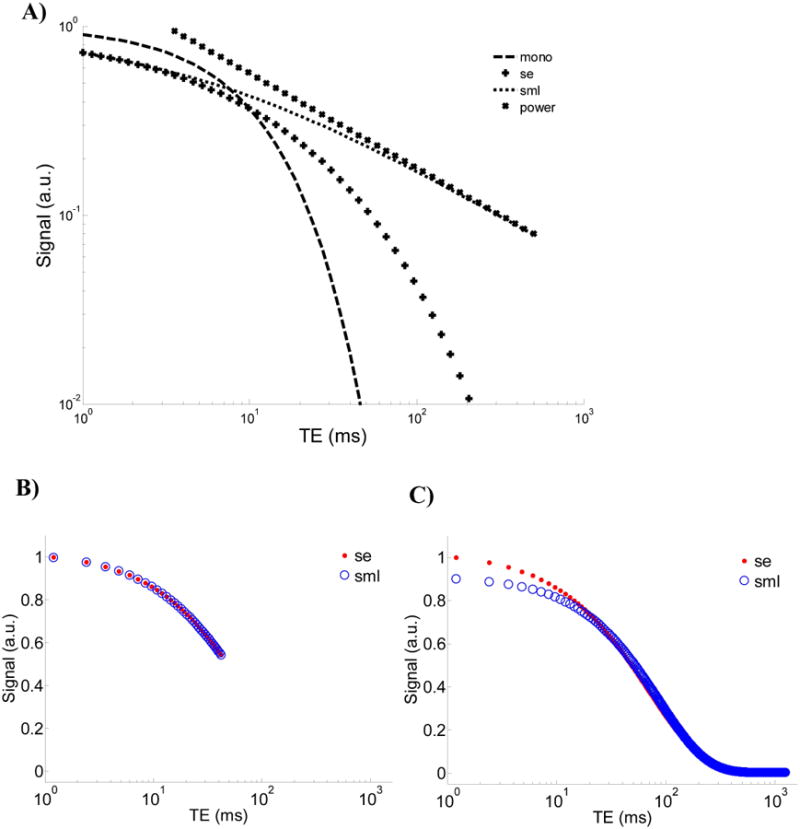
A) Comparison of different models: i) the exponential function exp(-t), ii) the stretched exponential function exp(-t0.5), iii) the stretched Mittag-Leffler function Eα(-t0.5), and iv) the power function t-0.5/ Γ(0.5). B) Plots of the stretched exponential and the stretched Mittag-Leffler models showing similar decays over small arguments of time and C) the deviation at the small arguments of time when fit using the complete decay signal.
The SE model can be motivated from several physical perspectives. It can be obtained as a solution of the Bloch equations under the assumption that the transverse decay time constant exhibits a power law time-dependence such that T2(t) = τt1–α where τ and α are positive constants, with α ranging over the interval (0, 1], and t = 0 coinciding with the 90 degree excitation pulse. Given this notation, transverse magnetization takes the form M⃗xy(t) = M⃗xy(0)·exp(−tα/(ατ)) where the quantity ατ corresponds to the aggregate constant T2,se used in the present work. For values of α that approach unity, T2,se loses its time-dependence and is equal to the constant τ, so that the transverse relaxation signal model approaches a monoexponential. One alternative approach for deriving the SE from the Bloch equations uses a right-handed fractional integral operator (18).A second way of deriving the SE function is through use of a fractal generalization of diffusion in both space and time (19). Stretched exponential relaxation has also been observed extensively in other non-NMR systems and shown to arise from non-stationary step lengths in a random walk process (20). Although a derivation has not been produced directly for NMR relaxation, this interpretation is plausible, given the complex porous structure of cartilage. Certainly, the empirical success of the SE model in our analysis of transverse relaxation in cartilage is motivation for attempting to establish a corresponding physical picture.
A further interpretation of the SE model, which also applies to the SML model, is that it represents a compact empirical approximation of an underlying distribution of relaxation times of the system. A similar interpretation has also been suggested in the context of the luminescence decay law (21,22). In Figure 4 we illustrate this idea in control and degraded BNC, showing a comparison of the NNLS-derived T2 distribution (A) and the corresponding SE T2 distribution (B), where the SE distribution was computed based on the analytical form provided by Berberan-Santos and Valeur (22). From this comparison it is apparent that the SE distribution appears as a smooth continuous distribution that resembles the overall envelope of peaks in the NNLS distribution. Comparison of control and degraded samples also illustrates the manner in which smaller values of αse reflect a larger skewness of the distribution towards more rapidly relaxing T2 values; the amplitude of the more rapidly relaxing NNLS-derived T2 components have been shown to positively correlate with the concentration of cartilage proteoglycan (23). In this case, the SE model provides a particularly simple representation of these distributions that, as we have shown above, has relatively modest SNR requirements. We note that the SE function represents a restricted family of specific forms for the superposition of a continuum of exponentials (see figures 1 and 3 in (22)), which is to say that the SE functional form is much more constrained than an arbitrary distribution of underlying exponentials.
Figure 4.
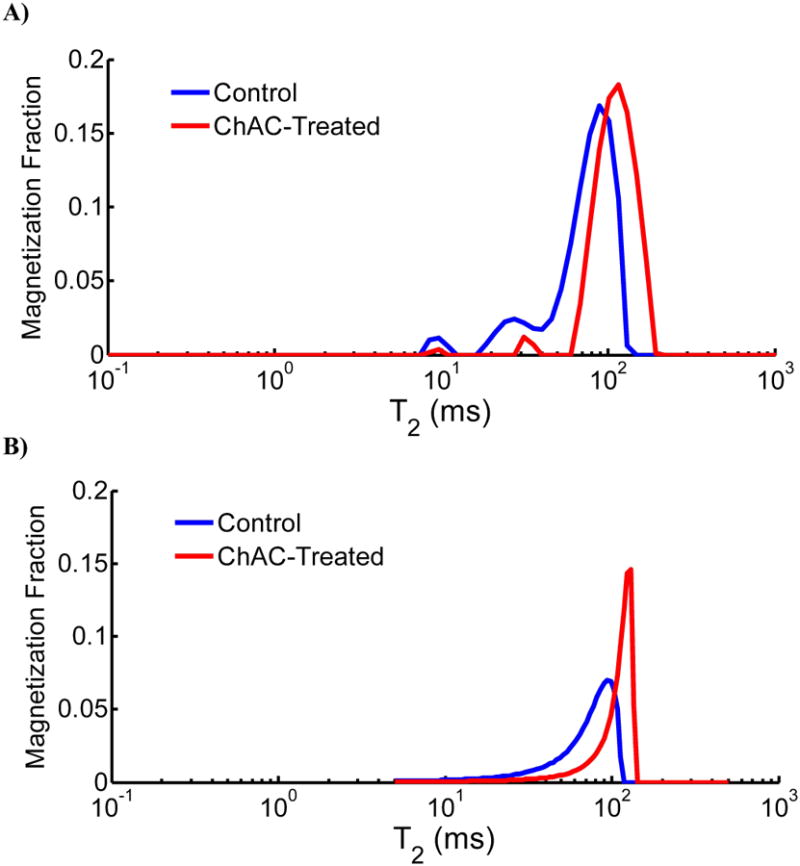
A) Representative NNLS-derived T2 distributions from control and Ch AC-treated BNC. B) Corresponding T2 distributions of the stretched exponential fits (control T2se=70 msα and αse=0.88; Ch AC-treated T2se=108msα and αse=0.94) for the same samples in A). The stretched exponential T2 distribution appears as a smooth continuous distribution that resembles the overall envelope of the peaks in the NNLS-derived T2 distribution.
The SE provides a good approximation to the SML in the short time limit (24). This is seen in Figure 3A, in which the SML coincides with the SE at early times but then becomes a power law at later times. In spite of this close correspondence at early times (Figure 3B), when fitting signals which decay over several time scales, the SML can deviate from the SE at small values of time (Figure 3C). The misfit observed in Figure 3C is similar to that of the experimental data in Figure 2A.
Simulations
High SNR simulated decay signals from each model were used to examine the extent to which experimental data may be used to distinguish among the four models investigated. Input model parameters were based on experimentally derived model parameters in both control and degraded cartilage under high SNR conditions. For the models under comparison, the simulation results in Table 1 demonstrate the ability to discriminate between the correct model and incorrect models based on MSE. Simulation results from Table 2 also indicate high accuracy and precision for experimental conditions with high SNR. These results indicate that fit errors had negligible influence on parameter estimates for each model, suggesting that the experimental acquisition conditions were sufficient for examining model parameters as they relate to e.g. proteoglycan content.
Simulations using more modest SNR, fewer echoes and longer echo times provide insight into the feasibility for obtaining accurate and reproducible measurements under clinical conditions using these signal models. As reflected in Table 2, monoexponential, SE, and SML models exhibited favorable accuracy and precision under simulated clinical imaging conditions. The stretching parameters, α, showed accuracy within 2% and precision within 8% under SNR values of 40. Although αsml showed higher precision than αse in these simulations, the experimentally-determined range of αsml was much smaller between control and enzymatically degraded samples, indicating that a greater SNR would be needed for using αsml to detect modest loss of sGAG. For example, for SNR of 100, the derived values of αse were within approximately 3% of the true value. This indicates sufficient precision to detect differences between control and degraded BNC; αse increased on average by 7.28% with degradation (see Table 4). On the other hand, estimates of αsml were within 1.27% of the true value for SNR of 100. This shows better precision compared with αse; however, since this parameter showed a small increase of 1.35% between control and degraded samples, these differences are likely undetectable using the SML model. The parameter w1 derived from the biexponential analysis showed poor accuracy and precision at these lower SNR levels. Aside from the substantial bias of greater than 25% as reflected by the accuracy, the dispersion of greater than 35% would obscure the observation of the expected decrease in w1 due to degradation, which was on the order of 27% for the in vitro BNC samples. These simulations indicate a more stringent SNR requirement for the biexponential model compared with the other models, for these particular acquisition and tissue parameters investigated. Again, this is likely attributable to the fact that the biexponential model involves an additional fitting parameter.
Experimental
There have been many recent studies describing non-monoexponential transverse relaxation in nasal cartilage (6), articular cartilage (23,25), and engineered cartilage (26,27). In the current work we closely examine the misfit between transverse relaxation models and multi-echo spin echo decay data from BNC using data with extremely high SNR and high-frequency echo sampling, to empirically explore alternative relaxation models under the most optimal acquisition conditions. As expected, the monoexponential model shows large deviations from the data with the oscillations of the residual curve over the entire decay (Figure 2). This analysis shows a consistent pattern of misfit across all samples in both normal and degraded BNC, showing deviations of the data from monoexponential decay at early (1-10ms), intermediate (10-100 ms), and late (>100ms) times; specifically, the monoexponential model undershoots at early and late times while it overshoots at intermediate times. In control BNC (Figure 2A), the SML model also shows misfit at the early and intermediate times similar to the monoexponential model though it shows close representation of the true signal at the later times, owing to its known heavy-tail characteristics (see Figure 4A). The biexponential model shows a similar pattern of oscillations to the monoexponential and SML models at early and intermediate times, though with substantially smaller amplitude to within a percent of the total signal. The SE, in contrast, shows substantially smaller misfit over the course of the entire decay in both normal and degraded BNC, reflecting its ability to capture non-monoexpenential decay features in the transverse relaxation signal. In contrast to Figure 2A, the SE in Figure 2B shows a smaller improvement in misfit compared with the SML and biexponential models for this representative degraded BNC sample. This smaller difference in MSEs between models in degraded samples is attributed to larger values of α, smaller value of w1 and the observation that as α approaches 1 and w1 approaches zero, all three anomalous relaxation models fit the data equally well (ref. Table 1 first row). This is also reflected in Table 4 when comparing the average MSEs for the SE and biexponential models. When comparing the MSE between models for each given sample decay, the SE MSE was consistently lowest among the four models for all experimental data. In particular, we note that the biexponential model, in addition to requiring an additional fitting parameter, also does not provide as good a fit to the observed data as the SE.
Multiexponential relaxation studies in cartilage have attributed specific T2 components to water protons bound to or in close proximity to matrix macromolecules. For example, component fractions with T2s of ∼25 ms have been shown to correlate with sGAG in native cartilage (23) and engineered cartilage (27). In the current work, w1 with a T2 value ranging from 24 ms to 87 ms correlated with sGAG. Collagen has also been associated with more rapidly decaying signal (typically < 1ms) as observed in the analysis of multi-echo ultra-short echo time (UTE) decay data (28). This approach models these matrix-associated decay features at early and intermediate times as independent compartments with corresponding relaxation times.
In the current work, the SE model closely represents the decay signal over early and intermediate times. This is apparent from the small residuals observed from fits to normal and degraded BNC. The extent to which the SE model exhibits this deviation from monoexponential relaxation at early and intermediate times is dictated by the extent to which αse deviates from 1. This is in contrast to the SML function for which smaller values of αsml also result in more prolonged signal at later times compared with the SE model. Given these observations, it is not surprising that the slope of the correlation between αse and sGAG is substantially steeper than that of αsml and sGAG (Figure 1); this is based on the observations of the previously mentioned studies that show matrix components to be more closely associated with the early and intermediate time behavior rather than the late time behavior of the signal decay.
Conclusion
The SE, SML, and biexponential anomalous relaxation models presented in this work provide an alternative and physically plausible model of T2 relaxation in cartilage. The stretching parameters, αse and αsml, reflect the microstructural complexity of the underlying matrix. The short T2 component fraction w1, is interpreted as reflecting PG-associated water. We find that transverse relaxation data in cartilage is described much more accurately over the entire acquisition time by the SE model than by the conventional monoexponential model. With this, the modest SNR requirements for obtaining reproducible SE parameter values, and the well-defined correlation with sGAG, αse shows potential for providing a clinical biomarker of cartilage matrix composition and integrity.
Acknowledgments
This work was supported by the Intramural Research Program of the NIH, National Institute on Aging and by R01 EB 007537 and MTM2013-41704-P.
Contract/Grant Sponsors: National Institutes of Health, Intramural Research Program of the National Institute on Aging and the National Institutes of Health extramural program Contract/Grant Number R01 EB 007537; Grant Number MTM2013-41704-P from the Government of Spain.
References
- 1.Mosher TJ, Smith HE, Collins C, Liu Y, Hancy J, Dardzinski BJ, Smith MB. Change in knee cartilage T2 at MR imaging after running: a feasibility study. Radiology. 2005;234(1):245–249. doi: 10.1148/radiol.2341040041. [DOI] [PubMed] [Google Scholar]
- 2.Mosher TJ, Liu Y, Yang QX, Yao J, Smith R, Dardzinski BJ, Smith MB. Age dependency of cartilage magnetic resonance imaging T2 relaxation times in asymptomatic women. Arthritis and Rheumatism. 2004;50(9):2820–2828. doi: 10.1002/art.20473. [DOI] [PubMed] [Google Scholar]
- 3.Mosher TJ, Collins CM, Smith HE, Moser LE, Sivarajah RT, Dardzinski BJ, Smith MB. Effect of gender on in vivo cartilage magnetic resonance imaging T2 mapping. J Magn Reson Imaging. 2004;19(3):323–328. doi: 10.1002/jmri.20013. [DOI] [PubMed] [Google Scholar]
- 4.Menezes NM, Gray ML, Hartke JR, Burstein D. T2 and T1rho MRI in articular cartilage systems. Magnetic Resonance in Medicine. 2004;51(3):503–509. doi: 10.1002/mrm.10710. [DOI] [PubMed] [Google Scholar]
- 5.Reiter DA, Lin PC, Fishbein KW, Spencer RG. Multicomponent T2 relaxation analysis in cartilage. Magnetic Resonance in Medicine. 2009;61(4):803–809. doi: 10.1002/mrm.21926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Reiter DA, Roque RA, Lin PC, Doty SB, Pleshko N, Spencer RG. Improved specificity of cartilage matrix evaluation using multexponential transverse relaxation analysis applied to pathomimetically degraded cartilage. NMR in Biomedicine. 2011 doi: 10.1002/nbm.1690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Celik H, Bouhrara M, Reiter DA, Fishbein KW, Spencer RG. Stabilization of the Inverse Laplace Transform of Multiexponential Decay through Introduction of a Second Dimension. Journal of Magnetic Resonance. 2013;236:134–139. doi: 10.1016/j.jmr.2013.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Graham SJ, Stanchev PL, Bronskill MJ. Criteria for analysis of multicomponent tissue T2 relaxation data. Magnetic Resonance in Medicine. 1996;35(3):370–378. doi: 10.1002/mrm.1910350315. [DOI] [PubMed] [Google Scholar]
- 9.Magin RL, Li W, Velasco MP, Trujillo J, Reiter DA, Morgenstern A, Spencer RG. Anomalous NMR relaxation in cartilage matrix components and native cartilage: Fractional-order models. Journal of Magnetic Resonance. 2011 doi: 10.1016/j.jmr.2011.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kohlrausch R. Theorie des elektrischen Rückstandes in der Leidener Flasche. Annalen der Physik. 1854;167(2):179–214. [Google Scholar]
- 11.Farndale RW, Buttle DJ, Barrett AJ. Improved quantitation and discrimination of sulfated glycosaminoglycans by use of dimethylmethylene blue. Biochimica et Biophysica Acta. 1986;883(2):173–177. doi: 10.1016/0304-4165(86)90306-5. [DOI] [PubMed] [Google Scholar]
- 12.Wald A, Wolfowitz J. On a test whether two samples are from the same population. Annals of Mathematical Statistics. 1940;11:147–162. [Google Scholar]
- 13.Whittall KP, Mackay AL. Quantitative interpretation of NMR relaxation data. Journal of Magnetic Resonance. 1989;84(1):134–152. [Google Scholar]
- 14.James DR, Liu YS, Demayo P, Ware WR. Distributions of Fluorescence Lifetimes - Consequences for the Photophysics of Molecules Adsorbed on Surfaces. Chemical Physics Letters. 1985;120(4-5):460–465. [Google Scholar]
- 15.Magin R, Feng X, Baleanu D. Solving the Fractional Order Bloch Equation. Concepts in Magnetic Resonance Part A. 2009;34A(1):16–23. [Google Scholar]
- 16.Magin RL. Fractional Calculus in Bioengineering. Connecticut: Begell House Publishers, Inc.; 2006. [Google Scholar]
- 17.Johnston DC. Stretched exponential relaxation arising from a continuous sum of exponential decays. Physical Review B. 2006;74(18) [Google Scholar]
- 18.Kilbas AA, Srivastava HM, Trujillo JJ. Theory and applications of fractional differential equations. Amsterdam: Elsevier; 2006. [Google Scholar]
- 19.Chen W. Time-space fabric underlying anomalous diffusion. Chaos, Solitons and Fractals. 2006;28:923–929. [Google Scholar]
- 20.Shlesinger MF, Montroll EW. On the Williams-Watts Function of Dielectric-Relaxation. Proceedings of the National Academy of Sciences of the United States of America-Physical Sciences. 1984;81(4):1280–1283. doi: 10.1073/pnas.81.4.1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Berberan-Santos MN, Bodunov EN, Valeur B. Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential) Chemical Physics. 2005;315(1-2):171–182. [Google Scholar]
- 22.Berberan-Santos MN, Valeur B. Luminescence decays with underlying distributions: General properties and analysis with mathematical functions. Journal of Luminescence. 2007;126(2):263–272. [Google Scholar]
- 23.Reiter DA, Roque RA, Lin PC, Irrechukwu O, Doty S, Longo DL, Pleshko N, Spencer RG. Mapping Proteoglycan-Bound Water in Cartilage: Improved Specificity of Matrix Assessment Using Multiexponential Transverse Relaxation Analysis. Magnetic Resonance in Medicine. 2011 doi: 10.1002/mrm.22673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Carpinteri A, Mainardi F. Fractals and fractional calculus in continuum mechanics. New York: Springer; 1997. [Google Scholar]
- 25.Du J, Diaz E, Carl M, Bae W, Chung CB, Bydder GM. Ultrashort echo time imaging with bicomponent analysis. Magnetic Resonence in Medicine. 2012;67(3):645–649. doi: 10.1002/mrm.23047. [DOI] [PubMed] [Google Scholar]
- 26.Irrechukwu ON, Reiter DA, Lin PC, Roque RA, Fishbein KW, Spencer RG. Characterization of engineered cartilage constructs using multiexponential T2 relaxation analysis and support vector regression. Tissue Eng Part C Methods. 2012;18(6):433–443. doi: 10.1089/ten.tec.2011.0509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Reiter DA, Irrechukwu O, Lin PC, Moghadam S, Von Thaer S, Pleshko N, Spencer RG. Improved MR-based characterization of engineered cartilage using multiexponential T2 relaxation and multivariate analysis. NMR in Biomedicine. 2012;25(3):476–488. doi: 10.1002/nbm.1804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pauli C, Bae WC, Lee M, Lotz M, Bydder GM, D'Lima DL, Chung CB, Du J. Ultrashort-echo time MR imaging of the patella with bicomponent analysis: correlation with histopathologic and polarized light microscopic findings. Radiology. 2012;264(2):484–493. doi: 10.1148/radiol.12111883. [DOI] [PMC free article] [PubMed] [Google Scholar]


