Joint Model of Iron and Hepcidin During the Menstrual Cycle in Healthy Women

Abstract

Hepcidin regulates serum iron levels, and its dosage is used in differential diagnostic of iron-related pathologies. We used the data collected in the HEPMEN (named after HEPcidin during MENses) study to investigate the joint dynamics of serum hepcidin and iron during the menstrual cycle in healthy women. Ninety menstruating women were recruited after a screening visit. Six fasting blood samples for determination of iron-status variables were taken in the morning throughout the cycle, starting on the second day of the period. Non-linear mixed effect models were used to describe the evolution of iron and hepcidin. Demographic and medical covariates were tested for their effect on model parameters. Parameter estimation was performed using the SAEM algorithm implemented in the Monolix software. A general pattern was observed for both hepcidin and iron, consisting of an initial decrease during menstruation, followed by a rebound and stabilising during the second half of the cycle. We developed a joint model including a menstruation-induced decrease of both molecules at the beginning of the menses and a rebound effect after menses. Iron stimulated the release of hepcidin. Several covariates, including contraception, amount of blood loss and ferritin, were found to influence the parameters. The joint model of iron and hepcidin was able to describe the fluctuations induced by blood loss from menstruation in healthy non-menopausal women and the subsequent regulation. The HEPMEN study showed fluctuations of iron-status variables during the menstrual cycle, which should be considered when using hepcidin measurements for diagnostic purposes in women of child-bearing potential.

Electronic supplementary material

The online version of this article (doi:10.1208/s12248-016-9875-4) contains supplementary material, which is available to authorized users.

INTRODUCTION

Iron is a very important element in mammals, and it is the most abundant trace element in humans with a total body amount of 2.5–4.5 g (1). It participates in cellular respiration, in DNA repair and synthesis and in oxygen transfer (2). It is naturally present in the body, with most of the body iron (60%) used within the red blood cell haemoglobin to bind oxygen. There is no regulated pathway to excrete iron from the body, and as a result, body iron levels are mainly regulated by daily absorption of iron from food, via modulation of the rate of iron entry through the duodenal mucosa, which affects net iron absorption. Serum iron levels are maintained stable by a complex regulation network, affected by the rate of iron recycling from macrophages and transfer from other tissue stores. Figure 1 shows a simplified schematic of iron circulation in the body: ferric iron (iron(III)) absorbed from food is first reduced to ferrous iron (iron(II)) and absorbed by enterocytes through binding with the divalent metal transporter 1 (DMTP1), As free ferrous iron catalyses the formation of free radical from reactive oxygen species, protective mechanisms have evolved to protect the cells from its toxicity. Iron is stored in hepatocytes, enterocytes and macrophages as ferritin, a complex formed by apoferritin binding iron in the ferric state. Export of iron from duodenal enterocytes and macrophages into plasma is mediated by the iron transporter ferroportin. Hepcidin, a hormone peptide mainly synthesised by the hepatocytes (3,4), binds to ferroportin resulting in its internalisation and degradation (5–7), thereby blocking iron export. Ferric iron resulting from oxidation of iron released by ferroportin is taken up by transferrin which transports it mainly to the liver for storage and the bone marrow for production of red blood cells.

Fig. 1.

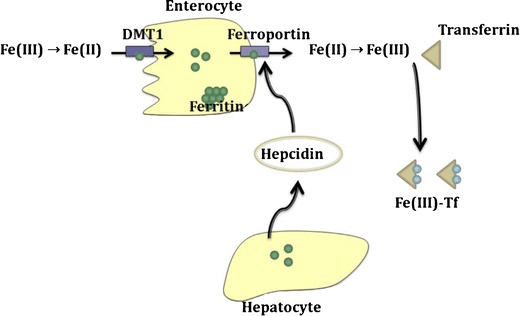
Simplified processes of iron absorption and circulation in the mammalian body

Once iron has entered the body, it is surprisingly difficult to remove it by other means than bleeding, either natural or accidental, as only a very small amount of iron passes into urine or is excreted in the intestine (8). Natural bleeding occurs in women during their period every month, where they generally lose 10 to 40 mg of iron. This triggers the regulation network and leads to fluctuations in iron levels throughout the menstrual cycle, as evidenced in an epidemiological study in 1712 women aged 18 to 44 years, with regular menstrual periods, which reported significant variation of iron status during the menstrual cycle (9). Menstruating women also tend to have lower serum hepcidin than men of similar age, as reflected in the normal laboratory ranges (10). The most prevalent iron disorder is anaemia (too little iron), but there is also a range of iron overload disorders (hemochromatosis), with both genetic (thalassemia) and non-genetic causes, which lead to long-term organ toxicity. The differential diagnostic of these pathologies involves dosing serum iron, haemoglobin and ferritin, as well as the two key players of the iron regulation network, ferroportin and hepcidin.

Hepcidin production decreases in response to low concentrations of circulating iron, in order to restore normal levels, and when erythropoiesis is activated, to release iron for the synthesis of erythrocytes (11). This stimulates both the release of stored iron and the absorption of dietary iron. Conversely, hepcidin concentrations increase when iron stores are high (12,13) and in the presence of inflammation (14,15), which decreases intestinal absorption and iron release from storage. Reduced hepcidin levels can be observed as the result of hypoxia, while inflammation or infection can stimulate hepcidin production. Measuring hepcidin along with serum iron can be useful in differential diagnostic of iron-related disorders, particularly chronic anaemia. Indeed, low levels of serum iron are associated with high serum hepcidin in anaemia from chronic inflammatory disease but with low serum hepcidin in iron-deficiency anaemia (de Kroot et al. 2011). There is no specific indication for dosing hepcidin during menses per se but when non-menopausal women are affected by anaemia timing for dosing hepcidin during cycle should be taken into account to interpret the results. Because hepcidin and iron concentrations are so intimately linked, we can expect hepcidin levels to also respond to iron loss through bleeding.

We therefore designed the HEPMEN (named after HEPcidin during MENses) study to investigate the evolution of iron-status variables in healthy menstruating women during their menstrual cycle and help decide when to measure hepcidin for diagnostic purposes. In this paper, we develop the first joint model for iron and hepcidin concentrations during the menstrual cycle.

METHODS

Experimental Design

The HEPMEN study was a multicenter observational study performed in four university hospitals in France (Brest, Nantes, Rennes, Tours). It included 90 healthy women aged 19 to 44 years with regular menstrual cycles and menses length between 3 and 5 days. No treatments were administered during the study. Sixty-one percent of the women took daily oral contraceptives. Demographic variables were recorded during an inclusion visit, including age, height, weight, body mass index, waist circumference and Higham’s score, which evaluates the abundance of menstrual periods (16). Higham’s score was obtained as the mean of the three last scores calculated by the patients.

Sampling Design

Fasting blood samples (4 mL) were collected from each woman on six occasions distributed during the menstrual cycle in order to measure concentrations of serum hepcidin, serum iron, transferrin saturation, serum transferrin, serum ferritin and haemoglobin. The visits were planned at the same time each day, between 8 am and 9 am. The sampling protocol was optimised using the PFIM software (17,18) to maximise the information collected in the study in view of a joint modelling of iron and hepcidin. For the optimisation, we used the pharmacokinetic model of hepcidin developed by Xiao et al. (19) and reflecting the changes in hepcidin concentrations in monkeys after an administration of an antibody, where hepcidin was modelled through a turnover model. We used the same model for iron, as a simplification of the iron regulatory system. We used the typical 1 mg daily iron loss reported in medical literature and a baseline iron value of 1 mg/L to compute the input and output parameters to the iron model. Iron loss during menses was estimated to be 0.05 day⁻¹ based on typical blood loss and iron concentrations. For hepcidin, we used the elimination rate reported in (19), as well as a baseline value of 10 nmol/L for hepcidin, the average value from data available in house as part of routine measurements performed in healthy volunteers taking part in clinical trials. Finally, we assumed two linear models to account for the effect of iron on hepcidin and vice versa, with parameters, respectively, equal to 0.5 and 0.2 which gave a plausible magnitude of variation during the cycle compared to iron changes in menstruating women reported in (9) and assuming similar variations for hepcidin. A sigmoid model was not identifiable because of the very rapid turnover of hepcidin. We assumed an inter-individual variability of 30% for most parameters, except the elimination rate of hepcidin and the effect of hepcidin on iron, which were fixed to allow the optimisation algorithm to converge. We limited the number of samples to six per subject and used the Fedorov-Wynn algorithm to optimise over a discrete set of sampling times (one per day of the cycle) with the following constraints: three time-points between day 1 (beginning of menses) and day 6; one point during the rebound after menses (between days 6 and 12); one point mid-cycle (between days 12 and 19) and one point at the end of the cycle (between days 26 and 29). The first blood sample was collected on the second day of menses, and the optimal protocol was then adjusted based on the day of the week that menses began, to avoid sampling during weekends. This also served to make the protocol more robust as it allowed the samples to be spread out during the cycle.

Ethics Statement

This study was reviewed by the ethical committee of Rennes and approved by the National Security Agency of the Medicine and the products of health (ANSM). Signed, written informed consent was obtained from all participants.

Bioanalytical Methods

The samples were collected in the four participating hospitals. Blood samples were collected in fasting subjects, in the morning between 8 and 9 am. Samples for hepcidin determination were collected on dry tubes and then centrifuged at 1500g during 20 min at 4°C. Except for the sample collected at the inclusion visit, which was treated on site, all serum samples were frozen at −80°C and sent to the Laboratory of Rennes’s hospital for centralised analyses. Laboratory assays were performed in the biochemistry laboratory at the Rennes University Hospital (Pontchaillou, Rennes, France). The assays of serum iron, transferrin and ferritin were performed on a cobas ® 8000 (Roche Diagnostics GmbH, Mannheim). Serum iron was quantified in a colorimetric manner using a ferrozine method (Iron2 Iron Gen2 Roche-ref. 03183696122). Serum transferrin was measured by immunochemical turbidimetry (Tina-quant Transferrin ver.2 ref. 05588855 190), and transferrin saturation was calculated using the formula: transferrin saturation (%) = (iron (μmol/L)/(transferrin (g/L) × 25) × 100). The Ferritin level was determined with an electrochemiluminescence immunoassay (Ferritin ECLIA Roche ref. ms_04491785190). The laboratory’s within-run (intra-assay) precision and between-run (inter-assay) precision were, respectively, 1.4 and 2.5% for iron, 2 and 2.5% for transferrin and 1.5 and 4.1% for ferritin. The lower quantification limit was 0.9 μmol/L, 0.1 g/L and 0.5 μg/L for iron, transferrin and ferritin, respectively. Serum hepcidin-25 was quantified using a competition CE-marked Enzyme Immunoassay (EIA) kit (S-1337; Bachem Torrance USA) following the instructions of the manufacturer. Serum samples were diluted in supplied standard diluent and analysed in duplicate at 450 nm on a microplate reader (Victor®-PerkinElmer Massachusetts USA). Hepcidin concentrations were interpolated from standard curves generated by logistic four-parameter non-linear curve fitting. The intra-assay and inter-assay coefficient of variation was 3.5 and 6.3%, respectively, and the lower quantification limit was 0.01 nmol/L.

Statistical Model

The data consisted of repeated measurements in a population of women. Non-linear mixed effect models were used for the analysis as they are well suited to longitudinal data (20). The observation yij measured at time tij for a subject i was modelled using the following equation:

$$y_{ij}=f({\theta }_i,t_{ij},z_i)+{\epsilon }_{ij}$$ 1

where n_i denotes the number of observations in subject i, j the index of the observation (j = 1,…, n_i), f the structural model, θ_i the individual parameters for subject i, ε_ij the measurement error and z_i the individual covariates.

The between-subject variability was modelled through a log-normal distribution for the parameters θ_i so that the kth component of θ_i was defined as:

$${\theta }_{ik}={\mu }_k{e}^{b_{ik}}$$ 2

where μ_k is a population fixed effect and b_ik is the corresponding individual random effect. Continuous covariates such as body mass index (BMI) were entered in the model through an exponential model, modifying Eq. (2) to

$${\theta }_{ik}={\mu }_k{\left({\mathrm{BMIi}}_i/\mathrm{tBMI}\right)}^{\beta \mathrm{B}\mathrm{M}\mathrm{I}}{e}^{bik}$$

where tBMI is a typical value of weight (either the median in the population or a set value) and β_BMI the estimated effect. For a categorical covariate such as contraception, the reference value of the parameter for women taking contraception was assumed to follow Eq. (2) while for women not taking contraception, Eq. (2) was modified to

$${\theta }_{ik}={\mu }_k{e}^{\beta \mathrm{contraception}}{e}^{bik}$$

A combined error model was used to describe the variance of the residual error for both serum iron and serum hepcidin:

$$\mathrm{v}\mathrm{a}\mathrm{r}\left({\epsilon }_{ij}\right)={(a+bf({\theta }_i,t_{ij},z_{ij}))}^2$$ 3

where the variance parameters a (additive part) and b (proportional part) are, respectively, a_iron and b_iron for iron and a_Hep and b_Hep for hepcidin.

The maximum likelihood estimates of the parameters were obtained using the SAEM algorithm implemented in the Monolix software (4.3.2 version standalone Windows, 32 bits) (21). The log-likelihood was computed using importance sampling (22).

Model Building

To build the joint model, we first explored structural models separately for iron and hepcidin and then combined the two models testing different link functions to describe the mutual regulation. The separate fits also provided appropriate initial estimates for the parameters of the joint model. A diagonal covariance matrix was used at this stage to represent the inter-individual variability, and we tested whether there was significant covariance between certain parameters. During model building, log-likelihood ratio tests (LRT) were used to compare nested models, including variability structures; non-nested models were compared using the Bayesian information criterion (BIC).

In a second stage, we included covariates in the model through a stepwise procedure. The covariate data included the demographic variables recorded at the inclusion visit, as well as reference values of martial settings: serum transferrin, serum ferritin, haemoglobin and transferrin saturation.

The evolution of all the iron-status variables is shown in Fig. 2. The plots show a similar evolution for iron, hepcidin and saturation of serum transferrin, which all exhibit a decrease during menses, followed by a moderate rebound for hepcidin and a marked rebound for the other two variables. Transferrin, ferritin and haemoglobin do not seem to consistently vary during the cycle but show considerable inter-individual variability. Transferrin saturation on the other hand was highly correlated with iron (ρ = 0.92). Therefore, only a reference value was included in the model as a covariate. In order to ensure consistency across all recruiting centres, the reference values were taken as the concentrations obtained at the last appointment for each woman. We did not use the measurements collected at the inclusion visit because these were obtained at different moment during the menstrual cycle, in non-fasted conditions, and also because these samples were analysed in each participating centre while all other samples collected during the protocol were analysed centrally with the same analytical method. Inclusion of covariates was performed using a two stage stepwise approach: first, exploring the relationships for each parameter separately and then building the full covariate model. In the first stage, for each parameter, a full covariate model including all potential relationships was built. Covariates with a p value for the Wald test larger than 0.2 were removed from the model in one step, and then backward selection was applied to remove non-significant covariates one at a time, with a threshold of 0.05 for the Wald test, starting with the covariate which had the largest non-significant covariate. In the second stage, a model was created with all the previous covariate-parameter relationship and backward selection was again applied using the same approach, until all covariates remaining in the model were significant according to the Wald test.

Fig. 2.

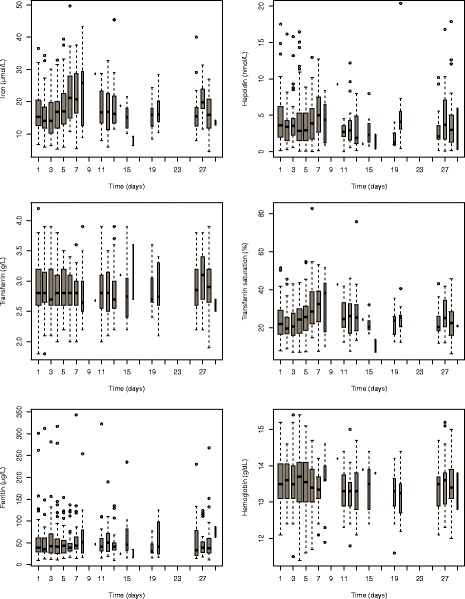
Evolution of iron-status variables during the menstrual cycle in the Hepmen study, shown as boxplots. The Y-axis for the hepcidin plot was set to 0–20, excluding seven outlying observations from the plot to better show the evolution during the cycle. The width of each box is proportional to the number of observations collected on each day

Finally, the covariance structure was refined, by testing again for correlations between parameters and by removing variances when needed. The final model was adjusted to obtain the estimates of the parameters and their standard errors.

Three subjects were identified by the clinicians as having abnormal hepcidin concentrations. Two of them had a very high serum hepcidin at one or two visits (four to seven times higher than all other concentrations for that subject), and the concentrations were high at all visits for the third subject (two to three times larger than the highest concentration of hepcidin in the data set). A sensitivity analysis was performed with the final model to evaluate their impact on parameter estimates.

Iron Model

In the absence of perturbation, iron regulation maintains stable levels of serum iron in the body. To reflect the endogenous levels of iron, we described the baseline evolution of iron through a turnover model (23). In this model, the change in iron concentrations is the result of two compensating mechanisms: constant endogenous secretion characterised by a parameter ksyn_I, reflecting the release of iron from storage, and first-order elimination characterised by a parameter kout I, reflecting the uptake of iron and its disappearance from serum. The equation for this model, denoting Ir(t) serum iron levels at time t, is:

$$d\mathrm{I}\mathrm{r}\left(t\right)/dt={\mathrm{ksyn}}_{\mathrm{I}}-{\mathrm{kout}}_{\mathrm{I}}\mathrm{I}\mathrm{r}\left(t\right)$$ 4

In menstruating women, blood loss during menses results in iron loss. This was included in the turnover model as an increase in the elimination koutI, which was assumed to be koutI + kloss for a duration of dloss days. We tested whether dloss could be estimated from the data or whether it should be fixed to the duration of menses. Because Higham’s score (HiS) reflects the quantity of blood lost during menses, we tested the assumption that it influenced kloss through a loglinear function:

$$\mathrm{kloss}={\alpha }_{\mathrm{loss}}ln\left(\mathrm{HiS}\right)$$

In the standard turnover model, concentrations of iron would return at their steady-state level after the end of the perturbation, but here, the data showed a marked overshoot of iron around mid-cycle, reminiscent of the pattern observed when an organism adapts to change input conditions, a situation known as tolerance (24). We tested several tolerance models including push-pull models (25) or effect-compartment models (26) which could reflect the regulation of iron namely through hepcidin.

Alternatively, an empirical model was built by assuming that iron release into serum increases by a parameter krelI during a period of time starting mid-menses (tbeg) and lasting drel days. Because of identifiability issues, tbeg was estimated using a grid approach between 1 and 5 days.

Hepcidin Model

As hepcidin showed a similar evolution as iron, the models described above were also applied to hepcidin. Because there were more fluctuations during the cycle than for iron, we tested for periodic changes in the model parameters using sinusoidal functions for baseline ksyn_H or kout_H:

$${\mathrm{k}\mathrm{o}\mathrm{u}\mathrm{t}}_{\mathrm{H}}={\mathrm{k}\mathrm{o}\mathrm{u}\mathrm{t}}_{\mathrm{H}0}+\mathrm{R}\mathrm{b}\ast \cos (2\ast a\cos (-1)\ast \left(t\text{-}\mathrm{d}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\right)/\mathrm{l}\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}))$$

where l cycle is the duration of the cycle, Rb the magnitude of variation and decal the day in the cycle when kout_H is equal to its average value.

Joint Model

The two separate models for iron and hepcidin were then combined, and we investigated the interaction between the two martial variables. We tested whether a mutual regulation could explain the rebound observed at the end of menses, by adding a linear or sigmoid effect of one variable on the synthesis of the other. For example, the effect of hepcidin on iron release into serum was modelled through equations such as

$${\mathrm{ksyn}}_{\mathrm{I}}={\mathrm{\alpha }}_{\mathrm{H}}\left(\mathrm{He}\left(t\right)-\mathrm{He}\left(0\right)\right)$$

$$\mathrm{or}{\mathrm{ksyn}}_{\mathrm{I}}={\mathrm{\alpha }}_{\mathrm{H}}\left(\mathrm{He}\left(t\right)-\mathrm{He}\left(0\right)\right)/\left(\mathrm{He}\left(t\right)-\mathrm{He}\left(0\right)+\mathrm{He}50\right)$$

The final model is illustrated in Fig. 3. Iron and hepcidin production were characterised by a zero-order rate constant (ksyn_I and ksyn_H, respectively), their elimination were characterised by a first-order rate constant (kout_I and kout_H, respectively), and the production of hepcidin was influenced by the changes in iron concentrations through a linear model. The final model for iron (Ir) and hepcidin (He) was described by the following system of differential equations:

$$\left\{\begin{array}{l}\frac{d\mathrm{I}\mathrm{r}\left(t\right)}{dt}={\mathrm{ksyn}}_{\mathrm{I}}\left(t\right)-{\mathrm{kout}}_{\mathrm{I}}.\mathrm{Ir}\left(t\right)\hfill \\ \frac{d\mathrm{He}\left(t\right)}{dt}={\mathrm{ksyn}}_{\mathrm{H}}\left(t\right)\left(1+\mathrm{\alpha }\left(\mathrm{Ir}\left(\mathrm{t}\right)-{\mathrm{I}\mathrm{r}}_0\right)\right)-{\mathrm{kout}}_{\mathrm{H}}.\mathrm{He}\left(t\right)\hfill \end{array}\right.$$ 4

starting from initial conditions:

$$\left\{\begin{array}{l}\mathrm{I}\mathrm{r}\left(t=0\right)=\frac{{\mathrm{ksyn}}_{{\mathrm{I}}_0}}{{\mathrm{kout}}_{{\mathrm{I}}_0}}\hfill \\ \mathrm{He}\left(t=0\right)=\frac{{\mathrm{ksyn}}_{{\mathrm{H}}_0}}{{\mathrm{kout}}_{{\mathrm{H}}_0}}\hfill \end{array}\right.$$ 5

where t = 0 is the beginning of the cycle; ksyn_I, kout_I, ksyn_H and kout_H vary according to the schedule in Fig. 3 (right) and dloss denotes the length of menses of each subject and was fixed to individual observed values, while drel denotes the length of the time period over which release is increased and was estimated. In Fig. 3, dcycle was fixed to the length of the cycle for each woman.

Fig. 3.

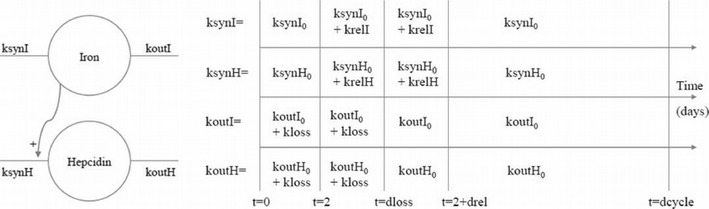
Model for iron and hepcidin in non-menopausal women (left), and values of the parameters controlling the turnover of both molecules according to the time in menstrual cycle (right)

Model Evaluation

Model evaluation was based on visual inspection of diagnostic graphs (27): individual fits, evaluating the predictive capacity of the model, plots of the predictions versus observations, evaluating the quality of the structural model, scatterplots of the NPDE (normalised prediction distribution errors) versus time and predicted concentrations, assessing the structural and statistical models (28), and VPC (Visual Predictive Check), evaluating the ability of the model to reproduce the observed data. NPDE and VPC were based on 1000 simulated datasets. These graphs were produced for all the runs during the analysis and used in combination with the statistical criteria to guide model building.

To evaluate the stability of the final model, a run assessment was performed using Monolix: 10 runs were performed with a different seed for the random number generator, and different initial parameters, randomly chosen within a range of ±20% centred on the estimates from the final model. The 10 sets of estimates parameters were then compared to those obtained with the final run. We also re-estimated the parameters for the final model excluding the three subjects identified by the clinicians as having abnormal values of hepcidin to assess their influence on parameter estimates.

RESULTS

Evolution of Iron-Status Variable During the Study

Ninety (90) menstruating women were included in the analysis. Their demographic and biological characteristics are shown in Table I. The population was homogeneous, with small standard deviations for the demographic covariates. Biological variability at the end of cycle visit ranged from small (5.2%) for haemoglobin to large (83.4%) for ferritin and was intermediate for serum transferrin (17.0%) and transferrin saturation (34.9%).

Table I.

Characteristics of Covariates at the Last Visit (End of Menstrual Cycle)

Demographic variables		Biological covariates (at the last visit)
Covariate	Mean (SD)	Covariate	Mean (SD)
Age	27.6 (6.3)	Serum transferrin	2.94 (0.5)
Height (cm)	165.4 (6.1)	Serum ferritin	53.14 (44.3)
Weight (kg)	61.8 (9.2)	Haemoglobin	13.48 (0.7)
Body mass index (kg/m2)	22.6 (3.0)	Transferrin saturation	23.81 (8.3)
Waist circumference (cm)	77.2 (9.6)
Higham’s score	96.6 (60.5)

SD standard deviation

Among the 90 patients, 67 had 6 blood samples, 20 had 5 and 3 subjects had 4. Overall, 514 measurements of iron and hepcidin were available. Since large variations were supposed to occur at the beginning of the cycle, per protocol, the bulk of the samples was collected during the first part of the cycle, with fewer samples from day 14 onwards.

Observed variations of serum iron and serum hepcidin throughout the menstrual cycle are shown in Fig. 2 as boxplots, along with the other iron-status variables. Spaghetti plots of the individual profiles is provided in the Appendix (Figure S1). Considerable fluctuations were observed in both iron and hepcidin levels with large variations in the shape of the individual profiles. A general pattern was observed in the boxplots of Fig. 2, consisting of an initial decrease during menses, followed by a rebound, and a stabilisation during the second half of the cycle. The rebound was marked, as both concentrations increased after the end of menses to reach higher values than baseline concentrations. The boxplots in Fig. 2 show a similar evolution for iron, hepcidin and saturation of serum transferrin. The other iron-status variables (transferrin, ferritin and haemoglobin) do not seem to consistently vary during the cycle but show considerable inter-individual variability.

Iron Modelling

In a first step, iron and hepcidin were modelled separately to help guide the joint modelling and provide appropriate initial estimates. Table S1 in Supplementary material shows the steps of the model building for each variable.

The turnover model with blood loss starting with menses was first adjusted to the data (model I1). The duration of blood loss could be fixed to the length of the menses (model I2). As expected, this model could not describe the rebound observed at mid-cycle in serum concentrations. We then tested various tolerance models (models I3 and I4), but they failed to reproduce the extent of the rebound. An empirical model assuming that iron release into serum increases by a parameter krel I during a period of time starting during menses and lasting drel days performed better (models I6 and I7), and a grid search showed mid-menses (day 2) performed well in terms of statistical criterion. An alternative was to fix the beginning of the rebound at the end of menses (model 5).

We tested whether dloss could be estimated from the data, but better estimates were found when dloss was fixed to the length of menses for every woman and when drel was estimated without between-subject variability. Because kloss represents the rate of iron lost during menses, we tested whether we could set kloss to be linearly related to Higham’s score, which evaluates the abundance of menstrual periods, but this did not improve the results. The final model reflected the evolution of iron adequately, as shown by the diagnostic graphs (Supplementary Figure S1), with a residual error around 30%.

Hepcidin Modelling

The evolution of hepcidin during the menstrual cycle paralleled on average the evolution of iron, as shown in Fig. 1. We used the same baseline model as for iron, with parameters ksynH, and koutH, and again tested various assumptions to handle the mid-cycle rebound of hepcidin concentrations. The residual error remained large for all model tested, however, decreasing from 0.49 to 0.46 when the rebound was included. A model where kout_H was assumed to have a sigmoidal periodicity throughout the cycle was tested and improved the residual error to 0.4; however, this model was not kept in the following because it induced large fluctuations in the second part of the cycle where we did not have sufficient data to confidently validate such behaviour and also because for some subjects, kout_H became very small and as a result, hepcidin concentrations did not return to baseline at the end of the cycle. Diagnostic graphs for the final hepcidin model are shown in Supplementary Figure S2.

Iron and Hepcidin Modelling

The two separate models for iron and hepcidin were then combined, and we investigated the interaction between the two martial variables. Table II shows key models tested in the joint analysis. In the first model, we combined the separate models for iron and hepcidin without a link between the two. We then tested a model where hepcidin modifies the release of iron (ksynI, model 2), and this model had a similar BIC, while a model where iron modifies the release of hepcidin ksynH (model 3) performed slightly better. A model including both link functions on the other hand had a worse BIC (model 4), so the effect of hepcidin on iron was not kept in the model. We then tested different assumptions concerning the link between the two variables: we could assume the same (relative) loss during menses (same kloss) and the same duration for the rebound. In model 6, the duration of the rebound had a rather large estimation error (72%), but we could assume the inter-individual variability was negligible (model 7). We compared this joint model with a model where hepcidin concentration is a linear function of iron (He(t) = α Ir(t)); although the BIC decreased by a little over four points (BIC = 5715.7), the residual error for hepcidin increased back to 50% and we did not keep this model. Because in some subjects the rebound for iron or hepcidin was not apparent, we also tested mixture models to accommodate different profiles within the population, but these did not provide better estimates (models 8 and 9). Finally, we also refined the residual error models. To avoid numerical problems with a proportional error model, we used a combined residual error model for the model building. In the final model, the additive part of the iron residual error was very small and poorly estimated and could be removed without changing the value of the log-likelihood or the estimated parameters (model 9) or fixed to a small value (model 11, where a_I was fixed to 0.001).

Table II.

Models Tested in the Joint Analysis of Iron and Hepcidin

Number	Description	BIC (IS)
1	Separate models for iron and hepcidin	5751.3
2	Model with ksynI linear function of hepcidin concentration	5751.0
3	Model with ksynH linear function of iron concentration	5749.4
4	Model with both variables acting on each other	5768.4
5	ksynH linear function of iron concentration, same kloss	5736.5
6	ksynH linear function of iron concentration, same drel	5728.9
7	ksynH linear function of iron concentration, same drel, no IIV	5728.7
8	Mixture model on krelI	5735.2
9	Mixture model on krelH	5735.3
10	ksynH linear function of iron concentration, no rebound for hepcidin	5731.8
11	Final model, proportional error model	5712.0
12	Final model, aIron fixed to 0.001	5720.0

The log-likelihood (LL) was computed by importance sampling for all models tested. A combined error model was used except when indicated otherwise

BIC Bayesian information criterion, IS importance sampling

Therefore, in the final model (Fig. 3), turnover models were used to describe both iron and hepcidin evolution, and the changes in iron concentrations drive the production of hepcidin. The four production and elimination parameters were modelled as time dependent, and their variations during the cycle are depicted on the right hand side of Fig. 3. The same parameter kloss increased the elimination of both responses during menses, while the synthesis of iron and hepcidin increases by krelI and krelH, respectively, for the same duration drel starting from day 2 of menses. Throughout the menstrual cycle, serum iron affected the synthesis of hepcidin through a linear relationship involving a parameter α.

The joint model provided a good fit for iron, with a residual error around 29%, while the residual error was larger for hepcidin (48%), which was reflected in a large variability in the VPC plots although the median profile appeared adequately predicted. The additive part of the error model was estimated with a large estimation error; it was kept in the model to avoid numerical problems during the estimation process, but its estimated value was very small and does not influence the results.

Effect of Covariates

The parameter estimates for the joint structural model are reported in the first column of Table III (model without covariates). There was substantial inter-individual variability for several parameters, so the next step in the analysis was to test whether covariates could explain part of the variability. Covariate model building was performed starting from model 7 in Table II, assuming a combined residual error model again to avoid running into numerical issues. For each parameter, we first built a full model with all potential parameter-covariate relationship; in a second step, we removed all the relationships for which the p value of the Wald test for the covariate was higher than 0.2 (intermediate model); then, the covariate model for the parameter was obtained by removing one by one all non-significant relationships (reduced model). Each of these steps is presented in models 2 to 28. Except for model 22 (selection on parameter krelH), all the reduced models had lower BIC than the base model. No covariate was found to influence drel, while for koutI, the intermediate model was the same as the final parameter model. The selected relationships were then combined in a full model (model 29), and descending selection was again performed to obtain the final model (model 30). A proportional error model was tested for the final model and found to yield similar parameter estimates and log-likelihood values. The steps of the analysis are shown in Table IV.

Table III.

Estimates of the Parameters and Their Variability for Both Models With and Without Covariates

	Model without covariate		Model with covariates
Parameter	Estimate (RSE)	Variability (RSE)	Estimate (RSE)	Variability (RSE)
ksynI (μmol.d. L−1)	5.48 (10)	13 (64)	7.57 (8)	15 (15)
koutI (d−1)	0.33 (10)	14 (51)	0.42 (8)	0 (-)
kloss (d−1)	0.08 (27)	129 (20)	0.14 (19)	95 (19)
krelI (μmol.d.L−1)	2.23 (14)	70 (19)	2.55 (13)	55 (22)
drel (d)	5.44 (10)	0 (−)	5.74 (5)	0 (−)
ksynH (nmol.d.L−1)	1.86 (9)	50 (12)	2.48 (5)	24 (19)
koutH (d−1)	0.58 (9)	51 (12)	0.82 (7)	57 (9)
krelH (nmol.d.L−1)	0.21 (25)	156 (13)	0.28 (21)	103 (17)
α (−)	0.03 (35)	64 (67)	0.03 (31)	87 (38)
b Iron (−)	0.29 (4)		0.29 (4)
a Hep (nmol.L−1)	0.14 (48)		0.17 (50)
b Hep (−)	0.48 (7)		0.47 (8)
−2LL (IS)	5631.0		5558.5
BIC (IS)	5721.0		5680.0

The variability is in %

RSE relative standard error, in %, d day, BIC Bayesian Information Criterion, IS importance sampling, −2LL objective function

Table IV.

Covariate Models Tested in the Joint Analysis of Iron and Hepcidin. Full Base (N = 90)

Number	Description	LL (IS)	BIC (IS)
1	Base model, no covariates	5634.17	5728.7
2	Parameter ksynH, full model (all covariates)	5599.25
3	Parameter ksynH, removing covariates with p > 0.2	5597.77
4	Parameter ksynH, reduced model after stepwise pruning	5601.50	5718.49
5	Parameter koutH, full model (all covariates)	5605.83
6	Parameter koutH, removing covariates with p > 0.2	5605.46
7	Parameter koutH, reduced model after stepwise pruning	5602.22	5714.72
8	Parameter ksynI, full model (all covariates)	5591.01
9	Parameter ksynI, removing covariates with p > 0.2	5584.00
10	Parameter ksynI, reduced model after stepwise pruning	5588.82	5701.31
11	Parameter koutI, full model (all covariates)	5589.64
12	Parameter koutI, removing covariates with p > 0.2	5582.85
13	Parameter koutI, reduced model after stepwise pruning	5582.85	5704.34
14	Parameter kloss, full model (all covariates)	5613.80
15	Parameter kloss, removing covariates with p > 0.2	5620.61
16	Parameter kloss, reduced model after stepwise pruning	5620.61	5724.11
17	Parameter krelI, full model (all covariates)	5625.23
18	Parameter krelI, removing covariates with p > 0.2	5616.80
19	Parameter krelI, reduced model after stepwise pruning	5619.53	5727.52
20	Parameter krelH, full model (all covariates)	5627.29
21	Parameter krelH, removing covariates with p > 0.2	5625.87
22	Parameter krelH, reduced model after stepwise pruning	5628.21	5731.71
23	Parameter drel, full model (all covariates)	5634.81
24	Parameter drel, removing covariates with p > 0.2	–
25	Parameter drel, reduced model after stepwise pruning	–	–
26	Parameter α, full model (all covariates)	5627.67
27	Parameter α, removing covariates with p > 0.2	5633.77
28	Parameter α, reduced model after stepwise pruning	5626.46	5725.46
29	Joint model combining separate parameter models	5636.71	5731.21
30	Final model after stepwise pruning	5565.16	5691.16
31	Final model, aIron fixed to 0.001	5563.23	5684.73
32	Final model, proportional error model	5558.49	5679.98

LL log-likelihood, BIC Bayesian information criterion, IS importance sampling

After stepwise model building, the following six covariates were found to affect one or several parameters in the model: method of contraception, BMI, Height and Higham’s score, as well as the end of cycle values of haemoglobin and ferritin. After covariate inclusion, the between-subject variability for the parameter kout_I was very small, and we removed it from the final model. The estimates of the effects of these covariates are shown in Table V. For each continuous parameter-covariate relationship, we show the values of the 10th and 90th percentile of the distribution of this covariate in our population (column 4) and the corresponding predicted values of the parameter for that relationship, in order to illustrate the typical individual variability for this parameter. For example, the release of iron during the rebound effect, characterised by parameter krelI, can be expected to vary between 3.80 for women with a BMI of 19.3 and 1.32 for a BMI of 26.6. The table also shows that women without contraception eliminate iron about 22% faster than women taking contraception.

Table V.

Estimates of the Covariates Effects (β) on the Parameters of the Final Model

Parameter	Covariate	Estimate of β (RSE)	Covariate distribution (10th–90th percentile)	Estimate (10th–90th percentile)
koutI	No contraception	0.20 (23)	0–1	0.38–0.46
krelI	BMI	−3.31 (31)	19.3–26.6	3.80–1.32
	Haemoglobina	6.93 (31)	12.5–14.6	1.54–4.53
ksynH	Higham	0.66 (11)	38.2–160.2	0.61–1.58
koutH	Higham	0.83 (14)	38.2–160.2	0.18–0.59
	Ferritina	−0.60 (16)	18.6–97.4	0.50–0.18
krelH	Height	32.70 (16)	158.0–173.0	0.03–0.58
	Ferritina	−1.95 (18)	18.6–97.4	0.57–0.03

RSE relative standard error, in %, 10–90, Assessment mean (min/max) of five values estimated during the run assessment step; Covariate distribution: values of the 10th and the 90th percentile of the covariate; Estimate: values of the parameter corresponding to the 10th and 90th percentiles respectively.

^aBaseline

The method of contraception was significant in the final model, where we found that women with contraception have a lower elimination of iron throughout the cycle, and consequently maintain higher iron concentrations than women without contraception. This result is consistent with the observed serum iron values, as we found iron concentrations at the last visit to be significantly higher for the women with contraception (p value 0.008 according to a Wilcoxon test). Higham’s score increases both the production and the elimination of hepcidin, and the net effect results in higher concentrations of hepcidin with faster return to equilibrium for high scores. Subjects with high concentrations of ferritin at the end of the cycle visit tended to have slower elimination of hepcidin but also less rebound after menses, resulting in higher concentrations with dampened fluctuations throughout the cycle. The height of the subjects had an important effect on the release of hepcidin at the end of menses, with tall women showing a much more pronounced rebound than short women. This effect was not related to weight or body mass index and remained highly significant in all covariate models tested in the analysis. The final model with a proportional error model was subjected to a run assessment, and all effects remained significant in the repeated runs (additional details, including a figure showing the estimates of parameters and their standard errors across 10 runs starting with different seeds and conditional estimates, are given in the Appendix).

To highlight the importance of including covariates, Table IV compares the estimates of the parameters and their standard errors in the models with and without covariates. The estimates of the fixed parameters were similar in both models but the between-subject variabilities were generally smaller in the model with covariates. The model with covariates also performed better with respect to the minimal value of the objective function and the value of both residual errors. The precisions of the estimates in the final model were reasonable, with standard-errors less than 30%.

Model Evaluation

Individual fits of iron and hepcidin are shown in Fig. 4 for the first nine subjects in the dataset. The two responses for each subject are shown overlayed on the same figure; iron is represented in red and hepcidin in blue, respectively, with closed and open circles for measured values. The model adequately described the evolution of both serum concentrations throughout the menstrual cycle for most subjects, although in some subjects iron fluctuated daily and did not follow a recognisable evolution (subject 6 for iron and subject 2 for hepcidin, for example). The diagnostic VPC in Fig. 5 supports the good model adequacy for iron, since the observed median profile as well as the 10th and 90th percentiles remain in their prediction intervals. The hepcidin serum concentrations were more difficult to predict because of the high variability, and the individual fits and the diagnostic VPC reflected these results, which can be seen in particular in the higher variability for the 90th percentile of data in Fig. 5 (upper right). The evolution of hepcidin was poorly adjusted in some subjects, especially when hepcidin did not return to a baseline level at the end of the cycle (subject 2 in Fig. 4 for example), and there was more diversity in the individual profiles. As a result, the VPC for hepcidin was less convincing than for iron, with a larger variability in particular in the magnitude of the rebound. This variability reflects the fact that the rebound does not appear in all subjects and also that hepcidin does not always follow the evolution of iron. However, the model adequately described the median and the 10th percentile for hepcidin, suggesting that we can capture the average evolution of hepcidin. Finally, Fig. 5 shows the plots of predicted versus observed values, for iron (top) and hepcidin (bottom), using either population (left) or individual predictions (right). As can be expected from the poor predictions for some observations, the plots show some outliers poorly predicted by the model, but the bulk of the observations are distributed around the line of identity. The NPDE (normalised prediction distribution errors) versus time, in Fig. 5 (bottom), supports this conclusion. As expected, the majority of the residuals of both iron and hepcidin fall within the interval (−1.96, 1.96), indicating no major model misspecification (28). Figure 6 presents the plots of the observed versus predicted concentrations for iron (top) and hepcidin (bottom), with population (left) and individual (right) predictions, with again more residual variability apparent for the second iron-status variable.

Fig. 4.

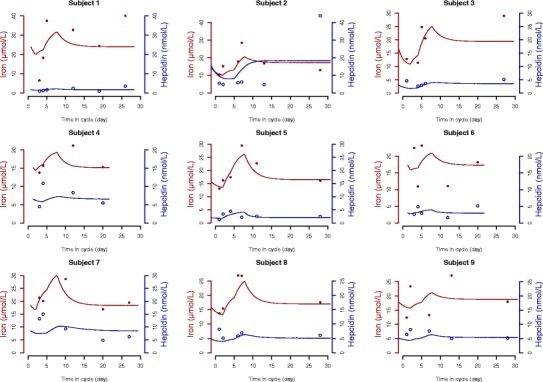
Individual fits for the first nine subjects in the dataset, for iron (red, closed symbols) and hepcidin (blue, open circles). The symbols on the individual fits represent individual measured concentrations, and the solid lines represent model predictions

Fig. 5.

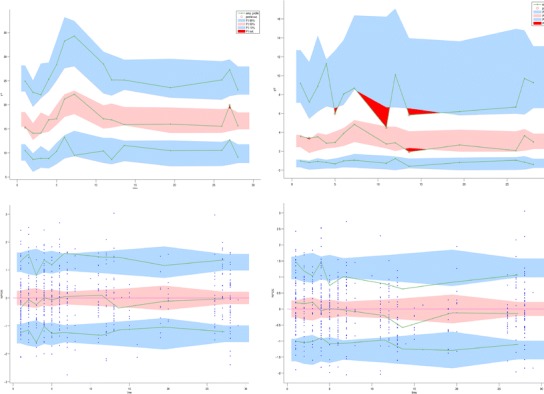
Diagnostic VPC (top) and graphs of the NPDE (bottom), as obtained with the Monolix software for iron (left) and hepcidin (right). The solid lines represent the 10th, 50th and 90th empirical percentiles of the measured concentrations in the diagnostics VPC and of empirical percentiles of the residuals in the NPDE graphs. The coloured areas represent the 90% prediction interval associated with the 10th, 50th and 90th theoretical percentile in the first case and the confidence interval in the second

Fig. 6.

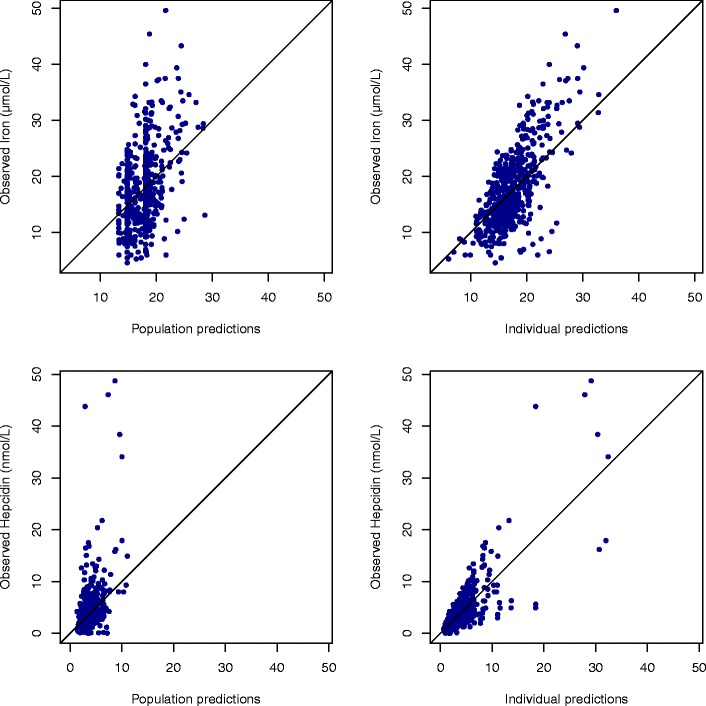
Prediction versus observations for iron (top) and hepcidin (bottom), with population predictions (left) and individual predictions (right)

Finally, we performed two assessments of the model robustness. First, we ran a run assessment to assess the stability when changing initial conditions and random number generator seed; the estimates of the parameters remained stable across the different runs, revealing no major problem of stability. Second, the model was adjusted again with the dataset excluding the three subjects with abnormal values of hepcidin. The fixed estimates of the model parameters (fixed and random variability) were similar to those obtained in the full dataset, but the residual error of hepcidin decreased to 0.45; a couple of covariate effects were also slightly modified but remained significant. This suggests that the model considered the outlier data as noise and confirmed the robustness of the model estimates.

DISCUSSION

The objective of the present study was to model the evolution of serum iron and serum hepcidin concentrations throughout the menstrual cycle in healthy non-menopausal women. Hepdicin has attracted interest as a major player in the regulation of iron metabolism, and since the development of an analytical method to measure its serum concentration, it is being introduced in the array of diagnostic tools for iron disorders (7). Little is known however about the within-subject variations to be expected, in particular in women: significant diurnal variations of hepcidin have been reported (29), and gender, as well as age, has been shown to impact the values of hepcidin concentrations in normal subjects (10,30,31). In addition, the evolution of martial settings including serum iron shows significant variations during the menstrual cycle (9). To our knowledge, ours is the first study to propose a joint model of these two variables and the first to propose a model explaining the fluctuations of hepcidin during the menstrual cycle.

We used a population approach via non-linear mixed effect models to design the experiment and model the data collected (18,19). This enabled us to limit the number of samples in each woman, as an important loss of blood could have interfered with iron regulation and therefore modified concentrations of iron-status variables. Non-linear mixed effect models are also able to handle longitudinal data with different sampling times for each subject; this allowed us to adapt the sampling schedule to cover the entire menstrual cycle over the population, while adjusting to weekdays for the visits. An added benefit was the bolstered inclusion rate as the protocol was not deemed to be too invasive.

The evolution of the two variables was jointly described using two linked turnover models with increased elimination from blood loss during menses. Menses were found to have a similar impact on both iron and hepcidin, as we could use the same parameter kloss to model the increased elimination of the two variables. We found that iron levels modified the release of hepcidin, but we could not identify a regulatory effect of hepcidin on iron. The elimination rate of hepcidin, characterising the rate of turnover and the speed at which the system adjusts to perturbations, was estimated in our study to be around 0.82 day⁻¹ (half-life of 0.9 day). This reflects the equilibration time for the iron regulatory system rather than the actual elimination half-life of hepcidin alone, which on its own is a very short-lived hormone, with a half-life estimated to a few minutes in monkeys (19). The fact that kout_I and kout_H are close supports this interpretation, as the elimination rate constant for iron was estimated to be 0.42 day⁻¹ (half-life of 1.7 days).

A second feature of the model was the increased release of both hepcidin and iron beginning during menses, which was included in the model through the parameters krelI and krelH, to describe the rebound observed mid-cycle. Rebound effects are characteristic of systems including regulation loops and can reflect tolerance building up in the system as it adjusts to changing inputs (24). Various tolerance models have been proposed, including push-pull models (25), effect compartment models (26) and precursor models (32). We attempted to introduce mutual or one-way regulation of iron and hepcidin to account for this phenomenon, but none of the different tolerance models tested was able to describe adequately the observed rebound, generally falling short of the peak. We also explored introducing the other iron-status variables into the model, as they are known to be involved in iron circulation, but contrary to iron and hepcidin, they showed little variation during the menstrual cycle, except for transferrin saturation which was highly correlated with iron concentrations, and were therefore unable to explain the variations during the first part of the cycle. Thus, the iron network was simplified in this study where iron was only related to hepcidin. Interestingly, the increase in iron was about nearly four times as large (41%) as the increase in hepcidin (11%), which can be related to the fact that hepcidin is driven mainly by iron in our model, while iron is also influenced by deep regulation mechanisms. The impact of iron on hepcidin was relatively small (α = 0.03) but significant, as models without the link function were found to perform worse. We also tested removing the rebound for hepcidin so that the hepcidin profile was entirely driven by changes in iron concentration but again the statistical criterion was slightly worse, showing that both intrinsic hepcidin rebound and iron changes influence the evolution of hepcidin.

There was a considerable between-subject variability in baseline concentrations for both iron and hepcidin, reflected in large inter-individual variability in key parameters in the model, notably the elimination rate of hepcidin. Variability in iron-status variable loss during menses, or the extent of the rebound effect, also impacts the within-subject variability during the menstrual cycle on top of the fluctuations introduced by blood loss during menses and the subsequent system regulation. It is interesting to note that the study was performed in a relatively homogenous population of healthy women, where we excluded subjects with low iron concentrations or haemoglobin at baseline. For diagnosis purposes, this suggests that non-menopausal women are likely to exhibit significant variations within their cycle on top of the within-subject variability, even in the absence of iron-related disorders. Blood loss during menses is the main cause of iron deficiency in young women. It varies between 20 and 80 mL during a period, representing a loss of 10 to 40 mg of iron for women with regular menstrual cycles (16,33). This is significant compared to the unregulated 1 mg eliminated daily through skin, intestinal and urinary cell desquamation, the only other physiological way to eliminate iron (2). Additional sources of variability may include dietary factors, which were not monitored or controlled in this study.

The joint model proved very satisfactory to describe the evolution of iron, with a residual variability of 30%, while the residual variability remained larger for hepcidin (47%) even after covariate inclusion, indicating more unexplained fluctuations for this variable. This reflects the observed data, as the evolution of iron was more consistent across the women than the evolution of hepcidin. Indeed, in about two thirds of the subjects, the rebound of hepcidin was small or non-existent, or the evolution of hepcidin was quite different from the evolution of iron. Graphical diagnostics illustrated this higher variability. We experimented with various other models for hepcidin, including a mixture of subjects with or without rebound, as well as a cyclic menstrual variation in the elimination rate constant of hepcidin during the cycle. Although this last model was promising, with a reduced residual variability, it had the disadvantage of predicting large fluctuations in the second part of the cycle, where the data to evaluate it was limited, so it was not kept in the final analysis. A total of six iron-status variables were measured during the study, but only iron and hepcidin are included in the model because the others did not show significant variations during the menstrual cycle. The exception was transferrin saturation which was almost completely correlated with iron and did not bring additional information for the modelling. However, the typical (baseline) value of these variables was taken into account as a covariate. Our results suggest that in this group of healthy women, menses are the main determinant of iron changes during a monthly cycle, and iron and hepcidin are the most reactive iron-status variables.

The experimental design for the HEPMEN study was optimised based on three assumptions: (i) a simplified turnover model of iron assuming only release and elimination of iron into the blood stream, (ii) a similar evolution of hepcidin with parameters estimated in monkeys and (iii) an additional elimination of both variables through blood loss during menses. As a result, the optimised protocol included more sampling times during the first part of the cycle where more variation was expected. The data collected in the HEPMEN study however showed a significant rebound of iron concentrations after the end of menses in most women, as well as of hepcidin in a large proportion of women. In addition, some women exhibited different patterns for hepcidin evolution which could not be adequately described by the model. It would therefore be interesting to collect additional data in the second part of the menstrual cycle to further refine the model and evaluate the plausibility of cyclic changes that could be associated with hormone status.

In the present study, we also investigated the impact of a number of covariates, both demographic and biological, on the variability of iron and hepcidin. Most covariate effects we found had an impact on the steady-state levels of iron and hepcidin. At the end of the cycle, the model predicts that hepcidin and iron both stabilise to a value representing the steady-state of the system in the absence of the perturbation induced by menses or abnormal bleeding. The average baseline value of iron was estimated to be 18 μmol.L⁻¹, or equivalently 1 mg/L, and the average baseline value of hepcidin was estimated to be 3.0 nmol.L⁻¹. Those values are similar to baseline of previous studies with similar population where iron baseline was estimated to 16.6 μmol.L⁻¹ (9) and hepcidin baseline was estimated between 2.6 and 4.8 nmol.L⁻¹ depending on age (10). These baseline levels were found to be affected by contraception method for iron and by serum ferritin for hepcidin.

We found that women without contraception had a higher elimination of iron, which led to steady-state concentrations of iron lower by about 20% compared to women using contraception. It has been shown that contraception regulates the abundance of menses (34) and therefore limits iron loss (35), which can explain this finding. Iron concentrations at steady-state were also affected by body size, as we found that iron absorption decreased when the body mass index increased. This result was observed in several studies revealing that iron concentration was lower for people with a high body mass index (36,37). A study performed on women aged between 18 to 25 years with a measured BMI ≥27.5 kg/m² revealed the presence of inflammation with increasing body mass index. However, inflammation is a factor increasing hepcidin production and consequently decreasing iron absorption. Finally, our model confirmed previous findings that haemoglobin concentrations have an impact on iron concentrations (38). We found that iron concentrations were lower when haemoglobin concentrations were low. The production of haemoglobin is dependent on serum iron which binds to transferrin and moved to the bone marrow where it is used to produce erythrocytes (2). High haemoglobin concentration decreases this stimulation, leaving more circulating iron in blood, which is reflected in our model by an increased rebound of iron after menses. Similarly, several covariates were also found to affect levels of hepcidin. Higham’s score had an effect both on the production and elimination of hepcidin. The net result is that hepcidin concentrations are lower in women experiencing high blood loss during menses. High blood loss would also result in more iron loss, which would lead to higher hepcidin release to compensate. Finally, our model confirmed previous observations of a significant correlation between hepcidin and ferritin (39,40). In healthy women, high concentrations of ferritin correlate with high concentrations of iron, which would trigger an increase of hepcidin to regulate iron release from storage.

An unexpected finding was that height had a strong effect on the release of hepcidin at the end of menses, with tall women showing a more pronounced rebound after menses. This was not attributable to a particular subgroup of subjects, as the effect was quite strong and remained present in all models tested. As weight or BMI are more often used as determinant of body size in PK/PD analyses, we also considered these covariates in the analysis, but they did not have the same impact as height.

CONCLUSION

In summary, a joint turnover model with time-varying production and elimination rate constants was developed to describe serum iron and serum hepcidin concentrations throughout the menstrual cycle. The elimination rate constant increased during menses, reflecting the loss of blood, and the secretion rate constant was assumed to increase during the first part of the cycle, describing the observed rebound in both molecules at the end of menses. An increased excretion of hepcidin in response to increased concentration of iron reflecting iron regulation was also modelled. This model allowed a better understanding of the evolution of hepcidin throughout the cycle and its relationship with iron changes. It was able to describe the significant variations of both variables throughout the cycle and highlighted a large daily variability reflected by the high residual of hepcidin. The model will be applied to analyse the variations of iron and hepcidin throughout the cycle and determine the optimal time to measure the concentrations of those molecules (41–43).

Compliance with Ethical Standards

This study was reviewed by the ethical committee of Rennes and approved by the National Security Agency of the Medicine and the products of health (ANSM).

Competing Interest

The authors report no conflict of interest concerning this study. All contributing authors are members of French hospitals and French medical research institutions.

Informed Consent

Signed, written informed consent was obtained from all participants.