Does a coupling capacitor enhance the charge balance during neural stimulation? An empirical study

Abstract

Due to their DC-blocking characteristic, coupling capacitors are widely used to prevent potentially harmful charge buildup at the electrode–tissue interface. Although the capacitors can be an effective safety measure, it often seems overlooked that coupling capacitors actually introduce an offset voltage over the electrode–tissue interface as well. This work investigates this offset voltage both analytically and experimentally. The calculations as well as the experiments using bipolar-driven platinum electrodes in a saline solution confirm that coupling capacitors introduce an offset, while they barely contribute to the passive charge balancing. In particular cases, this offset is shown to reach potentially dangerous voltage levels that could induce irreversible electrochemical reactions. This work therefore suggests that when the use of coupling capacitors is required, the offset voltage should be analyzed for all operating conditions to ensure it remains within safe boundaries.

Introduction

Neural stimulation is becoming an increasingly popular clinical treatment methodology for a wide variety of diseases. In most cases, an implantable pulse generator (IPG) is used to deliver stimulation pulses to electrodes that are placed in the target area. The safety of the device is of major concern, since a faulty stimulation signal can cause irreversible damage to the neural tissue. It is especially important to prevent the flow of DCs through the electrodes [3, 7].

The use of coupling capacitors between the stimulator and the electrodes is widely considered to be an effective safety mechanism [10, 11], and indeed, various advantages concerning the use of coupling capacitors have been identified [4]. The first important advantage is the prevention of DCs in the event of device failure [9]. If, for example, one of the electrodes shorts to the supply voltage, the coupling capacitor will prevent a prolonged DC current through the electrodes.

The second important advantage that is attributed to coupling capacitors is that they improve the performance of passive charge-balancing techniques [4, 14, 15]. Charge balancing is important for polarizable electrodes to keep the electrode–tissue interface within an electrochemically safe regime [7]. A coupling capacitor helps due to its high-pass characteristics, which limits the flow of DCs, and hence, no net charge can be injected into the tissue.

A disadvantage of coupling capacitors is that their required value is often too high to be integrated on an IC [15], and hence, they are realized using bulky external components. Many studies have focused on designing stimulator output stages with accurate charge-balancing circuits [8, 13] in order to eliminate the need of coupling capacitors. Others have proposed high-frequency operation to reduce their size [5]. Indeed, the results seem to suggest that the proposed mechanisms are good enough to prevent charge accumulation on the tissue even without coupling capacitors. However, it is not clear how these systems can guarantee safety in the event of a device failure. For this reason, many stimulator systems still require the use of coupling capacitors.

Although widely used, it often seems overlooked that a coupling capacitor eliminates control over the DC voltage across the electrodes. As will be shown in this work, it is therefore possible for an offset voltage V_os to develop over the electrode–tissue interface, even when the electrodes and capacitors are shorted in between the stimulation pulses and charge-balanced biphasic stimulation is used.

If V_os becomes too large, the electrode–tissue interface may leave the electrochemically safe regime, triggering the production of potentially dangerous reaction products. In this case, the intended safety mechanisms of the coupling capacitor create the opposite result: A potentially dangerous situation is created. In this work, the value of V_os is analyzed over various operating conditions, both analytically and experimentally. This gives insight in when V_os is exceeding a predefined safe regime.

Methods

A basic setup of a biphasic stimulator system is depicted in Fig. 1a: The coupling capacitor C_c is connected in series with the stimulator and the electrodes. The stimulation source in Fig. 1a is a biphasic constant current stimulator with a cathodic first stimulation pulse with amplitude I_c and duration t_c. The anodic charge cancelation phase follows with amplitude I_a and duration t_a. Most stimulator systems apply a passive charge-balancing scheme [15], in which the series connection of the electrodes and coupling capacitor are shorted after the stimulation cycle by closing switch S₁ to discharge C_dl. The duration of shorting t_dis is determined by the repetition rate f_stim = 1/t_stim of the stimulation, since S₁ needs to be opened again when the next stimulation cycle starts.

Fig. 1.

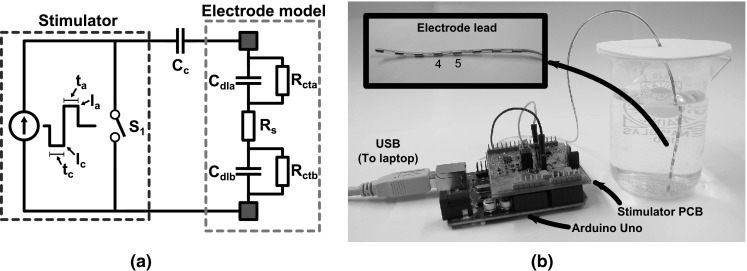
a A basic setup of a biphasic constant current stimulator system is shown that includes a coupling capacitor C _c and an electrode model. b A picture of the measurement setup is shown with a detail of the electrode lead where contacts 4 and 5, which were used for stimulation, are indicated

As shown in Fig. 1a, the electrodes are modeled as a resistance R_s in series with capacitors (C_dla and C_dlb) and resistors (R_cta and R_ctb) that model the electrode–tissue interfaces of both electrodes [6]. The electrodes used in this study are single percutaneous octrode leads (manufactured by ANS, currently St. Jude Medical): They consist of eight ring-shaped platinum contacts that are distributed on a single lead. Each electrode has a diameter of 1.5 mm and a width of 3 mm (area 0.14 cm²). A picture of the electrodes is depicted in Fig. 1b. These types of electrodes are typically used for spinal cord stimulation, and the stimulation amplitudes used in this paper are based on the specifications of the EON™ IPG (also from St. Jude Medical) [16]. The electrodes were submerged in a phosphate-buffered saline (PBS) solution containing the following: 1.059 mM KH₂PO₄, 155.172 mM NaCl, 2.966 mM Na₂HPO₄–7H₂O (pH 7.4, Gibco^® Life technologies™). The electrodes were connected in a bipolar fashion by selecting contacts 4 and 5 as the anode and cathode (see Fig. 1b). The other contacts were left floating.

Using an HP4194A impedance analyzer (excitation amplitude 0.1 V), it was found that for these electrodes in the PBS solution, R_s ≈ 100 Ω and C_dl ≈ 1.5 μF. Here, C_dl is the capacitive part of both electrode–tissue interfaces combined. The value of R_ct ≈ 1 MΩ (also combining both interfaces) was determined by measuring the voltage over the electrodes due to a 5-nA DC from a Keithley 6430 sub-femtoamp sourcemeter.

Determining V_os

After the anodic phase, both C_c and C_dl will be charged. Upon closing S₁, these capacitors will be discharged with a time constant:

$${\mathit{\tau }}_{\text{dis}}=R_s{C}_{\text{eq}}{C}_{\text{eq}}=\frac{C_c{C}_{\text{dl}}}{C_c+C_{\text{dl}}}$$ 1

If S₁ would be closed sufficiently long, a pseudosteady state is reached in which:

$$V_{\text{Cc}}+V_{\text{Cdl}}=0$$ 2

Here, V_Cc is the voltage over C_c. If S₁ is closed even longer, C_dl will continue to discharge through R_ct with time constant τ₂ = R_ctC_dl until V_Cdl = 0 V and the actual steady state is reached. However, usually t_dis ≪ τ₂, and therefore, only the pseudosteady state is reached.

Note that Eq. (2) does not guarantee that V_Cdl = 0 in pseudosteady state: It is an under-determined equation, and V_Cc = −V_Cdl can have any value. Only when both C_c and C_dl are ideal capacitors, the same current is flowing through both capacitors during a stimulation cycle, which causes V_Cc = V_Cdl = 0 V in pseudosteady state. If these requirements are not met (e.g., when R_ct ≠ ∞), the current though C_c does not equal to the current through C_dl, which will cause V_Cdl = -V_Cc ≠ 0 in pseudosteady state. This charge imbalance can accumulate over many stimulation cycles, which creates an offset in V_Cdl [2].

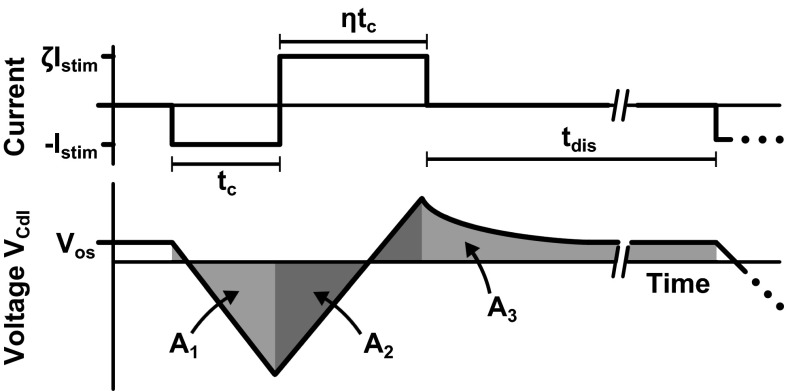
We refer to Fig. 2 to analyze V_Cdl when after many stimulation cycles the offset voltage V_os is stable. In order for this voltage to be stable, the average current through R_ct must be zero such that no charge is lost that causes an inequality in the charge accumulated on C_dl with respect to C_c. Therefore, it must hold that the average value of V_Cdl (and hence the area as indicated in Fig. 2) is zero as well.

Fig. 2.

Schematic plot of V _Cdl during a biphasic stimulation cycle with charge mismatch. When V _os is stable, the area A ₁ + A ₂ + A ₃ equals zero

To find the value of V_os for which this requirement is met, it is assumed that the cathodic stimulation phase is characterized by a duration t_c and amplitude I_c = I_stim. In the anodic phase, both the duration t_a = ηt_c and the amplitude I_a = ζI_stim can include mismatch. Furthermore, it is assumed that t_dis ≪ τ₂ (such that pseudosteady state is reached) and that R_ct is large enough to be neglected in the analysis (but as stated above, it must be finite). The areas A₁, A₂ and A₃ are found as:

$$A_1={\int }_0^{t_{\text{c}}}\left(V_{\text{os}}-\frac{I_{\text{stim}}t}{C_{\text{dl}}}\right)\text{d}t=V_{\text{os}}{t}_{\text{c}}-\frac{I_{\text{stim}}{t}_{{}_{\text{c}}}^2}{2C_{\text{dl}}}$$ 3a

$$A_2={\int }_0^{\mathit{\eta }{t}_{\text{c}}}\left(V_{\text{os}}-\frac{I_{\text{stim}}{t}_{\text{c}}}{C_{\text{dl}}}+\frac{\mathit{\zeta }{I}_{\text{stim}}t}{C_{\text{dl}}}\right)\text{d}t=V_{\text{os}}\mathit{\eta }{t}_{\text{c}}-\frac{I_{\text{stim}}\mathit{\eta }{t}_{\text{c}}^2}{C_{\text{dl}}}+\frac{\mathit{\zeta }{I}_{\text{stim}}{\left(\mathit{\eta }{t}_{\text{c}}\right)}^2}{2C_{\text{dl}}}$$ 3b

$$A_3={\int }_0^{t_{\text{dis}}}\left(V_{\text{os}}-\left(1-\mathit{\zeta }\mathit{\eta }\right)\frac{I_{\text{stim}}{t}_{\text{c}}}{C_{\text{dl}}}exp\left(\frac{-t}{R_{\text{s}}{C}_{\text{dl}}}\right)\right)\text{d}t=V_{\text{os}}{t}_{\text{dis}}-\left(1-\mathit{\zeta }\mathit{\eta }\right)I_{\text{stim}}{t}_{\text{c}}{R}_{\text{s}}$$ 3c

By setting A₁ + A₂ + A₃ = 0 and solving for V_os, the following equation is obtained:

$$V_{\text{os}}=\frac{(0.5+\mathit{\eta }-0.5\mathit{\zeta }{\mathit{\eta }}^2)I_{\text{stim}}{t}_{\text{c}}^2+(1-\mathit{\zeta }\mathit{\eta })I_{\text{stim}}{C}_{\text{dl}}{t}_{\text{c}}}{C_{\text{dl}}{t}_{\text{c}}(1+\mathit{\eta })+t_{\text{dis}}}$$ 4

If ζ = η = 1, which means that perfectly charge-balanced stimulation is applied, the following equation holds:

$$V_{\text{os}}=\frac{I_{\text{stim}}{t}_{\text{c}}^2}{C_{\text{dl}}(2t_{\text{c}}+t_{\text{dis}})}=\frac{I_{\text{stim}}{t}_{\text{c}}^2}{C_{\text{dl}}(t_{\text{stim}})}$$ 5

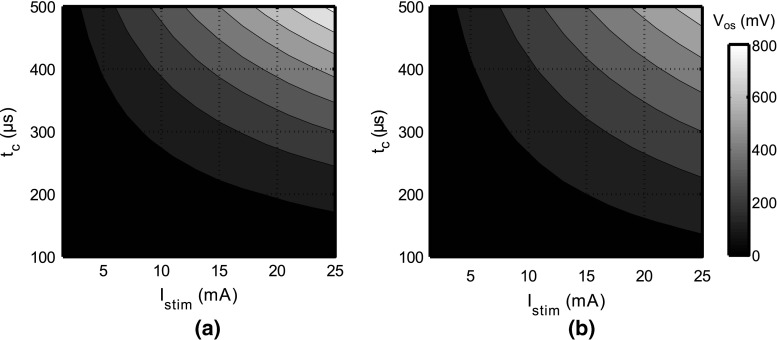
In Fig. 3a, the value of V_os is depicted for a charge-balanced stimulation cycle with f_stim = 200 Hz. This cycle includes a coupling capacitor. For small I_stim and t_c, the value of V_os is small and will have negligible influence on the system. However, for larger stimulation intensities, V_os starts to increase toward several hundreds of millivolts (up to 800 mV for the maximum intensity).

Fig. 3.

Overview of the pseudosteady-state offset voltages V _os for a variety of stimulation settings. a A perfectly charge-balanced stimulation waveform is chosen, and V _os is determined according to Eq. (5) with f _stim = 200 Hz. b A monophasic stimulation waveform is used, and V _os is determined using Eq. (4) with η = 0

Equation (4) can also be used to analyze monophasic stimulation patterns by choosing η = 0. In Fig. 3b, the values of V_os are plotted for this situation. Somewhat surprisingly, these values are smaller than the biphasic charge-balanced stimulation. However, this can be explained by the fact that due to the relatively low value of R_s, the discharge current during t_dis is larger than I_stim, and hence, the electrodes discharge faster toward pseudosteady state as compared to the biphasic stimulation waveform.

Verifying V_os

To verify Eq. (4), the response of an electrode system was analyzed using both simulations and measurements in a saline bath. To simulate the response of these electrodes, the circuit from Fig. 1 was implemented in a simulator (LT-Spice). Switch S₁ was chosen to have R_off = 10 MΩ to mimic the limited output impedance of the current source and R_on = 10 Ω. The stimulation current was chosen to be I_stim = 1.5 mA (ζ = 1), while an 8 % charge mismatch was introduced by making t_c = 460 μs and t_a = 500 μs (η = 1.087). After the stimulation cycle, switch S₁ was closed for t_dis = 9 ms before the next stimulation pulse is started. This makes the stimulation repetition rate slightly higher than 100 Hz.

Using Eq. (1), it is found that t_dis > 60 τ_dis, which means that V_Cdl and V_Cc can be assumed to have reached their pseudosteady-state values. Also τ₂ = 1.5 s ≫ τ_dis, which means that the system will stay in pseudosteady state and will not have the opportunity to fully discharge.

The value of C_c should be chosen well above C_dl in order to limit the contribution of C_c to the voltage headroom of the stimulator [15]. In this particular case, it was chosen to make C_c = 8.8 μF, based on the availability of components for the measurements. The circuit was simulated over many stimulation cycles (up to 200 s) to analyze the voltage over C_dl and C_c. To minimize leakage introduced by the simulation setup, the minimum conductance of the SPICE simulator was lowered from G_min = 1 pΩ⁻¹ to G_min = 1 fΩ⁻¹. After a simulation, MATLAB was used to select the time stamps that correspond to pseudosteady state to obtain the values of V_os over many stimulation cycles.

After simulations, a stimulation circuit was built using discrete components as depicted in Fig. 4. Transistor Q₁ (2N3906) implements a current source together with resistor R₂ and the opamp (LMV358). The output current I_stim is controlled using the PWM signal V_in that is filtered using R₁ = 1 MΩ and C₁ = 1 μF. Using the H-bridge topology implemented with MOSFET devices (NTZD3155C), the current can be injected bidirectionally through the load during the cathodic and anodic stimulation phase. An Arduino Uno is used to control the switches: During the cathodic phase, switches SW_P1 and SW_N1 are closed, while during the anodic phase, switches SW_P2 and SW_N2 are closed. The tissue is shorted in between the stimulation pulses by closing SW_P1 and SW_P2. Diodes D₁ and D₂ (CD0603–B00340) are needed to prevent unwanted current flow through the body diodes of SW_N1 and SW_N2: If C_dl is charged beyond 0.6 V during the cathodic phase, the body diodes of SW_N1 and SW_N2 otherwise become forward biased when the stimulation direction is reversed.

Fig. 4.

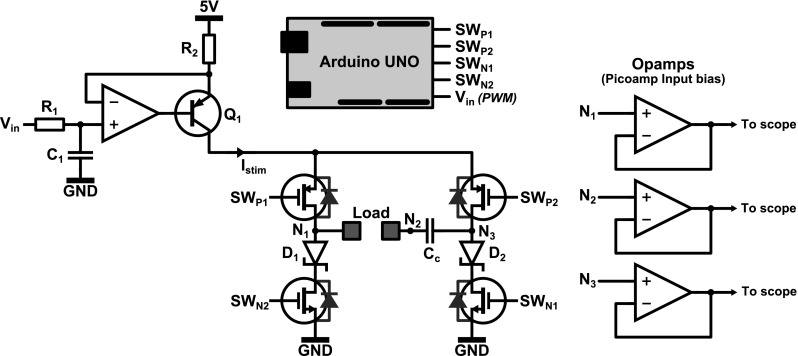
Measurement setup used to verify the influence of the coupling capacitor C _c on the charge cancelation. A constant current source implemented using Q ₁ is connected to the load via an H-bridge configuration (MOSFET switches), which allows bidirectional stimulation. An Arduino Uno is used for the control of the circuit, while buffers are used to prevent loading of the system during measurements

The Arduino was programmed with four different stimulation settings as summarized in Table 1. The first setup uses no coupling capacitor, and it is verified that C_dl is indeed charged back to 0 V after a stimulation cycle. The second setup uses a low-intensity stimulation cycle with a positive charge mismatch, while the third setup uses a high-intensity stimulation cycle (close to the maximum stimulation intensity possible before the current source would clip to the 5 V supply voltage). The fourth experiment uses a monophasic stimulation waveform. All measurements were taken after stimulation was enabled sufficiently long (at least 5 min) to allow the voltages to settle.

Table 1.

Stimulation settings used during measurements

Nr.	Waveform	I stim (mA)	t c (μs)	Mismatch η	f stim (Hz)	Incl. C c?
1	Biphasic	1.5	460	1.085 (t a = 500 μs)	110	No
2	Biphasic	1.5	460	1.085 (t a = 500 μs)	110	Yes
3	Biphasic	15	200	0.75 (t a = 150 μs)	400	Yes
4	Monophasic	15	200	0	100	Yes

The load of the circuit in Fig. 4 first consisted of the electrode model from Fig. 1 (R_s = 100 Ω, C_dl = 1.5 μF, R_ct = 1 MΩ). Subsequently, the electrode model was replaced by the electrodes that were submerged in the PBS solution.

To measure the response of the system, the relevant output signals are buffered using picoampere input bias operational amplifiers (AD8625, powered with ±8 V) in order to prevent the measurement equipment from loading the system. It was found using simulations and measurements that a 10 MΩ ||12 pF standard probe largely distorts the measurement, as will be discussed further in the last section.

Results

Figure 5 shows the simulation results of the circuit from Fig. 1. In Fig. 5a, the value of V_Cdl in pseudosteady state is shown over many stimulation cycles. When no coupling capacitor is used, V_Cdl can discharge almost completely. When C_c is added in Fig. 5a, it is seen that after several stimulation cycles, V_Cdl = 20.7 mV. Indeed, the introduction of C_c causes an offset in V_Cdl in pseudosteady state. Furthermore, the simulated values correspond well with Eq. 4, which predicts V_os = 20.6 mV.

Fig. 5.

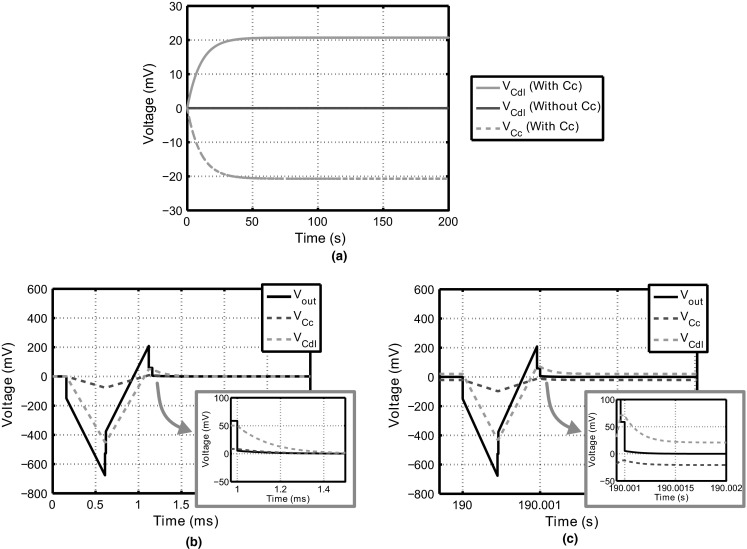
Simulation results of the circuit from Fig. 1. a The voltages V _Cdl and V _Cc are shown during the interval t _open over a large number of stimulation cycles. As can be seen, the coupling capacitor causes an offset. b, c The transient voltages are shown for the system with C _c and R _p = ∞ just after stimulation is initiated and after 190 s, respectively

In Fig. 5b, c, the simulated transient behavior of the voltages in the circuit including C_c is shown for two time instances. Figure 5b shows the voltages right after the first stimulation cycle, while Fig. 5c shows the voltages during a stimulation cycle after 190 s of simulation time, where the offset is clearly visible.

In Fig. 6, the measurement results are presented for all experiments listed in Table 1. In all figures, V_out refers to the voltage measured over the output of the current source (between nodes N₁ and N₃ in Fig. 3) and V_el is the voltage over the electrode (nodes N₁ and N₂). For saline measurements, it is not possible to measure V_Cdl directly, and hence, V_el is shown instead.

Fig. 6.

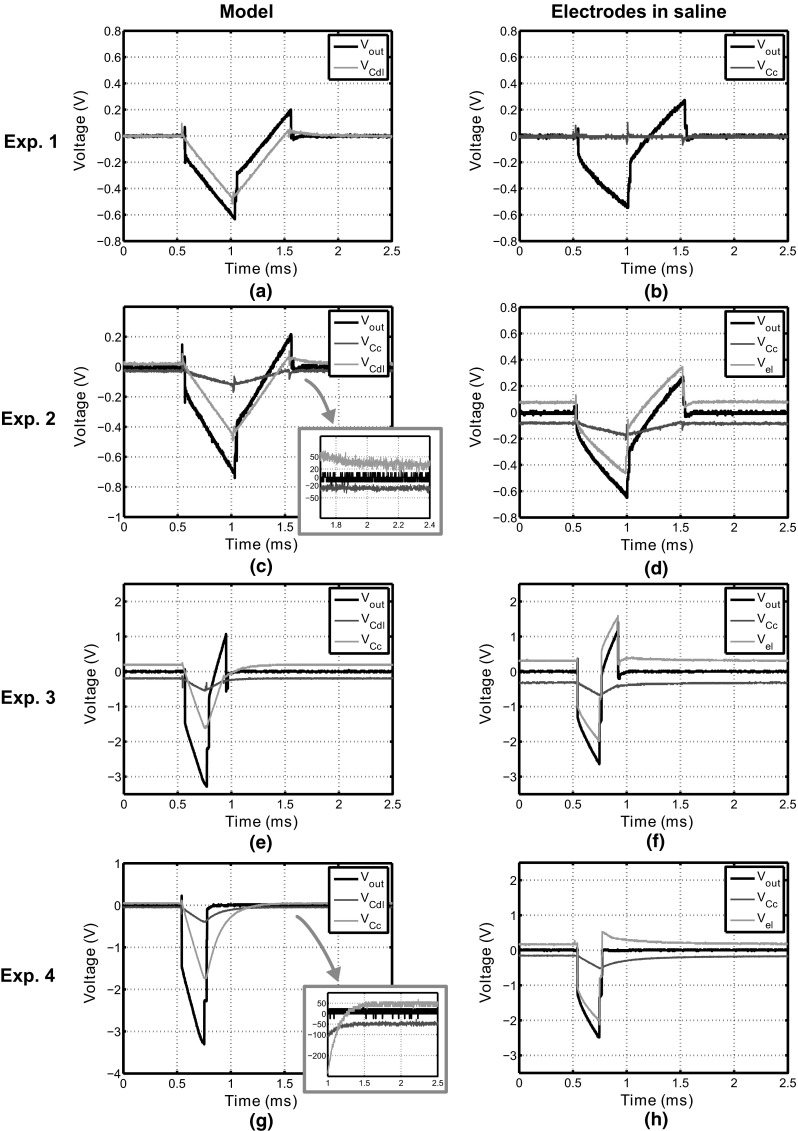
Measurement results from the experimental setup depicted in Fig. 4 with the load consisting of the electrode model (left column) and the electrodes in saline (right column). For both loads, four stimulation settings are used as described in Table 1. As can be seen, the offset voltage depends on the stimulation settings used, but is zero when no coupling capacitor is used (experiment 1)

Discussion

The measured values for V_os are summarized in Table 2 and compared with the values calculated using Eq. (4). It is seen that the measurements with the model correspond well to the calculated values, indicating that the circuit implementation is working as expected. For the saline measurements, the values of V_os are higher than expected, and hence, the model underestimates the offset value introduced. This is most likely due to complex nonlinear behavior of the electrode–tissue interface that cannot be modeled using the simple capacitance C_dl. The electrode model is a small-signal model (C_dl was found using a sinusoidal excitation of 0.1 V), and the measurement results show that the validity of the model is limited during a stimulation cycle. From these results and the plots in Fig. 6, we can draw three important conclusions.

1. First of all, coupling capacitors barely improve the way in which V_Cdl returns to equilibrium. The only way in which C_c contributes is by making τ_dis (Eq. 1) smaller during the t_dis interval [4]. This causes the interface to discharge toward equilibrium slightly faster. However, since C_c ≫ C_dl, the influence on τ_dis is negligible, and hence, coupling capacitors barely improve the charge cancelation.

2. Second of all, coupling capacitors introduce an offset in the pseudosteady-state value of the electrodes. The value of V_os can be predicted using Eq. (4), although it was found that this equation underestimated the offset measured from the electrodes in saline.

Table 2.

Calculated and measured values of V _os for the experiments summarized in Table 1

Experiment	Equation (4) (mV)	Measurement (model) (mV)	Measurement (saline) (mV)
1	0	0	0
2	21.6	25	80
3	201	200	320
4	50	50	165

The question is whether or not V_os introduces potential safety issues. For small values of V_os, no problems are likely to occur: As long as no irreversible faradaic reactions are triggered, no harmful effects are to be expected. Even more so, V_os will increase the amount of charge that can be injected [1], because V_os reduces the peak voltage of V_Cdl during a stimulation cycle.

However, when V_os increases toward the threshold of irreversible faradaic reactions (600–900 mV for platinum electrodes [12]), problems can be expected. In this case, the interface is experiencing a significant offset voltage during the t_dis interval, during which irreversible reactions might occur. For high stimulation intensities, Fig. 3 predicts values of V_os that are close to or exceed the maximum safe voltage window.

• 3Finally, secondary effects can have a strong effect on V_os. Using the settings of experiment 2, measurements were repeated with both the model and the electrodes as load. This time, the voltages were not buffered using the picoampere input bias opamps, but 10 MΩ ||12 pF probes (referenced to ground) were connected to N₁, N₂ and N₃ directly. This has a large impact on the offset voltage: It increases from 25 mV to 2 V (model) and from 80 mV to 0.6 V (saline).

All in all, it can be concluded that in contrast to what many other studies have suggested [4, 14, 15], the introduction of C_c does not improve the charge-balancing process and it is furthermore associated with the loss of control over the pseudosteady-state value of V_Cdl. Instead of ensuring safety by returning the electrode interface voltage back to 0 V, the coupling capacitor introduces an unwanted offset in the interface voltage that is hard to control by the stimulator and, moreover, is sensitive to secondary effects.

Although this work suggests that coupling capacitors are not beneficial for charge cancelation purposes, they still protect the electrodes and tissue from DCs in case of a device or software failure. Depending on the application, this could require the need to still use these capacitors. In that case, the results from this study show that the stimulation settings should be limited to ensure that under all operating conditions, V_os does not exceed any predefined safety window.

It is possible to discharge both C_c and C_dl completely by introducing an additional switch over C_c. In this case, C_c and C_dl are shorted individually and are guaranteed to discharge toward 0 V in pseudosteady state, which would eliminate the offset. However, in this case, it is unclear how the coupling capacitor is contributing to the charge-balancing process: It does not improve τ_dis and V_Cdl will have the same response as compared to the circuit without C_c. Furthermore, the additional switch introduces a single-fault device failure risk. Therefore, the advantages of a coupling capacitor are not exploited when C_c is discharged separately.

This work focused on passive charge-balancing techniques. Active charge-balancing techniques use feedback to bring the electrode voltage back to safe values after a stimulation cycle [15] and can therefore help to overcome the offset problem. However, if these schemes require a coupling capacitor to protect in the event of a device failure, it is important to measure the voltage over the electrodes only and not to include the coupling capacitor. This requires an additional sensing pin if the coupling capacitors are realized using external components. Only then, the feedback mechanism will help to remove the offset.

In this study, only one type of electrode was considered. Smaller electrodes have different impedance levels, and more research is needed to find the pseudosteady-state response in this case. Note that Eq. (4) is only valid under the assumption that τ_dis ≫ t_dis, which might not be the case for high impedance electrodes. Finally, it would also be interesting to determine the influence of the coupling capacitors in vivo.

Conclusions

In this work, the influence of coupling capacitors on the charge-balancing properties is studied during neural stimulation. In contrast to what previous work suggests, coupling capacitors were found not to improve the charge-balancing process. Even more so, they introduce an offset voltage in the electrodes, which cannot be removed by conventional means such as passive discharging. The value of the offset voltage depends on the stimulation and electrode parameters. When using coupling capacitors, it is therefore important to ensure that this offset voltage does not exceed any safety boundaries for all possible operating conditions.