Isolation–By–Distance–and–Time in a stepping–stone model

Abstract

With the great advances in ancient DNA extraction, genetic data are now obtained from geographically separated individuals from both present and past. However, population genetics theory about the joint effect of space and time has not been thoroughly studied. Based on the classical stepping–stone model, we develop the theory of Isolation by Distance and Time. We derive the correlation of allele frequencies between demes in the case where ancient samples are present, and investigate the impact of edge effects with forward–in–time simulations. We also derive results about coalescent times in circular and toroidal models. As one of the most common ways to investigate population structure is principal components analysis (PCA), we evaluate the impact of our theory on PCA plots. Our results demonstrate that time between samples is an important factor. Ancient samples tend to be drawn to the center of a PCA plot.

1. Introduction

Geography plays a central role in the pattern of genetic differentiation within a species. Seminal work on describing the evolution of continuous populations was done by Wright and Malécot. They studied genetic differentiation and inbreeding in continuously distributed populations [1, 2]. The resulting idea is that, under the assumption of local dispersion, genetic differentiation accumulates with distance. This pattern of genetic structure is called Isolation–By– Distance (IBD), which is detected by computing measures of differentiation such as F_ST [1, 3, 4], or correlation coefficients [5, 6]. Understanding the effect of geographic distance on population structure is an important task for population geneticists, as it is a source of neutral genetic variation [7, 8]. Furthermore, IBD has been observed in humans and many other species [9, 10, 11, 12, 13].

The role of geography in neutral genetic variation has been widely studied partly because of the many population genetic studies of individuals sampled from different locations in present–day populations. Because of the development of methods for sequencing DNA from fossils, genomes of individuals alive at previous times are now available to bring new information about the evolutionary processes that affected a species in the past. Since the first studies of ancient DNA (aDNA) three decades ago [14, 15], techniques to retrieve DNA molecules from ancient bones have tremendously developed [16].

In modern evolutionary biology, the similarity of differentiation in space and time has been recognized [17, 18, 19]. Theoretical developments predict the effect of time on F_ST and related quantities [20]. Epperson [21] studied patterns of isolation by distance and time in ecology by using stochastic spatial time series and identity by descent probabilities. However such theoretical studies remain scarce.

The effect of separation in time can be studied using classical statistical methods in population genetics, such as principal component analysis (PCA) [22]. PCA is widely used to determine relatedness between individuals, and is a convenient way to represent geographic patterns [23]. But PCA can also capture the differentiation between ancient and modern samples: the percentage of variance explained by time can be expressed on the same scale as the percentage of variance explained by geography [20]. Unfortunately, PCA does not give a complete picture of how quantities such as F_st and correlation coefficients evolve in time and space.

In this article we generalize the theory of IBD to allow for difference in the times at which different individuals are sampled. We call this the theory of isolation by distance and time (IBDT). We base our work on the stepping–stone model of [24] and add to the theoretical results already derived for this model [6, 25, 26, 27, 28, 29]. We start by briefly reviewing the original results for the infinite stepping–stone model at equilibrium and the decay of correlation of allele frequencies with distance. Then, we extend the original work to derive the correlation between individuals separated by distance and time. We perform simulations that show the validity of the analytic results, even in the case of a finite number of populations where some demes are subject to edge effect. We also derive the expected coalescence times between samples separated by time and space in circular and toroidal models [30, 31]. Finally we consider the consequences of IBDT on PCA in the common case of a dataset made up of a large proportion genomes from present–day individuals and few ancient genomes.

2. The stepping–stone model

The stepping–stone model describes the distribution of allele frequencies in an infinite set of demes in different locations of the space represented by Cartesian coordinates. We start by describing the 1-Dimensional case. Let p(k) be the frequency of one allele at a bi-allelic locus in population k and p̄ be the average allele frequency. In each generation, p(k) is updated with the following three steps [32]:

• Exchange a proportion m_i of migrants with demes at a distance i.

• Exchange a proportion m_∞ of migrants with a deme that has fixed allele frequency p̄. The meaning of this step is discussed later.

• Sample gametes of the next generation in the population.

In the case considered by [6], migrants are exchanged only between neighboring locations in the first step, so that m_i = 0, i > 1. The second step consists of the exchange of migrants with an external population at rate m_∞. This event is equivalent to reversible mutation with equilibrium allele frequency m_∞. In general m₁ >> m_∞. Random sampling of step 3 is represented by a random change in the allele frequency ε(k), with E[ε(k)] = 0, and E[ε(k)²] = p(k)(1–p(k))/2N_e, where N_e is the effective population size of a deme [33, 34].

Our interest is in the changes in allele frequency in one generation. We consider p̃(k) = p̄–p(k), the deviation from the average frequency. Given these three steps,

$${\stackrel{\sim }{p}}^{\prime }(k)=(1-{\sum }_{i=1}^{\infty }{m}_i-m_{\infty })\stackrel{\sim }{p}(k)+\frac{m_1}{2}(\stackrel{\sim }{p}(k-1)+\stackrel{\sim }{p}(k+1))+\frac{m_2}{2}(\stackrel{\sim }{p}(k-2)+\stackrel{\sim }{p}(k+2))+\cdots +\epsilon (k).$$ (1)

To simplify the notation, we define the operators S and L,

$$S\stackrel{\sim }{p}(k)=\stackrel{\sim }{p}(k+1),S^i\stackrel{\sim }{p}(k)=\stackrel{\sim }{p}(k+i),i\in \mathbb{Z},$$ (2)

$$L=m_0{S}^0+{\sum }_{i=1}^{\infty }\frac{m_i}{2}(S^i+S^{-i}),$$ (3)

where $m_0=1-{\sum }_{i-1}^{\infty }{m}_i-m_{\infty }$, so that,

$${\stackrel{\sim }{p}}^{\prime }(k)=L\stackrel{\sim }{p}(k)+\epsilon (k).$$ (4)

The quantity of interest in this model is the correlation of allele frequencies between two demes at locations k₁ and k₂. Let r(k) be the correlation coefficient of allele frequencies between populations that are k steps apart. Assuming equilibrium, we have

$$r(k)=\frac{\rho (k)}{\rho (0)}=\frac{E[\stackrel{\sim }{p}(k_1)\stackrel{\sim }{p}(k_2)]}{\rho (0)}=\frac{E[L\stackrel{\sim }{p}(k_1)L\stackrel{\sim }{p}(k_2)]}{\rho (0)},$$ (5)

where ρ(k) is the covariance in frequencies in demes k steps apart. The within-population variance of allele frequencies, ρ(0), value is detailed in [25]. The mathematical treatment of equation (5) by [25] using the spectral representation of a correlation [35] gives the general formula

$$r(k)=\frac{C}{2\pi }{\int }_0^{2\pi }\frac{cos(k\theta )d\theta }{1-{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^2},$$ (6)

where C is the normalizing constant chosen so that r(0) = 1.

In the case of a stepping-stone model where migrants are exchanged only between neighboring demes (m_i = 0, i > 1), r can be approximated by an exponential function of k:

$$r(k)=e^{-\sqrt{\frac{2m_{\infty }}{m_1}k}},$$ (7)

as detailed in [6]. This simple formula conveys the important idea that in one dimension, the correlation of allele frequencies between populations decays exponentially with distance. In the 2–Dimensional and 3–Dimensional cases, the correlation function is more difficult to approximate. Using modified Bessel function, it has been shown that correlation at a given distance is lower in these cases than in the 1–Dimensional case [25].

3. Isolation–by–Distance–and–Time

3.1. 1-Dimensional case

We are here interested in the case where genetic samples are collected from demes that are in different locations and at different times (measured in generations). Let ρ(k, t) be the covariance between allele frequencies of two demes separated by k steps and t generations. We denote the coordinates of these demes by (k₁, t₁) and (k₂, t₂), and the deviations in allele frequencies p̃(k₁)^(t₁) and p̃(k₂)^(t₂). Since we assume the distribution of allele frequencies is stationary in both time (equilibrium distribution) and space (all migration rates are equal), we can consider these coordinates to be (0, 0) and (k, t) with no loss of generality. Following previous notation

$$\rho (k,t)=E[{\stackrel{\sim }{p}(k_1)}^{(t_1)}{\stackrel{\sim }{p}(k_2)}^{(t_2)}]=E[\stackrel{\sim }{p}{(k)}^{(t)}\stackrel{\sim }{p}{(0)}^{(0)}].$$ (8)

To characterize the evolution of the covariance between allele frequencies with respect to time t, we iteratively apply the operator L defined in equation (3). This operation describes the potential trajectories of an allele. This process leads to

$$\rho (k,t)=L^t\rho (k)$$ (9)

with ρ(k) = ρ(k, 0) (see Appendix A).

Let r(k, t) be the correlation between allele frequencies of two demes separated by k steps and t generations, equations (5) and (9), combined with the general formula of equation (6) gives

$$r(k,t)=\frac{C}{2\pi }{\int }_0^{2\pi }\frac{{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^{t}cos(k\theta )d\theta }{1-{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^2}.$$ (10)

and the constant C is set such that r(0, 0) = 1 (Appendix B).

This equation reduces to

$$r(k,t)=\frac{C}{2\pi }{\int }_0^{2\pi }\frac{{[1-m_1-m_{\infty }+m_{1}cos(\theta )]}^{t}cos(k\theta )d\theta }{1-{(1-m_1-m_{\infty }+m_{1}cos(\theta ))}^2}$$ (11)

in the standard stepping–stone model, where demes only exchange migrants with their closest neighbors at rate m₁/2. An exact formula for this integral can be calculated and is notable for its size and lack of utility (Appendix C).

One noteworthy feature of equation (10) is that the decay of the correlation with time is not affected by the effective population size N_e. This result is different from what is expected for an isolated population: the level of differentiation as a function of the number of generations separating two samples is larger when the effective population size is small, reflecting the increased magnitude of genetic drift. However, in the particular case of an equilibrium stepping-stone model, the covariance of allele frequencies between the demes is not a function of the effective population size, a result already known in the spatial context (see equation (7)) [6]. This result becomes clear when considered in terms of coalescence times. Between the time the first and second samples are taken, the trajectory of the first sample depends only on the migration process. There is no possibility of coalescence.

3.2. Two dimensions and more

So far, we have focused on the 1-Dimensional case for the sake of simplicity. However, it is important to investigate the decay in higher dimensions as it is common in practice to have samples taken from a 2-Dimensional or even 3-Dimensional habitat. The general formula for the correlation in higher dimensions can be obtained with no more theoretical development. In their work on the stepping–stone model, Kimura and Weiss derived a general formula for the correlation that can be extended to any number of dimensions. In their work they only gave approximations for 1, 2 or 3 dimensions as these are the practical cases. Using general formula (3.11) of [25], we can write the correlation 10 in 2 dimensions

$$r(k_1,k_2,t)=\frac{C_2}{{(2\pi )}^2}{\int }_0^{2\pi }{\int }_0^{2\pi }\frac{g^t({\theta }_1,{\theta }_2)cos(k_1{\theta }_1)cos(k_2{\theta }_2)d{\theta }_{1}d{\theta }_2}{1-g^2({\theta }_1,{\theta }_2)},$$ (12)

where $g({\theta }_1,{\theta }_2)={\sum }_{i_1=0}^{\infty }{\sum }_{i_2=0}^{\infty }{m}_{i_1{i}_2}cos(i_1{\theta }_1)cos{i}_2{\theta }_2$. The generalization to obtain the correlation in n dimensions is straight–forward (Appendix D).

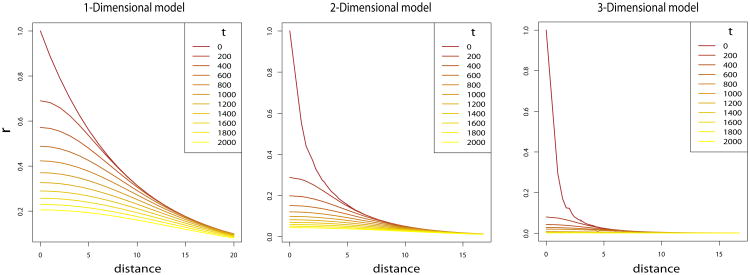
We perform a numerical integration of equation (12) to investigate the decay of correlation with distance and time in one or more dimensions. Correlation decreases as a function of distance and time in 1, 2 and 3 dimensional models (Figure 1). In addition, for the same values of the migration and mutation rates the decrease in correlation is more rapid in both time and space in higher dimensional models, consistent with previous results for space only [36, 26]. The more rapid decay can be explained by the random walk followed by the genealogy of a gene. In a higher dimension model the probability for the gene to move away from its original deme is larger. Numerical integration was done using the R package cubature.

Figure 1.

Correlation as a function of distance between demes k steps appart in 1, 2 and 3-Dimensional models. The correlation is evaluated for different number of generations t between the demes. The migration and mutation rates are used for all models, and m₁ = .01 and m_∞ = 4.10⁻⁴. Migration rates are the proportion of individuals leaving the population.

3.3. Simulations in one dimension and two dimensions

In realistic examples, there is only a finite number of demes. As a consequence, correlation patterns are affected by edge effects [37]. Another effect of there being a finite number of demes is that the overall allele frequency can drift away from the expected allele frequency. An alternative is to consider a finite, non-circular model, and to deal with edge issues independently [38]. To investigate to what extent the analytic theory developed in the previous section is valid in a finite stepping–stone model with temporal sampling, we performed simulations.

Backward in time simulation software such as ms [39], or fastsimcoal [40], are usually used to investigate IBD in a stepping–stone model [23]. Temporal sampling can be investigated using Serial SimCoal software [41]. Another approach is to simulate gene trees where lineages from isolated demes are joined to the stepping–stone demes at a chosen time in the past [20]. Mutations are then randomly placed on the gene tree. Such a simulation is needed to understand the influence of time and distance on genetic differentiation, but it assumes an infinite sites mutation model because of the way mutations are placed on the branches of the gene tree. The infinite site model, unlike the reversible mutation model, does not have a true equilibrium at each site.

We wrote a C program that performs forward in time simulations. The program is available upon request. The simulation program precisely follows the model presented in the previous section. At the initial time, the allele frequencies in all the demes are equal to the allele frequencies in the external infinite–sized population. Then the program runs for 150, 000 generations until the stationary distribution of the allele frequencies is reached.

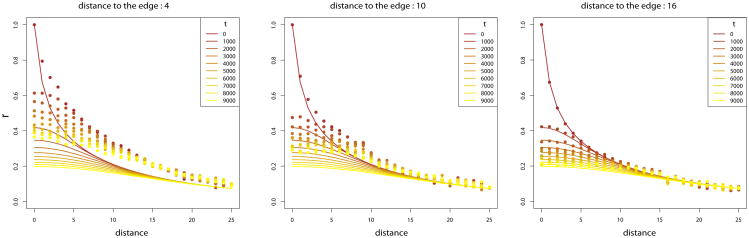
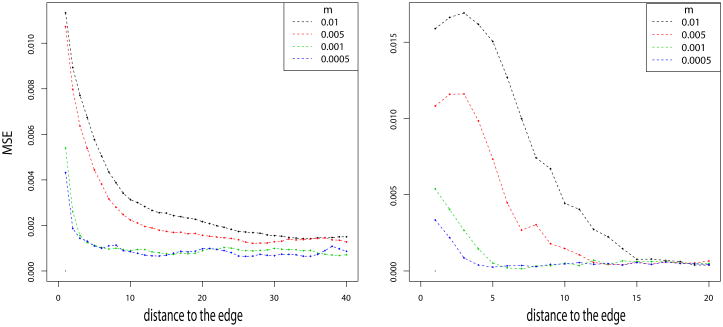
In the 1-Dimensional case, we simulate 100 demes. For the 2-Dimensional case, we simulate a total of 2500 demes on a 50 × 50 grid. We assume all the demes have the same effective population size. We sample the allele frequencies at several times in the past. Correlation between demes fit very closely the theory of equations (11) and (12) provided that demes are taken sufficiently far away from the edge of the grid (Figure 2). As predicted by [26, 42], the edge effect increases the correlation between demes, and is present when comparing present and ancient samples. In both 1 and 2 dimensions, the edge effect is less strong with lower migration rates (Figure 3). In the 1-Dimensional model, the magnitude of the edge effect decreases monotonically with distance from the edge in one dimension but not in two. The non-monotonicity indicates a more complex interaction with the boundary in two dimensions than in one.

Figure 2.

Comparison between theoretical results and simulations on a 2-Dimensional square with m₁ = .02 and m_∞ = 10⁻⁵. The solid lines represent the theory prediction. The dots represent the simulation results evaluated for demes at a distance 4, 10 or 16 from the edges. Since in the simulations several pairwise comparisons between demes have the same distance in space and time, we keep the mean of these pairwise correlations.

Figure 3.

Mean squarred error between simulations and theory in 1 and 2 Dimensions as a function of the distance to the edge. The error is evaluated for m_∞ = 10⁻⁵ and m₁ = .01, .005, .001, .0005.

Only the classical stepping-stone model with migration between nearest neighbors is simulated here. However, the general formula (10) gives the correlation in the case with long distance migration between demes. The decrease in correlation with distance is weaker if there is long distance migration (Figure S1). The effective migration rate between demes is larger, and consequently, edge effects in the simulation would have a greater impact in the case where (m_i > 0, i = 2 … ∞), accordingly to Figure (3).

4. Coalescence times

4.1. Coalescence times in one dimension

Coalescence times in a stepping–stone model can be derived under some assumptions. In particular, we consider a case with migration only between neighboring demes and low mutation rate. Expected coalescence times between genes that are in different demes is a function of the locations of these demes. These coalescence times are of interest because they are closely related to F_ST and coefficients of identity–by–descent [30]. Under the assumption of a circular 1-Dimensional stepping-stone model with n_d demes, two genes A₁ and A₂ have an expected coalescence time

$$E[T_{A_1{A}_2}]=2N_e{n}_d+(n_d-k)\frac{k}{2m},$$ (13)

where N_e is the effective population size per deme, m the migration rate between neighboring demes (previously m₁), and k is the distance between the two demes [30]. Considering a circular arrangement of the demes makes the analysis simpler, as only the distance between the demes matters, and there are no edge effects. In addition it has been shown that linear/planar and circular/toroidal stepping stone models are very similar when considering populations away from the edges [26, 42]. To study a case similar to the infinite stepping–stone model, we assume n_d is large.

We extend the previous theoretical result in the case where two genes are sampled at different times. Let us assume that the sampled genes are in populations k_A1 and k_A2. The number of generations between the two sampling times is t = t₁ – t₂, and we assume, with no loss of generality, that t₁ = 0 and t₂ = t generations in the past. The coalescence process between these two genes can be divided into three phases. The first phase corresponds to the genealogy that traces back to the ancestor of the present gene, called $A_1^{(t)}$, at generation t. This ancestor is in population $k_{A_1^{(t)}}$. The two other parts correspond to the time until the coalescence event between $A_1^{(t)}$ and A₂. They are respectively the time until the gene $A_1^{(t)}$ and A₂ are in the same deme, then the time to the common ancestor of these two genes. This part has already been described, and the expectation is given in equation (13) [30]. The expected coalescence time between A₁ and A₂ is then written

$$E[T_{A_1{A}_2}]=t+E[T_{A_1^{(t)}{A}_2}].$$ (14)

The variable $T_{A_1^{(t)}{A}_2}$ is the coalescence time between a random gene in the unknown population $k_{A_1^{(t)}}$ and a random gene in population k₂. To represent the uncertainty about the population $k_{A_1^{(t)}}$, we derive the probability distribution of the position $k_{A_1^{(t)}}$ at time t, given position k_A1 at time 0. Using this probability distribution we rewrite the expectation (14) as

$$E[T_{A_1{A}_2}]=t+\sum _{x=0}^{n_d-1}E[T_{A_1^{(t)}{A}_2}|k_{A_1^{(t)}}=x]p(k_{A_1^{(t)}}=x).$$ (15)

To describe the probability distribution of position $k_{A_1^{(t)}}$ at time t given that a gene is in population k_A1 at time 0, we consider a random walk with transition matrix

$$M=\left(\begin{array}{cccccc}1-m& \frac{m}{2}& 0& \dots & 0& \frac{m}{2}\\ \frac{m}{2}& 1-m& \frac{m}{2}& \dots & 0& 0\\ 0& \frac{m}{2}& 1-m& \dots & 0& 0\\ \dots & & & & & \\ \frac{m}{2}& 0& 0& \dots & \frac{m}{2}& 1-m\end{array}\right).$$ (16)

Using standard results about Markov chains [43], we know that the vector of probabilities for the position at time t, $P_{k_{A_1^{(t)}}}$ is expressed such as

$$P_{k_{A_1^{(t)}}}=P_{k_{A_1}}{M}^t$$ (17)

with P_kA1 is the initial probability distribution of gene A₁'s position. The initial probability distribution is trivial and P_kA1 is a vector of 0 with a 1 in the $k_{A_1}^{\mathit{\text{th}}}$ entry Exact formula for this matrix power can be obtained using tridiagonal matrix properties [44]. However we can also express an approximation for the probability distribution of this process at time t. This random process is symmetrical, centered in k_A1, and using classical results about Brownian motion, has a variance proportional to t. We can approximate the probability distribution by a Normal distribution, and

$$P(k_{A_1^{(t)}}=x|k_{A_1})=\mathcal{N}(x;k_{A_1},mt).$$ (18)

The accuracy of this approximation can be verified with simulations using equation (17). The approximation is relevant for sufficiently large values of t, depending on the migration rate. Because the normal distribution has an infinite support, the approximation needs a sufficiently large number of demes n_d to be accurate. the mean squarred error between coefficients of $P_{k_{A_1^{(t)}}}$ and the Gaussian approximation is a function of parameters m, t and n_d (Figure S2). The expected coalescence time in a 1-Dimensional circle can then be written

$$E[T_{A_1{A}_2}]=2N_e{n}_d+t+\frac{1}{\sqrt{2\pi mt}}{\int }_0^{n_d-1}(n_d-|x-k_{A_2}|)\frac{|x-k_{A_2}|}{2m}{e}^{-\frac{{(x-k_{A_1})}^2}{2mt}}\mathit{\text{dx}}.$$ (19)

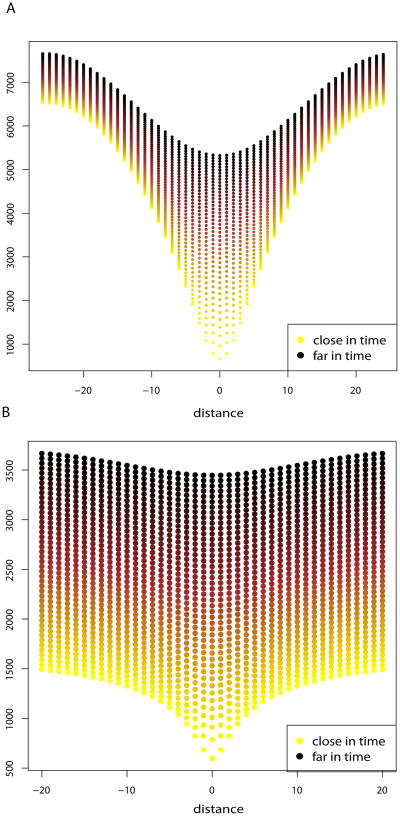
Coalescence time between genes is an increasing function of distance and time between demes (Figure 4). Asymptotically, when t is large, the expected time for two genes to be in the same population can be approximated by a linear function of time between the samples. The right part of equation (19) is the integral of a product of a positive function that depends only on the distance between demes and a Gaussian kernel with variance mt. As the time gets large, relatively to m, the Gaussian kernel becomes flat, and the integral is almost constant (Figure 4). In practice, this implies that in a population at equilibrium, the geography does not matter when the sample is very old.

Figure 4.

Panel A: Expected time for two genes to be in a same deme in a 1–Dimensional circular stepping–stone model with N_e = 100, m = .01, and n_d = 51 demes as a function of the distance between demes. Panel B: Expected time for two genes to be in a same deme in a 2–Dimensional toroidal stepping–stone model with N_e = 100, m = .01, and n_d = 51 × 51 demes as a function of the distance between demes. Colors indicate the time between samples. Sampling consists in 45 time points evenly separated by 50 generations. As the time between samples gets large, the influence of the geography is less important especially in 2 dimensions.

4.2. Coalescence times in two dimensions

In the case of a 2-Dimensional habitat with n_d1 × n_d2 demes, the expected coalescence time between two genes A₁ and A₂ is

$$E[T_{A_1{A}_2}]=N_e{n}_{d1}{n}_{d2}+\frac{S(i_1,i_2)}{2N_{e}m},$$ (20)

where S(i₁, i₂) is a function of i₁ and i₂ given in equation (8b) of [31], the number of demes between the two genes. We assume in this case that the migration in each direction is the same.

Using the same conditioning as in equation (14), we can derive the expectation for the coalescence time of genes A₁ in population k_A1 and A₂ in population k_A2 at t generations in the past, where k_A1 and k_A2 are 2-Dimensional vectors. We have

$$E[T_{A_1{A}_2}]=t+\sum _{x_1=0}^{n_{d1}-1}\sum _{x_2=0}^{n_{d2}-1}E[T_{A_1^{(t)}{A}_2}|{\mathit{k}}_{{\mathit{A}}_{\mathbf{1}}^{(\mathit{t})}}=(x_1,x_2)]p{\mathit{k}}_{{\mathit{A}}_{\mathbf{1}}^{(\mathit{t})}}=(x_1,x_2)).$$ (21)

The probability distribution of the position of gene A₁ at time t, ${\mathit{k}}_{{\mathit{A}}_{\mathbf{1}}^{(\mathit{t})}}$ is known using the same random walk as in the 1-Dimensional case. The distribution can be approximated by a bivariate Normal distribution with mean k_A1, and covariance matrix Ω, where Ω is diagonal with terms mt/2 in the diagonal. In the anisotropic case where migration rates are different in the two dimensions, m₁ and m₂, Ω would have m₁t and m₂t as diagonal terms. The evaluation of this function for samples separated in distance and time shows a similar pattern to the 1-Dimensional case (Figure 4). However for a same migration rate, the expected times for two genes to be in the same deme in the 2–Dimensional toroidal model are smaller than in the 1–Dimensional circular model. Then, if there is the same number of demes, with same effective population sizes, e.g. n_dN_e = n_d1n_d2N_e, the expected coalescence times are smaller in the 2–Dimensional case. This result is already known when comparing samples taken at the same generation and remains true when t is positive [31].

5. Connection with PCA

Because there is a close connection between PCA and coalescence times [45], our results are relevant to using PCA to compare ancient and modern samples. PCA is a useful way to represent the main axes of variation in data and has proven to be a powerful tool to infer genetic relationships when applied to ancient DNA data [46, 47].

5.1. Ancient samples are shrunk towards 0

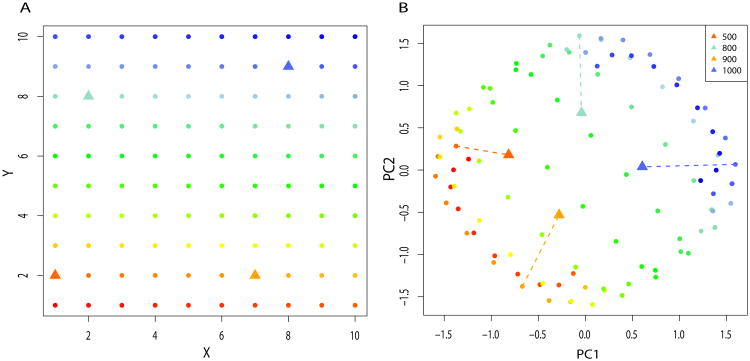
In population genetics, PCA is usually performed by computing the eigenvectors, and eigenvalues of the matrix of covariances in the genotypes of different individuals. Although there are other ways to compute principal components, this one is convenient in population genetics because the number of variables is usually larger by several orders of magnitude than the number of samples. The effect of differences in the sampling times can be evaluated using the dependence of the covariance matrix described by equation (10). To illustrate, consider a 2-Dimensional even repartition of 10 × 10 demes, and ancient samples taken in several randomly chosen demes at different times t = 500, 800, 900, 1000 generations in the past (Figure 5A). By calculating the theoretical covariance matrix and its first two eigenvectors, we obtain the first two principal components that reproduce geography of the demes [23, 48]. Figure (5B) shows that principal components mimic the geography of the present demes, but ancient demes are not superposed on the corresponding present-day sample from the same deme. Instead, ancient samples move towards the center of the first and second principal components. In addition, the intensity of the shrinkage effect increases with the time between present and ancient samples.

Figure 5.

Panel A. Sampling scheme of a 10 × 10 grid of demes. Triangles represent demes where ancient individuals are sampled at 500, 800, 900 or 1000 generations in the past. The demes are colored according to their geographic location. Panel B. First 2 eigenvectors of the covariance matrix between populations of Panel A. Parameters used are m₁ = .01 and m_∞ = 10⁻⁵. Color code is the same as in Panel A. Lines start from the position of the present deme where an ancient sample is taken, and end at the PC coordinates of the ancient sample.

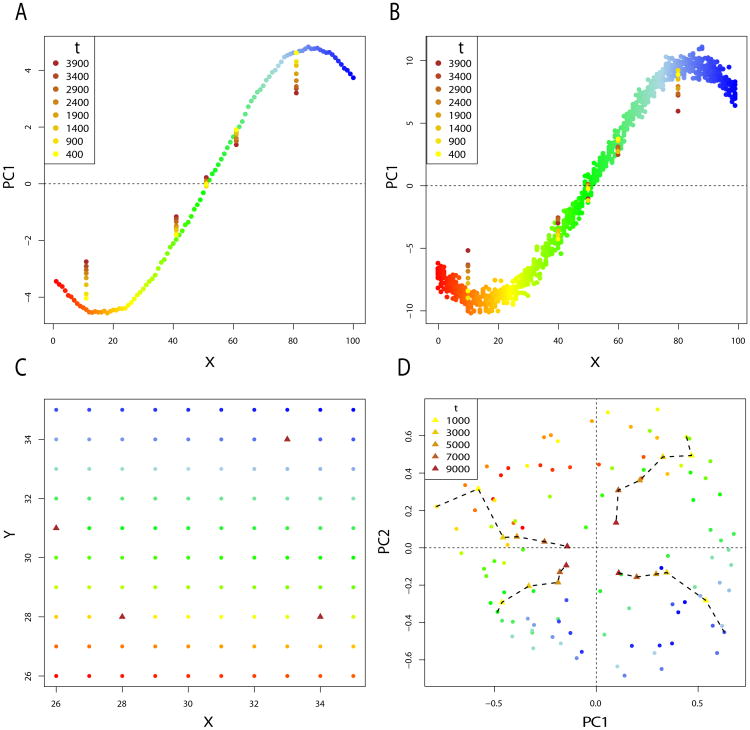
Using 100 demes from a 1-Dimensional simulation described above, we apply PCA to the allele frequencies at the 6000 simulated loci. To remove the edge effect, we simulate 200 demes, and consider only the 100 demes in the center. We also include allele frequencies from past generations for several demes. PC1 shows the 1-Dimensional pattern of isolation–by–distance as expected, and ancient samples are closer to 0 (Figure 6A). The distance between ancient individuals and the center of the principal component decreases as the sampling time increases. In practice, the true allele frequencies are not known, and the covariance matrix is estimated from the data. When working with sampled individuals instead of allele frequencies, the same pattern is still visible. A sub-sampling of 10 diploid individuals for each deme at the present time, and 1 diploid individual for each ancient deme shows the same shrinkage of PC scores for ancient individuals (Figure 6B).

Figure 6.

Panel A. First principal component for the 1-Dimensional simulation, with m₁ = .01 and m_∞ = 4.10⁻⁵. PCA is performed on allele frequency data from each of the 100 demes, and ancient allele frequencies are taken in 5 populations at 8 times in the past. Panel B. First principal component for the 1-Dimensional simulation. In each deme, 10 diploid individuals are sampled at the present time. One diploid individual is sampled in 5 demes at 8 times in the past. Panel C. Sampling scheme of a 10 × 10 grid of populations. Demes marked by a triangle are demes where ancient individuals were sampled. Panel D. plot of PC1 and PC2 for the 2-Dimensional simulation with m₁ = .001 and m_∞ = 10⁻⁵. Ancient samples are taken at different times in the past for 4 demes.

When applying PCA on allele frequencies from the 2-Dimensional simulations, the time effect is visible on the first two components. We study the case of a 10 × 10 grid, with no edge effects, and ancient samples taken from 4 demes at different times in the past (Figure 6C). The first and second principal components reproduce the geography of the samples, and the ancient samples are moved towards the center of the plot (Figure 6D). the dashed lines representing this shrinkage are not straight because of the residual variance captured by the principal components.

This shrinkage effect of time can be understood considering the shape of the covariance function. The first and second principal components represent the 2–dimensional IBD pattern. This pattern causes the covariance matrix at time t = 0 to have a “block Toeplitz with Toeplitz blocks” form [49]. However the pairwise covariance between present-day individuals (t = 0) and between ancient and present-day individuals (t > 0) does not have the same shape (Figure 1). Equation (10) implies that in a stepping–stone model the covariance as a function of distance flattens when comparing present and ancient individuals. As a consequence, the scores of ancient samples are moved towards the center of the principal components reproducing the local correlation pattern. Thus ancient samples can cluster with present-day samples at different locations, even in an equilibrium stepping–stone model.

5.2. One component for the time differentiation

Links between PCA and population genetics quantities, such as coalescence times and F_ST have been studied [45, 50, 51] and show that these values can be estimated from principal components. In the 2–population case, [45] showed that the distance between individuals on the appropriate principal component is approximately a linear function of the square root of the time, Δ, until the lineages of the two individuals are in the same deme. If there are ancient and present-day samples, they can be considered as two groups, and Δ is the time corresponding to the first two parts of the coalescence process between the lineages, described in the previous section. The time separating the individuals is a source of variance important enough to be reflected in the principal components [20]. In this case, one component separates the two groups and the distance between groups is approximately proportional to √Δ. In Appendix E, we compute the expectation of Δ if there are several present-day and one ancient individuals sampled.

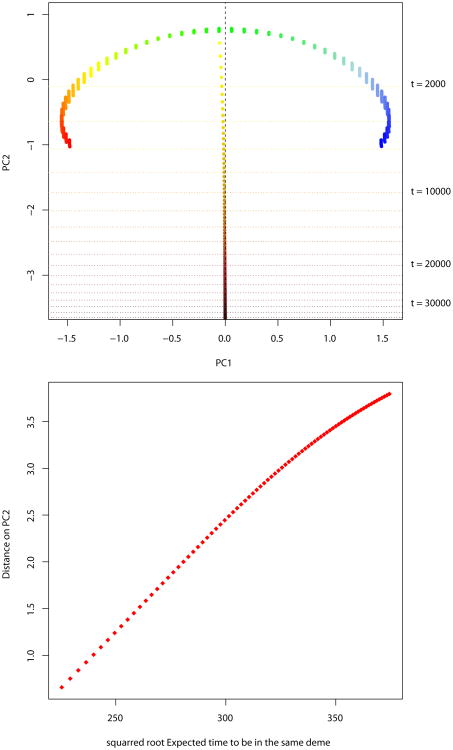
We analyze the case with 50 contiguous populations sampled from a circular 1-Dimensional stepping–stone model with n_d = 1000. We assume m₁ = 0.1, and one deme is sampled in the past. We apply PCA by computing the eigenvectors of the individuals correlation matrix. The first principal component represents the IBD pattern between the present demes. The second principal component corresponds to the differentiation between the ancient deme, and the present demes (Figure 7A). The average distance on PC2 between the two groups (present and ancient) is an increasing function that can be approximated by a linear function of the square root of Δ (Figure 7B).

Figure 7.

Panel A. Principal components for a 1-Dimensional stepping–stone with 50 present demes, and 1 ancient deme. The PCA is performed several times, with an ancient deme sampled at different times. The results of all the PCA are plotted on the same graph. Panel B. Average distance between present demes and ancient deme on PC2 as a function of √Δ.

6. Conclusions and discussion

We have generalized the Kimura–Weiss theory of a stepping–stone model to the case where samples are taken at different times, a theory we call isolation-by distance-and-time (IBDT). The correlation between individuals decreases as a function of both geographic distance and time. This result is accentuated in higher dimensions. When considering IBDT patterns, the edge effect applies when considering a linear model with a finite number of demes, in a way similar to the standard stepping–stone model. However simulations shows that in both 1 and 2 dimensions, this effect decreases at a rate depending of the migration rate. We have also derived the expected coalescence times under the assumption of a circular or toroidal model and low mutation rate. As the time between samples increases, the coalescence time between samples can be approximated by a linear function of time.

The connection between IBDT theory and PCA is of interest as it gives insights about what to expect from the PC plots that compare ancient and present-day samples. When considering the relationship between principal components and geography, ancient samples may not cluster with the population at the same location. Such a result can occur even in a population at equilibrium in a stepping–stone model, with no complex demographic history. This behavior of PCA is important to note as it could result in the inference of a non-existent past demographic event. The genetic differentiation created by time can be observed on another principal component. An important question that remains is under what conditions is the proportion of variance explained by time larger than the proportion of variance explained by geography. In this event, the first principal component would not reflect the geography of the samples but rather the times separating the samples.

The limitations of PCA for investigating population structure in a spatio–temporal context highlights the need for new theoretical developments to analyze population structure when present-day and ancient samples are combined. This is especially apparent when considering the complex demographic scenarios already inferred about the history of modern humans [52]. Important theoretical work has already been done to test specific hypothesis [53, 54]. Another way to test different past demographic events is with simulation-intensive methods, such as Approximate Bayesian Computations [55, 56]. In this case, theoretical developments on mechanistic models such as the stepping–stone model are important to perform simulations efficiently [57].

In the article we considered the case where PCA is applied on all the individuals, both ancient and modern, at the same time. However PCA is also commonly used in a 2-step procedure where principal components are constructed based on a subset of individuals, present–day individuals, and the rest, ancient individuals, are projected onto these components [46, 47]. This approach leads to biases in the principal component projections similar to the shrinkage induced by the time between samples [58]. Such effect can be accounted for and corrected [59], but is different from the case we address here, since we use no projections.

We studied the classical stepping–stone model under the assumptions of a stationary distribution of the allele frequencies in both time and space. These assumptions are not valid in all cases. The time–stationary distribution is not reached when recent events such as range expansions occurred, causing asymmetry in the site frequency spectrum [60, 61]. Spatial non–stationarity and anisotropy are present when the migration pattern is uneven between all populations, or migration is asymmetric [62, 63, 64]. The correlation of allele frequencies is then not only a function of space and time, but also of the location of each deme.

A stepping–stone model is not the only model to describe spatial population structure. As an alternative to discrete models, continuous models can also be considered to study evolutionary processes [65, 66, 67]. Isolation–by-Distance– and–Time can be studied in a continuous framework. In the same way, results about coalescence times in a stepping–stone model can be connected to previous theory on coalescence in a continuous population [68]. Different models are especially useful since it is acknowledged that continuous stepping–stone models are a source of difficulties because of the assumption incompatibilities in a continuous framework [69].

Appendix A: derivation of r(k, t)

Using the notations in [25], we calculate the covariance of the allele frequencies ρ(k) between two populations that are spatially separated by k units of distance. This quantity is defined by

$$\rho (k)=E[\stackrel{\sim }{p}(0)\stackrel{\sim }{p}(k)].$$ (22)

In the case where the demes are also separated by t units of time, we define

$$\rho (k,t)=E[\stackrel{\sim }{p}{(0)}^{(0)}\stackrel{\sim }{p}{(k)}^{(t)}].$$ (23)

and in the particular case of t = 1,

$$\rho (k,1)=E[\stackrel{\sim }{p}{(k)}^{(1)}\stackrel{\sim }{p}{(0)}^{(0)}]=E[\stackrel{\sim }{p}{(k)}^{\prime }\stackrel{\sim }{p}(0)]=E[(L\stackrel{\sim }{p}(k)+\epsilon (k))\stackrel{\sim }{p}(0)]=E[L\stackrel{\sim }{p}(k)\stackrel{\sim }{p}(0)]+E[\epsilon (k)\stackrel{\sim }{p}(0)]=LE[\stackrel{\sim }{p}(k)\stackrel{\sim }{p}(0)]=L\rho (k).$$

By induction, we show that for any value of t > 0

$$\rho (k,t)=L^t\rho (k).$$ (24)

Let's assume that for a time t > 0 equation (24) is true,

$$\rho (k,t+1)=E[\stackrel{\sim }{p}{(k)}^{(t+1)}\stackrel{\sim }{p}{(0)}^{(0)}]=E[(L\stackrel{\sim }{p}{(k)}^{(t)}+\epsilon {(k)}^{(t)})\stackrel{\sim }{p}(0)]=E[L\stackrel{\sim }{p}{(k)}^{(t)}\stackrel{\sim }{p}(0)]+E[\epsilon {(k)}^{(t)}\stackrel{\sim }{p}(0)]=LE[\stackrel{\sim }{p}{(k)}^{(t)}\stackrel{\sim }{p}(0)]=L\rho (k,t)=L^t\rho (k).$$

Then to obtain the correlation of allele frequencies r(k, t) between two demes, we have ρ(0, 0) = ρ(0) and

$$r(k,t)=\frac{\rho (k,t)}{\rho (0,0)}=\frac{L^t\rho (k)}{\rho (0)}=L^{t}r(k).$$ (25)

Appendix B: general formulation of r in 1 Dimension

We established in equation (11) that r(k, t) = L^tr(k), and using the general expression in equation (6) we have,

$$r(k,t)=L^t\frac{C}{2\pi }{\int }_0^{2\pi }\frac{cos(k\theta )d\theta }{1-{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^2}=\frac{C}{2\pi }{\int }_0^{2\pi }\frac{L^{t}cos(k\theta )d\theta }{1-{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^2}.$$

It is now demonstrated that

$$L^{t}cos(k\theta )={[\sum _{i=0}^{\infty }{m}_{i}cos(i\theta )]}^{t}cos(k\theta ),$$ (26)

where $m_0=(1-m_{\infty }-{\sum }_{i=1}^{\infty }{m}_i)$. In the particular case of t = 1 we have

$$Lcos(k\theta )={\sum }_{i=0}^{\infty }\frac{m_i}{2}(S^{+i}cos(k\theta )+S^{-i}cos(k\theta ))={\sum }_{i=0}^{\infty }\frac{m_i}{2}(cos((k+i)\theta )+cos((k-i)\theta ))={\sum }_{i=0}^{\infty }\frac{m_i}{2}(2cos(i\theta )cos(k\theta ))=[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]cos(k\theta )$$

Now assuming that formula (26) holds for any value t > 0, we have

$$L^{t+1}cos(k\theta )=L[L^{t}cos(k\theta )]=L[{\sum }_{i_1=0}^{\infty }\cdots {\sum }_{i_t=0}^{\infty }{m}_{i_1}\dots m_{i_t}cos(i_1\theta )\dots cos(i_t\theta )]cos(k\theta )={\sum }_{i_{t+1}=0}^{\infty }[{\sum }_{i_1=0}^{\infty }\cdots {\sum }_{i_t=0}^{\infty }{m}_{i_1}\dots m_{i_t}cos(i_1\theta )\dots cos(i_t\theta )]\times \frac{m_{i_{t+1}}}{2}(cos((k+i_{t+1})\theta )+cos((k-i_{t+1})\theta ))={\sum }_{i_{t+1}=0}^{\infty }{\sum }_{i_1=0}^{\infty }\cdots {\sum }_{i_t=0}^{\infty }{m}_{i_1}\dots m_{i_t}{m}_{i_{t+1}}cos(i_1\theta )\dots cos(i_t\theta )cos(i_{t+1}\theta )cos(k\theta )={[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^{t+1}cos(k\theta ).$$

We can conclude by induction that formula (26) is true for any positive t. Then, using equation (26), a general formula for r(k, t) can be expressed

$$r(k,t)=\frac{C}{2\pi }{\int }_0^{2\pi }\frac{{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^{t}cos(k\theta )d\theta }{1-{[{\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )]}^2}.$$ (27)

Constant C is set such that r(0, 0) = 1. We do not analytically investigate this constant, however details about the case t = 0 can be found in [25].

Appendix C: general derivation

Let's assume the particular stepping-stone model: ${\sum }_{i=0}^{\infty }{m}_{i}cos(i\theta )=1-m_1-m_{\infty }+m_{1}cos(\theta )$. Now the correlation between 2 demes k steps appart and t generations is

$$r(k,t)=\frac{C}{2\pi }{\int }_0^{2\pi }\frac{{[1-m_1-m_{\infty }+m_{1}cos(\theta )]}^{t}cos(k\theta )d\theta }{1-{[1-m_1-m_{\infty }+m_{1}cos(\theta )]}^2}.$$

The fraction can be decomposed in two parts r(k, t) = C/(2π)(A₁(k, t)+A₂(k, t)) using partial fraction expansion, where

$$\begin{array}{c}{A}_1(k,t)={\int }_0^{2\pi }\frac{{[1-m_1-m_{\infty }+m_{1}cos(\theta )]}^{t}cos(k\theta )d\theta }{1-[1-m_1-m_{\infty }+m_{1}cos(\theta )]}\\ A_2(k,t)={\int }_0^{2\pi }\frac{{[1-m_1-m_{\infty }+m_{1}cos(\theta )]}^{t}cos(k\theta )d\theta }{1+[1-m_1-m_{\infty }+m_{1}cos(\theta )]}\end{array}$$

Let α = m₀/m₁, we can expand A₁ and A₂,

$$\begin{array}{c}{A}_1(k,t)=-m_1^{t-1}\sum _{g=0}^t\left(\begin{array}{c}t\\ g\end{array}\right){\alpha }^{t-g}{\int }_0^{2\pi }\frac{{cos}^g(\theta )cos(k\theta )d\theta }{\alpha -\frac{1}{m_1}+cos(\theta )},\\ A_2(k,t)=m_1^{t-1}\sum _{g=0}^t\left(\begin{array}{c}t\\ g\end{array}\right){\alpha }^{t-g}{\int }_0^{2\pi }\frac{{cos}^g(\theta )cos(k\theta )d\theta }{\alpha +\frac{1}{m_1}+cos(\theta )},\end{array}$$

To get rid of the integral, we can use the fact that

$${\int }_0^{2\pi }\frac{{cos}^t(\theta )cos(k\theta )d\theta }{x+cos(\theta )}=\frac{1}{2^t}\sum _{g=0}^t{a}_g^{(t)}{\int }_0^{2\pi }\frac{cos((k+g)\theta )+cos((k-g)\theta )d\theta }{x+cos(\theta )},$$

Where

g	0	1	2	3	4	5	Sum
$a_g^{(1)}$	0	1					2 × 1 = 2
$a_g^{(2)}$	2	0	1				2 × 1+2=4
$a_g^{(3)}$	0	3	0	1			2 × (1 + 3) = 8
$a_g^{(4)}$	6	0	4	0	1		16
$a_g^{(5)}$	0	10	0	5	0	1	32

and as given in [25]

$$\frac{1}{2\pi }{\int }_0^{2\pi }\frac{cos(k\theta )d\theta }{x+cos(\theta )}=\{\begin{array}{cc}\frac{1}{\sqrt{x^2-1}}{(\sqrt{x^2-1}-x)}^k,& x>1(\text{expression}{A}_2),\\ \frac{{(-1)}^{k+1}}{\sqrt{x^2-1}}{(\sqrt{x^2-1}+x)}^k,& x<-1(\text{expression}{A}_1).\end{array}$$

This leads us to the expressions for A₁ and A₂,

$$\begin{array}{c}{A}_1(k,t)=-m_1^{t-1}{\sum }_{g=0}^t\left(\begin{array}{c}t\\ g\end{array}\right){\alpha }^{t-g}\frac{2\pi }{2^g}{\sum }_{j=0}^g\{a_j^{(g)}\frac{{(-1)}^{k+j}}{\sqrt{{(\alpha -\frac{1}{m_1})}^2-1}}{(\alpha -\frac{1}{m_1}+\sqrt{{(\alpha -\frac{1}{m_1})}^2-1})}^{k+j}+a_j^{(g)}\frac{{(-1)}^{k-j}}{\sqrt{{(\alpha -\frac{1}{m_1})}^2-1}}{(\alpha -\frac{1}{m_1}+\sqrt{{(\alpha -\frac{1}{m_1})}^2-1})}^{k-j}\}\\ A_2(k,t)=m_1^{t-1}{\sum }_{g=0}^t\left(\begin{array}{c}t\\ g\end{array}\right){\alpha }^{t-g}\frac{2\pi }{2^g}{\sum }_{j=0}^g\{a_j^{(g)}\frac{1}{\sqrt{{(\alpha +\frac{1}{m_1})}^2-1}}{(\sqrt{{(\alpha +\frac{1}{m_1})}^2-1}-(\alpha +\frac{1}{m_1}))}^{k+j}+a_j^{(g)}\frac{1}{\sqrt{{(\alpha +\frac{1}{m_1})}^2-1}}{(\sqrt{{(\alpha +\frac{1}{m_1})}^2-1}-(\alpha +\frac{1}{m_1}))}^{k-j}\}\end{array}$$

Appendix D: higher dimensions

The 2-Dimensional case of the analysis can be detailed by changing the operators L and S. We note the cartesian coordinates of each deme with the couple (k₁, k₂), and we define the operators S₁ and S₂ such as

$$\begin{array}{c}{S}_1\stackrel{\sim }{p}(k_1,k_2)=\stackrel{\sim }{p}(k_1+1,k_2)\text{and}{S}_2\stackrel{\sim }{p}(k_1,k_2)=\stackrel{\sim }{p}(k_1,k_2+1).\\ S_1^{i_1}\stackrel{\sim }{p}(k_1,k_2)=\stackrel{\sim }{p}(k_1+i_1,k_2)\text{and}{S}_2^{i_2}\stackrel{\sim }{p}(k_1,k_2)=\stackrel{\sim }{p}(k_1,k_2+i_2).\end{array}$$

The operator L in two dimensions becomes

$$L=(1-\sum _{i_1}\sum _{i_2}{m}_{i_1{i}_2}-m_{\infty })\frac{(S_1^0+S_2^0)}{2}+\sum _{i_1}\sum _{i_2}\frac{m_{i_1{i}_2}}{4}(S_1^{i_1}+S_1^{-i_1})(S_2^{i_2}+S_2^{-i_2})$$

where m_i1i2 is the migration rate between demes separated by i₁ and i₂ steps. The correlation in 2 dimensions can be written using the spectral decomposition and for two demes we have

$$r(k_1,k_2,0)=\frac{C_2}{{(2\pi )}^2}{\int }_0^{2\pi }{\int }_0^{2\pi }\frac{cos(k_1{\theta }_1)cos(k_2{\theta }_2)d{\theta }_{1}d{\theta }_2}{1-{({\sum }_{i_1,i_2=0}^{\infty }{m}_{i_1{i}_2}cos(i_1{\theta }_1)cos(i_2{\theta }_2))}^2}$$

for two populations that are separated by k₁ and k₂ steps at the same generation. Using the same trigonometric properties as in appendix B, we have

$$L^{t}cos(k_1{\theta }_1)cos(k_2{\theta }_2)={[\sum _{i1}\sum _{i2}(m_{i_1{i}_2}cos(i_1{\theta }_1)cos(i_2{\theta }_2))]}^{t}cos(k_1{\theta }_1)cos(k_2{\theta }_2)$$

and m₀₀ = (1 – Σ_i1Σ_i2 m_i1i2 – m_∞). As a consequence, the correlation of allele frequencies in 2 dimensions between two populations separated by k₁ and k₂ steps, and t generations is

$$r(k_1,k_2,t)=\frac{C_2}{{(2\pi )}^2}{\int }_0^{2\pi }{\int }_0^{2\pi }\frac{{[{\sum }_{i_1=0}^{\infty }{\sum }_{i_2=0}^{\infty }{m}_{i_1{i}_2}cos(i_1{\theta }_1)cos(i_2{\theta }_2)]}^{t}cos(k_1{\theta }_1)cos(k_2{\theta }_2)d{\theta }_{1}d{\theta }_2}{1-{({\sum }_{i_1=0}^{\infty }{\sum }_{i_2=0}^{\infty }{m}_{i_1{i}_2}cos(i_1{\theta }_1)cos(i_2{\theta }_2))}^2}.$$

To go further, and especially investigate the 3-Dimensional case that can be relevant in practice, it is possible to extend the calculations in n-dimensional models, where two populations are separated by t generations and a vector of steps (k₁,…k_n). Redefining the operators S and L, we can show that the correlation is

$$r(k_1,\dots ,k_n,t)=\frac{C_n}{{(2\pi )}^n}{\int }_0^{2\pi }\cdots {\int }_0^{2\pi }\frac{{[{\sum }_{i_1,i_n=0}^{\infty }{m}_{i_1\dots i_n}cos(i_1{\theta }_1)\dots cos(i_n{\theta }_n)]}^{t}cos(k_1{\theta }_1)\dots cos(k_n{\theta }_n)d{\theta }_1\dots d{\theta }_n}{1-{({\sum }_{i_1,\dots ,i_n=0}^{\infty }{m}_{i_1\dots i_n}cos(i_1{\theta }_1)\dots cos(i_n{\theta }_n))}^2}$$

Appendix E: expected coalescence time between two groups

We detail the case where two groups are present in the data, the present demes and the ancient deme. The quantity Δ is the time for two genes in different groups to be in the same group. In the case where there is one ancient deme k₂ and one present deme k₁, using equation (19) we have

$$E[\mathrm{\Delta }|k_1]=E[T_{A_1{A}_2}]-2N_e{n}_d=t+\frac{1}{\sqrt{2\pi m_{1}t}}{\int }_0^{n_d}(n_d-|x-k_2|)\frac{|x-k_2|}{2m_1}{e}^{-\frac{{(x-k_1)}^2}{2m_{1}t}}\mathit{\text{dx}}.$$

In the practical case we consider several present time demes 1… n_p, and one ancient deme. The expectation of Δ has to be conditioned by the probability that A₁ is in a given present population k₁.

$$E(\mathrm{\Delta })=\sum _{i=1}^{n_p}p(k_1=j)E[\mathrm{\Delta }|k_1=j].$$ (28)

Since we consider a stepping–stone model where all the populations have the same effective population size, we have p(k₁ = j) = 1/n_p, j = 1…n_p.